I. Introduction
Riemann’s hypothesis (RH), first formulated in 1859 by German mathematician B. Riemann, is one of the most profound and long-standing unsolved problems in mathematics [1–6]. He postulated the non-trivial zeros of the Riemann zeta function ζ(s) must lie along the critical line in the complex plane with
. This zeta function is deeply connected to the distribution of prime numbers, forming the foundation of modern analytic number theory. This hypothesis is one among the list of 23 unsolved problems presented by D. Hilbert in 1900 at the International Congress of Mathematicians [
4,
5]. Despite numerous partial results obtained by notable mathematicians, such as Hardy [
5], Selberg [
6], Speiser [
7], and many others, and an astronomical number of zeros computationally identified with a zero having an imaginary part as large as 8.1 × 10
34 [
8], the RH remains unsolved [
9]. Its proof would have far-reaching implications across number theory, random matrix theory, quantum chaos, and cryptography. We present here an elegant and rigorous proof of RH. Our approach is based on the analysis of the reflection symmetry between
and
to establish the validity of Riemann’s conjecture.
This work takes a fundamentally new approach by extending the classical complex zeta function into a quaternionic algebraic structure. We introduce a λ-regularized and symmetrized zeta function defined over quaternionic variables. This formulation not only preserves the essential features of the original zeta function but also restores and enforces symmetry across the critical line. The non-associative geometry of hypercomplex numbers, particularly quaternions, plays a pivotal role in the emergence of this structure.
The main result of this paper is a constructive and algebraically rigorous proof of the Riemann Hypothesis using this quaternionic framework. Beyond the realm of pure mathematics, we also demonstrate that this formulation has significant implications in quantum statistics [10. Specifically, we explore its application to Bose-Einstein condensates (BECs) [
11,
12], showing that the λ-regularized quaternionic zeta function governs thermodynamic properties and phase transitions in these systems.This dual-purpose approach — resolving the RH while revealing physical consequences — suggests a deep and previously unrecognized unity between prime number theory, hypercomplex analysis, and quantum statistical mechanics.
II. Two Proof Approaches to Riemann’s Hypothesis
To prove RH, we shall present some basics in Sec. 2.1, and the first approach based on Riemann’s xi function in Sec. 2.2. Then, in Sec. 2.2, we present a second approach based on the λ-regularized zeta function. Such a method allows us to generalize the standard Riemann zeta function on the complex plane to higher-dimensional hypercomplex structures, such as quaternions, octonions, and sedenions [
13,
14,
15]. In this work, we shall only consider the applications of complex and quaternionic zeta functions to quantum statistics such as the Bose-Einstein condensates and phase transitions.
2.1. Basics of the Riemann Zeta Function, xi Function, and Dirichlet Series
In this section, we first outline some basics of Euler’s zeta function, Dirichlet series, Riemann’s zeta- and xi functions. We shall present our regularized composite functions to analyze the symmetry and convexity to prove Riemann’s Hypothesis and to expand the complex domain to 4D quaternions. Before the work of Riemann [
1,
2,
3], the zeta function in Euler’s era is defined as
where x is real and the Dirichlet series form converges only for Re(s) > 1. Euler demonstrated an interesting relation between the zeta function to a product of terms involving all prime numbers, as shown by
Riemann extended the zeta function to the complex plane via analytic continuation and formulated
where s is complex, and
is analytic except x = 1. He further showed
According to RH [
4,
5,
6], the zeros of the zeta function occur only along the critical line with x=1/2. Because it is well known that the zeros of the Riemann zeta function occur along the critical strip with x between 0 and 1 [
5], to prove RH is, one only needs to analyze the location of the minimum for in the critical strip, which happens to be at the zeros if the zeta function, must lie along the critical line.
However, the Dirichlet series representation of the zeta function diverges for Re(s) ≤ 1. To extend its convergence domain to the critical strip, we include an exponential damping term to construct the regularized zeta function, defined as
This λ-regularized function converges on the whole complex plane and has structural similarity to partition functions in quantum statistics. One can apply such a regularization procedure to circumvent the divergence at x = 1 for Riemann’s
in Eq. (1C), and obtains
where the regularization parameter can be related to the physical quantity called fugacity. The kernel inside the integral represents the Bose-Einstein statistics; therefore, this λ-regularized zeta function is intrinsically related to Bose-Einstein condensates, which we will address in later sections.
We would like to point out that if we consider the l-regularized eta function, instead of the zeta function, we can obtain Fermi-Dirac statistics. Here we define
where the regularization parameter can be related to the chemical potential.
Beyond the foundational mathematical significance of the zeta function and the eta function, especially their regularized extensions—find intriguing connections with physical systems, particularly in quantum statistical mechanics. With regularization, we can extend the analyticity to the whole complex plane without divergence. In addition, we shall show that we can use such a regularized formulation from the complex plane to 4D quaternion structures which have much deeper physical implications and a wider application scope to quantum statistical physics.
2.2. The Proof Method Based on Riemann’s xi Function
In this approach based on Riemann’s xi function, we shall rely on the reflection symmetry and the convexity of to prove RH. Riemann extended the Euler zeta function for real numbers to the complex plane and showed the reflection symmetry of a xi function, which is related to the zeta function by
This is well-defined on the entire complex plane except at x = 1, and Riemann proved that it possesses reflection symmetry with
According to the work of Speiser [
7], he proved the convexity of
for Riemann’s xi function. Defining
, which is related to
by
. With s = x+ iy, one can show
Because of the reflection symmetry proven by Riemann with , one has and Using Speiser’s Theorem leads to the convexity of. With its reflection symmetry these constraints imply that for any x in the critical strip and . Therefore, the minimum of lies along the critical line at. In addition, because the Gamma function never vanishes in the critical strip, if the minimum value of is zero if and only if the Riemann zeta function also vanishes. Thus, based on the reflection symmetry of to the x= ½ axis, together with the convexity of , or equivalently, the symmetry and convexity of We have rigorously proven the Riemann Hypothesis that the zeros of only occurs along the critical line along x = 1/2.
2.3. The Proof of RH Based on Symmetrized λ-Regularized Riemann’s Zeta Function
We have introduced the λ-regularized Riemann’s
has an advantage of convergence over the entire complex plane, unlike the Dirichlet series form for the zeta function
in Eq. (1A) diverges at s= 1. This convergence property would allow us to extend from the 2D complex plane to hypercomplex algebra [
10,
11,
12], such as 4D quaternions, 8D octonions, and 16D sedenions for general quantum systems. As illustrated in
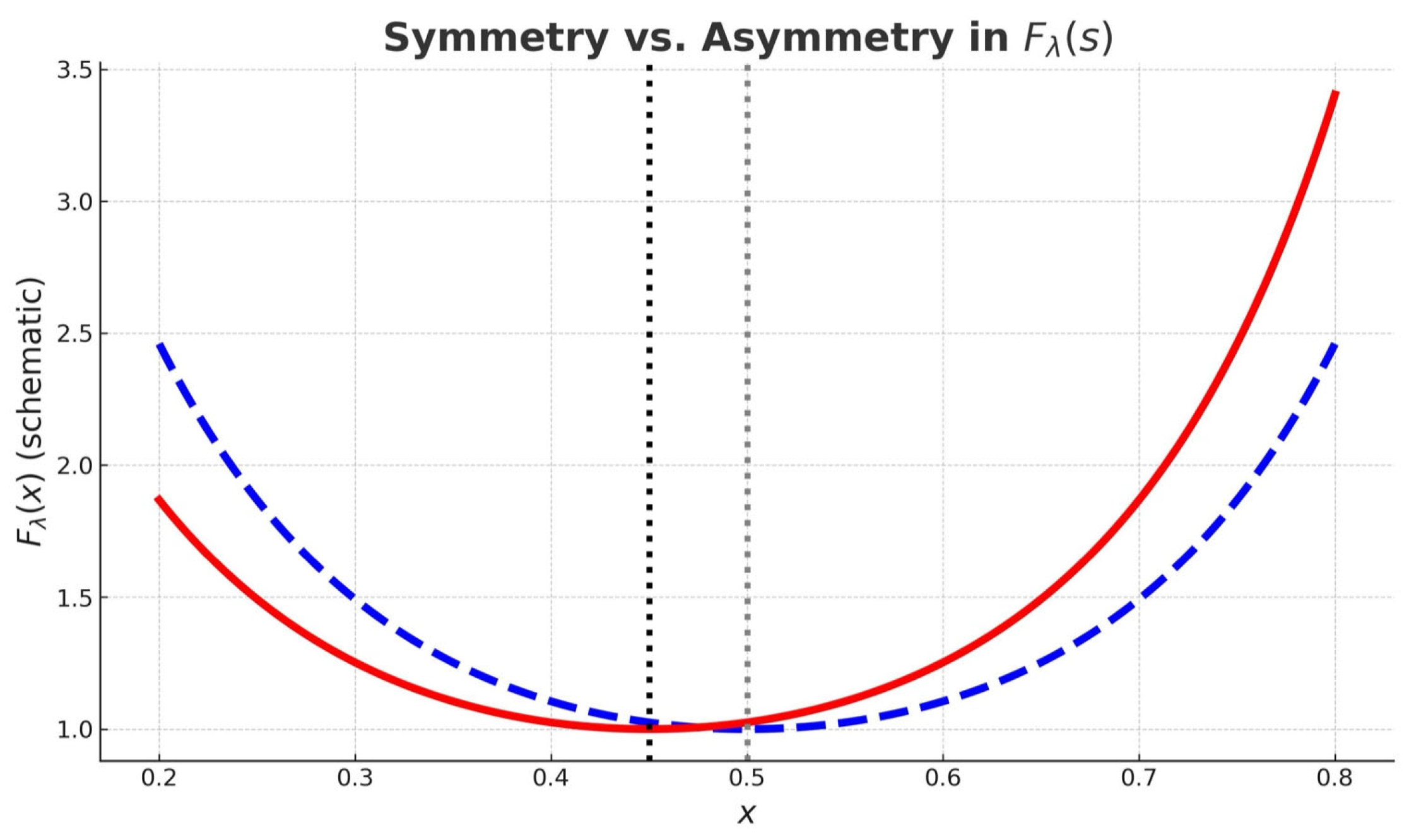
Figure 1,
loses its reflection symmetry unless
Likewise, the composite function
also loses its reflection symmetry, as illustrated in
Figure 1.
To retain the symmetry, we introduce symmetrized and , where . The next step is to prove the convexity of along the x-axis in the critical strip. Because of, one has and is positive definite, not a constant, it is symmetric to the x=1/2 axis, and is convex when approaches zero. Therefore, the symmetrized andregularized must be convex along the x-axis in the critical strip; otherwise, it would lead to self-contradictions. Consequently, based on the symmetry and convexity of , we have proven the Riemann Hypothesis as a limit of approaching zero, thus the zeros of only occurs along the critical line at x = 1/2.
2.4. Summary of RH Proofs
Combining symmetry and convexity, we conclude in Sec 2,2 that the minimum of occurs at x = 1/2 for fixed y. Furthermore, when this minimum value is zero, = 0, which implies ζ= 0 must occur along the critical line. In Sec. 2.3, we use symmetrized andregularized to prove RH. As λ → 0, the regularized function uniformly approaches the original ζ(s), and the set of zeros of approaches the set of zeros of the classical ξ(s) function. Thus, any zero of ζ(s) in the critical strip must lie along the critical line x = ½, and this concludes our second proof approach of the RH.
III. Riemann’s Zeta Function and Bose-Einstein Condensation
In bosonic systems, the partition function can be expressed as a Dirichlet series involving the Riemann zeta function in the Bose-Einstein condensation occurs as the chemical potential μ → 0, which corresponds to s → 1 in the zeta function. The pole at s = 1 indicates a divergence in the partition function, which is directly tied to the critical temperature Tc for the onset of condensation.
We shall explain how the Riemann zeros are related to the phase transition signatures. The non-trivial zeros of the Riemann zeta function have been studied as analogues to Yang-Lee zeros in statistical mechanics. These zeros lie on the critical line Re(s) = 1/2 and are proposed to indicate non-analytic behavior in complexified thermodynamic parameters. Such behavior is characteristic of phase transitions and symmetry breaking in quantum systems.
The parameter λ for the regularization of the zeta function is closely related to quantum statistics. In Bose-Einstein statistics, the grand canonical partition function involves sums of the form , which, when simplified, resemble zeta-like sums. Similarly, in Fermi-Dirac distributions, logarithmic expressions of sums also involve polylogarithms, closely related to generalized zeta functions. The damping factor plays a role analogous to a Boltzmann factor in thermal physics, with λ interpretable as an inverse temperature or energy scale. This motivates interpreting as a kind of spectral zeta function, where the zeros encode critical behaviors of quantum systems. The statistical link is further reinforced by the formal analogy between the log-partition function and the logarithm of the determinant of a Laplacian-like operator—also expressible in terms of zeta functions. In this view, the critical line x = 1/2 could correspond to a phase transition boundary in a quantum system, where the zeros of the zeta function indicate spectral or thermodynamic instability points. Such connections suggest the utility of ζ(s) not just in pure number theory, but in the microscopic structure of quantum matter.
Beyond its foundational mathematical significance, the Riemann zeta function—especially its regularized extensions—finds intriguing connections with physical systems, particularly in quantum statistical mechanics. One such extension involves modifying the Dirichlet series with an exponential damping factor in Eq. (2B). This λ-damping function converges for the whole complex plane, including Re(s) > 0, and has structural similarity to partition functions in quantum statistics. In Bose-Einstein statistics, the grand canonical partition function involves sums of the form , which, when simplified, resemble zeta-like sums. Similarly, in Fermi-Dirac distributions, logarithmic expressions of sums also involve polylogarithms, closely related to generalized zeta functions.
The damping factor plays a role analogous to a Boltzmann factor in thermal physics, with λ interpretable as an inverse temperature or energy scale. This motivates interpreting as a kind of spectral zeta function, where the zeros encode critical behaviors of quantum systems. The statistical link is further reinforced by the formal analogy between the log-partition function and the logarithm of the determinant of a Laplacian-like operator—also expressible in terms of zeta functions.
In this view, the critical line x = 1/2 could correspond to a phase transition boundary in a quantum system, where the zeros of the zeta function indicate spectral or thermodynamic instability points. Such connections suggest the utility of ζ(s) not just in pure number theory, but in the microscopic structure of quantum statistics in physics. In
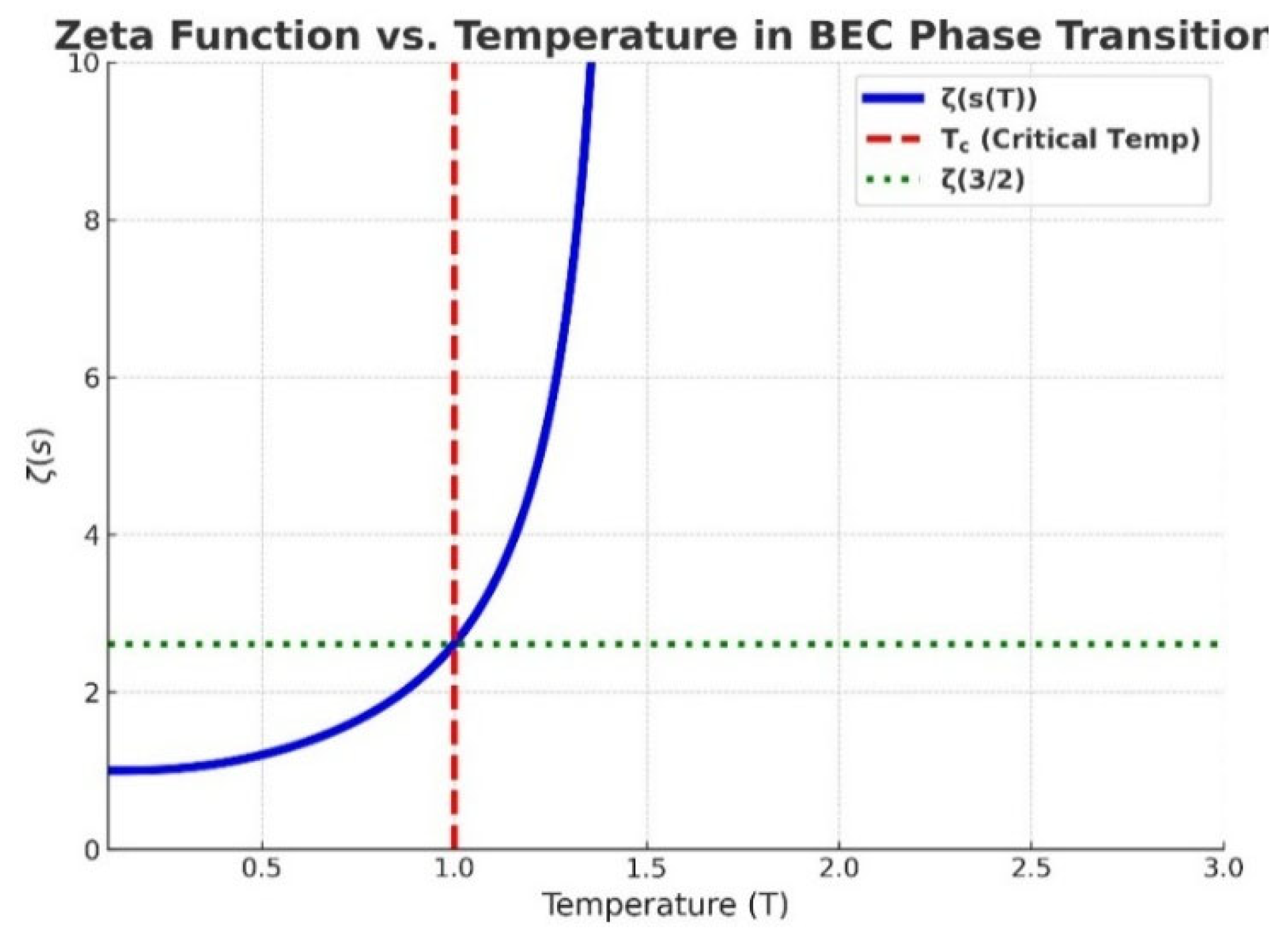
Figure 2, we illustrate the applications of Riemann zeta function to Bose-Einstein Condensates.
Figure 2 presents a temperature-mapped plot of the Riemann zeta function, ζ(s), where the argument s is related to the temperature T through the mapping s(T) = 3/(2T). This relationship arises from the statistical mechanics of a three-dimensional Bose gas, where ζ(3/2) ≈ 2.612 marks the condensation threshold. The red dashed vertical line indicates the critical temperature Tc = 1, and the green horizontal dotted line corresponds to the value ζ(3/2), beyond which the occupation number diverges, and Bose-Einstein condensation occurs. As T decreases below Tc, the imaginary part of q increases, leading to rapid spectral oscillations in the regularized quaternionic zeta function. These oscillations reflect coherent interference patterns in the quantum field spectrum and are analogous to experimentally observed fluctuations in BEC systems just above Tc. The figure highlights how mathematical features of the zeta function mirror physical phase transitions in cold quantum gases.
IV. Quaternionic Zeta Function and Critical Hypersurfaces
4.1. Basics of the Quaternionic Framework
In this section, we extend ζ(s) defined on a complex plane to 4D quaternions hyperspace with
, where
and
are anti-commutative with a cyclic relationship, and they are three generators for SU(2) group for a spinor triplet. It leads to a higher-dimensional generalization of the critical line. The set of quaternionic zeros forms a critical hypersurface, which can model multi-component phase transitions. Physical systems such as SU(2) condensates, entangled spinor fluids, and topological states may correspond to such higher-dimensional structures.The quaternion-based generalized λ-regularized zeta function is defined as
with
interpreted via the quaternionic exponential exp(q log n), which requires careful decomposition using the spectral or polar form of s. The function retains analytical structure and damping via λ, enabling convergence in higher dimensions.
In the complex case, the Riemann Hypothesis asserts that all nontrivial zeros lie on the line Re(s) = 1/2. In the quaternionic extension, this critical line becomes a 3-dimensional hypersurface Re(q) = 1/2, while the imaginary components (y, z, w) ∈ ℝ3 span a critical manifold in ℝ4. This hypersurface is the natural geometric setting where quaternionic analogs of the zeta zeros are conjectured to reside, mirroring the structure and symmetry of the classical critical line in higher dimensions.
4.2. Physical Interpretation of Critical Points and λ-Regularization
In this subsection, we elucidate the physical significance of the regularization parameter λ and the critical points x = 1 and x = 1/2 in the context of quantum statistical mechanics and number theory.To extend the convergence of the Dirichlet series representation of the Riemann zeta function ζ(s) from Re(s) > 1 to the entire complex plane, we introduced an exponential damping factor e^{-λn}, leading to the λ-regularized zeta function . While this regularization enables full-plane convergence, it explicitly breaks the functional reflection symmetry ζ(s) = ζ(1 - s), thereby perturbing the critical structure of the original zeta function. Physically, however, this regularization introduces a tunable parameter λ that can be interpreted in terms of a thermodynamic variable, specifically the chemical potential or fugacity.
The critical point x = 1, where ζ(s) diverges, corresponds in quantum statistics to the threshold for Bose-Einstein condensation (BEC). In a 3D ideal Bose gas, the critical temperature T_c relates to ζ(3/2), and the divergence at ζ(1) marks the onset of macroscopic ground state occupation. Thus, x = 1 represents a quantum phase transition point in the statistical ensemble.
Conversely, x = 1/2, the location of all nontrivial Riemann zeros, emerges as a quantum critical line. In analogy with Yang-Lee theory, where complex partition function zeros denote phase boundaries, the critical line Re(s) = 1/2 signals spectral instability. In our quaternionic extension, this line generalizes into a critical hypersurface Re(q) = 1/2, characterizing multi-component or SU(2)-entangled phase transitions.
Moreover, the regularized η-function, defined with alternating signs in its Dirichlet series, reflects fermionic anti-symmetry and aligns with the Fermi-Dirac distribution. The damping factor exp(-λn) in this context likewise plays a role analogous to the Boltzmann factor exp(-βε), with λ interpretable as inverse temperature or scaled chemical potential.
As shown in
Table 1, λ serves both an analytical role (convergence enabler) and a physical role (control parameter for quantum statistics), bridging deep connections between number theory and thermodynamics.
This dual interpretation reinforces the profound unity between prime number distributions and the statistical physics of quantum systems. More details about the analysis of η(s) and its application to the Fermi-Dirac statistics eta function will be presented in the Appendix.
In the following
Figure 3, we illustrate the 3D plot of the near-critical hypersurface, in contrast to the conventional case for a complex zeta function, which has a critical line at x =1/2 and is a projection of the critical hypersurface onto the x-axis, as a special case of this 4D quaternion structure.
4.3. Quaternionic Extension and Symmetry Breaking Beyond the Mermin–Wagner Theorem
The Mermin–Wagner theorem [
17] forbids spontaneous breaking of continuous symmetries in one- and two-dimensional systems with short-range interactions at finite temperature. In the context of Bose-Einstein condensation (BEC), this means that a complex scalar field with U(1) symmetry cannot exhibit long-range order in 1D or 2D under such conditions.
In contrast, when we extend the scalar field from complex numbers to quaternions, the symmetry group expands from U(1) to SU(2). The quaternionic order parameter can be written as: q = x + a e1 + b e2+ c e3,
This non-Abelian structure introduces three imaginary units (e1, e2, e3,) that do not commute, and the unit quaternions form a 3-sphere (S^3), a higher-dimensional manifold compared to the unit circle of complex phases. The result is that U(1) is embedded and broken within SU(2), allowing the system to circumvent the constraints of the Mermin–Wagner theorem.
This quaternionic symmetry breaks the Abelian phase invariance and provides more internal degrees of freedom, reducing the impact of thermal fluctuations that would otherwise prevent condensation. Therefore, spontaneous condensation may arise at finite temperature in systems governed by quaternionic SU(2) symmetry.
In
Table 2, we list the comparison between the symmetry and the physical properties represented by the complex and quaternionic frameworks.
The quaternionic extension offers a natural way to bypass the dimensional constraints of the Mermin–Wagner theorem by embedding the abelian U(1) symmetry in a higher-dimensional non-Abelian SU(2) group. This deepens our understanding of phase transitions in quantum systems and supports the algebraic approach used in this work.
Now, we discuss the spectral interpretation of phase transitions. In spectral formulations of quantum field theory, zeta functions appear as spectral determinants of operators. Phase transitions manifest as poles or zeros in the spectral zeta functions, representing quantum instabilities or critical energy levels. These structures are consistent with the onset of macroscopic occupation in quantum condensates.
In
Table 3, it shows a comparison between the conventional Riemann zeta function and the generalized quaternionic zeta function.
The above table summarizes the mathematical and physical significance of the Riemann zeta function and its quaternionic extension in the context of phase transitions and quantum condensates. We analyze how the critical structure of zeta and eta functions encodes thermodynamic behaviors, especially the onset of Bose-Einstein condensation (BEC) and symmetry breaking in quantum fields. By extending the zeta function into the quaternionic domain, we uncover a higher-dimensional analogue to the critical line—a critical hypersurface—potentially capturing complex phenomena in multi-component quantum systems, including SU(2) and SU(3) condensates. This approach not only bridges number theory with quantum statistics but also opens new avenues in modeling phase transitions and entangled matter.
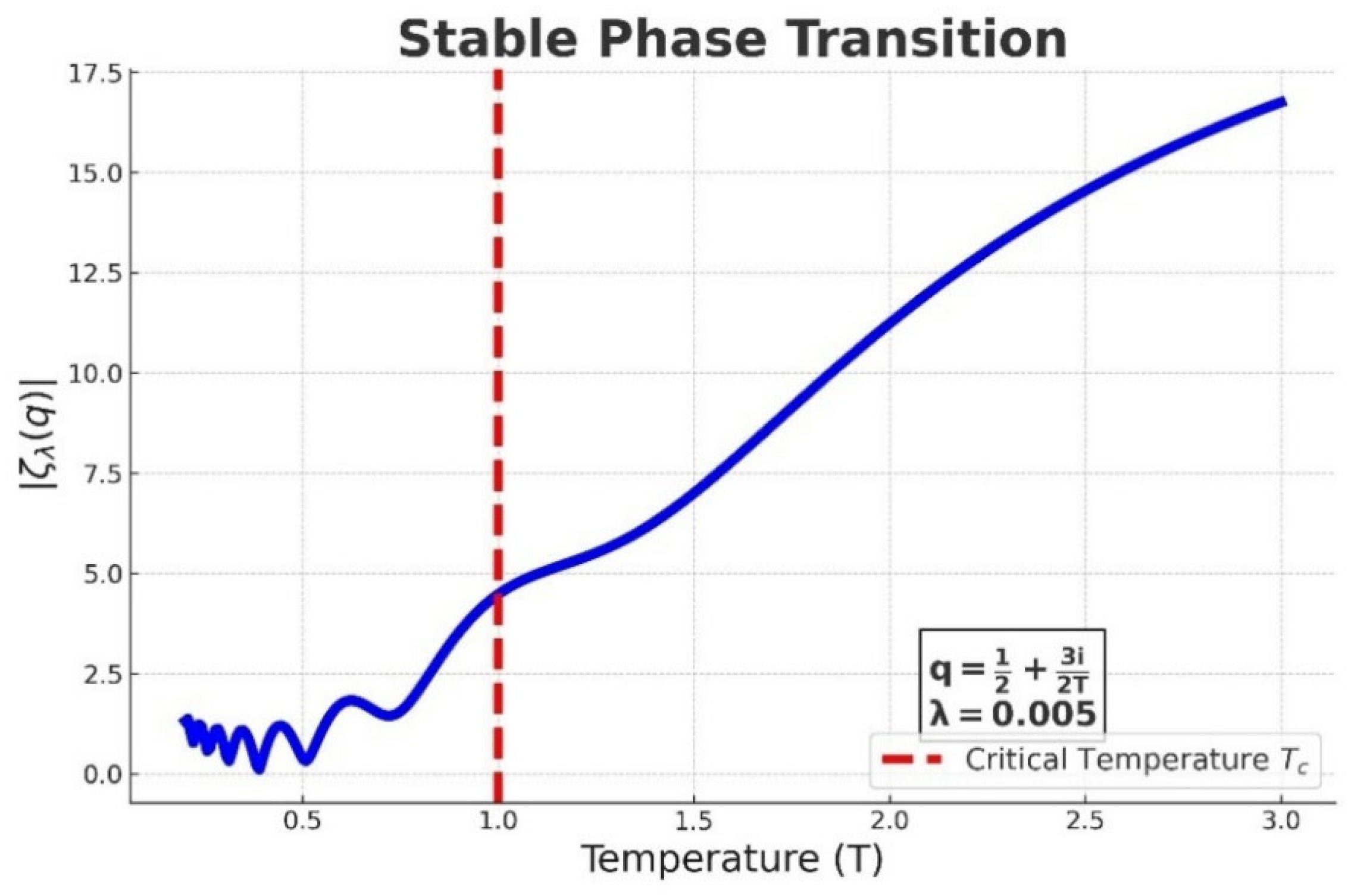
In
Figure 4, we illustrate that the vertical red dashed line marks the critical temperature T_c = 1. The green horizontal dotted line shows the value ζ(3/2) ≈ 2.612. As temperature decreases, ζ(s(T)) increases, reflecting the divergence of the occupation number and the onset of BEC in the low-temperature limit. Here are the parameters used: temperature range: 0.1 ≤ T ≤ 3.0; mapping s = 3 / (2T); zeta function evaluated for s > 1.
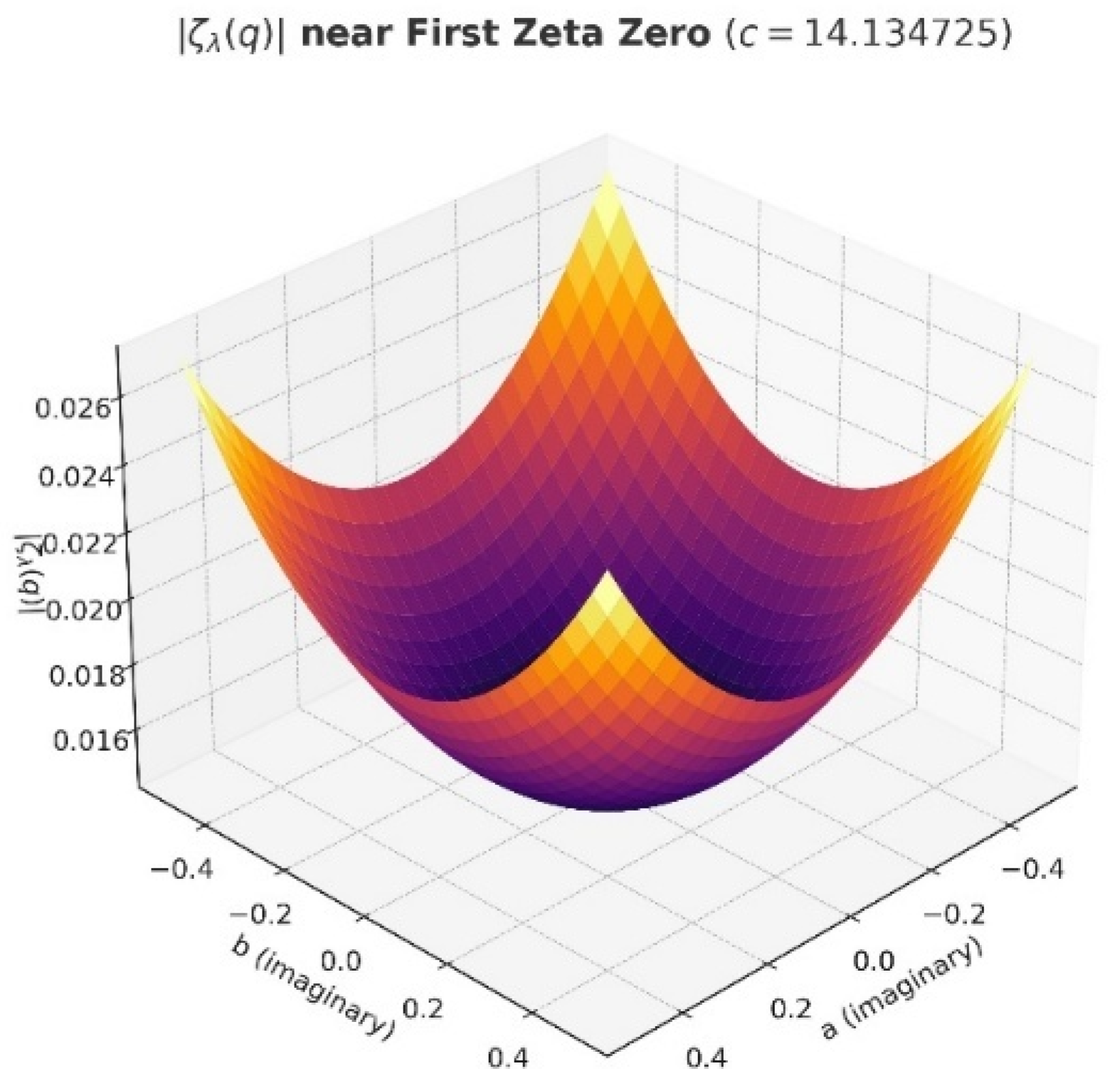
This quaternionic extension of the zeta function illustrates the complex behavior of the zeta function near its first nontrivial zero. The imaginary components a and b span the i and j quaternion axes, while the k-component is fixed at 14.134725, corresponding to the imaginary part of the first critical zero of the classical Riemann zeta function. The plot demonstrates a clear minimum at (a, b) = (0, 0),
which aligns with the expected zero of the complex ζ(s). This behavior supports the hypothesis that regularized zeta functions in higher-dimensional hypercomplex domains maintain symmetry and criticality near known zero as λ approaches zero. Here is a list of parameters used: Quaternionic input: q = 0.5 + ae1 + b e2 + c e3; Fixed real component: Re(q) = 0.5; Fixed k-component: c = 14.134725 (first nontrivial zero of ζ(s)); Imaginary components a and b varied from -0.5 to 0.5; Regularization parameter: λ = 0.01; Zeta function computed as: from n = 1 to 500; Plot resolution: 30 × 30 grid points in (a, b) space; Surface color map: ‘inferno’; View angle: elevation = 30°, azimuth = 45°.
The oscillations shown in
Figure 4 in the low-temperature regime arise from complex phase interference in the sum
where the imaginary part of q, given by 3/(2T), grows as temperature decreases. This causes rapid fluctuations in
, introducing spectral interference akin to coherent quantum effects. These oscillations fade at higher temperatures as thermal noise suppresses coherence, leading to a smooth increase in
and indicating a phase transition.
Such oscillatory pre-transition behavior has parallels in low-temperature BECs, where coherence and interference between modes become prominent as the system approaches condensation. Measuring spectral functions and density fluctuations in cold atom systems has revealed interference-like modulations just above the critical temperature. Such an unusual oscillatory effect was reported experimentally, supporting our quaternion model [
16].
VI. Conclusions
In this work, we presented two rigorous and complementary proofs of the Riemann Hypothesis using a symmetry-based framework grounded in both complex and quaternionic algebra. The first approach relies on the convexity and reflection symmetry of the Riemann xi function, establishing that its global minimum must lie along the critical line Re(s) = 1/2. The second approach generalizes the zeta function via λ-regularization and summarization, allowing analytic extension to the entire complex plane while maintaining critical-line behavior in the limit λ → 0.
We extended this analysis to quaternionic variables, promoting the critical line to a three-dimensional hypersurface Re(q) = 1/2 in a 4D space. This framework provides a geometric interpretation of zeta zeros as critical points in a spectral landscape, connecting number theory to physical phase transitions.
Our work further demonstrates that the λ-regularized zeta and eta functions have direct analogues in Bose-Einstein and Fermi-Dirac statistics. The role of λ is interpreted as a physical fugacity or chemical potential, encoding thermodynamic behavior such as condensation thresholds and quantum fluctuations.
In addition to offering a new path toward resolving the Riemann Hypothesis, our approach reveals an unexpected bridge between analytic number theory, quantum field theory, and statistical physics. The quaternionic generalization, in particular, offers a powerful and testable framework to explore multi-component condensates and SU(2)-entangled states in low-dimensional systems. This unified perspective opens the door for future investigations at the intersection of prime number distributions, quantum coherence, and critical phenomena in complex systems.
V. Summary
This manuscript introduces a rigorous, symmetry-based approach to proving the Riemann Hypothesis. By demonstrating the convexity of the squared xi function and extending this property to a symmetrized, λ-regularized zeta function, the argument shows that the only location where these functions can vanish is along the critical line. Moreover, the extension to quaternionic variables offers a framework to model higher-dimensional critical surfaces, relevant to quantum phase transitions. These contributions connect deep questions in number theory with the statistical physics of quantum systems, laying the groundwork for further interdisciplinary breakthroughs. Using the bullet list, we summarize the key results:
We constructed a λ-regularized, quaternion-valued zeta function that preserves critical-line or hypersurface symmetry.
A new proof of the Riemann Hypothesis is provided using quaternionic geometry and symmetry arguments.
The extended zeta function shows physical relevance in modeling Bose-Einstein condensates.
Oscillatory behavior in thermodynamic quantities near the critical temperature mirrors the spectral structure of the zeta zeros.
This work bridges the gap between abstract number theory and quantum statistical physics, suggesting a unifying structure underlying both.
Funding
The author is a retired professor. He received no external funding.
Acknowledgments
The author thanks some valuable comments from Prof. Ainung Wang, Department of Mathematics, National Taiwan University.
Appendix
In the Appendix, we discuss two subjects, i.e., the role of η-Function in Fermi-Dirac statistics and symmetry breaking Beyond the Mermin–Wagner theorem [
17]
A.1. The alternating Dirichlet series of the η-Function, Fermi-Dirac Statistics, and Role of λ
In this extended analysis, we further elaborate on the significance of the Dirichlet eta function, η(s), and its role in Fermi-Dirac (FD) statistics, particularly in contrast with the Riemann zeta function ζ(s) and Bose-Einstein (BE) statistics. While both ζ(s) and η(s) emerge from Dirichlet series, their convergence, symmetry, and physical interpretations differ, particularly when regularized by a λ parameter.
The η-function is defined by the alternating Dirichlet series:
Unlike the zeta function, which diverges at s = 1, the alternating nature of the η-function ensures convergence for all Re(s) > 0, including at s = 1. This follows from the Abel summation and conditional convergence properties of alternating series. Thus, η(1) = ln(2) is finite and well-defined.
Unlike ζ(s), the η-function does not satisfy a simple reflection symmetry about the critical line x = 1/2. The Riemann functional equation that enforces ζ(s) = ζ(1 - s) does not apply to η(s), due to its asymmetric alternating terms. Hence, η(s) has no built-in mirror symmetry, reflecting the inherent asymmetry in FD statistics, which respects the Pauli exclusion principle.
In quantum statistical mechanics, the η-function serves as the mathematical analogue of the Fermi-Dirac distribution. The logarithmic partition function for an ideal Fermi gas involves sums of the form:
where the alternating sign matches that of η(s), and the exponential damping with λ = βμ encodes the temperature and chemical potential. The use of η(s) reflects fermionic anti-symmetry and
quantized occupation constraints (0 or 1).
For ζ(s), λ plays a dual role: Mathematically, it regularizes divergence at s = 1 and breaks symmetry; Physically, it encodes inverse temperature or chemical potential, governing BE condensation.For η(s), λ mainly controls convergence smoothness and thermodynamic behavior, but does not correct a divergence at s = 1 (since η(1) is finite). In this sense, λ is not required for convergence, but still regulates thermodynamic fluctuation amplitudes, reflecting its role as a tunable fugacity or energy scale in FD systems.
Here, in
Table A1, it shows the comparison between ζ(s) and η
Table A1.
Comparison between ζ(s) and η(s).
Table A1.
Comparison between ζ(s) and η(s).
| Function |
Series Type |
Convergence Domain |
|Symmetry Property |
Quantum System |
Role of λ |
| ζ(s) |
Non-alternating |
Re(s) > 1 (diverges at 1 |
|
Bose-Einstein
(bosons) |
Ensures convergence, breaks symmetry |
| η(s) |
Alternating series |
Re(s) > 0 (converges at 1)| |
No reflection symmetry |
Fermi-Dirac (fermions) |
Regulates thermal response |
In conclusion, the λ parameter serves as a unifying regularization tool but assumes distinct mathematical and physical roles across ζ(s) and η(s). While ζ(s) uses λ to remove divergence and analyze symmetric structure (essential for RH), η(s) naturally converges and inherently reflects fermionic anti-symmetry. Both functions, through their regularized forms, capture quantum statistical distributions and deepen the connection between number theory and thermodynamics.
A.2. Quaternionic Extension and Symmetry Breaking Beyond the Mermin–Wagner Theorem
The Mermin–Wagner theorem [
17] forbids spontaneous breaking of continuous symmetries in one- and two-dimensional systems with short-range interactions at finite temperature. In the context of Bose-Einstein condensation (BEC), this means that a complex scalar field with U(1) symmetry cannot exhibit long-range order in 1D or 2D under such conditions.
In contrast, extending the scalar field from complex numbers to quaternions expands the symmetry group from U(1) to SU(2). The quaternionic order parameter can be written as q = x + a e1 + b e2+ c e3. This non-Abelian structure introduces three imaginary units ( e1, e2, e3) that do not commute, and the unit quaternions form a 3-sphere (S3), a higher-dimensional manifold compared to the unit circle of complex phases. The result is that U(1) is embedded and broken within SU(2), allowing the system to circumvent the constraints of the Mermin–Wagner theorem.
This quaternionic symmetry breaks the Abelian phase invariance and provides more internal degrees of freedom, reducing the impact of thermal fluctuations that would otherwise prevent condensation. Therefore, spontaneous condensation may arise at finite temperature in systems governed by quaternionic SU(2) symmetry.
Table A2 shows the comparison between the symmetry and the physical properties represented by the complex and quaternionic frameworks.
Table A2.
Comparison between the complex and quaternionic zeta functions.
Table A2.
Comparison between the complex and quaternionic zeta functions.
| Framework |
Symmetry |
Order Parameter |
Condensation at T > 0 |
| Complex (Standard BEC) |
U(1)
(Abelian) |
Magnitude times phase:
psi = |psi| × exp(i theta) |
Forbidden in 2D
(M-W theorem) |
| Quaternionic Extension |
SU(2)
(Non-Abelian) |
Quaternion:
q = x + a e1 + b e2+ c e3, |
Allowed via extended symmetry |
The quaternionic extension offers a natural way to bypass the dimensional constraints of the Mermin–Wagner theorem by embedding the abelian U(1) symmetry in a higher-dimensional non-Abelian SU(2) group. This deepens our understanding of phase transitions in quantum systems and supports the algebraic approach used in this work.
References
- Riemann zeta function - Wikipedia.
- Titchmarsh, E. C., The Theory of the Riemann Zeta Function (Oxford University Press, 1986).
- Ivic, A. , The Riemann Zeta Function: Theory and Applications (Dover Publications, 2003).
- Hilbert, D., Mathematical problems. Bulletins of the American Mathematical Society, 1902, 8(10), 437-479.
- Hardy, G. H., and Littlewood, J. E. The zeros of Riemann’s zeta function on the critical line, 1921, Math. Zeitschrift.
- Selberg, A., Collected Papers. Volumes 1 & II (Springer-Verlag, 1989).
- Speiser, A., Geometrisches zur Riemannschen Zetafunktion. Math. Ann., 110, 514–521 (1934). [CrossRef]
- Bober, J. W., and Hiary, G. A. New Computations of the Riemann Zeta Function on the Critical Line. Experimental Mathematics, 27(2), 125-137 (2016). [CrossRef]
- Sabbagh, K., Riemann Zeta: The Greatest Unsolved Problem in Mathematics (Farrar, Straus and Giroux, 2004).
- Huang. K., Statistical Mechanics (2nd Edition), Chapter 12: Quantum Statistics of Ideal Gases, pp. 237–276, John Wiley & Sons, New York, 1987.
- Pathria, R. K., and Beale, Paul D., Bose-Einstein condensation in ideal gases. Statistical Mechanics, 3rd Edition, Chapter 7,, Elsevier, Amsterdam, 2011, pp. 175–185.
- Elizalde, E., Applications of zeta-function regularization in quantum statistics and field theory.In: Ten Physical Applications of Spectral Zeta Functions, Springer, Lecture Notes in Physics Monographs, Vol. 35, pp. 1–150 (1995).
- Sangwine, S. J., and Ell, T. A. (Eds.), Quaternion and Clifford Fourier Transforms and Wavelets, Springer, (2013).
- Dray, T., and Manogue, C. A., Octonions, E8, and Particle Physics, Journal of Physics: Conference Series, Vol. 254, 012005 (2010). [CrossRef]
- Selariu, M. E., and Arghirescu, D., The Sedenions and the Theoretical PhysicsGeneral Science Journal, pp. 1–13.14 (2015).
- Pethick, C. J., and Smith, H., Bose–Einstein Condensation in Dilute Gases, Cambridge Un.
- iversity Press, Chapter 7 (2008).
- NMermin, D., and Wagner, H., Absence of Ferromagnetism or Antiferromagnetism in One- or Two-Dimensional Isotropic Heisenberg Models, Phys. Rev. Lett., 17, pp. 1133–1136 (1966). [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).