Seismicity Before and After the 2023 M7.7 and M7.5 Turkey Earthquakes

1. Introduction

On February 6, 2023 (UTC), a devastating earthquake of magnitude (M) 7.7 struck the East Anatolian fault zone (EAFZ) bounding the Arabian and Anatolian tectonic plates (Figure 1). This quake, which occurred near the city of Kahramanmaraş in the Mediterranean region of Turkey, was followed about nine hours later by a M7.5 quake approximately 90 km to the north of the initial M7.7 quake. The epicenter of the M7.5 quake was on the Sürgü fault. The broad context of the doublet quakes (the M7.7 and 7.5 quakes) is that they occurred under the current tectonic stress that created the EAFZ. The EAFZ accommodates the westward movement of Turkey into the Aegean Sea. Although the relative plate motions in the region around the EAFZ are low (typically less than 10 mm/yr), even regions of slow plate motions can host extremely damaging earthquakes [1].

During the 20th century, much of the North Anatolian fault zone (NAFZ) ruptured from east to west in a series of M7 or larger earthquakes [1]. In this same period, seismicity along the EAFZ experienced M6 earthquakes, with most of the activity on the northern section. The activity on the southern section of the EAFZ started with the Jan. 24, 2020 M6.8 quake. Figure 1b shows how the remainder of the southern section was activated during the 2023 doublet quakes and following events, where seismicity (M≥5.5) from 1965 to the M7.7 quake (thin circles) were overlaid with seismicity after the M7.7 quake (thick circles) and fault segments of the doublet quakes (green) [2,3].

The focal mechanism of the 2020 M6.8 quake indicates faulting on a near-vertical left-lateral plane trending SW-NE [4]. A slip on this plane is consistent with the orientation of regional faults and local plate motions. The M7.7 quake involved a left-lateral strike slip along SW-NE trending faults [2]. A predominant mechanism of the M7.5 quake was a left-lateral strike-slip fault motion along SW-NE and E-W trending faults [3].

The preceding M7.7 quake promoted the subsequent M7.5 quake, largely by unclamping of stress loaded on the epicentral patch of the future rupture [5]. Chen et al. [6] also showed that the M7.5 quake was promoted by historical earthquakes and finally triggered by the M7.7 quake. As performed in several studies [5,6,7,8,9], it is of interest to analyze the interaction between the doublet quakes. However, this possibility is out of scope in the present study. Rather, we focused on seismicity before and after the doublet quakes.

Kwiatek et al. [10] reported seismicity transients starting approximately 8 months before the 2023 M7.7 quake. One of the main characteristics of the transients was seismic activation (see also [11]). Seismicity was composed of isolated spatiotemporal clusters near a future M7.7 epicenter. Four clusters were recognized within 50 km of the future epicenter, referred to as C1, C2, C3, and C7 [10]. Clusters C1 and C2 emerged within 8 months prior to the M7.7 quake. Clusters C2 and C7 were located on and around a fault segment (segment 2 defined in the Data section), where the M7.7 quake initiated. Cluster C7 emerged in 2017-2018. Cluster C3 was activated in 2015, 2016, and 2021. The other main characteristic was the low b-value of the Gutenberg-Richter (GR) frequency-magnitude relation of earthquakes [12]. This relation will be defined in the Method section. Clusters C1 and C2 were responsible for the low b-values [10]. The authors also showed non-Poissonian inter-event time statistics and magnitude correlations of seismicity. Local comparable seismic transients have not been observed, at least not since 2014.

Seismicity after the doublet quakes was still active. About 4500 M≥3 earthquakes occurred around the causative faults during the period since the M7.7 quake until Oct. 16, 2024, when we used the AFAD catalog (see the Data section). Two M6-class earthquakes occurred after the doublet quakes, a M6.4 quake on Feb. 20, 2023 [13] and a M5.9 quake on Oct. 16, 2024 [14] around the south and north ends of the M7.7 rupture, respectively. Given that the fault end zones generally calculate increases in stress [7], the areas surrounding these M6-class quakes were hypothesized to be heading toward failure, using the stress calculation. In the present study, this hypothesis was proven by using currently available earthquake data and fault models.

Although active seismicity continues, the post-doublet-quake sequence undergoes the Omori-Utsu (OU) power-law decay over time [15] (see the Method section). Toda and Stein [5] estimated the duration of the post-doublet-quake sequence to be 1-2.5 years. This duration was defined as the period of a larger occurrence rate computed from using the OU relation than that computed from using ordinary earthquakes before the 2020 M6.8 quake. Re-evaluation of the duration of this sequence would provide the basis of a time-dependent seismic hazard assessment along the NAFZ, because almost 1.5 years have passed since the M7.7 quake (as of Oct. 2024).

We studied seismicity before and after the doublet quakes, using earthquake catalogs created by the Disaster and Emergency Management Authority (AFAD), Lomax [16], and Kwiatek et al. [10], to demonstrate that the result does not depend on the choice of catalog. We first confirmed previously-reported seismicity transients during the pre-doublet-quake sequence [10], using the statistical Epidemic-Type Aftershock Sequence (ETAS [17]) and GR models. Taking both physics-based and statistical approaches, we then investigated the post-doublet-quake sequence to indicate that the two M6-class quakes were promoted by the doublet quakes and to discuss a comparison between our study and a previous study [5], based on currently-observable data.

2. Methods

2.1. OU Relation and ETAS Model

Seismicity after a large earthquake is often correlated with the OU relation [15] in the time domain, given as λ_OU=k(c+t)^-p, where λ_OU is the number of earthquakes per unit time at t with M larger than or equal to a minimum magnitude (M_th), and p, c, and k are constants. The rate- and state-dependent friction law [18] assumes p=1 as a standard form. Variability in p is possible: p>1 and p<1 for special cases with rapidly and slowly decreasing stress, respectively. The ETAS model described below considers an earthquake sequence as a result of the onset of the OU power-law decay following each previous event.

In the framework of the ETAS model [17], all earthquakes are decomposed into Poisson background activity and clustering activity. The occurrence rate of the Poisson background activity is a constant μ. The ETAS model assumes that each earthquake is followed by earthquakes in the form of the OU relation. The rate of earthquake occurrence at t following the i-th earthquake (time t_i and magnitude M_i) is given by ν_i(t)=K₀exp{α(M_i-M_th)}(t-t_i+c)^-p for t>t_i, where K₀ and α are constants. The rate of occurrence of the whole earthquake series at t becomes $\lambda \left(t|H_t\right)=\mu +{\sum }_{S<t_i<t}{\nu }_i\left(t\right)$. The summation is performed for all i satisfying t_i<t. Here, H_t represents the history of occurrence times with associated magnitudes from the data {(t_i, M_i)} before time t. The parameter set θ=(μ, K₀, α, c, p) represents the characteristics of seismic activity. The units of the parameters are day^-1, day^-1, no unit, day, and no unit, respectively. θ is given by using the maximum-likelihood estimate. AIC (Akaike Information Criterion [19]), useful for assessing the goodness of fit of the model to data, is obtained from the maximum log-likelihood and the number of adjusted parameters.

It is possible to visualize how well or poorly the ETAS model fits an earthquake sequence by comparing the cumulative number of earthquakes with the rate calculated by the model [20]. Ordinary time can be converted to transformed time in such a way that the transformed sequence follows the Poisson process (uniformly distributed occurrence times) with unit intensity (occurrence rate). Visualization can be achieved in two ways: one graph using ordinary time and the other using transformed time. If the model presents a good approximation of observed seismicity, an overlap of both observation rate and model rate is expected.

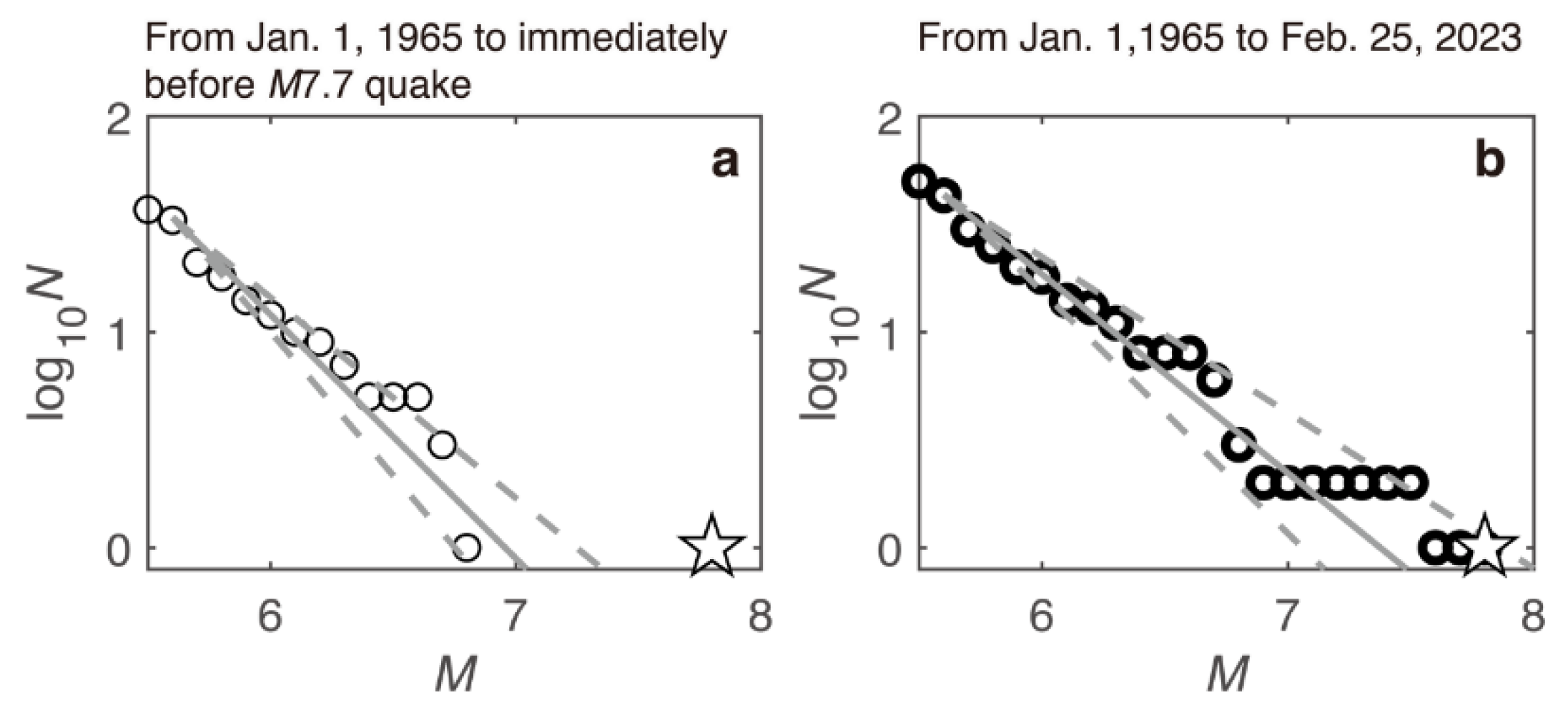
2.2. GR Relation

The GR relation [12] is given by log₁₀N=a-bM, where N is the number of earthquakes with a magnitude larger than or equal to M in the given time window, and a and b are constants. b is used to describe the relative occurrence of large and small events in the given time window (i.e., a high b-value indicates a larger proportion of small earthquakes, and vice versa) [21,22,23,24,25]. The b-value is calculated based on earthquakes with a magnitude above the completeness magnitude M_c, above which all events are considered to be detected by a seismic network.

The results of laboratory experiments indicated a systematic decrease in the b-value approaching the time of the entire fracture [26,27,28]. In this context, a decrease in b and/or low b-values have been reported for the period leading up to large-size earthquakes in Sumatra, Japan, and Chile [28,29,30]. Although underlying physical processes associated with the temporal changes in b remain unclear, and the role of b as a stress meter is unproven, there are indications of such processes and role from laboratory experiments [26] and numerical simulations [32]. One possible physical model showed that the decrease in b was caused by a rapid increase in shear stress, promoting micro-crack growth [26]. Another possible model showed that an increased stress level in slowly slipping parts of a fault facilitates earthquake rupture growth, resulting in the temporal decrease in b prior to a large earthquake (mainshock) [32].

2.3. Stress-Change Calculation

We used Coulomb, a graphic-rich deformation and stress-change software for earthquakes, tectonics, and volcanoes [33,34] to calculate how earthquakes promote or inhibit failure on nearby faults. Static stress changes caused by the displacement of a fault (source fault) were calculated. Displacements in the elastic half space were used to calculate the 3D strain field; this was multiplied by elastic stiffness to derive the stress changes. A typical value for Poisson’s ratio (PR=0.25), Young’s modulus (E=8×10⁵ bar), and friction coefficient (μ=0.4) was used in this study, resulting in a shear modulus of G=E/[2(1+PR)] = 3.3×10⁵ bar. The shear and normal components of the stress change were resolved on specified receiver fault planes. A receiver fault consists of planes, each characterized by specified strike, dip, and rake, on which the stresses imparted by the source faults are resolved. The Coulomb failure criterion, in which failure is hypothesized to be promoted (inhibited) when the Coulomb failure is positive (negative), was used.

3. Data

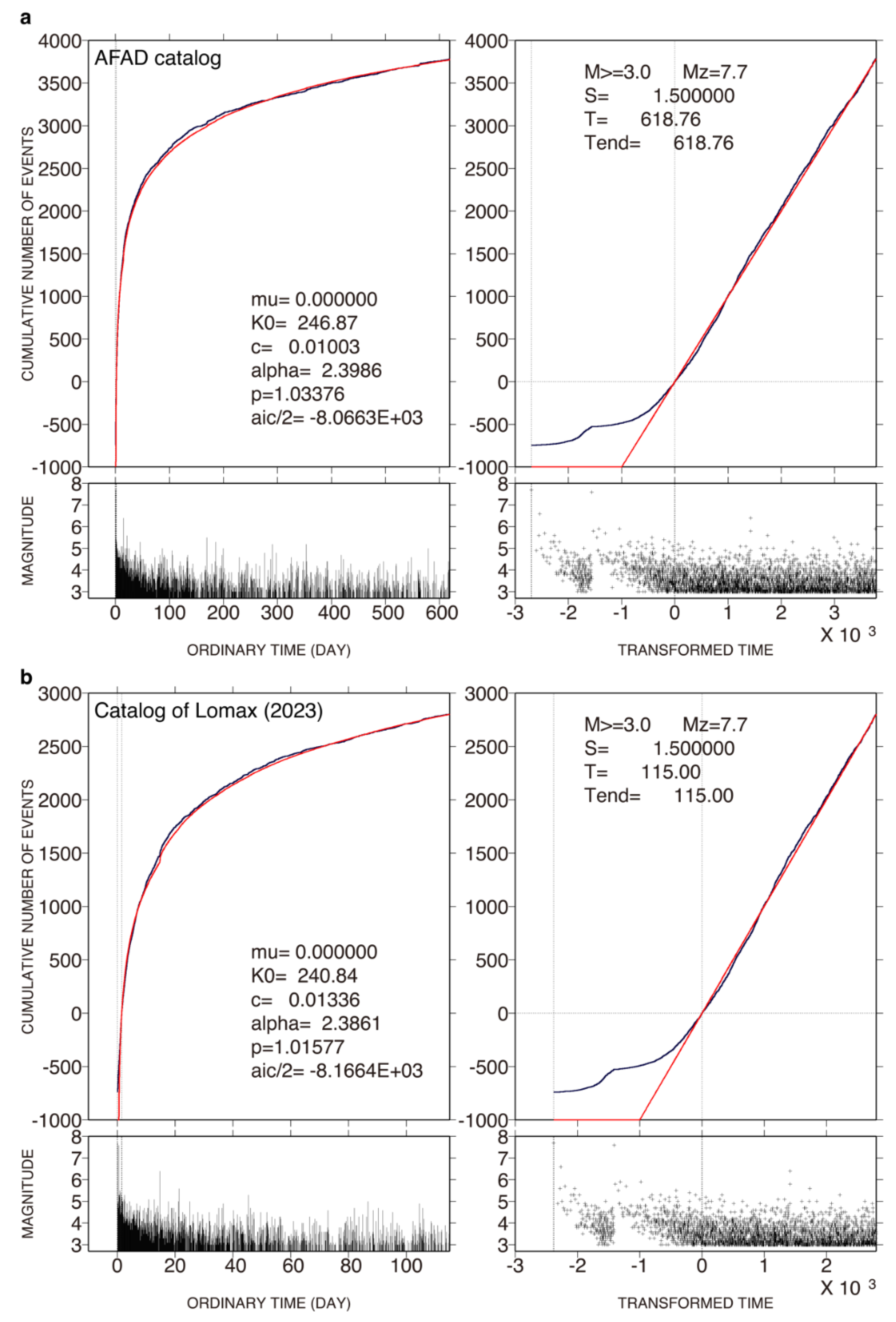
3.1. Earthquake Catalogs

For analyses of long-term seismicity (Figure 1), we created an earthquake catalog based on the ISC-GEM catalog (version 9.1, released on Jun. 27, 2022) [35,36,37,38] and the ANSS catalog [39]. The catalog we created contains earthquakes with M≥5.5 during the period Jan. 1, 1965-Dec. 31, 2018 obtained from the ISC-GEM catalog and during the period Jan. 1, 2019-Feb. 25, 2023 obtained from the ANSS catalog.

For analyses of short-term seismicity, we used three earthquake catalogs created by the Disaster and Emergency Management Authority (AFAD), Lomax [16], and Kwiatek et al. [10] to demonstrate that the result does not depend on the choice of catalog. We downloaded the catalog, including earthquakes of M≥1.0 from Jan. 1, 2014 to Oct. 16, 2024. This timing of Jan. 1, 2014 coincided with the effective incorporation of seismic stations to the generation of the local seismicity catalogue by AFAD, leading to a visible improvement of the consistency of magnitude estimates since the selected time [10]. Although we filtered out events specified as explosion, downthrow, volcanic, and unknown when downloading the catalog, it is known that it includes clusters corresponding to quarry-blast activity [10]. In this study, the events located within areas of the quarry-blast shown in Figure 2 of Kwiatek et al. [10] were excluded from the catalog. According to Kwiatek et al. [10], the AFAD catalog has M_c=1.5 within a 50 km radius from the M7.7 quake during a period from Jan. 1, 2023 to immediately before the M7.7 quake (Feb. 6, 2023).

The Lomax catalog [16] (version 3.0. released on Jun. 28, 2023), which includes earthquakes from Jan. 1 to May 31, 2023, is an NLL-SSST-coherence hypocenter catalog, where NLL-SSST-coherence [40,41] is an enhanced, absolute-timing earthquake location procedure that 1) iteratively generates spatially varying travel-time corrections to improve multi-scale location precision, and 2) uses waveform similarity to improve fine-scale location precision. Relocations were performed with merged phase arrival data available from AFAD (https://deprem.afad.gov.tr/event-catalog) and KOERI (http://www.koeri.boun.edu.tr/sismo/2/bultenler) [16]. All events in the AFAD catalog with M≥1.5 are used for relocation [16].

The catalog of Kwiatek et al. [10] is an enhanced seismicity catalog lowering the magnitude detection threshold around the M7.7 and 7.5 quakes for a period from Jan. 1, 2023 to immediately before the M7.7 quake (Feb. 6, 2023). This catalog was generated by using an AI-based workflow [10]. When the events located within areas identified as quarry blasts were excluded, only events representing earthquakes remained. The catalog has M_c=0.5 in the 50 km radius around the M7.7 quake [10].

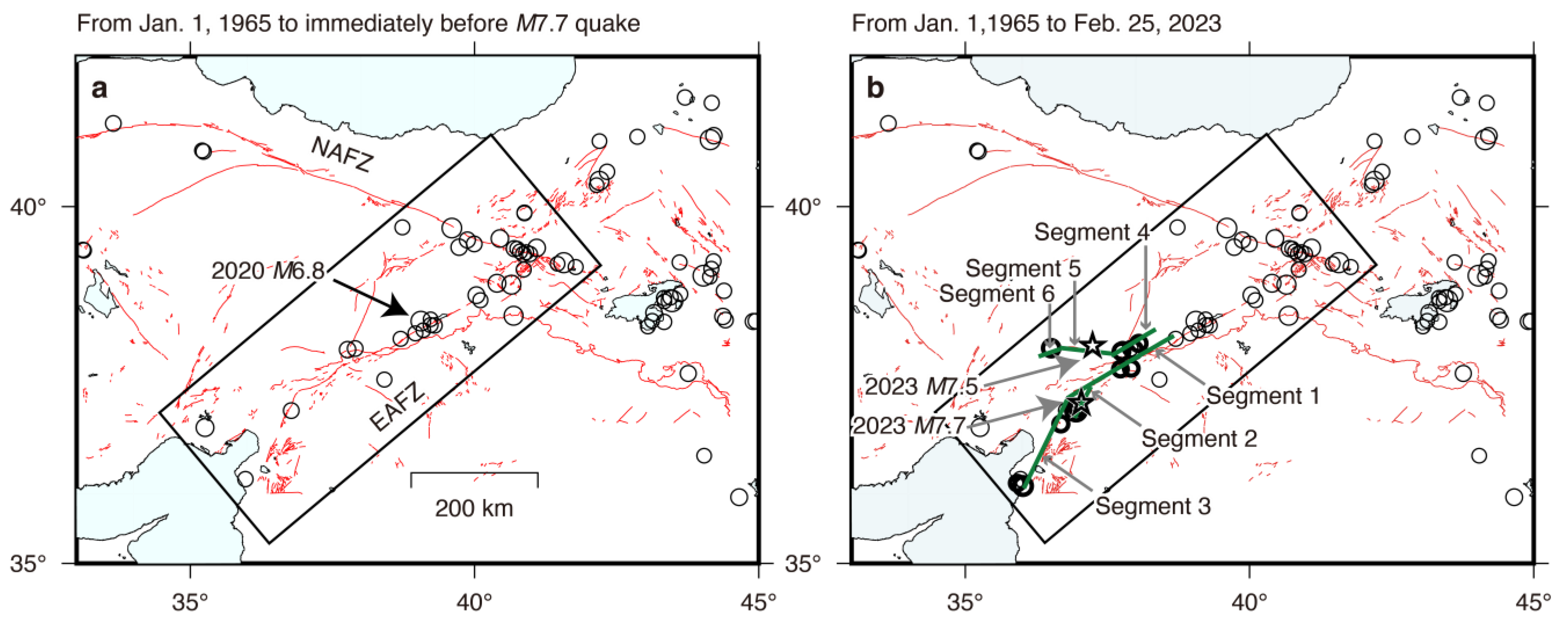
3.2. Fault Models

The fault model of the M7.7 quake is based on the work by the United States Geological Survey (USGS) [2]. This is a finite-fault model (also called a variable slip) with numerous small patches of slips, each having information on the location of a rectangular patch, strike, dip, and rake. The model that includes analysis of both teleseismic and regional seismic and geodetic observations represents three plane segments 1, 2, and 3, showing two main ruptures on segments 1 and 3 with one strand (segment 2) near the M7.7 hypocenter (Figure 1). Considering the location of the M7.7 hypocenter, the rupture initiated on segment 2, and the rupture radiation was bilateral along segments 1 and 3. This is consistent with the rupture model of the M7.7 quake [42]. A slip distribution for the rupture along segments 1 and 3 shows peak-slip values of >10 m, but along segment 2, it shows peak-slip values of about 1.5 m. The model representing the three segments involves predominantly near-vertical left-lateral strike-slip faulting.

Similarly, the finite-fault model of the M7.5 quake, based on work by the USGS [3], was used. This model represents three segments 4, 5, and 6 that involve predominantly near-vertical left-lateral strike-slip faulting (Figure 1). Considering the location of the M7.5 hypocenter, the rupture initiated on central segment 5, and the rupture radiation was bilateral along two segments (4 and 6) located at both ends of segment 5, consistent with the rupture model of the M7.5 quake [42]. A slip distribution for the rupture along segment 5 shows peak-slip values of >10 m, while along segments 4 and 6, it shows peak-slip values <10 m.

To calculate how the doublet quakes promoted or inhibited the M6.4 quake, a moment tensor solution of the M6.4 quake reported by the USGS [13] was used. The moment tensor contains two nodal planes (NPs). Both NPs were used as receiver faults of changes in Coulomb stress imparted by the doublet quakes. Similarly, a moment tensor solution of the M5.9 quake reported by the USGS [14] was used.

4. Results

4.1. Pre-Doublet-Quake Sequence

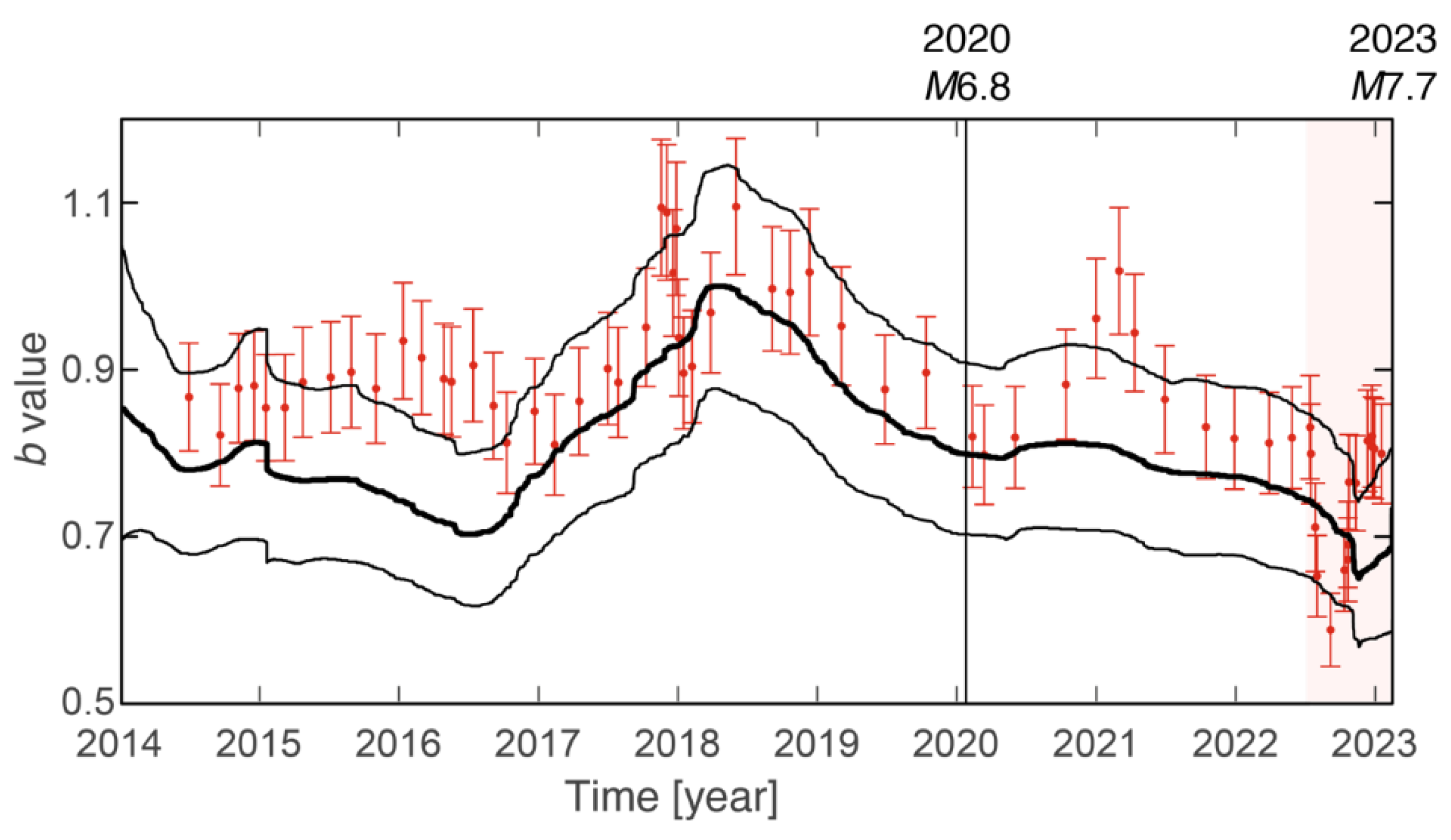
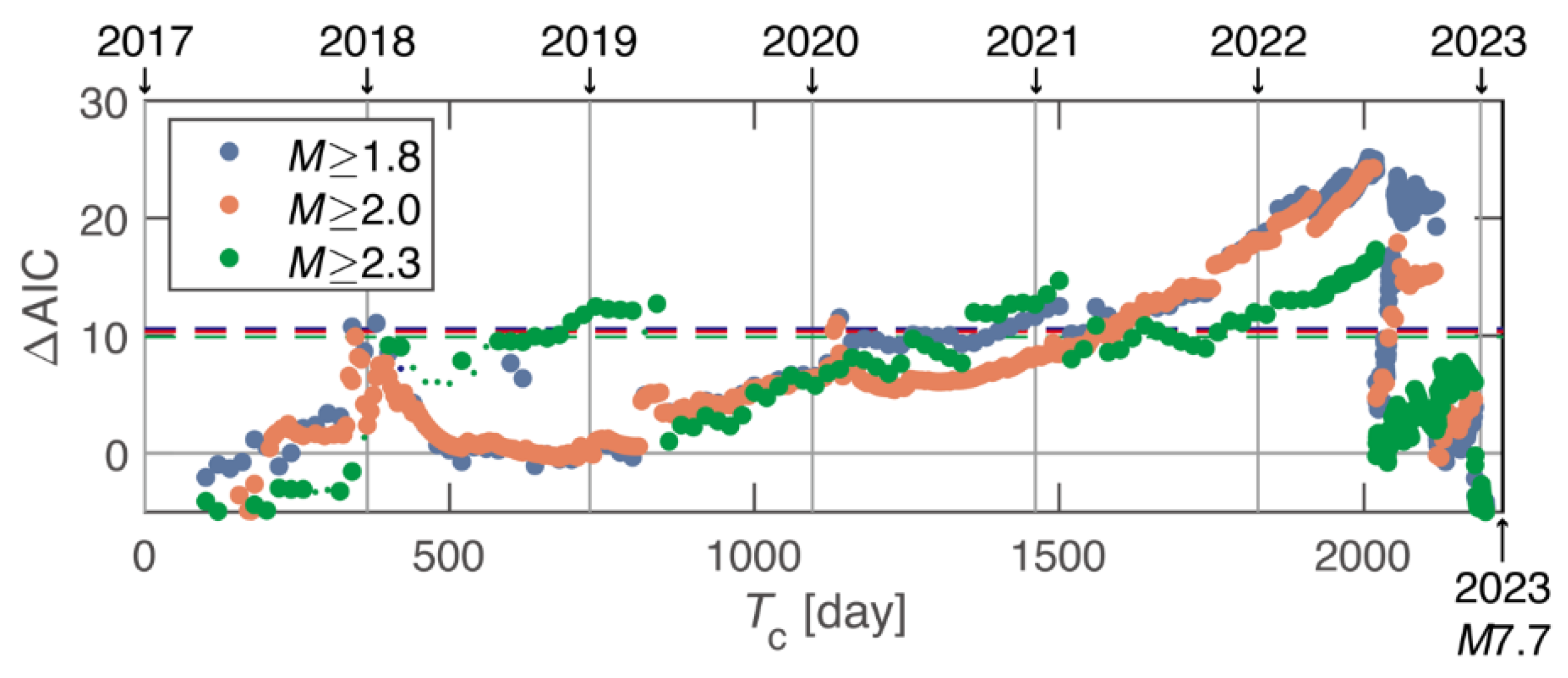
4.1.1. b-Value and Change in Seismicity Rate

We confirmed the previously-reported seismicity transients: low b-values and seismic activation starting approximately 8 months before the 2023 M7.7 quake in the region within a 50 km radius surrounding the future M7.7 epicenter [10].

We first considered unbiased time-dependent b-values (Figure 2), using our method [24] where the b-value function of time is represented by a broken line connecting the sequence of earthquakes under a smoothness constraint in piecewise slopes, using the empirical Bayesian smoothing technique. Unlike Kwiatek et al. [10], who used a moving event window of 120 events and attributed each calculated b-value to the origin time of the last event in each window, the method we used does not assume a moving window. Therefore, it has the advantage of obtaining unbiased b-values as a function of time [24]. Results (black data) based on use of the AFAD catalog show that b reached values as low as ~0.6 during the period from July 2022 to immediately before the M7.7 quake (pink region). Also included for comparison is the timeseries of b-values (red data) reproduced from Figure 3b of Kwiatek et al. [10]. Regardless of whether the previous method [10] or our method was used, the results were similar. The lowest b-values are related to two clusters, referred to as C1 and C2 by Kwiatek et al. [10].

We next showed that seismic activation, as suggested previously [10], is statistically significant, conducting a change point analysis. For this analysis, ΔAIC=AIC_single-AIC_2stage was used as a function of the change-point time T_c [20,24,43,44]. Here, AIC_single is AIC for the standard (single) ETAS model that considers a constant θ-value over time, and AIC_2stage is AIC for the two-stage ETAS model that considers different θ-values in subperiods before and after T_c, where both models are fitted to earthquakes of M≥M_th. If ΔAIC≥2q, the two-stage model is better fitted to the data than the single model, detecting candidate changes in occurrence rate, where q is the degree of freedom to search for the best candidate T_c from the data. q depends on sample size (number of earthquakes of M≥M_th) [45,46]. The result for M_th=2 (red data in Figure 3) shows that the two-stage ETAS model was much better than the single ETAS model during T_c=1600~2100 days, where events during the period from Jan. 1, 2017 to immediately before the M7.7 quake in the AFAD catalog were used. The most significant T_c was 2015 days (Jul. 9, 2022). The results for M_th=1.8 (blue data) and 2.3 (green data) indicate that the most significant T_c was 2008 days (Jul. 2, 2022) and 2019 days (Jul. 13, 2022), respectively. This feature, i.e., that the most significant T_c-values are about 8 months before the M7.7 quake, was observed regardless of M_th-values.

We fitted the ETAS model to earthquakes (M≥2) before T_c=2015 days (Jul. 9, 2022) (Figure 4a,b). For this fitting, three time-intervals were considered [24]. One interval is called the target interval, for which θ was computed. The seismicity in this period may be affected by earthquakes which occurred before this period due to the long-lived nature represented by the OU relation. To consider this effect, another time interval, which is precursory to the target interval (called the precursory interval), was chosen and earthquakes in this period were considered in the computation. The precursory interval is defined by 0 to S. The target interval is defined by S to T. The third time interval defined by T to T_end is called the prediction interval. θ in this interval is the same as that computed for the target interval. We set S=0.01 days, T=T_c=2015 days (Jul. 9, 2022), and T_end=2225.71 days (immediately before the M7.7 quake). The occurrence rate (black) after T=T_c=2015 days (during the prediction interval) was larger than the extrapolated rate (red), indicating relative activation. Here, the extrapolated rate is the occurrence rate computed by using the ETAS model, in which θ was obtained by fitting to earthquakes (M≥2) before T=T_c=2015 days (the target interval).

4.1.2. Background Activity and Clustering Activity

We further analyzed seismicity during the 8 months before the 2023 M7.7 quake to explore the reason for the change in the rate of earthquake occurrence (Figure 5). We took a reductionism approach, by decomposing all earthquakes into Poisson background activity and clustering activity. We measured μ (a solo parameter of the Poisson background activity) and K₀ (a parameter representing the clustering activity), where the other three parameters (α, c, p) were constants. We used a non-stationary ETAS approach [24,43,46,47] to seismicity before the M7.7 quake. The standard (single) ETAS model, which is the stationary ETAS model, can be temporally extended to the non-stationary ETAS model in such a way that μ and K₀ are assigned as a function of t. The function μ(t) is represented by a broken line connecting the sequence (t_i, μ(t_i)) for the i-th earthquake, using a Bayesian function. Similarly, K₀(t) is represented by a broken line connecting the sequence (t_i, K₀(t_i)).

We obtained the α, c, and p-values obtained for the standard (single) ETAS fitting to the earthquakes (M≥2) over the period from 2014 to immediately before the M7.7 quake in the region within a 50 km radius surrounding the future M7.7 epicenter. Then, the obtained α, c, and p-values were assumed to be applicable to the non-stationary ETAS model with μ(t), K₀(t), and λ(t). Namely, the α, c, and p-values were independent of t. Given the predefined α=1.43, c=0.028, and p=1.17 for M_th=2 (M≥2), μ (red), K₀ (blue), and λ (grey) were computed for each earthquake (inset of Figure 5). Visual inspection shows that μ was nearly constant over time. However, K₀ was visually larger after mid-2022 than before it, although the timeseries of K₀ before mid-2022 showed one tall peak in 2016. Focusing on the time-dependent K₀, we included, in Figure 5, the average (horizontal solid line) of K₀-values for the periods before and after Jul. 9, 2022 (T_c=2015 days) (vertical dashed line). The average of K₀-values after Jul. 9, 2022 was nearly equal to K₀-values around the tall peak in 2016. The result shows that K₀ was larger after the start of seismic activation than before it, suggesting that clustering had an influence on months-long activation surrounding the M7.7-quake nucleation region. The increase in K₀ is consistent with the emergence of clusters C1 and C2 [10] within 8 months prior to the M7.7 quake. The same analysis was conducted for M≥1.5 (Figure S1), supporting our result.

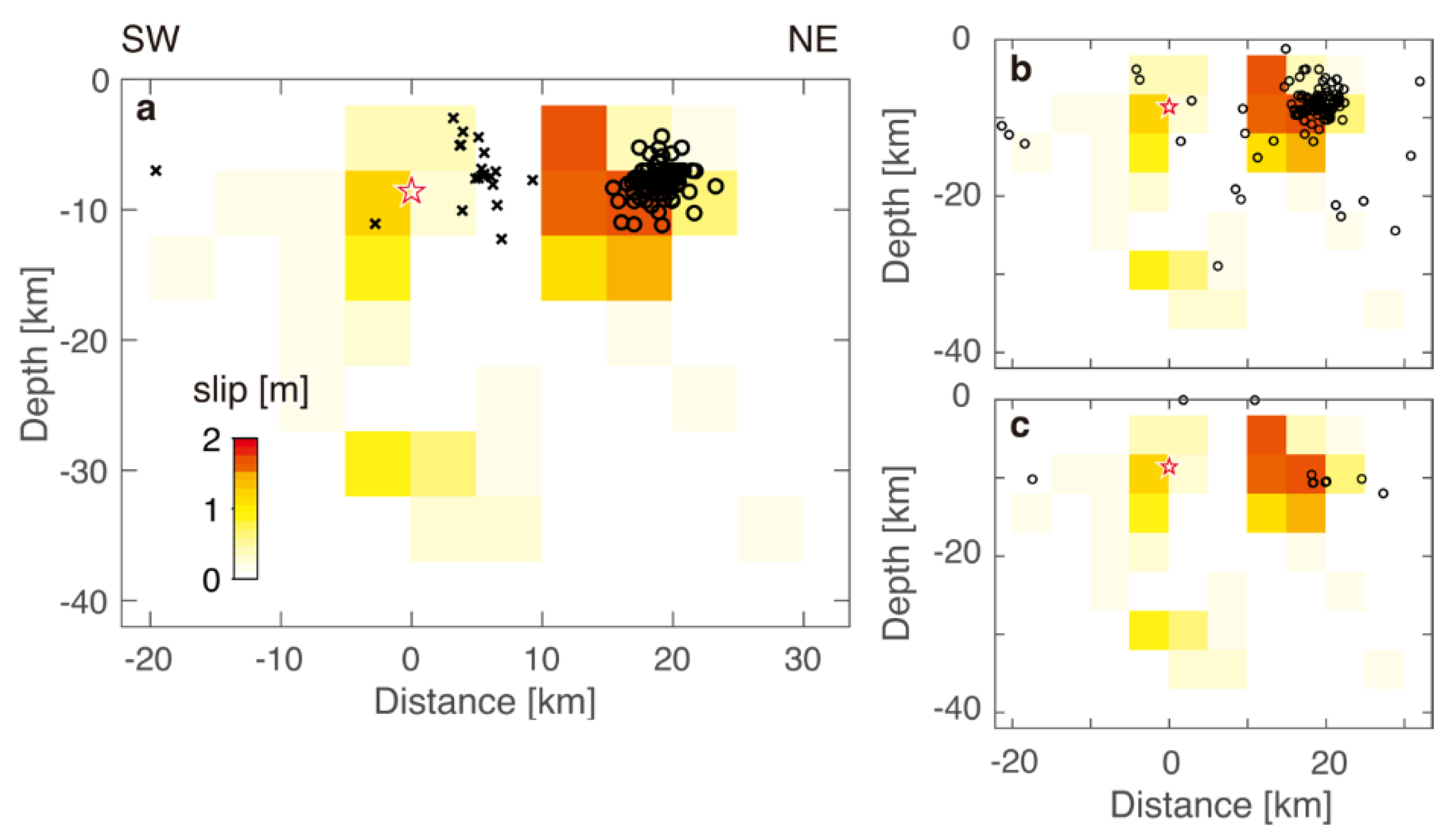
4.1.3. Slip Distribution of the M7.7 Quake and Preceding Seismicity

A cross-sectional view (Figure 6a) shows the slip distribution on segment 2 where the M7.7 quake initiated [2] and seismicity after the start of the activation (circles) (from Jul. 1, 2022 to immediately before the M7.7 quake). To create this cross-section, we used the AFAD catalog and retrieved M≥2 events within 7.5 km from the segment (width of 15 km). The retrieved events mostly consisted of events within cluster C2 [10]. An area of high-slip values of >1.5 m (red) was separated by about 10 km from the M7.7 hypocenter (star). This high-slip area overlaps with seismicity after the start of the activation (circles). A similar result was obtained (Figure 6b), using the catalog of Kwiatek et al. [10], into which events during the period from Jan. 1, 2023 to immediately before the M7.7 quake were included. We considered M≥0.5 events, because M_c for the catalog was 0.5 [10]. We similarly investigated the catalog of Lomax [16]. The number of earthquakes (M≥1.5, from Jan. 1, 2023 to immediately before the M7.7 quake) was inadequate (Figure 6c), although the result is consistent with those in Figure 6a,b. Given that cluster C2 contributed to the display of low b-values (b=0.6 [10]), our result indicates that the zone of low b-values coincided with the location of a future high-slip area on segment 2. This is similar to the result obtained by Nanjo et al. [30], who compared the slip distribution of the 2011 M9 Tohoku earthquake in Japan and the distribution of areas with low b-values of seismicity since 2008 to immediately before the Tohoku earthquake. Those authors showed that the zones of extremely low b-values coincided remarkably with locations of an extremely large co-seismic slip.

Also included in Figure 6a is the distribution of a swarm (crosses) in late 2017 to early 2018, shown as an upward convex around 340 days in ordinary time in Figure 4a or 40 in transformed time in Figure 4b. This swarm corresponds to cluster C7 [10]. The majority of this swarm overlaps with a low-slip area (white to light yellow). Cluster C7 displayed a high b-value (b=0.9 [10]). The observation between a high b-value and a low slip is also consistent with a previous study [30].

4.2. Post-Doublet-Quake Sequence

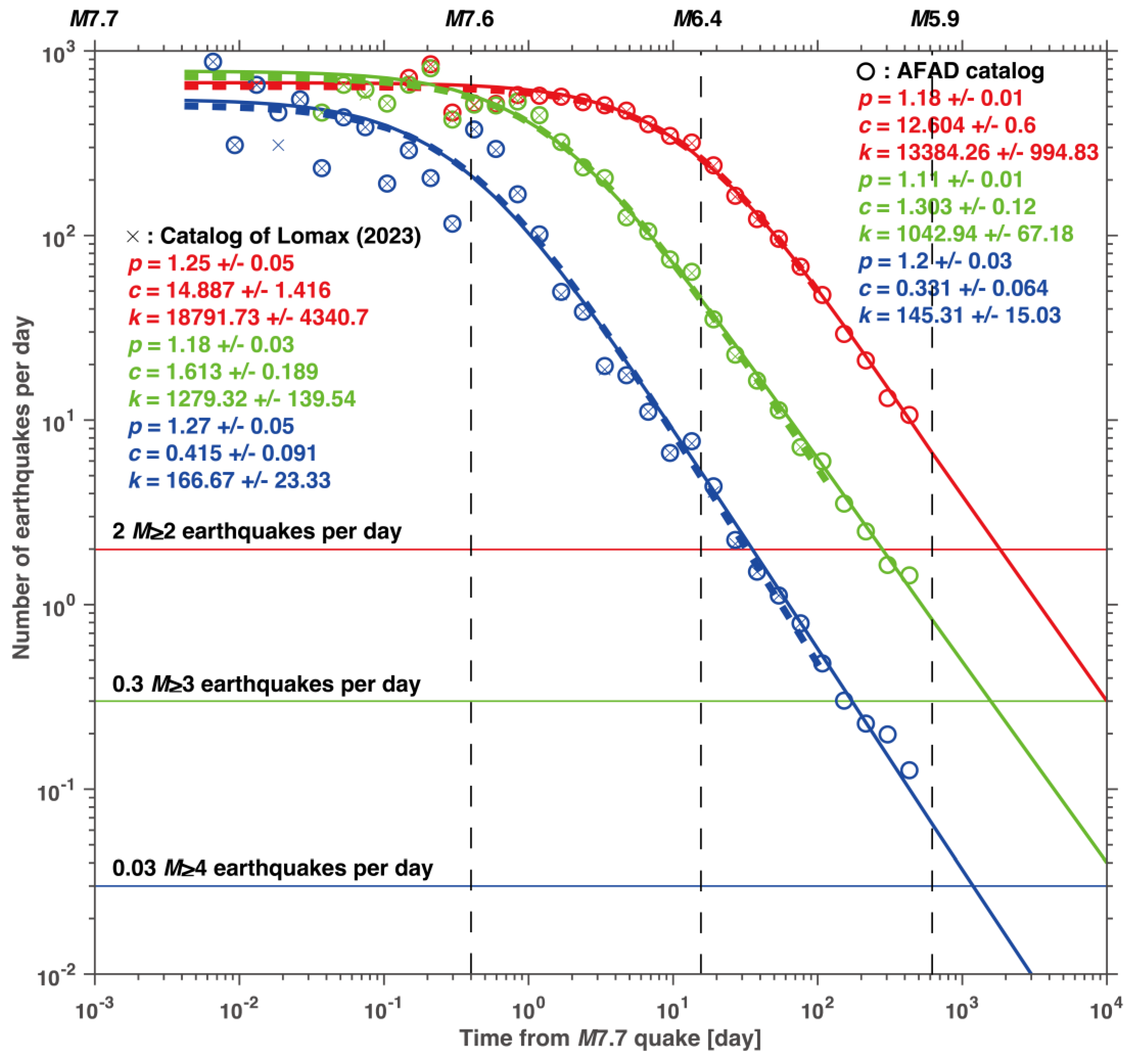
4.2.1. Seismicity Immediately After the Doublet Quakes

We calculated Coulomb stresses imparted by the doublet quakes and their relationship to seismicity within 5 days after the M7.7 quake (Figure 7a), where we used the USGS source models of the M7.7 and 7.5 quakes [2,3] and the AFAD earthquake catalog. In creating Figure 7a, the stresses were resolved on idealized faults oriented parallel to segment 1 (strike/dip/rake=60°/85°/3°) of the M7.7 source [2] and, therefore, similar to the broad character of the EAFZ. We observed a lack of seismicity at the zone of increase in Coulomb stress beyond the north end of the M7.7 rupture, noting that the area, which lacked seismicity, closely matched the area of the M6.8 rupture (Figure 7b). To create this figure, the same Coulomb stress calculation as was used in Figure 7a was conducted, but we used seismicity within 1 day after the 2020 M6.8 earthquake, which outlined the 2020 M6.8-quake source. Stress in the area beyond the north end of the M7.7 rupture was released by the 2020 M6.8 quake so that the increase in stress imparted by the doublet quakes was insufficient to induce the following events in this area. This is consistent with the result obtained by Toda and Stein [5], who showed that the 2020 M6.8 quake locally dropped the stress by ~10 bars, and the M7.7 quake then increased the stress there by 1-2 bars, resulting in a hole in seismicity after the M7.7 quake.

4.2.2. Seismicity Until the M6.4 Quake

The largest event (M6.4) after the doublet quakes occurred on Feb. 20, 2023 in an area around the south end of the M7.7 rupture. In creating Figure 8a, we conducted the same stress calculation as that in Figure 7a, but resolved stresses on faults oriented parallel to the NP1 (strike/dip/rake=225°/53°/-27°) of the M6.4 source [13]. The fault that ruptured during the M6.4 quake was promoted toward failure. The same resolution was conducted for the NP2 (strike/dip/rake=333°/69°/-139°), and a similar result was obtained (Figure 8b). Över et al. [11] obtained a result consistent with Figure 8a.

A map view based on data from the AFAD catalog for the period from Feb. 12, 2023 to immediately before the M6.4 quake (Figure 9a) shows that the eventual epicenter fell in a region of low b-values (red), where the period until Feb. 11, 2023 was not considered to remove the effect of the main aftershock sequence, revealing strong temporal variability in b. To create this map, we computed b-values [21,22] for events falling in a cylindrical volume, with height=30 km and sampling radius r=20 km, centered at each node on a 0.05°×0.05° grid, and plotted a b-value at the corresponding node. According to a previous study [48], r was searched by mapping b-values with a range of r=10-30 km to find optimal r (Figures S2 and S3). A nearly identical pattern of b-values, when sampled with r=15-20 km, was observed. Using r=10 km did not reveal details because it only reduced coverage. Sampling with r≥25 km resulted in smoothed b-values. For r=30 km, the low b-value zone lost its crispness and moved toward the outside. This is because the small volumes containing information about the low b-values were located at the edge of seismically active regions. At the locus of the b-value anomaly, the sample became a mixture of different distributions when r was increased. As a result, the anomaly was visually reduced. Thus, the optimal r was in the range of 15-20 km. In Figure 9, r=20 km was used, but using r=15 km, which slightly reduced coverage, did not change the conclusion. The corresponding M_c maps are given in Figure S2, where M_c was simultaneously calculated when calculating the corresponding b-value [22]. A similar feature was observed in Figure 9b by using the catalog of Lomax [16], where the mapping procedure was the same as that used for Figure 9a (see Figures S4 and S5).

4.2.3. Seismicity Until the M5.9 Quake

The second largest event (M5.9) after the doublet quakes occurred on Oct. 16, 2024 in an area around the north end of the M7.7 rupture. The same stress calculation as in Figure 7a was conducted, but different receiver faults [14] were used. Namely, we used two NPs of the M5.9 source: strike/dip/rake=244°/43°/-8° in Figure 10a and 340°/84°/-133° in Figure S6b. The result shows that the fault that ruptured during the M5.9 quake was promoted toward failure by the double quakes, irrespective of the plane that was used (Figure 10a and Figure S6b). We conducted the same stress calculation as in Figure 10a and Figure S6b, except that the M6.8-quake fault [4] was added into source faults. A similar feature was observed (Figure 10b and Figure S6a).

A map view based on use of the AFAD catalog for the period from Feb. 21, 2023 to Oct. 15, 2024 shows a zone of relatively low b-values (yellow to green) around the future epicenter (Figure 11a). The mapping procedure was the same as that in Figure 9a. The optimal r was in the range of 15-20 km (Figures S7 and S8). Similar to Figure 9a, we decided to use r=20 km in Figure 11a. This feature generally appears when using the catalog of Lomax [16] (Figure 11b, Figures S9 and S10).

5. Discussion

As was pointed out in the Introduction, we discussed a comparison of the duration of the post-doublet-quake sequence between our study and a previous study [5] to provide information that might possibly be used when evaluating a time-dependent seismic hazard along the NAFZ. As the basis of this comparison, we first confirmed that the overall seismicity after the doublet quakes around the causative faults decayed with time (black curve in Figure 12a), where earthquakes of M≥3 in the AFAD catalog for the period from the M7.7 quake to Oct. 16, 2024 in the study region shown in Figure 11 were used. Visual inspection (Figure 12a) shows that the standard (single) ETAS model (red curve) fits the data after the M7.7 quake well, suggesting no pronounced activation and quiescence. Similar results were obtained for M≥4 (Figure S11). The results were not induced by catalog selection bias, because similar results were observed when using the catalog of Lomax [16] (Figure 12b and Figure S12). The well-fitted results of the standard (single) ETAS model to the data (Figure 12, Figures S11 and S12) allowed us to assume that use of the OU relation is enough to capture an essential aspect of seismicity decay following the doublet quakes and to estimate the expected duration of the post-doublet-quake sequence, as described below.

As was done by Toda and Stein [5], we correlated the earthquake sequence with the OU relation, where we used events of M≥3 (green circles in Figure 13) in the AFAD catalog (from immediately after the M7.7 quake to Oct. 16, 2024 in the region considered for Figure 11). A similar correlation was obtained by using the catalog of Lomax [16] (green crosses). We used the ordinary occurrence rate of 0.3 M≥3 earthquakes per day (horizontal green line), based on the number of M≥3 earthquakes in the AFAD catalog during the period from 2014 to immediately before the 2020 M6.8 quake in the region considered for Figure 11. The intersection between the horizontal green line and the green curve shows an expected duration of about 1-2×10³ days. Similar expected durations were obtained for M≥2 (red) and M≥4 (blue) (Figure 13).

Our expected duration was longer than that (1-2.5 years) obtained by Toda and Stein [5]. We assumed a more stable fitting of the OU relation to data in the present study than in the previous study. This is because Toda and Stein fitted the OU relation to earthquakes during the period of about 100 days since the M7.7 quake while we completed this process for a period of 618 days since the M7.7 quake, i.e., the period (about 100 days) considered by Toda and Stein was shorter than the period (618 days) we considered. Similar to Toda and Stein [5], we considered the earthquake sequence of M≥4.5 to obtain the estimated duration (Figure S13). This sequence is correlated with the OU relation. An ordinary occurrence rate of 0.006 M≥4.5 earthquakes per day was used. The expected duration was about 1-2×10³ days. This is similar to the expected durations obtained for M≥2, 3, and 4, and longer than that in a previous study [5].

During the 20th century, much of the northern section of the EAFZ ruptured, as described in the Introduction. Starting with the 2020 M6.8-quake sequence, much of the southern section ruptured (Figure 1). There is no doubt that the M7.7 quake was not the almighty earthquake [49], which would rupture an entire plate boundary at once and leave no stress that could produce any other kind of earthquake. Regional and global earthquake magnitude frequency distributions obey a GR relation (e.g., [29,30,31,48,50]), but it is unclear if individual fault zones do. Namely, earthquake magnitude-frequency on fault zones is suggested to be distributed in a GR relation or characteristic. Parsons et al. [51] used data from California, USA and found that individual fault zones have characteristic magnitude distributions, with a greater number of large earthquakes relative to small earthquakes than expected from a GR trend (e.g., [52]).

We conducted a simple test to examine whether seismicity along the EAFZ obeys a GR relation or not (Figure 14), where a lower magnitude threshold (M=5.5) was set to ensure the homogeneity of earthquake recording since 1965. To create Figure 14, we used the same catalog as that used in Figure 1 (see the Data section). Analysis of the b-value [21,22] shows that the M7.7 quake (star) followed the GR trend with b~1 (Figure 14b), indicating that the EAFZ does not have a characteristic magnitude distribution, where we used earthquakes during the period from Jan. 1, 1965 to Feb. 25, 2023. As a reference, we conducted a similar analysis, using data before the M7.7 quake. Figure 14a, which indicates the GR distribution with b~1, shows that the M7.7 quake (star) deviates from this distribution, where the M7.7 quake was not included in the GR fitting. A comparison between these figures (Figure 14a,b) indicates that the M7.7 quake and the following events, including the M7.5 quake, affected the whole magnitude range, such that the M7.7 quake continued to follow the GR trend (Figure 14b). A similar feature was observed for the effect of the 2004 Sumatran megaquake, in Indonesia, on a global catalog [50]. Our result supports the observation that the M7.7 quake was not an outlier (neither an almighty earthquake nor a characteristic earthquake), but was instead harmonized with small earthquakes along the EAFZ. If an almighty earthquake or a characteristic earthquake of the EAFZ existed, it would be much larger than the M7.7 quake.

Figure 14. Cumulative number of earthquakes as a function of M. (a) Earthquakes during the period from Jan. 1 1965 to immediately before the M7.7 quake (the top outside of axes) in the rectangle shown in Figure 1a were used. Solid line represents the GR relation with b=1.13 and a=7.86. The GR relation, taking the upper and lower bounds (standard deviation) of b-values (b=1.33 and 0.93), is shown by dashed lines, where the standard deviation of the b-values of the bootstrap samples was used to define these bounds. Also included for comparison is the M7.7 quake (star), where this quake was not included in the data to which the GR relation was fitted. (b) Earthquakes during the period given at the top outside of axes in the rectangle shown in Figure 1a were used. The GR relation with b=0.92±0.20 and a=6.80 is shown by a solid line and dashed lines, respectively. The M7.7 quake (star) was included in the data to which the GR relation was fitted.

Figure 14. Cumulative number of earthquakes as a function of M. (a) Earthquakes during the period from Jan. 1 1965 to immediately before the M7.7 quake (the top outside of axes) in the rectangle shown in Figure 1a were used. Solid line represents the GR relation with b=1.13 and a=7.86. The GR relation, taking the upper and lower bounds (standard deviation) of b-values (b=1.33 and 0.93), is shown by dashed lines, where the standard deviation of the b-values of the bootstrap samples was used to define these bounds. Also included for comparison is the M7.7 quake (star), where this quake was not included in the data to which the GR relation was fitted. (b) Earthquakes during the period given at the top outside of axes in the rectangle shown in Figure 1a were used. The GR relation with b=0.92±0.20 and a=6.80 is shown by a solid line and dashed lines, respectively. The M7.7 quake (star) was included in the data to which the GR relation was fitted.

The feature that the M7.7 quake continued to follow the GR trend (Figure 14b) implies that underlying mechanism of earthquake occurrence did not differ from small events to large events. A phenomenon served by the mechanism we focused on is earthquake clustering, namely seismicity prior and subsequent to the M7.7 quake. Given that this quake and the M7.5 quake that occurred about nine hours later were defined as the doublet quakes, this paper reported the characteristics of seismicity before and after the doublet quakes. The possibility to analyze the interaction between the doublet quakes was out of scope in the present study because several studies [5,6,7,8,9] performed in-depth analyses of it.

There are three features of the pre-doublet-quake sequence:

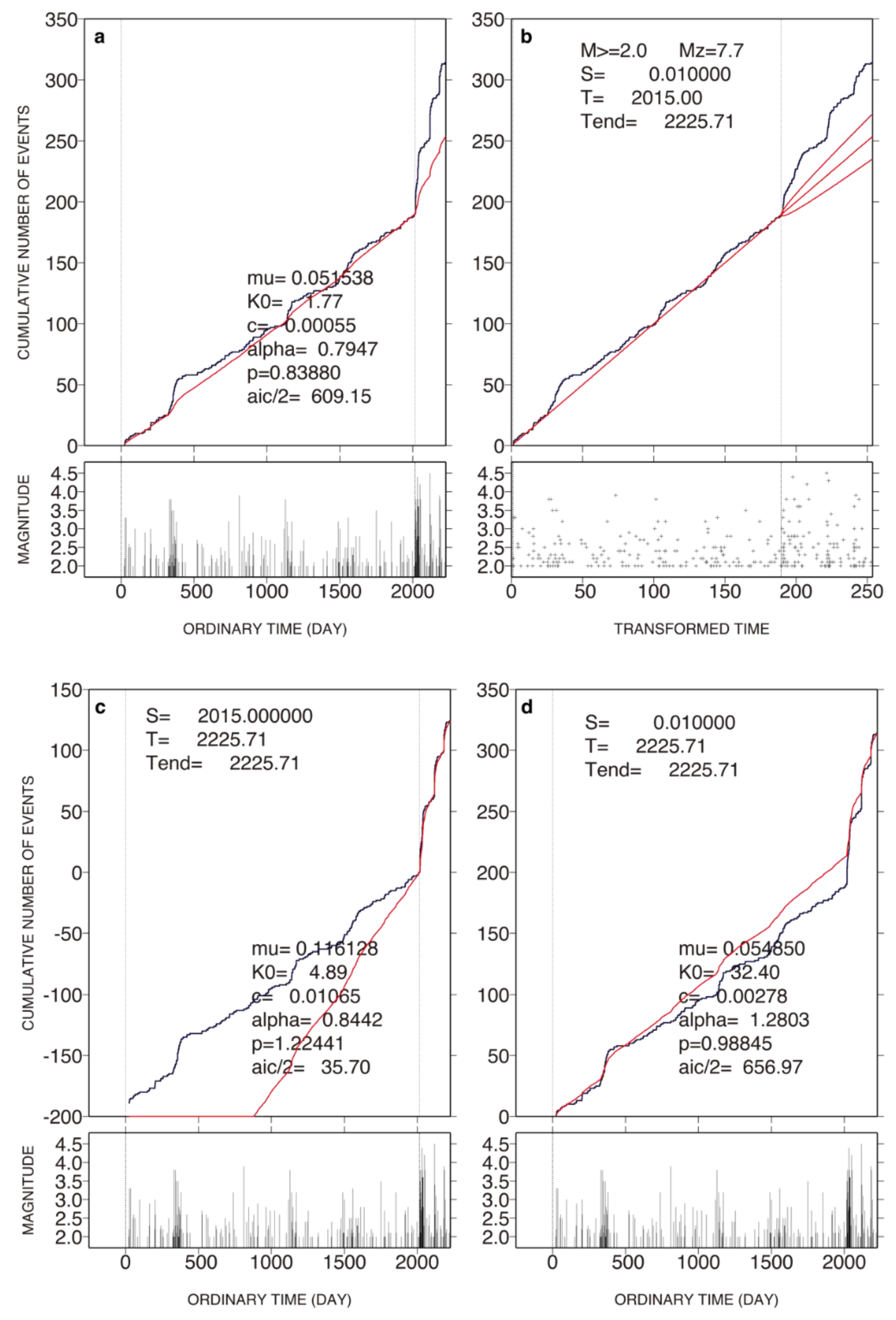
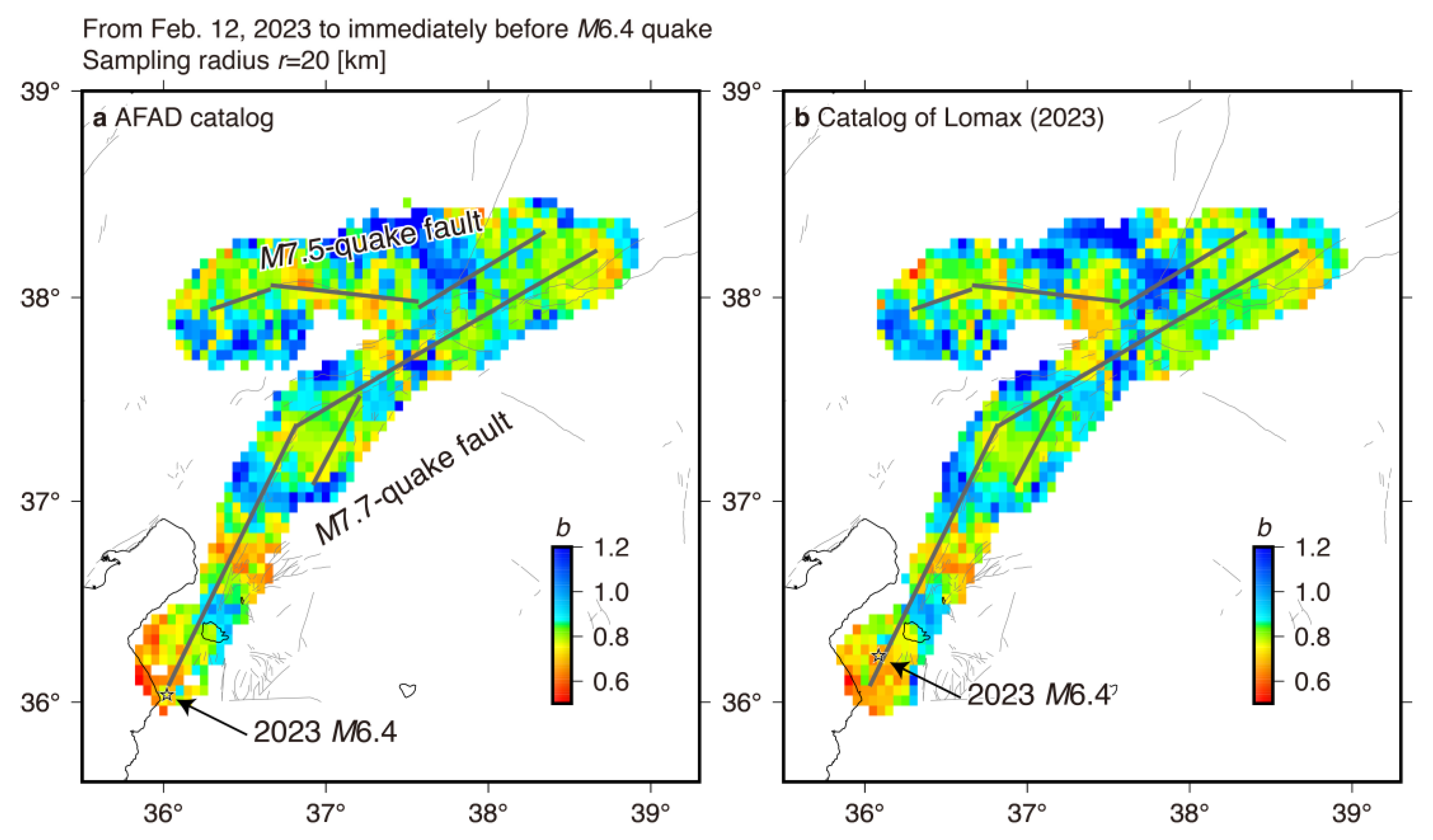
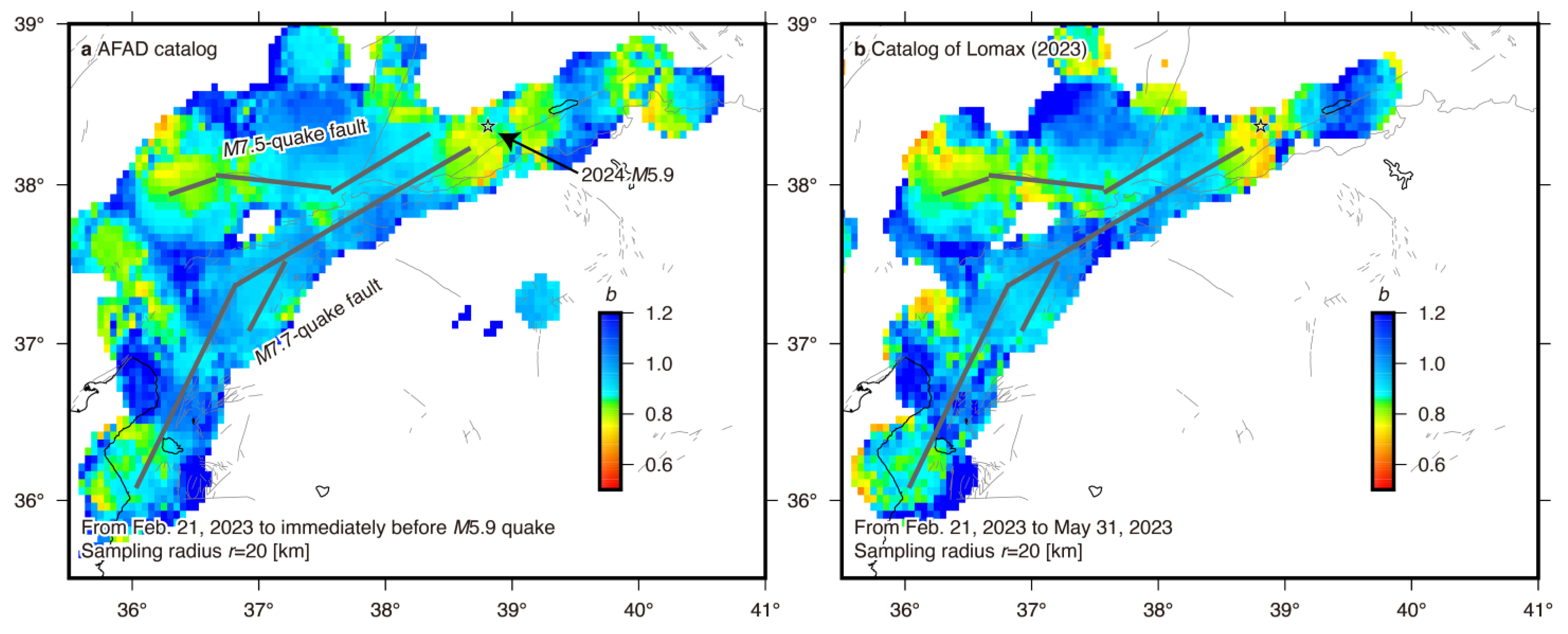
• Seismicity transients began in mid-2022 within 50 km of the future M7.7 epicenter. We revealed that the occurrence rate after mid-2022 was significantly larger than that before it, showing seismic activation. Small b-values were observed after the start of activation. The transients reported previously [10,11] were confirmed by our study, which applied the ETAS model and the Bayesian b-value model to events in two different earthquake catalogs.
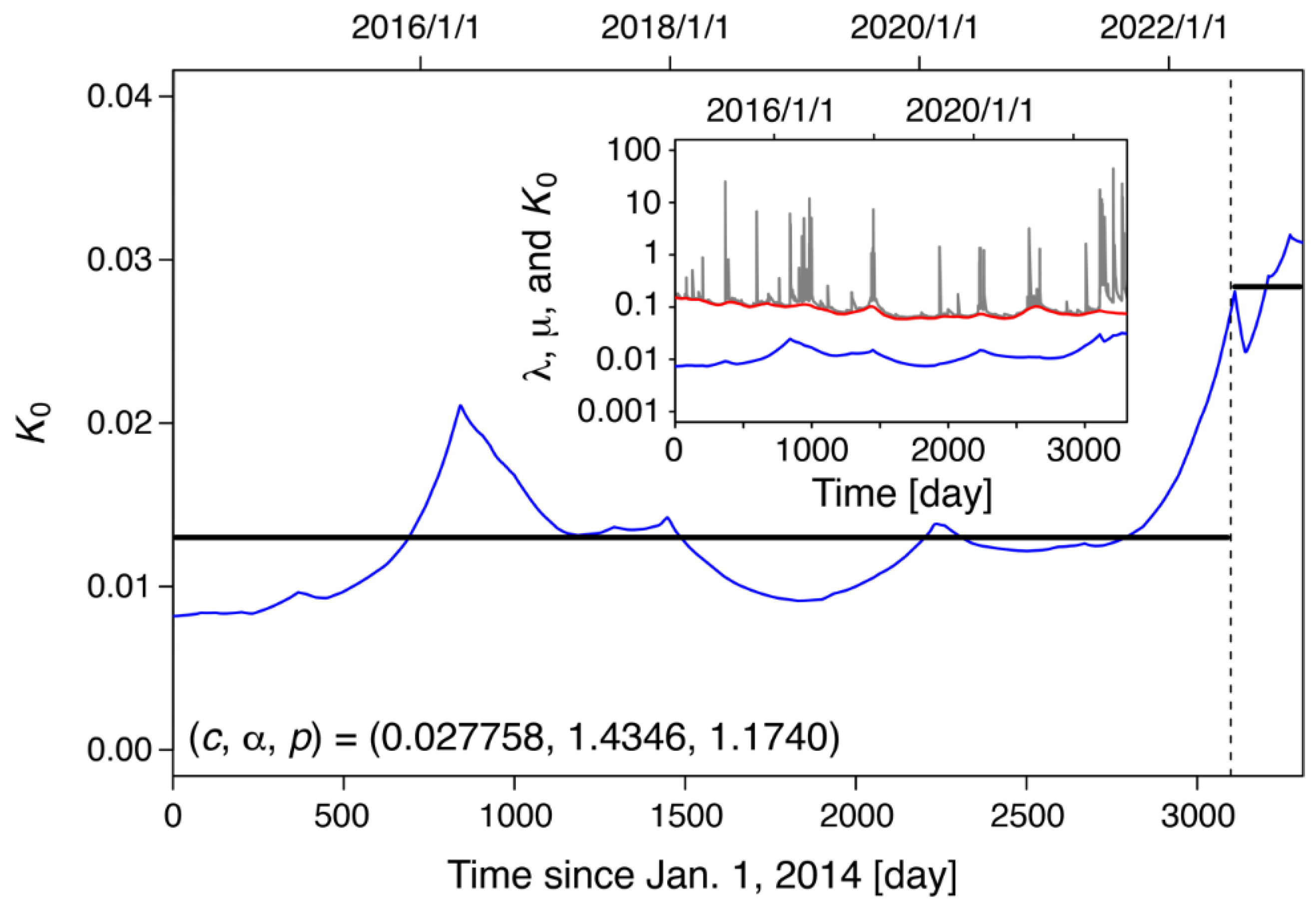
• Seismicity within 50 km of the future M7.7 epicenter decomposed into two types of activity: background and clustering. The parameter representing background activity was almost constant over time while that representing clustering activity was smaller before the start of activation than after it. Seismic activation is interpreted as the effect of clustering activity. This was attributed to the emergence of two clusters near the future M7.7 epicenter [10].
• A high-slip area on the segment (referred to as segment 2 in this study) from which the M7.7 rupture started, overlaps with seismicity after the start of activation. This seismicity mostly consisted of events of the cluster displaying low b-values. A similar result was observed for the 2011 Tohoku megaquake [30], where a correlation between areas of low b-values and areas of large co-seismic displacement was shown. A cluster of high b-values that emerged in 2017-2018 overlapped with a low-slip area on the same segment.

There are three features pertaining to seismicity after the doublet quakes:

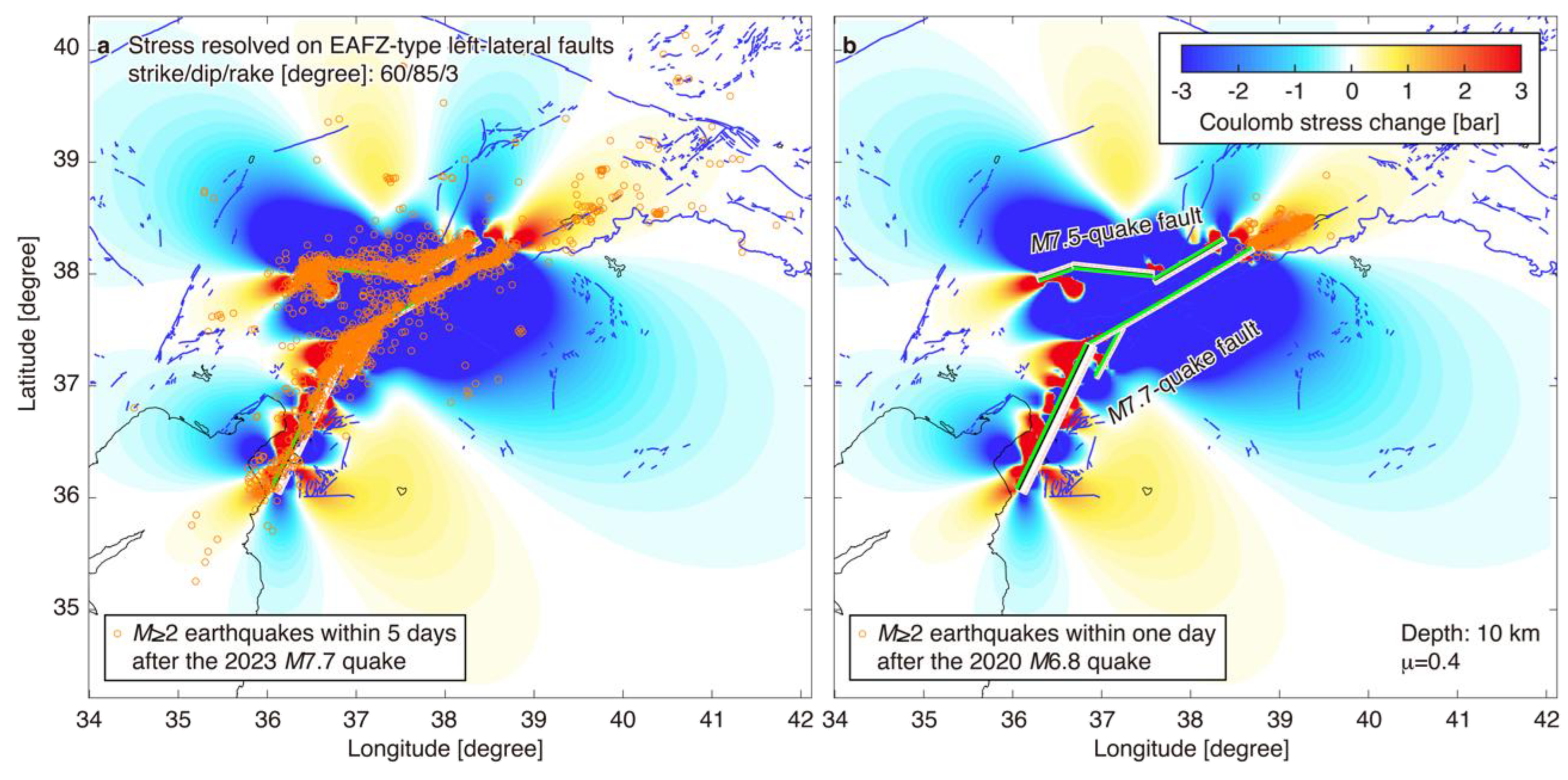
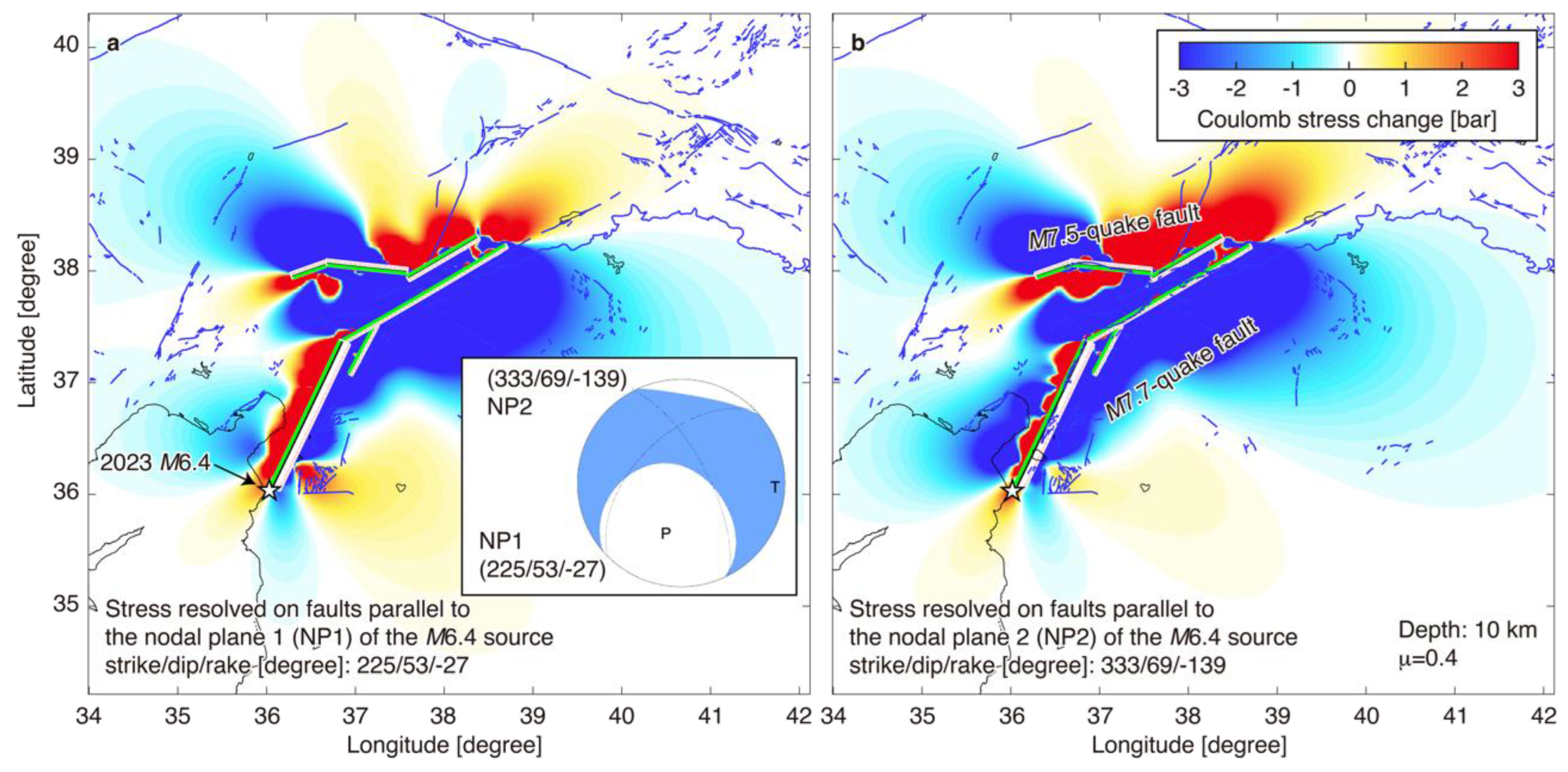
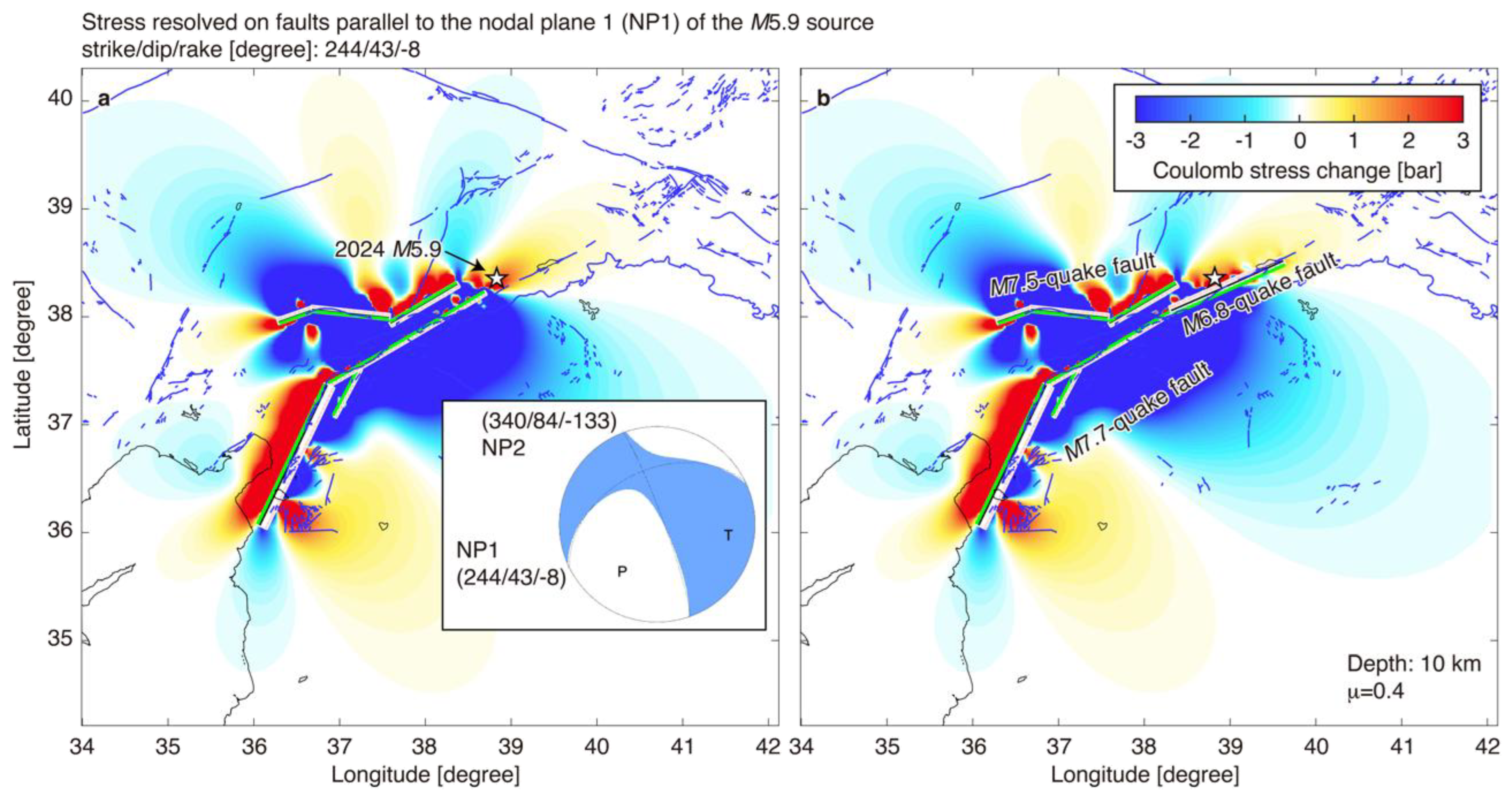
• Seismicity following the 2020 M6.8 quake suggests that the south end of the M6.8 rupture was close to the north end of the M7.7 rupture. There was a lack of post-M7.5-quake seismicity at the zone of increase in Coulomb stress imparted by the doublet quakes beyond the north end of the M7.7 rupture, noting that this area, which lacked seismicity, closely matched the area of the 2020 M6.8 rupture. Our result is consistent with a previous finding [5].
• Locations of the two M6-class quakes around the north and south ends of the M7.7-quake rupture were in relatively high-stress regions compared with the surrounding ones, as implied by the b-value and Coulomb-stress analyses. The region around the hypocenters of the M6-class quakes became closer to failure by the doublet quakes. A similar result was obtained when adding the 2020 M6.8 fault to source faults of Coulomb stress changes.
• The decay of seismic activity with time after the M7.7 quake around the causative faults was well modeled by the standard (single) ETAS model, indicating no pronounced activation or quiescence. This decay also followed the OU relation. Our estimation of the duration of the post-doublet-quake sequence was 1-2×10³ days (2.7-5.5 years), a longer duration than that proposed by an earlier study [5]. The difference between the present study and the previous study emerged from the fact that the former used events within 618 days since the M7.7 quake while the latter used events within about 100 days.