Prerpints.org logo
Preprint
Article

Adsorption of CuSO4 on Anatase TiO2 (101) Surface: A DFT Study

This version is not peer-reviewed.

Submitted:

13 February 2025

Posted:

17 February 2025

You are already at the latest version

Abstract
The rapid growth of industrial activities has increased environmental pollution, and so-lar-driven heterogeneous photocatalysis using TiO2 has emerged as a promising solution. However, its wide bandgap limits its efficiency, prompting research into various optimi-zation strategies. One of these approaches is surface functionalization. Thus, this study investigates the adsorption of CuSO4 on the anatase TiO2 (101) surface using density func-tional theory calculations. The adsorption process induced a magnetic moment of 0.97 µB and a slight reduction in overall bandwidth. A preferential adsorption geometry pattern with an energy of -4.31 eV was identified. Charge transfer analysis revealed a net transfer from the TiO2 surface to the CuSO4 molecule, with increased net atomic charges for atoms involved in new chemical bond formation, indicating a chemisorption process. These electronic structure modifications are expected to influence the electronic and catalytic properties of the material. The findings provide insights into the CuSO4 adsorption mechanism on anatase TiO2 (101) surface and its impact on the properties of the material, contributing to a deeper understanding of this system.
Keywords: 
TiO2 (101)
;  
CuSO4
;  
DFT + U
;  
vdW
;  
chemisorption
;  
surface
Subject: 
Chemistry and Materials Science  -   Surfaces, Coatings and Films

1. Introduction

The rapid growth of industrial activities and population has accelerated the dispersion of harmful chemicals into the environment, leading to the presence of persistent organic pollutants even in remote areas [1,2]. This global issue calls for cleaner, more sustainable production and consumption policies, along with the development of innovative technologies for air, soil, and water treatment [3].
In this sense, solar-driven heterogeneous photocatalysis is a promising and sustainable solution for removing organic and biological contaminants from water [4,5]. Among materials, Titanium dioxide (TiO2) is a key material in several high-technology applications, including photocatalysis, biomaterials, and novel photovoltaic solar cells [6,7,8]. Its use in photoelectrochemical processes is particularly crucial for enabling efficient large-scale solar electricity production, addressing the growing global need for sustainable energy.
TiO2, particularly in its anatase phase, has proven to be a promising material due to its unique electronic and catalytic properties, making it suitable for applications in photocatalysis, sensors, solar cells, and environmental remediation [9,10,11]. The anatase TiO2 (101) surface is known for its high stability and favorable energetic properties [6,12,13]. Studies have demonstrated that the anatase TiO2 (101) surface is the most energetically favorable and commonly observed surface in natural and synthetic anatase crystals [14,15]. By examining how different molecules interact with this surface, researchers can develop insights into improving TiO2-based materials for various applications [16,17].
However, the wide bandgap of anatase-phase TiO2 (3.2 eV) significantly constrains its photocatalytic efficiency under solar irradiation [18]. To address this limitation, researchers have explored various strategies, including doping [19], morphological engineering [20,21], surface functionalization [22], and synthesis of substoichiometric titanium oxides, specifically Magnéli phases [23,24]. These approaches aim to modulate the electronic structure and optical properties of TiO2, thereby enhancing its photocatalytic performance across a broader spectrum of light.
Photocatalysis is an advanced oxidation process (AOP) that facilitates the degradation of organic compounds by generating hydroxyl radicals (HO•). Nevertheless, optimizing the efficiency of photocatalysts remains challenging, requiring extensive experimental testing, often based on trial-and-error methods.
In this context, computational simulation of molecular adsorption on metal oxide surfaces has emerged as a key tool for understanding catalytic and adsorption mechanisms. This study investigates the adsorption of the copper (II) (CuSO4) molecule on the anatase (101) surface of TiO2 using first-principles methods based on Density Functional Theory (DFT).
To the best of our knowledge, no density functional theory (DFT) focused on the surface adsorption of this molecule. Therefore, provides unique insights that complement experimental findings [25,26]. This approach offers a deep atomic-level understanding of the adsorption process.

2. Computational Details

The present work has been conducted using the Vienna ab initio Simulation Package (VASP) [27,28], which is based on first-principles Density Functional Theory (DFT) within the Generalized Gradient Approximation (GGA) method [29]. In this approach, the valence electronic states are represented using a set of periodic plane waves, and the interaction between core and valence electrons is implemented through the projector augmented wave (PAW) method [30]. The Perdew-Burke-Ernzerhof (PBE) [31] parameterized GGA functionals are used to describe the exchange-correlation interaction. The valence configuration employed in our calculations for each atom is as follows: 3p63d24s2 for Ti, 3d104s14p6 for Cu, 2s22p4 for O, and 3s23p4 for S. Additionally, to account for the strong correlation between d electrons, an intra-site Coulomb repulsion U-term was included in the calculations, specifically, the rotationally invariant (Dudarev) approach to the GGA + U , [32] resulting in the so-called DFT + U method [33]. The utilized U parameters values were 3.5 eV for the Ti atom [34] and 7 eV for the Cu atom [35]. Furthermore, spin-polarized calculations within the DFT+U framework were applied throughout the study.
GGA and hybrid functionals have limitations in accurately capturing long-range electron correlations necessary for modelling van der Waals (dispersive) forces. This shortcoming arises because these functionals approximate the exchange-correlation energy based on local or semi-local density gradients and, in the case of hybrid functionals, include a portion of non-local Hartree-Fock exchange [36]. However, they do not inherently account for long-range dispersive interactions, which are essential for accurately modelling adsorption processes. To address this, we have employed the DFT-D3 dispersion correction method developed by Grimme, which includes a Becke-Johnson damping function [37,38]. This method enhances the accuracy of our adsorption studies by incorporating van der Waals interactions.
This study employed a cut-off kinetic energy of 550 eV which was determined by converging the total energy to less than 1 meV/atom. The Brillouin zone sampling was performed using a Γ-centered Monkhorst-Pack (MP) scheme [39]. A 3 × 2 × 1 k-point mesh was used for structural optimization of the 144-atom periodic slab, while a higher-resolution 7 × 5 × 1 mesh was implemented for subsequent static calculation to compute properties. To prevent artificial interactions between periodic slabs, a vacuum space of 20 Å and dipole correction were applied [40,41].
To accurately model the isolated CuSO4 molecule within the context of periodic calculations, it was placed in a cubic supercell with dimensions of 15 × 15 × 15 ų. The molecule was then geometrically optimized without constraints, using the same kinetic energy cut-off as employed for the slab calculations. This approach ensures consistency in the representation of both the adsorbed and free molecular states.

3. Results and Discussion

3.1. Pristine Surface

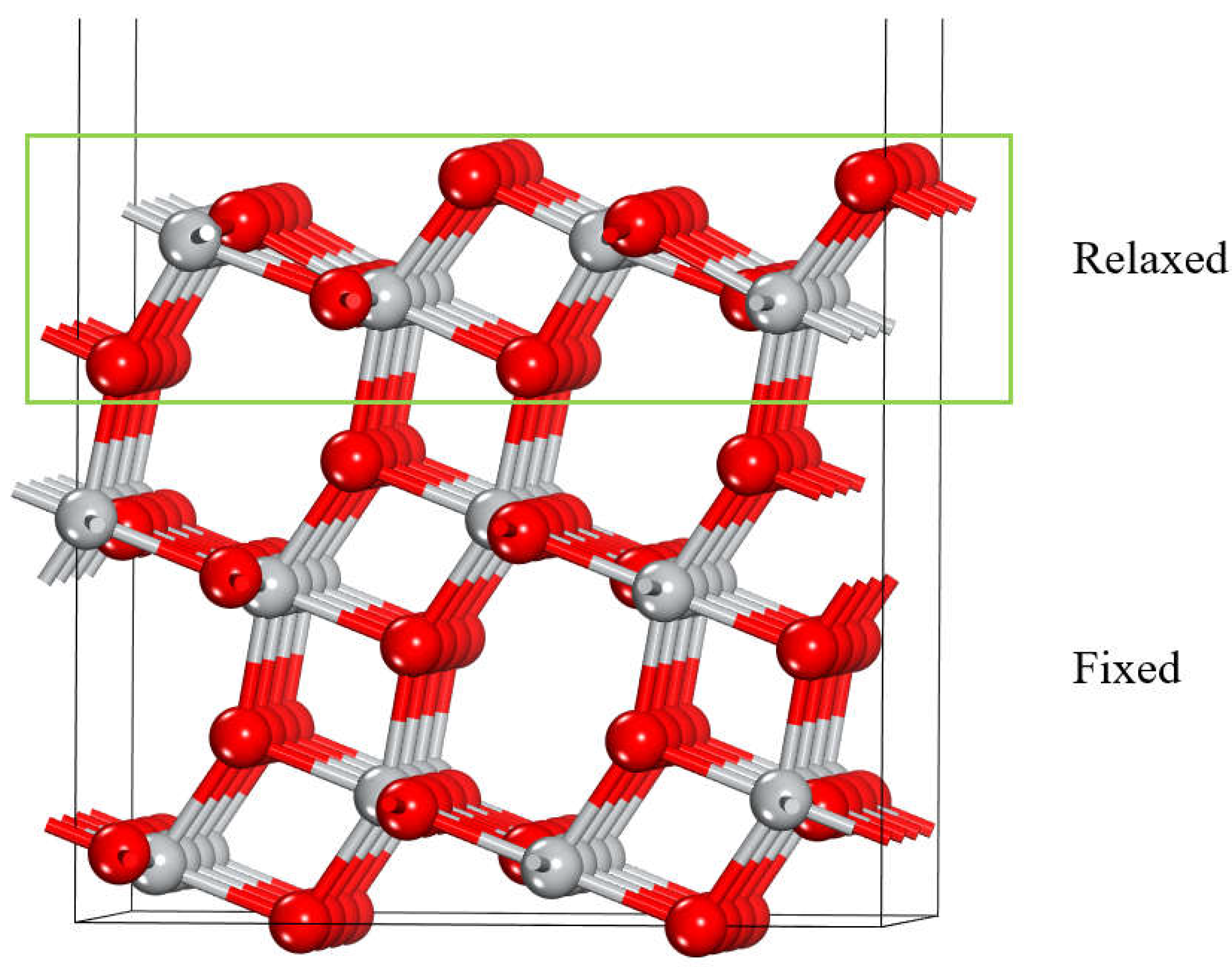
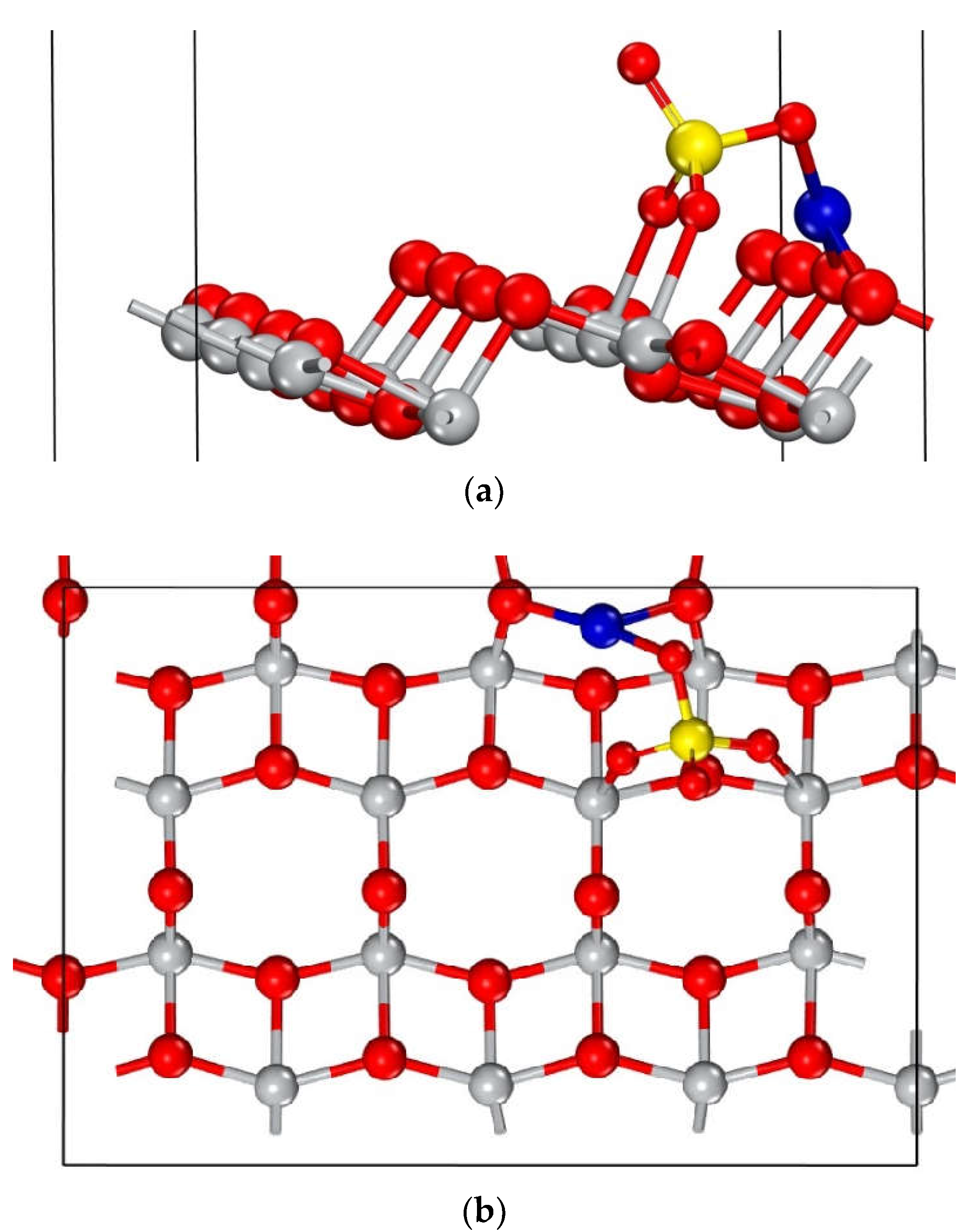
To model the anatase (101) TiO2 surface a slab was constructed using a (3 × 3) 12-atom primitive unit cell, resulting in a periodic slab containing 144 atoms. The slab consists of three trilayers, each containing an upper and bottom layers of O atoms bonded with a middle layer of titanium atoms. Prior to adsorption, the uppermost trilayer was fully relaxed while the undelaying layers were constrained to their bulk positions, as illustrated in Figure 1.
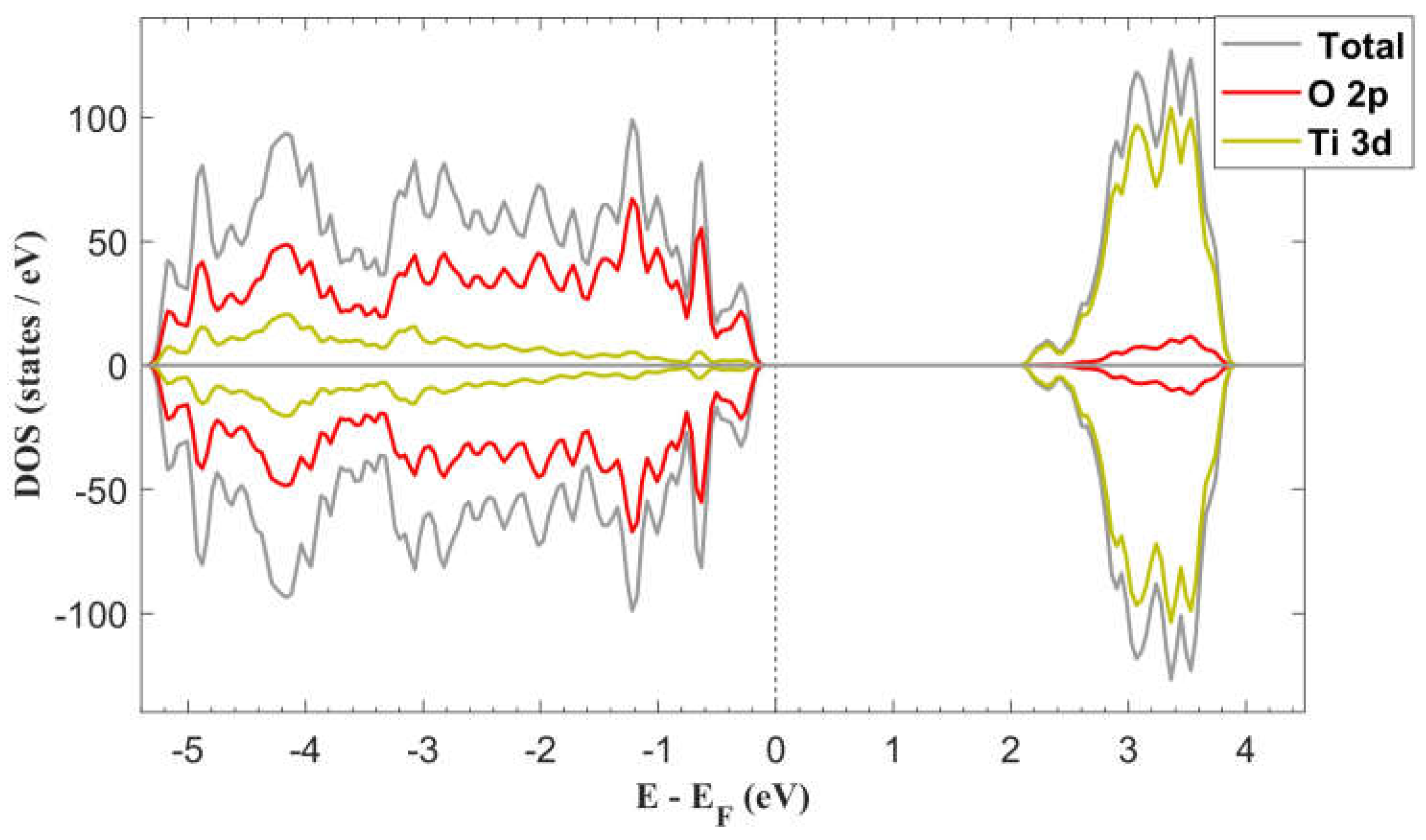
The computed total density of states (DOS) of the pristine surface is presented in Figure 2. It can observe hybridization between O 2p and 3d states in the valence band (VB) with mayor contributions of O 2p states. In the case of the conduction band (CB) is primarily constituted of Ti 3d states, with a small contribution from O 2p states. This composition is consistent with previous works [42,43].
The computed band gap width was 2.05 eV, which is smaller than the well-established value of 3.2 eV for bulk anatase TiO2. This underestimation is a known limitation of DFT methodologies. To address this issue, we implemented the Generalized Gradient Approximation plus Hubbard U (GGA+U) approach with U = 3.5 eV. This modification resulted in a modest improvement of the band gap width, increasing from 2.05 eV to 2.27 eV, representing a 10.73% enhancement. While this adjustment partially mitigates the bandgap underestimation inherent to standard DFT calculations, it is important to note that our primary focus remains on elucidating the effects induced by the adsorption process rather than achieving perfect agreement with experimental band gap values.

3.2. Free Molecule

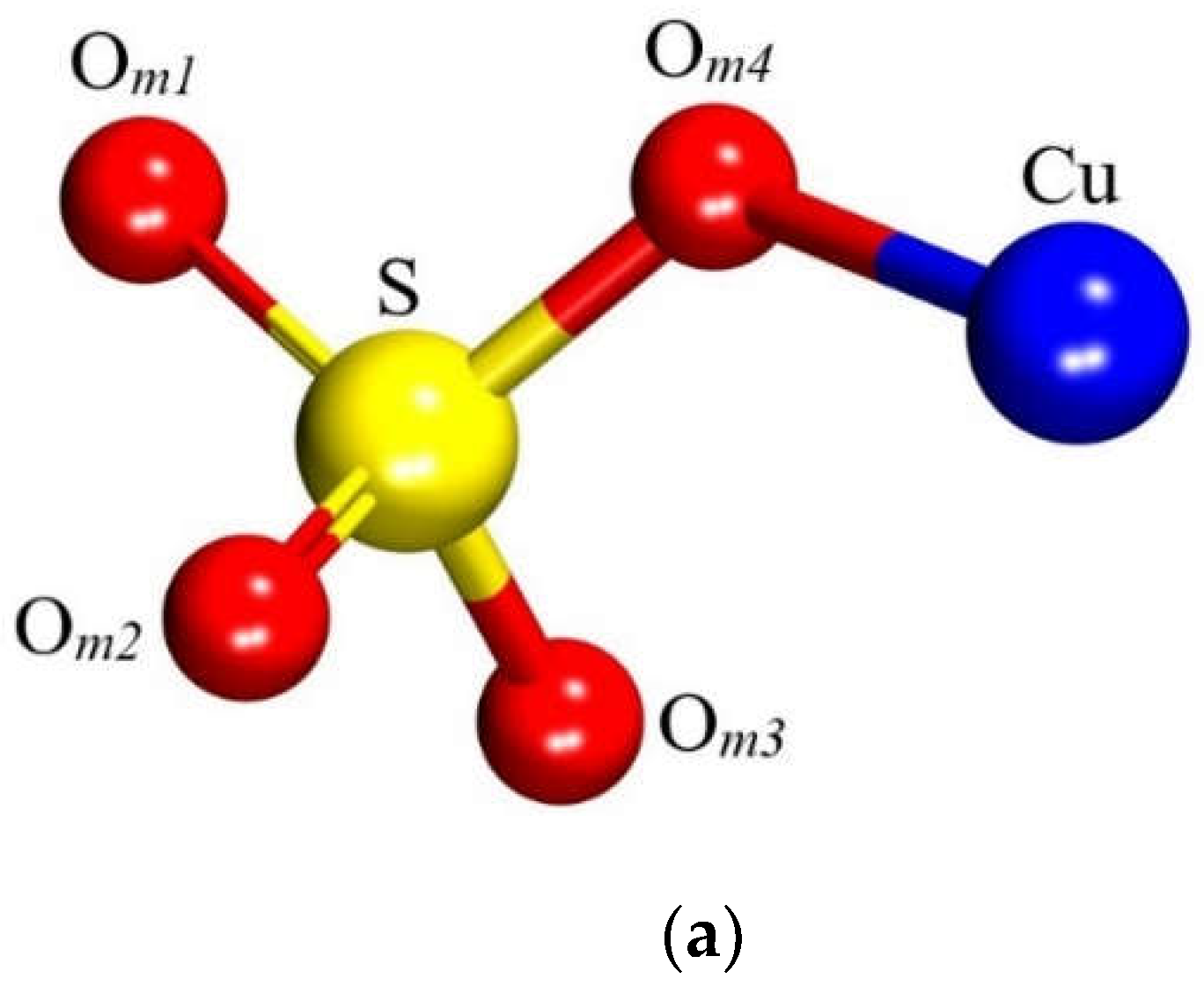
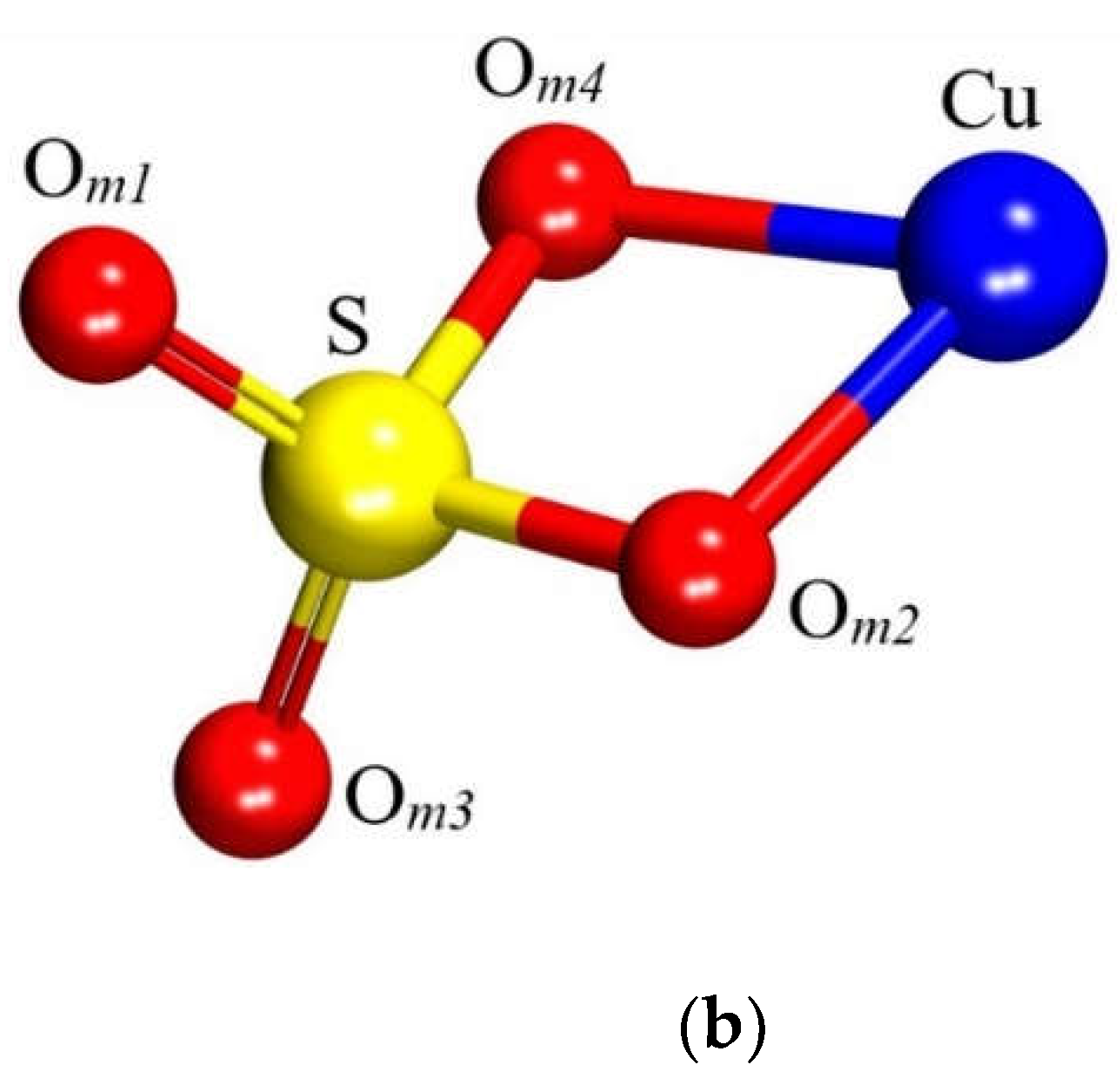
The dehydrated state of CuSO4 was selected to model the molecule. The free molecule was constructed by positioning it at the center of a 15 × 15 × 15 ų cubic supercell and subjecting it to full atomic relaxation. The optimized molecular structure is presented in Figure 3 and Table 1.
The atomic relaxation within this model led to the approximation of Cu and its nearest O atom, designated as Om2. Prior to optimization, these atoms were separated by 3.25 Å and afterwards, the distance is found to be 1.85 Å, which is identical to Cu ̶ Om4(Table 1). This structural rearrangement can be attributed to the breaking of bonds that the Cu atom originally formed within its crystalline structure (chalcocyanite) and subsequent relaxation that led the isolated molecule to adopt a more energetically favorable state.

3.3. Adsorption on Anatase TiO2 (101) Surface

The anatase phase of TiO2 is widely recognized as the most prevalent form in photovoltaic applications [45], with the (101) surface being particularly significant due to its thermodynamic stability [46]. Consequently, this study employs the anatase TiO2 (101) surface as the substrate for investigating the adsorption behavior of CuSO4.
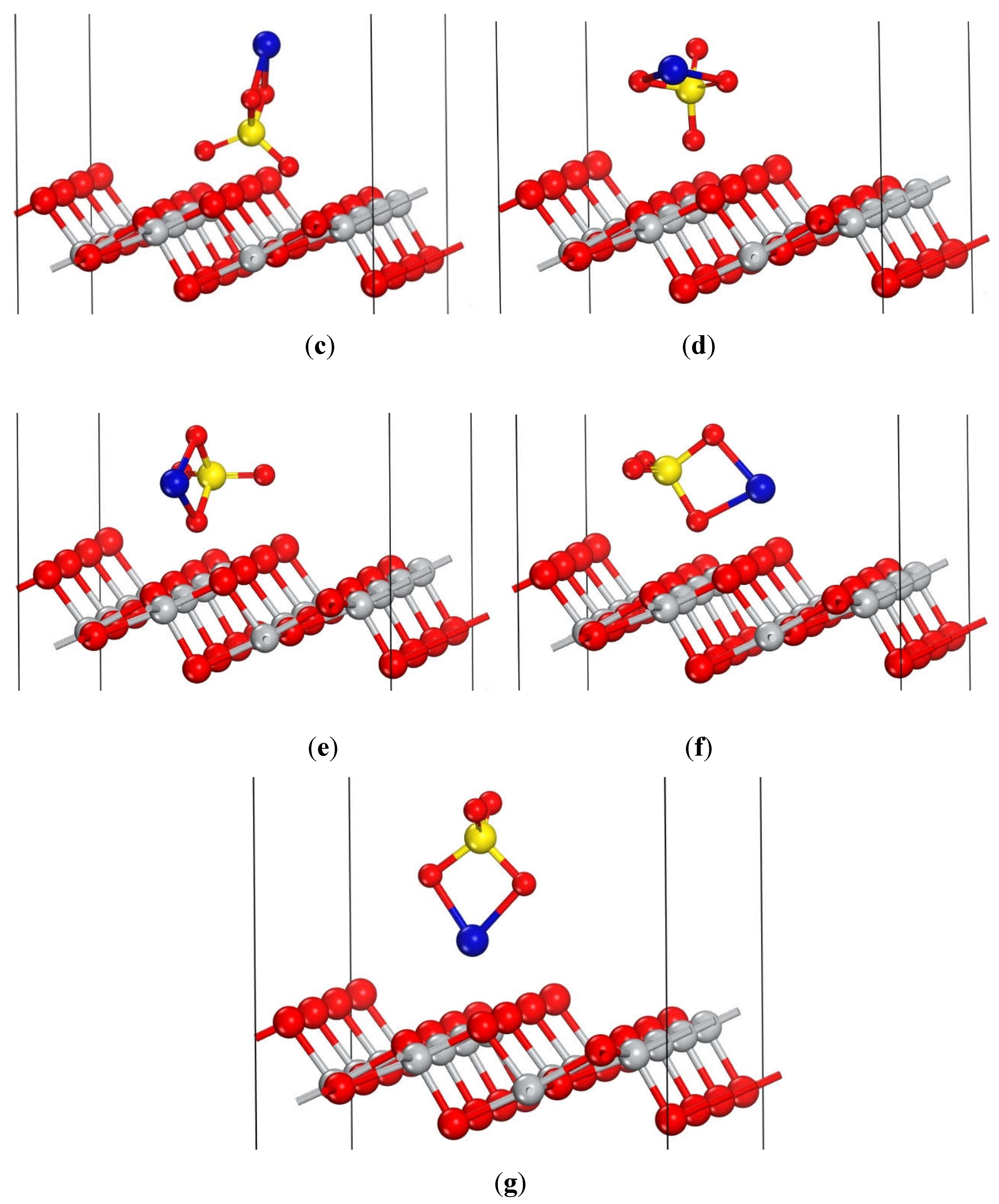
To determine the optimal adsorption geometry of CuSO4 on the anatase TiO2 (101) surface, seven distinct initial orientations of the CuSO4 molecule were systematically explored, each positioned over different adsorption sites on the surface. These initial configurations are illustrated in Figure 4.
Following the initial placement of the CuSO4 molecule, a comprehensive atomic relaxation was performed. This optimization procedure was conducted without imposing any constraints on the atomic displacements of both the adsorbed molecule and the atoms within the uppermost trilayer of the TiO2 surface. Upon completion of the geometry optimization, the adsorption energy (Eads) for each configuration was calculated using the following equation:
E a d s = E s u r f + m o l − E s u r f − E f r e e ( m o l )
Where E s u r f + m o l refers to energy of the surface with the adsorbate, E s u r f is the energy of the pristine surface while E f r e e ( m o l ) represents the energy of the free molecule. Computed adsorption energies are shown in Table 2.
As can be observed in Table 2, configurations that achieved the lowest adsorption energies are b, d and f, all of which reach an identical adsorption structure. The second most favorable configuration was e, which is depicted in Figure 5.
However, the adsorption geometry with the lowest adsorption energy corresponds to configurations b, d, and f, which have been selected for further analysis due to its higher likelihood of occurrence. Its structure closely resembles configuration e, as is illustrated in Figure 6.
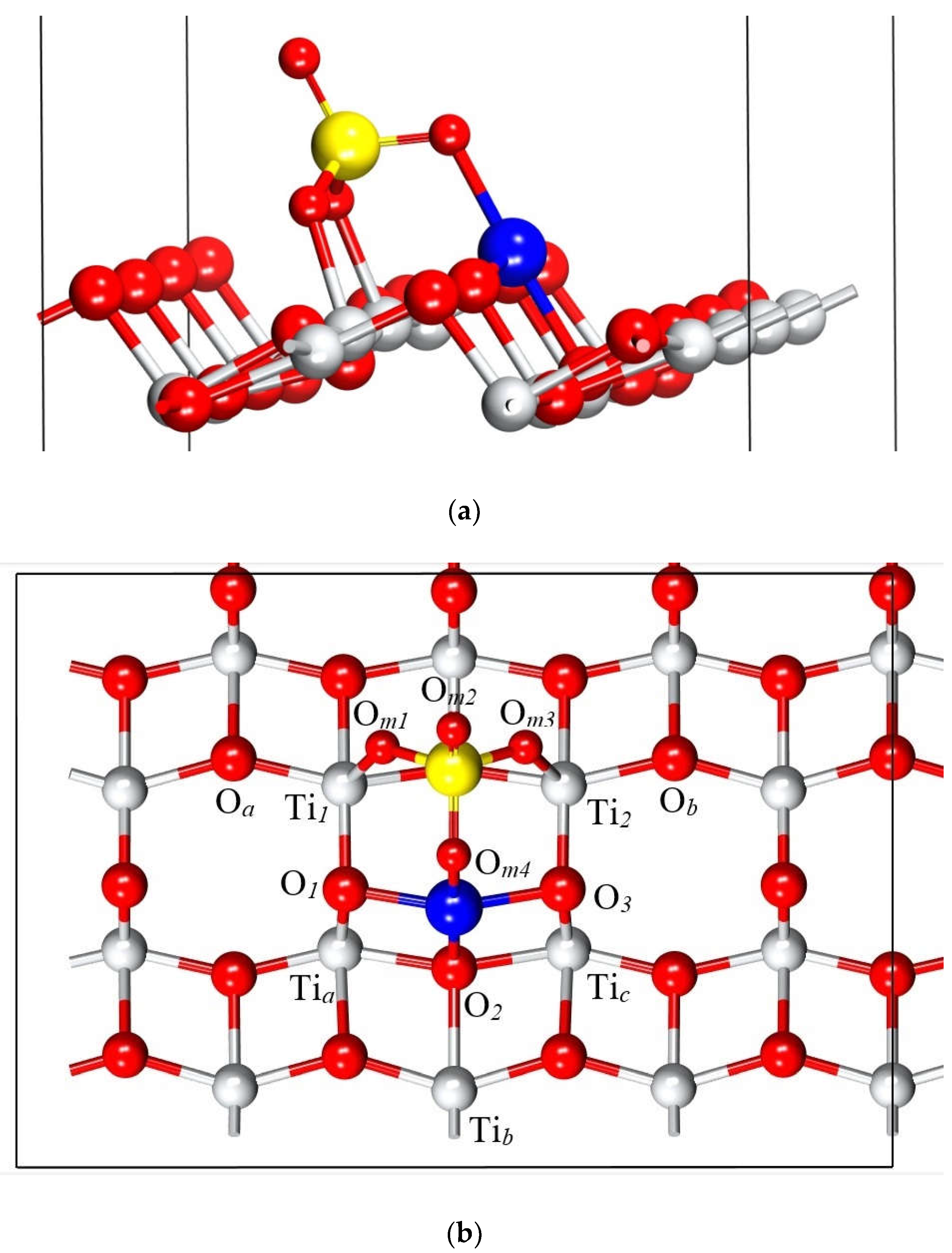
Figure 6 illustrates the resulting structure of the adsorption process, highlighting the formation of bonds between the molecule and the surface, which indicates a chemisorption mechanism. Notably, the molecule binds to the surface through its oxygen and copper atoms. This interaction significantly alters the geometry of both the molecule and the uppermost surface layers, inducing atomic displacements in these regions. To quantify these changes, the interatomic distances and angles of the atoms labelled in Figure 6b were measured and are presented in Table 3. The newly formed bonds are between Om1 and Om3 of the molecule with Ti1 and Ti2on the surface, while the Cu atom interacts with surface oxygen atoms O1, O2, and O3. As a result of this process, the surface atoms tend to displace towards the molecule, predominantly in the upwards direction. Ti1and Ti2 move about 0.13 Å, while O1 and O3 show a minor displacement of 0.03 Å. O2, located in a deeper layer, experiences a more significant displacement of 0.21 Å.
The bond length between the O1 and O2 atoms with the Cu atom is 1.94 Å which is consistent with the 1.95 Å observed in the monoclinic crystal structure of Copper (II) oxide (CuO) [47]. In the case of Om‒Ti bonds measure 2.02 Å, which is close to the experimental within the bulk of 1.98 Å (Table 3) [48].
Atomic charges were calculated using Bader population analysis [49] and are presented in Table 4. The data reveals that atoms that exhibited the most significant changes in atomic charge are those belonging to the molecule. This observation is consistent with the fact that the molecule receives a net charge of 0.11 e from the surface. Furthermore, Table 4 also demonstrates that atoms directly involved in bond formation experience an increase in their net atomic charge, suggesting an ionic character to these chemical bonds.
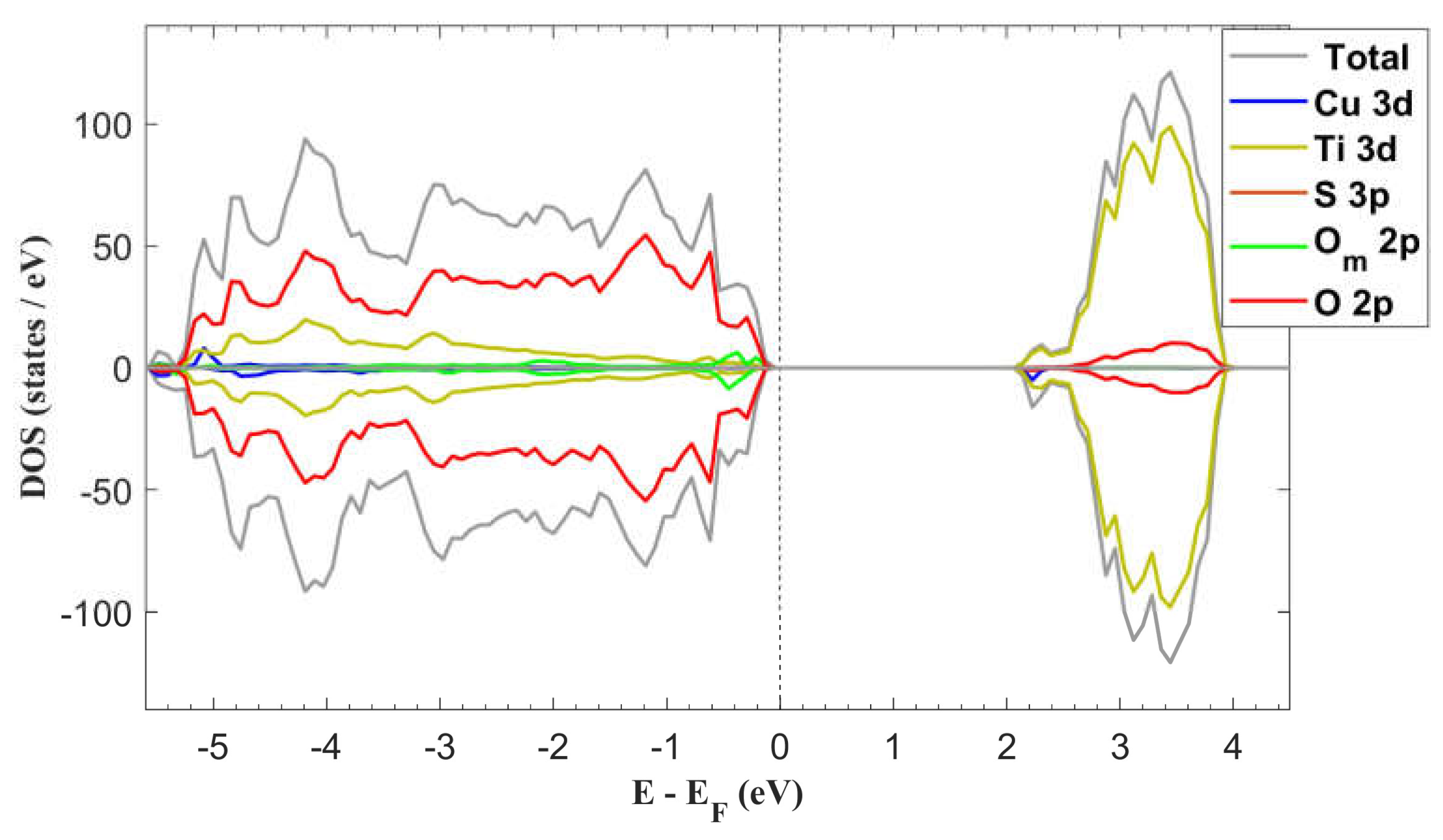
The computed DOS of the system with the adsorbed molecule is presented in Figure 7. Analysis of this data reveals a band gap width of 2.19 eV, which is narrower than the 2.27 eV observed for the pristine surface. Regarding the band’s composition it can be noticed that the VB exhibits some minor presence of O 2p and Cu 3d states from the molecule. Sulphur states are also present at deep energy levels within the VB, but their intensity is very small and thus not distinguishable in the graph.
The DOS exhibits asymmetrical contributions from the molecular atomic states, resulting in an induced magnetic moment within the system. Following the adsorption process, the total magnetic moment measures 0.97 µB, arising from both the molecule and its interacting surface atoms. The predominant contribution comes from the Cu 3d states at 0.72 µB, while the Ti 3d and O 2p states contribute 0.02 µB and 0.23 µB, respectively.
The induced magnetic moment coupled with bandgap narrowing, could alter the optical absorption properties of the material and potentially enhance the catalytic performance. This phenomenon aligns with previous experimental observations, including the favorable influence of CuSO4 on the catalytic activity observed in [25] and the reported photoexcitation under blue light irradiation [26]. While these studies attribute enhanced activity to the formation of intermediate energy levels within the bandgap, our computational analysis suggests that the effect primarily originates from bandgap narrowing.

4. Conclusions

This study presents a first-principles analysis of CuSO4 adsorption on the anatase TiO2 (101) surface, employing density functional theory (DFT) calculations. The key findings are as follows:
(1) Adsorption geometry: A preferential adsorption pattern was identified, characterized by the lowest adsorption energy of -4.31 eV. This configuration was consistently obtained regardless of the initial approach of the molecule to the surface, suggesting its prevalence in real samples.
(2) Adsorption Mechanism: The substantial adsorption energy and the formation of new chemical bonds between CuSO4 and the TiO2 surface provide strong evidence for a chemisorption process.
(3) Charge Transfer: Atomic charge analysis reveals a net charge transfer from the TiO2 surface to the CuSO4 molecule. Atoms directly involved in forming new chemical bonds exhibit increased net atomic charges, indicating the ionic nature of these bonds.
(4) Electronic Structure Modification: The adsorption process induces a magnetic moment and a slight reduction in the bandwidth. These electronic structure alterations are expected to impact on the electronic and catalytic properties of the material.

Author Contributions

Conceptualization, F.M., D.C., A.S., S. A. and J.C.; methodology, F..M., D.C., S.A; software, F.M.; validation, S.A., J.C. and A.S.; formal analysis, D.C, F.M, S.A..; investigation, F.M., D.C., A.S., S. A. and J.C.; writing—original draft preparation, F.M., D.C., A.S., S. A. and J.C.; X.X.; writing—review and editing, F.M., D.C., A.S., S. A. and J.C.; funding acquisition, D.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

n/a.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Pastorino, P.; Prearo, M. High-mountain lakes, indicators of global change: Ecological characterization and environmental pressures. Diversity 2020, 12, 260. [Google Scholar] [CrossRef]
  2. Wang, X.; Wang, C.; Zhu, T.; Gong, P.; Fu, J.; Cong, Z. Persistent organic pollutants in the polar regions and the Tibetan Plateau: A review of current knowledge and future prospects. Environ. Pollut. 2019, 248, 191–208. [Google Scholar] [CrossRef] [PubMed]
  3. Vergragt, P.; Akenji, L.; Dewick, P. Sustainable production, consumption, and livelihoods: Global and regional research perspectives. J. Clean. Prod. 2014, 63, 1–12. [Google Scholar] [CrossRef]
  4. Ren, G.; Han, H.; Wang, Y.; Liu, S.; Zhao, J.; Meng, X.; Li, Z. Recent advances of photocatalytic application in water treatment: A review. Nanomaterials 2021, 11, 1804. [Google Scholar] [CrossRef]
  5. López, M.C.; Fernández, M.I.; Martínez, C.; Santaballa, J.A. Photochemistry for pollution abatement. Pure Appl. Chem. 2013, 85, 1437–1449. [Google Scholar] [CrossRef]
  6. Stashans, A.; Marcillo, F.; Castillo, D. Dopamine adsorption configurations on anatase (101) surface. Surf. Rev. Lett. 2015, 22, 1550052. [Google Scholar] [CrossRef]
  7. Castillo, D.; Ontaneda, J.; Stashans, A. Geometry of dopamine adsorption on rutile (110) surface. Int. J. Mod. Phys. B 2014, 28, 1450071. [Google Scholar] [CrossRef]
  8. Grätzel, M. Dye-sensitized solar cells. J. Photochem. Photobiol. C Photochem. Rev. 2003, 4, 145–153. [Google Scholar] [CrossRef]
  9. Yan, L.; Du, J.; Jing, C. How TiO2 facets determine arsenic adsorption and photooxidation: Spectroscopic and DFT studies. Catal. Sci. Technol. 2016, 6, 1526–1538. [Google Scholar] [CrossRef]
  10. Eddy, D.R.; Permana, M.D.; Sakti, L.K.; Sheha, G.A.N.; Solihudin; Hidayat, S.; Takei, T.; Kumada, N.; Rahayu, I. Heterophase polymorph of TiO2 (Anatase, Rutile, Brookite, TiO2 (B)) for efficient photocatalyst: Fabrication and activity. Nanomaterials 2023, 13, 704. [Google Scholar] [CrossRef]
  11. Gao, J.; Jia, S.; Liu, J.; Yang, X.; Chen, Z.; Wang, X. Enhanced effect of adsorption and photocatalytics by TiO2 nanoparticles embedded porous PVDF nanofiber scaffolds. J. Mater. Res. 2021, 36, 1538–1548. [Google Scholar] [CrossRef]
  12. Li, Y.; Gao, Y. Interplay between water and TiO2 anatase (101) surface with subsurface oxygen vacancy. Phys. Rev. Lett. 2014, 112, 206101. [Google Scholar] [CrossRef]
  13. Liu, L.; Li, K.; Chen, X.; Liang, X.; Zheng, Y.; Li, L. Amino acid adsorption on anatase (101) surface at vacuum and aqueous solution: A density functional study. J. Mol. Model. 2018, 24, 107. [Google Scholar] [CrossRef]
  14. Hengerer, R.; Bolliger, B.; Erbudak, M.; Grätzel, M. Structure and stability of the anatase TiO2 (101) and (001) surfaces. Surf. Sci. 2000, 460, 162–169. [Google Scholar] [CrossRef]
  15. Diebold, U. Structure and properties of TiO2 surfaces: A brief review. Appl. Phys. A 2003, 76, 681–687. [Google Scholar] [CrossRef]
  16. Sakar, M.; Prakash, R.M.; Do, T.-O. Insights into the TiO2-based photocatalytic systems and their mechanisms. Catalysts 2019, 9, 680. [Google Scholar] [CrossRef]
  17. Irfan, F.; Tanveer, M.U.; Moiz, M.A.; Husain, S.W.; Ramzan, M. TiO2 as an effective photocatalyst mechanisms, applications, and dopants: A review. Eur. Phys. J. B 2022, 95, 184. [Google Scholar] [CrossRef]
  18. Degefu, D.M.; Liao, Z. Photocatalytic degradation of volatile organic compounds using nanocomposite of P-type and N-type transition metal semiconductors. J. Sol-Gel Sci. Technol. 2021, 98, 605–614. [Google Scholar] [CrossRef]
  19. Xing, M.; Wu, Y.; Zhang, J.; Chen, F. Effect of synergy on the visible light activity of B, N and Fe co-doped TiO2 for the degradation of MO. Nanoscale 2010, 2, 1233–1239. [Google Scholar] [CrossRef]
  20. Liu, M.; Piao, L.; Lu, W.; Ju, S.; Zhao, L.; Zhou, C.; Li, H.; Wang, W. Flower-like TiO2 nanostructures with exposed {001} facets: Facile synthesis and enhanced photocatalysis. Nanoscale 2010, 2, 1115–1117. [Google Scholar] [CrossRef]
  21. Zhang, P.; Shao, C.; Zhang, Z.; Zhang, M.; Mu, J.; Guo, Z.; Liu, Y. TiO2@carbon core/shell nanofibers: Controllable preparation and enhanced visible photocatalytic properties. Nanoscale 2011, 3, 2943–2949. [Google Scholar] [CrossRef] [PubMed]
  22. Luan, Y.; Jing, L.; Xie, Y.; Sun, X.; Feng, Y.; Fu, H. Exceptional photocatalytic activity of 001-facet-exposed TiO2 mainly depending on enhanced adsorbed oxygen by residual hydrogen fluoride. ACS Catal. 2013, 3, 1378–1385. [Google Scholar] [CrossRef]
  23. Jagminas, A.; Ramanavičius, S.; Jasulaitiene, V.; Šimėnas, M. Hydrothermal synthesis and characterization of nanostructured titanium monoxide films. RSC Adv. 2019, 9, 40727–40735. [Google Scholar] [CrossRef] [PubMed]
  24. Domaschke, M.; Zhou, X.; Wergen, L.; Romeis, S.; Miehlich, M.E.; Meyer, K.; Peukert, W.; Schmuki, P. Magnéli-phases in anatase strongly promote cocatalyst free photocatalytic hydrogen evolution. ACS Catal. 2019, 9, 3627–3632. [Google Scholar] [CrossRef]
  25. Yu, Y.; Miao, J.; Wang, J.; He, C.; Chen, J. Facile synthesis of CuSO4/TiO2 catalysts with superior activity and SO2 tolerance for NH3-SCR: Physicochemical properties and reaction mechanism. Catal. Sci. Technol. 2017, 7, 1590–1601. [Google Scholar] [CrossRef]
  26. Luna, M.D.G.; Garcia-Segura, S.; Mercado, C.H.; Lin, Y.-T.; Lu, M.-C. Doping TiO2 with CuSO4 enhances visible light photocatalytic activity for organic pollutant degradation. Environ. Sci. Pollut. Res. 2020, 27, 24604–24613. [Google Scholar] [CrossRef]
  27. Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
  28. Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
  29. Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671. [Google Scholar] [CrossRef]
  30. Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
  31. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
  32. Dudarev, S.; Botton, G.; Savrasov, S.; Humphreys, C.; Sutton, A. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study. Phys. Rev. B 1998, 57, 1505. [Google Scholar] [CrossRef]
  33. Liechtenstein, A.; Anisimov, V.; Zaanen, J. Density-functional theory and strong interactions: Orbital ordering in Mott-Hubbard insulators. Phys. Rev. B 1995, 52, R5467. [Google Scholar] [CrossRef]
  34. Stashans, A.; Bravo, Y. Large hole polarons in Sc-doped TiO2 crystals. Mod. Phys. Lett. B 2013, 27, 1350113. [Google Scholar] [CrossRef]
  35. Mishra, A.K.; Roldan, A.; de Leeuw, N.H. CuO Surfaces and CO2 Activation: A Dispersion-Corrected DFT+U Study. J. Phys. Chem. C 2016, 120, 2198–2214. [Google Scholar] [CrossRef]
  36. Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
  37. Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
  38. Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
  39. Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
  40. Neugebauer, J.; Scheffler, M. Adsorbate-substrate and adsorbate-adsorbate interactions of Na and K adlayers on Al (111). Phys. Rev. B 1992, 46, 16067. [Google Scholar] [CrossRef]
  41. Makov, G.; Payne, M. Periodic boundary conditions in ab initio calculations. Phys. Rev. B 1995, 51, 4014. [Google Scholar] [CrossRef]
  42. Rafique, M.; Shuai, Y.; Hassan, M. Structural, electronic and optical properties of CO adsorbed on the defective anatase TiO2 (101) surface; A DFT study. J. Mol. Struct. 2017, 1142, 11–17. [Google Scholar] [CrossRef]
  43. Liu, Q.-L.; Zhao, Z.-Y. DFT study on microstructures and electronic structures of Pt mono-/bi-doped anatase TiO2 (101) surface. RSC Adv. 2015, 5, 17984–17992. [Google Scholar] [CrossRef]
  44. Wildner, M.; Giester, G. Crystal structure refinements of synthetic chalcocyanite (CuSO4) and zincosite (ZnSO4). Miner. Petrol. 1988, 39, 201–209. [Google Scholar]
  45. Diebold, U. The surface science of titanium dioxide. Surf. Sci. Rep. 2003, 48, 53–229. [Google Scholar] [CrossRef]
  46. Lazzeri, M.; Vittadini, A.; Selloni, A. Structure and energetics of stoichiometric TiO2 anatase surfaces. Phys. Rev. B 2001, 63, 155409. [Google Scholar] [CrossRef]
  47. Marabelli, F.; Parravicini, G.B.; Salghetti-Drioli, F. Optical gap of CuO. Phys. Rev. B 1995, 52, 1433–1436. [Google Scholar] [CrossRef]
  48. Burdett, J.K.; Hughbanks, T.; Miller, G.J.; Richardson, J.W.; Smith, J.V. Structural electronic relationships in inorganic solids: powder neutron diffraction studies of the rutile and anatase polymorphs of titanium dioxide at 15 and 295 K, J. Am. Chem. Soc. 1987, 109, 3639–3646. [Google Scholar] [CrossRef]
  49. Henkelman, G.; Arnaldsson, A.; Jonsson, H. A Fast and Robust Algorithm for Bader Decomposition of Charge Density. Comput. Mater. Sci. 2006, 36, 354–360. [Google Scholar] [CrossRef]
Preprints 149334 g001
Figure 1. TiO2 anatase (101) surface structure. Red and grey spheres represent O and Ti atoms.
Figure 1. TiO2 anatase (101) surface structure. Red and grey spheres represent O and Ti atoms.
Preprints 149334 g001
Preprints 149334 g002
Figure 2. DFT+U total DOS and partial DOS (PDOS) of anatase TiO2 (101) surface. The bandgap with is 2.27 eV.
Figure 2. DFT+U total DOS and partial DOS (PDOS) of anatase TiO2 (101) surface. The bandgap with is 2.27 eV.
Preprints 149334 g002
Preprints 149334 g003aPreprints 149334 g003b
Figure 3. CuSO4 molecule structure. (a) Experimental and (b) modelled.
Figure 3. CuSO4 molecule structure. (a) Experimental and (b) modelled.
Preprints 149334 g003aPreprints 149334 g003b
Preprints 149334 g004
Figure 4. Initial adsorption structures of the CuSO4 on the anatase TiO2 (101) surface, prior geometry optimization. Atoms are represented by colored spheres: Cu (blue), S (yellow), O (red), and Ti (grey). For clarity, only the uppermost atoms of the TiO2 surface are displayed.
Figure 4. Initial adsorption structures of the CuSO4 on the anatase TiO2 (101) surface, prior geometry optimization. Atoms are represented by colored spheres: Cu (blue), S (yellow), O (red), and Ti (grey). For clarity, only the uppermost atoms of the TiO2 surface are displayed.
Preprints 149334 g004
Preprints 149334 g005
Figure 5. Adsorption geometry of configuration e: (a) Side and (b) top views. The blue, yellow, red and grey spheres represent atoms of Cu, S, O and Ti, respectively.
Figure 5. Adsorption geometry of configuration e: (a) Side and (b) top views. The blue, yellow, red and grey spheres represent atoms of Cu, S, O and Ti, respectively.
Preprints 149334 g005
Preprints 149334 g006
Figure 6. Most favorable adsorption geometry of CuSO4 on the anatase TiO2 (101) surface: (a) Side and (b) top views. The blue, yellow, red, and white spheres represent atoms of Cu, S, O, and Ti, respectively.
Figure 6. Most favorable adsorption geometry of CuSO4 on the anatase TiO2 (101) surface: (a) Side and (b) top views. The blue, yellow, red, and white spheres represent atoms of Cu, S, O, and Ti, respectively.
Preprints 149334 g006
Preprints 149334 g007
Figure 7. Total DOS and partial DOS (PDOS) of anatase TiO2 (101) surface with one adsorbed molecule. The corresponding band gap width is 2.19 eV.
Figure 7. Total DOS and partial DOS (PDOS) of anatase TiO2 (101) surface with one adsorbed molecule. The corresponding band gap width is 2.19 eV.
Preprints 149334 g007
Table 1. Interatomic distances and relevant angles of the CuSO4 molecule comparing the experimental [44] and the modelled structures.
Table 1. Interatomic distances and relevant angles of the CuSO4 molecule comparing the experimental [44] and the modelled structures.
Distance (Å) Angle (°)
Atoms Exp. Modelled Atoms Exp. Modelled
S ̶ Om1 1.46 1.44 S ̶ Om4 ̶ Cu 123.44 94.04
S ̶ Om2 1.46 1.60 Om1 ̶ S ̶ Om3 110.52 119.39
S ̶ Om3 1.46 1.44
S ̶ Om4 1.52 1.60
Cu ̶ Om4 2.04 1.85
Cu ̶ Om3 3.71 3.46
Cu ̶ Om2 3.25 1.85
Cu ̶ Om1 4.33 3.51
Table 2. Computed adsorption energies.
Table 2. Computed adsorption energies.
Configuration Eads (eV)
a –2.06
b –4.31
c –1.25
d –4.31
e –4.00
f –4.31
g –2.67
Table 3. Interatomic distances and relevant angles for the pristine surface and the surface with the adsorbate. Atoms labels adhere to the notation established in Figure 6b.
Table 3. Interatomic distances and relevant angles for the pristine surface and the surface with the adsorbate. Atoms labels adhere to the notation established in Figure 6b.
Bond length (Å) Angle (°)
Atoms Free
molecule		 Adsorbed molecule Atoms Free
molecule		 Adsorbed molecule
S ̶ Om1 1.45 1.53 Ti1 ̶ Om1 ̶ S ̶ 132.57
S ̶ Om2 1.57 1.42 S ̶ Om3 ̶ Ti2 ̶ 132.62
S ̶ Om3 1.45 1.53 S ̶ Om4 ̶ Cu 93.82 112.29
S ̶ Om4 1.57 1.51 Om1 ̶ S ̶ Om3 116.04 107.58
Cu ̶ Om4 1.91 1.92
Atoms Pristine surface Adsorbed molecule Atoms Pristine surface Adsorbed molecule
Om1 ̶ Ti1 ̶ 2.02 Oa ̶ Ti1 ̶ Om1 ̶ 102.16
Om3 ̶ Ti2 ̶ 2.02 Om3 ̶ Ti2 ̶ Ob ̶ 102.24
Ti1 ̶ Oa 1.98 1.97 Ti1 ̶ O1 ̶ Tia 100.96 101.53
Ti2 ̶ Ob 1.98 1.97 Ti2 ̶ O3 ̶ Tic 100.96 101.52
Cu ̶ O1 ̶ 1.94 Tia ̶ O2 ̶ Tic 155.23 152.98
Cu ̶ O2 ̶ 2.02 Cu ̶ O2 ̶ Tib ̶ 108.19
Cu ̶ O3 ̶ 1.94
O1 ̶ Tia 1.94 1.96
O2 ̶ Tib 2.06 2.16
O3 ̶ Tic 1.94 1.96
Table 4. Atomic charges of the atoms labelled in Figure 6b.
Table 4. Atomic charges of the atoms labelled in Figure 6b.
Atomic charge (e)
Atom Free molecule Adsorbed molecule
Cu 1.00 1.14
S 4.20 3.77
Om1 –1.24 –1.26
Om2 –0.85 –1.27
Om3 –1.68 –1.26
Om4 –1.43 –1.23
Atom Pristine surface Adsorbed molecule
Ti1 2.26 2.32
Ti2 2.26 2.32
Tia 2.30 2.30
Tib 2.26 2.24
Tic 2.30 2.30
O1 –1.03 –1.09
O2 –1.18 –1.23
O3 –1.03 –1.09
Oa –1.20 –1.19
Ob –1.20 –1.19
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

39

Views

28

Comments

0

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

Email

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated