Numerical Method to Obtain the Resistance of Reinforced Concrete and Composite Steel Concrete Sections Subjected to Axial Forces and Biaxial Bending Based on Simplex (Linear Programming)

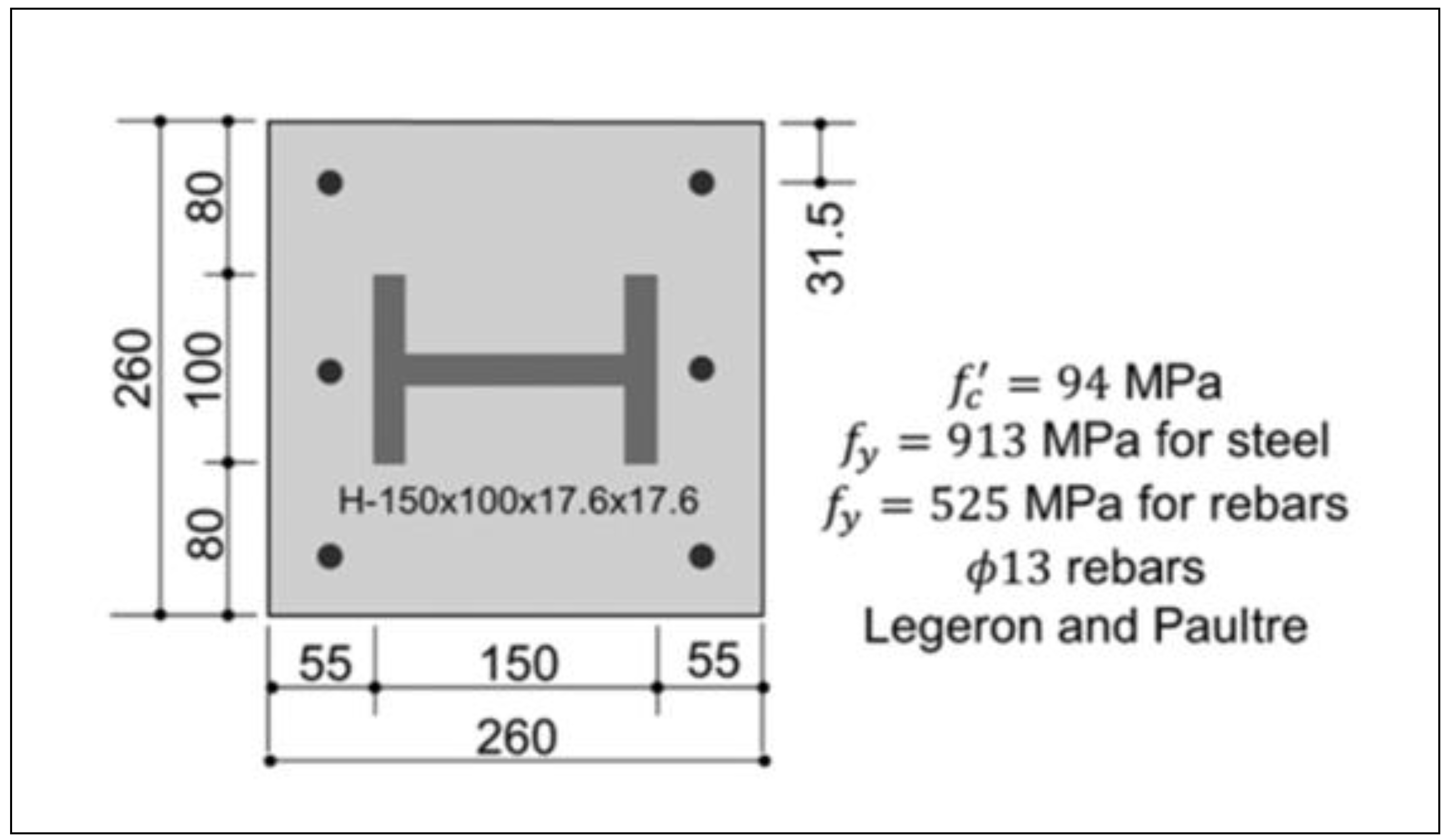
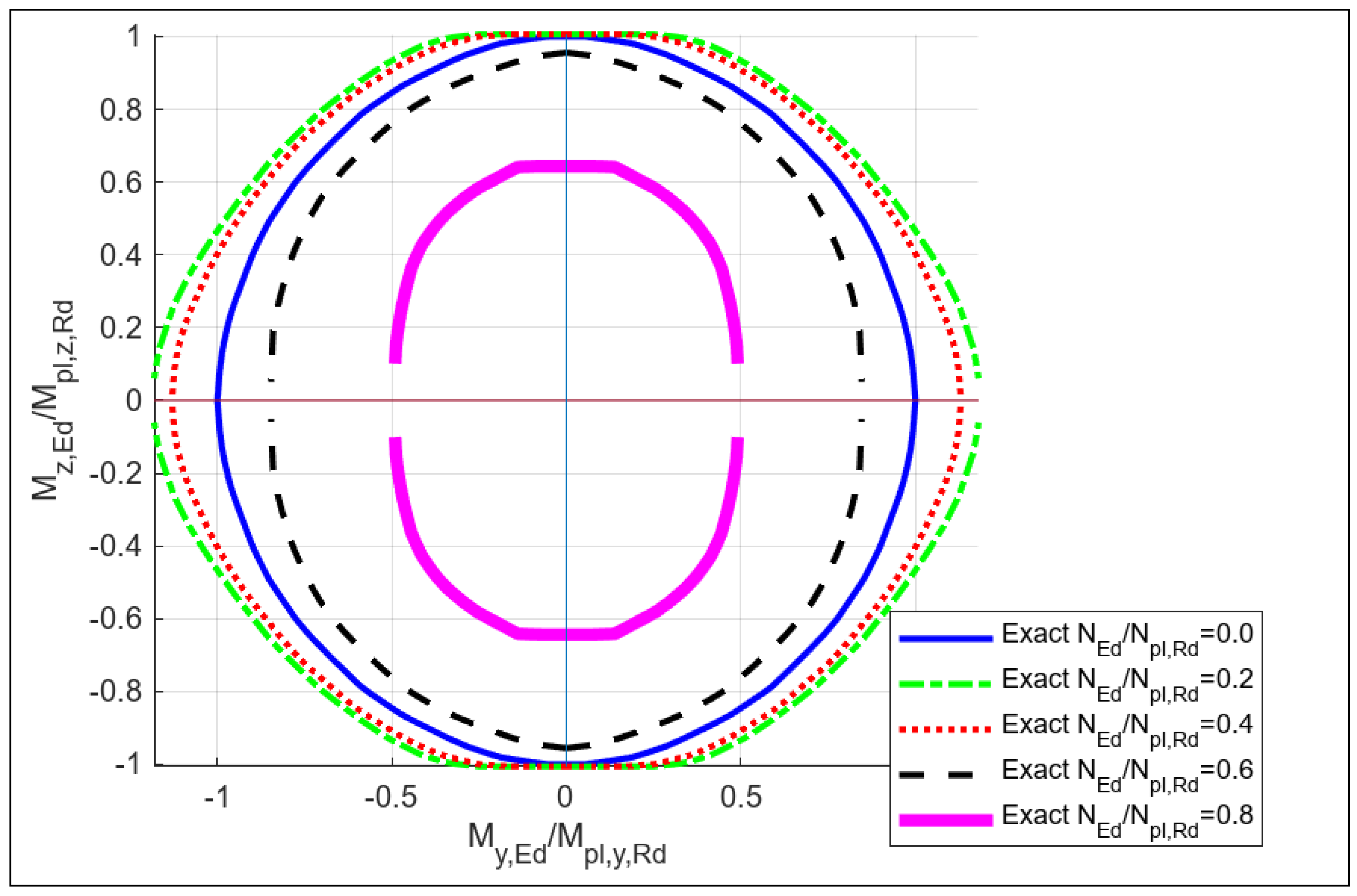
1. Introduction

Designing cross sections of reinforced concrete is a routine task in structural engineering and typically involves structures such as reinforced concrete buildings, bridges, and underground constructions. Cross sections come in various shapes, and when combined with bending moments acting on both axes simultaneously along with axial force, this makes the design a highly non-linear problem.

Using computer programs to design reinforced concrete cross sections is now standard practice. Bentz [1] discusses how a computer application can handle reinforced concrete sections of any shape, including any placement of reinforcement bars. Papanikolao [2] emphasizes that the algorithm used to determine the ultimate strength of various cross sections, as well as the material constitutive laws, line subdivision, and stress integration methods, are key elements of these algorithms.

Regarding the material constitutive laws for concrete in compression, Eurocode 2 defines concrete in compression as parabolic-linear for designing reinforced concrete cross sections (clause 3.1.7), and this relationship is followed in this study. Rosati et al. [3] also use parabolic-linear behavior for concrete. Papanikolaou [2] explores the impact of using completely arbitrary material laws for concrete in compression.

The efficiency of algorithms largely depends on how the section is subdivided and the stress integration method. Charalampakis and Koumousis [4] divide any section using curvilinear trapezoids and employ closed-form solutions to compute internal forces, achieving exact results. Sfakianakis [5] suggests computing internal forces without subdividing the section, using fiber integration, though this may yield approximate results based on mesh division. Dias da Silva et al. [6] apply a closed-form algorithm for multi-rectangular sections followed by Gauss–Legendre integration, showing that closed-form solutions are preferred for computational efficiency. Rodriguez and Aristizabal-Ochoa [7] propose an algorithm that subdivides sections into polygons and performs closed-form integration per polygon. Pallarès et al. [8] perform closed-form integration without section subdivision, while De Vivo and Rosati [9] introduce an integration scheme using boundary integrals.

This paper introduces a new approach that uses fibre section model combined with simplex (linear programming).

2. Analysis of Plastic Resistance of Different Sections

The static or lower bound theorem is applied. The equilibrium and plastic condition are satisfied in order to achieve plastification factor equal or smaller than the plastic one.

The following method has been implemented in a computer program.

The Software can be found in the following blog:

https://antonioagueroramonllin.blogs.upv.es/

Section with Fibers NMyMz:

https://laboratoriosvirtuales.upv.es/webapps/sectionfibersNMyMz.html

2.1. Method to Obtain Plastic Parameters

The following tables explain how to obtain the plastic resistance. The cross section is divided into n fibers of Area A(i), coordinates y(i),z(i) of its centroid. The normal stress σ(i) values at each fiber are optimized to maximize the different linear functions in the tables with the corresponding linear constraints, this problema can be solved using simplex (Linear programming).

Case 1: Computation of plastic parameters:

Maximize	$N={\displaystyle \sum _{i=1}^n}A\left(i\right)\sigma \left(i\right)$	$My={\displaystyle \sum _{i=1}^n}z\left(i\right)A\left(i\right)\sigma \left(i\right)$	$Mz=-{\displaystyle \sum _{i=1}^n}y\left(i\right)A\left(i\right)\sigma \left(i\right)$
Constraints	$My={\displaystyle \sum _{i=1}^n}z\left(i\right)A\left(i\right)\sigma \left(i\right)=0$	$N={\displaystyle \sum _{i=1}^n}A\left(i\right)\sigma \left(i\right)=0$	$My={\displaystyle \sum _{i=1}^n}z\left(i\right)A\left(i\right)\sigma \left(i\right)=0$
	$Mz=-{\displaystyle \sum _{i=1}^n}y\left(i\right)A\left(i\right)\sigma \left(i\right)=0$	$Mz=-{\displaystyle \sum _{i=1}^n}y\left(i\right)A\left(i\right)\sigma \left(i\right)=0$	$N={\displaystyle \sum _{i=1}^n}A\left(i\right)\sigma \left(i\right)=0$
	$-fy<\sigma \left(i\right)<fy$ Steel $-fc<\sigma \left(i\right)<0$ concrete

Case 2: Computation of plastic parameters maximum:

Maximize	$N={\displaystyle \sum _{i=1}^n}A\left(i\right)\sigma \left(i\right)$	$My={\displaystyle \sum _{i=1}^n}z\left(i\right)A\left(i\right)\sigma \left(i\right)$	$Mz=-{\displaystyle \sum _{i=1}^n}y\left(i\right)A\left(i\right)\sigma \left(i\right)$
Constraints	$-fy<\sigma \left(i\right)<fy$ Steel $-fc<\sigma \left(i\right)<0$ concrete

2.2. Method to Obtain Interaction Diagram

To obtain the interaction diagram N My Mz, the plastification factor ξ (is the factor by which internal forces must be multiplied to reach the plastic resistance of cross section) can be obtained for each combination in of N1, My1, Mz1 applying the static or lower bound theorem:

Maximize	ξ
constraint	$N={\displaystyle \sum _{i=1}^n}A\left(i\right)\sigma \left(i\right)=\mathrm{N}1$
	$My={\displaystyle \sum _{i=1}^n}z\left(i\right)A\left(i\right)\sigma \left(i\right)=\mathrm{M}\mathrm{y}1$
	$Mz=-{\displaystyle \sum _{i=1}^n}y\left(i\right)A\left(i\right)\sigma \left(i\right)=\mathrm{M}\mathrm{z}1$
	$-fy<\sigma \left(i\right)<fy$Steel $-fc<\sigma \left(i\right)<0$ concrete

3. Comparison with Experimental Results and Other Authors

3.1. Reinforced Concrete Section

Ppred= Load predicted by the numerical method.

Ptest= Load obtained with the test.

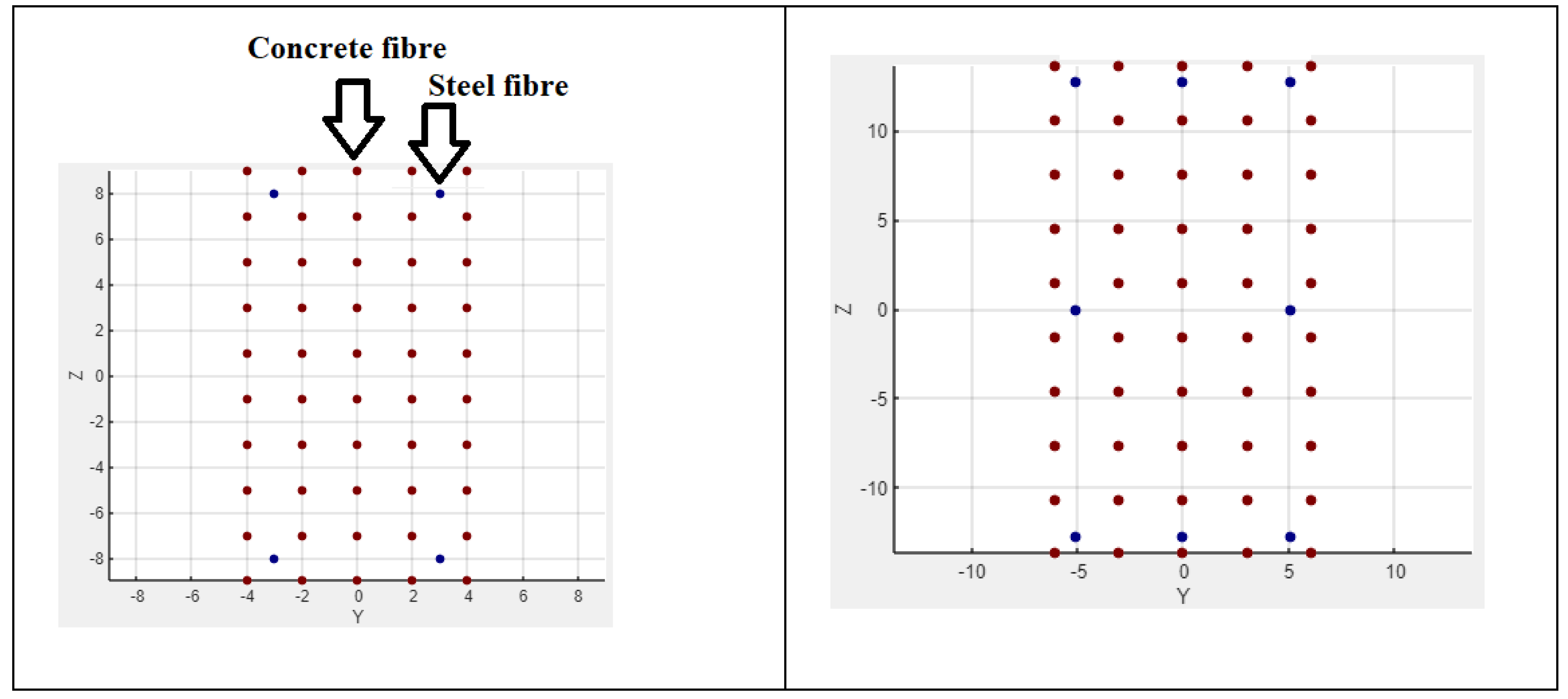
Figure 1. (a) Fibre section Luis Test. (b) Ramamurthy Tests.

Figure 1. (a) Fibre section Luis Test. (b) Ramamurthy Tests.

Luis [8,10] Test.

Test	P (kN)	Ppred/Ptest
		Vaz Rodrigues	Proposal
10_05_3	473	1.15	1.16
10_05_4	175	1.09	1.11
10_1_4	166	1.12	1.108
10_2_2	899	1.17	1.09
10_2_3	436	1.27	1.19
10_2_4	142	1.44	1.264

Ramamurthy [11] Test.

Test	Ppred/Ptest
	Vaz Rodrigues	Proposal
A1	1.06	1.085
A2	0.97	0.994
A3	0.99	1.022
A4	0.96	0.989
A5	0.91	0.921
A6	0.99	1.043
A7	0.92	0.954
A8	1.05	1.074
A9	0.92	0.95
A10	1.08	1.184
A11	1.12	1.26
A12	1.07	1.153
A13	0.94	1.048
A14	0.88	0.929
A15	0.91	1.023
B3	0.94	1.057
B4	0.98	1.109
B6	0.97	1.138
B7	0.88	1.025
B8	0.92	1.075
C6	0.88	1.022
R138	0.83	0.91
R238	0.83	0.886
R338	0.85	0.879
D2	1.08	0.996
D3	1.02	0.93
D5	0.98	1.018
D6	0.85	1.078
E1	1.27	0.82
E2	1.34	0.843
E3	1.2	0.978
E4	1.11	1.195
F2	1.41	1.224
F4	1.4	1.249
F5	1.17	1.159
G2	1.21	0.881
G3	1.42	1.138
G4	1.29	1.016

Mean Value	Proposal	Vaz Rodrigues
Luis Tests	1.1537	1.2067
Ramamurthy Tests	1.033	1.0421

Standard deviation Value	Proposal	Vaz Rodrigues
Luis Tests	0.0657	0.1297
Ramamurthy Tests	0.1129	0.1698

4. Examples of Interaction Diagram

Interaction diagram Luis test and Rama. Test A1…

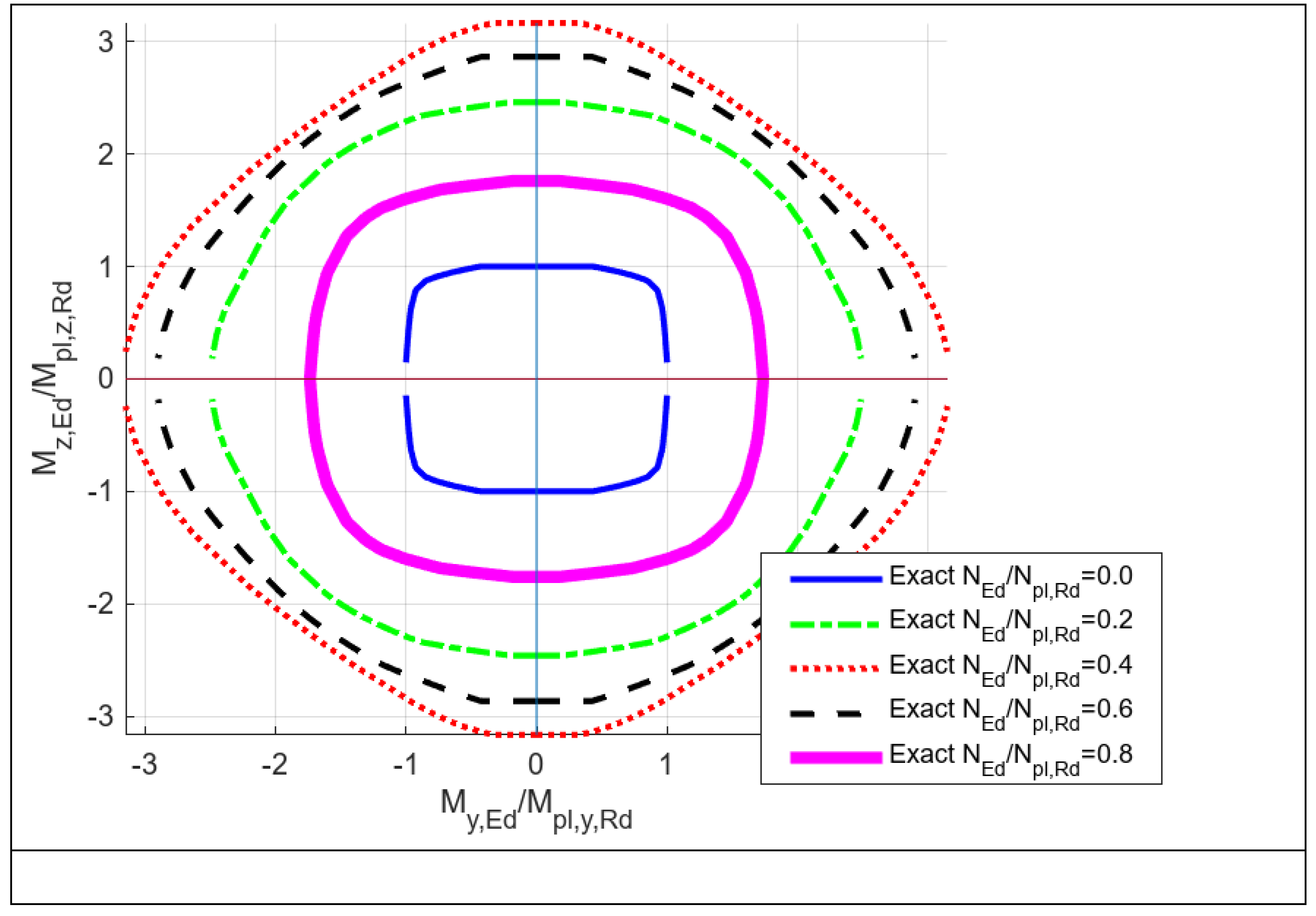
Figure 2. Luis Test interaction diagram.

Figure 2. Luis Test interaction diagram.

Luis Test:

Units kN,cm

Mypl = -1543.530 Mzpl = -701.205 Npl = -1586.501

Myplmax = -4930.410 Nc = -705.600Mzc = -0.000

Mzplmax = -2219.344 Nc = -846.720Myc = 0.000

Nplmax = -1586.501 Mzc = -0.000Myc = 0.000

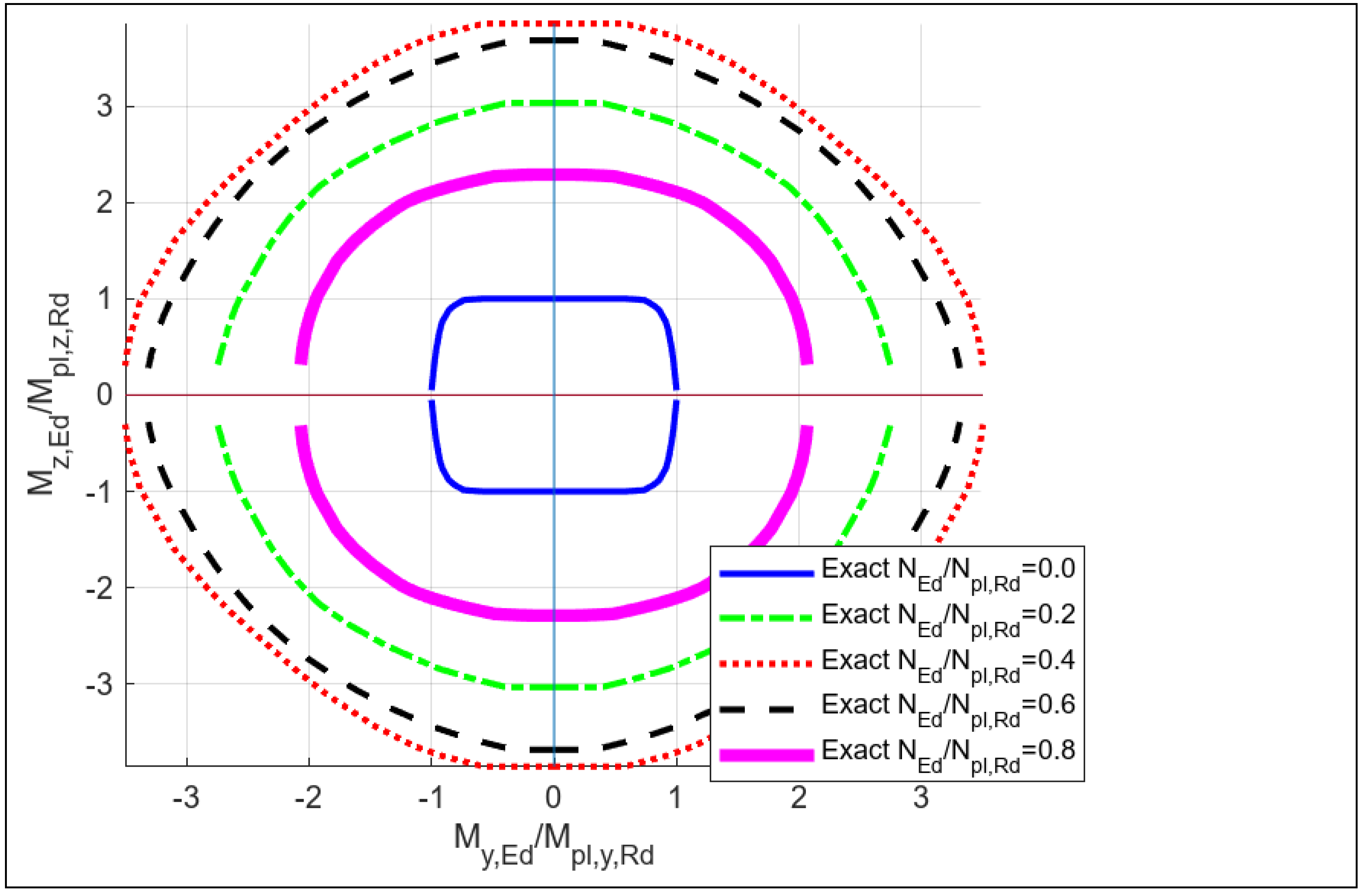
Figure 3. Ramamurthy Test A1 to A15 interaction diagram.

Figure 3. Ramamurthy Test A1 to A15 interaction diagram.

Ramamurthy Test A1-A15

Mypl = -6133.744 Mzpl = -2770.356 Npl = -2423.834

Myplmax = -11914.623 Nc = -1095.302Mzc = -0.000

Mzplmax = -5370.853 Nc = -1291.040Myc = -0.000

Nplmax = -2423.834 Mzc = 0.000Myc = -0.000

Interaction diagram composite section

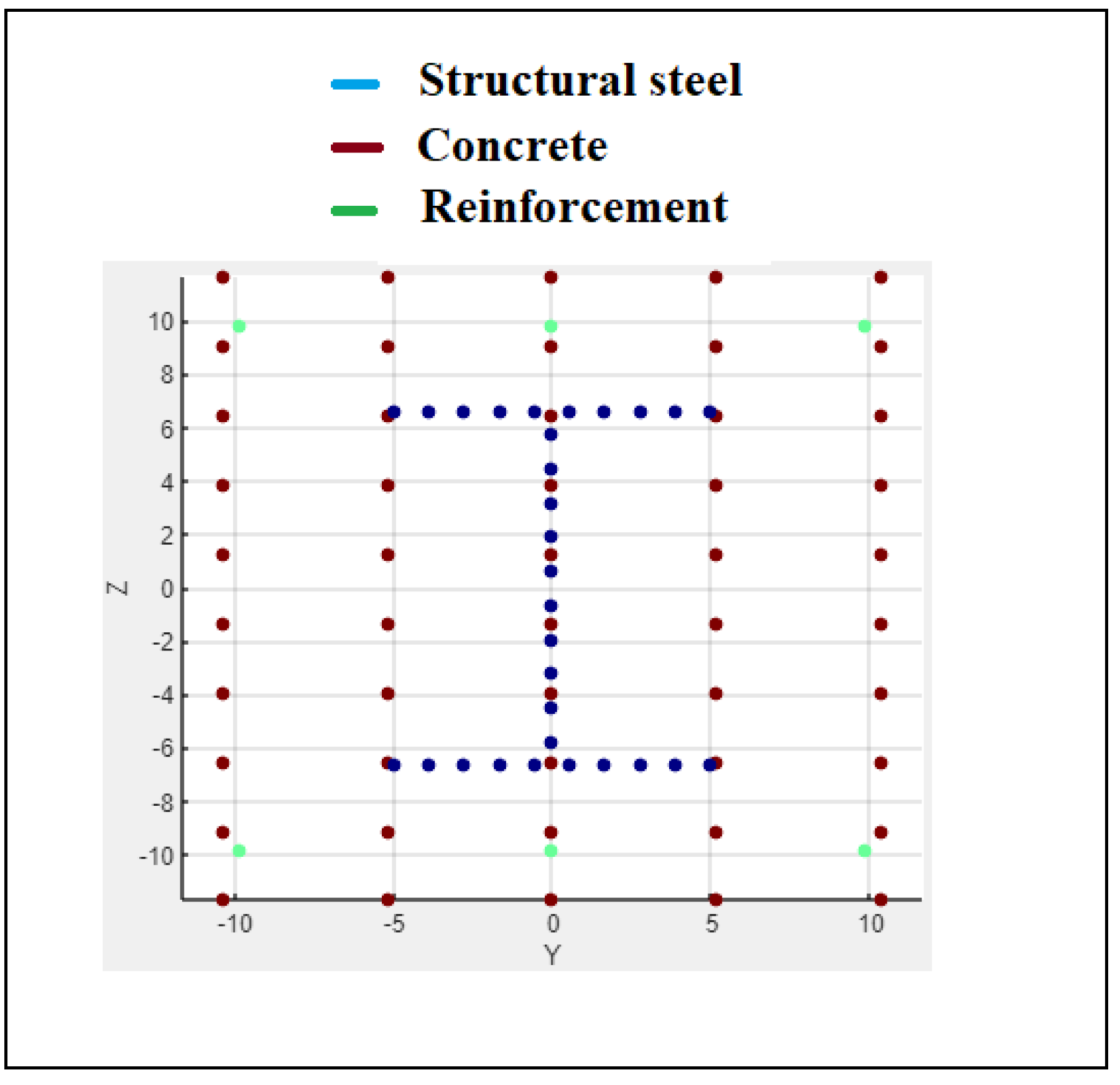
Figure 4. Composite section fiber model.

Figure 4. Composite section fiber model.

Figure 5. Composite section real section.

Figure 5. Composite section real section.

Figure 6. Composite section interaction diagram.

Figure 6. Composite section interaction diagram.

Composite 1

Units kN,cm

Mypl = -41746.732 Mzpl = -29347.220 Npl = -11195.526

Myplmax = -49862.610 Nc = -2859.480Mzc = 0.000

Mzplmax = -29515.840 Nc = -5415.443 Myc = 0.000

Nplmax = -11195.526 Mzc = 0.000Myc = -0.000

5. Conclusions

In this paper, we propose a novel algorithm based on the simplex method to calculate the ultimate strength of reinforced concrete and steel concrete composite sections under biaxial bending and axial force. The proposed algorithm is validated by comparing its analytical results with methods suggested by other authors and with experimental results available in the literature.

Further research: To take into account the fire effects at each fiber there Will be a Temperature related to new tensión and compression resistance at Steel fy(i,T) and a new compression resistance in concrete fc(i,T). So the input needed to solve this problema is Temperature map along the cross section, the software by Agüero [12] can be updated.