Prerpints.org logo
Preprint
Article

This version is not peer-reviewed.

A Machine Learning-Driven Geophysical–Geotechnical Approach for Improved Engineering Site Assessment

Submitted:

10 February 2025

Posted:

13 February 2025

You are already at the latest version

Abstract

Subsurface geological formations are vital for validating deep engineering design assumptions, particularly in weathered terrains where unstable ground conditions pose risks. Geophysical investigations often face challenges due to inverse problem uncertainties and inadequate subsurface data. While resistivity and seismic P-wave velocity (Vp) imaging offer valuable insights, subsurface complexity necessitates integrated approaches for reliable characterization. This study introduces a machine learning-assisted geophysical–geotechnical framework combining electrical resistivity tomography, seismic refraction tomography, and borehole-based standard penetration tests (SPT-N). ML optimization metrics, including k-means clustering, PCA, Silhouette, elbow, and supervised linear regression, enhance analytical precision. A field survey over an 800 m segment in Kabota-Tawau, Sabah, Malaysia, utilized 490 collocated resistivity–Vp datasets to optimize cluster identification and interpretation accuracy. The analysis delineated four lithological units based on resistivity and Vp variations correlating with surface-subsurface properties. Clustering demonstrated strong performance, with an R² value approaching 1, a Silhouette score of 0.78, and an 88% reduction in the sum of square errors. Vulnerable zones, including weathered layers, fractures, and faults, were identified as critical for geotechnical consideration. In contrast, relatively weathered bedrock with hard-to-very-hard properties was deemed optimal for deep structural foundations requiring minimal reinforcement. This non-invasive approach enhances subsurface characterization, offering a reliable framework for construction site suitability and groundwater resource identification. It provides significant value for sedimentary regions with similar geological settings, advancing geotechnical and environmental planning.

Keywords: 
Geophysical–geotechnical investigation
;  
statistical correlation
;  
p-wave velocity (Vp) soil penetration test
;  
machine learning (ML)
;  
k-means clustering
;  
supervised regression modeling
Subject: 
Environmental and Earth Sciences  -   Geophysics and Geology

Introduction

Society faces critical challenges that demand innovative solutions to address various geophysical challenges. The challenges lie in showcasing the implications of environmental variability, monitoring and easing polluted air, assessing infrastructure susceptibility to natural and human-induced hazards, analyzing the future accessibility and extraction of water and subsurface minerals, and understanding the underlying factors of ground failures, seismic events, and flooding events [1,2]. Addressing these issues requires an interdisciplinary approach, encompassing physics, geology, hydrology, and other fields that collectively contribute to geosciences. This discipline seeks to unravel the complexities of earth’s systems and their interconnected components [3]. Advancements in statistical evaluation, specifically through ML, are transforming geoscience research by uncovering hidden patterns within vast datasets. ML offers remarkable benefits across multiple domains, enabling breakthroughs that drive impactful innovations [4].
A diverse array of applications, involving neural networks, deep learning, natural language processing, language detection, and computer vision, have significantly profited from the utilization of ML techniques. Various unsupervised machine learning algorithms, including k-means, hierarchical, density-based, and fuzzy-based clustering [5], is proposed as effective means for data analysis, showcasing robust reliability measures. Integrating geoscience approaches with ML enables the resolution of several geophysical challenges, including the identification of surface-subsurface geological structures [6,7,8]. The examination of subsurface soil-rock components shows substantial intricacies and problems in geosciences, particularly due to the complicated and diverse characteristics of their core formations [9]. This occurrence impedes the analysis and comprehension of subsurface data [10,11].
Subsurface assessment provides a comprehensive evaluation of the geological and physical attributes of the earth’s subsurface strata. To accurately comprehend the subsurface’s nature and properties, it is essential to conduct thorough studies and analyses of various geophysical, geological, and geochemical data analyses in the investigated region. Comprehending physical parameters, like the strength, durability, and permeability of subsurface geological structures, is crucial for guaranteeing the safety of engineering operations [3]. Combination of diverse geophysical methodologies, including electrical resistivity tomography (ERT) and seismic refraction tomography (SRT), together with borehole data and machine learning, offers a robust strategy for identifying the spatial variation of physical properties, such as electrical resistivity, conductivity, and seismic velocity [12,13,14], environmental characteristics [15,16], temporal dimensions, and geochemical characteristics [8] of the region under investigation. This multidisciplinary framework enhances the resolution and accuracy of subsurface characterization, enabling a deeper understanding of geological structures and processes. This strategy surpasses the efficacy of using these technologies individually or relying only on traditional measures. By combining these two inversion outputs with machine learning, it may be possible to resolve the uncertainties in the inverse problem and improve our understanding of the subsurface [17].
Utilizing the models of p-wave velocity (Vp) and electrical resistivity (ER) in conjunction with machine learning for subsurface exploration allows for establishing clear relationships between physical and geotechnical properties at specific depths [18,19]. This technique streamlines the subsurface categorization of the explored area through its unique lithology, thereby improving the interpretation of subsurface conditions and enhancing the accuracy of predictions for engineering and environmental applications. The research conducted by [15] examined the correlations between the electrical resistivity tomography and seismic refraction tomography of a significantly weathered swelling mudstone subjected to diverse freezing, thawing, wetting, and drying circumstances. An increase in the frequency of wetting-drying cycles demonstrated a substantial surge in resistivity. Prior research by, [12,20] examined the characteristics of granite by ERT and SRT assessments. The study results revealed a significant improvement in the depiction of some geological features that may have possibly been overlooked or misinterpreted. Furthermore, they used cluster analysis to combine the subsurface images and develop a conceptual subsurface model.
Moreover, the analysis of subsurface soil-rock characteristics in diverse environments has been conducted using Vp and resistivity data, along with machine learning, as shown in earlier research [17,20,21,22]. Akingboye & Bery, (2023) established strong empirical associations between Vp and resistivity in tropical granitic terrains utilizing geotomographic data and supervised statistical modeling. However, the use of machine learning (ML) in geophysical research is still underutilized in areas like Kabota-Tawau, Sabah, Malaysia. This constraint prevents a more comprehensive advancement in the characterization and optimization of both surface and subsurface features. Also, it is important to note that there are not many well-documented empirical correlations between Vp and resistivity, especially in the case of tropical sedimentary terrain.
The application of emerging and increasingly popular technologies in geological studies remains underexplored, yet their potential to enhance and optimize the understanding of surface and subsurface features across diverse environments is immense. This study builds on the foundational works of [17,23] in granitic landscapes and draws partially on the insights of [22] in Malaysia. By leveraging these prior investigations, this research seeks to integrate innovative techniques to decipher the surface-subsurface geology of the study area and establish empirical relationships between Vp and resistivity datasets acquired from the site. This research is particularly significant for developing a robust analytical framework to accurately characterize soil-rock conditions in a cost-efficient manner. The methodology involves two discrete stages: first, inversion and interpolation of the geophysical datasets to identify coincidence positions; second, application of k-means clustering to the resulting extracted datasets from the interpolated mesh models to classify lithologies within the specified area. The analysis further explores correlations between the Vp and resistivity variables to establish their interconnectivity with borehole-based standard penetration test (SPT-N) datasets. SPT-N is a globally recognized subsurface engineering evaluation method widely used to assess soil strength and consistency, offering insights into soil properties such as density, shear strength, and bearing capacity. The proposed methodological framework is expected to significantly enhance the ability to model accurate soil-rock conditions and provide a cost-effective framework for infrastructure designs.

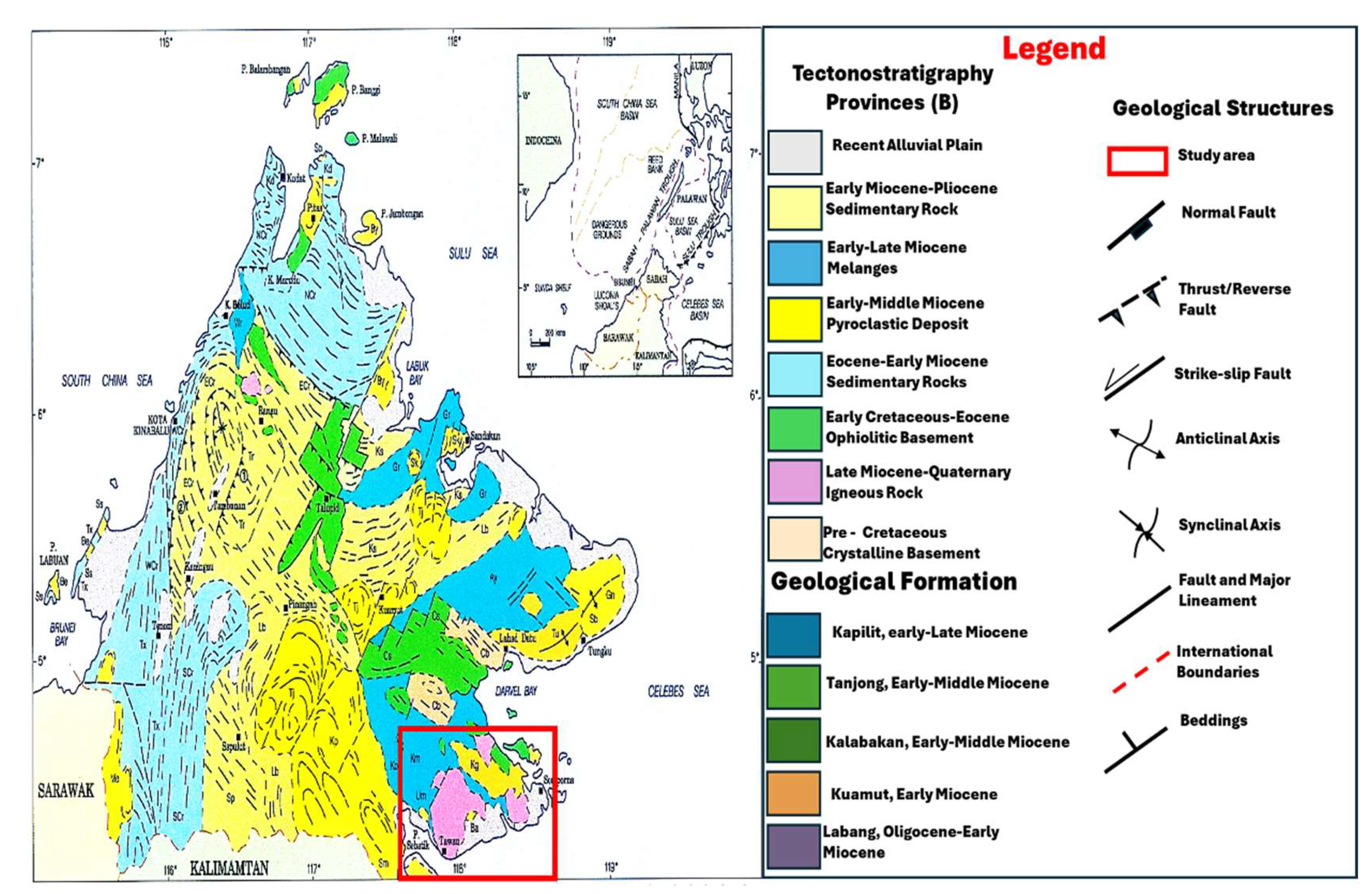
Location and Geology of the Study Area

Kabota-Tawau region of Sabah, the study area located in northern Borneo, is bounded by the South China Sea to the west, the Sulu Sea to the northeast, and the Celebes Sea to the southeast, as illustrated in Figure 1. Positioned in the northeastern area of the island of Borneo, this region holds significant importance. [24]. The intricate tectonic framework of southeast Sabah has revealed a diverse array of lithologies and sedimentary structures, reflecting a variety of depositional environments. These range from continental settings, such as coal deposits, to shallow marine environments characterized by cross-bedded sandstones, and deep marine settings with turbidite formations. However, the fossil content within these rock units is sparse, providing limited biostratigraphic data from foraminifera or macrofossil species. [25].
The northern area of Borneo, Sabah, has an intricate geological past that has significantly influenced its tectonic development [26,27,28]. This region’s rock formations are categorized into five distinct tectonostratigraphic provinces according to age and lithology aas explained in [29]: (i) an ophiolite complex or basement underlying the sedimentary sequences; (ii) sedimentary layers ranging from the Eocene to Lower Miocene; (iii) pyroclastic deposits from the Early to Middle Miocene; (iv) chaotic deposits and mélanges from the Middle Miocene; and (v) shallow marine to fluvial-deltaic sediments from the Early to Late Miocene. The Tawau Hills, a component of Sabah Parks, encompass an area of 280 km² and are located around 25 km northwest of Tawau town. This area has seen several tectonic events since the early Tertiary period [25,30] The principal geological formations in western Sabah are the Crocker Formation and the Rajang Group.

Methodology

The study employed an integrated approach using SRT and ERT to explore the geological characteristics beneath the surface of the study site. Field locations for SRT and ERT data collection were carefully selected to facilitate an extensive evaluation and profiling of lithological strata, including their properties and subsurface attributes. The survey design strategically positioned geophysical profiles near three existing boreholes (BH1, BH2, and BH3), as depicted in the aerial geophysical data acquisition map in Figure 2a. This strategic setup enabled cost-effective and efficient data collection.
The aerial map (Figure 2a) illustrates two Lines, L1, spanning 500 m, and L2, measuring 300 m. These lines were arranged to align spatially with BH1, BH2, and BH3. Traverse 1 (L1) stretches from the northern section of the study area toward its eastern edge, while Traverse 2 (L2) begins at the terminus of L1 and extends southward. BH1 and BH3 were located near L1, whereas BH2 was situated along L2. These boreholes served as constraints for geophysical modeling of the subsurface lithologies and determining the SPT-N of the subsurface soils. The ERT and SRT measurements along L1 and L2 were conducted with respective lengths of 500 m and 300 m (Figure 2b). An electrode spacing (ΔE) and geophone spacing (ΔG) of 5.0 m were maintained for optimal resolution (Figure 2b). The configurations of the ERT and SRT traverses are represented by blue and red lines, respectively, in the map, providing a clear visualization of the survey layout. This integrated approach facilitated a detailed subsurface investigation, enhancing the interpretation of lithological and geotechnical properties in the research region.

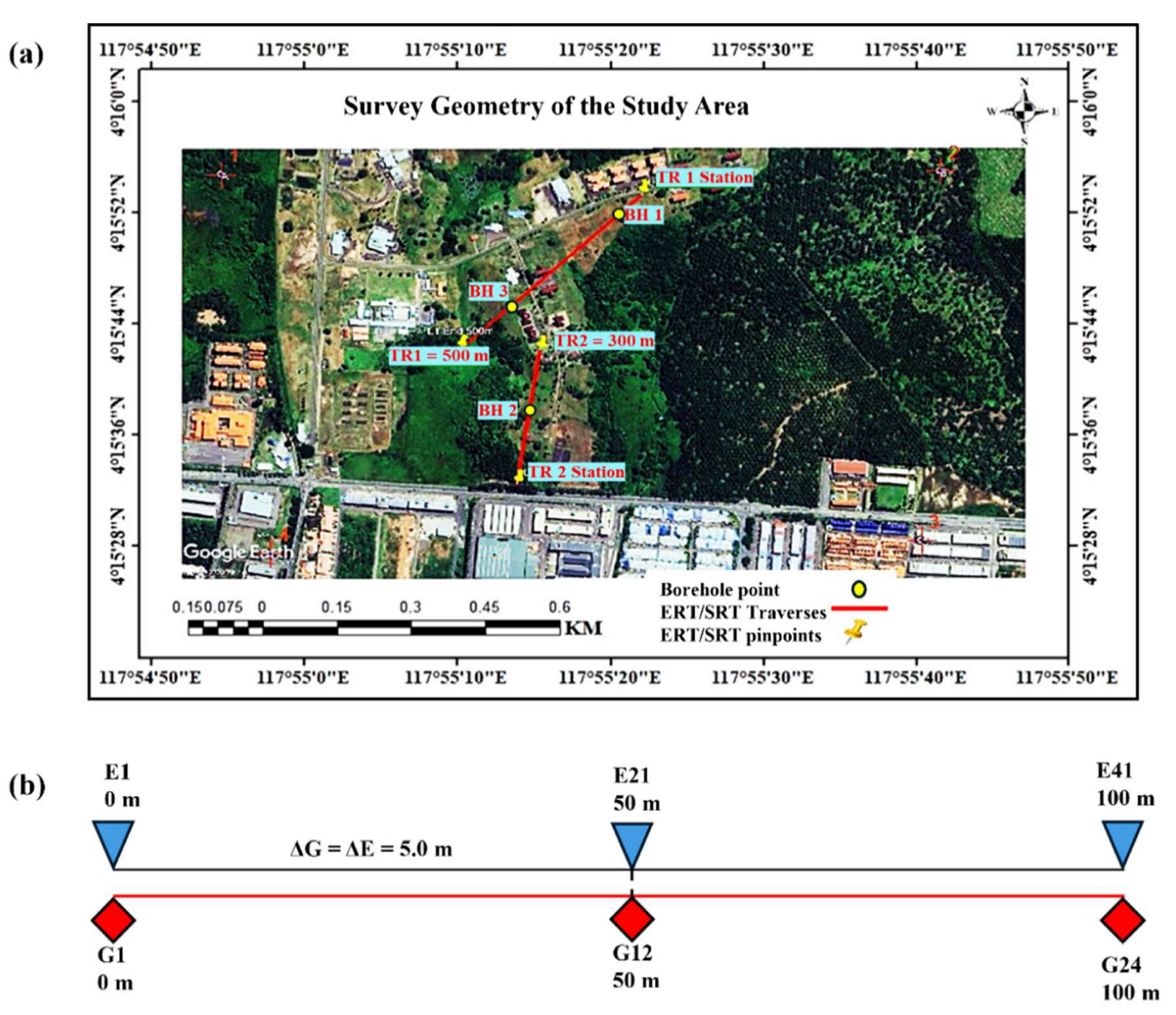
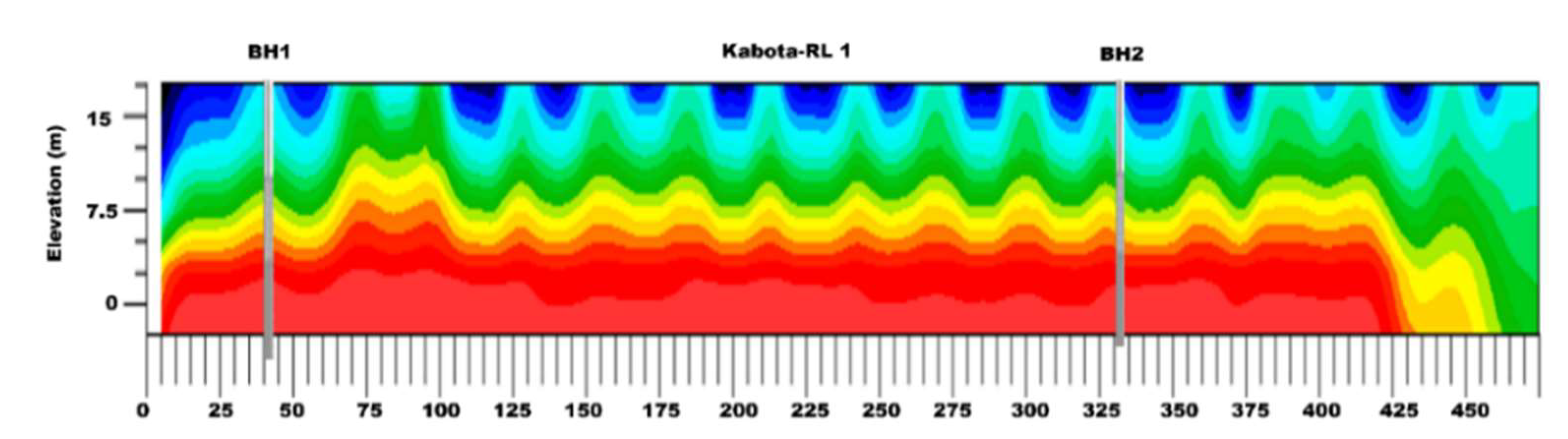
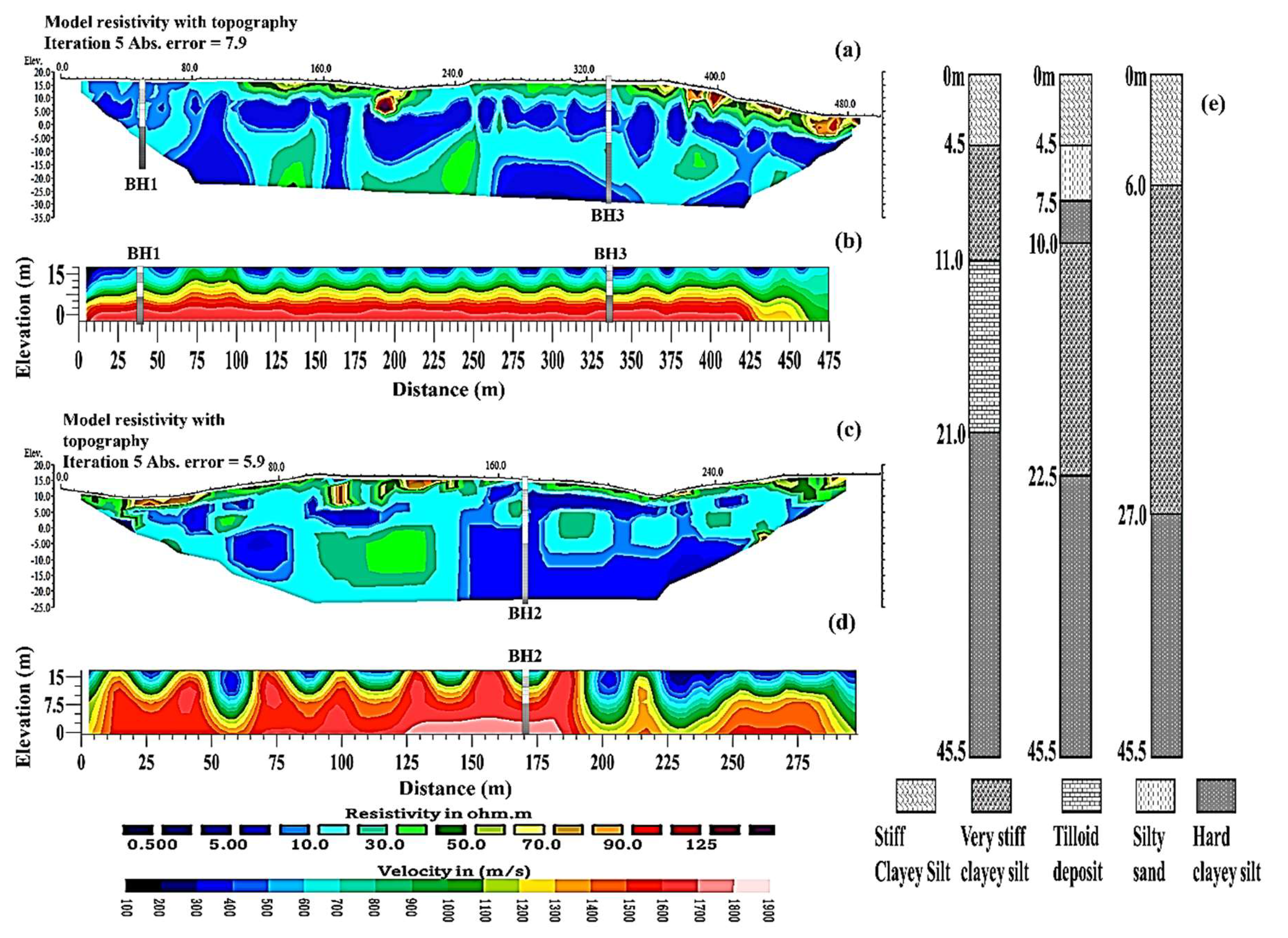
ERT and SRT Field Data Acquisition

The ABEM SAS Terrameter 4000 and ES 10-64C models of the ABEM LUND Resistivity System, together with their associated accessories, were employed to assess the electrical resistivity responses of soil-rock units. This imaging system performs high-resolution 2-D electrical imaging surveys using multiple electrodes and permits the selection of preferred protocols. For this study, the Wenner-Schlumberger array was employed, which combines the Wenner-alpha and Schlumberger arrays [31]. This configuration enhances the system’s ability to investigate at greater depths while ensuring sensitivity to horizontal and vertical structures, resulting in an improved signal-to-noise ratio for the resistivity models. The resulting resistivity figures were of high quality, with minimal or negligible error impact [32].
For SRT, the ABEM Terraloc Mk 8 equipment was used to measure Vp via seismic refraction techniques. The data collection process involved both forward and reverse shooting. The optimal number of shots per point was maintained at 7–10, with offsets set 30 m beyond the first and last geophones. At each offset, 10 shots were fired into the subsurface, providing a robust dataset for constructing high-fidelity subsurface models with enhanced spatial resolution. Inline shots were positioned at the midpoint of the geophone spread, representing the center between the first 12 and the final 12 receivers. This placement maximized coverage and ensured uniform data acquisition across the survey area. The combination of forward and reverse shooting and inline shots enabled the generation of detailed and accurate seismic velocity models, complementing the resistivity data for a comprehensive subsurface evaluation.

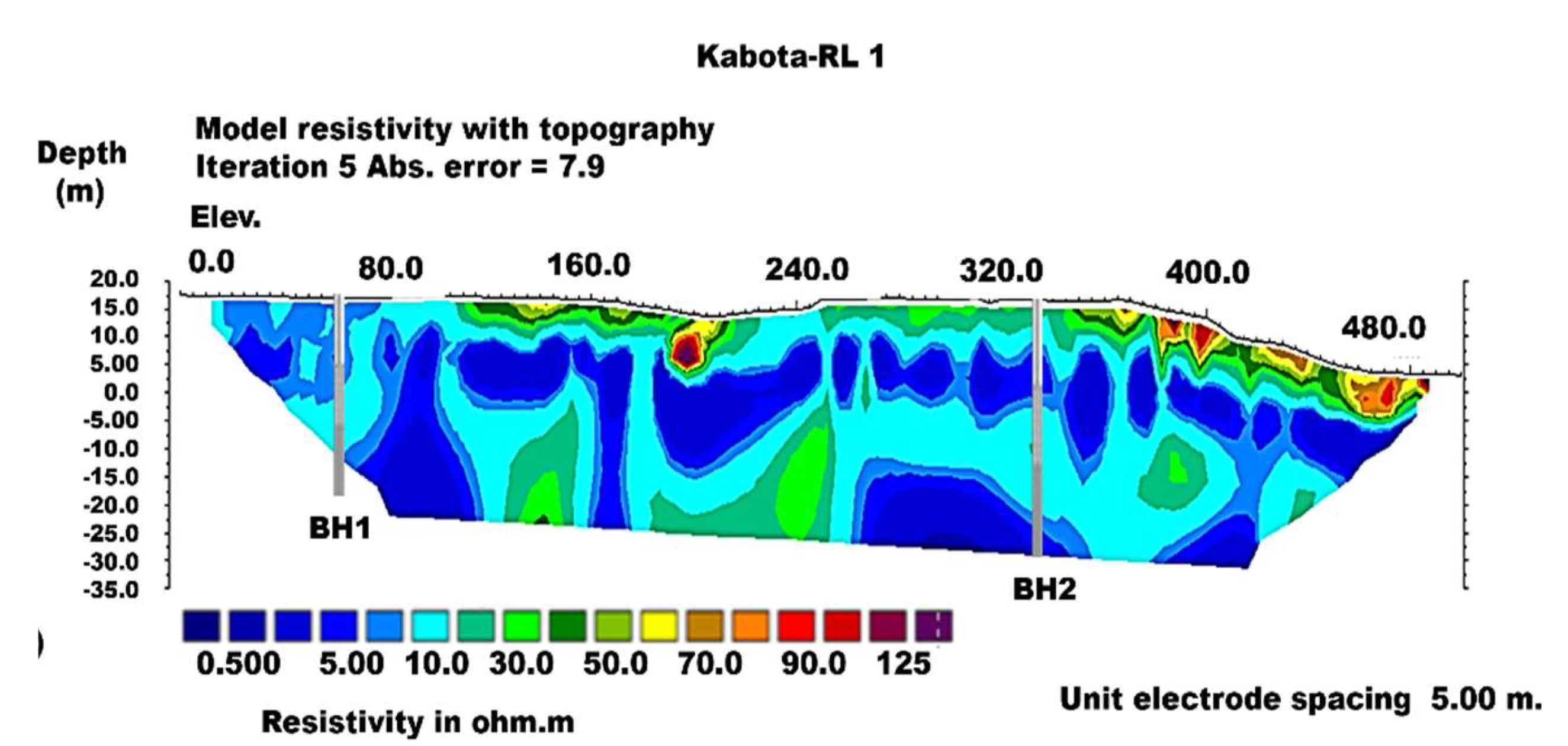
Field Data Modeling and Processing for ERT

Inversion and modeling techniques were employed during the processing of data to create accurate resistivity sections of the subsurface. The apparent resistivity data provided an initial approximation of the resistivity distribution, which was refined through inversion. The RES2DINV software, as outlined by [33,34], was employed to invert the field-measured apparent resistivity data. This process utilized the finite element method combined with strong smoothness-constrained least-squares inversion (L2-norm) and a four-node configuration. The method allowed for the customization of damping factors and flatness filters to account for varying data characteristics. The damping factor was set at 0.05, with a minimum value of 0.01, to enhance the resolution and precision of the inversion models. The iterative process continued until the absolute error was reduced to 7.9% and 5.9% for lines L1 and L2, respectively, within a maximum of five iterations. The final inversion results are presented in Figure 3, which displays the inverse resistivity sections with topography for both traverses.

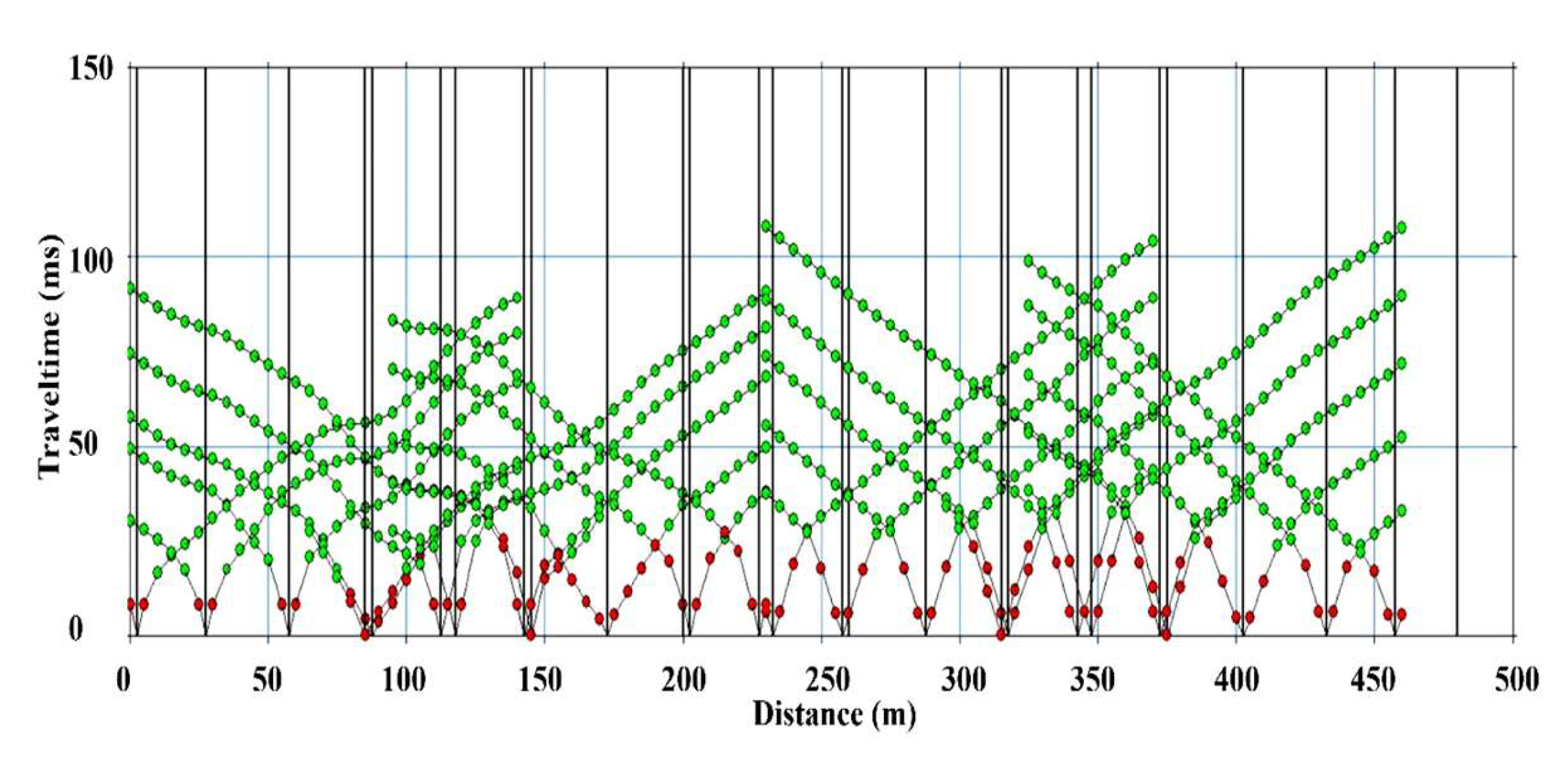
Field Data Modeling and Processing for SRT

An 800 m seismic profile was recorded along the same ERT data traverses (Figure 2) to construct a regional 2-D Vp model, which was combined with the electrical resistivity model. Advanced SRT processing techniques, including trace editing, filtering, and picking first-arrival times, were applied using SeisOpt@2D software [35]. The auto-gain control method was used to address hidden and masked layers, particularly where low-velocity zones lay beneath high-velocity layers or where thin layers lacked sufficient velocity contrast. Weak Vp signals were enhanced, and the first arrivals were manually analyzed using SeisImagerTM [36], as illustrated in Figure 4. The inversion of first-arrival travel times combined the finite-difference solution of the Eikonal problem with the multi-stencils fast marching method and simulated annealing global optimization, using the Refraction Inversion and Optimization Technique (RIOT) in high-resolution mode. This approach minimized structural artifacts and provided precise Vp models, as illustrated in Figure 5. The final models were visualized with SurferTM software [37], incorporating topography and uniform color scaling for clearer subsurface characterization.
Most importantly, the ERT and SRT inversion models were constrained using data from BH1, BH2, and BH3, which enhanced model accuracy and ensured a detailed understanding of the subsurface lithology. This integrated approach also effectively addressed hidden and masked layers, providing a comprehensive view of the subsurface properties in the research region.

Results

Lithological Profiles for the Assessed Boreholes

Borehole logs in the study area uncovered a spectrum of lithological profiles, starting with stiff clayey silt layers at the surface and extending to highly resistant lithologic units at greater depths with their Vp and resistivity signatures (Figure 6a–e). Previous studies (Akingboye & Bery, 2023; Bauer et al., 2010; Colombo et al., 2008) demonstrate that rock/soil characteristics can be integrated utilizing joint inversion methods to integrate various geophysical parameters, based on an assumed relationship between simulated physical properties. (such as porosity and water saturation) and observed lithologies. However, these methods require adjustments based on drilling log data to accurately reflect subsurface conditions.
In this study, the inversion results for Vp and resistivity were improved using borehole data, improving the accuracy of subsurface layer delineation, their depths, and thicknesses. The inversion models reveal distinct soil profile classifications, such as surficial and weathered soils (Figure 6a–d). These include a topsoil layer of stiff clayey silt, a middle layer of stiff to hard clayey/silty weathered units, and a deeper layer of hard to very hard clayey/silty weathered materials. Resistivity values for these strata extend from 0.5–30 Ωm (topsoil), >30–70 Ωm (weathered units), to >70–125 Ωm (hard weathered units), while Vp values span from 100–700 m/s (topsoil), 700–1100 m/s (weathered units), to 1100–1900 m/s (harder layers). These values align with different subsurface lithologies, including topsoil, medium stiff to very stiff clayey silt, and highly weathered/fractured units. The Vp models for L1 and L2 show similar trends, with hard to very hard lithologic units at or near the surface.
A distinct feature in the study area is a dense, grey, mottled brown silty sand layer located between 4.5 and 10 m depth under the stiffly layered topsoil near BH2 (Figure 6c–e). This strata is deemed appropriate for light-to-moderate construction [40,41,42]. Beneath the extremely stiff clayey silty layer near BH1 (Figure 6a–b, e), a layer unit composed of coarse blocks and a muddy matrix was observed between 11 and 21.45 m depth. This layer, exhibiting weak, light brownish, and dark grey deposits, is extensively fractured and displaying tilloid features, making it unsuitable for civil construction [38]. In contrast, a clayey silt or silty clay layer from 21.0 to 45.5 m near BH1, 22.5 to 45.5 m near BH2, and 27.0 to 45.5 m near BH3 are hard to very hard, with a color range from pale brown to grey (Figure 6a–e). This section is suitable for high-load-bearing structures [43,44]. The borehole logs present key insights related to the lithological configuration and depths of the earth layers, confirming the weathered overburden materials’ extent and indicating significant weathering over time [30,45]. Despite depths reaching up to 55 m, neither the resistivity nor Vp models suggest the presence of bedrock, highlighting the distinctive nature of the area due to extensive weathering.
The topsoil layer thickness typically ranges from 2 m to 15 m (Figure 6). The weathered layer boundaries under L1 and L2 exhibit different characteristics: L1 has a sharp boundary (Figs. 6a–b), while L2 shows an undulating boundary (Figs. 6c–d). The stiffness of the weathered layers ranges from hard to extremely hard, with thickness values between 2 and 7 m. Notably, the topsoil towards the eastern region of L2, near BH1, has a depth of about 7 m. These features suggest a considerable load-bearing capacity across the region, particularly where the geological structure includes a mix of hard and very hard lithologies. The regions exhibiting low resistivity values (<10 Ωm) may indicate pronounced weathering and fracturing, often associated to water saturation [6]. The geological characteristics in the study area exert significant structural influences on environmental considerations, especially infrastructure and groundwater resource management. The variations in Vp and resistivity values, as observed, are directly linked to the physical and geomechanical properties of the underlying rock and soil structures, supporting findings from [17,46].

Discussion

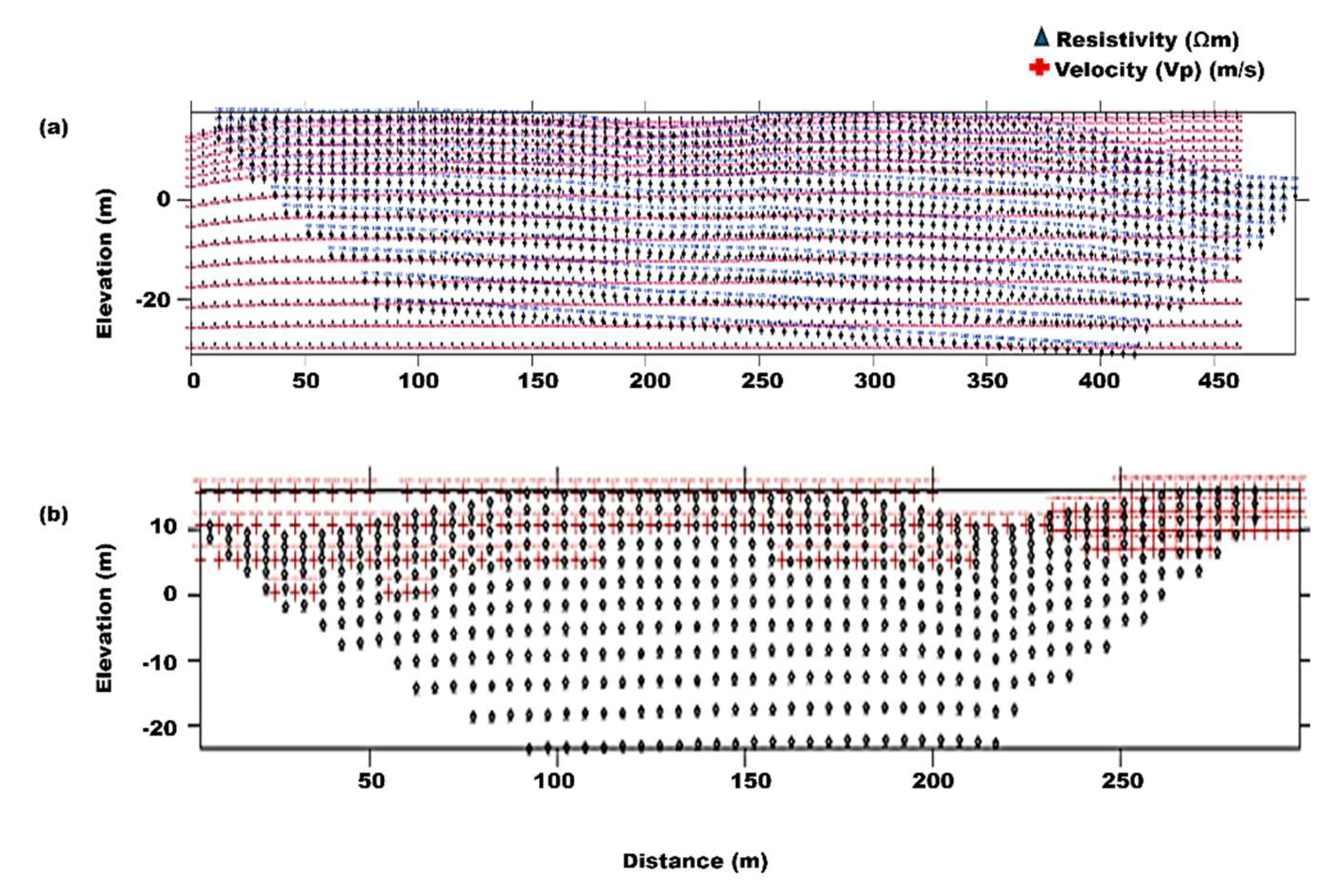
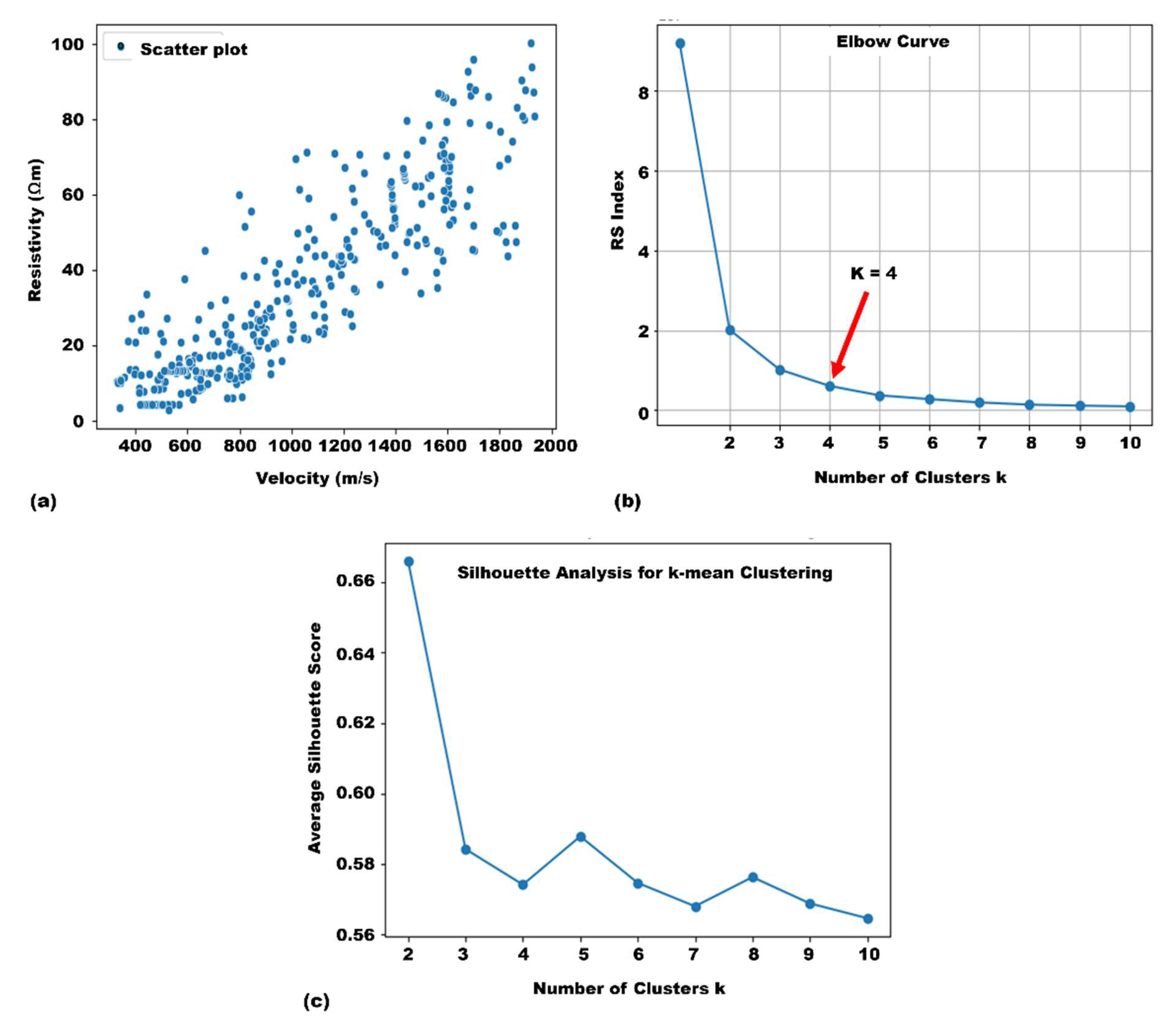
Integrated Application of Geotomographic Analysis and k-Means Clustering

The spatial alignment of the ERT and SRT data points was achieved through interpolation of the modeled ERT and SRT meshes of Figure 6a–d. In this integration, most ERT stations were positioned at the same locations as the seismic shooting stations, providing a direct spatial overlap. To combine the Vp and resistivity data, univariate models were overlaid on a shared mesh grid that covered the study area. The interpolated mesh sections were mapped onto the final grid, as illustrated in Figure 7. From this final grid, 491 data points were carefully selected, ensuring uniform spatial resolution and consistent space intervals between points. Following the interpolation of the inversion models mapped onto the shared grid, the points that coincided in space were grouped, forming a “joint parameter space” (JPS), as defined by [47]. The scatterplot for these coincident points, presented in Figure 8a, provides insights into the connections between resistivity and Vp values. This aids in uncovering associations within the data, which is essential for a more robust analysis of subsurface conditions.
To further enhance the comprehension of the region and optimize the results, a clustering technique was applied to the data. Clustering, as a technique for grouping observations based on specific criteria, is widely used in data analysis [48,49]. Within the context of this study, the k-means clustering algorithm was chosen to classify the data points into clusters by minimizing the sum of squared errors (SSE). As illustrated in Eq. 1, the Within-Cluster Sum of Squares (WCSS) is a key metric in k-means clustering analysis. It measures the compactness of clusters by quantifying the variability of data points within each cluster. This approach, first introduced by [50] and later expanded by [51], identifies cluster centroids by iteratively adjusting their positions to minimize the total SSE across all clusters. The k-means algorithm is particularly effective in identifying centroids in partitioned datasets, making it a valuable tool in geophysical data analysis [18].
Identifying the optimal number of clusters, k, poses a challenge, as highlighted by [52]. Several methods are employed to assess clustering quality, with the Elbow and Silhouette methods being the mostly used. These methods were used in this study to validate the uniqueness and consistency of the clusters. The Elbow method involves plotting the SSE as a function of k and identifying the point where the rate of decrease slows, while the Silhouette method evaluates the compactness and separation of the [53]. Both methods, as shown in Figs. 8b and 8c, provided validation for the clustering results, ensuring the reliability and relevance of the identified clusters. By employing k-means clustering, along with the Elbow and Silhouette validation techniques, the study was able to identify distinct subsurface layer classification, enhancing geophysical model interpretation. This integrated approach not only helped refine the spatial characterization of subsurface features but also provided a more accurate understanding of the underlying geological structures.
W C S S = ∑ k = 1 k ∑ x i ϵ C k ( c k − x i ) 2 (1)
Where x i is a point in C k being the mean of the kth cluster, WCSS is the within-cluster sum of squares or SSE.
Figure 8a presents a scatterplot of the modified dataset after the application of the Principal Component Analysis (PCA), showing a single, expanded cluster without clear segmentation or centroid assignment. This plot illustrates the data in its raw, unsegmented form, highlighting the complete arrangement of the data points before clustering. In contrast, Figure 8b illustrates the association between the number of clusters (k) and the R-squared index (RS index), which quantifies the goodness of fit for the clusters formed. The RS index is useful for assessing how well the data points fit within their assigned clusters, with higher values indicating better cluster cohesion. Additionally, Figure 8c shows the Silhouette scores, which provide an evaluation of the degree of similarity in data points are within their clusters compared to those in other clusters. A high Silhouette score suggests well-separated and distinct clusters, while a low score demonstrates that some data points might be inadequately assigned to their respective clusters. The k-means clustering algorithm employed in the current research operates iteratively to partition the dataset into k-distinct clusters [54]. Initially, centroids are randomly placed, and each data point is assigned to the cluster whose centroid is nearest, typically using Euclidean distance as described in Eq. 2. After the initial assignment, the centroids are recalculated as the average of all points in each cluster. The new centroids are then used to reassign the data points, and the process is iterated until convergence is achieved — which happens when the centroids no longer change significantly between iterations, indicating stable clusters. The iterative process of k-means ensures that the data points are grouped into clusters that are as compact and well-separated as possible, with minimal overlap. The clustering process is fine-tuned using validation methods such as the RS index and Silhouette scores to ensure that the final clustering solution is both meaningful and reliable. These metrics guide the determination of the ideal number of clusters (k), ensuring that the model reveals the core patterns in the data without overfitting or underfitting. The estimation of the Silhouette coefficients, s ( i ) , requires the application of Eq. 3 [55,56], and Eq. 4 [57] in ccases where the C I = 1 , C I < 1 , and C I = 0 , respectively. To assess the correctness of the cluster analysis and obtain a value of s(i) near +1, it is essential that a i < < b i . This signifies that the data has been effectively partitioned into clusters [58].
d e u c ( a , b ) = ∑ i = 1 n a i − b i 2 (2)
s i = 0 , i f C I = 1 (3)
s i = 1 − a i b i ,   i f   a i < b ( i ) 0 ,   i f   a i = b ( i )   b i a i − 1 ,   i f   a i > b ( i ) (4)
Where s i represents the silhouette width of the point (i),  a i is the average distance between the i t h point and all the points within the clusters i = 1 ,   2 ,   … , n ,  b i is the average distance from point (i) to all points in the nearest neighboring cluster (the next best cluster it could belong to) and d e u c is the Euclidean distance.
Assessing the most suitable number of clusters (k) is a significant challenge when using the k-means algorithm, as no established theoretical method exists for accurately redefining k. The process often involves executing clustering algorithms with different k values and selecting the optimal k based on predefined criteria, balancing effective clustering with meaningful physical interpretation. Cluster validity, which uses external criteria to determine k, is a common approach [47,59,60]. Researchers have introduced a range of assessment measures, such as the Bayesian Information Criterion (BIC) and Akaike Information Criterion (AIC), to address this challenge [47,61,62]. However, achieving an optimal k remains complex, even with these objective measures. This research, therefore, prioritizes two primary criteria—compactness and separation—for evaluating and selecting the best clustering approach [49,63,64]. Additionally, the RS index, as outlined in Eq. 5, is employed as a validation metric, consistent with the work of [65,66]. These measures aim to ensure robust clustering outcomes.
R S = S S t − S S w S S t = S S b S S t (5)
Where S S t is the total sum of squares distance between the points in the dataset, S S w is the sum of squares distance within each cluster, and S S b is the square distance between points belonging to the distinct groups.
The RS index for a given cluster set is computed as the ratio of S S b to S S t (see Eq. 5). S S b quantifies the dispersion among the clusters Since S S t = S S b + S S w , then, as S S b increases, S S w decreases, and vice versa. The degree of contrast between groupings in clustering directly correlates with the similarity within each group: greater distinctions lead to more uniform clusters, and vice versa. The RS index quantifies this relationship by measuring dissimilarity across clusters (low inter-class similarity) and uniformity within clusters (high intra-class similarity). RS values range from 0 to 1, where an RS of 0 indicates no disparities between groups, while an RS of 1 signifies significant variations. The optimal number of clusters is determined when introducing an additional cluster no longer considerably alters the dataset’s information content. To identify this optimal k, clustering was iteratively performed for values of k extending from 2 to 11. An inflection point, often referred to as the “elbow,” was observed in the RS curve, as demonstrated in Figure 8b. This inflection at k = 4 marks the ideal number of clusters, validating it as a suitable constraint for the chosen clustering approach.

K-Mean Clustering with Validity Index

The k-means clustering algorithm, widely recognized in data analysis for recognizing patterns, is distinguished by its assured convergence [18]. [19] utilized the elbow and silhouette methods to detect patterns in the dataset, revealing masked subsurface layers. PCA was employed to streamline dataset dimensions while ensuring critical traits, streamlining the clustering process. The results derived from the clustering are illustrated in Figure 9a, with each point in the JPS correlating to a specific location in the research area. This allows clusters in the JPS to be projected back onto the spatial domain, with each cluster being characterized by a combination of Vp and resistivity values, defined by the cluster centers (x), as detailed in Table 1. The k-means algorithm effectively partitions the JPS into distinct clusters. However, identify the ideal number of clusters (k) remains a challenge, as no definitive standards exist for its selection. This highlights the importance of employing clustering validity indices to assess and validate the clustering results.
Employing a clustering validity index together with a clustering approach is a well-established approach to identify the ideal number of clusters. The appropriate value of k can be identified by analyzing the peak or lowest index value, based on the chosen validity index. These indices are generally classified into two classes: external and internal. Internal indices assess the data’s inherent properties, while external indices rely on external information, such as labels. Internal measures are commonly used to improve clustering algorithms, while external indices are primarily used for validation purposes [67]. Internal validity indices, such as the silhouette and elbow methods, are particularly effective in determining the optimal k value and other clustering characteristics, such as handling skewed distributions [68,69]. The silhouette index, introduced by [70] and discussed by [67], quantifies both the separation between clusters and the cohesion within each cluster. It evaluates the closeness (cohesion) of data points within a cluster and the distance (separation) between clusters. The ideal value of k corresponds to the highest silhouette value (not the average), indicating the most efficient clustering partition. The optimal silhouette coefficient can be derived using Eq. 6.
s i = b i − a ( i ) M a x { a , b i } (6)
The ideal number of clusters, k, is revealed by the highest silhouette value, which indicates well-defined clusters with minimal overlap. The silhouette coefficient spans from -1 to 1, with higher values demonstrating significant clustering. A mean silhouette score of 0.67 was set as the threshold for quality, with clusters exceeding this value considered well-separated. Figure 9b shows that the k = 4 configuration provides the best clustering, as it has the highest average silhouette score, indicating compact and distinct clusters. This conforms to the RS-index near 1 (Figure 8b), confirming the reliability of the clustering results. Silhouette coefficients of 0.78 and 0.75 were estimated for clusters 4 and 2, while clusters 1 and 3 exhibit a Silhouette value of 0.74, compared to the average Silhouette value of 0.67 as suggested by k-mean (refer to the red, blue, and green lines in Figure 9b). Cluster 4, with a score of 0.78, was identified as the most optimal for the study.
Figure 10 (a–d) depict the inter-cluster distances and data point distribution per cluster, which strengthens the case for the clustering method’s analytical success. Since RS, average silhouette, and the silhouette values of the best-performing clusters are all <1 (see Silhouette scores of the best four performing clusters in Table 1 and the average silhouette coefficients of different clusters, ranging from 1 to 10 (Table 2), This reveals that the arrangement of clusters (lithology) is based on well-defined entities.
As shown in Eq. 1, the SSE provides another approach for validating clustering validity. Table 2 provides the SSE outcomes for cluster examination, involving the the rate of change of SSE for k between 2 and 6. At k=4, the SSE shows the highest rate of change. The rate of change (%change) is realized by applying Eq. 7, where i ≥ 2. Cluster analysis sorts the modified dataset according to the resistivity distribution and Vp range within the clusters.
% c h a n g e = ( S S E o f k i − 1 − S S E o f k i ) * 100 S S E o f k i 7
Figure 11 presents average histograms for each cluster, detailing their associated resistivity and Vp values. These histograms assess the effectiveness of clustering in distinguishing the subsurface characteristics within the study area. The centroid distributions provided in Table 1 further support this analysis. To visualize spatial clustering, density maps and density maps with contours (Figs. 11a–b) highlight sections where cluster boundaries, fractures, interconnections, or overlaps may occur within the subsurface units [6]. The analysis reveals overlapping lithologic units at specific depths, indicative of complex geological arrangements with gradual transitions between strata, as suggested by [71]. Using cluster centroids derived from the modified dataset facilitates the identification of these transitional zones. Table 3 summarizes the clustering results, including the resistivity and Vp ranges as well as their centroid values for each lithologic unit. These clusters correspond to distinct lithologies within the study area: Cluster 1: Clayey topsoil; Cluster 2: Stiff to extremely stiff clayey/silty units; Cluster 3: Extremely stiff to hard clayey/silty units, and Cluster 4: Hard to very hard clayey/silty units. The resistivity values of these layers range from 0 – 20 Ωm, 5 - 30 Ωm, <30 – 50 Ωm, and 50 to >125 Ωm, respectively, with corresponding Vp of <100-700 m/s, 700 to <1100 m/s, 1100-1400 m/s, and <1400 to >1900 m/s. This classification aids in identifying transitions and potential zones of interest for further geotechnical or hydrological investigations. Figure 12 captures a broad range of Vp and resistivity values, reflecting the spatial variability of subsurface lithologies across the study area. These results significantly enhance understanding of the temporal evolution and interconnections of lithologic properties, providing valuable insights for interpreting subsurface conditions and their geotechnical implications.

Resistivity-Vp Correlations for Identified Lithologic Units

This research primarily focuses on modeling and establishing of an integrated resistivity-Vp statistical relationship for the lithologies identified in the study area. The initial phase involved independently examining resistivity and Vp values alongside their geotechnical attributes, specifically SPT-N values, to understand their individual and combined behavior. Statistical associations were determined by regressing the integrated datasets from the mesh models (Figure 7). Regression analysis is a key method for quantifying relationships between variables, although it can be limited in addressing nonlinear data in complex scenarios [21,72]. Nevertheless, it provides a framework for predicting outcomes, visualizing trends, and analyzing causal or correlational dynamics.
In this study, 491 data points were analyzed using simple linear regression (SLR) to explore the correlation between resistivity (ρ\rho) and Vp. The regression plot (Figure 13) reveals a positive trend between resistivity and Vp. The relationship is expressed in Eq. 8, showing A robust linear association with R2 of 0.801. This suggests that Vp, as the independent variable, accounts for 80.1% of the variability in resistivity. This high R2R^2 value underscores the robustness of the linear model in describing the resistivity-Vp relationship. The integrated resistivity-Vp equation reflects the sensitivity of these parameters to lithological variations and clay content at the study sites, as noted by [22,73]. The strong correlation highlights the suitability of the model for interpreting subsurface materials and provides a reliable tool for geotechnical and geophysical assessments in the region.
ρ = 0.0501 V p − 15.614 ( R 2 = 0.801 ) 8
To enhance model accuracy and improve correlation efficiency between Vp and resistivity for each lithologic unit, Vp and resistivity values along the line of fit in Figure 13 were extracted for targeted prediction accuracy (Figure 14). From the 491 data points initially used for the SLR in Figure 13, 51 were selected to represent specific lithologies: topsoil (clayey/silty sand), completely weathered layers (medium clayey silt), highly weathered/fractured units (stiff to hard clayey silt), and relatively weathered bedrock (very hard to hard clayey silt/silty clay), as summarized in Table 5. This sample size aligns with datasets validated in prior studies, such as [74], 31 [75], and 32 [17], ensuring reliable regression analysis. Lithology-specific regression models, summarized in Eqs. 9–12, yielded high R2 values of 0.9656, 0.9770, 0.9590, and 0.9639, corresponding to prediction accuracies of 96.56%, 97.70%, 95.90%, and 96.39% for clusters 1 through 4, respectively. These lithology-based empirical relationships provide more accurate resistivity modeling by capturing the nuanced correlations for each lithology, especially in regions with complex soil-rock boundaries, fractures, and faulted layers.
ρ c l u s t e r 1 = 3.554 V p + 503.64 ( R 2 = 0.9656 ) 9
ρ c l u s t e r 2 = 4.7276 V p + 741.4 ( R 2 = 0.9770 ) 10
ρ c l u s t e r 3 = 5.0778 V p + 987.19 ( R 2 = 0.9590 ) 11
ρ c l u s t e r 4 = 2.988 V p + 1409.80 ( R 2 = 0.9639 ) 12
The evaluation of R2 values for each lithologic unit reveals that the combined resistivity-Vp empirical correlations surpass those reported by Zeng et al. (2018), which ranged from 0.641 to 0.816, as cited in [17]. While the findings of [17,76] align with the current research’s resistivity-Vp correlation (Figure 13), the distinct lithology-based empirical models exhibit excellent R2 values, demonstrating improved accuracy and predictive capability. Variations in equipment, geological conditions, and evaluation methodologies likely account for the differences between the cited studies and this investigation. As noted by [17], factors such as soil and rock conditions, root mean square error (RMSE), model uncertainty, and statistical assumptions significantly influence the predictive power of empirical relationships. The higher R2 values of the lithology-based models provide enhanced characterization of both surface and subsurface layers within the study area and similar geological contexts. These correlations are particularly advantageous in regions with limited borehole data, saturated or loose soils, or where seismic refraction is impractical. The refined resistivity-Vp relationships offer a robust framework for subsurface modeling, improving geophysical assessments in comparable settings.
Figure 15 highlights the correlation between SPT-N values from boreholes BH1, BH2, and BH3 with measured resistivity and Vp of the subsurface lithologies. At SPT-N values of 15–25 blows, Vp and resistivity were below 500 m/s and 7.6 Ωm, respectively. For SPT-N values exceeding 50 blows, Vp and resistivity increased to 520 m/s and 13.4 Ωm, respectively. These correlations provide critical insights into subsurface material properties and geotechnical conditions. An SPT-N value of 25 generally indicates dense, compacted materials such as dense clay, silt, or weathered rock [8,21]. Resistivity and Vp values below 15 Ωm and 1000 m/s suggest unconsolidated or poorly compacted materials, likely indicative of weathered or loose formations. Such materials may have poor drainage due to fine-grained composition (e.g., clay or silt), resulting in high water retention and saturation. These conditions reduce resistivity and influence subsurface hydrology and foundation stability [8], [21]. Saturated, stiff clay or silt, characterized by high blow counts and low resistivity/Vp values, aligns with findings of compacted but water-saturated materials [77,78]. SPT-N values exceeding 50 blows, which indicate highly compacted soils or potential bedrock, were excluded from the correlation analysis. According to [73], such values suggest resistance beyond standard SPT capabilities, often representing dense sands, gravels, hard clays, or cemented layers suitable for foundation applications. These high blow counts reflect robust layers, offering high bearing capacity and minimal deformation under loads.
From all the borehole data collected in the research area, five sets of SPT (N) and geophysical data were chosen based on the depth of the SPT-N used for correlation analysis. These datasets were used to measure the precision of the statistical correlations created between SPT-N and geophysical data for the study area. The precision of the SPT-N values for the selected data was evaluated using the empirical relationships in Eqs. 13 and 14, respectively. Table 4 delineates the efficacy of predictive equations that correlate measured and estimated geophysical datasets using borehole data at corresponding depths. The correlation between Vp and SPT (N) exhibits percentage matches between 90% and 100%, whereas the correlation between resistivity and SPT (N) demonstrates percentage matches between 93% and 99.9% throughout the study area. Percentage matching reflects the accuracy, showing how closely the predicted values match the observed values. The study accurately describes the layers of soil and rock below the surface in the study area, showing a strong statistical link between SPT (N) and the datasets. This association underscores the differences in lithological characteristics, including density, porosity, and compaction, vital for geotechnical and geological assessments. The integration of these prediction models shows substantial possibilities for enhancing subsurface research, minimizing borehole drilling expenses, and effectively evaluating geological conditions over extensive regions.
The relationships between SPT-N, resistivity, and Vp are quantified with strong correlation coefficients (R2) of 0.9052 for resistivity and 0.9192 for Vp, demonstrating predictive accuracies of 90.52% and 91.92%, respectively. Positive slopes in Eqs. 13 and 14 confirm a direct relationship, where increasing SPT-N corresponds to higher resistivity and Vp, indicative of increasing soil density or strength. This trend suggests a transition from low-density/strength to high-density/strength materials, marking a progression toward highly compacted or weathered lithologies [17,79]. These robust regression models underline the reliability of the geophysical parameters in evaluating soil properties and subsurface conditions.
ρ = 0.1309 ( N ) + 6.8711 ( R 2 = 0.9052 ) 13
V p = 36.12 N − 273.41 ( R 2 = 0.9192 ) 14
As presented in Table 5, dense lithology with low resistivity and Vp may effectively sustain loads due to their density but needs further consideration for drainage. Saturated, low-resistivity clays or silts may have settling problems under load if water content changes, thereby compromising the integrity of foundations over time. Layers below the ground that have these low parameter values and moderate SPT-N may not be strong enough to hold heavy loads without extra soil reinforcement. Examining the site for foundation placement may indicate the need for ground enhancement, as these strata may be prone to settling, particularly under dynamic loads.
Conclusion
This study highlights the effective use of k-means clustering, augmented by PCA, Silhouette, and Elbow methods, alongside supervised linear regression, to characterize subsurface lithological units in the Kabota-Tawau area of Sabah, Malaysia. By integrating resistivity and Vp data obtained from ERT and SRT models, this research enhances the identification of lithological boundaries and improves geotechnical assessments through the inclusion of SPT-N values. The combined geophysical and geotechnical approaches provided crucial insights into subsurface properties, weak zones, and spatial variations in resistivity, Vp, and SPT-N. Positive correlations between these parameters confirm that increasing SPT-N values are associated with higher resistivity and Vp, suggesting a transition from low-density/strength to high-density/strength materials, which is useful for evaluating the suitability of subsurface conditions for engineering applications in similar sedimentary regions.
K-means clustering successfully delineated distinct lithological units, identifying key resistivity and Vp ranges for each unit. Machine learning metrics, such as PCA, RS index, and silhouette score, refined the clustering process, resulting in reliable models with a silhouette score of 0.67 and an RS value approaching 1. A significant reduction in SSE (88.96%) further validates the precision of the clustering method. The R² values exceeding 0.801 for the resistivity-Vp empirical correlations demonstrate strong accuracy and predictive capability, with a confidence level of over 80%. This approach effectively classified the subsurface lithologies, identified weak zones, and highlighted key areas for geotechnical and geomechanical evaluation, especially in regions with limited borehole data. However, the assumption in k-means clustering of spherical, equally sized clusters may not always be accurately representing the complexities of subsurface formations. Future research could improve accuracy by applying advanced clustering techniques, such as fuzzy or hierarchical clustering, which are better suited to handle complex geological structures. Furthermore, incorporating machine learning algorithms like Support Vector Machines (SVM) or Random Forests could enhance the prediction of lithological boundaries by better modeling non-linear interactions.

Data availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author upon reasonable request.

Author Contributions

MDD: Conceptualization, Methodology, Data – curation & validation, Writing – review & editing, Resources, and Supervision. AAB: Conceptualization, Methodology, Data – curation & validation, Writing – review & editing, Resources, Funding, and Supervision. ASA: Conceptualization, Methodology, Data – curation & validation, Writing – review & editing, and Supervision. MUA: Writing – review & editing, Resources and Supervision. JG: Writing – review & editing and Resources. GAB: Writing – review & editing, and Resources. EM: Writing – review & editing, and Resources. NNO: Writing – review & editing, and Resources

Funding

The authors express their gratitude to the Malaysian Ministry of Higher Education (MoHE) for providing financial support via the Fundamental Research Grant Scheme (203.PFIZIK.6712108), as well as to Universiti Sains Malaysia for the Short-Term Grant (304/PFIZIK/6315489), which have enabled the funding of this research endeavors. Funding through TETFund is also acknowledged.

Acknowledgments

The authors would like to express gratitude and appreciation to individuals who have contributed to the completion of this paper. Special appreciation to the Editor and the reviewers for their valuable comments and recommendations, which have greatly contributed to improving the quality of our paper. The authors express their gratitude to Universiti Sains Malaysia, laboratory staff at the School of Physics (Geophysics Programme), as well as the postgraduate students, and TETfund for their valuable assistance in the process of field data acquisition and manuscript development. We also would like to thank Universiti Sains Malaysia for the GoT Incentive (R502-KR-GOT001-0000000157-K134) and Malaysian Higher Education (MoHE) for the FRGS grant (203.PFIZIK.6712108) for the research financial support.

Competing Interest

The authors assert that they do not have any competing interests or personal ties that might have potentially influenced the research presented in this manuscript.

Ethical Approval

All ethical standards have been duly followed during the research.

Consent to Participate

Not Applicable

Consent to Publish

Not Applicable

Financial interests

The authors declare that they have no conflict of interest.

References

  1. M. U. Aka, O. E. M. U. Aka, O. E. Agbasi, O. Nsidibe Ndaraka, and O. A. Derikuma, “Assessment of Geologic Effect of Road Submergence Depths on Soil Subgrade Strength in Eket, South-South Nigeria,” Int. J. Sci. Res. Manag., vol. 10, no. 06, pp. 09–21, Jun. 2022. [Google Scholar] [CrossRef]
  2. A. N. Salleh et al., “Journal of Asian Earth Sciences Application of geophysical methods to evaluate soil dynamic properties in Penang Island, Malaysia,” J. Asian Earth Sci., vol. 207, no. 20, p. 104659, Mar. 20 July 2021. [CrossRef]
  3. A. Karpatne, I. A. Karpatne, I. Ebert-Uphoff, S. Ravela, H. A. Babaie, and V. Kumar, “Machine Learning for the Geosciences: Challenges and Opportunities,” IEEE Trans. Knowl. Data Eng., vol. 31, no. 8, pp. 1544–1554, Aug. 2019. [Google Scholar] [CrossRef]
  4. A. Latrach, M. L. A. Latrach, M. L. Malki, M. Morales, M. Mehana, and M. 2023. [Google Scholar] [CrossRef]
  5. S. Bernardinetti and P. P. G. Bruno, “The Hydrothermal System of Solfatara Crater (Campi Flegrei, Italy) Inferred From Machine Learning Algorithms,” Front. Earth Sci., vol. 7, Nov. 2019. [CrossRef]
  6. O. Ali and C. Sheng-Chang, “Characterization of well logs using K-mean cluster analysis,” J. Pet. Explor. Prod. Technol., vol. 10, no. 6, pp. 2245– 2256, 2020. [CrossRef]
  7. A. Arbelaitz, I. A. Arbelaitz, I. Gurrutxaga, J. Muguerza, J. M. Pérez, and I. Perona, “An extensive comparative study of cluster validity indices,” Pattern Recognit., vol. 46, no. 1, pp. 2013. [Google Scholar] [CrossRef]
  8. A. S. Akingboye, A. A. A. S. Akingboye, A. A. Bery, M. B. Aminu, M. D. Dick, G. A. Bala, and T. O. Ale, “Surface–subsurface characterization via interfaced geophysical–geotechnical and optimized regression modeling,” Model. Earth Syst. Environ., vol. 10, no. 4, pp. 5121–5143, Aug. 2024. [Google Scholar]
  9. B. Benjumea et al., “Undercover karst imaging using a Fuzzy c-means data clustering approach (Costa Brava, NE Spain),” Eng. Geol., vol. 293, no. 2021. [CrossRef]
  10. J. S. Whiteley, J. E. J. S. Whiteley, J. E. Chambers, S. Uhlemann, P. B. Wilkinson, and J. M. Kendall, “Geophysical Monitoring of Moisture-Induced Landslides: A Review,” Rev. Geophys., vol. 57, no. 1, pp. 2019. [Google Scholar] [CrossRef]
  11. R. Zavqiddin, Y. R. Zavqiddin, Y. Oʻgʻli, and E. Z. Abdaaliyevna, “3D Technological System of Management of Geological Exploration Processes of Mining Enterprises,” vol. 5, no. 11, pp. 254–261, 2022.
  12. K. Hellman, M. K. Hellman, M. Ronczka, T. Günther, M. Wennermark, C. Rücker, and T. Dahlin, “Structurally coupled inversion of ERT and refraction seismic data combined with cluster-based model integration,” J. Appl. Geophys., vol. 143, pp. 169–181, Aug. 2017. [Google Scholar] [CrossRef]
  13. C. V. A. LE, N. N. K. C. V. A. LE, N. N. K. NGUYEN, and T. Van NGUYEN, “Zastosowanie metody klastrowania w różnych parametrach geofizycznych do badania środowiska podpowierzchniowego,” Inżynieria Miner., vol. 1, no. 2, pp. 39–47, Jan. 2023. [Google Scholar] [CrossRef]
  14. M. H. Loke, J. E. M. H. Loke, J. E. Chambers, D. F. Rucker, O. Kuras, and P. B. Wilkinson, “Recent developments in the direct-current geoelectrical imaging method,” J. Appl. Geophys., vol. 95, pp. 135–156, Aug. 2013. [Google Scholar] [CrossRef]
  15. Z. Zeng, L. Kong, M. Wang, and H. M. Sayem, “Assessment of engineering behaviour of an intensely weathered swelling mudstone under full range of seasonal variation and the relationships among measured parameters,” Can. Geotech. J., vol. 55, no. 12, pp. 1837– 1849, 2018. [CrossRef]
  16. M. Hasan and Y. Shang, “Investigating the groundwater resources of weathered bedrock using an integrated geophysical approach,” Environ. Earth Sci., vol. 82, no. 9, p. 20 May; 23. [CrossRef]
  17. A. S. Akingboye and A. A. Bery, “Development of novel velocity–resistivity relationships for granitic terrains based on complex collocated geotomographic modeling and supervised statistical analysis,” Acta Geophys., vol. 71, no. 6, pp. 2675–2698, Mar. 2023. [CrossRef]
  18. E. Piegari, G. E. Piegari, G. De Donno, D. Melegari, and V. Paoletti, “A machine learning-based approach for mapping leachate contamination using geoelectrical methods,” Waste Manag., vol. 157, no. 22, pp. 121–129, Feb. 20 November 2023. [Google Scholar] [CrossRef]
  19. N. Zamri et al., “A comparison of unsupervised and supervised machine learning algorithms to predict water pollutions,” Procedia Comput. Sci., vol. 204, no. 2021, pp. 2022. [CrossRef]
  20. M. Ronczka, K. M. Ronczka, K. Hellman, T. Günther, R. Wisén, and T. Dahlin, “Electric resistivity and seismic refraction tomography: a challenging joint underwater survey at Äspö Hard Rock Laboratory,” Solid Earth, vol. 8, no. 3, pp. 671–682, Jun. 2017. [Google Scholar] [CrossRef]
  21. M. D. Dick, A. A. M. D. Dick, A. A. Bery, A. S. Akingboye, K. R. Ekanem, and E. Moses, “Subsurface lithological characterization via machine learning-assisted electrical resistivity and SPT-N modeling: A case study from Sabah, Malaysia,” Earth Syst. Environ. 2024. [Google Scholar]
  22. M. D. Dick, A. A. M. D. Dick, A. A. Bery, N. N. Okonna, K. R. Ekanem, Y. Bashir, and A. S. Akingboye, “A novel machine learning approach for interpolating seismic velocity and electrical resistivity models for early-stage soil-rock assessment,” Earth Sci. Informatics, Apr. 2024. [Google Scholar] [CrossRef]
  23. F. A. F. Da, C. G. Böhm, and S. P. M. Giorgi, “Petro - physical Characterization of the Shallow Sediments in a Coastal Area in NE Italy from the Integration of Active Seismic and Resistivity Data,” Surv. Geophys., no. 012345 6789, 2023. [CrossRef]
  24. E. James, A. A. E. James, A. A. Ghani, O. O. Akinola, and J. Asis, “Petrology and Geochemical Features of Semporna Volcanic Rocks, South-east Sabah, Malaysia,” Sains Malaysiana, vol. 50, no. 1, pp. 2021; 21. [Google Scholar] [CrossRef]
  25. S. Tahir, B. S. Tahir, B. Musta, and I. A. Rahim, “Geological heritage features of Tawau volcanic sequence, Sabah,” Bull. Geol. Soc. Malaysia, vol. 56, no. 56, pp. 2010; 85. [Google Scholar] [CrossRef]
  26. K. M. Leong, “Geological Setting of Sabah,” Petroleum Geology and Resources of Malaysia. pp. 475–497, 1999.
  27. C. S. Hutchison, “The North-West Borneo Trough,” Mar. Geol., vol. 271, no. 1–2, pp. 2010; 43. [CrossRef]
  28. R. J. Morley et al., “Sequence biostratigraphic framework for the Oligocene to Pliocene of Malaysia: High-frequency depositional cycles driven by polar glaciation,” Palaeogeogr. Palaeoclimatol. Palaeoecol., vol. 561, no. 20, p. 110058, Jan. 20 October 2021. [CrossRef]
  29. R. Hall, “Contraction and extension in northern Borneo driven by subduction rollback,” J. Asian Earth Sci., vol. 76, pp. 2013. [CrossRef]
  30. M. Madon, C. L. M. Madon, C. L. Kim, and R. Wong, “The structure and stratigraphy of deepwater Sarawak, Malaysia: Implications for tectonic evolution,” J. Asian Earth Sci., vol. 76, pp. 2013. [Google Scholar] [CrossRef]
  31. A. S. Akingboye and A. C. Ogunyele, “INSIGHT INTO SEISMIC REFRACTION AND ELECTRICAL RESISTIVITY TOMOGRAPHY TECHNIQUES IN SUBSURFACE INVESTIGATIONS,” Rud. Zb., vol. 34, no. 1, pp. 93–111, Feb. 2019. [CrossRef]
  32. M. H. Loke, “Rapid 2D resistivity forward modelling using the finite-difference and finite-element methods,” 2002.
  33. D. H. Griffiths and R. D. Barker, “Electrical Imaging in Archaeology,” J. Archaeol. Sci., vol. 21, no. 2, pp. 153–158, Mar. 1994. [CrossRef]
  34. M. H. Loke and J. W. Lane, Jr, “Inversion of Data from Electrical Resistivity Imaging Surveys in Water-Covered Areas,” Explor. Geophys., vol. 35, no. 4, pp. 266–271, Dec. 2004. [CrossRef]
  35. P. Kearey and M. Brooks, An introduction to geophysical exploration. 2nd edition. 1991.
  36. Geometrics, “SeisImager/SW TM Manual Windows Software for Analysis of Surface Waves Pickwin TM v. 4.0.1.5 WaveEq TM v. 2 Including explanation of surface wave data acquisition using Geometrics Seismodule Controller Software for ES-3000, SmartSeis ST, Geode, and Strata,” vol. 50, no. m, 2009.
  37. G. Software, “Golden Software (2021) Surfer User’s Guide. Golden Software, LLC. 1431 p. www.GoldenSoftware.com”.
  38. K. Bauer et al., “Exploring the Groß Schönebeck (Germany) geothermal site using a statistical joint interpretation of magnetotelluric and seismic tomography models,” Geothermics, vol. 39, no. 1, pp. 35–45, Mar. 2010. [CrossRef]
  39. S. W. Colombo D, Cogan M, Hallinan S, Mantovani M, Virgilio M, “Near-surface P-velocity modelling by integrated seismic, EM, and gravity data: examples from the middle East. 2008.
  40. R. D. Agustina, H. R. D. Agustina, H. Pazha, and H. Sugilar, “Identification of subsurface basement rock using geoelectrical resistivity method in development area (campus 2 UIN Sunan Gunung Djati Bandung),” IOP Conf. Ser. Mater. Sci. Eng., vol. 434, no. 2018; 1. [Google Scholar] [CrossRef]
  41. S. N. M. Akip Tan et al., “Correlation of Resistivity Value with Geotechnical N-Value of Sedimentary Area in Nusajaya, Johor, Malaysia,” J. Phys. Conf. Ser., vol. 995, no. 2018; 1. [CrossRef]
  42. C. C. Tsai, T. Kishida, and C. H. Kuo, “Unified correlation between SPT–N and shear wave velocity for a wide range of soil types considering strain-dependent behavior,” Soil Dyn. Earthq. Eng., vol. 126, no. June, p. 10 5783, 2019. [CrossRef]
  43. J. A. Díaz-Rodríguez, “Characterization and engineering properties of Mexico City lacustrine soils,” Proc. Int. Work. Characterisation Eng. Prop. Nat. Soils, no. February, pp. 725–755, 2003, [Online]. Available: https://s3.amazonaws.com/academia.edu.documents/40141579/Characterisation_and_engineering_propert20151118-18961-1mjkv31.pdf? 1538.
  44. F. Schnaid, Geocharacterisation and properties of natural soils by insitu tests, vol. 38, no. 9. 2005. [CrossRef]
  45. A. Burton-Johnson, C. G. A. Burton-Johnson, C. G. Macpherson, and R. Hall, “Internal structure and emplacement mechanism of composite plutons: Evidence from Mt Kinabalu, Borneo,” J. Geol. Soc. London., vol. 174, no. 1, pp. 2017. [Google Scholar] [CrossRef]
  46. M. N. A. Anuar, M. H. Arifin, H. Baioumy, and M. Nawawi, “A geochemical comparison between volcanic and non-volcanic hot springs from East Malaysia: Implications for their origin and geothermometry,” J. Asian Earth Sci., vol. 217, no. May, p. 10 4843, 2021. [CrossRef]
  47. M. G. Di Giuseppe, A. M. G. Di Giuseppe, A. Troiano, C. Troise, and G. De Natale, “k-Means clustering as tool for multivariate geophysical data analysis. An application to shallow fault zone imaging,” J. Appl. Geophys., vol. 101, pp. 108–115, Feb. 2014. [Google Scholar] [CrossRef]
  48. A. K. Jain, “Data clustering: 50 years beyond K-means,” Pattern Recognit. Lett., vol. 31, no. 8, pp. 651–666, Jun. 2010. [CrossRef]
  49. K. Sumiran, “An Overview of Data Mining Techniques and Their Application in Industrial Engineering,” Asian J. Appl. Sci. Technol., vol. 2, no. 2, pp. 947–953, 2018, [Online]. Available: www.ajast.
  50. S. P. Lloyd, “Least Squares Quantization in PCM,” IEEE Trans. Inf. Theory, vol. 28, no. 2, pp. 1982. [CrossRef]
  51. MacQueen, James and others, “Some methods for classification and analysis of multivariate observations,” Proc. fifth Berkeley Symp. Math. Stat. Probab., vol. 1, no. 14, pp. 281–297, 1967, [Online]. Available: http://books.google.de/books?
  52. A. Fujita, D. Y. A. Fujita, D. Y. Takahashi, and A. G. Patriota, “A non-parametric method to estimate the number of clusters,” Comput. Stat. Data Anal., vol. 73, pp. 2014; 39. [Google Scholar] [CrossRef]
  53. F. Batool and C. Hennig, “Clustering with the Average Silhouette Width,” Comput. Stat. Data Anal., vol. 158, p. 10 7190, 2021. [CrossRef]
  54. J. Singh, S. P. J. Singh, S. P. Mohanty, and D. K. Pradhan, “Introduction to SRAM,” in Robust SRAM Designs and Analysis, New York, NY: Springer New York, 2013, pp. 1–29. [CrossRef]
  55. A. Likas, N. A. Likas, N. Vlassis, and J. J. Verbeek, “The global k-means clustering algorithm,” Pattern Recognit., vol. 36, no. 2, pp. 2003. [Google Scholar] [CrossRef]
  56. A. Rajabi, M. Eskandari, M. J. Ghadi, L. Li, J. Zhang, and P. Siano, “A comparative study of clustering techniques for electrical load pattern segmentation,” Renew. Sustain. Energy Rev., vol. 120, no. November 2019, 2020. [CrossRef]
  57. P. Fränti and S. Sieranoja, “How much can k-means be improved by using better initialization and repeats?,” Pattern Recognit., vol. 93, pp. 2019. [CrossRef]
  58. R. C. De Amorim and C. Hennig, “Recovering the number of clusters in data sets with noise features using feature rescaling factors,” Inf. Sci. (Ny)., vol. 324, pp. 2015. [CrossRef]
  59. M. L. Lee, Y. L. M. L. Lee, Y. L. Lee, S. L. Goh, C. H. Koo, S. H. Lau, and S. Y. Chong, “Case Studies and Challenges of Implementing Geotechnical Building Information Modelling in Malaysia,” Infrastructures, vol. 6, no. 10, p. 145, Oct. 2021. [Google Scholar] [CrossRef]
  60. S. Sardari, M. S. Sardari, M. Eftekhari, and F. Afsari, “Hesitant fuzzy decision tree approach for highly imbalanced data classification,” Appl. Soft Comput. J., vol. 61, pp. 2017. [Google Scholar] [CrossRef]
  61. K. Husain, M.R.; Ishak, A.M., Redzuan, N., Kalken, T.V., Eds.; Brown, “Malaysian national water balance system (NAWABS) for improved river basin management: Case study in the Muda River basin.,” in In Proceedings of the 37th IAHR World Congress, Kuala Lumpur, Malaysia, 1, 2017. [Google Scholar]
  62. M. Ramze Rezaee, B. P. F. M. Ramze Rezaee, B. P. F. Lelieveldt, and J. H. C. Reiber, “A new cluster validity index for the fuzzy c-mean,” Pattern Recognit. Lett., vol. 19, no. 3–4, pp. 1998. [Google Scholar] [CrossRef]
  63. T. Bohlin, “Validation techniques,” in Interactive System Identification: Prospects and Pitfalls, Berlin, Heidelberg: Springer Berlin Heidelberg, 1991, pp. 220–243. [CrossRef]
  64. J. Saha and J. Mukherjee, “CNAK: Cluster number assisted K-means,” Pattern Recognit., vol. 110, p. 10 7625, 2021. [CrossRef]
  65. P. Govender and V. Sivakumar, “Application of k-means and hierarchical clustering techniques for analysis of air pollution: A review (1980–2019),” Atmos. Pollut. Res., vol. 11, no. 1, pp. 2020; 56. [CrossRef]
  66. M. Halkidi, M. M. Halkidi, M. Vazirgiannis, and Y. Batistakis, “Quality Scheme Assessment in the Clustering Process,” in Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 2000, pp. 265–276. [CrossRef]
  67. R. Ünlü and P. Xanthopoulos, “Estimating the number of clusters in a dataset via consensus clustering,” Expert Syst. Appl., vol. 125, pp. 2019; 39. [CrossRef]
  68. Y. Liu, Z. Y. Liu, Z. Li, H. Xiong, X. Gao, and J. Wu, “Understanding of internal clustering validation measures,” Proc. - IEEE Int. Conf. Data Mining, ICDM, pp. 2010. [Google Scholar] [CrossRef]
  69. E. Rendón, I. E. Rendón, I. Abundez, A. Arizmendi, and E. M. Quiroz, “Internal versus External cluster validation indexes,” Int. J. Comput. Commun., vol. 5, no. 1, pp. 27--34, 2011, [Online]. Available: http://w.naun.org/multimedia/UPress/cc/20-463.
  70. P. J. Rousseeuw, “Silhouettes: A graphical aid to the interpretation and validation of cluster analysis,” J. Comput. Appl. Math., vol. 20, no. C, pp. 1987; 65. [CrossRef]
  71. L. Ge et al., “Current Trends and Perspectives of Detection and Location for Buried Non-Metallic Pipelines,” Chinese J. Mech. Eng. (English Ed., vol. 34, no. 2021; 1. [CrossRef]
  72. A. Pérez-López, M. A. Pérez-López, M. García-López, and M. González-Gil, “Integrated Interpretation of Electrical Resistivity Tomography for Evaporite Rock Exploration: A Case Study of the Messinian Gypsum in the Sorbas Basin (Almería, Spain),” Minerals, vol. 13, no. 2023; 2. [Google Scholar] [CrossRef]
  73. A. Hegde and A. Anand, “Resistivity Correlations with SPT-N and Shear Wave Velocity for Patna Soil in India,” Indian Geotech. J., vol. 52, no. 1, pp. 2022. [CrossRef]
  74. M. Hasan and Y. Shang, “Geophysical evaluation of geological model uncertainty for infrastructure design and groundwater assessments,” Eng. Geol., vol. 299, p. 106560, Mar. 2022. [CrossRef]
  75. B. Balarabe and A. A. Bery, “Modeling of soil shear strength using multiple linear regression (MLR) at Penang, Malaysia,” J. Eng. Res., vol. 9, no. 3A, pp. 40–51, Sep. 2021. [CrossRef]
  76. D. Colombo and T. Keho, “The non-seismic data and joint inversion strategy for the near surface solution in Saudi Arabia,” in SEG Technical Program Expanded Abstracts 2010, Society of Exploration Geophysicists, Jan. 2010, pp. 1934–1938. [CrossRef]
  77. G. M. Deynoux, M. G. M. Deynoux, M., Miller, J. M. G., Domack, E. W., Eyles, N., Fairchild, I. J., & Young, “Earth’s glacial record,” in Glaciers, Cambridge University Press, 2004, pp. 303–334. [CrossRef]
  78. K. A. Hatta and S. B. A. Syed Osman, “Correlation of Electrical Resistivity and SPT-N Value from Standard Penetration Test (SPT) of Sandy Soil,” Appl. Mech. Mater., vol. 785, pp. 702–706, Aug. 2015. [CrossRef]
  79. J. T. D. Gonçalves, M. A. B. J. T. D. Gonçalves, M. A. B. Botelho, S. L. Machado, and L. G. Netto, “Correlation between field electrical resistivity and geotechnical SPT blow counts at tropical soils in Brazil,” Environ. Challenges, vol. 5, no. 2021. [Google Scholar] [CrossRef]
Preprints 148851 g001
Figure 1. A generalized geological map of Sabah, Malaysia adapted from [29].
Figure 1. A generalized geological map of Sabah, Malaysia adapted from [29].
Preprints 148851 g001
Preprints 148851 g002
Figure 2. (a) Aerial map showing geophysical data acquisition for the study area, with defined ERT and SRT transects (L1 and L2) and borehole locations. (b) Layout of the two survey traverses.
Figure 2. (a) Aerial map showing geophysical data acquisition for the study area, with defined ERT and SRT transects (L1 and L2) and borehole locations. (b) Layout of the two survey traverses.
Preprints 148851 g002
Preprints 148851 g003
Figure 3. Generated 2-D composite ERT inversion model with topography for L1 with 500 m length.
Figure 3. Generated 2-D composite ERT inversion model with topography for L1 with 500 m length.
Preprints 148851 g003
Preprints 148851 g004
Figure 4. A typical ray-path illustration for the processed Vp data for L1 in the research region.
Figure 4. A typical ray-path illustration for the processed Vp data for L1 in the research region.
Preprints 148851 g004
Preprints 148851 g005
Figure 5. Generated RIOT’s Vp models for L1 with 500 m length.
Figure 5. Generated RIOT’s Vp models for L1 with 500 m length.
Preprints 148851 g005
Preprints 148851 g006
Figure 6. Inversion models for ERT and SRT showing (a and b) L1, (c and d) L2, and (e) created borehole logs for BH1, BH2, and BH3 in the study area.
Figure 6. Inversion models for ERT and SRT showing (a and b) L1, (c and d) L2, and (e) created borehole logs for BH1, BH2, and BH3 in the study area.
Preprints 148851 g006
Preprints 148851 g007
Figure 7. Depictions of the interpolated ERT–SRT mesh models generated for (a) L1 and (b) L2.
Figure 7. Depictions of the interpolated ERT–SRT mesh models generated for (a) L1 and (b) L2.
Preprints 148851 g007
Preprints 148851 g008
Figure 8. (a) Visualization of the 491 extracted data points from the mesh model in a scatter plot (b) Plot of RS index against the number of clusters based on k-means analysis. (c) Silhouette score for k-means clustering.
Figure 8. (a) Visualization of the 491 extracted data points from the mesh model in a scatter plot (b) Plot of RS index against the number of clusters based on k-means analysis. (c) Silhouette score for k-means clustering.
Preprints 148851 g008
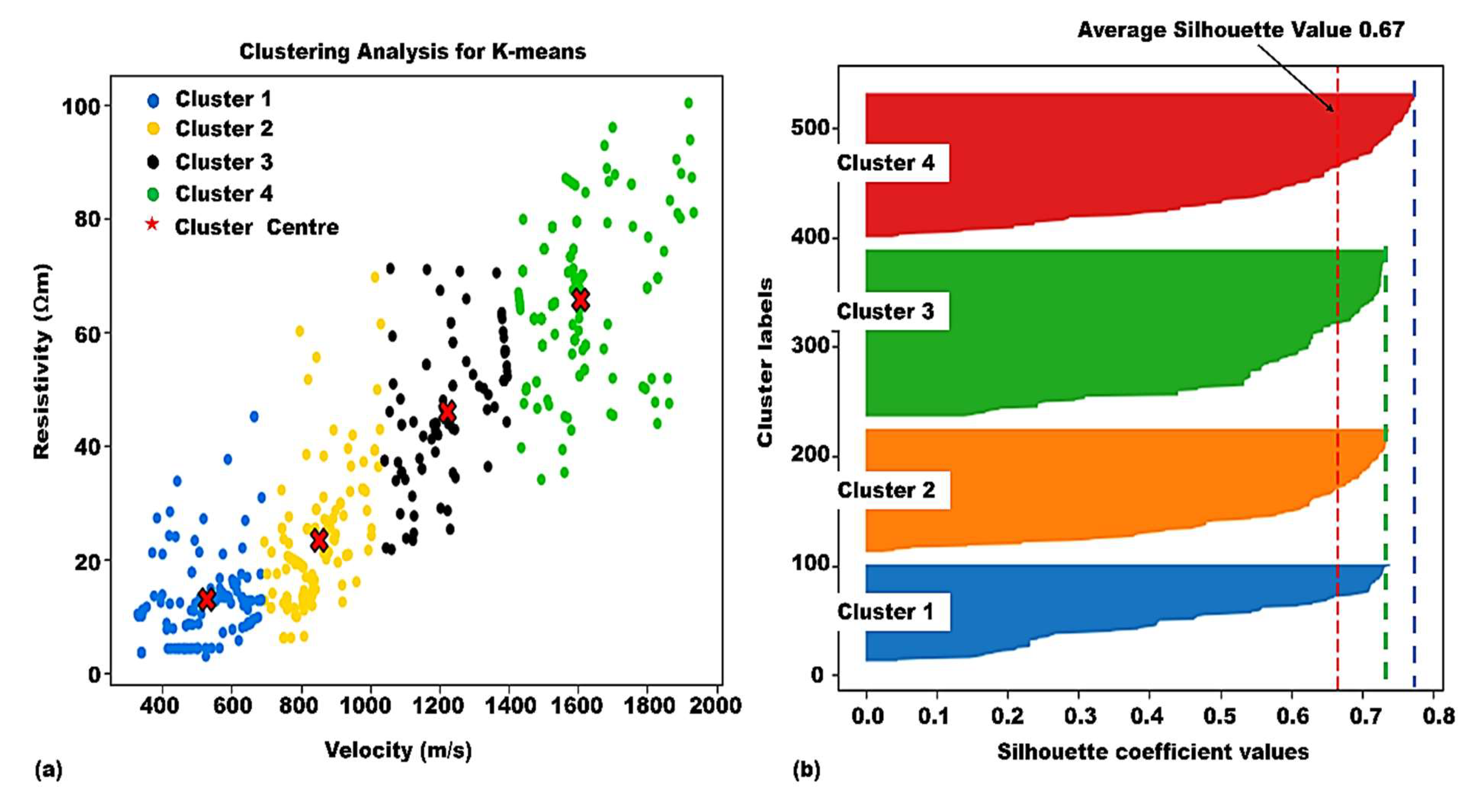
Preprints 148851 g009
Figure 9. (a) Clusters of parameters identified from the transformed dataset using the k-means algorithm revealing the partitioning achieved post-inversion. (b) Silhouette plot illustrating k on four clusters with an average silhouette score of 0.67.
Figure 9. (a) Clusters of parameters identified from the transformed dataset using the k-means algorithm revealing the partitioning achieved post-inversion. (b) Silhouette plot illustrating k on four clusters with an average silhouette score of 0.67.
Preprints 148851 g009
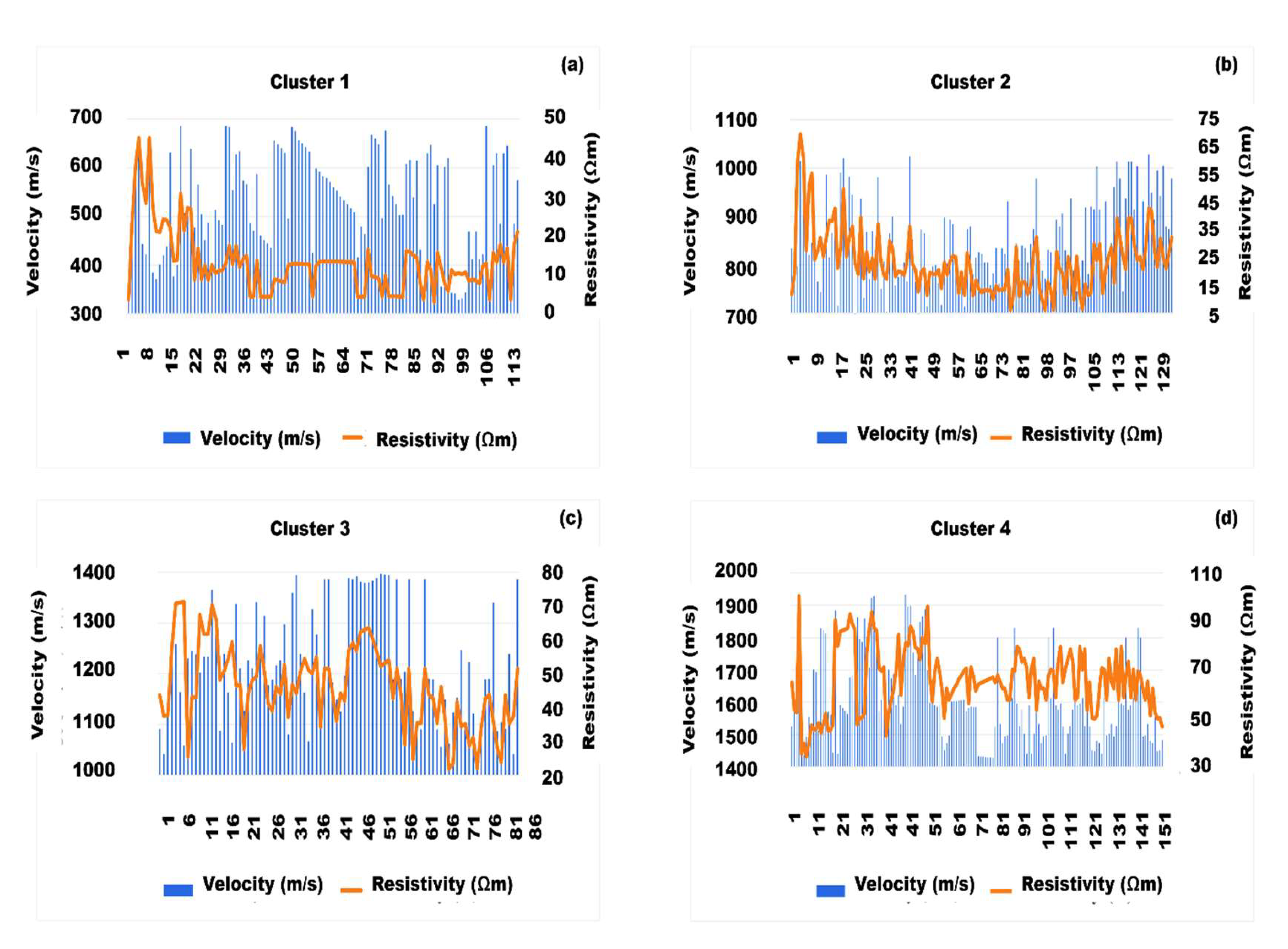
Preprints 148851 g010
Figure 10. Inter-cluster spacings calculated for cluster (!-4), highlighting resistivity arrangement within clusters through histograms illustrating the range of Vp data these clusters.
Figure 10. Inter-cluster spacings calculated for cluster (!-4), highlighting resistivity arrangement within clusters through histograms illustrating the range of Vp data these clusters.
Preprints 148851 g010
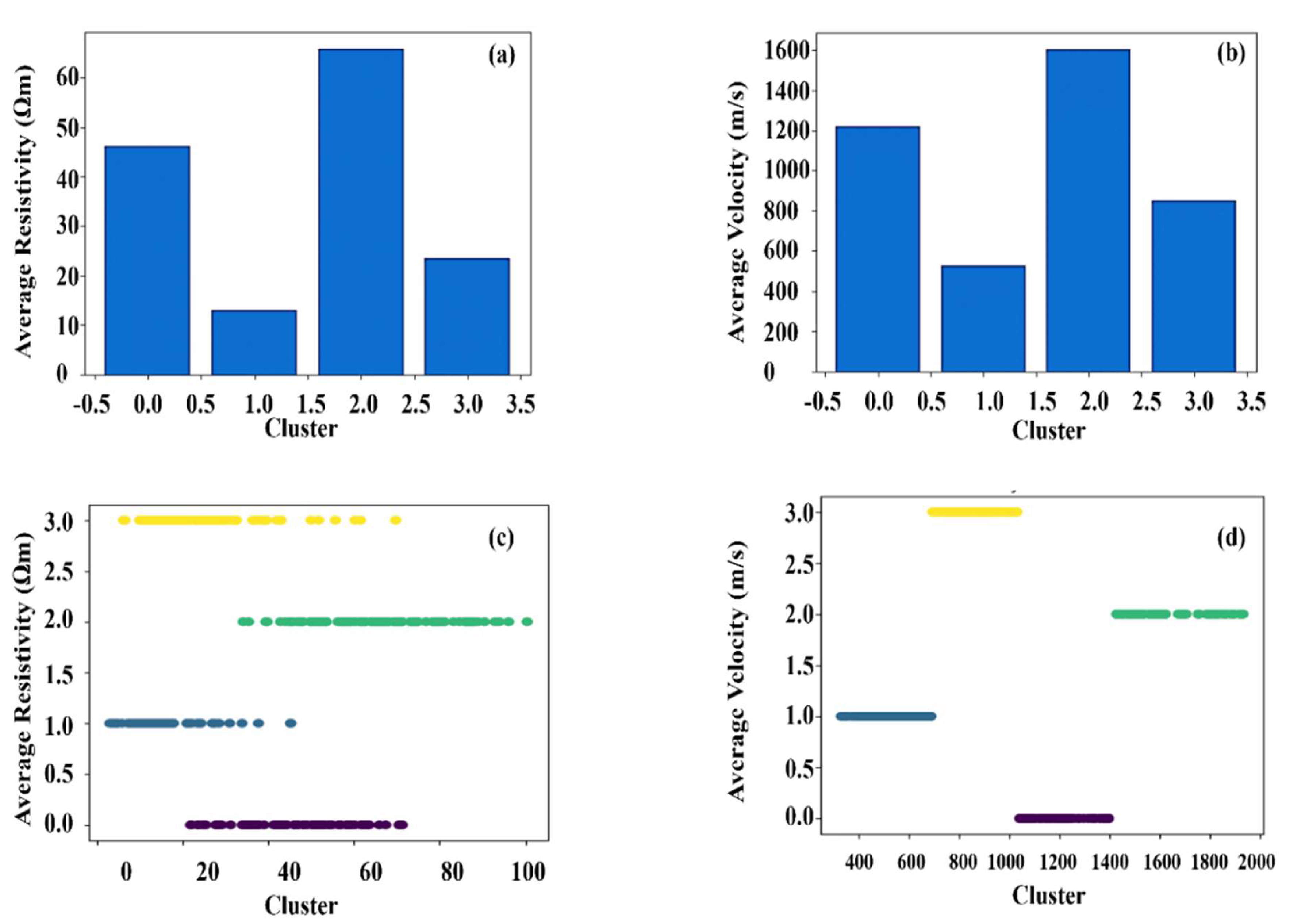
Preprints 148851 g011
Figure 11. Average histogram plots and the cluster range of parameters in each of the clusters.
Figure 11. Average histogram plots and the cluster range of parameters in each of the clusters.
Preprints 148851 g011
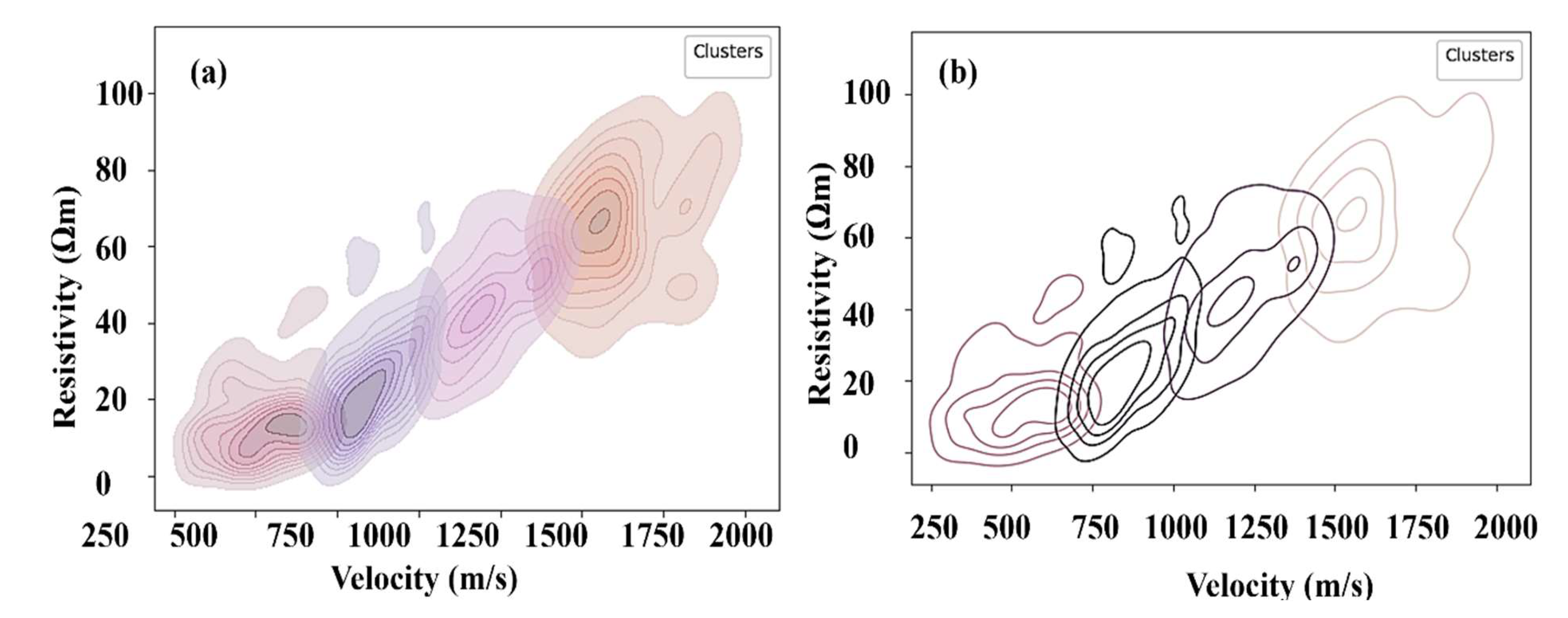
Preprints 148851 g012
Figure 12. Density plots demonstrating (a) clusters and (b) overlapping ranges in different clusters.
Figure 12. Density plots demonstrating (a) clusters and (b) overlapping ranges in different clusters.
Preprints 148851 g012
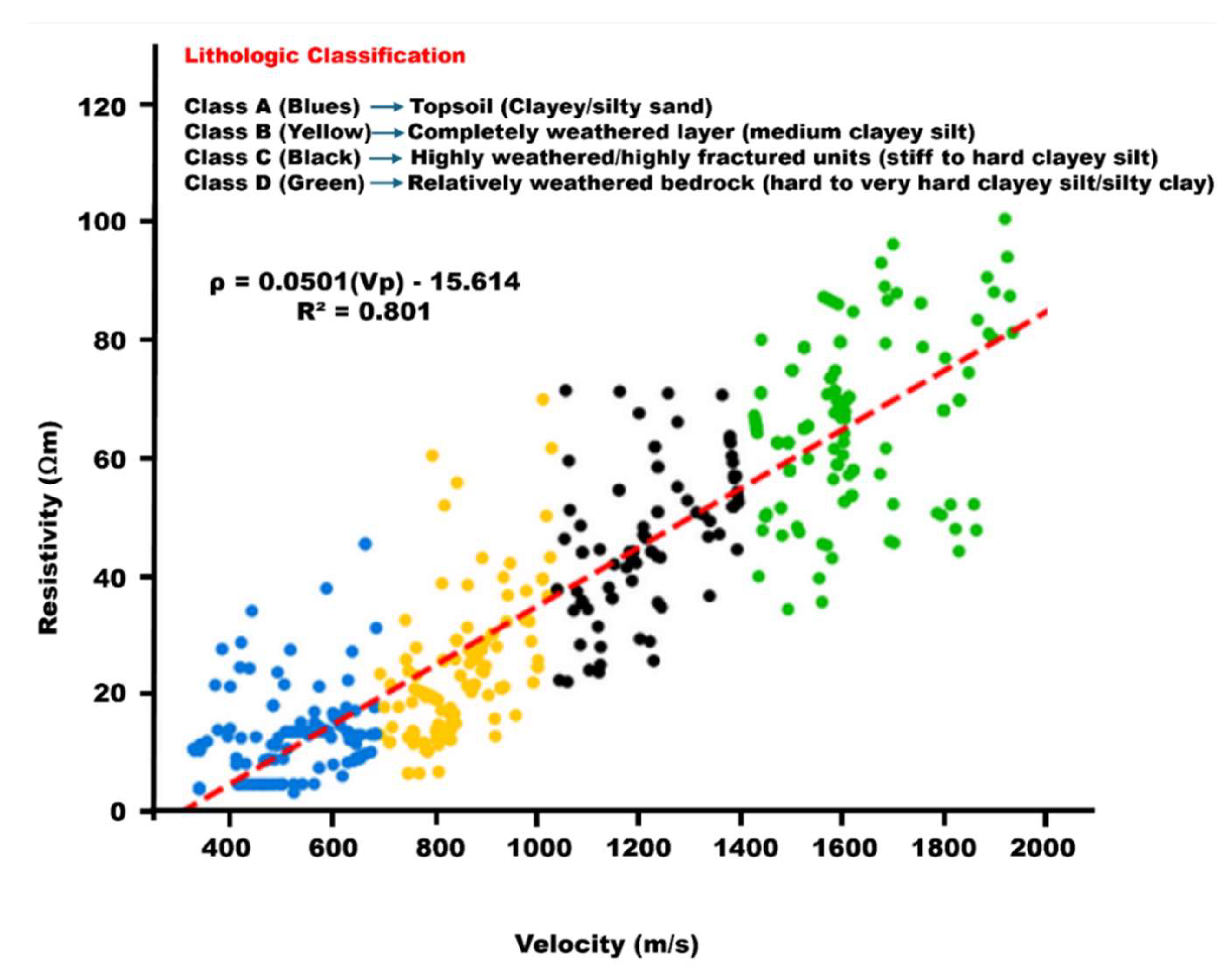
Preprints 148851 g013
Figure 13. Visualization of resistivity–Vp correlation for 491 integrated data points.
Figure 13. Visualization of resistivity–Vp correlation for 491 integrated data points.
Preprints 148851 g013
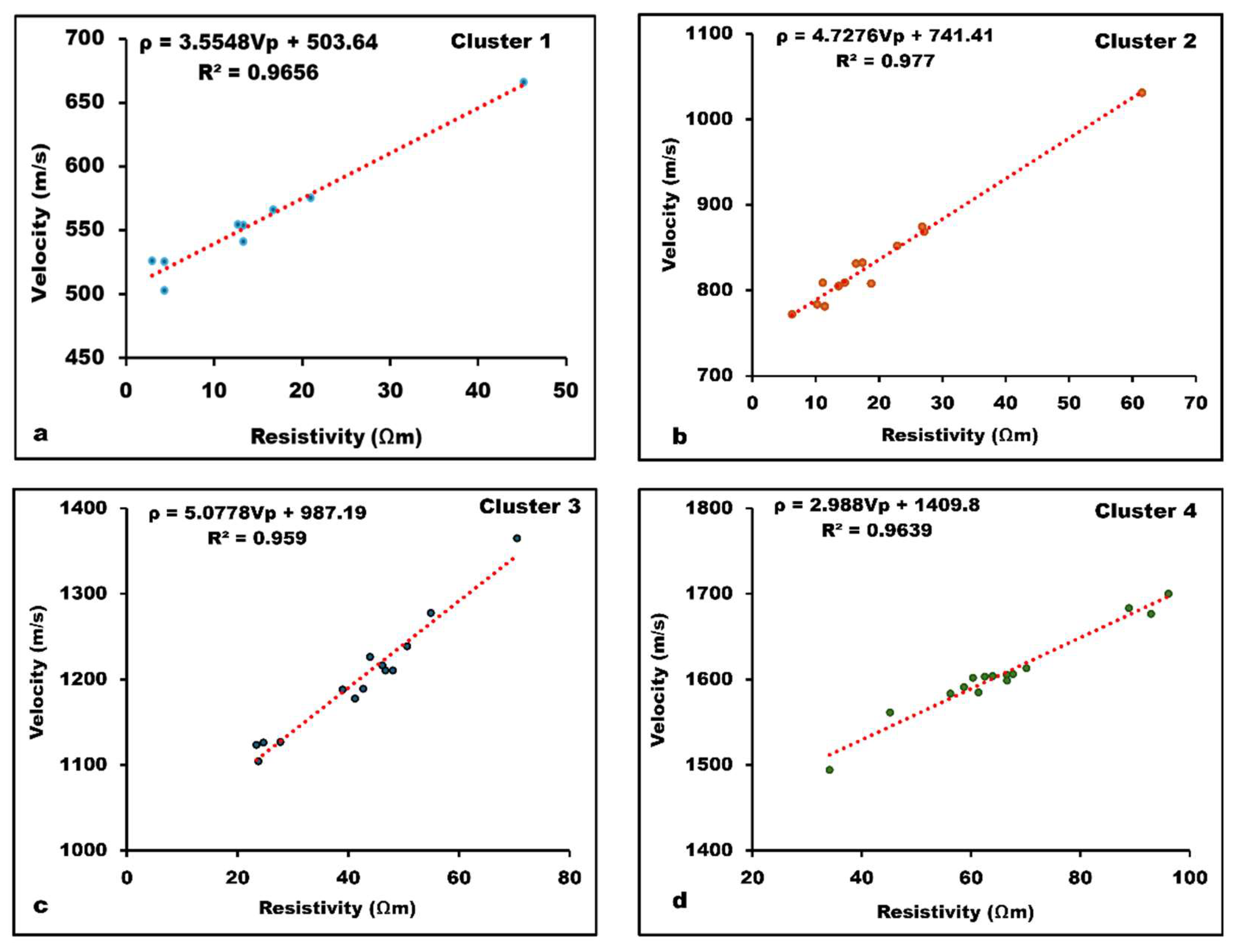
Preprints 148851 g014
Figure 14. Resistivity-Vp regression plot for data point along the line of fit for a specific lithologic unit at Site 1.
Figure 14. Resistivity-Vp regression plot for data point along the line of fit for a specific lithologic unit at Site 1.
Preprints 148851 g014
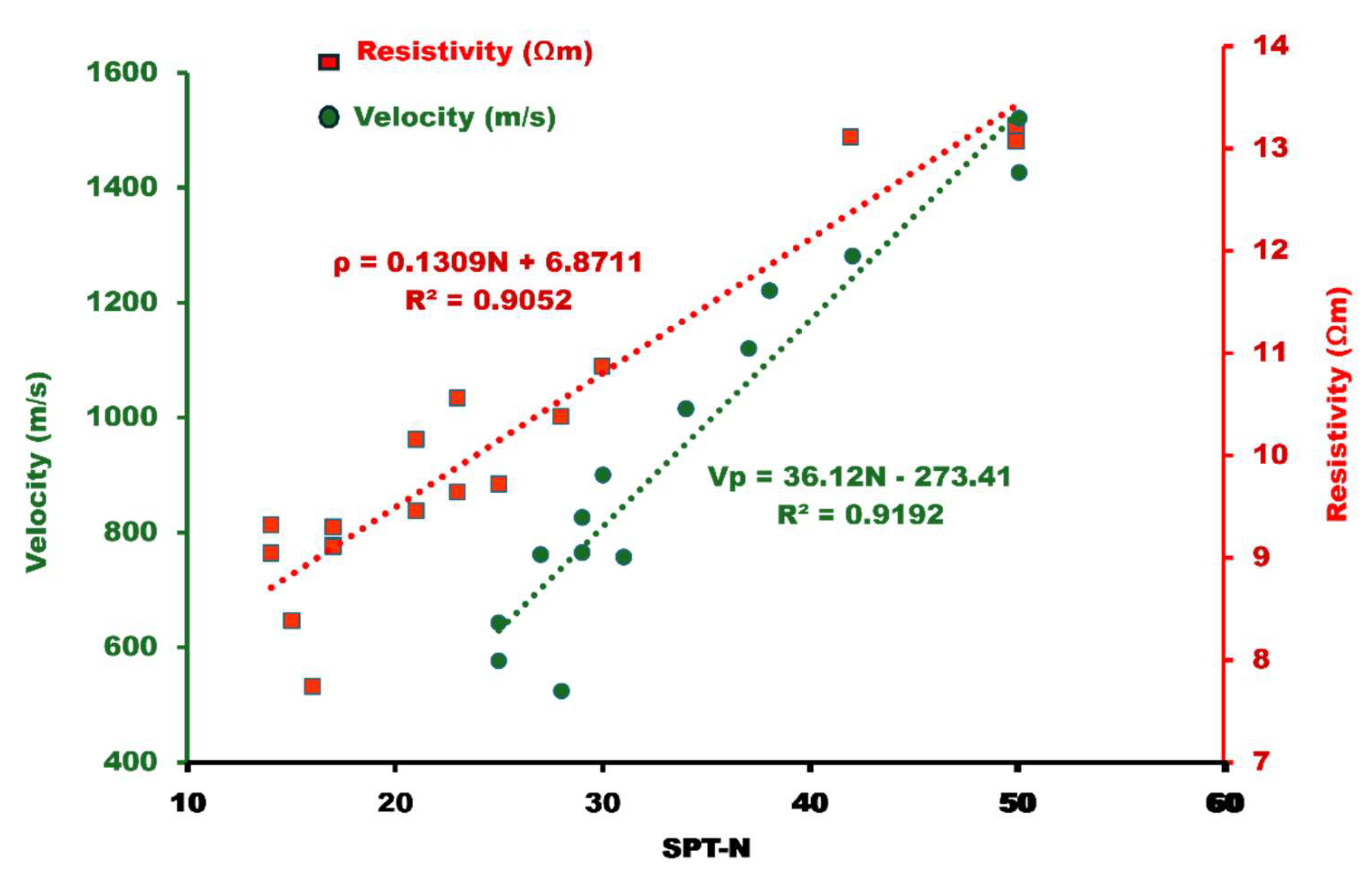
Preprints 148851 g015
Figure 15. SPT-N correlation with seismic velocity and resistivity corresponding to the depth of the SPT-N.
Figure 15. SPT-N correlation with seismic velocity and resistivity corresponding to the depth of the SPT-N.
Preprints 148851 g015
Table 1. Organizing datasets into clusters based on spatial arrangement of of centroids.
Table 1. Organizing datasets into clusters based on spatial arrangement of of centroids.
Number of clusters (k) Vp Centroids (m/s) Resistivity Centroids (Ωm) Silhouette value for each cluster
1 (Blue) 529.02 13.13 0.74
2 (Yellow) 851.86 23.58 0.75
3 (Black) 1221.50 46.11 0.74
4 (Green) 1604.95 65.89 0.78
Table 2. Average Silhouette scores, RS values for each k, and SSE results for spherical and overlapping clusters.
Table 2. Average Silhouette scores, RS values for each k, and SSE results for spherical and overlapping clusters.
Silhouette score for k Average Silhouette score for k WCSS (or SSE)x107 %change of SSE
2 0.58 2.01 ---
3 0.57 102 98.01
4 0.67 9.21 88.96
5 0.59 6.05 1420.69
6 0.58 3.68 64.33
Table 3. Clustering analysis showing Vp-resistivity relationships for lithologic units.
Table 3. Clustering analysis showing Vp-resistivity relationships for lithologic units.
Cluster Vp centroids Resistivity centroids Range of ρvalues (Ωm) Range of Vpvalues (m/s) Lithological units
1 529.02 13.13 0.5–20 <100–700 topsoil (clayey silt)
2 851.86 23.58 5–30 700–1100 completely weathered soil unit (medium-stiff clayey silt)
3 1221.50 46.11 30–50 1100–1400 highly weathered/fractured units (very stiff to hard clayey silt)
4 1604.95 65.89 50 to >125 1400 to >1900 relatively weathered/fractured units (hard to very hard clayey silt)
Table 4. Performance of the predicted equations and their percentage matching.
Table 4. Performance of the predicted equations and their percentage matching.
S/N Velocity (Vp) (m/s) Resistivity (Ωm)
SPT (N) Obs. Vp (m/s) Pred. Vp (m/s) Percentage Matching SPT (N) Observed Resistivity (Ωm) Predicted Resistivity (Ωm) Percentage Matching (%)
1 30 899.55 810.19 90.07 14 9.3154 8.7037 93.4335
2 29 825.58 774.07 93.76 17 9.1196 9.0964 99.7456
3 50 1520.34 1532.59 100.81 17 9.1056 9.0964 99.8990
4 27 760.86 701.83 92.24 30 10.8702 10.7981 99.3367
5 25 641.99 629.59 98.07 42 13.1114 12.3689 94.3369
Table 5. Summary of the resistivity-Vp regression analysis for specific lithologic units and their engineering implications.
Table 5. Summary of the resistivity-Vp regression analysis for specific lithologic units and their engineering implications.
Lithologic units/Clusters Range of Vp values (m/s) Range of ρ values (Ωm) R2 values Engineering Implication
Cluster 1: Topsoil (Clayey/silty sand) <100–700 0–20 0.9656 Unconsolidated lithology which is unsuitable for engineering structures
Cluster 2: Completely weathered layer (medium clayey silt) 700–1100 5– 30 0.9770 Not ideal for extensive construction projects; moderate compaction is recommended for lighter structures with enhanced reinforcement.
Cluster 3: Highly weathered/highly fractured units (stiff to hard clayey silt) 1100–1400 30–50 0.9590 Moderate compaction is needed, along with excavation of loose soils and sealing water paths, to strengthen the load-bearing capacity.
Cluster 4: Relatively weathered bedrock (hard to very hard clayey silt/silty clay) 1400 to >1900 50 to >125 0.9639 Well-compacted, making the layer more reliable for supporting heavy loads, complex, and stable structures. Sealing continuous water sections further improves load-bearing capacity.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
bsky
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

Privacy Settings

© 2025 MDPI (Basel, Switzerland) unless otherwise stated