Submitted:
31 January 2025
Posted:
04 February 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Materials and Methods
2.1. Sensors and Measurements
2.1.1. Research Grade Sensor: Palas Fidas Frog
- PM1.0: Particulate Matter with an aerodynamic diameter ≤ 1.0 m (unit is g/m3).
- PM2.5 Particulate Matter with an aerodynamic diameter ≤ 2.5 m (unit is g/m3).
- PM4.0: Particulate Matter with an aerodynamic diameter ≤ 4.0 m (unit is g/m3).
- PM10.0: Particulate Matter with an aerodynamic diameter ≤ 10.0 m (unit is g/m3).
- Total PM Concentration: The overall concentration of particulate matter across different size fractions (unit is g/m3).
- Particle Count Density: The number of particles per unit volume of air (unit is number of particles/cm3 or #/cm3).
2.2. Low Cost Sensor: LoRaWAN Prototype
-
PPD42NS: Particle CounterThe PPD42NS (Figure 2 (a)) [17] is the primary PM sensor in the LoRa Node It is an affordable optical sensor designed to measure parameters associated with particulate matter (PM) concentrations for two size ranges, detected via two separate channels. Channel 1 measures parameters associated with particulates larger than 1 m in diameter, while Channel 2 measures parameters associated with particulates larger than 2.5 m in diameter. The measurement range for PM concentration is approximately 0 to 28,000 g/m3 for both >1 m (P1) and >2.5 m (P2) particle sizes.The sensor operates based on the Low Pulse Occupancy (LPO) principle. When particles pass through the sensor’s optical chamber, they scatter the light emitted by an LED. This scattered light is detected by a photodiode, which outputs a pulse width-modulated (PWM) signal. The duration of the PWM signal is proportional to the particle count and size. LPO is defined as the amount of time during which this PWM signal is low during a fixed sampling interval (15 seconds in this study). The standard error for LPO is approximately 0.02 units for both channels under low-concentration conditions (< 50 g/m3). Under high-concentration conditions (≥ 50 g/m3), the error varies non-linearly [18,19].The following parameters are measured by the PPD42NS:
- –
- P1 LPO: Represents the total time for Channel 1 (indicating the presence of particles larger than 1 m) during which the sensor signal is low in a 15-second sampling period. It is also referred to as the > 1 μm LPO and is measured in milliseconds.
- –
- P1 Ratio: Represents the proportion of time the sensor signal is low for Channel 1 (indicating the presence of particles larger than 1 m) during the sampling period. It is also referred to as the > 1 μm ratio.
- –
- P1 Concentration: Measures the PM concentration of particles larger than 1 m in diameter. It is also referred to as the > 1 μm concentration and is measured in g/m3.
- –
- P2 LPO: Represents the total time for Channel 2 (indicating the presence of particles larger than 2.5 m) during which the sensor signal is low in a 15-second sampling period. It is also referred to as the > 2.5 μm LPO and is measured in milliseconds.
- –
- P2 Ratio: Represents the proportion of time the sensor signal is low for Channel 2 (indicating the presence of particles larger than 2.5 m) during the sampling period. It is also referred to as the > 2.5 μm ratio.
- –
- P2 Concentration: Measures the PM concentration of particles larger than 2.5 m in diameter. It is also referred to as the > 2.5 μm concentration and is measured in g/m3.
-
BME280: Climate SensorThe BME280 (Figure 2 (b)) is the climate sensor used in the LoRa Node. It measures Air Temperature (referred to as Temperature), Atmospheric Pressure (referred to as Pressure), and Relative Humidity (referred to as Humidity), which are critical for understanding environmental conditions and calibrating the PM sensor. The BME280 sensor can measure temperatures ranging from -40 °C to 85 °C with an accuracy of ±0.5 °C, pressure from 300 hPa to 1100 hPa with an accuracy of ±1.0 hPa, and humidity from 0% to 100% with an accuracy of ±3%,[20].
2.3. Data Collection
2.4. Supervised Machine Learning Approach for Calibration
2.4.1. Super Learner
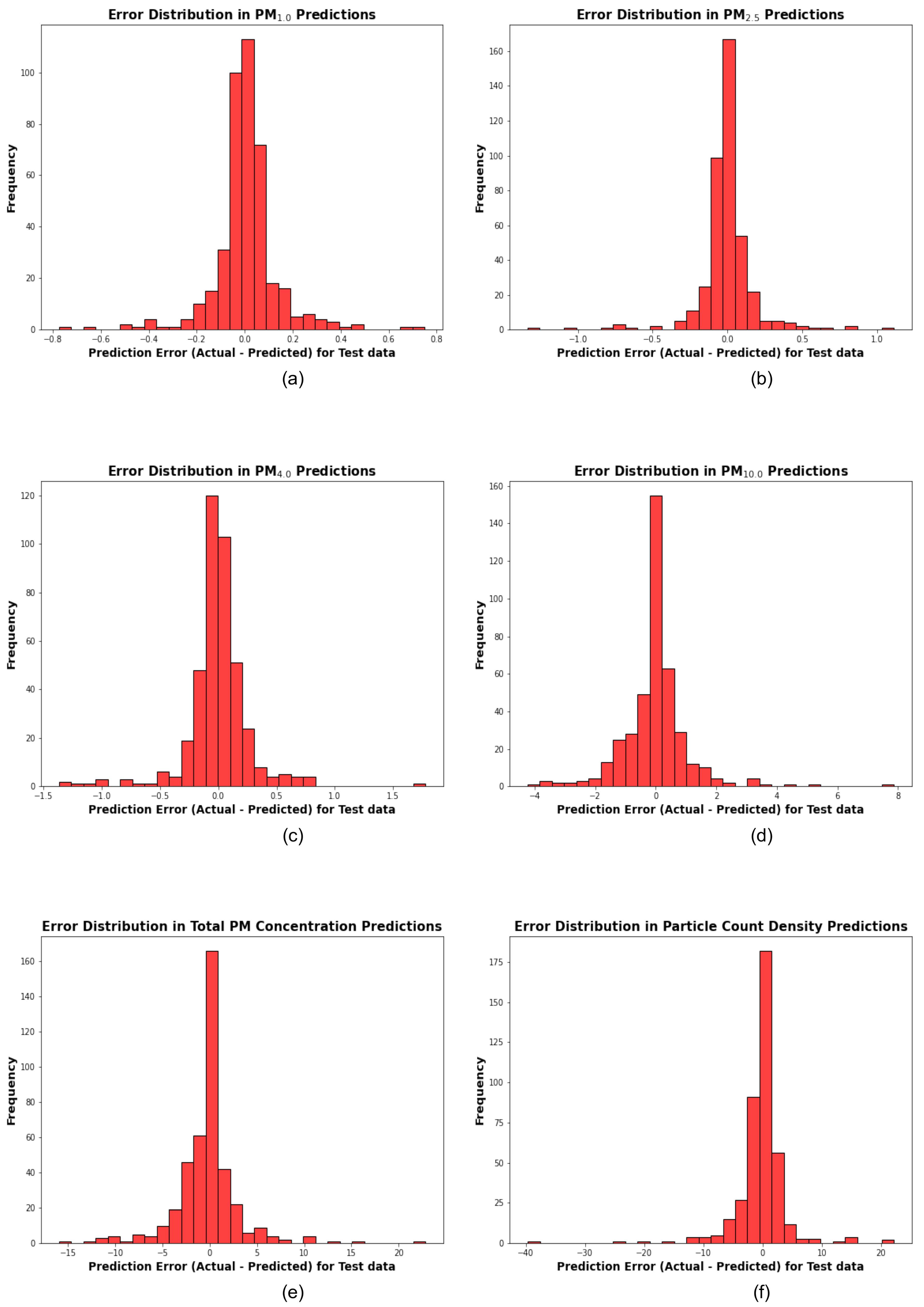
2.4.2. Metric for Calibration
- is the actual target value for the i-th data point,
- is the predicted target value for the i-th data point,
- is the mean of all target values, and
- N is the total number of data points.
2.4.3. Hyperparameter Tuning
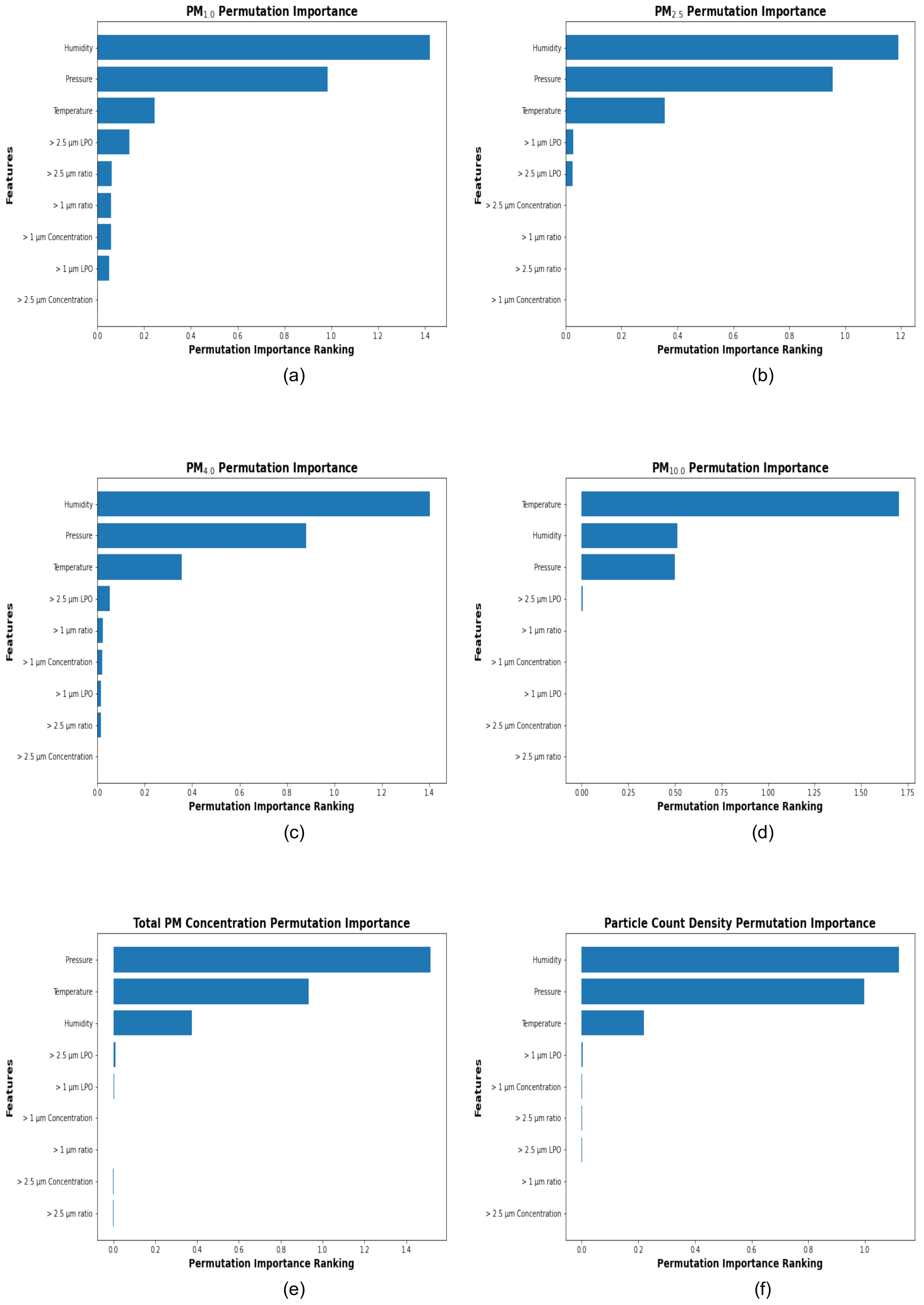
2.4.4. Permutation Importance
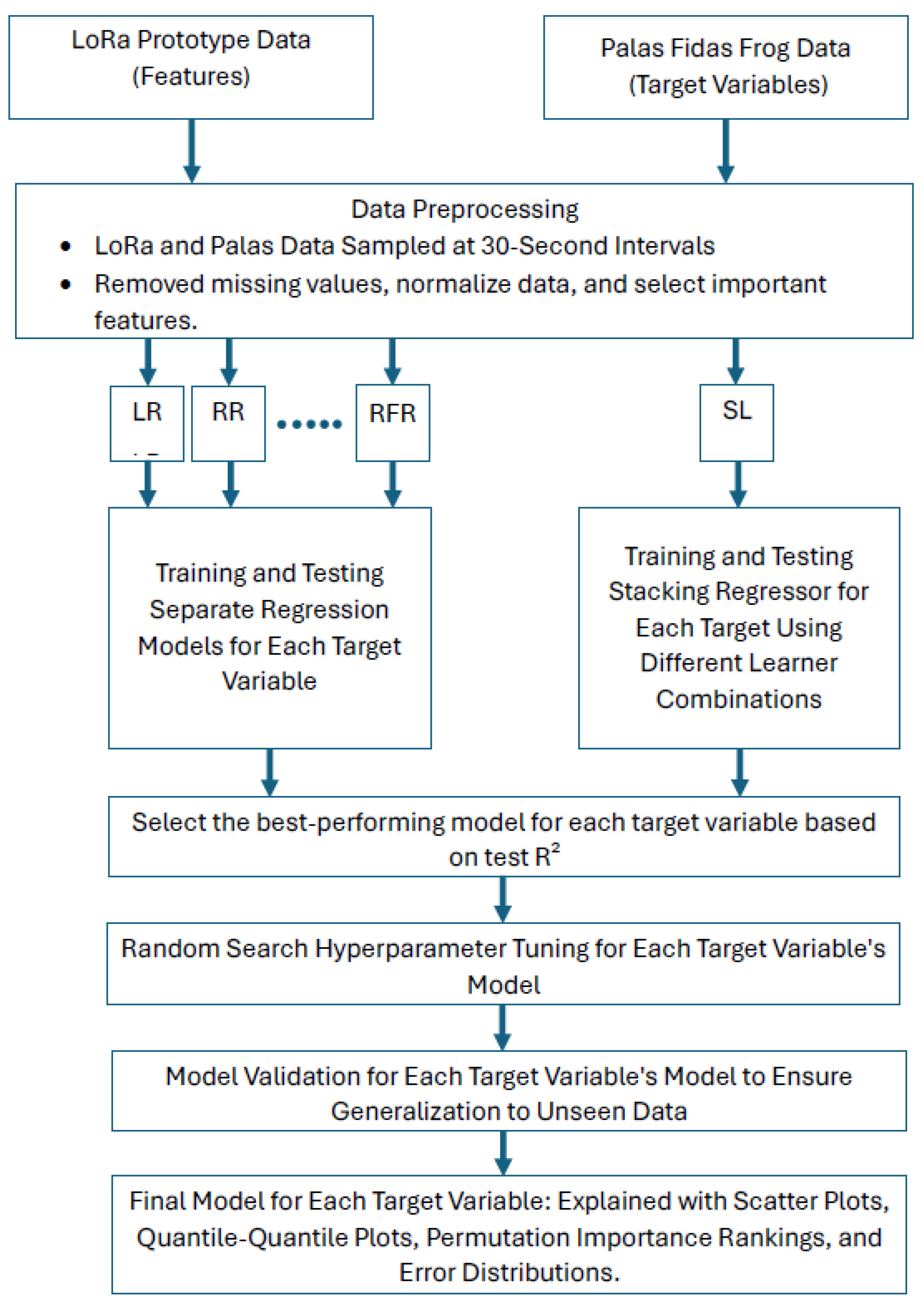
2.4.5. Basic Machine Learning Work Flow
2.4.6. Data Preprocessing
3. Results
4. Challenges and Future Work
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| General Technical Terms | |
| CSV | Comma-Separated Values |
| FEM | Federal Equivalent Method |
| IoT | Internet of Things |
| LoRaWAN | Long Range Wide Area Network |
| LPO | Low Pulse Occupancy |
| Probability Density Function | |
| PM | Particulate Matter |
| PM1.0 | Particulate Matter with an aerodynamic diameter ≤ 1.0 m |
| PM2.5 | Particulate Matter with an aerodynamic diameter ≤ 2.5 m |
| PM4.0 | Particulate Matter with an aerodynamic diameter ≤ 4.0 m |
| PM10.0 | Particulate Matter with an aerodynamic diameter ≤ 10.0 m |
| PWM | Pulse Width Modulation |
| Quantile - Quantile | |
| R2 | R-squared or Coefficient of Determination |
| UTD | University of Texas at Dallas |
| WLAN | Wireless Local Area Network |
| WSTC | Waterview Science and Technology Center |
| Model and Method-Related Terms | |
| DT | Decision Tree |
| EB | Ensemble Bagging |
| KNN | K-Nearest Neighbors |
| LightGBM | Light Gradient Boosting Machine |
| LR | Linear Regression |
| NN | Neural Networks |
| RF | Random Forest |
| RR | Ridge Regression |
| SL | Super Learner |
| XGBoost | Extreme Gradient Boosting |
References
- Zimmerman, N.; Presto, A.A.; Kumar, S.P.; Gu, J.; Hauryliuk, A.; Robinson, E.S.; Robinson, A.L.; Subramanian, R. A machine learning calibration model using random forests to improve sensor performance for lower-cost air quality monitoring. Atmospheric Measurement Techniques 2018, 11, 291–313. [Google Scholar] [CrossRef]
- Alfano, B.; Barretta, L.; Del Giudice, A.; De Vito, S.; Di Francia, G.; Esposito, E.; Formisano, F.; Massera, E.; Miglietta, M.L.; Polichetti, T. A review of low-cost particulate matter sensors from the developers’ perspectives. Sensors 2020, 20, 6819. [Google Scholar] [CrossRef]
- Concas, F.; Mineraud, J.; Lagerspetz, E.; Varjonen, S.; Liu, X.; Puolamäki, K.; Nurmi, P.; Tarkoma, S. Low-cost outdoor air quality monitoring and sensor calibration: A survey and critical analysis. ACM Transactions on Sensor Networks (TOSN) 2021, 17, 1–44. [Google Scholar] [CrossRef]
- Clarity. Low-Cost Sensors for Comprehensive Air Quality Management, 2025. Available at: https://www.clarity.io/blog/low-cost-sensors-for-comprehensive-air-quality-management (Accessed: 2025-01-31).
- Caldas, F.; Soares, C. Machine learning in orbit estimation: A survey. Acta Astronautica 2024. [Google Scholar] [CrossRef]
- Styp-Rekowski, K.; Michaelis, I.; Stolle, C.; Baerenzung, J.; Korte, M.; Kao, O. Machine learning-based calibration of the GOCE satellite platform magnetometers. Earth, Planets and Space 2022, 74, 138. [Google Scholar] [CrossRef]
- Naimi, A.I.; Balzer, L.B. Stacked generalization: An introduction to super learning. European Journal of Epidemiology 2018, 33, 459–464. [Google Scholar] [CrossRef]
- Wijeratne, L.O.H. Coupling Physical Measurement with Machine Learning for Holistic Environmental Sensing. PhD thesis, University of Texas at Dallas, Dallas, Texas, USA, 2021.
- de Carvalho Silva, J.; Rodrigues, J.J.; Alberti, A.M.; Solic, P.; Aquino, A.L. LoRaWAN—A low power WAN protocol for Internet of Things: A review and opportunities. In Proceedings of the 2017 2nd International Multidisciplinary Conference on Computer and Energy Science (SpliTech). IEEE, 2017, pp. 1–6.
- Haxhibeqiri, J.; De Poorter, E.; Moerman, I.; Hoebeke, J. A survey of LoRaWAN for IoT: From technology to application. Sensors 2018, 18, 3995. [Google Scholar] [CrossRef]
- Adelantado, F.; Vilajosana, X.; Tuset-Peiro, P.; Martinez, B.; Melia-Segui, J.; Watteyne, T. Understanding the Limits of LoRaWAN. IEEE Communications Magazine 2017, 55, 34–40. [Google Scholar] [CrossRef]
- Thu, M.Y.; Htun, W.; Aung, Y.L.; Shwe, P.E.E.; Tun, N.M. Smart air quality monitoring system with LoRaWAN. In Proceedings of the 2018 IEEE International Conference on Internet of Things and Intelligence System (IOTAIS). IEEE, 2018, pp. 10–15.
- Bonilla, V.; Campoverde, B.; Yoo, S.G. A Systematic Literature Review of LoRaWAN: Sensors and Applications. Sensors 2023, 23, 8440. [Google Scholar] [CrossRef]
- Palas GmbH. Fidas Frog Product Datasheet, 2025. Available at: https://www.palas.de/en/product/download/fidasfrog/datasheet/pdf (Accessed: 2025-01-02).
- Palas GmbH. Palas Fidas Frog: Mobile Fine Dust Aerosol Spectrometer, 2025. Available at: https://www.palas.de/en/frog#techniquePage (Accessed: 2025-01-31).
- Lock, J.A.; Gouesbet, G. Generalized Lorenz–Mie theory and applications. Journal of Quantitative Spectroscopy and Radiative Transfer 2009, 110, 800–807. [Google Scholar] [CrossRef]
- Seeed Studio. Grove Dust Sensor Product Datasheet, 2025. Available at: https://www.mouser.com/datasheet/2/744/Seeed_101020012-1217636.pdf (Accessed: 2025-01-11).
- Canu, M.; Galvis, B.; Morales, R.; Ramírez, O.; Madelin, M. Understanding the Shinyei PPD24NS Low-Cost Dust Sensor. In Proceedings of the 2018 IEEE International Conference on Environmental Engineering, Milan, Italy, 2018.
- Austin, E.; Novosselov, I.; Seto, E.; Yost, M.G. Laboratory Evaluation of the Shinyei PPD42NS Low-Cost Particulate Matter Sensor. PLOS ONE 2015, 10, e0137789. [Google Scholar]
- Bosch Sensortec. BME280: Combined Humidity and Pressure Sensor Datasheet, 2025. Available at: https://www.bosch-sensortec.com/media/boschsensortec/downloads/datasheets/bst-bme280-ds002.pdf (Accessed: 2025-01-11).
- El Naqa, I.; Murphy, M.J. What is Machine Learning?; Springer, 2015.
- Sykes, A.O. An Introduction to Regression Analysis. Coase-Sandor Institute for Law and Economics Working Paper 1993, 20, 1–39. [Google Scholar]
- Ruwali, S.; Fernando, B.; Talebi, S.; Wijeratne, L.; Waczak, J.; Madusanka, P.M.; Lary, D.J.; Sadler, J.; Lary, T.; Lary, M.; et al. Estimating Inhaled Nitrogen Dioxide from the Human Biometric Response. Advances in Environmental and Engineering Research 2024, 5, 1–12. [Google Scholar] [CrossRef]
- Ruwali, S.; Fernando, B.A.; Talebi, S.; Wijeratne, L.; Waczak, J.; Sooriyaarachchi, V.; Hathurusinghe, P.; Lary, D.J.; Sadler, J.; Lary, T.; et al. Gauging ambient environmental carbon dioxide concentration solely using biometric observations: A machine learning approach. Medical Research Archives 2024, 12. [Google Scholar]
- Ruwali, S.; Talebi, S.; Fernando, A.; Wijeratne, L.O.; Waczak, J.; Dewage, P.M.; Lary, D.J.; Sadler, J.; Lary, T.; Lary, M.; et al. Quantifying Inhaled Concentrations of Particulate Matter, Carbon Dioxide, Nitrogen Dioxide, and Nitric Oxide Using Observed Biometric Responses with Machine Learning. BioMedInformatics 2024, 4, 1019–1046. [Google Scholar] [CrossRef]
- Dong, X.; Yu, Z.; Cao, W.; Shi, Y.; Ma, Q. A Survey on Ensemble Learning. Frontiers of Computer Science 2020, 14, 241–258. [Google Scholar] [CrossRef]
- Sibindi, R.; Mwangi, R.W.; Waititu, A.G. A Boosting Ensemble Learning-Based Hybrid Light Gradient Boosting Machine and Extreme Gradient Boosting Model for Predicting House Prices. Engineering Reports 2023, 5, e12599. [Google Scholar] [CrossRef]
- Cohen, W.W.; Carvalho, V.R. Stacked Sequential Learning. CRF Technical Report 2005, 1, 1–17. [Google Scholar]
- Džeroski, S.; Ženko, B. Is Combining Classifiers with Stacking Better than Selecting the Best One? Machine Learning 2004, 54, 255–273. [Google Scholar] [CrossRef]
- Ozer, D.J. Correlation and the Coefficient of Determination. Psychological Bulletin 1985, 97, 307. [Google Scholar] [CrossRef]
- Bergstra, J.; Bengio, Y. Random Search for Hyper-Parameter Optimization. Journal of Machine Learning Research 2012, 13, 281–305. [Google Scholar]
- Altmann, A.; Toloşi, L.; Sander, O.; Lengauer, T. Permutation Importance: A Corrected Feature Importance Measure. Bioinformatics 2010, 26, 1340–1347. [Google Scholar] [CrossRef] [PubMed]
- Zender-Świercz, E.; Galiszewska, B.; Telejko, M.; Starzomska, M. The effect of temperature and humidity of air on the concentration of particulate matter-PM2.5 and PM10. Atmospheric Research 2024, 312, 107733. [Google Scholar] [CrossRef]
- Kim, M.; Jeong, S.G.; Park, J.; Kim, S.; Lee, J.H. Investigating the impact of relative humidity and air tightness on PM sedimentation and concentration reduction. Building and Environment 2023, 241, 110270. [Google Scholar] [CrossRef]
- Lou, C.; Liu, H.; Li, Y.; Peng, Y.; Wang, J.; Dai, L. Relationships of relative humidity with PM 2.5 and PM 10 in the Yangtze River Delta, China. Environmental Monitoring and Assessment 2017, 189, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Cheng, Y.; Zhang, Y.; He, Y.; Gu, Z.; Yu, C.; et al. Impact of air humidity fluctuation on the rise of PM mass concentration based on the high-resolution monitoring data. Aerosol and Air Quality Research 2017, 17, 543–552. [Google Scholar] [CrossRef]
- Haikerwal, A.; Akram, M.; Del Monaco, A.; Smith, K.; Sim, M.R.; Meyer, M.; Tonkin, A.M.; Abramson, M.J.; Dennekamp, M. Impact of fine particulate matter (PM 2.5) exposure during wildfires on cardiovascular health outcomes. Journal of the American Heart Association 2015, 4, e001653. [Google Scholar] [CrossRef]
- Péré, J.; Bessagnet, B.; Mallet, M.; Waquet, F.; Chiapello, I.; Minvielle, F.; Pont, V.; Menut, L. Direct radiative effect of the Russian wildfires and its impact on air temperature and atmospheric dynamics during August 2010. Atmospheric Chemistry and Physics 2014, 14, 1999–2013. [Google Scholar] [CrossRef]
- Shaposhnikov, D.; Revich, B.; Bellander, T.; Bedada, G.B.; Bottai, M.; Kharkova, T.; Kvasha, E.; Lezina, E.; Lind, T.; Semutnikova, E.; et al. Mortality related to air pollution with the Moscow heat wave and wildfire of 2010. Epidemiology 2014, 25, 359–364. [Google Scholar] [CrossRef]
- Alvarez, H.B.; Echeverria, R.S.; Alvarez, P.S.; Krupa, S. Air quality standards for particulate matter (PM) at high altitude cities. Environmental Pollution 2013, 173, 255–256. [Google Scholar] [CrossRef]
- Chen, Z.; Cheng, S.; Li, J.; Guo, X.; Wang, W.; Chen, D. Relationship between atmospheric pollution processes and synoptic pressure patterns in northern China. Atmospheric Environment 2008, 42, 6078–6087. [Google Scholar] [CrossRef]
- Li, H.; Guo, B.; Han, M.; Tian, M.; Zhang, J. Particulate matters pollution characteristic and the correlation between PM (PM2.5, PM10) and meteorological factors during the summer in Shijiazhuang. Journal of Environmental Protection 2015, 6, 457–463. [Google Scholar] [CrossRef]
- Czernecki, B.; Półrolniczak, M.; Kolendowicz, L.; Marosz, M.; Kendzierski, S.; Pilguj, N. Influence of the atmospheric conditions on PM 10 concentrations in Poznań, Poland. Journal of Atmospheric Chemistry 2017, 74, 115–139. [Google Scholar] [CrossRef]
- Kaiser Permanente. Air Quality Program Expands with Kaiser Permanente Grant, 2025. Available at: https://about.kaiserpermanente.org/news/press-release-archive/air-quality-program-expands-with-kaiser-permanente-grant (Accessed: 2025-01-31).
- New York City Department of Health and Mental Hygiene. Air Quality: NYC Community Air Survey (NYCCAS), 2025. Available at: https://www.nyc.gov/site/doh/data/data-sets/air-quality-nyc-community-air-survey.page (Accessed: 2025-01-31).
- Breathe London. Breathe London: Mapping Air Pollution in Real-Time, 2025. Available at: https://www.breathelondon.org/ (Accessed: 2025-01-31).
- Chu, J. A new approach could change how we track extreme air pollution events, 2021. Available at: https://news.mit.edu/2021/new-approach-could-change-how-we-track-extreme-air-pollution-events-0630 (Accessed: 2025-01-31).
- Rika Sensors. The Importance of Air Quality Sensors, 2025. Available at: https://www.rikasensor.com/blog-the-importance-of-air-quality-sensors.html (Accessed: 2025-01-31).
- Jayaratne, R.; Liu, X.; Thai, P.; Dunbabin, M.; Morawska, L. The influence of humidity on the performance of a low-cost air particle mass sensor and the effect of atmospheric fog. Atmospheric Measurement Techniques 2018, 11, 4883–4890. [Google Scholar] [CrossRef]
- Papadimitriou, C.H. Computational complexity; Encyclopedia of Computer Science, 2003; pp. 260–265.
- Wong, J.; Manderson, T.; Abrahamowicz, M.; Buckeridge, D.L.; Tamblyn, R. Can hyperparameter tuning improve the performance of a super learner?: A case study. Epidemiology 2019, 30, 521–531. [Google Scholar] [CrossRef]
- Chou, Y. R Parallel Processing for Developing Ensemble Learning with SuperLearner, 2019. Available at: https://yungchou.wordpress.com/2019/01/16/r-parallel-processing-for-developing-ensemble-learning-with-superlearner/ (Accessed: 2025-01-31).
- UNICEF. Sustainable Development Goals, 2025. Available at: https://www.unicef.org/sustainable-development-goals (Accessed: 2025-01-30).
- United Nations. Sustainable Development Goal 3: Ensure healthy lives and promote well-being for all at all ages, 2025. Available at: https://sdgs.un.org/goals/goal3 (Accessed: 2025-01-31).
- Clarity Movement, Co. . The Myriad Use Cases for Low-Cost Air Quality Sensors, 2025. Available at: https://www.clarity.io/blog/the-myriad-use-cases-for-low-cost-air-quality-sensors (Accessed: 2025-01-30).
- United Nations. Sustainable Development Goal 7: Ensure access to affordable, reliable, sustainable and modern energy for all, 2025. Available at: https://sdgs.un.org/goals/goal7 (Accessed: 2025-01-31).
- United Nations. Sustainable Development Goal 11: Make cities and human settlements inclusive, safe, resilient, and sustainable, 2025. Available at: https://sdgs.un.org/goals/goal11 (Accessed: 2025-01-31).
- United Nations. Sustainable Development Goal 9: Build resilient infrastructure, promote inclusive and sustainable industrialization and foster innovation, 2025. Available at: https://sdgs.un.org/goals/goal9 (Accessed: 2025-01-31).
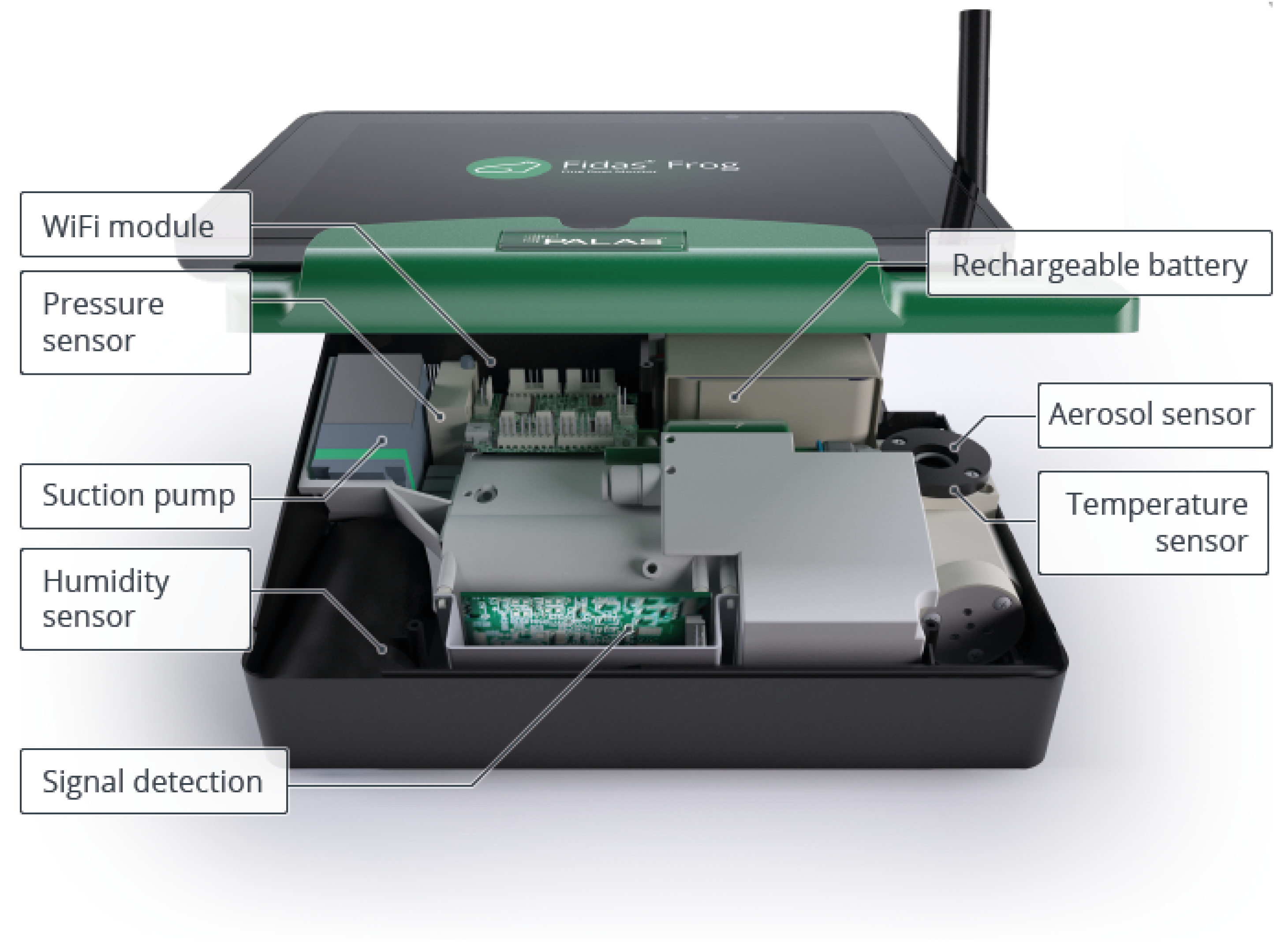

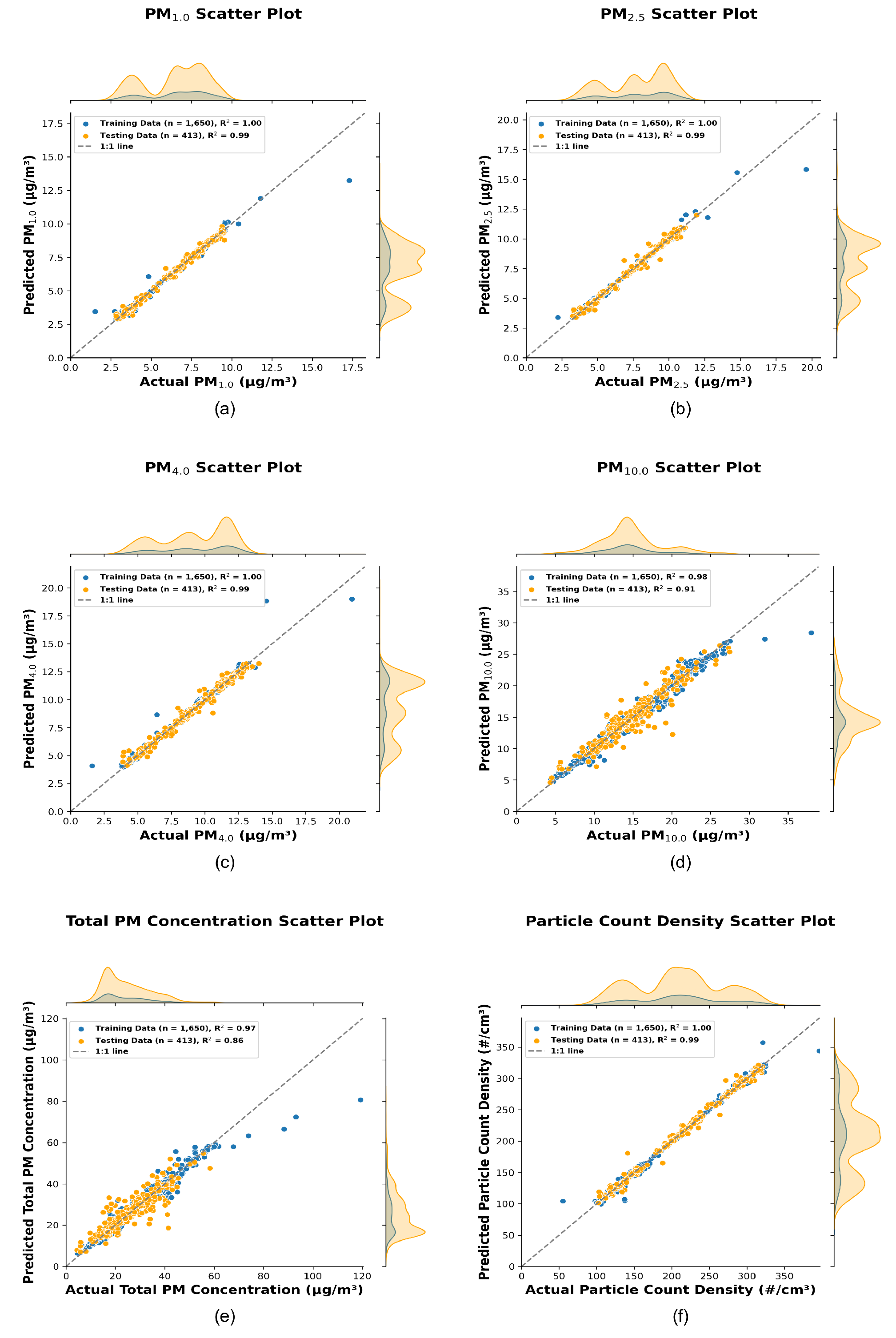
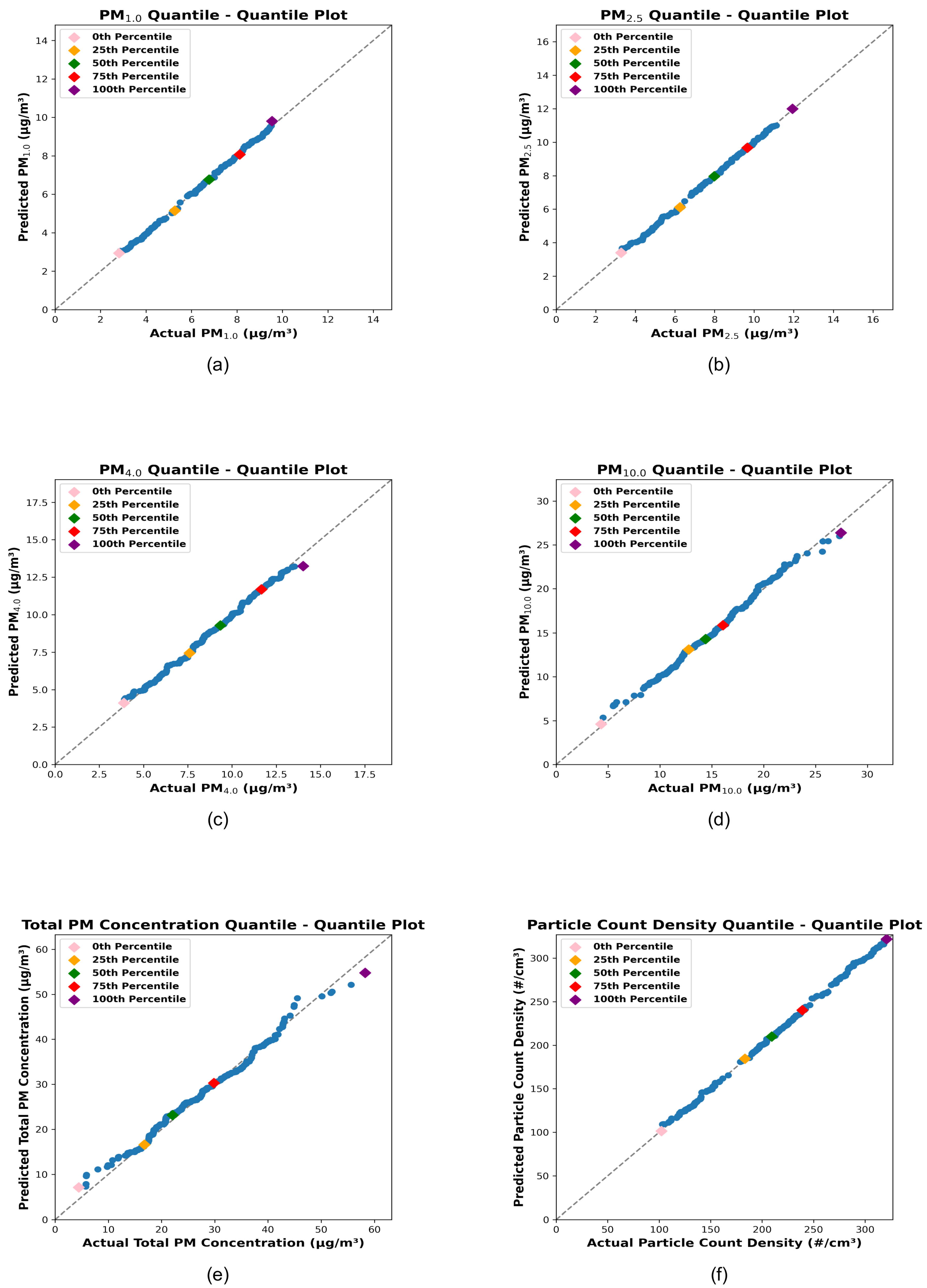
| Specification | Palas Fidas Frog | LoRaWAN Prototype |
|---|---|---|
| Measurement Range (PM) | 0 – 100 mg/m3 | 0 – 28,000 g/m3 |
| Particle Size Range | 0.18 – 93 m | > 1 m, > 2.5 m |
| Measurement Uncertainty | 9.7% (PM2.5), 7.5% (PM10) | 2% |
| Power Source | Battery-operated | Solar-powered |
| Cost | Approximately $20,000 USD | $100 – $200 USD |
| Model | PM1.0 | PM2.5 | PM4.0 | PM10.0 | Total PM Conc. | Particle Count Density | Avg. | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Train | Test | Train | Test | Train | Test | Train | Test | Train | Test | Train | Test | Train | Test | |
| Random Forest | 1.00 | 0.97 | 1.00 | 0.98 | 1.00 | 0.97 | 0.99 | 0.89 | 0.97 | 0.80 | 1.00 | 0.99 | 0.99 | 0.93 |
| Ensemble Bagging | 1.00 | 0.96 | 1.00 | 0.97 | 1.00 | 0.97 | 0.98 | 0.90 | 0.96 | 0.80 | 1.00 | 0.99 | 0.99 | 0.93 |
| Light Gradient Boosting Machine | 1.00 | 0.95 | 1.00 | 0.95 | 0.99 | 0.96 | 0.96 | 0.90 | 0.92 | 0.80 | 1.00 | 0.98 | 0.98 | 0.92 |
| Extreme Gradient Boosting | 1.00 | 0.97 | 1.00 | 0.98 | 1.00 | 0.96 | 0.99 | 0.87 | 0.99 | 0.71 | 1.00 | 0.99 | 1.00 | 0.91 |
| Decision Tree | 1.00 | 0.97 | 1.00 | 0.98 | 1.00 | 0.96 | 1.00 | 0.81 | 1.00 | 0.67 | 1.00 | 0.99 | 1.00 | 0.90 |
| Neural Network | 0.95 | 0.88 | 0.94 | 0.88 | 0.93 | 0.88 | 0.63 | 0.59 | 0.45 | 0.40 | 0.95 | 0.92 | 0.81 | 0.76 |
| K-Nearest Neighbors | 0.97 | 0.86 | 0.96 | 0.86 | 0.96 | 0.87 | 0.82 | 0.59 | 0.73 | 0.46 | 0.96 | 0.90 | 0.90 | 0.76 |
| Linear Regression | 0.48 | 0.46 | 0.51 | 0.50 | 0.56 | 0.55 | 0.16 | 0.17 | 0.21 | 0.21 | 0.40 | 0.38 | 0.39 | 0.38 |
| Ridge Regression | 0.48 | 0.46 | 0.51 | 0.50 | 0.56 | 0.55 | 0.15 | 0.17 | 0.21 | 0.21 | 0.40 | 0.38 | 0.39 | 0.38 |
| Target Variable | Base Learners | Meta Learner | R2 Train | R2 Test |
|---|---|---|---|---|
| PM1.0 | Linear Regression, K-Nearest Neighbors, Extreme Gradient Boosting, Neural Network, |
Random Forest | 1.00 | 0.99 |
| PM2.5 | K-Nearest Neighbors, Decision Tree, Bagging Regressor, Neural Network |
Random Forest | 1.00 | 0.99 |
| PM4.0 | Linear Regression, K-Nearest Neighbors, Decision Tree, Extreme Gradient Boosting |
Random Forest | 1.00 | 0.99 |
| PM10.0 | K-Nearest Neighbors, Random Forest, Extreme Gradient Boosting, Light Gradient Boosting Machine |
Neural Network | 0.98 | 0.91 |
| Total PM Concentration | K-Nearest Neighbors, Random Forest, Extreme Gradient Boosting, Light Gradient Boosting Machine |
Neural Network | 0.97 | 0.86 |
| Particle Count Density | Linear Regression, Ridge Regression, Decision Tree, Light Gradient Boosting Machine |
Random Forest | 1.00 | 0.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





