Robust Client Selection Strategy Using an Improved Federated Random High Local Performance Algorithm to Address High Non-IID Challenges

1. Introduction

In the context of Federated Learning (FL), the process of client selection plays a pivotal role in determining the most suitable participants for model training. Effective client selection contributes to accelerated convergence, improved global model accuracy, optimal utilization of heterogeneous data, and enhanced computational capabilities across various devices, ultimately leading to superior model performance [1]. Concurrently, it is essential to ensure communication efficiency and minimize computational resource consumption.

Engaging all clients can present significant challenges, including the potential unavailability of certain clients at specific times and communication bottlenecks arising from network infrastructure limitations. Consequently, an efficient client selection strategy focuses on identifying a smaller subset of clients for participation, which offers multiple advantages, such as reduced communication costs, improved resource efficiency, and enhanced model generalization [2].

A significant challenge in Federated Learning (FL) relates to suboptimal client selection and excessive diversity in model aggregation. Client heterogeneity can arise from statistical disparities, such as imbalanced datasets or substantial variations in da-ta volume across clients, which may lead to diminished model accuracy and prolonged convergence times [3]. Furthermore, the non-independent and identically distributed (Non-IID) characteristics of the data compound this challenge. Each client possesses training samples from a limited range of classes and demonstrates imbalanced sample distributions during the training process. The Non-IID challenge can be categorized into two distinct levels: high-level and low-level issues. High-level issues emerge when each client is assigned only a few labels for local model training. Conversely, low-level issues occur when clients have access to a broader range of labels, albeit not the complete set.

The challenges associated with heterogeneous client selection and low-quality data are particularly evident in the random client selection mechanism employed by the Feder-ated Averaging algorithm (FedAvg). As previous research has indicated [4], FedAvg may result in suboptimal global model aggregation [5-6], leading to increased delays and diminished model accuracy, especially when addressing Non-IID data across cli-ents [7-9]. In response to the issues arising from random client selection, various strategies have been developed that incorporate bias values to select clients based on their number of training samples and elevated local loss. One such strategy, was highlighted in [10], proposed the Power-of-Choice algorithm (PoC), which prioritizes clients exhibiting higher local loss values to enhance convergence rates. Nevertheless, the PoC approach may deviate from the optimal central loss function, potentially compromising overall model accuracy due to its singular focus on accelerating convergence. To refine the PoC methodology, the FedChoice algorithm was introduced [11]. This algorithm aims to improve global model convergence by favoring clients with higher loss values, thereby increasing their likelihood of participating in local model training and subsequent integration into the global model

This study presents an improved version of the Fed-RHLP algorithm, building upon the initial iteration introduced in [12]. The primary objective of this improvement is to refine the process of robust client selection by identifying a more suitable and reduced subset of clients, thereby addressing the challenges posed by significant Non-IID is-sues. The improved Fed-RHLP algorithm prioritizes the selection of clients with three key characteristics: a substantial number of samples, demonstrated label diversity, and high local model performance across both local updates and global aggregation. Concurrently, the algorithm allows for the inclusion of lower-quality clients, enabling them to contribute their local datasets during the training and aggregation phases. The implementation of this algorithm results in accelerated convergence and im-proved accuracy, particularly in scenarios characterized by high Non-IID conditions. Moreover, it ensures fairness by facilitating proportional participation from the majority of clients.

2. Materials and Methods

2.1. Exploring Issues of Client Selection Methods

In the context of Federated Learning (FL), the selection of diverse clients, combined with limited data samples and suboptimal data quality, can impede convergence rates and contribute to the development of an inaccurate global model. Numerous studies have proposed client selection methodologies designed to address the statistical discrepancies encountered during the global model aggregation process. The challenge of statistical heterogeneity originates from multiple sources, including, variations in data distributions, inconsistent sampling practices, and non-independent and identically distributed (Non-IID) data or imbalanced datasets [13]. To manage this heterogeneity, it is crucial to implement client selection strategies during the training process that ensure convergence across the system, considering the diversity of statistical heterogeneity [14]. Furthermore, additional complexities arise from variations in model architectures, network conditions, and hardware capabilities among participating clients. These factors collectively exacerbate the existing challenges, diminishing the server's ability to perform effective model aggregation and resulting in a global model with compromised precision [15]. A comprehensive review and analysis of the challenges and limitations associated with these algorithms can be conducted as follows:

FedAvg represents a straightforward approach that involves the random selection of clients for local model updates, specifically employing Convolutional Neural Networks (CNNs) to distribute computational tasks among clients and address challenges associated with centralized machine learning. This method applies gradient de-scent to perform local updates on the models of a randomly selected subset of clients, which are subsequently aggregated to create a global model. Although FedAvg aver-ages the updates from individual client models, it may encounter significant divergence from the optimal model, particularly when the training data distribution of a single client markedly differs from the heterogeneous and non-IID data distribution [16 - 17].

The ideal model equation for FedAvg can be decomposed into two primary components: 1) Local Updates: Each client k refines its model w_(t+1)^k through gradient descent, employing a step size determined by η, (the learning rate). This process is influenced by the client's local dataset and the gradient g_k of the loss function and 2) Global aggregation: The locally updated models from the clients are amalgamated to form the global model w_(t+1 ), with the aggregation weighted proportionally to the size of each client's dataset n_k relative to the total dataset size n, as shown in equation (1).

$$\begin{gathered} \forall \mathit{k},{\mathit{w}}_{\mathit{t}+1}^{\mathit{k}}\leftarrow {\mathit{w}}_{\mathit{t}}-{\mathit{n}\mathit{g}}_{\mathit{k}} \\ {w}_{t+1}\leftarrow \sum _{k=1}^K{\displaystyle \frac{n_k}{n}}{w}_{t+1}^k \end{gathered}$$

(1)

The problems with FedAvg can be demonstrated through the following example, as shown in Figure 1.

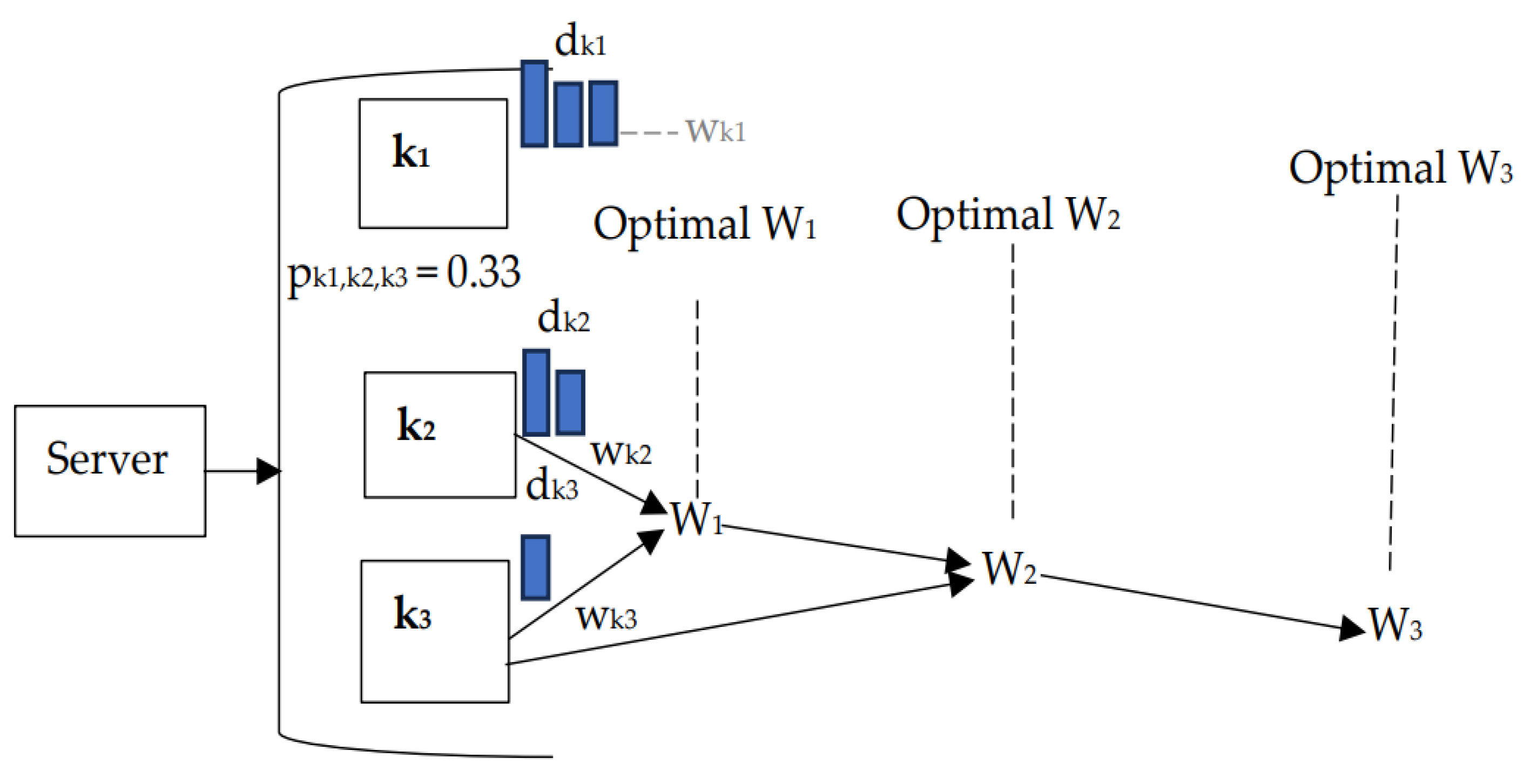
In Figure 1, it is assumed that three clients (K = 3), represented as k1, k2, and k3, each responsible for updating their local models (wk1, wk2, and wk3) with local dataset (dk) and then contribute to aggregating a global model (Wt) in communication round (t). In the random client selection process, the probability of selecting a client (pk) for local updates is equally distributed, with a probability value of pk = 1/K (0.33). We assume that k1 has 100 samples with 3 labels (nk = 100, Lk =3), k2 has 50 samples with 1 label (nk = 50, Lk =2), and k3 has 20 samples with 1 label (nk = 20, Lk =1). If clients with low data quantity and few labels (k2 and k3) are frequently selected for up-dates, this can cause significant divergence.

Upon examining client selection methodologies such as the Power-of-Choice (PoC) algorithm and the FedChoice algorithm, it becomes evident that bias values are allocated to clients based on the volume of training samples and elevated local loss. A significant concern emerges when a client with a substantial number of samples is selected, particularly if these samples are predominantly from a single label. This scenario detrimentally affects the diversity of datasets utilized in model updates and global aggregation [18]. The issue of label scarcity further compounds this challenge, as certain clients may lack adequate labelled data due to resource constraints or insufficient motivation for labelling tasks. Such complications contribute to suboptimal model performance and impede the development of a well-generalized model across varied datasets. Ideally, client selection should encompass a range of labels alongside a considerable number of samples [19 - 20]. This approach ensures that local model training effectively captures diverse patterns, thereby enhancing the global model's generalization [21]. When addressing the bias gap arising from an exclusive reliance on large sample sizes for client selection in local loss estimation and model up-dates within the PoC and FedChoice frameworks, as well as the conventional practice of utilizing all clients for local model performance assessment in Fed-RHLP, it becomes apparent that these approaches may result in a deficiency of local dataset diversity and significant execution time de-lays. This issue is evident, as shown in Figure 2.

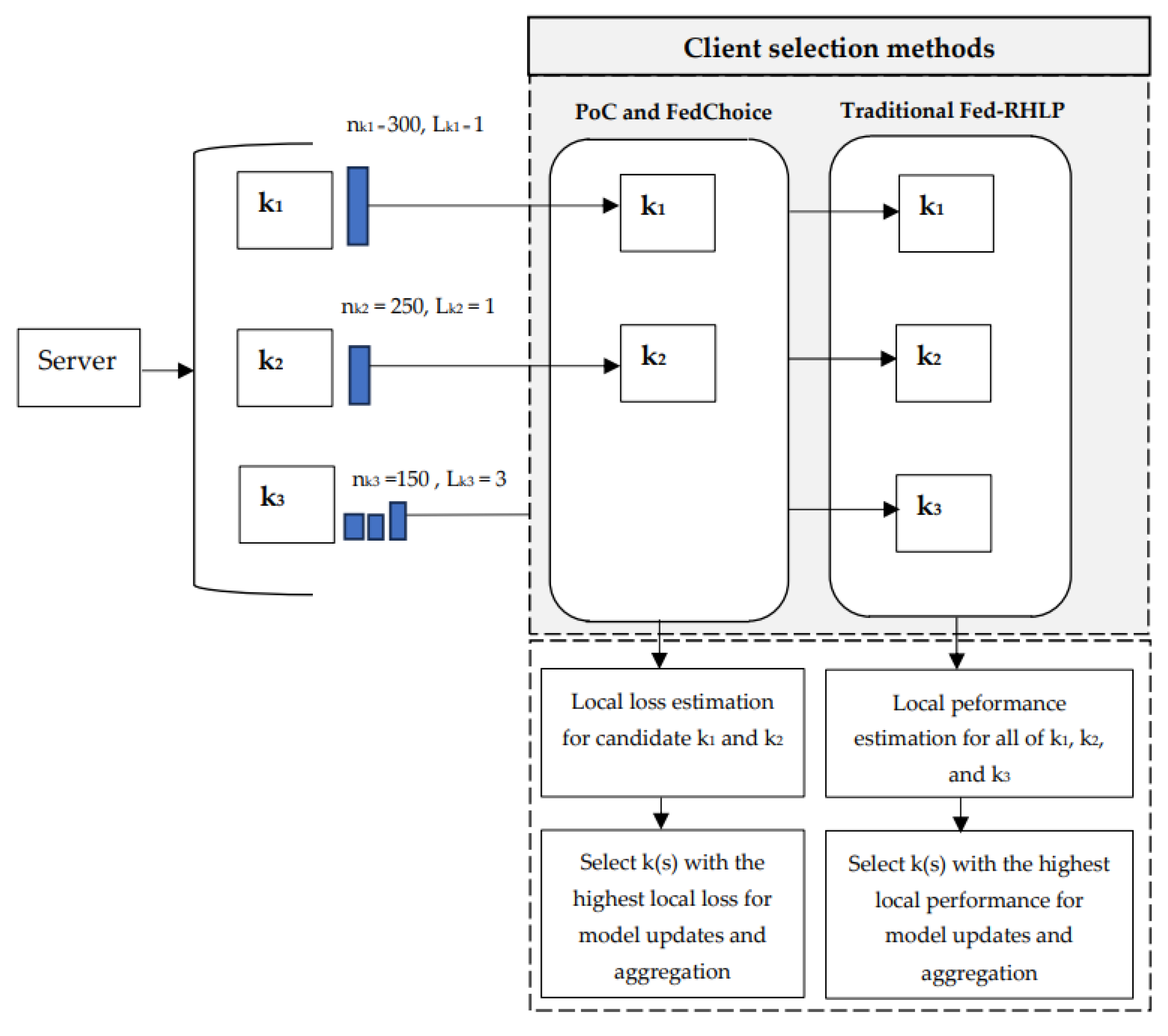
In Figure 2, the comparison of client selection methods for local model updates in the PoC, FedChoice, and traditional Fed-RHLP algorithm is shown. In the example, there are three clients (k1, k2, and k3).

The PoC and FedChoice algorithms assume that the server selects only two clients as candidates for local loss estimation in each communication round. These algorithms prioritize clients with larger local datasets for participation. The probability of selecting each client (k) based on its local dataset size is calculated as P_k= n_k/(∑_(k=1)^K▒n_k ). For k1, with a local dataset size of nk1 = 300, the probability is calculated as Pk1 = 300/700 = 0.43. For k2, with nk2 = 250, Pk2 = 250/700 = 0.36. Finally, for k3, with nk3 = 150, Pk3 = 150/700 = 0.21. As a result, k1 has the highest probability of being selected, followed by k2, which has a higher probability than k3. This selection process often leads to clients with a single label, such as k1 and k2, being selected repeatedly for local model training. Consequently, this reduces the diversity of the aggregated global model.

The traditional Fed-RHLP algorithm, proposed in [12], uses all clients (k1, k2, and k3) to estimate the clients' local model performance (LPk) by sending the global model (W) to each client for estimating with the local dataset (dk). Subsequently, the LPk of each client is converted into a weight for local mod-el performance (WLPk), which is added to a biased roulette wheel for randomly selecting model up-dates and aggregation based on clients’ local model performance, as shown in Equations (2)–(4).

$${LP}_k=f\left(W;d_k\right)$$

(2)

$$TotalLP=\sum _{k=1}^N{LP}_k$$

(3)

$${WLP}_k={\displaystyle \frac{{LP}_k}{TotalLP}}$$

(4)

The conventional Fed-RHLP algorithm is marked by significant computational demands, particularly in situations where certain clients are unavailable for processing at specific times. Additionally, the random selection of a large number of clients complicates the identification of those with high-quality datasets. This scenario may lead to missed processing opportunities and impede the accurate identification of clients eligible for participation.

2.2. Developing the Improved Federated RHLP Algorithm for Efficient Client Selection

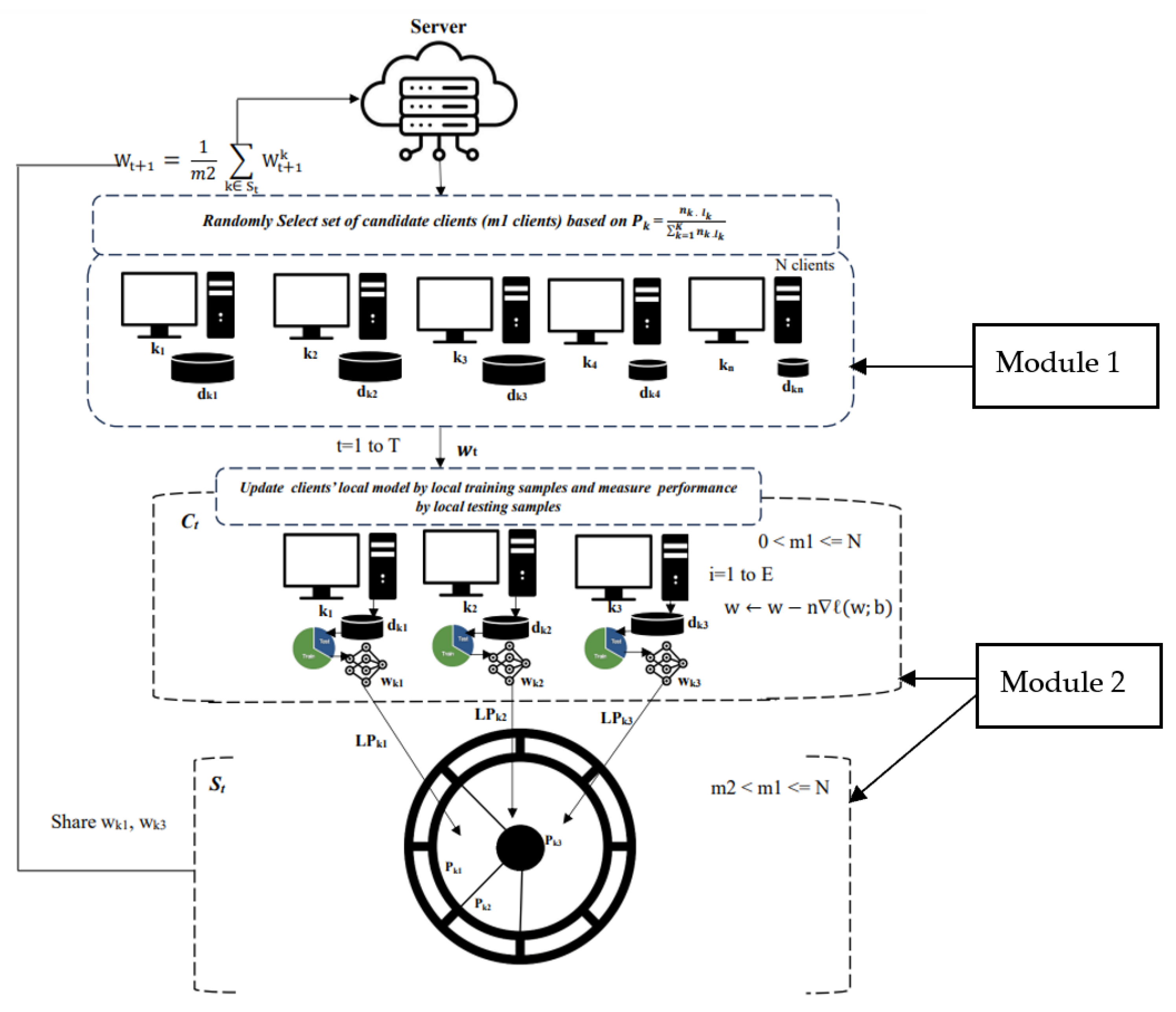
The Improved Federated RHLP algorithm exhibits enhanced efficiency by increasing the accuracy of global model aggregation and accelerating the convergence rate. This improvement is achieved through its dual-bias approach, consisting of Module 1 and Module 2. These modules incorporate fac-tors such as the number of samples, label diversity, and the high performance of local models from cli-ents into the processes of model updates and aggregation, as shown in Figure 3.

In Figure 3, the architecture of the Improved RHLP algorithm is developed in two modules:

Module 1: Candidate client selection

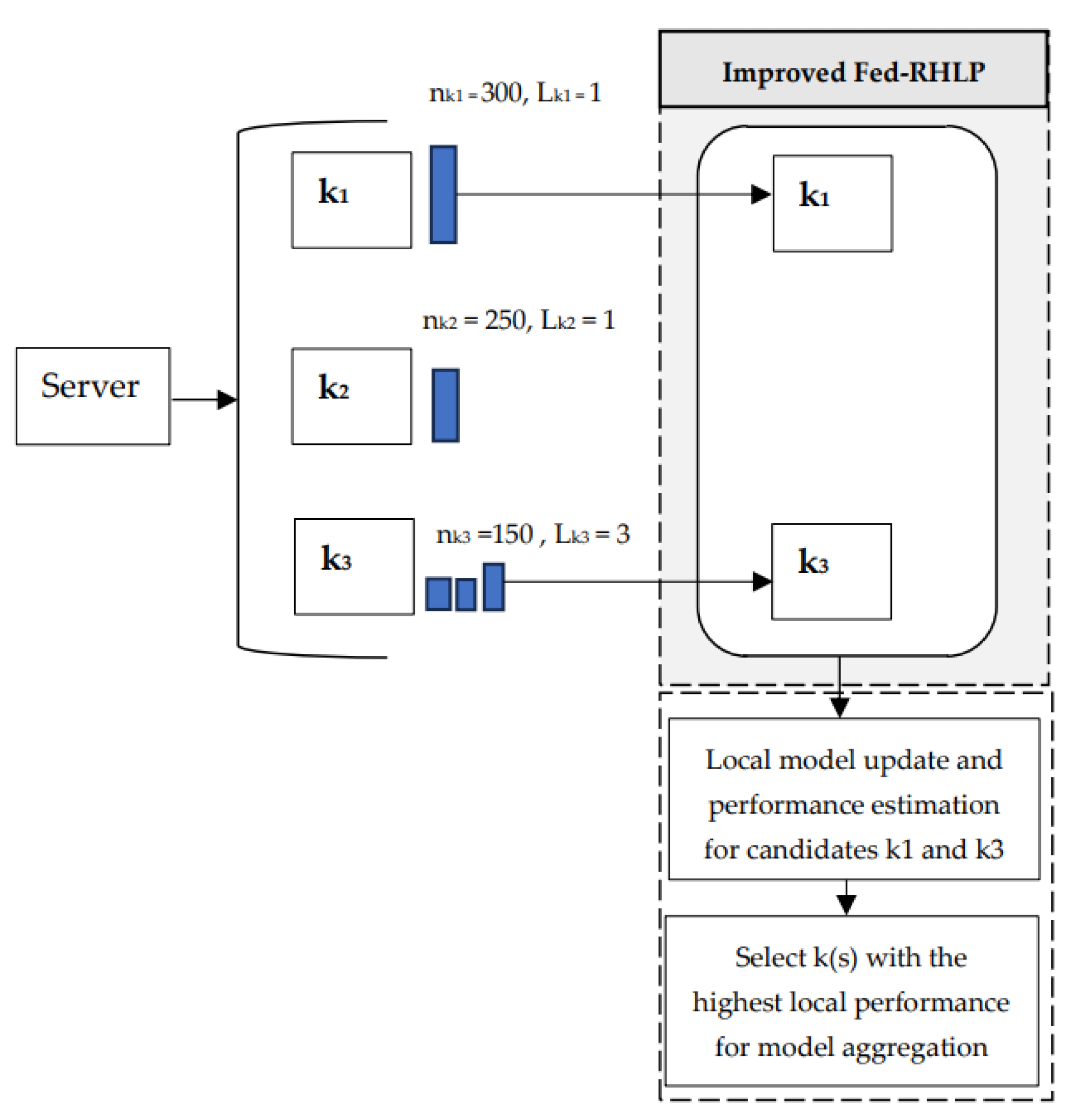
The client selection process requires improvement to more effectively select a smaller set of candidate clients (Ct) in each communication round, prioritizing based on the number of samples (nk) and label diversity (Lk). In the example (Figure 4), the probability of selecting each client (k) is calculated as ${\mathit{P}}_{\mathit{k}}$= ${\displaystyle \frac{{\mathit{n}}_{\mathit{k}.{\mathit{L}}_{\mathit{k}}}}{\sum _{\mathit{k}=1}^{\mathit{K}}{\mathit{n}}_{\mathit{k}.{\mathit{L}}_{\mathit{k}}}}}$ For k1, Pk1 = (300 x 1) /1,000 = 0.3; for k2, Pk2 = (250 x 1) /1,000 = 0.25; for k3, Pk3 = (150 x 3) /1,000 = 0.45. As a result, k3 has the highest likelihood of being chosen for local model updates and performance estimation, followed by k1, which has a higher probability than k2. This pro-posed selection process ensures that clients with more diverse labels and larger datasets are prioritized, leading to a more diverse and robust aggregated global model.

Module 2: High local model performance updates and aggregation

The local model performance is measured in the algorithm by splitting each candidate’s local dataset (dk) into training samples (d_traink), where (d_traink) is further split into batches of size B for locally updating the model (wk) by using the Stochastic Gradient Descent (SGD) Tech-nique, and small test samples (d_testk), which are used for testing local model performance of each client (LPk) with LPk=ʄ(wk;d_testk). High-performing local models, calculated from $\mathit{T}\mathit{o}\mathit{t}\mathit{a}\mathit{l}\mathit{L}\mathit{P}=\sum _{\mathit{k}{\mathit{C}}_{\mathit{t}}}{\mathit{L}\mathit{P}}_{\mathit{k}}$ and using Equation (4) to determine the weight of local model performance (WLPk), are then randomly selected using a biased roulette wheel mechanism for global model aggregation. The de-tails of the improved RHLP algorithm are presented in the pseudocode in Figure 5.

2.3. Experiment Setup

This study employs Convolutional Neural Networks (CNNs), recognized as a highly effective deep learning algorithm suitable for tasks involving image classification [22]. The experimental procedure is organized into three distinct phases, which are outlined in the following sections.

2.3.1. Dataset Preparation

In this study, we address the challenge posed by imbalanced and non-independent identically distributed (Non-IID) datasets that are distributed among clients, a critical concern in the realm of federated learning (FL) [23]. Such imbalances have a profound impact on the efficacy of model training [24]. The effectiveness of the improved Fed-RHLP algorithm was evaluated through comparisons with FedAvg, Power-of-Choice (PoC), and FedChoice, specifically focusing on Non-IID scenarios utilizing the MNIST and Fashion-MNIST (FMNIST) datasets.

The structures of these datasets are described and illustrated in Figure 5.

Figure 6 shows the use of two datasets: (a) the MNIST dataset and (b) the FMNIST dataset. Both datasets contain a total of 70,000 images, each being a 28 × 28 grayscale image. The MNIST dataset consists of handwritten digit images (ranging from 0 to 9) [25], while the FMNIST dataset contains fashion item images categorized into 10 classes [26]. Both datasets are split into 60,000 training images and 10,000 test images.

To demonstrate the resilience of the improved Federated RHLP algorithm, we constructed Non-IID challenges to assess the algorithm's robustness at two distinct levels: 1) High Non-IID Challenge: Each client was assigned 1–2 classes for local model updates, and 2) Low Non-IID Challenge: Each client was assigned 5–6 classes for local model updates. The datasets were distributed among 100 clients, with each client receiving a varying proportion of data samples, ranging from 10% to 30%, to support the training of their local models.

2.3.2. Setting Up Algorithms, CNN Model Structures, and Hardware Specifications

Setting Up Algorithms

The algorithms will be run for 200 communication rounds to aggregate the global model. The SGD optimization algorithm is used in CNN for local model updates over five local epochs (E). The batch size is set to 64 , and the learning rate for SGD is 0.01 [27 - 30].

In each communication iteration, the Improved Federated RHLP, PoC, and FedChoice algorithms identify a subset of candidate clients (Ct), comprising 10% (C=0.1) of the total pool of 100 clients. Subsequently, a smaller group of clients (St) is selected in varying proportions [31] of 2%, 4%, 6%, 8%, and 10%. When the selection for St reaches 10%, the number of candidate clients is increased by 15% (adding 15 additional candidates) to ensure a sufficiently random selection process. Additionally, in the Improved Federated RHLP approach, each client's local dataset is divided into local testing samples, randomly ranging between 3% and 5%, with the remaining data allocated for training in local model updates and performance evaluation. In contrast, the FedAvg approach does not designate predefined candidate clients but directly selects fractions of 2%, 4%, 6%, 8%, and 10% of clients for model training.

Setting Up CNN Model Structures

The structure of the CNN model is configured for training on the MNIST and FMNIST datasets, as outlined below:

1) MNIST Dataset:

The CMM model architecture comprises two convolutional layers. In the first layer, 10 feature maps are produced using 5 × 5 filters. The second layer increases the number of feature maps to 20, also employing 5 × 5 filters. To reduce the risk of overfitting, a dropout layer with a rate of 0.5 is applied after the second convolutional layer. The network architecture further includes two fully connected layers: the first layer reduces 320 features to 50 neurons, and the second layer maps these 50 neurons to 10 output classes, representing the digits 0 to 9.

2) FMNIST Dataset:

The CNN model architecture comprises two convolutional layers. The initial layer generates 32 feature maps using 3 × 3 filters with a padding of 1. A max pooling layer with a 2 × 2 kernel and a stride of 2 follows this first layer. The subsequent convolutional layer increases the number of feature maps to 64, again employing a 3 × 3 filter size. This is followed by another max pooling layer, utilizing the same 2 × 2 kernel and stride of 2. The model further incorporates three fully connected layers: The first layer transforms 2,304 features into 600 neurons. A dropout layer with a rate of 0.25 is introduced after this layer to mitigate the risk of over-fitting. The second fully connected layer reduces the 600 features to 120 neurons. The final layer maps the 120 features to 10 output classes, representing various fashion items.

Setting Up Hardware Component Specifications

This experiment prepares the hardware specifications for setting up and executing the algorithms, as outlined in Table 1.

2.3.3. Algorithm Performance Evaluation

The global model of the algorithms was evaluated three times over 200 communication rounds, using 10,000 global test samples from the MNIST and FMNIST datasets. The formula for evaluating the Improved RHLP algorithm, compared with other benchmark algorithms, involves measuring prediction accuracy, con-vergence speed, and reduced execution time [11]. The calculation methods for these three-performance metrics are shown in Equations (5) – (7).

$$\mathbf{A}\mathbf{c}\mathbf{c}\mathbf{u}\mathbf{r}\mathbf{a}\mathbf{c}\mathbf{y}\left(\mathbf{\%}\right)={\displaystyle \frac{(\mathbf{T}\mathbf{o}\mathbf{t}\mathbf{a}\mathbf{l} \mathbf{n}\mathbf{u}\mathbf{m}\mathbf{b}\mathbf{e}\mathbf{r} \mathbf{o}\mathbf{f} \mathbf{t}\mathbf{e}\mathbf{s}\mathbf{t} \mathbf{s}\mathbf{a}\mathbf{m}\mathbf{p}\mathbf{l}\mathbf{e}\mathbf{s}-\mathbf{N}\mathbf{u}\mathbf{m}\mathbf{b}\mathbf{e}\mathbf{r} \mathbf{o}\mathbf{f} \mathbf{i}\mathbf{n}\mathbf{c}\mathbf{o}\mathbf{r}\mathbf{r}\mathbf{e}\mathbf{c}\mathbf{t}\mathbf{l}\mathbf{y} \mathbf{p}\mathbf{r}\mathbf{e}\mathbf{d}\mathbf{i}\mathbf{c}\mathbf{t}\mathbf{e}\mathbf{d} \mathbf{s}\mathbf{a}\mathbf{m}\mathbf{p}\mathbf{l}\mathbf{e}\mathbf{s})\mathbf{x}100}{\mathbf{T}\mathbf{o}\mathbf{t}\mathbf{a}\mathbf{l} \mathbf{n}\mathbf{u}\mathbf{m}\mathbf{b}\mathbf{e}\mathbf{r} \mathbf{o}\mathbf{f} \mathbf{t}\mathbf{e}\mathbf{s}\mathbf{t} \mathbf{s}\mathbf{a}\mathbf{m}\mathbf{p}\mathbf{l}\mathbf{e}\mathbf{s}}}$$

(5)

$$\mathbf{C}\mathbf{o}\mathbf{n}\mathbf{v}\mathbf{e}\mathbf{r}\mathbf{g}\mathbf{e}\mathbf{n}\mathbf{c}\mathbf{e} \mathbf{s}\mathbf{p}\mathbf{e}\mathbf{e}\mathbf{d}\left(\mathbf{\%}\right)={\displaystyle \frac{(\mathbf{H}\mathbf{i}\mathbf{g}\mathbf{h}\mathbf{e}\mathbf{r} \mathbf{r}\mathbf{o}\mathbf{u}\mathbf{n}\mathbf{d}-\mathbf{L}\mathbf{o}\mathbf{w}\mathbf{e}\mathbf{r} \mathbf{r}\mathbf{o}\mathbf{u}\mathbf{n}\mathbf{d})\mathbf{x}100}{\mathbf{H}\mathbf{i}\mathbf{g}\mathbf{h}\mathbf{e}\mathbf{r} \mathbf{r}\mathbf{o}\mathbf{u}\mathbf{n}\mathbf{d}}}$$

(6)

$$\mathbf{e}\mathbf{d}\mathbf{u}\mathbf{c}\mathbf{e}\mathbf{d} \mathbf{e}\mathbf{x}\mathbf{e}\mathbf{c}\mathbf{u}\mathbf{t}\mathbf{i}\mathbf{o}\mathbf{n} \mathbf{t}\mathbf{i}\mathbf{m}\mathbf{e}\left(\mathbf{\%}\right)={\displaystyle \frac{(\mathbf{H}\mathbf{i}\mathbf{g}\mathbf{h}\mathbf{e}\mathbf{r} \mathbf{e}\mathbf{x}\mathbf{e}\mathbf{c}\mathbf{u}\mathbf{t}\mathbf{i}\mathbf{o}\mathbf{n} \mathbf{t}\mathbf{i}\mathbf{m}\mathbf{e}-\mathbf{L}\mathbf{o}\mathbf{w}\mathbf{e}\mathbf{r} \mathbf{e}\mathbf{x}\mathbf{e}\mathbf{c}\mathbf{u}\mathbf{t}\mathbf{i}\mathbf{o}\mathbf{n} \mathbf{t}\mathbf{i}\mathbf{m}\mathbf{e})\mathbf{x}100}{\mathbf{H}\mathbf{i}\mathbf{g}\mathbf{h}\mathbf{e}\mathbf{r} \mathbf{e}\mathbf{x}\mathbf{e}\mathbf{c}\mathbf{u}\mathbf{t}\mathbf{i}\mathbf{o}\mathbf{n} \mathbf{t}\mathbf{i}\mathbf{m}\mathbf{e}}}$$

(7)

3. Results

The Improved Fed-RHLP was assessed for its overall model accuracy and benchmarked against various algorithms across different ratios of selected clients. This evaluation was conducted using the MNIST and FMNIST datasets, which respectively represent high and low degrees of Non-IID challenges. The results are shown below

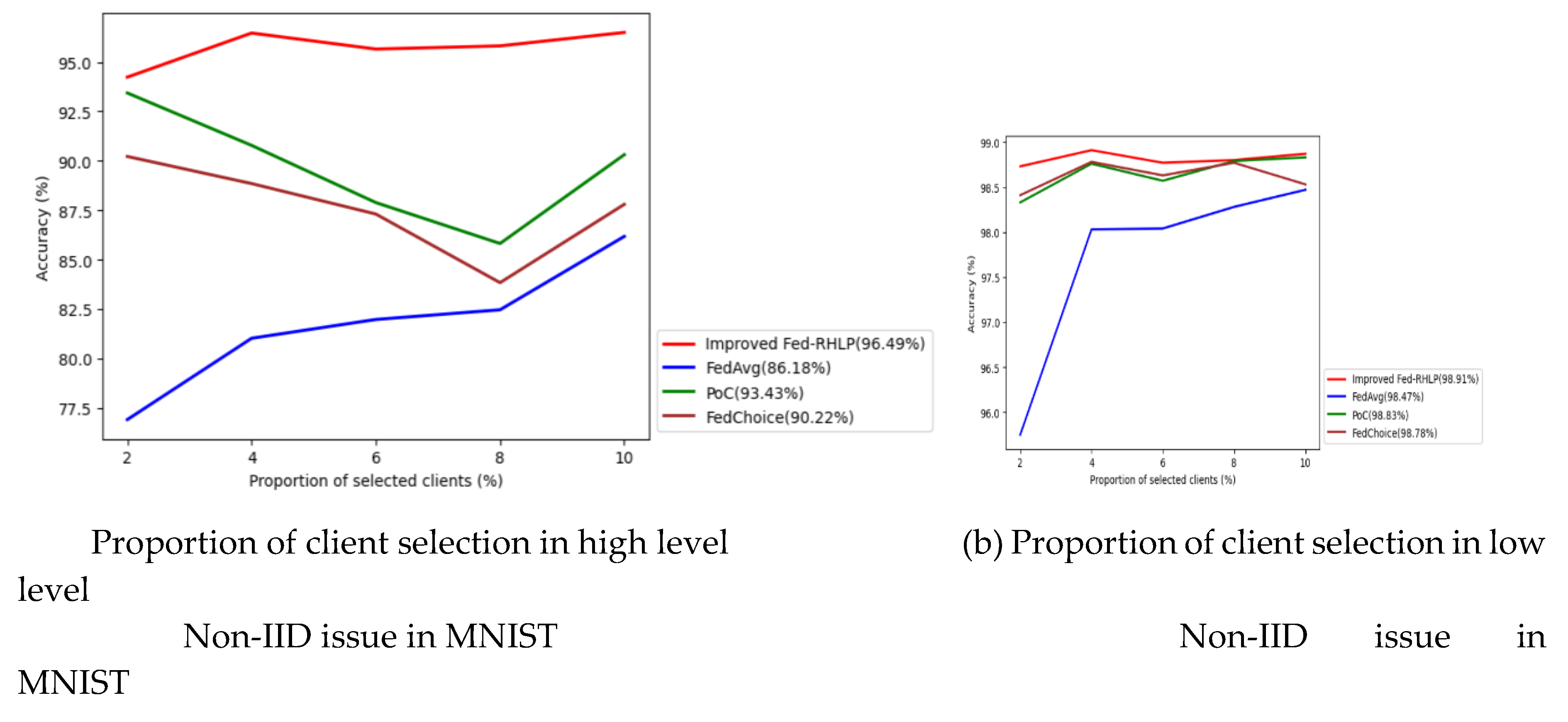
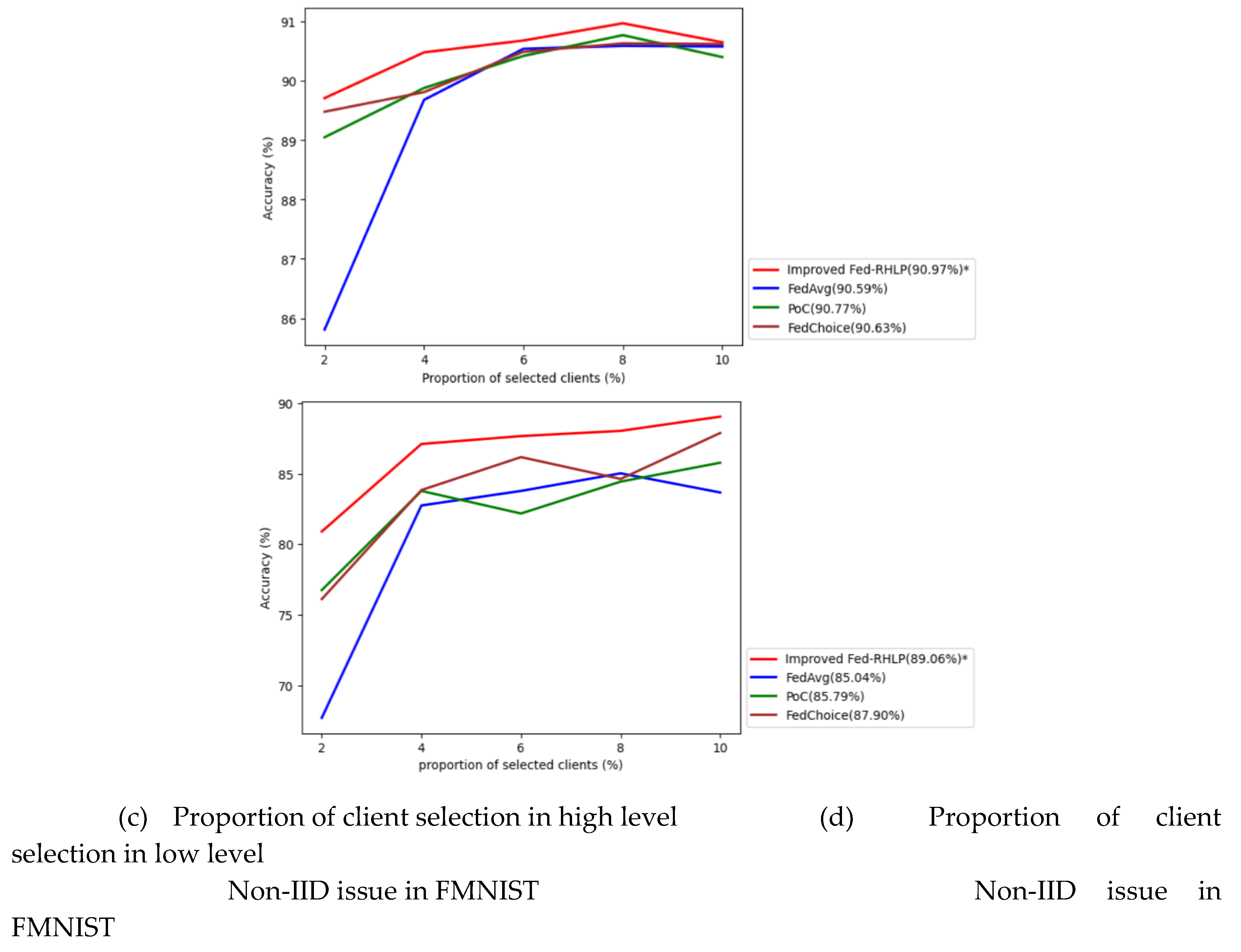
The data depicted in Figure 7 demonstrates that the improved Fed-RHLP exhibits superior global model ac-curacy compared to alternative client selection algorithms, irrespective of the severity of Non-IID challenges, as substantiated by the results derived from the MNIST and FMNIST datasets. In scenarios characterized by high Non-IID issues, the improved Fed-RHLP significantly outperforms its competitors across all client selection pro-portions. Conversely, under conditions of low Non-IID challenges, the algorithm provides a modest advantage over alternative approaches.

In scenarios characterized by high Non-IID challenges within the MNIST dataset, the improved Fed-RHLP achieves a peak global model accuracy of 96.49% when employing a selection proportion of 10%. This performance demonstrates notable improvements: 10.31% higher than FedAvg (highest accuracy: 86.18% at a 10% selection proportion) 3.06% higher than PoC (highest accuracy: 93.43% at a 2% selection proportion) and 6.27% higher than FedChoice (highest accuracy: 90.22% at a 2% selection proportion). Similarly, in the context of high Non-IID issues within the FMNIST dataset, the improved Fed-RHLP attains a global model accuracy of 89.06% at a selection pro-portion of 10%. This represents performance improvements of: 4.02% higher than FedAvg (highest accuracy: 85.04% at a 8% selection proportion), 3.27% higher than PoC (highest accuracy: 85.79% at a 10% selection proportion) and 1.16% higher than FedChoice (highest accuracy: 87.90% at a 10% selection proportion).

In scenarios characterized by low Non-IID challenges within the MNIST dataset, the improved Fed-RHLP achieves a peak global model accuracy of 98.91% with a selection proportion of 4%. This performance demonstrates marginal improvements: 0.44% higher than FedAvg (highest accuracy: 98.47% at a 10% selection proportion), 0.08% higher than PoC (highest accuracy: 98.83% at a 10% selection proportion), and 0.14% higher than FedChoice (highest accuracy: 98.78% with a 4% selection proportion). Similarly, in the context of low Non-IID issues in the FMNIST dataset, the improved Fed-RHLP attains a maximum global model accuracy of 90.97% with a selection proportion of 8%. This represents incremental performance improvements of: 0.38% higher than FedAvg (highest accuracy: 90.59% at a 8% selection proportion), 0.20% above PoC (highest accuracy: 90.77% at a 8% selection proportion), and 0.34% greater than FedChoice (highest accuracy: 90.63% at a 8% selection proportion).

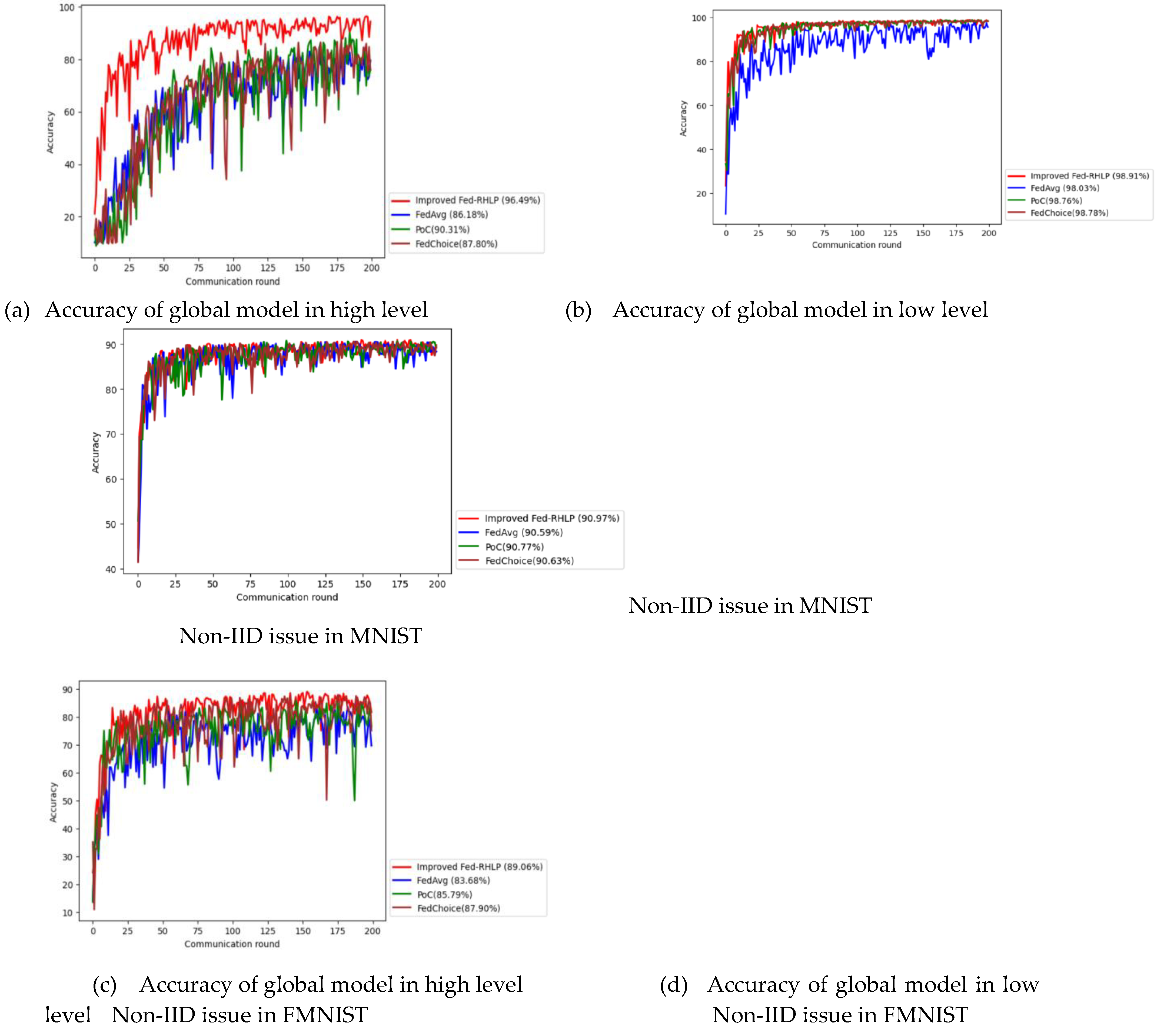
Additionally, the improved Fed-RHLP underwent assessment for its convergence speed and execution time, benchmarked against alternative algorithms across both high and low levels of Non-IID challenges. The evaluation focused on achieving the highest global model accuracy under the following parameters: High Non-IID Conditions: MNIST: 10% client selection proportion FMNIST: 10% client selection proportion and in Low Non-IID Conditions: MNIST: 4% client selection proportion, FMNIST: 8% client selection proportion respectively. The results are presented as follows.

Figure 8a–d show that the improved Fed-RHLP achieves higher global model accuracy, faster convergence speed, and reduced execution time compared to FedAvg, PoC, and FedChoice when tested on MNIST and FMNIST under both high and low levels of Non-IID issues. The insights from the results are presented in Table 2 and Table 3 .

From Table 2 and Table 3, the testing results on the MNIST and FMNIST datasets demonstrate that the improved Fed-RHLP exhibits significant advantages in addressing high Non-IID levels compared to other algorithms.

In the context of the MNIST dataset characterized by high Non-IID challenges, the improved Fed-RHLP demonstrates exceptional performance, achieving an accuracy of 96.49%. This result surpasses that of FedAvg, PoC, and FedChoice by margins of 10.31%, 6.18%, and 8.69%, respectively. At an accuracy level of 80%, Fed-RHLP exhibits both faster convergence and reduced execution time compared to all other algorithms. Most notably, it reaches 90% accuracy within merely 41 communication rounds, which represents a 77.84% improvement over PoC, accompanied by a 74.51% reduction in execution time. In scenarios with low Non-IID levels, Fed-RHLP significantly outperforms FedAvg, achieving an 80.77% enhancement in convergence speed and a 58.79% decrease in execution time. Additionally, the algorithm marginally exceeds the performance of PoC and FedChoice.

In the context of the FMNIST dataset characterized by high Non-IID challenges, the improved Fed-RHLP demonstrates a peak accuracy of 89.06%. This performance exceeds that of FedAvg, PoC, and FedChoice by mar-gins of 5.38%, 3.27%, and 1.16%, respectively. When achieving an accuracy of 80%, Fed-RHLP exhibits remarkable convergence characteristics: 72.73% more rapid convergence than FedAvg, 61.54% faster than PoC and 28.57% quicker than FedChoice. Correspondingly, the algorithm achieves significant reductions in execution time: 68.09% reduction compared to FedAvg, 65.75% reduction compared to PoC, and 36.55% reduction compared to FedChoice. In scenarios with low levels of Non-IID, Fed-RHLP demonstrates a marginal advantage over FedAvg, PoC, and FedChoice.

In summary, the improved Fed-RHLP exhibits greater efficiency and precision in managing elevated Non-IID levels across both datasets, showing notable advancements in convergence speed and execution duration when compared to alternative algorithms.

4. Discussion and Conclusions

This paper presents an enhanced version of the Fed-RHLP algorithm designed to address challenges posed by Non-IID data distributions. It selects a focused and diverse group of clients for training using a dual-biased strategy, considering factors such as dataset size, label variety, and local model performance. The goal is to optimize both data diversity and the quality of the global model, aligning with the approach in [32]. The Oort algorithm also tackles the participant selection challenge by considering data and system diversity to choose suitable participants.

A key feature of the enhanced version of the Fed-RHLP algorithm is the prioritization of high-performing clients while still allowing lower-performing clients to contribute. Focusing on high-performing clients during model aggregation improves global model accuracy, while including lower-performing clients ensures fairness and maintains data diversity. This balance between high and low-performing clients accelerates convergence and helps the model generalize well across diverse data distributions.

Additionally, this method reduces the computational cost of federated learning by selectively choosing clients based on dataset characteristics and local model performance. By minimizing the number of clients required for each aggregation round, execution time is reduced, which is especially beneficial in resource-constrained or large-scale scenarios. As outlined in [33], the approach improves computational efficiency and addresses communication overhead by dynamically selecting the best client models to share. This reduces unnecessary communication, lowers costs, and accelerates aggregation, making it especially valuable in federated settings with limited network bandwidth. The result is a more efficient FL framework with reduced computational load and faster model updates.

In conclusion, the enhanced Fed-RHLP algorithm improves both accuracy and convergence, especially in Non-IID environments with significant data heterogeneity. By balancing the involvement of high- and low-performing clients, the algorithm ensures fairness and increases the diversity of contributions to the global model. This balance accelerates convergence and reduces computational costs, making it an effective solution for federated learning in diverse data environments.

5. Future Works

In future work, we aim to improve the Fed-RHLP algorithm by incorporating hierarchical federated learning (FL) structures. As the client pool expands, the central server faces heightened computational demands. To alleviate this, we propose dividing clients into smaller subgroups for localized aggregation before transmitting the results to the central server. This strategy will help reduce the computational load and enhance scalability, as well as decrease communication overhead and speed up the aggregation process. Additionally, we plan to adapt this hierarchical framework to handle various data distributions and model types, ensuring its effectiveness in diverse environments. Furthermore, we aim to dynamically adjust client participation in each round, considering factors such as fluctuating client participation ratios and local training epochs. This adjustment will be based on the influence of global model tuning and the contributions of client groups in each communication round, optimizing the efficiency of the global model.