The Symmetry Number Structure About Line-1/2

Liu Yajun

doi:10.20944/preprints202501.1995.v1

Submitted:

26 January 2025

Posted:

28 January 2025

Read the latest preprint version here

Abstract

In this paper, we discuss the symmetry number structure about line-1/2 . We find that using the symmetry characters of those structures we can give proofs of the number Conjectures: Goldbach Conjecture、Twins Prime Conjecture and Polignac’s conjecture and the Riemann Hypothesis. In this paper, we also gave concise proofs of the Fermat’ Last Theorem and the 3n+1 conjecture.

Keywords:

P/2n

;

Prime numbers Conjectures

;

Riemann Hypothesis

Subject:

Computer Science and Mathematics - Algebra and Number Theory

1. The Symmetry of P/2n and Prime Numbers Conjectures

We have

\frac{P}{2 n} = \{\begin{matrix} \frac{1}{2^{N + 1}} n = 2^{N} P \\ \frac{3}{4} n = 2 P = 3 \\ 1 n = 1 P = 2 \end{matrix}

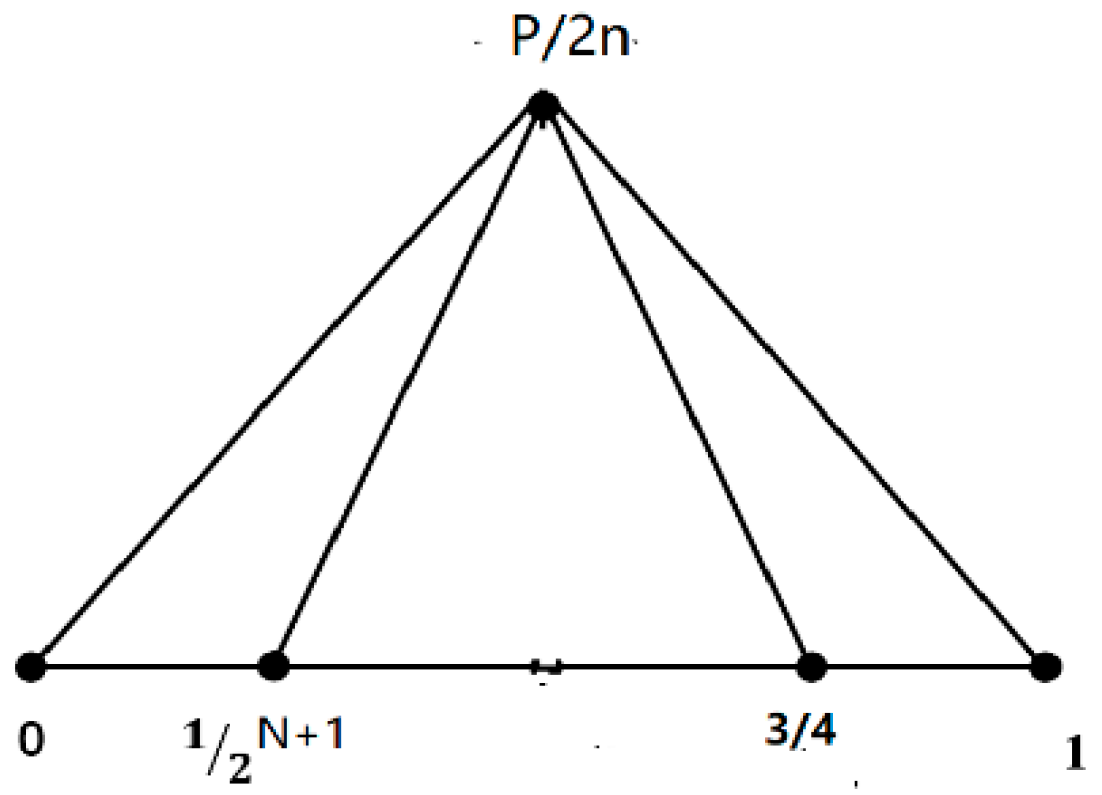
Figure 1. P/2n number structure with points [ 0 1/2^N+1 3/4 1].

N ~ (0, 1 ， 2 ， 3 ， 4 ， \dots \dots \dots .)

All natural numbers

n ~ (1 ， 2 ， 3 ， 4 ， \dots \dots \dots .)

All natural numbers excepted 0

P ~ (2 ， 3 ， 5 ， 7 ， \dots \dots \dots .)

All prime numbers

and

\frac{P}{2 n} = \{\begin{matrix} \frac{1}{2} - \frac{1}{2 n} P = n - 1 (n \geq 3) \\ \frac{1}{2} P = n \\ \frac{1}{2} + \frac{1}{2 n} P = n + 1 \end{matrix}

And We have

p0∈

P

~(0, n]

(n \geq 2)

And based on Bertrand -Chebyshev Theorem：when

n \geq 2

, there are at least a prime number between n and 2n.

pn∈

P

~[n, 2n)

(n \geq 2)

So we have:

0 < \frac{p 0}{2 n} \leq \frac{1}{2}

\frac{1}{2} \leq \frac{p n}{2 n} < 1

So we have

\frac{p 0}{2 n} = \frac{1}{2} - \frac{1}{2 n} (n \geq 3)

\frac{p n}{2 n} = \frac{1}{2} + \frac{1}{2 n}

So

(\frac{1}{2} - \frac{1}{2 n}) + (\frac{1}{2} + \frac{1}{2 n}) = \frac{p 0}{2 n} + \frac{p n}{2 n}

2 n = p 0 + p n (n \geq 3)

This is the proof of Goldbach conjecture.

and

\frac{p n}{2 n} - \frac{p 0}{2 n} = (\frac{1}{2} + \frac{1}{2 n}) - (\frac{1}{2} - \frac{1}{2 n})

p n - p 0 = 2

This is the proof of Twin Primes Conjecture

And we also have

0 < \frac{p 0}{2 n} = \frac{2 k_{1} + 1}{2 n} ≪ 1 / 2 (n \geq 3)

0 < 2 k_{1} + 1 ≪ n

0 < k_{1} ≪ \frac{n - 1}{2}

k_{1} i s a p o s i t i v e i n t e g e r

s o k 1 ~ 1,2, 3 ∙ ∙ ∙ ∙ ∙ ∙ [\frac{n - 1}{2}] (n \geq 3)

And

\frac{1}{2} ≪ \frac{p n}{2 n} = \frac{2 k_{2} + 1}{2 n} < 1

n ≪ 2 k_{2} + 1 < 2 n

\frac{n - 1}{2} ≪ k_{2} < \frac{2 n - 1}{2} (n \geq 3)

k_{2} i s a p o s i t i v e i n t e g e r

s o k_{2} ~ [\frac{n - 1}{2}], [\frac{n - 1}{2}] + 1, ∙ ∙ ∙ ∙ ∙ ∙ [\frac{2 n - 1}{2}] (n \geq 3)

we have

\frac{p n}{2 n} - \frac{p 0}{2 n} = \frac{{2 k}_{2} + 1}{2 n} - \frac{2 k_{1} + 1}{2 n}

p n - p 0 = 2 (k 2 - k 1)

{(p n - p 0)}_{m a x} = 2 ({k 2}_{m a x} - {k 1}_{m i n}) = 2 ([\frac{2 n - 1}{2}] - 1) = 2 (n - 2) (n \geq 3)

This is the proof of Polignac’s conjecture.

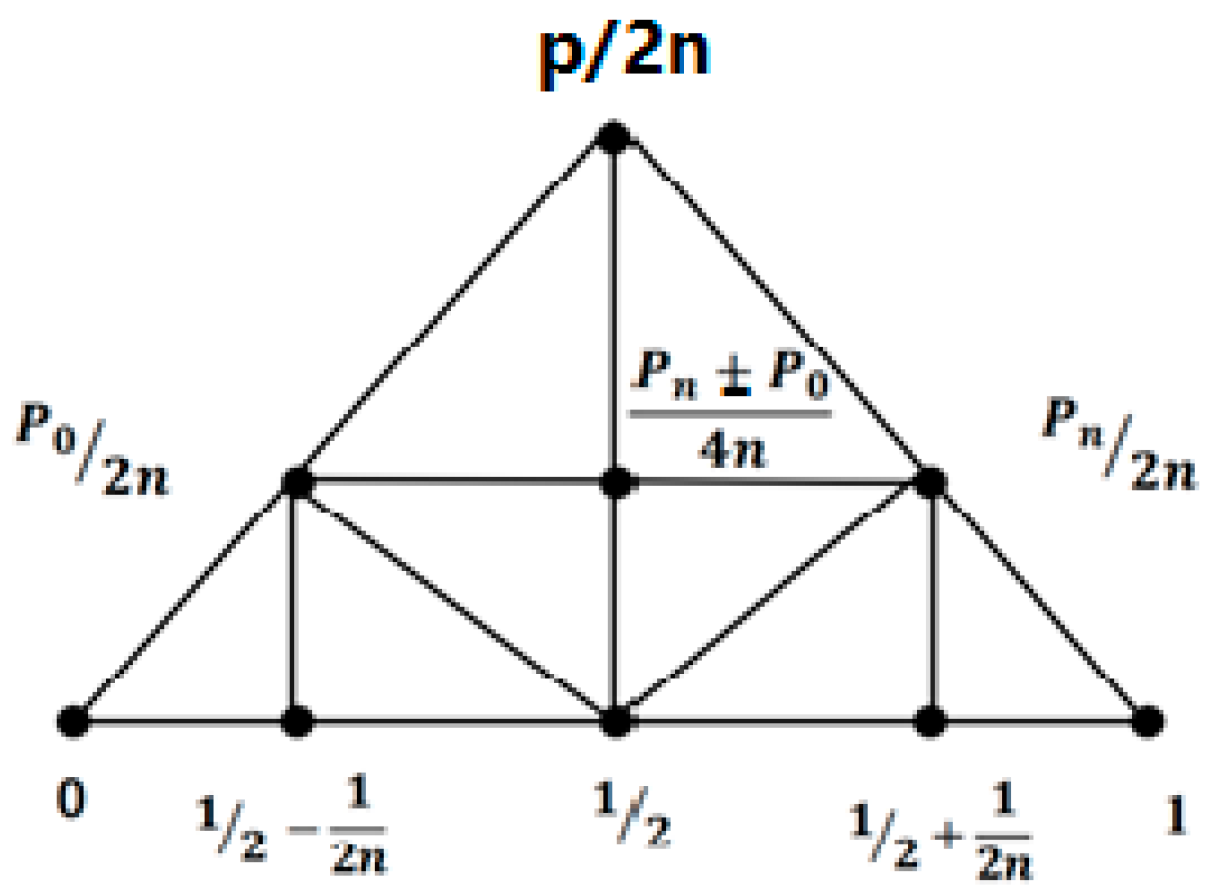
So we get a symmetry structure of P/2n asFigure 2

Figure 2. a symmetry structure of P/2n about line-1/2.

\frac{p 0}{2 n} = \frac{1}{2} - \frac{1}{2 n} (n \geq 3)

\frac{p n}{2 n} = \frac{1}{2} + \frac{1}{2 n}

\frac{p n \pm p 0}{4 n} = \frac{1}{2}

2. A Concise Proof of The Fermat’ Last Theorem

he Fermat’ Last Theorem:

x^{n} + y^{n} = z^{n}

(x, y, z \in n, x y z \neq 0 n > 2)

has no solution.

n ~ (1,2, 3,4, 5, 6 \dots \dots \dots .) a l l t h e n a t u r a l n u m b e r s e x c e p t e d 0

The equivalent proposition of this conjecture is

({{\frac{x}{z})}^{n} + (\frac{y}{z})}^{n} = 1

(x, y, z \in n, x y z \neq 0 n > 2)

has no solution.

We have

({{\frac{x}{z})}^{n} + (\frac{y}{z})}^{n} = 1 = \sum \frac{1}{2^{n}}

n ~ (1,2, 3,4, 5, 6 \dots \dots \dots .) a l l t h e n a t u r a l n u m b e r s e x c e p t e d 0

\begin{matrix} ({{\frac{x}{z})}^{n} + (\frac{y}{z})}^{n} = 1 \\ = (\frac{1}{2^{n}} - \frac{1}{2^{n}}) + 1 \\ = (\frac{1}{2} - \frac{1}{2^{n}}) + (\frac{1}{2} + \frac{1}{2^{n}}) \\ = \frac{1}{2^{n}} + (1 - \frac{1}{2^{n}}) \end{matrix}

Only When

n = 1

we have

(\frac{1}{2^{n}} - \frac{1}{2^{n}}) = (\frac{1}{2} - \frac{1}{2^{n}}) = 0

1 = (\frac{1}{2} + \frac{1}{2^{n}}) = (\frac{1}{2} + \frac{1}{2})

And Only When

n = 2

(\frac{1}{2^{n}}) = (\frac{1}{2} - \frac{1}{2^{n}}) = \frac{1}{4}

(1 - \frac{1}{2^{n}}) = (\frac{1}{2} + \frac{1}{2^{n}}) = \frac{3}{4}

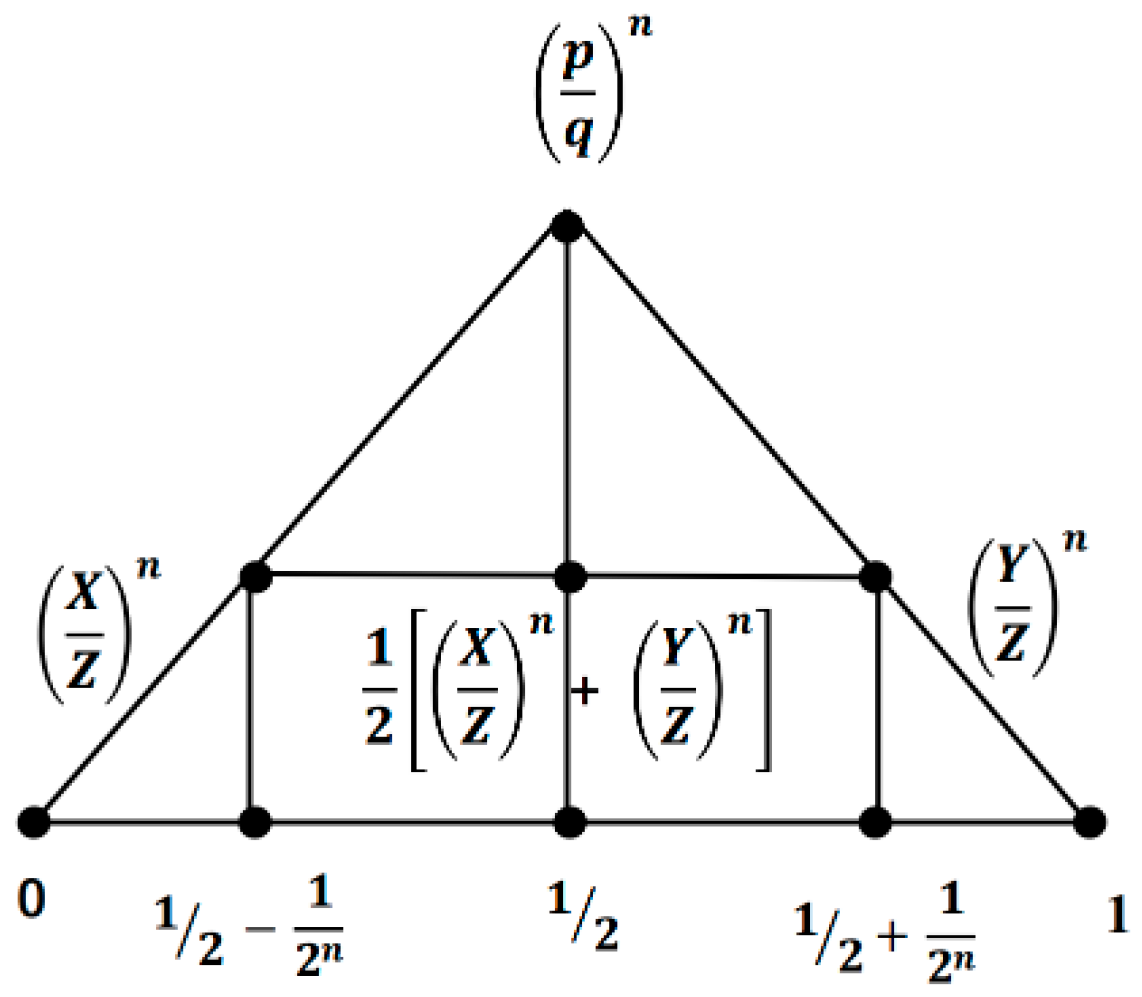
And We can get the figures as Figure 3.

Figure 3. D1/₂₊1/₂ with points 1/2-1/2ⁿ and 1/2-1/2ⁿ

n ~ (1 ， 2 ， 3 ， 4 ， \dots \dots \dots .) .

Figure 3. D1/₂₊1/₂ with points 1/2-1/2ⁿ and 1/2-1/2ⁿ

n ~ (1 ， 2 ， 3 ， 4 ， \dots \dots \dots .) .

n = 1 and n = 2

In fact we have

1 = \frac{1}{2^{1}} + \frac{1}{2^{1}} = \frac{1}{2^{2}} + \frac{3}{2^{2}} = \frac{1}{2^{3}} + \frac{7}{2^{3}} o r \frac{3}{2^{3}} + \frac{5}{2^{3}}

Figure 4. a symmetry structure of

{(\frac{p}{q})}^{n}

about line-1/2.

Figure 4. a symmetry structure of

{(\frac{p}{q})}^{n}

about line-1/2.

({\frac{p}{q})}^{n}

p, q is relatively prime and

n ~ (1 ， 2 ， 3 ， 4 ， \dots \dots \dots .)

1 / 2 [({{\frac{x}{z})}^{n} + (\frac{y}{z})}^{n}] = 1 / 2 \leftrightarrow ({{\frac{x}{z})}^{n} + (\frac{y}{z})}^{n} = 1

({\frac{x}{z})}^{n} = \frac{1}{2} - \frac{1}{2^{n}}

{(\frac{y}{z})}^{n} = \frac{1}{2} + \frac{1}{2^{n}}

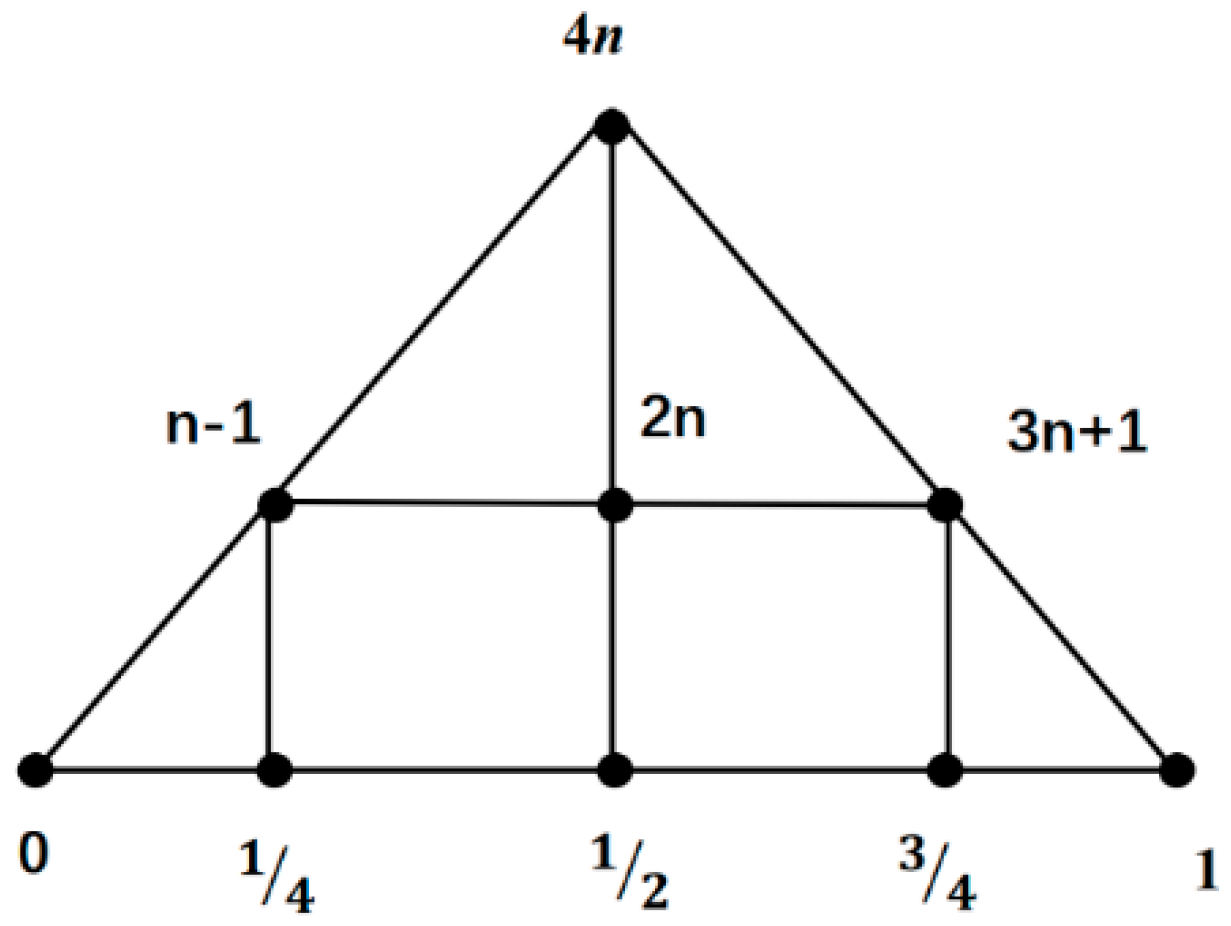
3. a concise proof of Collatz Conjecture

Collatz Conjecture:

f (n) = \{\begin{matrix} \frac{n}{2} i f n \equiv 0 (m o d 2) \\ 3 n + 1 i f n \equiv 1 (m o d 2) \end{matrix}

k \in N \to f^{k} (n) = 1

n ~ (1 ， 2 ， 3 ， 4 ， \dots \dots \dots .) a l l t h e n a t u r a l n u m b e r s e x c e p t e d 0

\frac{[\frac{n + 1}{2}] + [\frac{n - 1}{2}]}{[\frac{n}{2}]} = \frac{2 n + 2}{n + 1} = \frac{(n - 1) + (3 n + 1)}{2 n} = \frac{4 n}{2 n} = \frac{4}{2} = \frac{2}{1} = \frac{1}{\frac{1}{2}}

= \sum \frac{1}{2^{N}}

Figure 5. a symmetry structure of

4 n

about line-1/2.

Figure 5. a symmetry structure of

4 n

about line-1/2.

2 n = 1 / 2 [(n - 1) + (3 n + 1)]

\lim_{n \to \infty} (\frac{n - 1}{4 n}) = 1 / 4

\lim_{n \to \infty} (\frac{3 n + 1}{4 n}) = 3 / 4

4. The symmetry of L^1/2±ε _{(0 1/2 1)} and Riemann Hypothesis

Riemann Zeta-Function

ξ (s) = \sum_{n = 1} \frac{1}{n^{s}} \begin{matrix} = \prod \frac{1}{1 - p^{s}} \end{matrix} (s = a + b i)

S > 1 ξ (s) \to c o n s t

The trivial zero-points of Riemann Zeta-Function is -2n (n~1,2,3,…….)

Riemann Hypothesis: all the Non-trivial zero-point of Zeta-Function

Re (s) = \frac{1}{2}

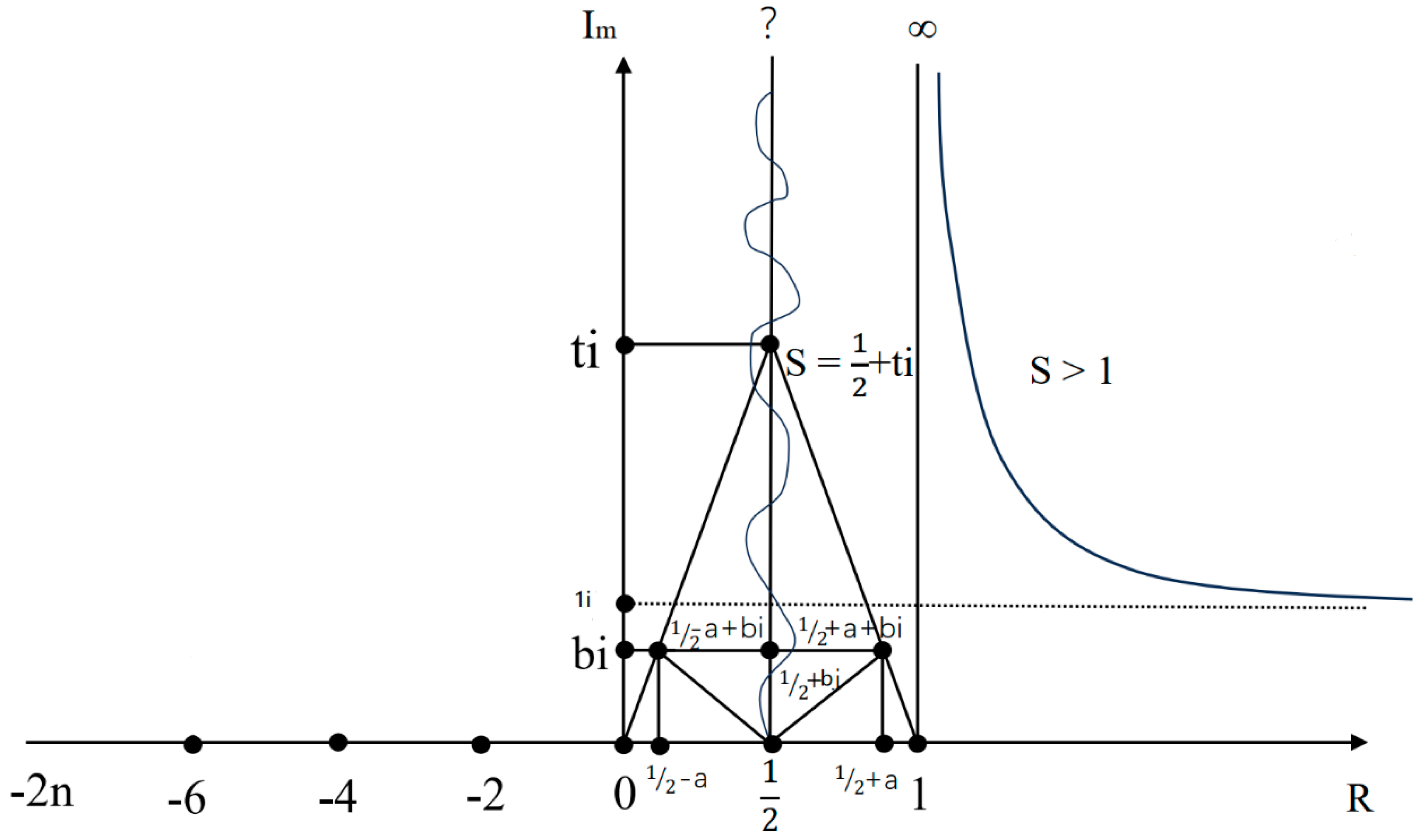
Figure 6. Riemann Hypothesis: all the non-trivial Zero points of Riemann zeta-function are on the 1/2 axis.

We can get a symmetry structure including all numbers about the line-1/2 as Figure 6

s = \frac{1}{2} + t i t \in R

z p 1 = \frac{1}{2} - a + b i z p 0 = \frac{1}{2} + b i z p 2 = \frac{1}{2} + a + b i

z p 1 + z p 2 = (\frac{1}{2} - a + b i) + (\frac{1}{2} + a + b i) = 1 + 2 b i

z p 2 - z p 1 = (\frac{1}{2} + a + b i) - (\frac{1}{2} - a + b i) = 2 a

a, b \in R 0 \leq a \leq \frac{1}{2}

As the Figure 7 If we have zero points of

ξ (s)

as

z p 1 = \frac{1}{2} - a + b i z p 2 = \frac{1}{2} + a + b i

And

s = \frac{1}{2} + t i

t \in R

is the first zero point on line-1/2

We can get a zero point as

z p 0 = \frac{1}{2} + b i b < t b, t \in R

It is contrary to that

s = \frac{1}{2} + t i

t \in R

is the first zero point on line-1/2

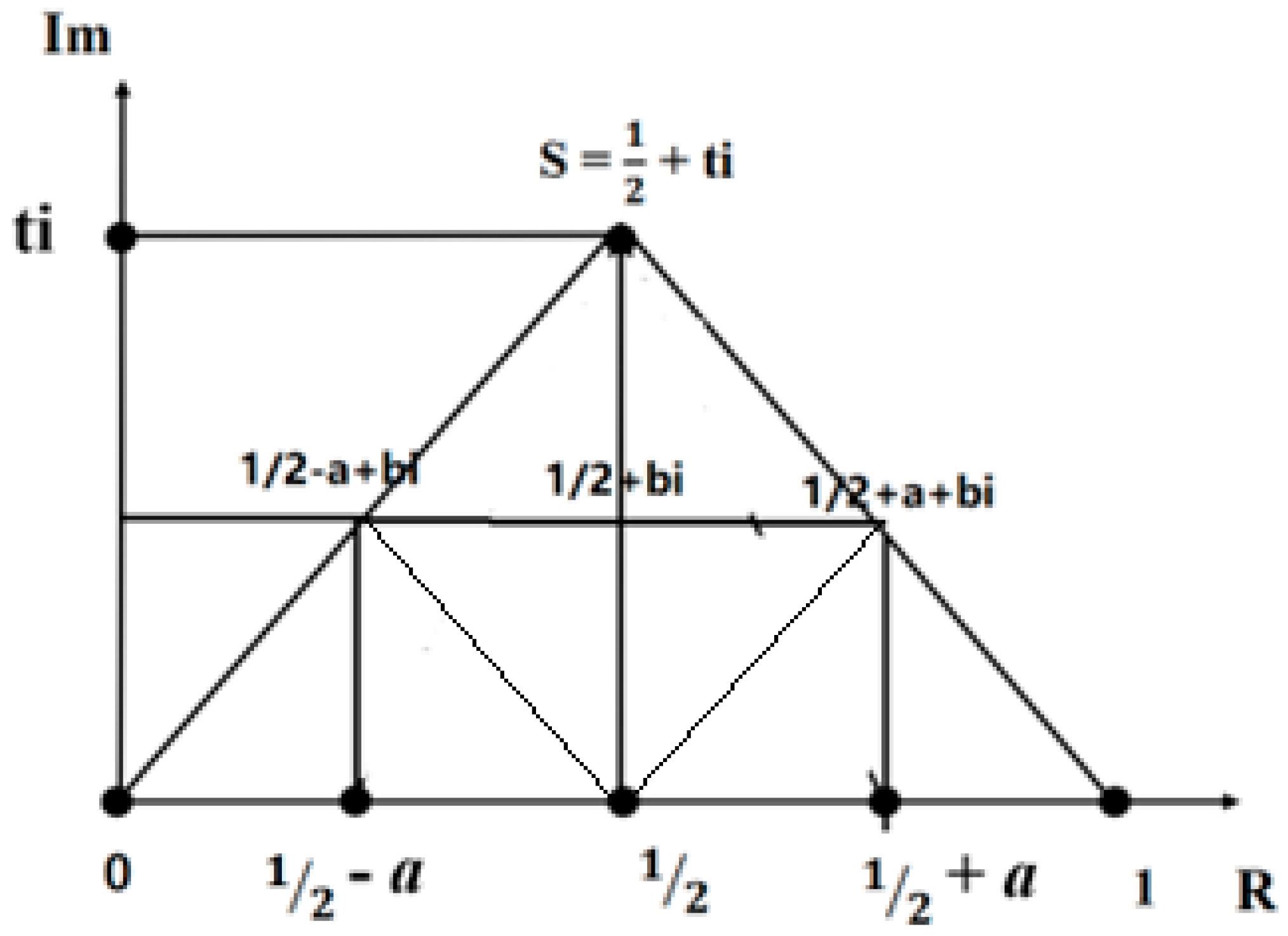
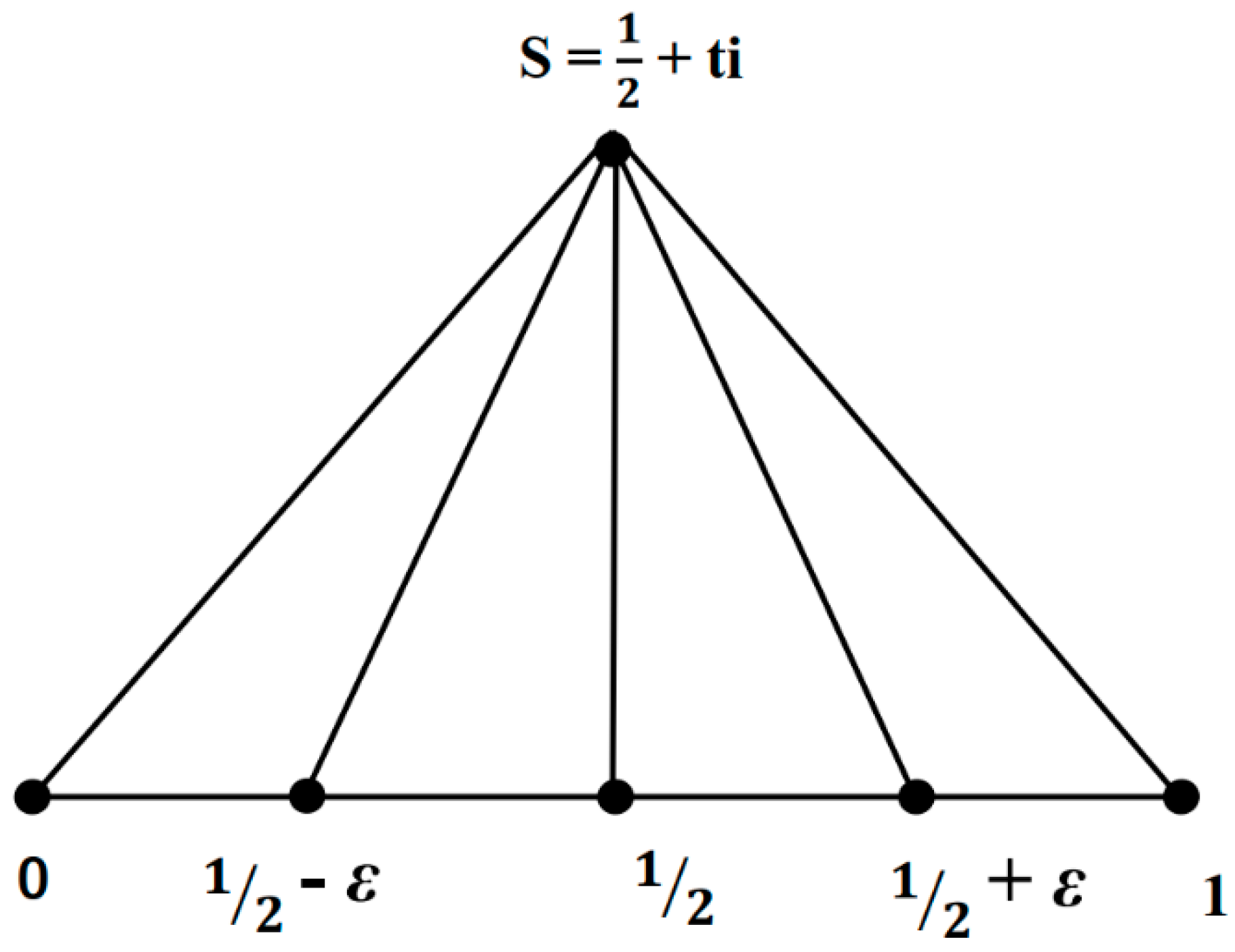
Figure 7. a symmetry structure about line1/2+/-a at the zero piont s=1/2+ti.

As the Figure 8. If we have zero points of

ξ (s)

as

z p 1 = \frac{1}{2} - a + b i z p 2 = \frac{1}{2} + a + b i

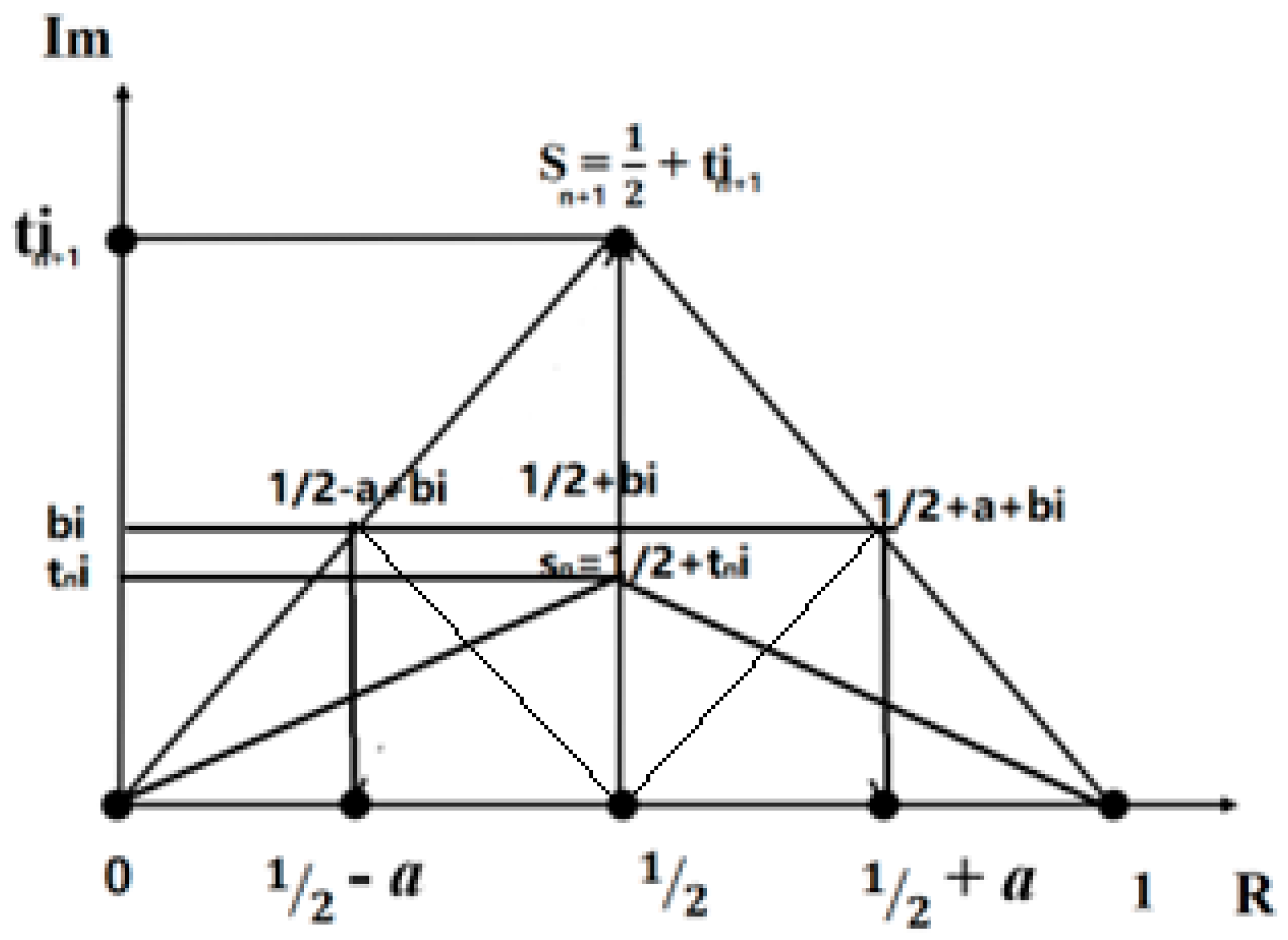
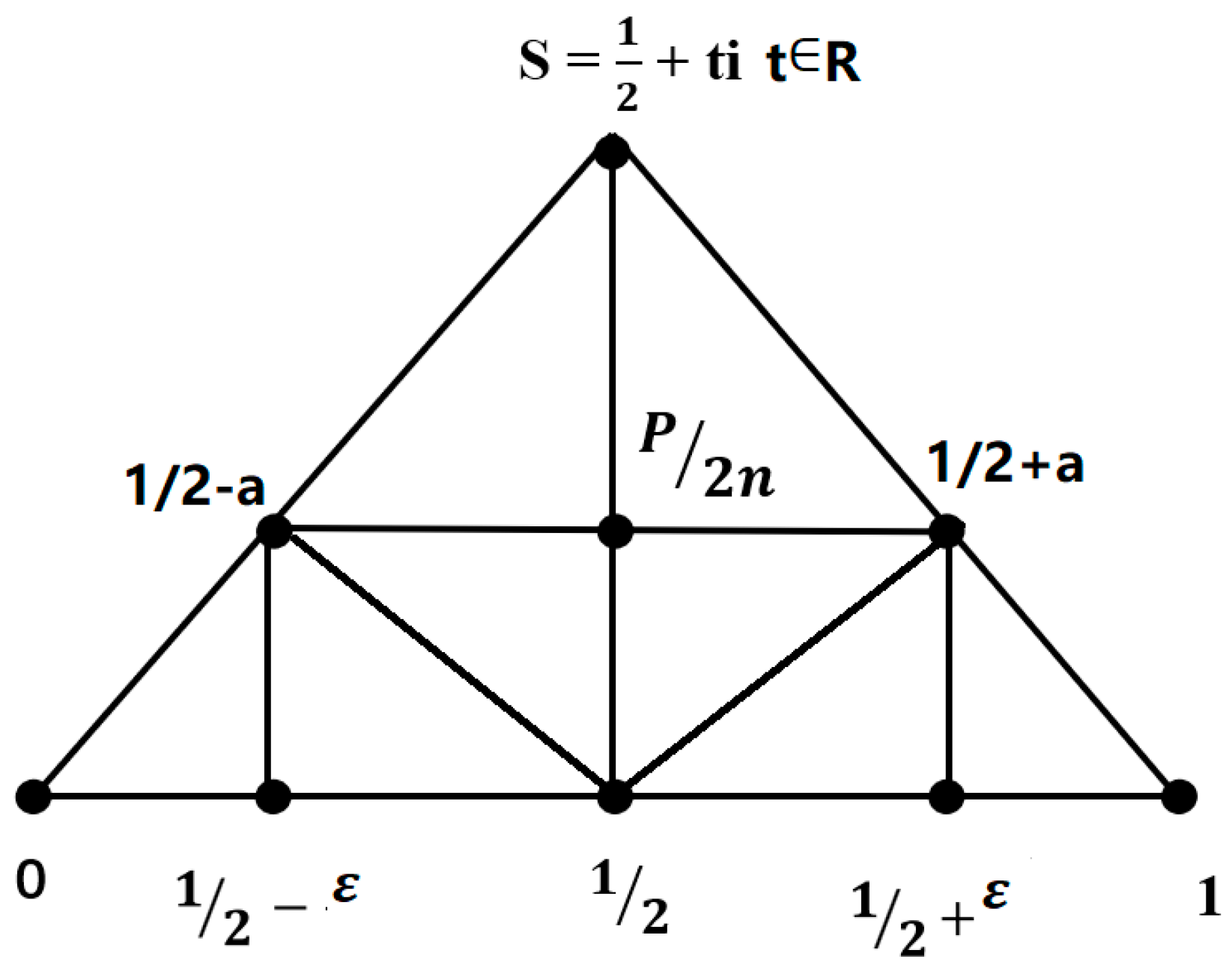
Figure 8. a symmetry structure about line1/2+/-a at the zero point s_n=1/2+t_ni and s_n+1=1/2+t_n+1i.

And

s_{n} = \frac{1}{2} + t_{n} i

t \in R

is the No. n zero point on line-1/2

s_{n + 1} = \frac{1}{2} + t_{n + 1} i

t \in R

is the No. n+1 zero point on line-1/2

We can get a zero point between

s_{n} a n d s_{n + 1} o n l i n e - 1 / 2

as

z p 0 = \frac{1}{2} + b i t_{n} < b < t_{n + 1} b, t \in R

It is contrary to that

s_{n} a n d s_{n + 1}

are the adjacent zero points on line-1/2

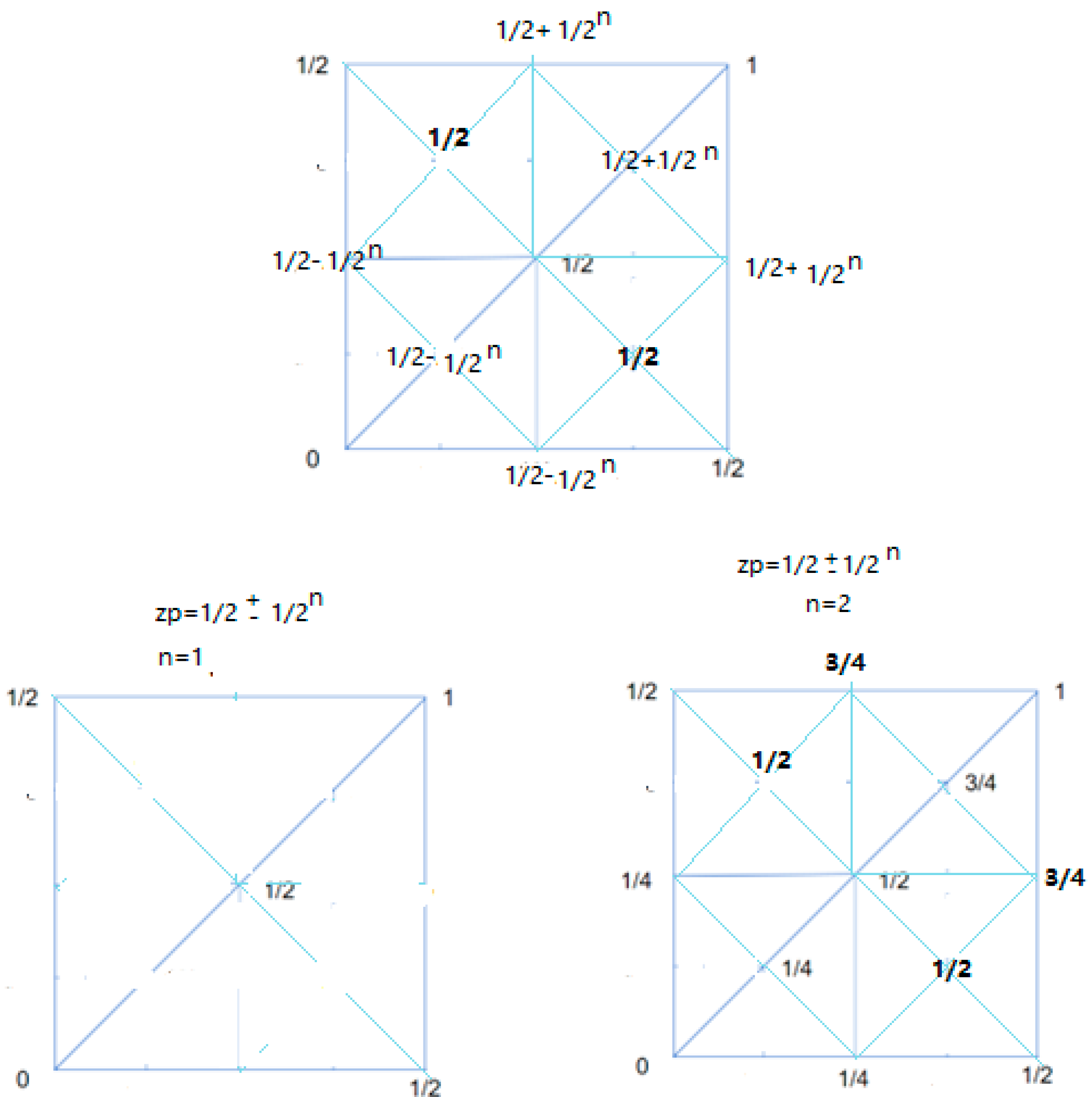
So on complex plane, We can have the symmetry structure about the line-1/2 with zp=1/2±a

(0 \leq a \leq \frac{1}{2} a \in R)

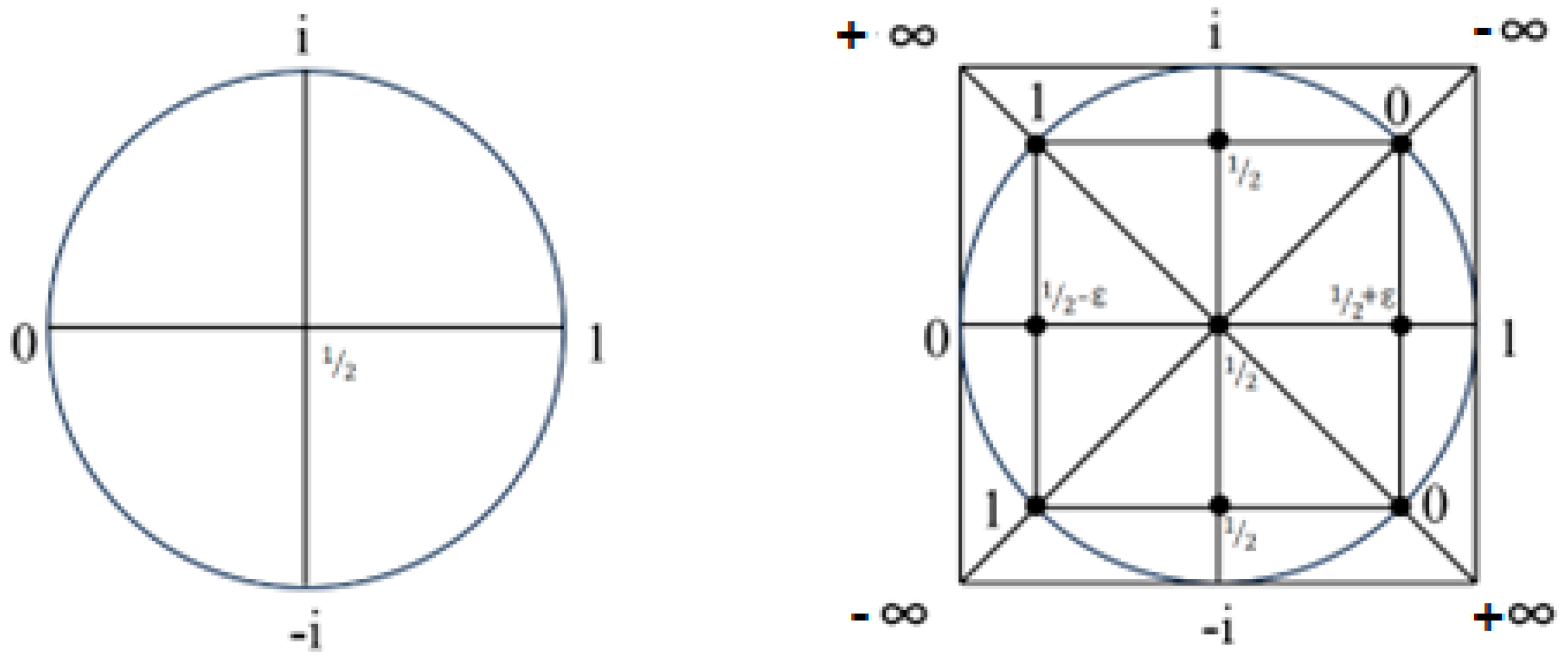
show as on Figure 9.

Figure 9. symmetry structure about the line-1/2 with zp=1/2±a.

S = \frac{1}{2} + t i (t \in R)

z p = \frac{1}{2} \pm a (0 \leq a \leq \frac{1}{2} a \in R)

z p 1 = \frac{1}{2} - a z p 0 = \frac{1}{2} z p 2 = \frac{1}{2} + a

z p 1 + z p 2 = (\frac{1}{2} - a) + (\frac{1}{2} + a) = 1

z p 2 - z p 1 = (\frac{1}{2} + a) - (\frac{1}{2} - a) = 2 a

This is mean that there are no zero points on line-1/2±

a (0 \leq a \leq \frac{1}{2} a \in R)

.

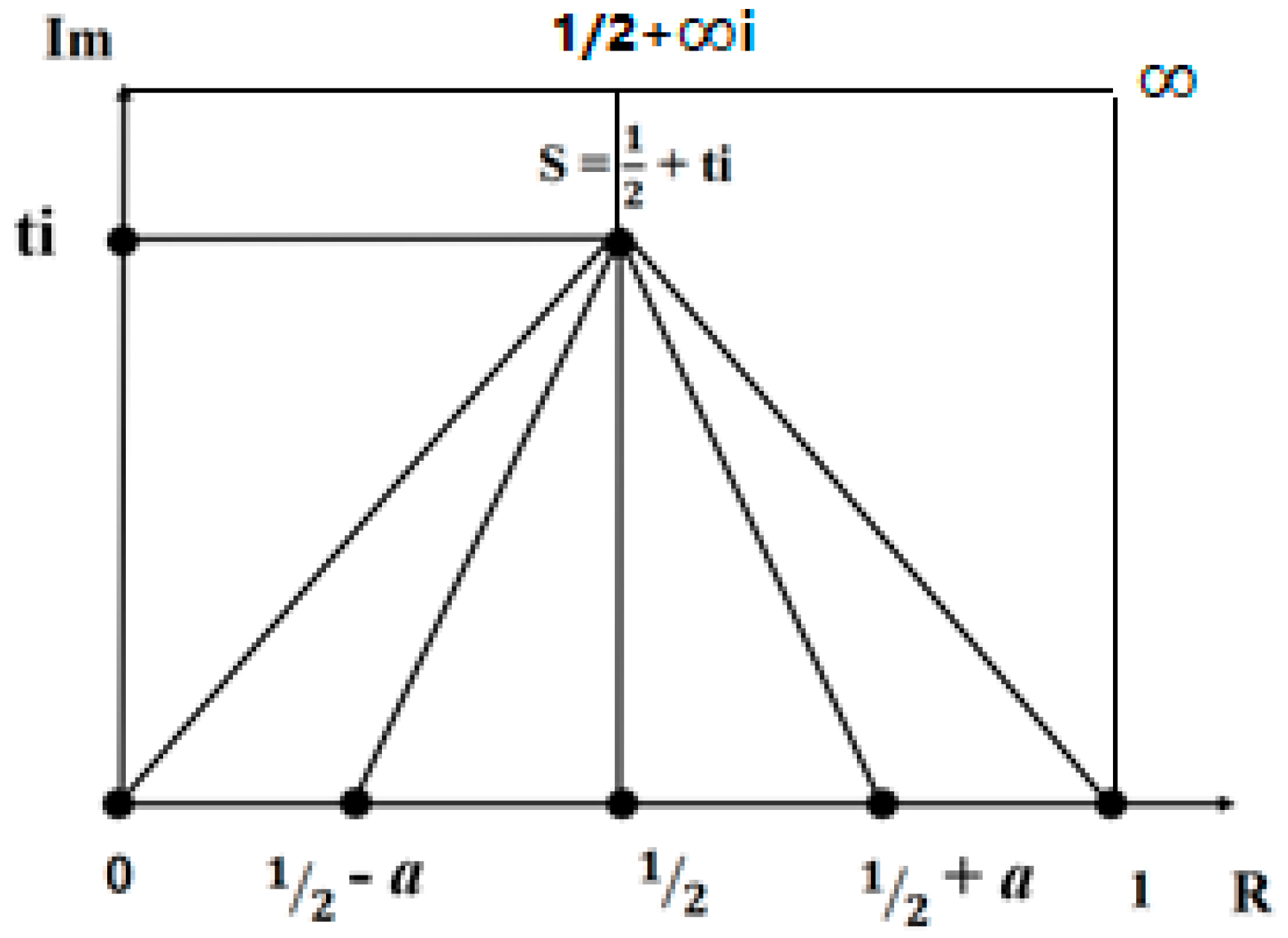
Hardy and Littlewood give a proof that there are infinite zero points on line-1/2 (Hardy and Littlewood. 1914 )

So we give a proof that all the non-trivial Zero points of Riemann zeta-function are on the Line-1/2. This is the proof of Riemann Hypothesis.

5. The Symmetry Number Structure about Line-1/2 including all numbers

In fact, we have a symmetry number structure about line-1/2 as Figure 10:

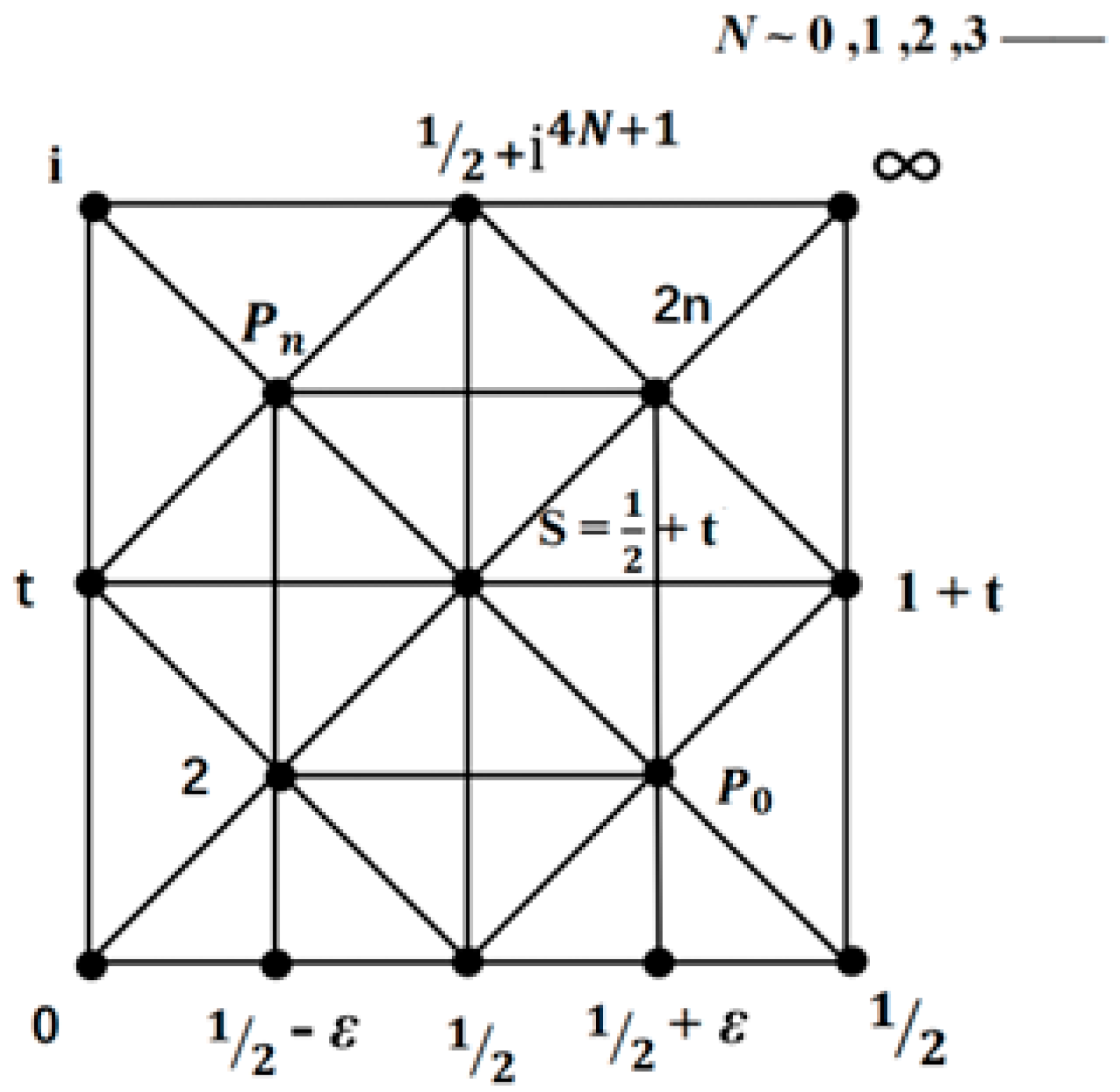
Figure 10. symmetry structure about the line-1/2 with zp=1/2±ε.

S = \frac{1}{2} + t i (t \in R)

z p = \frac{1}{2} \pm ε (ε = a + b i a, b \in R 0 \leq a \leq \frac{1}{2})

And we have

1 / 2 = 1 / 2 0 = 1 / 2 - 1 / 2 1 = 1 / 2 + 1 / 2

1 + (\pm {i)}^{2} = 0

1 + 1 / 2 (i + 1) (i - 1) = 0

\infty = 1 + 1 + 1 + 1 + \dots

We called it L^1/2±ε _{【0 1/2 1
】} and analytic continuation to

[\begin{matrix} + \infty & - \infty \\ - \infty & + \infty \end{matrix}]

we can get Figure 11.

Figure 11. The Symmetry of L^1/2±ε _{【0 1/2 1】} with

z p = \frac{1}{2} \pm ε .

Figure 11. The Symmetry of L^1/2±ε _{【0 1/2 1】} with

z p = \frac{1}{2} \pm ε .

So we have:

1 + [\begin{matrix} + \infty i - \infty \\ 0 1 / 2 1 \\ - \infty - i + \infty \end{matrix}] {[\begin{matrix} 1 1 / 2 0 \\ \frac{1}{2} - ε 1 / 2 \frac{1}{2} + ε \\ 1 1 / 2 0 \end{matrix}]}^{- 1} = 0

z p = \frac{1}{2} \pm ε

ε = a + b i (a, b \in R 0 \leq a \leq \frac{1}{2})

z p 1 = \frac{1}{2} - ε z p 2 = \frac{1}{2} + ε

We have

z p 1 + z p 2 = (\frac{1}{2} - ε) + (\frac{1}{2} + ε) = 1

z p 2 - z p 1 = (\frac{1}{2} + ε) - (\frac{1}{2} - ε) = 2 ε = 2 (a + b i)

And we have

n^{2} = \frac{1}{2} ∙ n ∙ 2 n = \sum_{N} \frac{1}{2} \sum_{N} \frac{1}{2^{N}} [(\frac{1}{2} - ε) + (\frac{1}{2} + ε)]

N ~ (0, 1 ， 2 ， 3 ， 4 ， \dots \dots \dots .)

All natural numbers

n ~ (1 ， 2 ， 3 ， 4 ， \dots \dots \dots .)

All natural numbers excepted 0

We can get a matrix (

n \times n

)

[\begin{matrix} 1 / 2 \dots \dots . . \frac{1}{2^{n}} (1 / 2 + ε) \\ \dots \dots 1 / 2 \dots \dots \dots . . \\ \frac{1}{2^{n}} (1 / 2 - ε) \dots \dots . . 1 / 2 \end{matrix}] (n \times n)

The tr(A)=1/2*n

Figure 12. The Symmetry of S∞+i.

We have

0 = \frac{1}{2} - \frac{1}{2} 1 = \frac{1}{2} + \frac{1}{2} 2 = 1 + 1

1 + i^{2} = 0 1 / 2 + i^{4 N + 1} = 1 / 2 + i

\infty = 1 + 1 + 1 + 1 + \dots

P 0 \in P \leq 2 n P n \in P \geq 2 n

N ~ (0 ， 1 ， 2 ， 3 ， 4 ， \dots \dots \dots .)

all the natural numbers.

n ~ (1 ， 2 ， 3 ， 4 ， \dots \dots \dots .)

All natural numbers excepted 0

P ~ (2 ， 3 ， 5 ， 7 ， \dots \dots \dots .)

All odd prime number

S = \frac{1}{2} + t (t \in R)

z p = \frac{1}{2} \pm ε (ε = a + b i a, b \in R 0 \leq a \leq \frac{1}{2})

And we find that

1 + e^{π i} =

0 (Euler’s Formula)

1 + i^{2} = 0 1 + \frac{1}{2} (i + 1) (i - 1) = 0 (1 + i) (1 - i) = \sum \frac{1}{2^{N}}

1 + e^{π i} = 0 1 + \frac{1}{2} (e^{i p π} - e^{i 2 N π}) = 0

N ~ (0 ， 1 ， 2 ， 3 ， 4 ， \dots \dots \dots .)

all the natural numbers.

p ~ (3 ， 5 ， 7 ， \dots \dots \dots .)

All odd prime number

2 (n \pm 1) = p n \pm p 0

p n - 2 n + p 0 = 2

And

2 n - p n + p 0 = 2

It is like the Euler’s Polyhedron Formula

We can get Figure 12. This is a symmetry number structure about line-1/2 including all numbers.

And we can get a symmetry number structure about line-1/2 as Figure 13. We should call it Reimann dynamic space.

Figure 13. Reimann dynamic space.

1 + i^{2} = 0

1 + 1 / 2 (i + 1) (i - 1) = 0

S = \frac{1}{2} + t i (t \in R)

z p = \frac{1}{2} \pm ε (ε = a + b i a, b \in R 0 \leq a \leq \frac{1}{2})

\frac{P}{2 n} = \{\begin{matrix} \frac{1}{2^{N + 1}} n = 2^{N} P \\ \frac{3}{4} n = 2 P = 3 \\ 1 n = 1 P = 2 \end{matrix}

N ~ (0, 1 ， 2 ， 3 ， 4 ， \dots \dots \dots .)

All natural numbers

n ~ (1 ， 2 ， 3 ， 4 ， \dots \dots \dots .)

All natural numbers excepted 0

P ~ (2 ， 3 ， 5 ， 7 ， \dots \dots \dots .)

All prime numbers

No datasets were generated or analyzed during the current study.

Competing Interests statement

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

Weisstein, Eric W. " Riemann Hypothesis." From MathWorld--A Wolfram Web Resource. Available online: https://mathworld.wolfram.com/ Riemann Hypothesis.
Weisstein, Eric W. " Goldbach conjecture." From MathWorld--A Wolfram Web Resource. Available online: https://mathworld.wolfram.com/ Goldbach conjecture.
Weisstein, Eric W. " Fermat Last Theorem." From Math World--A Wolfram Web Resource. Available online: https://mathworld.wolfram.com/Fermat Last Theorem.
Weisstein, Eric W. "Collatz Problem." From Math World--A Wolfram Web Resource. Available online: https://mathworld.wolfram.com/Fermat Last Theorem.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

The Symmetry Number Structure About Line-1/2

Abstract

Keywords:

Subject:

1. The Symmetry of P/2n and Prime Numbers Conjectures

2. A Concise Proof of The Fermat’ Last Theorem

3. a concise proof of Collatz Conjecture

4. The symmetry of L1/2±ε (0 1/2 1) and Riemann Hypothesis

5. The Symmetry Number Structure about Line-1/2 including all numbers

Competing Interests statement

References

4. The symmetry of L^1/2±ε _{(0 1/2 1)} and Riemann Hypothesis