2. The Generalized Golden Ratio (GGR)
In this section, we extend the well-known concept of the gold ratio in the -dimension vector space. Let be the normed vector space over real numbers . It means that exists such a real-valued function , which is denoted by and has the following properties:
, and means that
, for any real number
, for any elements and .
The function is called the length, or the norm, of the element .
Definition 1. In a normed vector space , the function which satisfies the conditions
, for any elements and
If
If
For any real number , is called the proportion.
As an example, when , the function is the proportion. This is the function that interests us the most.
Definition 2. Given a proportion
in the normed vector space
, two elements
and
are called
the golden pair, if the following holds:
The elements
and
are also called
the golden ratio elements, or
the golden pair.
Definition 3. If the elements and are golden ratio elements, for a proportion then the ratio is called the generalized golden ratio, or shortly GGR.
In the example below for the 1-D vector space, this number is the known golden ratio [
1]. Therefore, we use a similar name. In order not in any way to underestimate the historical nature of this number, we added a generalized meaning.
Example 1: Let
and the function
be the proportion. Here, we consider that
for real numbers. To find the golden ratio elements
and
, we consider the primary equation
It can be written as
or
The solutions of this equation are considered for the following two possible cases.
1. Case
: Then, the equation to be solved is
The solutions are
Such numbers are real only when
. Therefore,
A golden ratio is a positive number. The first number
is considered, but the second
is not, since it is negative. Thus, the golden ratio is
2. Case
: The following equation is considered:
with the solutions
Such numbers are real only when
. Therefore,
Here, is negative and also needs to be discarded, since the condition of consideration is violated, that is, . Thus, a golden pair cannot be composed from numbers of opposite signs. This example shows that for any number there is only one number that composes the golden ratio with . This number is . The golden pair is . In the 1D space , when setting the system of coordinates, we match each point to a certain number, implying by this number some measure of distance from the center of coordinates. Therefore, in the 1D case we deal with linear objects (segments on the real line ) which have the length and it is namely the value for which we obtained a certain proportion called the golden ratio. Two linear objects are in golden ratio, if the ratio of their measures (lengths) is equal to the number .
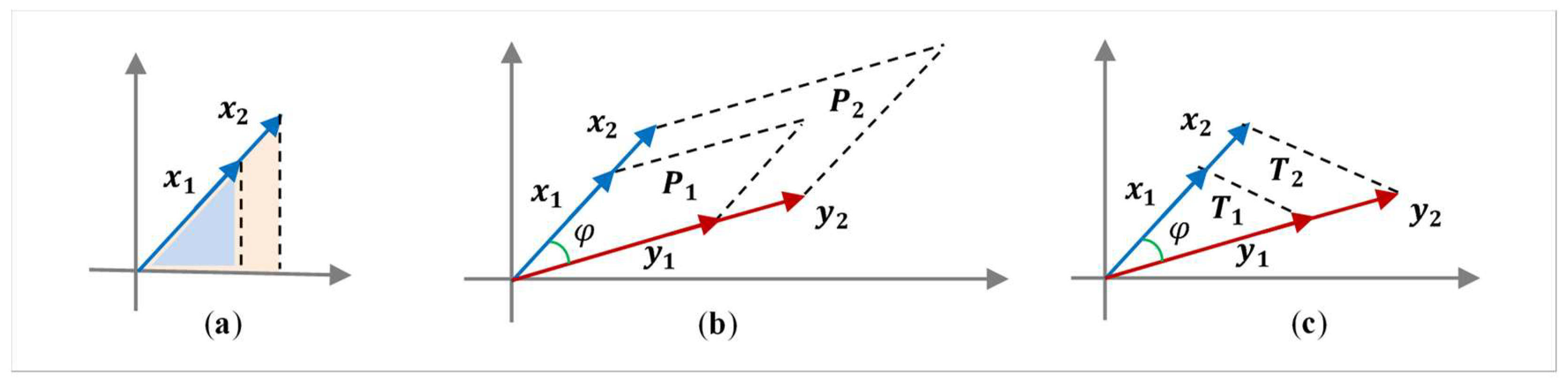
Now, we will try to move the idea of the golden ratio on the 2D plane (with 1D and 2D objects), considering the starting point 0 in a given system of coordinates. Before we start to work with equations, we need to prepare ourselves to all possible results and ability to explain them. The thing is that 2D objects includes the 1D objects and the golden ratio rule must remain unchanged for them. Let us consider two vectors
and the corresponding similar vector
(see
Figure 1 in part (a)). One can note that the 2D measures of the similar vectors
and
, or areas of their shadows are in the ratio
, not in
.
Now we consider that two vectors and are related into one 2D object, the parallelogram, , as shown in part (b). The similar vectors and are also related into another 2D object; the parallelogram . If these vectors are related, then this relation changes; it depends on the angle between these vectors. Then, the question arises how the proportions of these 2D objects cannot depend on connectedness of vectors. In the general case, this number, or the ratio, is the function of the angle, which we denote by When the angle between the vectors is zero, the 2D object is a line. Therefore, in order that the 1D golden ratio can manifest, it is necessary to request the condition . Note that instead of the parallelograms we can also consider other figures, including the triangles composed by these vectors, as shown in part (c). We can call these triangles the golden pair of triangles. Now, we will describe in detail the concept of the golden ratio in a multi-dimensional vector space.
Example 2: Consider the
-dimensional vector space
It is not difficult to show that the function
is the proportion. Here, the norms
and
We consider the golden ratio equation (rule)
written as
The following calculations are valid for this equation:
Here,
is the inner product in the space
, and
is the angle between the vectors
and
. Denoting the golden ratio by
, we obtain the equation
or
This equation has four roots , which are functions of the angle. Thus, the GGR depends on the angle. Since , the roots =, for Also, =.
A. Case
(vectors are collinear, or are in the same directions): The equation
can be written as
Therefore, we consider the solutions of the equation
, which are
The positive solution is
Given vector
, the golder pair of vectors
are in the same direction, and the pair of vectors
are in the opposite direction. The second equation
has two complex roots,
These complex coefficients of “similarity” are equal to 1 in absolute value, that is, they do not affect the length, but only rotation by
. One can say that the first equation in Eq. 8 defines similarity by length and the second equation similiarity by rotation.
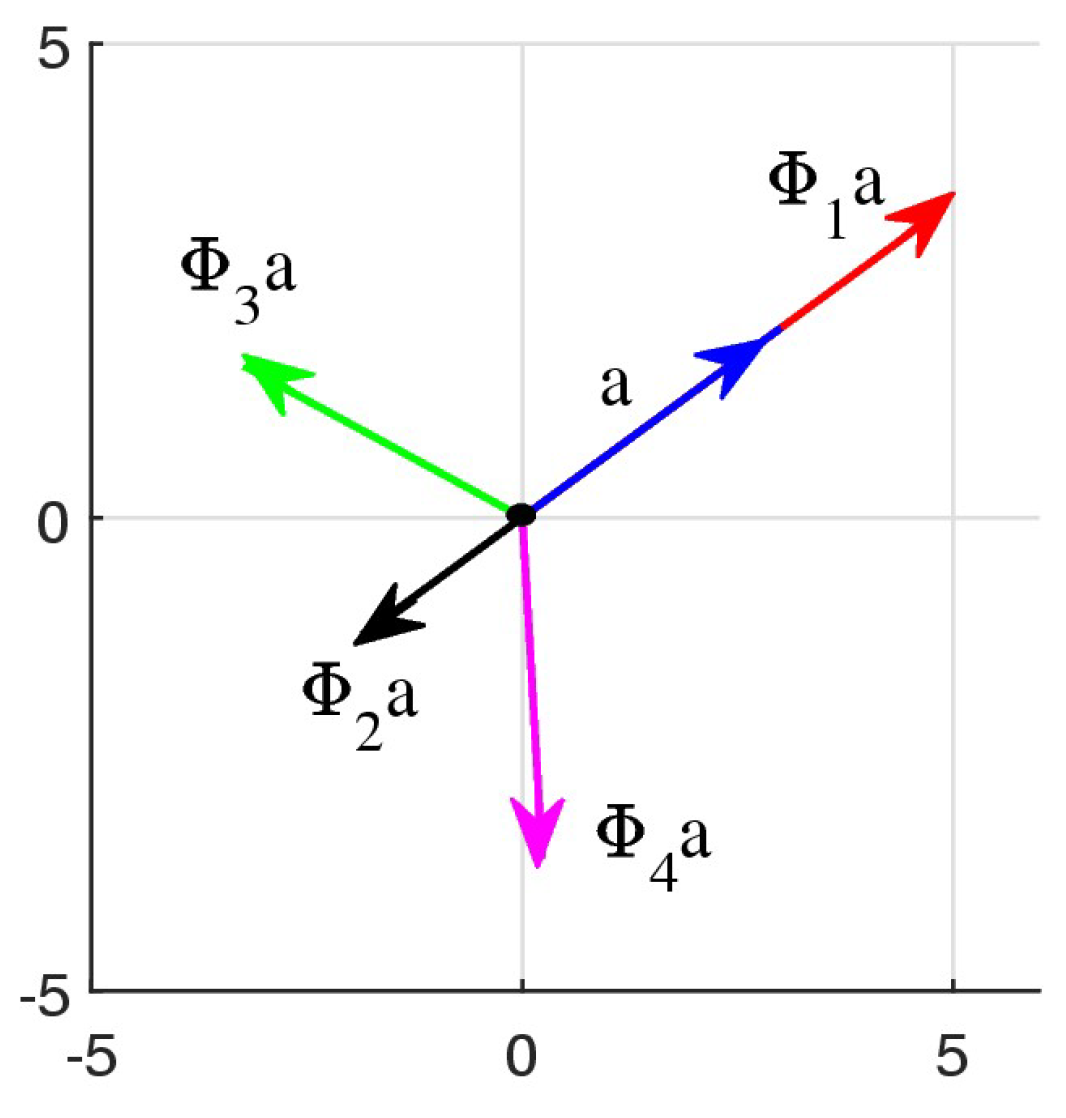
As an example,
Figure 3 shows the 2D vector
at an angle of
to the horizontal and four vectors
It is not difficult to see that and These equations hold for any vector .This figure illustrates the concept of similarity of the vector , or similarity by the angle . Among these fours vector, only the first one, is in the golden ratio with .
B. Case
(vectors are perpendicular): The equation
is reduced to two equations
Therefore, the first equation is considered and its two solutions are
The positive solution is
C. Case
(vectors are collinear in the opposite directions): The equation
can be written as
Therefore, we consider the solution of equation
, which are (see Eq. 4)
The positive solution is Thus, in the -dimensional space, when , two vectors in the opposite directions can compose a golden pair.
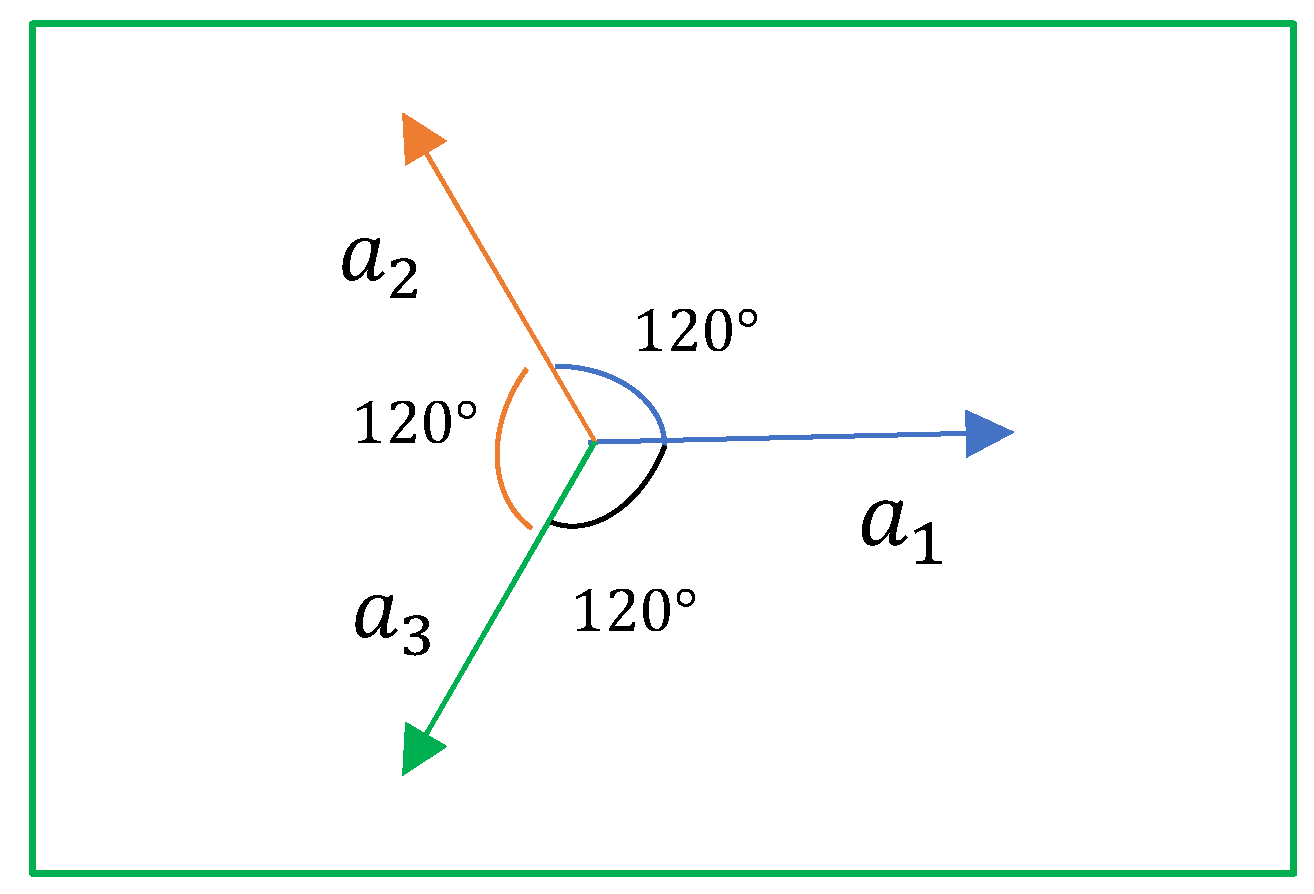
D. Case when the golden pair of vectors have the same length, that is
Then, Eq. 7 is
and the angles
. Two pairs of vectors with the angles
and 120 (in degrees) between them compose golden pairs when their lengths are equal.
Figure 4 shows three vectors
and
with the same length. Each of these vectors is in the golden ratio with two others.
3. Main Equation of Golden Ration and Its Analytical Solution
In this section, we describe the positive roots of Eq. 7, where
is a function of the angle
The equation is
with the initial condition
=1.61803398. For each angle
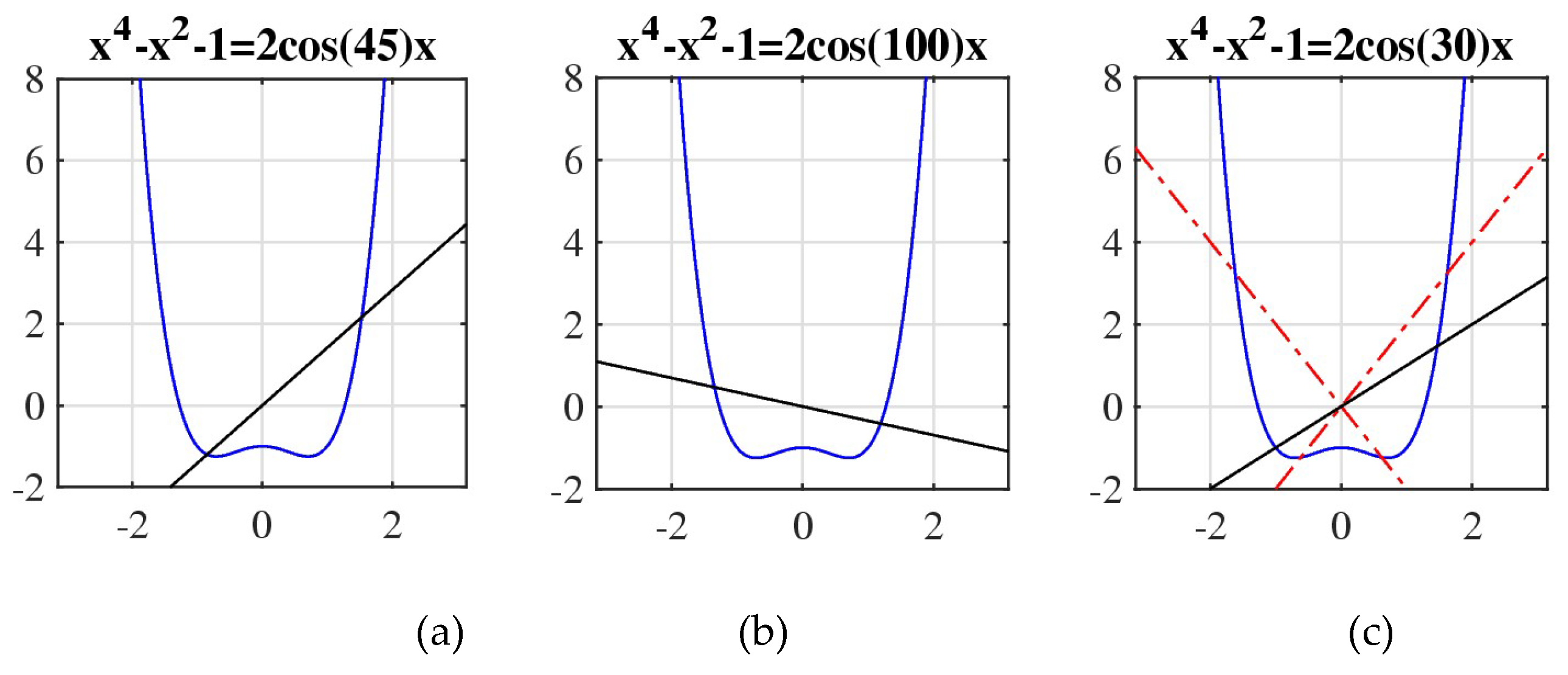
α, the quartic polynomial in this equation has four roots, and two of them are complex and therefore complex conjugate. We are looking for a positive solution of this equation, which should be only one. Equation 10 can be written as
The parabola
crosses the straight line with the slope
at two points. As illustration,
Figure 5 shows the graph of the polynomial
together with the line
, when
in part (a) and
in part (b).
For the angle
, the solutions of Eq. 10 are
The numbers are written here with 4 decimal precision. At points
and
, the parabola
crosses the straight line
, as shown in part (a). The second coordinate is positive. Thus, the required root
. For the angle
, the solutions of Eq. 10 are
The parabola
P(
x) crosses the straight line
at the point
and the positive point
. Therefore,
638778… .
The case with the angle
(when
…) is shown in
Figure 5 in part (c). Here, two lines
are also shown (in red) as the border lines for the lines
, when
One can see that all these lines
intersect the parabola at two points, one of which is positive and other one is negative.
3.1. Similarity Equation and Its Roots
Consider again the main equation of the gold ratio
We call the continuous roots of this equation the similarity functions and denote them by the symbols
. The analytical exact solution of this quartic equation is very complicated [12-15]. The standard procedure is to add an auxiliary parameter
to the quartic equation
, write it as
and then to request for a square polynomial in square brackets to be a square, that is,
To have such a multiple root
, the discriminant of the equation must be zero,
Then,
and the above quartic equation can be written as
and solved by two quadratic equations
Cubic Eq. 13 can be reduced to the following depressed cubic equation:
by changing the variable,
, as
. The Cardano’s solution for this equation states that it has a real root, if the following function is positive:
Figure 6 shows the graph of this polynomial
,
in part (a); it is positive. Therefore, the solution of Eq. 16 is
The graph of this function is shown in part (b). The function
can be used for solving Eq. 14, which will give us four solutions
. One can see that the solution formulas of the gold equation are cumbersome and difficult to visualize. Therefore, we now consider another approach, to describe the solutions, by using simple computer programs.
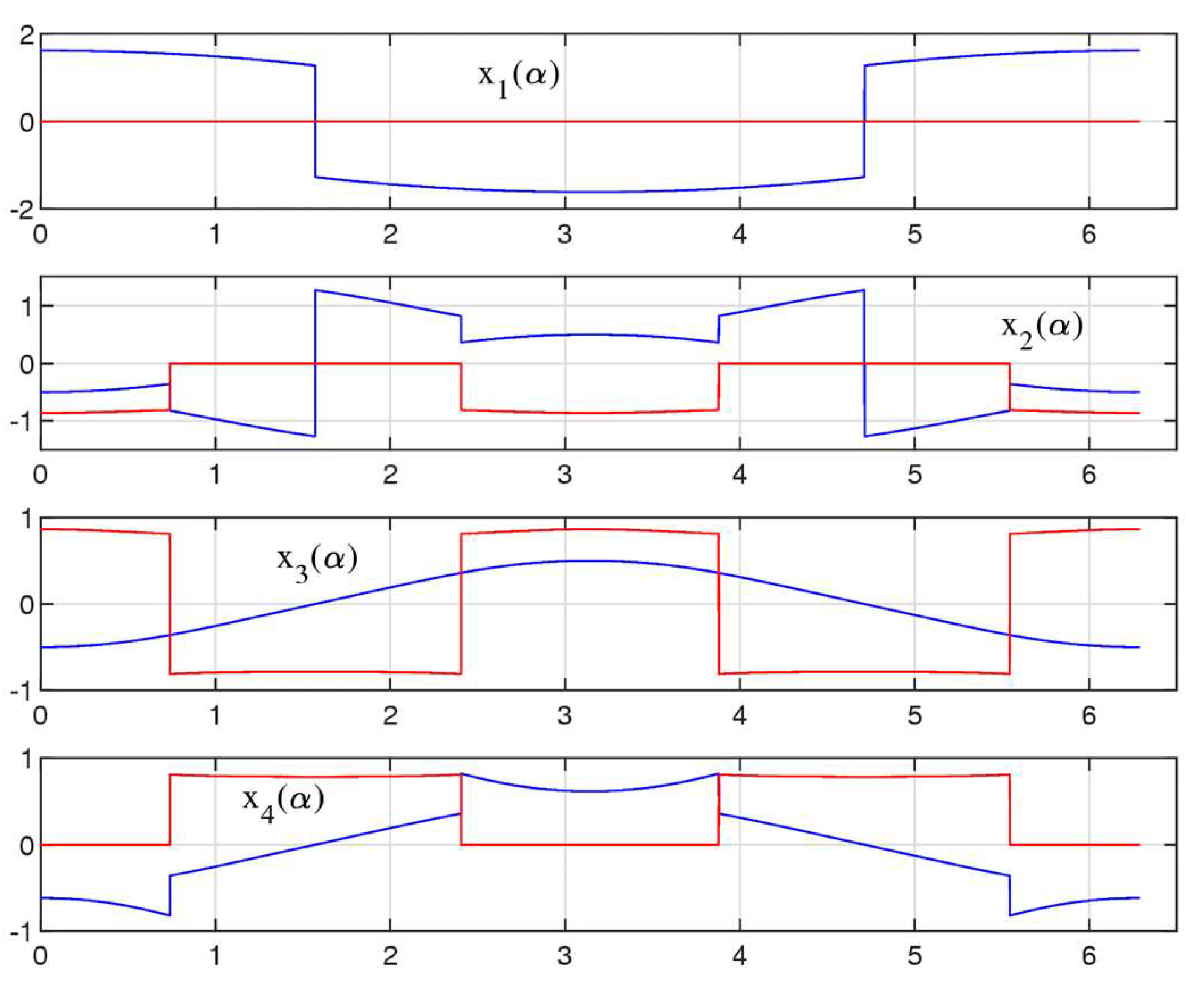
To analyze the equation of the generalized golden ratio, we compute its roots.
Figure 7 shows the graphs of four roots
,
, of Eq. 7. The real and imaginary parts of the roots are shown in blue and red colors, respectively. The angles
are in the interval
with step 0.0015 radians, or 1/12 degrees. These roots were calculated with the command
‘x=roots([1,0,-1,-2∗cos(a),-1])’, by using MATLAB function ‘
roots.m.’
The graphs of the roots are symmetric with respect to the vertical at angle-point
. In some parts these functions change sign. For example, the change of sign in the real part of the first solution
occurs at angles
and
and the jump is equals to
For other roots, the discontinuities can be seen at angle-points
and
. As shown in Eqs. 11-17 (see also
Figure 6), the analytical solutions (not the ones modeled above) should not have points of discontinuity.
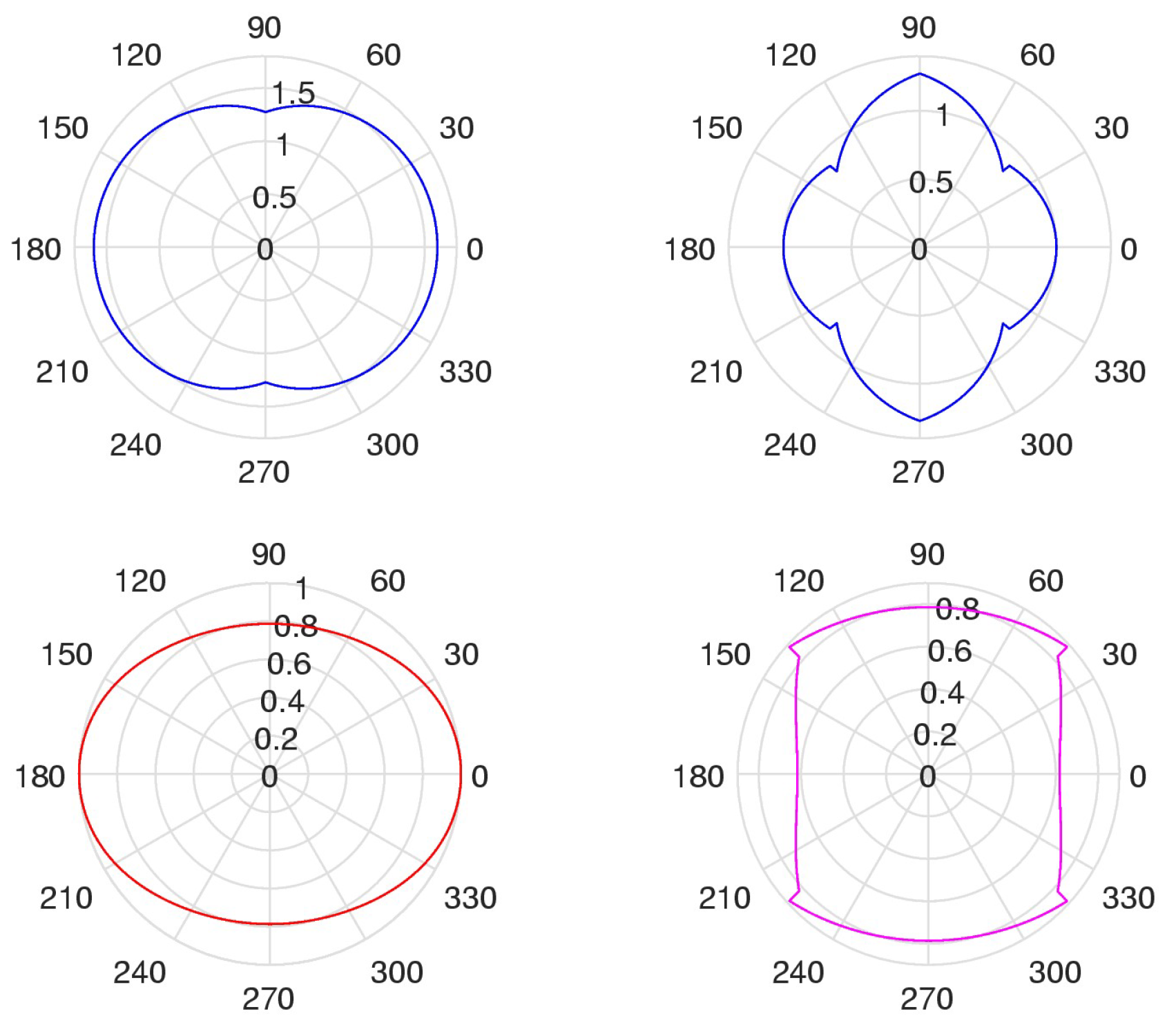
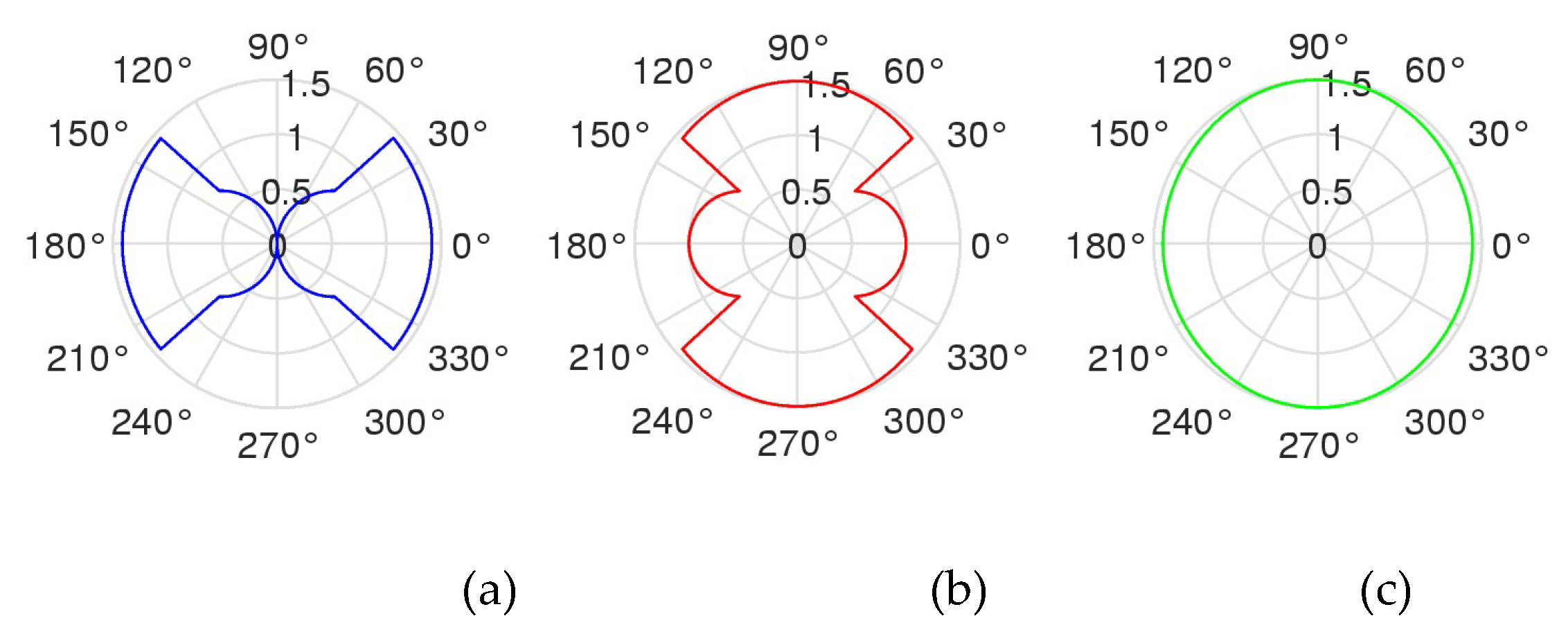
In
Figure 8, these four roots are plot in the polar form. The first plot is like the apple, the 2
nd as a four-petal flower, the 3
rd as the egg (Earth), and the 4
th plot is an unknown figure for us.
It is not difficult to note that the following holds for the roots of the above equation:
Thus,
equals to the sum of the first three roots with sign minus. The 4
th plot is the sum
in polar form.
Figure 9 shows the polar plots of the sum of roots
,
and
in the polar form in parts (a), (b), and (c), respectively. These figures are interesting.
3.2. Analyze of Solutions
It is not difficult to note from
Figure 7 that, for each angle, there are two real solutions of Eq. 10. Even more, there is only one positive solution for each angle (see also
Figure 5(c)). We will regroup the obtained set of roots
,
and
of the above equation in the following way. The corresponding codes for these four roots are given in Appendix.
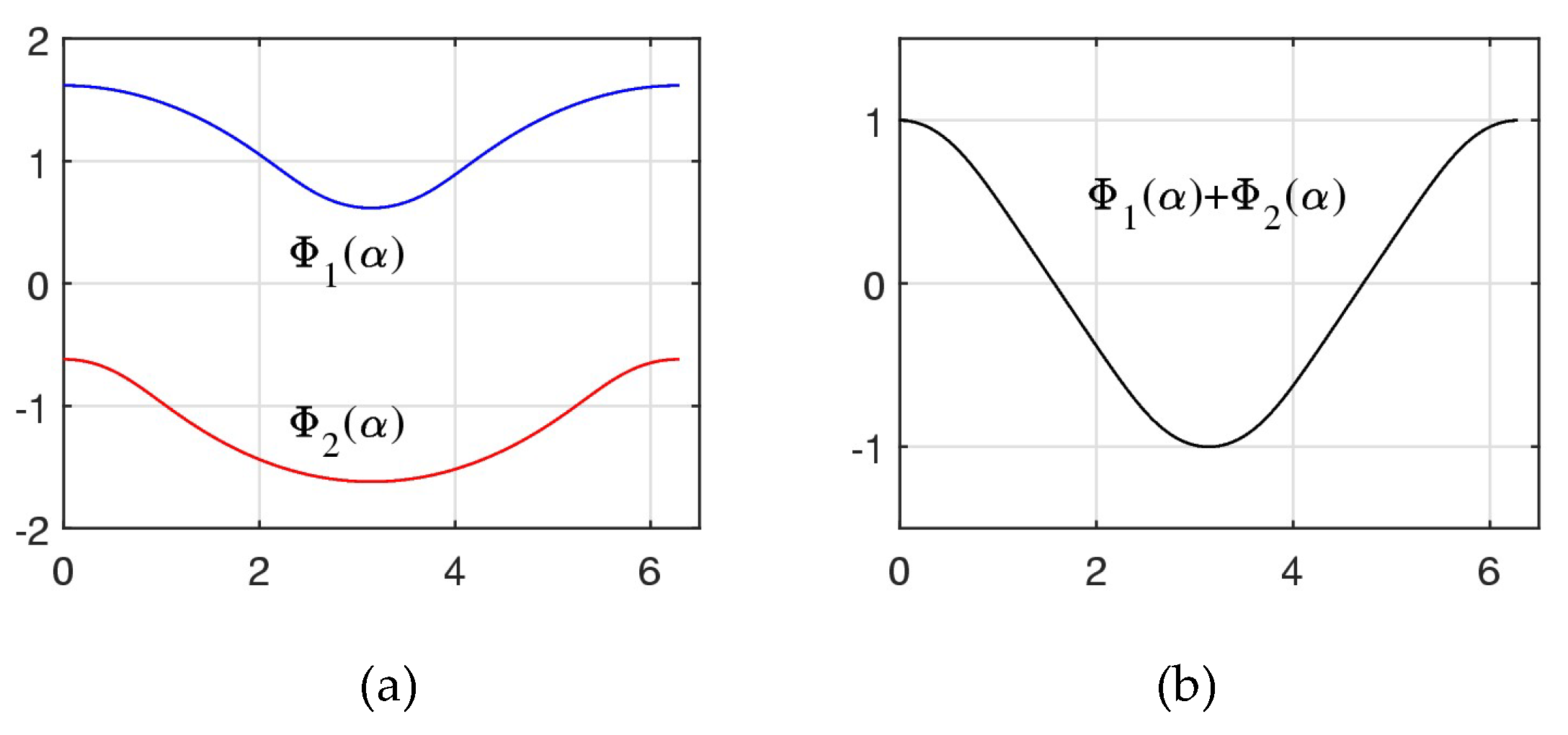
For each angle , the first two roots are real and the next two roots are complex conjugate. Then, the solutions are composed as follows:
Figure 11 shows these two roots (solutions) in part (a)
The functions
and
are continuous. The first function is positive and the second one is negative. Both functions are periodic; the period is
. It is interesting to note that
In part (b), the graph of the sum of these solutions is shown,
. The magnitude of this function
.
Figure 10.
(a) Two real solutions of Eq. 10 and (b) their sum.
Figure 10.
(a) Two real solutions of Eq. 10 and (b) their sum.
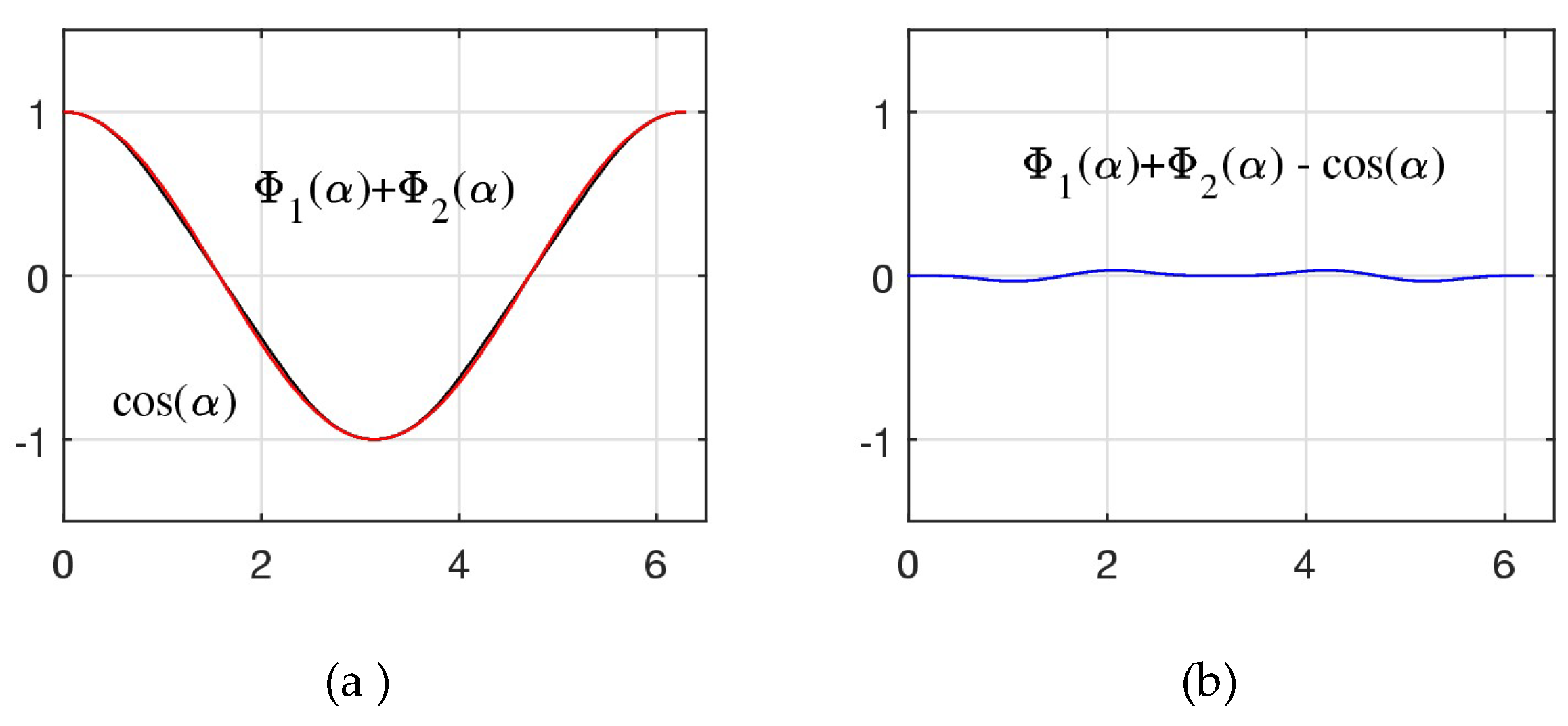
It is interesting to note that the graph of
in
Figure 10 in part (b) is similar to, but not exactly, the cosine function. This sum of two roots together with the cosine function
are shown in
Figure 11 in part (a). The difference of these functions is given in part (b). The maximum difference of these two functions is 0.0344590758 (the functions were calculated for
angles
in the interval
.
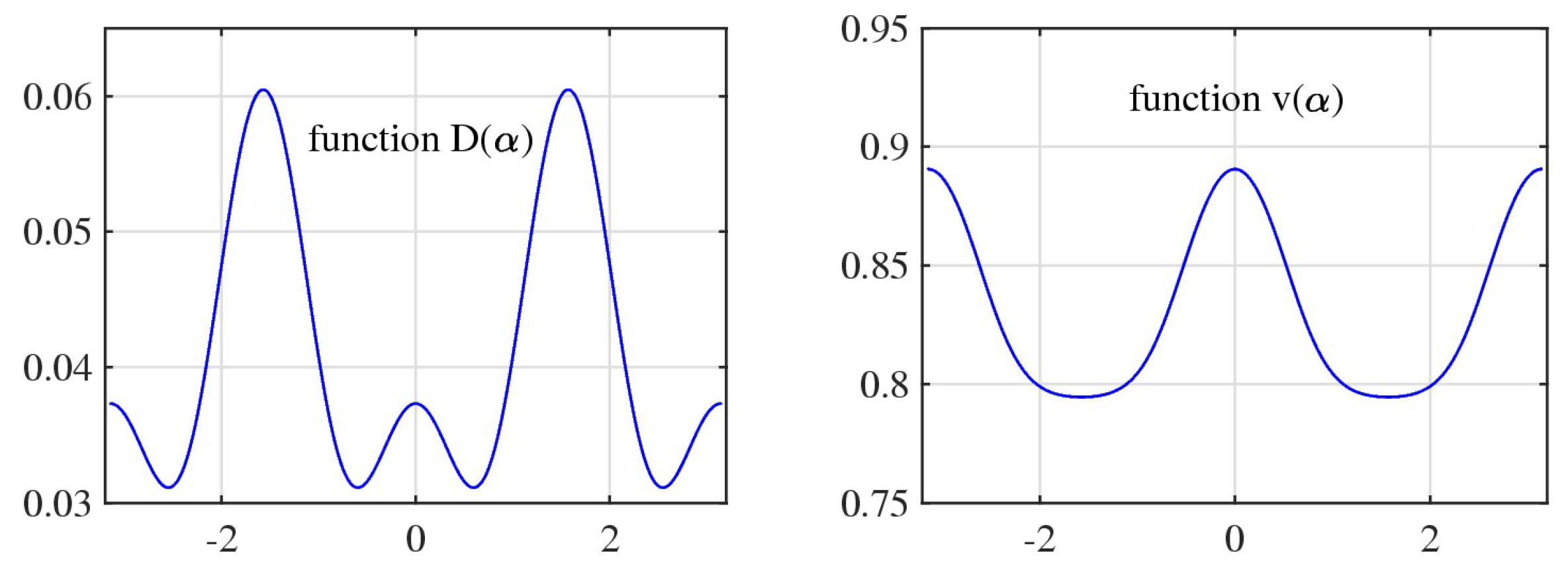
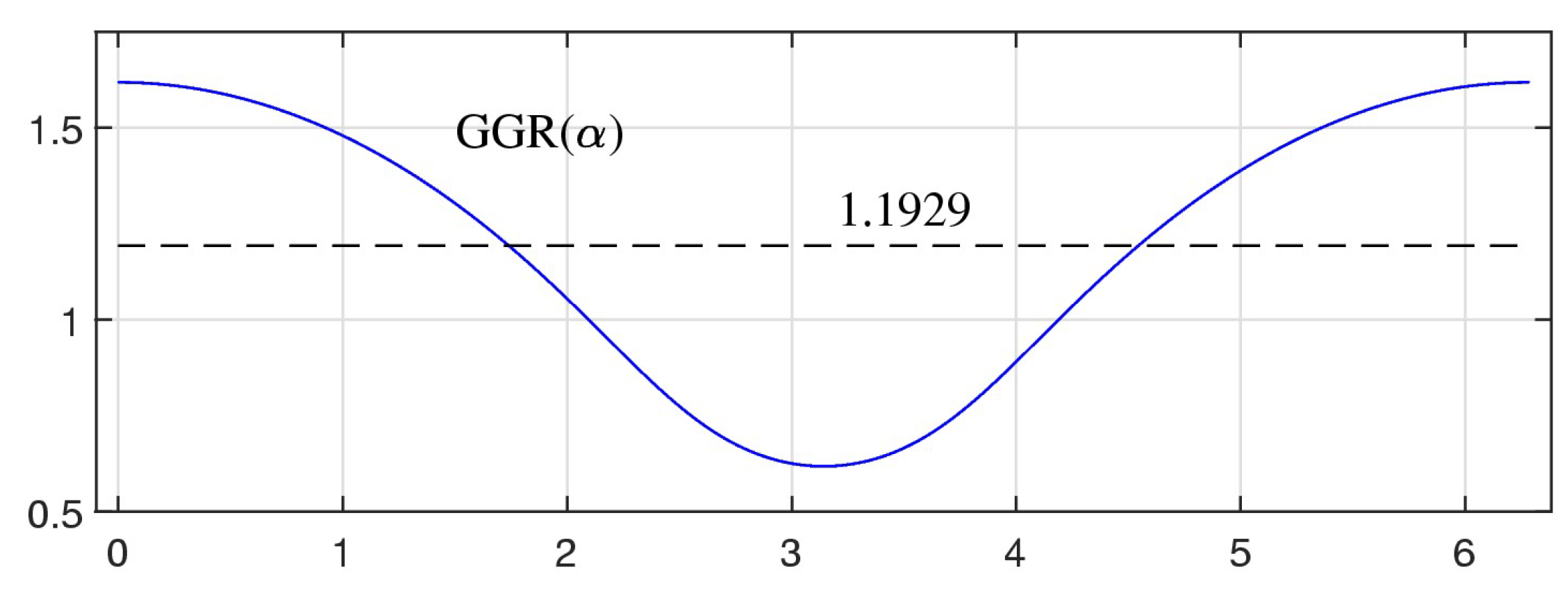
Figure 12 shows the graph of the positive roots
calculated in the interval of interval
. We call the function
with this graph
the general golden ratio function, or
the GGR function. For this function, the minimum is 0.6180 at the angle-point
, and the maximum is 1.6180 at
and
. The Golden ratio function equals to 1 at angles
and
. The mean of the Golden ratio in this interval equals to 1.192880, approximately at angles 1.7385 and 4.5447 in radians, or
and
.
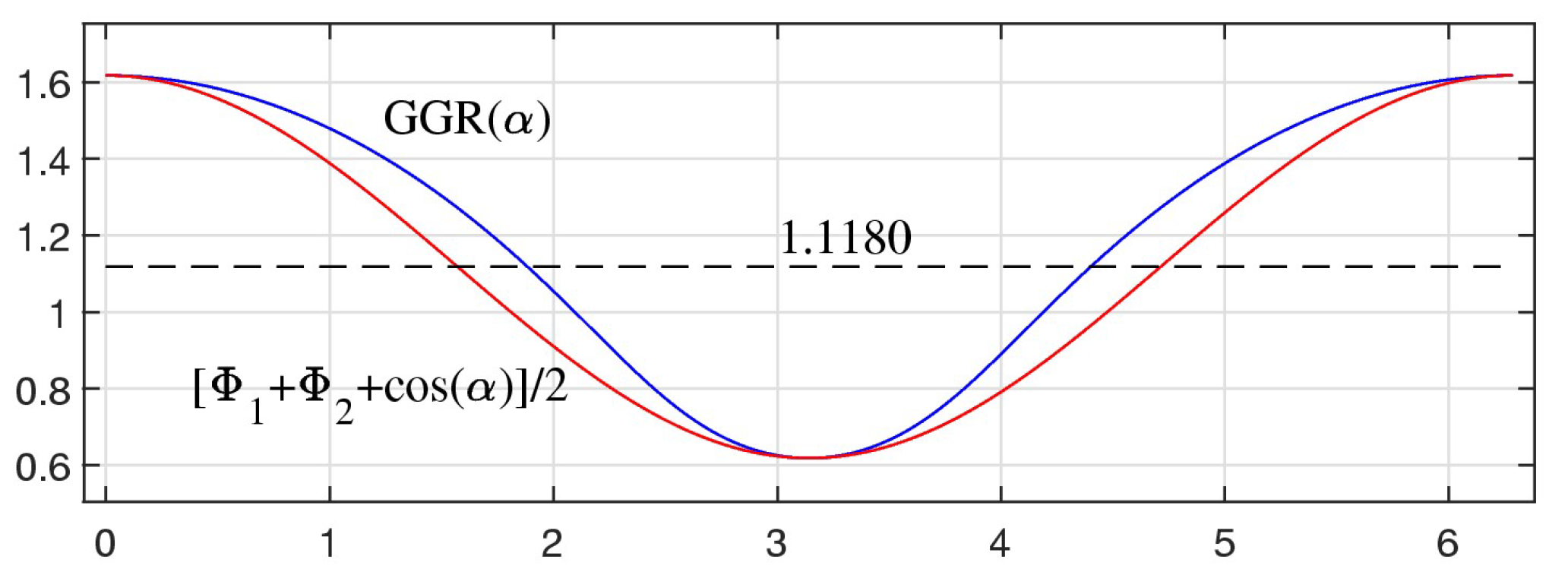
The GGR function
has approximately the form similar to the cosine function. Together with the GGR function, the following function is shown in
Figure 13:
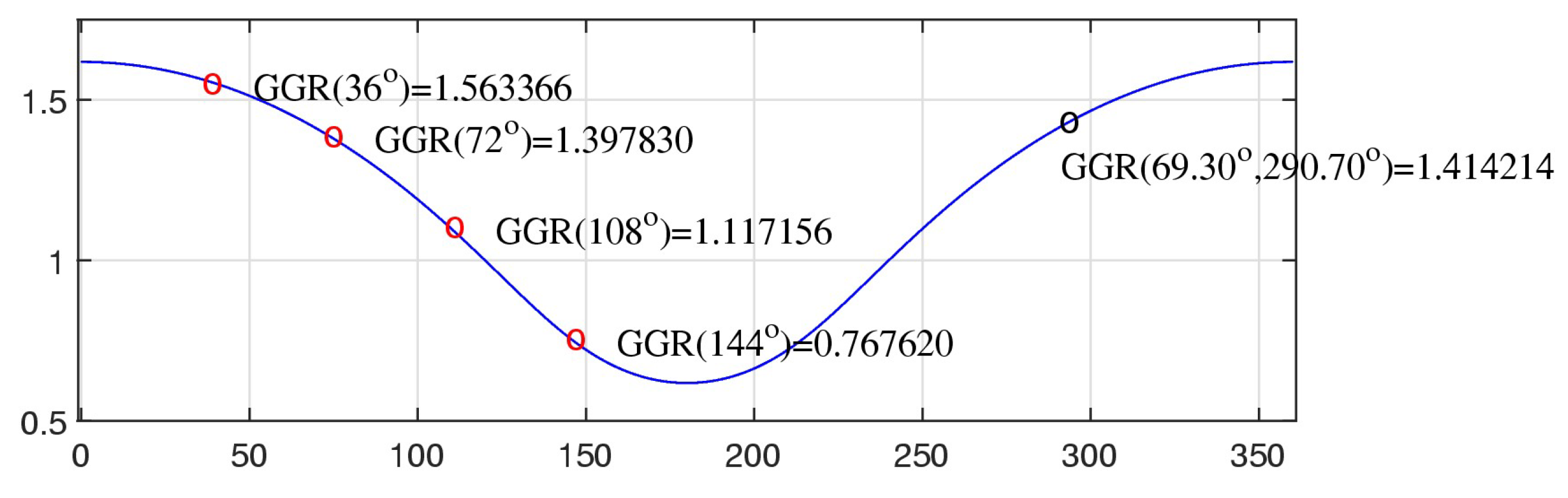
Figure 14 shows the graph of the GGR function versus angles in degrees in the interval
. A few points on the graph are marked for the values of this function at angles
and
plus the angle
at which the Golden ratio equals to
The complex roots of Eq. 10 can also be regrouped, by using the phases of two complex solutions and Namely, the following functions are calculated:
Note that. MATLAB-based codes for these functions are given in Appendix.
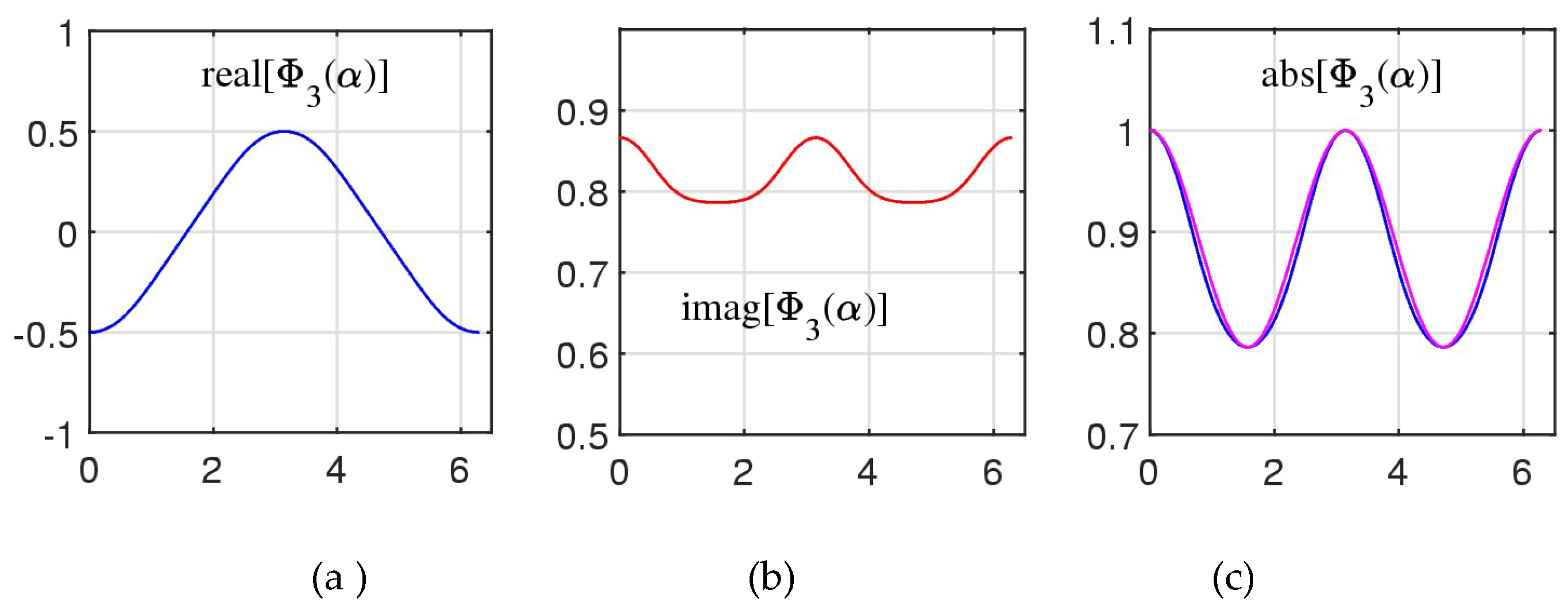
Figure 15 shows the graphs of the real and imaginary parts of the complex solution
in parts (a) and (b), respectively. One can note that the real part of the solution
has values in the interval
Absolute value of this function together with the function
is shown in part (c). Here,
The function
can be considered as an approximation of
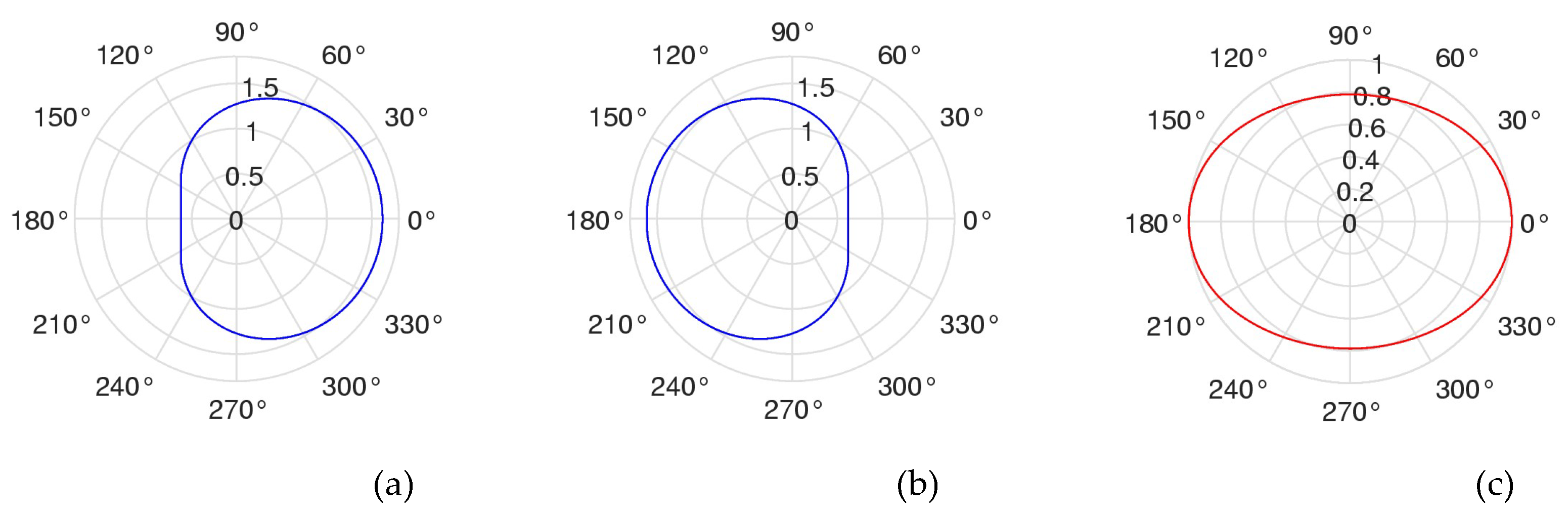
Figure 16 shows the magnitudes of three solutions
,
in the polar form. In comparison with the plots in
Figure 8, one can note the symmetry of plots of the real functions
and
The polar plots for other two complex functions
and
are the same; the functions are complex conjugate to each other.
3.3. Properties of the Roots
The following properties hold for the roots of the golden equation:
Also, from Eq. 7, we obtain the following identities:
Due to Eqs. 23 and 24, the real part
of the 3
rd solution (shown in
Figure 15) equals to
(see
Figure 10(b)). It is also not difficult to see that these solutions are transformed into each other under the transformation
. Indeed, the following identities are valid, for any angle
:
Thus, for each angle
, the real ratios can be in two states as
. This vector state changes with operator
as
The full 4D vector of states changes as
4. Examples of Golden Ratios
In this section, we consider a few examples of golden pair of vectors in the 1D and 2D vector spaces.
Example 3 (1D vectors):
For 1D vectors (real numbers), or the elements of the real line
, we define the inner product as
. Then, the angle is defined as
which means that the angle between similar elements may take only two values, 0 and π. Therefore, the set of similarity, that is, the set of numbers that are in golden ratios with the number
is defined as
When
that is,
the number
is in golden ratio with numbers of the set
When
that is,
, the golden pairs are defined by the similar set
These two sets are equal up to the sign. Here,
Note that
and
. Thus, for number
>0, the set of similarities equals to
For the unit vector
, the set of similarities is
The golden pairs are
and
Example 4 (2D vectors):
Consider two vectors
and
in the 2D real space
. The inner product is defined as
and the norm of the vector
equals to
. All unit vectors
have tips on the unit circle, that is, they are described by the set
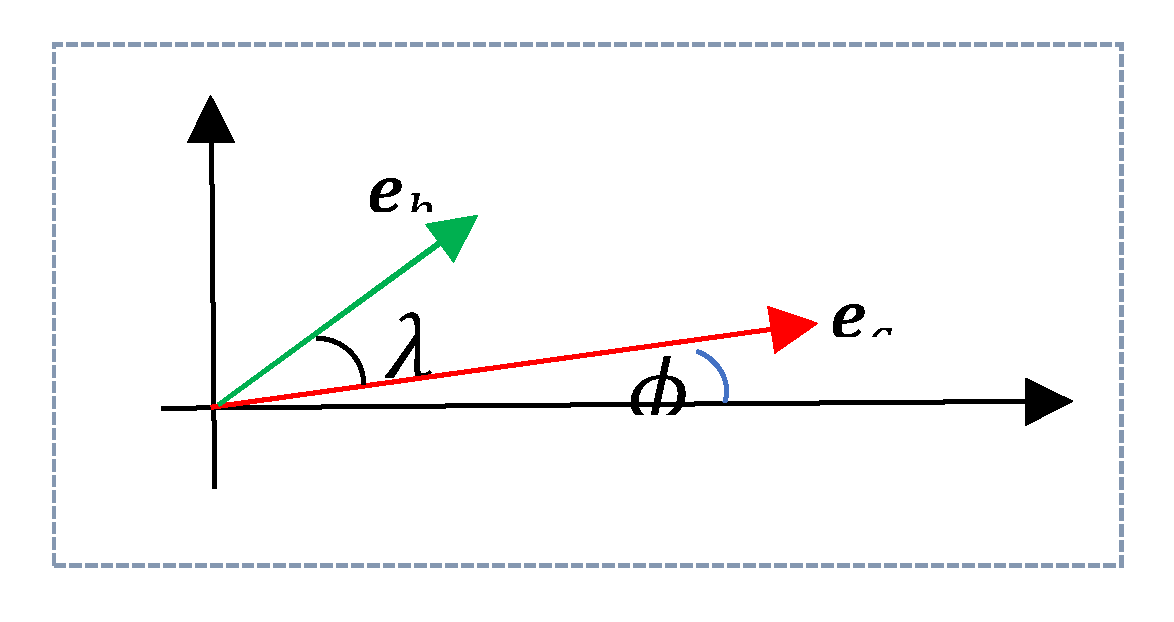
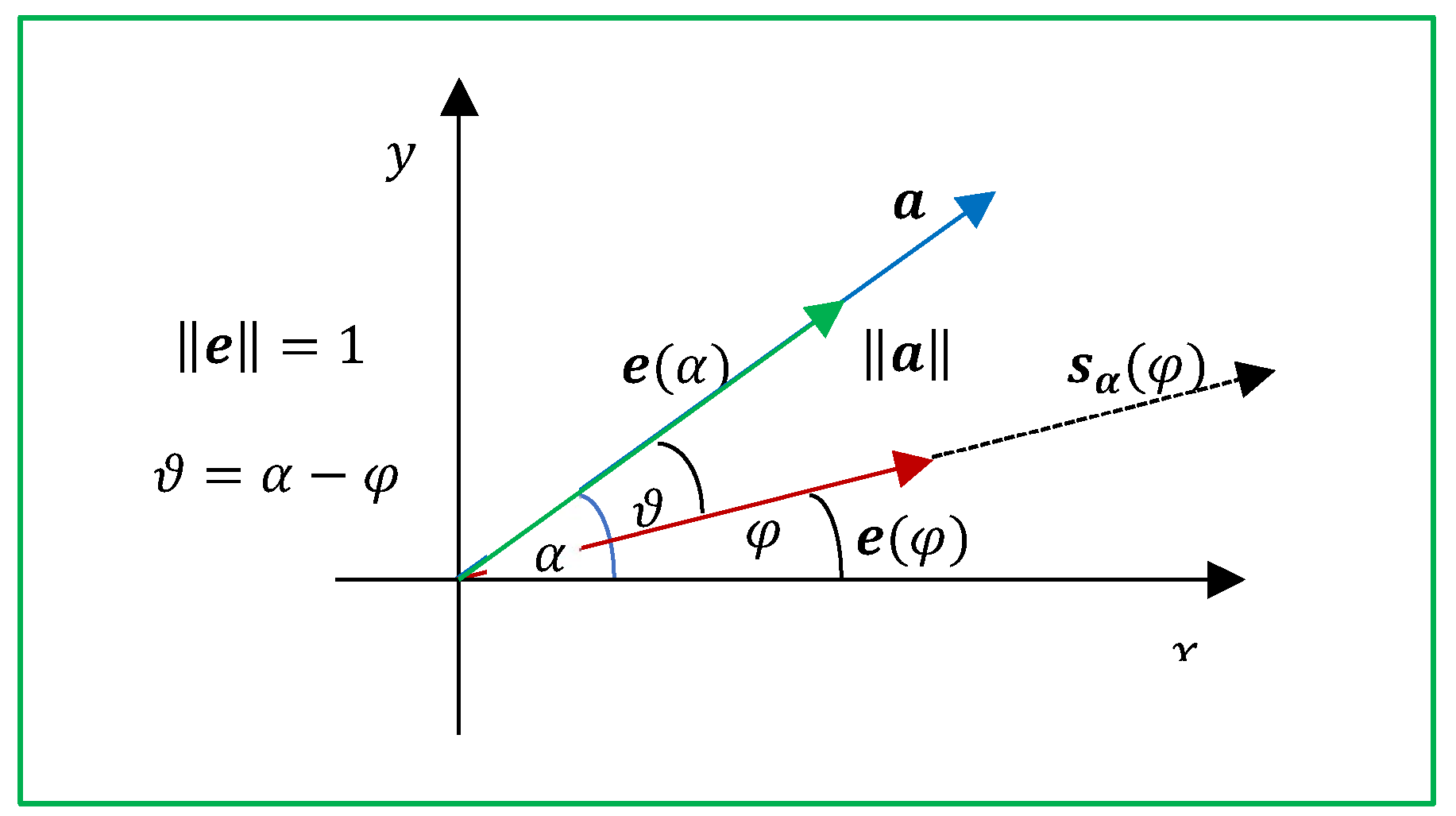
We consider the polar form of the vector
and the unit vector
at angle
to the horizontal (see
Figure 17).
Let us assume that the unit vector
composes the angle
with the vector
. The inner product of
with the unit vector
along the vector
equals to
Along the angle
, the vector that is in the golden ratio with the vector
equals to
Therefore, the set of similarity of the vector
is defined as
Thus, for a given vector
, a golden pair can be found along any direction. The golden ratio changes with angles. As an example,
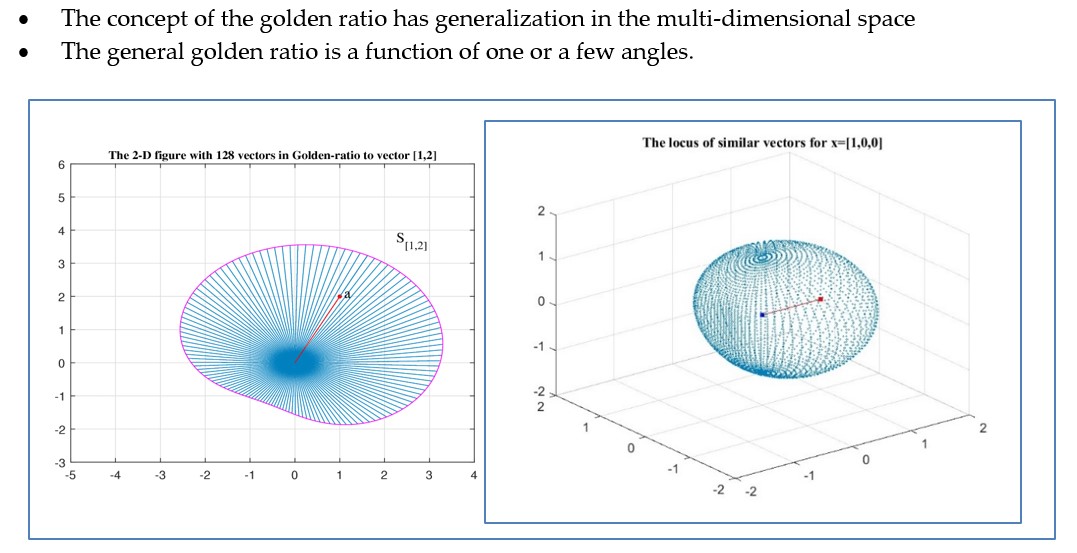
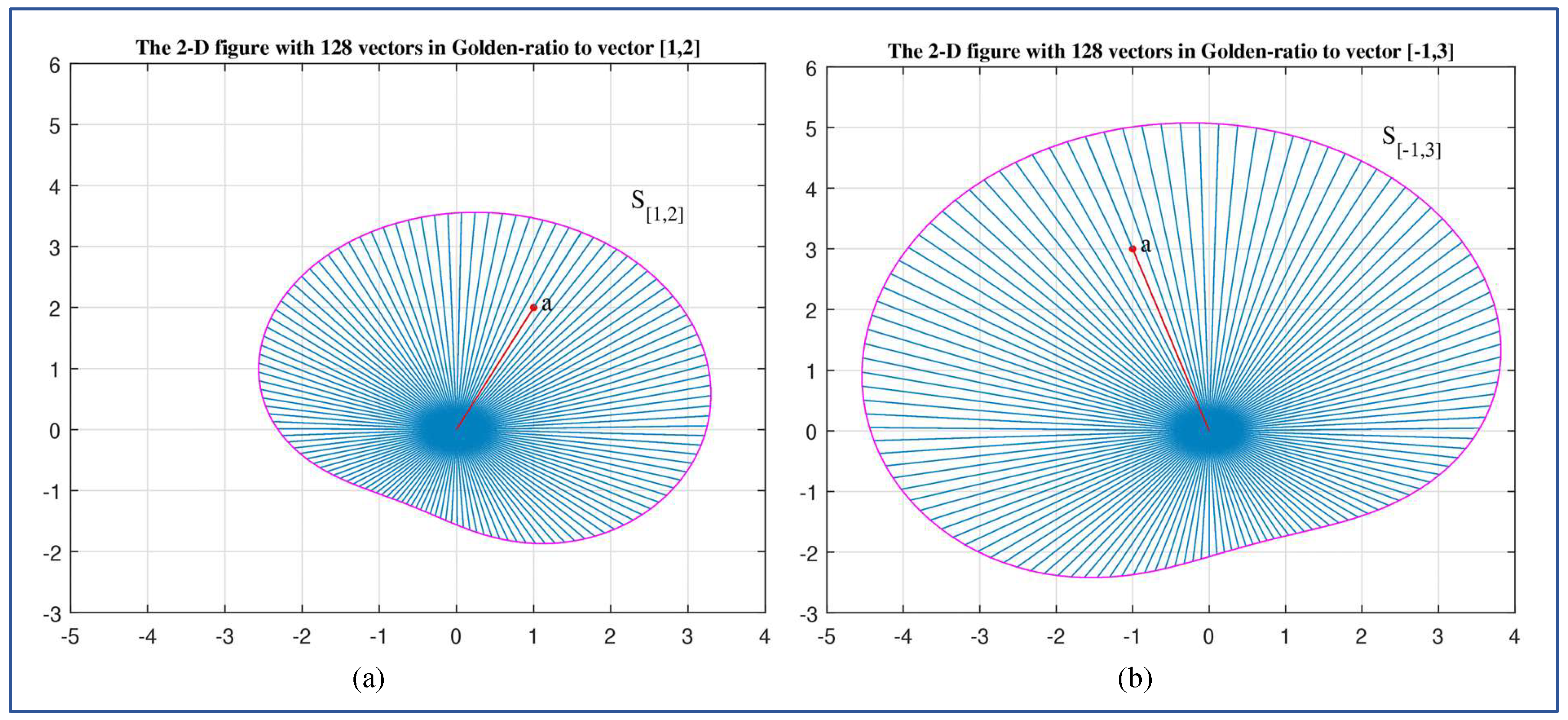
Figure 18 shows the locus of all similarity 2D vectors
that compose the golden pairs
for the vectors
and
in parts (a) and (b), respectively. The similarity sets of these vectors are
and
In these figures, the vectors are shown only for 128 uniformly distributed angles
from the interval
The tips of the vectors are not shown. The figures recall the same petal rotated by different angles and magnifications. The vectors
show the orientation of the corresponding sets of similarity
.
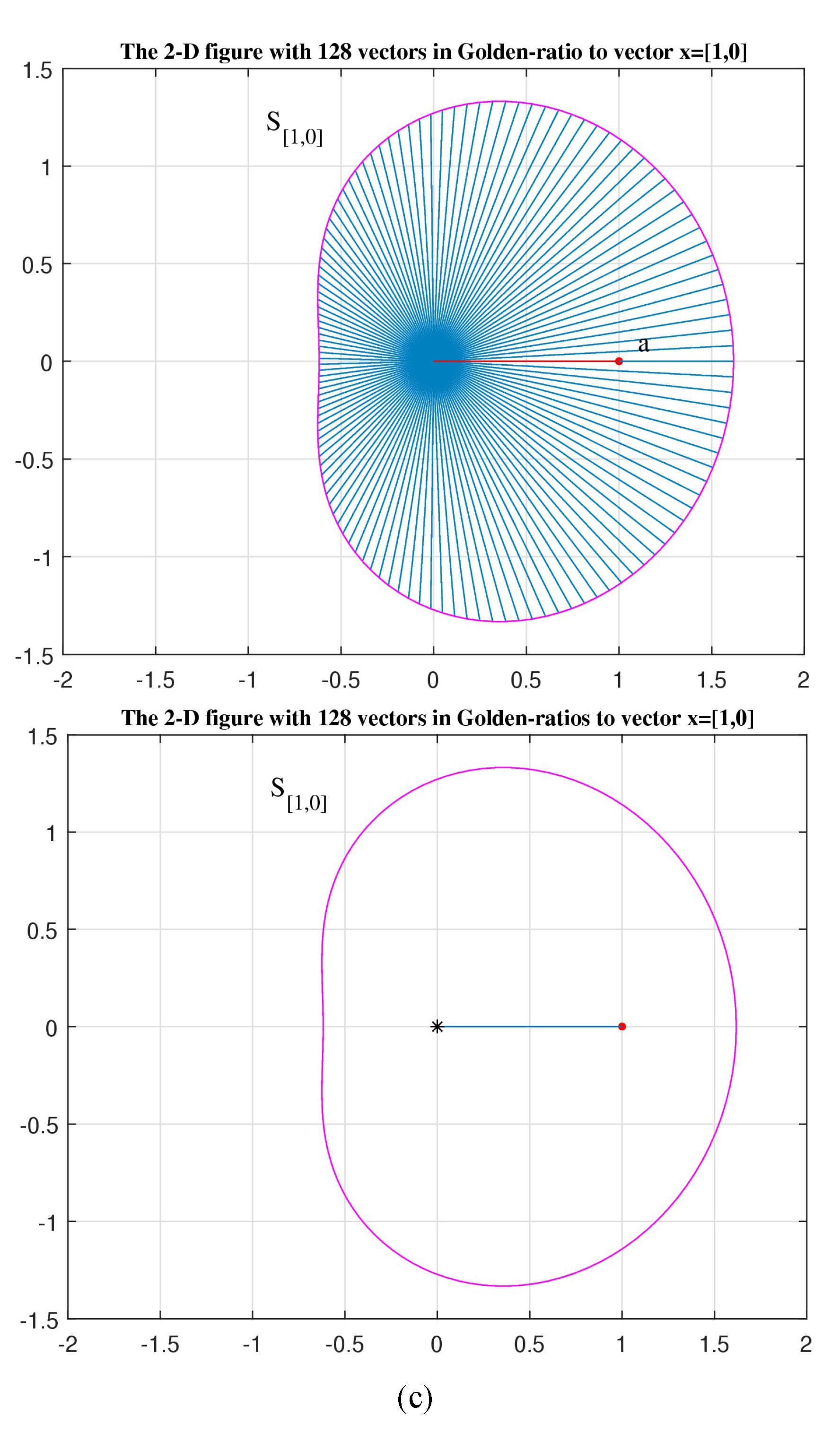
In part (c), the similarity figure is shown for the vector
The similarity set of this unit vector is
It should be noted that the figures of the sets of similarity in part (a) and (b) are the rotated figure of part (c) with magnification by the norms
and
of the vectors
and
, respectively. The figure for the set
can be obtained from the figure of the set
by rotation by the angle of
and magnified by the number
. Similarly, the figure of the similar set
in part (b) can be obtained from the figure of
by rotation of the angle
and magnified by the number
.
Figure 18.
(continuation) (c) The locus of 128 Golden pairs with the unit vector
Figure 18.
(continuation) (c) The locus of 128 Golden pairs with the unit vector
5. Field of Similarities
A. Philosophical digression: What is similarity in our case? Each vector affects its environment, stimulating its influence through the imposition of its likeness. The vector may represent a force, an impulse, or any action in the vector space. If you think about it, then we are all a certain vector of possibilities that we impose on the environment by projecting ourselves into it, and this projection is symbolically represented by a certain projection angle. (All our immediate environment is our projection, our likeness. This is a kind of vector shadow that is cast on the environment, and the ray symbolizes the angle of objectification of this shadow.)
The vector or force in its action can be expressed (presented) by one of its similarity vectors (or forces), in any direction. All these possible similarities, or states of vectors, do not describe the ideal unit circle in 2D case, for one qubit, and the unit sphere in 3D space for two qubits, as assumed in the quantum computing [
16]. Here, we have the figure of a petal in the 2D case (
Figure 18) and an apple in the 3D case (as shown in the next section).
B. Until now, we knew that if two vectors do not interact and the inner product is zero (that is, the angle is 90 degrees), then mutual influence is excluded. But what is interesting is that the similarity coefficient at this angle is not equal to zero! That is, the influence is still there. According to the printout, it appears that
C. Two roots of Eq. 10 are real, and . The second two are negative. Note that negative numbers do not exist in the nature. We can talk about two, three, etc. objects, which we can not only imagine, but also see (let’s say, 2, 2.5, and 3 apples). One cannot say that about negative numbers, only the imagination works here (let’s imagine - apples). We can say that being positive or negative number are two states, like heads and tails in the probability theory. After all, it was not for nothing that we got two states, , one refers to positive roots, and the other to negative ones. Two other solutions are complex, and ; they show us the 2D representation (the real solutions determine the 1D representation). Note that in English the words imaginary (for complex numbers) and the image have the same root.
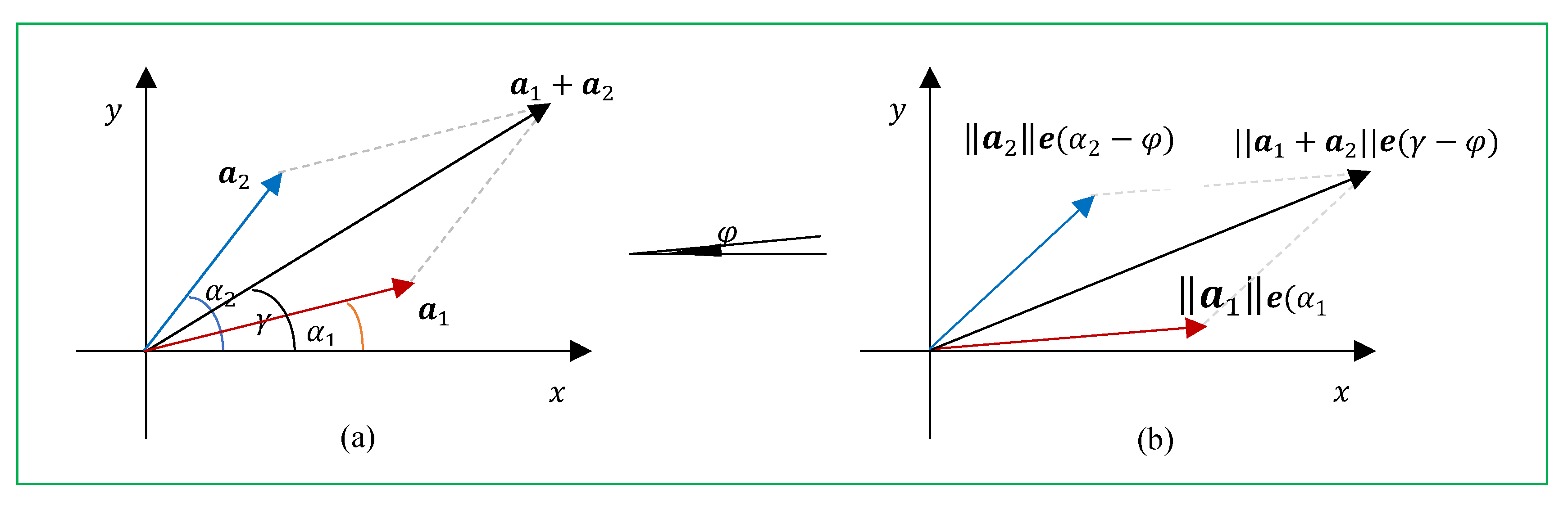
D. (The sum of similarity vectors) The following question arises. Is it possible to add similarity fields? If so, then what exactly does the sum of similarities mean? Let us consider two different vectors
and
at angles of
and
to the positive real axis, respectively. The corresponding sets of similarities are
These two sets can be written as
Then, their sum should be defined as the set of similarities
where the angle
Let us verify if the following is true:
Here, the summation is angle-wise, that is, the summation of vectors that correspond to the same angle
Therefore, this equation can be written as
All vectors have the same coefficient of similarity. Removing the similar term
from this equation, we obtain
This equation describes the well-known rule for summing vectors over projections. The following calculations are valid for the right part of this equation:
Here,
and
Thus, everything is correct in Eqs. 38 and 39.
Figure 19 illustrates this property in part (b), where the parallelogram is the result of the rotation of the original parallelogram in part (a), which is composed for the sum of vectors
and
.
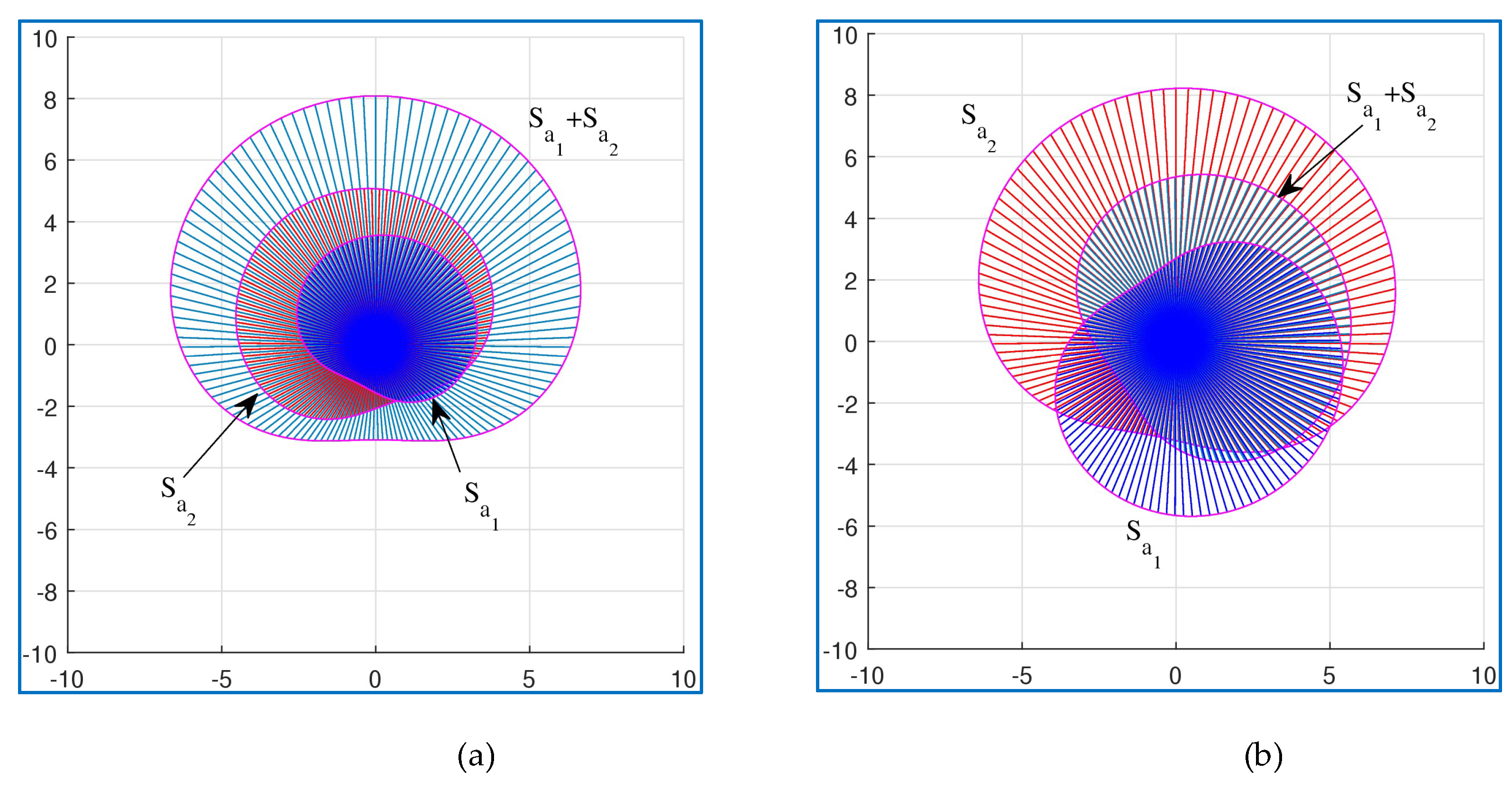
As examples,
Figure 20 illustrates the summation of the similarity sets for the vectors
and
in part (a) and for the vectors
, and for
in part (b).
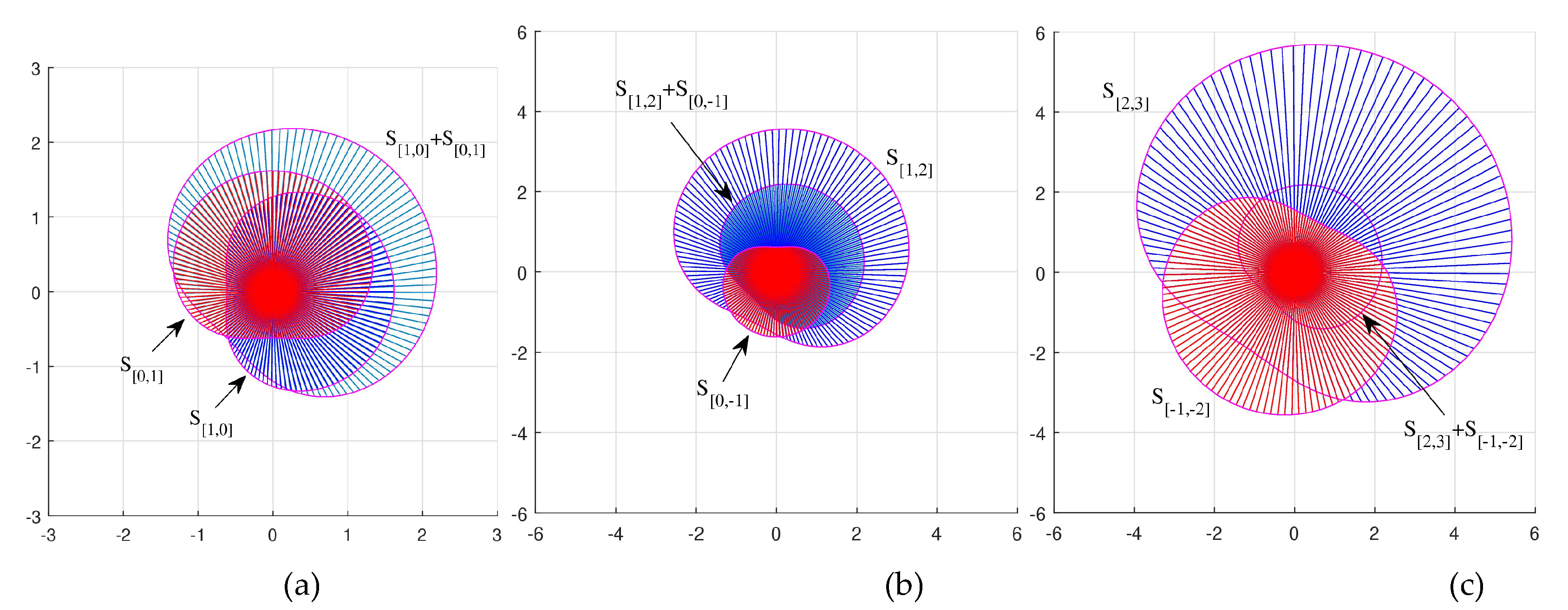
Figure 21 shows the same sum
of similarity sets, for three pairs of vectors
and
. Namely, for the vectors
and
in part (a), vectors
and
in part (b), and vectors
and
in part (c). If we assume the vectors represent forces and generate the similarity fields, then the above figures with the sums of similarity sets (fields) may illustrate the influence of fields on space, for example, attraction and repulsion.
It should be noted that we do not sum the similarity sets over equally directed rays. If we do that, that is, if consider the sum of the similar vectors
for each angle
, then, we need to find the vector
and angle
, such that
The solution of the equation
is unknown for us.
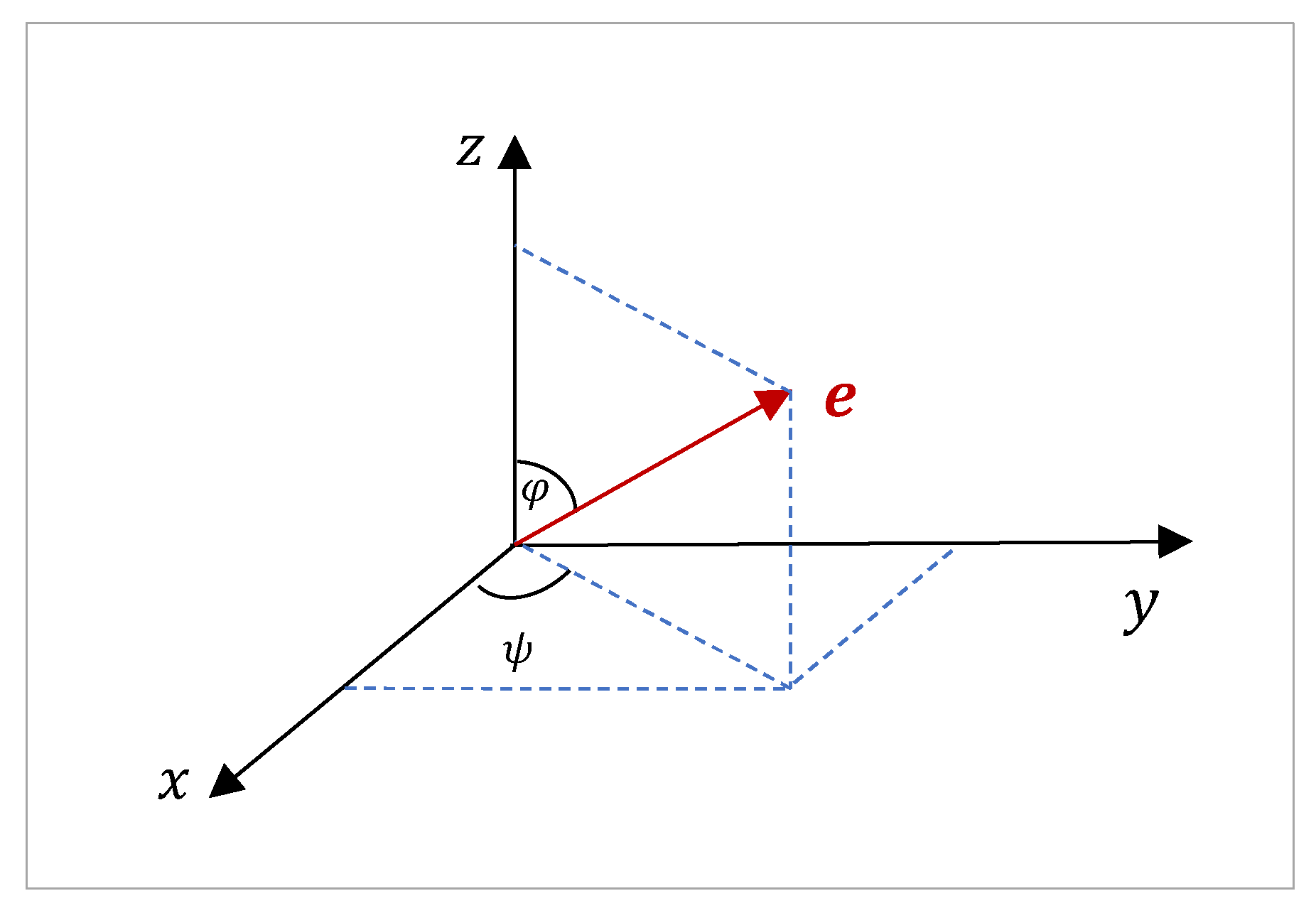
Example 5 (3-D vectors): We consider the traditional representation of the 3D unit vectors, namely the set
The geometry of the unit vector
is shown in
Figure 22.
The inner product of such a unit vector
with a vector
, where
, is calculated by
Thus,
The cosine of the angle between these two vectors is the function of 4 arguments, that is, the angle
between the vectors
and
is the function
. The similarity set, that is, the set of all vectors in golden ratios with the vector
is
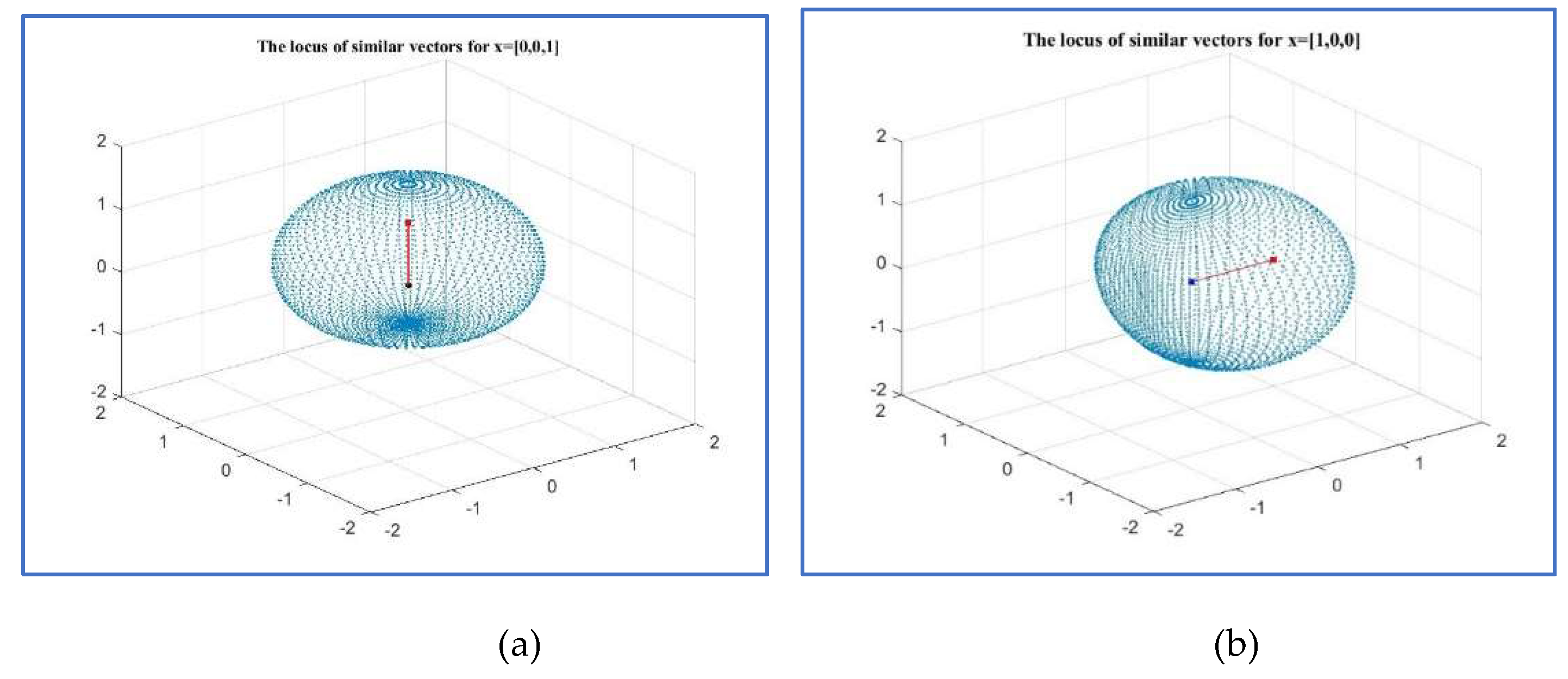
Let
be the unit vector
Figure 23 shows the locus of vectors being in the Golden ratio with this vector in part (a). In this case,
and
Therefore,
and the set of similiarity is
We also consider the unit vector
Then,
and
. Therefore,
and the similar set is
The locus of vectors of this similarity set is shown in part (b). In these two figures, as in the 2D case above, only the ends of the vectors as dots are shown. The angles
and
were taken with the step
in the intervals
and
, respectively.
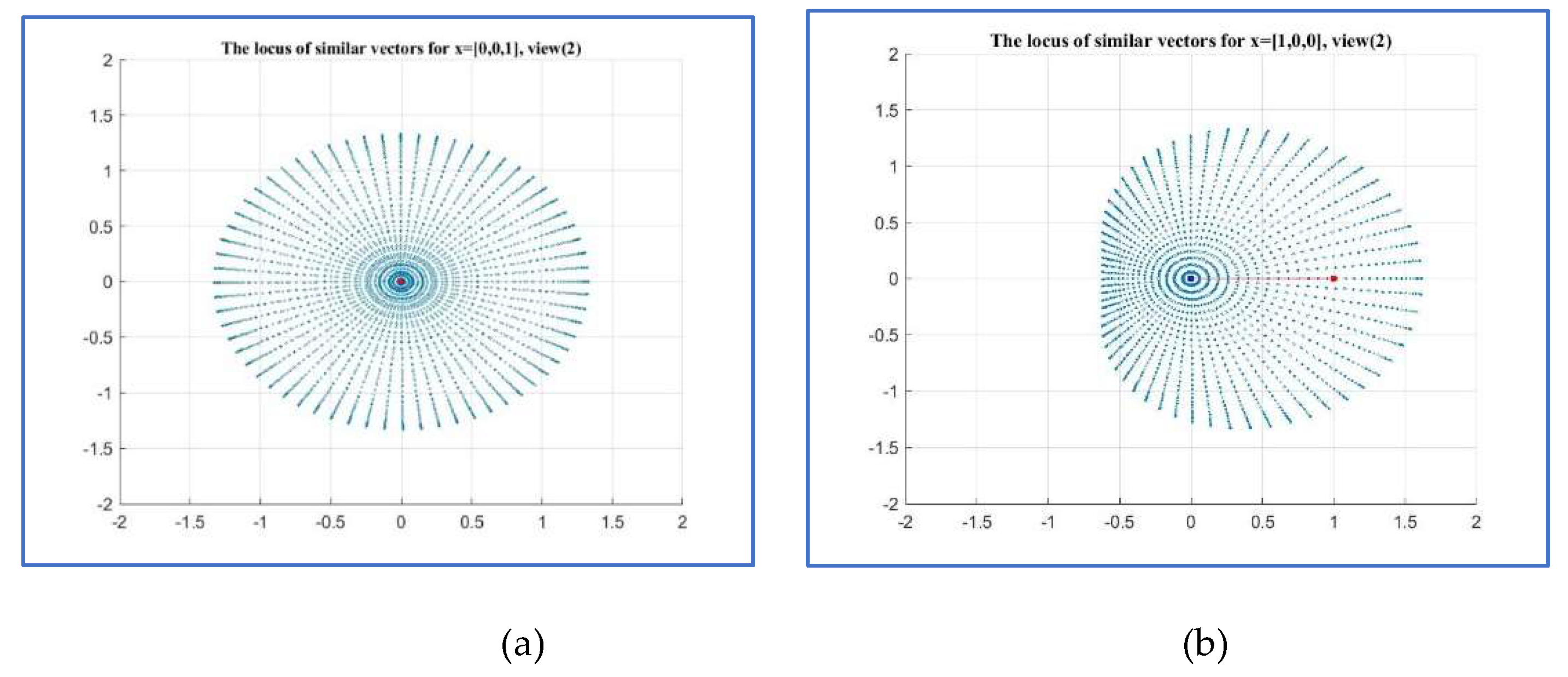
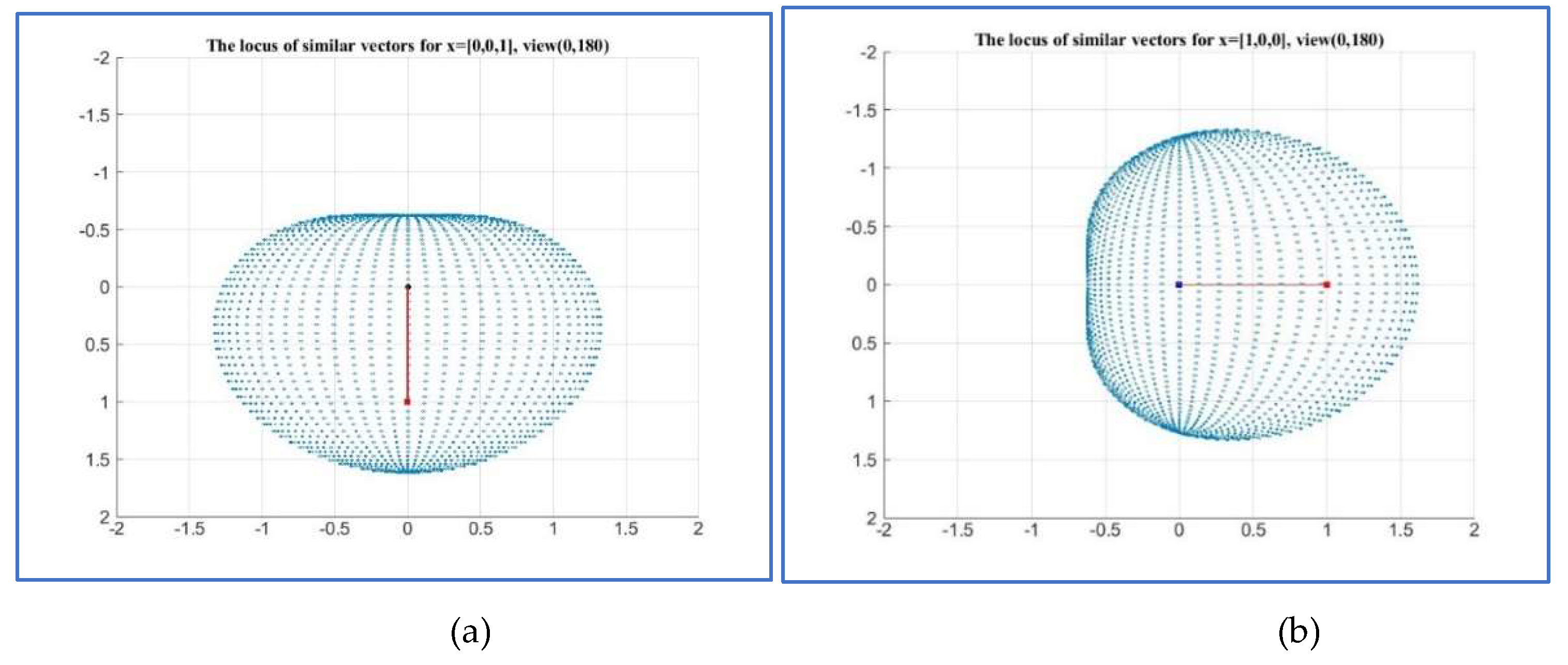
Figure 24 and
Figure 25 show these similar sets by different angles. Namely, by using the azimuth (AZ) of zero degree and vertical elevation (EL) of 90 and 180 degrees, respectively. For this, the MATLAB functions ‘view(2)’ and ‘view(0,180)’ were used.
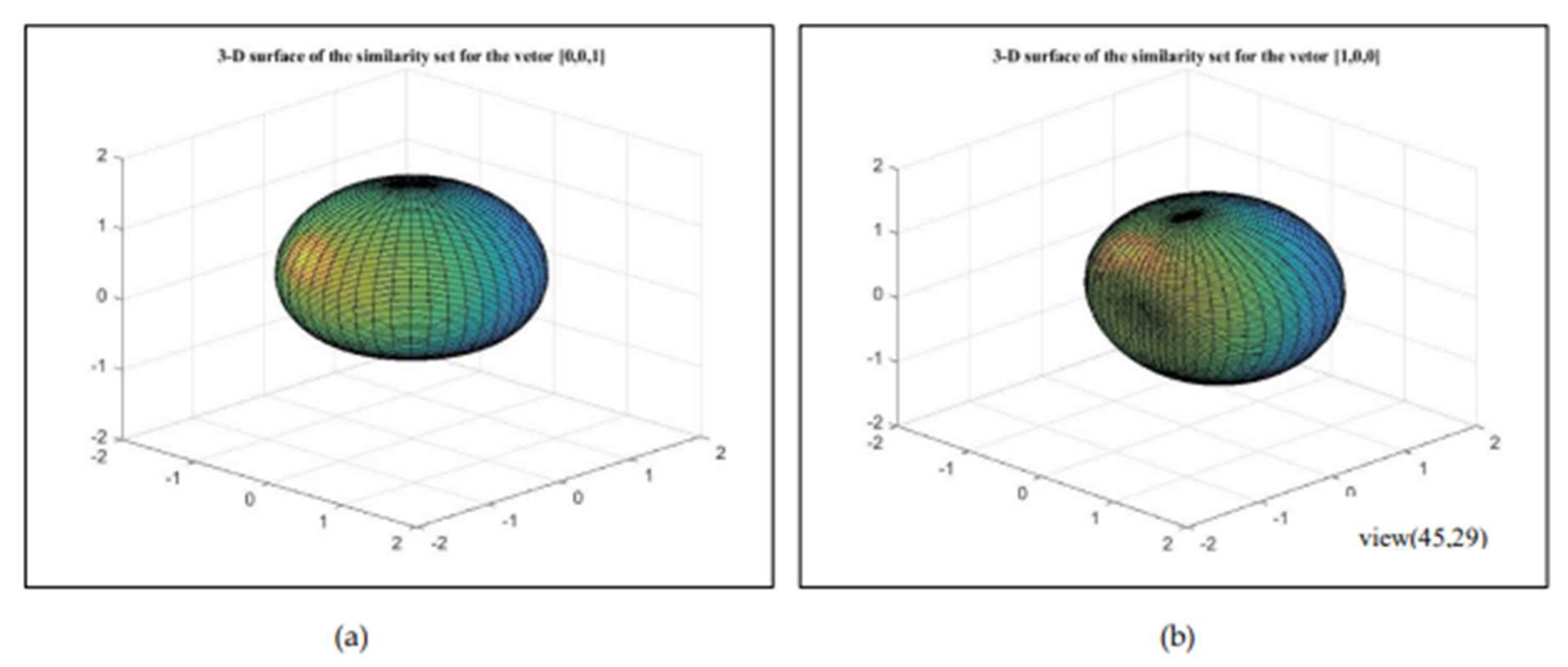
Figure 26 shows the 3D surface that is made up of the vertices of the vectors of a subset of
in part (a). Thus, this is the surface framing the vectors which are similar to the unit vector
In part (b), the similarity surface is shown for the unit vector
For both surfaces, the angles
and
were taken with the step
in the intervals
and
, respectively.
6. Similarity Triangles
In this section, we consider triangles as elements of the 6D vector space and introduce the concept of the inner product and norm of triangles. The tringles in golden ratio are described and the similarity sets are presented with examples.
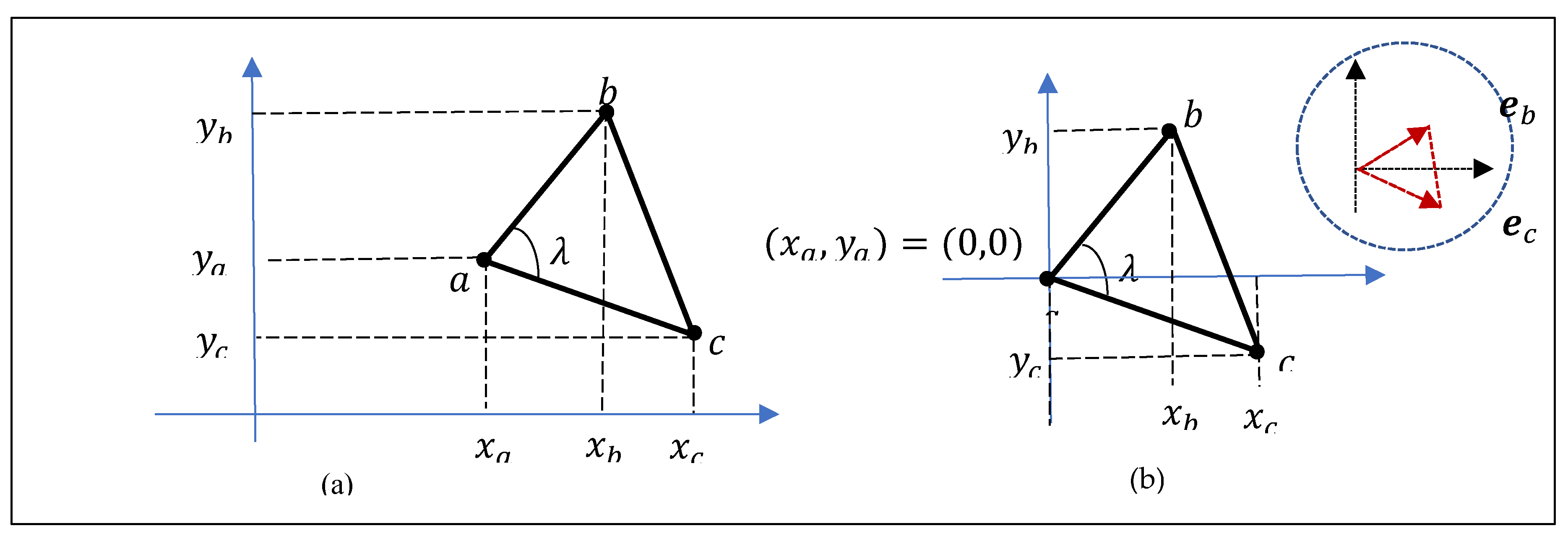
In order to show the similarity of three points (
) in the form of a triangle on the plane (see
Figure 27(a)), we need three 2D vectors, which we denote by
and
. The vectors
, and
These coordinate vectors compose the 6-D vector
Consider two 6D vectors that correspond to two triangles,
and
The inner product of these vectors is defined as
The norm of the vector is defined as
The norm
when a triangle degenerates into point, that is, when
, and this case is not considered.
A unit vector, or a triangle,
with norm 1 is defined as
We can zero the first 2D vector
and consider the unit vector
, for which
with condition that
and
Such 6D vector corresponds to a triangle with the point
at the center of the system of coordinates. Such an example is shown in
Figure 27 in part (b).
It is follows from Eq. 48, that
Here,
is the angle between 2D vectors
and
. This equation can be written as
Solutions of this equation can be written as (
Thus, we have a parameterized set of solutions; two parameters are the angles
and
The solutions can be written as
Here,
and
This system of solutions connects the lengths and the angle
between the sides of the triangle,
and
. Note that, to generalize this solution, we can add a zero element
with norm 0. Indeed, for a 2D vector
=1.
The vector
can be analytically written as
The angles
in Eqs. 51 and 52 are considered the same.
Thus, the vector is parameterized by two angles, that is,
In this system, the vector
is rotated counter clock-wise by the angle
and the vector
by the angle
(from the horizontal). We denote the set of such unit 6D vectors (triangles)
by
As examples,
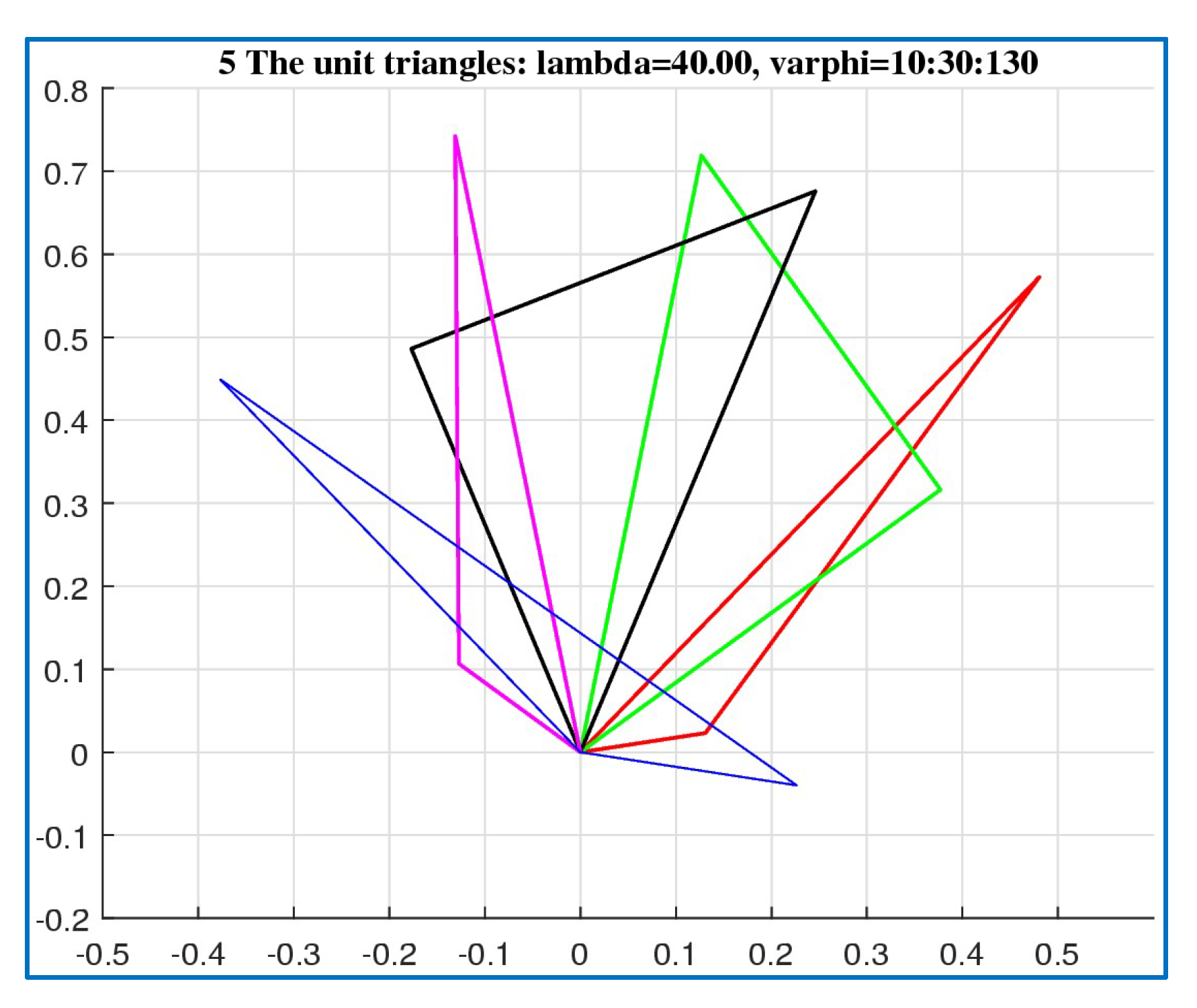
Figure 28 shows five unit triangles with the angle
. The first triangle with angle
is shown in red with vertices marked. Other four unit triangles are shown with the angles
and 130
Two other examples with unit triangles are shown in
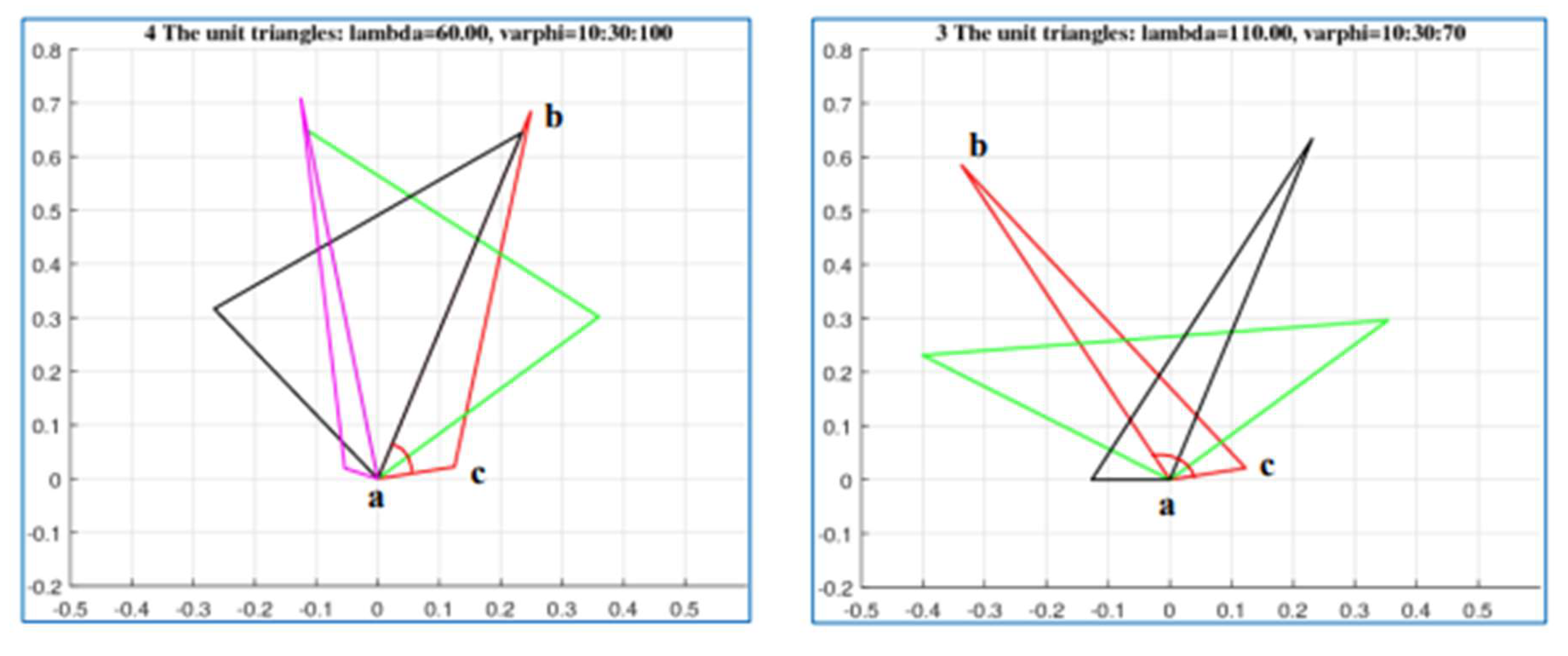
Figure 29. Four unit triangles with angle
are shown in part (a), when angles
and 100
In part (b), three unit triangles with angle
are shown, when angles
and
.
For a 6D vector
presenting a triangle, the similarity triangle, or the triangle in the general golden ratio with
, is defined as
Here,
) denotes the angle between vectors
and
, which is calculated by
The norm
is calculated as in Eq. 47 and the inner product is calculated by
As an example,
Figure 30 show the triangle described by the vector
in part (a). The angle between the vectors
and
equals to
and
. The similarity triangles
, and
for angle
, are shown in parts (b), (c), and (d), respectively.
For the vector
, the similarity set of triangles is defined as
Also, we can write this set as
As example,
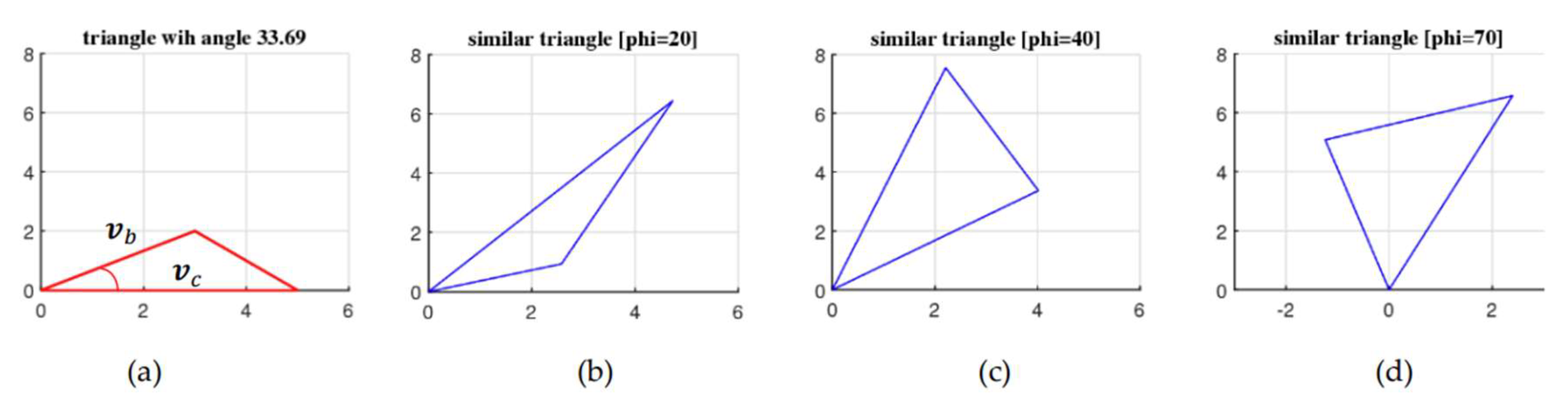
Figure 31 in part (a) shows the subset of the similarity set
, for the vector
which represents a right triangle with angle
between sides ab and ac (shown in red). The angle
is the angle between vectors
and
. The unit vectors
are calculated by Eq. 51 and 52, for 23 angles
The second parameter
, that is, the angle between the vectors
and
in the similarity triangles is the same as in the triangle for
. In part (b), the subset of another similarity set
is shown, for the vector
. This vector represents a triangle with angle of
between vectors
and
(shown in red). 26 angles of
are used, namely
, and the angle
In
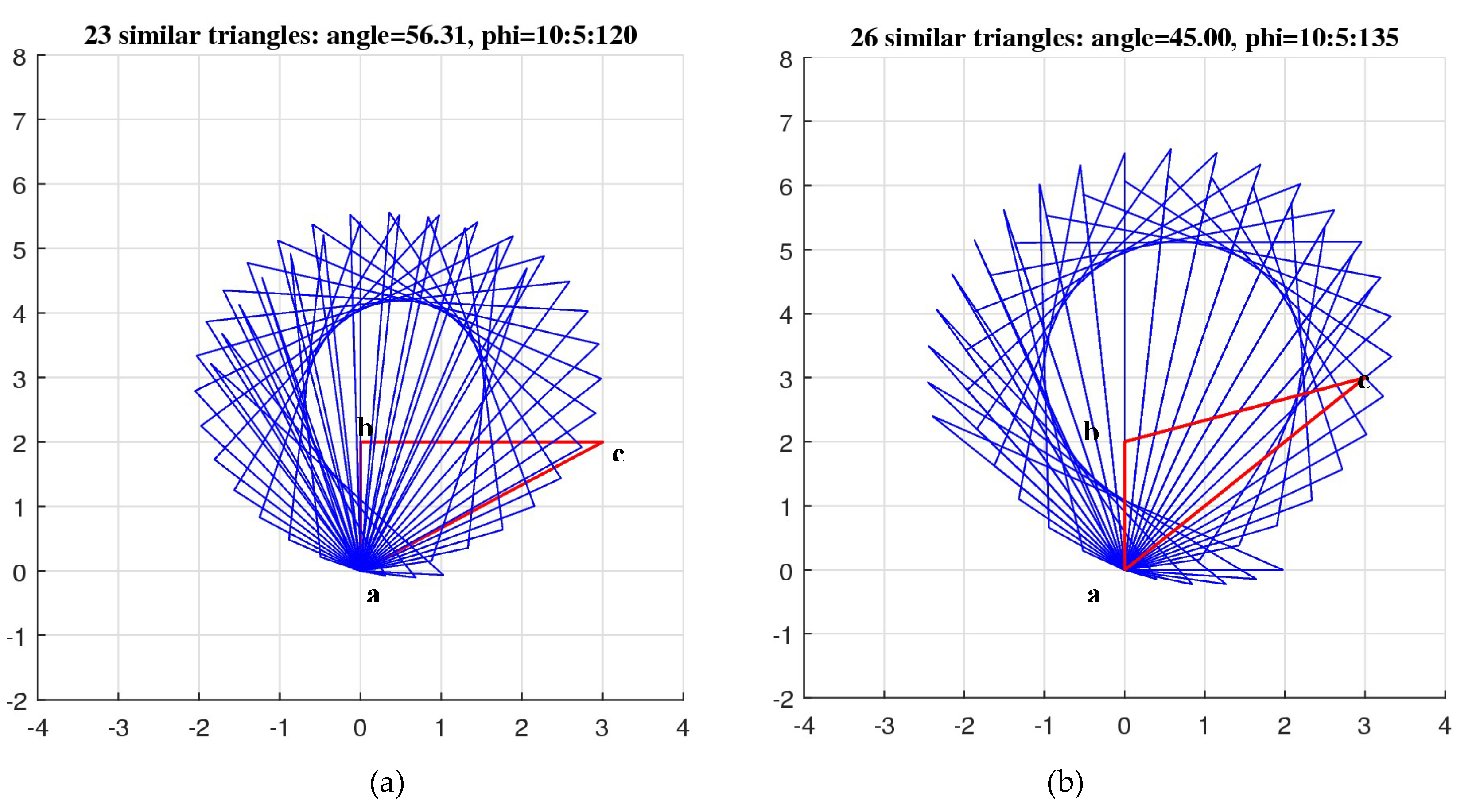
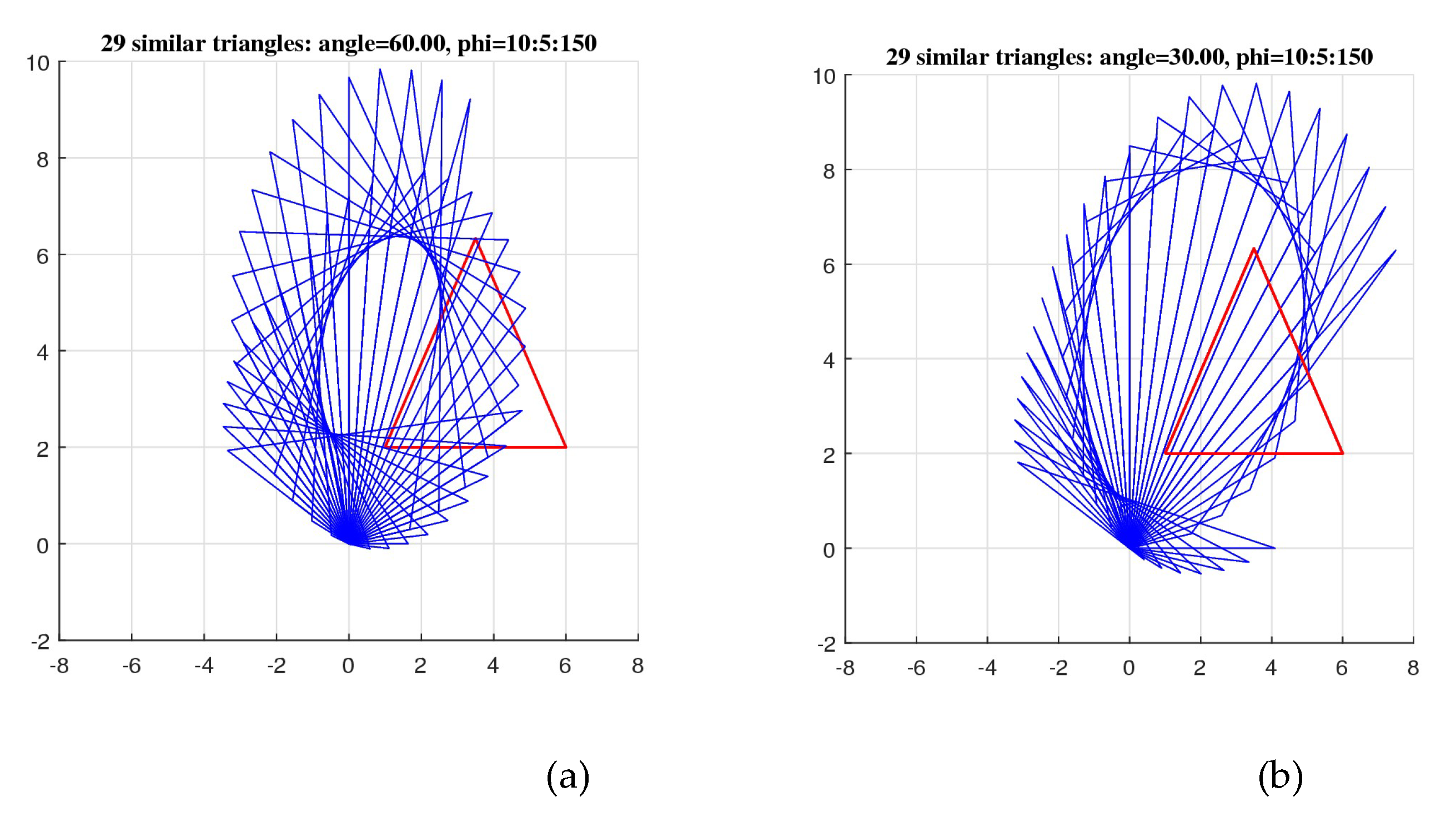
Figure 32, the similarity subsets are shown for the equilateral triangle with sides of length 5. The corresponding vector is
. The first point
of the triangle is not at the origin. In part (a), the subset of similarity triangles is shown for 29 angles
and angle
This is the case when
. In part (b), the subset is shown for the same 29 angles of
and the angle
What can be seen from the figures above, among similarity triangles there is no equal to the triangle with the vector
. It also not difficult to see from Eq. 53, that
only if
that is, when
, or
and
It is possible that other definitions of the inner product of triangles could lead to similarities that include the original triangle
.
As was mentioned above, to generalize this solution, we can add to unit vectors
a zero element
with a 2-D vector
Therefore in general, we can consider the similarity set of triangles of the vector-triangle
as a set parameterized by angles
and vector
,
To facilitate understanding, we can separate similarities, by fixing two parameters out of three. Also, we can consider these similarities separately (as spatial similarity, similarity in one fixed angle
, or similarity in rotation
). If we are interested in similarities with a fixed angle between two sides, then we should fix the value of λ by giving it the value of one of the angles of the original triangle. Adding a constant vector
leads to a spatial shift (translation) of the set of similarities.
7. Similarity of Figures (not Vectors)
The concepts of the similarity vectors and similarity sets of vectors, or golden vectors, are defined in the vector space. These concepts were described in detail and illustrated in
Section 6 on examples with triangles represented as vectors. In this section, we present the concept of similarity on figures, not as vectors. In general, it is difficult to describe many figures (objects), for example the 7-pointed star, in the vector space. The generalized golden function can also be used in the simple case for similar figures (or objects), considering the change of the size of a given figure according to this function, as the function of angle, that is, after rotation of the figure. Now we will illustrate this simplified concept of similar figures on examples in the 2D plane, which include the well-known figures, such as the pentagons, heptagons, stars, and spirals.
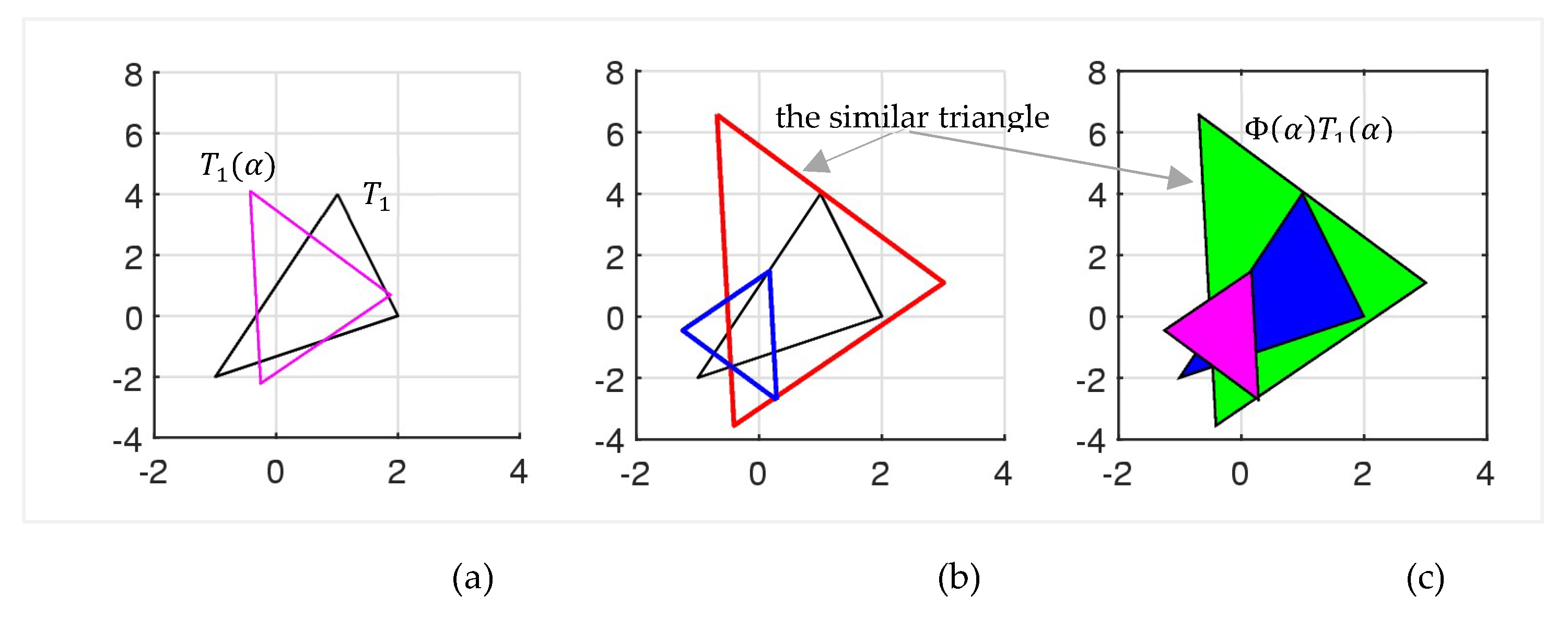
Example 6: (Triangle)
Let is consider the following three points on the place
, and
These points together compose one triangle, which we donote by
. We need to draw the triangles which are in golden ratio with the triangle
but rotated by
.
Figure 33 shows the original triangle in part (a) (in black color) together with the rotated triangle (in magenta). The solution of the golden equations for this angle are
Two roots are positive,
and
are positive, and only the first one is positive. The similar triangle, that is, the triangle in the golden ratio,
is shown in part (b). The small triangle in part (b) is
which is not in the golden ratio with
. In part (c), the original triangle is shown in blue and the triangle in the gold ratio with it in green.
The triangles that are in golden ratio with
at angles 30
, 140
, and -20
are shown in
Figure 34 in parts (a), (b), and (c), respectively. Note that the system of coordinates is not in the center of the triangle
and the golden pairs change the original form (angles) of the triangle.
7.1. Other Figures
Now, we consider a few more illustrative examples for the GGR function in the 2D vector space. The figures of regular polygons and stars are considered with their centers at the initial point of the coordinate system. The form of golden pairs for each of such figures is preserved, as shown below.
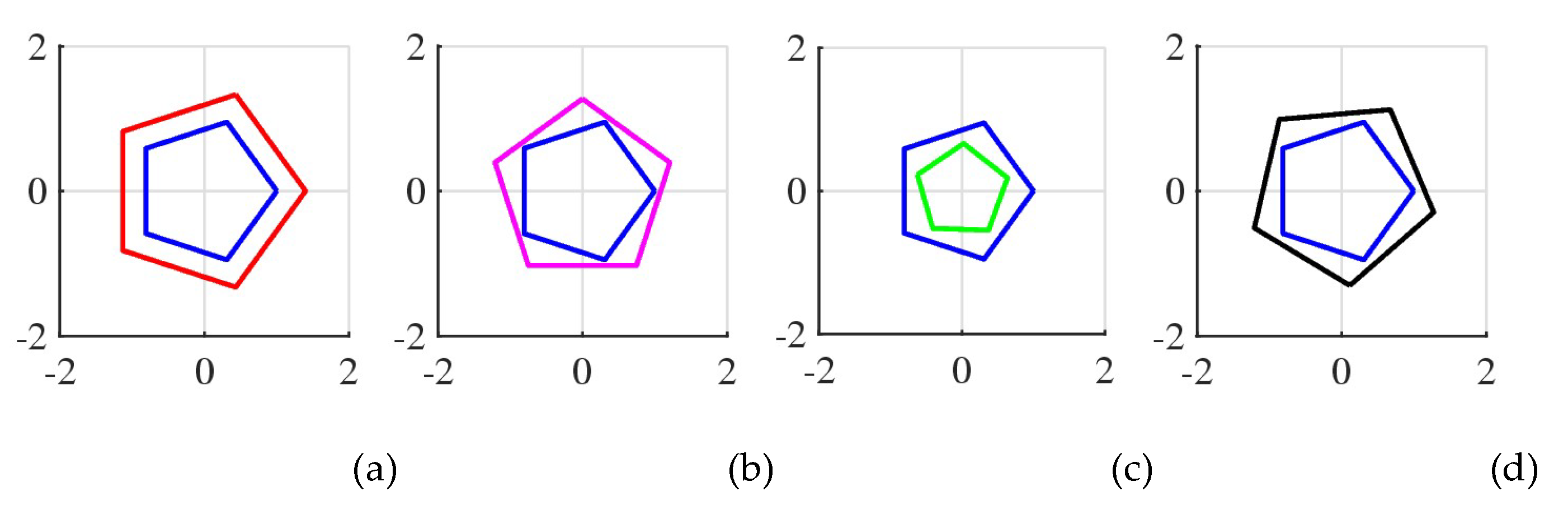
Example 7. Consider the pentagon,
, inside the unit circle, which is shown in
Figure 34 in the blue color. The hexagons that are in golden ratio with
at angles 72
, 90
, 160
, and 275
are shown in parts (a), (b), (c), and (d), respectively.
Figure 34.
The pentagon and its golden pairs for the angles 72,90, 160, and 275.
Figure 34.
The pentagon and its golden pairs for the angles 72,90, 160, and 275.
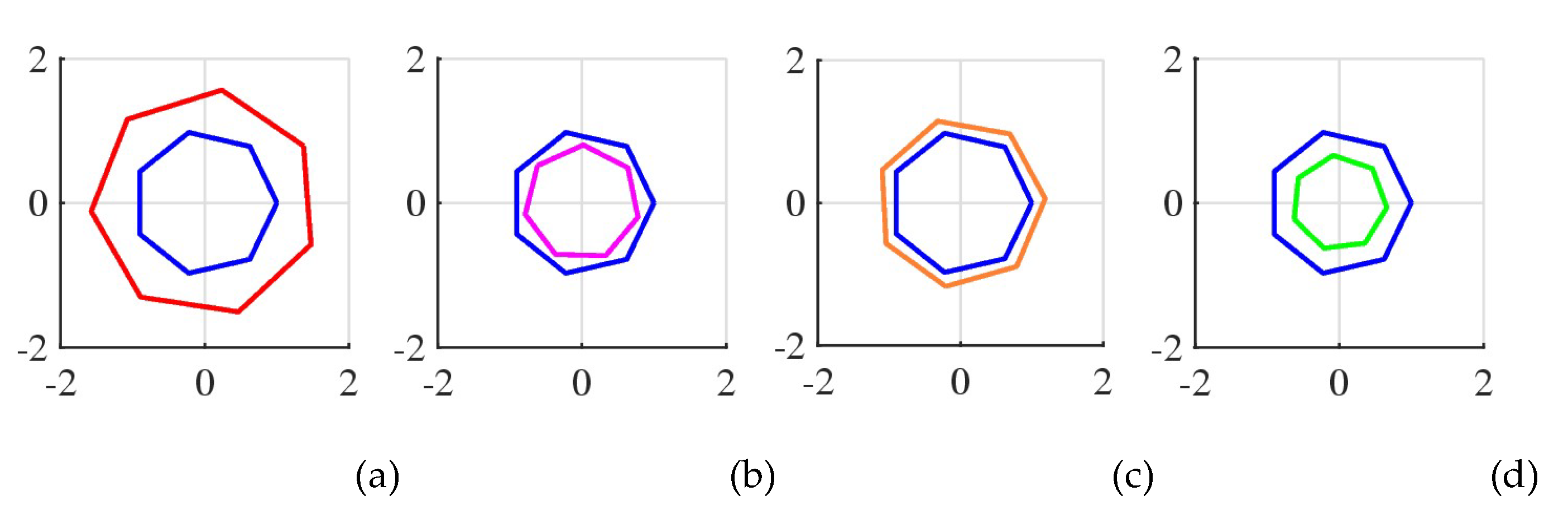
Example 8. Consider the heptagon,
, inside the unit circle, which is shown in
Figure 35 in the blue color. The heptagons that are in golden ratio with
at angles 30
, 140
, -100
, and 200
are shown in parts (a), (b), (c), and (d), respectively.
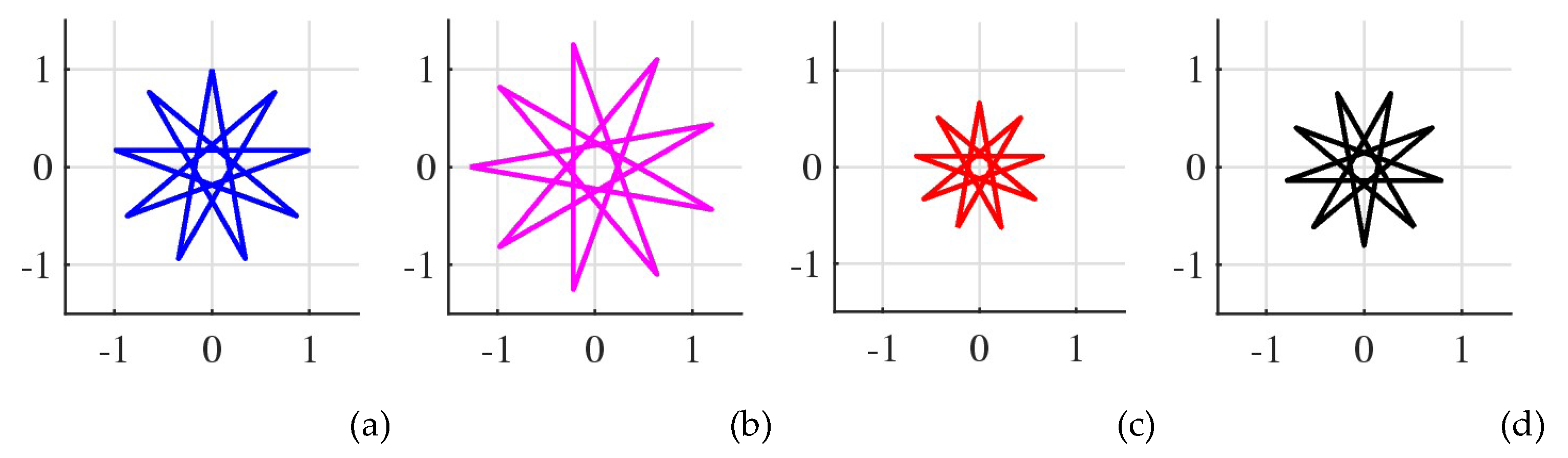
Example 9. Consider the 7-pointed star, or the regular heptagram,
inside the unit circle. This star is shown in
Figure 36 in the blue color. The heptagrams that are in golden ratio with
at angles 30
, 90
, 160
, and 220
are shown in parts (a), (b), (c), and (d), respectively.
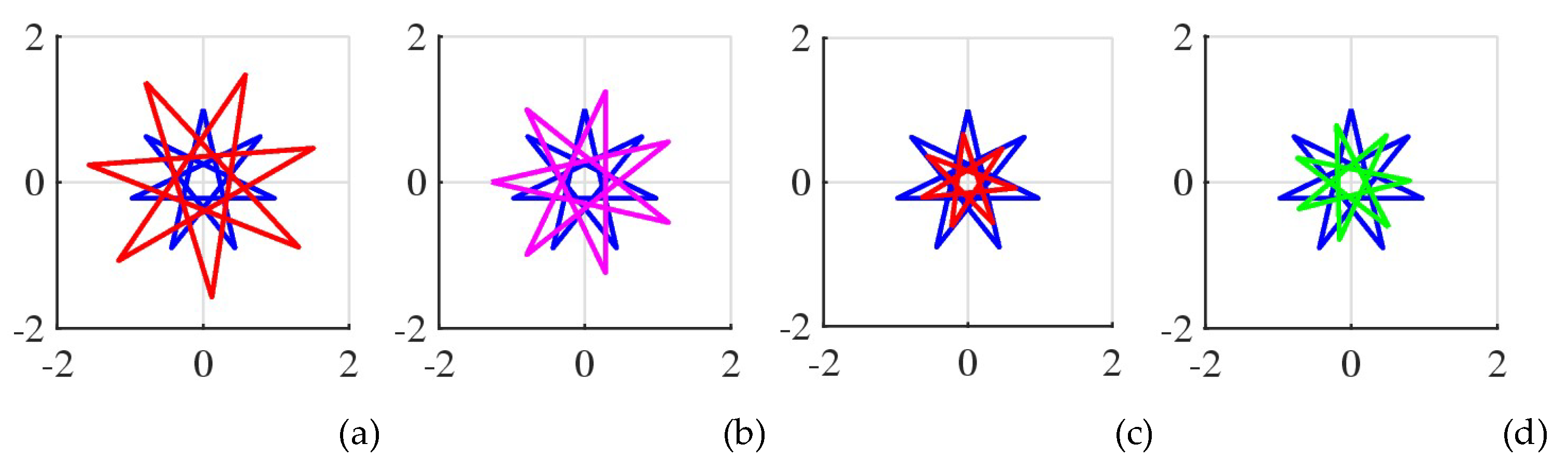
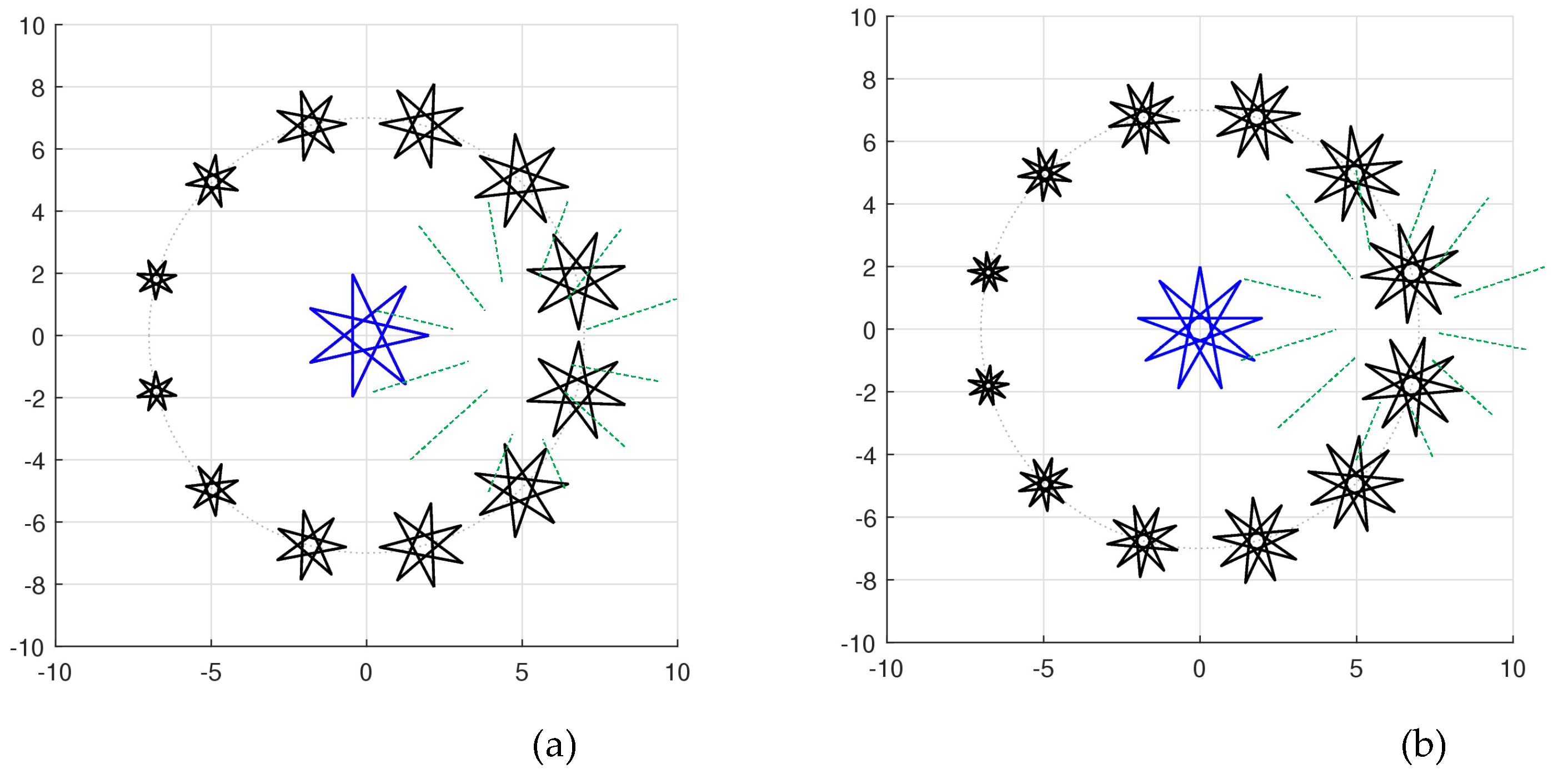
Example 10. Consider the 9-pointed star, or the regular enneagram,
inside the unit circle. This star is shown in
Figure 37 in part (a). The enneagrams that are in golden ratio with
at angles 90
, 160
, and 220
are shown in parts (b), (c), and (d), respectively.
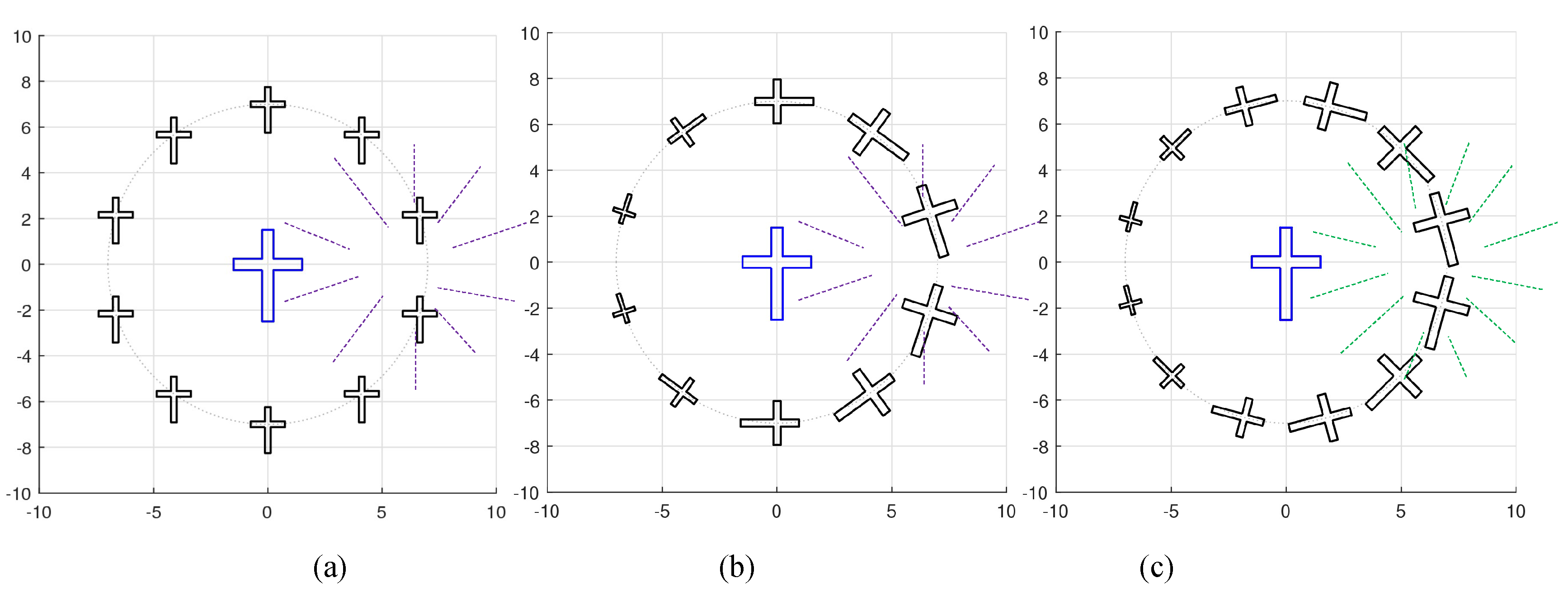
Example 11. Consider the figure with the cross, along with 10 crosses of half the size, each arranged in a circle, as shown in
Figure 38 in part (a). This is a traditional picture with complete symmetry and identical figures. There is complete symmetry and there is no movement in this picture. In part (b), 10 crosses on the circle are chosen from the golden pairs with angles 18
, 54
,
,
, …, and 342
. In part (c), the same cross in the center is shown together with 12 its golden pairs for by angles 15
,
,
,
, 145
, …, and 335
.
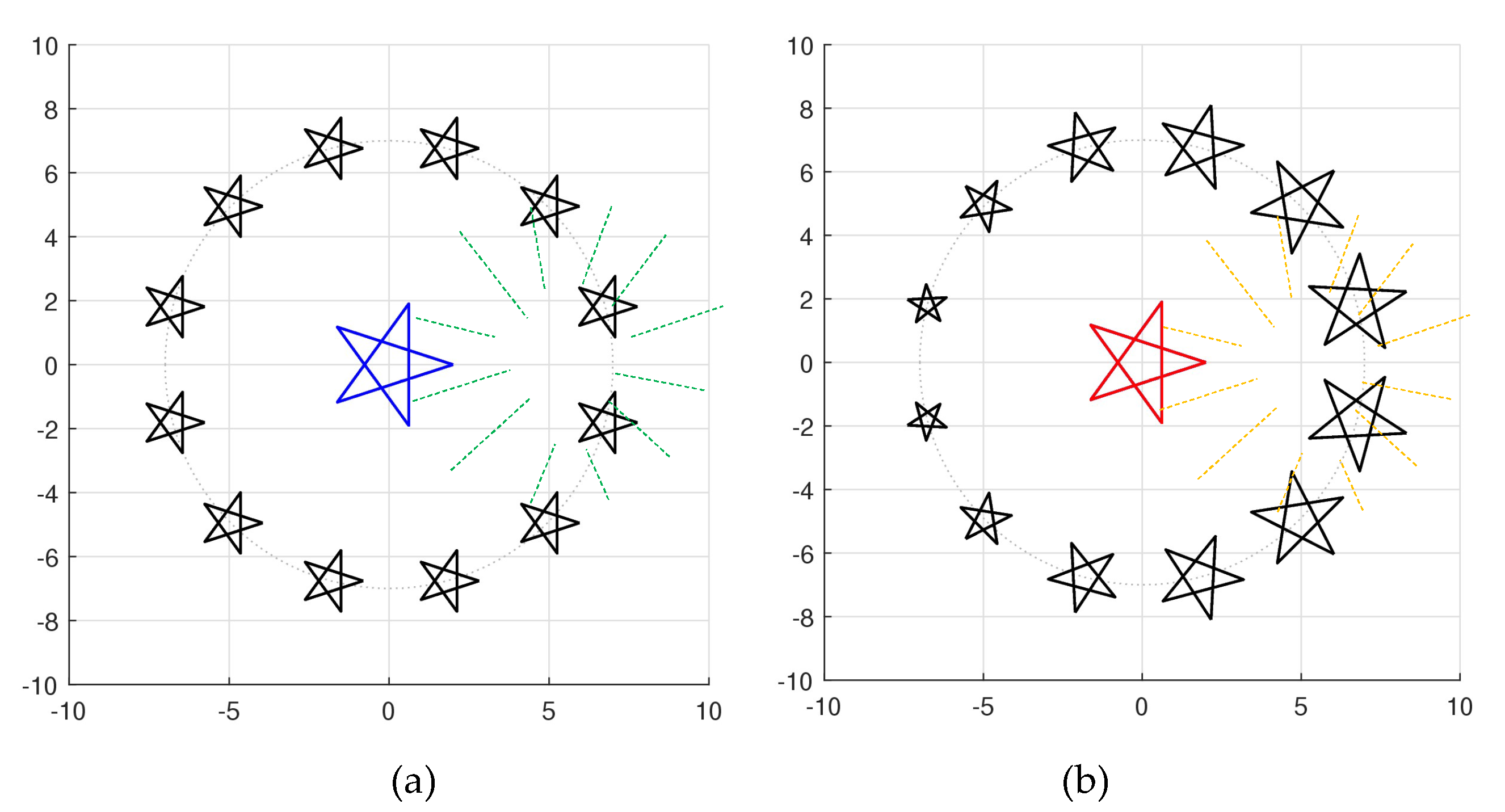
Example 12. Consider the 5-pointed star together with 12 starts of twice smaller starts which are shown in
Figure 39. In part (a), the traditional picture is shown, and in part (b), 12 starts are composing the golden pairs with the star in the center.
Example 13. Consider the 7-pointed star,
shown in the center of
Figure 40 in part (a) and 12 golden pair-starts placed around a circle. These golden pairs were calculated for star twice smaller size,
.
Figure 15(b) shows the similar picture for the 9-pointed star,
. The golden pairs of stars were calculated for angles 15
,
,
,
, 145
, …, and 335
.
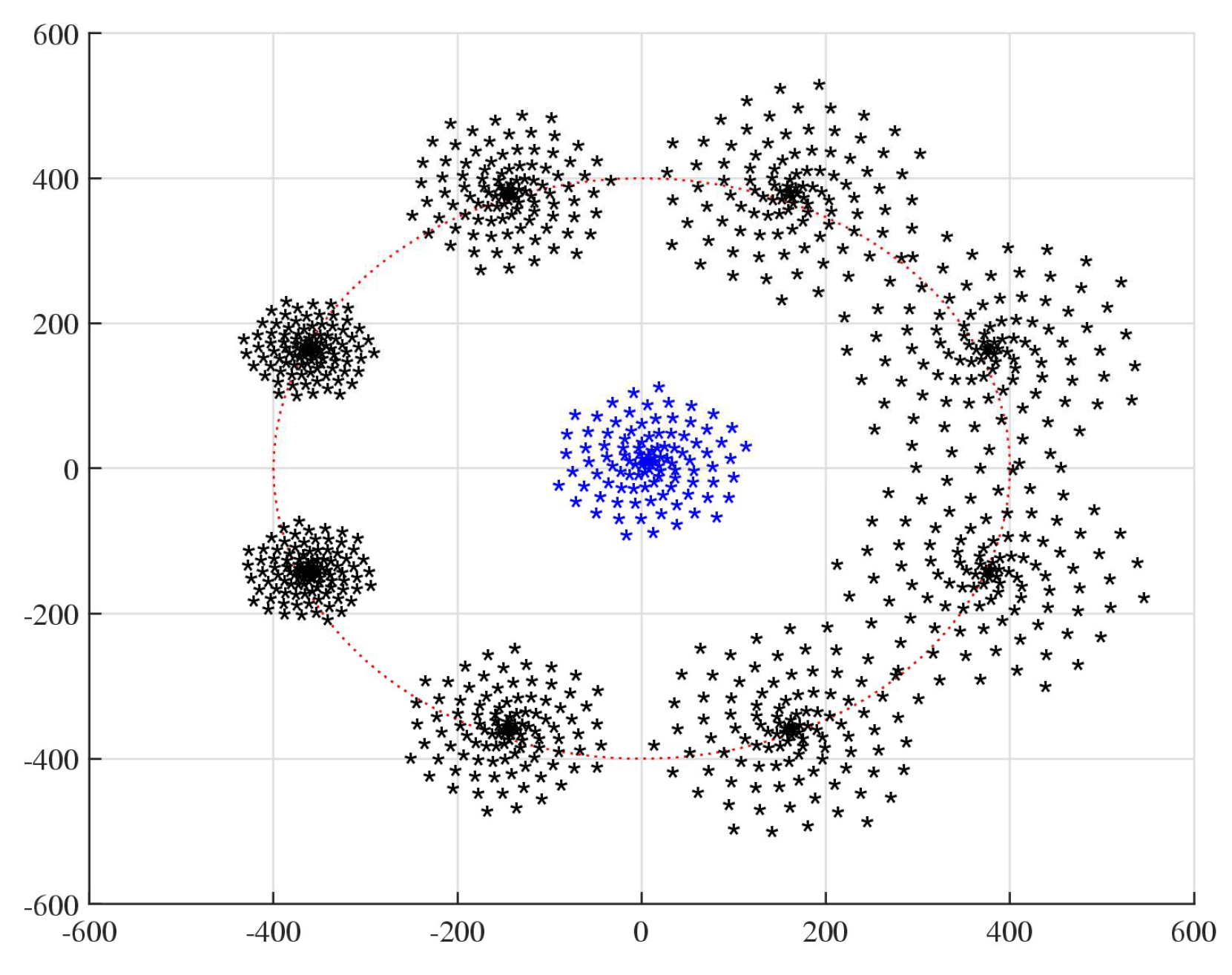
Example 14. Consider the locus of the first 108 points on the Archimedes spiral
}. We can call this figure a linear spiral
.
Figure 41 shows this spiral in the center together with 8 spirals which compose golden pairs with the spiral
/2 of twice smaller size. These 8 spirals are placed around a circle with distance of
.
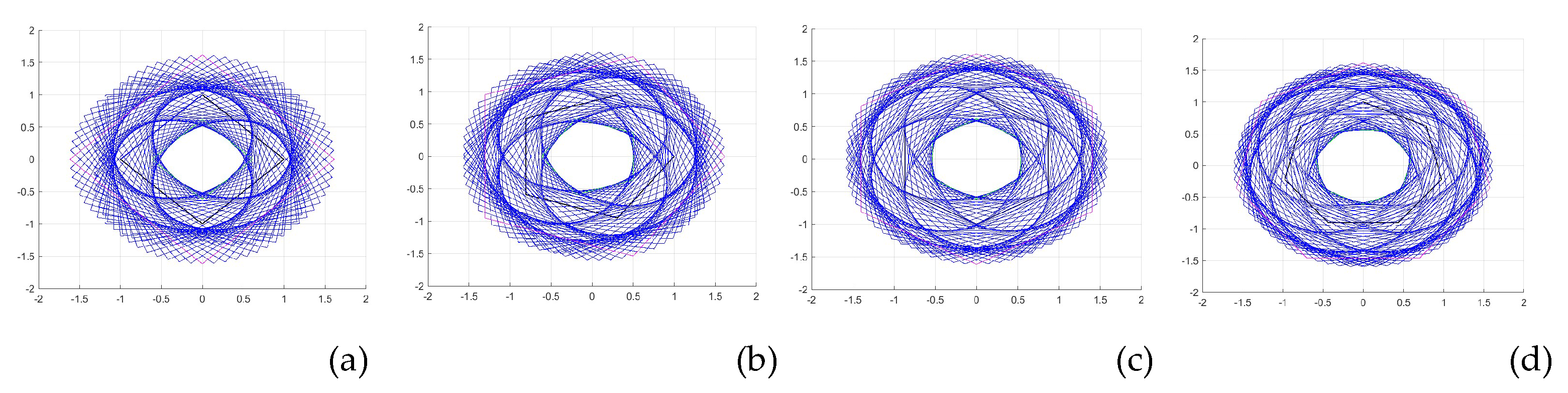
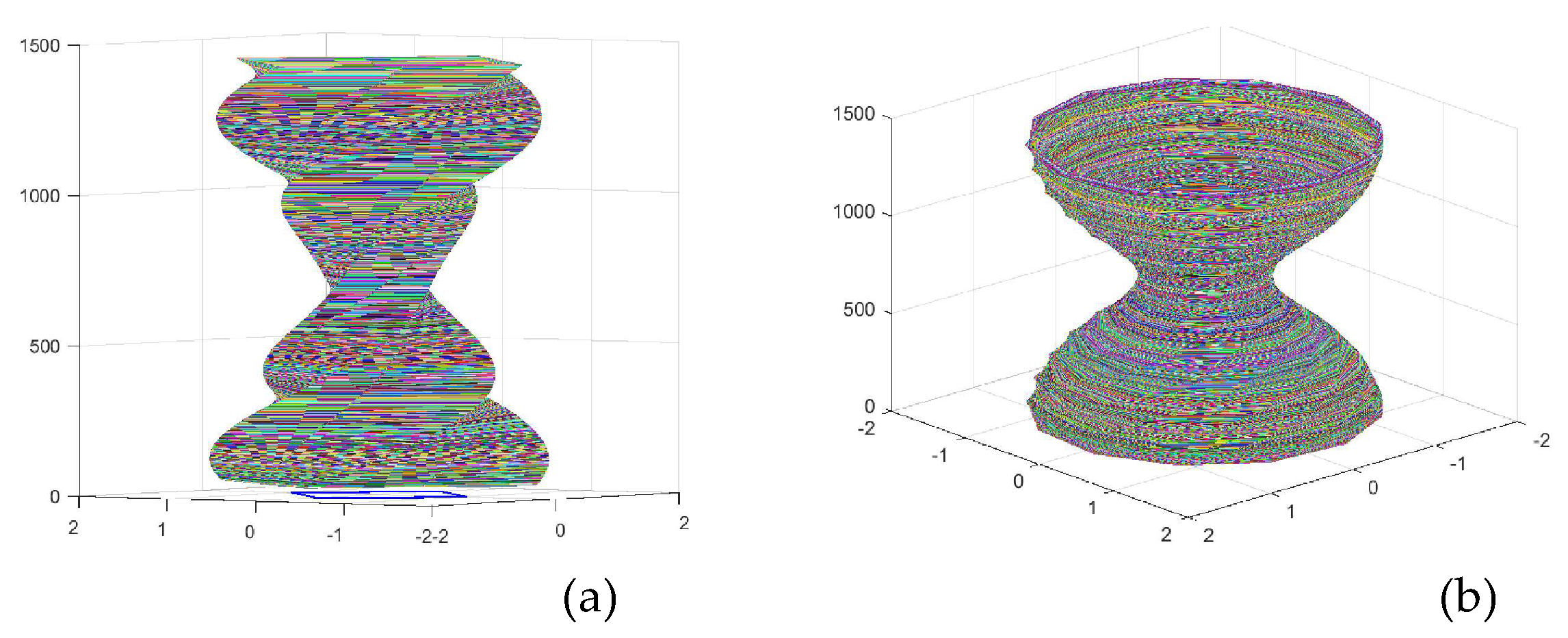
If we superimpose these shapes on top of each other, we get a 3D shape. As examples, Figs. 42 shows such 2D view for the -sided polygons , for and 7. The angles were taken from the interval with the step of 2 degree. The original polygons are shown on the x-y plane in the black color.
Figure 43 shows such shapes for the square in part (a) and for the twelve-sided polygon (dodecagon) in part (b). In these shapes, the polygons in golden ratios are colored randomly and angles
were taken from the interval
with the small step, 0.2
. These two figures exist in the nature.
Figure 1.
(a) The golden pair of vectors and these vectors with (b) the parallelograms and (c) triangles.
Figure 1.
(a) The golden pair of vectors and these vectors with (b) the parallelograms and (c) triangles.
Figure 3.
The vector and its four similarity vectors.
Figure 3.
The vector and its four similarity vectors.
Figure 4.
The golden pairs , and
Figure 4.
The golden pairs , and
Figure 5.
The graphs of the polynomial and lines, when (a) , (b) , and (b) .
Figure 5.
The graphs of the polynomial and lines, when (a) , (b) , and (b) .
Figure 6.
The positive functions (a) and (b) for the Cardano’s solution of the depressed equation.
Figure 6.
The positive functions (a) and (b) for the Cardano’s solution of the depressed equation.
Figure 7.
The graphs of the four roots of Eq. 10.
Figure 7.
The graphs of the four roots of Eq. 10.
Figure 8.
Polar plots of magnitudes of four roots of Eq. 10.
Figure 8.
Polar plots of magnitudes of four roots of Eq. 10.
Figure 9.
The polar plots of the sum of two roots: (a) , (b) , and (c) .
Figure 9.
The polar plots of the sum of two roots: (a) , (b) , and (c) .
Figure 11.
(a) The sum of real solutions and the cosine function and (b) their difference.
Figure 11.
(a) The sum of real solutions and the cosine function and (b) their difference.
Figure 12.
The general golden ratio function .
Figure 12.
The general golden ratio function .
Figure 13.
The general golden ratio function and the function .
Figure 13.
The general golden ratio function and the function .
Figure 14.
The General Golden ratio function with a few marked values on it.
Figure 14.
The General Golden ratio function with a few marked values on it.
Figure 15.
The complex solution : (a) the real part, (b) the imaginary part, and (c) the magnitude and its approximation . .
Figure 15.
The complex solution : (a) the real part, (b) the imaginary part, and (c) the magnitude and its approximation . .
Figure 16.
Polar plots of three roots in absolute scale: (a) (b) and (c)
Figure 16.
Polar plots of three roots in absolute scale: (a) (b) and (c)
Figure 18.
The locus of 128 golden pairs with the vectors (a) and (b)
Figure 18.
The locus of 128 golden pairs with the vectors (a) and (b)
Figure 19.
The parallelogram composed of the sum of two vectors (a) before and (b) after the rotation by the angle .
Figure 19.
The parallelogram composed of the sum of two vectors (a) before and (b) after the rotation by the angle .
Figure 20.
Sum of similarity sets for the 2-D vectors (a) , and (b) ,
Figure 20.
Sum of similarity sets for the 2-D vectors (a) , and (b) ,
Figure 21.
Sum of similarity sets for the 2D vectors (a) , , (b) , and (c) , .
Figure 21.
Sum of similarity sets for the 2D vectors (a) , , (b) , and (c) , .
Figure 22.
The unit vector in the 3D spherical coordinate system.
Figure 22.
The unit vector in the 3D spherical coordinate system.
Figure 23.
The geometry of the similarity sets of golden vectors with the 3D vectors (a) [0,0,1] and (b) [1,0,0].
Figure 23.
The geometry of the similarity sets of golden vectors with the 3D vectors (a) [0,0,1] and (b) [1,0,0].
Figure 24.
The view with AZ=0 and EL=90 degrees of the geometry of similarity sets of the Golden vectors with the 3D vectors (a) [0,0,1] and (b) [1,0,0].
Figure 24.
The view with AZ=0 and EL=90 degrees of the geometry of similarity sets of the Golden vectors with the 3D vectors (a) [0,0,1] and (b) [1,0,0].
Figure 25.
The view with AZ=0 and EL=180 degrees: The geometry of the similarity sets of the Golden vectors with the 3-D vectors (a) [0,0,1] and (b) [1,0,0].
Figure 25.
The view with AZ=0 and EL=180 degrees: The geometry of the similarity sets of the Golden vectors with the 3-D vectors (a) [0,0,1] and (b) [1,0,0].
Figure 26.
The 3-D surface of the similarity sets of the Golden vectors with the 3-D vectors (a) [0,0,1] and (b) [1,0,0].
Figure 26.
The 3-D surface of the similarity sets of the Golden vectors with the 3-D vectors (a) [0,0,1] and (b) [1,0,0].
Figure 27.
(a) Triangle for the vector and (b) the triangle with the vertex at the origin.
Figure 27.
(a) Triangle for the vector and (b) the triangle with the vertex at the origin.
Figure 28.
Five unit triangles with the angle
Figure 28.
Five unit triangles with the angle
Figure 29.
The unit triangles with the angle (a) and (b)
Figure 29.
The unit triangles with the angle (a) and (b)
Figure 30.
(a) The original triangle with angle and similarity triangles with the angle of (b) (c) and (d)
Figure 30.
(a) The original triangle with angle and similarity triangles with the angle of (b) (c) and (d)
Figure 31.
The similarity triangles for (a) the triangle with angle and (b) the triangle with angle . .
Figure 31.
The similarity triangles for (a) the triangle with angle and (b) the triangle with angle . .
Figure 32.
The similarity triangles for the equilateral triangle, when the angle (a) and (b) .
Figure 32.
The similarity triangles for the equilateral triangle, when the angle (a) and (b) .
Figure 33.
(a) The original and rotated triangles, (b) the original triangle and its two pairs, and (c) the same shaded triangles.
Figure 33.
(a) The original and rotated triangles, (b) the original triangle and its two pairs, and (c) the same shaded triangles.
Figure 35.
The heptagon and its golden pairs for the angles 30,140, -100, and 200. (roos4_2.m)
Figure 35.
The heptagon and its golden pairs for the angles 30,140, -100, and 200. (roos4_2.m)
Figure 36.
The heptagram and its golden pairs for the angles 30,90,160, and 220.
Figure 36.
The heptagram and its golden pairs for the angles 30,90,160, and 220.
Figure 37.
(a) The enneagram and its golden pairs for the angles (b) 90, (c) 160, and (d) 220.
Figure 37.
(a) The enneagram and its golden pairs for the angles (b) 90, (c) 160, and (d) 220.
Figure 38.
The cross together with (a) 10 equal small crosses, (b) 10 golden pairs, and (c) 12 golden pairs.
Figure 38.
The cross together with (a) 10 equal small crosses, (b) 10 golden pairs, and (c) 12 golden pairs.
Figure 39.
The star together with (a) 12 equal small stars and (b) 12 stars of the golden pairs.
Figure 39.
The star together with (a) 12 equal small stars and (b) 12 stars of the golden pairs.
Figure 40.
The 7-pointed and 9-pointed stars together with their 12 stars of the golden pairs.
Figure 40.
The 7-pointed and 9-pointed stars together with their 12 stars of the golden pairs.
Figure 41.
The 108-points on the Archimedes spiral together with eight golden-pairs.
Figure 41.
The 108-points on the Archimedes spiral together with eight golden-pairs.
Figure 42.
The 2-D view of 108 golden (a) squares, (b) pentagons, (c) hexagons, and (d) heptagons.
Figure 42.
The 2-D view of 108 golden (a) squares, (b) pentagons, (c) hexagons, and (d) heptagons.
Figure 43.
3D composition of golden figures for (a) the square and (b) the dodecagon.
Figure 43.
3D composition of golden figures for (a) the square and (b) the dodecagon.