Research on Relationship Between Aging Population Distribution and Real Estate Market Dynamics based on Neural Networks

1. Introduction

As the global population ages, structural changes in all areas of society have a profound impact on the economy, policy, and market behavior. The phenomenon of population aging is multi-faceted, encompassing not only an increase in the elderly population but also profound transformations in various domains, including the family structure, the labor market, social consumption patterns, medical needs, and social security systems. These transformations have directly or indirectly altered the relationship between demand and supply in various markets, most notably in the real estate sector, where the phenomenon of aging has become increasingly complex and multidimensional [1]. For instance, the demand for housing by elderly individuals has evolved beyond the mere need for basic living space, encompassing the demand for new housing forms and service requirements such as barrier-free facilities, senior apartments, and long-term care housing. Furthermore, the convergence of a diminishing labor market and a declining youth population may impede or alter the urbanization process, consequently leading to a diminished demand for real estate in primary cities and heightened pressure on secondary and tertiary cities [2].

The phenomenon of population aging will also profoundly affect the demand structure and price trend of the real estate market. On the one hand, the purchasing power of the elderly population is limited; however, their housing needs are evolving, with a growing preference for stable, low-maintenance and adaptable housing options. On the other hand, the decline in the young population may lead to a sustained sluggish demand for real estate in certain cities, thereby further exacerbating the differentiated development of the real estate market between regions [3]. In particular, in areas experiencing slower economic growth and significant population outflows, the real estate market may face the challenge of oversupply, potentially leading to long-term stagnation or decline in housing prices. Consequently, as the population ages, governments may be compelled to adopt more proactive housing policies to address the needs of the elderly population, including the development of senior housing and the active housing rental market, which are contributing to the transformation of the real estate market. Consequently, the accurate capture of the relationship between population aging and the real estate market, and the scientific prediction of real estate demand in different regions and market sectors, has become a topic of urgent importance in both academic and industry circles [5].

In recent years, with the advent of big data and artificial intelligence technology, data-driven analysis methods have gradually become the mainstream approach to studying the real estate market. Unlike conventional models that rely heavily on economic theories and assumptions about market behavior, data-driven methodologies leverage vast amounts of historical data to extract patterns and insights that may not be immediately apparent through traditional models. By processing and analyzing massive datasets—such as property transaction records, demographic shifts, interest rates, and even social media sentiment—these advanced techniques can identify complex and nuanced factors that influence real estate trends, offering a more comprehensive understanding of market dynamics [6]. The primary advantage of data-driven approaches lies in their ability to capture the micro-level dynamics of market changes, which are often too subtle or intricate to be effectively modeled by traditional methods. Through machine learning algorithms and deep learning techniques, these methodologies can uncover hidden relationships between various variables, identifying nonlinear patterns that would be difficult to discern through linear regression or time series analysis alone. This enables more precise modeling of real estate markets, allowing for the identification of emerging trends and the prediction of price movements with greater accuracy.

For instance, machine learning models can be trained to recognize the influence of factors such as neighborhood gentrification, infrastructure development, or even environmental changes, and predict their impact on property values. By continuously learning from new data inputs, these models are able to adapt to shifting market conditions, improving their forecasting accuracy over time. Furthermore, data-driven methods can incorporate a wide range of factors that might be overlooked in conventional models, including microeconomic variables like local employment rates, school rankings, or even weather patterns, thereby providing a more holistic and dynamic view of the real estate landscape.

However, the fundamental assumptions inherent in these methods are frequently linear, which does not adequately capture the intricate dynamics that characterize market behavior. For instance, conventional models presuppose that the relationship between demographic, economic, policy-related, and other factors is static and linear. However, in actual markets, these factors frequently exhibit strong temporal variation and interdependence, and their effects are often non-linear. This is especially evident in the complex social phenomenon of population aging, where traditional methods frequently underrepresent the intricate interactions and market feedback mechanisms between diverse factors [6].

2. Related Work

Francke and Korevaar (2021) [7] explore the short- and long-term impact of the pandemic on the housing market by analyzing the dynamics of the real estate market during historical pandemics. Their findings indicate that while the pandemic has exerted a substantial influence on house prices and population movements in the short term, market indicators generally revert to pre-pandemic trends with alacrity. This study demonstrates the real estate market's notable resilience and its capacity for rapid dynamic adjustment in the aftermath of a significant public health emergency.

Liu et al. (2022) [8] examined the dynamics of urban retail real estate rents in the era of e-commerce, focusing on the case of Guangzhou, China. Utilizing a big data approach, underpinned by population heat information, they constructed a model to elucidate the dynamics of urban management and the real estate market. The study demonstrates that the prevalence of e-commerce has not only resulted in a shift in the spatial distribution of traditional retail, but has also exerted a significant influence on the value structure of urban real estate markets.

In her 2022 study, Wilkinson [9] explores the impact of demographic change on health and socioeconomic disparities. She does this by analyzing trends in mortality among different classes in the process of population aging. The study posits that as the age distribution of the population rises, disparities in health and longevity between different socioeconomic classes are likely to widen, with far-reaching indirect implications for housing demand. In a related study, Corbae and D'Erasmo (2021) [10] constructed a quantitative model on banking dynamics, analyzing the dynamics of capital buffers in the financial, insurance, and real estate sectors. Their findings indicate that the financial and real estate sectors' profit models during periods of economic volatility are predominantly driven by "internal" factors, such as industry restructuring and enhanced efficiency in capital allocation.

The multi-objective optimisation approach proposed by Ciardiello et al. [11] focuses on the optimisation of building form and shell design with the aim of improving building energy efficiency, comfort, and environmental impact. The optimization method incorporates factors such as heat transfer, light, and ventilation in the building design process, which are of particular significance in an ageing society, especially with respect to the comfort of the living environment and the energy efficiency of the elderly. In their study, Yao et al. investigated the multi-objective optimisation of the design of transparent enclosures, including windows and glass walls, for rural dwellings in cold climate zones. The objective of this research is to enhance thermal insulation, natural illumination and indoor comfort, thereby addressing the diverse requirements of various climates and enhancing the energy efficiency of the constructed environment. This optimal design is of particular significance for ageing societies, especially those in cold climates.

3. Methodologies

3.1. Adjustment Door of LSTM

The LSTM network is predicated on a mechanism of updating its cellular state and gating operations. In traditional LSTMs, the cell state is updated by forgetting gates, input gates, and output gates. The oblivion gate determines the amount of state information transferred from the previous moment to the current moment; the input gate determines the amount of input information that must be written to the cell state at the current moment; and the output gate determines the output information at the current moment. However, when dealing with such a complex problem as the real estate market, which is driven by multiple factors and subject to cyclical fluctuations, the capabilities of standard LSTMs are often insufficient to capture the deeper market dynamics.

In order to enhance the expressive ability of the model, innovative extensions have been made to the standard LSTM. A novel "moderation gate" mechanism has been introduced, which is used to regulate the renewal process of the network in combination with external market factors (such as economic indicators, ageing population distribution, etc.). Specifically, we introduce external information into the LSTM's cell state update equation and dynamically adjust the influence of external information on cell state through a new gating operation. In order to introduce external market factors, a "moderation gate" was designed. This gate adjusts the weight of the hidden state and the cellular state of the input to the LSTM according to changes in the external environment. The adjustment gate is calculated as Equation (1).

$${\mathrm{r}}_{\mathrm{t}}=\mathsf{\sigma }\left({\mathrm{W}}_{\mathrm{r}}·\left[{\mathrm{h}}_{\mathrm{t}-1},{\mathrm{x}}_{\mathrm{t}},{\mathrm{f}}_{\mathrm{t}}\right]+{\mathrm{b}}_{\mathrm{r}}\right),$$

(1)

where ${\mathrm{r}}_{\mathrm{t}}$ denotes the output of the adjustment gate, whilst $\mathsf{\sigma }$ represents the sigmoid activation function. The weight matrix is denoted by ${\mathrm{W}}_{\mathrm{r}}$, and the $\left[{\mathrm{h}}_{\mathrm{t}-1},{\mathrm{x}}_{\mathrm{t}},{\mathrm{f}}_{\mathrm{t}}\right]$ means that the hidden state of the previous moment, the input of the current moment, and the external market factors ${\mathrm{f}}_{\mathrm{t}}$ (such as ageing population distribution, migration patterns, economic indicators, etc.) are connected and sent into the network by $\left[{\mathrm{h}}_{\mathrm{t}-1},{\mathrm{x}}_{\mathrm{t}},{\mathrm{f}}_{\mathrm{t}}\right]$. In this context, the external factor ${\mathrm{f}}_{\mathrm{t}}$ is not merely a conventional eigenvariable; it has the capacity to influence the computational process of the network. Consequently, it is imperative that it is weighted by a gating mechanism.

The purpose of the adjustment gate is to enable the dynamic adjustment of the update steps of the LSTM network in accordance with changes in external market factors. This enables the network to flexibly adjust the direction and amplitude of the forecast according to the prevailing economic environment, population structure and other relevant information. The introduction of regulatory gates has led to the enhancement of the updated formula for cell state. The original formula for updating the cell state is given by Equation (2):

$${\mathrm{C}}_{\mathrm{t}}={\mathrm{f}}_{\mathrm{t}}·{\mathrm{C}}_{\mathrm{t}-1}+{\mathrm{i}}_{\mathrm{t}}·{\tilde{\mathrm{C}}}_{\mathrm{t}}.$$

(2)

Following the implementation of the regulatory gate, the revised formula for the cell state is expressed as Equation (3):

$${\mathrm{C}}_{\mathrm{t}}={\mathrm{r}}_{\mathrm{t}}·\left({\mathrm{f}}_{\mathrm{t}}·{\mathrm{C}}_{\mathrm{t}-1}+{\mathrm{i}}_{\mathrm{t}}·{\tilde{\mathrm{C}}}_{\mathrm{t}}\right)+\left(1-{\mathrm{r}}_{\mathrm{t}}\right)·{\mathrm{C}}_{\mathrm{t}-1},$$

(3)

The output of the adjustment gate is denoted by ${\mathrm{r}}_{\mathrm{t}}$R. By modulating the gate, it is possible to dynamically control the weighting relationship between historical cell state ${\mathrm{C}}_{\mathrm{t}-1}$ and current cell state updates. In situations where market environments undergo substantial changes, the adjustment gate is used to assign greater importance to novel information, thereby amplifying the model's responsiveness to such market fluctuations. Conversely, in instances where market environments exhibit minimal or consistent changes, the adjustment gate is designed to preserve a greater proportion of historical state information, thus ensuring the model's stability.

In traditional LSTMs, the output gate determines the effect of cell state ${\mathrm{C}}_{\mathrm{t}}$ at the current moment on the output at the next moment. However, when external market factors are taken into account, the output gate also needs to be adjusted accordingly in order to fuse external information with internal memory. In the model under consideration, the output gate is calculated as Equation (4):

$${\mathrm{o}}_{\mathrm{t}}=\mathsf{\sigma }\left({\mathrm{W}}_{\mathrm{o}}·\left[{\mathrm{h}}_{\mathrm{t}-1},{\mathrm{x}}_{\mathrm{t}},{\mathrm{f}}_{\mathrm{t}}\right]+{\mathrm{b}}_{\mathrm{o}}\right),$$

(4)

The incorporation of the external market factor ${\mathrm{f}}_{\mathrm{t}}$ into the calculation of the output gate enables the model to adjust the output of the hidden state in accordance with changes in external factors. Consequently, in diverse market environments, the output gate will assign greater weight to the cell state based on external information.

3.2. Dynamic Adjustment

In order to enhance the training efficiency of the model, the Adaptive Moment Estimation optimizer is employed. In contrast to conventional Stochastic Gradient Descent (SGD) optimizers, Adam employs an adaptive adjustment of the learning rate for each parameter. This is achieved by calculating the first-order moment and the second-order moment. This approach has been shown to accelerate the training process and enhance the convergence speed. The update rules for the Adam optimizer are as Equations (5)–(9).

$${\mathrm{m}}_{\mathrm{t}}={\mathsf{\beta }}_1{\mathrm{m}}_{\mathrm{t}-1}+\left(1-{\mathsf{\beta }}_1\right){\nabla }_{\mathsf{\theta }}\mathrm{J}\left(\mathsf{\theta }\right),$$

(5)

$${\mathrm{v}}_{\mathrm{t}}={\mathsf{\beta }}_2{\mathrm{v}}_{\mathrm{t}-1}+\left(1-{\mathsf{\beta }}_2\right){\left({\nabla }_{\mathsf{\theta }}\mathrm{J}\left(\mathsf{\theta }\right)\right)}^2,$$

(6)

$${\widehat{\mathrm{m}}}_{\mathrm{t}}={\displaystyle \frac{{\mathrm{m}}_{\mathrm{t}}}{1-{\mathsf{\beta }}_1^{\mathrm{t}}}},$$

(7)

$${\widehat{\mathrm{v}}}_{\mathrm{t}}={\displaystyle \frac{{\mathrm{v}}_{\mathrm{t}}}{1-{\mathsf{\beta }}_2^{\mathrm{t}}}},$$

(8)

$${\mathsf{\theta }}_{\mathrm{t}}={\mathsf{\theta }}_{\mathrm{t}-1}-{\displaystyle \frac{\mathsf{\alpha }{\widehat{\mathrm{m}}}_{\mathrm{t}}}{\sqrt{{\widehat{\mathrm{v}}}_{\mathrm{t}}}+\mathsf{ϵ}}},$$

(9)

where ${\mathrm{m}}_{\mathrm{t}}$ and ${\mathrm{v}}_{\mathrm{t}}$ are the momentum term and the gradient square term, respectively, ${\mathsf{\beta }}_1$ and ${\mathsf{\beta }}_2$ are the decay rate, $\mathsf{\alpha }$ is the learning rate, and $\mathsf{ϵ}$ is the small constant that prevents the divide-zero error. The ADAM optimizer has the capacity to automatically adjust the learning rate of each parameter based on the momentum and square gradient of the historical gradient.

In order to enhance the model's generalization capabilities and prevent overfitting, a data augmentation strategy was employed. This is intended to enhance the diversity of the data, thereby enabling the model to more effectively adapt to changes in the market environment. The mean square error was employed as a loss function to quantify the discrepancy between the predicted and true values of the model. The MSE is defined as shown in Equation (10):

$$\mathcal{L}\left(\mathsf{\theta }\right)={\displaystyle \frac{1}{\mathrm{N}}}\sum _{\mathrm{t}=1}^{\mathrm{N}}{\left({\mathrm{y}}_{\mathrm{t}}-{\widehat{\mathrm{y}}}_{\mathrm{t}}\right)}^2,$$

(10)

where the actual value ${\mathrm{y}}_{\mathrm{t}}$ is shown as the predicted value of the model ${\widehat{\mathrm{y}}}_{\mathrm{t}}$, with the sample size $\mathrm{N}$ being the measurement of this value. In order to enhance the efficacy of the loss function, a weighted loss function is also introduced, assigning a greater weight to the prediction error of substantial fluctuations according to the various market fluctuations. The definition of this function is given by Equation (11):

$$\mathcal{L}\left(\mathsf{\theta }\right)={\displaystyle \frac{1}{\mathrm{N}}}\sum _{\mathrm{t}=1}^{\mathrm{N}}{{\mathrm{w}}_{\mathrm{t}}\left({\mathrm{y}}_{\mathrm{t}}-{\widehat{\mathrm{y}}}_{\mathrm{t}}\right)}^2,$$

(11)

where ${\mathrm{w}}_{\mathrm{t}}$ denotes the weight coefficient, which is generally subject to dynamic adjustment in accordance with market fluctuations. To illustrate this point, during periods of market volatility, ${\mathrm{w}}_{\mathrm{t}}$ will undergo an increase, thereby accentuating the influence of the error on the overall forecast accuracy at that particular juncture. The employment of a weighted loss function enables the model to prioritize prediction accuracy during periods of high market volatility, thereby enhancing its adaptability to the intricate dynamics of financial environment.

3.3. External Market Factors and the Moderation Gate

In this study, external market factors such as economic indicators, population dynamics, and migration patterns are integrated into the LSTM network through a mechanism called the moderation gate. This gate adjusts the influence of these external factors on the LSTM model, allowing it to adapt to changing economic conditions and market fluctuations.

3.3.1. Moderation Gate Mechanism

The key function of the moderation gate is to adjust the influence of external factors based on the current market situation. At each time step, the gate evaluates the market conditions and adjusts the weight of the hidden state and input information accordingly. External factors, such as GDP, inflation rates, and demographic shifts, can significantly affect markets like real estate.

By incorporating these external factors, the model becomes more sensitive to market fluctuations. For instance, during periods of economic instability, the gate may increase the weight of external factors, allowing the model to respond more rapidly to changes in the market. On the other hand, during more stable periods, the gate reduces the impact of external factors, allowing the model to rely more on historical trends.

3.3.2. Dynamic Adjustment of Cell State

The moderation gate not only increases the influence of external factors but also dynamically adjusts how the cell state is updated. When the market environment changes, the gate determines how to integrate these changes into the model’s memory. For example, during an economic downturn, external factors such as unemployment rates or consumer confidence may have a greater impact on the model’s predictions. In contrast, during a stable economic period, the model will place more weight on historical data. This dynamic adjustment mechanism ensures that the LSTM model can more accurately capture market changes, improving its predictive accuracy in complex and uncertain market conditions.

3.3.3. Adjustments to the Output Gate

In traditional LSTM networks, the output gate controls how much of the cell state influences the next prediction. However, when external market factors are introduced, the output gate needs to be adjusted as well, in order to properly fuse both internal memory and external inputs. The moderation gate influences the output gate’s weight, ensuring that the model’s predictions reflect both historical information and current market conditions. This adjustment guarantees that the model can adapt its outputs based on the varying market conditions. For example, in a volatile market, the output may give more weight to external factors, while in stable periods, the model will rely more on its historical memory.

4. Experiments

4.1. Experimental Setups

The Zillow Transaction and Assessment Dataset (ZTRAX) was utilized as the sole data source. The ZTRAX dataset, provided by Zillow, is one of the world's largest datasets of real estate transactions, containing detailed U.S.-wide real estate transaction records, appraisal data, property characteristics, and historical changes in home prices. The comprehensive nature of the dataset ensures its relevance to the study of real estate market dynamics across diverse geographical regions, spanning from the late 20th century to the present. This temporal breadth offers a substantial foundation for the investigation of long-term market trends. In order to combine the characteristics of the ageing population, we extracted fields from ZTRAX that are related to the dynamics of the real estate market, including house prices, transaction volumes, house types, construction years, etc., as time series input features.

The model was implemented with a 3-layer LSTM network consisting of 128 units per layer, equipped with dropout regularization (rate of 0.3) to prevent overfitting. We utilized the Adam optimizer with a learning rate of 0.001, applying learning rate decay during training. The loss function was Mean Squared Error (MSE), and weight decay was introduced (1e-5) to penalize large weights. The moderation gate, which dynamically adjusts the influence of external factors (e.g., economic indicators, population trends), was added to capture market shifts effectively. The experiments were run on a high-performance computing setup with an Intel Xeon Gold 6248R CPU (20 cores, 40 threads), NVIDIA Tesla V100 GPU (32 GB memory), and 128 GB RAM, ensuring the capacity to process and analyze large-scale datasets efficiently. The model was developed using TensorFlow 2.0 and Keras, with Pandas and NumPy for data manipulation, and Matplotlib and Seaborn for visualization. These computational resources and frameworks supported the extensive data preprocessing, model training, and evaluation, enabling us to explore the complex dynamics of the real estate market.

4.2. Experimental Analysis

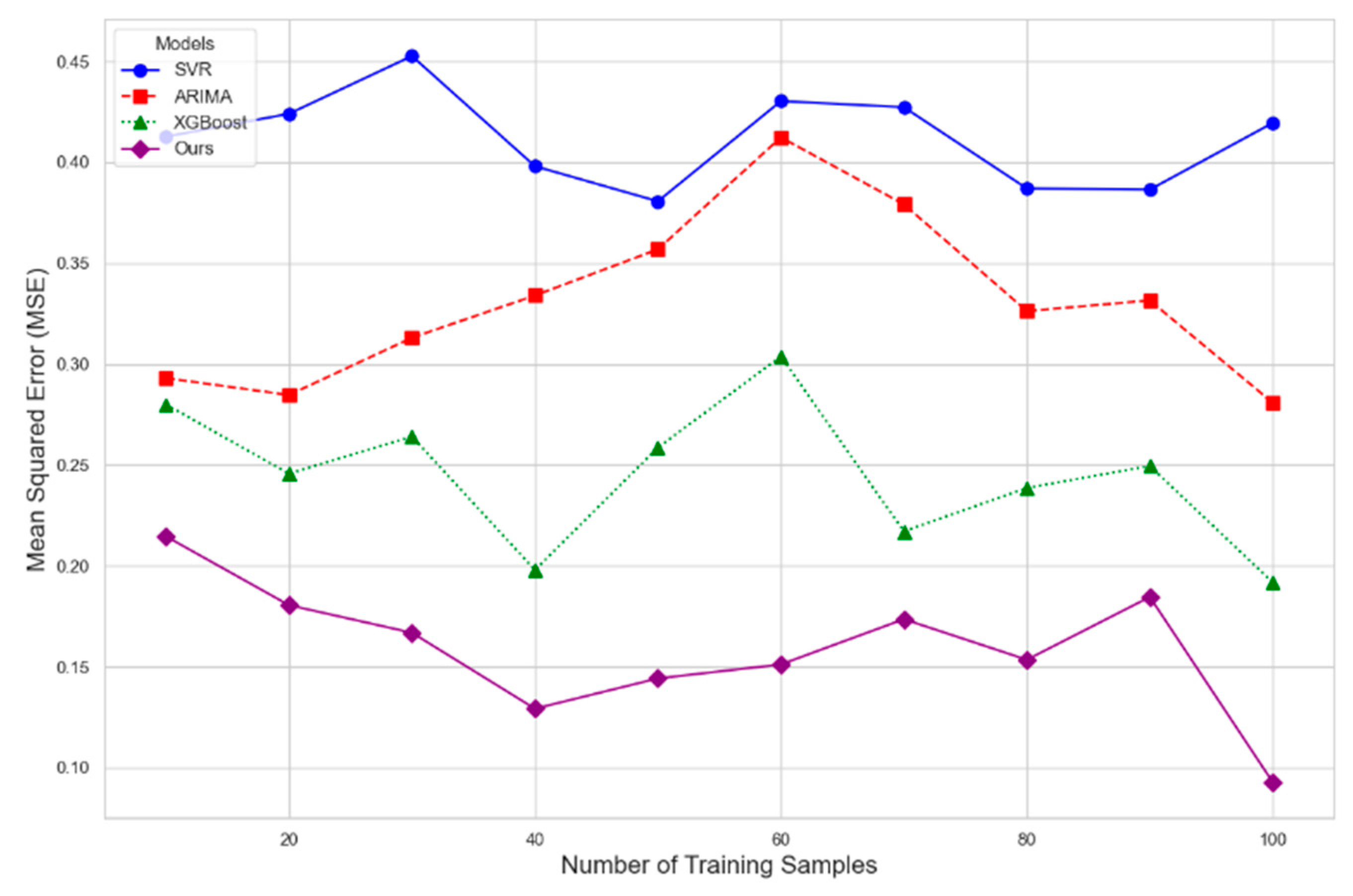
We used a variety of baseline models for comparison, including support vector regression (SVR), autoregressive integral moving average model (ARIMA), and gradient boosting method (XGBoost). The prediction performance of the four models VR, ARIMA, XGBoost, and the improved LSTM model (Ours) was evaluated using the Mean Square Error (MSE). The results presented in Figure 1 demonstrate that the error of SVR and ARIMA diminishes less with an increase in the number of training samples, indicating inherent limitations, particularly in the context of the intricate relationship between population aging and real estate market dynamics. In contrast, XGBoost and our LSTM models demonstrated a superior capacity to adapt to the nonlinear characteristics of the data, resulting in a substantial reduction in error as the sample size increased.

The coefficient of determination (R²) was utilized as an evaluation index to ascertain the fitting effect of various models in the real estate market forecast. The R² value is indicative of the extent to which the model interprets the variability of the data; a value closer to 1 is indicative of a superior fit. In the present experiment, the R² performance of SVR, ARIMA, XGBoost, and our improved LSTM model (Ours) was compared with different training sample counts. As demonstrated in Figure 2, the R² values of SVR and ARIMA exhibited a gradual increase with an increase in the number of training samples. However, this increase was marginal, suggesting their limitations in processing complex data. In contrast, the XGBoost and LSTM models demonstrated a substantial enhancement in performance with an increase in sample size, particularly the LSTM model, which exhibited a sustained increase in R² values.

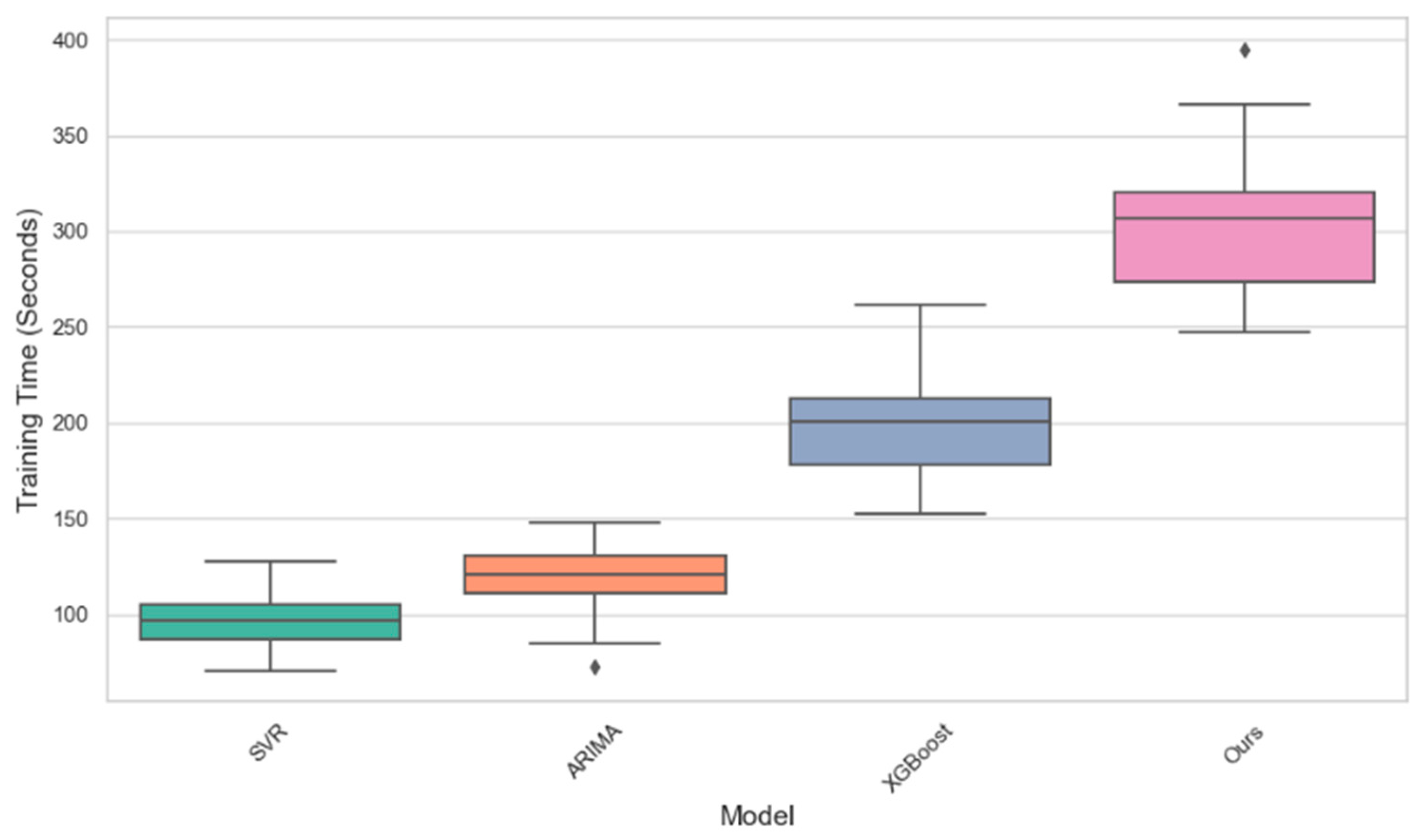
A comparison was made of the time differences between SVR, ARIMA, XGBoost, and our improved LSTM model (Ours) during training by boxplot. The results indicate that the training time for SVR and ARIMA is comparatively brief, with a relatively concentrated distribution of training time as Figure 3. This suggests that these two models are more efficient and better suited to processing smaller-scale datasets. In contrast, the XGBoost model requires a substantially longer training time and exhibits a more dispersed training time distribution, indicating a greater demand for computing resources, particularly during the processing of complex, non-linear data.

To further analyze the robustness of the models, we examined their performance under different market conditions, such as stable periods, market volatility, and economic downturns. This analysis is crucial because real estate markets are often influenced by external economic conditions, and a model that adapts well to such shifts is more useful in real-world applications. We simulated three market conditions based on the historical trends in the ZTRAX dataset: Stable Market, a period with steady price growth and low volatility; Volatile Market, a period of fluctuating prices and transaction volumes due to shifting economic indicators; Economic Downturn, a recessionary period characterized by falling house prices and transaction volumes.

The models were evaluated under each condition, and their performance was compared based on MSE, R², and Training Time. Table 1 summarizes the performance of the four models (SVR, ARIMA, XGBoost, and LSTM) under the different market conditions. The LSTM model consistently outperforms the other models across all market conditions, achieving the lowest MSE and highest R² in stable, volatile, and downturn markets. This demonstrates its superior ability to capture complex, nonlinear relationships and adapt to changing market dynamics. While XGBoost also performs well, especially in volatile conditions, it requires significantly more computational resources and training time compared to the more efficient SVR and ARIMA models. However, these simpler models struggle to handle the complexities of volatile and downturn markets, where their performance is noticeably inferior. Overall, the LSTM model offers the best trade-off between accuracy and model flexibility, though its longer training time may be a consideration in resource-constrained environments.

5. Conclusions

This study highlights the significant impact of aging population distribution on real estate market dynamics, effectively captured by our advanced neural network models, particularly the LSTM. While simpler models like SVR and ARIMA are efficient, they lack the ability to grasp the complex relationships as effectively as the LSTM and XGBoost models. Our findings suggest that as the population ages, the real estate market must adapt to shifting demands in housing types and services, influencing market trends and prices. Future research should focus on enhancing the efficiency and generalizability of these models to better predict and adapt to these demographic and market changes.