1. Introduction
Orthogonal Frequency Division Multiplexing (OFDM) is a widely used modulation technique in optical communication systems due to its high bandwidth efficiency, ability to mitigate narrowband interference and dispersion effects, and its suitability for high data rate transmission. With a cyclic prefix, OFDM can combat both inter-carrier interference (ICI) and inter-symbol interference (ISI) [
1]. When higher-order Quadrature Amplitude Modulation (QAM) is used with OFDM, it improves the link efficiency by allowing for high data rates with a low Bit Error Rate (BER) [
2]. A radio-over-fiber (RoF) system is capable of overcoming the limitations caused by the impairments in the optical domain since it leverages the low-loss transmission properties of optical fiber to transmit the mm-wave signals over long distances with minimal signal degradation [
3]. Moreover, RoF technology has several benefits, including excellent spectral efficiency, fast signaling, and low functional expenses [
4]. The end-to-end communication, in a mm-wave A-RoF system, necessitates the integration of both wireless and optical domain advancements which greatly increase the link distance [
5] in joint optimization of the 5G fronthaul (FH) for end-to-end C-RAN architectures [
6] achieving data rate up to 80 Gbit/s [
7]. The V-band frequency range enables high bandwidth [
8], high-throughput, and cost-efficient solutions for delivering high data rate [
9] communications in optical networks which are made possible by converged mm-waves A-RoF systems. However, chromatic dispersion in the standard single-mode fiber (SSMF) is creating ISI, especially in high-bit-rate systems (≥10 Gbit/s) that use OFDM. While narrowband transmitters can solve dispersion-related issues for data rates up to 2.5 Gbit/s, chromatic dispersion limits the transmission distance in high-data-rate systems [
10]. Therefore, it is necessary in the fiber to prevent deterioration of the output signal due to ISI which could be done either in the optical domain or using equalization techniques in the electrical.
The intensity-modulation and direct-detection (IM-DD) design with external modulators is the most commonly used technique for RoF transmissions [
11,
12]. In [
13] authors demonstrate nonlinear post-equalizers, such as a Volterra series-based equalizer and a neural network-based (NN) equalizer, to combat signal degradation in a 28 GHz mm-wave A-RoF FH link with transmission over a 10 km fiber using an optical single-sideband modulation format. In 64-QAM, both equalizers achieve BER< 3.8 × 10
-3 while, additionally, when the NN equalizer is used after OFDM 16-QAM along with least-square equalization it manages to obtain a better BER.
The proposed solution in [
14,
15] describes an artificial neural network nonlinear equalizer (ANN-NLE) for single-carrier 16-QAM and 64-QAM signals in a 60 GHz RoF communication system and validates the approach to ensure effectiveness in equalizing the signal and improving the transmission performance. Moreover, an experimental demonstration of the 60 GHz RoF system is conducted in utilizing an adaptive activated ANN-NLE to enhance the BER performance and effectively transmit 5 Gbit/s Binary Phase Shift Keying (BPSK) signal across a 10 km fiber while maintaining a forward error correction limit of 10
-3. The authors in [
16] demonstrate the feasibility of transmitting and receiving a 100 Gbit/s data rate link at 28 GHz. The performance of three modulation formats (16-PSK, 16-QAM, and 64-QAM) is tested for optical fiber lengths ranging from 5 km to 35 km using two detection systems: coherent and direct detection with a DSP block implemented in simulation software. In [
17] authors introduce an iterative block (IB) decision feedback equalization (DFE) method for an intensity modulation and direct-detection (IM/DD) based optical code division multiplexing (OCDM) system for a 50 km SSMF link. This method effectively reduces signal degradation caused by chromatic dispersion (CD) in the fiber. In [
18] authors propose an optical phase-locked loop (PLL) technique to generate mm-waves, and a pilot-assisted radio frequency (RF) method is used for phase offset equalization at the receiver side for 16-QAM modulation. In [
19], the authors present and demonstrate a convolutional neural network (CNN) and binary convolutional neural network (BCNN) decision schemes that effectively address both linear and nonlinear impairments resulting from signal modulation, transmission, and detection. The proposed schemes are very computationally efficient and the CNN and BCNN decision methods are showcased in a 5 Gb/s 60 GHz RoF system, covering a fiber reach of up to 20 km.
In [
20] authors propose a Volterra Nonlinear Equalizer (VNLE) for Directly modulated Laser (DML) based IM/DD systems and a simulation of Pulse Amplitude Modulation (PAM-4) signals for high baud rate transmission over 10 km SSFM. In [
21] authors are experimentally transmitting a single channel 112 Gb/s PAM-4 direct detection signal, and a high receiver sensitivity is achieved by the Maximum Likelihood Sequence Estimation (MLSE) algorithm. Moreover, in [
22,
23] the Least Mean Square Algorithm (LMS), Constant Modulus Algorithm (CMA), and Adaptive Median Algorithm (AMF) are implemented for equalization in a converged OFDM 5G mm-wave A-RoF system at 60 GHz. Quadrature Phase Shift keying (QPSK) and 16-QAM are used as modulation formats in the OFDM subcarriers. The maximum achieved transmission distance is 100 km after the equalization when QPSK is used while a transmission distance of 50 km is achieved after equalization for the 16-QAM case.
Table 1 delineates the various techniques examined in the literature review to address ISI and nonlinearities in converged mm-wave OFDM A-RoF systems, along with some notes related to their advantages and disadvantages. In addition,
Table 2 elaborates and compares specific parameters employed in the literature review articles.
To that end in the present paper, we propose two new algorithms, i.e., the Decision Feedback Equalizer (DFE) and the Maximum Likelihood Detection (MLD) for equalization in a converged OFDM 5G mm-wave A-RoF system at 60 GHz. The modulation schemes being used in this system are QPSK, 16-QAM, 64-QAM, and 128-QAM in all the OFDM subcarriers. The proposed algorithms are developed in MATLAB [
33] to equalize the distorted subcarriers. In this work, we use an SSMF of length up to 120 km since DFE and MLD are more adept at managing fiber distortions and noise. DFE effectively mitigates inter-symbol interference (ISI) by leveraging past decisions, rendering it particularly beneficial in dispersive SSMF channels. Meanwhile, MLD offers a near-optimal performance by evaluating all potential signal sequences and selecting the one that maximizes the probability of accurate detection, resulting in enhanced transmission distance relative to other known algorithms such as LMS and CMA.
The rest of the paper is organized as follows:
Section 2 briefly provides the simulation setup for a converged mm-wave A-RoF system at 60 GHz for testing the algorithms.
Section 3 provides the details of the different equalization algorithms used. Subsequently, section 4 compares the DFE and MLD algorithms about the modulation formats along the maximum fiber lengths achieved while section 5 provides details of the assessment of the proposed work against different well-known equalization algorithms. The relationship between RF input power and EVM for QPSK, 16-QAM, and 64-QAM modulation formats is considered in section 6 and section 7 presents the conclusions.
2. Simulation Setup
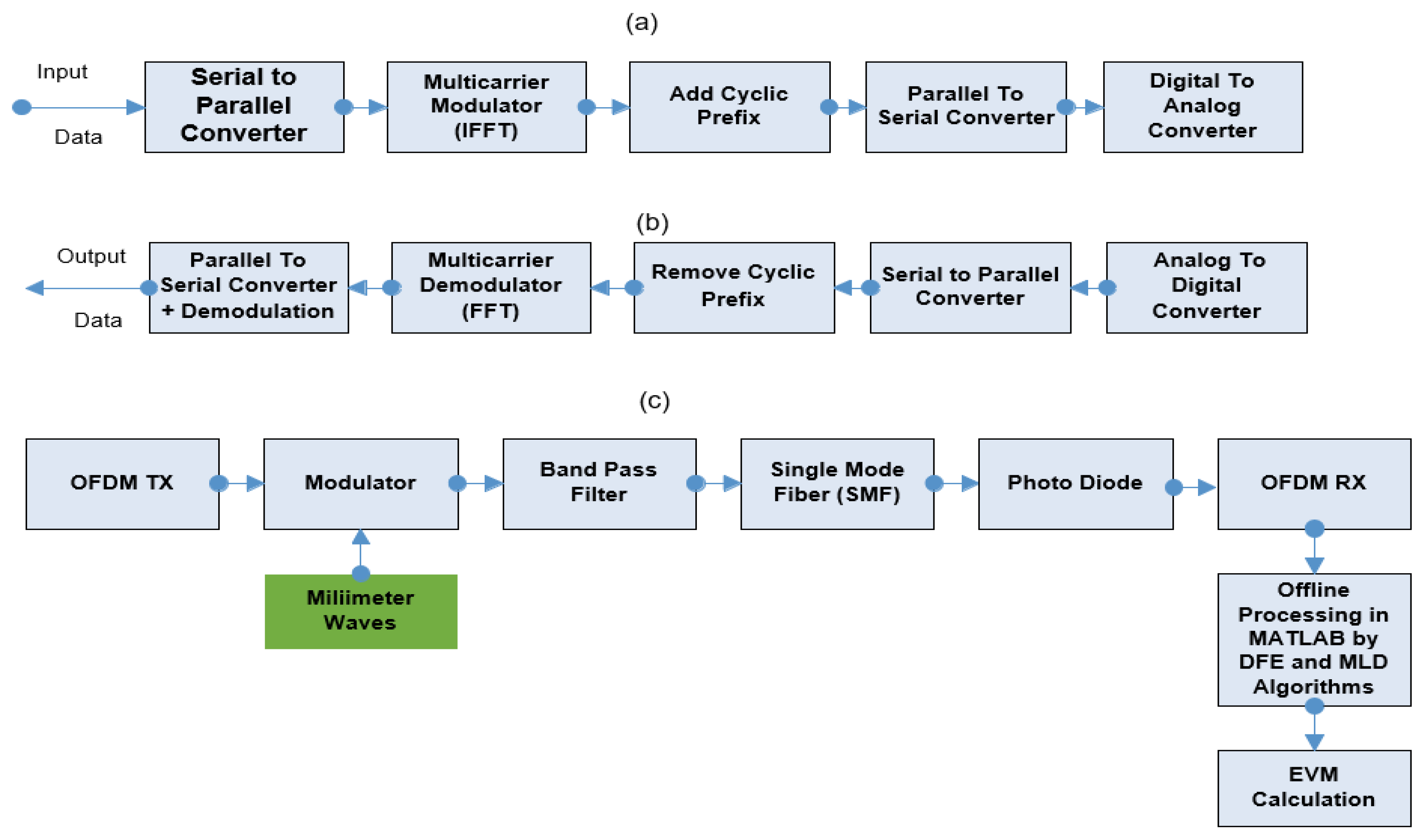
Figure 1 describes in block diagrams an (a) OFDM Tx, (b) OFDM Rx, and (c) a complete simulated setup of a converged 5G mm-wave A-RoF system at 60 GHz designed in VPI Photonics design suite [
32] and used to test the algorithms. The OFDM Tx depicted in
Figure 1a comprises a Pseudo Random Binary Sequence (PRBS) block that generates data at a rate relying upon the modulation level and the applied bitrate. The digital binary bits are distributed into data streams, and each stream is subsequently encoded using 4-QAM, 16-QAM, 64-QAM, or 128-QAM as modulation formats. The modulated data stream is converted from serial to parallel form, creating multiple parallel data streams. This procedure allows the data to be transmitted simultaneously on various subcarriers.
Next the Inverse Fast Fourier transform (IFFT) is performed transforming a complex frequency domain signal into a time domain signal which is then used to modulate the signal onto orthogonal subcarriers in the digital domain. A cyclic prefix (CP), introducing a guard time interval between symbols, is used to minimize inter-symbol interference (ISI). The parallel data streams are converted back to serial, and the output signal through a digital-to-analog converter (DAC) is transformed to an analog signal. Using a Mach-Zehnder modulator (MZM) the signal is modulated while an optical bandpass filter can be used to suppress the amplified spontaneous emission (ASE) noise. The produced 60 GHz mm-wave analog signal [
22,
23] is transmitted through a SSMF of different lengths with a 16 ps/nm/km dispersion while a photodiode is utilized to capture the optical signal, which is then converted into electrical and fed into an OFDM receiver for subcarrier recovery as shown in
Figure 1c. The electrical signal undergoes down-conversion to a baseband signal, followed by pulse shaping and an OFDM decoder as shown in
Figure 1b. The distorted electrical symbols from the OFDM constellations are captured and subsequently equalized in MATLAB using the DFE and MLD, algorithms.
Table 3 provides a summary of the simulation parameters used in this work.
3. Proposed Equalization Algorithms
3.1. Decision Feedback Equalizer
A Decision-Feedback Equalizer (DFE) is an algorithm that offers superior performance compared to a linear equalizer while maintaining the same low complexity. It is particularly beneficial when addressing significant channel distortion. The DFE structure consists of a feedforward and a feedback filter. The feedforward filter processes the current received symbols passing through the decision function. The current received symbols are then refined passing through the feedback filter which utilizes previously identified symbols that ideally have minimal, or no noise allowing for precise estimation and cancellation of ISI without enhancing the noise, provided that the previous decisions are correct. If the decisions are incorrect, the error propagates to the next decisions. One notable advantage of the DFE over linear equalizers is its ability to remove ISI without enhancing noise while a linear equalizer handles noise and signal equally, which might result in the amplification of noise [
24,
25,
26]. The following equation describes the DFE [
27]:
(1)
t(n)= f{y(n)} (2)
e(n)= y(n)-t(n) (3)
where y[n]: The equalized output signal of the nth symbol.
x[n-k]: The equalizer input sequence.
: The coefficients for the feedforward filter.
: The coefficients for the feedback filter.
: The order length of the feedforward filter.
: The order length of the feedback filter.
]: The previously detected symbols.
t(n): The equalizer decision sequence.
f{n}: Decision device function.
e(n): The error signal.
3.2. Maximum Likelihood Sequence Detection Algorithm
Maximum Likelihood Detection (MLD) is a widely recognized and highly effective approach suitable for practical applications and offers optimal detection performance. The idea is essential in signal processing, especially when identifying and interpreting symbols despite interference from noise and distortions. MLD is founded on the fundamental concept of statistical inference. It utilizes the likelihood function of detecting the received symbol based on a given set of potentially transmitted symbols. The objective is to optimize this likelihood to ascertain the most probable transmitted symbol [
28,
29,
30]. However, the main drawback of the MLD algorithm is that it needs accurate information on the potential transmitted symbols to compute the likelihood of each possible transmitted symbol. If the potential transmitted symbol is not accurate, the performance of the MLD may deteriorate dramatically, potentially leading to erroneous decisions and detection errors.
The Maximum Likelihood Detection (MLD) algorithm seeks to identify the transmitted symbol ‘s’ with the highest likelihood of receiving a given symbol ‘r’ in the presence of noise. The mathematical formula for MLD can be stated as [
31]:
(4)
where is the transmitted symbol.
r is the received signal vector.
s S is a transmitted symbol from the set of all transmitted symbols S.
H is the channel matrix, representing the effects of the transmission channel on the symbol.
.2 represents the squared Euclidean distance.
4. Comparisons of Results for DFE and MLD
The received signal, of the used setup shown in
Figure 1, is processed offline using the two proposed equalization algorithms and applying different modulation formats in the OFDM subcarriers in order to minimize the ISI caused by the dispersive transmission.
4.1. Equalization by Maximum Likelihood Detection (MLD) Algorithm
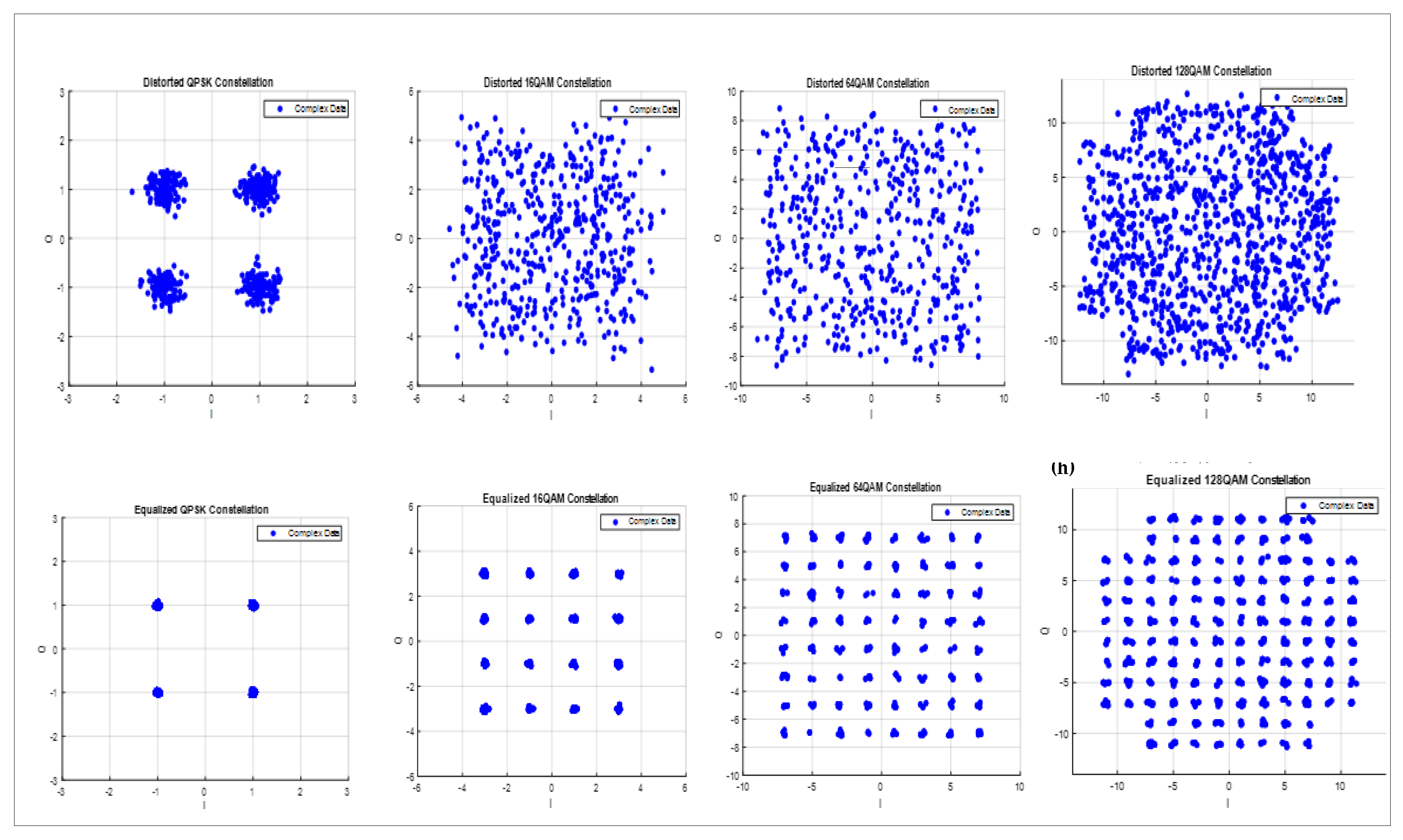
The MLD algorithm is applied to the distorted received data after the photodiode in the OFDM analyzer. The distorted OFDM subcarrier signals with the QPSK, 16-QAM, 64-QAM, and 128-QAM modulation formats result in the constellation diagram and EVM calculations that are shown in
Figure 2 before (2a, 2b, 2c, and 2d) and after equalization (2e, 2f, 2g, 2h) for the respected modulation formats and at the maximum attained fiber lengths for each case.
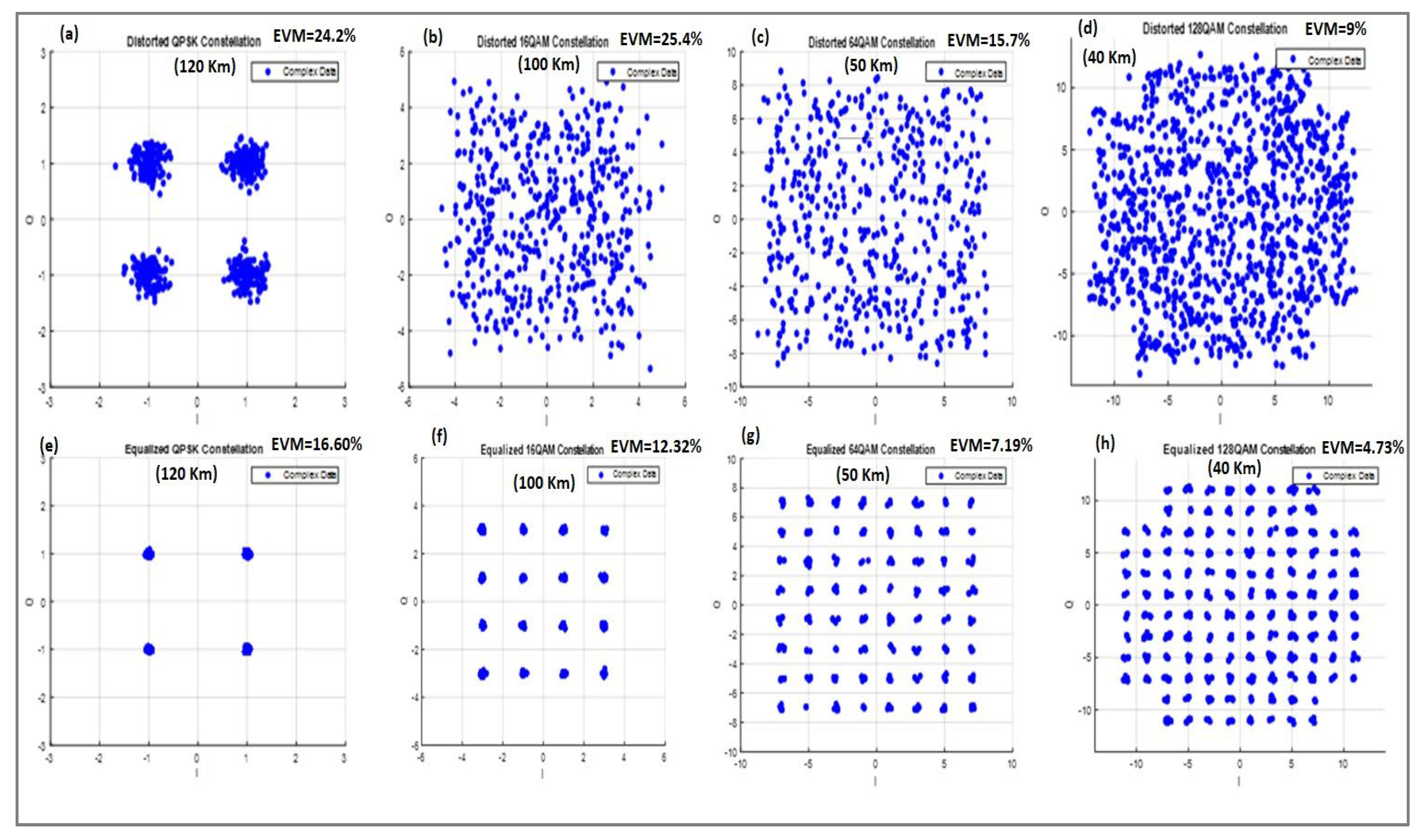
Maintaining the performance criteria of modern communication systems across different modulation schemes requires keeping the Error Vector Magnitude (EVM) of the received signal below the 3GPP proposed thresholds ensuring the quality and reliability of the signal, particularly as the complexity of the modulation format increases. The implementation of the proposed Maximum Likelihood Detection (MLD) algorithm is tested across different fiber lengths. For QPSK modulation on OFDM subcarriers, an EVM of 17.06% is achieved after equalization at a maximum fiber length of 120 km. When using 16-QAM modulation, the fiber length is reduced to 100 km, and an EVM of 12.40% after equalization. For higher-order modulations, such as 64-QAM and 128-QAM, the fiber lengths are 50 km and 40 km, respectively, to maintain compliance with the 3GPP threshold limits and EVM values of 7.35% for 64-QAM and 4.85% for 128-QAM are obtained.
All equalized EVM values successfully meet the stringent 3GPP threshold limits (17.5% for QPSK, 12.5% for 16-QAM, 8% for 64-QAM, and 5% for 128-QAM), demonstrating the effectiveness of the proposed MLD in maintaining signal integrity across various modulation formats and fiber lengths.
4.2. Equalization by Decision Feedback Equalizer
The DFE equalization is performed on the distorted data obtained at the OFDM receiver.
Figure 3 shows the constellation diagrams of QPSK, 16-QAM, 64-QAM, and 128-QAM obtained before and after the equalization at the maximum fiber length that can be achieved before (3a, 3b, 3c, and 3d) and after equalizing (3e, 3f, 3g, 3h) for the respected modulation formats. After equalization, the EVM of the equalized constellations is computed.
The proposed Decision Feedback Equalizer’s (DFE) performance is evaluated over various fiber lengths. For QPSK modulation in OFDM subcarriers, with a maximum fiber length of 120 km, an EVM of 16.60% is achieved while for 16-QAM modulation, at a maximum fiber length of 100 km, the EVM is 12.32% after equalization. In the cases of 64-QAM and 128-QAM modulations, EVMs of 7.19% and 4.73% are achieved for fiber lengths of 50 km and 40 km, respectively. Notably, all the equalized EVM values are below the 3GPP threshold.
Table 4 presents a comparison of MLD and DFE algorithms in terms of EVM for different modulation formats, respectively, presenting a slight superior performance of the DFE algorithm in mitigating ISI effects over different modulation schemes and fiber lengths in all cases.
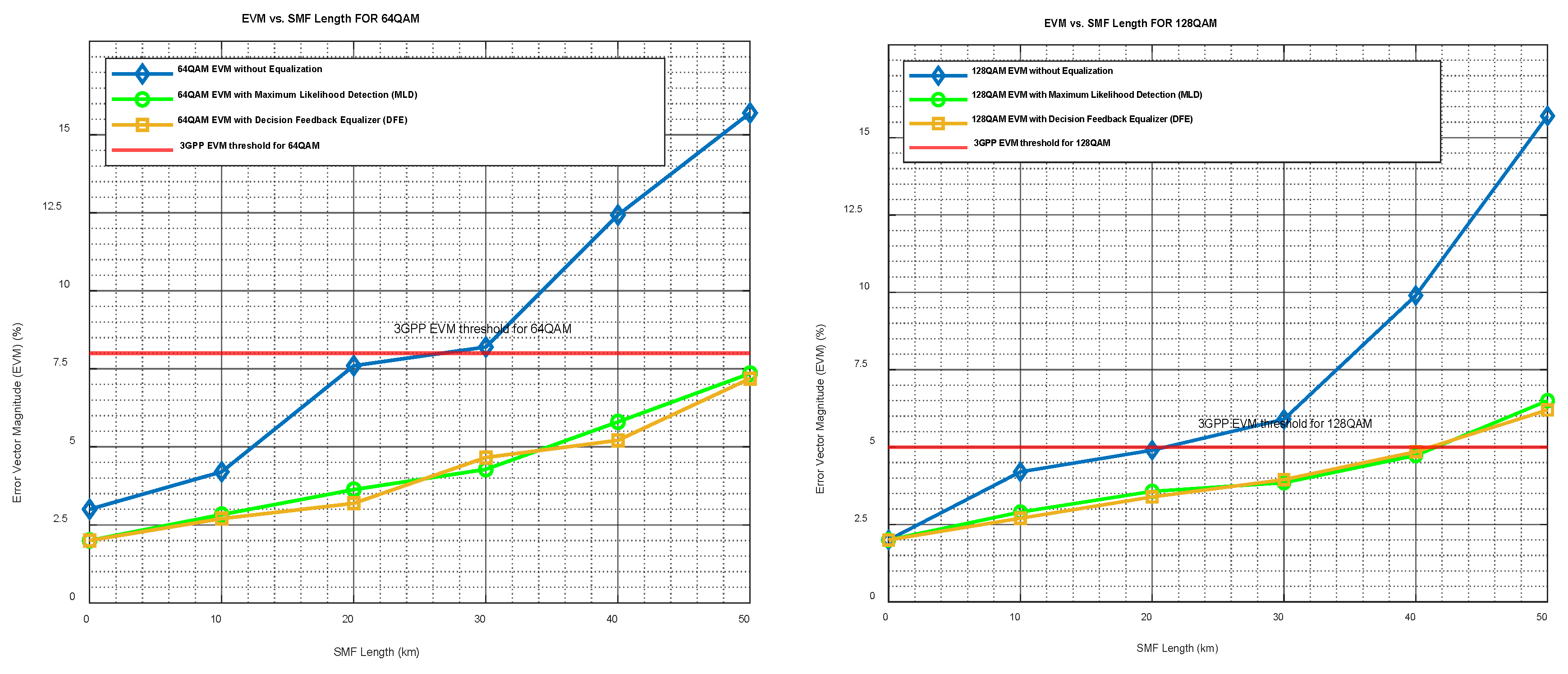
Figure 4 illustrates the EVM performance as a function of fiber length for both QPSK and 16-QAM modulation schemes. These results demonstrate the efficacy of both MLD and DFE techniques in compensating ISI within a converged mm-wave A-RoF system operating at 60 GHz. A comparative analysis of these two equalization algorithms reveals that the DFE slightly outperforms the MLD as shown in
Table 4.
Figure 5 presents the EVM results versus the fiber length both for 64-QAM and 128-QAM. A comparative analysis of these two equalization algorithms reveals that the DFE slightly outperforms the MLD as shown in
Table 4.
Moreover, when we compare the two algorithms in terms of computational complexity the DFE is performing better than the MLD because the latter assesses all potentially transmitted symbol sequences to identify the one that optimizes the likelihood of generating the observed received sequence and MLD’s complexity increases exponentially with the size of the signal constellation and the number of symbols in the sequence [
30], rendering it less efficient for systems with high modulation orders.
5. Assessment of Algorithms Against Prior Research Results
The performance of the proposed DFE and MLD algorithms is compared against the Least Mean Square (LMS) [
35] algorithm, the Constant Modulus Algorithm (CMA) [
34,
36,
37], and the Adaptive Median Filtering (AMF) [
38] algorithm, as reported in our previously published work [
21,
22]. Although the LMS is simpler and more efficient for linear channels, it is inadequate for severely dispersive channels. At the same time, AMF mainly intended for reducing noise, is less appropriate for equalization tasks in high-frequency, high-data-rate situations.
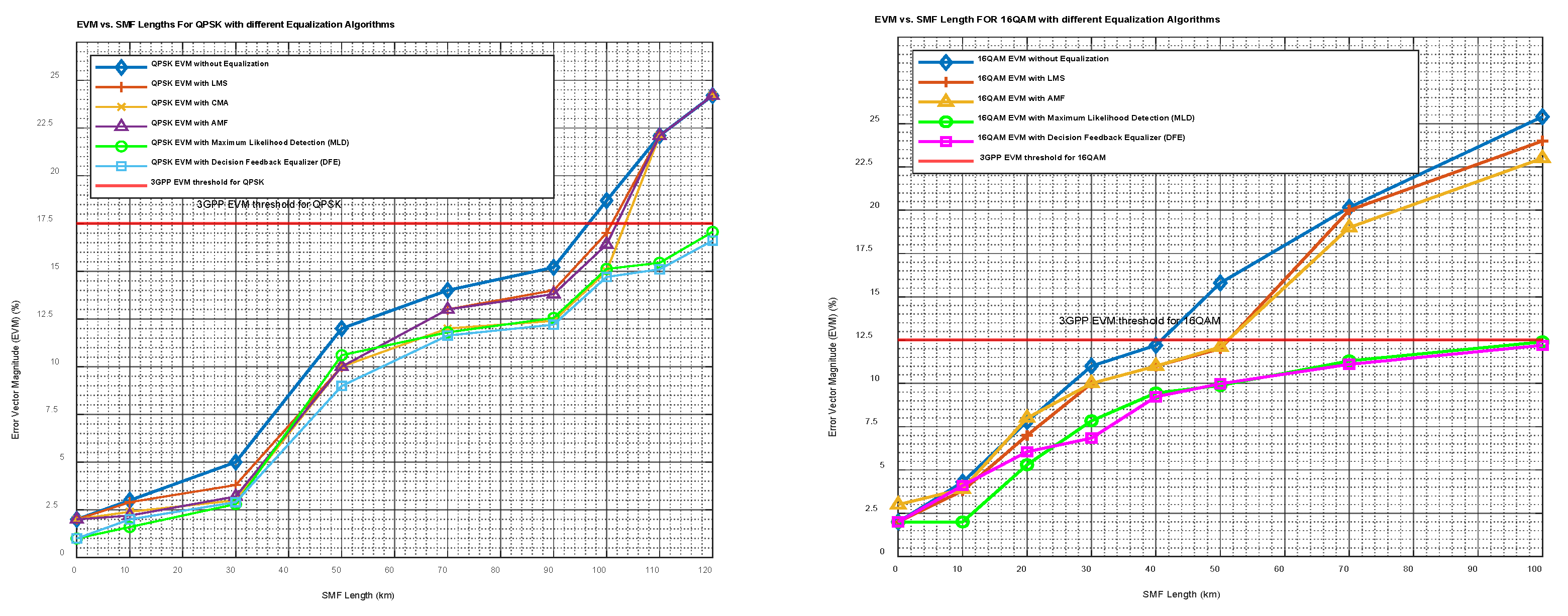
For QPSK modulation across all OFDM subcarriers, specifically, when comparing MLD and DFE with LMS, CMA, and AMF, for an SSMF of length 120 Km as shown in
Table 5 and
Figure 6 the LMS, CMA, and AMF algorithms do not provide an EVM value for QPSK, indicating that they failed to perform effectively under the given conditions or configuration. This suggests that LMS, CMA, and AMF may struggle to adapt to QPSK modulation over long fiber distances, making it unsuitable for this particular setup.
For QPSK, the MLD algorithm achieves an EVM of 17.06% over a fiber length of 120 km while the DFE algorithm slightly outperforms MLD in terms of EVM, with a value of 16.6%. However, both MLD and DFE can handle fiber lengths up to 120 km, indicating that both algorithms can maintain signal quality over similar transmission distances. The small improvement in EVM for DFE suggests that this algorithm may be better suited for compensating distortion in the dispersive channel compared to the MLD.
For 16-QAM modulation, the implementation of MLD and DFE algorithms allows for an extended transmission distance of up to 50 km beyond what is achievable with LMS and AMF algorithms, while maintaining EVM values below the 3GPP threshold, as shown in
Figure 6.
Specifically, when comparing MLD with LMS and AMF after equalization for 16-QAM modulation, as shown in
Table 5 and
Figure 6 MLD achieves an EVM improvement of 11.35% over LMS and a 10.60% improvement over AMF at a fixed fiber length of 100 km. The CMA algorithm is not employed in this scenario due to its limitations with multiple radii in the constellation points, rendering it ineffective for 16-QAM modulation [
39].
Further analysis reveals that DFE slightly outperforms MLD and outperforms LMS and AMF for 16-QAM modulation in OFDM subcarriers, demonstrating an EVM improvement of 0.80% over MLD, 11.43% over LMS, and 10.68% over AMF for the same fixed fiber length of 100 km. For 16-QAM modulation over a transmission distance of 50 km, a comparative analysis reveals significant improvements in EVM when using MLD and DFE algorithms.
These findings highlight the superior performance of MLD and DFE algorithms not only in improving signal quality (EVM for QPSK and 16-QAM) but also in extending the transmission distance and demonstrating robustness and effectiveness in high-performance optical communication systems. Moreover, when higher-order modulation schemes, such as 64-QAM and 128-QAM, are used for equalization approaches like LMS, CMA, and AMF, they do not give meaningful results. At the same time, the proposed MLD and DFE algorithms demonstrate their effectiveness in managing the challenges posed by higher modulation formats and dispersion in optical fibers preserving signal quality and meeting the 3GPP EVM threshold limits.
6. Relationship Between RF Input Power and EVM for Different Modulation Formats
The correlation between RF input power and EVM is crucial in optical communications, as it impacts signal quality, system performance, and overall efficiency. Increasing the RF input power can enhance the quality of the signal until a certain threshold, beyond which high power might cause non-linearities.
In general, in scenarios in which the power levels are low, the signal may be weak and susceptible to noise, which can result in high EVM values. The signal-to-noise ratio (SNR) can be improved by increasing the input power, which can first increase the signal quality by overcoming noise and improving the output signal, leading to reduced EVM values, and improvement in the demodulation performance.
Various modulation schemes have varied criteria for the quality of the signal and the required power level. Understanding the relationship between RF input power and EVM can help optimize the power levels and achieve the desired signal quality without consuming any additional power. Examining EVM across various RF input power levels can help determine the performance limits of every modulation scheme.
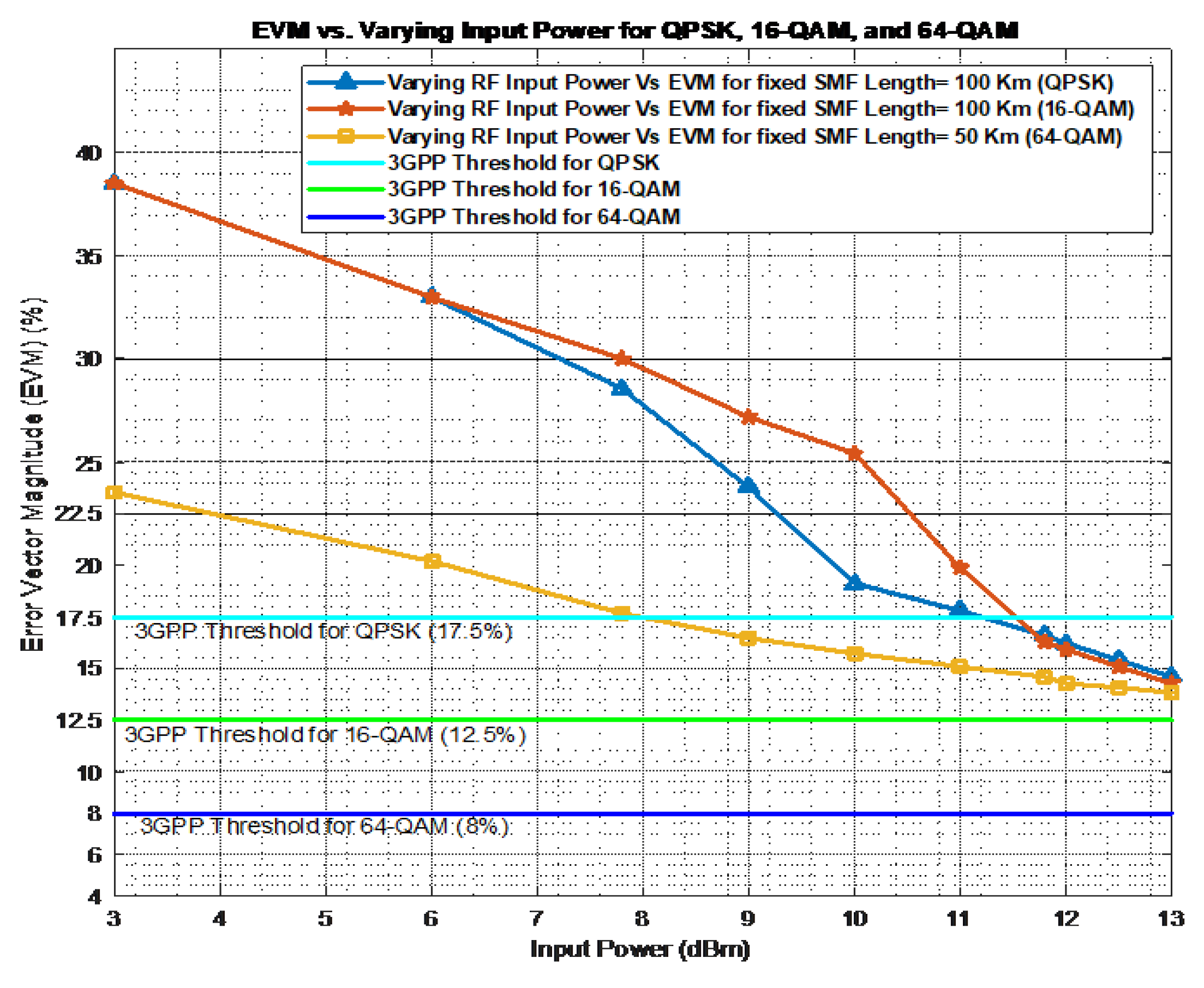
Figure 7 presents the EVM performance as a function of RF input power for the different modulation formats and the relevant maximum fiber lengths. For QPSK (100 km) the EVM is high at lower RF input power levels (3 dBm to 9 dBm), and the same applies for 16-QAM and 64-QAM. This indicates poor signal quality, due to significant effect of ISI and noise that are not adequately compensated. For RF input power levels from 9 to 11 dBm, there is a substantial decrease in EVM which suggests that increasing power helps to improve signal quality by overcoming to some extent the impairments. Beyond 11 dBm further increases in RF input power continue to reduce EVM, but at a slower rate indicating marginal benefits. Also, the EVM, in all cases, does not fall below the corresponding 3GPP thresholds except QPSK which at 11,5 dBm input power is just below the threshold.
On the contrary
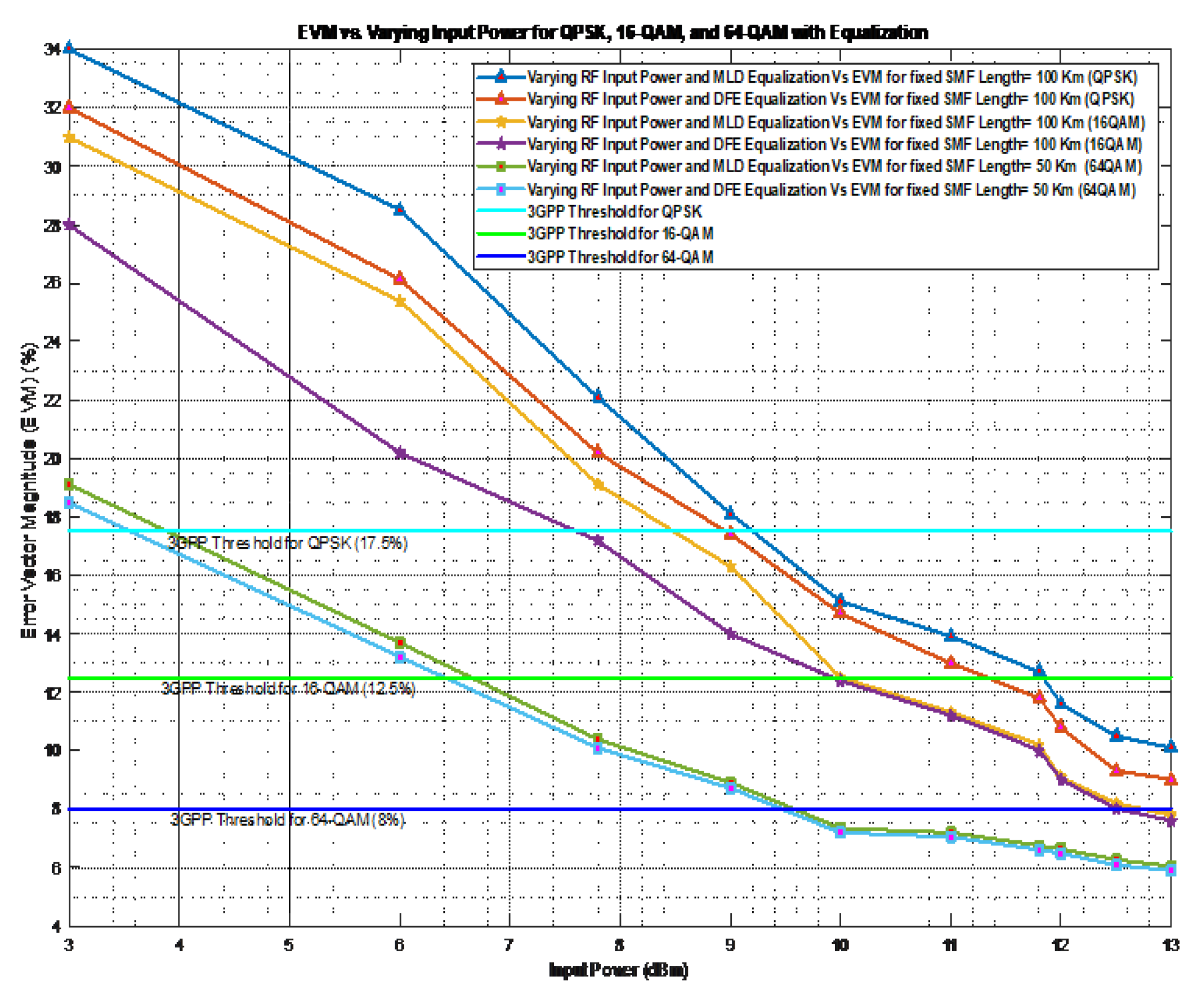
Figure 8, presents the EVM performance as a function of RF input power after equalization for the different modulation formats indicating that although the trend of the curves is similar as above the system can perform efficiently with less input power, for example for QPSK and 100 km fiber length when the DFE algorithm is used a 9 dBm input is sufficient while in the case of MLD a corresponding value is 9.5 dBm.
Within this scenario, the significance of equalization algorithms is of utmost importance since it is obvious from
Figure 8 that the signal in higher modulation formats such as 16-QAM, 64-QAM, or 128-QAM can only reach the corresponding 3GPP thresholds with equalization. The proposed algorithms, Maximum Likelihood Detection (MLD) and Decision Feedback Equalizer (DFE), are specifically developed to more efficiently reduce the impact of ISI and noise. By implementing these techniques, it is feasible to attain reduced EVM values and enhanced signal quality which is crucial for maximizing the performance in optical communication systems.
7. Conclusions
The DFE and MLD algorithms are implemented in MATLAB to eliminate the ISI in a dispersive channel in an SSMF, which degrades the system performance. A converged 5G mm-wave A-RoF system at 60 GHz is used as an example to test the two equalization algorithms. When assessing these two algorithms in the case of QPSK, 16-QAM, 64-QAM, and 128-QAM as a modulation format in OFDM subcarriers, the DFE algorithm performs slightly better than the MLD with an EVM improvement of 0.46%, 0.08%, 0.16%, and 0.12% respectively.
The proposed MLD and DFE algorithms, in comparison to the three most popular equalization algorithms LMS, CMA, and AMF, achieved better EVM values, and a fiber length that can extend up to 120 km. Moreover, algorithms such as LMS, CMA, and AMF fail miserably when applied to higher-order QAM constellations such as 64-QAM and 128-QAM while DFE and MLD allows us to reach EVMs of 7.19% and 7.35% for 64-QAM and 50 km SSMF distances, respectively, and 4.73% and 4.85% for 128-QAM and 40 km SSMF distances, respectively.
Finally, it is proven that if the equalization algorithms are used there is no need to increase the input power in order to achieve EVM values below the corresponding 3GPP thresholds, especially in higher modulation formats.
Author Contributions
Conceptualization, U.F. and A.M.; methodology, U.F.; software, U.F.; validation, U.F., A.M.; formal analysis, U.F.; investigation, U.F.; resources, A.M.; data curation, U.F.; writing—original draft preparation, U.F.; writing—review and editing, A.M.; visualization, U.F.; supervision, A.M.; project administration, A.M.; funding acquisition, A.M. All authors have read and agreed to the published version of the manuscript.
Funding
The work presented in this article was carried out within the 5G STEP FWD Innovative Training Network, which has received funding from the European Union’s Horizon 2020 Research and Innovation Programme 2018–2021 under the Marie Skłodowska-Curie Action grant agreement No.722429.
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
Not Applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gigabit-Capable Passive Optical Networks (NG-PON2): General Requirements,” ITU-T Recommendation G.989.1, 2013.
- Singya, Praveen Kumar, Parvez Shaik, Nagendra Kumar, Vimal Bhatia, and Mohamed-Slim Alouini. “A survey on higher-order QAM constellations: Technical challenges, recent advances, and future trends.” IEEE Open Journal of the Communications Society 2 (2021): 617-655.
- Mohamed, Abd El–Naser A., Ahmed Nabih Zaki Rashed, and Mohamed SF Tabbour. “Transmission characteristics of radio over fiber (ROF) millimeter wave systems in local area optical communication networks.” International Journal of Advanced Networks and Applications 2, no. 6 (2011): 876-886.
- Kumar, P.; Sharma, S.K.; Singla, S.; Gupta, V.; Sharma, A. A review on mmWave based energy efficient RoF system for next generation mobile communication and broadband systems. J. Opt. Commun. 2021, 45, 303–318. [Google Scholar] [CrossRef]
- Ali, Sevan H., and Raghad Zuhair Yousif Al-Maqdici. “Improving the performance of cost-effective millimeter wave-based front-haul RoF system for up to 140 km link length using pre-distortion device and FBG technique.” Soft Computing (2023): 1-16.
- Vagionas C, Ruggeri E, Kalfas G, Sirbu B, Leiba Y, Kanta K, Giannoulis G, Caillaud C, Cerulo G, Mallecot F, Raddo TR. An end-to-end 5G fiber wireless A-RoF/IFoF link based on a 60 GHz beam-steering antenna and an InP EML. InBroadband Access Communication Technologies XIV 2020 Jan 31 (Vol. 11307, pp. 63-68). SPIE.
- Dat, P.T.; Kanno, A.; Inagaki, K.; Rottenberg, F.; Louveaux, J.; Yamamoto, N.; Kawanishi, T. High-Speed Radio-on-Free-Space Optical Mobile Fronthaul System for Ultra-Dense Radio Access Network. Optical Fiber Communication Conference. LOCATION OF CONFERENCE, United StatesDATE OF CONFERENCE; p. W2A.37.
- Fatah, S.Y.A.; Hamad, E.K.I.K.I.; Swelam, W.; Allam, A.M.M.A.; Sree, M.F.A.; Mohamed, H.A. Design and Implementation of UWB Slot-Loaded Printed Antenna for Microwave and Millimeter Wave Applications. IEEE Access 2021, 9, 29555–29564. [Google Scholar] [CrossRef]
- Ishimura, S.; Bekkali, A.; Tanaka, K.; Nishimura, K.; Suzuki, M. 1.032-Tb/s CPRI-Equivalent Rate IF-Over-Fiber Transmission Using a Parallel IM/PM Transmitter for High-Capacity Mobile Fronthaul Links. J. Light. Technol. 2017, 36, 1478–1484. [Google Scholar] [CrossRef]
- Yu, H.; Doylend, J.; Lin, W.; Nguyen, K.; Liu, W.; Gold, D.; Dahal, A.; Jan, C.; Herrick, R.; Ghiurcan, G.A.; et al. 100Gbps CWDM4 Silicon Photonics Transmitter for 5G applications. Optical Fiber Communication Conference. LOCATION OF CONFERENCE, United StatesDATE OF CONFERENCE; p. W3E.4.
- Lim, C.; Tian, Y.; Ranaweera, C.; Nirmalathas, T.A.; Wong, E.; Lee, K.-L. Evolution of Radio-Over-Fiber Technology. J. Light. Technol. 2018, 37, 1647–1656. [Google Scholar] [CrossRef]
- Dat, P.T.; Kanno, A.; Inagaki, K.; Kawanishi, T. High-Capacity Wireless Backhaul Network Using Seamless Convergence of Radio-over-Fiber and 90-GHz Millimeter-Wave. J. Light. Technol. 2014, 32, 3910–3923. [Google Scholar] [CrossRef]
- Song, T.; Lim, C.; Nirmalathas, A. Performance Analysis of a 28 GHz Wideband Analog Radio-Over-Fiber Fronthaul With Channel Nonlinearity Compensation. J. Light. Technol. 2024, 42, 7588–7595. [Google Scholar] [CrossRef]
- Liu, S.; Xu, M.; Wang, J.; Lu, F.; Zhang, W.; Tian, H.; Chang, G.-K. A Multilevel Artificial Neural Network Nonlinear Equalizer for Millimeter-Wave Mobile Fronthaul Systems. J. Light. Technol. 2017, 35, 4406–4417. [Google Scholar] [CrossRef]
- Liu, S.; Wang, X.; Zhang, W.; Shen, G.; Tian, H. An Adaptive Activated ANN Equalizer Applied in Millimeter-Wave RoF Transmission System. IEEE Photon- Technol. Lett. 2017, 29, 1935–1938. [Google Scholar] [CrossRef]
- Gadze, J.D.; Akwafo, R.; Agyekum, K.A.-P.; Opare, K.A.-B. A 100 Gbps OFDM-Based 28 GHz Millimeter-Wave Radio over Fiber Fronthaul System for 5G. Optics 2021, 2, 70–86. [Google Scholar] [CrossRef]
- Ouyang, X.; Talli, G.; Power, M.; Townsend, P.D. Iterative Block Decision Feedback Equalization for IM/DD-Based OCDM to Compensate Chromatic-Dispersion-Induced Power Fading. J. Light. Technol. 2019, 37, 4349–4358. [Google Scholar] [CrossRef]
- Dodane, D.; Santacruz, J.P.; Bourderionnet, J.; Rommel, S.; Feugnet, G.; Jurado-Navas, A.; Vivien, L.; Monroy, I.T. Optical phase-locked loop phase noise in 5G mm-wave OFDM ARoF systems. Opt. Commun. 2022, 526. [Google Scholar] [CrossRef]
- Lee, Jeonghun, Jiayuan He, Yitong Wang, Chengwei Fang, and Ke Wang. “Experimental demonstration of millimeter-wave radio-over-fiber system with convolutional neural network (CNN) and binary convolutional neural network (BCNN). arXiv:2001.02018 (2020).
- Liu, T.; Wang, Y.; Zhou, J. Using Volterra Nonlinear Equalizer and Probabilistic Shaping in an IM/DD System. 2021 Photonics & Electromagnetics Research Symposium (PIERS). LOCATION OF CONFERENCE, ChinaDATE OF CONFERENCE; pp. 1209–1214.
- ,Zhang, J. L., et al. “Direct detection of a single-channel 112 Gb/s PAM-4 signal using an 18 GHz directly modulated laser and Maximum-Likelihood Sequence Estimation (MLSE) equalization.” Frontier Research and Innovation in Optoelectronics Technology and Industry. CRC Press, 2018. 385-391.
- Farooq, U.; Miliou, A. Channel Equalization for converged OFDM-Based 5G mm-wave A-RoF System at 60 GHz. 2021 IEEE 11th Annual Computing and Communication Workshop and Conference (CCWC). LOCATION OF CONFERENCE, United StatesDATE OF CONFERENCE; pp. 1263–1267.
- Farooq, Umar, and Amalia Miliou. “Assessment of different channel equalization algorithms for a converged OFDM-based 5G mm-wave A-RoF system at 60 GHz.” Applied Sciences 12, no. 3 (2022): 1511.
- Barry, J. “Equalization.” In Academic Press Library in Mobile and Wireless Communications, pp. 283-331. Academic Press, 2016.
- Pulford, Graham W. Developments in non-linear equalization. Australian National University, 1992.
- Chu, X.; Wang, W.; Wang, J.; Wu, F.; Luo, Y.; Guo, W.; Li, N.; Li, Y. A Novel Decision Feedback Equalization Structure for Nonlinear High-Speed Links. IEEE Access 2020, 8, 59135–59144. [Google Scholar] [CrossRef]
- Rontogiannis, A.; Berberidis, K. Efficient decision feedback equalization for sparse wireless channels. IEEE Trans. Wirel. Commun. 2003, 2, 570–581. [Google Scholar] [CrossRef]
- Su, Karen. “Efficient maximum likelihood detection for communication over multiple input multiple output channels.” Department of Engineering, University of Cambridge (2005).
- Xu, H. Simplified maximum likelihood-based detection schemes for M-ary quadrature amplitude modulation spatial modulation. IET Commun. 2012, 6, 1356–1363. [Google Scholar] [CrossRef]
- Rupp, M.; Gritsh, G.; Weinrichter, H. Approximate ML detection for MIMO systems with very low complexity. 2004 IEEE International Conference on Acoustics, Speech, and Signal Processing. LOCATION OF CONFERENCE, CanadaDATE OF CONFERENCE; pp. 809–809.
- Jalden, Joakim. “Maximum likelihood detection for the linear MIMO channel.” PhD diss., 2004.
- VPIphotonics: Simulation Software and Design Services. Available online: https://www.vpiphotonics.com/ (accessed on 1st June 2024).
- MATLAB. Available online: https://www.mathworks.com/products/matlab.html (accessed on day month year).
- Moshirian, S.; Ghadami, S.; Havaei, M. Blind Channel Equalization. arXiv arXiv:1208.2205, 2012.
- Smalley, D. Equalization Concepts: A Tutorial; Atlanta Regional Technology Center, Texas Instruments: Dallas, TX, USA, 1944; pp. 1–29. [Google Scholar]
- Treichler, J.; Agee, B. A new approach to multipath correction of constant modulus signals. IEEE Trans. Acoust. Speech, Signal Process. 1983, 31, 459–472. [Google Scholar] [CrossRef]
- Johnson, R.; Schniter, P.; Endres, T.; Behm, J.; Brown, D.; Casas, R. Blind equalization using the constant modulus criterion: a review. Proc. IEEE 1998, 86, 1927–1950. [Google Scholar] [CrossRef]
- Yazdi, H.S.; Homayouni, F. Impulsive Noise Suppression of Images Using Adaptive Median Filter. Int. J. Signal Processing Image Processing Pattern Recognit. 2010, 3, 1–12. [Google Scholar]
- Fernandes, C.A.R.; Mota, J.C.M.; Favier, G. Decision Directed Algorithms for Blind Equalization Based on Constant Modulus Criteria. In Proceedings of the 20◦ Colloquium on Signal and Image Processing, FRA, Novosibirsk, Russia, 20–24 June 2005. [Google Scholar]
Figure 1.
Block diagrams (a) OFDM Tx, (b) OFDM Rx, and (c) a converged OFDM-based 5G mm-wave A-RoF system.
Figure 1.
Block diagrams (a) OFDM Tx, (b) OFDM Rx, and (c) a converged OFDM-based 5G mm-wave A-RoF system.
Figure 2.
EVM measurements for the QPSK, 16-QAM, 64-QAM, and 128-QAM modulation using MLD equalization, (i) (a) (b), (c), and (d) respective constellation diagrams before equalization and (ii) (e), (f), (g), (h) after equalization.
Figure 2.
EVM measurements for the QPSK, 16-QAM, 64-QAM, and 128-QAM modulation using MLD equalization, (i) (a) (b), (c), and (d) respective constellation diagrams before equalization and (ii) (e), (f), (g), (h) after equalization.
Figure 3.
EVM measurements for the QPSK, 16-QAM, 64-QAM, and 128-QAM modulation using DFE equalization, (i) (a), (b), (c), and (d) respective constellation diagrams before equalization, and (ii), (e), (f), (g) and (h) after equalization.
Figure 3.
EVM measurements for the QPSK, 16-QAM, 64-QAM, and 128-QAM modulation using DFE equalization, (i) (a), (b), (c), and (d) respective constellation diagrams before equalization, and (ii), (e), (f), (g) and (h) after equalization.
Figure 4.
EVM results obtained before and after equalization vs. the fiber lengths for a QPSK and 16-QAM constellation after MLD and DFE.
Figure 5.
EVM results obtained before and after equalization vs. the fiber lengths for a 64-QAM and a 128-QAM constellation after MLD and DFE Equalization.
Figure 5.
EVM results obtained before and after equalization vs. the fiber lengths for a 64-QAM and a 128-QAM constellation after MLD and DFE Equalization.
Figure 6.
Comparisons of EVM results for MLD and DFE obtained before and after equalization vs. the fiber lengths for a QPSK constellation against LMS, CMA, and AMF algorithms and 16-QAM constellation against LMS, and AMF algorithms.
Figure 6.
Comparisons of EVM results for MLD and DFE obtained before and after equalization vs. the fiber lengths for a QPSK constellation against LMS, CMA, and AMF algorithms and 16-QAM constellation against LMS, and AMF algorithms.
Figure 7.
EVM results for QPSK, 16QAM, and 64-QAM modulation at the corresponding maximum fiber length vs RF input power levels without equalization.
Figure 7.
EVM results for QPSK, 16QAM, and 64-QAM modulation at the corresponding maximum fiber length vs RF input power levels without equalization.
Figure 8.
EVM results for QPSK, 16QAM, and 64-QAM modulation at the corresponding maximum fiber length vs RF input power levels with DFE and MLD equalization.
Figure 8.
EVM results for QPSK, 16QAM, and 64-QAM modulation at the corresponding maximum fiber length vs RF input power levels with DFE and MLD equalization.
Table 1.
Comments on the algorithms discussed in the literature review.
Table 1.
Comments on the algorithms discussed in the literature review.
| Literature Review |
Approach/Methods used |
Comments |
| [16] |
DSP unit in simulated software for 5 to 35 km direct and coherent detection 16-PSK, 16-QAM, and 64-QAM 100 Gbit/s data rate link at 28 GHz. |
- Simple technique.
- 28 GHz mm-wave frequency. |
| [17] |
Use of the iterative block (IB) decision feedback equalization (DFE) method for an intensity modulation and direct-detection (IM/DD) based optical code division multiplexing (OCDM) system. |
- Effectively compensates chromatic dispersion in an IM/DD-based system.
- Complex receiver structure for the IM/DD-OCDM system using costly hardware. |
| [18] |
Adaptive activated artificial neural network nonlinear equalizer (ANN-NLE) to enhance BER performance. |
- Complex Algorithm. |
| [19] |
Convolutional Neural Network (CNN) and Binary Convolutional Neural Network (BCNN) based decision schemes. |
- Complex Algorithm. |
| [21] |
Transmission of a single channel 112 Gb/s PAM-4 direct detection signal using the Maximum Likelihood Sequence Estimation (MLSE) algorithm. |
- Achieved the highest sensitivity for 112 Gb/s transmission.
- Complex Receiver Architecture. |
| [22,23] |
LMS, CMA, and AMF-based equalization in converged mm-wave A-RoF system at 60GHz. |
- Not suitable for higher-order modulation formats. |
[This
Work]
|
Converged OFDM-based mm-wave A-RoF system at 60 GHz with signal processing using DFE and MLD algorithms. |
- Compensation of higher-order modulation formats.
|
Table 2.
Literature review comparisons over specific parameters.
Table 2.
Literature review comparisons over specific parameters.
| Literature Review |
Frequency (GHz) |
Maximum Fiber Length (km) |
Modulation Format |
Algorithm |
Computational Complexity |
| [13] |
28
|
10 |
OFDM 16-QAM |
Voltera and Neural Network-based Equalizers |
Computational complex algorithms |
| [14] |
60 |
20 |
OFDM 16-QAM and 64-QAM |
Complex Valued (ANN-NLE) |
Computational complex algorithm |
| [16] |
28 |
5-35
|
16-PSK, 16-QAM and 64-QAM |
Built-in DSP Unit in simulation software |
Low complexity |
| [18] |
60 |
10
|
BPSK |
ANN-NLE |
Computational complex algorithm |
| [19] |
60 |
20
|
2-PAM |
Convolutional Neural Network (CNN) and Binary Convolutional Neural Network (BCNN) based decision schemes |
Computational complex algorithm
|
| [22] |
60 |
25 |
QPSK and 16-QAM |
LMS Algorithm |
Low complexity |
| [23] |
60 |
100 |
QPSK and 16-QAM |
LMS, CMA, and AMF Algorithms |
Low complexity |
| [This work] |
60 |
0-120 |
QPSK, 16-QAM, 64-QAM and 128-QAM |
DFE and MLD Algorithms |
Low complexity |
Table 3.
Simulation parameters.
Table 3.
Simulation parameters.
| Link Design Components |
Values |
| Carrier Frequency |
7.5 GHz |
| Laser CW |
10 dBm |
| Wavelength |
1553 nm |
| RIN |
-130 dB/Hz |
| Radio Frequency |
60 GHz mm-wave |
| Bit Rate Default |
40 Gbit/s |
| Bits per Symbol |
2,4,6,7 |
| SSMF Length |
Up to 120 km |
| Dispersion |
16 ps/nm/km |
| Dispersion Slope |
0.08 x 103 s/m3
|
| SSMF Attenuation Coefficient |
0.2 dB/Km |
| Photo Diode Model |
PIN |
| Responsivity |
0.8 A/W |
| Thermal Noise |
10-12 A/Hz1/2
|
| Shot Noise |
ON |
| Cyclic Prefix |
0.125 |
Table 4.
EVM improvement of DFE vs MLD across various modulation schemes and fiber lengths.
Table 4.
EVM improvement of DFE vs MLD across various modulation schemes and fiber lengths.
Modulation Scheme
|
EVM for MLD after equalization (%) |
EVM for DFE after equalization (%) |
EVM Improvement (%) |
Max fiber length (km) |
| QPSK |
17.06 |
16.60 |
0.46 |
120 |
| 16-QAM |
12.40 |
12.32 |
0.08 |
100 |
| 64-QAM |
7.35 |
7.19 |
0.16 |
50 |
| 128-QAM |
4.85 |
4.73 |
0.12 |
40 |
Table 5.
EVM and fiber length comparisons for the different equalization algorithms.
Table 5.
EVM and fiber length comparisons for the different equalization algorithms.
| Algorithm |
QPSK |
16-QAM |
| |
EVM (%) |
Fiber length (km) |
EVM (%) |
Fiber length (km) |
| MLD |
17.06 |
120 |
12.4 |
100 |
| DFE |
16.6 |
120 |
12.32 |
100 |
| LMS |
- |
120 |
23.75 |
100 |
| CMA |
- |
120 |
- |
100 |
| AMF |
- |
120 |
23.00 |
100 |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).