Geometrical Optics Stability Analysis of Rotating Visco-Diffusive Flows

1. Introduction

Consider a system of coupled nonlinear partial differential equations (PDEs) modeling a physical phenomenon in hydrodynamics or magnetohydrodynamics, incorporating additional factors such as fluid compressibility, rotation, density stratification, thermal gradients, or electromagnetic fields. Let the vector $\mathit{L}(\mathit{x},t)={(\mathit{u}(\mathit{x},t),p(\mathit{x},t),\dots )}^T$ represent the unknown functions governed by the system. This vector includes the fluid velocity field $\mathit{u}(\mathit{x},t)$ , pressure $p(\mathit{x},t)$ , and other quantities that may vary depending on the model, such as electromagnetic fields, temperature, or density, all of which depend on spatial coordinates $\mathit{x}$ and time t.

Assume the base state of the system, described by the vector ${\mathit{L}}_B(\mathit{x},t)={({\mathit{u}}_B(\mathit{x},t),p_B(\mathit{x},t),\dots )}^T$ , is known. To analyze its stability, we consider small perturbations such that $\mathit{L}(\mathit{x},t)={\mathit{L}}_B(\mathit{x},t)+{\mathit{L}}^{\prime }(\mathit{x},t)$ , where ${\mathit{L}}^{\prime }(\mathit{x},t)={({\mathit{u}}^{\prime }(\mathit{x},t),p^{\prime }(\mathit{x},t),\dots )}^T$ . Linearizing the governing nonlinear equations about the base state yields a system of linear partial differential equations.

Introducing a small parameter $0<ϵ\ll 1$ , we seek solutions to the linearized equations as asymptotic expansions in $ϵ$ :

$${\mathit{L}}^{\prime }(\mathit{x},t,ϵ)={\mathrm{e}}^{{\displaystyle \frac{i\Phi (\mathit{x},t)}{ϵ}}}\left({\mathit{L}}^{\left(0\right)}(\mathit{x},t)+ϵ{\mathit{L}}^{\left(1\right)}(\mathit{x},t,ϵ)\right)+ϵ{\mathit{L}}^{\left(r\right)}(\mathit{x},t,ϵ),$$

(1)

where $i=\sqrt{-1}$ , $\Phi$ is the wave phase (eikonal), and ${\mathit{L}}^{\left(j\right)}={({\mathit{u}}^{\left(j\right)},p^{\left(j\right)},\dots )}^T$ ($j=0,1,r$ ) are complex-valued amplitudes. The remainder ${\mathit{L}}^{\left(r\right)}$ is assumed to remain uniformly bounded in $ϵ$ over any fixed time interval [8,9,10,11,13,19,36,37].

Substituting (1) into the linearized system and collecting terms at orders ${ϵ}^{-1}$ and ${ϵ}^0$ yields a system of PDEs comprising the eikonal equation for $\Phi (\mathit{x},t)$ and transport equations for the amplitude ${\mathit{L}}^{\left(0\right)}(\mathit{x},t)$ , with initial conditions $\Phi (\mathit{x},0)={\Phi }_0\left(\mathit{x}\right)$ and ${\mathit{L}}^{\left(0\right)}(\mathit{x},0)={\mathit{L}}_0^{\left(0\right)}\left(\mathit{x}\right)$ .

Consider a fluid element following the trajectory:

$${\displaystyle \frac{d\mathit{x}}{dt}}={\mathit{u}}_B,\mathit{x}\left(0\right)={\mathit{x}}_0.$$

(2)

Since the eikonal and transport equations involve only the advective derivative along the base flow velocity ${\mathit{u}}_B$ [13,19,24], the eikonal equation becomes an ODE describing the evolution of the wave vector $\mathit{k}\left(t\right)=\nabla \Phi \left(\mathit{x}\right(t),t)$ along the streamline (2), with initial condition $\mathit{k}\left(0\right)={\mathit{k}}_0=\nabla {\Phi }_0\left({\mathit{x}}_0\right)$ . Similarly, the transport equations become a system of ODEs along the streamlines for the amplitudes ${\mathit{L}}^{\left(0\right)}(\mathit{x}\left(t\right),t)$ , forming the complete system of characteristic equations. These describe the motion of the perturbation envelope (viewed as a high-frequency wavelet [13]) initially localized at ${\mathit{x}}_0$ , along with the fluid elements passing through ${\mathit{x}}_0$ at $t=0$ [13,19,24].

For sufficiently small $ϵ$ , the leading-order terms dominate the solution (1) over an extended time [13,36]. This reduces the stability analysis to studying the growth rates of solutions of the transport ODEs, which are generally non-autonomous due to time dependence of the wave vector. Stability conditions are determined by the boundedness of solutions: the existence of unbounded solutions implies instability [13,19]. This localized analysis provides sufficient instability and necessary stability conditions along the trajectories of the flow [13,19].

The geometrical optics stability analysis has proven highly effective in addressing stability problems in ideal hydrodynamics and magnetohydrodynamics for 3D flows, both compressible and incompressible, characterized by complex streamlines. Applications span a broad range of systems, including circular Couette-Taylor flow [7], flows with elliptical [2,41,47,49] and hyperbolic [30,41] streamlines, chaotic streamline systems like the ABC flow [7], helical (swirling) compressible [8,32] and incompressible [10,32] flows, vortex rings with swirl [16,38], Kelvin–Helmholtz vortices [1], Riemann ellipsoids in celestial mechanics [33,45,53], geophysical flows [19], and hydromagnetic systems [12,28,34,44,46,50]. For ideal flows with elliptical streamlines subject to elliptical parametric instability, the periodic amplitude transport equations are effectively addressed either numerically [53,54] or through perturbation methods [34,44], in combination with Floquet theory [2].

Maslov [40] noted that high-frequency oscillations of the form $exp(i{ϵ}^{-1}\Phi (\mathit{x},t))$ rapidly decay due to viscosity, unless a quadratic dependence of viscosity on the small parameter $ϵ$ is assumed: $\nu ={ϵ}^2\tilde{\nu }$ . This assumption allowed the extension of geometrical optics stability analysis to the Navier-Stokes equations [36], where an integral transformation of the amplitude reduced the viscous transport equations to their inviscid form, revealing the stabilizing influence of viscosity [7,13,30,36]. Consequently, early applications of geometrical optics stability analysis were restricted to cases where viscosity or diffusivity had a purely stabilizing effect, even in visco-diffusive or multiple-diffusive settings [5,30].

To simplify mathematical complexity, studies often assumed a Prandtl number $Pr=1$ , representing an equal ratio of viscosity to diffusivity. Leblanc [31] highlighted the unique role of $Pr=1$ , stating: “The standard transformation used in non-stratified flows [30] is not valid here, except in the exceptional case where $Pr=1$ , which may be treated in closed form. In that case, introducing a change of variables reduces the amplitude equation to an inviscid homogeneous Hill’s equation. With the wave vector being periodic and bounded in time, inviscid resonances are either damped or eventually suppressed by diffusion.” For large Prandtl numbers but small viscosity and diffusivity, particularly with vanishing thermal diffusivity, Leblanc further reduced the problem to a damped Mathieu equation, demonstrating that under certain conditions “viscosity suppresses parametric instability.”

Similar observations have been made in magnetohydrodynamics, where both magnetic diffusion and viscous dissipation were considered [46]: “This shows first that if the diffusivities are equal, the only effect of dissipation is a reduction in growth rate. Second, assuming magnetic diffusivity is vanishingly small, the impact of dissipation primarily manifests as a decrease in the growth rate.”

Building on the works [21,22,23], which analyzed helical and azimuthal magnetorotational instabilities under the geometrical optics framework, it became clear that this method is effective even for systems with unequal diffusivities. In particular, it enabled the derivation of new analytical criteria for dissipation-induced instabilities, including the Goldreich-Schubert-Fricke instability [24], McIntyre instability [29,42,52], and salt-fingering double-diffusive instability [52].

Recently, Singh and Mathur [51] applied the geometrical optics approach to investigate the effect of the Schmidt number ($Sc$ ), defined as the ratio of viscosity to the diffusivity of the stratifying agent, on elliptical instability under stable stratification. Their findings revealed that $Sc\ne 1$ significantly alters inviscid instability behavior and introduces a new branch of oscillatory instability, absent when $Sc=1$ . This observation aligns with earlier studies that demonstrated damping broadens the region of combination parametric resonance in the context of solid mechanics [17,27].

These advancements have expanded the applicability of geometrical optics stability analysis to visco-diffusive and multi-diffusive rotating flows with circular and elliptical streamlines over a broad range of Prandtl, Schmidt, and magnetic Prandtl numbers [6,26,48,54]. The present paper reviews these developments, highlights their implications, and explores potential directions for advancing this method and its applications.

2. Singular Diffusionless Limit of Visco-Diffusive Instabilities in Magnetohydrodynamics

2.1. Governing Equations and the Background Fields

Following [23] we consider azimuthal magnetorotational instability (AMRI) as a visco-diffusive oscillatory instability. The dynamics of a viscous, electrically conducting, incompressible Newtonian fluid interacting with a magnetic field are governed by the coupled Navier-Stokes and induction equations [21,22,23,25]:

$$\left.\begin{array}{c}{\displaystyle \frac{\partial \mathit{u}}{\partial t}}+\mathit{u}·\nabla \mathit{u}-{\displaystyle \frac{1}{{\mu }_0\rho }}\mathit{B}·\nabla \mathit{B}+{\displaystyle \frac{1}{\rho }}\nabla P-\nu {\nabla }^2\mathit{u}=0,\hfill \\ {\displaystyle \frac{\partial \mathit{B}}{\partial t}}+\mathit{u}·\nabla \mathit{B}-\mathit{B}·\nabla \mathit{u}-\eta {\nabla }^2\mathit{B}=0,\hfill \end{array}\right\}$$

(3)

where $P=p+{\displaystyle \frac{{\mathit{B}}^2}{2{\mu }_0}}$ is the total pressure, p is the hydrodynamic pressure, $\rho$ is the density, $\nu$ the kinematic viscosity, $\eta ={\left({\mu }_0\sigma \right)}^{-1}$ the magnetic diffusivity, $\sigma$ the fluid’s conductivity, and ${\mu }_0$ the magnetic permeability of free space. The flow velocity field $\mathit{u}$ and magnetic field $\mathit{B}$ are subject to the incompressibility and solenoidal field constraints:

$$\nabla ·\mathit{u}=0,\nabla ·\mathit{B}=0.$$

(4)

For a differentially rotating flow in the gap between radii $r_1$ and $r_2>r_1$ and purely azimuthal magnetic field, the steady solution to (3) and (4) has the form:

$${\mathit{u}}_B\left(r\right)=r\Omega \left(r\right){\mathit{e}}_{\varphi },p=p_B\left(r\right),{\mathit{B}}_B\left(r\right)=B_{\varphi }^0\left(r\right){\mathit{e}}_{\varphi },$$

(5)

in cylindrical coordinates $(r,\varphi ,z)$ .

In the magnetized circular Couette-Taylor flow (5), the angular velocity profile $\Omega \left(r\right)$ and the azimuthal magnetic field $B_{\varphi }^0\left(r\right)$ are arbitrary functions of r subject to boundary conditions for an inviscid, non-resistive fluid. For viscous and resistive fluids, these profiles become $\Omega \left(r\right)=a+b{r}^{-2}$ and $B_{\varphi }^0\left(r\right)=cr+d{r}^{-1}$ , with coefficients determined by boundary conditions. In the context of local linear stability analysis, boundary conditions are neglected, and the steady state of the visco-diffusive system coincides with that of the diffusionless system.

2.2. Transport Equation for Amplitudes and Its Dispersion Relation

Linearizing equations (3)-(4) near the stationary solution (5), and seeking a solution in asymptotic form (1) under the assumptions $\nu ={ϵ}^2\tilde{\nu }$ and $\eta ={ϵ}^2\tilde{\eta }$ [40], we derive transport equations for the amplitudes ${\mathit{u}}^{\left(0\right)}$ and ${\mathit{B}}^{\left(0\right)}$ [21,22,23,28]:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d{\mathit{u}}^{\left(0\right)}}{dt}}& =& \left[{\displaystyle \frac{2\mathit{k}{\mathit{k}}^T}{{\left|\mathit{k}\right|}^2}}-\mathcal{I}\right]\mathcal{U}{\mathit{u}}^{\left(0\right)}-\tilde{\nu }{\left|\mathit{k}\right|}^2{\mathit{u}}^{\left(0\right)}+{\displaystyle \frac{1}{\rho {\mu }_0}}\left\{\left[\mathcal{I}-{\displaystyle \frac{2\mathit{k}{\mathit{k}}^T}{{\left|\mathit{k}\right|}^2}}\right]\mathcal{B}+{\mathit{B}}_B·\nabla \right\}{\mathit{B}}^{\left(0\right)},\hfill \\ \hfill {\displaystyle \frac{d{\mathit{B}}^{\left(0\right)}}{dt}}& =& \mathcal{U}{\mathit{B}}^{\left(0\right)}-\tilde{\eta }{\left|\mathit{k}\right|}^2{\mathit{B}}^{\left(0\right)}-(\mathcal{B}-{\mathit{B}}_B·\nabla ){\mathit{u}}^{\left(0\right)},\hfill \end{array}$$

(6)

where $\mathcal{I}$ is the $3\times 3$ identity matrix, and the gradients of the background fields are

$$\begin{array}{c}\hfill \mathcal{U}:=\nabla {\mathit{u}}_B=\Omega \left(\begin{array}{ccc}0& -1& 0\\ 1+2Ro& 0& 0\\ 0& 0& 0\end{array}\right),\mathcal{B}:=\nabla {\mathit{B}}_B={\displaystyle \frac{B_{\varphi }^0}{r}}\left(\begin{array}{ccc}0& -1& 0\\ 1+2Rb& 0& 0\\ 0& 0& 0\end{array}\right),\end{array}$$

(7)

with the time evolution of the wave vector $\mathit{k}=\nabla \Phi$ given by

$${\displaystyle \frac{d\mathit{k}}{dt}}=-{\mathcal{U}}^T\mathit{k},$$

(8)

where $d/dt={\partial }_t+{\mathit{u}}_B·\nabla$ . Equations (6) and (8) hold if ${\mathit{B}}_B·\mathit{k}=0$ .

Defining $\alpha =k_z{\left|\mathit{k}\right|}^{-1}$ and ${\left|\mathit{k}\right|}^2=k_r^2+k_z^2$ , we introduce the $\mathrm{Alfv}\acute{\mathrm{e}}\mathrm{n}$ angular velocity, viscous and resistive frequencies, and the hydrodynamic and magnetic Reynolds numbers [21,22]:

$${\omega }_{A_{\varphi }}={\displaystyle \frac{B_{\varphi }^0}{r\sqrt{\rho {\mu }_0}}},{\omega }_{\nu }=\tilde{\nu }{\left|\mathit{k}\right|}^2,{\omega }_{\eta }=\tilde{\eta }{\left|\mathit{k}\right|}^2,Re={\displaystyle \frac{\alpha \Omega }{{\omega }_{\nu }}},Rm={\displaystyle \frac{\alpha \Omega }{{\omega }_{\eta }}},$$

(9)

and the fluid and magnetic Rossby numbers [21]:

$$Ro={\displaystyle \frac{rD\Omega }{2\Omega }},Rb={\displaystyle \frac{rD{\omega }_{A_{\varphi }}}{2{\omega }_{A_{\varphi }}}},$$

(10)

where $D={\displaystyle \frac{d}{dr}}$ . Note that $Rm=RePm$ with $Pm={\displaystyle \frac{\nu }{\eta }}$ as the magnetic Prandtl number.

Seeking solutions to Eqs. (6) in modal form [12,23], ${\mathit{u}}^{\left(0\right)}=\widehat{\mathit{u}}{e}^{\alpha \Omega \lambda t+im\varphi }$ and ${\mathit{B}}^{\left(0\right)}=\sqrt{\rho {\mu }_0}\widehat{\mathit{B}}{e}^{\alpha \Omega \lambda t+im\varphi }$ , the amplitude equations yield

$$\mathit{A}\mathit{z}=\lambda \mathit{z},$$

(11)

where $\mathit{z}={({\widehat{u}}_R,{\widehat{u}}_{\varphi },{\widehat{B}}_R,{\widehat{B}}_{\varphi })}^T\in {\mathbb{C}}^4$ and $\mathit{A}={\mathit{A}}_0+{\mathit{A}}_1\in {\mathbb{C}}^{4\times 4}$ with

$${\mathit{A}}_0=\left(\begin{array}{cccc}-in& 2\alpha & inS& -2\alpha S\\ -{\displaystyle \frac{2(1+Ro)}{\alpha }}& -in& {\displaystyle \frac{2(1+Rb)}{\alpha }}S& inS\\ inS& 0& -in& 0\\ -{\displaystyle \frac{2Rb}{\alpha }}S& inS& {\displaystyle \frac{2Ro}{\alpha }}& -in\end{array}\right),{\mathit{A}}_1=\left(\begin{array}{cccc}{\displaystyle \frac{-1}{Re}}& 0& 0& 0\\ 0& {\displaystyle \frac{-1}{Re}}& 0& 0\\ 0& 0& {\displaystyle \frac{-1}{Rm}}& 0\\ 0& 0& 0& {\displaystyle \frac{-1}{Rm}}\end{array}\right).$$

(12)

Here, $n=m/\alpha$ is the modified azimuthal wavenumber, and $S={\omega }_{A_{\varphi }}/\Omega$ is the $\mathrm{Alfv}\acute{\mathrm{e}}\mathrm{n}$ angular velocity in units of $\Omega$ .

Defining a Hermitian matrix

$$\mathit{G}=\left(\begin{array}{cccc}0& -i& 0& iS\\ i& 0& -iS& 0\\ 0& iS& 4{\displaystyle \frac{Ro-Rb}{\alpha n}}& -i\\ -iS& 0& i& 0\end{array}\right),$$

(13)

the indefinite inner product in ${\mathbb{C}}^4$ becomes $[\mathit{x},\mathit{y}]={\overline{\mathit{y}}}^T\mathit{G}\mathit{x}$ [23,25], with the standard inner product $(\mathit{x},\mathit{y})={\overline{\mathit{y}}}^T\mathit{x}$ . The matrix ${\mathit{H}}_0=-i\mathit{G}{\mathit{A}}_0$ is Hermitian:

$${\mathit{H}}_0=\left(\begin{array}{cccc}-{\displaystyle \frac{2(S^{2}Rb-Ro-1)}{\alpha }}& in(S^2+1)& -{\displaystyle \frac{2S(1+Rb-Ro)}{\alpha }}& -2inS\\ -in(S^2+1)& 2\alpha & 2inS& -2\alpha S\\ -{\displaystyle \frac{2S(1+Rb-Ro)}{\alpha }}& -2inS& {\displaystyle \frac{2(S^{2}Rb+S^2+2Rb-3Ro)}{\alpha }}& in(S^2+1)\\ 2inS& -2\alpha S& -in(S^2+1)& 2\alpha S^2\end{array}\right).$$

(14)

The eigenvalue problem ${\mathit{A}}_0\mathit{z}=\lambda \mathit{z}$ transforms to Hamiltonian form with ${\mathit{H}}_0$ [23,25]:

$${\mathit{H}}_0\mathit{z}=i^{-1}\mathit{G}\lambda \mathit{z}.$$

(15)

The symmetry ${\mathit{A}}_0=-{\mathit{G}}^{-1}{\overline{{\mathit{A}}_0}}^T\mathit{G}$ ensures the spectrum of ${\mathit{A}}_0$ is symmetric about the imaginary axis.

The full eigenvalue problem (11) is a dissipative perturbation of the Hamiltonian problem (15):

$$({\mathit{H}}_0+{\mathit{H}}_1)\mathit{z}=i^{-1}\mathit{G}\lambda \mathit{z},$$

(16)

where ${\mathit{H}}_1=-i\mathit{G}{\mathit{A}}_1$ is complex and non-Hermitian:

$${\mathit{H}}_1=\left(\begin{array}{cccc}0& {\displaystyle \frac{1}{Re}}& 0& -{\displaystyle \frac{S}{Rm}}\\ -{\displaystyle \frac{1}{Re}}& 0& {\displaystyle \frac{S}{Rm}}& 0\\ 0& -{\displaystyle \frac{S}{Re}}& 4i{\displaystyle \frac{Ro-Rb}{\alpha nRm}}& {\displaystyle \frac{1}{Rm}}\\ {\displaystyle \frac{S}{Re}}& 0& -{\displaystyle \frac{1}{Rm}}& 0\end{array}\right).$$

(17)

The dispersion relation for the visco-diffusive system (16) follows as

$$p\left(\lambda \right):=det({\mathit{H}}_0+{\mathit{H}}_1-i^{-1}\mathit{G}\lambda )=0.$$

(18)

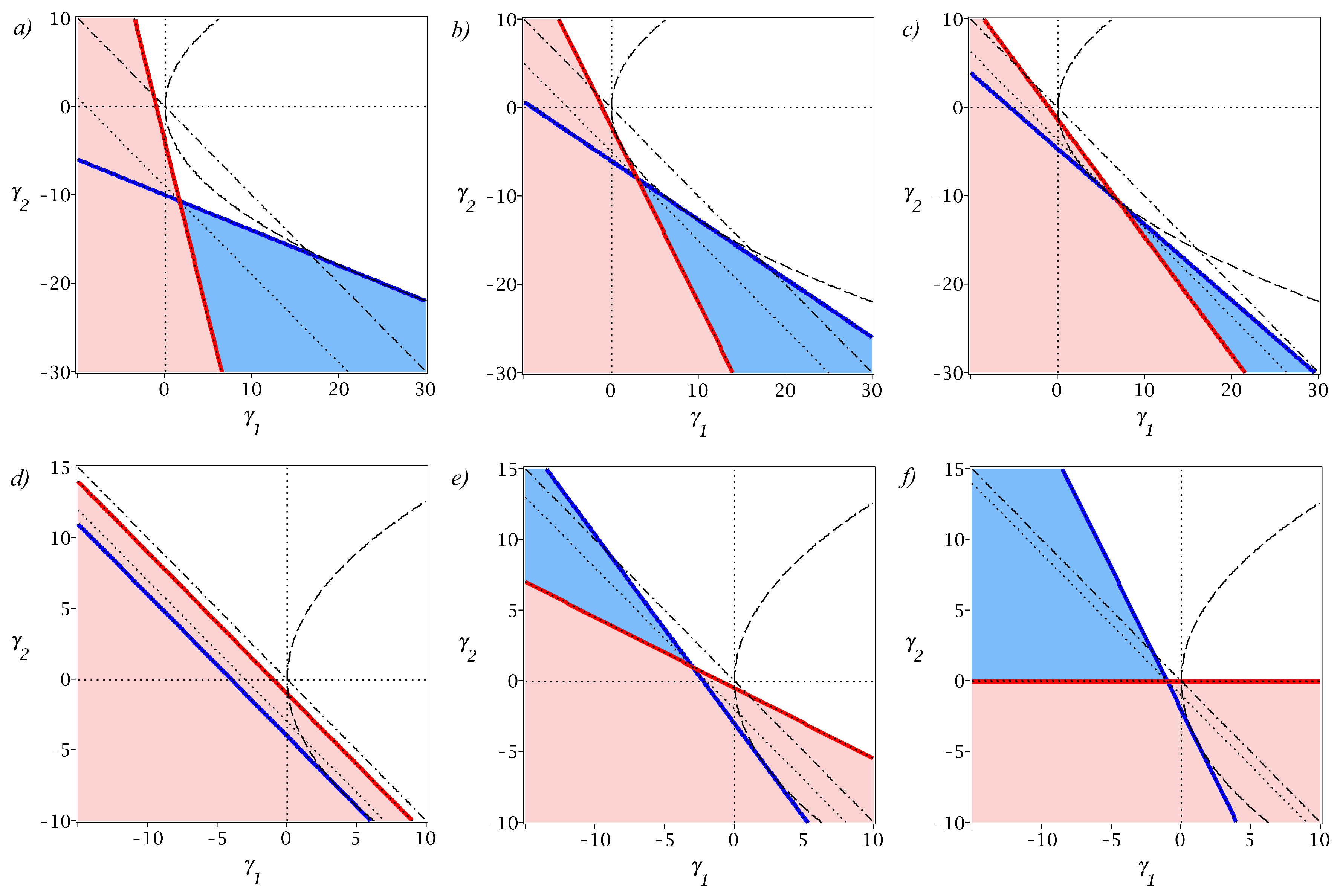
2.3. Krein Sign and Splitting of Double Eigenvalues with Jordan Block

A simple imaginary eigenvalue $\lambda =i\omega$ of the eigenvalue problem (15), with eigenvector $\mathit{z}$ , has a positive Krein sign if $[\mathit{z},\mathit{z}]>0$ and a negative Krein sign if $[\mathit{z},\mathit{z}]<0$ [23,25].

Let $\mathit{p}$ represent the parameters of the matrix ${\mathit{H}}_0$ , i.e., $\mathit{p}={(S,Ro,Rb,n)}^T\in {\mathbb{R}}^4$ . Suppose at $\mathit{p}={\mathit{p}}_0$ , the matrix ${\mathit{H}}_0=\mathit{H}\left({\mathit{p}}_0\right)$ has a double imaginary eigenvalue $\lambda =i{\omega }_0$ $({\omega }_0\ge 0)$ , with a Jordan chain consisting of eigenvector ${\mathit{z}}_0$ and associated vector ${\mathit{z}}_1$ , satisfying:

$${\mathit{H}}_0{\mathit{z}}_0={\omega }_0\mathit{G}{\mathit{z}}_0,{\mathit{H}}_0{\mathit{z}}_1={\omega }_0\mathit{G}{\mathit{z}}_1+i^{-1}\mathit{G}{\mathit{z}}_0.$$

(19)

Applying transposition and complex conjugation gives:

$${\overline{\mathit{z}}}_0^T{\mathit{H}}_0={\omega }_0{\overline{\mathit{z}}}_0^T\mathit{G},{\overline{\mathit{z}}}_1^T{\mathit{H}}_0={\omega }_0{\overline{\mathit{z}}}_1^T\mathit{G}-i^{-1}{\overline{\mathit{z}}}_0^T\mathit{G}.$$

(20)

From these, it follows that $[{\mathit{z}}_0,{\mathit{z}}_0]=0$ and $[{\mathit{z}}_0,{\mathit{z}}_1]=-[{\mathit{z}}_1,{\mathit{z}}_0]$ .

Varying the parameters along a curve $\mathit{p}=\mathit{p}\left(\epsilon \right)$ $(\mathit{p}\left(0\right)={\mathit{p}}_0)$ , where $\epsilon$ is a real parameter, yields:

$${\lambda }_{\pm }=i{\omega }_0\pm i{\omega }_1{\epsilon }^{1/2}+o\left({\epsilon }^{1/2}\right),{\mathit{z}}_{\pm }={\mathit{z}}_0\pm i{\omega }_1{\mathit{z}}_1{\epsilon }^{1/2}+o\left({\epsilon }^{1/2}\right),$$

(21)

with

$${\omega }_1=\sqrt{i{\displaystyle \frac{{\overline{\mathit{z}}}_0^T\Delta \mathit{H}{\mathit{z}}_0}{{\overline{\mathit{z}}}_1^T\mathit{G}{\mathit{z}}_0}}},\Delta \mathit{H}={\left.\sum _{s=1}^4{\displaystyle \frac{\partial \mathit{H}}{\partial p_s}}{\displaystyle \frac{d{p}_s}{d\epsilon }}\right|}_{\epsilon =0}={\overline{(\Delta \mathit{H})}}^T.$$

(22)

Given that ${\overline{\mathit{z}}}_0^T\Delta \mathit{H}{\mathit{z}}_0$ is real and ${\overline{\mathit{z}}}_1^T\mathit{G}{\mathit{z}}_0$ is imaginary, we assume ${\omega }_1>0$ . For $\epsilon >0$ , the eigenvalue $i{\omega }_0$ splits into ${\lambda }_{\pm }=i{\omega }_0\pm i{\omega }_1\sqrt{\epsilon }$ (stability). For $\epsilon <0$ , the split produces a pair of complex eigenvalues with real parts of opposite signs (instability). Thus, the curve $\mathit{p}\left(\epsilon \right)$ exhibits a linear Hamilton-Hopf bifurcation at ${\mathit{p}}_0$ , which is a regular point on the stability boundary.

For $\epsilon >0$ , the indefinite inner product of perturbed eigenvectors gives [23,25]:

$$[{\mathit{z}}_{+},{\mathit{z}}_{+}]=+2i{\omega }_1{\overline{\mathit{z}}}_0^T\mathit{G}{\mathit{z}}_1{\epsilon }^{1/2}+o\left({\epsilon }^{1/2}\right),[{\mathit{z}}_{-},{\mathit{z}}_{-}]=-2i{\omega }_1{\overline{\mathit{z}}}_0^T\mathit{G}{\mathit{z}}_1{\epsilon }^{1/2}+o\left({\epsilon }^{1/2}\right).$$

(23)

Hence, ${\lambda }_{+}$ and ${\lambda }_{-}$ have opposite Krein signs. As $\epsilon$ decreases towards zero, these eigenvalues merge at $i{\omega }_0$ and then split into complex eigenvalues for $\epsilon <0$ . The presence of opposite Krein signs is both a necessary and sufficient condition for the imaginary eigenvalues to leave the imaginary axis.

Below we demonstrate the Krein collision at the onset of the diffusionless azimuthal magnetorotational instability (AMRI) by calculating the roots of the dispersion relation both analytically and numerically.

2.4. Threshold of Oscillatory Instability in the Diffusionless Case

In the Hamiltonian case (${\displaystyle \frac{1}{Re}}=0$ , ${\displaystyle \frac{1}{Rm}}=0$ ), the dispersion relation $p_0\left(\lambda \right)=det({\mathit{H}}_0-i^{-1}\mathit{G}\lambda )=0$ has a compact form [12,23,25]:

$$p_0\left(\lambda \right)=4{\delta }^2+4{\left(i\lambda -n+n{S}^2\right)}^2-{\left(2\delta -{(i\lambda -n)}^2+n^2{S}^2\right)}^2=0,$$

(24)

where $\delta =Ro-Rb{S}^2$ . For $S=1$ , this factorizes into:

$${\left.p_0\left(\lambda \right)\right|}_{S=1}=[{\lambda }^3+4in{\lambda }^2+4(1-n^2+Ro-Rb)\lambda +8in(Ro-Rb)]\lambda =0.$$

(25)

The negative discriminant of the cubic polynomial factor provides the criterion for oscillatory instability [23,25]:

$$\begin{array}{c}\hfill 4n^4+({(Ro-Rb)}^2+20(Ro-Rb)-8)n^2+4{(Ro-Rb+1)}^3<0.\end{array}$$

(26)

Equality in (26) marks the transition from marginal stability to oscillatory instability via a linear Hamilton-Hopf bifurcation (see Figure 1). Marginal stability corresponds to one eigenvalue $\lambda$ being zero and simple, another simple and imaginary, and the last two forming a double imaginary eigenvalue with a Jordan block. At $Rb=-1$ , the critical fluid Rossby number is derived from (26):

$${Ro}_c\left(n\right)={\displaystyle \frac{{\beta }^{\frac{1}{3}}-n^2}{12}}-{\displaystyle \frac{n^2}{{\beta }^{\frac{1}{3}}}}\left(18-{\displaystyle \frac{n^2}{12}}\right)-2,\beta \left(n\right)=-n^2\left(n^4+540n^2-5832-24\sqrt{3{(n^2+27)}^3}\right).$$

(27)

Although Krein signs of the imaginary eigenvalues in Figure 1 can be evaluated numerically, it is instructive to analyze the case $Ro=Rb=-1$ and $S=1$ . Here, Eq. (25) yields a double semi-simple zero eigenvalue ${\lambda }_0=0$ with eigenvectors ${\mathit{z}}_1={(0,1,0,1)}^T$ and ${\mathit{z}}_2={(1,0,1,0)}^T$ , and two imaginary eigenvalues ${\lambda }_{\pm }=-2i(n\pm 1)$ with eigenvectors ${\mathit{z}}_{+}={\left(-i\alpha ,{\displaystyle \frac{-n}{2+n}},{\displaystyle \frac{in\alpha }{2+n}},1\right)}^T$ and ${\mathit{z}}_{-}={\left(i\alpha ,{\displaystyle \frac{n}{2-n}},{\displaystyle \frac{in\alpha }{2-n}},1\right)}^T$ . see Figure 1(left). These eigenvalues have opposite Krein signs [23,25]:

$${\displaystyle \frac{[{\mathit{z}}_{+},{\mathit{z}}_{+}]}{({\mathit{z}}_{+},{\mathit{z}}_{+})}}=-{\displaystyle \frac{2\alpha }{1+{\alpha }^2}}{\displaystyle \frac{2{(n+1)}^2}{1+{(n+1)}^2}}<0,{\displaystyle \frac{[{\mathit{z}}_{-},{\mathit{z}}_{-}]}{({\mathit{z}}_{-},{\mathit{z}}_{-})}}={\displaystyle \frac{2\alpha }{1+{\alpha }^2}}{\displaystyle \frac{2{(n-1)}^2}{1+{(n-1)}^2}}>0.$$

(28)

For instance, at $n=\sqrt{2}$ , ${\displaystyle \frac{1+{\alpha }^2}{2\alpha }}{\displaystyle \frac{[{\mathit{z}}_{-},{\mathit{z}}_{-}]}{({\mathit{z}}_{-},{\mathit{z}}_{-})}}=1-{\displaystyle \frac{\sqrt{2}}{2}}\approx 0.2929$ , implying that ${\lambda }_{-}$ has a positive Krein sign. The solid circle representing ${\lambda }_{-}$ belongs to the branch labeled ${\lambda }_2$ in Figure 1(left), where all ${\lambda }_2$ eigenvalues for ${Ro}_c<Ro<-1$ have positive Krein signs. Conversely, according to (23) the ${\lambda }_1$ branch eigenvalues in Figure 1(left) have negative Krein signs in the same range.

Thus, the onset of nonaxisymmetric oscillatory instability (diffusionless AMRI) involves a Krein collision between modes of positive and negative Krein sign. Krein sign directly relates to the energy sign of a mode, and the linear Hamilton-Hopf bifurcation represents a collision of imaginary eigenvalues with opposite Krein (energy) signs [23,25].

2.5. Dissipative Perturbation of Simple Imaginary Eigenvalues

The complex non-Hermitian matrix of the dissipative perturbation, ${\mathit{H}}_1$ , can be decomposed into Hermitian and anti-Hermitian components: ${\mathit{H}}_1={\mathit{H}}_1^H+{\mathit{H}}_1^A$ , where [23,25]

$${\mathit{H}}_1^H={\displaystyle \frac{S(Pm-1)}{2Rm}}\left(\begin{array}{cccc}0& 0& 0& 1\\ 0& 0& -1& 0\\ 0& -1& 0& 0\\ 1& 0& 0& 0\end{array}\right),{\mathit{H}}_1^A={\displaystyle \frac{1}{Rm}}\left(\begin{array}{cccc}0& Pm& 0& -{\displaystyle \frac{S(Pm+1)}{2}}\\ -Pm& 0& {\displaystyle \frac{S(Pm+1)}{2}}& 0\\ 0& -{\displaystyle \frac{S(Pm+1)}{2}}& 4i{\displaystyle \frac{Ro-Rb}{\alpha n}}& 1\\ {\displaystyle \frac{S(Pm+1)}{2}}& 0& -1& 0\end{array}\right).$$

At large $Rm$ , the increment $\delta \lambda$ to a simple imaginary eigenvalue $\lambda$ with eigenvector $\mathit{z}$ is determined using standard perturbation theory [23,25]:

$$\delta \lambda =i{\displaystyle \frac{{\overline{\mathit{z}}}^T{\mathit{H}}_1\mathit{z}}{{\overline{\mathit{z}}}^T\mathit{G}\mathit{z}}}=i{\displaystyle \frac{({\mathit{H}}_1\mathit{z},\mathit{z})}{[\mathit{z},\mathit{z}]}}.$$

(29)

The increment due to the Hermitian component, $\delta {\lambda }^H=i{\displaystyle \frac{({\mathit{H}}_1^H\mathit{z},\mathit{z})}{[\mathit{z},\mathit{z}]}}$ , is purely imaginary. Notably, ${\mathit{H}}_1^H=0$ when $Pm=1$ , implying that frequencies are unaffected by the Hermitian component of the dissipative perturbation when the contributions of viscosity and resistivity are equal.

In contrast, the increment due to the anti-Hermitian component, $\delta {\lambda }^A=i{\displaystyle \frac{({\mathit{H}}_1^A\mathit{z},\mathit{z})}{[\mathit{z},\mathit{z}]}}$ , is real. For example, the eigenvalues ${\lambda }_{+}$ and ${\lambda }_{-}$ in Figure 1(left) acquire the increments:

$$\delta {\lambda }_{\pm }^A=-{\displaystyle \frac{Pm+1}{2Rm}}=-{\displaystyle \frac{1}{h}}=-{\displaystyle \frac{1}{2}}\left({\displaystyle \frac{1}{Re}}+{\displaystyle \frac{1}{Rm}}\right),\delta {\lambda }_{\pm }^H=0,$$

(30)

where h is the harmonic mean of the two Reynolds numbers.

In the vicinity of the critical Rossby number for the Hamilton-Hopf bifurcation, ${Ro}_c\approx -1.07855$ , the real increment $\delta {\lambda }^A$ to the imaginary eigenvalues ${\lambda }_1$ (with negative Krein sign) and ${\lambda }_2$ (with positive Krein sign) is shown in Figure 2(left) for fixed $Rm={10}^3$ and varying $Pm$ (where the fluid Reynolds number is calculated as $Re=Rm/Pm$ ).

Eigenvalues with a negative Krein sign become dissipatively destabilized when $Pm>1$ , i.e., when fluid viscosity dominates over ohmic losses. Interestingly, eigenvalues with a positive Krein sign can also develop positive growth rates. This occurs for $Pm<1$ , where electrical resistivity outweighs kinematic viscosity.

The interval of negative real increments in Figure 2(left) shrinks as the deviation from the critical Rossby number, $\Delta Ro=Ro-{Ro}_c$ , approaches zero. At $\Delta Ro=0$ , the stable interval reduces to a single point: $Pm=1$ . Thus, weak ohmic diffusion ($Pm<1$ ) destabilizes positive-energy waves, while weak kinematic viscosity ($Pm>1$ ) destabilizes negative-energy waves, provided $|Ro-{Ro}_c|$ is sufficiently small.

2.6. Diffusionless and Double-Diffusive Criteria Meet at $Pm=1$

We extend the sensitivity analysis of eigenvalues for the diffusionless Hamiltonian eigenvalue problem under visco-diffusive perturbation by directly computing the stability boundaries using the algebraic Bilharz stability criterion. This criterion ensures that all roots of a complex polynomial of degree n lie to the left of the imaginary axis in the complex plane if all even-order principal minors of the $2n\times 2n$ Bilharz matrix, constructed from the real and imaginary parts of the polynomial coefficients, are positive [25].

Applying the Bilharz criterion to (18), we plot the neutral stability curves in the plane of inverse Reynolds numbers, ${Rm}^{-1}$ and ${Re}^{-1}$ , for various values of $\Delta Ro=Ro-{Ro}_c$ , where ${Ro}_c$ is defined in (27). These plots, shown in Figure 2(right), correspond to $S=1$ , $Rb=-1$ , and $n=\sqrt{2}$ . Notably, the diagonal line corresponding to $Pm=1$ remains within the stability domain for $\Delta Ro\ge 0$ and is the only tangent to the stability boundary at the cuspidal origin when $Ro={Ro}_c$ .

Furthermore, at $Ro={Ro}_c$ and $Re=Rm$ , the spectrum of the double-diffusive system with $S=1$ and $Rb=-1$ includes double complex eigenvalues, also known as exceptional points [25]:

$${\lambda }_d={\lambda }_c\left(n\right)-{Rm}^{-1}.$$

(31)

Here, the imaginary eigenvalue ${\lambda }_c\left(n\right)$ is determined by (25) for $Ro={Ro}_c\left(n\right)$ , as specified in (27).

2.7. Visco-Diffusive Instability at $Pm\ne 1$

As $Re=Rm>0$ , varying $Ro$ at fixed $Rb=-1$ , $S=1$ , and n leads to a bifurcation at $Ro=R{o}_c$ of the double complex eigenvalue (31) with a negative real part of $-R{m}^{-1}$ , as shown in Figure 3(left). At $Pm=1$ , dissipation shifts the Hamilton-Hopf bifurcation to the left in the complex plane, so the oscillatory instability in the visco-diffusive system with equal viscosity and resistivity occurs through the classical Hopf bifurcation at $Ro\left(Rm\right)<R{o}_c$ , with $Ro\left(Rm\right)$ approaching $R{o}_c$ as $Rm\to \infty$ .

When the magnetic Prandtl number deviates slightly from $Pm=1$ , the shifted Hamilton-Hopf bifurcation unfolds into two quasi-hyperbolic eigenvalue branches, passing close in an avoided crossing [20] centered at the exceptional point ${\lambda }_d$ of (31) with real part $-h^{-1}$ , where $h={\displaystyle \frac{2}{\frac{1}{Re}+\frac{1}{Rm}}}$ is the harmonic mean of the fluid and magnetic Reynolds numbers ($Re\ne Rm$ ), as seen in Figure 3(left).

The unfolding of the eigenvalue crossing into an avoided crossing depends on the sign of $Pm-1$ . For $Pm<1$ ($Pm>1$ ), the complex eigenvalues, originating from the imaginary eigenvalues of the diffusionless system with positive (negative) Krein sign, form a branch that bends rightward and crosses the imaginary axis at some $Ro(Re,Rm)\ne R{o}_c$ , as shown in Figure 3(left), cf. [20]. The critical values $Ro(Re,Rm)$ of the visco-diffusive system lie on a surface in the $({Re}^{-1},{Rm}^{-1},Ro)$ -space, with a self-intersection along the $Ro$ -axis, as depicted in Figure 3(right). The angle of the self-intersection tends to zero as $Ro\to R{o}_c$ , and at the point $(0,0,R{o}_c)$ , the surface has a singularity, known as the Whitney umbrella [3,25,27].

Near the $Ro$ -axis, the instability threshold forms a ruled surface [3], with each ruler’s slope determined by $Pm$ . As the Reynolds numbers approach infinity while $Pm$ remains fixed, the $Ro$ -axis is approached along a ruler corresponding to that value of $Pm$ . For all values of $Pm$ except $Pm=1$ , a ruler leads to a limiting value of $Ro$ greater than $R{o}_c$ , extending the instability interval compared to the diffusionless system, as seen in Figure 3(right). The plane $Pm=1$ divides the neutral stability surface near $Ro=R{o}_c$ into two regions: one for positive energy modes destabilized by dominant ohmic diffusion at $Pm<1$ and one for negative energy modes destabilized by dominant fluid viscosity at $Pm>1$ , as shown in Figure 3(right). The ray defined by $Re=Rm>0$ , $Ro=R{o}_c$ lies within the stability domain and contains exceptional points (31) that govern the eigenvalue behavior shown in Figure 3(left). The Whitney umbrella singularity of the neutral stability surface is the reason for persistence of diffusive destabilization even in the limit of vanishing dissipation [3,25,27,42].

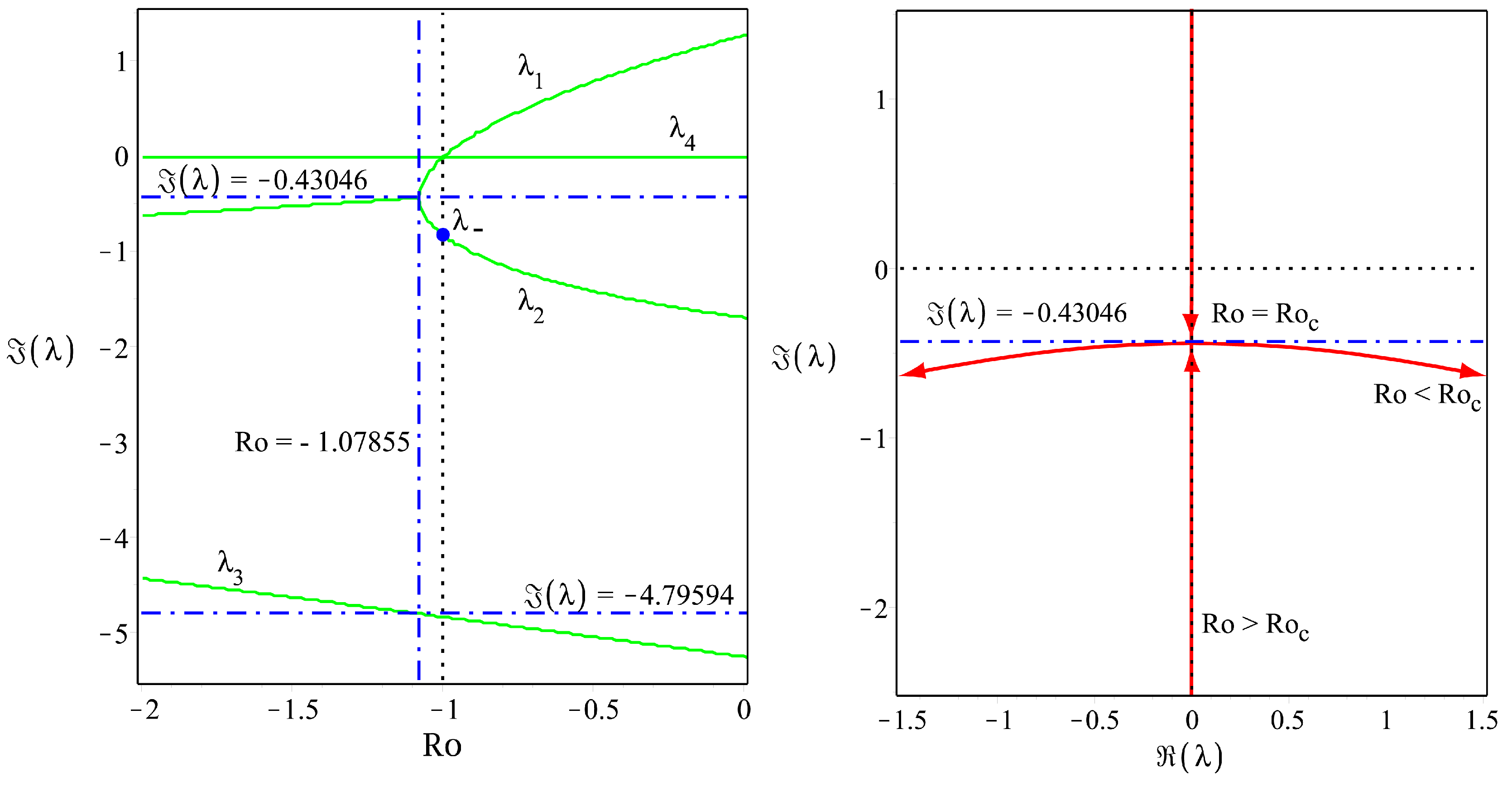
3. Diffusive Instabilities of Baroclinic Lenticular Vortices

3.1. Nonlinear Equations of Motion and the Base State

Following [29], we model a circular lenticular vortex immersed in a deep, vertically stratified viscous incompressible Newtonian fluid under gravity and rotation. The coordinate system $(\tilde{r},\tilde{\theta },\tilde{z})$ rotates with angular velocity $(0,0,f/2)$ , where f (the Coriolis parameter) can be positive or negative. Gravity $(0,0,-g)$ is antiparallel to the $\tilde{z}$ -axis, and the centrifugal force is negligible [29,42]. The ambient fluid is linearly stratified along the direction of gravity, incorporating viscosity ($\nu$ ) and diffusion ($\kappa$ ) of the stratifying agent, unlike McIntyre’s study [42], which considered viscosity and thermal diffusion.

The baroclinic vortex, modeled as an ellipsoid with angular velocity $(0,0,\tilde{\Omega }(\tilde{r},\tilde{z}))$ , is embedded in a motionless (in the rotating frame), stratified fluid far from the vortex core, with boundaries assumed non-influential. Adopting the Boussinesq-Oberbeck approximation, we describe the stable background density gradient as $-{\displaystyle \frac{{\rho }_0{N}^2}{g}}$ , where $N=\sqrt{-{\displaystyle \frac{g}{{\rho }_0}}{\displaystyle \frac{\mathrm{d}\tilde{\rho }}{\mathrm{d}\tilde{z}}}}$ is the Brunt-Väisälä frequency. The total density is then given as [29]:

$$\tilde{\rho }(\tilde{r},\tilde{z})={\rho }_0-{\rho }_0{\displaystyle \frac{N^2}{g}}\tilde{z}+{\tilde{\rho }}_A(\tilde{r},\tilde{z}),$$

(32)

where the density anomaly ${\tilde{\rho }}_A$ captures the vortex’s internal stratification.

Introducing characteristic scales $R,Z,U,W$ , with $W=\alpha U$ and $\alpha =Z/R$ , and the time scale $R/U$ yields the scales ${\rho }_{0}fRU$ for pressure and ${\rho }_{0}fU/\left(g\alpha \right)$ for density [29]. The horizontal Froude number $F_h$ , vortex Rossby number $Ro$ , and Burger number $Bu$ are defined as:

$$F_h={\displaystyle \frac{U}{RN}},Ro={\displaystyle \frac{U}{fR}},Bu={\displaystyle \frac{{\alpha }^{2}R{o}^2}{F_h^2}}.$$

(33)

Anticyclonic (cyclonic) eddies correspond to $Ro<0$ ($Ro>0$ ) for $U>0$ . The Schmidt and Ekman numbers are given by:

$$Sc={\displaystyle \frac{\nu }{\kappa }},Ek={\displaystyle \frac{\nu }{f{R}^2}}={\displaystyle \frac{Ro}{Re}},$$

(34)

where $Re=UR/\nu >0$ is the Reynolds number. Both $Ek$ and $Ro$ can be positive or negative but share the same sign.

The background flow is assumed to be purely azimuthal:

$${\mathit{u}}_B=\left(0,r\Omega (r,z),0\right),$$

(35)

where $\Omega (r,z)=(R/U)\tilde{\Omega }=e^{-r^2-z^2}>0$ is the dimensionless angular velocity. Then, from (32), the dimensionless density is:

$$\rho (r,z)={\displaystyle \frac{g\alpha }{fU}}-z{\displaystyle \frac{Bu}{Ro}}+{\rho }_A(r,z),$$

(36)

with the density anomaly:

$${\rho }_A(r,z)=-z\Omega \left(1+Ro\Omega \right),$$

(37)

and $r=\tilde{r}/R$ , $z=\tilde{z}/Z$ .

With the scaling adopted, the dimensionless equations of motion are:

$$\begin{array}{cc}\hfill \nabla ·\mathit{u}& =0,\hfill \end{array}$$

(38a)

$$\begin{array}{cc}\hfill Ro{\displaystyle \frac{d\mathit{u}}{dt}}+{\mathit{e}}_z\times \mathit{u}& =-{\nabla }_{\alpha }P-{\displaystyle \frac{\rho }{{\alpha }^2}}{\mathit{e}}_z+Ek\mathcal{D}\mathit{u},\hfill \end{array}$$

(38b)

$$\begin{array}{cc}\hfill Ro{\displaystyle \frac{d\rho }{dt}}& ={\displaystyle \frac{Ek}{Sc}}\mathcal{D}\rho ,\hfill \end{array}$$

(38c)

where $t=\tilde{t}U/R$ , $\mathit{u}={(u_r,u_{\theta },u_z)}^T$ is the velocity field, P is the pressure, $d/dt={\partial }_t+\mathit{u}·\nabla$ , $\mathcal{D}={\nabla }_h^2+{\alpha }^{-2}{\partial }_z^2$ , ${\nabla }_h^2$ is the horizontal Laplacian, and ${\nabla }_{\alpha }={({\partial }_r,r^{-1}{\partial }_{\theta },{\alpha }^{-2}{\partial }_z)}^T$ is the modified gradient operator [29].

3.2. Linearization and Geometrical Optics Equations

Linearizing (38) about the base state (35), assuming $Ek={ϵ}^2\widetilde{Ek}$ [29,40], and seeking solutions in the asymptotic form (1), we derive transport equations for the leading-order amplitudes ${\mathit{u}}^{\left(0\right)}$ and ${\rho }^{\left(0\right)}$ of a localized wave packet moving along the base flow streamlines [29]:

$$\begin{array}{ccc}\hfill Ro{\displaystyle \frac{d{\mathit{u}}^{\left(0\right)}}{dt}}& =& -Ek{\mathit{u}}^{\left(0\right)}-Ro\left(\mathcal{I}-2{\displaystyle \frac{\mathcal{K}}{{\beta }^2}}\right)\mathcal{U}{\mathit{u}}^{\left(0\right)}-\left(\mathcal{I}-{\displaystyle \frac{\mathcal{K}}{{\beta }^2}}\right){\mathit{e}}_z\times {\mathit{u}}^{\left(0\right)}-\left(\mathcal{I}-{\displaystyle \frac{\mathcal{K}}{{\beta }^2}}\right){\mathit{e}}_z{\displaystyle \frac{{\rho }^{\left(0\right)}}{{\alpha }^2}},\hfill \\ \hfill Ro{\displaystyle \frac{d{\rho }^{\left(0\right)}}{dt}}& =& -{\displaystyle \frac{Ek}{Sc}}{\rho }^{\left(0\right)}-\left({\mathcal{B}}^{T}Ro-{\mathit{e}}_z^{T}Bu\right){\mathit{u}}^{\left(0\right)},\hfill \end{array}$$

(39)

where $Ek=\widetilde{Ek}\left|{\mathit{k}}_{\alpha }^T\mathit{k}\right|$ , $d/dt={\partial }_t+{\mathit{u}}_B·\nabla$ , $\mathcal{I}$ is the $3\times 3$ identity matrix, $\mathcal{U}=\nabla {\mathit{u}}_B$ , and $\mathcal{B}=\nabla {\rho }_A$ , given by:

$$\mathcal{U}=\left(\begin{array}{ccc}0& -\Omega & 0\\ \Omega +r{\partial }_r\Omega & 0& r{\partial }_z\Omega \\ 0& 0& 0\end{array}\right),\mathcal{B}=\left(\begin{array}{c}-z{\displaystyle \frac{\partial \Omega }{\partial r}}\left(1+2Ro\Omega \right)\\ 0\\ -z{\displaystyle \frac{\partial \Omega }{\partial z}}\left(1+2Ro\Omega \right)-\Omega \left(1+Ro\Omega \right)\end{array}\right).$$

(40)

The matrix $\mathcal{K}={\mathit{k}}_{\alpha }{\mathit{k}}^T$ in (39) is defined by the wavevector $\mathit{k}=\nabla \Phi ={(k_r,k_{\theta },k_z)}^T$ and its scaled counterpart ${\mathit{k}}_{\alpha }={\nabla }_{\alpha }\Phi ={(k_r,k_{\theta },k_z/{\alpha }^2)}^T$ , where $\mathit{k}$ satisfies the eikonal equation:

$${\displaystyle \frac{d\mathit{k}}{dt}}=-{\mathcal{U}}^T\mathit{k}.$$

(41)

From (41), we find $k_r$ and $k_z$ to be constants, while $k_{\theta }=0$ . Introducing scaled wavenumbers $q_r=k_r/\beta$ and $q_z=k_z/\beta$ , where ${\beta }^2={\mathit{k}}^T{\mathit{k}}_{\alpha }=k_r^2+k_{\theta }^2+k_z^2/{\alpha }^2$ , we have $q_r=\sqrt{1-q_z^2/{\alpha }^2}$ . The matrix $\mathcal{K}$ can then be expressed as:

$$\mathcal{K}={\mathit{q}}_{\alpha }{\mathit{q}}^T,\mathit{q}={(q_r,0,q_z)}^T,{\mathit{q}}_{\alpha }={(q_r,0,q_z/{\alpha }^2)}^T.$$

3.3. Dispersion Relation

As shown in [24,29], eliminating $u_z^{\left(0\right)}$ from (39) reduces the system to three equations for $u_r^{\left(0\right)}$ , $u_{\theta }^{\left(0\right)}$ , and ${\rho }^{\left(0\right)}$ . Introducing the complex growth rate $\lambda$ and azimuthal wavenumber m via the ansatz:

$$\left(u_r^{\left(0\right)},u_{\theta }^{\left(0\right)},{\rho }^{\left(0\right)}\right)=\left({\widehat{u}}_r^{\left(0\right)},{\widehat{u}}_{\theta }^{\left(0\right)},{\widehat{\rho }}^{\left(0\right)}\right)exp\left(\lambda t+im\theta \right),$$

yields the eigenvalue problem $\mathcal{H}\xi =\widehat{\lambda }\xi$ , where $\xi ={\left({\widehat{u}}_r^{\left(0\right)},{\widehat{u}}_{\theta }^{\left(0\right)},{\widehat{\rho }}^{\left(0\right)}\right)}^T$ , $\widehat{\lambda }=Ro\left(\lambda +im\Omega \right)+Ek$ , and $\mathcal{H}$ is a $3\times 3$ matrix:

$$\mathcal{H}=\left(\begin{array}{ccc}0& {\displaystyle \frac{q_z^2}{{\alpha }^2}}{\displaystyle \frac{2j}{r^2}}& {\displaystyle \frac{q_r{q}_z}{{\alpha }^2}}\\ -{\displaystyle \frac{r^2\left(q_z{\kappa }_r^2-q_r{\kappa }_z^2\right)}{2q_{z}j}}& 0& 0\\ -{\displaystyle \frac{Ro\left(q_z{\partial }_r{\rho }_A-q_r{\partial }_z{\rho }_A\right)+q_{r}Bu}{q_z}}& 0& Ek{\displaystyle \frac{Sc-1}{Sc}}\end{array}\right),$$

where $j(r,z)$ is the angular momentum per unit mass, ${\kappa }_r$ the epicyclic frequency, and ${\kappa }_z$ the vertical oscillation frequency, given by:

$$j={\displaystyle \frac{r^2}{2}}\left(1+2Ro\Omega \right),{\kappa }_r^2=r^{-3}{\displaystyle \frac{\partial j^2}{\partial r}},{\kappa }_z^2=r^{-3}{\displaystyle \frac{\partial j^2}{\partial z}}.$$

The dispersion relation $p\left(\widehat{\lambda }\right)=det\left(\mathcal{H}-\widehat{\lambda }\mathcal{I}\right)$ is a cubic polynomial:

$$p\left(\widehat{\lambda }\right)={\widehat{\lambda }}^3+Ek{\displaystyle \frac{1-Sc}{Sc}}{\widehat{\lambda }}^2+\left({\gamma }_1+{\gamma }_2\right)\widehat{\lambda }+Ek{\displaystyle \frac{1-Sc}{Sc}}{\gamma }_1,$$

(42)

where

$${\gamma }_1={\displaystyle \frac{q_z}{{\alpha }^2}}\left(q_z{\kappa }_r^2-q_r{\kappa }_z^2\right),{\gamma }_2={\displaystyle \frac{q_r}{{\alpha }^2}}\left[Ro\left(q_z{\displaystyle \frac{\partial {\rho }_A}{\partial r}}-q_r{\displaystyle \frac{\partial {\rho }_A}{\partial z}}\right)+q_{r}Bu\right]$$

(43)

and ${\partial }_r{\rho }_A$ and ${\partial }_z{\rho }_A$ are given by (40). The parameters ${\gamma }_1$ and ${\gamma }_2$ represent shear effects from differential rotation and buoyancy effects from ambient density stratification, respectively. Both can take positive or negative values depending on the vortex and stratification properties.

3.4. Stability Analysis

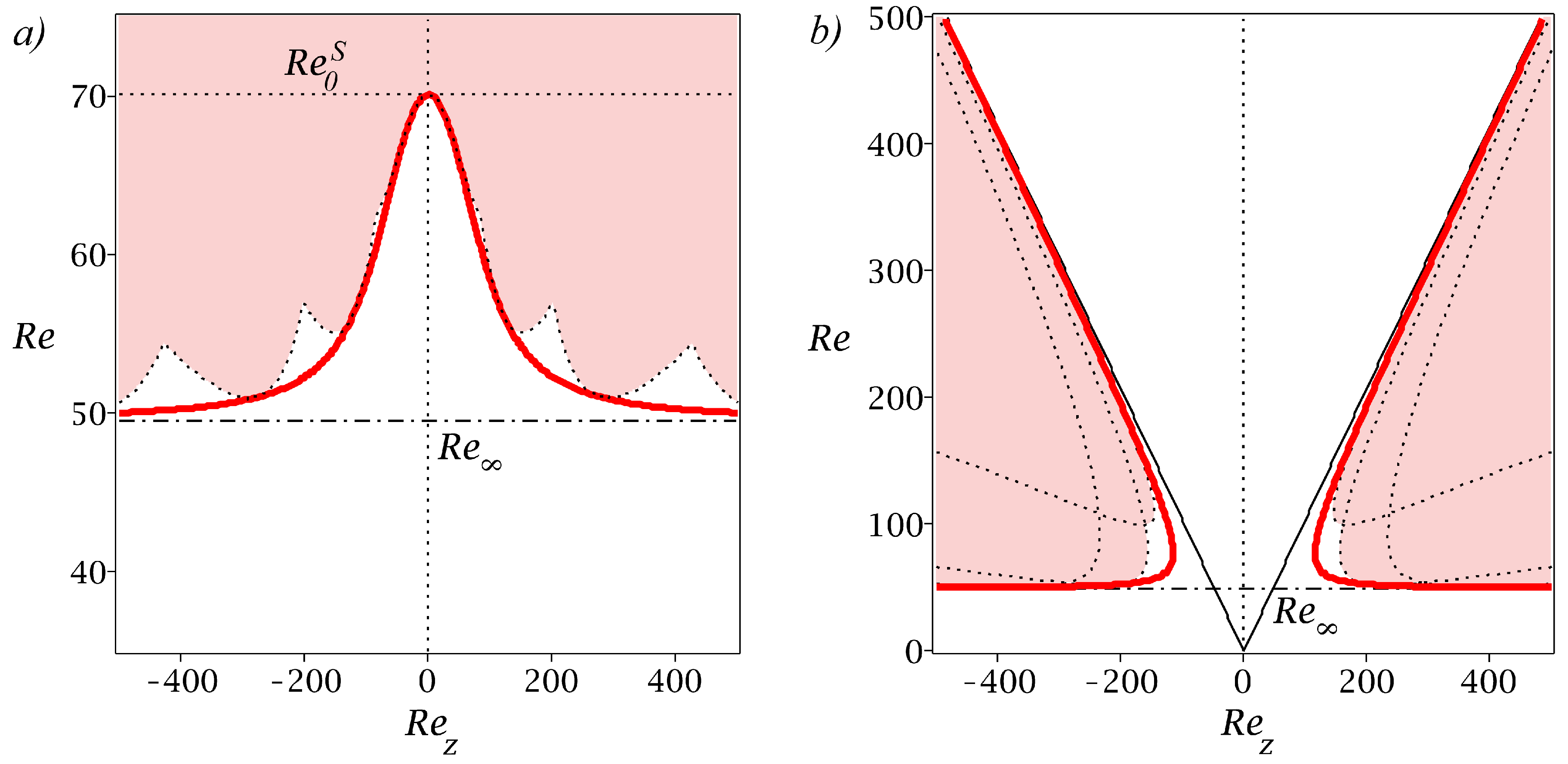
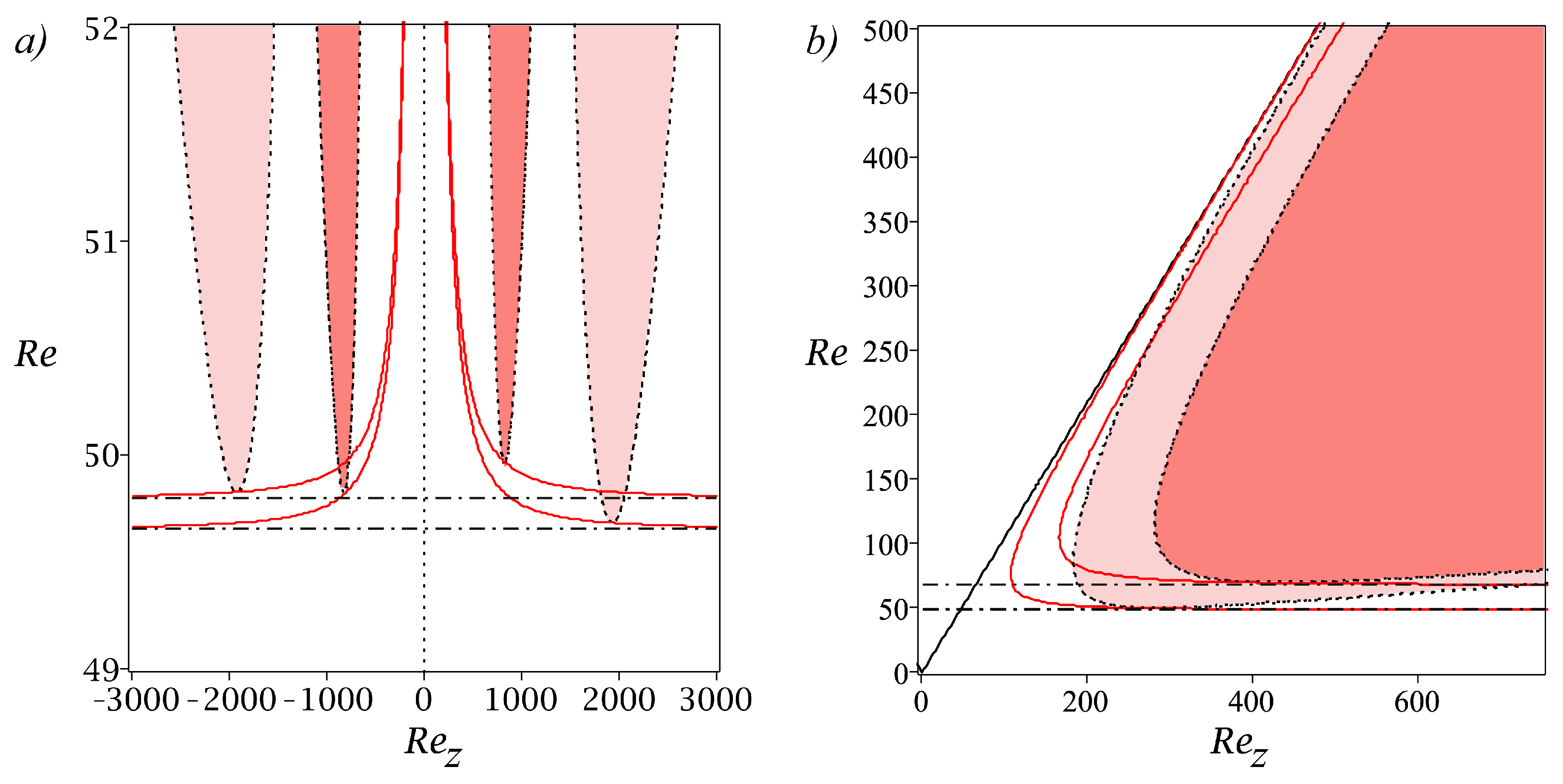
3.4.1. Diffusionless and $Sc=1$ Cases

When $Ek=0$ or $Sc=1$ , the dispersion relation (42) simplifies, factorizing into a product of quadratic and linear polynomials in $\widehat{\lambda }$ , allowing explicit solutions.

In these cases, the eigenvalues associated with centrifugal instability are given by [29]:

$${\lambda }^{\pm }=-{\displaystyle \frac{im\Omega }{Ro}}\pm {\displaystyle \frac{1}{Ro}}\sqrt{-\left({\gamma }_1+{\gamma }_2\right)},$$

(44)

leading to the instability criterion:

$${\gamma }_1+{\gamma }_2<0.$$

(45)

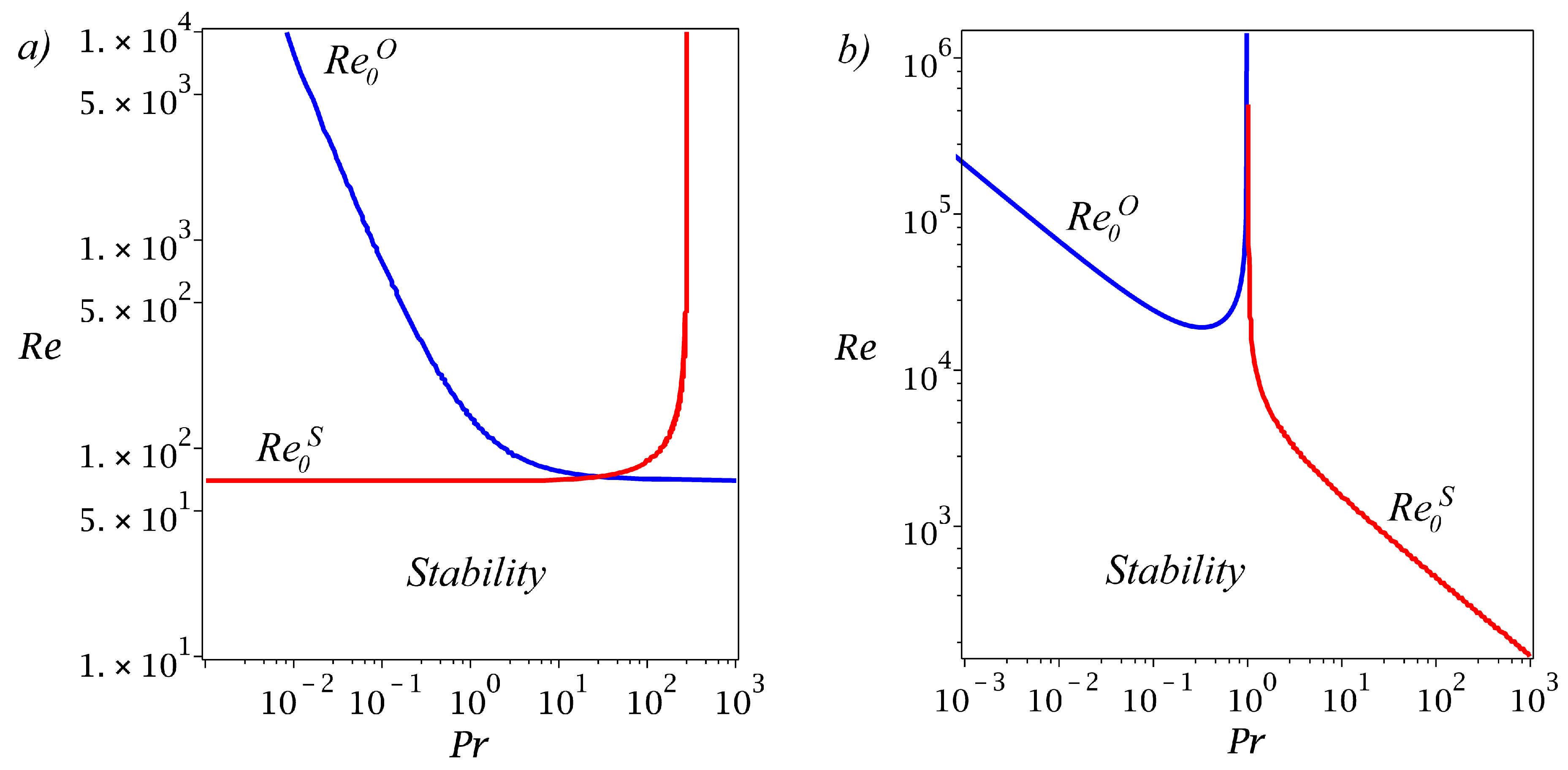
3.4.2. Criteria for Visco-Diffusive Monotonic and Oscillatory Instabilities

Applying the Bilharz criterion to (42) with $Ek/Ro=1/Re>0$ , the base flow is stable for $Sc>0$ and $m=0$ if and only if the following three inequalities are satisfied simultaneously [29]:

$$\begin{array}{cc}\hfill 2{(Sc+1)}^{2}E{k}^2+Sc(2Sc{\gamma }_1+{\gamma }_2(Sc+1))& >0,\hfill \end{array}$$

(46a)

$$\begin{array}{cc}\hfill (Sc+2)E{k}^2+Sc({\gamma }_1+{\gamma }_2)& >0,\hfill \end{array}$$

(46b)

$$\begin{array}{cc}\hfill E{k}^2+Sc{\gamma }_2+{\gamma }_1& >0.\hfill \end{array}$$

(46c)

Conditions (46) are linear in ${\gamma }_1$ and ${\gamma }_2$ , allowing the stability domain to be represented in the $({\gamma }_1,{\gamma }_2)$ -plane [29,51]. The stability region is the intersection of the half-planes defined by (46a)–(46c), as shown in Figure 4.

The intersection of the neutral stability lines corresponding to the criteria (46) defines a codimension-2 point with coordinates [29,51]:

$${\gamma }_1=E{k}^2{\displaystyle \frac{1+Sc}{1-Sc}},{\gamma }_2={\displaystyle \frac{2E{k}^2}{Sc(Sc-1)}}.$$

(47)

At this point, the slopes of the lines defining the inequalities (46a), (46b), and (46c) are:

$$\begin{array}{c}\hfill {\sigma }_1=-{\displaystyle \frac{2Sc}{Sc+1}},{\sigma }_2=-1,{\sigma }_3=-{\displaystyle \frac{1}{Sc}}.\end{array}$$

(48)

The relationships between the slopes depend on $Sc$ [29]:

$$\begin{array}{ccc}\hfill \left.\begin{array}{c}\hfill -1\ge {\sigma }_1>-2\\ \hfill {\sigma }_2=-1\\ \hfill -1\le {\sigma }_3<0\end{array}\right\}& \mathrm{if}& 1\le Sc<+\infty ,\hfill \\ \hfill \left.\begin{array}{c}\hfill 0>{\sigma }_1>-1\\ \hfill {\sigma }_2=-1\\ \hfill -\infty <{\sigma }_3<-1\end{array}\right\}& \mathrm{if}& 0<Sc<1.\hfill \end{array}$$

(49)

Actually, reversed inequality (46c) determines monotonic axisymmetric (MA) instability, corresponding to a monotonically growing perturbation, while the reversed inequality (46a) stands for oscillatory axisymmetric (OA) instability, i.e. growing oscillation.

For $0<Sc<1$ , the slope of the neutral stability line defining (46c) is steeper than that defining (46a), Figure 4(a-c). This causes the stability domain to be convex, with a wedge extending into the region of centrifugal instability. The codimension-2 point, a well-known phenomenon in hydrodynamics [24], existing for ${\gamma }_2<0$ , separates OA and MA instability regions. Diffusion destabilizes centrifugally stable vortices due to difference of the slopes ${\sigma }_1$ and ${\sigma }_3$ from ${\sigma }_2=-1$ , if the absolute values of ${\gamma }_1$ and ${\gamma }_2$ are large enough, as shown in Figure 4(a-c).

At $Sc=1$ , the slopes (48) converge (${\sigma }_1={\sigma }_2={\sigma }_3=-1$ ), and the stability boundaries of the diffusionless and visco-diffusive systems coincide for $Ek\to 0$ . However, for $Ek\ne 0$ , viscosity and diffusion can stabilize centrifugally unstable diffusionless vortices, Figure 4(d).

For $Sc>1$ , the codimension-2 point reappears at infinity for ${\gamma }_2>0$ and moves along an asymptotic direction until it reaches the final location at ${\gamma }_1=-E{k}^2$ and ${\gamma }_2=0$ as $Sc\to \infty$ (Figure 4(f)). This qualitative change in location of the codimension-2 point is accompanied by the exchange of the stability criteria: the condition (46c) becomes dominating over (46a) and vice versa, Figure 4(e,f).

Figure 4 provides evidence that stability boundary consisting of two straight lines that intersect at a codimension-2 point in the $({\gamma }_1,{\gamma }_2)$ -plane exhibit a qualitative change at $Sc=1$ such that for $Sc<1$ ($Sc>1$ ) the upper (lower) line corresponds to the onset of MA instability and the lower (upper) line to the onset of OA instability.

Even as $Ek\to 0$ , these qualitative phenomena persist, aligning with the properties of McIntyre instability [42] and other dissipation-induced instabilities [3,25,27]. The existence of the codimension-2 point qualitatively distinguishes the diffusive case from the diffusionless one, where the onset of instability corresponds to the monotonic axisymmetric centrifugal instability only, Figure 4(d). Hence, the oscillatory axisymmetric instability is a genuine dissipation-induced instability [25] which is as important as the monotonic axisymmetric one despite its relatively low growth rate, because in a large set of parameters the oscillatory axissymmetric modes are the first to be destabilized by the differential diffusion of mass and momentum.

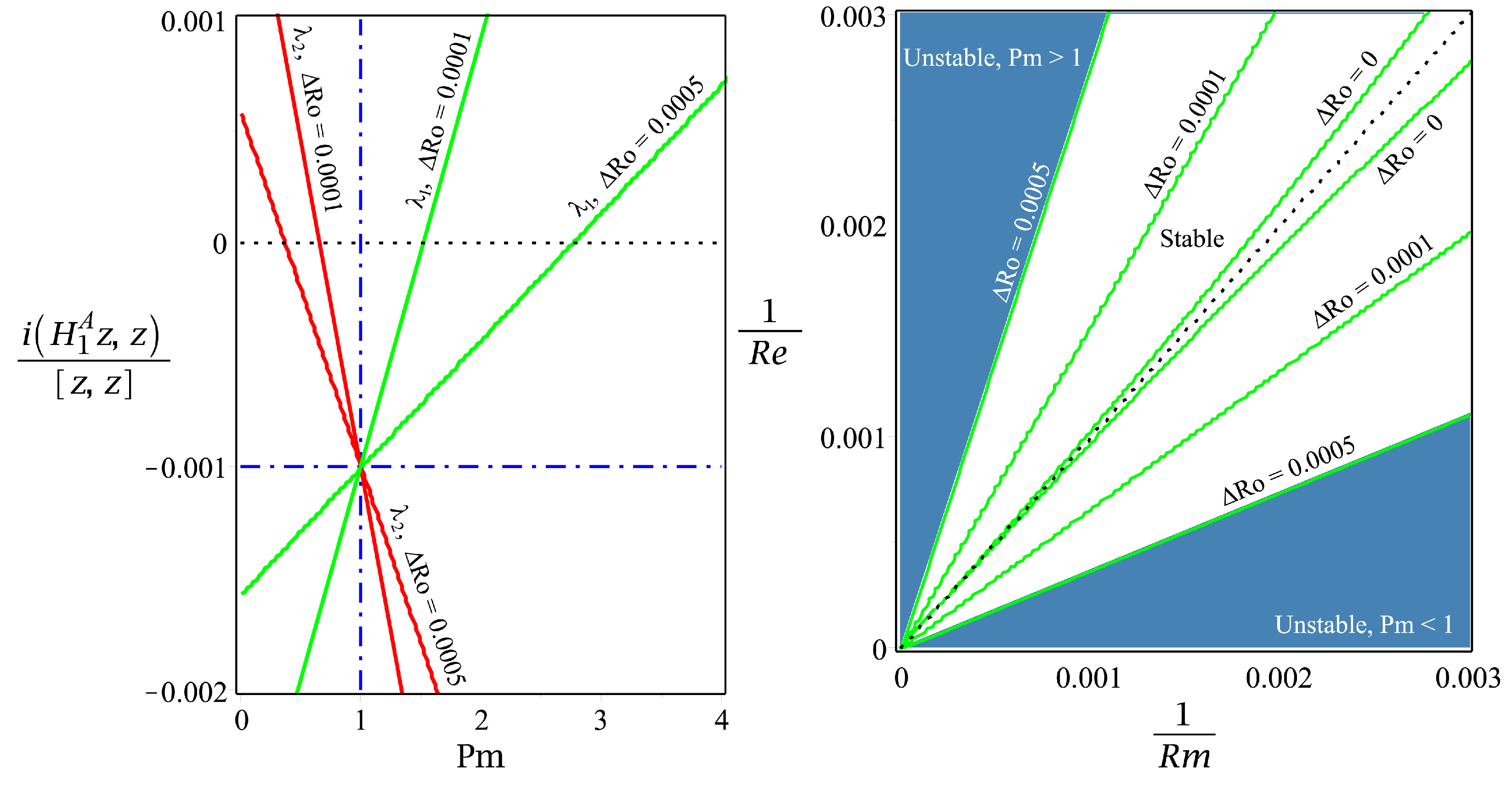
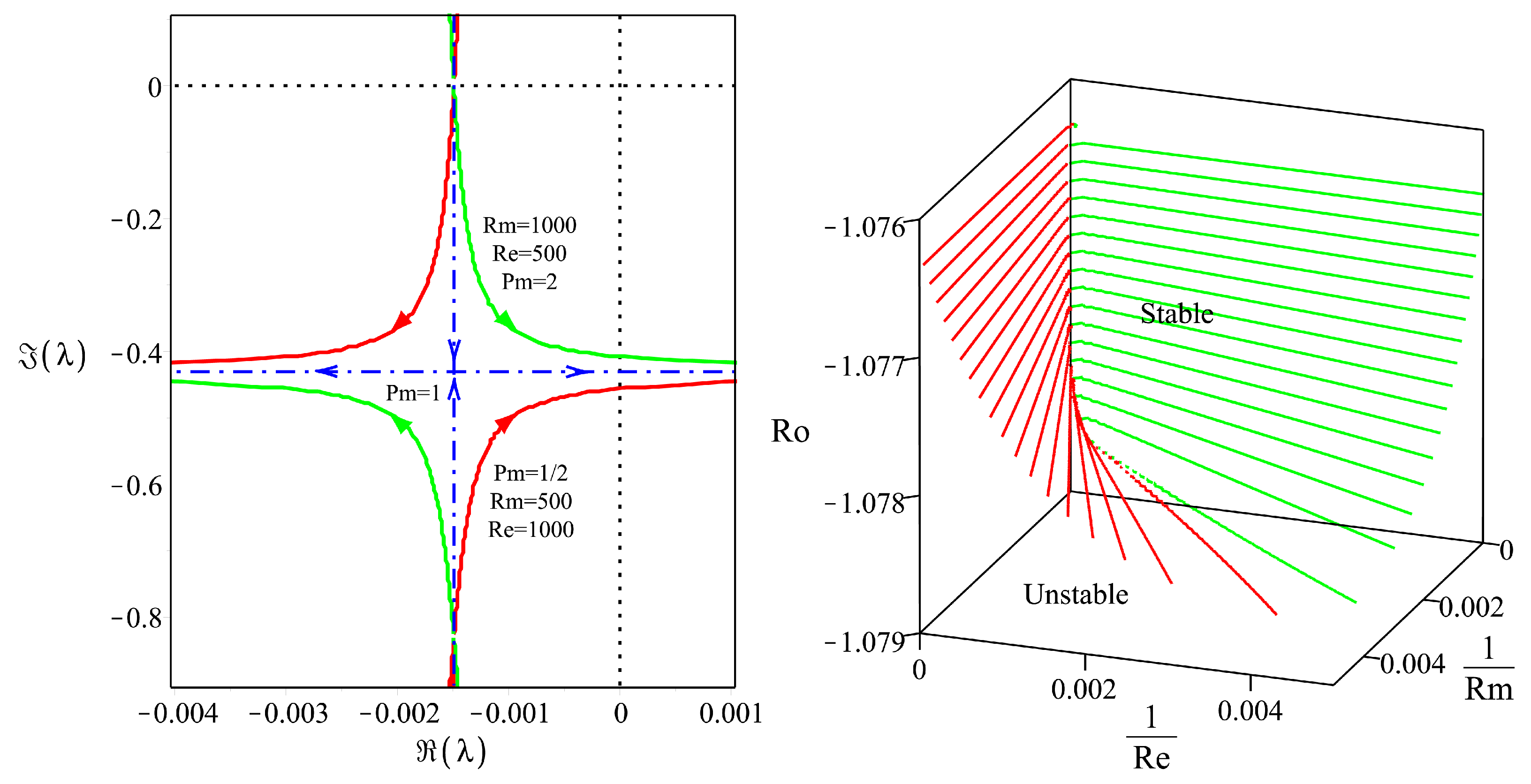
4. Spiral Poiseuille Flow with Radial Temperature Gradient

4.1. Nonlinear Equations of Motion

Following [4,24,26], we consider an incompressible Newtonian fluid with constant reference density $\rho$ and constant thermal expansion coefficient $\alpha$ , kinematic viscosity $\nu$ , and thermal diffusivity $\kappa$ within an infinitely long cylindrical annulus with a gap width $d=R_2-R_1$ , where $R_1$ is the radius of the inner cylinder at temperature $T_1$ , rotating with angular velocity ${\Omega }_1$ , and $R_2$ is the radius of the outer cylinder at temperature $T_2=T_1-\Delta T$ , rotating with angular velocity ${\Omega }_2$ . The Z-axis of the cylindrical coordinates $(R,\phi ,Z)$ aligns with the common rotation axis of the cylinders. We assume the inner cylinder velocity, $V_0={\Omega }_1{R}_1$ , as the velocity scale, d as the length scale, $d/V_0$ as the time scale, and $\rho V_0^2$ as the pressure scale to write the dimensionless governing equations in the Boussinesq-Oberbeck approximation:

$$\begin{array}{ccc}\hfill & \nabla ·\mathit{u}=0,& \hfill \end{array}$$

(50a)

$$\begin{array}{ccc}& {\displaystyle \frac{d\mathit{u}}{dt}}+\nabla p-{\displaystyle \frac{1}{Re}}{\nabla }^2\mathit{u}+\gamma {\displaystyle \frac{v^2}{r}}{\mathit{e}}_r\theta =0,& \hfill \end{array}$$

(50b)

$$\begin{array}{ccc}& {\displaystyle \frac{d\theta }{dt}}-{\displaystyle \frac{1}{RePr}}{\nabla }^2\theta =0.& \hfill \end{array}$$

(50c)

Here p is pressure, $\mathit{u}=(u,v,w)$ the velocity field, $\theta ={\displaystyle \frac{T-T_2}{\Delta T}}$ the temperature deviation, $\Delta T=T_1-T_2$ , ${\displaystyle \frac{d}{dt}}={\displaystyle \frac{\partial }{\partial t}}+\mathit{u}·\nabla$ , $r={\displaystyle \frac{R}{d}}$ , and $z={\displaystyle \frac{Z}{d}}$ . The dimensionless control parameter $Re={\displaystyle \frac{V_{0}d}{\nu }}$ in Eq. (50) is the Reynolds number associated with the rotation of the inner cylinder, $Pr={\displaystyle \frac{\nu }{\kappa }}$ is the Prandtl number, and $\gamma =\alpha \Delta T$ , with $\gamma <0$ for inward heating $(T_1<T_2)$ [24,26].

4.2. Base State

We assume the base flow to be the Spiral Poiseuille Flow (SPF), which combines the annular Poiseuille flow, characterized by an axial velocity driven by an external pressure gradient, and the circular Couette flow, defined by the azimuthal velocity profile induced by the differential rotation of the cylinders. The two-component dimensionless velocity field of SPF and the base temperature distribution are expressed as

$${\mathit{u}}_B\left(r\right)=\left(0,V\left(r\right),S^{-1}W\left(r\right)\right),{\theta }_B\left(r\right)=\Theta \left(r\right),$$

(51)

where $S={\displaystyle \frac{V_0}{W_m}}$ is the swirl parameter, $W_m$ is the mean velocity of the annular Poiseuille flow, and $W\left(r\right)$ , $V\left(r\right)$ , and $\Theta \left(r\right)$ are the dimensionless axial, azimuthal, and temperature profiles, respectively. Defining the axial Reynolds number as $R{e}_z={\displaystyle \frac{W_{m}d}{\nu }}$ , we can write $S={\displaystyle \frac{Re}{R{e}_z}}$ .

The axial velocity profile $W\left(r\right)$ of SPF is given by [4]:

$$W\left(r\right)={\displaystyle \frac{2{(1-\eta )}^{2}ln\eta }{{\eta }^2-({\eta }^2+1)ln\eta -1}}\left[r^2-r_2^2+{\displaystyle \frac{1}{ln\eta }}{\displaystyle \frac{1+\eta }{1-\eta }}ln\left({\displaystyle \frac{r}{r_2}}\right)\right].$$

(52)

The azimuthal velocity profile $V\left(r\right)$ in (51) corresponds to the circular Couette flow [4,24]:

$$V\left(r\right)={\displaystyle \frac{\eta }{1+\eta }}\left({\displaystyle \frac{1-\mu }{{(1-\eta )}^2}}{\displaystyle \frac{1}{r}}-{\displaystyle \frac{{\eta }^2-\mu }{{\eta }^2}}r\right).$$

(53)

The temperature profile $\Theta \left(r\right)$ in (51) is expressed as [4,24]:

$$\Theta \left(r\right)={\displaystyle \frac{ln\left[r\right(1-\eta \left)\right]}{ln\eta }}.$$

(54)

Here, the geometric and rotational parameters are defined as follows:

• $\eta =R_1/R_2$ , the ratio of the inner ($R_1$ ) to outer ($R_2$ ) cylinder radii,
• $\mu ={\Omega }_2/{\Omega }_1$ , the ratio of the angular velocities of the outer (${\Omega }_2$ ) to inner (${\Omega }_1$ ) cylinders,
• $r_1={\displaystyle \frac{\eta }{1-\eta }}$ , the inner radius in dimensionless form,
• $r_2={\displaystyle \frac{1}{1-\eta }}$ , the outer radius in dimensionless form, and
• $r_g=\sqrt{r_1{r}_2}={\displaystyle \frac{\sqrt{\eta }}{1-\eta }}$ , the geometric mean radius, at which we will evaluate all parameters in subsequent analyses.

4.3. Geometrical Optics Equations

After linearization of the governing equations (50) about the base SPF flow (51), assuming $Re\sim {ϵ}^{-2}$ in the linearized equations [40] and seeking solution in the asymptotic form (1), we find the transport equations for the leading-order amplitudes ${\mathit{u}}^{\left(0\right)}$ and ${\theta }^{\left(0\right)}$ of the localized wave packet moving along the streamlines of the base flow written in the stationary frame [24,26]:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d{\mathit{u}}^{\left(0\right)}}{dt}}+{\displaystyle \frac{{\left|\mathit{k}\right|}^2}{Re}}{\mathit{u}}^{\left(0\right)}& =& -\left(\mathcal{I}-{\displaystyle \frac{\mathit{k}{\mathit{k}}^T}{{\left|\mathit{k}\right|}^2}}\right)\left(\gamma {\displaystyle \frac{V^2}{r}}{\mathit{e}}_r-Ri{\mathit{e}}_z\right){\theta }^{\left(0\right)}\hfill \\ & & -\left(\mathcal{I}-2{\displaystyle \frac{\mathit{k}{\mathit{k}}^T}{{\left|\mathit{k}\right|}^2}}\right)\mathcal{U}{\mathit{u}}^{\left(0\right)}-2\gamma \Theta \Omega \left(\mathcal{I}-{\displaystyle \frac{\mathit{k}{\mathit{k}}^T}{{\left|\mathit{k}\right|}^2}}\right){\mathit{e}}_r{\mathit{e}}_{\phi }^T{\mathit{u}}^{\left(0\right)},\hfill \\ \hfill {\displaystyle \frac{d{\theta }^{\left(0\right)}}{dt}}+{\displaystyle \frac{{\left|\mathit{k}\right|}^2}{RePr}}{\theta }^{\left(0\right)}& =& -{\left(\nabla \Theta \right)}^T{\mathit{u}}^{\left(0\right)},\hfill \end{array}$$

(55)

where $\mathcal{I}$ is the $3\times 3$ identity matrix, and the eikonal equation determining the evolution of the wavevector $\mathit{k}=(k_r,k_{\phi },k_z)={ϵ}^{-1}\nabla \Phi$ , $\mathit{k}·{\mathit{u}}^{\left(0\right)}=0$ , in the stationary frame:

$${\displaystyle \frac{d\mathit{k}}{dt}}=-{\mathcal{U}}^T\mathit{k}.$$

(56)

The gradients of the base state are given by

$$\mathcal{U}=\nabla {\mathit{u}}_B=\left(\begin{array}{ccc}0& -\Omega & 0\\ (1+2Ro)\Omega & 0& 0\\ {\displaystyle \frac{1}{S}}DW& 0& 0\end{array}\right),\nabla \Theta =\left(\begin{array}{c}D\Theta \\ 0\\ 0\end{array}\right)$$

(57)

with $D={\displaystyle \frac{d}{dr}}$ , $\Omega ={\displaystyle \frac{V}{r}}$ , and the Rossby number defined as $Ro={\displaystyle \frac{rD\Omega }{2\Omega }}$ [21].

4.4. Dispersion Relation

From Eq. (56), it follows that under the condition [8,10,26]

$$k_{\phi }=-\overline{DW}{k}_z,\mathrm{with}\overline{DW}={\displaystyle \frac{DW}{2\Omega RoS}},$$

(58)

the components of the wave vector $\mathit{k}$ remain time-independent in the rotating frame: $k_r=\mathrm{const}.$ , $k_{\phi }=\mathrm{const}.$ , $k_z=\mathrm{const}.$ . This condition describes the most unstable and exponentially growing 3D perturbations in swirling flows that exhibit helical symmetry, i.e., remain invariant along circular helices with a pitch of $2\pi r\overline{DW}$ [8,10,26]. Additionally, under the constraint (58) the amplitude equations (55) are autonomous in the rotating frame [8,10,26].

Writing explicitly the material derivative in the left side of the amplitude equations, explicitly computing its right hand side, exploiting the relation

$${\left|\mathit{k}\right|}^2=k_r^2+k_z^2\left[1+{\overline{DW}}^2\right],$$

(59)

and assuming ${\mathit{u}}^{\left(0\right)},{\theta }^{\left(0\right)}\sim e^{st+\mathrm{i}m\phi +i{k}_{z}z}$ , where $s=\sigma +\mathrm{i}\omega$ , $\sigma ,\omega \in \mathbb{R}$ , is the complex growth rate, and $m=k_{\phi }r$ and $k_z$ are the integer azimuthal and real axial wavenumbers, we find the dispersion relation as the characteristic polynomial

$$p\left(\lambda \right)=-det(\mathcal{H}-\lambda \mathcal{I})=a_3{\lambda }^3+a_2{\lambda }^2+a_1\lambda +a_0$$

(60)

of the matrix $\mathcal{H}$ , where $\lambda =\sigma +\mathrm{i}\left(\omega +m\Omega +k_{z}W/S\right)$ and

$$\mathcal{H}=\left(\begin{array}{ccc}-2\Omega \overline{DW}{\displaystyle \frac{k_r{k}_z}{{\left|\mathit{k}\right|}^2}}-{\displaystyle \frac{{\left|\mathit{k}\right|}^2}{Re}}\hfill & 2\Omega (1-\gamma \Theta )\left(1-{\displaystyle \frac{k_r^2}{{\left|\mathit{k}\right|}^2}}\right)\hfill & -r\gamma {\Omega }^2\left(1-{\displaystyle \frac{k_r^2}{{\left|\mathit{k}\right|}^2}}\right)\hfill \\ -2\Omega \left(Ro+{\displaystyle \frac{k_r^2+k_z^2}{{\left|\mathit{k}\right|}^2}}\right)\hfill & 2\Omega (1-\gamma \Theta )\overline{DW}{\displaystyle \frac{k_r{k}_z}{{\left|\mathit{k}\right|}^2}}-{\displaystyle \frac{{\left|\mathit{k}\right|}^2}{Re}}\hfill & -r\gamma {\Omega }^2\overline{DW}{\displaystyle \frac{k_r{k}_z}{{\left|\mathit{k}\right|}^2}}\hfill \\ -D\Theta \hfill & 0\hfill & {\displaystyle \frac{{\left|\mathit{k}\right|}^2}{Re}}{\displaystyle \frac{Pr-1}{Pr}}-{\displaystyle \frac{{\left|\mathit{k}\right|}^2}{Re}}\hfill \end{array}\right).$$

(61)

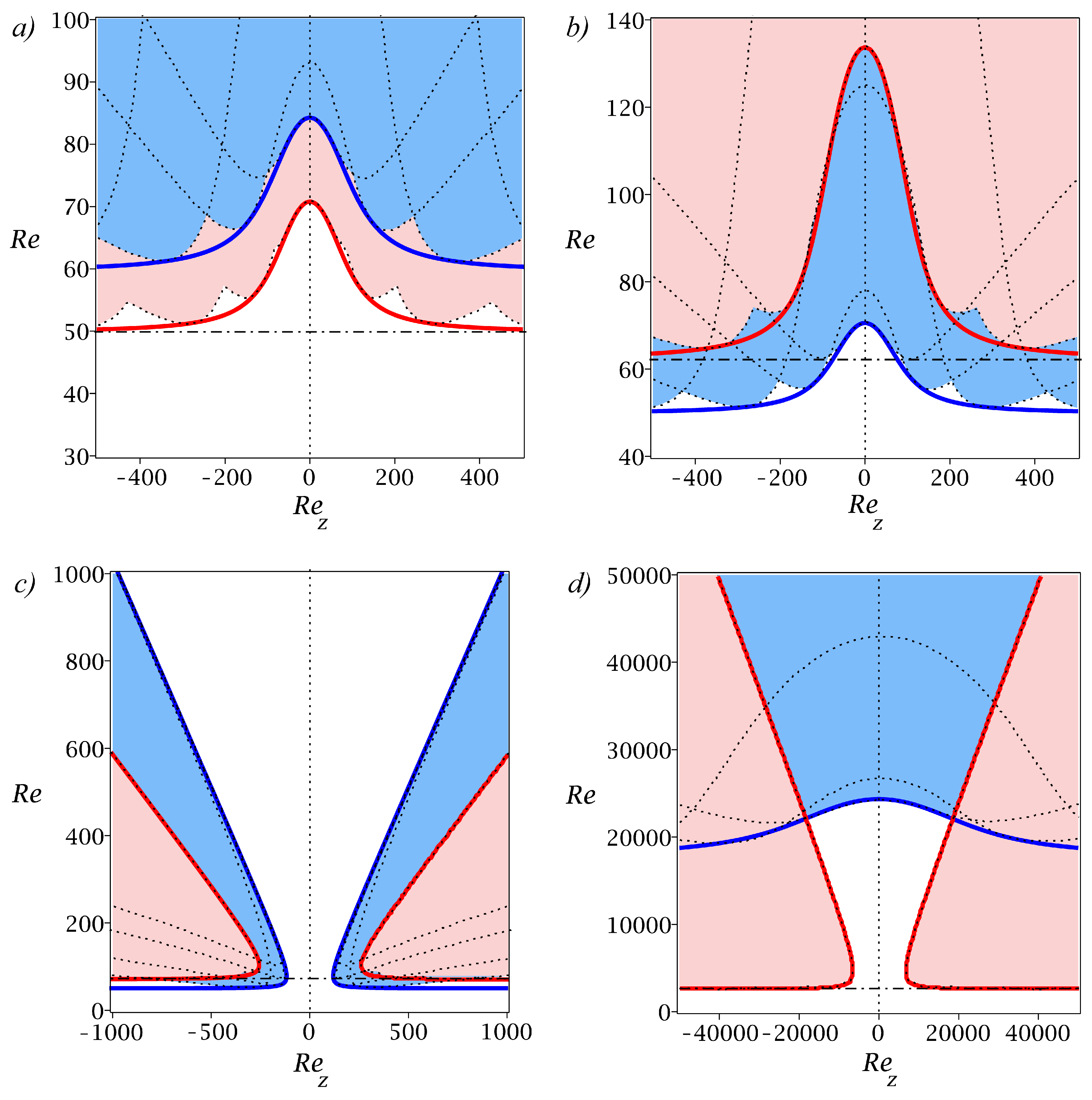
4.5. Stability Analysis

The dispersion relation (60) has real coefficients. Consequently, the stability conditions of the base flow $(\sigma <0)$ are determined by the Liénard-Chipart stability criterion: $a_0>0$ , $a_2>0$ , and $a_1{a}_2-a_0>0$ [25]. Note that $a_2={\displaystyle \frac{k_r{k}_z}{{\left|\mathit{k}\right|}^2}}{\displaystyle \frac{DW}{SRo}}\gamma \Theta +{\displaystyle \frac{2Pr+1}{Pr}}{\displaystyle \frac{{\left|\mathit{k}\right|}^2}{Re}}$ is positive in both the isothermal case $(\gamma =0)$ and the pure azimuthal circular Couette flow with a radial temperature gradient $(DW=0)$ . In these cases, the inequality $a_0<0$ extends the Rayleigh centrifugal instability criterion, while the inequality $a_1{a}_2-a_0<0$ characterizes oscillatory instability [24,29,42].

4.5.1. Pure Azimuthal Circular Couette Flow with the Radial Temperature Gradient

The condition $a_0=0$ defines the neutral stability boundary in the $(Pr,Re)$ -plane for the non-oscillatory (stationary) Goldreich-Schubert-Fricke (GSF) instability [6,24]. The neutral stability curves are parameterized by the axial wavenumber $k_z$ , with $a_0=0$ leading to a polynomial equation in $k_z$ . The envelope of this family of curves can be determined through three equivalent approaches: (1) computing the discriminant of the polynomial, (2) solving the equations $a_0\left(k_z\right)=0$ and ${\displaystyle \frac{d{a}_0\left(k_z\right)}{d{k}_z}}=0$ simultaneously, or (3) expressing $Re$ as a function of $k_z$ from $a_0=0$ and minimizing $Re$ with respect to $k_z$ [18]. All approaches yield the same expression for the envelope:

$$R{e}_0^S={\displaystyle \frac{3\sqrt{3}{k}_r^2}{2\Omega }}{\displaystyle \frac{1}{\sqrt{4(R{o}_R^S-Ro)(1-\gamma \Theta )}}},$$

(62)

where $R{o}_R^S$ is the modified Rayleigh line for non-isothermal flows [26]:

$$R{o}_R^S=-1+{\displaystyle \frac{rD\Theta \gamma Pr}{4\left(1-\gamma \Theta \right)}}.$$

(63)

The same procedure applied to the equation $a_1{a}_2=a_0$ yields the envelope of the neutral stability curves for the oscillatory instability:

$$R{e}_0^O={\displaystyle \frac{3\sqrt{3}{k}_r^2}{2\Omega }}{\displaystyle \frac{Pr+1}{Pr\sqrt{4(R{o}_R^O-Ro)(1-\gamma \Theta )}}},$$

(64)

where

$$R{o}_R^O=-1+(R{o}_R^S+1){\displaystyle \frac{Pr+1}{2P{r}^2}}.$$

(65)

Note that $R{o}_R^O=R{o}_R^S$ and $R{e}_0^O=2R{e}_0^S$ at $Pr=1$ . Moreover, rewriting Eq. (62) and Eq. (64) in terms of the Taylor number $Ta={\displaystyle \frac{2Re\Omega }{3\sqrt{3}{k}_r^2}}$ exactly reproduces the result of [24].

The criterion for the stationary GSF instability given by the inequality $Re>R{e}_0^S$ can be written in terms of the Rayleigh discriminant $N_{\Omega }^2=4(1+Ro){\Omega }^2$ and the square of the centrifugal Brunt-Väissälä frequency $N^2=-\gamma {\Omega }^{2}rD\Theta$ as follows:

$$N_{\Omega }^2(1-\gamma \Theta )+Pr{N}^2+{\displaystyle \frac{27k_r^4}{4R{e}^2}}<0,$$

(66)

while the criterion for oscillatory instability $Re>R{e}_0^O$ takes the form:

$$N_{\Omega }^2(1-\gamma \Theta )+{\displaystyle \frac{Pr+1}{2Pr}}{N}^2+{\displaystyle \frac{{(Pr+1)}^2}{4P{r}^2}}{\displaystyle \frac{27k_r^4}{R{e}^2}}<0.$$

(67)

Setting $\gamma =0$ and $N=0$ in (66) exactly reproduces the centrifugal instability criterion for isothermal viscous Couette-Taylor flow found in [7] by local geometrical optics approach.

In Figure 5, the envelopes (62) and (64) are depicted in the $(Pr,Re)$ -plane by red and blue curves, respectively, with the instability domain located above these curves. In the Rayleigh-unstable case ($\mu <{\eta }^2$ ) shown in Figure 5(a), for outward heating ($\gamma >0$ ), the envelopes intersect, forming a codimension-2 point at a specific value of $Pr$ , which is detailed in [24]. In this scenario, the GSF instability dominates for $Pr<1$ , while the oscillatory instability becomes critical for $Pr>1$ .

Conversely, for Rayleigh-stable flow ($\mu >{\eta }^2$ ), inward heating destabilizes the system through an oscillatory instability mechanism when $Pr<1$ and through GSF when $Pr>1$ , as illustrated in Figure 5(b). This behavior was first identified using the local geometrical optics approach in [24] and later confirmed by numerical global stability analysis in [43]. The parameters characterized by low Prandtl numbers and high Reynolds numbers, corresponding to oscillatory instability as shown in Figure 5(b), are particularly relevant to the dynamics of accretion disks in astrophysics [14,15].

4.5.2. Isothermal Spiral Poiseuille Flow (SPF)

Setting $\Theta \equiv 0$ and $\gamma =0$ in the matrix (61) corresponds to the isothermal spiral Poiseuille flow. Under these conditions, the dispersion relation simplifies, separating into a linear equation with no physical significance and a quadratic polynomial. The quadratic polynomial determines centrifugal instability via the sole relevant condition of the Liénard-Chipart criterion: $a_0<0$ . Computing the discriminant of $a_0=0$ , considered as a polynomial in $k_z$ , yields the envelope of the neutral stability curves in the $(R{e}_z,Re)$ -plane [26]:

$$E(R{e}_z,Re)={\displaystyle \frac{N_{\Omega }^2}{{\Omega }^2}}-{\displaystyle \frac{4{\overline{DW}}^2}{1+{\overline{DW}}^2}}+{\displaystyle \frac{27}{4{\Omega }^2}}{\displaystyle \frac{k_r^4}{R{e}^2}}=0.$$

(68)

The centrifugal instability of the isothermal viscous swirling flow is then determined by the condition $E(R{e}_z,Re)<0$ [26] that for isothermal inviscid swirling flows $(Re\to \infty )$ reduces to the result

$${\displaystyle \frac{N_{\Omega }^2}{{\Omega }^2}}-{\displaystyle \frac{4{\overline{DW}}^2}{1+{\overline{DW}}^2}}<0,$$

(69)

previously obtained in [8,10] using the local geometrical optics approach, and in [35,39] via the global stability analysis. The equality in (69) determines asymptotes to the envelope (68) shown in Figure 6(b) by oblique straight lines for the Rayleigh-stable flow. The envelope (68) also has a horizontal asymptote [26]

$$R{e}_{\infty }={\displaystyle \frac{3\sqrt{3}{k}_r^2}{4\Omega \sqrt{-Ro}}}\mathrm{as}\left|R{e}_z\right|\to \infty$$

(70)

as shown in Figure 6(a,b) by the dot-dashed line.

4.5.3. Spiral Poiseuille Flow with Radial Temperature Gradient (SPFRT)

The radial temperature gradient induces a splitting of the envelope bounding the domain of centrifugal instability in swirling flows [26].

For Rayleigh-unstable, non-isothermal swirling flows, the envelope comprises two branches that intersect at $R{e}_z=0$ and $Re=R{e}_0^S$ , where $R{e}_0^S$ is defined in (62). A linear approximation for the branches of the envelope near the intersection is given by the formula [26]:

$${\displaystyle \frac{Re\left(R{e}_z\right)}{R{e}_0^S}}=1\pm \gamma \Theta {\displaystyle \frac{\sqrt{2}}{9k_r^2}}{\displaystyle \frac{DW}{Ro}}R{e}_z+o\left(R{e}_z\right).$$

(71)

The horizontal asymptote (70) also splits, with the new values of $R{e}_{\infty }$ determined as the roots of the bicubic equation:

$$b_3{(\Omega Re)}^6+b_2{(\Omega Re)}^4+b_1{(\Omega Re)}^2+b_0=0,$$

(72)

where the coefficients are defined as:

$$\begin{array}{ccc}\hfill b_3& =& 16[{(\gamma \Theta )}^2+A]A^5,\hfill \\ \hfill b_2& =& k_r^4[27{(\gamma \Theta )}^6-265A{(\gamma \Theta )}^4-492A^2{(\gamma \Theta )}^2-216A^3]A^2,\hfill \\ \hfill b_1& =& 3k_r^8[-144{(\gamma \Theta )}^8-96A{(\gamma \Theta )}^6-8A^2{(\gamma \Theta )}^4+216A^3{(\gamma \Theta )}^2+243A^4],\hfill \\ \hfill b_0& =& 1024k_r^{12}{(\gamma \Theta )}^6,\hfill \\ \hfill A& =& 4(1-\gamma \Theta )(1+R{o}_R^S-Ro),\hfill \end{array}$$

(73)

and where $R{o}_R^S$ is the modified Rayleigh line (63).

Using perturbation theory for $\left|\gamma \right|\ll 1$ , an approximate expression for the splitting of the horizontal asymptote can be derived from (72):

$$\begin{array}{ccc}\hfill {\displaystyle \frac{R{e}_{\infty }\left(\gamma \right)}{R{e}_{\infty }}}& =& 1+\gamma \Theta \left[{\displaystyle \frac{1}{2}}+{\displaystyle \frac{Pr}{4}}{\displaystyle \frac{Rt}{Ro}}\pm {\displaystyle \frac{1}{\sqrt{-6Ro}}}\right]+o\left(\gamma \right),\hfill \end{array}$$

(74)

where $R{e}_{\infty }$ is defined in (70), and $Rt={\displaystyle \frac{rD\Theta }{2\Theta }}$ [24].

In Figure 7(a), the envelope of the centrifugal instability domains of the Rayleigh-unstable SPF with a radial temperature gradient (SPFRT) is split, exhibiting two horizontal asymptotes at $R{e}_{\infty }\approx 49.66$ and $R{e}_{\infty }\approx 49.80$ . These values, derived from (74), are indistinguishable from the exact results given by (72). Furthermore, as predicted by (74), these values demonstrate that the temperature gradient not only splits the isothermal horizontal asymptote $R{e}_{\infty }\approx 49.60$ shown in Figure 6(a) for the same parameter values as in Figure 7(a), but also shifts it downward. Note that the splitting of the envelope introduces asymmetry in the instability domains with respect to the sign of $k_z$ : for $R{e}_z>0$ , the critical $Re$ corresponding to the lower branch of the envelope has $k_z>0$ , whereas for $R{e}_z<0$ , the critical $Re$ corresponding to the lower branch has $k_z<0$ , Figure 7(a).

Figure 7(b) illustrates that the splitting of the envelope of the centrifugal instability domains for the Rayleigh-stable SPFRT results in not only the two horizontal asymptotes from (74) as $|R{e}_z|\to \infty$ , but also two oblique asymptotic lines as $Re\to \infty$ . The outer branch of the envelope follows the asymptotic line given by the expression:

$${\displaystyle \frac{N_{\Omega }^2}{{\Omega }^2}}(1-\gamma \Theta )+Pr{\displaystyle \frac{N^2}{{\Omega }^2}}={\displaystyle \frac{{\overline{DW}}^2}{1+{\overline{DW}}^2}}{(2-\gamma \Theta )}^2$$

(75)

If the left-hand side of (75) exceeds its right-hand side, this inequality defines the centrifugal stability of the SPFRT. The inner branch of the envelope lies within the centrifugal instability domain and has the asymptote:

$${\displaystyle \frac{N_{\Omega }^2}{{\Omega }^2}}\left(1-\gamma \Theta \right)+Pr{\displaystyle \frac{N^2}{{\Omega }^2}}={\displaystyle \frac{4{\overline{DW}}^2}{1+{\overline{DW}}^2}}\left(1-\gamma \Theta \right).$$

(76)

Since the splitting of the envelope of the centrifugal instability domains is small for $\left|\gamma \right|\ll 1$ , we can derive a simple approximation by substituting $D\Theta =-{\displaystyle \frac{N^2}{\gamma {\Omega }^{2}r}}$ into the equation $a_0=0$ , calculating the discriminant of the resulting equation (treated as a polynomial in $k_z$ ), and then taking the limit as $\gamma \to 0$ while keeping the centrifugal Brunt-Väissälä frequency N fixed. This procedure yields the following approximate expression for the envelope:

$${\displaystyle \frac{N_{\Omega }^2}{{\Omega }^2}}+Pr{\displaystyle \frac{N^2}{{\Omega }^2}}-{\displaystyle \frac{4{\overline{DW}}^2}{1+{\overline{DW}}^2}}+{\displaystyle \frac{27k_r^4}{4{\Omega }^{2}R{e}^2}}=0.$$

(77)

The approximation (77) represents a non-isothermal extension of the envelope (68) for the centrifugal instability domains of viscous swirling flows and is valid when $\left|\gamma \right|\ll Pr$ . It forms a single smooth curve (see Figure 8) that aligns closely with the minimal splitting of individual neutral stability curves for specific $k_z$ . This splitting is so subtle that it is imperceptible to the naked eye in Figure 8.

Applying the above procedure to the equation $a_1{a}_2=a_0$ , we derive a similar approximation for the envelope of the oscillatory instability domains of SPFRT in the $(R{e}_z,Re)$ -plane, shown as thick blue lines in Figure 8:

$${\displaystyle \frac{N_{\Omega }^2}{{\Omega }^2}}+{\displaystyle \frac{N^2}{{\Omega }^2}}{\displaystyle \frac{Pr+1}{2Pr}}-{\displaystyle \frac{4{\overline{DW}}^2}{1+{\overline{DW}}^2}}+{\displaystyle \frac{{(Pr+1)}^2}{P{r}^2}}{\displaystyle \frac{27k_r^4}{4{\Omega }^{2}R{e}^2}}=0$$

(78)

The approximation (78) is valid when $\left|\gamma \right|\ll Pr$ . Requiring the left-hand side of (78) to be negative extends the criterion (67) to swirling flows with a radial temperature gradient.

A comparison of Figure 8(a),(b) with Figure 5(a) reveals that the Rayleigh-unstable SPFRT with an outward temperature gradient ($\gamma >0$ ) can exhibit either centrifugal instability (at small $Pr$ ) or oscillatory instability (at large $Pr$ ). The transition between these regimes occurs at a critical $Pr$ , corresponding to a codimension-2 point in the $(Pr,Re)$ -plane at $R{e}_z=0$ , as shown in Figure 5(a).

The Rayleigh-stable SPFRT depicted in Figure 8(c), (d) can exhibit oscillatory instability in the presence of an outward temperature gradient ($\gamma >0$ ) at large $Pr$ , as shown in Figure 8(c), when $|R{e}_z|$ exceeds a critical value. For an inward temperature gradient ($\gamma <0$ ), Figure 5(b) indicates that stability is lost via oscillatory instability at small $|R{e}_z|$ and via centrifugal instability at large axial Reynolds numbers when $Pr<1$ , consistent with the numerical results of [4]. For $Pr>1$ , this behavior is reversed.

5. Conclusions

The geometrical optics local stability analysis, initially developed for the hydrodynamics of ideal fluids, was revisited and extended to visco-diffusive rotating flows. This approach was applied to three cases: the azimuthal magnetorotational instability (AMRI) in magnetized differentially rotating flows, the McIntyre instability in baroclinic lenticular vortices, and instabilities in the spiral Poiseuille flow with a radial temperature gradient (SPFRT).

The influence of the hydrodynamic ($Pr$ ) and magnetic ($Pm$ ) Prandtl numbers, and Schmidt ($Sc$ ) number on the onset of stationary and oscillatory instabilities was explored, with a focus on the exchange of instabilities near the critical value where the ratio of viscosity to diffusivity equals one. It was demonstrated that AMRI can be interpreted as a dissipative unfolding of the linear Hamilton-Hopf bifurcation, represented by the Whitney umbrella singularity on the neutral stability surface. This singularity explains the persistence of diffusive destabilization even in the limit of vanishing dissipation, provided $Pm\ne 1$ . The thresholds for diffusive and diffusionless AMRI coincide only at $Pm=1$ .

A similar critical behavior was observed in the visco-diffusive McIntyre-like instability of lenticular vortices, where $Sc=1$ acts as the boundary between oscillatory and stationary instabilities, determining the transition between these regimes. The method also proved effective in deriving stability criteria for swirling flows with radial temperature gradients, highlighting the role of $Pr$ in the exchange between stationary and oscillatory instabilities.

This analysis offers a robust framework for deriving instability criteria analytically, even for parameter values inaccessible in numerical or physical experiments, providing valuable insights and guidance for future studies.