Submitted:
31 December 2024
Posted:
31 December 2024
You are already at the latest version
Abstract
Keywords:
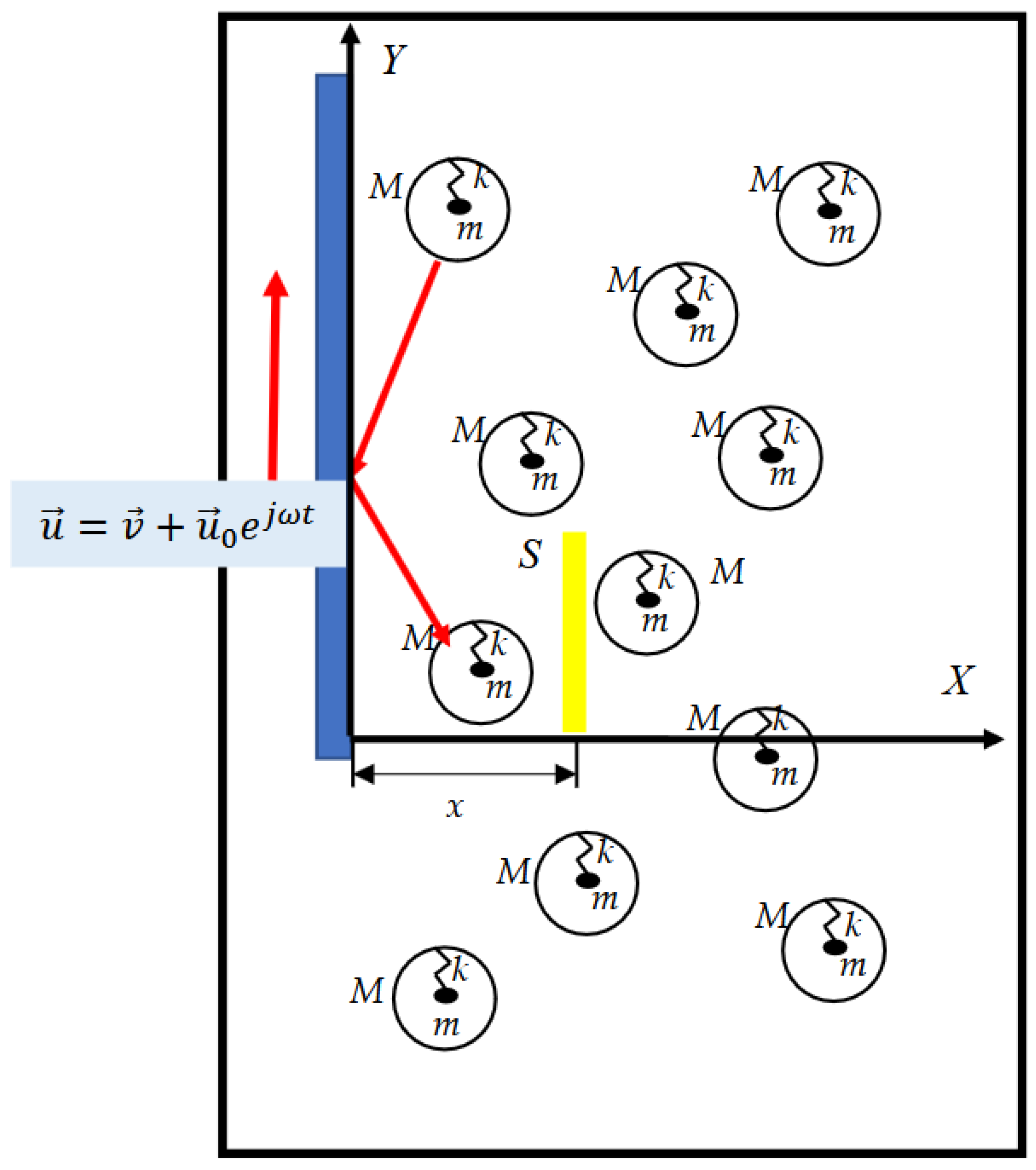
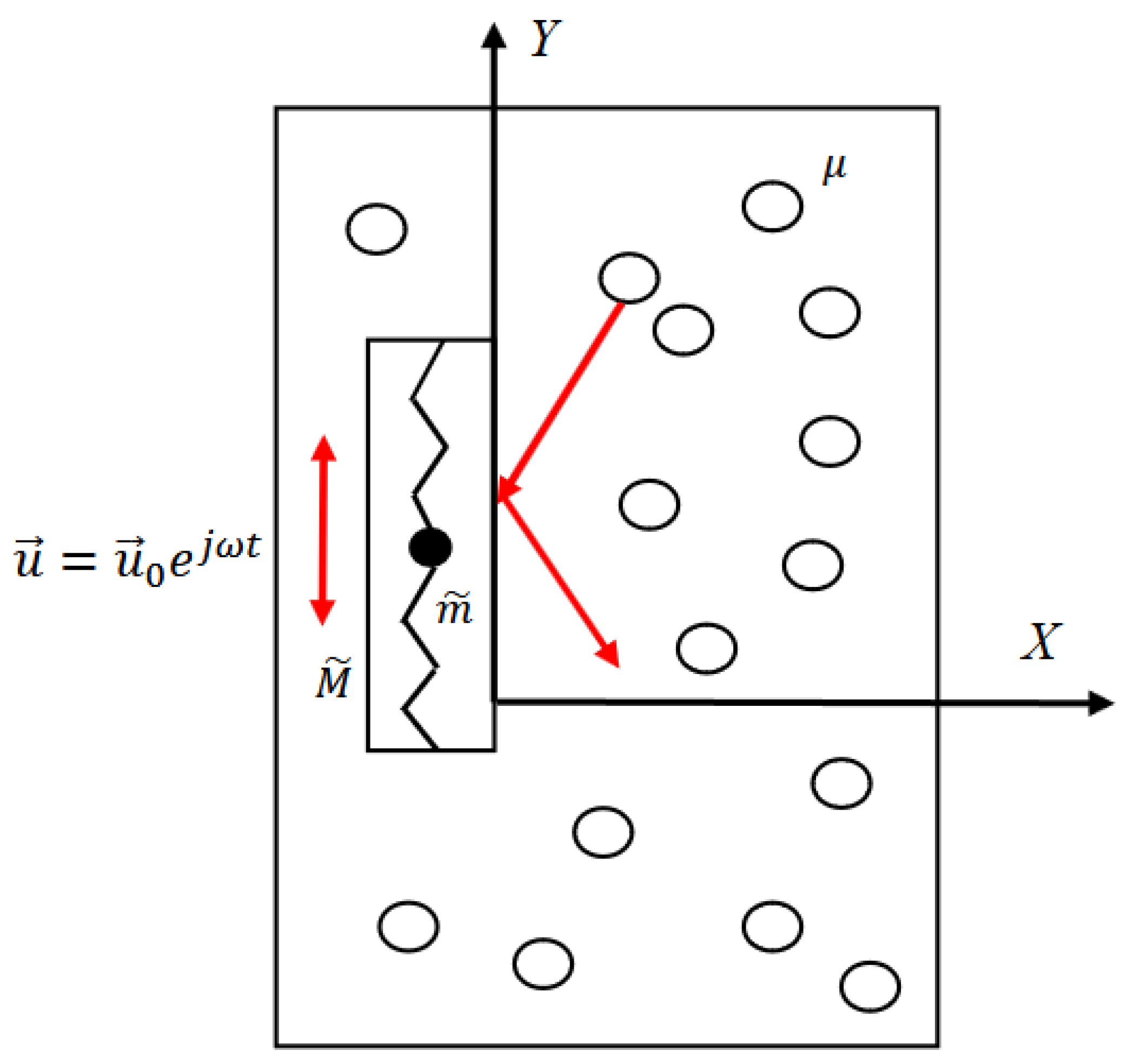
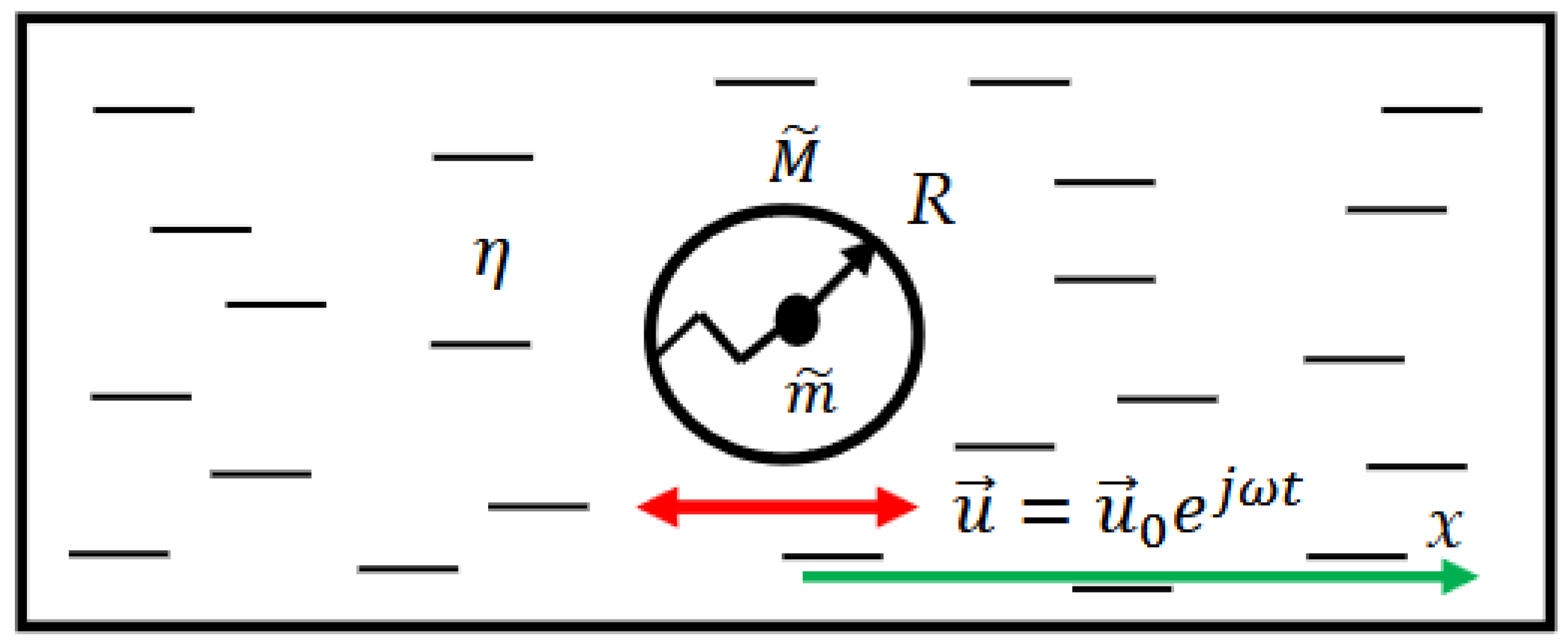
1. Introduction
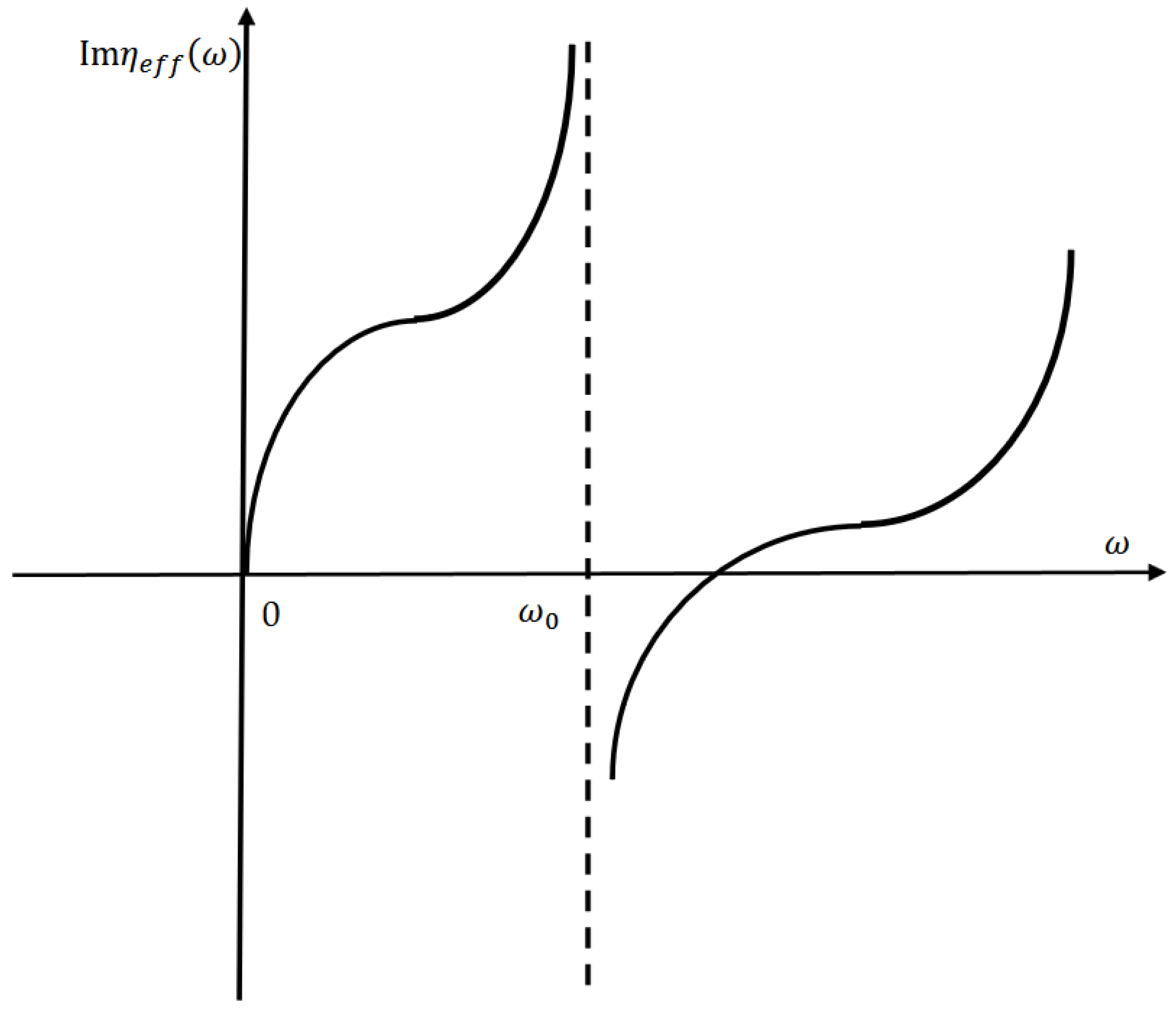
2. Results
3. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
References
- Veselago, V.G. The electrodynamics of substances with simultaneously negative values of e and u. Sov. Phys. Usp. 1968, 10, 509–514. [Google Scholar] [CrossRef]
- Cui, T.J.; Smith, D.; Liu, R. Metamaterials. Theory, Design, and Applications, Springer, NY., USA, 2010.
- Jiao, P.; Mueller, J.; Raney, J.R.; Zheng, X.; Alavi, A.H. Mechanical metamaterials and beyond. Nat. Commun, 2023, 14, 6004. [Google Scholar] [CrossRef] [PubMed]
- Yang, F.; Zhang, Z.; Xu, L.; Liu, Z.; Jin, P.; Zhuang, P.; Lei, M.; Liu, J. ; Jiang, J-H. Controlling mass and energy diffusion with metamaterials, Rev. Mod. Phys. 2024, 96, 015002. [Google Scholar]
- Singh, A.K.; Abegaonkar, M.P.; Koul, S.K. Metamaterials for Antenna Applications, CRC Press, Boca Raton, Fl. USA, 2022.
- Felbacq, D.; Bouchitté, G. Metamaterials Modelling and Design, Taylor & Francis, Pan Stanford Publishing, Singapore, 2017.
- Marques, R.; Martin, F.; Sorolla, M. Metamaterials with Negative Parameters: Theory, Design, and Microwave Applications (Wiley Series in Microwave and Optical Engineering Book 183), J. Wiley & Sons, Hoboken, USA, 2008.
- Engheta, N.; Ziolkowski, R.W. Electromagnetic Metamaterials: Physics and Engineering Explorations, IEEE Press, Hoes Lane, NJ, USA, 2006.
- Semouchkina, E. Dielectric Metamaterials and Metasurfaces in Transformation Optics and Photonics, Woodhead Publishing, Cambridge, MA, USA, 2021.
- Cai, W.; Shalaev, V. Optical Metamaterials. Fundamentals and Applications, Chapter 5, Springer, New York, 2010.
- Wu, W.; Hu, W.; Qian, G.; Liao, H.; Xu, H.; Berto, F. Mechanical design and multifunctional applications of chiral mechanical metamaterials: A review. Materials & Design 2019, 180, 107950.
- Kshetrimayum, R.S. A Brief Intro to Metamaterials. IEEE Potentials. 2004, 23, 44–46. [Google Scholar] [CrossRef]
- Bormashenko Ed. Bioinspired Materials and Metamaterials, CRC Press, Boca Raton, USA, 2025.
- Li, Y. , Li, W., Han, T.; Fan, S..; Qui S-W. Transforming heat transfer with thermal metamaterials and devices. Nat. Rev. Mater. 2021, 6, 488–507. [Google Scholar] [CrossRef]
- Milton, G.W.; Willis, J.R. On modifications of Newton’s second law and linear continuum elastodynamics. Proc. R. Soc. A 2007, 463, 855–880. [Google Scholar] [CrossRef]
- Liu, X.N.; Hu, G.K.; Huang, G.L.; Sun, C.T. An elastic metamaterial with simultaneously negative mass density and bulk modulus. Appl. Phys. Lett. 2011, 98, 251907. [Google Scholar] [CrossRef]
- Rodrigues, I.C.; Steele, G.A.; Bothner, D. Photon Pressure with an Effective Negative Mass Microwave Mode, Phys. Rev. Lett. 2024, 132, 203603. [Google Scholar] [CrossRef] [PubMed]
- Chan, C.T.; Li, J.; Fung, K.H. On extending the concept of double negativity to acoustic waves. JZUS A 2006, 7, 24–28. [Google Scholar] [CrossRef]
- Huang, H.H.; Sun, C.T.; Huang, G.L. On the negative effective mass density in acoustic metamaterials. Int. J. Eng. Sci. 2009, 47, 610–617. [Google Scholar] [CrossRef]
- Bhatt, A.; Banerjee, A. Double attenuation peaks in metamaterial with simultaneous negative mass and stiffness, Phys. Lett. A 2022, 443, 128201. [Google Scholar] [CrossRef]
- Bormashenko, Ed.; Legchenkova, I. Negative effective mass in plasmonic systems. Materials 2020, 13, 1890. [Google Scholar] [CrossRef]
- Bormashenko, Ed; Legchenkova, I. ; Frenkel, M. Negative Effective Mass in Plasmonic Systems II: Elucidating the Optical and Acoustical Branches of Vibrations and the Possibility of Anti-Resonance Propagation. Materials 2020, 13, 512. [Google Scholar]
- Golovkin, B.G. High temperature negative mass plasma. Ann. Math. Phys. 2024, 7, 118–137. [Google Scholar]
- Liu, Z.Y.; Zhang, X.X.; Mao, Y.W.; Zhu, Y.Y.; Yang, Z. Y.; Chan, C.N.; Sheng, P. Locally resonant sonic materials, Science, 2000, 289, 1734-1736.
- Lončar, J.; Igrec, B.; Babić, D. Negative-inertia converters: Devices manifesting negative mass and negative moment of inertia. Symmetry 2022, 14, 529. [Google Scholar] [CrossRef]
- Peralta, I.; Fachinotti, V.D.; Álvarez Hostos, J.C. A Brief Review on Thermal Metamaterials for Cloaking and Heat Flux Manipulation, Adv. Eng. Mater. 2020, 22, 1901034. [Google Scholar]
- Liu, J.; Deng, J.; Chen, D.; Huang, Q. ; Pan. G.; Design and performance of ultra-broadband composite meta-absorber in the 200Hz-20kHz range, J. Sound & Vibration, 2024, 574, 118229. [Google Scholar]
- Liao, G.; Luan, C.; Wang, Z.; Liu, J.; Yao, X.; Fu, J. Adv. Mater. Techn. 2021, 6, 2000787. [CrossRef]
- Lim, C.W. From Photonic Crystals to Seismic Metamaterials: A Review via Phononic Crystals and Acoustic Metamaterials. Arch. Computat. Methods Eng. 2022, 29, 1137–1198. [Google Scholar]
- Bacri, J.-C.; Perzynski, R.; Shliomis, M.I.; Burde, G.I. “Negative-Viscosity” Effect in a Magnetic Fluid, Phys. Rev. Lett. 1995, 75, 2128. [Google Scholar] [CrossRef] [PubMed]
- Shliomis, M.I.; Morozov, K.I. Negative viscosity of ferrofluid under alternating magnetic field. Physics Fluids 1994, 6, 2855–2861. [Google Scholar] [CrossRef]
- Li, W.; Li, Z.; Han, W.; Li, Y.; Yan, S.; Zhao, Q.; Chen, F. Measured viscosity characteristics of Fe3O4 ferrofluid in magnetic and thermal fields, Phys. Fluids 2023, 35, 012002. [Google Scholar] [CrossRef]
- Paras, R.; Anupam, B. Negative viscosity effects on ferrofluid flow due to a rotating disk. Int. J. Appl. Electromagnetics & Mechanics 2013, 41, 467–478. [Google Scholar]
- Sivashinsky, G.; Yakhot, V. Negative viscosity effect in large-scale flows. Physics of Fluids 1985, 28, 1040–1042. [Google Scholar] [CrossRef]
- Malkin, A.Ya. , Rheology Fundamentals, Toronto: Canada: ChemTec Publ., 1994.
- Macosco, C.W. Rheology Principles, Wiley-VCH, Weinheim, Germany, 1994.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




