A Non-Turing Computer Architecture for Artificial Intelligence with Dynamic Rule Learning and Generalization Abilities Using Images or Texts

1. Introduction

In recent years, the research of deep neural network models has witnessed significant progress as various large language models are proposed and evolved at a fast pace. However, currently, these models still cannot achieve reasonable performance in logical and mathematical reasoning without much human intervention, although more than 10 billion trainable parameters are placed in their latest neural networks. The failure of these sophisticated models in some seemingly simple math problems inspired us to propose a non-Turing computer structure to address this challenge. The number of previous works on non-Turing machines is relatively small ([1,2,3,4,5,6,7]), which mostly discuss it conceptually and psychologically without giving any specific workable architecture like the Turing one. Among these, [2,7] argued that analog or natural computations should be used to conduct calculations involving continuous real numbers. The potential adaptivity of this type of model, however, is only restricted to the range between the discrete approximation of a continuous number and its unrepresented portion. Moreover, it lacks the interactions among the discrete domain and the continuous domain to solve the problem in their model as well. Recently, [8] and its variants investigated so-called Neural Turing Machines, which use neural networks like LSTM [9] as the controller to make the entire system differentiable for end-to-end training. Compared with this structure, the abstract controller in the proposed non-Turing machine (which will be called “Ren machine" for simplicity below) can still be discrete/binary-based for logic reasoning. This novel structure allows the flexibility of switching back and forth between the abstract domain and the specific domain to better approach a solution to a given problem with rules summarized or learned from thought/tool experiments during the process. What’s more, it also enables the interactive collaborations of specific contents and abstract contents on both types of tapes to command and instruct the controller for completing a task.

2. Related Work

There are early works studying the multi-tape variants of Turing machines such as [10,11]. It is proved that these multi-tape Turing machines are not essentially different from their single-tape prototype – simply increasing the number of tapes does not give rise to the capacity to compute any new functions, though their complexity of computing or realizing a function can be improved to some degree. Furthermore, various types of interactive multi-tape Turing machines have also been proposed and analyzed in the theoretical computer science community ([12,13,14,15]). However, one fundamental characteristic of these architectures that makes them different from Ren machine is that they only consider a single type of domain (namely, the abstract bit domain). As a result, even interactions in the single abstract domain are considered in some of these works, their potential reasoning ability and the ability of rule summarization, learning, and generalization are unlikely to go beyond the Turing machine’s limit. What is more, their research focuses on the computability/realizability of an assumed static function on these architectures, while using unconventional and nondeterministic computations based on autonomous rule formation and generalization in thought/tool experiments to solve practical problems (such as collision avoidance in robotics, mathematical reasoning in theorem proving, etc.) is not discussed due to its infeasibility on these Turing variants. Compared with these existing structures, the proposed Ren machine provides a more general architecture containing tapes not only in the abstract domain but also in the specific domain, and its computation and reasoning are hence implemented based on the mapping rules that are known in advance or learned from experiments among these domains.

3. The Proposed Architecture

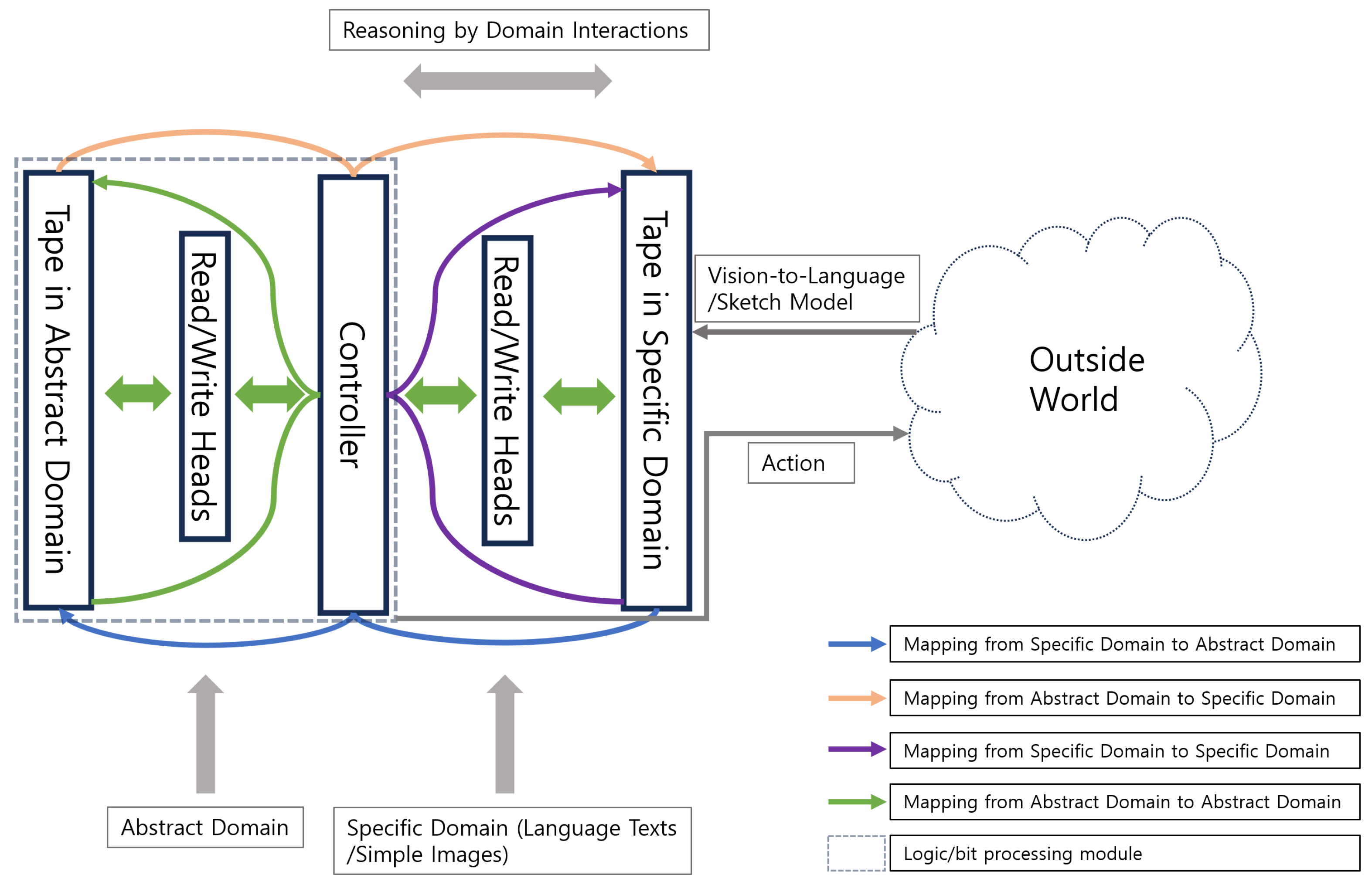
The components and their relations of Ren machine are elaborated in Figure 1. This structure consists of a controller and two types of read/write heads and tapes, one in the specific domain and the other in the abstract domain. The interactions inter and intra the specific domain and the abstract domain are realized by different types of mappings annotated in this figure. These mappings can be implemented by applying prior knowledge or learned rules (e.g., neural networks or memorized tables) or simply rendering using a built-in function on the screen. Note that the writing and reading processes utilizing the heads in the specific domain are affected by the environment in the real world. As a result, some information from the outside world is also involved during these processes. As discussed above, the read/write heads and tapes in the specific domain are essential parts of a Ren machine because of their important effects on autonomous rule formation and generalization.

4. Experiment

In the first experiment, we aim to autonomously find a method of computing the product of any positive integers by using very basic algebraic rules that are already known. The following diagram shows the workflow of Ren machine to calculate an expression where it learned the distributive rule of multiplication by experiments generated in the specific domain and used the rule to get the correct result of the expression.

In this process, when it is recognized that a potential rule is technically applicable to any objects in either the abstract domain or the specific domain, the rule will be formed, called, and applied to them as a trial to move towards a solution even if it seems that applying this rule to the objects is ‘meaningless’ (certainly a search strategy like reinforcement learning with simplicity and regularity rewards could be added for more ‘efficient’ lookup). New rules are summarized or learned from thought or tool experiments generated from prior knowledge and existing rules that have already been learned so far. For example, in the computing process demonstrated in Figure 2, the distributive rule is learned by the cooperation of specific observations and abstract prior knowledge. Specifically, Ren machine can compute the multiplication of any small integers like $12\times 30$, $10\times 30$, and $2\times 30$ using multiple additions by the original definition of multiplication. Then it finds that actually the equation $\boxed{12\times 30=10\times 30+2\times 30}$ holds true. Then it generates an example in the specific domain accordingly by simply displaying the equation on the screen. Using a similar procedure, it can generate a large number of examples (images) in the specific domain showing that the distributive property exists. Then neural networks can be trained to learn the transformation between the images on the left side of the equation and those on the right side of the equation with a high confidence. It is shown in the experiment that such neural networks (e.g. LLaMA [16], ChatGPT [17]) are able to generalize to other pairs of integers that are unseen in the training, even when the integers are very large. After applying the transformation in the visual domain, we can use computer vision models such as YOLO [18] to convert the equation back into the abstract domain. This procedure eventually enables Ren machine to autonomously learn a general method of calculating the multiplications of arbitrary positive integers. The accuracy of the reasoning process is guaranteed by the high accuracy of each reasoning step: each rule it uses is valid with a probability higher than $99.9\%$; therefore the theoretical overall accuracy of the multi-step reasoning process is over $98.0\%$.

We conduct the test of computing the multiplications in 20 pairs of positive integers listed as follows:

1234*3456,	12345*34567,	123456*345678,	1234567*3456789,	12345678*34567891
2345*4567,	23456*45678,	234567*456789,	2345678*4567891,	23456789*45678912
3456*5678,	34567*56789,	345678*567891,	3456789*5678912,	34567891*56789123
4567*6789,	45678*67891,	456789*678912,	4567891*6789123,	45678912*67891234

The results in this experiment show that the accuracy ($100\%$) achieved by the proposed method on Ren machine is significantly higher than that ($80\%$) achieved by the state-of-the-art large language model used in Microsoft Copilot [19].

In the second experiment, we present how the proposed Ren machine completes the proof of the conclusion that “the summation of interior angles of a triangle is ${180}^{\circ }$ in Euclidean space" using the rules that are learned in advance and the prior knowledge base.

In this workflow, first, it is assumed that the machine knows from prior experiences that a flat angle (i.e., a straight line) is ${180}^{\circ }$, which also appears in the target conclusion to be proved. Then, a language model can be trained to generate a text prompt like “According to the question, first generate a triangle, then generate a line passing through one of its vertices" to potentially help prove the conclusion with the added auxiliary line. Next, rules based on a language-to-image model and a structured display of geometric objects (a line and a triangle) are used to map the texts to simple images in the specific domain. As we find, current LLM-based methods are not able to generate a structured image according to text prompts correctly. However, we can train image-to-image models to rotate and translate geometric objects in proper directions so that the straight line passes through one vertex of the triangle and becomes parallel to the opposite edge. After that, an annotation mapping rule in the specific domain can be applied to label the involved angles in the generated image. Sequentially, the rules of interior alternate angles and flat angle that are learned and memorized before can be used to convert the images in the specific domain to the symbolic angular equations in the specific domain, as shown in Figure 3. Finally, one can complete the proof by applying the stored substitution rule in the specific (symbol) domain to the generated equations.

5. Conclusions and Discussion

In this paper, we propose a non-Turing architecture, Ren machine, that solves a problem by autonomously learning rules and building knowledge bases from generated experiments in the process of approaching an answer. It can input and output by using two types of read/write heads in both the specific domain and the abstract domain. The mappings among these domains can be conducted based on learned rules such as neural networks, memorized tables, or simply built-in rendering functions. In this way, the controller can be commanded/instructed cooperatively by both the contents on the tape in the abstract domain and those in the specific domain. In the experiments, it is demonstrated that this flexible mechanism enables Ren machine to solve the multiplication problem of positive integers in a self-directed manner with a higher accuracy rate compared with other state-of-the-art LLM methods. The machine’s superior reasoning ability is also shown in proving a theorem in Plane Geometry. Assume a thought chain for solving a problem has a length of 1000 and each rule it uses is valid with a probability of $0.99999$, then the thought chain achieves an accuracy rate of $0.{99999}^{1000}\approx 0.99$. More advantages of Ren machine could be further explored by coping with the problems that cannot be solved by Turing machine intrinsically. As we know, the halting problem is the problem of determining whether an arbitrary program will terminate or continue to run forever. This problem is proven to be undecidable on Turing machine, meaning that there exists no general algorithm on Turing machine that can solve the halting problem for all possible pairs of program and input. On the other hand, on Ren machine, since the controller is connected with the specific domain using another type of read/write heads, it can also be commanded/instructed by the contents shown on the tape in the specific domain. Thus, the halting problem can be addressed with significantly high accuracy, if one includes a clock in the specific domain to count the time that a program has been running for, or uses neural networks to recognize the text patterns of never-ending programs, or counts the number of steps from their printouts on the screen, etc. In this regard, instead of pretending to be human in conversation, if a machine can actively generate rules from thought/tool experiments, for generalizing them to approach an answer to the problem it tries to solve, then it can be closer to the real artificial general intelligence.