Submitted:
23 December 2024
Posted:
24 December 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Materials and Methods
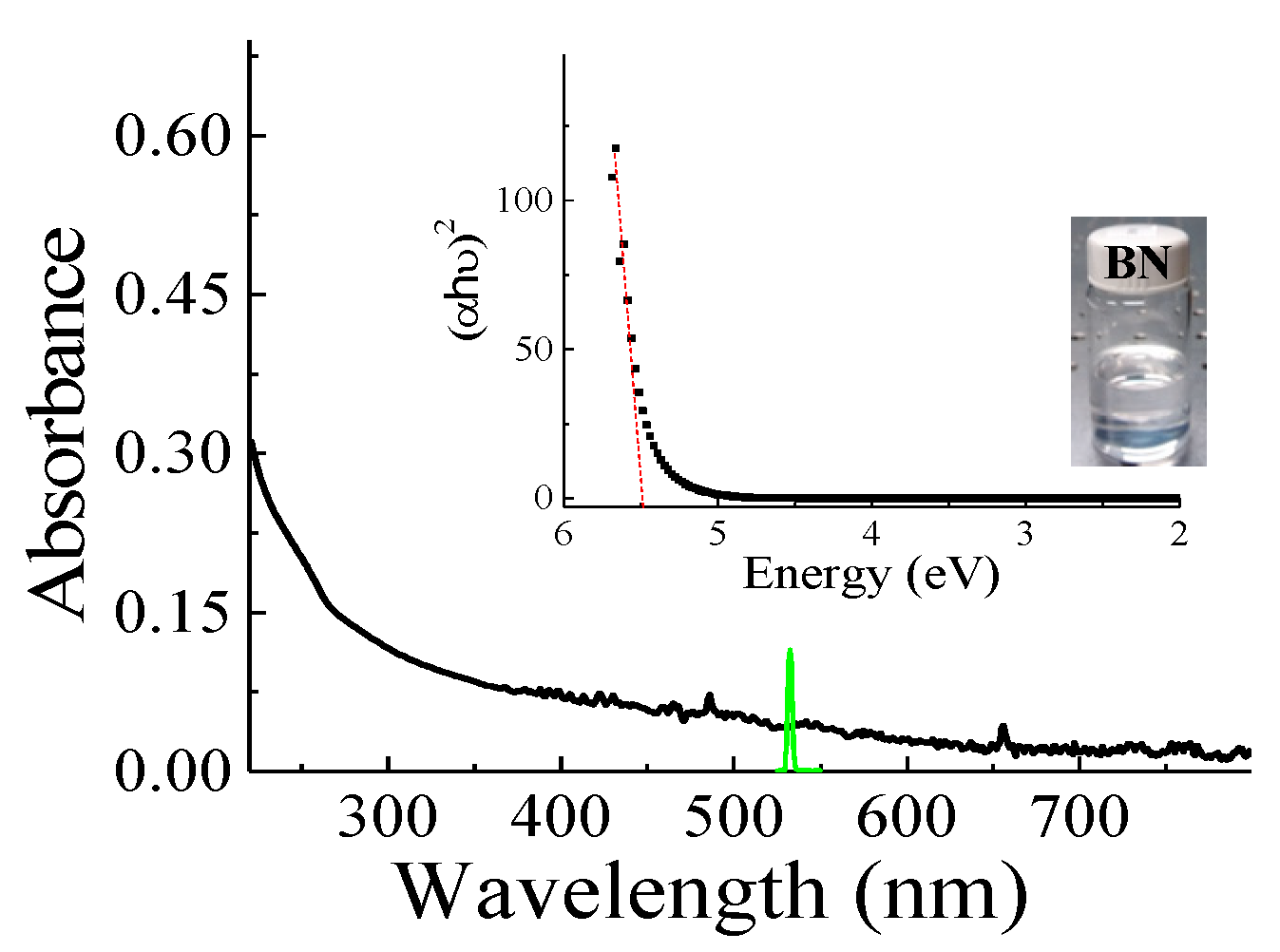
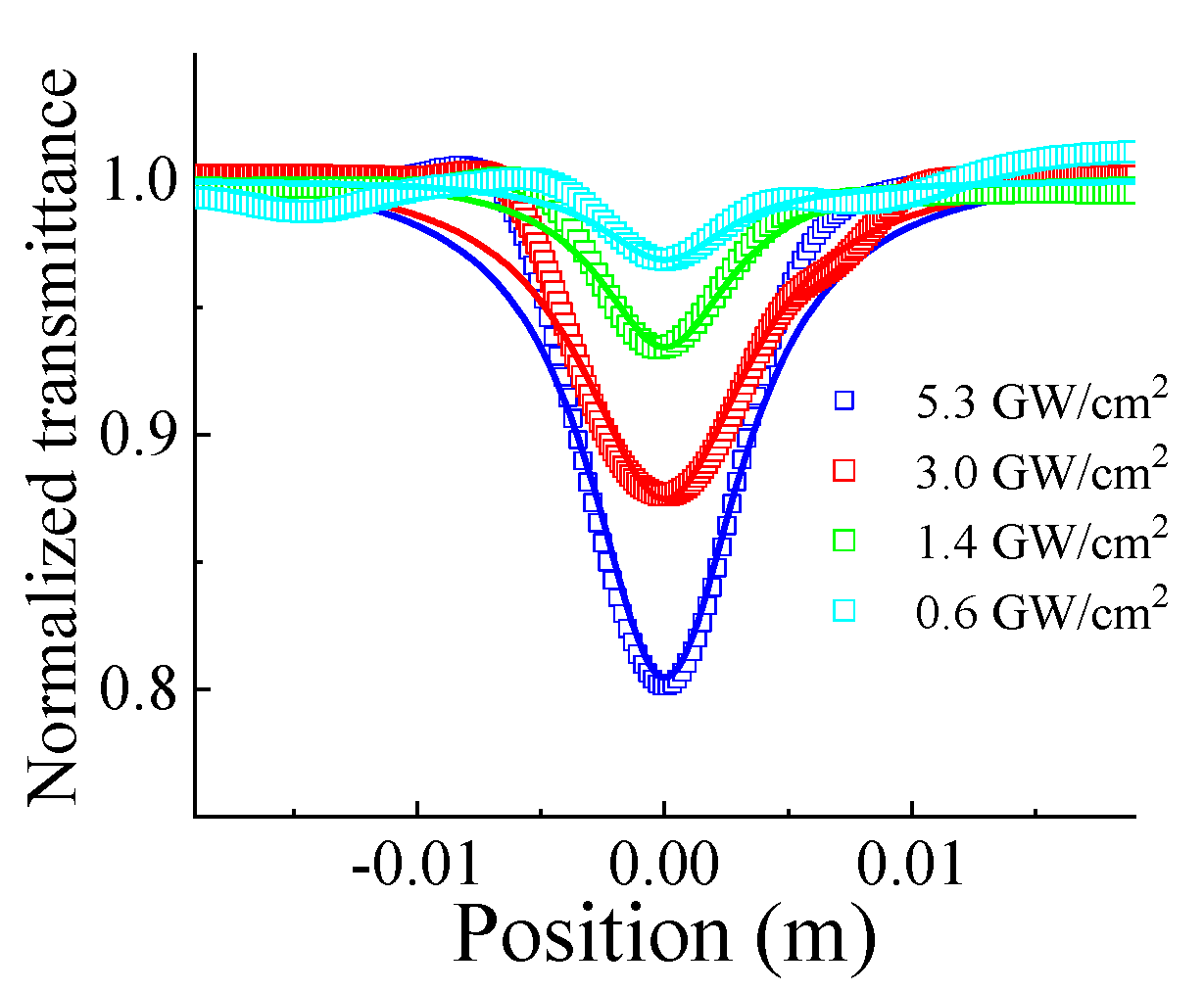
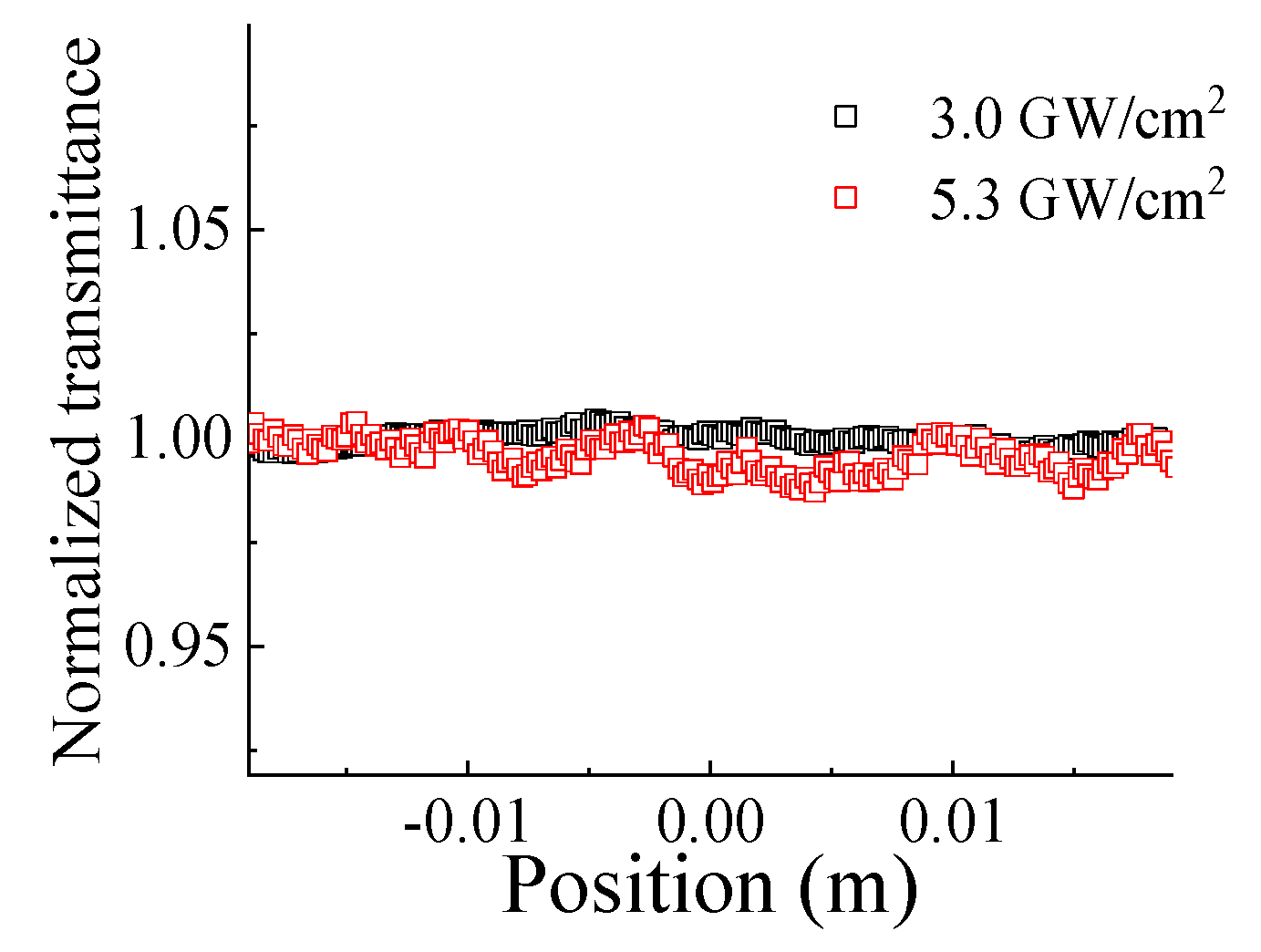
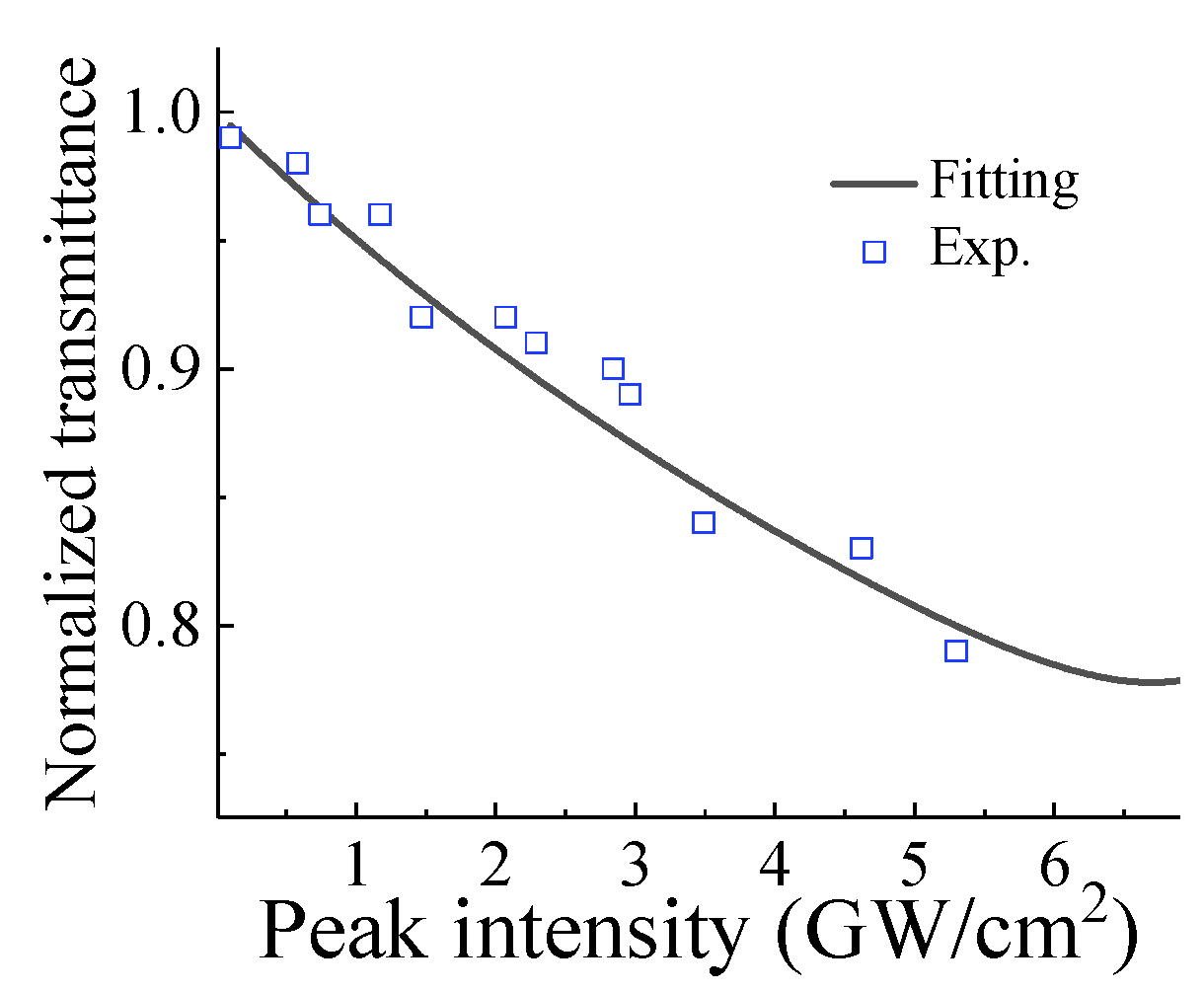
3. Results and Discussion
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- lavin, N. R.; Jespersen, M. L.; Check, M. H.; Hu, J. J.; Hilton, A. M.; Fisher, T. S.; Voevodin, A. A. Synthesis of few-layer large area hexagonal-boron nitride by pulsed laser deposition. Thin Solid Films 2014, 572, 245–250. [Google Scholar]
- umbhakar, P.; Kole, A. K.; Tiwary, C. S.; Biswas, S.; Vinod, S.; Tijerina, J. T.; Chatterjee, U.; Ajayan, P.M. Nonlinear Optical Properties and Temperature-Dependent UV–Vis Absorption and Photoluminescence Emission in 2D Hexagonal Boron Nitride Nanosheets. Adv. Optical Mater. 2015, 3, 828–835. [Google Scholar] [CrossRef]
- hao, G.; Zhang, F.; Wu, Y.; Hao, X.; Wang, Z.; Xu, X. One-Step Exfoliation and Hydroxylation of Boron Nitride Nanosheets with Enhanced Optical Limiting Performance. Adv. Optical Mater. 2016, 4, 141–146. [Google Scholar]
- iswas, S.; Tiwary, C. S.; Vinod, S.; Kole, A. K.; Chatterjee, U.; Kumbhakar, P.; Ajayan, P. M. Nonlinear Optical Properties and Temperature-Dependent Photoluminescence in hBN-GO Heterostructure 2D Material. J. Phys. Chem. C 2017, 121, 8060–8069. [Google Scholar]
- oan, T. C.; Majety, S.; Grenadier, S.; Li, J.; Lin, J. Y.; Jiang, H. X. Hexagonal boron nitride thin film thermal neutron detectors with high energy resolution of the reaction products. Nucl. Instrum. Meth. Phys. Res. Sect. A 2015, 783, 121–127. [Google Scholar]
- ersisyan, H. H.; Lee, T. H.; Lee, K. H.; An, Y. S.; Lee, J. S.; Lee, J. H. Few-atomic-layer boron nitride nanosheets synthesized in solid thermal waves. RSC Advances 2015, 5, 8579–8584. [Google Scholar] [CrossRef]
- su, A.; Han, W.; Yong, C. S.; Maily, B.; Xu, Z.; Lili, Y.; Yumeng, S.; Yi, H. L.; Dubey, M.; Ki, K. K.; Jing, K.; Palacios, T. Large-Area 2-D Electronics: Materials, Technology, and Devices. Proc. IEEE 2013, 101, 1638–1652. [Google Scholar]
- iu, Z.; Gong, Y.; Zhou, W.; Ma, L.; Yu, J.; Idrobo, J. C.; Jung, J.; MacDonald, A. H.; Vajtai, R.; Lou, J.; Ajayan, P. M. Ultrathin high-temperature oxidation-resistant coatings of hexagonal boron nitride. Nature Comm. 2013, 4, 2541. [Google Scholar]
- ttaccalite, C.; Grüning, M.; Amara, H.; Latil, S.; Ducastelle, F. Two-photon absorption in two-dimensional materials: The case of hexagonal boron nitride. Phys, Rev. B 2018, 98, 165126. [Google Scholar] [CrossRef]
- chell, A. W.; Tran, T. T.; Takashima, H.; Takeuchi, S.; Aharonovich, I. Nonlinear excitation of quantum emitters in hexagonal boron nitride multiplayers. APL Photonics 2016, 1, 091302. [Google Scholar]
- . Wang, G.; Zhang, S.; Zhang, X.; Zhang, L.; Cheng, Y.; Fox, D.; Zhang, H.; Coleman, J. N.; Blau, W. J.; Wang, J. Tunable nonlinear refractive index of two-dimensional MoS2, WS2, and MoSe2 nanosheet dispersions. Photon. Res. 2015, 3, A51–A55. [Google Scholar] [CrossRef]
- oyd, R. W. Nonlinear Optics, Academic Press, Elsevier, USA, 2003.
- . Neupane, T.; Yu, Y.; Rice, Q.; Tabibi, B.; Seo, F. J. Third-order optical nonlinearity of tungsten disulfide atomic layer with resonant excitation. Optical materials 2019, 96, 109271. [Google Scholar] [CrossRef]
- . Wang, W.; Wu, Y.; Wu, Q.; Hua, J.; Zhao, J. Coherent Nonlinear Optical Response Spatial Self-Phase Modulation in MoSe2 Nano-Sheets. Sci. Rep. 2016, 6, 22072. [Google Scholar] [CrossRef] [PubMed]
- . Durbin, S. D.; Arakelian, S. M.; Shen, Y. R. Laser-induced diffraction rings from a nematic-liquid-crystal film. Opt. Lett. 1981, 6, 411–413. [Google Scholar] [CrossRef]
- ahae, M. S.; Said, A. A.; Wei, T. H.; Hagan, D. J.; Van Stryland, E. W. Sensitive Measurement of Optical Nonlinearities Using a Single Beam. IEEE J Quantum Electron 1990, 26, 76–769. [Google Scholar]
- eupane, T.; Rice, Q.; Jung, S.; Tabibi, B.; Seo, F.J. Cubic Nonlinearity of Molybdenum Disulfide Nanoflakes. J. Nanosci. Nanotechnol 2020, 20, 4373–4375. [Google Scholar] [CrossRef]
- eupane, T.; Yu, Y.; Rice, Q.; Tabibi, B.; Seo, F. J. Third-order optical nonlinearity of tungsten disulfide atomic layer with resonant excitation. Optical materials 2019, 96, 109271. [Google Scholar] [CrossRef]
- eo, J. T.; Yang, Q.; Kim, W. J.; Heo, J.; Ma, S. M.; Austin, J.; Yun, W.S.; Jung, S.S.; Han, S.W.; Tabibi, B.; Temple, D. Optical nonlinearities of Au nanoparticles and Au/Ag coreshells. Optics Letters 2009, 34, 307–309. [Google Scholar]
- a, S. M.; Seo, J. T.; Yang, Q.; Battle, R.; Brown, H.; Lee, K.; Creekmore, L.; Jackson, A.; Skyles, T.; Tabibi, B. Third-Order Nonlinear Susceptibility and Hyperpolarizability of CdSe Nanocrystals with Femtosecond Excitation. J. Korean Phys. Soc. 2006, 48, 1379. [Google Scholar]
- . Neupane, T.; Tabibi, B.; Seo, F. J. Spatial self-phase Modulation in WS2 and MoS2 Atomic Layer. Optical Materials Express 2020, 10, 831–842. [Google Scholar] [CrossRef]
- . Neupane, T.; Wang, H.; Yu, W. W.; Tabibi, B.; Seo, F. J. Second-order hyperpolarizability and all-optical switching of intensity-modulated spatial self-phase modulation in CsPbBr1.5I1.5 perovskite quantum dot. Optics and Laser Technology 2021, 140, 107090. [Google Scholar] [CrossRef]
- . Callen, W. R.; Huth, B. G.; Pantell, R. H. Optical Patterns of Thermally Self-Defocused Light. Appl. Phys. Lett. 1967, 11, 103–105. [Google Scholar] [CrossRef]
- Neupane, T.; Tabibi, B.; Kim, K.-J.; Seo, F.J. Spatial Self-Phase Modulation in Graphene Oxide Monolayer. Crystal 2023, 13, 271. [Google Scholar] [CrossRef]
- urlbut, W.C.; Lee, Y. S.; Vodopyanov, K. L.; Kuo, P. S.; Fejer, M. M. Multiphoton absorption and nonlinear refraction of GaAs in the mid-infrared. Optics Letter 2007, 32, 668. [Google Scholar] [CrossRef]
- oleman, J. N.; Khan, U.; Young, K.; Gaucher, A.; De, S.; Smith, R. J.; Shvets, I. V.; Arora, S. K.; Stanton, G.; Kim, H.; Lee, K.; Kim, G. T.; Duesberg, G. S.; Hallam, T.; Boland, J. J.; Wang, J. J.; Donegan, J. F.; Grunlan, J. C.; Moriarty, G.; Shmeliov, A.; Nicholls, R. J.; Perkins, J. M.; Grieveson, E. M.; Theuwissen, K.; Mccomb, D. W.; Nellist, P. D.; Nicolosi, V. Two-Dimensional Nanosheets Produced by Liquid Exfoliation of Layered Materials. Science 2011, 331, 568–571. [Google Scholar] [CrossRef] [PubMed]
- eupane, T.; Poudyal, U.; Tabibi, B.; Kim, K.-J.; Seo, F.J. Cubic Nonlinearity of Graphene Oxide Monolayer. materials 2023, 16, 6664. [Google Scholar] [CrossRef]
- ox, M. Optical properties of solids, second edition Oxford University press, page 81 (2010).
- . Nalda, R. de; Coso, R. del; Requejo-Isidro, J.; Olivares, J.; Suarez-Garcia, A.; Solis, J.; Afonso, C. N. Limits to the determination of the nonlinear refractive index by the Z-scan method. J. Opt. Soc. Am. B 2002, 19, 289. [Google Scholar] [CrossRef]
- . Falconieri, M. Salvetti, G. Simultaneous measurement of pure-optical and thermo-optical nonlinearities induced by high- repetition-rate, femtosecond laser pulses: application to CS2. Appl. Phys. B 1999, 69, 133.
- . Martin, K.; Spinks, D. Measurement of the speed of sound in ethanol/water mixture. Ultrasound Med. Biol. 2001, 27, 289–291. [Google Scholar] [CrossRef]
- . Khabibullin, V. R.; Usoltseva, L. O.; Galkina, P. A.; Galimova, V. R.; Volkov, D. S.; Mikheev, I. V.; Proskurnin, M. A. Measurement Precision and Thermal and Absorption Properties of Nanostructure in Aqueous Solutions by Transient and Steady-State Thermal-Lens Spectrometry. Phys. chem. 2023, 3, 156–197. [Google Scholar] [CrossRef]
- . Gnoli, A.; Razzari, L.; M. Righini, M. Z-scan measurements using high repetition rate lasers: how to manage thermal effects. Opt. Express 2005, 13, 7976–7981. [Google Scholar] [CrossRef]
- . Ganeev, R. A.; Ryasnyansky, A. I.; Baba, M.; Suzuki, M.; Ishizawa, N.; Turu, M.; Sakakibara, S.; Kuroda, H. Nonlinear refraction in CS2. Appl. Phys. B 2004, 78, 433–438. [Google Scholar] [CrossRef]
- . Burkins, P.; Kuis, R.; Basaldua, I.; Johnson, A. M.; Swaminathan, S. R.; Zhang, D.; Trivedi, S. Thermally Managed Z-scan methods investigation of the size-dependent nonlinearity of graphene oxide in various solvents. J. Opt. Soc. Am. B 2016, 33, 2395–2401. [Google Scholar] [CrossRef]
- ang, Q.; Seo, J. T.; Creekmore, S.; Temple, D.; Mott, A.; Min, N.; Yoo, K.; Kim, S. Y.; Jung, S. Distortions in Z-scan spectroscopy. Appl. Phys. Lett 2003, 82, 19–21. [Google Scholar] [CrossRef]
- . Yin, L.; Agrawal, G. P. Impact of two-photon absorption on self-phase modulation in silicon waveguides. Optics Letters 2007, 32, 2031–2033. [Google Scholar] [CrossRef]
- . Ulmer, T. G.; Tan, R. K.; Zhou, Z.; Ralph, S. E.; Kenan, R. P.; Verber, C. M. Two-photon absorption-induced self-phase modulation in GaAs-AlGaAs waveguides for surface-emitted second-harmonic generation. Optics Letters 1999, 24, 756–758. [Google Scholar] [CrossRef]
- . Huy, M. C. P.; Baron, A.; Lebrun, B.; Frey, R.; Delay, P. Characterization of self-phase modulation in liquid filled hollow photonic bandgaps fibers. J. Opt. Soc. Am. B 2010, 27, 1886–1893. [Google Scholar]
- . Dekker, R.; Driessen, A.; Wahlbrink, T.; Moormann, C.; Niehusmann, J.; Forst, M. Ultrafast Kerr-induced all-optical wavelength conversion in silicon waveguides using 1.55 µm femtoseconds pulses. Optics Express 2006, 14, 8336–8346.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




