1. Introduction
Optoelectronic oscillators (OEOs) have emerged as an indispensable technology in microwave photonics due to their ability to generate microwave signals with ultra-low phase noise and broad bandwidth. OEOs have been extensively utilized in high-performance applications such as radar systems, communications, and signal processing. By incorporating optical components such as modulators and photodetectors, OEOs overcome the limitations of traditional microwave oscillators, significantly improving phase noise performance and spectral purity [
1]. The hybrid nature of OEOs, which combines optical and electronic feedback loops, allows them to generate high-frequency microwave signals, making them ideal for applications that demand precise and stable signal generation.
The development of OEOs began in the late 1990s, following the seminal work of Yao and Maleki, who introduced a fiber-based OEO architecture. This design utilized a long, low-loss optical fiber as an energy storage element, achieving a high-quality factor and reducing phase noise [
2]. This foundational work led to various advancements in OEO architectures, including dual-loop OEOs [
3], coupled OEOs (COEOs) [
4], and high-Q resonator-based OEOs [
5]. These innovations have not only improved the phase noise performance but also enhanced the flexibility and tunability of OEO systems, broadening their applications in modern technology.
One of the most attractive features of OEOs is their ability to generate ultra-low phase noise signals, which are crucial in applications like radar and communication systems that require short-term frequency stability [
6]. Traditional electronic oscillators struggle to maintain signal quality as frequency increases, but OEOs leverage the advantages of photonics to achieve stable, high-frequency microwave signals, making them superior for these high-performance applications [
7]. The integration of optical delay lines or high-quality resonators in the OEO feedback loop has been key to achieving this low phase noise, as these components provide the high-quality factor necessary for noise reduction [
8].
In recent years, there has been growing interest in integrated OEOs, which aims to miniaturize the technology while maintaining excellent performance. Photonic integration platforms [
9,
10,
11], such as silicon and indium phosphide, have enabled the fabrication of compact OEOs with low power consumption, which are critical for next-generation communication systems and sensors [
12]. Additionally, techniques for mode control and frequency tunability, such as the use of tunable microwave photonic filters [
13] and optoelectronic parametric processes [
14,
15], have expanded the versatility of OEOs in producing a variety of microwave signals, including chirped and complex waveforms.
This review explores the evolution of OEOs, focusing on their transition from traditional fiber-based architectures to advanced integrated systems. We discuss the fundamental principles that support their operation, analyze key technological advancements in designs such as hybrid integration, parity-time symmetric systems, and micro-ring resonator-based configurations, and examine their performance improvements in terms of phase noise, frequency tunability, and compactness. By presenting a comprehensive overview of these developments, this review highlights the current state of OEO technology and its growing potential for applications in fields such as radar, wireless communications, and precision instrumentation, while addressing the challenges that remain for achieving high-performance, fully integrated systems.
2. OEO Configurations and Architectures
2.1. Single-Loop OEOs
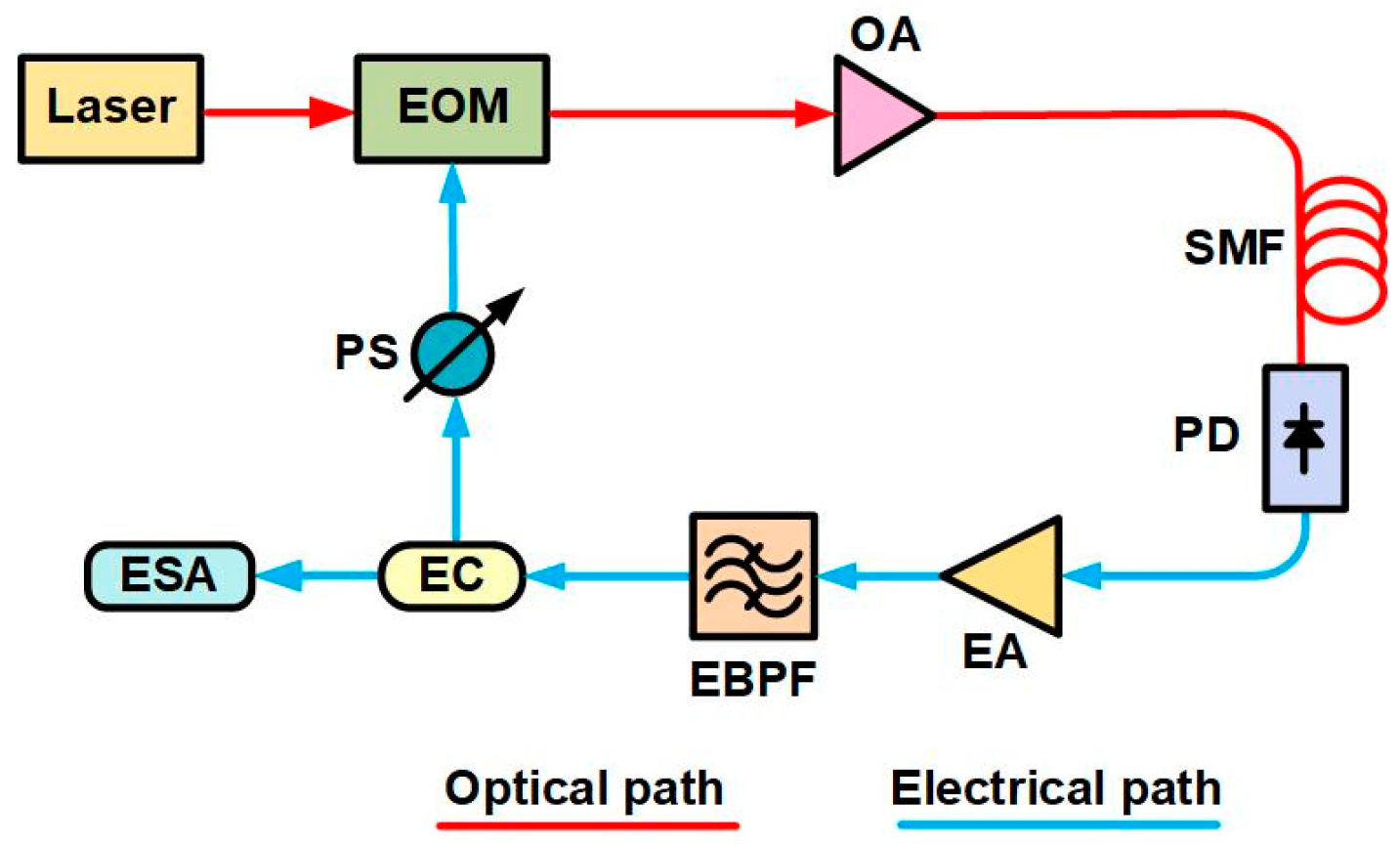
A typical single-loop OEO is depicted schematically in
Figure 1. The optical carrier generated by a laser diode (LD) is intensity modulated by the feedback signal using an electro-optic modulator (EOM). This modulator can be either a Mach-Zehnder modulator (MZM) [
4,
16,
17] or an electroabsorption modulator (EAM), the latter offering the advantages of low driving voltage and high integration capability [
18,
19]. The modulated optical signal, after amplification by an optical amplifier (OA), propagates through a length of single-mode fiber (SMF) and is subsequently converted into an electrical signal by a photodetector (PD). The electrical signal is then amplified by an electrical amplifier (EA), and an electrical bandpass filter (EBPF) is employed to perform mode selection. The filtered signal is divided into two parts by an electrical coupler (EC). One part is adjusted via a phase shifter (PS) and fed back to the EOM, thereby establishing a closed positive feedback loop. Another part is output or observed with an electrical signal analyzer (ESA).
When a MZM is used and the driving signal applied to the modulator is
Vin(
t), the output of the MZM is
where,
Ein(
t) is the optical carrier from the LD,
φ=
πVb/
Vπ, is the phase shift induced by the DC bias voltage
Vb, and
Vπ is the half-wave voltage of the MZM. After transmission through the OEO loop, the output signal of the PS
Vout(
t) can be obtained as
where,
R is the responsivity of the PD,
Rd is the load impedance of the photodetector, γ is the amplitude attenuation due to the EBPF, EC and PS,
Ge is the voltage gain of the EA,
Go is the gain of the OA,
Po is the average output power of the LD,
and
L are, respectively, the attenuation coefficient and length of the fiber.
Then, the small-signal open-loop gain of the OEO is
To achieve a stable oscillation in an OEO, optical and electrical amplifiers are used to provide sufficient gain to make the net gain |
Gs| greater than 1. Additionally, the phase matching condition to be satisfied is [
1]
Here, k represents the mode number, ωk denotes the angular frequency of the k-th mode, τ is the time delay determined by the physical length of the feedback loop, is the frequency-dependent phase induced by the dispersive components in the loop, and φ0 is the initial phase. Theoretical analysis has suggested that modes satisfying the gain and phase matching conditions can initiate oscillation. The frequency spacing between two adjacent oscillation modes, known as the Free Spectral Range (FSR), is inversely proportional to the loop delay. Typically, an EBPF is employed to select oscillation modes. Within the EBPF’s passband, the strongest primary mode, located near the center frequency, may coexist with weaker side modes if the FSR is smaller than the filter bandwidth. However, due to the saturation of the gain medium and the nonlinear behavior of the EOM, the gains of oscillating modes gradually converge to unity. As a result, only the mode closest to the EBPF’s center frequency survives, forming a stable oscillation.
2.2. Performance Parameters
2.2.1. Side Mode Suppression Ratio
The Side Mode Suppression Ratio (SMSR) is a critical parameter that quantifies the spectral purity of an OEO. It is defined as the ratio of the power of the main oscillation mode to the maximum power of the side modes. A higher SMSR indicates superior spectral purity, which is essential for applications requiring clean and stable signals.
As discussed earlier, the single-frequency mode in OEOs is typically selected using an EBPF. However, in long fiber loops, the small FSR results in a higher density of side modes within the EBPF passband, which degrades the SMSR. To address this issue, one common approach involves employing a multi-loop structure, which increases the effective FSR through gain competition among multiple sets of modes [
20]. Another effective strategy to suppress side modes and achieve single-frequency oscillation is replacing long optical fibers with high-Q optical resonators as the optical energy storage medium, where Q-factor is defined as
Q=
2πfoscτ and
fosc is the oscillation frequency. High-Q optical resonators, such as microring resonators (MRRs), significantly improve spectral purity due to their large FSRs and high Q-factors [
5].
2.2.2. Phase Noise
According to Leeson model, the output phase noise power spectral density of an OEO can be expressed as [
21]
where,
Sϕi(
f) is the input phase noise power spectral density, and
f is the frequency offset from the oscillation frequency. The input phase noise in OEOs includes relative intensity noise (RIN), shot noise, thermal noise, and flicker noise. The RIN originates from the laser, whose intensity fluctuations are converted into current fluctuations by the photodetector. Shot noise is mainly caused by the statistical fluctuations of carriers within the OEOs. Thermal noise primarily originates from RF amplifiers and PDs, resulting from the random motion of electrons excited by heat. Flicker noise is a low-frequency noise source from RF amplifiers and PD, impacting the phase noise near the oscillation frequency. The total input phase noise power spectral density
Sϕi can be expressed as,
where,
NRIN is the RIN noise of the laser,
Iph is the photocurrent,
e is the electron charge,
kB is the Boltzmann constant,
Te is the room temperature,
NF is the noise figure of the EA,
b-1 is the total flicker noise coefficient of EA and PD, and
Posc is the oscillation power before EA.
2.3. Multi-Loop OEOs
In single-loop OEOs, a long optical fiber with low transmission loss is commonly employed to construct a resonant cavity with a high Q-factor, enabling the generation of low-phase-noise signals. However, the use of long fibers introduces a small FSR, which complicates mode selection and can lead to issues such as mode hopping and a degraded SMSR. To address these challenges, multi-loop OEOs have been proposed [
20,
22].
2.3.1. Dual-Loop OEOs
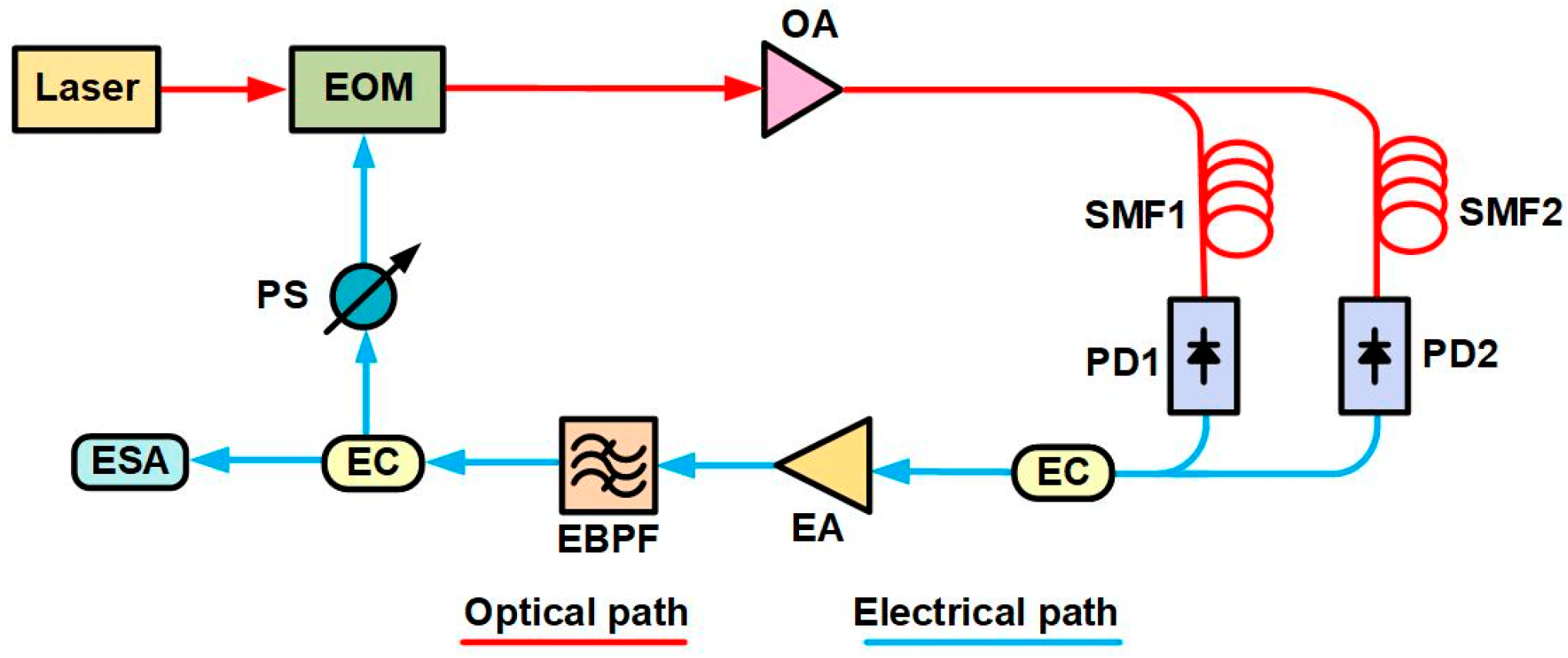
As illustrated in
Figure 2, in a typical dual-loop OEO configuration, the modulated optical signal is amplified and divided by an optical coupler into two paths, each feeding a long and a short optical fiber loop. These signals are converted into electrical signals by two PDs and then combined by an EC. In this configuration, an EA and a PS are also used to satisfy the gain and the phase conditions for oscillating, and an EBPF is for mode section. The long optical loop forms a high-Q resonant cavity, reducing the phase noise of the output signal, while the short loop assists in mode selection, thereby improving the SMSR. By designing the fiber lengths of the loops in a multiple relationship, the system allows for different oscillation modes to form in each loop. Only the common modes in the two loops are output. In this case, the oscillation frequency can be expressed as,
where
m and
n are integers, and
FSR1 and
FSR2 are the FSR of the long and short fiber loops, respectively. Due to the Vernier effect, the equivalent mode spacing of the dual-loop OEO is significantly increased, optimizing the SMSR while maintaining low phase noise.
While the dual-loop architecture effectively improves SMSR and reduces phase noise, it also introduces challenges. The use of longer fibers in the loops increases accumulated dispersion, which can degrade the near-carrier phase noise. A trade-off must be carefully considered in the design of dual-loop OEOs to achieve optimal performance.
In a multi-loop OEO, optical coupling technology can be used as an alternative to electrical coupling. In the optical domain, polarization division multiplexing enables the use of a polarization beam splitter (PBS) to divide the modulated optical signal into two loops, which are later recombined in the optical domain with a polarization beam combiner (PBC) [
23,
24]. This approach eliminates the need for multiple independent PDs, simplifying the system architecture.
Additionally, multi-loop OEOs can incorporate multiple laser sources by leveraging wavelength division multiplexing (WDM) technology. Wavelength division multiplexers are used in the optical domain to split and combine signals based on their wavelengths. Compared to polarization-based methods, WDM-based systems offer the advantage of reduced interference between beams of different wavelengths, as opposed to the orthogonal polarizations in PBS or PBC configurations. This significantly mitigates the beating noise caused by random interference, enhancing the signal quality and stability [
25].
2.3.2. Coupled OEOs
Both single-loop and dual-loop OEOs utilize long optical fibers to achieve a high Q-factor, which is essential for reducing phase noise. However, increasing the length of the optical fiber also amplifies its dispersion and sensitivity to environmental perturbations, which can negatively impact the stability of the OEOs. To address these issues and maintain a high Q-factor with shorter optical fibers, the coupled optoelectronic oscillator (COEO), also known as a regenerative mode-locked laser, has been investigated [
26,
27].
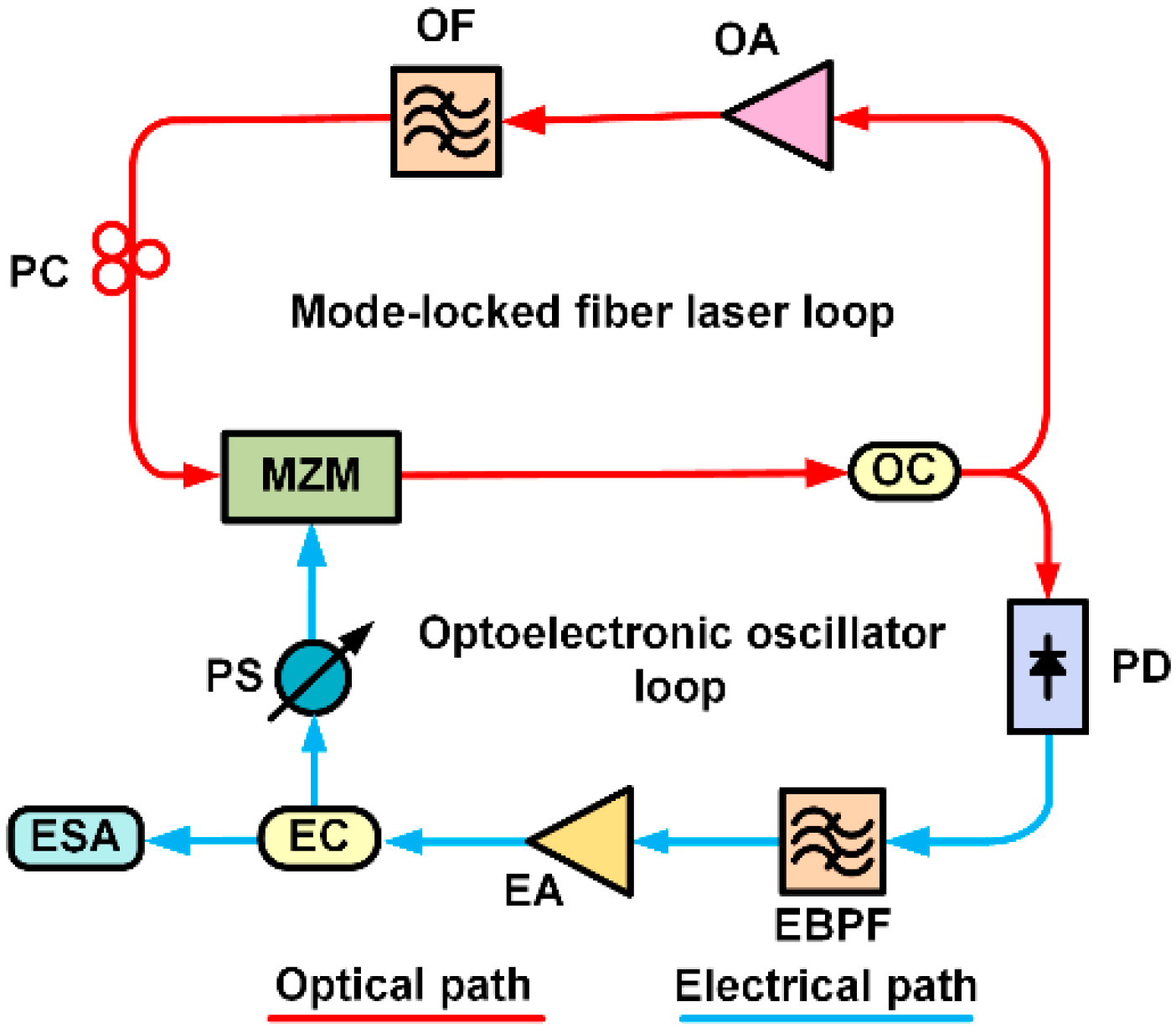
A typical COEO configuration is shown in
Figure 3, consisting of two coupled loops: a mode-locked laser loop and an OEO loop. The mode-locked laser loop is formed by an optical coupler (OC), an OA, an optical filter (OF), a polarization controller (PC), and a MZM. The OEO loop includes a PD, an EBPF, an EA, a PS and a shared MZM. Unlike traditional OEOs, COEOs do not require external light sources, as the optical signal is generated within the mode-locked laser loop.
In COEOs, one part of the optical signal produced by the mode-locked laser loop serves as the light source for the OEO loop. After photoelectric conversion, filtering and amplification, the signal is fed back to the MZM to modulate the gain of the mode-locked laser loop. When the modulation frequency, determined by center of the EBPF, matches an integer multiple of the FSR of the laser loop, mode-locking occurs. This ensures that only a subset of the laser modes oscillates in phase, with the mode spacing corresponding to the oscillation frequency of the OEO loop. These selected laser modes are injected into the OEO loop, amplifying the desired oscillation mode while suppressing others. After multiple iterations, the COEO reaches a stable state, producing a microwave signal with low phase noise and simultaneously outputting an optical pulse with low timing jitter.
The integration of the mode-locked laser loop in the COEO architecture significantly enhances the equivalent Q-factor, reducing the phase noise of the output signal for a given optoelectronic loop delay. This reduces the system’s dependency on long optical fibers, increasing the FSR and relaxing the performance requirements of the EBPF. Consequently, COEOs achieve improved SMSR and overall system stability while maintaining compactness and efficiency.
2.3.3. Parity-Time Symmetric OEOs
Recently, the Parity-Time (PT)-Symmetric OEO has emerged as a novel approach to achieving single-frequency oscillation without relying on narrowband filters. Compared to conventional methods, PT-symmetric OEOs generate high-spectral-purity signals even with small FSRs. A typical PT-symmetric OEO consists of two coupled loops of identical lengths: one providing gain and the other providing loss. The PT-symmetry condition requires the gain and loss to be balanced in magnitude. By manipulating the gain, loss, and coupling ratio between the loops, PT-symmetry can be selectively broken for a specific mode, allowing it to dominate and achieve stable single-mode oscillation.
The oscillation mode is governed by a set of coupled differential equations that describe the amplitudes of the
nth longitudinal mode
an(1, 2) in each loop [
28]:
where
g and
γ represent the net gain or loss in the responding loop,
μ is the coupling coefficient between the two loops,
ωn is the angular frequency of the
nth mode,
ωn(1,2) are the resonance frequencies of each loop, and ∆
ωn(1, 2) =
ωn-
ωn(1,2)
are the detuned frequencies of each loop. The solution to these equations provides the eigenfrequencies of the system, enabling the identification of the stable oscillation mode when PT symmetry is broken.
PT-symmetric OEOs often adopt a dual-loop structure, where the gain and loss in each loop are controlled via amplifiers and attenuators [
28] or with polarization-based methods [
29,
30]. In addition, a single-loop PT-symmetric OEO based on WDM has been proposed. In this design, the gain, loss, and coupling ratio of equivalent loops are adjusted by tuning the input wavelength based on the reflection characteristics of a chirped fiber Bragg grating (CFBG) [
31].
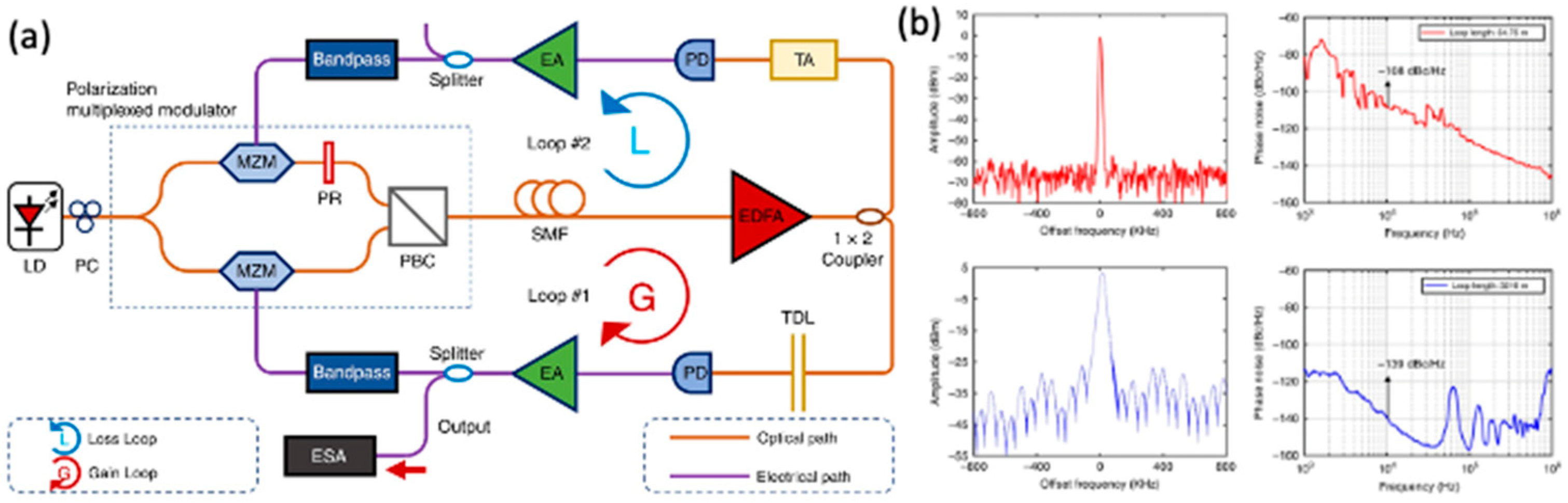
In a PT-symmetric dual-loop OEO configuration, as shown in
Figure 4(a) [
28], a stable single-mode oscillation can be achieved with ultralow phase noise. For example, a single-frequency signal at 4.0703 GHz exhibited a phase noise of -108 dBc/Hz at a 10 kHz offset. When a longer loop length of 3216 m was employed, an ultralow phase noise of -139 dBc/Hz at a 10 kHz offset was achieved. These results demonstrate the potential of PT-symmetric OEOs for producing high-spectral-purity signals while maintaining low phase noise.
2.4. Recent Progress
The performance comparison of single-frequency OEOs is summarized in
Table 1. High SMSR and low phase noise are crucial for single-frequency OEOs to achieve excellent spectral purity and stable signal performance. Using a WDM based dual-loop architecture, a 20-GHz oscillating signal with a SMSR as high as 70 dB and a phase noise of −120.6 dBc/Hz at 10-kHz offset frequency has been produced [
25]. In a single-loop OEO with a high-Q optical ring resonator, a SMSR of 59 dB is achieved [
32] . In addition, a PT-symmetric OEO without a narrowband EBPF generates a 6.19 GHz signal with a SMSR of 55 dB and a phase noise of -139 dBc/Hz at 10-kHz offset frequency [
28]. And a 9.867 GHz signal with a lower phase noise of −142.5 dBc/Hz at the offset frequency of 10 kHz is also generated in a PT-symmetric OEO using polarization control [
29].
3. Operation Frequency and Stability
To meet various application requirements, OEOs have evolved beyond single-frequency operation to include frequency-tunable and broadband configurations. The critical performance parameters for microwave sources include operating frequency, frequency stability, phase noise, and tunability, which directly affect the effectiveness and versatility of the OEOs in diverse scenarios. Frequency-tunable OEOs provide flexibility in selecting operating frequencies, enabling their deployment in dynamic communication networks and adaptive radar systems. Broadband OEOs, on the other hand, can generate signals over a wide range of frequencies, broadening their scope for use in multi-functional platforms.
To enhance the performance of OEOs, particularly in terms of frequency stability, advanced techniques such as phase-locked loops (PLL) and injection locking (IL) have also been introduced. PLL-based OEOs achieve improved frequency stability by locking the oscillation frequency to a stable external reference, reducing drift and ensuring precise control. Similarly, IL techniques stabilize the oscillation frequency by injecting a highly stable signal into the system, suppressing undesired modes and enhancing phase noise performance. These approaches not only enhance the reliability of OEOs but also expand their application potential in environments demanding stringent frequency control, such as satellite communications and secure data links.
3.1. Frequency Stability
3.1.1. Frequency Stability and Influencing Factors
For OEOs, frequency stability is influenced by various factors. First, the high-Q components in OEOs, such as long optical fibers and narrowband electrical filters, are susceptible to environmental influences. Especially, the optical fibers affected by temperature may change the cavity lengths, leading to unstable output frequencies. Additionally, the dispersion and nonlinear effects of the optical fibers also impact the frequency stability. The noises introduced by active components, such as lasers, photodetectors, and amplifiers, also affect frequency stability. In addition, multiple modes oscillating in the loop result in multimode noise and mode competition, which can cause issues like mode hopping and drifting, affecting frequency stability. Frequency stability can be described as short-term frequency stability and long-term frequency stability. Phase noise is a frequency-domain representation of short-term frequency stability. Time jitter is a time-domain representation of short-term frequency stability. Allan variance is a time-domain representation of long-term frequency stability.
3.1.2. Methods to Improve Frequency Stability
Enhancing the frequency stability of OEOs involves approaches such as environmental condition control, phase noise suppression, and SMSR enhancement. Temperature control, through temperature-stabilized chambers or temperature-insensitive optical fibers, can mitigate thermal effects [
34]. Multi-core optical fibers (MCFs) can create multi-loop OEOs, where co-located loops share the same environmental conditions, reducing optical fiber length requirements while enhancing stability [
6].
PLL, self-phase-locked loop (SPLL), IL, and self-injection locking (SIL) techniques are widely implemented to further improve frequency stability. In a PLL, the phase error voltage is derived by comparing the OEO output signal with an external reference, and it is fed back to an electrical phase shifter for phase drift compensation, effectively converting the OEO into a voltage-controlled oscillator (VCO). For example, a PLL-stabilized OEO generating a 2.5 GHz signal with a phase noise of -134 dBc/Hz at 10-kHz offset frequency significantly reduces Allan deviation and enhances long-term stability [
3]. However, PLL systems are susceptible to phase noise from external reference signals. To address this issue, SPLL uses a delay-line frequency discriminator (DLFD) to generate the error signal. By comparing the delayed OEO output signal with its original, the SPLL achieves phase compensation by controlling the bias voltage of the used MZM in the oscillating loop [
35], [
36].
On the other hand, IL enhances the frequency stability of OEOs by synchronizing the oscillation frequency with an external electrical or optical reference signal. In electrical IL, the oscillation frequency of the OEO is pulled to match the frequency of the injected signal when they are sufficiently close, maintaining a constant phase difference between the two [
37]. This method minimizes the impact of environmental fluctuations and improves phase noise performance near the carrier frequency. Additionally, the injected signal amplifies the energy of the locked oscillation mode, enhancing mode competition and improving the SMSR.
For instance, an electrical injection-locked dual OEO operating at 10 GHz, as described in [
38], uses the RF output signal of a high-Q long-fiber master OEO to lock a short-fiber slave OEO. This configuration suppresses side modes and preserves the master OEO's high-Q properties, achieving phase noise below -110 dBc/Hz at low offset frequencies. Similarly, a COEO employing optical IL couples an external optical reference signal into a mode-locked laser loop [
39]. This approach achieves over 8 dB spur suppression in the RF spectrum. These results highlight the effectiveness of IL in reducing phase noise and improving SMSR, making it a vital technique for frequency stabilization in OEOs.
The phase noise performance of OEOs using IL is inherently constrained by the noise of the external source. To address this, the SIL technique has been proposed, wherein a portion of the output oscillation signal is coupled out, delayed, and reinjected into the OEO loop as a locking signal. Low-loss optical fiber delay lines are typically used to counteract the high loss of electrical delay lines; however, the use of long optical fibers reduces the FSR and increases environmental sensitivity. A dual-loop self-injection locking (DSIL) structure can suppress side modes and mitigate these challenges [
8]. To eliminate reliance on long optical fibers, a frequency-conversion-based SIL OEO was proposed in [
40]. As shown in
Figure 5, this method uses a coupler to split the oscillation signal, which is then reinjected into the loop after passing through a frequency conversion filter—an equivalent narrowband filter consisting of a frequency conversion pair and a narrowband intermediate frequency (IF) filter. Although residual phase noise from the local oscillator (LO) persists, it can be minimized by reducing the locking bandwidth or achieving delay matching. This frequency-conversion SIL OEO achieves a SMSR exceeding 70 dB at 10-GHz oscillation. And the phase noise at 10-kHz offset frequency is nearly 30 dB lower than traditional injection-locked OEOs under identical experimental conditions, demonstrating substantial improvements in frequency stability.
The combination of PLL, SPLL, IL, and SIL techniques significantly enhances the performance of OEOs by leveraging the strengths of each method. For instance, integrating PLL and IL enables precise phase compensation and frequency locking, achieving low phase noise and high side-mode suppression ratios, as demonstrated by a 9.5-GHz OEO with a phase noise of -143 dBc/Hz at a 10 kHz offset and an Allan deviation of 1.22×
[
41]. Similarly, combining PLL with DSIL reduces environmental sensitivity and further improves stability, achieving significant phase noise reductions and Allan deviation improvements compared to free-running configurations [
42]. These results highlight the effectiveness of combining stabilization techniques to meet stringent frequency stability requirements.
3.2. Frequency-Tunable OEOs
A frequency-tunable OEO is capable of adjusting the frequency of its output microwave signal over a defined range, generating high-frequency, broadband-tunable, and low-phase-noise RF signals. This adaptability makes it a crucial component for advanced applications in communication systems, radar, and electronic warfare. Frequency tuning in OEOs can be achieved using either tunable electrical filters or tunable microwave photonic filters (MPFs) [
43,
44].
A widely used tunable electrical filter is the Yttrium Iron Garnet (YIG) filter, which allows its center frequency to be adjusted by varying the driving voltage [
45,
46]. However, YIG filters have limitations. They require precise voltage control, and their tuning range, bandwidth, and anti-interference capability may constrain both frequency stability and overall tuning performance. These constraints have motivated the exploration of alternative solutions.
Tunable MPFs have emerged as a superior alternative for frequency-tunable OEO designs, offering wider tuning ranges, greater reconfigurability, and stronger anti-interference capabilities. Various MPF-based architectures have been demonstrated. For instance, in an OEO, a tunable single-bandpass MPF has been constructed using a non-sliced broadband optical source (BOS) cascaded with a phase modulator (PM) and a dispersion-compensating fiber (DCF) [
47], and frequency tunability in a range of 10.23 to 26.69 GHz is achieved. In another OEO, the MPF is composed of a tunable band-pass optical filter (TBPOF) combined with a PM to provide flexible tuning capabilities from 3.5 to 17.1 GHz [
6]. Other approaches involve fiber Bragg grating (FBG)-based structures, including Fabry-Pérot FBGs (FBG-FP) [
48], linearly chirped FBGs (LCFBG) [
49], and phase-shifted FBGs (PS-FBG) [
50,
51,
52].
In addition, MPFs based on stimulated Brillouin scattering (SBS) exhibit significant advantages, including high gain and narrowband filtering characteristics [
27,
53]. For example, an agilely tunable dual-loop OEO utilizing SBS achieves a narrowband MPF through a combination of phase modulation and selective sideband amplification via SBS [
55]. The oscillation frequency in this configuration is determined by the frequency of signal wave, pump wave and Stokes frequency shift. By adjusting the wavelength of the pump laser, the system achieves a wide frequency tuning range from DC to 60 GHz. The measured single-sideband (SSB) phase noise remains stable at approximately -100 dBc/Hz at a 10 kHz offset for all oscillation frequencies, with dual-loop fiber lengths ranging from 2 km to 4 km.
Table 2 provides a summary of the frequency tuning methods and characteristics of frequency-tunable OEOs. In terms of tuning range, MPF-based OEOs demonstrate significant advantages over YIG-based OEOs, achieving tuning ranges of several tens of GHz [
48,
53]. However, both YIG-based and MPF-based OEOs typically exhibit tuning steps at a MHz level, primarily due to the bandwidth limitations of tunable electrical filters and tunable MPFs.
Recent advancements have introduced tunable OEOs capable of finer tuning steps at the kHz level. For instance, a frequency-tunable PT-symmetric OEO is reported in [
54], where a dual-parallel MZM (DPMZM) functions as an optical phase shifter. By controlling the bias voltage of the parent MZM, the total phase of the OEO loop is adjusted, enabling fine-tuning within a kHz-level range. However, the stability of this design is limited due to its polarization dependence, which is highly sensitive to environmental fluctuations, resulting in poor output signal stability.
A more robust approach is presented in [
4], which describes a finely tunable COEO based on IL and a PLL. By precisely controlling the frequency of the injected signal and adjusting a tunable optical delay line, the system achieves a tuning range of 1.76 MHz with an exceptionally fine tuning step of 10 Hz. Furthermore, this design ensures excellent frequency stability in the output signals, addressing the limitations in polarization-sensitive designs.
3.3. Broadband OEOs
3.3.1. Multi-Frequency OEOs
To address the growing demands for multi-mode and multi-band operations in wireless communication applications [
2], significant research has been conducted on multi-frequency OEOs capable of simultaneously generating multiple stable oscillation frequencies. Multi-frequency OEOs are generally categorized into serial-structure multi-frequency OEOs and parallel-structure multi-frequency OEOs.
A typical serial-structure multi-frequency OEO consists of a single loop equipped with a multi-bandpass MPF. The multi-bandpass MPF can be constructed using technologies such as multi-channel optical notch filters (ONFs) [
56], FBG-FP filters [
57,
58] or SBS [
59]. While serial-structure multi-frequency OEOs are relatively simple in design, they are prone to gain competition between oscillation modes, which can lead to instability.
In contrast, parallel-structure multi-frequency OEOs offer a more robust solution by using independent loops for each oscillation frequency [
60]. This architecture increases system complexity but allows the gain in each loop to be tuned independently, mitigating gain competition between frequencies and ensuring stable oscillation. This design also ensures good phase coherence between the generated signals, making it a preferred choice for applications requiring simultaneous multi-band operation.
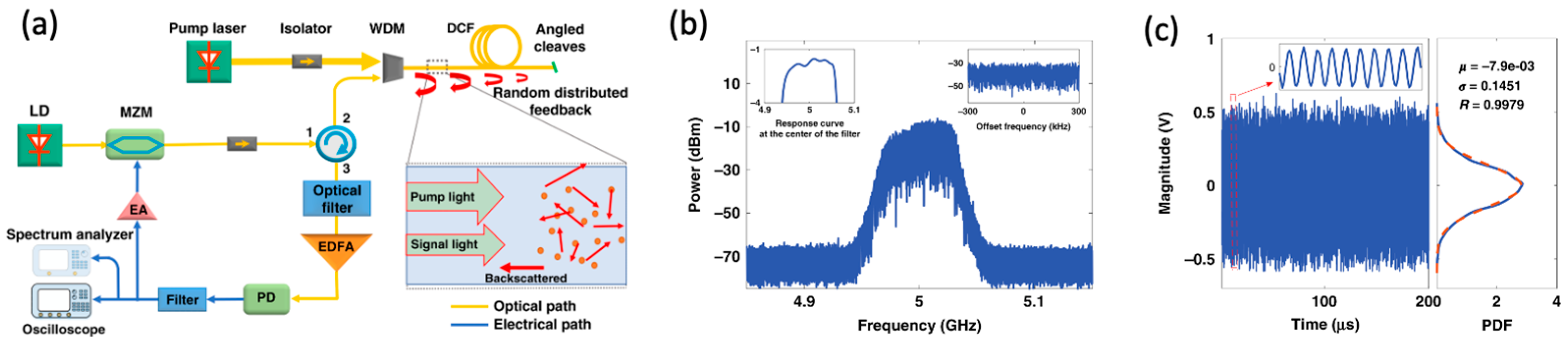
A noteworthy example of a parallel-structure design is the broadband random OEO leveraging Rayleigh scattering [
61]. This configuration employs distributed Raman amplification to enhance both incident and backscattered light within the feedback loop, creating a distributed random feedback mechanism. Unlike traditional multi-frequency OEOs with fixed cavity lengths, the Rayleigh scattering mechanism eliminates discrete longitudinal modes, enabling continuous broadband frequency oscillations from DC to 40 GHz. Experimental results, as shown in
Figure 6(b), illustrate the capability of this OEO to generate ultra-wideband microwave signals with a random amplitude and frequency distribution. These characteristics demonstrate the potential of multi-frequency OEOs not only for wireless communication but also for noise radar systems, secure communications, and random bit generation.
By combining robust architectures, such as parallel-structure loops, with innovative mechanisms like Rayleigh scattering, multi-frequency OEOs are poised to meet the demands of next-generation multi-band communication systems, offering both versatility and high performance.
3.3.2. Frequency-Scanning OEOs
In addition to single-frequency microwave signals, OEOs can generate linearly chirped waveforms (LCWMs) through rapid frequency scanning, which are critical for applications in spread-spectrum communication systems and radar systems. Although broadband frequency-tunable OEOs can theoretically produce LCWMs, their frequency-scanning speed is inherently limited. This limitation arises because the OEO operates in an unstable state during frequency tuning, requiring a new oscillation mode to re-establish from noise at each frequency step. This process makes it challenging to directly generate high-quality LCWMs.
To address this issue, frequency-scanning OEOs based on Fourier domain mode locking (FDML) have been proposed. In FDML-based OEOs, a tunable MPF is employed, with a center frequency fast scanning. FDML operation is achieved when the frequency scanning period of the MPF is equal to or a fraction of the round-trip time within the cavity. Under this condition, the OEO operates in a quasi-stationary state, with multiple longitudinal modes spanning the entire scanning range simultaneously excited and sustained within the cavity. By rapidly tuning the MPF, the OEO can directly output a broadband and high-performance LCWM.
Several advanced configurations of FDML-based OEOs have been developed to enhance their performance and flexibility. These include harmonically FDML OEOs [
63], dual-chirp FDML OEOs [
64], and polarization-manipulated FDML OEOs [65, 66]. A recent example of an FDML-based OEO [
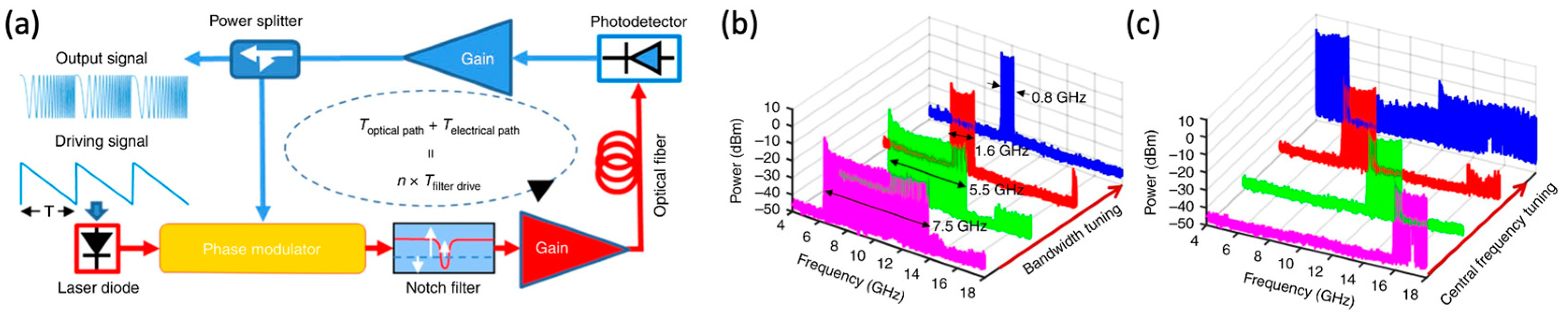
62] demonstrates its ability to overcome the mode-building time limitations during frequency scanning. This configuration simultaneously excites thousands of longitudinal modes with fixed phase relationships, ensuring quasi-stationary operation and enabling faster scanning speeds, leading to the generation of LCWMs with a chirp rate of 0.34 GHz/μs and a time-bandwidth product (TBWP) of 166,650. The experimental setup employs a tunable MPF synchronized with a periodic driving signal to facilitate continuous frequency sweeping.
Figure 7(a) illustrates the experimental setup, where the synchronization between the MPF and cavity round-trip time ensures stable FDML operation. The experimental results, shown in
Figure 7(b) and (c), highlight the reconfigurability of both center frequency and tuning range. These results demonstrate the superior performance of the FDML-based OEO, offering broadband frequency scanning and high-quality LCWM generation.
The advancements in FDML-based OEOs not only improve the speed and quality of LCWMs but also broaden their application scope. From radar systems requiring high-speed chirps to secure communications and high-frequency sensing, the demonstrated capabilities of these systems represent a significant step forward in the development of next-generation OEOs.
4. Integrated Optoelectronic Oscillators: Advances and Challenges
Classical OEO designs have historically relied on discrete components, including long optical fiber delay lines and electrical bandpass filters, while effective at achieving low phase noise. These designs are inherently bulky due to the length of the fiber required to achieve high Q-factors, and they are often power-hungry, limiting their scalability and practical applications in modern communication systems like 5G and 6G networks [
67,
68]. Furthermore, the reliance on discrete electrical and optical components limits the potential for system miniaturization and scalability, posing a significant challenge as modern applications demand more compact, power-efficient, and integrated solutions [
69,
70].
Recent advances in photonic integration have offered a promising solution to these limitations, enabling the development of integrated OEOs. These integrated designs combine key components—such as modulators, resonators and detectors—onto a single chip, resulting in systems that are not only smaller and more power-efficient but also capable of tunable performance across a wide frequency range. Moreover, integrated OEOs leverage novel filtering techniques, such as PT symmetry and micro-ring resonators, to achieve single-mode oscillation and wideband tunability without relying on large external filters [
71,
72]. For example, integrated designs have demonstrated tunability across a broad frequency range up to 42.5 GHz, which surpasses many traditional designs [
73]. This section reviews the transition from classical to integrated OEOs, highlighting key technological achievements in the field and examining the ongoing challenges that researchers and engineers face in further refining these systems.
4.1. Achievements in Integrated OEO Designs
Recent innovations have resulted in significant advancements in integrated OEO technologies. One of the most notable is the monolithic integration of OEO components on a SiGe BiCMOS silicon photonic platform, which achieved a phase noise of -115 dBc/Hz at a 100 kHz offset from a 750 MHz signal. This design drastically reduced system size and power consumption compared to traditional discrete-component designs [
74]. Another example of monolithic integration is the use of silicon photonic platforms to achieve a wide frequency tuning range from 3 GHz to 7 GHz with a phase noise of -80 dBc/Hz at a 10 kHz offset, showing the potential for low-cost, scalable OEOs for high-frequency applications [
69]. Moreover, the use of directly modulated dual-mode lasers in integrated OEOs has allowed for tunable generation of microwave signals from 28 GHz to 41 GHz, with a phase noise of -106 dBc/Hz, showcasing the potential of integrated designs for higher-frequency applications [
70]. Another notable development includes the use of a tunable optoelectronic oscillator based on a dual-frequency semiconductor laser, which demonstrated tunability from 14.2 GHz to 25.2 GHz and a phase noise of -106.363 dBc/Hz at 10 kHz offset [
75].
4.1.1. Si-Based OEOs
The silicon micro-ring-based OEO presents a novel approach to microwave signal generation, leveraging the compactness and integrability of silicon photonics. This architecture combines a laser source, an intensity modulator, and a silicon add-drop micro-ring resonator (MRR) to generate wideband tunable microwave signals through direct intensity-modulation-to-microwave conversion. The silicon micro-ring acts as an optical bandpass filter, selecting a single sideband of the modulated signal, which subsequently beats with the laser source to produce the desired microwave frequency. By tuning the wavelength separation between the laser and the resonance of the ring resonator [
76], this OEO achieves a frequency tuning range from 5.9 GHz to 18.2 GHz—the widest range reported for silicon-based OEOs to date.
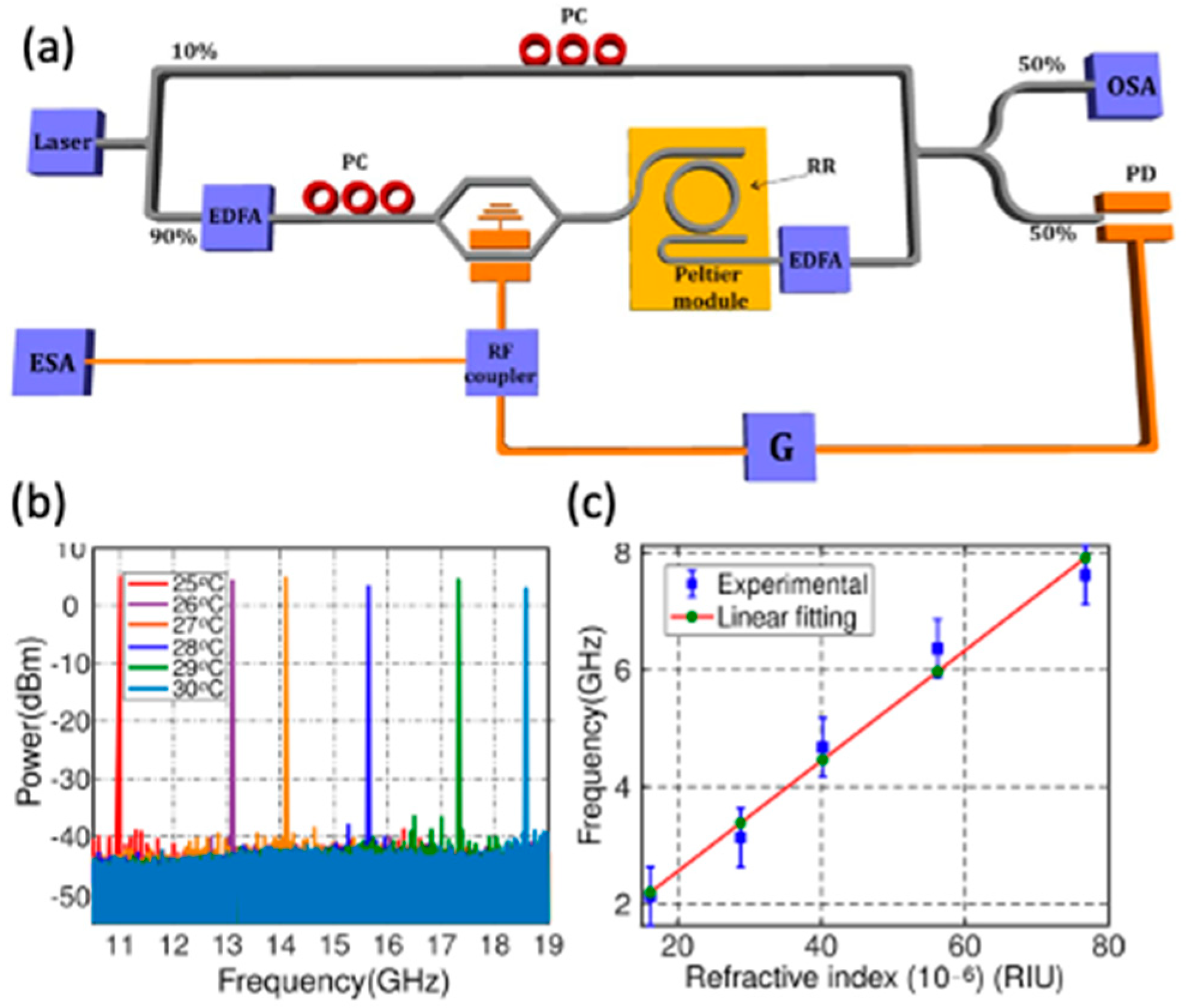
As shown in
Figure 8 (a), this design demonstrates exceptional phase noise performance, achieving −110 dBc/Hz at a 1 MHz offset across the tuning range. The micro-ring resonator, fabricated using silicon-on-insulator (SOI) technology, offers a high optical quality factor (Q ~ 8.1 × 10⁴), critical for improving the purity and stability of the generated signals. Moreover, the tunability is achieved through thermal control of the ring resonator or by sweeping the laser wavelength, providing a flexible and efficient frequency selection mechanism.
The proposed silicon OEO also extends its functionality into sensing applications. By monitoring the oscillation frequency shifts corresponding to variations in the ring's resonance, it achieves a refractive index sensitivity of 94350 GHz/RIU, with a detection limit as low as 10⁻⁸ RIU. These results highlight the potential of silicon micro-ring-based OEOs in microwave generation and photonic sensing, paving the way for advanced applications in radar, communication systems and lab-on-a-chip technologies.
4.1.2. Integrated PT Symmetric OEOs
In [
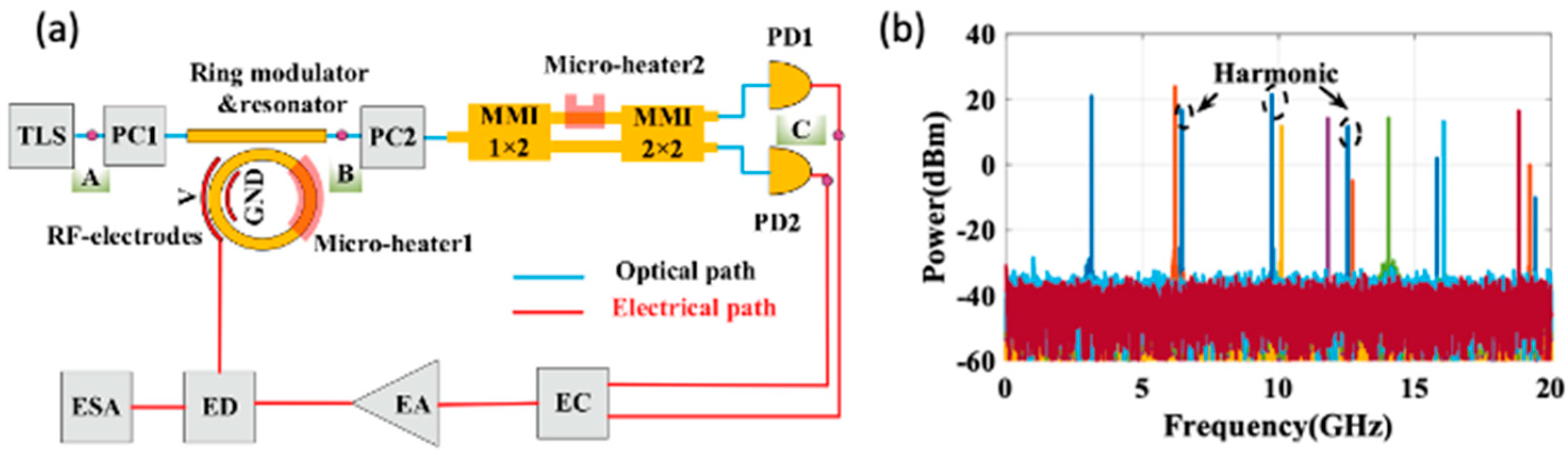
72], Ahmadfard and Hosseini present a novel design of a tunable PT symmetric OEO that integrates essential components such as a MRR with a high Q-factor and an adjustable optical power splitter, as shown in
Figure 9 (a). The operation of the proposed PT-symmetric OEO relies on the interaction between two coupled feedback loops. Each loop is geometrically identical, with one providing gain and the other loss. As explained in
Section 2.3.3, the PT symmetry is achieved when the gain and loss coefficients are balanced. As the symmetry is broken, a single mode with higher gain dominates, while other modes are suppressed, resulting in a stable single-mode oscillation. The system incorporates a tunable MPF based on the integrated MRR to provide precise control over the generated microwave frequency.
The SSB phase noise of the proposed OEO was calculated at two frequencies: 6.2 GHz and 11.5 GHz. The phase noise at a 10 kHz offset was measured as -79.22 dBc/Hz at 6.2 GHz and -76.5 dBc/Hz at 11.5 GHz. The SMSR was approximately 40 dB, indicating stable single-mode operation without the need for an additional microwave filter. By tuning the laser wavelength, the oscillation frequency can be varied from 0 to 20 GHz, covering a wide range of potential applications. The stability of the system is maintained through precise control of the gain and loss within the two feedback loops, adjusted using micro-heaters integrated into the power splitter.
4.1.3. Hybrid Integrated OEOs
Hybrid integrated OEOs have emerged as a promising solution to address the challenges of size, cost, and performance in traditional OEO designs. By combining photonic integration with advanced packaging techniques, these systems achieve a high level of compactness and performance, making them suitable for modern communication and sensing applications. A notable example of this approach is the hybrid-integrated wideband tunable OEO, which integrates a distributed feedback (DFB) laser chip with a silicon photonic chip and electronic components through microstrip interconnections [
77].
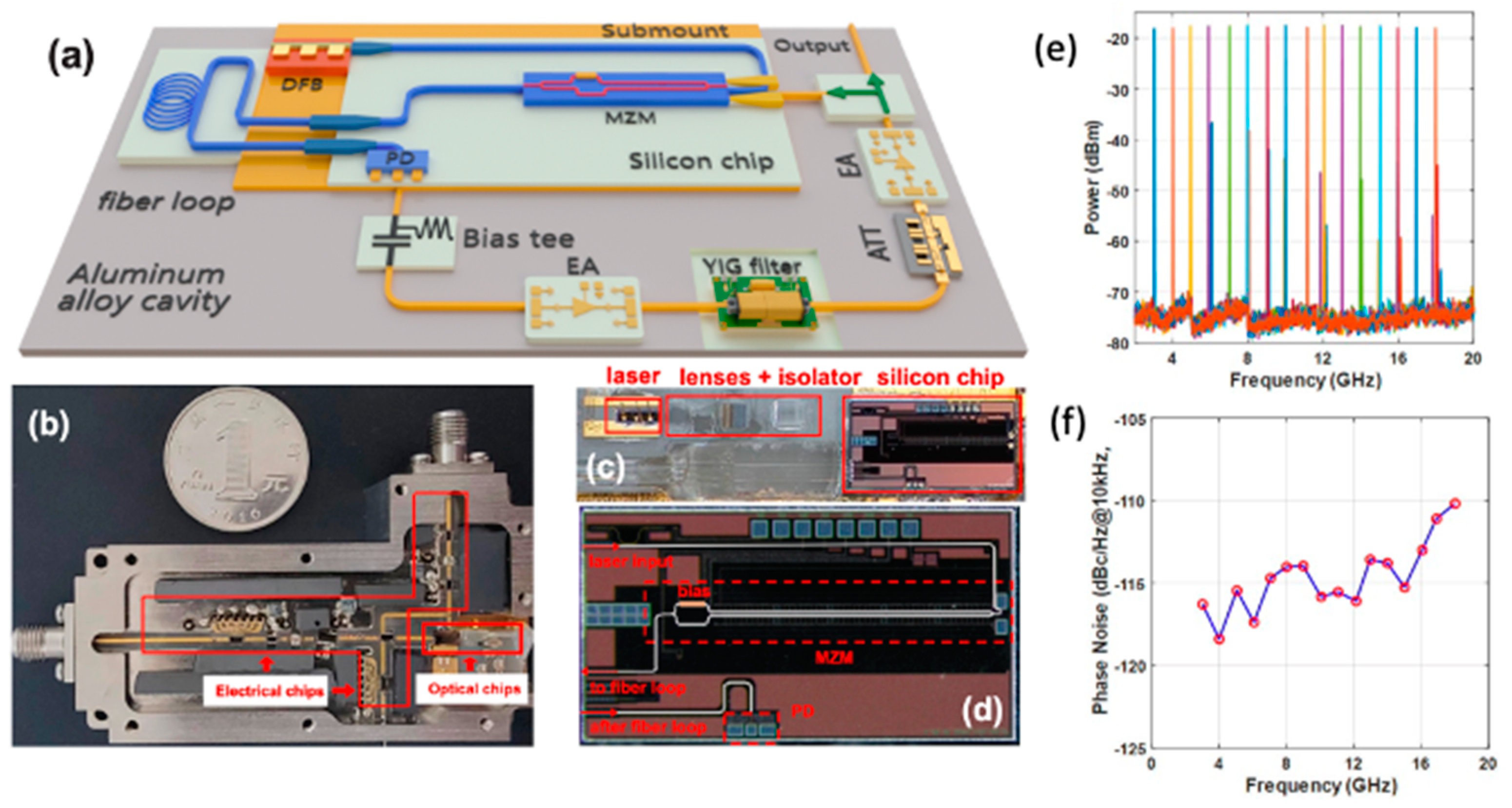
As shown in
Figure 10 (a), this hybrid design incorporates a polarization-maintaining fiber ring as the high-Q optical energy storage element, enabling the generation of ultra-low-phase-noise microwave signals. The architecture also features a YIG filter for frequency tuning. The filter is controlled via an external magnetic field to provide a wide tunability range from 3 GHz to 18 GHz covering essential frequency bands such as C, X, and Ku, which are critical for radar and communication systems. Experimental results demonstrate a phase noise of −128.04 dBc/Hz at a 10 kHz offset for a 10 GHz signal.
The hybrid structure leverages advanced silicon photonic components, including a high-speed MZM and a germanium-doped PD, to ensure efficient modulation and wide operational bandwidth. These optical and electronic chips are packaged into an aluminum alloy cavity with dimensions of 3 cm × 7 cm × 1.4 cm, significantly reducing the physical footprint. Moreover, a temperature control system is employed to mitigate thermal fluctuations, improving long-term frequency stability. The inclusion of the YIG filter further enhances the OEO’s tuning capability while maintaining superior phase noise characteristics.
4.2. Comparison of Current Methods
The performance of integrated OEOs has come to rival, and in some cases surpass, traditional OEOs in terms of frequency tunability and phase noise. Traditional OEOs rely heavily on long fiber delay lines to achieve low phase noise, but this comes with trade-offs in system size and frequency agility[
67,
69]. Integrated OEOs, on the other hand, achieve similar or better phase noise performance while significantly reducing size and power consumption. For example, an all-optical gain OEO, which eliminates the need for traditional electrical amplifiers, achieved a tuning range of 14.2 GHz to 25.2 GHz, while maintaining low phase noise [
75]. In comparison, a traditional fiber-based OEO design would struggle to achieve such a tuning range without becoming impractically large and power-hungry.
Additionally, integrated designs have introduced innovations such as PT symmetry, which improves mode selection and stability. A PT-symmetric OEO, based on a dual-wavelength approach, achieved tunability from 1 GHz to 22 GHz and phase noise ranging from -122 to -130 dBc/Hz at a 10 kHz offset [
71]. Such advancements in integrated designs offer a promising alternative to traditional configurations, particularly for applications requiring compact, power-efficient solutions.
Table 3 shows a comparison among various research works since 2017 (partially integrated and compact OEOs). Early silicon-based designs achieved a phase noise of −80 dBc/Hz at 5.4 GHz [
69], while InP-based dual-mode lasers extended the frequency range to 37.5–43.59 GHz with improved phase noise of −94.87 dBc/Hz [
78]. Innovations in PT-symmetric architectures have further pushed the boundaries, with silicon microring resonators (MDRs) and PS-FBGs achieving phase noise levels of −124 dBc/Hz and −125 dBc/Hz across 2–12 GHz and 1–22 GHz, respectively [
84], [
71]. Most recently, hybrid integration techniques achieved a record phase noise of −128.04 dBc/Hz over a 3–18 GHz range [
77], while a PM + MRR configuration in 2024 offered the widest tuning range of 3–42.5 GHz with a phase noise of −93 dBc/Hz [
73]. These advancements underscore the potential of integrated OEOs for next-generation communication and sensing applications. And the demonstrated design exemplifies the potential of hybrid-integrated OEOs in meeting the stringent requirements of next-generation radar, wireless communication, and electronic warfare applications.
4. Discussion and Conclusions
This review has traced the evolution of OEOs, from traditional designs reliant on long fiber loops to emerging integrated systems leveraging advanced photonic technologies. OEOs have proven to be versatile tools for generating high-frequency, low-phase-noise microwave and millimeter-wave signals, making them indispensable in applications ranging from radar and communications to electronic warfare and precision instrumentation. The transition to integrated OEOs marks a significant milestone, enabling compact, power-efficient, and tunable architectures without sacrificing performance. However, these advancements bring new challenges and opportunities for future research.
One of the key challenges facing OEOs is further reducing phase noise, especially for ultra-precise applications such as satellite communications and quantum systems. Dispersion in optical fibers and nonlinearity in modulators continue to hinder progress in minimizing noise levels. Moreover, achieving full integration of OEO components, including high-Q resonators, tunable filters, and modulators, remains a formidable technical hurdle. Integrated designs also face thermal sensitivity and polarization stability issues, which must be addressed to ensure reliable operation in practical environments.
Another critical area is enhancing frequency tunability and stability. While significant strides have been made in developing wideband frequency-tunable and broadband OEOs, maintaining high spectral purity and low phase noise across the tuning range remains challenging. Advanced designs, such as PT-symmetric OEOs and coupled-loop architectures, have shown promise in addressing these issues, but further refinement is necessary to achieve optimal performance. For multi-frequency and frequency-scanning OEOs, overcoming gain competition and ensuring phase coherence remain important directions for future work.
Looking ahead, advancements in materials, such as silicon nitride and lithium niobate, offer opportunities for improving environmental stability and device integration. The application of machine learning for adaptive control and optimization could enhance the performance of multi-frequency and broadband OEOs. Moreover, the development of application-specific designs tailored to fields such as radar, optical communications, and quantum information systems will continue to expand the versatility of OEOs. By addressing these challenges, OEOs can realize their full potential, enabling transformative advancements in next-generation communication, sensing, and radar systems.
Author Contributions
Resources and Review, Q.L., J.P.; Project Administration and Supervision, J.Y..; All authors contributed to data analysis and manuscript writing. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by National Natural Science Foundation of China (NSFC) under Grant No. 61771029 and 61201155.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yao, X.S.; Maleki, L. Optoelectronic microwave oscillator. J. Opt. Soc. Am. B 1996, 13, 1725–1735. [Google Scholar] [CrossRef]
- Yao, X.; Maleki, L. Optoelectronic oscillator for photonic systems. IEEE J. Quantum Electron. 1996, 32, 1141–1149. [Google Scholar] [CrossRef]
- Spencer, D.T.; Srinivasan, S.; Bluestone, A.; Guerra, D.; Theogarajan, L.; Bowers, J.E. A low phase noise dual loop optoelectronic oscillator as a voltage controlled oscillator with phase locked loop. 2014 IEEE Photonics Conference, Citeseer, 2014, p. 412. Available online: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=5e3e6084fe6b5d448a2c803c6e57c4f2f8f 3466f (accessed on 17 November 2024).
- Qiu, J.; Wei, B.; Yang, L.; Jin, X. Finely Tunable Coupled Optoelectronic Oscillator Based on Injection Locking and Phase Locked Loop. J. Light. Technol. 2023, 41, 5863–5869. [Google Scholar] [CrossRef]
- Cui, T.; Liu, D.; Liu, F.; Zhang, Z.; Tang, Z.; Cui, N.; Pan, S. Tunable optoelectronic oscillator based on a high-Q microring resonator. Opt. Commun. 2023, 536, 129299. [Google Scholar] [CrossRef]
- Huang, L.; Deng, L.; Fu, S.; Tang, M.; Cheng, M.; Zhang, M.; Liu, D. Stable and Compact Dual-Loop Optoelectronic Oscillator Using Self-Polarization-Stabilization Technique and Multicore Fiber. J. Light. Technol. 2018, 36, 5196–5202. [Google Scholar] [CrossRef]
- Xue, Z.; Li, S.; Xue, X.; Zheng, X.; Zhou, B. Photonics-assisted joint radar and communication system based on an optoelectronic oscillator. Opt. Express 2021, 29, 22442–22454. [Google Scholar] [CrossRef]
- Zhang, L.; Poddar, A.; Rohde, U.; Daryoush, A. Analytical and Experimental Evaluation of SSB Phase Noise Reduction in Self-Injection Locked Oscillators Using Optical Delay Loops. IEEE Photon J. 2013, 5, 6602217. [Google Scholar] [CrossRef]
- Bian, Y.; Hirokawa, T.; Lee, W.S.; Chandran, S.; Giewont, K.; Aboketaf, A.; Liu, Q.; Sporer, R.; Rakowski, M.; Dezfulian, K.; et al. 300-mm monolithic CMOS silicon photonics foundry technology [Invited]. CLEO: Applications and Technology; p. ATu3H.1.
- Hirokawa, T.; Bian, Y.; Giewont, K.; Aboketaf, A.; Chandran, S.; Cho, J.-K.; Chowdhury, Z.; Lee, W.S.; Liu, Q.; Sharma, P.; et al. Latest Progress and Challenges in 300 mm Monolithic Silicon Photonics Manufacturing. Optical Fiber Communication Conference; p. Th3H.2.
- Liu, Q.; Aboketaf, A.; Pal, S.; Mosleh, S.; Banihashemian, S.F.; Pavadai, S.; Lee, J.-C.; Bian, Y.; Gong, M.; Orner, B.; et al. High-Power Micro-Ring Modulator and Multi-Channel Coupled Ring Resonator for WDM Design on a 300-mm Monolithic Foundry Platform. Optical Fiber Communication Conference; p. M3A.2.
- Zou, F.; Zou, L.; Yang, B.; Ma, Q.; Zou, X.; Zou, J.; Chen, S.; Milosevic, D.; Cao, Z.; Liu, H. Optoelectronic oscillator for 5G wireless networks and beyond. J. Phys. D: Appl. Phys. 2021, 54, 423002. [Google Scholar] [CrossRef]
- Liu, Q.; Ge, J.; Fok, M.P. Microwave photonic multiband filter with independently tunable passband spectral properties. Opt. Lett. 2018, 43, 5685–5688. [Google Scholar] [CrossRef]
- Wu, T.; Jiang, Y.; Ma, C.; Jia, Z.; Bai, G.; Zi, Y.; Huang, F. Simultaneous Triangular Waveform Signal and Microwave Signal Generation Based on Dual-Loop Optoelectronic Oscillator. IEEE Photon- J. 2016, 8, 1–10. [Google Scholar] [CrossRef]
- Yan, J.; Liang, A.; Xin, F.; Liu, Q. An Optical Microwave Generator based on Stimulated Brillouin Scattering with Fine Tunability. In Proceedings of the CLEO: QELS_Fundamental Science, San Jose, CA, USA, 13–18 May 2018; p. 2. [Google Scholar]
- Liu, M.; Liu, S.; Yang, L.; Du, C.; Liu, H.; Pan, S. Improving the Quality of Arbitrary Periodic Waveform via Injection-Locking of an Optoelectronic Oscillator. IEEE Trans. Microw. Theory Tech. 2024, 72, 6678–6685. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, Y.; Wang, B. Low-Phase-Noise Ultra-Wide Arbitrary Waveforms Generation Using a Wideband Injection-Locked Optoelectronic Oscillator. J. Light. Technol. 2024, 42, 7693–7702. [Google Scholar] [CrossRef]
- Zhou, P.; Pan, S.; Zhu, D.; Guo, R.; Zhang, F.; Zhao, Y. A Compact Optoelectronic Oscillator Based on an Electroabsorption Modulated Laser. IEEE Photon- Technol. Lett. 2013, 26, 86–88. [Google Scholar] [CrossRef]
- Zhao, S.; Yan, J. Low phase noise optoelectronic oscillator based on an electroabsorption modulated laser. Appl. Opt. 2019, 58, 4512–4517. [Google Scholar] [CrossRef]
- Eliyahu, D.; Maleki, L. Low phase noise and spurious level in multi-loop opto-electronic oscillators. IEEE International Frequency Control Sympposium and PDA Exhibition Jointly with the 17th European Frequency and Time Forum, 2003. 2003; pp. 405–410.
- Leeson, D. A simple model of feedback oscillator noise spectrum. Proc. IEEE 1966, 54, 329–330. [Google Scholar] [CrossRef]
- Hasanuzzaman, G.K.M.; Kanno, A.; Dat, P.T.; Iezekiel, S. Self-Oscillating Optical Frequency Comb: Application to Low Phase Noise Millimeter Wave Generation and Radio-Over-Fiber Link. J. Light. Technol. 2018, 36, 4535–4542. [Google Scholar] [CrossRef]
- Yang, J.; Jin-Long, Y.; Yao-Tian, W.; Li-Tai, Z.; En-Ze, Y. An Optical Domain Combined Dual-Loop Optoelectronic Oscillator. IEEE Photon- Technol. Lett. 2007, 19, 807–809. [Google Scholar] [CrossRef]
- Hasanuzzaman, G.K.M.; Iezekiel, S.; Kanno, A. 94.5 GHz Dual-loop Optoelectronic Oscillator. 2023 International Conference on Electrical, Computer and Communication Engineering (ECCE); pp. 1–4.
- Jia, S.; Yu, J.; Wang, J.; Wang, W.; Wu, Q.; Huang, G.; Yang, E. A Novel Optoelectronic Oscillator Based on Wavelength Multiplexing. IEEE Photon- Technol. Lett. 2015, 27, 213–216. [Google Scholar] [CrossRef]
- Li, X.; Zhu, D.; Ding, J.; Hu, X.; Pan, S. Simulation investigation of coupled optoelectronic oscillator with high supermode suppression ratio. Seventh Asia Pacific Conference on Optics Manufacture and 2021 International Forum of Young Scientists on Advanced Optical Manufacturing (APCOM and YSAOM 2021); p. 391.
- Zeng, H.; Yan, J. GHz repetition rate tunable optical pulses generation using a SBS-based coupled optoelectronic oscillator. Opt. Commun. 2023, 555, 130234. [Google Scholar] [CrossRef]
- Liu, Y.; Hao, T.; Li, W.; Capmany, J.; Zhu, N.; Li, M. Observation of parity-time symmetry in microwave photonics. Light. Sci. Appl. 2018, 7, 38. [Google Scholar] [CrossRef]
- Zhang, J.; Yao, J. Parity-time-symmetric optoelectronic oscillator. 2018.
- Zhang, F.; Lin, X.; Wu, Z.; Xia, G. A Symmetric Parity–Time Coupled Optoelectronic Oscillator Using a Polarization–Dependent Spatial Structure. Photonics 2023, 10, 1236. [Google Scholar] [CrossRef]
- Fu, J.; Dai, Z.; Han, X.; Yao, J. Wavelength-Space Parity-Time Symmetric Optoelectronic Oscillator Using a Chirped Fiber Bragg Grating. IEEE Photon- Technol. Lett. 2023, 36, 187–190. [Google Scholar] [CrossRef]
- Chen, J.; Zheng, Y.; Xue, C.; Zhang, C.; Chen, Y. Filtering effect of SiO2 optical waveguide ring resonator applied to optoelectronic oscillator. Opt. Express 2018, 26, 12638–12647. [Google Scholar] [CrossRef] [PubMed]
- Y. Yu et al., “Frequency stabilization of the tunable optoelectronic oscillator based on anultra-high-Q microring resonator,” IEEE J. Sel. Top. Quantum Electron., vol. 26, no. 2, pp. 1–9, 2019.
- Kaba, M.; Li, H.-W.; Daryoush, A.; Vilcot, J.-P.; Decoster, D.; Chazelas, J.; Bouwmans, G.; Quiquempois, Y.; Deborgies, F. Improving thermal stability of opto-electronic oscillators. IEEE Microw. Mag. 2006, 7, 38–47. [Google Scholar] [CrossRef]
- Zhang, L.; Poddar, A.K.; Rohde, U.L.; Daryoush, A.S. Comparison of Optical Self-Phase Locked Loop Techniques for Frequency Stabilization of Oscillators. IEEE Photon- J. 2014, 6, 1–15. [Google Scholar] [CrossRef]
- Y. Wang and J. Yan, “Stability improvement of a dual-loop optoelectronic oscillator based on self-phase locking,” Appl. Opt., vol. 61, no. 30, pp. 8912–8916, 2022.
- Jiang, Y.; Bai, G.; Hu, L.; Li, H.; Zhou, Z.; Xu, J.; Wang, S. Frequency Locked Single-Mode Optoelectronic Oscillator by Using Low Frequency RF Signal Injection. IEEE Photon- Technol. Lett. 2013, 25, 382–384. [Google Scholar] [CrossRef]
- Zhou, W.; Blasche, G. Injection-locked dual opto-electronic oscillator with ultra-low phase noise and ultra-low spurious level. IEEE Trans. Microw. Theory Tech. 2005, 53, 929–933. [Google Scholar] [CrossRef]
- Williams, C.; Quinlan, F.; Davila-Rodriguez, J.; Delfyett, P.J. Optical Injection Locking of a Coupled Optoelectronic Oscillator. Conference on Lasers and Electro-Optics; p. CThF3.
- Guan, S.; Cen, Q.; Yin, F.; Xu, K.; Dai, Y. Self-Injection-Locked Optoelectronic Oscillator Based on Frequency Conversion Filtering. J. Light. Technol. 2021, 40, 1888–1894. [Google Scholar] [CrossRef]
- Zhenghua, Z.; Chun, Y.; Zhewei, C.; Yuhua, C.; Xianghua, L. An Ultra-Low Phase Noise and Highly Stable Optoelectronic Oscillator Utilizing IL-PLL. IEEE Photon- Technol. Lett. 2015, 28, 516–519. [Google Scholar] [CrossRef]
- Fu, R.; Jin, X.; Zhu, Y.; Jin, X.; Yu, X.; Zheng, S.; Chi, H.; Zhang, X. Frequency stability optimization of an OEO using phase-locked-loop and self-injection-locking. Opt. Commun. 2017, 386, 27–30. [Google Scholar] [CrossRef]
- Liu, Y.; Choudhary, A.; Marpaung, D.; Eggleton, B.J. Integrated microwave photonic filters. Adv. Opt. Photon- 2020, 12, 485–555. [Google Scholar] [CrossRef]
- Liu, Q.; Fok, M.P. Adaptive photonic RF spectral shaper. Opt. Express 2020, 28, 24789–24798. [Google Scholar] [CrossRef] [PubMed]
- Eliyahu, D.; Maleki, L. Tunable, ultra-low phase noise YIG based opto-electronic oscillator. IEEE MTT-S International Microwave Symposium - IMS 2003; pp. 2185–2187.
- H. Qi, D. H. Qi, D. Lu, and L. Zhao, “A Frequency-Tunable Coupled Optoelectronic Oscillator,” in 2021 Asia Communications and Photonics Conference (ACP), Oct. 2021, pp. 1–3. Accessed: Nov. 17, 2024. [Online]. Available: https://ieeexplore.ieee.org/abstract/document/9738407.
- Peng, H.; Xie, X.; Zhang, C.; Sun, T.; Guo, P.; Chen, F.; Zhu, L.; Hu, W.; Chen, Z. Widely Tunable Dual Loop Optoelectronic Oscillator based on a Single-Bandpass Microwave Photonic Filter and a Recirculating Delay Line. Asia Communications and Photonics Conference; p. AF3A.5.
- Wang, A.; Wo, J.; Zhang, J.; Luo, X.; Xu, X.; Zhang, D.; Du, P.; Yu, L. Radio-frequency arbitrary waveform generation based on dispersion compensated tunable optoelectronic oscillator with ultra-wide tunability. Chin. Opt. Lett. 2017, 15, 100603. [Google Scholar] [CrossRef]
- Li, C.; Wang, Y.; Wang, W.; Xu, Z.; Zhao, B.; Wang, H.; Tang, D. Widely Tunable Optoelectronic Oscillator Using a Dispersion-Induced Single Bandpass MPF. IEEE Photon- Technol. Lett. 2017, 30, 7–10. [Google Scholar] [CrossRef]
- Li, W.; Yao, J. A Wideband Frequency Tunable Optoelectronic Oscillator Incorporating a Tunable Microwave Photonic Filter Based on Phase-Modulation to Intensity-Modulation Conversion Using a Phase-Shifted Fiber Bragg Grating. IEEE Trans. Microw. Theory Tech. 2012, 60, 1735–1742. [Google Scholar] [CrossRef]
- Yang, B.; Jin, X.; Zhang, X.; Zheng, S.; Chi, H.; Wang, Y. A Wideband Frequency-Tunable Optoelectronic Oscillator Based on a Narrowband Phase-Shifted FBG and Wavelength Tuning of Laser. IEEE Photon- Technol. Lett. 2011, 24, 73–75. [Google Scholar] [CrossRef]
- Z. Dai, Z. Z. Dai, Z. Fan, P. Li, and J. Yao, “Frequency-tunable parity-time-symmetric optoelectronic oscillator using a polarization-dependent Sagnac loop,” J. Light. Technol., vol. 38, no. 19, pp. 5327–5332, 2020.
- Shi, M.; Yi, L.; Hu, W. SBS-based OEO with high tuning resolution and wide tuning range by selecting different-order phase modulation sideband as pump. Optical Fiber Communication Conference; p. M1H.4.
- Ding, Q.; Wang, M.; Zhang, J.; Mu, H.; Wang, C.-C.; Fan, G. A Precisely Frequency-Tunable Parity-Time-Symmetric Optoelectronic Oscillator. J. Light. Technol. 2020, 38, 6569–6577. [Google Scholar] [CrossRef]
- Peng, H.; Zhang, C.; Xie, X.; Sun, T.; Guo, P.; Zhu, X.; Zhu, L.; Hu, W.; Chen, Z. Tunable DC-60 GHz RF Generation Utilizing a Dual-Loop Optoelectronic Oscillator Based on Stimulated Brillouin Scattering. J. Light. Technol. 2015, 33, 2707–2715. [Google Scholar] [CrossRef]
- Zhou, P.; Zhang, F.; Pan, S. A Multi-frequency Optoelectronic Oscillator based on a Single Phase-Modulator. CLEO: Applications and Technology.; p. JTh2A.39.
- Yin, B.; Wang, M.; Wu, S.; Tang, Y.; Feng, S.; Zhang, H. High sensitivity axial strain and temperature sensor based on dual-frequency optoelectronic oscillator using PMFBG Fabry-Perot filter. Opt. Express 2017, 25, 14106–14113. [Google Scholar] [CrossRef]
- Wu, B.; Wang, M.; Dong, Y.; Tang, Y.; Mu, H.; Li, H.; Yin, B.; Yan, F.; Han, Z. Magnetic field sensor based on a dual-frequency optoelectronic oscillator using cascaded magnetostrictive alloy-fiber Bragg grating-Fabry Perot and fiber Bragg grating-Fabry Perot filters. Opt. Express 2018, 26, 27628–27638. [Google Scholar] [CrossRef] [PubMed]
- Zhou, P.; Zhang, F.; Pan, S. A tunable multi-frequency optoelectronic oscillator based on stimulated Brillouin scattering. 2015 14th International Conference on Optical Communications and Networks (ICOCN); pp. 1–3.
- Zhang, J.; Wang, Y.; Li, X.; Liu, Z.; Wo, J. Tunable multi-frequency optoelectronic oscillator based on a microwave photonic filter and an electrical filter. Opt. Quantum Electron. 2021, 53, 1–10. [Google Scholar] [CrossRef]
- Ge, Z.; Hao, T.; Capmany, J.; Li, W.; Zhu, N.; Li, M. Broadband random optoelectronic oscillator. Nat. Commun. 2020, 11, 1–8. [Google Scholar] [CrossRef]
- Hao, T.; Cen, Q.; Dai, Y.; Tang, J.; Li, W.; Yao, J.; Zhu, N.; Li, M. Breaking the limitation of mode building time in an optoelectronic oscillator. Nat. Commun. 2018, 9, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Hao, T.; Tang, J.; Li, W.; Zhu, N.; Li, M. Harmonically Fourier Domain Mode-Locked Optoelectronic Oscillator. IEEE Photon- Technol. Lett. 2019, 31, 427–430. [Google Scholar] [CrossRef]
- Hao, T.; Tang, J.; Shi, N.; Li, W.; Zhu, N.; Li, M. Dual-chirp Fourier domain mode-locked optoelectronic oscillator. Opt. Lett. 2019, 44, 1912–1915. [Google Scholar] [CrossRef] [PubMed]
- Zhu, S.; Fan, X.J.; Xu, B.R.; Sun, W.H.; Li, M.; Zhu, N.H.; Li, W. Polarization Manipulated Fourier Domain Mode-Locked Optoelectronic Oscillator. J. Light. Technol. 2020, 38, 5270–5277. [Google Scholar] [CrossRef]
- Hao, T.; Tang, J.; Li, W.; Zhu, N.; Li, M. Tunable Fourier Domain Mode-Locked Optoelectronic Oscillator Using Stimulated Brillouin Scattering. IEEE Photon- Technol. Lett. 2018, 30, 1842–1845. [Google Scholar] [CrossRef]
- Hao, T.; Liu, Y.; Tang, J.; Cen, Q.; Li, W.; Zhu, N.; Dai, Y.; Capmany, J.; Yao, J.; Li, M. Recent advances in optoelectronic oscillators. Adv. Photon- 2020, 2, 044001. [Google Scholar] [CrossRef]
- Ilgaz, M.A.; Batagelj, B. Opto-Electronic Oscillators for Micro- and Millimeter Wave Signal Generation. Electronics 2021, 10, 857. [Google Scholar] [CrossRef]
- Zhang, W.; Yao, J. A silicon photonic integrated frequency-tunable optoelectronic oscillator. 2017 International Topical Meeting on Microwave Photonics (MWP).; pp. 1–4.
- Pan, B.; Lu, D.; Zhang, L.; Zhao, L. A Widely Tunable Optoelectronic Oscillator Based on Directly Modulated Dual-Mode Laser. IEEE Photon- J. 2015, 7, 1–7. [Google Scholar] [CrossRef]
- Liu, P.; Xie, Z.; Lin, D.; Lu, M.; Cheng, W.; Hu, G.; Yun, B.; Cui, Y. Parity-time symmetric tunable OEO based on dual-wavelength and cascaded PS-FBGs in a single-loop. Opt. Express 2021, 29, 35377–35386. [Google Scholar] [CrossRef] [PubMed]
- Ahmadfard, F.; Hosseini, S.E. Design and simulation of a tunable parity-time symmetric optoelectronic oscillator utilizing integrated components. Sci. Rep. 2024, 14, 1–14. [Google Scholar] [CrossRef]
- Y. Tian et al., “Integrated ultra-wideband tunable Fourier domain mode-locked optoelectronic oscillator,” 2024, Accessed: Nov. 17, 2024. [Online]. Available: https://www.researchsquare.com/article/rs-4743222/latest.
- Dziallas, G.; Fatemi, A.; Peczek, A.; Tarar, M.; Kissinger, D.; Zimmermann, L.; Malignaggi, A.; Kahmen, G. A −115 dBc/Hz Integrated Optoelectronic Oscillator in a BiCMOS Silicon Photonic Technology. 2021 IEEE/MTT-S International Microwave Symposium - IMS), IEEE, 2021, pp. 23–26. Accessed: Nov. 17, 2024. [Online]. Available: https://ieeexplore.ieee.org/abstract/document/9574906/.
- Li, J.; Pu, T.; Zheng, J.; Zhang, Y.; Shi, Y.; Shao, W.; Zhang, X.; Meng, X.; Liu, J.; Liu, J.; et al. All-optical gain optoelectronic oscillator based on a dual-frequency integrated semiconductor laser: potential to break the bandwidth limitation in the traditional OEO configuration. Opt. Express 2021, 29, 1064–1075. [Google Scholar] [CrossRef] [PubMed]
- Do, P.T.; Alonso-Ramos, C.; Le Roux, X.; Ledoux, I.; Journet, B.; Cassan, E. Wideband tunable microwave signal generation in a silicon-micro-ring-based optoelectronic oscillator. Sci. Rep. 2020, 10, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Hao, T.; Cen, Q.; Li, M.; Shi, N.N.; Li, W.; Xiao, X.; Qi, N.; Dong, J.; Dai, Y.; et al. Hybrid-integrated wideband tunable optoelectronic oscillator. Opt. Express 2023, 31, 16929–16938. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Lu, D.; Guo, L.; Deng, Q.; Zhao, W.; Zhao, L. An Optoelectronic Oscillator based on Self-Injection-Locked Monolithic Integrated Dual-mode Amplified Feedback Laser. Asia Communications and Photonics Conference; p. Su2A.10.
- Han, J.-Y.; Hao, Y.-Z.; Tang, M.; Wang, F.-L.; Xiao, J.-L.; Yang, Y.-D.; Huang, Y.-Z. Wideband frequency-tunable optoelectronic oscillator with a directly modulated AlGaInAs/InP integrated twin-square microlaser. Opt. Express 2018, 26, 31784–31793. [Google Scholar] [CrossRef]
- Tang, J.; Hao, T.; Li, W.; Domenech, D.; Baños, R.; Muñoz, P.; Zhu, N.; Capmany, J.; Li, M. Integrated optoelectronic oscillator. Opt. Express 2018, 26, 12257–12265. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Zheng, J.; Pu, T.; Zhang, Y.; Shi, Y.; Li, J.; Li, Y.; Zhu, H.; Chen, X. Simple frequency-tunable optoelectronic oscillator using integrated multi-section distributed feedback semiconductor laser. Opt. Express 2019, 27, 7036–7046. [Google Scholar] [CrossRef] [PubMed]
- Teng, C.; Zou, X.; Li, P.; Pan, W.; Yan, L. Wideband Frequency-Tunable Parity-Time Symmetric Optoelectronic Oscillator Based on Hybrid Phase and Intensity Modulations. J. Light. Technol. 2020, 38, 5406–5411. [Google Scholar] [CrossRef]
- Fan, Z.; Zhang, W.; Qiu, Q.; Yao, J. Hybrid Frequency-Tunable Parity-Time Symmetric Optoelectronic Oscillator. J. Light. Technol. 2020, 38, 2127–2133. [Google Scholar] [CrossRef]
- Li, P.; Dai, Z.; Fan, Z.; Yan, L.; Yao, J. Parity-time-symmetric frequency-tunable optoelectronic oscillator with a single dual-polarization optical loop. Opt. Lett. 2020, 45, 3139–3142. [Google Scholar] [CrossRef]
- Liu, P.; Zheng, P.; Yang, H.; Lin, D.; Hu, G.; Yun, B.; Cui, Y. Parity-time symmetric frequency-tunable optoelectronic oscillator based on a Si3N4 microdisk resonator. Appl. Opt. 2021, 60, 1930–1936. [Google Scholar] [CrossRef] [PubMed]
- Zou, F.; Zou, L.; Lai, Y.; Xie, C.; Luo, J.; Milosevic, D.; Yan, L.; Pan, W.; Liu, Y.; Cao, Z.; et al. Parity-Time Symmetric Optoelectronic Oscillator Based on an Integrated Mode-Locked Laser. IEEE J. Quantum Electron. 2021, 57, 1–9. [Google Scholar] [CrossRef]
- Wang, L.; Liu, Y.; Chen, Y.; Gou, W.; Cui, S.; Xiao, X.; Yu, Y.; Zhang, X. Generation of Reconfigurable Linearly Chirped Microwave Waveforms Based On Fourier domain Mode-Locked Optoelectronic Oscillator. J. Light. Technol. 2022, 40, 85–92. [Google Scholar] [CrossRef]
- Gou, W.; Wang, L.; Liu, Y.; Chen, Y.; Yu, Y.; Yu, Y.; Zhang, X. Generation of phase-coded LFM signals based on Fourier domain mode-locked optoelectronic oscillator. J. Light. Technol. 2023, 41, 6142–6148. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).