Towards High-Resolution Multipitch Estimation for Expressive Pipa Music Annotation Using Morphological Analysis of Photoelectric Signals

1. Introduction

Performers manipulate the sound properties, including frequency (pitch), timing, amplitude, and timbre (harmonic spectrum) above and beyond the pitch and duration determined by composers to enrich the musical expressiveness and human perception [1]. The playing techniques like tremolo and vibrato often accompany with intensive strength and pitch variations corresponding to the amplitude modulation (AM) and frequency modulation (FM) of the vibration signal from signal processing perspective, which are widely present in world music. In practice, some monophonic pitch annotation tools like Tony [2], employing the short-time approaches under the local stationarity hypothesis, doesn’t perform well on complex playing techniques, over half of the notes require manual correction [3,4], not to mention in polyphonic settings [5,6].

As a traditional Chinese plucked string instrument, pipa boasts a long history and profound cultural heritage, with its origins tracing back to around the 2nd century BC. The earliest form of the may have originated from instruments in Central Asia and the Western Regions, such as Persia or India. This instrument gradually made their way into China through trade and cultural exchanges along the Silk Road, evolving and localizing over time to become the pipa we are familiar with today. The modern pipa has 4-string, 6 ledges and 24 frets which is performed with celluloid-made fakenails wore on each right finger. More than 60 playing techniques has been developed by the musicians[7] and the mixture of these techniques greatly enhances the expressiveness of music.

Automatic pipa transcription (APT), as a subtask of AMT dedicated to pipa, aims to build a multi-pitch estimation system capable of handling complex playing techniques, that extract features such as string number, F0 (fundamental frequency), boundaries (attack/transient/offset) and notes. In order to get the high-resolution multi-pitch annotation on plucked string instruments, Xi [8] and Wang [9] have mounted respectively electromagnetic pickups on guitar and optical switches on pipa, the multipitch estimation task is thus converted into the single pitch estimation on different strings. Although these two works provide a process with three steps, i.e. source separation to reduce the mutual resonance among the strings, boundary detection and pitch estimation, all steps are based on short-time algorithms and neither of these works investigate the annotation efficiency on boundary and pitch.

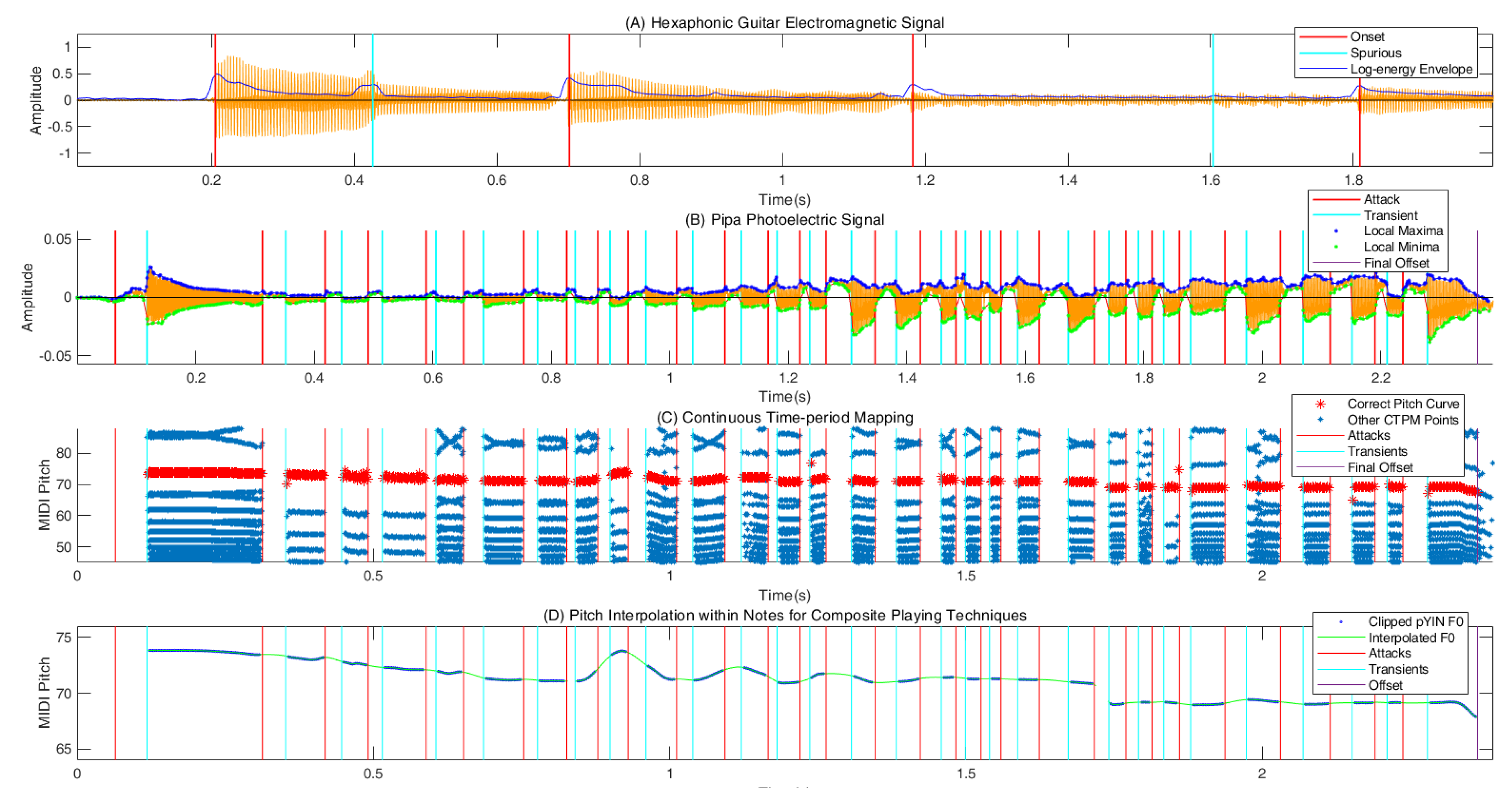
From time-domain perspective, the electromagnetic signal has a waveform similar to that of audio and the photoelectric one directly captures the string displacement which has different morphological features. Figure 1(A) shows a clip of the electromagnetic signal with two sliding tones that bring two spurious energy peaks located around 0.4 and 1.6 seconds (cyan lines). Concretely, the plucks severely bend the strings and make the photoelectric signal behave like arched form as shown in Figure 1(B). This feature doesn’t exist in audio and electromagnetic signal and provides a new indicator to extract the attack and transient points that circumvents the amplitude impacts from pitch shift techniques like vibrato and sliding. Given the accuracy boundaries, we could focus on the pitch estimation of the non-stationary vibration signal within each clip. Besides, the pitch period extraction directly from complex-structured waveform without any signal shaping is still a challenging work.

In Figure 1(B), a segment of The Love of the Wei River with mixed playing techniques is taken as an example. The tremolo composed by a series of intensive plucking, vibrato, sliding techniques imitate the vocal style of Qin Opera by controlling the intensity and pitch. Figure 1(C) presents a novel time-frequency representation, and the pitch curves red points were extracted from this representation. The gaps in CTPM through time correspond to the attack-transient intervals in which the signals don’t exhibit the periodicity. In the traditional annotation process, the pitch throughout time could be segmented based on the detected boundaries. The start and the end of a tremolo note are often derived from the musician’s professional experience and the reference score that reflect a certain subjectiviy, thus we manually implement the note segmentation under tremolo and don’t delve into its automation in this paper. As shown in Figure 1(D), the cubic interpolation was used to fill the pitch intervals within the tremolo notes. This step effectively removes abnormal pitch fluctuations at plucks and helps the future analysis of pitch shift techniques under tremolo.

In this paper, we investigate the pitch annotation process and algorithm performance on the string displacement of expressive pipa music by examining boundary detection in terms of recall, F-score and resolution and pitch estimation in terms of Intersection over Union (IoU), pitch deviation and running time. In section II, we briefly review the related works of commonly used onset detector and pitch estimators for annotation. The proposed fully time-domain methods on boundary and pitch were elaborated in Section III. The experimental results and related discussion were assigned in Section IV. Section V concludes this paper and enumerates the improvement and promising research points.

2. Related Works

The monophonic transcription consists of the unvoiced/voice detection (UVD) (or called voice activity detection (VAD) [10]) and pitch estimation steps. The annotation of a new particular instrument is generally implemented by completely explainable unsupervised algorithms that can be categorized into parametric, non-parametric and time-domain approaches, where the former two hypothesize the local stationarity of the short-time signal. A typical parametric approach, non-linear least square (NLS [11]), decomposes the signal into the linear combination of the Fourier bases adhering to the property of the stationary waves and harmonic structure. Shi proposed the Bayesian non-linear least square (BNLS [12]) by modeling the order prior and temporal continuity on pitch and voice activity. Most of the non-parametric approaches like the autocorrelation function (ACF [13]), capture the period of speech and music signal and neglect the timbral characteristics. A state-of-the-art pYIN [14] addresses not only the impact from local strength changes, but also temporal continuity on pitch and voice activity. However, the UVD/VAD of the pYIN and BNLS based on the framewise signal reconstruction quality may not meet the complex music structure [2].

As a task to identify the sudden change of signal, the boundary detection provides another path to limit the note range. Since deleting is much easier than adding, high recall and high resolution are the prerequiste to the manual annotation. The framewise root mean square (RMS) envelope of the high-pass signal, referred as to log-energy in the following of this paper, has been used in intensive plucking like tremolo [15]. It has a high recall and resolution suitable for annotation. SpecFlux [16], SuperFlux [17] and ComplexFlux [18] are another three common algorithms in which the first one has been also applied to the guitar annotation [8] and the latter two partially suppress the impact of vibrato and tremolo using maximum filtering from spectral perspective.

The time-domain pitch estimators aims to capture a sequence of zero-crossings (ZCs) or extrema as different sorts of pitch markers (PMs), the period pitch achieved by the distance of two adjacent PMs naturally disentangles to amplitude envelopes and doesn’t require window size selection. Multiple local candidates within a period may lead to difficulty in pitch marker selection. The empirical mode decomposition (EMD [19]), as a generic algorithm using the mean curve of upper and lower envelopes passing through the extrema, has been already applied to the endpoint detection [20] and pitch estimation [21] in speech. Although, it doesn’t ensure the periodicity of intrinsic mode function (IMF).

Hess [22] summarized the two categories of time-domain pitch estimators, the first relies on the pre-processing that simplifies the signal structure and reduces the candidate numbers of pitch markers, however a moderate low-pass filter is not easy to select and an arbitrary filter inevitably warp the original signal. DIO algorithm [23] analyzes the PM candidates after low-pass filtering of different cut-off frequencies, this algorithm has a high running speed and comparable performance to the short-time pitch estimators at that time. The second category is based on the thresholding of the raw signal, most of the related works have been appeared before 90s and require a simple waveform structure. Besides, the cascaded approaches first estimate a pitch curve by a robust short-time detector and then captures the PMs with the reference pitch. The granular synthesis [24] using non-positive-to-positive ZCs and time-scale modification using extrema in the pitch-synchronous overlap add (PSOLA [25]) split the waveform into clips with time-varying lengths referred to the pitch periods obtained by the short-time approaches. In following article, we proposed time-domain approaches on the relatively complex signal without filtering.

3. Methodology

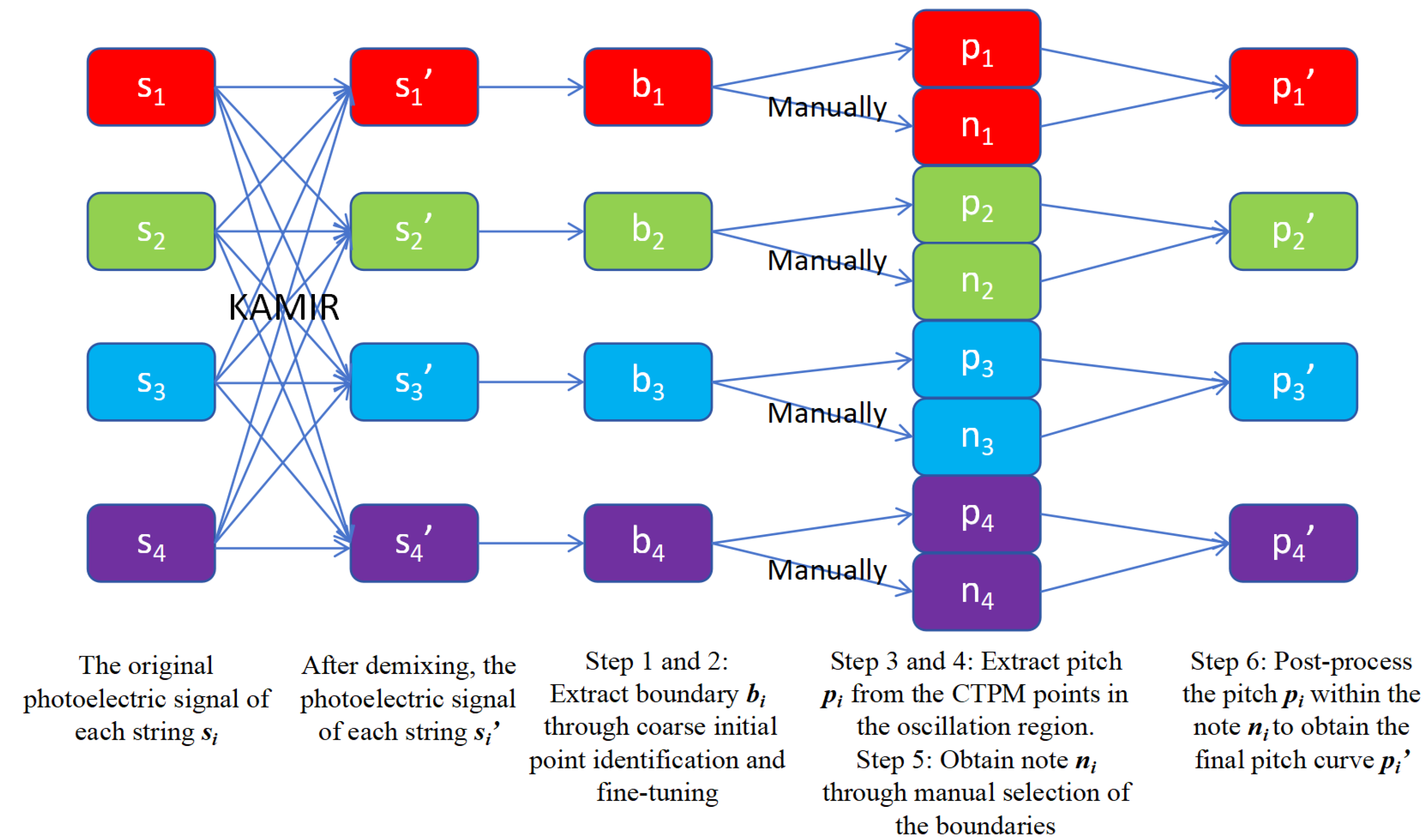
The proposed multipitch annotation process based on photoelectric sensors is shown in Figure 2. After removing the string resonance using kernel additive model interference reduction (KAMIR) algorithm [9,26], the monophonic string displacement signals could be processed by the following fully time-domain steps to obtain the APT-required features, i.e. string number, pitch, boundaries, and notes. The first three steps detect the boundaries, the last three process pitch and notes:

• Coarse onset detection: Localize the coarse attack-transient pairs with the arched waveform determined by analyzing the ZC intervals or envelope zero-crossings;
• Onset fine-tuning: Remove the attack-transient pair if the transient doesn’t meet the conditions of sudden change to improve the precision. Fine-tune the remaining transients and attacks by searching extrema and inflections;
• Vibration signal extraction: Determine the offset between transient and next attack (the next attack may coincide with offset), extract the the voiced area between transient and offset for pitch analysis;
• Pitch marking: Select an initial pitch marker pair, track forward and backward the pitch markers via the continuous time-period mapping (CTPM);
• Manual note segmentation: Manually select an attack-offset pair as the boundaries of a note;
• Pitch interpolation: Smooth the pitch curve within a note, interpolate the pitch curve clips to fill the gaps within tremolo notes.

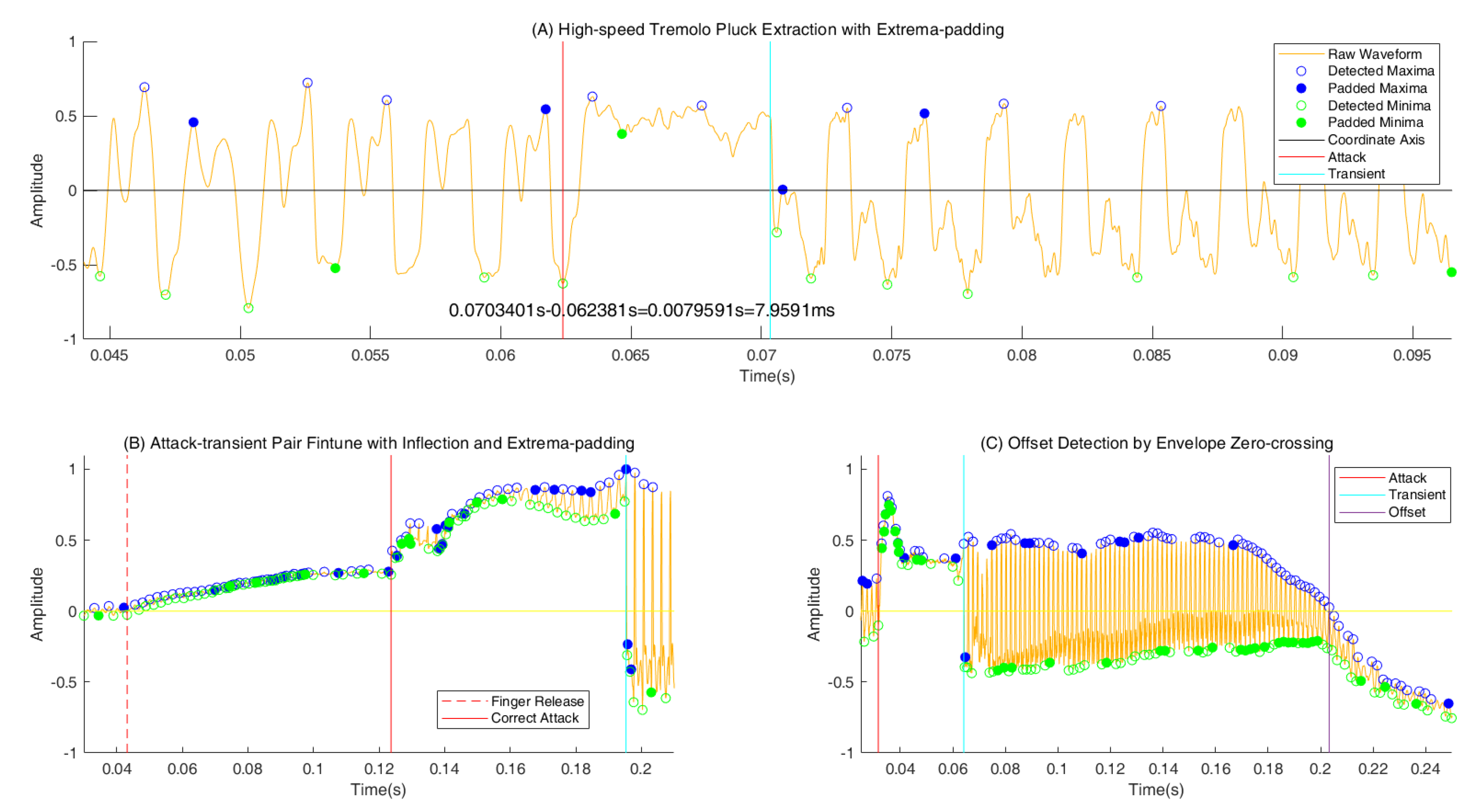
Onset Fine-tuning The sudden change is the key to distinguish the real transient and the impacts of mutual resonance waveform deviating from time axis. In this step, the sudden change is determined by the width ratio of upper and lower envelopes at adjacent extrema points so that a lot of false positives could be eliminated during silence. The correct transient is annotated at the previous extrema before the sudden change. In Figure 3(B), the correct attack is located at the inflection after the detected coarse attack instant produced by finger release. Similarly, the inflection is determined by the soar in the absolute value of the mean curve slope. The attack-transient interval range approximately between 3.5-150 ms also provides a threshold to remove the false positives from silence areas.

Vibration Signal Area Extraction As shown in Figure 3(C), the offset of a note is defined at the extrema closest to the instant when the envelope passes through the axis after transient. Therefore, given the boundaries with a sample-level resolution, a clip of signal within transient-offset pair in non-tremolo note and multiple clips in tremolo note count in voiced areas for subsequent pitch estimation.

3.1. Pitch Estimation

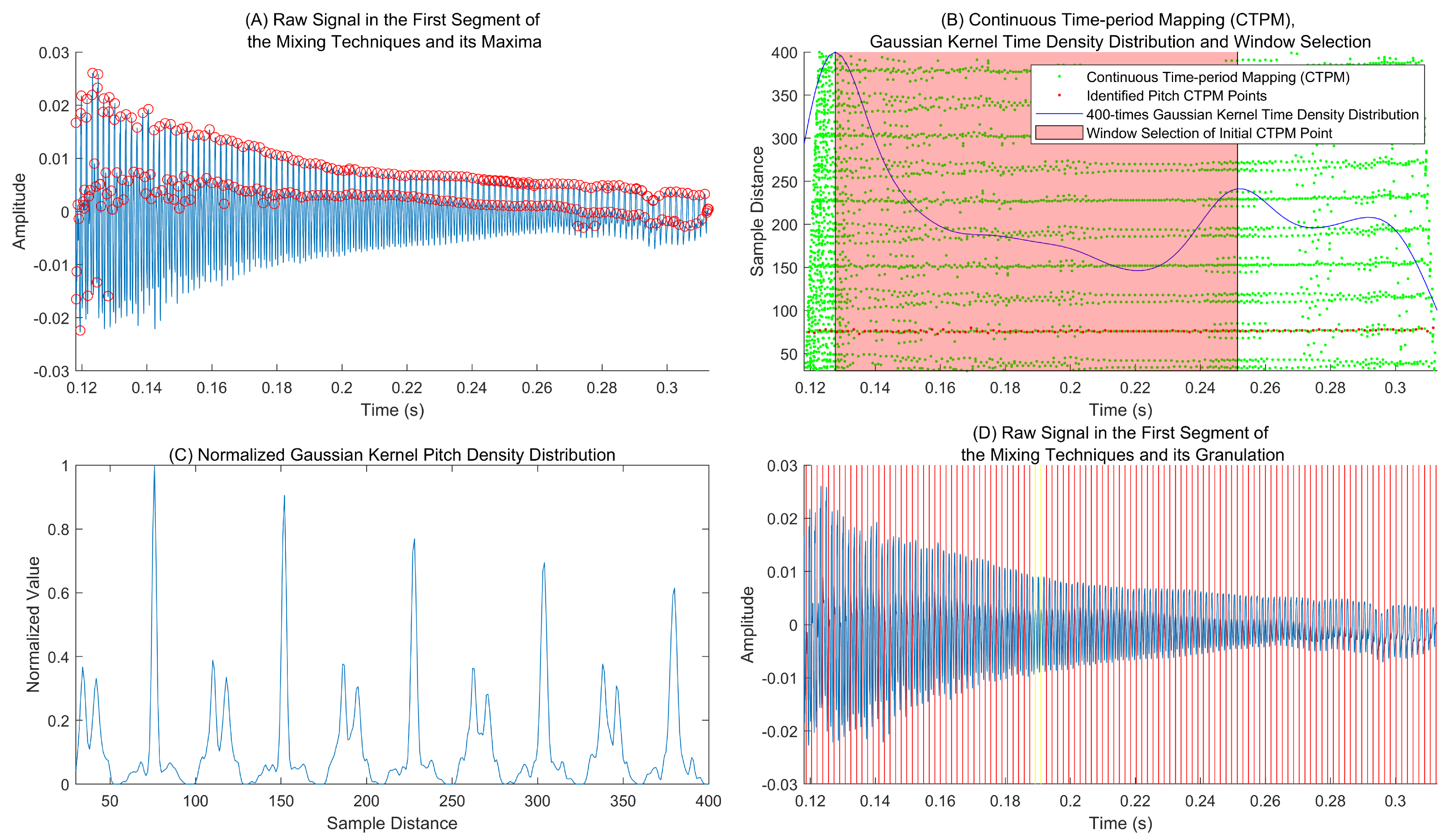
The pitch estimation process is shown in Figure 4. First, we extract zero-crossings or extrema with a minimal distance of 9.09 ms as shown in Figure 4(A). Next, the CTPM and its time-domain density function are calculated to select a window (See Figure 4(B)). This window help to extract the initial pitch points through the pitch density function (See Figure 4(C)). The yellow bars in Figure 4(D) represent the pairs of extrema points corresponding to the initial CTPM points. Starting from these initial point pair, the tracked pitch markers in both directions indicated by red lines in Figure 4(D) also correspond to the red CTPM pitch points shown in Figure 4(B). Some details in the process are described by the follows:

Continuous Time-Period Mapping (CTPM) Since the pitch markers are not easy to select if a few of ZC or extrema candidates occur within a period, we propose a novel time-period representation to analyze the pitch structure of signal. The continuous-valued time instant of the $i^{th}$ pitch marker candidate $t_i$ is achieved by the linear interpolation for zero-crossings and the parabolic interpolation for extrema. To avoid the excessive shift and envelope asymmetry of signal, we eliminate the mean curves of upper and lower envelopes (the first IMF of EMD) from the split signal. The relevant formulas are described by the follows:

$$\begin{array}{cccc}\hfill p_{i,j}& ={\displaystyle \frac{1}{t_{i+j}-t_i}}\hfill & \hfill T_{i,j}& ={\displaystyle \frac{t_{i+j}+t_i}{2}}\hfill \end{array}$$

(1)

$$\begin{array}{cccc}\hfill t_i& ={\displaystyle \frac{1}{2p_{i,j}}}-T_{i,j}\hfill & \hfill t_{i+j}& ={\displaystyle \frac{1}{2P_{i,j}}}+T_{i,j}\hfill \end{array}$$

(2)

With $i,j>=1$, the pitch period $p_{i,j}$ and its time instant $T_{i,j}$ of a point in CTPM has the one-to-one correspondence with $t_i$ and $t_{i+j}$, only the distance $t_{i+j}-t_i$ following the register of particular instrument counts in CTPM candidate points.

Pitch Marker Pair Initialization Known a reference pitch, the pitch marker is usually initialized from the extrema in the entire waveform [27]. Herein, we propose to select the basin of time-domain CTPM marginal distribution as the pitch-sparse window with time-varying length to extract the initial period (See pink area in Figure 4(B)) and the approximate initial instant is defined at the lowest point of the basin. Since CTPM points are continuously valued in both time and period, a Gaussian kernel density estimation method [28] is used to implement the marginal distribution. Assuming the timestamps of K CTPM points within a certain range are $T_k$ (k = 1,...,K), the corresponding time-domain distribution density can be formulated by the follows:

$$\mathrm{P}\left(\mathrm{t}\right)={\displaystyle \frac{1}{\mathrm{K}{10}^{-2}\sqrt{2\pi }}}\sum _{k=1}^{K}exp\left(-{\displaystyle \frac{{\left(t-T_k\right)}^2}{2\times {10}^{-4}}}\right)$$

(3)

where the standard deviation of the Gaussian kernel is ${10}^{-2}$ second. After obtaining the $P\left(t\right)$ distribution, the extrema serve as two ends of the basin. The minimal window length is set to the maximum of 0.1 second and the total length of the audio segment. Once the window is chosen, similarly to equation 3, the period-domain marginal distribution $P\left(I\right)$ of CTPM candidate points can be implemented by equation 4, assuming the variance of the Gaussian kernel as one sample distance and the periods of L CTPM points within the selected range $I_l$ (l=1,...,L):

$$\mathrm{P}\left(\mathrm{I}\right)={\displaystyle \frac{1}{\mathrm{L}\sqrt{2\pi }}}\sum _{l=1}^{L}exp\left(-{\displaystyle \frac{{\left(I-I_l\right)}^2}{2}}\right)$$

(4)

Inspired by the non-parametric pitch estimation methods like ACF [13], we propose to use the first peak greater than $\lambda \times$ the maximum with $\lambda \in (0,1)$ as the approximate period of initial CTPM point so that the corresponding pitch marker pair can be achieved, and the other pitch markers can be inferred before and after this pair using equation 5.

Pitch Mark Tracking The continuous reference interval $I_{n+1}$ is updated by the current interval $I_n$ and the distance $t_{i_n\pm j_n}-t_{i_n}$, and a momentum parameter $\beta$ is used for the pitch marker tracking:

$$I_{n\pm 1}=\beta I_n+(1-\beta )(t_{i_n\pm j_n}-t_{i_n})$$

(5)

where $j_n=arg{min}_j\left(\right|t_{i_n\pm j}-(t_{i_n}\pm I_n)\left|\right)$, n represents the number in the PM sequence, and $i_{n\pm 1}=i_n\pm j_n$.

3.2. Annotation Process and Processing of the Pitch Curves in Tremolo Notes

Above all, we categorize the processes into the pitch estimation before segmentation (PES) and the segmentation before pitch estimation (SPE). The original pYIN and BNLS attributed to PES process determine the voice activity by the quality of signal reconstruction after pitch estimation. Our proposed approach belongs to the SPE process in which the boundary detection provides a structural prior to constrain the pitch ranges to estimate. The pitch curve throughout the time could be also achieved by setting the voicing probability to 1 in pYIN and BNLS, then assigned by the corrected boundaries into each voiced clip. VAD from original pYIN and BNLS is thus replaced by the correct boundaries and we also name this process directly as PES in this paper.

Subsequently, the attack-offset pairs need to be manually selected through the music score or musicians’ experience to implement the note segmentation. The pitch gaps within tremolo notes are finally filled by cubic interpolation for future studies of playing techniques. Notably, the pitch curves need to be smoothed by an outlier-robust method, e.g. robust locally weighted scatterplot smooth (rLoWeSS [29]) algorithm used in this paper, to ensure the pitch continuity after the proposed pitch marking. 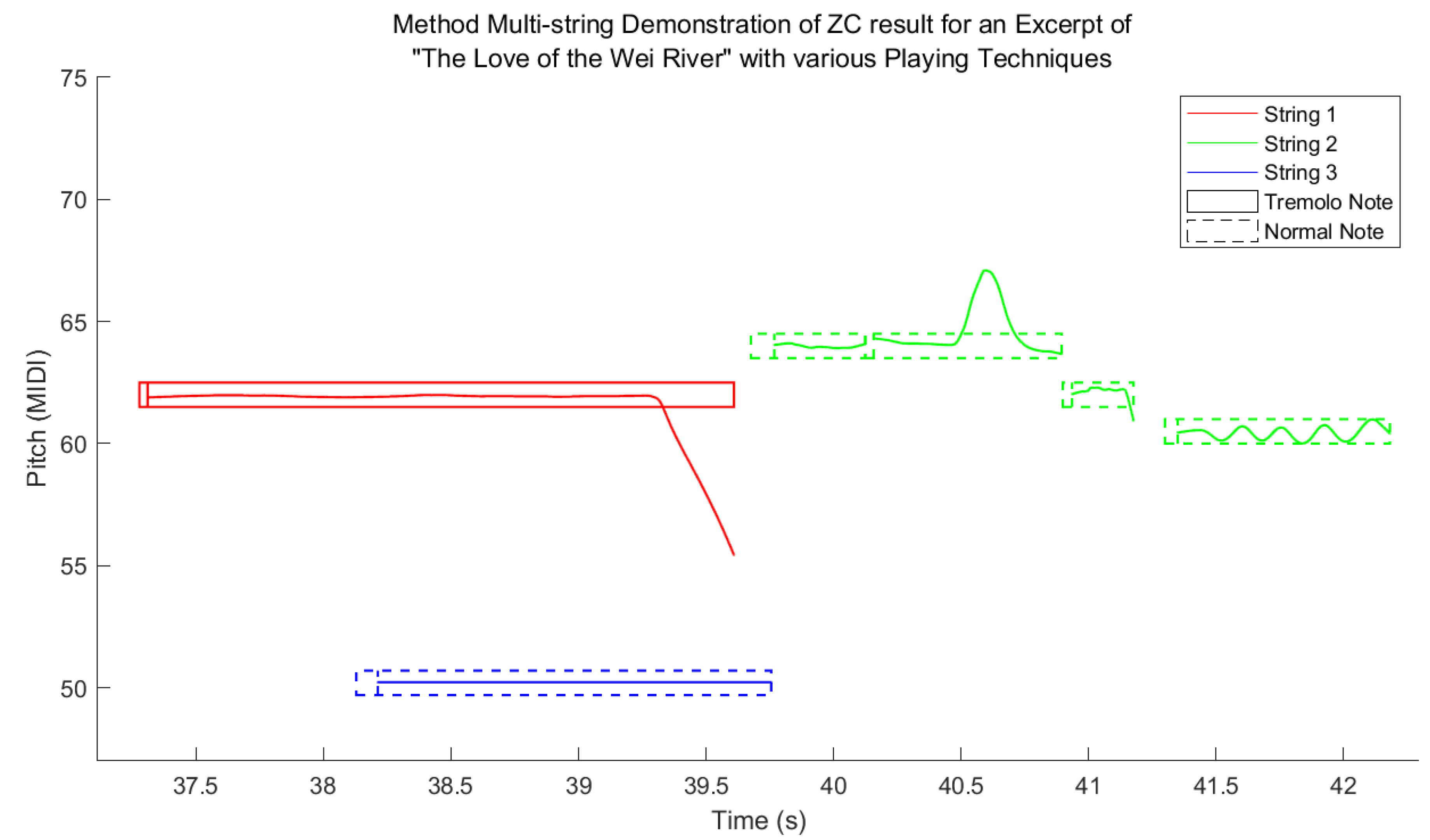Figure 5 demonstrates the final APT annotation of another expert of The Love of the Wei River including polyphonic notes, tremolo, vibrato, bending and sliding techniques, where the first attack-transient intervals in the tremolo notes like those in the normal notes are not filled.

4. Experiments

4.1. Datasets and Evaluation Metrics

In this section, we examine the transcription performance on the enhanced PipaSet which consists of 4 excerpts of naturally performed famous traditional Chinese music pieces from the collection of pipa grade examination [7], i.e. two low-level pieces Jasmine Flower (LvL. 1) and Nanni Bay (LvL. 2) and two high-level ones, The Love of the Wei River (LvL. 8, new added) and Ambush from Ten sides (LvL. 8). The high-level pieces are characterized by longer durations, higher polyphony, and higher degree of technical complexity. Only vibrato and sliding are presented as playing techniques in Jamine Flower. The tremolo techniques in Nanni Bay and The Love of the Wei River are not particularly fast. Vibrato, sliding and tremolo even their mixed ones are widely present in The Love of the Wei River and Ambush from Ten Sides in which the latter has a large quantity of tremolo plucks with attack-transient intervals shorter than 9.09 ms. The other playing techniques like harmonic, twisting and percussion take a very small proportion. 4 channels of photoelectric signals totaling 984 seconds were recorded with 44100 Hz of sampling rate and 24 bit of depth.

The boundaries are re-annotated following the framework of sample-level precision as outlined in Section 3.1. Since the attacks and transients are only distinguished by the proposed methods in this paper, we merge them together for evaluation with the other algorithms. Moreover, only the initial attack-transient pair of tremolo note is considered in note onset evaluation regardless of the ground-truth or the estimated ones, as all the playing techniques are excluded in a note segment. The accuracy metrics F-score (F), precision (P) and recall (R) are implemented by mir_eval [30] with a tolerance of 50 ms ($\pm 25$ ms). In order to avoid the impact of the note numbers performed on different strings and measure the annotation efficiency, the final F/P/R is weighted by pluck number ratio of each string. A note is identified as a tremolo if at least 2 plucks or 4 peaks present. The corresponding metric, Tremolo Note Recognition (TNR), is shown in Table 2. Given the correct note segments, the results on tremolo pluck localization are examined by the Pluck Detection (PD) metric. Additionally, we select the Intersection over Union (IoU) to evaluate the VAD results of existing pitch algorithms and the proposed boundary detectors. Due to the unavailability of a perfect reference F0, the median of the pitch estimated using the PES/SPE processing method is rounded to the integer MIDI value and compared with the correct MIDI pitch height. Notice that pitch continuity between segments is eliminated in SPE process based method.

Through statistical analysis and parameter scanning, the following parameters were obtained: envelope width ratio (EWR) > 0.77, sudden slope change (SSC) > 2.5, momentum $\beta =0.8$, pitch peak ratio $\lambda =0.765$, and rLoWeSS range multiplier of 0.1.

4.2. Experimental Results

4.2.1. Boundary Results

According to the results in Table 1, the extrema-padding method achieves $6\%$ and $24\%$ recall improvements respectively to those of log-energy and SpecFlux. The extrema (without padding) and ZC based methods have the same overall F-score, thus $19.25\%$ and $8.25\%$ increases compared to the log-energy and SpecFlux. Although the proposed methods and the log-energy have sufficiently high recalls and resolution, our proposed ones generally outperform the log-energy in F-score.

As shown in Table 2, the extrema-padding method has a $14\%$ TNR recall improvement compared to the log-energy, the extrema (without padding) method shows $21.33\%$ and $33.67\%$ TNR F-score increases compared to the SpecFlux and log-energy methods. Extrema-padding method has a $34\%$ recall and $21.66\%$ F-score improvement compared to log-energy under PD metric. Our proposed detection method outperforms other algorithms in terms of F-score for tremolo cases on all pieces, and the padding method achieves better recall and F-score in Ambush from Ten Sides.

Table 1. Average note onset detection performance and mean absolute error (MAE) of true positives to ground-truths.

Methods	Jasmine Flower		Nanni Bay		The Love of the Wei River		Ambush from Ten Sides
	F/P/R (%)	MAE (ms)	F/P/R (%)	MAE (ms)	F/P/R (%)	MAE (ms)	F/P/R (%)	MAE (ms)
SpecFlux	80/91/72	21.9	84/83/86	21.3	30/22/46	19.6	57/60/55	18.3
SuperFlux	70/96/55	21.7	80/88/73	21.3	27/27/26	21.4	60/72/52	18.0
ComplexFlux	72/96/58	21.4	78/88/70	21.3	25/23/28	21.2	59/76/49	17.7
Log-Energy	80/71/92	2.3	58/42/93	2.9	22/13/92	3.0	47/43/54	5.6
ZC	88/85/92	1.8	89/87/92	2.4	55/40/90	4.0	52/81/38	6.5
Extrema w/o padding	90/85/96	2.4	89/84/94	2.5	54/39/88	2.9	51/69/40	6.8
Extrema w/ padding	83/73/95	2.5	81/70/95	2.7	42/27/92	3.7	54/43/73	7.0

Table 1. Average note onset detection performance and mean absolute error (MAE) of true positives to ground-truths.

Methods	Jasmine Flower		Nanni Bay		The Love of the Wei River		Ambush from Ten Sides
	F/P/R (%)	MAE (ms)	F/P/R (%)	MAE (ms)	F/P/R (%)	MAE (ms)	F/P/R (%)	MAE (ms)
SpecFlux	80/91/72	21.9	84/83/86	21.3	30/22/46	19.6	57/60/55	18.3
SuperFlux	70/96/55	21.7	80/88/73	21.3	27/27/26	21.4	60/72/52	18.0
ComplexFlux	72/96/58	21.4	78/88/70	21.3	25/23/28	21.2	59/76/49	17.7
Log-Energy	80/71/92	2.3	58/42/93	2.9	22/13/92	3.0	47/43/54	5.6
ZC	88/85/92	1.8	89/87/92	2.4	55/40/90	4.0	52/81/38	6.5
Extrema w/o padding	90/85/96	2.4	89/84/94	2.5	54/39/88	2.9	51/69/40	6.8
Extrema w/ padding	83/73/95	2.5	81/70/95	2.7	42/27/92	3.7	54/43/73	7.0

Table 2. Tremolo note recognition (TNR), pluck detection (PD) performance and mean absolute error (MAE) of true positives to ground-truths.

Methods	Nanni Bay			The Love of the Wei River			Ambush from Ten Sides
	TNR (%)	PD (%)	MAE (ms)	TNR (%)	PD (%)	MAE (ms)	TNR (%)	PD(%)	MAE (ms)
SpecFlux	77/62/100	83/97/73	20.3	57/40/100	67/99/51	17.2	64/88/50	60/98/43	17.9
SuperFlux	87/77/100	69/97/53	20.1	67/50/100	45/100/29	17.8	55/95/39	49/98/33	17.8
ComplexFlux	91/83/100	62/97/46	19.5	67/50/100	46/99/30	17.4	55/90/39	43/98/28	17.7
Log-Energy	45/29/100	86/96/79	3.2	53/36/100	68/98/52	5.5	63/68/59	67/96/51	6.9
ZC	100/100/100	98/100/96	3.0	89/80/100	93/99/87	6.5	69/100/52	65/99/48	8.0
Extrema w/o padding	95/91/100	99/100/99	2.7	89/80/100	98/99/96	4.7	78/97/65	74/98/60	7.5
Extrema w/ padding	56/38/100	99/98/99	2.8	62/44/100	98/97/100	5.0	82/73/93	89/95/85	7.1

Table 2. Tremolo note recognition (TNR), pluck detection (PD) performance and mean absolute error (MAE) of true positives to ground-truths.

Methods	Nanni Bay			The Love of the Wei River			Ambush from Ten Sides
	TNR (%)	PD (%)	MAE (ms)	TNR (%)	PD (%)	MAE (ms)	TNR (%)	PD(%)	MAE (ms)
SpecFlux	77/62/100	83/97/73	20.3	57/40/100	67/99/51	17.2	64/88/50	60/98/43	17.9
SuperFlux	87/77/100	69/97/53	20.1	67/50/100	45/100/29	17.8	55/95/39	49/98/33	17.8
ComplexFlux	91/83/100	62/97/46	19.5	67/50/100	46/99/30	17.4	55/90/39	43/98/28	17.7
Log-Energy	45/29/100	86/96/79	3.2	53/36/100	68/98/52	5.5	63/68/59	67/96/51	6.9
ZC	100/100/100	98/100/96	3.0	89/80/100	93/99/87	6.5	69/100/52	65/99/48	8.0
Extrema w/o padding	95/91/100	99/100/99	2.7	89/80/100	98/99/96	4.7	78/97/65	74/98/60	7.5
Extrema w/ padding	56/38/100	99/98/99	2.8	62/44/100	98/97/100	5.0	82/73/93	89/95/85	7.1

Both log-energy and the proposed algorithms correctly estimate samples with a resolution that meets the annotation requirements. However, the latter method has more zero deviation at corrected sample points so that only few boundaries requires manual adjustments. our proposed methods reduces the MAE by approximately $80\%$ compared to the first three short-time methods. Finally, the Table 3 validate the effectiveness of the boundary detection in VAD metric comform to the annotation process of plucked string instruments [2,8].

4.2.2. Pitch Results

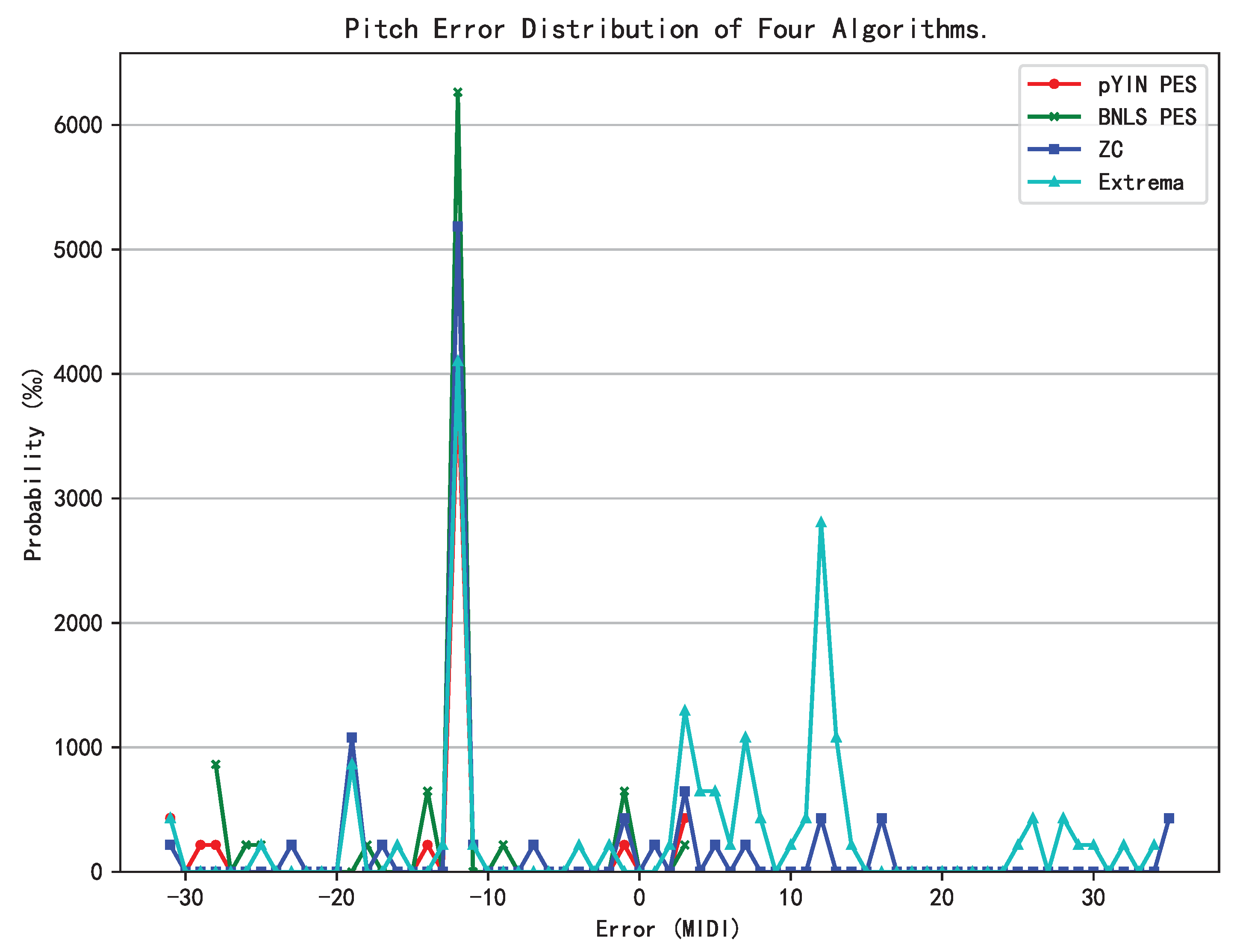
According to the results in Table 3, the ZC-based pitch annotation has a slight performance loss compared to the pYIN and BNLS under PES process. Very catastrophic results arise in pYIN and BNLS under SPE process.

Finally, Figure 6 presents a MIDI-level pitch deviation (estimated vs. true) among the proposed pitch estimation algorithms and the two short-time ones. It shows that the errors from the all algorithms primarily concentrate in the sub-harmonic notes corresponding to the octave errors.

4.2.3. Running Speed

All the algorithms proposed in this paper are implemented in Matlab. Even without any code optimization, the method still has overwhelming speed advantages. Running on hardware with an AMD R7-5800H CPU, 32GB RAM and Matlab 2023b with the correct boundaries, the zero-crossing-based pitch estimation demonstrates a 26 and 27 times speed-up to the C++ implemented pYIN1 in the SPE and PES processes, 108 and 65 times compared to the Matlab version of BNLS2.

5. Discussion

The results of boundary detection and tremolo analysis depict a significant improvement on the first three excerpts, the recalls in Ambush from Ten Sides decrease due to the loss of boundaries caused by the insufficient attack-transient intervals shorter than 9.09 ms produced by high-speed tremolo. The extrema-padding alleviates this issue at the expense of a precision decrease. Therefore, we recommend the extrema-padding onset detector for very intensive tremolo plucking annotation if the tremolo rate exceeds 10 Hz.

For quasi-periodic part of signals, the extrema generally generate more candidates than the ZCs, this results in higher difficulty in initial pitch selection than ZC and an inferior pitch performance referring to Figure 6. Very catastrophic results arise in pYIN and BNLS under SPE process as shown in Table 3, this implies that our proposed method can effectively resist the non-stationarity caused by AM-FM signals in relatively short time, while short-time approaches rely on the signal context and inherent pitch continuity for better results to some extent.

Since the tremolo and pitch shift techniques require theoretically high resolution respectively in time and frequency, the window selection become tough for high-resolution music transcription. The key point of a signal and the CTPM proposed in this paper are appropriate solutions to deal with AM-FM characteristics and the lack of pitch synchronism in EMD-like algorithms, but the noise-sensitive drawback still exists. Owning to the photoelectric sensor which have a direct contact with the vibration source, the external noise is excluded so that this system has the similarity to the guitar pickup that can be applied to a live performance full of complex ambient noise. Meanwhile according to the sound synthesis theory of pipa instrument[31], the bass audio recordings may produce a salient high-order harmonic components comparing to the F0 due to the small body size of pipa, the string vibration not modulated by the body resonance reflects waveform structure with fewer oscillation within a period.

6. Conclusion and Future work

This paper proposes a high-resolution transcription and annotation algorithm for pipa photoelectric signals, based on zero-crossing and extremum points in the full time domain. The method leverages the morphological advantages of photoelectric sensor signals over audio and electromagnetic signals during plucking. Additionally, a novel time-period representation method, CTPM, is introduced for waveform structure visualization and pitch recognition tasks. After benchmarking the performance of 6 short-time onset detection and pitch estimation algorithms in complex playing technique, it is evident that the proposed zero-crossing and extremum-based boundary detection method achieves superior F-scores in note onset recognition while maintaining a high recall rate. In high-speed tremolo scenarios, the extrema boundary detection method with padding-point improves the recall rate significantly. For the pitch estimation of vibration signal, our proposed method has ultimately achieved a relatively high level of performance and greater efficiency. Combining with the post-processing, the AMT task on mixed playing techniques could be addressed by our proposed annotation process.

In the future, we will focus on improving the algorithm in terms of accuracy and resolution, particularly in the specific scenarios such as high-speed tremolo. The dataset will also be scaled up to further validate the reliability of the algorithm under a funding afterwards. The proposed CTPM, as a novel time-frequency representation, holds a potential for more exploration in signals from other sensors, like the audio and electromagnetic pickup. Additionally, the transcribed pitch curves can be used for pitch shift technique analysis using similar morphological methods. Finally, the single-track multipitch estimation remain challenging and promising as the future direction.