A Novel Bio-Inspired Bird Flocking Node Scheduling Algorithm for Dependable Safety-Critical Wireless Sensor Network Systems

1. Introduction

The WSNs have become integral to modern safety-critical systems, including applications in healthcare, military operations, and industrial monitoring [1,2,3]. These systems demand high levels of reliability, energy efficiency, and robustness to ensure the dependable operation of the sensors, even under challenging conditions. However, achieving these goals in a dynamic, resource-constrained environment poses significant challenges, particularly with regard to efficient node scheduling and to manage the network resources efficiently. In safety-critical applications, where system failures can result in catastrophic consequences, ensuring that the network continues to function reliably is paramount. This bio-inspired algorithm not only enhances energy efficiency and extends network lifespan but also improves fault tolerance and redundancy, essential for maintaining the continuous operation of WSNs in hazardous environments [4].

The MOOP is concerned with optimising three important functional objectives; coverage, connectivity, and network lifetime in WSN. Improving the network lifetime while maintaining the other objectivise (connectivity and coverage) is not a trivial task especially in a resource constrained environment such as the WSN. Inspired by the collective behavior observed in bird flocking, bio-inspired algorithms have emerged as a promising solution for addressing complex optimisation problems of the WSNs such as the MOOP [13]. Bird flocking models, characterized by self-organization, adaptability, and efficient coordination, offer a natural framework for optimizing sensor node activities in a network. The Bio-Inspired Bird Flocking Node Scheduling Algorithm applies these principles to WSNs, enabling nodes to coordinate their sensing, communication, and energy through sleep/awake schedules in a decentralized manner, while minimizing energy consumption and ensuring the network's dependability. To enhance the process of maintaining the optimisation objectives a Lyapunov function is introduced within the bird flocking node scheduling algorithm. By mimicking the flocking behavior of birds, where individual birds respond to local stimuli while contributing to the global objective. That can be achieved through adapting the sleep/awake schedule to contribution to the global objective which is providing a scalable and robust solution for dependable WSN systems.

Hence, the main contribution of this paper is two folds: First, Propose a novel implementation of the Bio-Inspired Bird Flocking Node Scheduling Algorithm. Second evaluate the effectiveness of the proposed algorithm against the BAT Bio inspired node scheduling algorithm. This evaluation is conducted through MATLAB simulation where number of optimal solutions are presented. This has the benefit to offer improvements in network service availability, and reliability that are the crucial attributes for a dependable safety-critical WSN.

This paper is structured as follows: Section 2 discusses related work represented in the literature. Section 3 introduces the proposed Bird Flocking with its mathematical representation, Section 3.1 presenting the formulation of the problem and Section 3.2 discussing the use-case scenario of the Bird Flocking node scheduling algorithm. Section 4 covers the experimentation and the discussion of the results of this work. Finally, Section 5 presents our conclusion.

2. Related Work

The Bio-inspired algorithms have been widely used by the scientific community for solving hard optimisation problems, as extensively surveyed in [5],. In what follows we will investigate and analyse the most representative examples of the bio inspired approach that address the MOOP. For example, several bio-inspired computational approaches, like the Genetic Algorithm, focus solely on energy optimization [6,7]. Another example is the BAT bio inspired algorithms that attempt to solve the optimization problems in complex systems such as WSNs, specifically, by utilizing a cost function to find the best possible value of the solution in the search space [8]. Other bio-inspired flocking techniques were used to detect anomalies in the stream of data in the WSNs. The interested reader may refer to the comprehensive survey of node scheduling schemes in WSN [9].

In paper [9], the authors solve the problem of topology management in WSNs. First, the solution is restricted to 2D space. Second, they are trying to use the density distribution of the sensor nodes in the network. In particular, the authors are using the flocking model in which the agent is moving into a space in a fixed time. When these agents encounter another agent, they will form a flock if they are similar in density. Since these flocks form a swarm so the offline computation can easily be avoided using this approach. The approach assumes the agents are ON when sensor nodes are active which is not the case in the WSNs as sensor nodes alternate between ON and OFF rendering the density changeable.

In [10] the author proposed a distributed energy-efficient algorithm for ensuring coverage to address the MOOP in WSN. The main idea is the application of Firefly to grid-based computing used for WSN systems. Unlike bat optimization techniques, a firefly in a higher energy state flies at a greater altitude, while in a low-energy state, it descends and settles on surfaces like leaves. Taking several fireflies in this case, a part will fly another will rest, which creates an equilibrium or optimization sense when applied to WSN. Hence, in [10] the method involves dividing the network area into square cells and selecting the node with the highest energy in each cell as an aggregator. The firefly algorithm is then used to choose and maintain the most suitable node in each cell, maximizing coverage while minimizing energy demand and extending the network lifetime.

Th research in [11] proposes a Bat-Naturally Inspired Algorithm (NIA) for target-connected coverage in WSNs. The algorithm uses two bats in a binary search space: one locates active nodes, and the other identifies paths to the sink node for connectivity. Unlike binary-based methods, this approach adapts continuous search spaces to account for energy depletion over time, though it assumes nodes remain in an active state without node scheduling. However, the proposed study in [11] introduces node scheduling with a sleep-wake cycle, adding complexity by requiring management of multiple node states while focusing on active nodes for sink connectivity.

The authors in [12], addressed the MOOP by introducing the clustering approach in which fuzzy logic is utilised. The main idea behind this work is to construct a fitness function in which swarms work collaboratively to optimise a fitness function and send data from all sensor nodes to the Base station. [12] attempted to reduce the residual energy of each sensor node in which the minimum amount of energy is consumed. Using a fuzzy controller can ensure that effective routing is done considering the above condition as the backbone. Our approach for the Bat Node scheduling algorithm is similar to the approach of [12] which addresses the MOOP using Particle Swarm Optimization (PSO). The proposed BAT approach will have the same formulation for the MOOP, but the involved parameters are different.

An interesting example proposed by [13] a cuckoo search based on Cauchy optimization in which it addresses both coverage and routing in WSNs. The main idea is to use a dynamic cluster radius for routing based on a non-uniform clustering type of WSN. [13] addressed the coverage and routing challenges in the network but did not address the connectivity issues, and node scheduling i.e., in confirmation with Time Division Multiple Access (TDMA) which is practical while implementing in real life. The results indicate that the proposed algorithms outperform traditional methods in terms of coverage, energy efficiency, and network stability. However, the packet delivery rate is not considered, [13] present a very unrealistic view of energy loss of less than 1% which is the case if fewer packets are delivered and almost no control packets are generated in this case. The research suggests that while the proposed algorithms show promise, there is room for further exploration of the complex structure of WSNs.

Another interesting approach in [14] that utilises a hybrid Multi-objective Optimization technique that integrates cascading firefly and Greywolf algorithms to improve connectivity, coverage and network lifetime in WSNs. [14] coupled with the Pareto front in which the optimal solution provides insights on the trade-off between the three optimised objectives. The algorithms complement one another in terms of their strength. For example, firefly's optimization techniques are better for connectivity and Greywolf's optimization techniques are better for coverage, now in this case if they are applied in a cascading manner, they will complement one another resulting in better connectivity and coverage. The difficulty of this type of hybrid approach is in the increase of computational complexity and more convergence time required for optimization.

Another example that addressed the MOOP is proposed by [15] in which a node deployment algorithm using Firefly Optimization (FA) to achieve target location coverage and sensor node connectivity is introduced. To ensure the best Quality of Service (QoS) [15] introduced a multi-objective fitness function that considers factors like maximum survival, distance from the base station, coverage, number of sensor nodes, and connectivity. Furthermore, [15] introduced the distance to the base station as an important factor for delay-sensitive applications. [15] achieved fault tolerance through the p-coverage and q-connectivity which make the network perform efficiently in the complex. Although [15] address connectivity, coverage and lifetime in homogenous network scenarios, the authors did not consider heterogeneous which is the common deployment scenario in WSNs. Until for a specific purpose the WSN coverage should not be limited to a target-based coverage, as better coverage means better utilization for WSNs.

Furthermore, the authors in [16] proposed to improve the existing Graywolf algorithm optimization techniques and provide an energy saving coverage model. The model ensures that at least each point in the target area is covered by at least one sensor node. This work is an improvement over the existing Greywolf algorithm used in WSN, it has significant improvement over the original which provides better coverage and energy saving in the process.

In summary, the literature highlights gaps in existing bio-inspired approaches, with most algorithms focusing on one or two objectives of the MOOP, primarily energy. However, our previous work with BAT [17] tackled all three objectives simultaneously, which is crucial for reliable systems in WSNs. Building on this, we propose further improvements by incorporating the concept of Flocking Bird Algorithms. In nature, bird flocks sustain their energy while traveling long distances, and we adapt this concept to address the multi-objective optimization problem in this work.

3. Flocking Bird Node Scheduling Algorithm

The Flocking Bird Algorithm in WSNs is a bio-inspired approach that mimics the collective behavior of bird flocks to enhance network functions like energy efficiency, routing, and load balancing. By simulating natural flocking behaviors, this algorithm addresses multi-objective optimization challenges, including energy conservation, connectivity, and extending network lifetime[18,19], [20,21,22]. This algorithm is especially effective in situations requiring distributed, decentralized control, enabling nodes to adapt naturally to environmental changes or network conditions, much like birds flocking together.

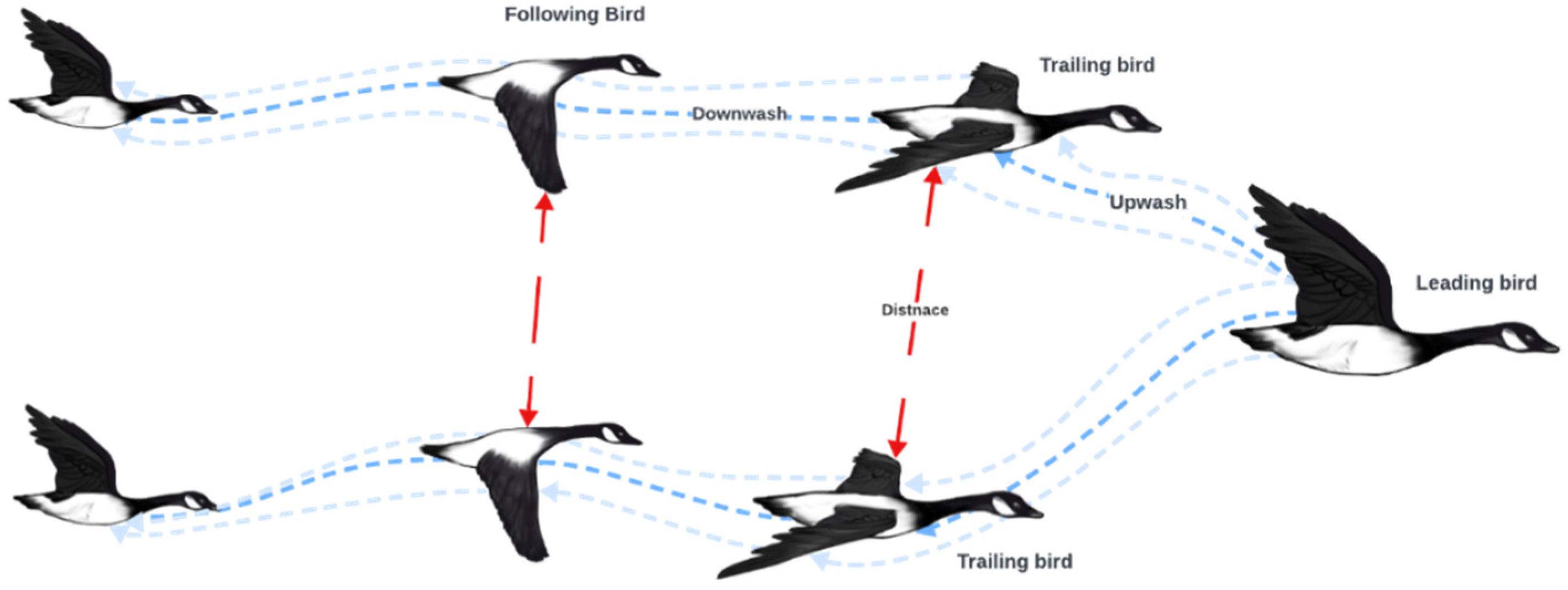
For example, geese are capable of flying hundreds to over a thousand kilometres without deviating from their flight path, depending on their species and environmental conditions. They rely on a combination of energy reserves, environmental cues, and aerodynamic efficiency to stay on course over long migration distances as shown in Figure 1. Factors such as species, energy reserves, and environmental conditions influence how far geese can travel without veering off their route. Migratory species, like the Canada Goose, are particularly renowned for their remarkable long-distance flights [20].

Figure 1 illustrates the migration behavior of bird flocks in sustaining an overall process, utilizing: (a) the leading bird’s energy, (b) collaborative effort between trailing and leading birds, and (c) the wind factor. Notably, the leading bird, with the highest energy level among the flock, uses wind dynamics to create upwash and downwash effects. The leading bird uses aerodynamic effects to create upwash and downwash, helping the trailing birds conserve energy. The upwash effect from the leader’s wing flapping reduces drag and lift needs for birds flying slightly to the sides, enhancing their efficiency. Meanwhile, downwash occurs directly behind the leader, so birds avoid this area to reduce drag. By taking advantage of the upwash, trailing birds save energy, and roles are rotated to share the energy cost of leading, allowing the flock to migrate over long distances more efficiently.

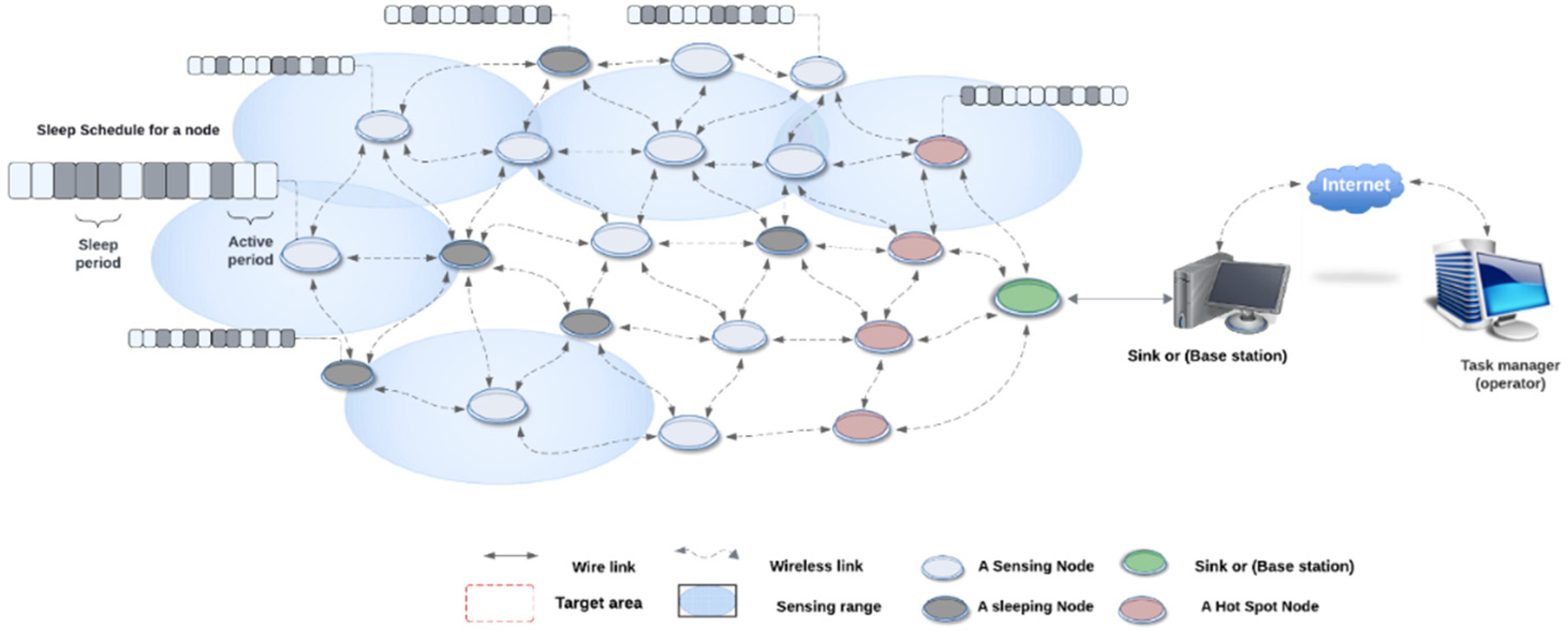
Subsequently, the key parameters of the migration behavior of bird flocking model are summarized in Table 1. On the other hand, Figure 2 represents the integration of a bio-inspired bird flocking model with Lyapunov functions for WSN. This integration aims to address three core functional objectives: coverage, connectivity, and network lifetime.

The relationship between bio-inspired flocking bird algorithms and Lyapunov functions in WSNs lies in the integration of biological principles of collective behaviour with mathematical tools for stability analysis. This synergy allows for the design of efficient, adaptive, and stable control mechanisms in WSNs, enhancing their performance and reliability to meet the demands of various applications. Hence, the main parameters introduced in this work are: Initial Energy (E_i​), Connectivity (R_c​), Coverage (N_d​), and adaptive Sleep/Awake Schedule (Ssec​).

3.1. Problem Formulation

In this study, we draw an analogy between the migration process of birds flocking and the deployment of WSN nodes to define the problem and set the objective of the bird flocking scheduling algorithm. The objective here is to use the Lyapunov function to maintain energy efficiency and network connectivity while ensuring stability in the sleep-awake scheduling of nodes. To understand the application of the bird flocking node scheduling algorithm stability using Lyapunov's function in WSN, it is essential to first break down the concept of stability within the frameworks of both flight dynamics and Lyapunov's stability theory [23]. As this approach ensures that nodes in the network are optimally scheduled to optimize energy while maintaining coverage, and connectivity. On the one hand, the bird flight stability refers to a bird's ability to maintain a steady flight path or return to it following a disturbance, such as wind gusts. Achieving this stability involves balancing and controlling the aerodynamic forces and momentum acting on the bird. On the other hand, the Lyapunov's stability theorem serves as a mathematical tool for determining the stability of equilibrium points in dynamic systems. The approach involves defining a scalar function, known as the Lyapunov function, which is analogous to the concept of energy in a physical system.

Thus, the Lyapunov function $V\left(x\right)$ is defined in terms of the system's state variables $x$ . For stability, this function must remain positive, $V\left(x\right)>0$, except at the equilibrium point, where $V\left(x\right)=0$.

While the Stability Condition is deemed stable if $V\left(x\right)\le 0$ (where $V\left(x\right)$ is the time derivative of $V\left(x\right).$ If $V\left(x\right)<0$, the system is asymptotically stable, indicating that it will return to the equilibrium state following a disturbance. Therefore, the stability check function can be formulated by

If $V\left(x\right)$ is positive definite and $V\left(x\right)\le 0$, the bird's flight is stable.

If $V\left(x\right)$ is strictly negative, the flight is asymptotically stable, signifying that the bird will return to a steady flight after experiencing a disturbance. To have a better understanding of how the bird flocking model maintain stability during migration process, let us consider a scenario where a bird pitches upward due to a disturbance:

State Variables: Let$x$ represent the pitch angle, and $x\mathrm{\text{'}}$ denote the pitch rate.

Lyapunov Function: Define $V(x,x\mathrm{\text{'}})={\displaystyle \frac{1}{2}}m{x\mathrm{\text{'}}}^2+{\displaystyle \frac{1}{2}}k{x\mathrm{\text{'}}}^2$, where m and k are constants associated with the bird's inertia and stiffness.

Stability Analysis: Calculate $V(x,x\mathrm{\text{'}})=mx\mathrm{\text{'}}x\mathrm{\text{'}}\mathrm{\text{'}}+kxx\mathrm{\text{'}}$. If $V(x,x\mathrm{\text{'}})\le 0$ under normal flight conditions, the pitch is stable according to Lyapunov's theorem.

In other words, Lyapunov's theorem offers a systematic approach to evaluate the stability of a bird's flight by analyzing the dynamics through a carefully defined Lyapunov function. This analysis provides valuable insights into how birds maintain stability in their flight despite external disturbances. In summary, our work is founded on previously collected data that includes sleep/awake states, energy levels, communication requirements, and scheduling parameters. The main aim of our proposed algorithm is to optimize the overall system metrics in which the objective is to maintain coverage, connectivity and network lifetime. Algorithm 1 describes the functionality of our proposed Bird Flocking solution.

3.2. Use Case Scenario of the Bird Flocking Algorithm

In this use-case scenario, the following steps outline the functionality of Algorithm 1, which adapts the behavior of Bird Flocking techniques to address the MOOP in WSN. The algorithm prioritizes key metrics such as coverage, connectivity, and network lifetime to meet the dependability requirements:

• The first step is the group selection of cluster head nodes: The group of cluster heads (CHs) to be turned ON for the current round is determined using (r mod k) + 1. Cluster heads that belong to this group are identified as ON_CH, while those that don't belong are identified as OFF_CH.
• The second step is the identification of the Lyapunov Scheduling function: For each ON_CH, a Lyapunov metric is calculated, which is the queue backlog at that cluster head weighted by V_weight. This metric determines the priority of turning cluster heads on. The cluster heads are then sorted in descending order of the Lyapunov metric to prioritize those with higher backlog, ensuring that nodes with the largest queues get served.
• The third step is turning ON the Cluster Heads and the Children nodes: After calculating the Lyapunov metrics and reordering the cluster heads based on their importance, the corresponding nodes (including the children) are marked as ON in the ON array.
• The fourth step is finalizing the nodes in the network: Nodes that are not turned ON are removed from the network by setting their entries in net to 0.
• The fifth step is returning the values: The Lyapunov function returns the updated-ON array. It is important to note, the Lyapunov function is used to optimize the scheduling of cluster heads by minimizing queue backlogs across the network. The higher the backlog, the higher the priority for activating the respective cluster head. Additionally, the Extra-ON rule ensures that nodes located too far from active cluster heads have a nearby cluster head turned on to improve coverage. The scheduling decision is made by selecting and scheduling cluster heads based on both their distance and queue backlog, ensuring network stability and efficiency.

4. Experimentation and Discussion

In this study, a simulation-based experiment is conducted to analyze the performance of the proposed Bird Flocking node scheduling algorithm. The experiments were conducted using MATLAB R2018b-based event-driven programming simulator. A comparative analysis is performed to evaluate the proposed Bird Flocking node scheduling algorithm against the BAT node scheduling algorithm. Thus, in this experiment, the following assumptions and parameters are considered, as detailed in Table 1.

The simulation consists of multiple rounds, with each round involving sensing and reporting of the collected data back to the base station. The parameters used in this study, including simulation settings, coverage, and node configurations, are consistent with those commonly found in the literature [9,24,25]. These values are adopted for the simulator environment. Furthermore, a realistic energy model commonly referenced in [7] is adopted for this simulation. However, the successful deployment of Flocking Bird systems in WSNs necessitates careful attention to specific various system parameters and considerations such as coverage, connectivity, energy constrains, and adaptive sleep/awake schedule.

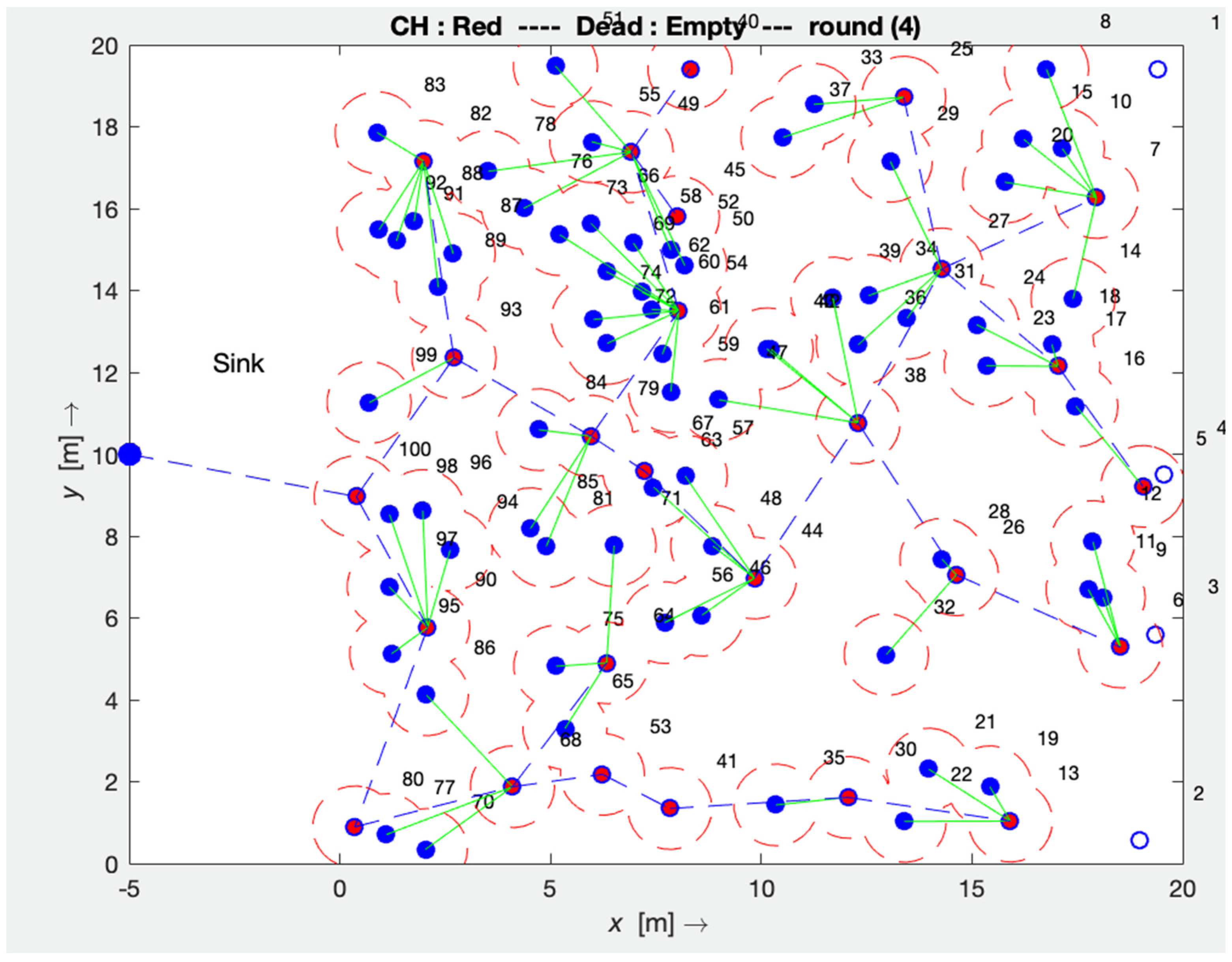
Figure 4 illustrates the simulation step up of the Bird Flocking node scheduling algorithm in WSN. The assumptions and the metrics used to compare the algorithms in this experiment are shown below:

4.1. All Used Energy

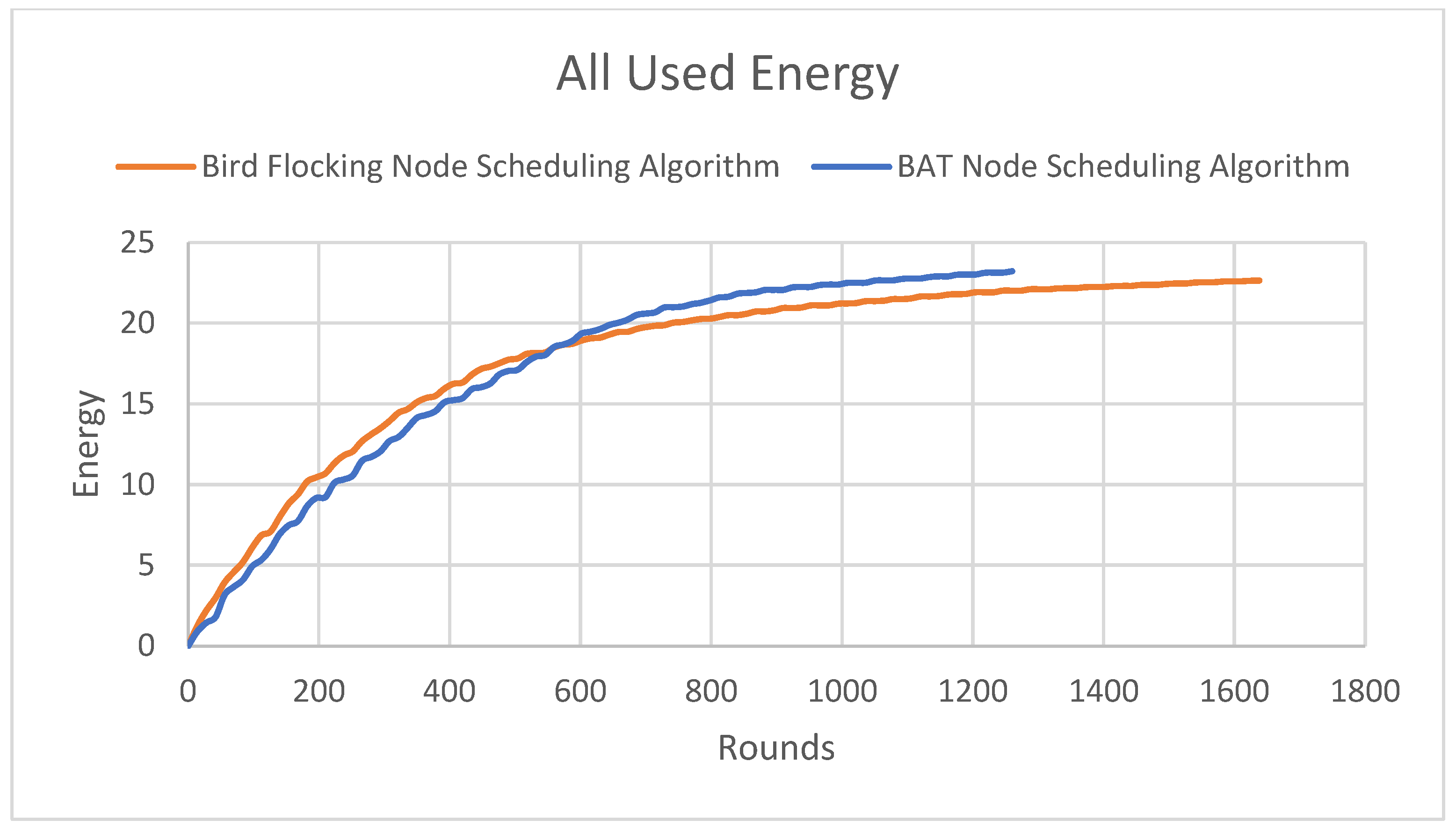
The used energy metric assesses network energy consumption over the simulation rounds. Figure 5 illustrates this metric, with the Y-axis representing the energy expended by nodes and the X-axis indicating the round number. The Bird Flocking node scheduling algorithm demonstrated superior energy efficiency compared to the BAT node scheduling algorithm, meeting performance requirements.

The Bird Flocking node scheduling algorithm achieved an energy consumption level of 24 joules by the 1650^th round, whereas the BAT node scheduling algorithm reached the same consumption level at the 1250^th round. This demonstrates that the Bird Flocking algorithm conserves energy over significantly more rounds, achieving more than three times the efficiency in terms of rounds compared to the BAT algorithm. Since energy management is a critical network parameter, optimizing its use is essential. As discussed, the Bird Flocking algorithm leverages energy as a key optimization factor, maintaining stable energy usage based on node distance.

It is important to note, the Bat and Bird Flocking node scheduling Algorithms both enhance energy efficiency in WSNs through different approaches. The Bat node scheduling Algorithm reduces energy consumption by dynamically adjusting communication range and transmission power, minimizing unnecessary retransmissions, and finding optimal node schedules. In contrast, the Bird node scheduling Flocking Algorithm focuses on cooperative energy management by optimizing sleep/wake cycles, minimizing idle times, and balancing energy loads across the network. While the Bat Algorithm is better for individual node optimization, the Bird Flocking Algorithm is more suited for network-wide cooperation and energy conservation. The choice depends on whether the focus is on node-level efficiency or overall network coordination. Given its high efficiency in coverage, connectivity, and network lifetime, the proposed Bird Flocking algorithm can be applied to a broad range of safety-critical systems, such as forest fire detection systems, skyscraper fire monitoring, and nuclear power plant systems.

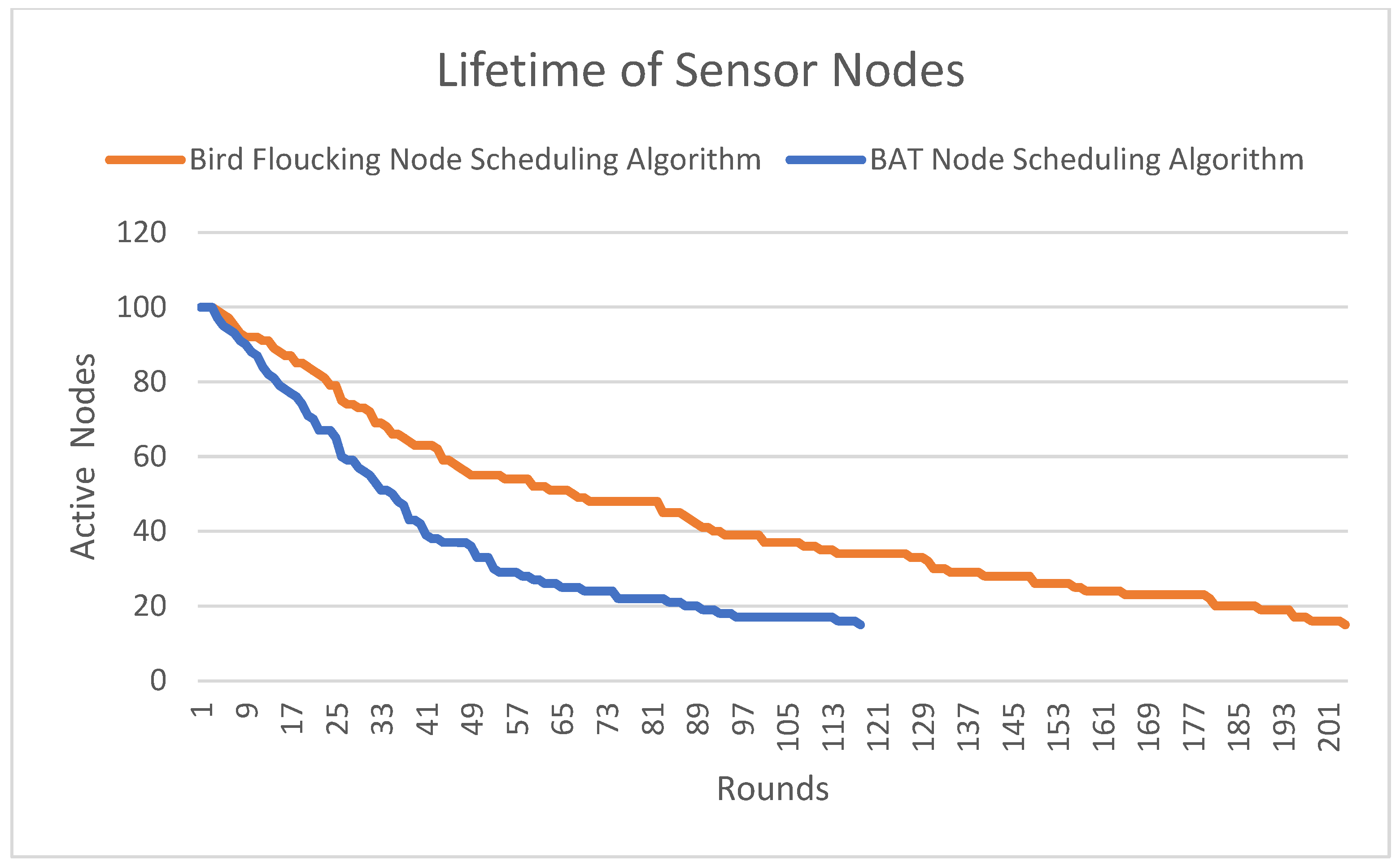
4.2. Lifetime of Sensor Nodes

The lifetime of a sensor node is evaluated by monitoring the number of active nodes across simulation rounds. In this analysis, the Y-axis represents the count of active nodes, while the X-axis indicates the simulation rounds. As illustrated in Figure 6, the Bird Flocking node scheduling algorithm demonstrates a significant improvement in energy efficiency and node longevity. Specifically, 16 nodes remain active at 203^rd rounds when using the Bird Flocking node scheduling algorithm, whereas, with the BAT node scheduling algorithm, only 16 nodes remain at 117^th rounds.

Consequently, the proposed Bird Flocking node scheduling algorithm significantly outperforms the BAT algorithm in sustaining node lifespan. This improvement is attributed to the Lyapunov function's capability to stabilize key system variables, such as the energy consumption levels of each node, thereby optimizing the duty cycle and extending the operational life of each node. In other words, Lyapunov function has the ability to introduce predetermined schedules for nodes across their operational lifetime, allowing them to know their ON/OFF states without disruption from randomization.

This deterministic approach in stochastic scheduling, as seen in the BAT node scheduling algorithm, enhances network lifetime, coverage, and connectivity by identifying optimal scheduling solution for the WSNs. In contrast, the Bird Flocking node scheduling algorithm employs adaptive, distributed decision-making and cooperative behavior to optimize energy usage and achieve effective load balancing through sleep/awake schedule. Figure 2 supports this, highlighting the optimal node schedule solution in terms of energy and distance. Further analysis of the Bird Flocking node scheduling algorithm using AI techniques could yield additional insights . Additionally, implementing the Bird Flocking algorithm alongside the Lyapunov function resulted in stable solutions that sustained message dissemination across the network, supporting prolonged QoS levels of availability and reliability.

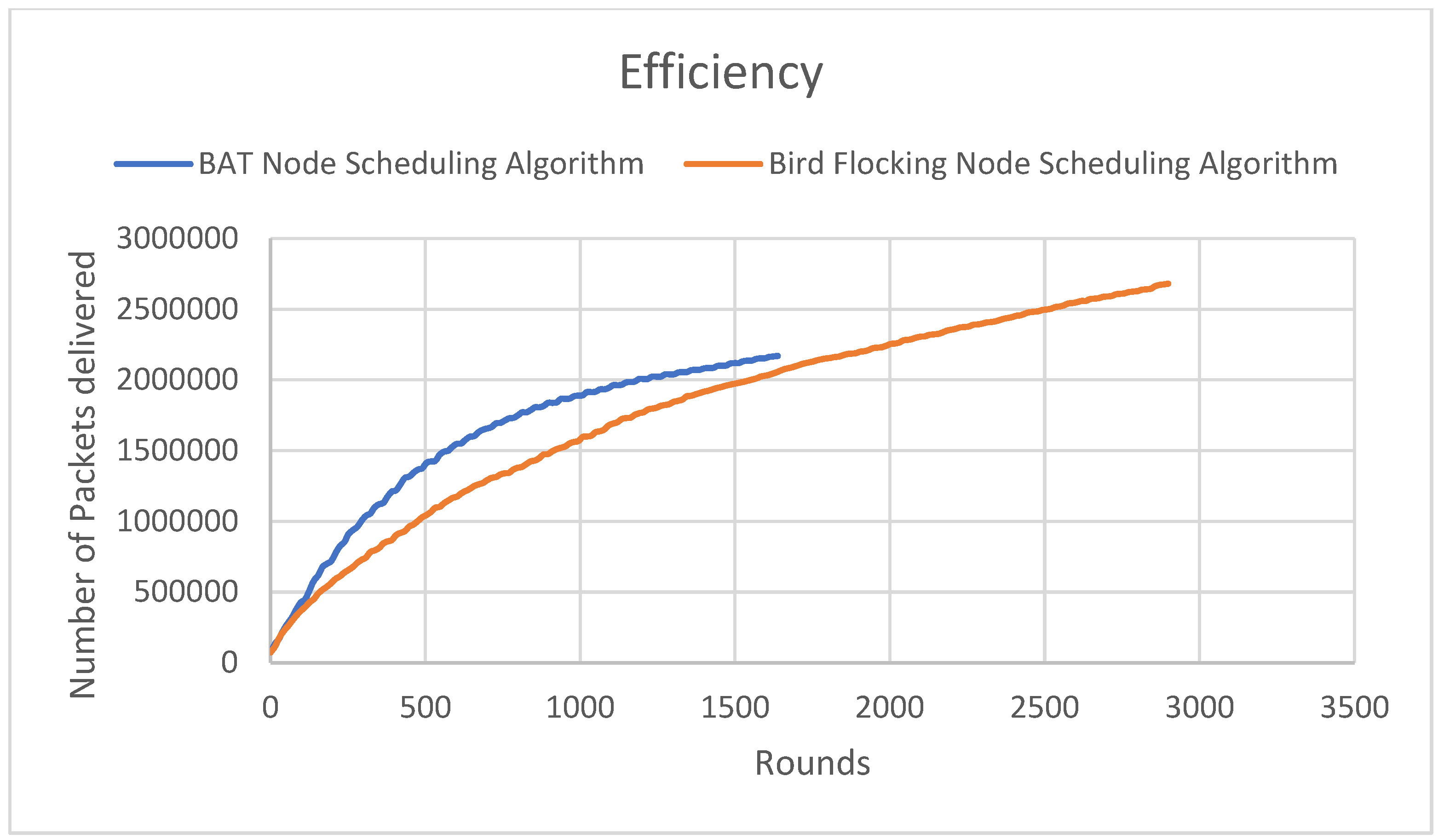
4.3. Efficiency

Throughout the network’s lifetime, packets are continuously sent and received, allowing us to compare the throughput of the BAT node scheduling algorithm with the proposed Bird Flocking node scheduling algorithm. The correlation observed is that a longer network lifetime results in a greater number of packets sent and received, indicating higher efficiency. Figure 7 illustrates this efficiency, with the Y-axis representing the number of packets sent and received and the X-axis indicating the number of rounds.

Figure 7 shows that the Bird Flocking node scheduling algorithm achieves higher efficiency than the BAT node scheduling algorithm, with the former algorithm reaching a throughput of 2,681,517 packets at the longest recorded simulation lifetime, around the 2898^th round. The Bird Flocking Node Scheduling Algorithm delivers a higher number of packets compared to the Bat Node Scheduling Algorithm because it promotes better energy efficiency, adaptive load balancing, and fewer sleep cycles, resulting in more active nodes available to transmit data. Conversely, the Bat algorithm's focus on individual energy optimization and more rigid scheduling which can reduce the overall packet delivery rate.

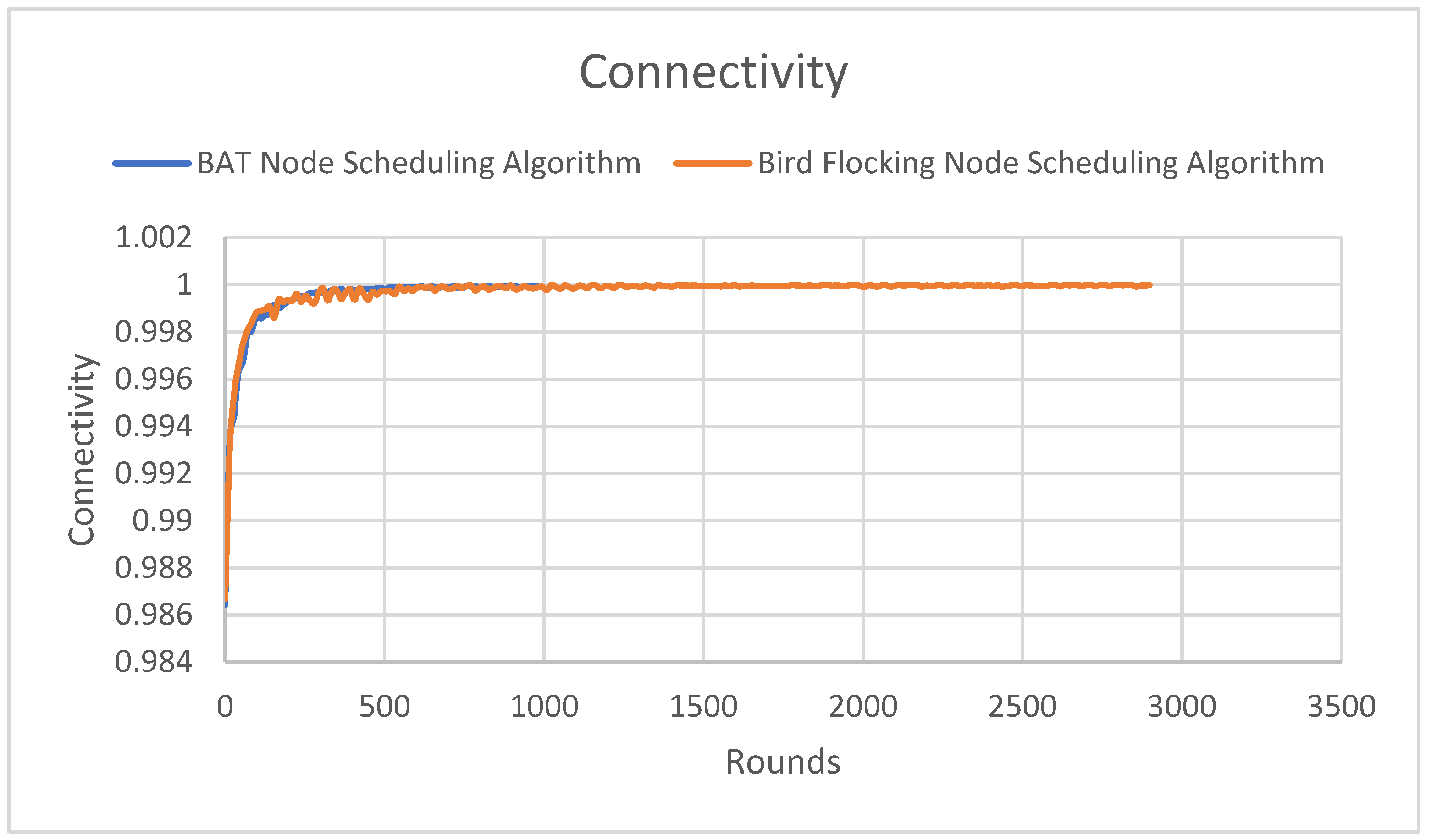
4.4. Connectivity

In this metric, we assess the connectivity of the sensor nodes within the network. As shown in Figure 8, the Y-axis represents connectivity performance, measured as a numerical value (e.g., the fraction of nodes connected in the network). The X-axis represents time, measured in terms of the number of rounds. For this scenario, the network consists of 150 nodes. For example, if the connectivity is 0.98, the total number of connected nodes is calculated as 150 × 0.98 = 149 connected nodes.

As shown in Figure 8, from 336th to 2884th rounds, the Bird Flocking node scheduling algorithm maintained a connectivity value of 1, indicating the network remained fully active with superior connectivity compared to other algorithms. It is important to note that fluctuations in setup cost for both the Bird Flocking and Bat Node Scheduling algorithms occurred between round 28 and 420 for the BAT algorithm, and between round 84 and 500 for the Bird Flocking algorithm. These fluctuations primarily result from the initial synchronization, node activation patterns, and energy management strategies. Both algorithms experience these fluctuations as they adjust to optimize energy usage, connectivity, and load balancing. However, the Bird Flocking algorithm outperforms the Bat Node Scheduling algorithm in terms of node connectivity due to its emphasis on adaptability, cooperation, and energy-efficient load balancing. These features ensure that nodes remain connected for longer periods and can dynamically adjust to changing network conditions. In contrast, the Bat algorithm’s focus on individual energy optimization often results in less effective coordination, leading to poorer connectivity over time.

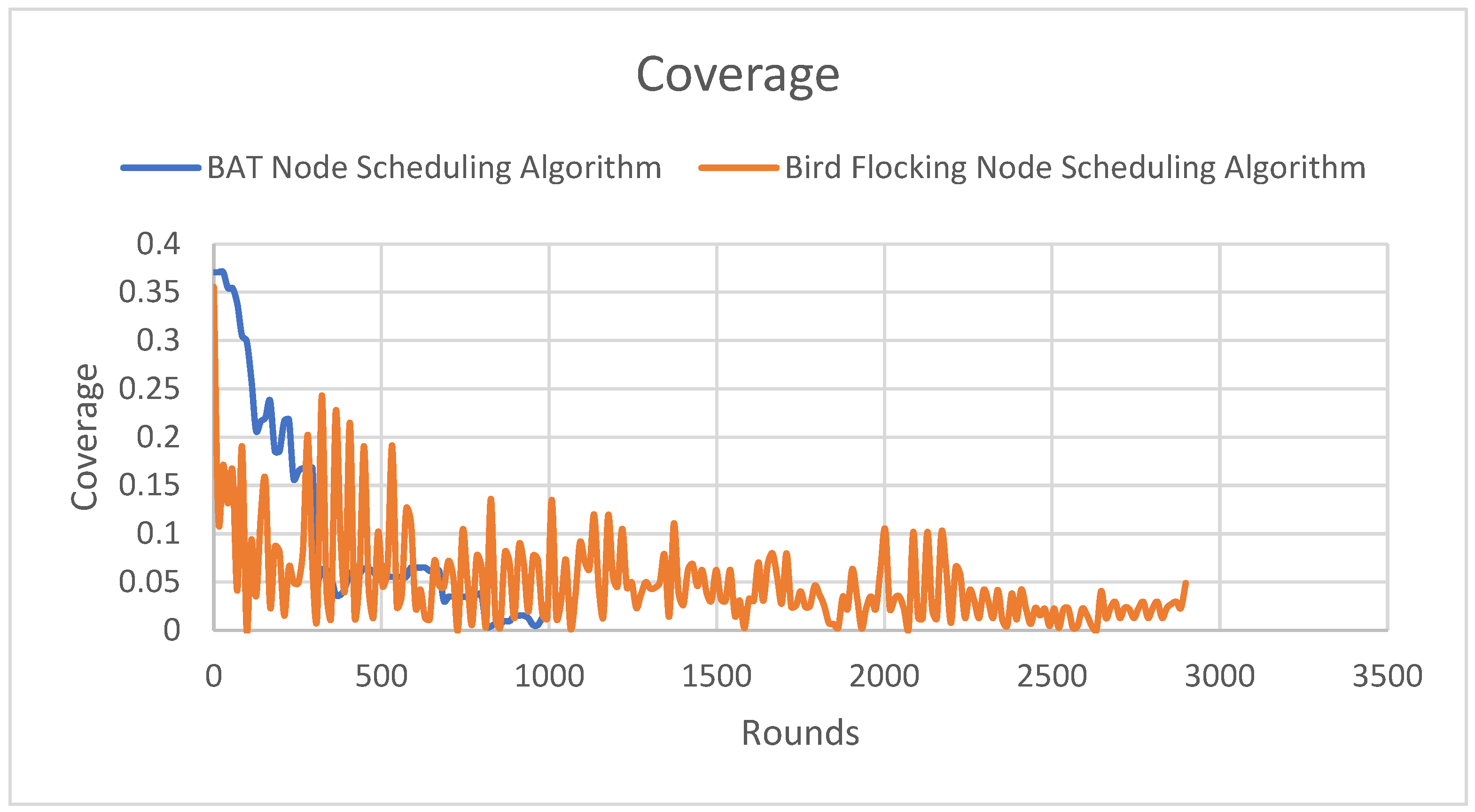
4.5. Coverage

Coverage is a metric that measures the ratio of all node coverage to the area to be monitored. In , the Y-axis is the ratio of the coverage to the total area to be monitored, and the X-axis is the number of rounds.

The Bird Flocking node scheduling algorithm notably maintained improved coverage up to the 2898^th round, whereas the BAT node scheduling algorithm recorded zero coverage by round 966^th, as nodes had already depleted their energy reserves. Coverage here refers to the fraction of the area monitored by the network. For instance, if the target area is 100 m², a coverage rate of 0.8 would mean that 80 m² of that area is being monitored. In summary, the Bird Flocking algorithm typically offers superior coverage compared to the Bat Node Scheduling algorithm, that is because of its adaptive scheduling and cooperative behavior. These features allow more nodes to stay active and contribute to maintaining a broader coverage across the network. On the other hand, while the Bat algorithm focuses on energy efficiency, its tendency for more frequent sleep cycles and less flexibility in adapting to network changes can result in reduced coverage, as fewer nodes are available for sensing at any given time.

5. Conclusions

To enhance coverage, connectivity, and network lifetime in WSNs, various scheduling algorithms are available, yet evaluating or identifying the best algorithm can be challenging. Bio-inspired computation has advanced the exploration of search spaces, and our main contribution is to investigate whether a Bird Flocking node scheduling algorithm offers superior solutions compared to the previously developed BAT node scheduling algorithm. The new Bird Flocking node scheduling algorithm demonstrates extended network lifetime, thereby enhancing service availability and contributing to more reliable WSNs. Moreover, the Bird Flocking algorithm, combined with the Lyapunov function, effectively optimizes network parameters such as connectivity, coverage, and lifetime. Our results indicate substantial improvements across these dimensions, with the Lyapunov function affirming the Bird Flocking node scheduling algorithm as optimal across potential fitness and objective functions within the defined search space—though this leaves room for future algorithms to potentially exceed its performance. With enhanced network lifetime, coverage, and connectivity, this work strengthens the dependability of WSNs. Simulation parameters were chosen to align closely with real-time WSN scenarios, emphasizing the practical relevance of our approach.