A New Generalized Bessel Function and Solutions of New Class of Fractional Kinetic Equations

1. Introduction

In contemporary engineering and physics, a profound understanding of applied mathematics, specifically pertaining to the fundamental characteristics of special functions, is indispensable. Special functions play a crucial role in various applications within the realm of physical sciences. The discipline of analysis, devoted to the examination of these specialized functions, traces its roots back to the early days of calculus, making it one of the most venerable fields of study. In recent decades, the discovery of novel special functions and their application to unexplored mathematical domains has reignited enthusiasm and rekindled scholarly curiosity in this area.

The investigation of Bessel functions holds significant relevance in the examination of crucial differential equations, (see for example [1]). These functions, rooted in Bessel function theory, find widespread application in diverse fields such as information theory, radiophysics, hydrodynamics, and nuclear physics. Notably, there has been a resurgence of interest in the exploration of Bessel functions within the context of fractional calculus theory, we may mention for example [2,3,4,5,6,7] and references therein.

Fractional calculus, which extends the concepts of differentiation and integration to arbitrary orders, is an intriguing branch of applied mathematics that has recently received a significant amount of attention from mathematicians and physicists. It is a powerful tool for studying a wide range of scientific problems, with many breakthroughs in control theory, hydrology, chaotic dynamics, kinetic theories, biophysics, bioengineering, quantum mechanics, diffusion processes, statistical mechanics, polymer sciences, thermodynamics, signal and image processing, astrophysics, and cosmology where many of the associated models amount to replace the time and space derivatives in an evolution equation with fractional derivatives of real orders (see [8,9,10,11,12,13,14,15]).

This subfield dates back to the late 17th century and evolved from the traditional definitions of calculus integral and derivative operators in much the same way that fractional exponents evolved from integer exponents. Several authors have stated that fractional-order operators are not only more suitable for modelling but also have advantages over integer-order operators.

It is important to recognize that there are multiple definitions for fractional-order derivatives, including divided-difference and infinite-sum types, such as the Grünwald-Letnikov fractional derivative, Weyl, Caputo, Feller, Riesz, Erdelyi-Kober fractional derivatives, and others. However, when it comes to fractional integration, the Riemann-Liouville (RL) and Caputo operators remain the most widely utilized and well-known methods. In modeling problems involving the concepts of nonlocality and memory effect, which are not well explained by integer-order calculus, fractional calculus stands out. Indeed, fractional calculus deals with the concept of the derivative operator, which is a local operator in integer order calculus but non-local in fractional calculus [16,17].

Indeed, fractional derivatives and integrals offer a more precise description of complex physical systems. These operators have been successfully incorporated into classical and quantum dynamical theories, demonstrating their utility in exploring novel fractal concepts [18]. They have introduced fresh perspectives and bridged gaps in traditional calculus that have yet to be fully assimilated or comprehended. Fractional calculus has proven effective in solving various physics problems, spanning classical to quantum domains. It is now recognized as a powerful tool for characterizing non-equilibrium complex systems exhibiting scale-invariant properties, dissipation, and long-range correlations that defy representation using traditional analytic functions and ordinary differential operators.

Presently, there are two prevailing approaches to describing fractional calculus. The first approach, known as the Riemann-Liouville approach, involves iteratively applying the integral operator n times and replacing it with a single integral using the well-known Cauchy formula. In this formulation, the factorial $n!$ is replaced with the Gamma function, enabling the definition of fractional integrals for non-integer orders. The Riemann and Caputo fractional derivatives have also been rigorously defined using integrals [19]. The second trend in fractional derivatives was pioneered by Grunwald-Letnikov. Their method involves iteratively applying the derivative n times and then fractionalizing the binomial coefficients using the Gamma function.

As they are used to model relevant systems, fractional differential equations have grown in popularity across a wide range of applied sciences. These equations play a vital role not just in the field of mathematics, but also in physics, control systems, dynamical systems, and engineering. They make it easier to create mathematical models that represent a wide variety of physical phenomena. Kinetic equations, in particular, are fundamental in mathematical physics and natural science because they describe the continuous motion of substances. As a result, as seen in previous research [6,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34], there has been a pursuit of extending and generalising fractional kinetic equations by incorporating diverse fractional calculus operators.

The structure of this paper is outlined as follows. Section 2 gathers the necessary concepts and definitions, and additionally introduces new and more generalized Bessel functions in the same section. In Section 3, we derive new Riemann-Liouville fractional integral and derivative formulas for the defined Bessel function. Section 4 is divided into three subsections. In SubSection 4.1, we explore the solutions of a novel type of fractional kinetic equation related to the generalized Bessel function. SubSection 4.2 presents various special cases of our main results. The graphical interpretation of the main findings is the focus of SubSection 4.3. Finally, concluding remarks are provided in Section 5.

2. Preliminaries and Basic Concepts

It is important to note that Riemann-Liouville and Caputo fractional derivatives are nonlocal operators with convolutional integrals with weak singularities. In the physical system, these non-local fractional derivatives introduce inherent memory and genetic effects.

The RL fractional integral and derivative of order $\alpha \in [n-1,n)$ are defined as follows (see, e.g., [8]):

• The left-side RL fractional integral

  $${(}_{RL}{D}_{0^{+}}^{-\alpha }f)\left(x\right)={(}_{RL}{I}_{0^{+}}^{\alpha }f)\left(x\right)={\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}\underset{0}{\overset{x}{\int }}{\displaystyle \frac{f\left(t\right)}{{\left(x-t\right)}^{1-\alpha }}}dt,$$

  (2.1)
• The right-side RL fractional integral

  $${(}_{RL}{D}_{-}^{-\alpha }f)\left(x\right)={(}_{RL}{I}_{-}^{\alpha }f)\left(x\right)={\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}\underset{x}{\overset{\infty }{\int }}{\displaystyle \frac{f\left(t\right)}{{\left(t-x\right)}^{1-\alpha }}}dt,$$

  (2.2)
• The left-side RL fractional derivative

  $$\begin{array}{cc}\hfill {(}_{RL}{D}_{0^{+}}^{\alpha }f)\left(x\right)& ={\left({\displaystyle \frac{d}{dx}}\right)}^n{(}_{RL}{I}_{0^{+}}^{n-\alpha }f)\left(x\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{\mathsf{\Gamma }\left(n-\alpha \right)}}{\left({\displaystyle \frac{d}{dx}}\right)}^n\underset{0}{\overset{x}{\int }}{\displaystyle \frac{f\left(t\right)}{{\left(x-t\right)}^{\alpha -n+1}}}dt,\hfill \end{array}$$

  (2.3)
• The right-side RL fractional derivative

  $$\begin{array}{cc}\hfill {(}_{RL}{D}_{-}^{\alpha }f)\left(x\right)& ={\left({\displaystyle \frac{-d}{dx}}\right)}^n{(}_{RL}{I}_{-}^{n-\alpha }f)\left(x\right)\hfill \\ \hfill & ={\displaystyle \frac{{\left(-1\right)}^n}{\mathsf{\Gamma }\left(n-\alpha \right)}}{\left({\displaystyle \frac{d}{dx}}\right)}^n\underset{x}{\overset{\infty }{\int }}{\displaystyle \frac{f\left(t\right)}{{\left(t-x\right)}^{\alpha -n+1}}}dt,\hfill \end{array}$$

  (2.4)

Lemma 2.1. 

Let $\Re \left(\alpha \right)>0,\Re \left(\rho \right)>-1$and $t>0,$ then

$$RL{I}_{0^{+}}^{\alpha }{t}^{\rho }={\displaystyle \frac{\mathsf{\Gamma }\left(\rho +1\right)}{\mathsf{\Gamma }\left(\rho +\alpha +1\right)}}{t}^{\rho +\alpha },$$

(2.5)

and

$$RL{I}_{-}^{\alpha }{t}^{-\rho }={\displaystyle \frac{\mathsf{\Gamma }\left(\rho -\alpha \right)}{\mathsf{\Gamma }\left(\rho \right)}}{t}^{\alpha -\rho }.$$

(2.6)

We now review the essential definitions that will be used in the sequel.

Definition 2.1. 

The Fox-Wright function, denoted as _pψ_q(x), is defined by a formula in which p represents the numerator and q represents the denominator of the function.

$${}_p\mathrm{\psi }_q\left(x\right)={}_p\mathrm{\psi }_q\left(\begin{array}{c}{\left(a_i,{ϵ}_i\right)}_{1,p}\\ {\left(b_j,{\nu }_j\right)}_{1,q}\end{array};x\right)=\sum _{n=0}^{\infty }{\displaystyle \frac{{\displaystyle \prod _{i=1}^p}\mathsf{\Gamma }\left(a_i+n{ϵ}_i\right)}{{\displaystyle \prod _{j=1}^q}\mathsf{\Gamma }\left(b_j+n{\nu }_j\right)}}{\displaystyle \frac{x^n}{n!}}$$

(2.7)

where $a_i,b_j\in \mathbb{R}(i=1,2,...,p;j=1,2,...,q)$ and such that ${\displaystyle \sum _{j=1}^q}{\nu }_j-{\displaystyle \sum _{i=1}^p}{ϵ}_i>-1.$ In particular, when ${ϵ}_i={\nu }_j=1,{}_p\mathrm{\psi }_q\left(x\right)$ immediately reduced to the generalized hypergeometric function _pF_q (see [35,36]).

Mittag-Leffler functions arise as inherent solutions to equations involving fractional order differentials and integrals.

In 1903, Mittag-Leffler [37] introduced and named the function after himself, defining it using a power series representation.

$$E_{\wp }\left(\xi \right)=\sum _{r=0}^{\infty }{\displaystyle \frac{{\xi }^r}{\mathsf{\Gamma }\left(r\wp +1\right)}},\Re \left(\wp \right)>0$$

(2.8)

Wiman generalised this function in 1905 [38] as

$$E_{{\wp }_1,{\wp }_2}\left(\xi \right)=\sum _{r=0}^{\infty }{\displaystyle \frac{{\xi }^r}{\mathsf{\Gamma }\left(r{\wp }_1+{\wp }_2\right)}},\Re \left({\wp }_1\right),\Re \left({\wp }_2\right)>0$$

(2.9)

In the present paper, we take into account a brand-new generalised Bessel function with the following form:

$$J_{{\sigma }_1,{\sigma }_2,\varphi ,\omega }^{ϵ,\eta ,{\chi }_1,{\chi }_2}\left(\xi \right)=\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-\omega \right)}^n{\left({\chi }_1\right)}_{{\sigma }_{2}n}}{n!\mathsf{\Gamma }\left(n\eta +ϵ+\frac{\varphi +1}{2}\right){\left({\chi }_2\right)}_{{\sigma }_{1}n}}}{\left({\displaystyle \frac{\xi }{2}}\right)}^{ϵ+2n},$$

(2.10)

where $ϵ,\eta ,{\chi }_1,{\chi }_2,\varphi ,\omega ,\xi \in \mathbb{C},\Re \left(\eta \right)>0,\Re \left(ϵ\right)>0,{\sigma }_1,{\sigma }_2\in \mathbb{N},$and ${\left(\chi \right)}_0=1,{\left(\chi \right)}_{{\sigma }_{2}n}={\displaystyle \frac{\mathsf{\Gamma }\left(\chi +{\sigma }_{2}n\right)}{\mathsf{\Gamma }\left(\chi \right)}}$ denotes the generalized pochhammer symbol (see, e.g [39]).

Remark 2.1. 

The series (2.10) generalizes many special cases as follows

(i)

Putting ${\sigma }_1={\sigma }_2=0,$ and $\eta =1$ in (2.10), we obtain the generalized Bessel function of the first kind, ${\omega }_{ϵ,\varphi ,\omega }\left(t\right)$ defined by [40].

$${\omega }_{ϵ,\varphi ,\omega }\left(\xi \right)=\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-\omega \right)}^n}{n!\mathsf{\Gamma }\left(n+ϵ+\frac{\varphi +1}{2}\right)}}{\left({\displaystyle \frac{\xi }{2}}\right)}^{ϵ+2n},\xi \in \mathbb{C}.$$

(2.11)

(ii)

Setting ${\sigma }_1={\sigma }_2=0,$$\eta =1,$ and $\varphi =\omega =1,$ in (2.10), the generalized Bessel function $J_{{\sigma }_1,{\sigma }_2,\varphi ,\omega }^{ϵ,\eta ,{\chi }_1,{\chi }_2}\left(\xi \right)$ reduced to the familiar Bessel function of the first kind of order $ϵ$, given by [40].

$$J_{ϵ}\left(\xi \right)=\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-1\right)}^n}{n!\mathsf{\Gamma }\left(n+ϵ+1\right)}}{\left({\displaystyle \frac{\xi }{2}}\right)}^{ϵ+2n},\xi \in \mathbb{C}.$$

(2.12)

(iii)

If we put ${\sigma }_1={\sigma }_2=0,$ and $\varphi =-\omega =1,$ in (2.10), then the generalized Bessel function $J_{{\sigma }_1,{\sigma }_2,\varphi ,\omega }^{ϵ,\eta ,{\chi }_1,{\chi }_2}\left(\xi \right)$ reduced to generalized type of modified Bessel function of the first kind, $I_{ϵ}^{\eta }\left(\xi \right)$ defined by [41].

$$I_{ϵ}^{\eta }\left(\xi \right)=\sum _{n=0}^{\infty }{\displaystyle \frac{1}{n!\mathsf{\Gamma }\left(n\eta +ϵ+1\right)}}{\left({\displaystyle \frac{\xi }{2}}\right)}^{ϵ+2n},\xi \in \mathbb{C}.$$

(2.13)

(iv)

Setting ${\sigma }_1={\sigma }_2=0,\eta =1,$ and $\varphi =-\omega =1,$ in (2.10), we have the familiar modified Bessel function of the first kind of order $ϵ$, $I_{ϵ}\left(\xi \right)$ given by [40].

$$I_{ϵ}\left(\xi \right)=\sum _{n=0}^{\infty }{\displaystyle \frac{1}{n!\mathsf{\Gamma }\left(n+ϵ+1\right)}}{\left({\displaystyle \frac{\xi }{2}}\right)}^{ϵ+2n},\xi \in \mathbb{C}.$$

(2.14)

(v)

Putting ${\sigma }_1={\sigma }_2=0,$$\varphi =2,$ and $\omega =1,$ in (2.10), we obtain the spherical Bessel function of order $ϵ$, $j_{ϵ}\left(\xi \right)$ defined by [40].

$$j_{ϵ}\left(\xi \right)=\sqrt{{\displaystyle \frac{\pi }{2}}}\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-1\right)}^n}{n!\mathsf{\Gamma }\left(n+ϵ+\frac{3}{2}\right)}}{\left({\displaystyle \frac{\xi }{2}}\right)}^{ϵ+2n},\xi \in \mathbb{C}.$$

(2.15)

(vi)

Setting $\varphi =\omega =1,$ and ${\sigma }_1=0,$ in (2.10), we the generalized Bessel function $J_{{\sigma }_1,{\sigma }_2,\varphi ,\omega }^{ϵ,\eta ,{\chi }_1,{\chi }_2}\left(t\right)$ reduced to

$$J_{{\sigma }_1,{\sigma }_2,\varphi ,\omega }^{ϵ,\eta ,{\chi }_1,{\chi }_2}\left(\xi \right)={\left({\displaystyle \frac{\xi }{2}}\right)}^{ϵ}{\tilde{J}}_{ϵ,q}^{\eta ,{\chi }_1}\left({\displaystyle \frac{{\xi }^2}{4}}\right),$$

(2.16)

where ${\tilde{J}}_{ϵ,q}^{\eta ,{\chi }_1}\left(\xi \right)$ is the generalized matland Bessel function defined by [42]

$${\tilde{J}}_{ϵ,q}^{\eta ,{\chi }_1}\left(\xi \right)=\sum _{n=0}^{\infty }{\displaystyle \frac{{\left({\chi }_1\right)}_{{\sigma }_{2}n}{\left(-\xi \right)}^n}{n!\mathsf{\Gamma }\left(n\eta +ϵ+1\right)}},\xi \in \mathbb{C}.$$

(2.17)

(vii)

Putting $\varphi =\omega =1,$ and ${\sigma }_1={\sigma }_2=0,$ in (2.10), we the generalized Bessel function $J_{{\sigma }_1,{\sigma }_2,\varphi ,\omega }^{ϵ,\eta ,{\chi }_1,{\chi }_2}\left(t\right)$ reduced to

$$J_{{\sigma }_1,{\sigma }_2,\varphi ,\omega }^{ϵ,\eta ,{\chi }_1,{\chi }_2}\left(\xi \right)={\left({\displaystyle \frac{\xi }{2}}\right)}^{ϵ}{\tilde{J}}_{ϵ}^{\eta }\left({\displaystyle \frac{t^{\xi 2}}{4}}\right),$$

(18)

where ${\tilde{J}}_{ϵ}^{\eta }\left(\xi \right)$ is the familiar matland Bessel function given by [43].

$${\tilde{J}}_{ϵ}^{\eta }\left(\xi \right)=\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-\xi \right)}^n}{n!\mathsf{\Gamma }\left(n\eta +ϵ+1\right)}},\xi \in \mathbb{C}.$$

(2.19)

Inspired by the preceding discussions and the existing literature on Bessel functions, this study intends to conduct additional research involving the generalised Bessel function (2.10). To begin, we provide fractional integral and differential formulations, as shown below.

3. Fractional Calculus Approach of $J_{{\sigma }_1,{\sigma }_2,\varphi ,\omega }^{ϵ,\eta ,{\chi }_1,{\chi }_2}\left(\xi \right)$

In this section, we derive the Riemann-Liouville fractional integration and fractional differentiation of the recently defined generalized Bessel function, denoted as $J_{{\sigma }_1,{\sigma }_2,\varphi ,\omega }^{ϵ,\eta ,{\chi }_1,{\chi }_2}\left(\xi \right)$. The obtained results are presented as follows.

3.1. Fractional Integral Forms

Theorem 3.1. 

Suppose λ and η are complex numbers such that the real part of λ is greater than 0 and the real part of η is greater than $0.$ Additionally, assume that the conditions stated in equation (2.10) are satisfied. Under these circumstances, the following formula for fractional integration is valid.

$$\begin{array}{cc}\hfill I_{0+}^{\lambda }\left(t^{\eta -1}{J}_{{\sigma }_1,{\sigma }_2,\varphi ,\omega }^{ϵ,\eta ,{\chi }_1,{\chi }_2}\left(t\right)\right)\left(\xi \right)=& {\displaystyle \frac{\mathsf{\Gamma }\left({\chi }_2\right)}{2^{ϵ}\mathsf{\Gamma }\left({\chi }_1\right)}}{\xi }^{\lambda +ϵ+\eta -1}\hfill \\ \hfill & \times {}_2\mathsf{\Psi }_3\left[\begin{array}{c}\left({\chi }_1,{\sigma }_2\right),\left(ϵ+\eta ,2\right);\\ \left(ϵ+{\displaystyle \frac{\varphi +1}{2}},\eta \right),\left({\chi }_2,{\sigma }_1\right),\left(\lambda +ϵ+\eta ,2\right);\end{array}{\displaystyle \frac{-\omega {\xi }^2}{4}}\right]\hfill \end{array}$$

(3.1)

Proof. 

Denoting the left-hand side of (3.1) by ${\Im }_1.$ Using (2.10), we obtain

$$\begin{array}{ccc}\hfill {\Im }_1& =& I_{0+}^{\lambda }\left(t^{\eta -1}\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-\omega \right)}^n{\left({\chi }_1\right)}_{{\sigma }_{2}n}}{n!\mathsf{\Gamma }\left(n\eta +ϵ+\frac{\varphi +1}{2}\right){\left({\chi }_2\right)}_{{\sigma }_{1}n}}}{\left({\displaystyle \frac{t}{2}}\right)}^{ϵ+2n}\right)\left(\xi \right)\hfill \\ & =& \sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-\omega \right)}^n{\left({\chi }_1\right)}_{{\sigma }_{2}n}{\left(\frac{1}{2}\right)}^{ϵ+2n}}{n!\mathsf{\Gamma }\left(n\eta +ϵ+\frac{\varphi +1}{2}\right){\left({\chi }_2\right)}_{{\sigma }_{1}n}}}{I}_{0+}^{\lambda }\left(t^{ϵ+2n+\eta -1}\right)\left(\xi \right)\hfill \end{array}$$

Using (2.5) of Lemma 2.1, we get

$$\begin{array}{ccc}\hfill {\Im }_1& =& \sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-\omega \right)}^n{\left({\chi }_1\right)}_{{\sigma }_{2}n}{\left(\frac{1}{2}\right)}^{ϵ+2n}}{n!\mathsf{\Gamma }\left(n\eta +ϵ+\frac{\varphi +1}{2}\right){\left({\chi }_2\right)}_{{\sigma }_{1}n}}}{\displaystyle \frac{\mathsf{\Gamma }\left(ϵ+2n+\eta \right)}{\mathsf{\Gamma }\left(\lambda +ϵ+2n+\eta \right)}}{\xi }^{\lambda +ϵ+2n+\eta -1}\hfill \\ & =& {\displaystyle \frac{\mathsf{\Gamma }\left({\chi }_2\right)}{2^{ϵ}\mathsf{\Gamma }\left({\chi }_1\right)}}{\xi }^{\lambda +ϵ+\eta -1}\sum _{n=0}^{\infty }{\displaystyle \frac{\mathsf{\Gamma }\left({\chi }_1+{\sigma }_{2}n\right)\mathsf{\Gamma }\left(ϵ+2n+\eta \right)}{\mathsf{\Gamma }\left(n\eta +ϵ+\frac{\varphi +1}{2}\right)\mathsf{\Gamma }\left({\chi }_2+{\sigma }_{1}n\right)\mathsf{\Gamma }\left(\lambda +ϵ+2n+\eta \right)}}{\displaystyle \frac{{\left(\frac{-\omega {\xi }^2}{4}\right)}^n}{n!}}.\hfill \end{array}$$

In view of the definition of the Fox-Wright function (2.7), we have

$${\Im }_1={\displaystyle \frac{\mathsf{\Gamma }\left({\chi }_2\right)}{2^{ϵ}\mathsf{\Gamma }\left({\chi }_1\right)}}{\xi }^{\lambda +ϵ+\eta -1}{}_2\mathsf{\Psi }_3\left[\begin{array}{c}\left({\chi }_1,{\sigma }_2\right),\left(ϵ+\eta ,2\right);\\ \left(ϵ+{\displaystyle \frac{\varphi +1}{2}},\eta \right),\left({\chi }_2,{\sigma }_1\right),\left(\lambda +ϵ+\eta ,2\right);\end{array}{\displaystyle \frac{-\omega {\xi }^2}{4}}\right]$$

as desired. □

Theorem 3.2. 

Suppose λ and η are complex numbers such that the real part of λ is greater than 0 and the real part of η is greater than $0.$ Additionally, assume that the conditions stated in equation (2.10) are satisfied. Under these circumstances, the following formula for fractional integration is valid.

$$\begin{array}{cc}\hfill I_{0-}^{\lambda }\left(t^{-\eta }{J}_{{\sigma }_1,{\sigma }_2,\varphi ,\omega }^{ϵ,\eta ,{\chi }_1,{\chi }_2}\left({\displaystyle \frac{1}{t}}\right)\right)\left(\xi \right)=& {\displaystyle \frac{\mathsf{\Gamma }\left({\chi }_2\right)}{2^{ϵ}\mathsf{\Gamma }\left({\chi }_1\right)}}{\xi }^{\lambda -\eta -ϵ}\hfill \\ \hfill & \times {}_2\mathsf{\Psi }_3\left[\begin{array}{c}\left({\chi }_1,{\sigma }_2\right),\left(\eta -ϵ-\lambda ,2\right);\\ \left(ϵ+{\displaystyle \frac{\varphi +1}{2}},\eta \right),\left({\chi }_2,{\sigma }_1\right),\left(\eta +ϵ,2\right);\end{array}{\displaystyle \frac{-\omega }{4{\xi }^2}}\right]\hfill \end{array}$$

(3.2)

Proof. 

Denoting the left-hand side of (3.1) by ${\Im }_2$. Using (2.10), we have

$$\begin{array}{ccc}\hfill {\Im }_2& =& I_{0-}^{\lambda }\left(t^{-\eta }\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-\omega \right)}^n{\left({\chi }_1\right)}_{{\sigma }_{2}n}}{n!\mathsf{\Gamma }\left(n\eta +ϵ+\frac{\varphi +1}{2}\right){\left({\chi }_2\right)}_{{\sigma }_{1}n}}}{\left({\displaystyle \frac{1}{2t}}\right)}^{ϵ+2n}\right)\left(\xi \right)\hfill \\ & =& \sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-\omega \right)}^n{\left({\chi }_1\right)}_{{\sigma }_{2}n}{\left(\frac{1}{2}\right)}^{ϵ+2n}}{n!\mathsf{\Gamma }\left(n\eta +ϵ+\frac{\varphi +1}{2}\right){\left({\chi }_2\right)}_{{\sigma }_{1}n}}}{I}_{0+}^{\lambda }\left(t^{-\left(ϵ+2n+\eta \right)}\right)\left(\xi \right)\hfill \end{array}$$

Using (2.6) of Lemma 2.1, we get

$$\begin{array}{ccc}\hfill {\Im }_2& =& \sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-\omega \right)}^n{\left({\chi }_1\right)}_{{\sigma }_{2}n}{\left(\frac{1}{2}\right)}^{ϵ+2n}}{n!\mathsf{\Gamma }\left(n\eta +ϵ+\frac{\varphi +1}{2}\right){\left({\chi }_2\right)}_{{\sigma }_{1}n}}}{\displaystyle \frac{\mathsf{\Gamma }\left(ϵ+2n+\eta -\lambda \right)}{\mathsf{\Gamma }\left(ϵ+2n+\eta \right)}}{\xi }^{\lambda -ϵ-2n-\eta }\hfill \\ & =& {\displaystyle \frac{\mathsf{\Gamma }\left({\chi }_2\right)}{2^{ϵ}\mathsf{\Gamma }\left({\chi }_1\right)}}{\xi }^{\lambda -ϵ-\eta }\sum _{n=0}^{\infty }{\displaystyle \frac{\mathsf{\Gamma }\left({\chi }_1+{\sigma }_{2}n\right)\mathsf{\Gamma }\left(ϵ+2n+\eta -\lambda \right)}{\mathsf{\Gamma }\left(n\eta +ϵ+\frac{\varphi +1}{2}\right)\mathsf{\Gamma }\left({\chi }_2+{\sigma }_{1}n\right)\mathsf{\Gamma }\left(ϵ+2n+\eta \right)}}{\displaystyle \frac{{\left(\frac{-\omega }{4{\xi }^2}\right)}^n}{n!}}.\hfill \end{array}$$

In view of the definition of the Fox-wright function (2.7), we arrive at the desired result. □

3.2. Fractional Derivative Forms

Theorem 3.3. 

Let $\lambda ,\eta \in \mathbb{C}$ be such that $\Re \left(\lambda \right)>0,\Re \left(\eta \right)>0,$ and the conditions given in (2.10) are satisfied, then the following fractional integral formula holds true

$$\begin{array}{cc}\hfill D_{0+}^{\lambda }\left(t^{\eta -1}{J}_{{\sigma }_1,{\sigma }_2,\varphi ,\omega }^{ϵ,\eta ,{\chi }_1,{\chi }_2}\left(t\right)\right)\left(\xi \right)=& {\displaystyle \frac{\mathsf{\Gamma }\left({\chi }_2\right)}{2^{ϵ}\mathsf{\Gamma }\left({\chi }_1\right)}}{\xi }^{ϵ+\eta -\lambda -1}\hfill \\ \hfill & \times {}_2\mathsf{\Psi }_3\left[\begin{array}{c}\left({\chi }_1,{\sigma }_2\right),\left(ϵ+\eta ,2\right);\\ \left(ϵ+{\displaystyle \frac{\varphi +1}{2}},\eta \right),\left({\chi }_2,{\sigma }_1\right),\left(ϵ+\eta -\lambda ,2\right);\end{array}{\displaystyle \frac{-\omega {\xi }^2}{4}}\right]\hfill \end{array}$$

(3.3)

Proof. 

Denoting the left-hand side of (3.3) by ${\Im }_3.$ Using (2.10) and (2.3), we obtain

$$\begin{array}{ccc}\hfill {\Im }_3& =& {\left({\displaystyle \frac{d}{d\xi }}\right)}^m\left[I_{0+}^{m-\lambda }\left(t^{\eta -1}{J}_{{\sigma }_1,{\sigma }_2,\varphi ,\omega }^{ϵ,\eta ,{\chi }_1,{\chi }_2}\left(t\right)\right)\left(\xi \right)\right]\hfill \\ & =& {\left({\displaystyle \frac{d}{d\xi }}\right)}^m\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-\omega \right)}^n{\left({\chi }_1\right)}_{{\sigma }_{2}n}{\left(\frac{1}{2}\right)}^{ϵ+2n}}{n!\mathsf{\Gamma }\left(n\eta +ϵ+\frac{\varphi +1}{2}\right){\left({\chi }_2\right)}_{{\sigma }_{1}n}}}{I}_{0+}^{m-\lambda }\left(t^{ϵ+2n+\eta -1}\right)\left(\xi \right)\hfill \end{array}$$

Using (2.5) of Lemma 2.1, we have

$$\begin{array}{ccc}\hfill {\Im }_3& =& {\left({\displaystyle \frac{d}{d\xi }}\right)}^m\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-\omega \right)}^n{\left({\chi }_1\right)}_{{\sigma }_{2}n}{\left(\frac{1}{2}\right)}^{ϵ+2n}}{n!\mathsf{\Gamma }\left(n\eta +ϵ+\frac{\varphi +1}{2}\right){\left({\chi }_2\right)}_{{\sigma }_{1}n}}}{\displaystyle \frac{\mathsf{\Gamma }\left(\eta +ϵ+2n\right)}{\mathsf{\Gamma }\left(m-\lambda +\eta +ϵ+2n\right)}}{\xi }^{m-\lambda +\eta +ϵ+2n-1}\hfill \\ & =& \sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-\omega \right)}^n{\left({\chi }_1\right)}_{{\sigma }_{2}n}{\left(\frac{1}{2}\right)}^{ϵ+2n}}{n!\mathsf{\Gamma }\left(n\eta +ϵ+\frac{\varphi +1}{2}\right){\left({\chi }_2\right)}_{{\sigma }_{1}n}}}{\displaystyle \frac{\mathsf{\Gamma }\left(\eta +ϵ+2n\right)}{\mathsf{\Gamma }\left(m-\lambda +\eta +ϵ+2n\right)}}{\left({\displaystyle \frac{d}{d\xi }}\right)}^m\left[{\xi }^{m-\lambda +\eta +ϵ+2n-1}\right],\hfill \end{array}$$

after some simplification

$$\begin{array}{ccc}\hfill {\Im }_3& =& \sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-\omega \right)}^n{\left({\chi }_1\right)}_{{\sigma }_{2}n}{\left(\frac{1}{2}\right)}^{ϵ+2n}}{n!\mathsf{\Gamma }\left(n\eta +ϵ+\frac{\varphi +1}{2}\right){\left({\chi }_2\right)}_{{\sigma }_{1}n}}}{\displaystyle \frac{\mathsf{\Gamma }\left(\eta +ϵ+2n\right)}{\mathsf{\Gamma }\left(\eta +ϵ+2n-\lambda \right)}}{\xi }^{\eta +ϵ+2n-\lambda -1}\hfill \\ & =& {\displaystyle \frac{\mathsf{\Gamma }\left({\chi }_2\right)}{2^{ϵ}\mathsf{\Gamma }\left({\chi }_1\right)}}{\xi }^{ϵ+\eta -\lambda -1}\sum _{n=0}^{\infty }{\displaystyle \frac{\mathsf{\Gamma }\left({\chi }_1+{\sigma }_{2}n\right)\mathsf{\Gamma }\left(\eta +ϵ+2n\right)}{\mathsf{\Gamma }\left(\eta n+ϵ+\frac{\varphi +1}{2}\right)\mathsf{\Gamma }\left({\chi }_2+{\sigma }_{1}n\right)\mathsf{\Gamma }\left(\eta +ϵ+2n-\lambda \right)}}{\displaystyle \frac{{\left(\frac{-\omega {\xi }^2}{4}\right)}^n}{n!}}.\hfill \end{array}$$

In view if the definition of the Fox-wright function (2.7), we have

$${\Im }_3={\displaystyle \frac{\mathsf{\Gamma }\left({\chi }_2\right)}{2^{ϵ}\mathsf{\Gamma }\left({\chi }_1\right)}}{\xi }^{ϵ+\eta -\lambda -1}{}_2\mathsf{\Psi }_3\left[\begin{array}{c}\left({\chi }_1,{\sigma }_2\right),\left(ϵ+\eta ,2\right);\\ \left(ϵ+{\displaystyle \frac{\varphi +1}{2}},\eta \right),\left({\chi }_2,{\sigma }_1\right),\left(ϵ+\eta -\lambda ,2\right);\end{array}{\displaystyle \frac{-\omega {\xi }^2}{4}}\right].$$

as required. □

Theorem 3.4. 

Let $\lambda ,\eta \in \mathbb{C}$ be such that $\Re \left(\lambda \right)>0,\Re \left(\eta \right)>m-\Re \left(\lambda \right),$and the conditions given in (2.10) are satisfied, then the following fractional integral formula holds true

$$\begin{array}{cc}\hfill D_{0-}^{\lambda }\left(t^{-\eta }{J}_{{\sigma }_1,{\sigma }_2,\varphi ,\omega }^{ϵ,\eta ,{\chi }_1,{\chi }_2}\left({\displaystyle \frac{1}{t}}\right)\right)\left(\xi \right)=& {\displaystyle \frac{\mathsf{\Gamma }\left({\chi }_2\right)}{2^{ϵ}\mathsf{\Gamma }\left({\chi }_1\right)}}{\xi }^{-\lambda -\eta -ϵ}\hfill \\ \hfill & \times {}_2\mathsf{\Psi }_3\left[\begin{array}{c}\left({\chi }_1,{\sigma }_2\right),\left(\lambda +\eta +ϵ,2\right);\\ \left(ϵ+{\displaystyle \frac{\varphi +1}{2}},\eta \right),\left({\chi }_2,{\sigma }_1\right),\left(\eta +ϵ,2\right);\end{array}{\displaystyle \frac{-\omega }{4{\xi }^2}}\right]\hfill \end{array}$$

(3.4)

Proof. 

Denoting the left-hand side of (3.4) by ${\Im }_4$. Using (2.10) and (2.4), we have

$$\begin{array}{ccc}\hfill {\Im }_4& =& I_{0-}^{m-\lambda }\left(t^{-\eta }{J}_{{\sigma }_1,{\sigma }_2,\varphi ,\omega }^{ϵ,\eta ,{\chi }_1,{\chi }_2}\left({\displaystyle \frac{1}{t}}\right)\right)\left(\xi \right)\hfill \\ & =& {\left({\displaystyle \frac{-d}{d\xi }}\right)}^m\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-\omega \right)}^n{\left({\chi }_1\right)}_{{\sigma }_{2}n}{\left(\frac{1}{2}\right)}^{ϵ+2n}}{n!\mathsf{\Gamma }\left(n\eta +ϵ+\frac{\varphi +1}{2}\right){\left({\chi }_2\right)}_{{\sigma }_{1}n}}}{I}_{0+}^{m-\lambda }\left(t^{-\left(\eta +ϵ+2n\right)}\right)\left(\xi \right)\hfill \end{array}$$

Using (2.6) of Lemma 2.1, we obtain

$$\begin{array}{ccc}\hfill {\Im }_4& =& {\left({\displaystyle \frac{-d}{d\xi }}\right)}^m\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-\omega \right)}^n{\left({\chi }_1\right)}_{{\sigma }_{2}n}{\left(\frac{1}{2}\right)}^{ϵ+2n}}{n!\mathsf{\Gamma }\left(n\eta +ϵ+\frac{\varphi +1}{2}\right){\left({\chi }_2\right)}_{{\sigma }_{1}n}}}{\displaystyle \frac{\mathsf{\Gamma }\left(\eta +ϵ+2n-m+\lambda \right)}{\mathsf{\Gamma }\left(\eta +ϵ+2n\right)}}{\xi }^{m-\lambda -\eta -ϵ-2n}\hfill \\ & =& \sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-\omega \right)}^n{\left({\chi }_1\right)}_{{\sigma }_{2}n}{\left(\frac{1}{2}\right)}^{ϵ+2n}}{n!\mathsf{\Gamma }\left(n\eta +ϵ+\frac{\varphi +1}{2}\right){\left({\chi }_2\right)}_{{\sigma }_{1}n}}}{\displaystyle \frac{\mathsf{\Gamma }\left(\eta +ϵ+2n-m+\lambda \right)}{\mathsf{\Gamma }\left(\eta +ϵ+2n\right)}}\hfill \\ & & \times {\displaystyle \frac{{\left(-1\right)}^m\mathsf{\Gamma }\left(m-\lambda -\eta -ϵ-2n+1\right)}{\mathsf{\Gamma }\left(1-\lambda -\eta -ϵ-2n\right)}}{\xi }^{-\lambda -\eta -ϵ-2n}\hfill \end{array}$$

Using the identity ${\displaystyle \frac{\mathsf{\Gamma }\left(\sigma -\varrho \right)}{\mathsf{\Gamma }\left(-\varrho \right)}}={\left(-\varrho \right)}_{\sigma }={\displaystyle \frac{{\left(-1\right)}^{\sigma }\mathsf{\Gamma }\left(\varrho +1\right)}{\mathsf{\Gamma }\left(\varrho -\sigma +1\right)}},$ we have

$$\begin{array}{ccc}\hfill {\Im }_4& =& \sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-\omega \right)}^n{\left({\chi }_1\right)}_{{\sigma }_{2}n}{\left(\frac{1}{2}\right)}^{ϵ+2n}}{n!\mathsf{\Gamma }\left(n\eta +ϵ+\frac{\varphi +1}{2}\right){\left({\chi }_2\right)}_{{\sigma }_{1}n}}}{\displaystyle \frac{\mathsf{\Gamma }\left(\lambda +\eta +ϵ+2n\right)}{\mathsf{\Gamma }\left(\eta +ϵ+2n\right)}}{\xi }^{-\lambda -\eta -ϵ-2n}\hfill \\ & =& {\displaystyle \frac{\mathsf{\Gamma }\left({\chi }_2\right)}{2^{ϵ}\mathsf{\Gamma }\left({\chi }_1\right)}}{\xi }^{-\lambda -ϵ-\eta }\sum _{n=0}^{\infty }{\displaystyle \frac{\mathsf{\Gamma }\left({\chi }_1+{\sigma }_{2}n\right)\mathsf{\Gamma }\left(\lambda +\eta +ϵ+2n\right)}{\mathsf{\Gamma }\left(n\eta +ϵ+\frac{\varphi +1}{2}\right)\mathsf{\Gamma }\left({\chi }_2+{\sigma }_{1}n\right)\mathsf{\Gamma }\left(\eta +ϵ+2n\right)}}{\displaystyle \frac{{\left(\frac{-\omega }{4{\xi }^2}\right)}^n}{n!}}.\hfill \end{array}$$

In view of the definition of the Fox-wright function (2.7), we arrive at the desired result. □

4. Fractional Kinetic Equation

In light of the kinetic equation’s effectiveness and importance in certain astrophysical problems, the authors devise a new generalised form of the fractional kinetic equation involving a newly defined Bessel function of the first kind.

Haubold and Mathai [21] have formulated a functional differential equation that relates the rate of reaction change, the rate of destruction, and the rate of production in the following manner:

$${\displaystyle \frac{dN}{dt}}=-d\left(N_t\right)+p\left(N_t\right),$$

(4.1)

where $N=N\left(t\right)$ is the rate of reaction, $d=d\left(N\right)$ is the rate of destruction, ${\sigma }_1=p\left(N\right)$ is the rate of production, and $N_t\left(t^{*}\right)=N\left(t-t^{*}\right),t^{*}>0.$

When spatial fluctuations or inhomogeneities in the quantity $N\left(t\right)$ are ignored, Haubold and Mathai studied a special case of the equation, which is given by the equation.

$${\displaystyle \frac{d{N}_i}{dt}}=-{\omega }_i{N}_i\left(t\right),$$

(4.2)

together with the initial condition that $N_i\left(t=0\right)=N_0$, is the number of density of species i at time $t=0,c_i>0.$ If the index i is dropped and the typical kinetic equation (4.2) is integrated, we receive

$$N\left(t\right)=N_0-\omega {}_{0}D_t^{-1}N\left(t\right),$$

(4.3)

where ${}_{0}D_t^{-1}$ is the special case of the Riemann-Liouville integral operator ₀$D_t^{-\nu }$ defined in (2.1).

Haubold and Mathai [21] have given the fractional generalization of the standard kinetic equation (4.3) as

$$N\left(t\right)=N_0-{\omega }^{\nu }{}_{0}D_t^{-\nu }N\left(t\right).$$

(4.4)

Then the solution for $N\left(t\right)$ is a Mittag-Leffler function $E_{\nu }\left(.\right)$

$$N\left(t\right)=N_0{E}_{\nu }\left(-{\omega }^{\nu }{t}^{\nu }\right)=N_0\sum _{r=0}^{\infty }{\displaystyle \frac{{\left(-1\right)}^r{\left(ct\right)}^{\nu r}}{\mathsf{\Gamma }\left(\nu r+1\right)}}$$

(4.5)

In addition, Saxena and Kalla [22] thought about the subsequent fractional kinetic equation

$$N\left(t\right)-N_{0}f\left(t\right)=-{\omega }^{\nu }{}_{0}D_t^{-\nu }N\left(t\right),$$

(4.6)

where $f\left(t\right)\in L\left(0,\infty \right).$

We now utilize the Laplace transform technique to obtain the solution for an integral equation more encompassing than the one referenced as (4.6). This is achieved by employing the findings presented in the work by [32].

$$L{\{}_{RL}{D}_t^{-\nu }\psi \left(t\right)\}=s^{-\nu }\Psi \left(s\right),$$

(4.7)

where

$$L\left\{\psi \left(t\right)\right\}=\Psi \left(s\right)=\underset{0}{\overset{\infty }{\int }}{e}^{-st}\psi \left(t\right)dt,\Re \left(s\right)>0.$$

(4.8)

In the following subsection, we solve novel fractional kinetic equations that incorporate the recently introduced generalised Bessel function, as defined in Equation (4.6). Furthermore, we create a variety of distinct special scenarios.

4.1. Solution of Fractional Kinetic Equation

Within this subsection, we explore the resolution of the fractional kinetic equation linked to the generalized Bessel function outlined in section 2.

Remark 4.1. 

The solutions we are about to deduce for the appropriate fractional kinetic equations will be ascertained using the generalized Mittag-Leffler function $E_{ϵ,\nu }\left(x\right)$ introduced by [38], as defined in Equation (2.9).

Theorem 4.1. 

If $d>0,\nu >0,ϵ,\eta ,{\chi }_1,{\chi }_2,\varphi ,\omega \in \mathbb{C},\Re \left(\eta \right)>0,\Re \left(ϵ\right)>0,$ and ${\sigma }_1,{\sigma }_2\in \mathbb{N},$then the solution of the equation

$$N\left(t\right)=N_0{J}_{{\sigma }_1,{\sigma }_2,\varphi ,\omega }^{ϵ,\eta ,{\chi }_1,{\chi }_2}\left(t\right)-d^{\nu }{}_{0}D_t^{-\nu }N\left(t\right),$$

(4.9)

is given by the following formula:

$$N\left(t\right)=N_0\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-\omega \right)}^n{\left({\chi }_1\right)}_{{\sigma }_{2}n}\mathsf{\Gamma }\left(ϵ+2n+1\right)}{n!\mathsf{\Gamma }\left(n\eta +ϵ+\frac{\varphi +1}{2}\right){\left({\chi }_2\right)}_{{\sigma }_{1}n}}}{\left({\displaystyle \frac{t}{2}}\right)}^{ϵ+2n}{E}_{\nu ,ϵ+2n+1}\left(-d^{\nu }{t}^{\nu }\right)$$

(4.10)

where $E_{\nu ,n+2i+1}\left(.\right)$ is the generalized Mittag-Leffler function.

Proof. 

By employing the Laplace transform to both sides of (4.9) and utilizing (4.7), we arrive at the result

$$L\left\{N\left(t\right)\right\}=N_{0}L\left\{J_{{\sigma }_1,{\sigma }_2,\varphi ,\omega }^{ϵ,\eta ,{\chi }_1,{\chi }_2}\left(t\right)\right\}-d^{\nu }L\left\{{}_{0}D_t^{-\nu }N\left(t\right)\right\}$$

$$N\left(s\right)=N_0\underset{0}{\overset{\infty }{\int }}{e}^{-st}\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-\omega \right)}^n{\left({\chi }_1\right)}_{{\sigma }_{2}n}}{n!\mathsf{\Gamma }\left(n\eta +ϵ+\frac{\varphi +1}{2}\right){\left({\chi }_2\right)}_{{\sigma }_{1}n}}}{\left({\displaystyle \frac{t}{2}}\right)}^{ϵ+2n}dt-d^{\nu }{s}^{-\nu }N\left(s\right)$$

Hence,

$$\begin{array}{ccc}\hfill N\left(s\right)\left[1+{\left({\displaystyle \frac{s}{d}}\right)}^{-\nu }\right]& =& N_0\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-\omega \right)}^n{\left({\chi }_1\right)}_{{\sigma }_{2}n}{\left(\frac{1}{2}\right)}^{ϵ+2n}}{n!\mathsf{\Gamma }\left(n\eta +ϵ+\frac{\varphi +1}{2}\right){\left({\chi }_2\right)}_{{\sigma }_{1}n}}}\underset{0}{\overset{\infty }{\int }}{e}^{-st}{t}^{ϵ+2n}dt\hfill \\ & =& N_0\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-\omega \right)}^n{\left({\chi }_1\right)}_{{\sigma }_{2}n}{\left(\frac{1}{2}\right)}^{ϵ+2n}}{n!\mathsf{\Gamma }\left(n\eta +ϵ+\frac{\varphi +1}{2}\right){\left({\chi }_2\right)}_{{\sigma }_{1}n}}}{\displaystyle \frac{\mathsf{\Gamma }\left(ϵ+2n+1\right)}{s^{ϵ+2n+1}}}\hfill \end{array}$$

Therefore,

$$N\left(s\right)=N_0\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-\omega \right)}^n{\left({\chi }_1\right)}_{{\sigma }_{2}n}\mathsf{\Gamma }\left(ϵ+2n+1\right){\left(\frac{1}{2}\right)}^{ϵ+2n}}{n!\mathsf{\Gamma }\left(n\eta +ϵ+\frac{\varphi +1}{2}\right){\left({\chi }_2\right)}_{{\sigma }_{1}n}}}{\displaystyle \frac{1}{s^{ϵ+2n+1}}}{\displaystyle \frac{1}{\left[1+{\left(\frac{s}{d}\right)}^{-\nu }\right]}}$$

$$N\left(s\right)=N_0\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-\omega \right)}^n{\left({\chi }_1\right)}_{{\sigma }_{2}n}\mathsf{\Gamma }\left(ϵ+2n+1\right){\left(\frac{1}{2}\right)}^{ϵ+2n}}{n!\mathsf{\Gamma }\left(n\eta +ϵ+\frac{\varphi +1}{2}\right){\left({\chi }_2\right)}_{{\sigma }_{1}n}}}\sum _{r=0}^{\infty }{\left(-1\right)}^r{d}^{\nu r}{s}^{-\left(ϵ+2n+\nu r+1\right)}$$

(4.11)

Taking Laplace inverse of (4.11) and using $L^{-1}\left[s^{-\nu }\right]={\displaystyle \frac{t^{\nu -1}}{\mathsf{\Gamma }\left(\nu \right)}}$, we obtain

$$\begin{array}{ccc}\hfill N\left(s\right)& =& N_0\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-\omega \right)}^n{\left({\chi }_1\right)}_{{\sigma }_{2}n}\mathsf{\Gamma }\left(ϵ+2n+1\right){\left(\frac{1}{2}\right)}^{ϵ+2n}}{n!\mathsf{\Gamma }\left(n\eta +ϵ+\frac{\varphi +1}{2}\right){\left({\chi }_2\right)}_{{\sigma }_{1}n}}}\sum _{r=0}^{\infty }{\left(-d^{\nu }\right)}^r{\displaystyle \frac{t^{ϵ+2n+\nu r}}{\mathsf{\Gamma }\left(ϵ+2n+\nu r+1\right)}}\hfill \\ & =& N_0\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-\omega \right)}^n{\left({\chi }_1\right)}_{{\sigma }_{2}n}\mathsf{\Gamma }\left(ϵ+2n+1\right)}{n!\mathsf{\Gamma }\left(n\eta +ϵ+\frac{\varphi +1}{2}\right){\left({\chi }_2\right)}_{{\sigma }_{1}n}}}{\left({\displaystyle \frac{t}{2}}\right)}^{ϵ+2n}\sum _{r=0}^{\infty }{\displaystyle \frac{{\left(-d^{\nu }{t}^{\nu }\right)}^r}{\mathsf{\Gamma }\left(ϵ+2n+\nu r+1\right)}}.\hfill \end{array}$$

In view of (2.9), we get the required result. □

Theorem 4.2. 

If $d>0,\nu >0,ϵ,\eta ,{\chi }_1,{\chi }_2,\varphi ,\omega \in \mathbb{C},\Re \left(\eta \right)>0,\Re \left(ϵ\right)>0,$ and ${\sigma }_1,{\sigma }_2\in \mathbb{N},$then the solution of the equation

$$N\left(t\right)=N_0{J}_{{\sigma }_1,{\sigma }_2,\varphi ,\omega }^{ϵ,\eta ,{\chi }_1,{\chi }_2}\left(d^{\nu }{t}^{\nu }\right)-d^{\nu }{}_{0}D_t^{-\nu }N\left(t\right),$$

(4.12)

is given by the following formula:

$$N\left(t\right)=N_0\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-\omega \right)}^n{\left({\chi }_1\right)}_{{\sigma }_{2}n}\mathsf{\Gamma }\left(\left(ϵ+2n\right)\nu +1\right)}{n!\mathsf{\Gamma }\left(n\eta +ϵ+\frac{\varphi +1}{2}\right){\left({\chi }_2\right)}_{{\sigma }_{1}n}}}{\left({\displaystyle \frac{d^{\nu }{t}^{\nu }}{2}}\right)}^{ϵ+2n}{E}_{\nu ,\left(ϵ+2n\right)\nu +1}\left(-d^{\nu }{t}^{\nu }\right)$$

(4.13)

Proof. 

Applying the laplace transform to the both sides of (4.12), and using (4.7), we obtain

$$L\left\{N\left(t\right)\right\}=N_{0}L\left\{J_{{\sigma }_1,{\sigma }_2,\varphi ,\omega }^{ϵ,\eta ,{\chi }_1,{\chi }_2}\left(d^{\nu }{t}^{\nu }\right)\right\}-d^{\nu }L\left\{{}_{0}D_t^{-\nu }N\left(t\right)\right\}$$

$$N\left(s\right)=N_0\underset{0}{\overset{\infty }{\int }}{e}^{-st}\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-\omega \right)}^n{\left({\chi }_1\right)}_{{\sigma }_{2}n}}{n!\mathsf{\Gamma }\left(n\eta +ϵ+\frac{\varphi +1}{2}\right){\left({\chi }_2\right)}_{{\sigma }_{1}n}}}{\left({\displaystyle \frac{d^{\nu }{t}^{\nu }}{2}}\right)}^{ϵ+2n}dt-d^{\nu }{s}^{-\nu }N\left(s\right)$$

Hence,

$$\begin{array}{ccc}\hfill N\left(s\right)\left[1+{\left({\displaystyle \frac{s}{d}}\right)}^{-\nu }\right]& =& N_0\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-\omega \right)}^n{\left({\chi }_1\right)}_{{\sigma }_{2}n}{\left(\frac{d^{\nu }}{2}\right)}^{ϵ+2n}}{n!\mathsf{\Gamma }\left(n\eta +ϵ+\frac{\varphi +1}{2}\right){\left({\chi }_2\right)}_{{\sigma }_{1}n}}}\underset{0}{\overset{\infty }{\int }}{e}^{-st}{t}^{\left(ϵ+2n\right)\nu }dt\hfill \\ & =& N_0\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-\omega \right)}^n{\left({\chi }_1\right)}_{{\sigma }_{2}n}{\left(\frac{d^{\nu }}{2}\right)}^{ϵ+2n}}{n!\mathsf{\Gamma }\left(n\eta +ϵ+\frac{\varphi +1}{2}\right){\left({\chi }_2\right)}_{{\sigma }_{1}n}}}{\displaystyle \frac{\mathsf{\Gamma }\left(\left(ϵ+2n\right)\nu +1\right)}{s^{\left(ϵ+2n\right)\nu +1}}}\hfill \end{array}$$

Therefore,

$$N\left(s\right)=N_0\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-\omega \right)}^n{\left({\chi }_1\right)}_{{\sigma }_{2}n}\mathsf{\Gamma }\left(\left(ϵ+2n\right)\nu +1\right){\left(\frac{d^{\nu }}{2}\right)}^{ϵ+2n}}{n!\mathsf{\Gamma }\left(n\eta +ϵ+\frac{\varphi +1}{2}\right){\left({\chi }_2\right)}_{{\sigma }_{1}n}}}{\displaystyle \frac{1}{s^{\left(ϵ+2n\right)\nu +1}}}{\displaystyle \frac{1}{\left[1+{\left(\frac{s}{d}\right)}^{-\nu }\right]}}$$

$$N\left(s\right)=N_0\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-\omega \right)}^n{\left({\chi }_1\right)}_{{\sigma }_{2}n}\mathsf{\Gamma }\left(\left(ϵ+2n\right)\nu +1\right){\left(\frac{d^{\nu }}{2}\right)}^{ϵ+2n}}{n!\mathsf{\Gamma }\left(n\eta +ϵ+\frac{\varphi +1}{2}\right){\left({\chi }_2\right)}_{{\sigma }_{1}n}}}\sum _{r=0}^{\infty }{\left(-1\right)}^r{d}^{\nu r}{s}^{-\left(\left(ϵ+2n+r\right)\nu +1\right)}$$

(4.14)

Taking Laplace inverse of (4.14) and using $L^{-1}\left[s^{-\nu }\right]={\displaystyle \frac{t^{\nu -1}}{\mathsf{\Gamma }\left(\nu \right)}}$, we obtain

$$\begin{array}{ccc}\hfill N\left(s\right)& =& N_0\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-\omega \right)}^n{\left({\chi }_1\right)}_{{\sigma }_{2}n}\mathsf{\Gamma }\left(\left(ϵ+2n\right)\nu +1\right){\left(\frac{d^{\nu }}{2}\right)}^{ϵ+2n}}{n!\mathsf{\Gamma }\left(n\eta +ϵ+\frac{\varphi +1}{2}\right){\left({\chi }_2\right)}_{{\sigma }_{1}n}}}\sum _{r=0}^{\infty }{\left(-d^{\nu }\right)}^r{\displaystyle \frac{t^{\left(n+2i+r\right)\nu }}{\mathsf{\Gamma }\left(\left(n+2i\right)\nu +r\nu +1\right)}}\hfill \\ & =& N_0\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-\omega \right)}^n{\left({\chi }_1\right)}_{{\sigma }_{2}n}\mathsf{\Gamma }\left(\left(ϵ+2n\right)\nu +1\right)}{n!\mathsf{\Gamma }\left(n\eta +ϵ+\frac{\varphi +1}{2}\right){\left({\chi }_2\right)}_{{\sigma }_{1}n}}}{\left({\displaystyle \frac{d^{\nu }{t}^{\nu }}{2}}\right)}^{ϵ+2n}\sum _{r=0}^{\infty }{\displaystyle \frac{{\left(-d^{\nu }{t}^{\nu }\right)}^r}{\mathsf{\Gamma }\left(\left(ϵ+2n\right)\nu +\nu r+1\right)}}\hfill \\ & =& N_0\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-\omega \right)}^n{\left({\chi }_1\right)}_{{\sigma }_{2}n}\mathsf{\Gamma }\left(\left(ϵ+2n\right)\nu +1\right)}{n!\mathsf{\Gamma }\left(n\eta +ϵ+\frac{\varphi +1}{2}\right){\left({\chi }_2\right)}_{{\sigma }_{1}n}}}{\left({\displaystyle \frac{d^{\nu }{t}^{\nu }}{2}}\right)}^{ϵ+2n}{E}_{\nu ,\left(ϵ+2n\right)\nu +1}\left(-d^{\nu }{t}^{\nu }\right),\hfill \end{array}$$

this completes the proof of theorem 4.1. □

Theorem 4.3. 

If $d>0,a>0,\nu >0,ϵ,\eta ,{\chi }_1,{\chi }_2,\varphi ,\omega \in \mathbb{C},\Re \left(\eta \right)>0,\Re \left(ϵ\right)>0,$${\sigma }_1,{\sigma }_2\in \mathbb{N},$ and $a\ne d,$ then the formula

$$N\left(t\right)=N_0\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-\omega \right)}^n{\left({\chi }_1\right)}_{{\sigma }_{2}n}\mathsf{\Gamma }\left(\left(ϵ+2n\right)\nu +1\right)}{n!\mathsf{\Gamma }\left(n\eta +ϵ+\frac{\varphi +1}{2}\right){\left({\chi }_2\right)}_{{\sigma }_{1}n}}}{\left({\displaystyle \frac{d^{\nu }{t}^{\nu }}{2}}\right)}^{ϵ+2n}{E}_{\nu ,\left(ϵ+2n\right)\nu +1}\left(-a^{\nu }{t}^{\nu }\right)$$

(4.15)

is a solution of the fractional kinetic equation

$$N\left(t\right)=N_0{J}_{{\sigma }_1,{\sigma }_2,\varphi ,\omega }^{ϵ,\eta ,{\chi }_1,{\chi }_2}\left(d^{\nu }{t}^{\nu }\right)-a^{\nu }{}_{0}D_t^{-\nu }N\left(t\right),$$

(4.16)

Proof. 

The proof of theorem 4.3 is parallel to theorems 4.1 and 4.2, so details of the proof are omitted. □

4.2. Special Cases

(i)

Choosing ${\sigma }_1={\sigma }_2=0,$ and $\eta =1,$ the generalized Bessel function (2.10), $J_{{\sigma }_1,{\sigma }_2,\varphi ,\omega }^{ϵ,\eta ,{\chi }_1,{\chi }_2}\left(t\right)$ reduced to the generalized type of Bessel function of the first kind, ${\omega }_{ϵ,\varphi ,\omega }\left(t\right)$ as we mentioned in (2.11).

Then theorems 4.1, 4.2, and 4.3 reduce to the following corollaries.

Corollary 4.1.  If $d>0,\nu >0,ϵ,\varphi ,\omega \in \mathbb{C},$ and$\Re \left(ϵ\right)>0,$ then the solution of the equation

$$N\left(t\right)=N_0{\omega }_{ϵ,\varphi ,\omega }\left(t\right)-d^{\nu }{}_{0}D_t^{-\nu }N\left(t\right),$$

(4.17)

is given by the following formula:

$$N\left(t\right)=N_0\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-\omega \right)}^n\mathsf{\Gamma }\left(ϵ+2n+1\right)}{n!\mathsf{\Gamma }\left(n+ϵ+\frac{\varphi +1}{2}\right)}}{\left({\displaystyle \frac{t}{2}}\right)}^{ϵ+2n}{E}_{\nu ,ϵ+2n+1}\left(-d^{\nu }{t}^{\nu }\right)$$

(4.18)

Corollary 4.2.  If $d>0,\nu >0,ϵ,\varphi ,\omega \in \mathbb{C},$ and$\Re \left(ϵ\right)>0,$ then the solution of the equation

$$N\left(t\right)=N_0{\omega }_{ϵ,\varphi ,\omega }\left(d^{\nu }{t}^{\nu }\right)-d^{\nu }{}_{0}D_t^{-\nu }N\left(t\right),$$

(4.19)

is given by the following formula:

$$N\left(t\right)=N_0\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-\omega \right)}^n\mathsf{\Gamma }\left(\left(ϵ+2n\right)\nu +1\right)}{n!\mathsf{\Gamma }\left(n+ϵ+\frac{\varphi +1}{2}\right)}}{\left({\displaystyle \frac{d^{\nu }{t}^{\nu }}{2}}\right)}^{ϵ+2n}{E}_{\nu ,\left(ϵ+2n\right)\nu +1}\left(-d^{\nu }{t}^{\nu }\right)$$

(4.20)

Corollary 4.3.  If $d>0,\nu >0,ϵ,\varphi ,\omega \in \mathbb{C},\Re \left(ϵ\right)>0,$ and $a\ne d,$then the formula

$$N\left(t\right)=N_0\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-\omega \right)}^n\mathsf{\Gamma }\left(\left(ϵ+2n\right)\nu +1\right)}{n!\mathsf{\Gamma }\left(n+ϵ+\frac{\varphi +1}{2}\right)}}{\left({\displaystyle \frac{d^{\nu }{t}^{\nu }}{2}}\right)}^{ϵ+2n}{E}_{\nu ,\left(ϵ+2n\right)\nu +1}\left(-a^{\nu }{t}^{\nu }\right)$$

(4.21)

is a solution of the fractional kinetic equation

$$N\left(t\right)=N_0{\omega }_{ϵ,\varphi ,\omega }\left(d^{\nu }{t}^{\nu }\right)-a^{\nu }{}_{0}D_t^{-\nu }N\left(t\right)$$

(4.22)

(ii)

Setting ${\sigma }_1={\sigma }_2=0,$$\eta =1,$ and $\varphi =\omega =1,$ the generalized Bessel function (2.10), $J_{{\sigma }_1,{\sigma }_2,\varphi ,\omega }^{ϵ,\eta ,{\chi }_1,{\chi }_2}\left(t\right)$ reduced to Bessel function of the first kind, $J_{ϵ}\left(t\right)$ as mentioned in (2.12).

Then theorems 4.1, 4.2, and 4.3 reduce to the following corollaries.

Corollary 4.4.  If $d>0,\nu >0,ϵ\in \mathbb{C},$ and$\Re \left(ϵ\right)>0,$then the solution of the equation

$$N\left(t\right)=N_0{J}_{ϵ}\left(t\right)-d^{\nu }{}_{0}D_t^{-\nu }N\left(t\right),$$

(4.23)

is given by the following formula:

$$N\left(t\right)=N_0\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-1\right)}^n\mathsf{\Gamma }\left(ϵ+2n+1\right)}{n!\mathsf{\Gamma }\left(n+ϵ+1\right)}}{\left({\displaystyle \frac{t}{2}}\right)}^{ϵ+2n}{E}_{\nu ,ϵ+2n+1}\left(-d^{\nu }{t}^{\nu }\right)$$

(4.24)

Corollary 4.5.  If $d>0,\nu >0,ϵ\in \mathbb{C},$ and$\Re \left(ϵ\right)>0,$then the solution of the equation

$$N\left(t\right)=N_0{J}_{ϵ}\left(d^{\nu }{t}^{\nu }\right)-d^{\nu }{}_{0}D_t^{-\nu }N\left(t\right),$$

(4.25)

is given by the following formula:

$$N\left(t\right)=N_0\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-1\right)}^n\mathsf{\Gamma }\left(\left(ϵ+2n\right)\nu +1\right)}{n!\mathsf{\Gamma }\left(n+ϵ+1\right)}}{\left({\displaystyle \frac{d^{\nu }{t}^{\nu }}{2}}\right)}^{ϵ+2n}{E}_{\nu ,\left(ϵ+2n\right)\nu +1}\left(-d^{\nu }{t}^{\nu }\right)$$

(4.26)

Corollary 4.6.  If $d>0,\nu >0,ϵ\in \mathbb{C},\Re \left(ϵ\right)>0,$ and $a\ne d,$then the formula

$$N\left(t\right)=N_0\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-1\right)}^n\mathsf{\Gamma }\left(\left(ϵ+2n\right)\nu +1\right)}{n!\mathsf{\Gamma }\left(n+ϵ+1\right)}}{\left({\displaystyle \frac{d^{\nu }{t}^{\nu }}{2}}\right)}^{ϵ+2n}{E}_{\nu ,\left(ϵ+2n\right)\nu +1}\left(-a^{\nu }{t}^{\nu }\right)$$

(4.27)

is a solution of the fractional kinetic equation

$$N\left(t\right)=N_0{J}_{ϵ}\left(d^{\nu }{t}^{\nu }\right)-a^{\nu }{}_{0}D_t^{-\nu }N\left(t\right)$$

(4.28)

(iii)

Choosing ${\sigma }_1={\sigma }_2=0,$ and $\varphi =-\omega =1,$ the generalized Bessel function (2.10), $J_{{\sigma }_1,{\sigma }_2,\varphi ,\omega }^{ϵ,\eta ,{\chi }_1,{\chi }_2}\left(t\right)$ reduced to generalized type of modified Bessel function of the first kind, $I_{ϵ}^{\eta }\left(t\right)$ as mentioned in (2.13).

Then theorems 4.1, 4.2, and 4.3 reduce to the following corollaries.

Corollary 4.7.  If $d>0,\nu >0,ϵ,\eta ,\varphi ,\omega \in \mathbb{C},\Re \left(\eta \right)>0$ and$\Re \left(ϵ\right)>0,$then the solution of the equation

$$N\left(t\right)=N_0{I}_{ϵ}^{\eta }\left(t\right)-d^{\nu }{}_{0}D_t^{-\nu }N\left(t\right),$$

(4.29)

is given by the following formula:

$$N\left(t\right)=N_0\sum _{n=0}^{\infty }{\displaystyle \frac{\mathsf{\Gamma }\left(ϵ+2n+1\right)}{n!\mathsf{\Gamma }\left(n\eta +ϵ+1\right)}}{\left({\displaystyle \frac{t}{2}}\right)}^{ϵ+2n}{E}_{\nu ,ϵ+2n+1}\left(-d^{\nu }{t}^{\nu }\right)$$

(4.30)

Corollary 4.8.  If $d>0,\nu >0,ϵ,\eta ,\varphi ,\omega \in \mathbb{C},\Re \left(\eta \right)>0$ and$\Re \left(ϵ\right)>0,$then the solution of the equation

$$N\left(t\right)=N_0{I}_{ϵ}^{\eta }\left(d^{\nu }{t}^{\nu }\right)-d^{\nu }{}_{0}D_t^{-\nu }N\left(t\right),$$

(4.31)

is given by the following formula:

$$N\left(t\right)=N_0\sum _{n=0}^{\infty }{\displaystyle \frac{\mathsf{\Gamma }\left(\left(ϵ+2n\right)\nu +1\right)}{n!\mathsf{\Gamma }\left(n\eta +ϵ+1\right)}}{\left({\displaystyle \frac{d^{\nu }{t}^{\nu }}{2}}\right)}^{ϵ+2n}{E}_{\nu ,\left(ϵ+2n\right)\nu +1}\left(-d^{\nu }{t}^{\nu }\right)$$

(4.32)

Corollary 4.9.  If $d>0,\nu >0,ϵ,\eta ,\varphi ,\omega \in \mathbb{C},\Re \left(\eta \right)>0,\Re \left(ϵ\right)>0,$ and $a\ne d,$then the formula

$$N\left(t\right)=N_0\sum _{n=0}^{\infty }{\displaystyle \frac{\mathsf{\Gamma }\left(\left(ϵ+2n\right)\nu +1\right)}{n!\mathsf{\Gamma }\left(n\eta +ϵ+1\right)}}{\left({\displaystyle \frac{d^{\nu }{t}^{\nu }}{2}}\right)}^{ϵ+2n}{E}_{\nu ,\left(ϵ+2n\right)\nu +1}\left(-a^{\nu }{t}^{\nu }\right)$$

(4.33)

is a solution of the fractional kinetic equation

$$N\left(t\right)=N_0{I}_{ϵ}^{\eta }\left(d^{\nu }{t}^{\nu }\right)-a^{\nu }{}_{0}D_t^{-\nu }N\left(t\right)$$

(4.34)

(iv)

Choosing ${\sigma }_1={\sigma }_2=0,\eta =1,$ and $\varphi =-\omega =1,$ the generalized Bessel function (2.10), $J_{{\sigma }_1,{\sigma }_2,\varphi ,\omega }^{ϵ,\eta ,{\chi }_1,{\chi }_2}\left(t\right)$ reduced to modified Bessel function of the first kind, $I_{ϵ}\left(t\right)$ as mentioned in (2.14).

Then theorems 4.1, 4.2, and 4.3 reduce to the following corollaries.

Corollary 4.10.  If $d>0,\nu >0,ϵ,\varphi ,\omega \in \mathbb{C},$ and$\Re \left(ϵ\right)>0,$then the solution of the equation

$$N\left(t\right)=N_0{I}_{ϵ}\left(t\right)-d^{\nu }{}_{0}D_t^{-\nu }N\left(t\right),$$

(4.35)

is given by the following formula:

$$N\left(t\right)=N_0\sum _{n=0}^{\infty }{\displaystyle \frac{\mathsf{\Gamma }\left(ϵ+2n+1\right)}{n!\mathsf{\Gamma }\left(n+ϵ+1\right)}}{\left({\displaystyle \frac{t}{2}}\right)}^{ϵ+2n}{E}_{\nu ,ϵ+2n+1}\left(-d^{\nu }{t}^{\nu }\right)$$

(4.36)

Corollary 4.11.  If $d>0,\nu >0,ϵ,\varphi ,\omega \in \mathbb{C},$ and$\Re \left(ϵ\right)>0,$then the solution of the equation

$$N\left(t\right)=N_0{I}_{ϵ}\left(d^{\nu }{t}^{\nu }\right)-d^{\nu }{}_{0}D_t^{-\nu }N\left(t\right),$$

(4.37)

is given by the following formula:

$$N\left(t\right)=N_0\sum _{n=0}^{\infty }{\displaystyle \frac{\mathsf{\Gamma }\left(\left(ϵ+2n\right)\nu +1\right)}{n!\mathsf{\Gamma }\left(n+ϵ+1\right)}}{\left({\displaystyle \frac{d^{\nu }{t}^{\nu }}{2}}\right)}^{ϵ+2n}{E}_{\nu ,\left(ϵ+2n\right)\nu +1}\left(-d^{\nu }{t}^{\nu }\right)$$

(4.38)

Corollary 4.12.  If $d>0,\nu >0,ϵ,\varphi ,\omega \in \mathbb{C},\Re \left(ϵ\right)>0,$ and $a\ne d,$then the formula

$$N\left(t\right)=N_0\sum _{n=0}^{\infty }{\displaystyle \frac{\mathsf{\Gamma }\left(\left(ϵ+2n\right)\nu +1\right)}{n!\mathsf{\Gamma }\left(n+ϵ+1\right)}}{\left({\displaystyle \frac{d^{\nu }{t}^{\nu }}{2}}\right)}^{ϵ+2n}{E}_{\nu ,\left(ϵ+2n\right)\nu +1}\left(-a^{\nu }{t}^{\nu }\right)$$

(4.39)

is a solution of the fractional kinetic equation

$$N\left(t\right)=N_0{I}_{ϵ}\left(d^{\nu }{t}^{\nu }\right)-a^{\nu }{}_{0}D_t^{-\nu }N\left(t\right)$$

(4.40)

(v)

Choosing ${\sigma }_1={\sigma }_2=0,$$\varphi =2,$ and $\omega =1,$ the generalized Bessel function (2.10), $J_{{\sigma }_1,{\sigma }_2,\varphi ,\omega }^{ϵ,\eta ,{\chi }_1,{\chi }_2}\left(t\right)$ reduced to spherical Bessel function, $j_{ϵ}\left(t\right)$ as mentioned in (2.15).

Then theorems 4.1, 4.2, and 4.3 reduce to the following corollaries.

Corollary 4.13.  If $d>0,\nu >0,ϵ,\varphi ,\omega \in \mathbb{C},$ and$\Re \left(ϵ\right)>0,$then the solution of the equation

$$N\left(t\right)=N_0{j}_{ϵ}\left(t\right)-d^{\nu }{}_{0}D_t^{-\nu }N\left(t\right),$$

(4.41)

is given by the following formula:

$$N\left(t\right)=\sqrt{{\displaystyle \frac{\pi }{2}}}{N}_0\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-1\right)}^n\mathsf{\Gamma }\left(ϵ+2n+1\right)}{n!\mathsf{\Gamma }\left(n+ϵ+\frac{3}{2}\right)}}{\left({\displaystyle \frac{t}{2}}\right)}^{ϵ+2n}{E}_{\nu ,ϵ+2n+1}\left(-d^{\nu }{t}^{\nu }\right)$$

(4.42)

Corollary 4.14.  If $d>0,\nu >0,ϵ,\varphi ,\omega \in \mathbb{C},$ and$\Re \left(ϵ\right)>0,$then the solution of the equation

$$N\left(t\right)=N_0{j}_{ϵ}\left(d^{\nu }{t}^{\nu }\right)-d^{\nu }{}_{0}D_t^{-\nu }N\left(t\right),$$

(4.43)

is given by the following formula:

$$N\left(t\right)=\sqrt{{\displaystyle \frac{\pi }{2}}}{N}_0\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-1\right)}^n\mathsf{\Gamma }\left(\left(ϵ+2n\right)\nu +1\right)}{n!\mathsf{\Gamma }\left(n+ϵ+\frac{3}{2}\right)}}{\left({\displaystyle \frac{d^{\nu }{t}^{\nu }}{2}}\right)}^{ϵ+2n}{E}_{\nu ,\left(ϵ+2n\right)\nu +1}\left(-d^{\nu }{t}^{\nu }\right)$$

(4.44)

Corollary 4.15.  If $d>0,\nu >0,ϵ,\varphi ,\omega \in \mathbb{C},\Re \left(ϵ\right)>0,$ and $a\ne d,$then the formula

$$N\left(t\right)=\sqrt{{\displaystyle \frac{\pi }{2}}}{N}_0\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-1\right)}^n\mathsf{\Gamma }\left(\left(ϵ+2n\right)\nu +1\right)}{n!\mathsf{\Gamma }\left(n+ϵ+\frac{3}{2}\right)}}{\left({\displaystyle \frac{d^{\nu }{t}^{\nu }}{2}}\right)}^{ϵ+2n}{E}_{\nu ,\left(ϵ+2n\right)\nu +1}\left(-a^{\nu }{t}^{\nu }\right)$$

(4.45)

is a solution of the fractional kinetic equation

$$N\left(t\right)=N_0{j}_{ϵ}\left(d^{\nu }{t}^{\nu }\right)-a^{\nu }{}_{0}D_t^{-\nu }N\left(t\right)$$

(4.46)

(vi)

Setting $\varphi =\omega =1,$ and ${\sigma }_1=0,$ the generalized Bessel function (2.10), $J_{{\sigma }_1,{\sigma }_2,\varphi ,\omega }^{ϵ,\eta ,{\chi }_1,{\chi }_2}\left(t\right)$ reduced to

$$J_{{\sigma }_1,{\sigma }_2,\varphi ,\omega }^{ϵ,\eta ,{\chi }_1,{\chi }_2}\left(t\right)=\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-1\right)}^n{\left({\chi }_1\right)}_{{\sigma }_{2}n}}{n!\mathsf{\Gamma }\left(n\eta +ϵ+1\right)}}{\left({\displaystyle \frac{t}{2}}\right)}^{ϵ+2n}={\left({\displaystyle \frac{t}{2}}\right)}^{ϵ}{\tilde{J}}_{ϵ,q}^{\eta ,{\chi }_1}\left({\displaystyle \frac{t^2}{4}}\right),$$

(4.47)

where ${\tilde{J}}_{ϵ,q}^{\eta ,{\chi }_1}\left(t\right)$ is the generalized matland Bessel function given in (2.16).

Then Theorems 4.1, 4.2, and 4.3 reduce to the following corollaries.

Corollary 4.16.  If $d>0,\nu >0,ϵ,\eta ,{\chi }_1\in \mathbb{C},\Re \left(\eta \right)>0,\Re \left(ϵ\right)>0,$ and $q\in \mathbb{N},$then the solution of the equation

$$N\left(t\right)=N_0{\left({\displaystyle \frac{t}{2}}\right)}^{ϵ}{\tilde{J}}_{ϵ,q}^{\eta ,{\chi }_1}\left({\displaystyle \frac{t^2}{4}}\right)-d^{\nu }{}_{0}D_t^{-\nu }N\left(t\right),$$

(4.48)

is given by the following formula:

$$N\left(t\right)=N_0\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-1\right)}^n{\left({\chi }_1\right)}_{{\sigma }_{2}n}\mathsf{\Gamma }\left(ϵ+2n+1\right)}{n!\mathsf{\Gamma }\left(n\eta +ϵ+1\right)}}{\left({\displaystyle \frac{t}{2}}\right)}^{ϵ+2n}{E}_{\nu ,ϵ+2n+1}\left(-d^{\nu }{t}^{\nu }\right)$$

(4.49)

Corollary 4.17.  If $d>0,\nu >0,ϵ,\eta ,{\chi }_1\in \mathbb{C},\Re \left(\eta \right)>0,\Re \left(ϵ\right)>0,$ and $q\in \mathbb{N},$then the solution of the equation

$$N\left(t\right)=N_0{\left({\displaystyle \frac{d^{\nu }{t}^{\nu }}{2}}\right)}^{ϵ}{\tilde{J}}_{ϵ,q}^{\eta ,{\chi }_1}\left({\displaystyle \frac{d^{2\nu }{t}^{2\nu }}{4}}\right)-d^{\nu }{}_{0}D_t^{-\nu }N\left(t\right),$$

(4.50)

is given by the following formula:

$$N\left(t\right)=N_0\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-1\right)}^n{\left({\chi }_1\right)}_{{\sigma }_{2}n}\mathsf{\Gamma }\left(ϵ+2n+1\right)}{n!\mathsf{\Gamma }\left(n\eta +ϵ+1\right)}}{\left({\displaystyle \frac{d^{\nu }{t}^{\nu }}{2}}\right)}^{ϵ+2n}{E}_{\nu ,\left(ϵ+2n\right)\nu +1}\left(-d^{\nu }{t}^{\nu }\right)$$

(4.51)

Corollary 4.18.  If $d>0,\nu >0,ϵ,\eta ,{\chi }_1\in \mathbb{C},\Re \left(\eta \right)>0,\Re \left(ϵ\right)>0,$$q\in \mathbb{N},$ and $a\ne d,$then the formula

$$N\left(t\right)=N_0\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-1\right)}^n{\left({\chi }_1\right)}_{{\sigma }_{2}n}\mathsf{\Gamma }\left(ϵ+2n+1\right)}{n!\mathsf{\Gamma }\left(n\eta +ϵ+1\right)}}{\left({\displaystyle \frac{d^{\nu }{t}^{\nu }}{2}}\right)}^{ϵ+2n}{E}_{\nu ,\left(ϵ+2n\right)\nu +1}\left(-a^{\nu }{t}^{\nu }\right)$$

(4.52)

is a solution of the fractional kinetic equation

$$N\left(t\right)=N_0{\left({\displaystyle \frac{d^{\nu }{t}^{\nu }}{2}}\right)}^{ϵ}{\tilde{J}}_{ϵ,q}^{\eta ,{\chi }_1}\left({\displaystyle \frac{d^{2\nu }{t}^{2\nu }}{4}}\right)-a^{\nu }{}_{0}D_t^{-\nu }N\left(t\right)$$

(4.53)

(vii)

Setting $\varphi =\omega =1,$ and ${\sigma }_1={\sigma }_2=0,$ the generalized Bessel function (2.10), $J_{{\sigma }_1,{\sigma }_2,\varphi ,\omega }^{ϵ,\eta ,{\chi }_1,{\chi }_2}\left(t\right)$ reduced to

$$J_{{\sigma }_1,{\sigma }_2,\varphi ,\omega }^{ϵ,\eta ,{\chi }_1,{\chi }_2}\left(t\right)=\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-1\right)}^n}{n!\mathsf{\Gamma }\left(n\eta +ϵ+1\right)}}{\left({\displaystyle \frac{t}{2}}\right)}^{ϵ+2n}={\left({\displaystyle \frac{t}{2}}\right)}^{ϵ}{\tilde{J}}_{ϵ}^{\eta }\left({\displaystyle \frac{t^2}{4}}\right),$$

(4.54)

where ${\tilde{J}}_{ϵ}^{\eta }\left(t\right)$ is matland Bessel function given in (2.17).

Then theorems 4.1, 4.2, and 4.3 reduce to the following corollaries.

Corollary 4.19.  If $d>0,\nu >0,ϵ,\eta \in \mathbb{C},\Re \left(\eta \right)>0,$ and $\Re \left(ϵ\right)>0,$then the solution of the equation

$$N\left(t\right)=N_0{\left({\displaystyle \frac{t}{2}}\right)}^{ϵ}{\tilde{J}}_{ϵ}^{\eta }\left({\displaystyle \frac{t^2}{4}}\right)-d^{\nu }{}_{0}D_t^{-\nu }N\left(t\right),$$

(4.55)

is given by the following formula:

$$N\left(t\right)=N_0\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-1\right)}^n\mathsf{\Gamma }\left(ϵ+2n+1\right)}{n!\mathsf{\Gamma }\left(n\eta +ϵ+1\right)}}{\left({\displaystyle \frac{t}{2}}\right)}^{ϵ+2n}{E}_{\nu ,ϵ+2n+1}\left(-d^{\nu }{t}^{\nu }\right)$$

(4.56)

Corollary 4.20.  If $d>0,\nu >0,ϵ,\eta \in \mathbb{C},\Re \left(\eta \right)>0,$ and $\Re \left(ϵ\right)>0,$then the solution of the equation

$$N\left(t\right)=N_0{\left({\displaystyle \frac{d^{\nu }{t}^{\nu }}{2}}\right)}^{ϵ}{\tilde{J}}_{ϵ}^{\eta }\left({\displaystyle \frac{d^{2\nu }{t}^{2\nu }}{4}}\right)-d^{\nu }{}_{0}D_t^{-\nu }N\left(t\right),$$

(4.57)

is given by the following formula:

$$N\left(t\right)=N_0\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-1\right)}^n\mathsf{\Gamma }\left(ϵ+2n+1\right)}{n!\mathsf{\Gamma }\left(n\eta +ϵ+1\right)}}{\left({\displaystyle \frac{d^{\nu }{t}^{\nu }}{2}}\right)}^{ϵ+2n}{E}_{\nu ,\left(ϵ+2n\right)\nu +1}\left(-d^{\nu }{t}^{\nu }\right)$$

(4.58)

Corollary 4.21.  If $d>0,\nu >0,ϵ,\eta \in \mathbb{C},\Re \left(\eta \right)>0,$ $\Re \left(ϵ\right)>0,$ and $a\ne d,$then the formula

$$N\left(t\right)=N_0\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(-1\right)}^n\mathsf{\Gamma }\left(ϵ+2n+1\right)}{n!\mathsf{\Gamma }\left(n\eta +ϵ+1\right)}}{\left({\displaystyle \frac{d^{\nu }{t}^{\nu }}{2}}\right)}^{ϵ+2n}{E}_{\nu ,\left(ϵ+2n\right)\nu +1}\left(-a^{\nu }{t}^{\nu }\right)$$

(4.59)

is a solution of the fractional kinetic equation

$$N\left(t\right)=N_0{\left({\displaystyle \frac{d^{\nu }{t}^{\nu }}{2}}\right)}^{ϵ}{\tilde{J}}_{ϵ}^{\eta }\left({\displaystyle \frac{d^{2\nu }{t}^{2\nu }}{4}}\right)-a^{\nu }{}_{0}D_t^{-\nu }N\left(t\right)$$

(4.60)

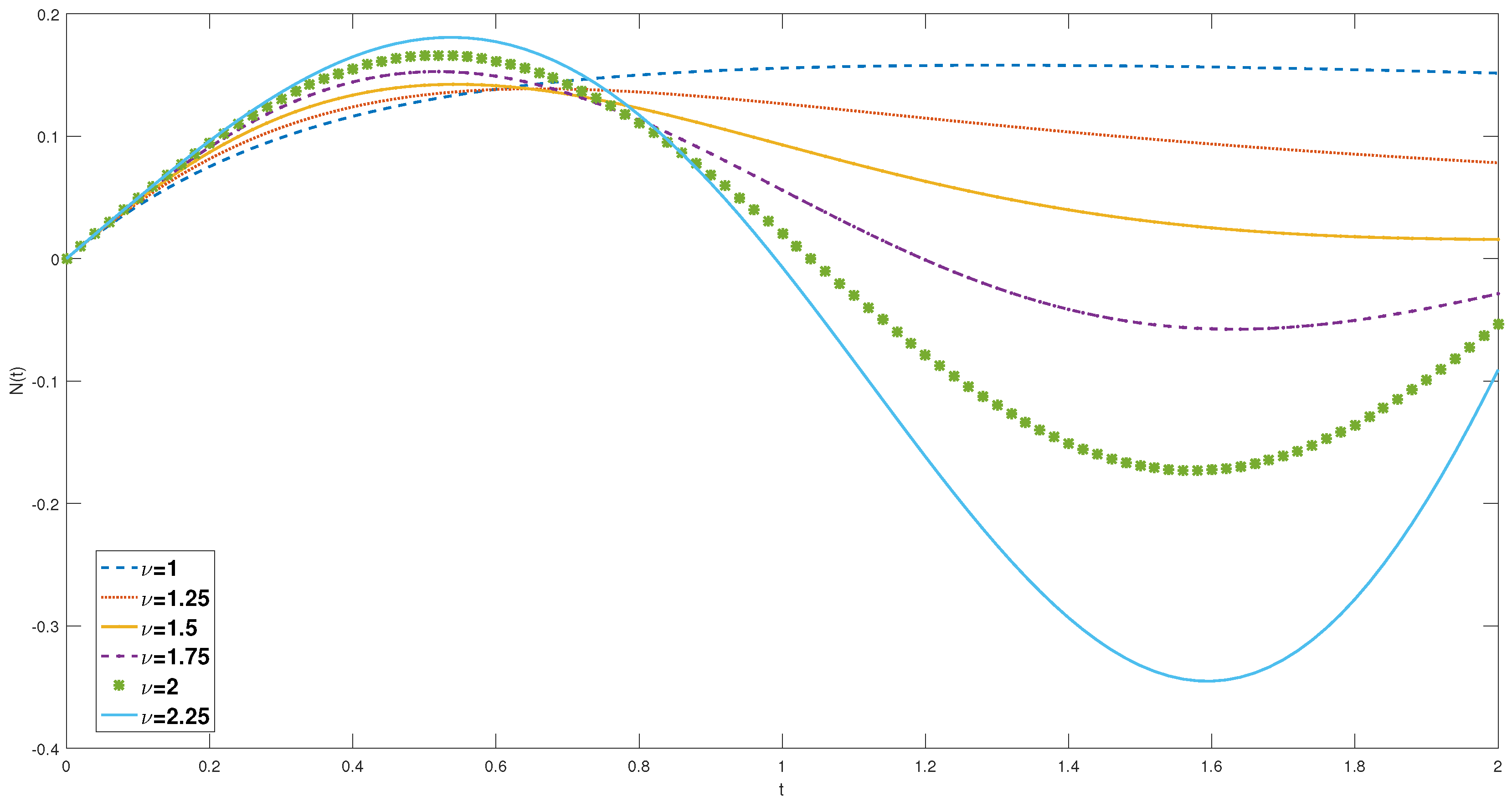
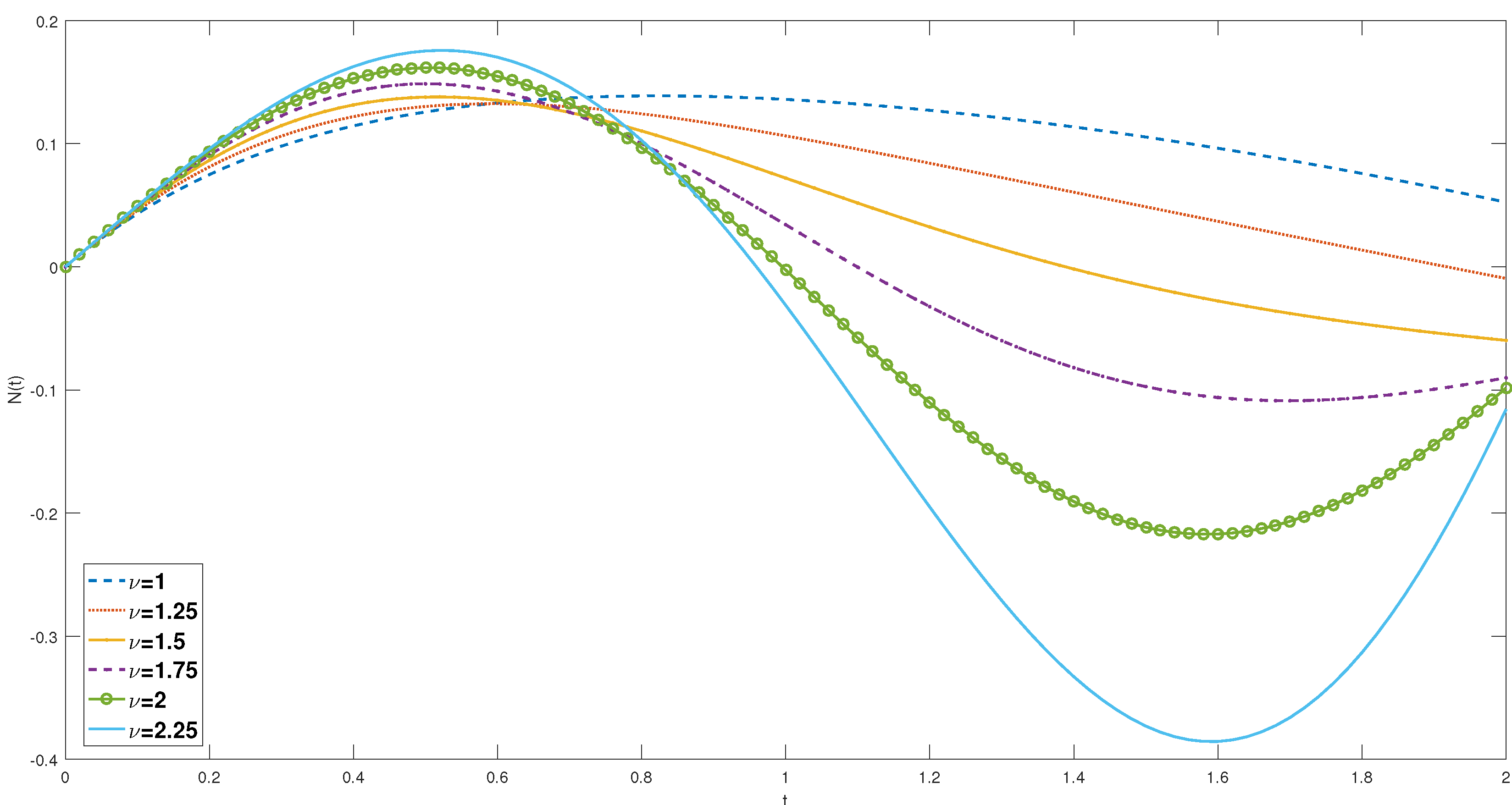
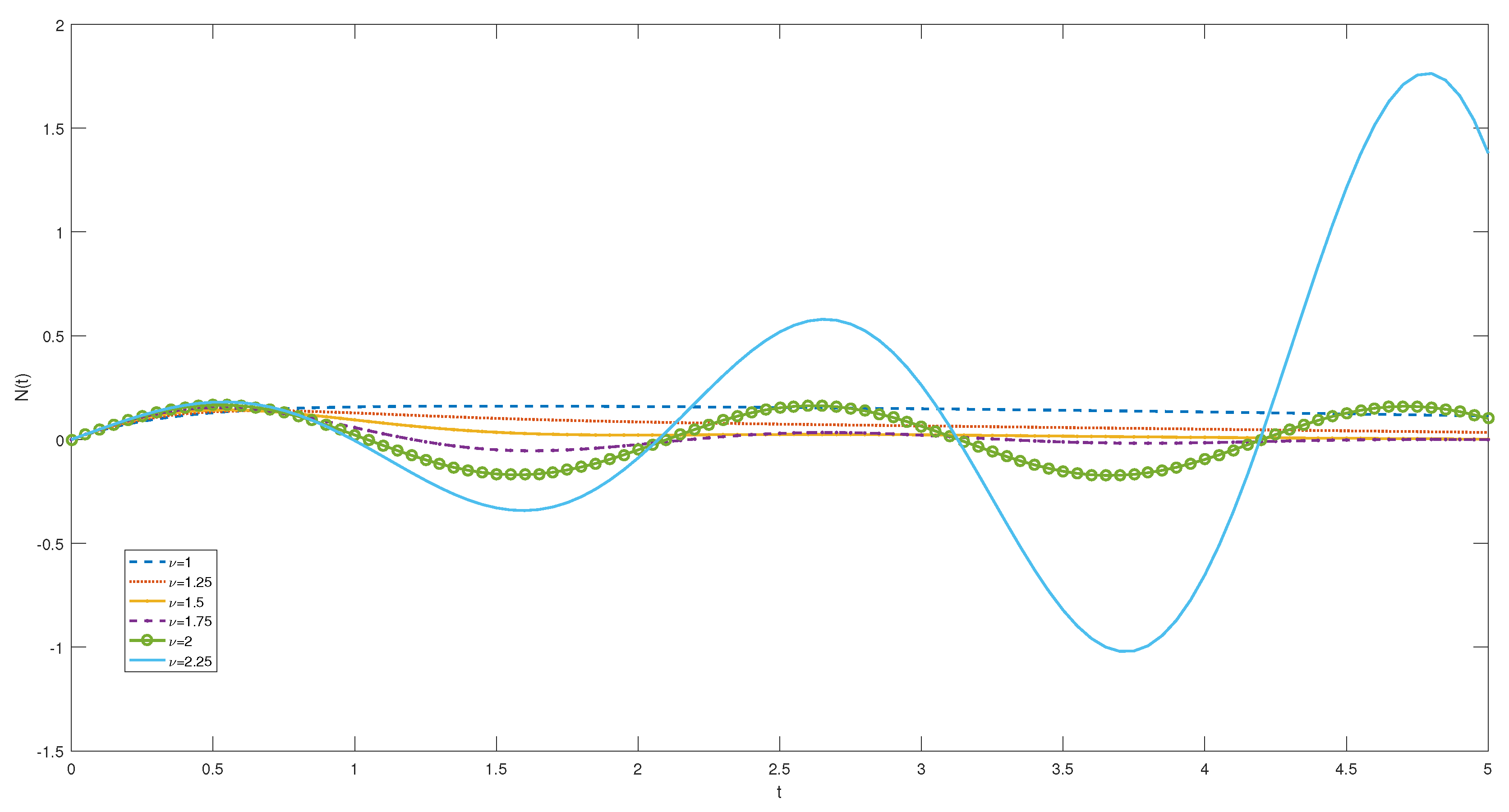
4.3. Graphical Interpretation

In this subsection, we present graphical representations that illustrate the main results obtained in Theorems 4.1, 4.2, and 4.3. These graphs depict the solution curves of equation (4.9) for various parameter values. Specifically, we consider the parameters $N_0=\omega =\eta =2$, ${\sigma }_1={\sigma }_2=ϵ=1$, $\varphi =d=3$, and $\nu =1,1.25,1.5,1.75,2,\mathrm{and}2.25$. The solution curves are shown in Figure 1 for the time interval $t=0:0.02:2$, where ${\chi }_1=1$ and ${\chi }_2=2$. Furthermore, Figure 2 presents the curves for the same parameter values, but with ${\chi }_1=4$ and ${\chi }_2=1$, and for the time interval $t=0:0.02:2$. Additionally, Figure 3 displays the curves for the time interval $t=0:0.05:5$, with ${\chi }_1=1$ and ${\chi }_2=4$.

From these figures, it is evident that $N\left(t\right)=0$ at the initial time $t=0$ for different parameter values. Moreover, it is observed that selecting $a=d$ in Theorems (2.16) and (2.18) yields identical solutions. Our observations also reveal that $N\left(t\right)$ exhibits both positive and negative values for different parameter settings.

5. Conclusion

The inclusion of convolution integrals with power-law or exponential-law memory kernels through fractional derivatives enhances the significance of fractional differential equations in elucidating the memory effects exhibited by complex systems.

The objective of this paper was to introduce a novel generalized Bessel function and establish formulas for fractional integrals and fractional derivatives. We conducted a comprehensive investigation of several intriguing fractional kinetic equations, considering a range of special functions [22,29,30,31,32]). Furthermore, we proposed a new and generalized solution for the fractional kinetic equation associated with the introduced generalized Bessel function, which we analyzed utilizing the Laplace integral transform technique. The main findings can serve as a basis for constructing a diverse set of kinetic equations and their potential solutions. Based on our graphical results, it can be concluded that $N\left(t\right)$ exhibits either positive or negative values across different parameter values and time intervals. The results obtained in this study have significant implications, as they have the potential to generate numerous established findings and potentially uncover new ones.

Our future work will be dedicated to further exploring and studying the recently introduced generalized Bessel function in the realm of solving fractional differential equations. We recognize the potential of this function in offering solutions to a wide array of fractional differential equations, which necessitates thorough investigation. Our focus will be on examining its properties, analyzing its behavior under different parameter configurations, and assessing its applicability across various scientific and engineering domains. Furthermore, we will investigate numerical methods and algorithms that can efficiently compute solutions involving the generalized Bessel function (see our previous work [6]). The aim of this research is to enhance the understanding and utilization of this function in solving intricate fractional differential equations, thereby advancing the field of fractional calculus.