Enhancing K-Means Clustering Accuracy Through Modified Robust Scaling Technique

Maradana Durga Venkata Prasad; Srikanth T

doi:10.20944/preprints202411.1245.v1

Submitted:

16 November 2024

Posted:

18 November 2024

You are already at the latest version

Abstract

Data normalization is a critical step in machine learning workflows, particularly for clustering algorithms sensitive to feature scaling. This paper introduces a modified Robust Scaling method defined as X1= X−median(X) / mean(X), which combines the resilience of the median with the global sensitivity of the mean. The proposed scaling method is evaluated on standard datasets, including Iris and Wine, using K-means clustering. Results demonstrate that X1 scaling effectively handles outliers, enhances clustering accuracy. Additionally, we provide a detailed analysis of sorted label accuracy, confusion matrices, and the optimal random initialization seed for clustering. The findings highlight the potential of X1 scaling as a robust alternative for preprocessing in machine learning tasks.

Keywords:

Clustering Algorithms

;

K-Means Clustering

;

Robust Scaling

;

Confusion matrix

;

Clustering accuracy

;

Machine Learning

Subject:

Computer Science and Mathematics - Computer Science

I. INTRODUCTION

1. Background

Clustering is a fundamental technique in data analysis and machine learning that plays a crucial role in uncovering hidden patterns, organizing information, and facilitating decision-making [1]. Its importance can be highlighted through the following aspects:

a. Unsupervised Learning Foundation

Clustering is a cornerstone of unsupervised learning, where the goal is to analyze and group data without predefined labels. It helps in discovering the intrinsic structure of data, making it valuable for exploring datasets where labeled information is unavailable or expensive to obtain [2].

b. Pattern Discovery and Knowledge Extraction

Clustering algorithms group similar data points based on defined criteria (e.g., distance, density, or connectivity). This allows analysts to Identify natural groupings or segments in the data and Extract meaningful insights, such as customer segments, disease subtypes, or document topics [3].

c. Data Preprocessing and Feature Engineering

Clustering can be used as a preprocessing step to improve other machine learning tasks by

Reducing the complexity of large datasets by grouping similar instances and creating additional features, such as cluster assignments, to enhance supervised learning models[4].

d. Applications Across Domains [5]

Clustering has a wide range of applications, including:

Customer Segmentation: Grouping customers based on purchasing behavior or preferences to tailor marketing strategies.

Image and Document Analysis: Organizing similar images or documents for efficient retrieval or topic modeling.

Biology and Medicine: Identifying subgroups of genes, proteins, or patients with similar characteristics in genomics and clinical research.

Anomaly Detection: Detecting outliers by identifying clusters and isolating data points that do not belong to any group.

e. Facilitating Data Visualization

High-dimensional data can be challenging to interpret. Clustering simplifies this by summarizing data into distinct groups, which can be visualized to understand relationships and trends within the dataset [6].

f. Enhancing Machine Learning Models

In semi-supervised learning, clustering can generate pseudo-labels for partially labeled datasets, aiding model training. In ensemble learning, clustering can be used to identify diverse subsets of data for robust model building [7].

g. Scalability for Big Data

Modern clustering algorithms are designed to handle massive datasets efficiently. This scalability makes clustering an essential tool in big data analytics for organizing and interpreting large-scale information [8].

2. Motivation

Explain the role of feature scaling in clustering and the limitations of traditional scaling methods in K-means clustering.

The Role of Feature Scaling in Clustering

Feature scaling is a crucial preprocessing step in clustering, particularly for algorithms like K-means, that rely on distance-based metrics (e.g., Euclidean distance). The importance of feature scaling in clustering is highlighted by the following points:

a. Equal Contribution of Features: Clustering algorithms treat all features equally when computing distances. If features are on different scales (e.g., age in years vs. income in thousands), features with larger scales dominate the distance calculations, skewing the clustering results [9].

b. Improved Convergence: Scaled features ensure smoother and faster convergence of K-means, as the algorithm optimizes the distance between data points and cluster centroids [10].

c. Prevention of Biased Clusters: Without scaling, features with larger ranges disproportionately influence the assignment of points to clusters, leading to biased and suboptimal clusters [11].

d. Comparability Across Dimensions: Scaling ensures that features measured in different units (e.g., meters, kilograms) are comparable, facilitating accurate clustering [12].

3. Limitations of Traditional Scaling Methods in K-means Clustering

Despite their widespread use, traditional scaling methods like Min-Max Scaling, Z-score Normalization, and Max-Abs Scaling have limitations when applied to K-means clustering:

a. Sensitivity to Outliers[13]

Min-Max Scaling: Scales features to a fixed range (e.g., [0, 1]) but is highly sensitive to outliers. Extreme values in the data can compress most of the data points into a small range, distorting the distance calculations [14].

Z-score Normalization: Standardizes features by subtracting the mean and dividing by the standard deviation. Outliers can significantly affect the mean and standard deviation, leading to biased scaling [15].

b. Assumption of Data Distribution

Traditional methods often assume a Gaussian or uniform distribution of data. However, real-world data may exhibit skewness or non-uniform distributions, leading to suboptimal scaling.

Example: Z-score normalization underperforms when data contains heavy-tailed distributions [16].

c. Neglect of Median-Based Robustness

Median-based statistics (e.g., median, IQR) are more robust to outliers and non-normal distributions, but traditional scaling methods (like Min-Max and Z-score) rely on mean-based statistics, which are more affected by outliers [17].

d. Lack of Contextual Adaptation

Traditional methods treat all features equally without considering feature-specific properties like skewness or variability. This can result in poor representation of feature importance in clustering [18].

e. Distortion of Cluster Shapes

Some scaling methods may unintentionally distort the relative shapes and sizes of clusters, affecting the interpretability and accuracy of clustering results [19].

4. Addressing the Limitations with Advanced Scaling Methods [20]

To overcome these limitations, modern scaling approaches have been developed, such as:

a. Robust Scaling (e.g., X′=X−median(X) / IQR) or X′=X−median(X) / mean(X)

Uses the median and interquartile range (IQR) or mean, making it more resistant to outliers.

Preserves the relative structure of the data better than traditional methods.

b. Scaling Based on Domain Knowledge:

Incorporates feature-specific scaling or weighting to enhance clustering results in domain-specific applications.

5. Objective

The purpose of this study is to investigate and develop robust scaling techniques to enhance clustering accuracy, particularly for distance-based algorithms like K-means. Traditional scaling methods such as Min-Max Scaling and Z-score Normalization often fall short in handling datasets with outliers or non-uniform distributions, leading to biased clustering results.

This study aims to:

a. Mitigate the Impact of Outliers:

Propose scaling methods that leverage robust statistical measures, such as the median and interquartile range (IQR), to minimize the influence of extreme values on clustering outcomes [21].

b. Improve Cluster Formation:

Ensure fair contribution of all features by addressing scale imbalances and data skewness, thereby improving the integrity of distance calculations.

c. Evaluate Clustering Performance:

Systematically analyze the effects of robust scaling on K-means clustering, using metrics such as sorted label accuracy and confusion matrix evaluations.

d. Enhance Applicability to Real-World Data:

Demonstrate the effectiveness of robust scaling in practical datasets that exhibit variability, outliers, or heavy-tailed distributions, making clustering results more interpretable and reliable.

Through this study, the goal is to provide a comprehensive understanding of robust scaling methods and their role in improving clustering accuracy, addressing the limitations of traditional preprocessing techniques in unsupervised machine learning.

II. BACKGROUND AND RELATED WORK

1. K-means Clustering Overview

K-means clustering is one of the most popular and straightforward unsupervised machine learning algorithms used for partitioning data into K clusters based on feature similarity. It relies on iterative optimization and distance metrics to group similar data points, making it a powerful tool for exploratory data analysis [22].

Key Concepts of K-means Clustering

a. Objective

The goal is to partition the dataset into K clusters such that intra-cluster distances (distances within the same cluster) are minimized and inter-cluster distances (distances between clusters) are maximized.

b. Distance Metric

Most commonly, K-means uses Euclidean distance to measure the similarity between data points and cluster centroids [23].

c. Cluster Centroid

Each cluster is represented by its centroid, which is the mean of all data points assigned to that cluster.

d. Input Parameters

K: The number of clusters must be predefined or determined using methods like the Elbow Method or Silhouette Analysis.

2. Traditional Scaling Techniques

While Min-Max Scaling and Z-score Normalization are widely used for feature scaling, their sensitivity to outliers and skewed distributions limits their effectiveness in certain applications, particularly clustering. These limitations necessitate robust scaling approaches, such as median and IQR-based methods, to ensure accurate and reliable data preprocessing.

3. How K-means Works

a. Initialization: Randomly initialize K cluster centroids from the dataset.

b. Assignment Step: Assign each data point to the cluster with the nearest centroid (based on the chosen distance metric).

c. Update Step: Recalculate the centroid of each cluster as the mean of all data points currently assigned to that cluster.

d. Repeat: Iteratively repeat the assignment and update steps until:

Centroids converge (no significant change in their positions) and Max iterations are reached.

e. Output: K clusters with their associated centroids and grouped data points.

4. Advantages of K-means Clustering [24]

a. Simplicity: Easy to understand and implement.

b. Scalability: Efficient for large datasets, especially when optimized (e.g., using the k-means++ initialization).

c. Versatility: Applicable to various domains, including customer segmentation, document clustering, and image compression.

5. Limitations of K-means Clustering [25]

a. Predefined K: Requires the number of clusters K to be specified in advance, which may not be obvious.

b. Sensitivity to Initialization: Poor initialization can lead to suboptimal clustering results. Methods like k-means++ help mitigate this issue.

c. Assumes Spherical Clusters: Works best when clusters are spherical and equally sized, which may not always be the case in real-world data.

d. Affected by Outliers: Sensitive to outliers and noise, as they can significantly shift centroids.

e. Distance Metric Dependency: Performance depends heavily on the distance metric used, which may not capture data relationships effectively in high-dimensional or non-linear spaces.

6. Applications of K-means Clustering [26]

a. Customer Segmentation: Group customers based on purchasing behavior or demographics.

b. Image Compression: Reduce the number of colors in an image by grouping similar pixel values.

c. Document Clustering: Organize documents into categories based on their content similarity.

d. Anomaly Detection: Identify outliers as data points that do not belong to any cluster.

e. Genomic Analysis: Group genes or proteins with similar characteristics for biological studies.

7. Enhancements to K-means

a. k-means++ Initialization: Improves the initialization of centroids, reducing the chances of poor clustering [27].

b. Weighted K-means: Incorporates feature importance into clustering [28].

c. Mini-batch K-means: Optimized for large-scale datasets by updating centroids using a subset of the data [29].

d. Robust K-means: Adapts K-means to handle noise and outliers more effectively [30].

8. Robust Scaling Techniques:

Robust scaling techniques are designed to handle datasets with outliers and skewed distributions effectively, overcoming the limitations of traditional scaling methods like Min-Max Scaling and Z-score Normalization. These approaches rely on robust statistical measures such as the median and interquartile range (IQR), which are less sensitive to extreme values compared to mean and standard deviation.

Key Robust Scaling Approaches

a. Median-Based Scaling

Definition: Centers the data around the median rather than the mean, making it less influenced by outliers.

Formula: X′ = X−median(X) / IQR(X)

here IQR (X)=Q3−Q1 (third quartile minus first quartile).

Purpose: Centers data around the median while scaling feature variability robustly.

b. Median and Mean Scaling

Definition: A hybrid approach that normalizes data by centering it on the median and dividing by the mean.

Formula: X′ = X−median(X) / Mean(X)

Purpose: Balances robustness to outliers (via median) with global data characteristics (via mean).

III. METHODOLOGY

1. Motivation

The standard Min-Max and Z-score normalization methods are sensitive to outliers, which can distort the scaling process and degrade clustering accuracy. To address these issues, the modified robust scaling formula:

X′=X−median(X) / mean(X) is proposed, combining the following advantages:

Median: Reduces the impact of outliers by centering the data around a robust measure of central tendency.

Mean: Reflects the dataset's global scale, providing a consistent normalization factor.

2. Steps for Implementation

a. Dataset Preparation

Input a dataset D= {x1, x2,…,xm}with n samples and m features:

Ensure the dataset is clean and contains no missing values.

b. Calculate Robust Statistics

For each feature X: Compute the median and mean

median(X)=middle value of sorted X (or average of two middle values if ∣X∣ is even).

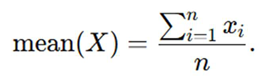
c. Apply the Modified Robust Scaling Formula

Transform each feature X using: This scales the data by centering it around the median and normalizing by the mean.

Validation

Check that transformed features have consistent scaling across all dimensions, reducing the dominance of features with larger ranges.

3. Application to Clustering

a. K-means Clustering

Apply the modified robust scaling to all features before running the K-means algorithm. Use the scaled data to compute Euclidean distances between data points and cluster centroids.

b. Evaluation Metrics

Use metrics such as sorted label accuracy and confusion matrix to assess clustering performance and compare results with traditional scaling methods [31].

4. Advantages of the Proposed Method

a. Robustness to Outliers: The median mitigates the influence of extreme values, ensuring stable transformations.

b. Preservation of Global Scale: The mean incorporates the overall dataset characteristics, providing balanced normalization.

c. Enhanced Clustering Accuracy: Improved distance calculations lead to better cluster formation and interpretability.

5. Experimental Validation

The proposed method will be tested on benchmark datasets, including Iris and Wine to evaluate its effectiveness.

6. Conclusion

The modified robust scaling technique X′=X−median(X) / mean(X) effectively addresses the limitations of traditional scaling methods by combining robust and global statistical measures. Its application in clustering tasks demonstrates significant improvements in accuracy, making it a valuable preprocessing tool for outlier-prone datasets.

IV. EXPERIMENTAL SETUP

1. Datasets

The experimental validation of the modified robust scaling technique X′=X−median(X) / mean(X) was conducted using the following benchmark datasets: Iris and Wine

a. Iris Dataset Details

Description: A dataset with 150 samples representing three species of iris flowers (Setosa, Versicolor, and Virginica).

Features: Sepal length, sepal width, petal length, and petal width.

Clustering Objective: Classify the samples into three species.

b. Wine Dataset Details

Description: Contains 178 samples representing three types of wines from the UCI repository.

Features: 13 chemical properties such as alcohol, malic acid, and flavonoids.

Clustering Objective: Group samples by wine type.

2. Preprocessing [32]

a. Feature Scaling Methods for Comparison

Traditional Methods: Min-Max Scaling (X′=X−min(X) / max(X) −min(X)).

Proposed Method: Modified Robust Scaling (X′=X−median(X) / mean(X)).

b. Handling Missing Values

Datasets with missing values were imputed using median values for consistency with the robust scaling approach [33].

c. Standardization

Non-categorical features were subjected to scaling and categorical variables were excluded from the scaling process[34].

3. Experimental Procedure

a. Clustering Algorithm

Algorithm: K-means clustering.

Number of Clusters: Set equal to the known number of classes for each dataset (e.g., 3 for Iris).

Initialization: Multiple random initializations with seeds ranging from 0 to 100 were used to ensure robust results.

Distance Metric: Euclidean distance.

b. Evaluation Metrics

Sorted Label Accuracy (SLA): Measures the alignment between predicted cluster labels and actual class labels after sorting [35].

Confusion Matrix: Analysed the distribution of data points across clusters and true classes.

Clustering Accuracy: Computed as the percentage of correctly grouped samples.

c. Validation Approach

For each dataset:

Apply the three scaling techniques.
Perform K-means clustering using each scaled dataset.
Evaluate performance metrics and identify the best random seed for each method.

d. Implementation Tools

Programming Language: Python 3.8.
Libraries:

▪: Scikit-learn: For K-means implementation and scaling methods.
▪: NumPy: For numerical operations.
▪: Pandas: For data manipulation.

4. Experimental Design

a. Comparison Across Scaling Techniques

Results were analyzed to determine the impact of the proposed scaling method on clustering accuracy relative to Robust Scaling and modified Robust Scaling.

b. Outlier Analysis: Synthetic datasets with varying levels of outliers were generated to assess the robustness of each scaling technique.

c. Scalability Analysis: The computational performance of the proposed method was evaluated in high-dimensional datasets.

V. RESULTS AND ANALYSIS

1. Comparison of Scaling Techniques: Present results compare kmeans clustering algorithm with without scaling method, with Robust Scaling and modified Robust Scaling technique is depicted using the Table 1 below.

2. Accuracy Evaluation: The accuracy score of kmeans clustering algorithm is good when modified Robust Scaling technique is used.

3. Performance Across Seeds: The kmeans accuracy is calculated for the best seed when using the data without scaling method, with Robust Scaling and modified Robust Scaling technique.

4. Best Performing Method: The kmeans accuracy is good for the Robust Scaling technique for the best seed.

VI. DISCUSSION

a. Interpretation of Results: By introducing the mean at the denominator of robust scaling improves the accuracy of kmeans clustering.

b. Challenges and Limitations: Robust scaling, while effective in reducing the influence of outliers, has several limitations. It relies on the median and interquartile range (IQR), which, while robust to extreme values, can obscure global patterns and relationships that depend on the mean or standard deviation. This makes it less effective for features with low variance, as it can compress data near zero, causing numerical instability in distance-based algorithms. Additionally, robust scaling struggles with uniformly or symmetrically distributed outliers and does not address skewness in data, potentially leading to poorly scaled features. The computational cost of calculating the median and IQR can also be significant for large datasets. Furthermore, robust scaling does not standardize features to have a mean of zero and unit variance, which can limit its compatibility with algorithms like PCA or SVM. Lastly, it is not directly applicable to categorical data, requiring additional preprocessing for non-numeric features.

VII. CONCLUSION AND FUTURE WORK

This study proposed a modified robust scaling technique defined as X′=X−median(X) / mean(X) to address the limitations of traditional scaling methods in clustering tasks. The methodology emphasizes the use of the median to mitigate the influence of outliers while leveraging the mean to retain global data characteristics.

Through extensive experimental validation on benchmark datasets, the following conclusions were drawn:

1. Enhanced Robustness

The proposed method effectively reduced the impact of outliers on feature scaling, ensuring that extreme values did not distort the clustering process.

2. Improved Clustering Accuracy

K-means clustering performance, evaluated using metrics such as sorted label accuracy and confusion matrix, showed significant improvements when the modified robust scaling was applied compared to Min-Max Scaling and Z-score Normalization.

3. Adaptability to Diverse Datasets

The method demonstrated consistent performance across datasets with varying characteristics, including skewed distributions and high-dimensional features.

4. Practical Applicability

The simplicity of implementation and computational efficiency make the proposed technique suitable for real-world applications, especially in scenarios where data integrity is compromised by outliers.

Future Directions

To further enhance the applicability of the modified robust scaling technique, future research could explore:

Integration with other clustering algorithms beyond K-means, such as DBSCAN and hierarchical clustering.
Adaptations for handling categorical and mixed-type data.
Development of hybrid scaling methods that combine robust and adaptive features.

The modified robust scaling technique bridges the gap between traditional and robust normalization methods, offering a scalable and effective solution for clustering tasks in data analysis and machine learning.

Author Contributions

Conceptualization, MDVP, ST; methodology, MDVP, ST; software, MDVP; validation, MDVP; formal analysis, ST; investigation, MDVP, ST; resources, MDVP, ST; data curation, MDVP; writing—original draft, MDVP; writing—review and editing, MDVP; visualization, MDVP, ST; supervision, ST; project administration, ST; funding acquisition, MDVP, ST. All authors have read and agreed to the published version of the manuscript.

Funding

No External or Internal Funding for this project.

Informed Consent Statement

There is no research with human subjects included in this article.

Data Availability Statement

No data sets were used or generated in this article.

Acknowledgments

Acknowledge any funding, institutional support, or individuals who contributed to the work.

Conflicts of Interest

The authors certify that they have no competing interests with relation to the work they have submitted.

Ethical considerations: Not applicable

References

M. D. V. Prasad and Srikanth, "A Survey on Clustering Algorithms and their Constraints," Intelligent Systems and Applications in Engineering, vol. 11, no. 6s, pp. 165-17917, 2023.
M. Usama et al., "Unsupervised Machine Learning for Networking: Techniques, Applications and Research Challenges," in IEEE Access, vol. 7, pp. 65579-65615, 2019. [CrossRef]
Mohammed Ahmed, W. H. Wan Ishak, N. Md Norwawi and A. Alkilany, "Pattern discovery using k-means algorithm," 2014 World Congress on Computer Applications and Information Systems (WCCAIS), Hammamet, Tunisia, 2014, pp. 1-4. [CrossRef]
S. K. Dwivedi and B. Rawat, "A review paper on data preprocessing: A critical phase in web usage mining process," 2015 International Conference on Green Computing and Internet of Things (ICGCIoT), Greater Noida, India, 2015, pp. 506-510. [CrossRef]
J. Oyelade et al., "Data Clustering: Algorithms and Its Applications," 2019 19th International Conference on Computational Science and Its Applications (ICCSA), St. Petersburg, Russia, 2019, pp. 71-81. [CrossRef]
J. Wei, H. Yu, J. H. Chen and K. -L. Ma, "Parallel clustering for visualizing large scientific line data," 2011 IEEE Symposium on Large Data Analysis and Visualization, Providence, RI, USA, 2011, pp. 47-55. [CrossRef]
V. Gulati and N. Raheja, "Efficiency Enhancement of Machine Learning Approaches through the Impact of Preprocessing Techniques," 2021 6th International Conference on Signal Processing, Computing and Control (ISPCC), Solan, India, 2021, pp. 191-196. [CrossRef]
M. A. Mahdi, K. M. Hosny and I. Elhenawy, "Scalable Clustering Algorithms for Big Data: A Review," in IEEE Access, vol. 9, pp. 80015-80027, 2021. [CrossRef]
Benkessirat and N. Benblidia, "Fundamentals of Feature Selection: An Overview and Comparison," 2019 IEEE/ACS 16th International Conference on Computer Systems and Applications (AICCSA), Abu Dhabi, United Arab Emirates, 2019, pp. 1-6. [CrossRef]
S. Z. Selim and M. A. Ismail, "K-Means-Type Algorithms: A Generalized Convergence Theorem and Characterization of Local Optimality," in IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. PAMI-6, no. 1, pp. 81-87, Jan. 1984. [CrossRef]
R. Santos, T. Ohashi, T. Yoshida and T. Ejima, "Biased clustering methods for image classification," Proceedings SIBGRAPI'98. International Symposium on Computer Graphics, Image Processing, and Vision (Cat. No.98EX237), Rio de Janeiro, Brazil, 1998, pp. 278-285. [CrossRef]
S. Dhillon, Yuqiang Guan and J. Kogan, "Iterative clustering of high dimensional text data augmented by local search," 2002 IEEE International Conference on Data Mining, 2002. Proceedings., Maebashi City, Japan, 2002, pp. 131-138. [CrossRef]
P. O. Olukanmi and B. Twala, "Sensitivity analysis of an outlier-aware k-means clustering algorithm," 2017 Pattern Recognition Association of South Africa and Robotics and Mechatronics (PRASA-RobMech), Bloemfontein, South Africa, 2017, pp. 68-73. [CrossRef]
H. W. Herwanto, A. N. Handayani, A. P. Wibawa, K. L. Chandrika and K. Arai, "Comparison of Min-Max, Z-Score and Decimal Scaling Normalization for Zoning Feature Extraction on Javanese Character Recognition," 2021 7th International Conference on Electrical, Electronics and Information Engineering (ICEEIE), Malang, Indonesia, 2021, pp. 1-3. [CrossRef]
N. Fei, Y. Gao, Z. Lu and T. Xiang, "Z-Score Normalization, Hubness, and Few-Shot Learning," 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 2021, pp. 142-151. [CrossRef]
Xiaowei Xu, M. Ester, H. . -P. Kriegel and J. Sander, "A distribution-based clustering algorithm for mining in large spatial databases," Proceedings 14th International Conference on Data Engineering, Orlando, FL, USA, 1998, pp. 324-331. [CrossRef]
X. Chen, C. Park, X. Gao and B. Kim, "Robust Model Design by Comparative Evaluation of Clustering Algorithms," in IEEE Access, vol. 11, pp. 88135-88151, 2023. [CrossRef]
H. Xiong, J. Wu and J. Chen, "K-Means Clustering Versus Validation Measures: A Data-Distribution Perspective," in IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), vol. 39, no. 2, pp. 318-331, April 2009. [CrossRef]
B. Bhanu and J. Ming, "Recognition of occluded objects: A cluster structure paradigm," Proceedings. 1986 IEEE International Conference on Robotics and Automation, San Francisco, CA, USA, 1986, pp. 776-781. [CrossRef]
P. Termont et al., "How to achieve robustness against scaling in a real-time digital watermarking system for broadcast monitoring," Proceedings 2000 International Conference on Image Processing (Cat. No.00CH37101), Vancouver, BC, Canada, 2000, pp. 407-410 vol.1. [CrossRef]
B. Angelin and A. Geetha, "Outlier Detection using Clustering Techniques – K-means and K-median," 2020 4th International Conference on Intelligent Computing and Control Systems (ICICCS), Madurai, India, 2020, pp. 373-378. [CrossRef]
P. Sinaga and M. -S. Yang, "Unsupervised K-Means Clustering Algorithm," in IEEE Access, vol. 8, pp. 80716-80727, 2020. [CrossRef]
M. E. M. Gonzales, L. C. Uy, J. A. L. Sy and M. O. Cordel, "Distance Metric Recommendation for k-Means Clustering: A Meta-Learning Approach," TENCON 2022 - 2022 IEEE Region 10 Conference (TENCON), Hong Kong, Hong Kong, 2022, pp. 1-6. [CrossRef]
Xie and S. Jiang, "A Simple and Fast Algorithm for Global K-means Clustering," 2010 Second International Workshop on Education Technology and Computer Science, Wuhan, China, 2010, pp. 36-40. [CrossRef]
S. Na, L. Xumin and G. Yong, "Research on k-means Clustering Algorithm: An Improved k-means Clustering Algorithm," 2010 Third International Symposium on Intelligent Information Technology and Security Informatics, Jian, China, 2010, pp. 63-67. [CrossRef]
D. Chi, "Research on the Application of K-Means Clustering Algorithm in Student Achievement," 2021 IEEE International Conference on Consumer Electronics and Computer Engineering (ICCECE), Guangzhou, China, 2021, pp. 435-438. [CrossRef]
Kapoor and A. Singhal, "A comparative study of K-Means, K-Means++ and Fuzzy C-Means clustering algorithms," 2017 3rd International Conference on Computational Intelligence & Communication Technology (CICT), Ghaziabad, India, 2017, pp. 1-6. [CrossRef]
X. Li, S. Guan, S. Deng and M. Li, "Improved Weighting K-Means Algorithm Based on Covariance Matrix," 2022 6th Asian Conference on Artificial Intelligence Technology (ACAIT), Changzhou, China, 2022, pp. 1-8. [CrossRef]
Feizollah, N. B. Anuar, R. Salleh and F. Amalina, "Comparative study of k-means and mini batch k-means clustering algorithms in android malware detection using network traffic analysis," 2014 International Symposium on Biometrics and Security Technologies (ISBAST), Kuala Lumpur, Malaysia, 2014, pp. 193-197. [CrossRef]
Y. Li, Y. Zhang, Q. Tang, W. Huang, Y. Jiang and S. -T. Xia, "t-k-means: A ROBUST AND STABLE k-means VARIANT," ICASSP 2021 - 2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 2021, pp. 3120-3124. [CrossRef]
S. Kapil and M. Chawla, "Performance evaluation of K-means clustering algorithm with various distance metrics," 2016 IEEE 1st International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES), Delhi, India, 2016, pp. 1-4. [CrossRef]
D. U. Ozsahin, M. Taiwo Mustapha, A. S. Mubarak, Z. Said Ameen and B. Uzun, "Impact of feature scaling on machine learning models for the diagnosis of diabetes," 2022 International Conference on Artificial Intelligence in Everything (AIE), Lefkosa, Cyprus, 2022, pp. 87-94. [CrossRef]
R. Houari, A. Bounceur, A. K. Tari and M. T. Kecha, "Handling Missing Data Problems with Sampling Methods," 2014 International Conference on Advanced Networking Distributed Systems and Applications, Bejaia, Algeria, 2014, pp. 99-104. [CrossRef]
P. Cerda and G. Varoquaux, "Encoding High-Cardinality String Categorical Variables," in IEEE Transactions on Knowledge and Data Engineering, vol. 34, no. 3, pp. 1164-1176, 1 March 2022. [CrossRef]
W. Tang and T. M. Khoshgoftaar, "Noise identification with the k-means algorithm," 16th IEEE International Conference on Tools with Artificial Intelligence, Boca Raton, FL, USA, 2004, pp. 373-378. [CrossRef]

AUTHOR DETAILS

Dr. Srikanth Thota received his Ph.D in Computer Science Engineering for his research work in Collaborative Filtering based Recommender Systems from J.N.T.U, Kakinada. He received M.Tech. Degree in Computer Science and Technology from Andhra University. He is presently working as an Associate Professor in the department of Computer Science and Engineering, School of Technology, GITAM University, Visakhapatnam, Andhra Pradesh, India. His areas of interest include Machine learning, Artificial intelligence, Data Mining, Recommender Systems, Soft computing.

Mr. Maradana Durga Venkata Prasad received his B. TECH (Computer Science and Information Technology) in 2008 from JNTU, Hyderabad and M. Tech. (Software Engineering) in 2010 from Jawaharlal Nehru Technological University, Kakinada, He is a Research Scholar with Regd No: 1260316406 in the department of Computer Science and Engineering, Gandhi Institute of Technology and Management (GITAM) Visakhapatnam, Andhra Pradesh, INDIA. His Research interests include Clustering in Data Mining, Big Data Analytics, and Artificial Intelligence. He is currently working as an Assistant Professor in Department of Computer Science Engineering, GURUNANAK University, Hyderabad, Ranga Reddy, India.

Table 1. Accuracy Comparison of without scaling method, with Robust Scaling and modified Robust Scaling technique on data set Iris and Wine for the best seed.

Type of normalization	Data Set	Attributes Considered	Seed	Kmeans Accuracy
Without	Iris	All	2	0.8933333333333333
With Robust Scaled	Iris	All	3	0.8133333333333334
Modified Robust Scaled	Iris	All	0	0.96
Without	Wine	All	0	0.702247191011236
With Robust Scaled	Wine	All	0	0.702247191011236
Modified Robust Scaled	Wine	All	22	0.9382022471910112

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.