Submitted:
16 November 2024
Posted:
18 November 2024
You are already at the latest version
Abstract
The paper develops the new formalism to treat both infinite and finite exceptional orthogonal polynomial (EOP) sequences as X-orthogonal subsets of X-Jacobi differential polynomial systems (DPSs). The new rational canonical Sturm-Liouville equations (RCSLEs) with quasi-rational solutions (q-RSs) were obtained by applying rational Rudjak-Zakhariev transformations (RRZTs) to the Jacobi equation re-written in the canonical form. The presented analysis was focused on the RRZTs leading to the canonical form of the Heun equation. It was demonstrated that the latter equation preserves its form under the second-order Darboux-Crum transformation. The associated Sturm-Liouville problems (SLPs) were formulated for the so-called ‘prime’ SLEs solved under the Dirichlet boundary conditions (DBCs). It was proven that one of the two X1-Jacobi DPSs composed of Heun polynomials contains both X1-Jacobi orthogonal polynomial system (OPS) and finite EOP sequence composed of the pseudo-Wronskian transforms of Romanovski-Jacobi (R-Jacobi) polynomials, while the second analytically-solvable Heun equation does not have the discrete energy spectrum. The quantum-mechanical realizations of the developed formalism were obtained by applying the Liouville transformation to each of the SLPs formulated in such a way.
Keywords:
1. Introduction
- i)
- the Liouville transformation from the CSLE to the Schrödinger equation;
- ii)
- the Darboux deformation of the corresponding Liouville potential;
- iii)
- the reverse Liouville transformation from the Schrödinger equation to the new CSLE using the same change of variable as at Step i),
2. The q-RSs of the JRef CSLE with the Simple-Pole Density Function
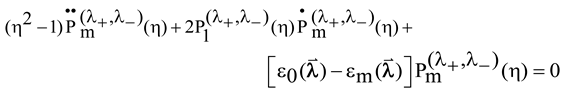
3. Rational Rudjak-Zakhariev Transforms of JRef CSLE
4. Form-Invariance of restr-HRef CSLE Under Two Sequential RZTs
- i)
- ,
- ii)
- ,
- iii)
- the ExpDiff for the pole of the JRef CSLE (1) at +1 lies within the limit-circle (LC) rangeand therefore this must be also true for the ExpDiff for the pole of the restr-HRef CSLE obtained from (35) by the corresponding DCT. By analogy with the conclusion made by us in [1] for the radial JRef potential and its linear-tangent-polynomial (LTP) counter-part on the line, we assert that the conventional rules of the quantum-mechanics must fail for all the Liouville potentials associated with the listed anomalous cases. We shall come back to this issue in Section 8.
5. Pseudo-Wronskian Representation of X1-Jacobi DPSs
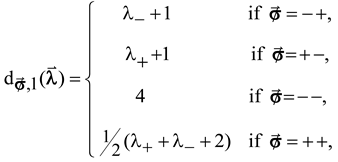
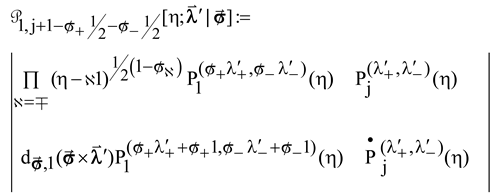
6. Energy Spectrum of ‘Prime’ SLEs Solved Under Dirichlet Boundary Conditions
6.1. X1-Jacobi OPS
6.2. Finite Orthogonal Subsequences of X1-Jacobi DPS
7. Liouville Potentials Shape-Invariant Under Second-Order DCTs
8. Discussion
9. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
Appendix A
Appendix B
Appendix C
Appendix D
References
- Natanson, G. Double-step shape-invariance of radial Jacobi-reference potential and breakdown of conventional rules of supersymmetric quantum mechanics. Axioms, 2024, 13, 273–26. [Google Scholar] [CrossRef]
- Natanzon G. A. Study of the one-dimensional Schrödinger equation generated from the hypergeometric equation. Vestn. Leningr. Univ. 1971. No 10, 22-28. English translation available online: arxiv.org/PS_cache/physics/pdf/9907/9907032v1.pdf.
- Gibbons, J. and Veselov A.P. On the rational monodramy-free potentials with sextic growth. J. Math. Phys. 2009, 50, 013513–25. [Google Scholar] [CrossRef]
- Sleeman, B.D.; Kuznetsov, V.B. §31.2: Heun functions: Normal form of Heun equation. In The NIST Handbook of Mathematical Functions; Olver, F.W., ed.; NIST: Gaithersburg, MD, USA, 201.
- Cooper, F.; Khare, A.; Sukhatme, U.P. Supersymmetry in Quantum Mechanics, Denver, World Scientific, 2001. [CrossRef]
- Pöschl, G.; Teller, F. Bemerkungen zur Quantenmechanik des anharmonischen Oszillators. Zs. Phys. 1933, 83, 143–151. [Google Scholar] [CrossRef]
- Quesne, C. Exceptional orthogonal polynomials, exactly solvable potentials and supersymmetry,” J. Phys. A 2008, 41, 392001, 6 pages. [CrossRef]
- Quesne, C. Solvable Rational Potentials and Exceptional Orthogonal Polynomials in Supersymmetric Quantum Mechanics. SIGMA 2009, 5, 084–24. [Google Scholar] [CrossRef]
- Bagchi, B.; Quesne, C.; Roychoudhury, R. Isospectrality of conventional and new extended potentials, second-order supersymmetry and role of PT symmetry. Pramana J. Phys. 2009, 73, 337–347. [Google Scholar] [CrossRef]
- Soltész, T.; Pethő, L.; Lévai, G. Unified supersymmetric description of shape-Invariant potentials within and beyond the Natanzon class. Symmetry 2024, 16, 174–25. [Google Scholar] [CrossRef]
- Natanson, G. Biorthogonal differential polynomial system composed of X-Jacobi polynomials from different sequences. 2018. Available online: researchgate.net/publication/322634977 (accessed on Jan. 22, 2018). [CrossRef]
- Natanson, G. X1-Jacobi differential polynomial system formed by solutions of Heun equation at fixed values of accessory parameter. 2018. Available online researchgate.net/publication/327235393 (accessed on 16 Nov. 2024). [CrossRef]
- Natanson, G. Two exceptional differential polynomial systems formed by Jacobi-seed Heun polynomials. 2019. Available online: researchgate.net/publication/336839244 (accessed on Oct. 30, 2019). [CrossRef]
- Bochner, S. Über Sturm-Liouvillesche Polynomsysteme, Math Z 1929, 29, 730-736. [CrossRef]
- Gȯmez-Ullate, D.; Kamran, N.; Milson, R. An extended class of orthogonal polynomials defined by a Sturm-Liouville problem. J. Math. Anal. Appl. 2009, 359, 352–367. [Google Scholar] [CrossRef]
- Gȯmez-Ullate, D.; Kamran, N.; Milson, R. An extension of Bochner’s problem: exceptional invariant subspaces. J Approx Theory 2010, 162, 987–1006. [Google Scholar] [CrossRef]
- Kwon, K.H.; .Littlejohn, L.L. Classification of classical orthogonal polynomials. J Korean Math Soc 1997, 34, 973-1008. Corpus ID:123032920.
- Natanson, G. Use of Wronskians of Jacobi polynomials with common complex indexes for constructing X-DPSs and their infinite and finite orthogonal subsets, 2019. Available from https://www.researchgate.net/publication/331638063 (accessed on March 10 2019). [CrossRef]
- Everitt, W.N.; Littlejohn, L.L. Orthogonal polynomials and spectral theory: a survey, In: Brezinski C.; Gori L.; Ronveaux A. editors. Orthogonal Polynomials and their Applications. IMACS Annals on Computing and Applied Mathematics, Vol.9, Basel: J.C. Baltzer, 1991, 21-55. ISSN 1012-2435.
- Everitt, W.N.; Kwon, K.H.; Littlejohn, L.L.; et al. Orthogonal polynomial solutions of linear ordinary differential equations”, J Comp & Appl Math 2001, 133, 85-109. [CrossRef]
- Chihara, T.S. An Introduction to Orthogonal Polynomials, Gordon and Breach, New York, 1978.
- Garcia-Ferrero, M.; Gomez-Ullate, D.; Milson, R. A Bochner type classification theorem for exceptional orthogonal polynomials. J. Math. Anal. & Appl. 2019, 472, 584–626. [Google Scholar] [CrossRef]
- Garcia-Ferrero, M.; Gomez-Ullate, D.; Milson, R. Classification of exceptional Jacobi polynomials, 2024. Available online: arXiv:2409.02656v1 (accessed on Sept 4 2024).
- Rudyak B., V.; Zakhariev B., N. New exactly solvable models for Schrödinger equation,” Inverse Problems. 1987, 3, 125-133.
- Schnizer, W. A.; Leeb, H. , Exactly solvable models for the Schrödinger equation from generalized Darboux transformations. J. Phys. A 1993, 26, 5145–5156. [Google Scholar] [CrossRef]
- Natanson, G. Single-source nets of algebraically-quantized reflective Liouville potentials on the line I. Almost-everywhere holomorphic solutions of rational canonical Sturm-Liouville equations with second-order poles. 2015. Available online: arXiv:1503.04798v2 (accessed on Dec 9 2015).
- Natanson, G. Gauss-seed nets of Sturm-Liouville problems with energy-independent characteristic exponents and related sequences of exceptional orthogonal polynomials I. Canonical Darboux transformations using almost-everywhere holomorphic factorization functions. 2013. Available online: arXiv:1305.7453v1 (accessed on May 31 2013).
- Natanson, G. Darboux-Crum Nets of Sturm-Liouville Problems Solvable by Quasi-Rational Functions I. General Theory. 2018. Available online: https://www.researchgate.net/publication/323831953 (accessed on 1 March 2018). [CrossRef]
- Gesztesy, F.; Simon, B.; Teschl, G. Zeros of the Wronskian and renormalized oscillation theory. Am. J. Math. 1996, 118, 571–594. [Google Scholar] [CrossRef]
- Romanovski, V.I. Sur quelques classes nouvelles de polynomes orthogonaux. C.R. Acad. Sci. 1929, 188, 1023–1025. [Google Scholar]
- Askey, R. An integral of Ramanujan and orthogonal polynomials,” J. Indian Math. Soc. 51 ( 1987), 27–36.
- Lesky, P.A. Vervollstandigungderklassischen Orthogonalpolynomedurch Erganzungen zum Askey—Schema der hypergeometrischen orthogonalen Polynome. Ost. Ak. Wiss. 1995, 204, 151–166. [Google Scholar]
- Lesky, P.A. Endliche und unendliche Systeme von kontinuierlichen klassichen Othogonalpolynomen. Z. Angew. Math. Mech. 1996, 76, 181–184. [Google Scholar] [CrossRef]
- Chen M., P.; Srivastava H., M. Orthogonality relations and generating functions for Jacobi polynomials and related hypergeometric functions, Appl. Math. Comput. 1995, 68, 153–188. [Google Scholar] [CrossRef]
- Koepf, W.; Masjed-Jamei, M. A generic polynomial solution for the differential equation of hypergeometric type and six sequences of orthogonal polynomials related to it,” Integral Transforms and Special Functions 2006, 17, 559-576. [CrossRef]
- Hetyei, G. Shifted Jacobi polynomials and Delannoy numbers. (2009). Available online: arXiv:0909.5512v2 (accessed on Dec 24 2009). [CrossRef]
- Yadav R., K.; Khare, A.; Mandal, B.P. The scattering amplitude for newly found exactly solvable potential. Ann. Phys. 2013, 331, 313–316. [Google Scholar] [CrossRef]
- Natanson, G. On quantization of Bagchi-Quesne-Roychoudhury potential by a finite X-orthogonal sequence of Heun eigenpolynomials. (Analytic and algebraic methods in physics XV, Prague, 10-13 September 2018). Slides are available online: researchgate.net/publication/326816855.
- Szego, G. Orthogonal Polynomials. (New York: Amer. Math. Soc., 1959) p.150.
- Rainville E.D. Special Functions. (The Macmillan Co., New York, 1960).
- Gȯmez-Ullate, D.;, Kamran N.; Milson R. On orthogonal polynomials spanning a non-standard flag. Contemp Math 2012, 563, 51–71. [CrossRef]
- Gȯmez-Ullate, D.; Marcellan, F.; Milson R., Asymptotic and interlacing properties of zeros of exceptional Jacobi and Laguerre polynomials,” J. Math. Anal. Appl. 2013, 399, 480–495. [CrossRef]
- Natanson, G. Survey of nodeless regular almost-everywhere holomorphic solutions for Exactly solvable Gauss-reference Liouville potentials on the line I. Subsets of nodeless Jacobi-seed solutions co-existent with discrete energy spectrum. 2016. Available online: arXiv:1606.08758. (accessed on 29 Oct 2016). [CrossRef]
- D. Gómez-Ullate, Y. D. Gómez-Ullate, Y. Grandati, and R. Milson, “Shape invariance and equivalence relations for pseudo-Wronskians of Laguerre and Jacobi polynomials.” J. Phys. A51 (2018), 345201, 28 pages.
- Liaw, C.; Littlejohn, L.L.; Stewart, J.; Wicks, Q. A spectral study of the second-order exceptional X1-Jacobi differential expression and a related non-classical Jacobi differential expression. J. Math. Anal. Appl. 2015, 422, 212–239. [Google Scholar] [CrossRef]
- Takemura, K. Multi-indexed Jacobi polynomials and Maya diagrams. J. Math. Phys. 2014, 55, 113501. [Google Scholar] [CrossRef]
- Everitt W N. Note on the X1-Jacobi orthogonal polynomials. 2008. Available online: arXiv:0812.0728v1 (accessed on Dec 3, 2008).
- Dimitrov, D.K.; Lun, Y.C. Monotonicity, interlacing and electrostatic interpretation of zeros of exceptional Jacobi polynomials, J. Approx. Theory 2014, 181, 18–29. [Google Scholar] [CrossRef]
- Horvath, A.P. Asymptotics for recurrence coefficients of X1-Jacobi polynomials and Christoffel function. Integral Transforms and Spec. Funct. 2020, 31, 87–106. [Google Scholar] [CrossRef]
- Martínez-Finkelshtein, A; Rakhmanov, E. A. On asymptotic behavior of Heine-Stieltjes and Van Vleck polynomials. Contemp. Math., 2010, 507, 209–232. [Google Scholar] [CrossRef]
- Natanson, G. Natanson, G. Breakup of SUSY Quantum Mechanics in the Limit-Circle Region of the Darboux/Pöschl-Teller Potential. 2019. Available online: https://www.researchgate.net/publication/334960618 (accessed on 1 October 2019).
- Everitt, W.N. A Catalogue of Sturm-Liouville Differential Equations. In Sturm-Liouville Theory, Past and Present; Amrein, W.O., Hinz, A.M., Pearson, D.B., Eds.; Birkhäuser Verlag: Basel, Switzerland, 2005; pp. 271–331. [Google Scholar] [CrossRef]
- Alhaidari A,D,; AssiI. A. Finite-Series Approximation of the Bound States for Two Novel Potentials. Physics 2022, 4, 1067–1080. [Google Scholar] [CrossRef]
- Raposo, A.P.; Weber H., J.; Alvarez-Castillo, D.E; Kirchbach, M. Romanovski polynomials in selected physics prob-lems,” Centr. Eur. J. Phys. 2007, 5, 253–284. [Google Scholar] [CrossRef]
- Weber H., J. Connections between Romanovski and other polynomials,” C. Eur. J. Math. 5 ( 2007), 581–595. [CrossRef]
- Avarez-Castillo D., E.; Kirchbach, M. , Exact spectrum and wave functions of the hyperbolic Scarf potential in terms of finite Romanovski polynomials,” Rev. Mex. Fis.E 2007, 53, 143–154. [Google Scholar]
- Quesne C, Extending Romanovski polynomials in quantum mechanics. J. Math. Phys. [CrossRef]
- Martınez-Finkelshtein, A. , Silva Ribeiro L. L.; Sri Ranga A.; Tyaglov M. Complementary Romanovski-Routh polynomials: From orthogonal polynomials on the unit circle to Coulomb wave functions. Proc. Amer. Math. Soc. 2019, 147, 2625–2640. [Google Scholar] [CrossRef]
- Masjed-Jamei, M. Special Functions and Generalized Sturm-Liouville Problems (Springer Nature Switzerland AG 2020), pp. 21-23. springer.com/book/10.1007/978-3-030-32820-7.
- Abo-Gabal, H.; Zaky, M.A.; Hafez, R.M; Doha, E.H. On Romanovski–Jacobi polynomials and their related approximation results. Numer. Methods Partial Differ. Equ.. 2020, 36, 1982–2017. [Google Scholar] [CrossRef]
- Youssri, Y.H.; Zaky, M.A.; Hafezd, R.M. Romanovski-Jacobi spectral schemes for high-order differential equations. Appl. Numer. Math. [CrossRef]
- Natanson, G. Rediscovery of Routh polynomials after hundred years in obscurity. In Recent Research in Polynomials; Özger, F., Ed.; IntechOpen: London, UK, 2023; 27p. [Google Scholar]
- Masjedjamei, M. Three finite classes of hypergeometric orthogonal polynomials and their application in functions approximation,” Integral Transforms and Special Functions 2002, 13, 169-190. [CrossRef]
- Masjed-Jamei, M.; Moalemi, Z.; Saad, N. Incomplete symmetric orthogonal polynomials of finite type generated by a generalized Sturm–Liouville theorem. J. Math. Phys. 0235; 01. [Google Scholar] [CrossRef]
- Erdelyi, A.; Bateman, H. Transcendental Functions; McGraw Hill: New York, NY, USA, 1953; Volume 1. [Google Scholar]
- Banerjee, S.; Yadav, R.K.; Khare, A.A.; Kumari, N.; Mandal, B.P. Solutions of (1+1)-dimensional Dirac equation associated with exceptional orthogonal polynomials and the parametric symmetry Int. J. Modern. Phys A 2023, 38, 2350069–23. [Google Scholar] [CrossRef]
- Yadav, R. K.; Khare, A.; Kumari, N.; Bagchi, B. and Mandal P. M. Parametric symmetries in exactly solvable real and PT symmetric complex potentials. J. Math. Phys. 2016, 57, 062106–22. [Google Scholar] [CrossRef]
- Odake, S.; Sasaki, R. Infinitely many shape invariant potentials and new orthogonal polynomials. Phys. Lett. B 2009, 679, 414–417. [Google Scholar] [CrossRef]
- Ho, C.-L.; Odake, S.; Sasaki, R. Properties of the Exceptional (Xl) Laguerre and Jacobi Polynomials. SIGMA 2011, 7, 107. [Google Scholar] [CrossRef]
- Yadav, R.K.; Khare, A.A.; Mandal, B.P. The scattering amplitude for one parameter family of shape invariant potentials related to Xm Jacobi polynomials. Phys. Lett. B 2013, 723, 433–435. [Google Scholar] [CrossRef]
- Yadav, R.K.; Banerjee, S. , Kumari N. ; Khare A.A.; Mandal B.P. One parameter family of rationally extended isospectral potentials, Ann. Phys. 2022, 436, 168679–27. [Google Scholar] [CrossRef]
- Andrianov, A.A.; Borisov, N.V.; Ioffe, M.V. The factorization method and quantum systems with equivalent energy spectra. Phys. Lett. 1984, 105, 19–22. [Google Scholar] [CrossRef]
- Sukumar, C.V. Supersymmetric quantum mechanics of one-dimensional system. J. Phys. A 1985, 18, 2917–2936. [Google Scholar] [CrossRef]
- Sukumar C., V. Supersymmetric quantum mechanics and the inverse scattering method. J. Phys. A 1985, 18, 2937–2955. [Google Scholar] [CrossRef]
- Gangopadhyaya, A.; Panigrahi P., K.; Sukhatme U., P. Analysis of inverse-square potentials using supersymmetric quantum mechanics,” J. Phys. A 1994, 27, 4295–4300. [Google Scholar] [CrossRef]
- Gangopadhyaya, A.; Mallow, J.V.; Rasinariu, C. Supersymmetric Quantum Mechanics. An Introduction (London: World Scientific Publishing, 2011), Ch. 12. [CrossRef]
- Weisstein, E.W. Jacobi Polynomials. MathWorld 2018. Available online: /en.wikipedia.org/wiki/Jacobi_Recurrence_relations (accessed on 15 July 2024).
- Abramowitz A; Stegun I. A. Handbook of Mathematical Functions (Washington DC: NBS, Applied Mathematics Series – 55, 1972) files.eric.ed.gov/fulltext/ED250164.pdf.
- Grandati, Y.; Bérard, A. Comments on the generalized SUSY QM partnership for Darboux- Pöschl-Teller potential and exceptional Jacobi polynomials. J Eng Math 2013, 82, 161–171. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




