Submitted:
12 November 2024
Posted:
13 November 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Areas of Interest and Datasets
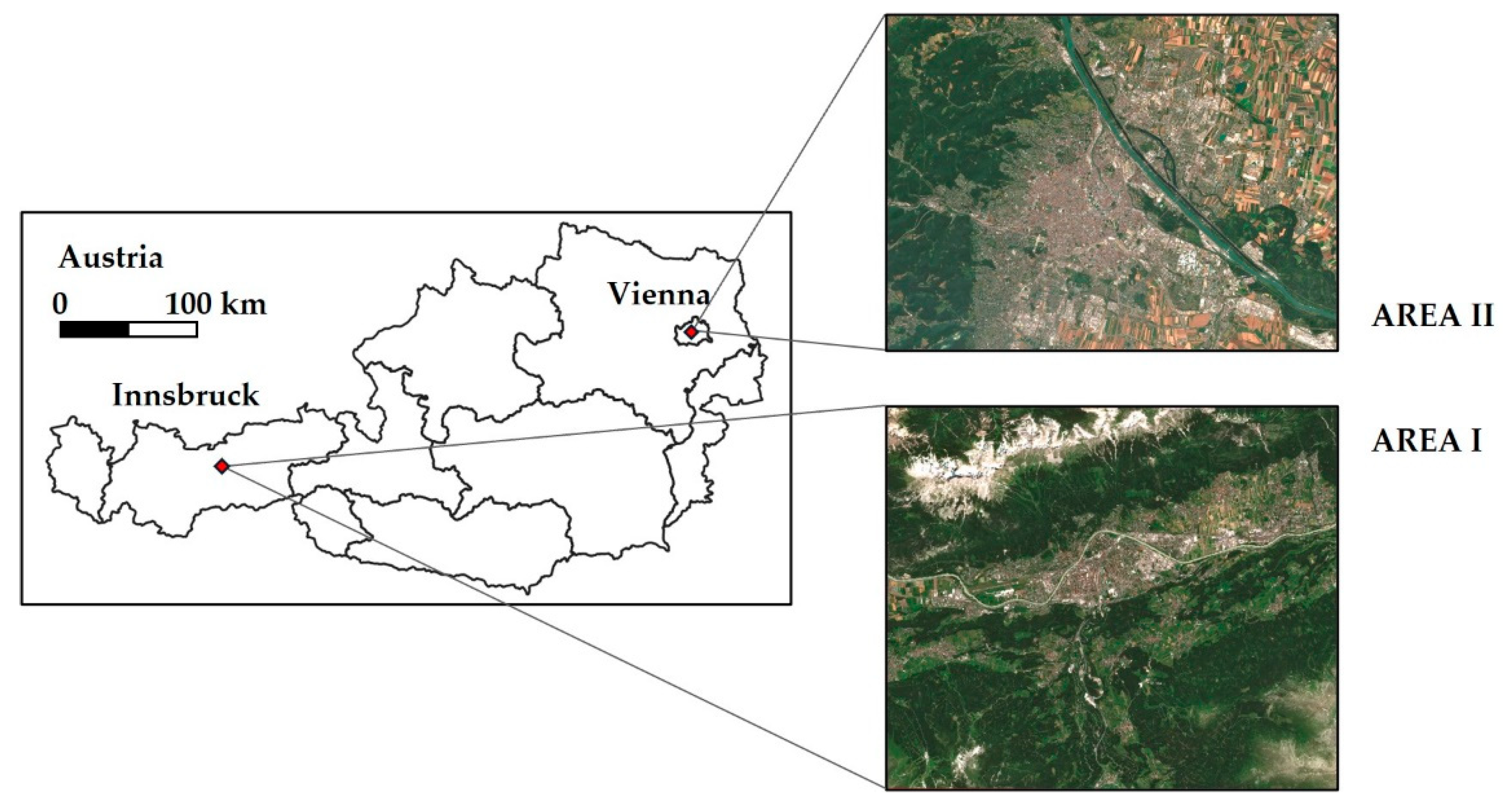
2.1. Areas of Interest
2.2. Land Surface Temperature
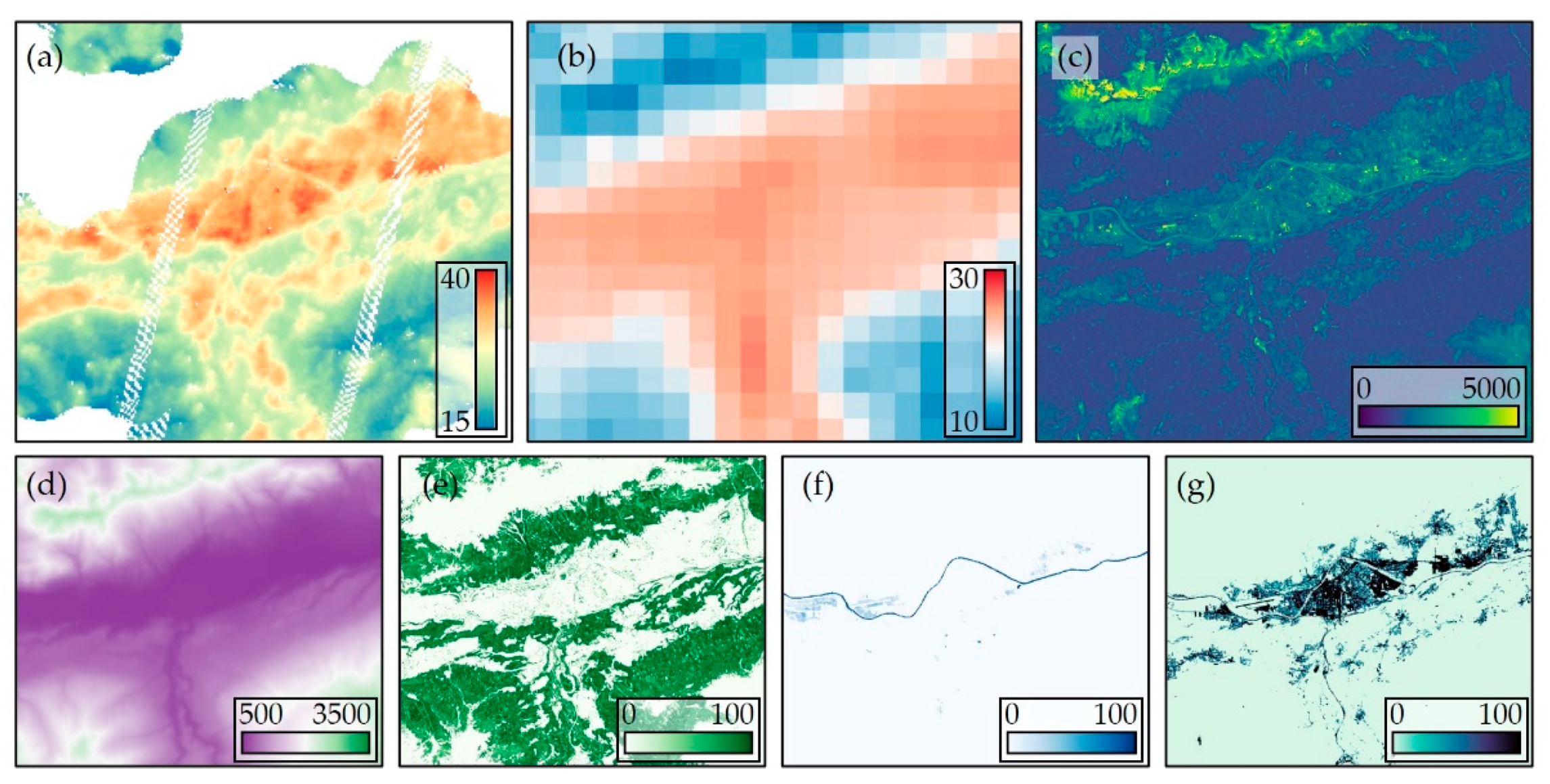
2.3. Input Datasets
2.3.1. ECOSTRESS: Label Dataset
2.3.2. INCA
2.3.3. Sentinel-2
2.3.4. Additional Input Datasets
- (i)
- tree cover density, a dataset which provides insights into vegetation distribution,
- (ii)
- water and wetness index, a dataset which indicates moisture levels and the presence of water bodies,
- (iii)
- imperviousness, a dataset which highlights the areas covered by artificial surfaces such as roads and buildings.
3. Methodology
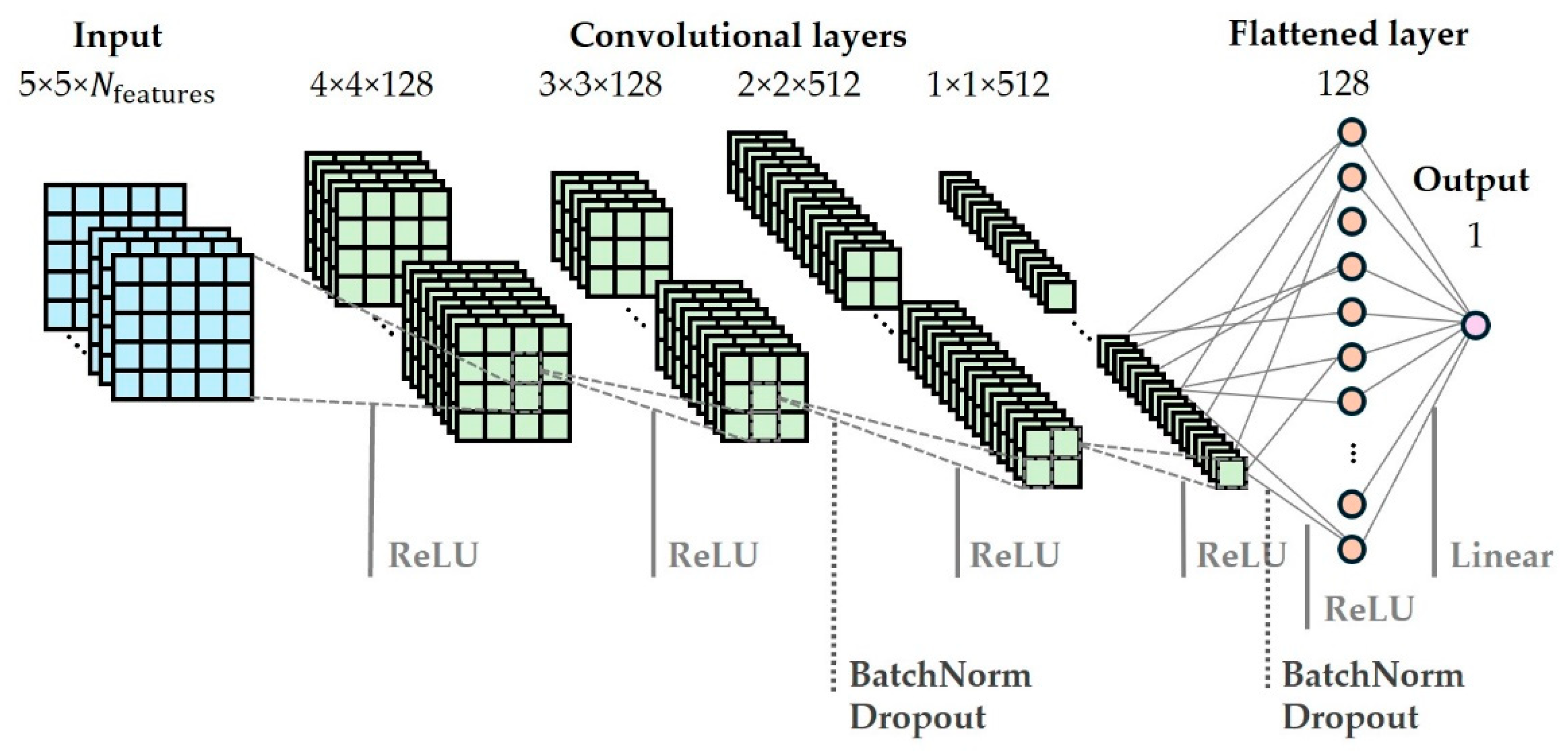
3.1. Convolutional Neural Network Architecture for Pixelwise Regression
3.2. Preparation of the Input Patches
4. Results
4.1. Model Training
4.2. Performance Evaluation
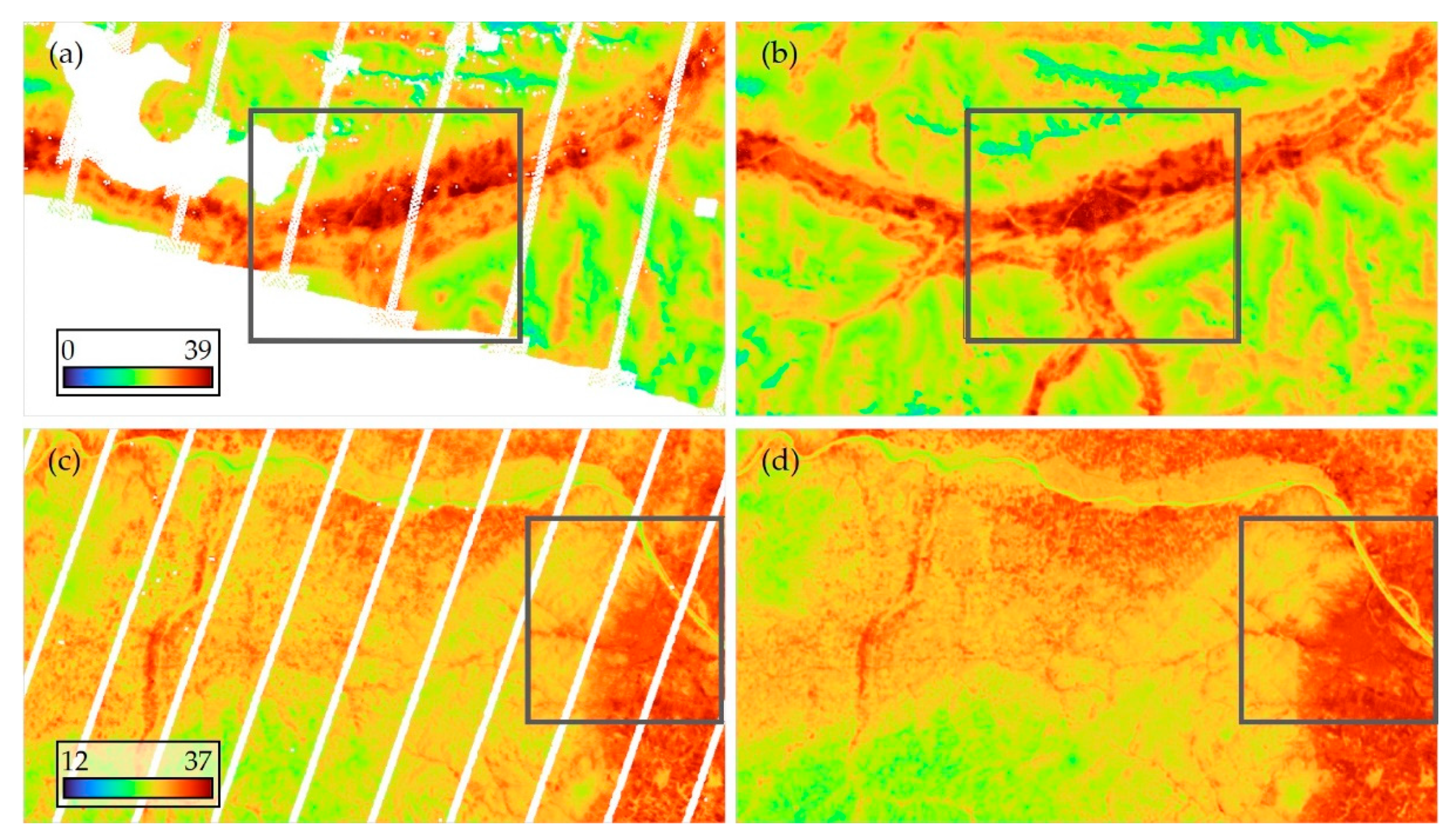
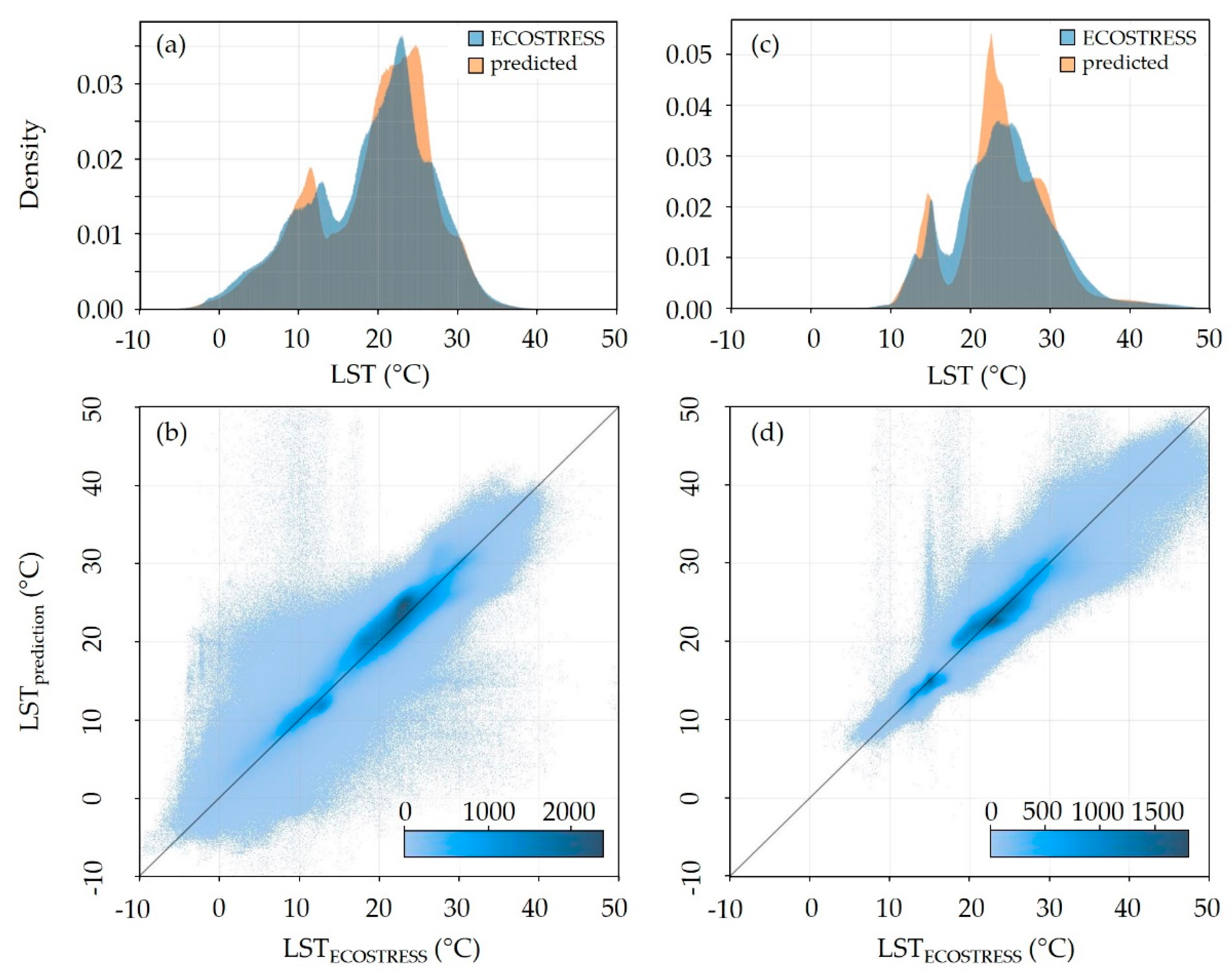
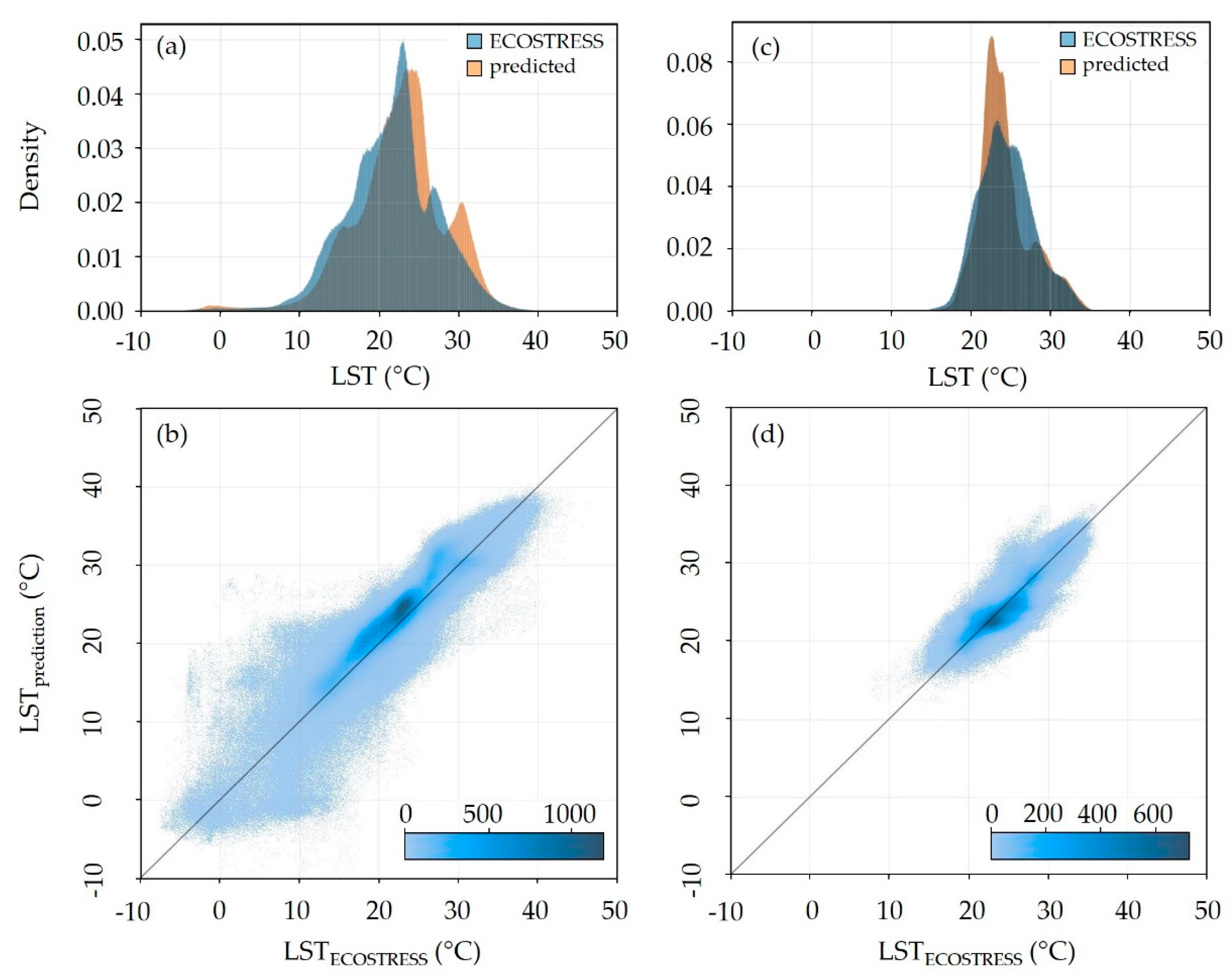
4.3. Qualitative Analysis of the Predictions
4.4. Quantitative Analysis of the Predictions
5. Discussion
5.1. Application of the Data Fusion Approach
5.2. Limitations of the Deep Learning Model
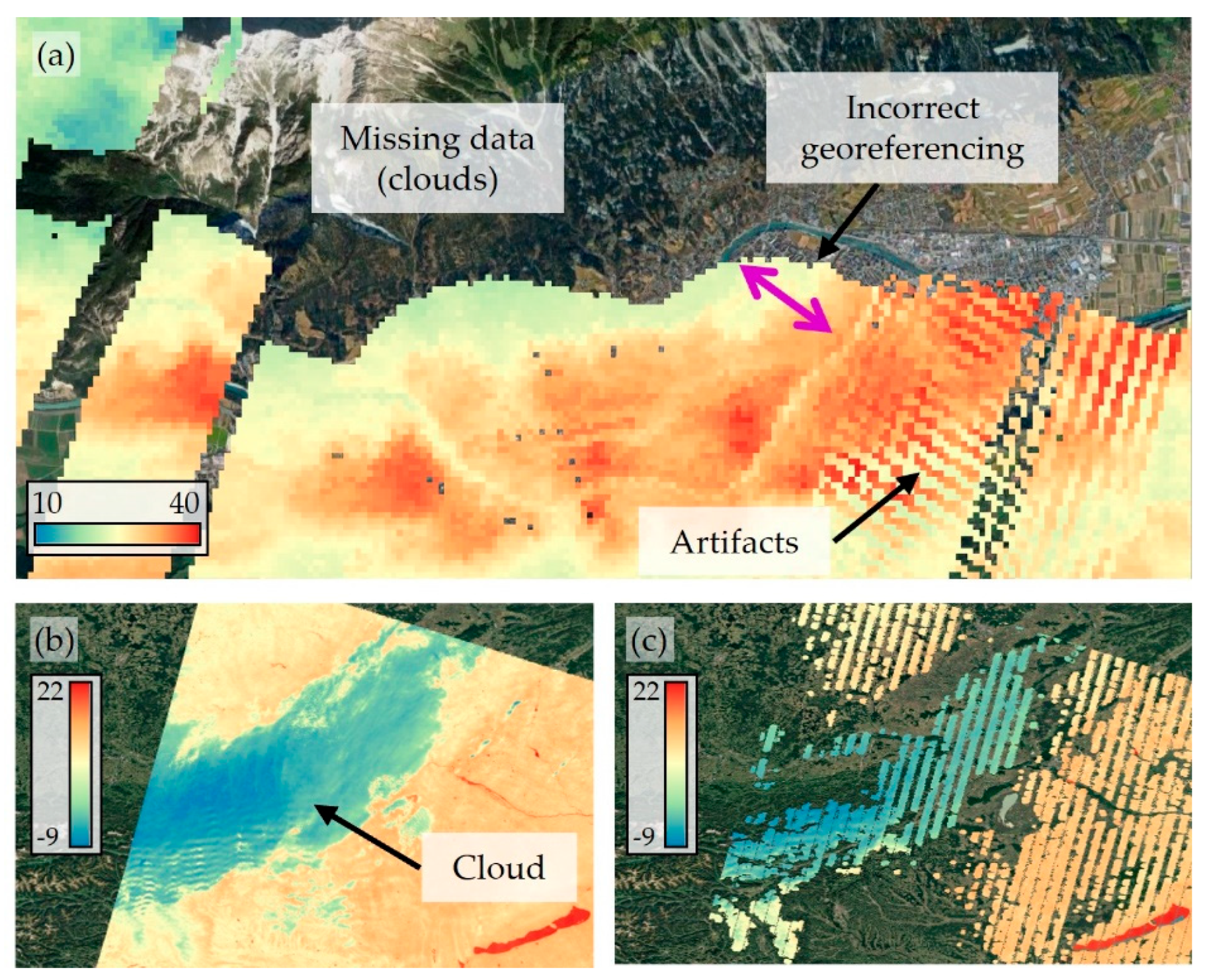
5.3. ECOSTRESS Data Quality
5.4. Future Directions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Turek-Hankins, L.L.; Coughlan de Perez, E.; Scarpa, G.; Ruiz-Diaz, R.; Schwerdtle, P.N.; Joe, E.T.; Galappaththi, E.K.; French, E.M.; Austin, S.E.; Singh, C.; et al. Climate Change Adaptation to Extreme Heat: A Global Systematic Review of Implemented Action. Oxford Open Climate Change 2021, 1, kgab005. [Google Scholar] [CrossRef]
- Oke, T.R. The Energetic Basis of the Urban Heat Island. Q. J. R. Meteorol. Soc. 1982, 108, 1–24. [Google Scholar] [CrossRef]
- Oke, T.R.; Mills, G.; Christen, A.; Voogt, J.A. Urban Climates; Cambridge University Press, 2017; ISBN 978-1-139-01647-6.
- Deilami, K.; Kamruzzaman, Md.; Liu, Y. Urban Heat Island Effect: A Systematic Review of Spatio-Temporal Factors, Data, Methods, and Mitigation Measures. Int. J. Appl. Earth Obs. Geoinf. 2018, 67, 30–42. [Google Scholar] [CrossRef]
- Logan, T.M.; Zaitchik, B.; Guikema, S.; Nisbet, A. Night and Day: The Influence and Relative Importance of Urban Characteristics on Remotely Sensed Land Surface Temperature. Remote Sens. Environ. 2020, 247, 111861. [Google Scholar] [CrossRef]
- Back, Y.; Bach, P.M.; Jasper-Tönnies, A.; Rauch, W.; Kleidorfer, M. A Rapid Fine-Scale Approach to Modelling Urban Bioclimatic Conditions. Sci. Total Environ. 2021, 756, 143732. [Google Scholar] [CrossRef]
- Back, Y.; Kumar, P.; Bach, P.M.; Rauch, W.; Kleidorfer, M. Integrating CFD-GIS Modelling to Refine Urban Heat and Thermal Comfort Assessment. Sci. Total Environ. 2023, 858, 159729. [Google Scholar] [CrossRef]
- Hart, M.A.; Sailor, D.J. Quantifying the Influence of Land-Use and Surface Characteristics on Spatial Variability in the Urban Heat Island. Theor. Appl. Climatol. 2009, 95, 397–406. [Google Scholar] [CrossRef]
- Kumar, P.; Debele, S.E.; Khalili, S.; Halios, C.H.; Sahani, J.; Aghamohammadi, N.; Andrade, M. de F.; Athanassiadou, M.; Bhui, K.; Calvillo, N.; et al. Urban Heat Mitigation by Green and Blue Infrastructure: Drivers, Effectiveness, and Future Needs. The Innovation 2024, 5. [Google Scholar] [CrossRef]
- Greene, S.; Kalkstein, L.S.; Mills, D.M.; Samenow, J. An Examination of Climate Change on Extreme Heat Events and Climate–Mortality Relationships in Large U.S. Cities. Wea. Climate Soc. 2011, 3, 281–292. [Google Scholar] [CrossRef]
- Vicedo-Cabrera, A.M.; Scovronick, N.; Sera, F.; Royé, D.; Schneider, R.; Tobias, A.; Astrom, C.; Guo, Y.; Honda, Y.; Hondula, D.M.; et al. The Burden of Heat-Related Mortality Attributable to Recent Human-Induced Climate Change. Nat. Clim. Chang. 2021, 11, 492–500. [Google Scholar] [CrossRef]
- Terzi, S.; Torresan, S.; Schneiderbauer, S.; Critto, A.; Zebisch, M.; Marcomini, A. Multi-Risk Assessment in Mountain Regions: A Review of Modelling Approaches for Climate Change Adaptation. J. Environ. Manag. 2019, 232, 759–771. [Google Scholar] [CrossRef] [PubMed]
- Intergovernmental Panel on Climate Change (IPCC) Climate Change 2022 – Impacts, Adaptation and Vulnerability: Working Group II Contribution to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press, 2023; ISBN 978-1-00-932584-4.
- Li, H.; Zhou, Y.; Li, X.; Meng, L.; Wang, X.; Wu, S.; Sodoudi, S. A New Method to Quantify Surface Urban Heat Island Intensity. Sci. Total Environ. 2018, 624, 262–272. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q.; Huang, X.; Yang, J.; Liu, Y. The Relationship between Land Surface Temperature and Artificial Impervious Surface Fraction in 682 Global Cities: Spatiotemporal Variations and Drivers. Environ. Res. Lett. 2021, 16, 024032. [Google Scholar] [CrossRef]
- Bowen, I.S. The Ratio of Heat Losses by Conduction and by Evaporation from Any Water Surface. Phys. Rev. 1926, 27, 779–787. [Google Scholar] [CrossRef]
- Mahmood, R.; Pielke Sr., R. A.; Hubbard, K.G.; Niyogi, D.; Dirmeyer, P.A.; McAlpine, C.; Carleton, A.M.; Hale, R.; Gameda, S.; Beltrán-Przekurat, A.; et al. Land Cover Changes and Their Biogeophysical Effects on Climate. Int. J. Climatol. 2014, 34, 929–953. [Google Scholar] [CrossRef]
- Schwingshackl, C.; Hirschi, M.; Seneviratne, S.I. Quantifying Spatiotemporal Variations of Soil Moisture Control on Surface Energy Balance and Near-Surface Air Temperature. J. Climate 2017, 30, 7105–7124. [Google Scholar] [CrossRef]
- Li, D.; Liao, W.; Rigden, A.J.; Liu, X.; Wang, D.; Malyshev, S.; Shevliakova, E. Urban Heat Island: Aerodynamics or Imperviousness? Sci. Adv. 2019, 5, eaau4299. [Google Scholar] [CrossRef]
- Anderson, M.C.; Norman, J.M.; Kustas, W.P.; Houborg, R.; Starks, P.J.; Agam, N. A Thermal-Based Remote Sensing Technique for Routine Mapping of Land-Surface Carbon, Water and Energy Fluxes from Field to Regional Scales. Remote Sens. Environ. 2008, 112, 4227–4241. [Google Scholar] [CrossRef]
- Dash, P.; Göttsche, F.-M.; Olesen, F.-S.; Fischer, H. Land Surface Temperature and Emissivity Estimation from Passive Sensor Data: Theory and Practice-Current Trends. Int. J. Remote Sens. 2002, 23, 2563–2594. [Google Scholar] [CrossRef]
- Dickinson, R.E. Land Surface Processes and Climate—Surface Albedos and Energy Balance. In Theory of Climate; Elsevier: Berlin/Heidelberg, Germany, 1983. [Google Scholar]
- Zhou, D.; Xiao, J.; Bonafoni, S.; Berger, C.; Deilami, K.; Zhou, Y.; Frolking, S.; Yao, R.; Qiao, Z.; Sobrino, J.A. Satellite Remote Sensing of Surface Urban Heat Islands: Progress, Challenges, and Perspectives. Remote Sens. 2019, 11, 48. [Google Scholar] [CrossRef]
- Wesley, E.J.; Brunsell, N.A. Greenspace Pattern and the Surface Urban Heat Island: A Biophysically-Based Approach to Investigating the Effects of Urban Landscape Configuration. Remote Sens. 2019, 11, 2322. [Google Scholar] [CrossRef]
- Granero-Belinchon, C.; Michel, A.; Lagouarde, J.-P.; Sobrino, J.A.; Briottet, X. Night Thermal Unmixing for the Study of Microscale Surface Urban Heat Islands with TRISHNA-Like Data. Remote Sens. 2019, 11, 1449. [Google Scholar] [CrossRef]
- Cammalleri, C.; Vogt, J. On the Role of Land Surface Temperature as Proxy of Soil Moisture Status for Drought Monitoring in Europe. Remote Sens. 2015, 7, 16849–16864. [Google Scholar] [CrossRef]
- Sun, J.; Salvucci, G.D.; Entekhabi, D. Estimates of Evapotranspiration from MODIS and AMSR-E Land Surface Temperature and Moisture over the Southern Great Plains. Remote Sens. Environ. 2012, 127, 44–59. [Google Scholar] [CrossRef]
- Galleguillos, M.; Jacob, F.; Prévot, L.; French, A.; Lagacherie, P. Comparison of Two Temperature Differencing Methods to Estimate Daily Evapotranspiration over a Mediterranean Vineyard Watershed from ASTER Data. Remote Sens. Environ. 2011, 115, 1326–1340. [Google Scholar] [CrossRef]
- Townshend, J.R.G.; Justice, C.O.; Skole, D.; Malingreau, J.-P.; Cihlar, J.; Teillet, P.; Sadowski, F.; Ruttenberg, S. The 1 Km Resolution Global Data Set: Needs of the International Geosphere Biosphere Programme. Int. J. Remote Sens. 1994, 15, 3417–3441. [Google Scholar] [CrossRef]
- Belward, A.; Bourassa, M.A.; Dowell, M.; Briggs, S. The Global Observing System for Climate: Implementation Needs 2016.
- Yu, Y.; Liu, Y.; Yu, P. Land Surface Temperature Product Development for JPSS and GOES-R Missions. In Comprehensive Remote Sensing; Elsevier: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Becker, F.; Li, Z. Surface Temperature and Emissivity at Various Scales: Definition, Measurement and Related Problems. Remote Sensing Reviews 1995, 12, 225–253. [Google Scholar] [CrossRef]
- Dash, P.; Göttsche, F.-M.; Olesen, F.-S.; Fischer, H. Retrieval of Land Surface Temperature and Emissivity from Satellite Data: Physics, Theoretical Limitations and Current Methods. J. Indian Soc. Remote Sens. 2001, 29, 23–30. [Google Scholar] [CrossRef]
- Qin, Z.; Karnieli, A. Progress in the Remote Sensing of Land Surface Temperature and Ground Emissivity Using NOAA-AVHRR Data. Int. J. Remote Sens. 1999, 20, 2367–2393. [Google Scholar] [CrossRef]
- Prata, A.J.; Caselles, V.; Coll, C.; Sobrino, J.A.; Ottlé, C. Thermal Remote Sensing of Land Surface Temperature from Satellites: Current Status and Future Prospects. Remote Sensing Reviews 1995, 12, 175–224. [Google Scholar] [CrossRef]
- Wark, D.Q.; Yamamoto, G.; Lienesch, J.H. Methods of Estimating Infrared Flux and Surface Temperature from Meteorological Satellites. J. Atmos. Sci. 1962, 19, 369–384. [Google Scholar] [CrossRef]
- Manoli, G.; Fatichi, S.; Bou-Zeid, E.; Katul, G.G. Seasonal Hysteresis of Surface Urban Heat Islands. Proc. Natl. Acad. Sci. U.S.A. 2020, 117, 7082–7089. [Google Scholar] [CrossRef] [PubMed]
- Dian, C.; Pongracz, R.; Dezső, Z.; Bartholy, J. Annual and Monthly Analysis of Surface Urban Heat Island Intensity with Respect to the Local Climate Zones in Budapest. Urban Clim. 2020, 31, 100573. [Google Scholar] [CrossRef]
- Benz, S.A.; Burney, J.A. Widespread Race and Class Disparities in Surface Urban Heat Extremes Across the United States. Earth’s Future 2021, 9, e2021EF002016. [Google Scholar] [CrossRef]
- Peng, S.; Piao, S.; Ciais, P.; Friedlingstein, P.; Ottle, C.; Bréon, F.-M.; Nan, H.; Zhou, L.; Myneni, R.B. Surface Urban Heat Island Across 419 Global Big Cities. Environ. Sci. Technol. 2012, 46, 696–703. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Oltra-Carrió, R.; Sòria, G.; Jiménez-Muñoz, J.C.; Franch, B.; Hidalgo, V.; Mattar, C.; Julien, Y.; Cuenca, J.; Romaguera, M.; et al. Evaluation of the Surface Urban Heat Island Effect in the City of Madrid by Thermal Remote Sensing. Int. J. Remote Sens. 2013, 34, 3177–3192. [Google Scholar] [CrossRef]
- Zhou, J.; Liu, S.; Li, M.; Zhan, W.; Xu, Z.; Xu, T. Quantification of the Scale Effect in Downscaling Remotely Sensed Land Surface Temperature. Remote Sens. 2016, 8, 975. [Google Scholar] [CrossRef]
- Zhou, B.; Rybski, D.; Kropp, J.P. The Role of City Size and Urban Form in the Surface Urban Heat Island. Sci. Rep. 2017, 7, 4791. [Google Scholar] [CrossRef]
- Onačillová, K.; Gallay, M.; Paluba, D.; Péliová, A.; Tokarčík, O.; Laubertová, D. Combining Landsat 8 and Sentinel-2 Data in Google Earth Engine to Derive Higher Resolution Land Surface Temperature Maps in Urban Environment. Remote Sens. 2022, 14, 4076. [Google Scholar] [CrossRef]
- Pu, R. Assessing Scaling Effect in Downscaling Land Surface Temperature in a Heterogenous Urban Environment. Int. J. Appl. Earth Obs. Geoinf. 2021, 96, 102256. [Google Scholar] [CrossRef]
- Pu, R.; Bonafoni, S. Reducing Scaling Effect on Downscaled Land Surface Temperature Maps in Heterogenous Urban Environments. Remote Sens. 2021, 13, 5044. [Google Scholar] [CrossRef]
- Masson, V.; Heldens, W.; Bocher, E.; Bonhomme, M.; Bucher, B.; Burmeister, C.; de Munck, C.; Esch, T.; Hidalgo, J.; Kanani-Sühring, F.; et al. City-Descriptive Input Data for Urban Climate Models: Model Requirements, Data Sources and Challenges. Urban Clim. 2020, 31, 100536. [Google Scholar] [CrossRef]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.-S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep Learning in Remote Sensing: A Comprehensive Review and List of Resources. IEEE Geosci. Remote Sens. 2017, 5, 8–36. [Google Scholar] [CrossRef]
- Ball, J.E.; Anderson, D.T.; Sr, C.S.C. Comprehensive Survey of Deep Learning in Remote Sensing: Theories, Tools, and Challenges for the Community. J. Appl. Remote Sens. 2017, 11, 042609. [Google Scholar] [CrossRef]
- Chlingaryan, A.; Sukkarieh, S.; Whelan, B. Machine Learning Approaches for Crop Yield Prediction and Nitrogen Status Estimation in Precision Agriculture: A Review. Comput. Electron. Agric. 2018, 151, 61–69. [Google Scholar] [CrossRef]
- Osco, L.P.; Marcato Junior, J.; Marques Ramos, A.P.; de Castro Jorge, L.A.; Fatholahi, S.N.; de Andrade Silva, J.; Matsubara, E.T.; Pistori, H.; Gonçalves, W.N.; Li, J. A Review on Deep Learning in UAV Remote Sensing. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102456. [Google Scholar] [CrossRef]
- Li, J.; Hong, D.; Gao, L.; Yao, J.; Zheng, K.; Zhang, B.; Chanussot, J. Deep Learning in Multimodal Remote Sensing Data Fusion: A Comprehensive Review. Int. J. Appl. Earth Obs. Geoinf. 2022, 112, 102926. [Google Scholar] [CrossRef]
- Yuan, Q.; Shen, H.; Li, T.; Li, Z.; Li, S.; Jiang, Y.; Xu, H.; Tan, W.; Yang, Q.; Wang, J.; et al. Deep Learning in Environmental Remote Sensing: Achievements and Challenges. Remote Sens. Environ. 2020, 241, 111716. [Google Scholar] [CrossRef]
- Huang, B.; Zhao, B.; Song, Y. Urban Land-Use Mapping Using a Deep Convolutional Neural Network with High Spatial Resolution Multispectral Remote Sensing Imagery. Remote Sens. Environ. 2018, 214, 73–86. [Google Scholar] [CrossRef]
- Cheng, G.; Xie, X.; Han, J.; Guo, L.; Xia, G.-S. Remote Sensing Image Scene Classification Meets Deep Learning: Challenges, Methods, Benchmarks, and Opportunities. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2020, 13, 3735–3756. [Google Scholar] [CrossRef]
- Corbane, C.; Syrris, V.; Sabo, F.; Politis, P.; Melchiorri, M.; Pesaresi, M.; Soille, P.; Kemper, T. Convolutional Neural Networks for Global Human Settlements Mapping from Sentinel-2 Satellite Imagery. Neural Comput. Appl. 2021, 33, 6697–6720. [Google Scholar] [CrossRef]
- Wang, L.; Scott, K.A.; Xu, L.; Clausi, D.A. Sea Ice Concentration Estimation During Melt From Dual-Pol SAR Scenes Using Deep Convolutional Neural Networks: A Case Study. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4524–4533. [Google Scholar] [CrossRef]
- Pyo, J.; Duan, H.; Baek, S.; Kim, M.S.; Jeon, T.; Kwon, Y.S.; Lee, H.; Cho, K.H. A Convolutional Neural Network Regression for Quantifying Cyanobacteria Using Hyperspectral Imagery. Remote Sens. Environ. 2019, 233, 111350. [Google Scholar] [CrossRef]
- Sobayo, R.; Wu, H.-H.; Ray, R.; Qian, L. Integration of Convolutional Neural Network and Thermal Images into Soil Moisture Estimation. In Proceedings of the 2018 1st International Conference on Data Intelligence and Security (ICDIS); April 2018; pp. 207–210. [Google Scholar]
- Hegazi, E.H.; Yang, L.; Huang, J. A Convolutional Neural Network Algorithm for Soil Moisture Prediction from Sentinel-1 SAR Images. Remote Sens. 2021, 13, 4964. [Google Scholar] [CrossRef]
- Ivanda, A.; Šerić, L.; Žagar, D.; Oštir, K. An Application of 1D Convolution and Deep Learning to Remote Sensing Modelling of Secchi Depth in the Northern Adriatic Sea. Big Earth Data 2024, 8, 82–114. [Google Scholar] [CrossRef]
- Tan, J.; NourEldeen, N.; Mao, K.; Shi, J.; Li, Z.; Xu, T.; Yuan, Z. Deep Learning Convolutional Neural Network for the Retrieval of Land Surface Temperature from AMSR2 Data in China. Sensors 2019, 19, 2987. [Google Scholar] [CrossRef]
- Mansourmoghaddam, M.; Rousta, I.; Ghafarian Malamiri, H.; Sadeghnejad, M.; Krzyszczak, J.; Ferreira, C.S.S. Modeling and Estimating the Land Surface Temperature (LST) Using Remote Sensing and Machine Learning (Case Study: Yazd, Iran). Remote Sens. 2024, 16, 454. [Google Scholar] [CrossRef]
- Han, J.; Fang, S.; Mi, Q.; Wang, X.; Yu, Y.; Zhuo, W.; Peng, X. A Time-Continuous Land Surface Temperature (LST) Data Fusion Approach Based on Deep Learning with Microwave Remote Sensing and High-Density Ground Truth Observations. Sci. Total Environ. 2024, 914, 169992. [Google Scholar] [CrossRef]
- Climate Data for Innsbruck and Vienna. Available online: en.wikipedia.org/wiki/Innsbruck, en.wikipedia.org/wiki/vienna (accessed on 7 June 2024).
- Oke, T.R. Boundary Layer Climates; 2nd ed.; Routledge, 1987;
- Matzarakis, A.; Rutz, F.; Mayer, H. Modelling Radiation Fluxes in Simple and Complex Environments: Basics of the RayMan Model. Int. J. Biometeorol. 2010, 54, 131–139. [Google Scholar] [CrossRef]
- Li, Z.-L.; Tang, B.-H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-Derived Land Surface Temperature: Current Status and Perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef]
- Xuanlan, Z.; Junbang, W.; Hui, Y.; Amir, M.; Shaoqiang, W. The Bowen Ratio of an Alpine Grassland in Three-River Headwaters, Qinghai-Tibet Plateau, from 2001 to 2018. J. Resour. Ecol. 2021, 12, 305–318. [Google Scholar] [CrossRef]
- Hulley, G.; Freepartner, R. ECOsystem Spaceborne Thermal Radiometer Experiment on Space Station (ECOSTRESS): Mission Level 2 Product User Guide; California Institute of Technology: Jet Propulsion Laboratory, 2019;
- Goffin, B.D.; Cortés-Monroy, C.C.; Neira-Román, F.; Gupta, D.D.; Lakshmi, V. At Which Overpass Time Do ECOSTRESS Observations Best Align with Crop Health and Water Rights? Remote Sens. 2024, 16, 3174. [Google Scholar] [CrossRef]
- Hulley, G.C.; Gottsche, F.M.; Rivera, G.; Hook, S.J.; Freepartner, R.J.; Martin, M.A.; Cawse-Nicholson, K.; Johnson, W.R. Validation and Quality Assessment of the ECOSTRESS Level-2 Land Surface Temperature and Emissivity Product. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–23. [Google Scholar] [CrossRef]
- NASA Earthdata Search Application. Available online: search.earthdata.nasa.gov (accessed on 13 June 2024).
- ECOSTRESS Swath to Grid Conversion Repository. Available online: git.earthdata.nasa.gov/projects/LPDUR/repos/ecostress_swath2grid (accessed on 13 June 2024).
- Haiden, T.; Kann, A.; Wittmann, C.; Pistotnik, G.; Bica, B.; Gruber, C. The Integrated Nowcasting through Comprehensive Analysis (INCA) System and Its Validation over the Eastern Alpine Region. Weather Forecast. 2011, 26, 166–183. [Google Scholar] [CrossRef]
- GeoSphere Austria Data Hub. Available online: data.hub.geosphere.at (accessed on 13 June 2024).
- European Space Agency Sentinel-2 User Handbook, ESA Standard Document Issue 1 Rev 2; ESA Communications, 2015.
- Google Cloud Sentinel-2 Data Collection. Available online: cloud.google.com/storage/docs/public-datasets/sentinel-2 (accessed on 13 June 2024).
- EEA Datahub. Available online: sdi.eea.europa.eu/catalogue/datahub (accessed on 13 June 2024).
- Copernicus Land Monitoring Service. Available online: land.copernicus.eu (accessed on 13 June 2024).
- Syrris, V.; Hasenohr, P.; Delipetrev, B.; Kotsev, A.; Kempeneers, P.; Soille, P. Evaluation of the Potential of Convolutional Neural Networks and Random Forests for Multi-Class Segmentation of Sentinel-2 Imagery. Remote Sens. 2019, 11, 907. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift; arXiv:1502. 0 3167, 2015. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Wang, Q.; Tang, Y.; Tong, X.; Atkinson, P.M. Filling Gaps in Cloudy Landsat LST Product by Spatial-Temporal Fusion of Multi-Scale Data. Remote Sens. Environ. 2024, 306, 114142. [Google Scholar] [CrossRef]
- Ma, J.; Shen, H.; Wu, P.; Wu, J.; Gao, M.; Meng, C. Generating Gapless Land Surface Temperature with a High Spatio-Temporal Resolution by Fusing Multi-Source Satellite-Observed and Model-Simulated Data. Remote Sens. Environ. 2022, 278, 113083. [Google Scholar] [CrossRef]
- Shi, J.; Hu, C. Evaluation of ECOSTRESS Thermal Data over South Florida Estuaries. Sensors 2021, 21, 4341. [Google Scholar] [CrossRef]
- Gorokhovich, Y.; Cawse-Nicholson, K.; Papadopoulos, N.; Oikonomou, D. Use of ECOSTRESS Data for Measurements of the Surface Water Temperature: Significance of Data Filtering in Accuracy Assessment. Remote Sens. Appl.: Soc. Environ. 2022, 26, 100739. [Google Scholar] [CrossRef]
- OroraTech GmbH. Available online: ororatech.com (accessed on 1 October 2024).
- Constellr GmbH. Available online: www.constellr.com (accessed on 1 October 2024).

| Dataset | Source | Resolution | Considered parameters |
|---|---|---|---|
| ECOSTRESS-LSTE | ECOSTRESS | 70 m | Land surface temperature, quality control |
| INCA | ZAMG, Austria | 1 km | Air temperature at 2 m, relative humidity at 2 m, global radiation, wind speed |
| Sentinel-2 | Sentinel-2 mission | 10/20 m | Bands B2, B3, B4, B8, B11, B12 |
| EU-DEM | Copernicus Land Monitoring Service | 25 m | Elevation, aspect, slope |
| Land cover | Copernicus Land Monitoring Service | 10 m | Tree cover density, water and wetness index, imperviousness |
| input layer | size: 5×5×15 |
| convolutional layers | kernel size: 2×2; stride: 1×1; filters: 128 (layers 1 and 2), 512 (layers 3 and 4) |
| dense layer | size: 128 |
| activation functions | rectified linear unit (‘relu’), for the final layer ‘linear’ |
| Optimizer | adam (with inverse time decay); learning rate schedule: initial_lr=0.001, decay_rate=1, steps=1000×number_samples/batch_size |
| loss function | mean absolute error |
| number of epochs | 50 |
| batch size | 512 |
| train/validation split | 80:20 |
| dropout rate | 0.1 |
| 32TPT | ||||||||||||
| date and time | hour range | MAE | ME | r2 | min | max | 10p | 15p | 85p | 90p | std | valid |
| 16.8.2023, 11:38:45 | 11:00-15:00 | 1.01 | 0.0 | 0.81 | -24.32 | 30.05 | -1.49 | -1.18 | 0.93 | 1.28 | 1.79 | 0.59 |
| 4.8.2022, 13:17:00 | 13:00-19:00 | 1.44 | -0.99 | 0.66 | -12.5 | 27.14 | -2.88 | -2.48 | 0.42 | 0.76 | 1.62 | 0.27 |
| 13.6.2023, 12:40:05 | 11:00-15:00 | 1.56 | -0.02 | 0.78 | -12.2 | 25.62 | -2.52 | -1.96 | 1.81 | 2.31 | 2.15 | 0.48 |
| 21.8.2022, 05:57:47 | 04:00-11:00 | 1.6 | 0.51 | 0.68 | -13.92 | 50.95 | -1.78 | -1.32 | 2.39 | 3.06 | 2.16 | 0.77 |
| 8.6.2023, 15:08:57 | 13:00-19:00 | 2.73 | -1.35 | 0.79 | -17.65 | 21.07 | -5.64 | -4.85 | 1.67 | 2.34 | 3.28 | 0.13 |
| 22.7.2023, 17:13:37 | 00:00-23:00 | 2.97 | 2.08 | -0.27 | -27.62 | 98.1 | -1.35 | -0.43 | 3.83 | 4.56 | 4.68 | 0.3 |
| 19.8.2023, 06:01:12 | 03:00-07:00 | 3.09 | 0.02 | 0.23 | -49.21 | 41.42 | -4.16 | -3.22 | 3.89 | 4.74 | 4.49 | 0.21 |
| 19.8.2023, 06:01:12 | 00:00-23:00 | 3.67 | -2.35 | -0.02 | -50.53 | 51.82 | -7.02 | -5.83 | 1.59 | 2.53 | 4.62 | 0.21 |
| ensemble statistics | - | 1.93 | 0.36 | 0.87 | -50.53 | 98.1 | -2.59 | -1.94 | 2.62 | 3.16 | 2.71 | 0.54 |
| 33UWP | ||||||||||||
| date and time | hour range | MAE | ME | r2 | min | max | 10p | 15p | 85p | 90p | std | valid |
| 2.7.2022, 5:26:25 | 00:00-23:00 | 0.85 | -0.14 | 0.46 | -6.81 | 28.6 | -1.43 | -1.16 | 0.74 | 1.04 | 1.38 | 0.62 |
| 2.7.2022, 5:26:25 | 03:00-07:00 | 0.98 | -0.46 | 0.49 | -5.69 | 25.87 | -1.83 | -1.58 | 0.65 | 0.92 | 1.27 | 0.62 |
| 15.8.2023, 07:36:45 | 04:00-11:00 | 1.1 | 0.0 | 0.69 | -7.39 | 8.05 | -1.77 | -1.4 | 1.38 | 1.74 | 1.43 | 0.66 |
| 2.7.2022, 5:26:25 | 04:00-11:00 | 1.1 | 0.03 | -0.13 | -16.65 | 56.41 | -1.65 | -1.37 | 1.23 | 1.56 | 2.01 | 0.62 |
| 16.8.2022, 11:38:39 | 00:00-23:00 | 2.18 | -0.72 | 0.81 | -20.24 | 17.37 | -4.45 | -3.42 | 1.85 | 2.41 | 2.97 | 0.41 |
| 12.8.2023, 13:13:33 | 07:00-11:00 | 2.26 | -0.65 | -0.15 | -13.32 | 62.62 | -3.9 | -3.35 | 1.98 | 3.06 | 2.84 | 0.24 |
| 18.6.2023, 10:13:08 | 00:00-23:00 | 2.55 | -2.14 | 0.4 | -17.4 | 7.81 | -5.7 | -4.88 | 0.27 | 0.72 | 2.59 | 0.53 |
| 18.6.2023, 10:13:08 | 00:00-23:00 | 2.61 | -2.39 | 0.4 | -17.34 | 62.68 | -5.59 | -4.81 | -0.21 | 0.33 | 2.33 | 0.53 |
| ensemble statistics | - | 1.6 | -0.15 | 0.87 | -33.14 | 135.46 | -2.68 | -2.08 | 1.78 | 2.27 | 2.22 | 0.59 |
| Model | MAE | ME | r2 | min | max | 10p | 15p | 85p | 90p | std | valid |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 32TPT, full day | 2.16 | -0.04 | 0.82 | -50.53 | 98.1 | -3.41 | -2.69 | 2.48 | 3.04 | 3.09 | 0.55 |
| 32TPT, afternoon | 1.96 | 1.06 | 0.81 | -27.3 | 27.14 | -1.56 | -0.92 | 3.02 | 3.47 | 2.29 | 0.48 |
| 33UWP, full day | 1.79 | -0.25 | 0.85 | -33.14 | 135.46 | -3.17 | -2.48 | 1.86 | 2.38 | 2.51 | 0.58 |
| 33UWP, afternoon | 1.39 | -0.19 | 0.73 | -9.71 | 10.44 | -2.4 | -1.94 | 1.58 | 2.06 | 1.77 | 0.61 |
| Model | MAE | r2 | ME | min | max | 10p | 15p | 85p | 90p | std | valid |
| 32TPT, extrapolating predictions | 3.12 | 0.72 | -0.35 | -52.81 | 56.51 | -5.41 | -4.28 | 3.42 | 4.33 | 4.14 | 0.55 |
| 33UWP, extrapolating predictions | 2.96 | 0.64 | 0.28 | -46.14 | 30.37 | -4.67 | -3.48 | 3.92 | 4.57 | 3.8 | 0.61 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





