A Green Computing Business Aggregation Strategy for LEO Satellite Networks

1. Introduction

The 6th generation mobile networks (6G) are expected to offer higher data transmission rates, broader coverage, and reduced latency to meet the extensive future demands in information transmission and processing [1]. Low Earth Orbit (LEO) satellite networks (LSNs) provide full coverage for remote regions and, compared to other satellite systems, offer lower latency, making them a critical component of 6G [2].

Despite these advantages, LSNs face significant challenges due to energy limitations, as LEO satellites rely on solar cells for power, leading to unstable energy supplies as satellites alternate between shadow and sunlight periods. This energy limitation affects the continuous operation and service reliability of LSNs [3].

To address these energy constraints, efficient solar energy acquisition is crucial. Perovskite-based solar cells have shown potential for improving energy conversion in space applications by increasing solar radiation absorption through optimized heat stimulation [4]. Additionally, effective onboard energy management can further optimize performance. For instance, managing energy usage across sunlit and shadow periods enhances transmission efficiency and coverage in high-mobility, large-scale connection scenarios [5].

Existing studies highlight that business aggregation in LSNs can yield significant green energy-saving effects. Studies [6,7] demonstrate that roughly 45% of LEO satellite nodes can be deactivated in low-demand regions without substantial latency increases. Furthermore, on-demand inter-satellite link management can reduce network energy consumption. However, these strategies lack quantification of latency costs associated with business aggregation.

This paper addresses the business aggregation challenge in LSNs. Our contributions are as follows: first, under a three-layer architecture comprising control, service, and user layers, we introduce an Energy-Delay Ratio (EDR) metric to assess the effectiveness of business aggregation; second, we propose an Optimal Consolidation Strategy for Business Efficiency (OCSBE) based on MDP-Double DQN optimization; finally, we validate the strategy’s effectiveness through simulation.

2. System Model

2.1. Network Model

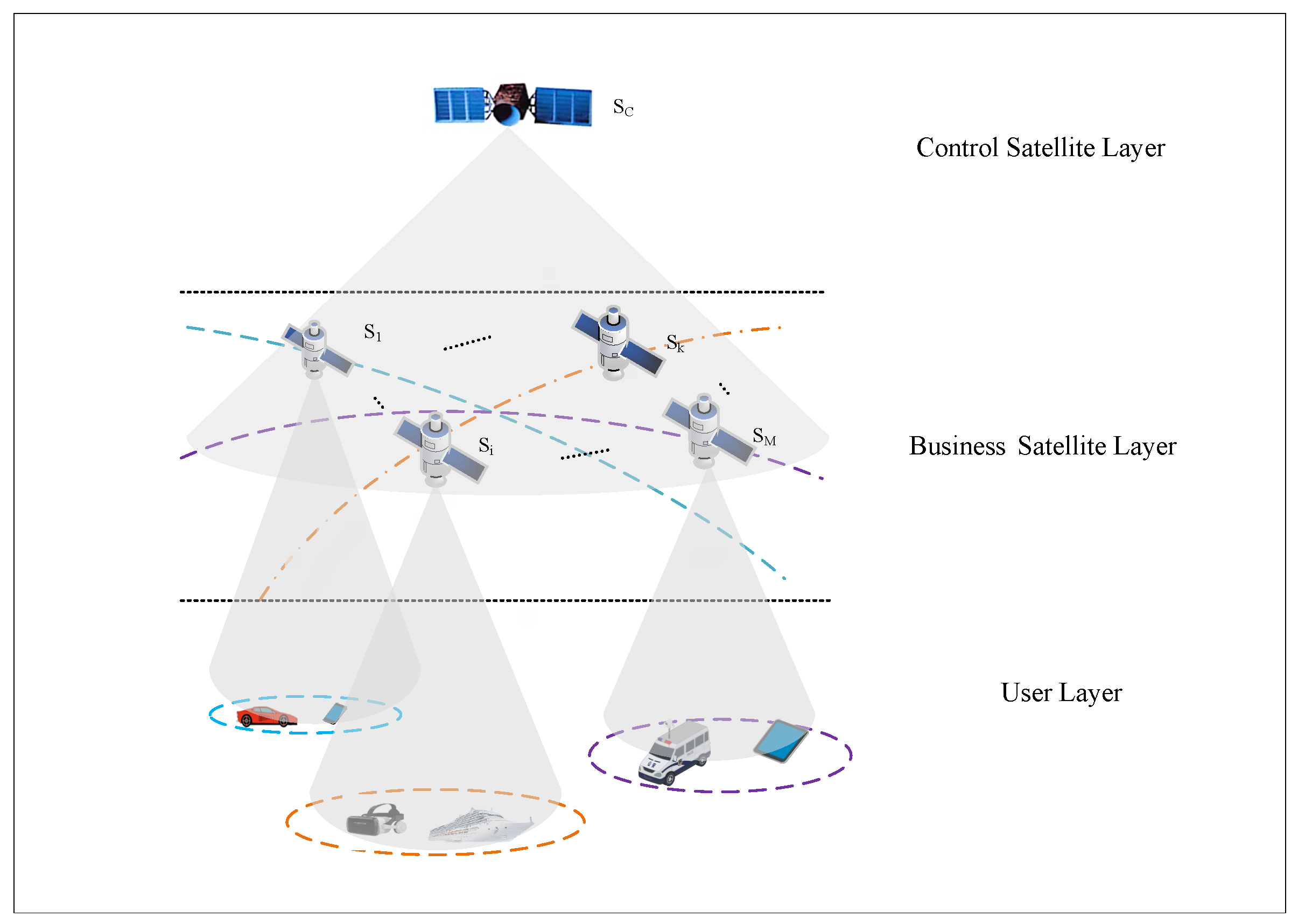
The layered LSNs network architecture is shown in Figure 1. The control satellite layer is composed of high-orbit satellites denoted as $S_c$, responsible for making aggregation decisions for the service satellites. The business satellite layer consists of M LEO satellites in low Earth orbit, responsible for handling specific businesses. Define the set of business satellites as $\mathbb{S}=\{S_1,\dots ,S_i,\dots ,S_k,\dots ,S_M\}$, where $S_i$ and $S_k$ represent any arbitrary business satellites. The user layer consists of various types of terminals located on the ground, which generate businesses and transmit them to the business satellites covering their region.

The set of businesses received by the business satellite layer is defined as $\mathcal{T}=\{T_1,\dots ,T_i,\dots ,T_k$, $\dots ,T_M\}$, where $T_i$ and $T_k$ are the businesses received by satellites $S_i$ and $S_k$, respectively. The set of business counts received by the business satellites is $\mathcal{N}=\{N_1,\dots ,N_i,\dots ,N_k,\dots ,N_M\}$, where $N_i$ and $N_k$ represent the number of businesses received by satellites $S_i$ and $S_k$, respectively. Define the sequence of businesses received by $S_i$ as $T_i=\{{\mathbb{T}}_{i1},\dots ,{\mathbb{T}}_{ij},\dots ,{\mathbb{T}}_{i{N}_i}\}$, where ${\mathbb{T}}_{ij}$ is the j-th business received by $S_i$. The attribute list for business ${\mathbb{T}}_{ij}$ is defined as ${\mathbb{T}}_{ij}=\{B_{ij},D_{ij}^{max}\}$, where $B_{ij}$ is the data size of business ${\mathbb{T}}_{ij}$, in bits, and $D_{ij}^{max}$ is its maximum tolerable delay, in seconds.

The LEO satellite orbit model is given by:

$$r\left(t\right)=(R+h)[1-ecos\alpha (t\left)\right]$$

(1)

where R is the Earth’s radius, h is the altitude of the satellite, e is the orbital eccentricity, and $\alpha \left(t\right)$ is the true anomaly angle.

The distance between two satellites $S_i$ and $S_k$ is calculated as:

$${\mathcal{D}}_{ik}=\sqrt{d_{ik}^2+{(h_i-h_k)}^2}$$

(2)

where $d_{ik}$ is the spherical distance between $S_i$ and $S_k$, and $h_i$, $h_k$ are their respective orbital heights.

2.2. Communication Model

The uplink channel capacity between a ground user and $S_i$ is:

$$C_{G{S}_i}=B_{G{S}_i}{log}_2\left(1+{\displaystyle \frac{P_{tx}{G}_{tx}{H}_{G{S}_i}}{N_{G{S}_i}}}\right)$$

(3)

where $B_{G{S}_i}$ is the channel bandwidth, $P_{tx}$ and $G_{tx}$ are the transmit power and antenna gain of the user equipment, $H_{G{S}_i}$ is the channel gain, and $N_{G{S}_i}$ is the noise power [8].

The transmission delay for business ${\mathbb{T}}_{ij}$ from the user to $S_i$ is given by:

$$D_{ij}={\displaystyle \frac{B_{ij}}{C_{G{S}_i}}}$$

(4)

The channel capacity between $S_i$ and $S_k$ is:

$$C_{S_i{S}_k}=B_{S_i{S}_k}{log}_2\left(1+{\displaystyle \frac{P_{TX}{G}_{TX}{H}_{S_i{S}_k}}{N_{S_i{S}_k}}}\right)$$

(5)

where $B_{S_i{S}_k}$ is the bandwidth, $P_{TX}$ is the transmission power, $G_{TX}$ is the antenna gain of $S_i$, $H_{S_i{S}_k}$ is the channel gain between $S_i$ and $S_k$, and $N_{S_i{S}_k}$ is the noise power.

The delay required for transmitting ${\mathbb{T}}_{ij}$ from $S_i$ to $S_k$ is:

$$D_{ijk}={\displaystyle \frac{B_{ij}}{C_{S_i{S}_k}}}$$

(6)

Since the computational results to be sent back to the ground are relatively small, the energy consumption and delay for the return transmission are negligible.

2.3. Computation Model

For a business ${\mathbb{T}}_{ij}$ being processed at $S_i$, the computation delay, assuming the existence of a ta business queue, is:

$$D_{ij}^c=\sum _{l=1}^{j-1}{\displaystyle \frac{B_{il}·\kappa }{f}}+{\displaystyle \frac{B_{ij}·\kappa }{f}}$$

(7)

where f is the CPU processor frequency of $S_i$ (in cycles/s), and $\kappa$ represents the computation capability (in cycles/bit).

The total delay for $S_i$ to process all businesses $T_i$ is:

$$D_i=\sum _{j=1}^{N_i}{\displaystyle \frac{B_{ij}·\kappa }{f}}$$

(8)

The energy consumed for computation at $S_i$ is:

$$E_c^i=P_c·D_i$$

(9)

where $P_c$ is the computation power of $S_i$.

3. Problem Modeling

Based on the operational modes of satellites, the working state of $S_i$ can be divided into three states: active, idle, and sleep. In the active state, the satellite performs business transmission and computation businesses, consuming the highest power, with average power consumption for transmission, reception, and computation modules denoted as $P_T^a$, $P_R^a$, and $P_C^a$, respectively. In the idle state, the satellite maintains a low-power mode for communication and computation modules, with power levels $P_T^{idle}$, $P_R^{idle}$, and $P_C^{idle}$. In the sleep state, the computation module is turned off to save power, with $P_C^{sleep}=0$, though communication functions remain active for rapid response [9,10].

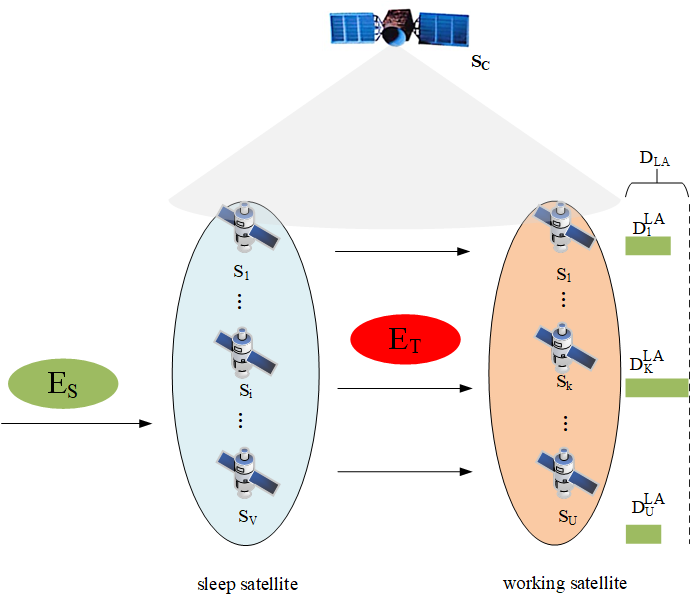
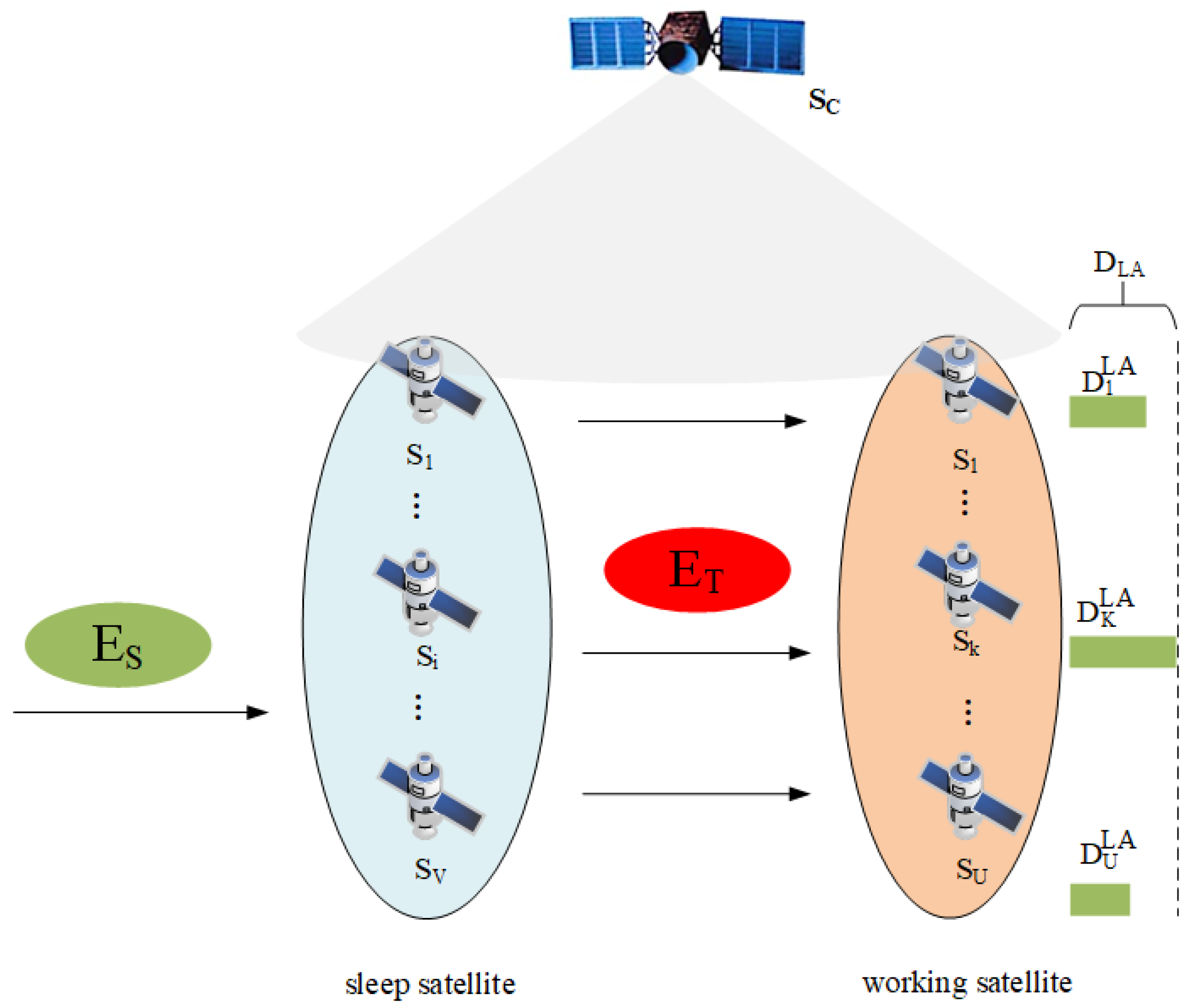
In specific scenarios, such as low business volume at night or in sparsely populated regions, certain satellites are underutilized. To enhance energy efficiency, a business aggregation strategy can be employed to consolidate businesses on a subset of satellites, allowing others to enter a sleep state.

As illustrated in Figure 2, the LSNs concentrate business processing on a subset of service satellites, allowing other satellites to enter a sleep state. Define the set of sleeping satellites as ${\mathbb{S}}^S=\{S_1,\dots ,S_U\}$ and working satellites as ${\mathbb{S}}^W=\{S_1,\dots ,S_V\}$, where U and V represent the number of sleeping and working satellites, respectively, such that $U+V=M$.

The energy consumption for transferring a business ${\mathbb{T}}_{ij}$ from a sleeping satellite $S_i$ to a working satellite $S_k$ is:

$$E_T^{ijk}=(P_T^a+P_R^a)·D_{ijk}$$

(10)

The total communication energy for aggregating businesses from ${\mathbb{S}}^S$ to ${\mathbb{S}}^W$ is:

$$E_T=\sum _{i=1}^V\sum _{j=1}^{N_i}{E}_T^{ijk}$$

(11)

The energy savings for a sleeping satellite $S_i$ is:

$$E_s^i=P_C^{idle}·\tau$$

(12)

where $\tau$ is the duration of the sleep period.

The total energy savings for all sleeping satellites ${\mathbb{S}}^S$ is:

$$E_s=\sum _{i=1}^V{E}_s^i$$

(13)

The net energy saved by business aggregation is:

$$\mathrm{\Delta }E=E_s-E_T$$

(14)

After receiving businesses from sleeping satellites, the working satellite $S_k$ updates its business queue. Suppose business ${\mathbb{T}}_{ij}$ is assigned a sequence number $N_a$ upon insertion; then the updated queue for $S_k$ is $T_k^{\prime }=\{{\mathbb{T}}_{k1},\dots ,{\mathbb{T}}_{k{N}_a},\dots ,{\mathbb{T}}_{k{N}_k^{\prime }}\}$, where $N_k^{\prime }$ represents the total number of businesses in $S_k$ after aggregation.

The computation delay for $S_k$ processing ${\mathbb{T}}_{k{N}_a}$ after aggregation is:

$$D_{ijk}^c=\sum _{l=1}^{N_a}{\displaystyle \frac{B_{kl}·\kappa }{f}}$$

(15)

The total computation delay for $S_k$ after aggregation is:

$$D_k^{LA}=\sum _{m=1}^{N_k^{\prime }}{\displaystyle \frac{B_{km}·\kappa }{f}}$$

(16)

The maximum delay for all working satellites after aggregation is:

$$D_{LA}=max(D_1^{LA},\dots ,D_V^{LA})$$

(17)

The maximum delay without aggregation is:

$$D_o=max(D_1,\dots ,D_M)$$

(18)

The delay increment due to aggregation is:

$$\mathrm{\Delta }D=D_{LA}-D_o$$

(19)

To comprehensively evaluate the impact of energy savings and delay increase, we define the Energy-Delay Ratio (EDR) as:

$$EDR={\displaystyle \frac{\mathrm{\Delta }E}{\mathrm{\Delta }D}}$$

(20)

where EDR represents the energy savings per unit delay increase (in J/s).

The optimization objective of the business aggregation strategy is defined as:

$$\begin{array}{c}\mathrm{maximize}\mathrm{EDR}\hfill \\ \mathrm{subject}\mathrm{to}\text{:}\hfill \\ D_{ij}+D_{ijk}+D_{ijk}^c<D_{ij}^{\max }\left(\mathrm{a}\right)\hfill \\ {\displaystyle \sum _{k=1}^M}{x}_{ijk}=1\left(\mathrm{b}\right)\hfill \\ 1\le U\le M\left(\mathrm{c}\right)\hfill \\ U+V=M\left(\mathrm{d}\right)\hfill \end{array}$$

(21)

where constraint (a) ensures that the business processing time is less than the maximum tolerable delay for the business; constraint (b) ensures that each business ${\mathbb{T}}_{ij}$ is assigned only once, with $x_{ijk}$ taking a value of 0 or 1 to indicate whether the business is assigned to business satellite $S_k$; constraint (c) defines the range of the number of working satellites; and constraint (d) ensures that the sum of working and sleeping satellites equals the total number of business satellites.

4. Problem Solution

The optimization problem includes both continuous and discrete variables, making it a Mixed-Integer Programming (MIP) problem. Due to the non-linear constraints, this problem can be classified as a Mixed-Integer Nonlinear Programming (MINLP) problem. To address this complex optimization, we decompose it into two sub-problems:

• Sub-problem 1: Determining the Set of Sleeping Satellites
• Sub-problem 2: Aggregating Businesses from Sleeping Satellites to Working Satellites

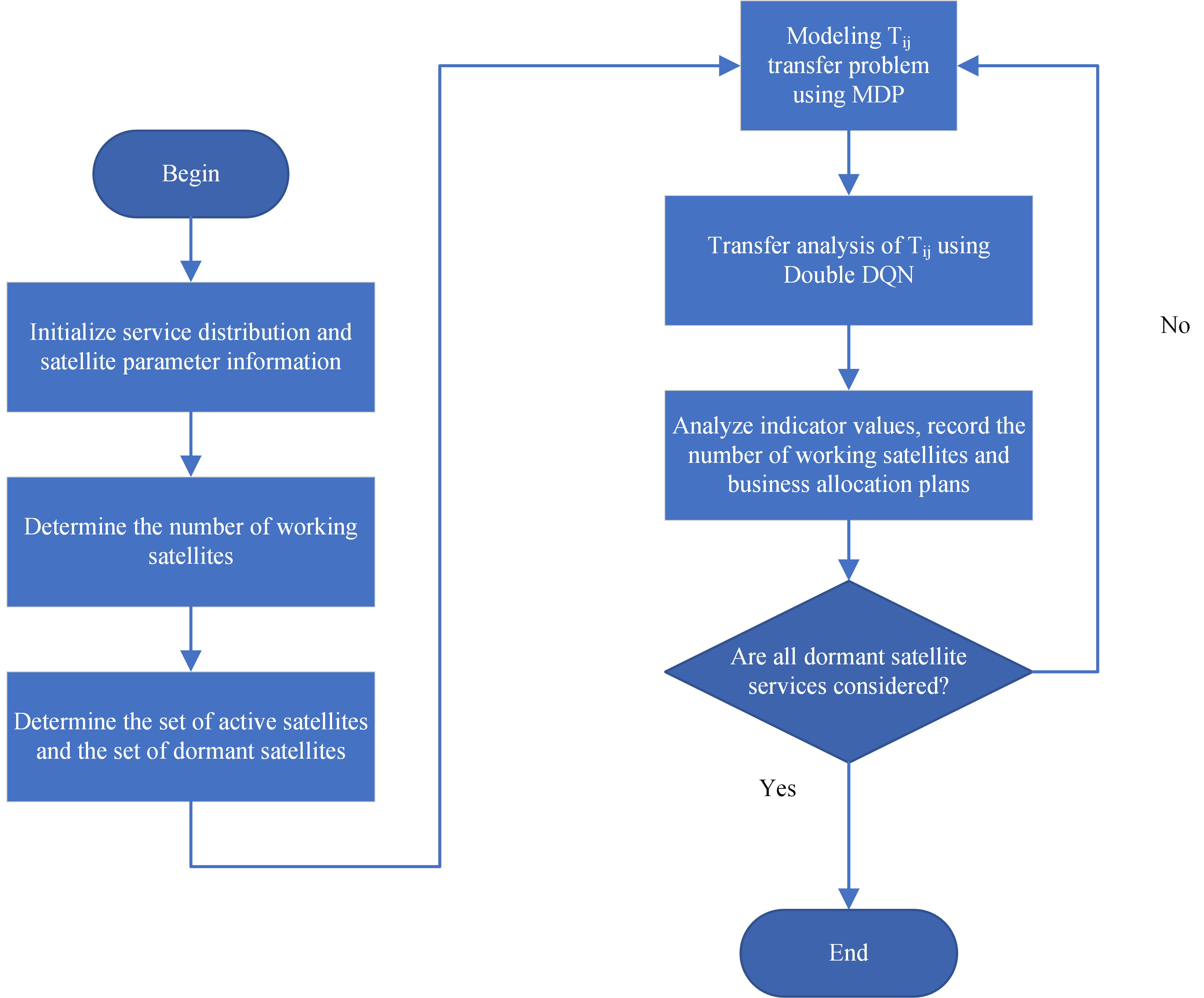
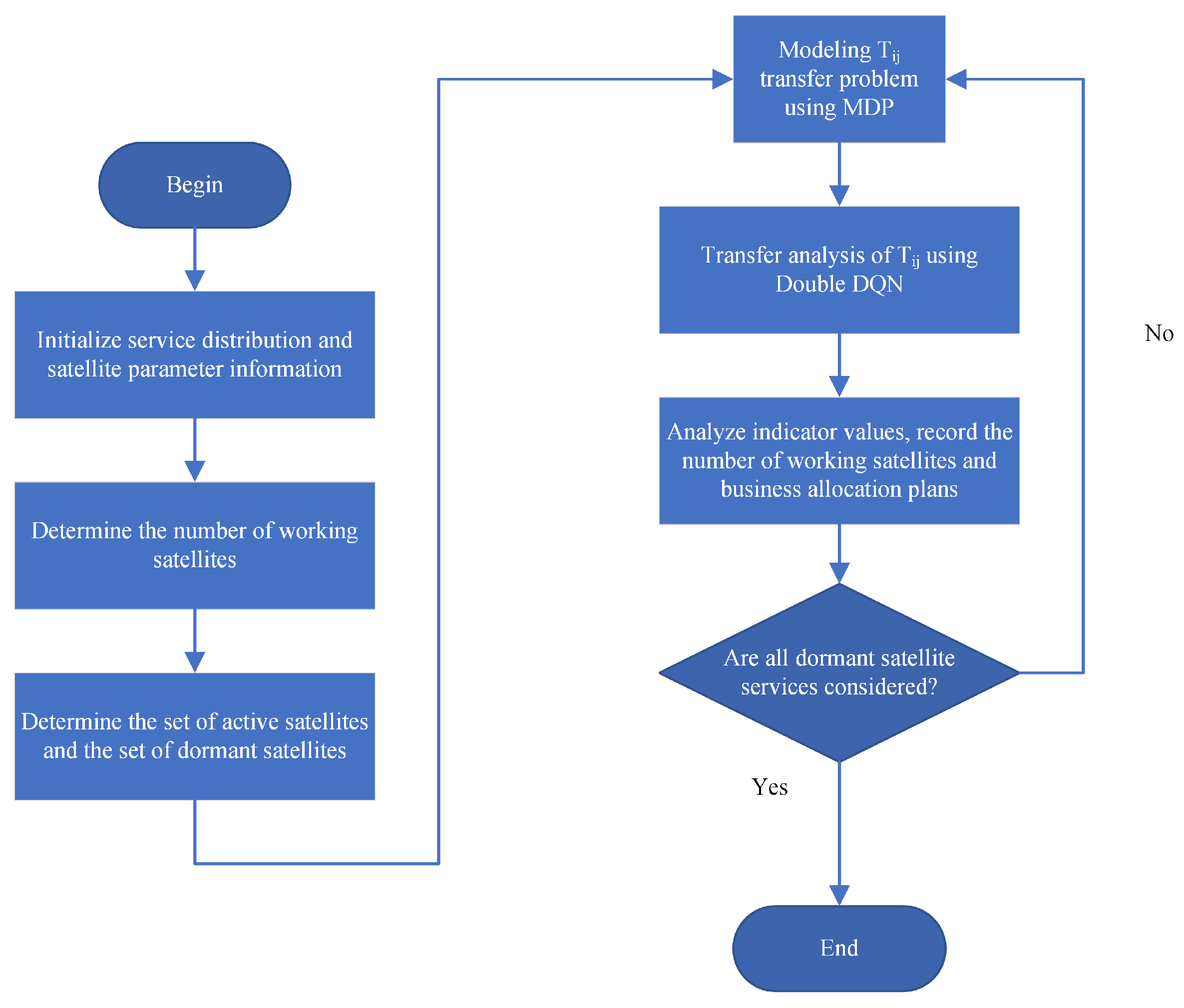
We propose the Optimal Consolidation Strategy for Business Efficiency (OCSBE) to aggregate businesses on service satellites. The procedure is illustrated in Figure 3.

• Step 1: Initialization. The control satellite initializes the process by collecting information on service distribution and satellite parameters.
• Step 2: Determine the Number of Working Satellites. Based on the current service volume, determine the number of satellites that will remain active.
• Step 3: Determine the Set of Active Satellites and the Set of Dormant Satellites. Classify satellites into active and dormant sets based on service demand.
• Step 4: Model the $T_{ij}$ Transfer Problem Using MDP. Use a Markov Decision Process (MDP) to model the transfer problem for $T_{ij}$.
• Step 5: Perform Transfer Analysis of $T_{ij}$ Using Double DQN. Conduct transfer analysis for $T_{ij}$ using a Double Deep Q-Network (Double DQN).
• Step 6: Analyze Indicator Values, Record the Number of Working Satellites and Business Aggregation Plans. Analyze indicator values, and record the number of active satellites and the business aggregation scheme.
• Step 7: Check if All Dormant Satellite Services Are Considered. Verify if all services for dormant satellites have been considered. If not, return to continue the process; if yes, end the process.

4.1. Determining the Set of Sleeping Satellites

For Sub-problem 1, this paper adopts the Capacity-Driven Sleep Satellite Quantity (CDSSQ) mechanism to determine the number of sleeping satellites. The design is as follows:

• Sorting Satellites: First, sort the business satellites in ascending order based on their business volume to obtain the list ${\mathbb{S}}^{\prime }=\{S_1,S_2,\dots ,S_k,\dots ,S_M\}$.
• Calculating the Number of Working Satellites: Determine the number of working satellites V using the relationship between the current business volume $B^c$ and the system’s maximum capacity $B^{max}$ as per Equation 22:

  $$V=⌈{\displaystyle \frac{B^c}{B^{max}}}·M⌉$$

  (22)

  where $B^c$ represents the current total business volume of ${\mathbb{S}}^{\prime }$; $B^{max}$ is the maximum computable business volume per satellite (measured in bits); and $\lceil ·\rceil$ denotes the ceiling function.
• Determining Satellite Sets: Based on the calculated number V and the sorted list ${\mathbb{S}}^{\prime }$, identify the set of working satellites ${\mathbb{S}}^W$ and the set of sleeping satellites ${\mathbb{S}}^S$.

4.2. Aggregating Businesses

We address this sub-problem by modeling it as a Markov Decision Process (MDP) and employing a Double Deep Q-Network (Double DQN) for business reassignment.

4.2.1. MDP Element Group

• Define the elements of the MDP as follows:
  • State Space ($s_t$):

    $$s_t=\{V,B_1,\dots ,B_i,\dots ,B_k,\dots ,B_M\}$$

    where $B_i$ represents the current business volume of satellite $S_i$.
  • Action Space ($a_t$):

    $$a_t=\{a_1,\dots ,a_k,\dots ,a_V\}$$
    Each action $a_k$ denotes assigning business ${\mathbb{T}}_{ij}$ to satellite $S_k$.
  • Transition Probability ($P(s_{t+1}\mid s_t,a_t)$): The probability of assigning business ${\mathbb{T}}_{ij}$ to satellite $S_k$ is represented as:

    $$P(B_k+B_{ij}\mid B_k,a_k)$$
    This denotes the probability of satellite $S_k$ transitioning from state $B_k$ to state $B_k+B_{ij}$ after action $a_k$.
  • Reward Function ($R(s_t,a_t)$): The reward for assigning business ${\mathbb{T}}_{ij}$ to satellite $S_k$ is defined as:

    $$R(B_k,a_k)={\displaystyle \frac{D_{ijk}·P_C^{idle}-D_{ijk}·(P_T^a+P_R^a)}{D_{ijk}+D_{ijk}^c-D_{ij}^c}}$$

    (23)

    where $D_{ijk}$ is the energy difference associated with the business transfer; $P_C^{idle}$ is the idle power consumption; $P_T^a$ and $P_R^a$ are the transmission and reception power consumptions, respectively; and $D_{ijk}^c$ and $D_{ij}^c$ represent delay components.
  • Discount Factor ($\gamma$):$\gamma$ is a discount factor between 0 and 1 that balances the importance of current and future rewards.

4.2.2. Double DQN

The Double DQN approach is designed to reduce the overestimation of Q-values by decoupling the action selection from the action evaluation. The implementation details are as follows:

Utilize Double DQN to learn the optimal business aggregation policy that maximizes cumulative rewards. Double DQN employs two Q-networks to mitigate the overestimation of Q-values:

• Online Network ($Q_o(s_t,a_t;\theta )$): The primary network used for selecting actions.
• Target Network ($Q_T(s_t,a_t;{\theta }^{-})$): A secondary network with parameters ${\theta }^{-}$ that are periodically updated to stabilize training.

• Action Selection Using $\epsilon$-Greedy Strategy: Based on the $\epsilon$-greedy policy, an action $a_k$ is selected in a given state $s_t$ as per:

  $$a_k=\left\{\begin{array}{cc}\mathrm{random}\mathrm{action}\hfill & \mathrm{if}\mathrm{random}<\epsilon \hfill \\ arg\underset{a}{max}{Q}_o(s_t,a;\theta )\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

  (24)

  where $\epsilon$ is a probability between 0 and 1 representing the likelihood of choosing a random action for exploration, and $Q_o(s_t,a;\theta )$ is the action-value function of the online network.
• Calculating Transition Probabilities: The probability of transferring business ${\mathbb{T}}_{ij}$ to satellite $S_k$ is computed as:

  $$P(B_k+B_{ij}\mid B_k,a_k)=\left\{\begin{array}{cc}{\displaystyle \frac{B_k^{max}-B_{ij}-B_k}{B_k^{max}}}\hfill & \mathrm{if}{B}_{ij}+B_k<B_k^{max}\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

  (25)

  where $B_k^{max}$ is the maximum business volume that satellite $S_k$ can handle, and $B_k$ represents the current business volume of satellite $S_k$.
• Reward Calculation: The reward for taking action $a_k$ in state $B_k$ is calculated as:

  $$R(B_k,a_k)={\displaystyle \frac{D_{ijk}·P_C^{idle}-D_{ijk}·(P_T^a+P_R^a)}{D_{ijk}+D_{ijk}^c-D_{ij}^c}}$$

  (26)
• Updating the Q-Values Using the Bellman Equation: Update the Q-value of the online network using the Bellman equation as shown:

  $$Q_o(s_t,a_k;\theta )\leftarrow Q_p(s_t,a_k;\theta )+\alpha \left[R(B_k,a_k)+\gamma \underset{a^{\prime }}{max}{Q}_T(s_{t+1},a^{\prime };{\theta }^{-})-Q_p(s_t,a_k;\theta )\right]$$

  (27)

  where: where $Q_p(s_t,a_k;\theta )$ is the previous Q-value before the update, $\alpha$ is the learning rate, $\gamma$ is the discount factor, and ${\theta }^{-}$ are the parameters of the target network.
• Convergence Check: Perform a convergence check to determine if the Q-values have stabilized:

  $$\mathrm{\Delta }Q=\left|Q_o(S_t,a_k;\theta )-Q_p(S_t,a_k;\theta )\right|<\delta$$

  (28)

  where $\delta$ is a small threshold value. If $\mathrm{\Delta }Q$ remains below $\delta$ for multiple consecutive updates, the Q-values are considered to have converged, indicating that the optimal business aggregation strategy for ${\mathbb{T}}_{ij}$ has been found.

Repeat the above steps to make aggregation decisions for all businesses that need to be transferred, and form the final business-working satellite mapping.

5. Simulation Analysis

5.1. Simulation Parameter Design

By using STK to build a three-layer network architecture scenario, the control satellite is set at an altitude of 2000 km, while the business satellites are distributed at altitudes ranging from 500 to 1500 km. The power range for the entire functional module transmitting inter-satellite signals is 10 W to 50 W [10], the power range for the entire functional module receiving signals is 5 W to 25 W [10], and the power range for the entire functional module performing computations is 60 W to 415 W [11]. The clock frequency of the satellite CPU is $2\times {10}^{10}$ cycles/s [12]. The parameters for LSNs are shown in Table 1.

The Double DQN strategy parameters are listed in Table 2. The learning rate was set to 0.001, ensuring a stable parameter update step size, with an epsilon decay rate of 0.995 to balance exploration and exploitation phases. The discount factor $\gamma$ was set to 0.99 to emphasize the importance of long-term rewards, and the training involved 500 episodes.

5.2. Strategy Simulation and Analysis

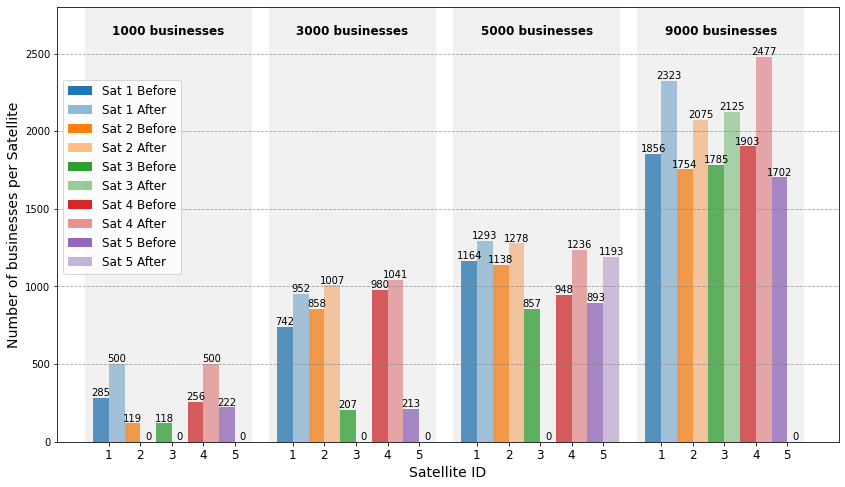
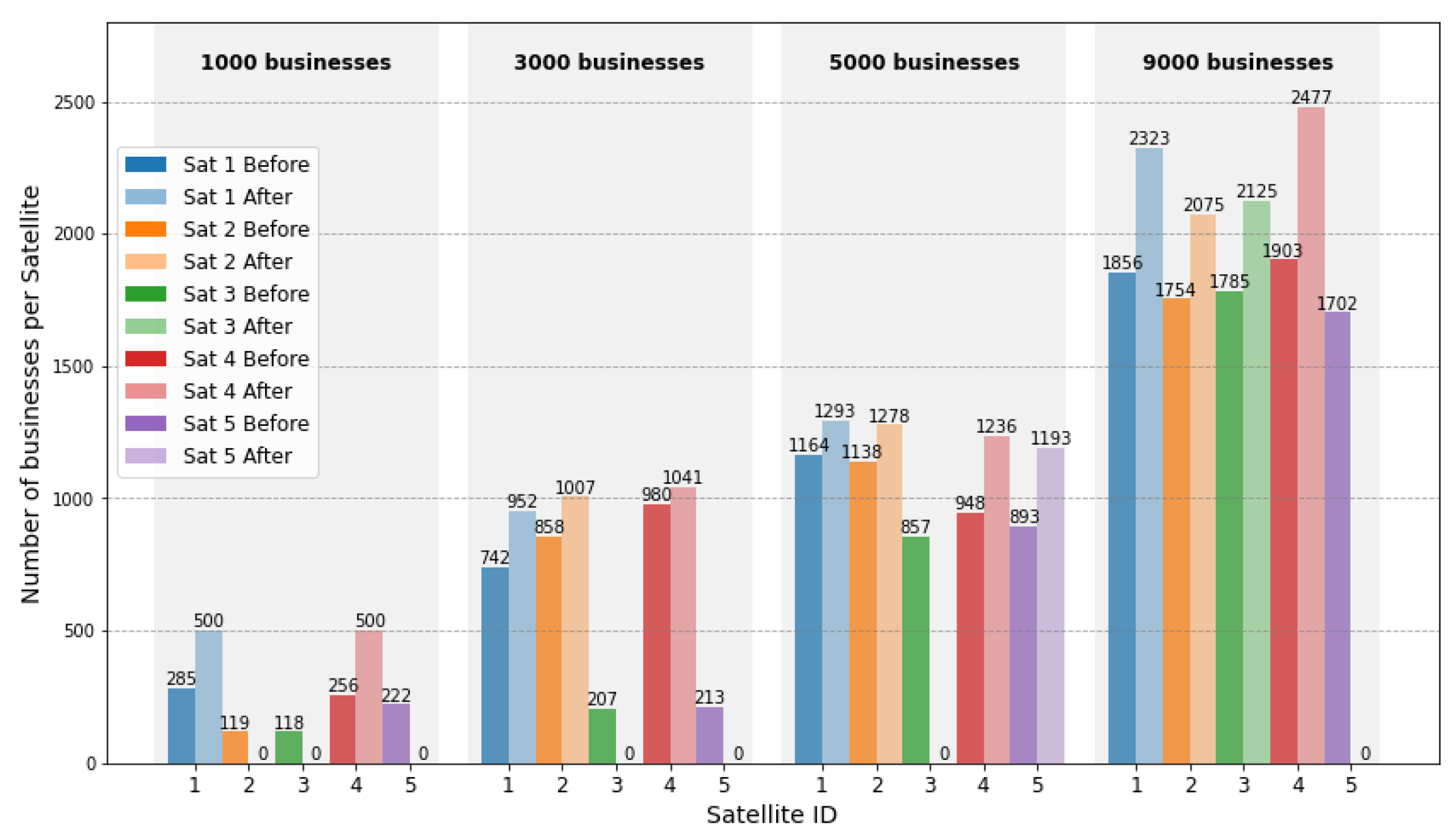
Figure 4 shows the performance of the proposed aggregation strategy. As business volume increases, the number of satellites involved in processing also grows. The strategy favors satellites with initially higher business volumes for aggregation, reducing transmission energy. Furthermore, the load distribution among working satellites becomes more balanced due to the reward-punishment mechanism, which optimizes the overall performance of the system.

To validate the performance advantage of the proposed strategy, this paper compares it with the following baseline strategies:

• Ant Colony Strategy (AC): This strategy generates aggregation decisions and resource aggregations by simulating ant colony behavior for global optimization.
• MDP-QL Strategy (MDP-QL): This strategy constructs a Q-table to generate aggregation decisions and resource aggregations, aiming to achieve global optimization.

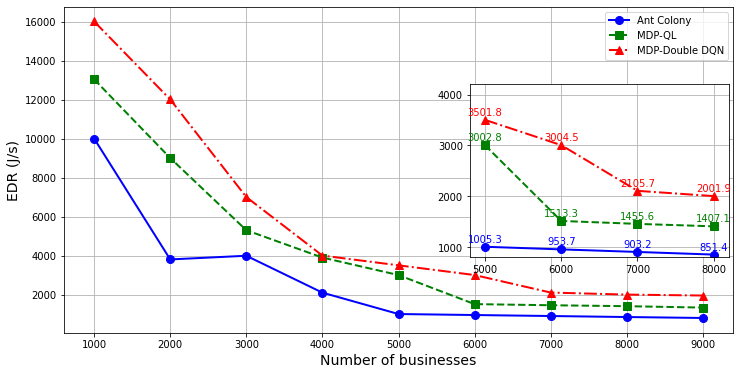
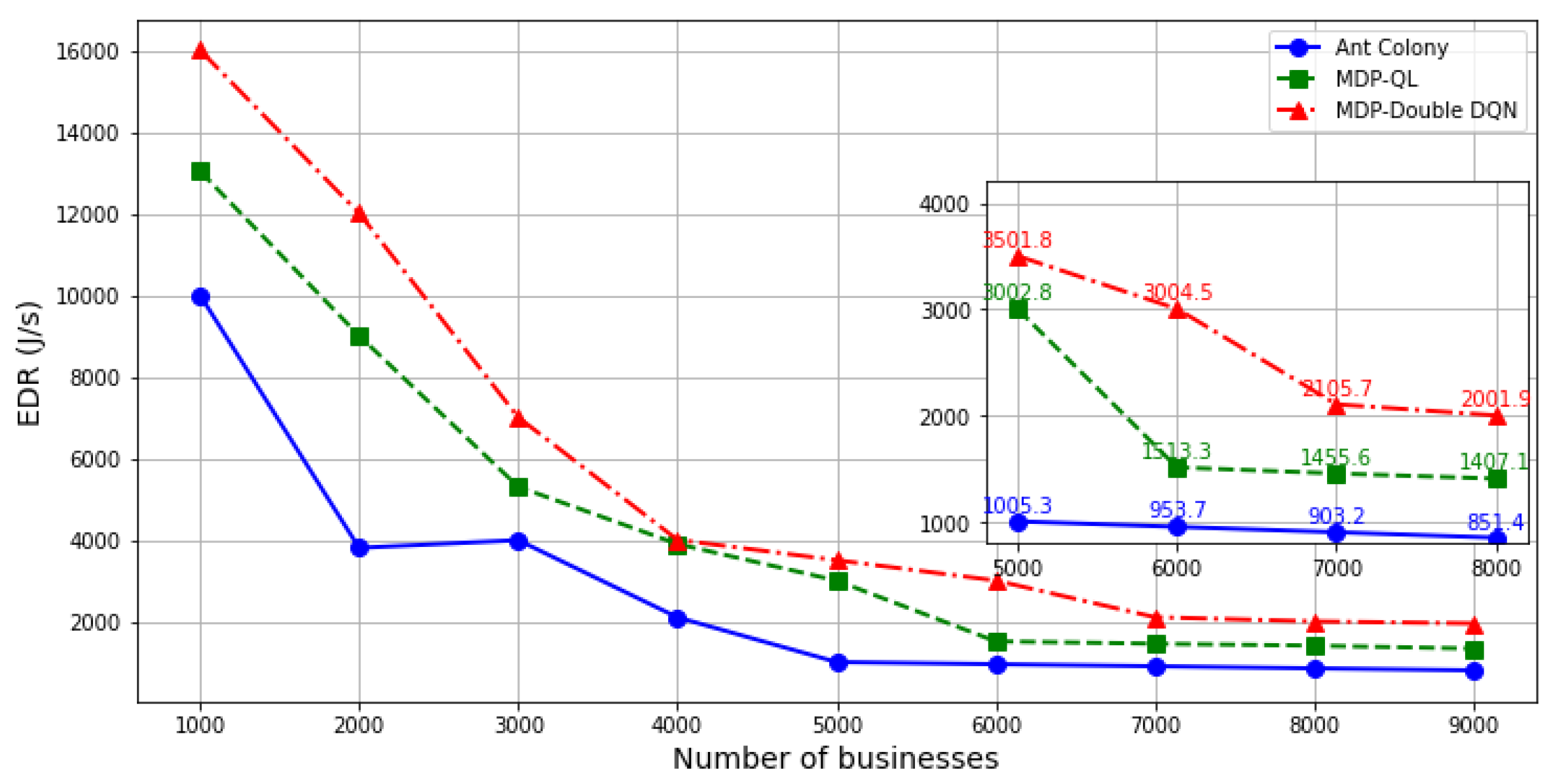
Figure 5 shows the performance comparison in terms of EDR across different strategies. With increasing business volume, the overall optimization goal declines and eventually converges. This is due to the increased transmission energy consumption and processing delays. The proposed strategy outperforms others across different business volumes because it utilizes reinforcement learning to effectively balance exploration and exploitation in continuous state spaces, achieving optimal performance.

Table 3 presents the delay increment and energy reduction ratio for different business volumes. When the business volume is low, the proposed aggregation strategy achieves significant energy savings with minimal delay increase. However, as the business volume grows, the energy savings decrease, making this strategy particularly advantageous in low-traffic scenarios.

6. Conclusion

In this paper, we propose a business aggregation strategy for Low Earth Orbit (LEO) Satellite Networks (LSNs) to address the energy limitations of LEO satellites. This strategy dynamically adjusts the working states of satellites based on the business volume, enabling certain satellites to enter a sleep state for energy conservation. By constructing a three-layer network architecture involving control satellites, service satellites, and user devices, and employing a Markov Decision Process (MDP) and Double Deep Q-Network (Double DQN), we optimize business scheduling and satellite state management.

The simulation results validate the effectiveness of the business aggregation strategy, demonstrating a 47.87% reduction in energy consumption under low business volume and a 4.36% reduction under high business volume. This shows that the proposed strategy is particularly effective in low-traffic scenarios where energy savings are critical.

The findings in this study provide practical guidance for energy-efficient management in LSNs, with potential applications in other energy-sensitive fields, such as data centers and smart grids, that require high energy-efficiency management.