Bioinformatics and Computational Biology: Exploring the Role of Biomathematics in Bioinformatics, Including the Analysis of Biological Data and the Development of Computational Tools

Akinbusola Olushola; Ayomide Adesiyan; Tolulope Ojo; Victoria Alao

doi:10.20944/preprints202411.0570.v1

Submitted:

02 November 2024

Posted:

08 November 2024

You are already at the latest version

Abstract

This study explores the intersection of bioinformatics, computational biology, and biomathematics, focusing on how mathematical models are applied to analyze biological data and develop computational tools. This study highlights the foundational role of biomathematics in biological research including genomics, proteomics, and systems biology. Key areas of focus include the use of statistical models, algorithms, and simulations to create computational tools to aid in data interpretation and drug discovery. Additionally, this paper delves into emerging trends such as artificial intelligence, machine learning, and big data in bioinformatics. By analyzing case studies and real-world applications, this study underscores the significance of biomathematics in advancing biological sciences and the potential for future innovations in personalized medicine and interdisciplinary approaches.

Keywords:

Bioinformatics

;

computational biology

;

biomathematics

;

mathematical models

;

biological data analysis

;

computational tools

;

genomics

;

proteomics

;

systems biology

;

drug discovery

Subject:

Computer Science and Mathematics - Mathematical and Computational Biology

Introduction

Background

Bioinformatics and computational biology are interdisciplinary fields that combine biological sciences and computational techniques to address complex biological questions. Bioinformatics refers explicitly to the use of software, algorithms, and data analysis methods to interpret large biological datasets (Pereira et al., 2020). The term has gained prominence with the rise of genomics, where high-throughput technologies have begun to produce vast amounts of genetic information. The need to manage, store, and analyze these data effectively has led to the development of specialized computational tools. On the other hand, computational biology often involves creating theoretical models to simulate biological processes, such as gene regulation, protein folding, or evolutionary dynamics (Pal et al., 2023). While bioinformatics focuses more on data management and analytical aspects, computational biology focuses on understanding the principles underlying biological phenomena.

Convergence of these fields represents the core of modern biological research. As we progress into the era of "big data," biology has become a data-intensive discipline that requires sophisticated computational methods. Sequencing technologies, for example, can generate terabytes of data that must be processed, analyzed, and interpreted to extract meaningful insights (Excedr, 2023). This convergence enables scientists to interpret biological data, generate new hypotheses, and predict biological behavior.

Biomathematics

The heart of bioinformatics and computational biology lies in the field of biomathematics, which provides the mathematical foundation for modeling biological systems. Biomathematics uses various mathematical tools, including differential equations, stochastic processes, and statistical methods, to describe biological phenomena (Mathematical Institute 2022). Developing these models is essential for understanding the intricate networks and dynamic processes that govern living organisms. In bioinformatics, biomathematics is crucial for analyzing data, especially when dealing with high-dimensional datasets such as gene expression profiles or protein interaction networks.

Biomathematics enable the transformation of biological problems into mathematical frameworks. This translation is critical for computational tools used in bioinformatics because mathematical models allow for predictions and simulations (Fischer, 2008). For example, mathematical models are used to simulate tumor growth in the study of diseases, such as cancer, enabling researchers to predict how a tumor might respond to different treatments. Similarly, biomathematics supports computational biology by providing a framework for simulating cellular processes or evolutionary mechanisms.

Research Statement

This study aims to explore the role of biomathematics in bioinformatics, focusing on its contribution to the analysis of biological data and the development of computational tools. The interplay between biology, computation, and mathematics is at the core of modern research, and this convergence has resulted in significant advancements in our understanding of complex biological systems. This study highlights the importance of interdisciplinary approaches in modern biological sciences by examining how biomathematics supports data interpretation and computational tool development.

Objectives and Research Questions

The key objectives of this study are as follows:

To understand the fundamental role of biomathematics in bioinformatics and computational biology.
To explore how mathematical models are employed in the analysis of biological data.
To evaluate the impact of computational tools underpinned by biomathematics in modern biological research.

These objectives were addressed through the following research questions.

How do biomathematics contribute to the analysis of large-scale biological data such as genomic and proteomic datasets?
What are the key mathematical models used in bioinformatics and how do they enhance the development of computational tools?
How have integrated biomathematics and bioinformatics advanced our understanding of biological systems and contributed to scientific discoveries?

Bioinformatics and Computational Biology: Foundations and Applications

Bioinformatics: Definition and Significance

Bioinformatics is the science of using computational tools to store, retrieve, analyze, and interpret biological data. It has become an essential discipline in modern biology because of the explosion of data from various biological experiments, particularly genomics and proteomics. The advent of high-throughput sequencing technologies has enabled scientists to generate vast amounts of data that require computational processing methods (Carleton, 2021). Bioinformatics allows researchers to handle such data efficiently and systematically, ensuring that large-scale datasets can be translated into meaningful biological insights.

The significance of bioinformatics lies in its ability to organize and analyze complex biological information. One of the primary goals of bioinformatics is to understand the structures and functions of genes and proteins. For example, bioinformatics tools can align DNA sequences to identify the genetic variants responsible for certain diseases. Similarly, bioinformatics is crucial for creating biological databases such as GenBank, Protein Data Bank (PDB), and Ensembl, which serve as repositories of genomic and proteomic data that researchers can access worldwide (Bayat 2002). These tools and resources have facilitated advancements in drug discovery, personalized medicine, and evolutionary biology.

Bioinformatics has allowed scientists to integrate various types of biological data, such as genomics, transcriptomics, and proteomics, into a cohesive framework. This integrative approach enhances our understanding of how different biological systems operate at multiple levels, leading to a more comprehensive understanding of cellular and molecular processes.

Computational Biology: Definition and Applications

Computational biology is a broad field that applies theoretical models, algorithms, and statistical techniques to understand biological systems. Unlike bioinformatics, which is primarily focused on managing and analyzing data, computational biology aims to model biological phenomena and simulate their behavior (Searls, 2024). These models can help scientists predict how biological systems behave under certain conditions. For example, computational biology is used to model the dynamics of populations in ecology, spread of infectious diseases, and regulatory networks of genes.

One of the major applications of computational biology is the simulation of biological processes on various scales, from molecules to ecosystems. At the molecular level, computational biology can model how proteins fold and interact with other molecules, which is crucial for understanding diseases such as Alzheimer's or designing new drugs (Searls, 2024). In systems biology, computational models help researchers to understand how different parts of a biological system, such as metabolic pathways or gene networks, interact.

Computational biology has also been used extensively in evolutionary studies. By simulating the evolutionary processes of a species over time, researchers can infer ancestral relationships, study the mechanisms of natural selection, and understand how specific traits have evolved (Searls, 2024). This approach, known as phylogenetic analysis, is crucial for studying evolutionary relationships among organisms and tracking the emergence of new pathogens.

Biomathematics in Bioinformatics: Supporting Biological Research

Biomathematics plays a fundamental role in supporting both bioinformatics and computational biology. It provides a mathematical framework that underpins the development of algorithms, models, and analytical tools (Lakhno 2019). In bioinformatics, biomathematics is used to construct models that analyze biological data, particularly in high-dimensional datasets such as those from genomic or proteomic experiments. These models help in pattern recognition, prediction of biological functions, and understanding complex biological networks.

For instance, machine learning algorithms are often built on statistical and mathematical principles, classify biological data, and predict outcomes. In cancer genomics, biomathematics aids in identifying genetic mutations that are likely to drive tumor growth and are merely bystanders (National Cancer Institute, 2020). The ability to distinguish these signals from noise is critical in the development of targeted therapies.

Mathematical models have also been used in computational biology to simulate biological processes. One example is the ordinary differential equation (ODE) model, which is widely used to describe the dynamics of biological systems (Parvinen 2022). In bioinformatics, these equations are employed to model gene regulatory networks, metabolic pathways, and even population dynamics in evolutionary biology. Also, the Boolean network model offers a parsimonious approach to investigating the intricate dynamics of biological systems. This model is valuable for elucidating the regulatory mechanisms underlying system properties and identifying potential points of intervention. (Julian et al., 2020). Imagine a network of switches, each switch can either be “on” and “off”. This simple setup can be used to represent complex biological systems.

Stochastic models incorporate randomness and help model biological systems with inherent variability, such as gene expression or population genetics. Combining biomathematics with computational tools has led to unprecedented advancements in biological research. These mathematical techniques provide a foundation for analyzing large, complex datasets typical of modern biology, offering insights into how biological systems behave in normal and diseased states.

Real-World Applications: Genomics, Proteomics, and Beyond

Bioinformatics and computational biology have revolutionized many areas of biological research with notable applications in genomics and proteomics. Bioinformatics tools assemble, annotate, and analyze whole genomes, leading to the discovery of genetic variation, gene function, and disease mechanisms (Hassan et al., 2022). The Human Genome Project is a prime example of how bioinformatics has been used to map the entire human genome (Collins & Fink, 1995). Computational tools have allowed scientists to sequence and annotate 3 billion base pairs of the human genome, providing a blueprint for understanding human biology and diseases.

In proteomics, bioinformatics is used to analyze the vast amounts of data generated from mass spectrometry experiments to study the structure and function of proteins. Bioinformatics tools help identify proteins from complex mixtures and map protein-protein interactions (Al-Amrani et al., 2021). This approach is vital for understanding cellular functions and identifying potential therapeutic targets in cancer and neurodegenerative disorders.

Another important application of bioinformatics and computational biology is in drug discovery. Pharmaceutical companies use bioinformatics tools to identify potential drug targets by analyzing genetic data and protein structures. Computational biology helps simulate how potential drugs interact with biological molecules, thereby accelerating drug development (Somda et al., 2023). By integrating genomics and proteomics data, bioinformatics facilitates the identification of biomarkers that can predict how patients will respond to a particular drug, paving the way for personalized medicine.

Finally, epidemiology has benefited greatly from computational biology. During the COVID-19 pandemic, bioinformatics and computational models have been used to track the evolution of the virus, model transmission patterns, and predict the effects of interventions, such as lockdowns and vaccinations (Napolitano et al., 2021). These models provide critical insights to guide public health strategies.

The convergence of bioinformatics, computational biology, and biomathematics has led to significant advancements in biological research. Using mathematical models and computational tools, scientists have been able to analyze complex datasets, simulate biological processes, and make previously impossible predictions. These tools have become indispensable in fields ranging from genomics to drug discovery, and their importance continues to grow as biological research becomes increasingly data-driven.

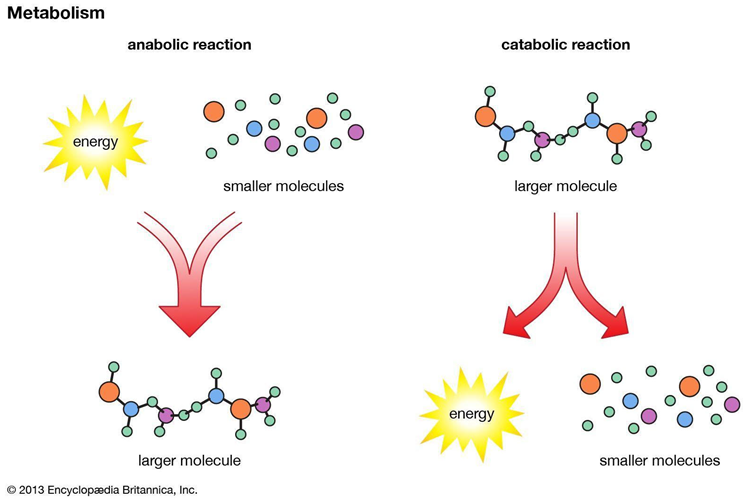
The Role of Biomathematics in Biological Data Analysis

Mathematical Models in Representing Biological Systems

Mathematical models are essential in biological research. They provide a framework for representing and understanding complex interactions that occur in biological systems. These models convert biological processes into quantitative terms, allowing for more precise predictions and simulations (Fischer 2008). Mathematical models can help scientists describe gene regulation, enzyme kinetics, population dynamics, and protein folding in bioinformatics and computational biology.

One of the most widely used forms of modeling is deterministic modeling, which assumes that the system evolves predictably. For example, the Michaelis-Menten equation is a deterministic model that describes enzyme kinetics, providing insights into how enzymes catalyze reactions at different substrate concentrations (McDonald & Tipton, 2022). Differential equations are another fundamental tool for modeling the rate of change in biological systems over time (Parvinen, 2022). These equations are employed to model everything from disease spread to cell-population dynamics.

However, stochastic models incorporate randomness and uncertainty into their framework. Biological processes, especially those occurring at the molecular level, often display a degree of variability that deterministic models cannot capture (Shmulevich and Aitchison, 2009). For instance, the Gillespie algorithm is a popular stochastic model used to simulate cell biochemical reactions considering the inherent randomness of molecular interactions (Mikolaj & Prusinkiewicz, 2019). Both deterministic and stochastic models serve as critical tools in biomathematics, providing different perspectives on how biological systems operate.

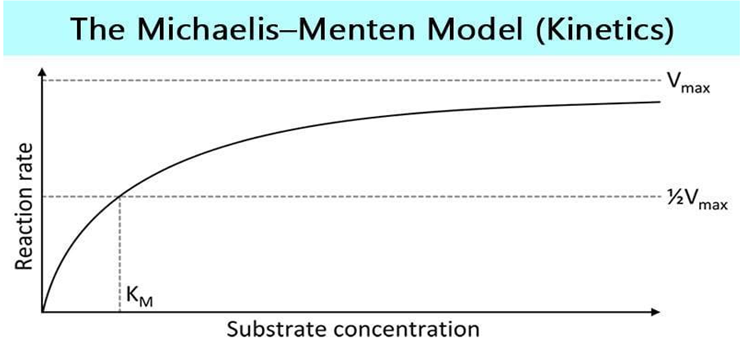
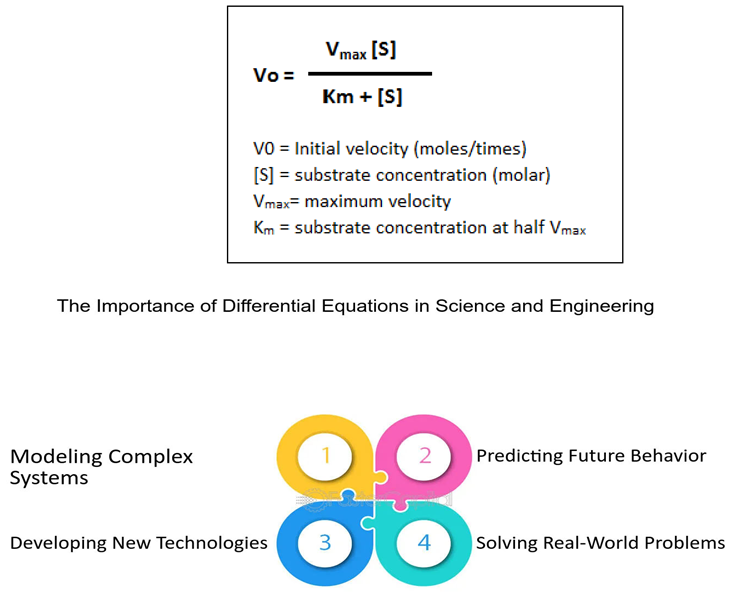
Data Analysis Techniques in Biomathematics

The sheer volume of biological data generated by modern experimental techniques requires advanced mathematical and computational tools for practical analyses. Statistical models are among the most commonly used methods in biomathematics for analyzing biological data (Fay and Gerow, 2018). These models help to identify patterns, make predictions, and draw inferences from large datasets. In genomics, regression models are frequently used to associate genetic variants with traits or diseases (Uffelmann et al., 2021). These models allow researchers to account for the complexities of genetic data, such as the interactions between genes and environmental factors.

Differential equations are pivotal in modeling dynamic systems, where the rate of change is crucial. They are used in various biological contexts such as modeling population growth or spreading infectious diseases (Parvinen, 2022). A classic example is the Lotka-Volterra model, which describes predator-prey interactions (Hoppensteadt, 2006). These equations can also be used to model cellular processes, such as how the concentrations of different molecules in a cell change over time.

Machine learning (ML) has emerged as a transformative tool for biological data analyses. By leveraging algorithms that can learn from data, machine-learning models can make predictions or classify biological data in ways that traditional models may struggle with (Yousef & Allmer, 2023). For instance, neural networks are used in image recognition tasks such as identifying cancerous cells in medical images.

For instance, a branch of Artificial neural networks called Convolutional Neural Networks are used in image recognition tasks such as identifying cancerous cells in medical images. CNNs are trained on large datasets of annoyed medical images. During this training process, it learns to associate specific patterns to with cancerous cells, enabling it to accurately classify new, unseen images.

In genomics, machine learning techniques, such as random forests or support vector machines (SVMs), are employed to classify genetic mutations, identify biomarkers, and predict disease outcomes (Huang, 2018). The power of machine learning lies in its ability to handle high-dimensional and noisy datasets, making it particularly suitable for complex biological problems.

Figure 1. A machine learning method based on the genetic and world competitive contests algorithms.

Types of Biological Data and Their Complexities

Biological research generates various types of data, each with its unique complexity. One of the most common types of data is genomic data, which involves DNA sequencing to identify genetic information. Genomic data are often massive, consisting of billions of base pairs, and require bioinformatic tools for alignment, annotation, and interpretation (Saraswathy et al., 2011). Beyond size, the inherent variability within genomes, such as single nucleotide polymorphisms (SNPs), makes analysis challenging. Genomic data are also hierarchical, spanning different levels, from individual genes to the entire genome, each requiring specific analytical approaches.

Another critical data type is proteomic data, which focuses on the large-scale study of proteins and the cell's workhorses. Unlike genomic data, which are relatively stable, proteomic data are highly dynamic in nature (Al-Amrani et al. 2021). Protein expression levels can vary depending on cellular conditions, and proteins undergo various modifications such as phosphorylation or glycosylation, further complicating their analysis. Mass spectrometry is a common technique used to generate proteomic data; however, interpreting the resulting spectra and mapping them back to the corresponding proteins requires sophisticated computational tools.

Metabolomic data represent the small molecules (metabolites) involved in metabolic processes. Similar to proteomics, metabolomic data are highly dynamic and context-dependent. Metabolic pathways are interconnected in complex networks and understanding how different metabolites interact requires systems biology approaches (Chen et al. 2022). Additionally, metabolomic data are influenced by environmental factors, making them more variable and challenging to interpret.

Each data type presents distinct challenges, but shares standard features: high dimensionality, variability, and the need for integration with other data types. For instance, combining genomic, proteomic, and metabolomic data (often called multi-omics data integration) is crucial for understanding diseases, such as cancer, where changes at different molecular levels interact to drive disease progression.

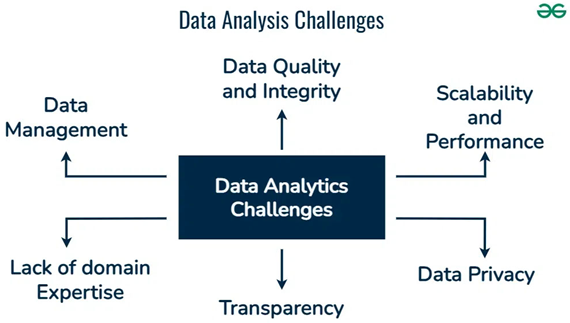
Challenges in Biological Data Analysis

The analysis of biological data is fraught with challenges stemming from the complexity and variability of the data. Therefore, data heterogeneity is a significant issue. Biological data often come from different sources (e.g., genomic, transcriptomic, and proteomic data) and may have different formats or scales (Li & Chen, 2014). Integrating these heterogeneous datasets into a unified model is difficult, but essential for understanding biological systems holistically. For example, while genomic data may provide information about the genetic predisposition to a disease, proteomic data might reveal how these genes are expressed under certain conditions. The challenge is to combine these insights to obtain a complete picture of biological systems.

Another challenge is the noise in the data. Biological experiments, especially high-throughput technologies such as sequencing and mass spectrometry, often generate noisy data owing to technical variability or biological fluctuations (Fan et al., 2014). This noise can obscure accurate biological signals, which makes it difficult to draw reliable conclusions. Techniques such as data smoothing, normalization, and statistical filtering are used to reduce noise; however, they come with trade-offs in terms of sensitivity and specificity. In some cases, essential signals may be lost during noise reduction.

Figure 2. Challenges in measuring and understanding biological noise.

Thus, scalability is a critical issue. Modern biological experiments can generate terabytes of data, and analyzing such vast datasets requires powerful computational resources and efficient algorithms (Almaden Genomics 2023). For example, analyzing a single human genome can require significant processing time and storage space, even with the most optimized algorithms. As biological datasets grow, the need for scalable algorithms has become increasingly pressing.

Biological variability adds to another layer of complexity. Unlike physical systems, biological systems are inherently variable, with significant differences between individuals, cells, or even molecules of the same type (Li & Chen, 2014). This variability can create models that generalize across different datasets or populations. Machine learning techniques, designed to handle variability, offer some solutions, but still need help with the high levels of uncertainty present in biological data.

Figure 3. biological variation.

Biomathematics play a crucial role in analyzing biological data and offering models and techniques for the inherent complexity and variability of living systems. Through mathematical models, scientists can represent biological systems in a structured and quantitative manner, enabling predictions and simulations that provide deep insights into biological phenomena. Essential techniques, such as statistical models, differential equations, and machine learning, are crucial for analyzing genomic, proteomic, and metabolomic data. However, biological data analysis is not without its challenges; data heterogeneity, noise, scalability, and biological variability all present significant hurdles that must be addressed to advance our understanding of life at the molecular level.

Development of Computational Tools Using Biomathematics

Computational Tool Development in Bioinformatics

The development of computational tools in bioinformatics involves a systematic approach to creating software, algorithms, and databases that can process and analyze complex biological data (Pereira et al., 2020). These tools are crucial for interpreting massive datasets generated by technologies, such as sequencing, proteomics, and metabolomics, which are central to modern biology. The development of computational tools typically involves several vital steps.

Problem Definition: The first step in developing a computational tool is to clearly define the biological problem it aims to solve. For example, a tool may be needed to identify homologous sequences in DNA, predict protein structures, or analyze gene expression patterns (Athar et al., 2024). The problem must be articulated with precision, outlining the specific biological data to be handled and the desired outcome of the analysis.
Data collection and preparation: Computational tools often require large amounts of biological data for effective functioning. The data must be collected from reliable sources, such as genomic databases (e.g., GenBank or Ensembl), and properly formatted for input into the tool (Matellio, 2024). This stage often involves data cleaning, annotation, and normalization to ensure that the data are consistent and ready for analysis.
Algorithm Design: The core of any bioinformatics tool is the algorithm that processes biological data and provides meaningful results. An algorithm must be chosen or designed based on this problem. For example, sequence alignment tools rely on dynamic programming algorithms to efficiently compare sequences (Clark and Lillard, 2024). Biomathematics heavily influences algorithm design because mathematical models often underpin the logic of these algorithms.
Software Development: Once the algorithm is defined, the next step is to implement it in software. This involves writing code in programming languages such as Python, R, or C++, and creating an interface that allows users to interact with the tool. User experience is a critical factor, as bioinformatics tools are used by biologists who may need a deeper understanding of the underlying algorithms (Pereira et al., 2020). The software must be intuitive and accessible, while still providing powerful analytical capabilities.
Testing and Validation: Before computational tool is released for public use, it must be rigorously tested. Testing involved running the tool on known datasets to ensure accurate and reliable results. The performance of the tool was also benchmarked against other tools to assess its speed, accuracy, and scalability (Pereira et al., 2020). The validation ensures that the tool provides meaningful insights into real-world biological research.
Distribution and Maintenance: Once tool is fully developed, it must be available to the scientific community. Many bioinformatics tools are distributed as open-source software, allowing researchers to freely use and modify them (Pereira et al., 2020). However, developers must continue to maintain and update software to accommodate new data types, fix bugs, and improve performance over time.

Algorithms and Models in Bioinformatics

At the heart of many bioinformatics tools, algorithms are based on mathematical models. These algorithms are designed to perform specific tasks, such as sequence alignment, structure prediction, or evolutionary analysis, and rely heavily on biomathematics to interpret biological data accurately. Some of the most popular algorithms used in bioinformatics include the following.

a): Hidden Markov Models (HMMs): HMMs are widely used in bioinformatics, particularly for sequence alignment and gene prediction. They are probabilistic models that describe systems with hidden states, such as the underlying structure of a protein or evolutionary relationships between DNA sequences. In sequence alignment, HMMs are used to model the probabilities of transitions between different sequence motifs, allowing the detection of conserved regions across genomes (Yoon, 2009). The biomathematical foundation of HMMs is based on the probability theory, where each state transition is governed by a set of probabilities.

Figure 4. Profile of hidden Markov model. (a) Multiple sequence alignment for constructing profile-HMM. (b) The ungapped HMM represents the consensus sequence of alignment. (c) Final profile of HMM that allows insertions and deletions.

Figure 4. Profile of hidden Markov model. (a) Multiple sequence alignment for constructing profile-HMM. (b) The ungapped HMM represents the consensus sequence of alignment. (c) Final profile of HMM that allows insertions and deletions.

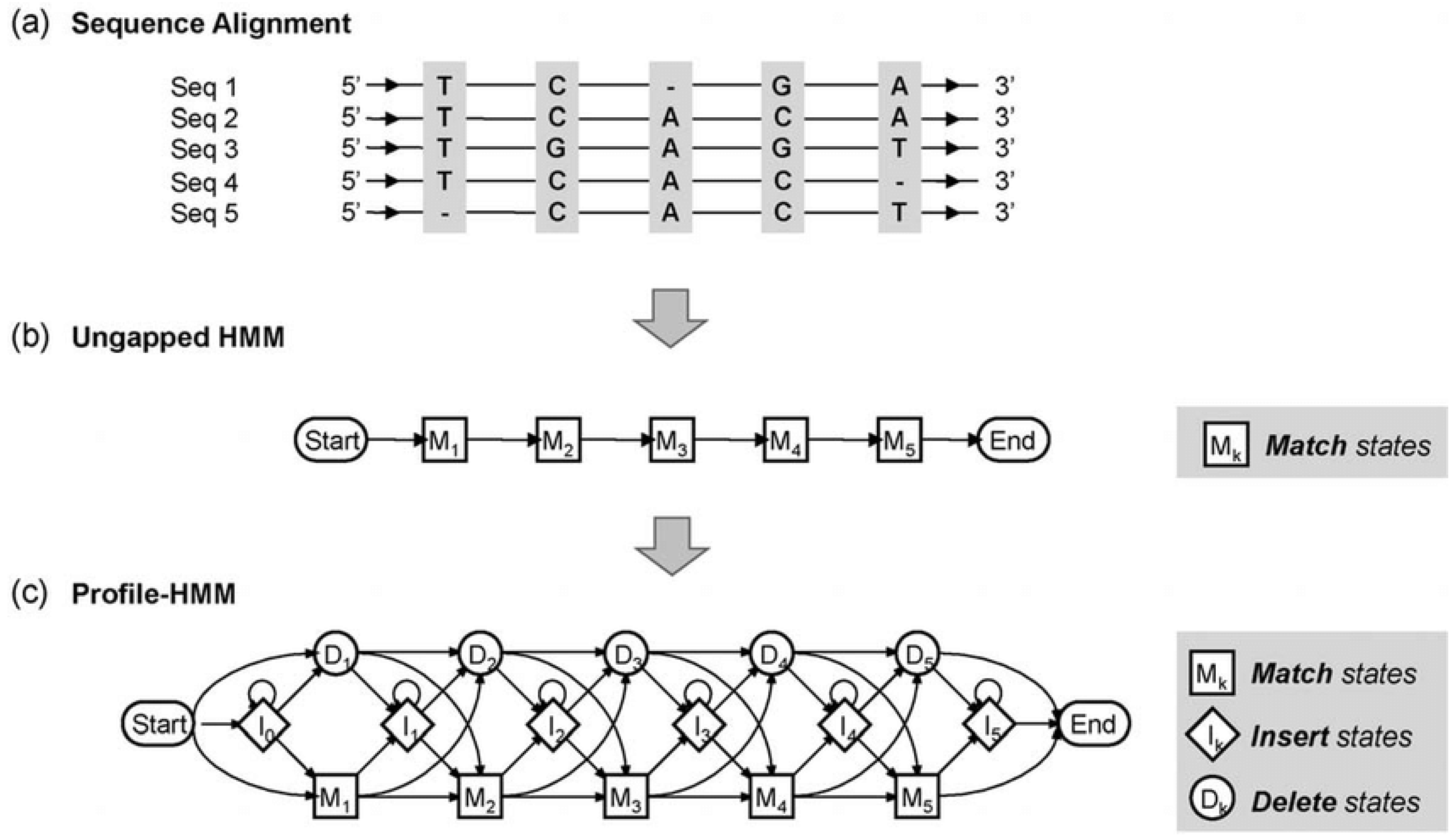
b): Bayesian Methods: Bayesian inference is another essential mathematical technique used in bioinformatics for phylogenetic analysis, gene expression profiling, and population genetics. Bayesian methods rely on Bayes’ theorem to update the probability of a hypothesis based on new data (Dey et al. 2010). This approach is beneficial for biological research in which uncertainty is inherent in the data. Bayesian models allow researchers to incorporate prior knowledge and uncertainty into their analyses, thus making them highly flexible and robust.

Figure 5. Model averaging strategies for structure learning in Bayesian networks with limited data.

Figure 5. Model averaging strategies for structure learning in Bayesian networks with limited data.

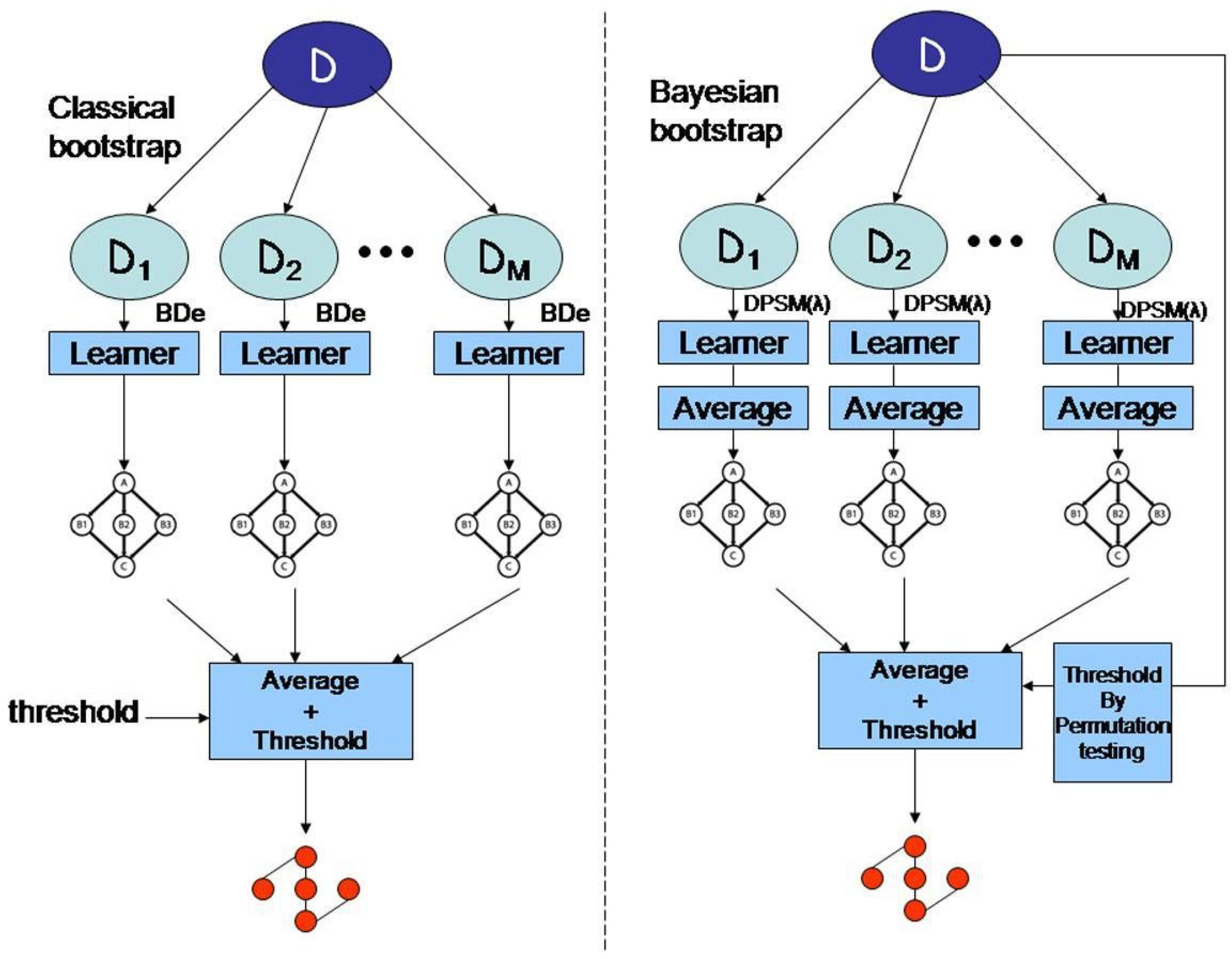
c): Dynamic Programming: Dynamic programming algorithms, such as the Needleman-Wunsch and Smith-Waterman algorithms, are fundamental to sequence alignment tools. These algorithms break down complex problems into smaller subproblems and solve them recursively. This approach is highly efficient in aligning large DNA or protein sequences and identifying homologous regions across genomes (Doerr et al. 2011). Dynamic programming is grounded in biomathematics, particularly in optimizing biological functions, where the goal is to find the best alignment or match between sequences.

Figure 6. Dynamic Programming.

Figure 6. Dynamic Programming.

Simulation Tools in Bioinformatics

Simulation tools are another critical component of bioinformatics, enabling researchers to model and predict biological phenomena that are too complex to observe directly (Molecular Modeling and Bioinformatics Group 2024). Biomathematics provides a foundation for many simulation tools that use mathematical equations and algorithms to replicate biological systems. Some standard simulation methods include the following.

I.: Monte Carlo Methods: Monte Carlo simulations are widely used in bioinformatics to model complex stochastic processes. These methods rely on random sampling to explore possible outcomes of biological systems. For example, Monte Carlo simulations can be used to model protein folding, in which the energy landscape of a protein is explored through random conformational changes (Giró et al., 1986). These simulations provide insights into the most likely structures that a protein can adopt based on its amino acid sequence. Monte Carlo methods are grounded in probability theory and are particularly useful when dealing with high-dimensional biological data.

II.: Agent-Based Modeling: In agent-based models, individual biological entities (e.g., cells, molecules, and organisms) are modeled as agents with specific behaviors. These agents interact with each other and with their environment, leading to emergent phenomena. Agent-based models are commonly used in systems biology to simulate complex interactions in biological systems, such as tumor growth and immune responses (Breitwieser et al., 2022). The biomathematical foundation of agent-based models lies in systems theory and differential equations, which describe the interactions between agents over time.

Figure 7. Data-driven Agent-based Simulation.

Figure 7. Data-driven Agent-based Simulation.

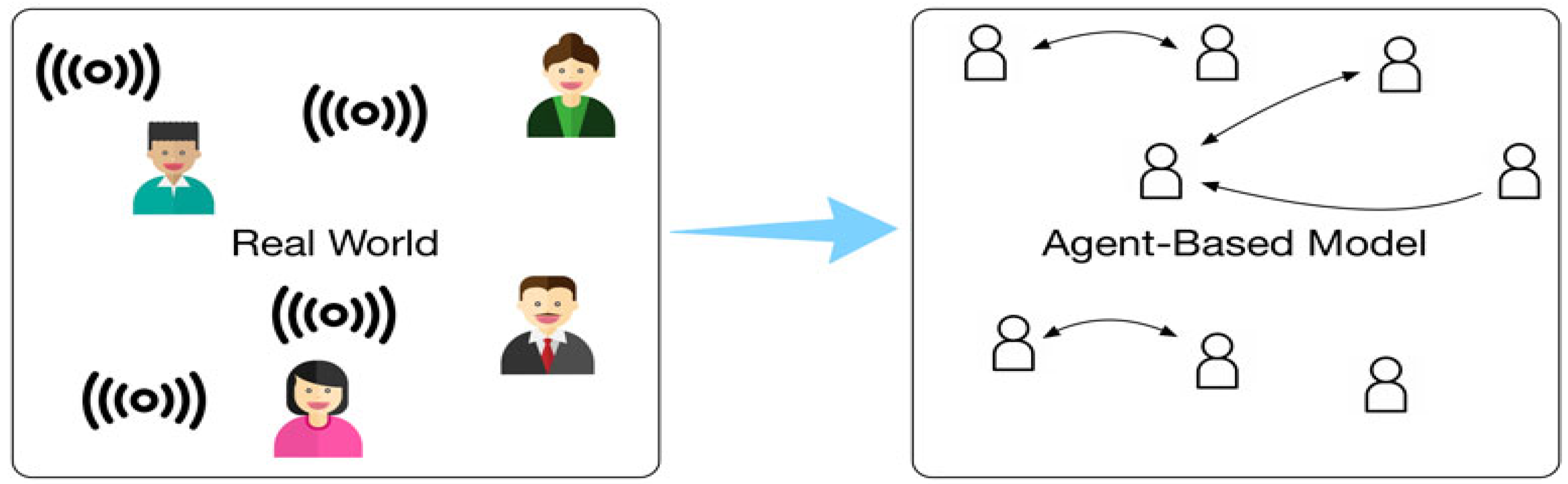
III.: Molecular Dynamics (MD) Simulations: MD simulations were used to model the physical movements of the atoms and molecules over time. These simulations are particularly useful for studying protein dynamics and drug and molecular interactions. MD simulations rely on principles of physics and biomathematics, such as Newton’s laws of motion, to calculate the trajectories of individual atoms in a biological system (Oyewusi et al., 2024). By simulating molecular motion, researchers can gain insights into the structural stability and function of biological macromolecules.

Case Studies: Tools Developed Using Biomathematical Approaches

Several well-known bioinformatic tools have been developed using biomathematical approaches, each of which plays a critical role in modern biological research.

i.: BLAST (Basic Local Alignment Search Tool (BLAST) is one of the most widely used bioinformatics tools for comparing nucleotide or protein sequences to sequence databases. It uses a heuristic algorithm to quickly identify regions of similarity between sequences (Samal et al., 2021). The biomathematical foundation of BLAST is based on dynamic programming and probabilistic models, which enables the tool to identify homologous sequences with high accuracy. BLAST has revolutionized the field of genomics by allowing researchers to annotate genes, identify conserved sequences, and study evolutionary relationships across species.

ii.: FASTA (Fast Alignment Search Tool): Like BLAST, FASTA is used for sequence alignment and searching databases for similar sequences. The FASTA algorithm uses heuristic methods and dynamic programming to align sequences efficiently (Alok & Shrivastava, 2022). The mathematical models used in FASTA allow it to handle large-scale genomic datasets and provide accurate alignments, making it a cornerstone of bioinformatic research.
iii.: RNA structure prediction tools: MFold and RNAfold use biomathematical approaches to predict the secondary structure of RNA molecules. These tools rely on dynamic programming algorithms and thermodynamic models to predict the most stable RNA structures based on nucleotide sequences (Afanasyeva et al., 2019). The biomathematical foundation of RNA structure prediction tools is based on statistical mechanics and thermodynamics, which allows researchers to model the folding process of RNA molecules and predict their functional structures.

Figure 8. Predicting RNA secondary structures from sequence and probing data.

Figure 8. Predicting RNA secondary structures from sequence and probing data.

The development of computational tools using biomathematics has transformed the field of bioinformatics by providing powerful algorithms and software for analyzing complex biological data. From sequence alignment tools, such as BLAST and FASTA, to simulation methods, such as Monte Carlo and molecular dynamics, biomathematical approaches form the backbone of modern bioinformatics. Researchers can develop tools that enable efficient analysis, prediction, and simulation of biological phenomena by leveraging mathematical models such as Hidden Markov Models, Bayesian methods, and dynamic programming. As biological data continue to grow in complexity and scale, the role of biomathematics in computational tool development will only become more critical, driving advances in genomics, proteomics, and systems biology.

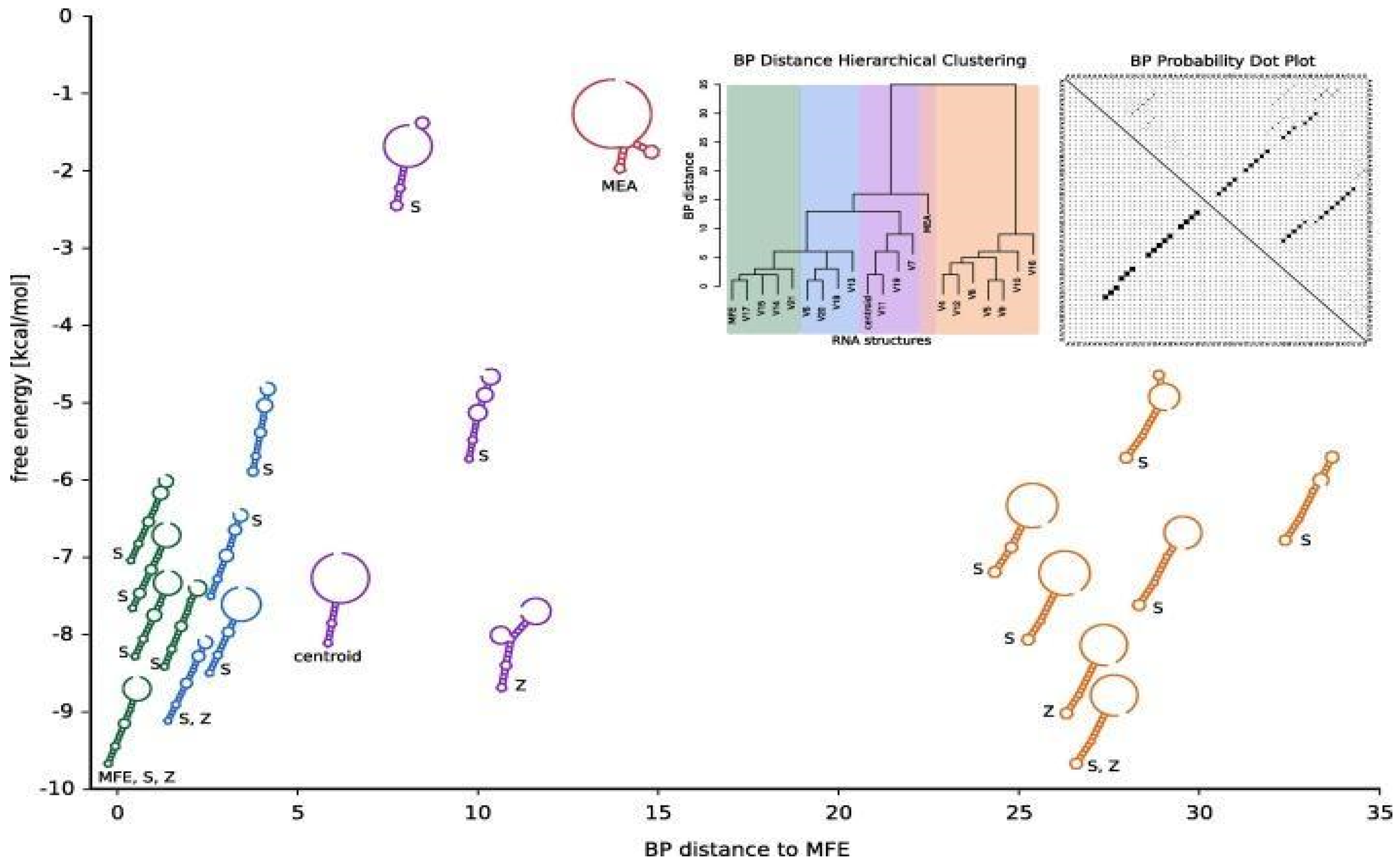
Biomathematics in Genomics and Proteomics

Biomathematics plays a pivotal role in genomics and proteomics by providing the necessary computational and statistical frameworks to analyze the vast, complex data generated in these fields. The mathematical models, algorithms, and techniques used in biomathematics enable researchers to interpret genomic sequences, understand protein structures, and model the interactions between genes and proteins (Hassan et al. 2022). This section explores how biomathematics contributes to genomic and proteomic data analysis, network analysis, comparative genomics, and phylogenetics.

Genomic Data Analysis

Genomic data analysis refers to the interpretation of the information derived from DNA sequencing and gene expression studies. With the advent of next-generation sequencing technologies, researchers have access to massive amounts of genomic data that require sophisticated mathematical approaches for meaningful interpretation.

Gene Expression and Differential Analysis

Biomathematics is central to the analysis of gene expression data and involves measuring the activity levels of genes under different conditions or tissues. This is typically performed using RNA sequencing (RNA-Seq) or microarray technologies, resulting in high-dimensional datasets that must be analyzed to determine which genes are upregulated or downregulated in response to a given stimulus.

Mathematical models, especially statistical methods, are critical for identifying differentially expressed genes (Rosati et al., 2024). Techniques such as linear and generalized linear models (GLMs) are commonly used to compare gene expression across multiple conditions. For example, the DESeq2 and edgeR packages in R are based on biomathematical models that apply statistical hypothesis testing to determine the significant differences in gene expression. These models account for biological and technical variabilities, ensuring that the identified changes are robust and reproducible.

Sequencing Data and Genomic Mapping

Mathematical models also support the interpretation of sequencing data, such as whole-genome, exome, and targeted sequencing. Algorithms based on graph theory and probabilistic models assemble raw sequencing reads into coherent genomic maps (Hassan et al., 2022). The Burrows-Wheeler Transform (BWT) and Suffix Arrays are examples of biomathematical concepts used in tools such as BWA and Bowtie for fast and efficient sequence alignment. Additionally, Hidden Markov Models (HMMs) are employed in gene prediction tools such as GENSCAN and Augustus, helping annotate genomes by identifying coding regions, introns, and exons. HMMs rely on probabilistic models that describe the transitions between different states (e.g., exons, introns, and intergenic regions), allowing for the accurate annotation of genes in newly sequenced genomes.

Variant Calling and Population Genomics

In population genomics, researchers have analyzed genetic variations between individuals or species. Variant calling identifies mutations in a population, such as single-nucleotide polymorphisms (SNPs), insertions, and deletions. Biomathematics contributes to this field through probabilistic models that calculate the likelihood of a variant to occur at a specific position in the genome. One popular approach is the Bayesian inference model, which is used in tools such as GATK’s HaplotypeCaller and FreeBayes (Clark et al., 2019). These tools model the uncertainty in sequencing data and use prior probabilities derived from population-level genetic data to generate accurate variant calls.

Proteomic Data Analysis

Proteomics, a large-scale study of proteins, poses significant challenges in data analysis for predicting protein structure and function. Biomathematics provides essential tools for interpreting proteomic data from peptide identification to structural prediction.

Protein Structure Prediction

One of the most critical applications of biomathematics in proteomics is the prediction of protein structures. Proteins fold into complex three-dimensional shapes, and their function is closely tied to this structure (Al-Amrani et al., 2021). Homology modeling, ab initio modeling, and fold recognition methods are commonly used to predict protein structures and rely heavily on mathematical models.

Homology modeling: This approach predicts protein structures based on their similarity to known structures. Mathematical algorithms, such as BLAST and PSI-BLAST, align sequences and identify structural homologs, which are then used as templates to build models of unknown proteins (Samal et al., 2021).
Ab initio modeling: Using physics-based simulations for proteins with no known homologs, ab initio modeling predicts the structures from scratch. Molecular dynamics (MD) simulations and energy minimization techniques are mathematical tools used in this approach. Rosetta, a leading tool in ab initio structure prediction, uses Monte Carlo simulations and scoring functions to evaluate the most likely protein conformations.
AlphaFold, an artificial intelligence-based tool, has revolutionized protein structure prediction using deep-learning algorithms trained on large datasets of known protein structures. The underlying biomathematics include optimization techniques, neural networks, and statistical models to predict the most probable folding pattern.

Functional Annotation of Proteins

Another area where biomathematics is crucial is understanding protein function based on its sequence or structure. Gene Ontology (GO) terms and Enzyme Commission (EC) numbers are often assigned to proteins based on sequence similarity using models such as HMMs and machine learning algorithms to predict functions based on known annotations (Makrodimitris et al., 2019). In mass spectrometry-based proteomics, biomathematical algorithms aid in peptide identification. Fourier transforms and machine-learning algorithms match experimental spectra to theoretical spectra from protein databases, enabling the identification of proteins in complex mixtures.

Network Analysis in Molecular Interactions

Based on graph theory, network analysis is an essential tool in bioinformatics for modeling the interactions between genes, proteins, and other molecules (Charitou et al., 2016). Biological systems are often represented as networks, where nodes correspond to biomolecules (e.g., genes and proteins) and edges represent interactions (e.g., physical interactions and regulatory relationships).

Graph Theory in Molecular Networks

Graph theory is a mathematical study of networks that is widely applied to biological systems, where molecular interactions form highly complex networks. In these models:

Nodes represent entities, such as genes, proteins, and metabolites.
Edges represent relationships, such as protein-protein interactions (PPIs), gene regulatory networks (GRNs), or metabolic pathways.

Graph theory metrics, such as degree centrality, betweenness centrality, and clustering coefficients, identify key molecules (hubs) or interactions (bottlenecks) in biological networks. These metrics help to prioritize genes or proteins for further experimental validation or as therapeutic targets.

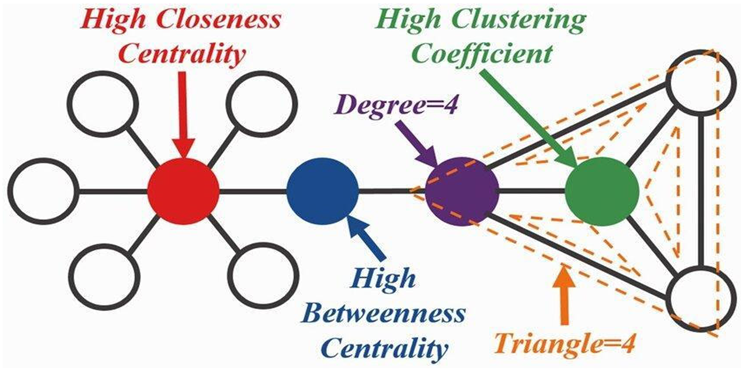
Systems Biology and Network Models

In systems biology, network models are used to study the emerging properties of biological systems. Dynamic Bayesian networks (DBNs) and ordinary differential equations (ODEs) are commonly used to model the temporal dynamics of gene regulatory networks. These models allow researchers to simulate how changes in one gene affect the expression of others over time, offering insights into the mechanisms driving complex biological behaviors, such as cell differentiation or tumor progression.

Comparative Genomics and Phylogenetics

Comparative genomics involves studying the similarities and differences between the genomes of different species, whereas phylogenetics explores the evolutionary relationships among species. Both fields rely heavily on biomathematics for sequence alignment, evolutionary modeling, and tree construction.

Comparative Genomics

Biomathematics play a key role in comparative genomics, where statistical models and algorithms compare gene sequences, gene order, and regulatory elements across species (Saada et al., 2024). Tools such as Mauve and CoGe use mathematical algorithms to align genomes and to identify conserved regions, syntenic blocks, and evolutionary breakpoints.

Phylogenetic Analysis

Phylogenetics aims to reconstruct the evolutionary history of a species by comparing its genetic sequences. Maximum likelihood and Bayesian inference are biomathematical approaches that are commonly used to infer phylogenetic trees.

Maximum likelihood models the evolution of DNA sequences based on statistical probability, generating a tree that best explains the observed data. Tools such as RAxML and PhyML are well known for this method.
Bayesian methods incorporate the prior knowledge of evolutionary processes and provide a probabilistic framework for tree construction. MrBayes is a tool that uses Bayesian inference to construct phylogenies and integrate uncertainties into the analysis.

Phylogenetic analysis is critical for understanding evolutionary relationships between species, tracing the origins of genes, and identifying evolutionarily conserved elements that may play key biological roles. Biomathematics is integral to genomics and proteomics, as it offers powerful tools for the analysis and interpretation of complex biological data. From gene expression analysis and genomic mapping to protein structure prediction and molecular network modeling, mathematical models and algorithms enable researchers to understand vast datasets. The applications of biomathematics in comparative genomics and phylogenetics further extend our understanding of evolutionary relationships and genome function across species. As technologies in genomics and proteomics continue to evolve, biomathematics will remain the cornerstone of biological research, driving advancements in personalized medicine, systems biology, and evolutionary biology.

Case Studies: Biomathematics in Drug Discovery and Systems Biology

Biomathematics has revolutionized the fields of drug discovery and systems biology, offering computational models and techniques to predict how drugs interact with biological systems and map complex biological networks. The application of mathematical models in these fields has also paved the way for personalized medicine, in which treatments are tailored to individual patients based on their genomic and molecular profiles. This study explored the role of biomathematics in drug discovery, systems biology, and personalized medicine, providing real-world case studies of biomathematical approaches that have contributed to drug development and treatment optimization.

Drug Discovery: Modeling Drug Interactions, Pharmacokinetics, and Pharmacodynamics

Drug discovery is an intricate process that involves the identification of new therapeutic compounds and understanding their interactions with biological systems. Mathematical models are vital for predicting these interactions, optimizing drug dosing, and ensuring safety and efficacy prior to clinical trials. The two primary areas where biomathematics are applied are pharmacokinetics (PK) and pharmacodynamics (PD).

Pharmacokinetics and Pharmacodynamics Modeling

Pharmacokinetics refers to the absorption, distribution, metabolism, and elimination of drugs from the body. Pharmacodynamics focuses on the biological effects of the drug and how it interacts with its target to produce therapeutic effects. Biomathematical models of PK/PD are essential for simulating drug behavior in the human body and for guiding decisions about dosing and drug delivery.

Compartmental models, commonly used in PK/PD modeling, break down the human body into compartments (e.g., bloodstream, liver, and kidney) with mathematical equations describing the transfer of the drug between compartments. For example, in a two-compartment model, the central compartment (e.g., blood) represents the initial distribution of the drug, whereas the peripheral compartment (e.g., tissue) accounts for the distribution to other parts of the body.

Case Study: Remdesivir in COVID-19 Treatment Remdesivir, an antiviral drug originally developed for Ebola, was repurposed for the treatment of COVID-19. Mathematical models of PK/PD were used to determine the optimal dosing regimen for remdesivir, balancing the need for effective antiviral action with the risk of adverse effects (Conway and Wiesch, 2021). A model used compartmental analysis to simulate drug concentrations in plasma and lung tissue, helping researchers determine the appropriate dose and administration schedule for hospitalized COVID-19 patients (Zhang et al., 2022). This biomathematical model has guided clinical trials and was instrumental in establishing remdesivir as one of the first approved treatments for COVID-19.

Molecular Docking and Drug Interactions

Biomathematics is also used in molecular docking, in which researchers predict how small molecules (drugs) interact with their target proteins. These models use mathematical algorithms to simulate the orientation, binding energy, and affinity of a drug for its target. Tools such as AutoDock and DOCK employ algorithms based on biomathematics to evaluate thousands of potential drug-target interactions, accelerating the drug discovery process.

Case Study: HIV Protease Inhibitors The development of HIV protease inhibitors (PIs), such as ritonavir and saquinavir, relies heavily on molecular docking models. Using quantum and statistical mechanics models, researchers have simulated how potential inhibitors would bind to the HIV protease enzyme, which is critical for viral replication (Ghosh et al., 2016). These models not only reduce the time needed to identify effective inhibitors but also guide structural modifications to improve the potency of drugs and minimize resistance.

Systems Biology: Modeling Complex Biological Systems

Systems biology focuses on understanding the interactions and behavior of biological systems such as cellular pathways, gene regulatory networks, and metabolic systems. Biomathematics play a central role in systems biology by providing mathematical frameworks to model these complex interactions.

Systems Biology and Network Models

Mathematical modeling in systems biology often involves the construction of dynamic models using differential equations to describe changes in biological systems over time. These models are used to simulate the behavior of cellular processes, such as activation of signaling pathways or regulation of gene expression.

One of the primary tools in systems biology is the ordinary differential equation (ODE) model, which describes how the concentrations of molecules (e.g., proteins and metabolites) change over time based on the rates of reactions between them. Stochastic models are also used when dealing with molecular systems that exhibit significant variability and randomness, such as gene expression noise, in bacterial populations.

Case Study: The MAPK Signaling Pathway in Cancer The mitogen-activated protein kinase (MAPK) signaling pathway plays a key role in cell proliferation and survival, making it a critical target for cancer therapies. Researchers have developed biomathematical models using ODEs to simulate the dynamics of the MAPK pathway in response to different growth factors and inhibitors (Fröhlich et al., 2023). This model has been used to predict how cancer cells would respond to RAF inhibitors, leading to the development of targeted therapies for melanoma. The model’s predictions were validated through experimental studies, and the insights gained from the model were crucial in designing combination therapies to overcome drug resistance.

Personalized Medicine: Tailoring Treatments Based on Genomic Data

Personalized medicine aims to customize treatment strategies based on an individual's genomic profile, offering a more targeted approach to health care. Mathematical models play a crucial role in interpreting genomic data and predicting patient response to specific treatments.

Pharmacogenomics and Biomarker Discovery

In personalized medicine, pharmacogenomic models are used to predict how variations in an individual's genome affect their responses to drugs. This is particularly important in cancer treatment, where tumor heterogeneity and genetic mutations can lead to variability in treatment outcomes.

Case Study: HER2-Positive Breast Cancer The development of trastuzumab (Herceptin) for HER2-positive breast cancer is a landmark example of personalized medicine. HER2 is overexpressed in a subset of breast cancers, leading to aggressive tumor growth. Mathematical models based on tumor genomics were used to identify HER2 as a key driver of cancer in these patients, leading to the development of trastuzumab, which specifically targets the HER2 receptor (Swain et al., 2023). By tailoring treatment to patients with HER2-positive tumors, biomathematics plays a crucial role in improving survival rates and reducing adverse effects in patients who are unlikely to benefit from traditional chemotherapy.

Predictive Models for Treatment Optimization

Biomathematics is also used to develop predictive models that optimize treatment strategies for individual patients. Machine-learning algorithms are commonly applied to genomic data to identify patterns associated with treatment success or failure. These models use patient data including genetic mutations, gene expression levels, and clinical factors to predict the most effective treatment regimen.

Case Study: Predicting Chemotherapy Response in Colorectal Cancer In a study a machine learning model was developed to predict how colorectal cancer patients would respond to chemotherapy (Russo et al., 2022). The model integrates genomic data (e.g., mutations in KRAS, BRAF, and PIK3CA genes) with clinical variables (e.g., tumor stage and patient age) to predict treatment outcomes. The model successfully identified patients who were likely to benefit from chemotherapy and those who would not, thereby allowing for more personalized treatment decisions. This biomathematical approach helped to optimize patient outcomes while minimizing unnecessary toxicity.

Case Study Examples: Biomathematical Applications in Drug Discovery and Treatment Strategies

Biomathematics have been applied in numerous real-world scenarios, driving advances in drug discovery, treatment optimization, and systems biology. Below are some key case studies that highlight the impact of biomathematics on these areas.

Case Study: The Development of Imatinib (Gleevec) for Chronic Myeloid Leukemia (CML): The development of imatinib, a tyrosine kinase inhibitor used to treat CML, relies heavily on biomathematical models of the BCR-ABL fusion protein, a key driver of CML. Using quantitative modeling of protein interactions and kinase activity, researchers were able to design a drug that specifically targeted the BCR-ABL protein, leading to high efficacy and long-term remission in CML patients (Lai et al., 2024). This biomathematical approach has accelerated the development of imatinib, making it one of the first examples of targeted cancer therapies.
Case Study: Insulin Dynamics and Diabetes Treatment: In the management of diabetes, mathematical models have been used to simulate insulin-glucose dynamics, leading to the development of insulin pumps and closed-loop systems for blood glucose control (Kovatchev et al., 2009). A mathematical model was developed to describe the interaction between insulin and glucose in the human body, providing a framework for optimizing insulin dosing in patients with diabetes. This model has been integrated into modern artificial pancreas systems, which automatically adjust insulin delivery based on real-time glucose measurements, improve patient outcomes, and reduce the burden of diabetes management.

Biomathematics is a powerful tool in drug discovery and systems biology that provides models and frameworks that enable researchers to simulate complex biological processes and predict drug interactions. These models have played a crucial role in the development of targeted therapies, optimization of treatment strategies, and advancement of personalized medicine. The real-world case studies highlighted in this section demonstrate the tangible impact of biomathematics on healthcare, from HIV treatment to cancer therapies and beyond. As biomathematics continues to evolve, its role in drug discovery and systems biology will expand, offering new opportunities for precision medicine and treatment of complex diseases.

Emerging Trends and Future Directions in Biomathematics and Bioinformatics

As the fields of bioinformatics and biomathematics continue to evolve, several emerging trends and future directions shape their trajectories. Innovations in machine learning and artificial intelligence (AI), the increasing significance of big data, and interdisciplinary collaborations are paving the way for new methodologies and applications (Journal Of Biomedical And Health Informatics, 2024). However, these advancements also bring forth challenges that need to be addressed to maximize their potential in biological research and healthcare. This section explores current trends, interdisciplinary approaches, and future challenges facing biomathematics and bioinformatics.

Machine Learning and AI: Revolutionizing Biomathematics in Bioinformatics

The integration of machine learning and AI into biomathematics has transformed the way biological data are analyzed and interpreted. Traditional mathematical models are often limited by their assumptions and the complexity of their biological systems. In contrast, machine learning algorithms can learn from data, uncover patterns, and make predictions without the need for explicit modeling of the underlying biological processes.

Applications of Machine Learning in Bioinformatics

Predictive Modeling: Machine learning algorithms are widely used to predict various biological outcomes, such as gene expression levels, protein-protein interactions, and patient responses to treatments (Mahood et al., 2020). For instance, gene expression prediction models employ techniques, such as random forests and support vector machines, to analyze large genomic datasets, allowing for accurate predictions of gene activity based on regulatory factors.

Figure 9. Steps involved in preprocessing and analysis of gene expression data.

Figure 9. Steps involved in preprocessing and analysis of gene expression data.

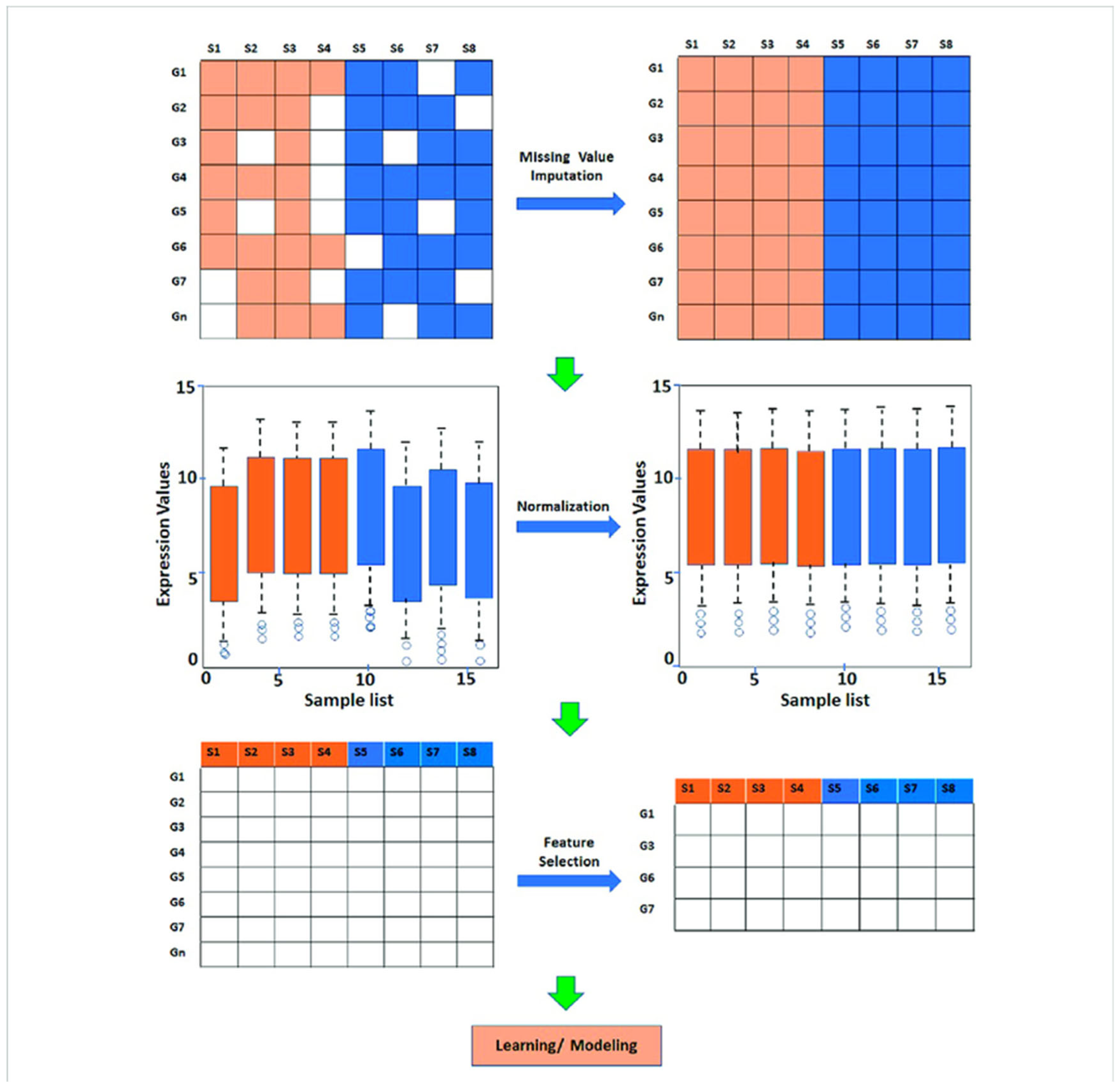
2.: Image Analysis: AI-driven image analysis is revolutionizing fields, such as medical imaging and histopathology. Convolutional neural networks (CNNs) are used to analyze histopathological images, helping in the early detection of cancers by identifying abnormal tissue structures (Priya et al., 2024). A notable example is the use of CNNs for detecting breast cancer in mammograms, which significantly improves diagnostic accuracy.

Figure 10. Deep Learning Approaches in Histopathology.

Figure 10. Deep Learning Approaches in Histopathology.

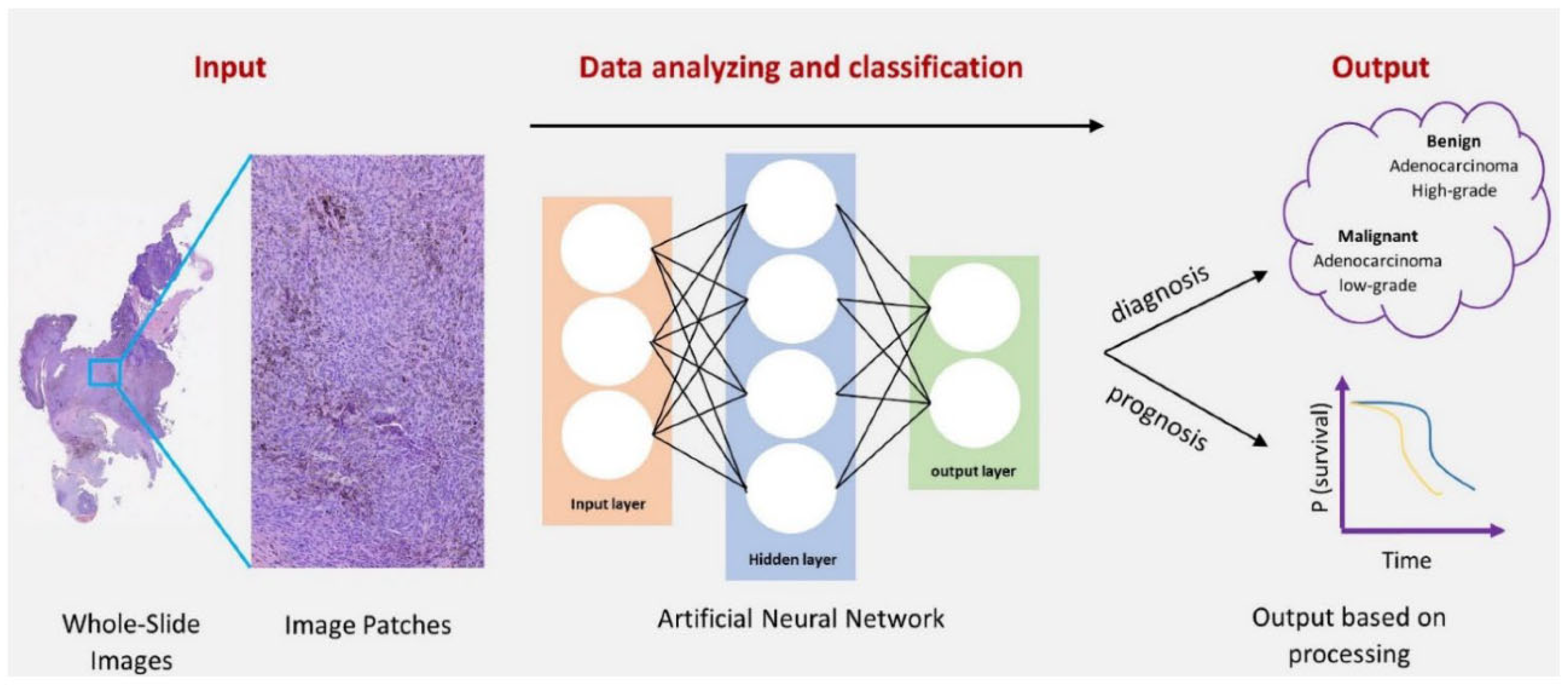
3.: Drug Discovery: Machine learning has also been applied in drug discovery to predict the efficacy and toxicity of new compounds. Deep learning models can analyze molecular structures and their interactions with biological targets, thereby accelerating the identification of promising drug candidates (Singh et al., 2023). Companies such as Atomwise and In silico Medicine utilize AI-driven platforms to predict molecular interactions and streamline the drug development process.

Figure 11. Deep Learning Driven Drug Discovery.

Figure 11. Deep Learning Driven Drug Discovery.

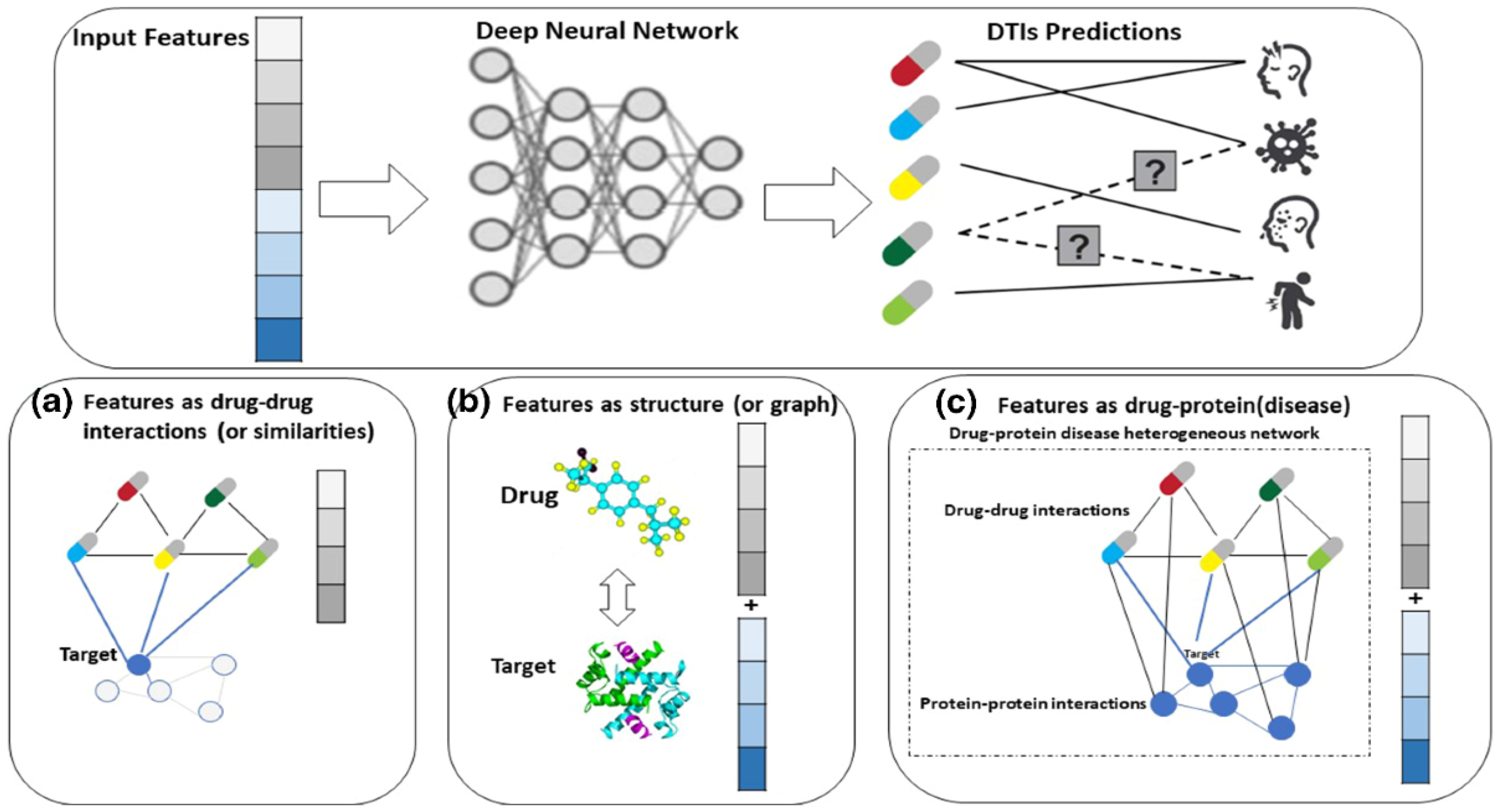
Big Data: Impact and Mathematical Models for Large Datasets

The rapid generation of biological data, particularly with advances in sequencing technologies and high-throughput experiments, has led to the emergence of "big data" in bioinformatics (Cremin et al., 2022). This data deluge presents both opportunities and challenges for researchers. Mathematical models play a crucial role in managing and interpreting large datasets.

Challenges of Big Data in Bioinformatics

Data Integration: Biological data are generated from various sources, including genomics, proteomics, transcriptomics, and metabolomics. Integrating heterogeneous data types into cohesive models requires sophisticated mathematical techniques (Greene et al. 2014). Approaches, such as multivariate analysis and network modeling, have been employed to correlate different datasets and uncover biological insights.
Scalability and Computational Efficiency: Mathematical models must be capable of efficiently handling large volumes of data. High-dimensional datasets often present computational challenges, necessitating the development of algorithms that can scale with data sizes (Biomatics, 2024). Techniques such as dimensionality reduction (e.g., principal component analysis) and parallel computing are essential for effectively managing and analyzing big data.
Real-time Data Analysis: The demand for real-time data analysis is increasing, especially in clinical settings. Algorithms that can analyze streaming data, such as the continuous monitoring of patient health metrics, must be developed (Pal et al., 2020). This requires dynamic mathematical models that are capable of adapting to incoming data and providing timely insights.

Integration with Other Disciplines: Interdisciplinary Approaches

The integration of biomathematics and bioinformatics with other scientific disciplines is a growing trend to enhance research capabilities and foster innovation. By combining insights and techniques from fields, such as physics, chemistry, and engineering, researchers can develop more robust models and methodologies.

Physics and Biophysics: The application of physical principles to biological systems has led to the development of models that describe molecular interactions and dynamics. For example, statistical mechanics is used to understand protein folding, whereas quantum mechanics helps to elucidate electron transfer in biochemical reactions (Goh & Wong, 2020).
Engineering: Techniques from engineering, such as systems engineering and control theory, are being increasingly applied in biological contexts (Goh & Wong, 2020). The development of biomedical devices such as biosensors and microfluidic systems leverages engineering principles to create tools for real-time biological monitoring and analysis.
Chemistry: Interplay between chemistry and biomathematics is particularly evident in drug design and discovery. Mathematical models that simulate chemical reactions and molecular interactions are crucial for predicting the behavior of new compounds (Goh & Wong, 2020). The field of cheminformatics employs mathematical and statistical methods to analyze chemical data and facilitate drug development.

Future Challenges: Addressing Computational Power, Data Privacy, and Ethical Concerns

As biomathematics and bioinformatics continue to advance, several challenges must be addressed to ensure sustainable progress.

Computational Power: The growing complexity of mathematical models and the increasing volume of biological data require substantial computational resources (Sharma, 2019). Researchers must seek innovative solutions to enhance the computational power, such as leveraging cloud computing and high-performance computing clusters.
Data Privacy and Security: With integration of personal genomic data into healthcare, ensuring data privacy and security is paramount. Ethical concerns regarding consent, data ownership, and potential misuse of sensitive information must be addressed (Bonomi et al., 2020). Developing frameworks that balance data accessibility for research and privacy protection is essential for fostering trust in genomic research.
Ethical Considerations: The use of AI and machine learning in healthcare raises ethical questions regarding accountability, bias, and transparency. As algorithms make increasingly autonomous decisions, ensuring fairness and minimizing bias in predictive models are crucial (Martinez-Martin & Magnus, 2019). Establishing ethical guidelines and frameworks for the use of AI in biomathematics and bioinformatics is vital to maintaining public trust and safety.

Emerging trends in biomathematics and bioinformatics, such as the integration of machine learning and AI, management of big data, and interdisciplinary collaborations, are shaping the future of biological research. However, addressing challenges related to computational power, data privacy, and ethical considerations is crucial to ensure that these advancements translate into meaningful applications in healthcare and research. As these fields continue to evolve, collaboration between mathematics, biology, and technology will play an essential role in unlocking new discoveries and improving patient outcomes.

Conclusions

The convergence of biomathematics, bioinformatics, and computational biology represents a significant advancement in the understanding and management of biological data. This study has explored various aspects of these interconnected fields, highlighting the crucial role of biomathematics in analyzing biological data, developing computational tools, and addressing the complexities inherent in biological systems. As we summarize the key findings, discuss their implications for research and practice, and suggest future research directions, it becomes evident that biomathematics are indispensable in the ongoing evolution of biological sciences.

Summary of Key Findings

Through this research, several major points have emerged regarding the role of biomathematics in bioinformatics and computational biology.

Biomathematics as a Foundation: Biomathematics serves as a foundational discipline in bioinformatics, providing mathematical frameworks and models that enable the analysis and interpretation of complex biological data. Through the application of statistical methods, differential equations, and computational algorithms, biomathematics facilitates a deeper understanding of biological processes such as tumor growth, genetic variation, and protein interactions.
Development of Computational Tools: The advancement of computational tools in bioinformatics relies heavily on biomathematical principles. The design and implementation of algorithms, databases, and software tools requires a strong mathematical foundation. Tools such as Hidden Markov Models (HMMs) and Bayesian methods exemplify how biomathematical approaches can enhance data analysis and modeling capabilities.
Application in Genomics and Proteomics: The role of biomathematics in genomics and proteomics has been emphasized, demonstrating its significance in interpreting genomic data, predicting protein structures, and analyzing molecular interactions. Techniques, such as network analysis and comparative genomics, have been instrumental in understanding the complexities of biological systems and their evolutionary relationships.
Interdisciplinary Collaboration: The integration of biomathematics with other disciplines, including physics, chemistry, and engineering, has opened new avenues for research and application. Interdisciplinary approaches facilitate the development of robust models, innovative methodologies, and enhanced technologies for biological research.
Emerging Trends and Future Directions: The impact of machine learning, big data, and AI on biomathematics and bioinformatics is underscored. These technologies are transforming the landscape of biological research and providing powerful tools for data analysis and modeling. However, they also present challenges related to the computational power, data privacy, and ethical considerations that must be addressed.

Implications for Research and Practice

The findings of this study have significant implications for both biological studies and computational biology.

Enhancing Research Capabilities: The integration of biomathematics into bioinformatics provides researchers with sophisticated tools to analyze large datasets and model complex biological systems. This enhances the capacity to uncover insights that were previously unattainable, such as understanding the genetic basis of diseases, predicting patient responses to treatment, and optimizing drug discovery processes.
Improving Clinical Applications: In clinical practice, the application of biomathematical models and computational tools can lead to more personalized medical approaches. By analyzing individual genomic data, healthcare providers can tailor treatments according to specific patient profiles, improve outcomes, and reduce adverse effects.
Guiding Policy and Ethical Considerations: As fields of biomathematics and bioinformatics continue to evolve, it is essential to establish guidelines and policies that address ethical considerations, data privacy, and the responsible use of AI in healthcare. Stakeholders, including researchers, policymakers, and clinicians, must collaborate to create frameworks to ensure the ethical application of these technologies.
Fostering Interdisciplinary Collaboration: The findings of this study highlight the importance of interdisciplinary collaboration in advancing biomathematics and bioinformatics. Encouraging partnerships among mathematicians, biologists, computer scientists, and engineers will foster innovation and lead to the development of more effective models and tools for biological research.

Future Research Directions

Several areas warrant further exploration to enhance biomathematical models and computational tools.

Advancements in Machine Learning Algorithms: Future research should focus on developing more sophisticated machine learning algorithms tailored to specific biological questions. This includes improving the predictive modeling capabilities, enhancing the interpretability of AI-driven models, and ensuring that they are robust against biases inherent in biological data.
Integration of Multi-Omics Data: As field of bioinformatics expands, integrating multi-omics data (genomics, transcriptomics, proteomics, and metabolomics) is a promising area for future research. Developing mathematical models that can effectively integrate and analyze these diverse datasets will provide a more comprehensive understanding of biological systems.
Real-Time Data Analysis Tools: The demand for the real-time analysis of biological data, particularly in clinical settings, necessitates the development of dynamic mathematical models and computational tools. Future studies should focus on creating algorithms that can analyze streaming data and provide actionable insights for healthcare professionals.
Ethics and Governance in Bioinformatics: Addressing the ethical implications of biomathematics and bioinformatics is crucial as these fields evolve. Future research should explore frameworks for ethical decision making, data governance, and public engagement to ensure that advancements are made responsibly and transparently.
Sustainability and Computational Efficiency: As biological datasets continue to grow, research into sustainable computing practices and efficient algorithms will be vital. Exploring methods to reduce the computational burden associated with large datasets will enhance the accessibility and usability of bioinformatics tools.

This study highlights the pivotal role of biomathematics in bioinformatics and computational biology. As we move forward, the collaboration of mathematical, biological, and computational sciences will be essential for addressing the complexities of biological systems, ultimately leading to significant advancements in healthcare and research. Embracing emerging trends, addressing challenges, and fostering interdisciplinary collaboration will ensure that the future of biomathematics and bioinformatics is both innovative and responsible, thus paving the way for transformative discoveries in biology and medicine.

References

Akinbusola, Victoria, (2024). Biomathematics in Cancer Research: Looking into How Mathematical Models Are Used to Understand Tumor Growth and the Effectiveness of Different Treatment Strategies. [CrossRef]
Akinbusola, Victoria (2024). Mathematical modeling of neural networks: Bridging the gap between mathematics and neurobiology. World Journal of Advanced Engineering Technology and Sciences, 2024,13(01), 516–526. [CrossRef]
Bayat A. (2002). Science, medicine, and the future: Bioinformatics. BMJ (Clinical research ed.), 324(7344), 1018–1022. [CrossRef]
Collins, F. S., & Fink, L. (1995). Human Genome Project. Alcohol health and research world, 19(3), 190–195.
Conway, J. M., & Abel Zur Wiesch, P. (2021). Mathematical Modeling of Remdesivir to Treat COVID-19: Can Dosing Be Optimized?. Pharmaceutics, 13(8), 1181. [CrossRef]
Fischer H. P. (2008). Mathematical modeling of complex biological systems: from parts lists to understanding systems behavior. Alcohol research & health: the journal of the National Institute on Alcohol Abuse and Alcoholism, 31(1), 49–59.
Greene, C. S., Tan, J., Ung, M., Moore, J. H., & Cheng, C. (2014). Big data bioinformatics. Journal of cellular physiology, 229(12), 1896–1900. [CrossRef]
Hassan, M., Awan, F. M., Naz, A., deAndrés-Galiana, E. J., Alvarez, O., Cernea, A., Fernández-Brillet, L., Fernández-Martínez, J. L., & Kloczkowski, A. (2022). Innovations in Genomics and Big Data Analytics for Personalized Medicine and Health Care: A Review. International journal of molecular sciences, 23(9), 4645. [CrossRef]
Kovatchev, B. P., Breton, M., Man, C. D., & Cobelli, C. (2009). In silico preclinical trials: a proof of concept in closed-loop control of type 1 diabetes. Journal of diabetes science and technology, 3(1), 44–55. [CrossRef]
Makrodimitris, S., van Ham, R. C. H. J., & Reinders, M. J. T. (2019). Improving protein function prediction using protein sequence and GO-term similarities. Bioinformatics (Oxford, England), 35(7), 1116–1124. [CrossRef]
Molecular Modeling and Bioinformatics Group. (2024). Tools Molecular Modeling and Bioinformatics Group. Irbbarcelona.org. https://mmb.irbbarcelona.org/www/tools.
Afanasyeva, A., Nagao, C., & Mizuguchi, K. (2019). Prediction of the secondary structure of short DNA aptamers. Biophysics and Physicobiology, 16, 287–294. [CrossRef]
Al-Amrani, S., Al-Jabri, Z., Al-Zaabi, A., Alshekaili, J., & Al-Khabori, M. (2021). Proteomics: Concepts and applications in human medicine. World Journal of Biological Chemistry, 12(5), 57–69. [CrossRef]
Almaden Genomics. (2023, February 6). Scalable and Effective Solutions for Bioinformatics. Almaden. https://almaden.io/blog/scalable-solutions-for-bioinformatics.
Alok, K., & Shrivastava. (2022). Introduction to bioinformatics (Database searching, Sequence alignment, and alignment affecting factors) Course Code -BOTY 4204 Course Title-Techniques in plant sciences, biostatistics and bioinformatics. https://mgcub.ac.in/pdf/material/20200406015638ec227591f9.pdf.
ATHAR, M., MANHAS, A., RANA, N., & IRFAN, A. (2024). Computational and bioinformatics tools for understanding disease mechanisms. Biocell, 48(6), 935–944. [CrossRef]
Biomatics. (2024). Big Data Challenges: Handling Big Data In Bioinformatics . https://biomatics.co.uk/big-data-challenges-handling-big-data-in-bioinformatics/.
Bonomi, L., Huang, Y., & Ohno-Machado, L. (2020). Privacy Challenges and Research Opportunities for Genomic Data Sharing. Nature Genetics, 52(7), 646–654. [CrossRef]
Breitwieser, L., Hesam, A., Montigny, de, Vavourakis, V., Iosif, A., Jennings, J., Kaiser, M., Manca, M., Meglio, D., AlArs, Z., Rademakers, F., Mutlu, O., & Bauer, R. (2022). BioDynaMo: a modular platform for highperformance agentbased simulation. Bioinformatics, 38(2), 453–460. [CrossRef]
Carleton, S. C. (2021, April 28). What is Bioinformatics? Graduate Blog. https://graduate.northeastern.edu/resources/what-is-bioinformatics/.
Charitou, T., Bryan, K., & Lynn, D. J. (2016). Using biological networks to integrate, visualize and analyze genomics data. Genetics Selection Evolution, 48(1), 27. [CrossRef]
Chen, Y., Li, E.-M., & Xu, L.-Y. (2022). Guide to Metabolomics Analysis: A Bioinformatics Workflow. Metabolites, 12(4), 357. [CrossRef]
Clark, A. J., & Lillard, J. W. (2024). A Comprehensive Review of Bioinformatics Tools for Genomic Biomarker Discovery Driving Precision Oncology. Genes, 15(8). [CrossRef]
Clark, L. V., Lipka, A. E., & Sacks, E. J. (2019). polyRAD: Genotype Calling with Uncertainty from Sequencing Data in Polyploids and Diploids. G3 GenesGenomesGenetics, 9(3), 663–673. [CrossRef]
Cremin, C. J., Dash, S., & Huang, X. (2022). Big data: Historic advances and emerging trends in biomedical research. Current Research in Biotechnology, 4, 138–151. [CrossRef]
Dey, D. K., Ghosh, S., & Mallick, B. K. (2010). Bayesian Modeling in Bioinformatics. CRC Press.
Doerr, B., Eremeev, A., Neumann, F., Theile, M., & Thyssen, C. (2011). Evolutionary algorithms and dynamic programming. Theoretical Computer Science, 412(43), 6020–6035. [CrossRef]
Excedr. (2023, November 27). What Is Bioinformatics & How Does It Compare to Computational Biology? Excedr.com. https://www.excedr.com/blog/what-is-bioinformatics-and-computational-biology#.
Fan, J., Han, F., & Liu, H. (2014). Challenges of Big Data analysis. Natl Sci Rev, 1(2), 293–314. [CrossRef]
Fay, D. S., & Gerow, K. (2018). A biologist’s guide to statistical thinking and analysis. In www.ncbi.nlm.nih.gov. WormBook. https://www.ncbi.nlm.nih.gov/books/NBK153593/.
Fröhlich, F., Gerosa, L., Muhlich, J., & Sorger, P. K. (2023). Mechanistic model of MAPK signaling reveals how allostery and rewiring contribute to drug resistance. Molecular Systems Biology, 19(2), e10988. [CrossRef]
Ghosh, A. K., Osswald, H. L., & Prato, G. (2016). Recent Progress in the Development of HIV-1 Protease Inhibitors for the Treatment of HIV/AIDS. Journal of Medicinal Chemistry, 59(11), 5172–5208. [CrossRef]
Giró, A., Valls, J., Padr, J. A., & Wagensberg, J. (1986). Monte Carlo simulation program for ecosystems. Bioinformatics, 2(4), 291–296. [CrossRef]
Goh, W. W. B., & Wong, L. (2020). The Birth of Bio-data Science: Trends, Expectations, and Applications. Genomics, Proteomics & Bioinformatics, 18(1), 5–15. [CrossRef]
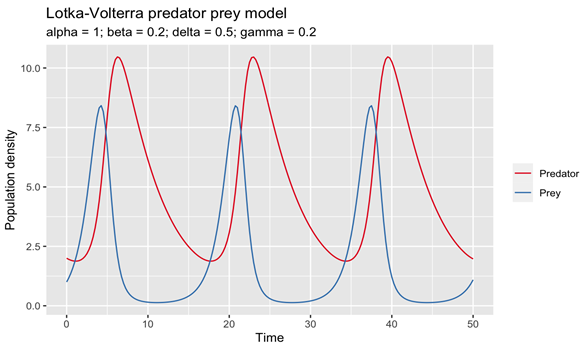
Hoppensteadt, F. (2006). Predator-prey model. Scholarpedia, 1(10), 1563. [CrossRef]
Huang, S. (2018). Applications of Support Vector Machine (SVM) Learning in Cancer Genomics. Cancer Genomics & Proteomics, 15(1). [CrossRef]
Journal Of Biomedical And Health Informatics. (2024). IEEE JOURNAL OF BIOMEDICAL AND HEALTH INFORMATICS J-B HI Special Issue on “Healthcare Information Systems for Disease Monitoring and Management in Smart Cities.” https://www.embs.org/jbhi/wp-content/uploads/sites/18/2023/06/JBHI_SmartCities_SI-1.pdf.
Lai, X., Jiao, X., Zhang, H., & Lei, J. (2024). Computational modeling reveals key factors driving treatmentfree remission in chronic myeloid leukemia patients. Npj Systems Biology and Applications, 10(1), 45. [CrossRef]
Lakhno, V. D. (2019). Mathematical biology and bioinformatics. Herald of the Russian Academy of Sciences, 81(5), 539–545. [CrossRef]
Li, Y., & Chen, L. (2014). Big Biological Data: Challenges and Opportunities. Genomics, Proteomics & Bioinformatics, 12(5), 187–189. [CrossRef]
Mahood, E. H., Kruse, L. H., & Moghe, G. D. (2020). Machine learning: A powerful tool for gene function prediction in plants. Applications in Plant Sciences, 8(7), e11376. [CrossRef]
Martinez-Martin, N., & Magnus, D. (2019). Privacy and ethical challenges in next-generation sequencing. Expert Review of Precision Medicine and Drug Development, 4(2), 95–104. [CrossRef]
matellio. (2024, February 28). Bioinformatics Software Development: Process, Use Cases, Insights, and More - Matellio Inc. Matellio Inc. https://www.matellio.com/blog/bioinformatics-software-development/.
Mathematical Institute. (2022). Bioinformatics, Biomathematics and Biostochastics. Uni-Tuebingen.de. https://www.math.uni-tuebingen.de/user/moehle/bio_e.htm.
Mikolaj, C., & Prusinkiewicz, P. (2019). GillespieLindenmayer systems for stochastic simulation of morphogenesis. In Silico Plants, 1(1), diz009. [CrossRef]
Napolitano, F., Xu, X., & Gao, X. (2021). Impact of computational approaches in the fight against COVID-19: an AI guided review of 17 000 studies. Briefings in Bioinformatics. [CrossRef]
National Cancer Institute. (2020, March 6). Mapping Cancer Genomic Evolution. Cancer.gov. https://www.cancer.gov/news-events/cancer-currents-blog/2020/mapping-genomic-evolution-as-cancer-develops#.
Olushola, A., Mart, J., (2022). Fraud Detection Using Machine Learning Techniques. [CrossRef]
Olushola, A., Mart, J., Alao, V., (2023). Implementations Of Artificial Intelligence In Health Care. [CrossRef]
Olushola, A., Mart, J., Alao, V., (2023). Predictive Modelling For Disease Outbreak Prediction. [CrossRef]
Oyewusi, H. A., Wahab, R. A., Akinyede, K. A., Albadrani, G. M., Al-Ghadi, M. Q., Abdel-Daim, M. M., Ajiboye, B. O., & Huyop, F. (2024). Bioinformatics analysis and molecular dynamics simulations of azoreductases (AzrBmH2) from Bacillus megaterium H2 for the decolorization of commercial dyes. Environmental Sciences Europe, 36(1). [CrossRef]
Pal, S., Bhattacharya, M., Lee, S.-S., & Chakraborty, C. (2023). Quantum Computing in the Next-Generation Computational Biology Landscape: From Protein Folding to Molecular Dynamics. Volume 66. [CrossRef]
Pal, S., Mondal, S., Das, G., Khatua, S., & Ghosh, Z. (2020). Big data in biology: The hope and presentday challenges in it. Gene Reports, 21, 100869. [CrossRef]
Parvinen, K. (2022). Ordinary Differential Equations. In E. D. Maria (Ed.), Systems Biology Modelling and Analysis: Formal Bioinformatics Methods and Tools (p. chapter 9). Wiley Online Library. [CrossRef]
Pereira, R., Oliveira, J., & Sousa, M. (2020). Bioinformatics and Computational Tools for Next-Generation Sequencing Analysis in Clinical Genetics. Journal of Clinical Medicine, 9(1), 132. [CrossRef]
Pereira, R., Oliveira, J., & Sousa, M. (2020). Bioinformatics and Computational Tools for Next-Generation Sequencing Analysis in Clinical Genetics. Journal of clinical medicine, 9(1), 132. [CrossRef]
Priya C V, L., V G, B., B R, V., & Ramachandran, S. (2024). Deep learning approaches for breast cancer detection in histopathology images: A review. Cancer biomarkers : section A of Disease markers, 40(1), 1–25. [CrossRef]
Rosati, D., Palmieri, M., Brunelli, G., Morrione, A., Iannelli, F., Frullanti, E., & Giordano, A. (2024). Differential gene expression analysis pipelines and bioinformatic tools for the identification of specific biomarkers: A Review. Computational and Structural Biotechnology Journal, 23. [CrossRef]
Russo, V., Lallo, E., Munnia, A., Spedicato, M., Messerini, L., D'Aurizio, R., Ceroni, E. G., Brunelli, G., Galvano, A., Russo, A., Landini, I., Nobili, S., Ceppi, M., Bruzzone, M., Cianchi, F., Staderini, F., Roselli, M., Riondino, S., Ferroni, P., Guadagni, F., … Peluso, M. (2022). Artificial Intelligence Predictive Models of Response to Cytotoxic Chemotherapy Alone or Combined to Targeted Therapy for Metastatic Colorectal Cancer Patients: A Systematic Review and Meta-Analysis. Cancers, 14(16), 4012. [CrossRef]
Saada, B., Zhang, T., Siga, E., Zhang, J., & Maria. (2024). WholeGenome Alignment: Methods, Challenges, and Future Directions. Applied Sciences, 14(11). [CrossRef]
Samal, K., Sahoo, J., Behera, L., & Dash, T. (2021). Understanding the BLAST (Basic Local Alignment Search Tool) Program and a Stepbystep Guide for its use in Life Science Research. Bhartiya Krishi Anusandhan Patrika, 36, 55–61. [CrossRef]
Saraswathy, N., Ramalingam, P., Saraswathy, N., & Ramalingam, P. (2011). 7 - Genome sequencing methods. In Woodhead Publishing Series in Biomedicine (pp. 95–107). Woodhead Publishing. [CrossRef]
Schwab, J.D., Kühlwein, S.D., Ikonomi, N., Kühl, M. and Kestler, H.A., 2020. Concepts in Boolean network modeling: What do they all mean?. Computational and structural biotechnology journal, 18, pp.571-582.
Searls, D. B. (2024, August 14). computational biology. Encyclopedia Britannica. https://www.britannica.com/science/computational-biology.
Sharma, H. (2019). HPCEnhanced Training of Large AI Models in the Cloud. [CrossRef]
Shmulevich, I., & Aitchison, J. D. (2009). Deterministic and stochastic models of genetic regulatory networks. Methods in enzymology, 467, 335–356. [CrossRef]
Singh, A.K. (2023). Convolutional Neural Network in Medical Image Analysis. [CrossRef]
Singh, S., Kumar, R., Payra, S., Singh, S. K., Singh, S., Kumar, R., Payra, S., & Singh, S. K. (2023). Artificial Intelligence and Machine Learning in Pharmacological Research: Bridging the Gap Between Data and Drug Discovery. Cureus, 15(8). [CrossRef]
Somda, D., Kpordze, S. W., Jerpkorir, M., Mahora, M. C., Ndungu, J. W., Kamau, S. W., Arthur, V., & Elbasyouni, A. (2023). The Role of Bioinformatics in Drug Discovery: A Comprehensive Overview. IntechOpen EBooks. [CrossRef]
Swain, S. M., Shastry, M., & Hamilton, E. (2023). Targeting HER2-positive breast cancer: advances and future directions. Nature reviews. Drug discovery, 22(2), 101–126. [CrossRef]
Uffelmann, E., Huang, Q. Q., Munung, Nchangwi Syntia, de Vries, Jantina, Okada, Y., Martin, A. R., Martin, H. C., Lappalainen, T., & Posthuma, D. (2021). Genomewide association studies. Nature Reviews Methods Primers, 1(1), 59. [CrossRef]
Yoon, B.-J. (2009). Hidden Markov Models and their Applications in Biological Sequence Analysis. Current Genomics, 10(6), 402–415. [CrossRef]
Yousef, M., & Allmer, J. (2023). Deep learning in bioinformatics. Turkish Journal of Biology, 47(6), 366–382. [CrossRef]
Zhang, P., Feng, K., Gong, Y., Lee, J., Lomonaco, S., & Zhao, L. (2022). Usage of Compartmental Models in Predicting COVID-19 Outbreaks. The AAPS Journal, 24(5). [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Bioinformatics and Computational Biology: Exploring the Role of Biomathematics in Bioinformatics, Including the Analysis of Biological Data and the Development of Computational Tools

Abstract

Keywords:

Subject:

Contents

Introduction

Background

Biomathematics

Research Statement

Objectives and Research Questions

Bioinformatics and Computational Biology: Foundations and Applications

Bioinformatics: Definition and Significance

Computational Biology: Definition and Applications

Biomathematics in Bioinformatics: Supporting Biological Research

Real-World Applications: Genomics, Proteomics, and Beyond

The Role of Biomathematics in Biological Data Analysis

Mathematical Models in Representing Biological Systems

Data Analysis Techniques in Biomathematics

Types of Biological Data and Their Complexities

Challenges in Biological Data Analysis

Development of Computational Tools Using Biomathematics

Computational Tool Development in Bioinformatics

Algorithms and Models in Bioinformatics

Simulation Tools in Bioinformatics

Case Studies: Tools Developed Using Biomathematical Approaches

Biomathematics in Genomics and Proteomics

Genomic Data Analysis

Gene Expression and Differential Analysis

Sequencing Data and Genomic Mapping

Variant Calling and Population Genomics

Proteomic Data Analysis

Protein Structure Prediction

Functional Annotation of Proteins

Network Analysis in Molecular Interactions

Graph Theory in Molecular Networks

Systems Biology and Network Models

Comparative Genomics and Phylogenetics

Comparative Genomics

Phylogenetic Analysis

Case Studies: Biomathematics in Drug Discovery and Systems Biology

Drug Discovery: Modeling Drug Interactions, Pharmacokinetics, and Pharmacodynamics

Pharmacokinetics and Pharmacodynamics Modeling

Molecular Docking and Drug Interactions

Systems Biology: Modeling Complex Biological Systems

Systems Biology and Network Models

Personalized Medicine: Tailoring Treatments Based on Genomic Data

Pharmacogenomics and Biomarker Discovery

Predictive Models for Treatment Optimization

Case Study Examples: Biomathematical Applications in Drug Discovery and Treatment Strategies

Emerging Trends and Future Directions in Biomathematics and Bioinformatics

Machine Learning and AI: Revolutionizing Biomathematics in Bioinformatics

Applications of Machine Learning in Bioinformatics

Big Data: Impact and Mathematical Models for Large Datasets

Challenges of Big Data in Bioinformatics

Integration with Other Disciplines: Interdisciplinary Approaches

Future Challenges: Addressing Computational Power, Data Privacy, and Ethical Concerns

Conclusions

Summary of Key Findings

Implications for Research and Practice

Future Research Directions

References

MDPI Initiatives

Important Links

Subscribe