Submitted:
31 October 2024
Posted:
01 November 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Notation
2.1. CoVaR in the Copula Setting
2.2. Portfolio Selection
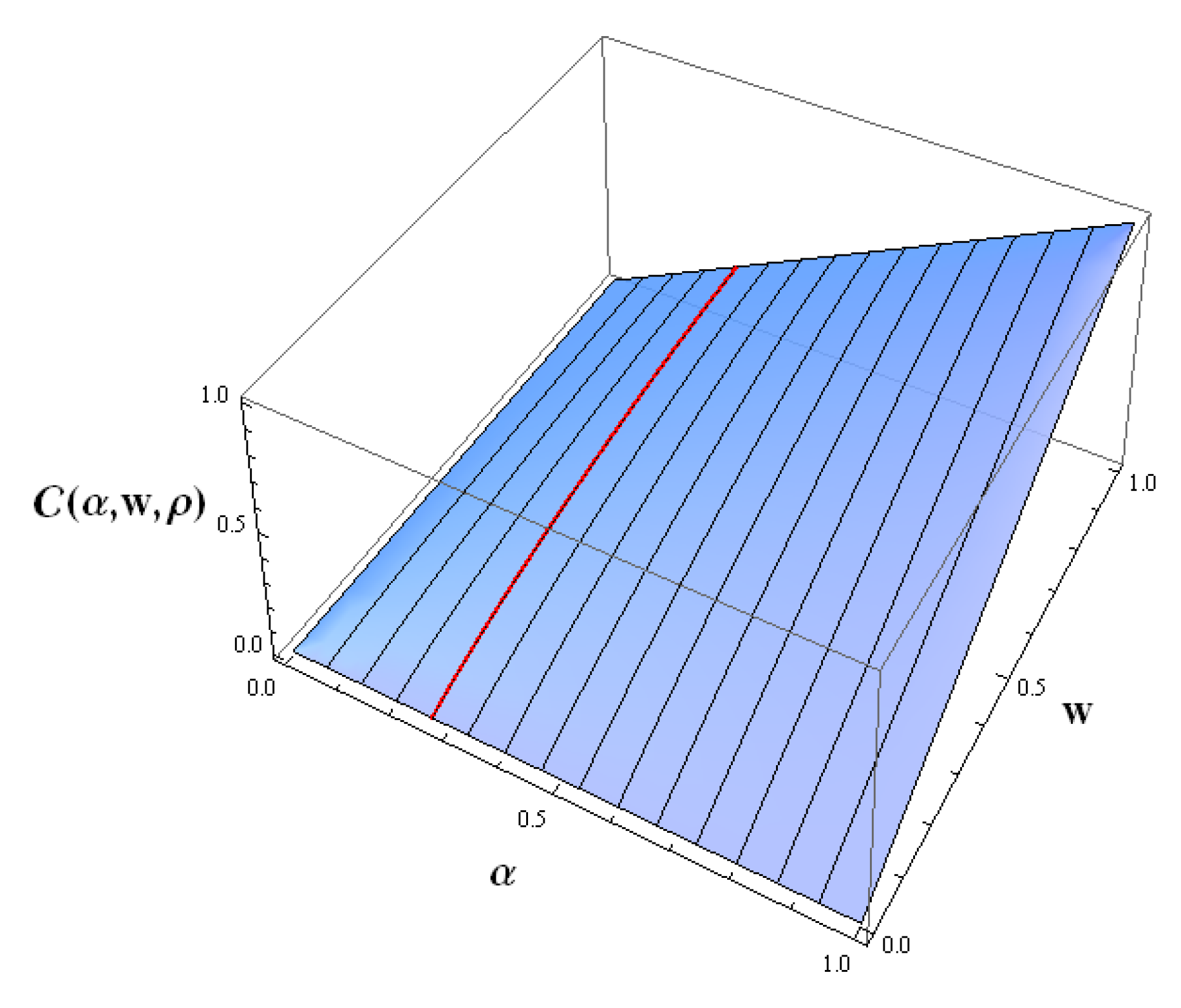
3. The Mean-CoVaR Model
4. Proofs and Auxiliary Results
4.1. Gaussian Copulas
- (1)
- (2)
- (3)
- .
4.2. The Optimization Problems
4.2.1. The Basic Problem
4.2.2. The Markowitz Problem
4.2.3. Critical Plane
4.2.4. Auxiliary Optimization Problem
4.2.5. Proof of Theorem 3.1
4.2.6. Proof of Theorem
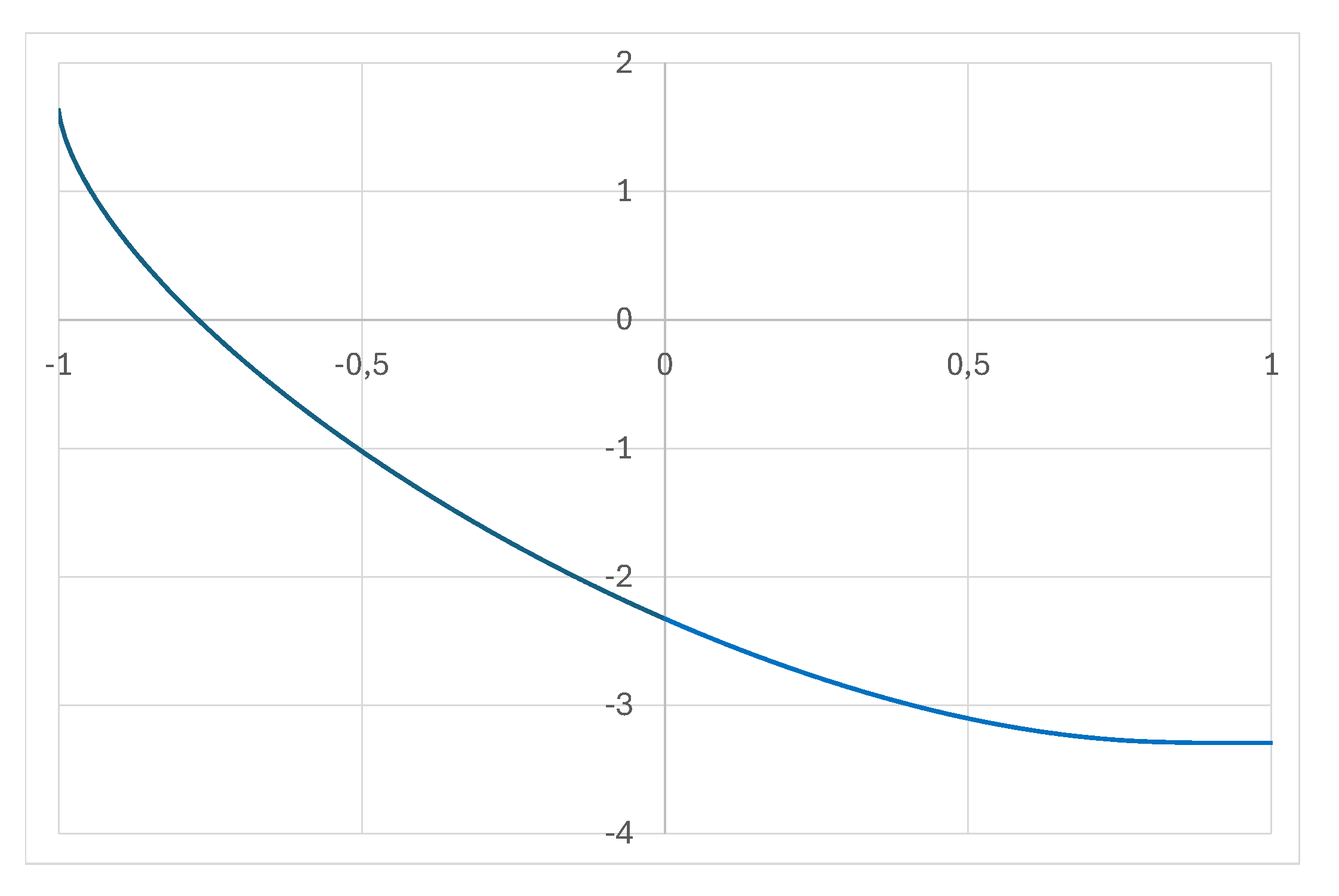
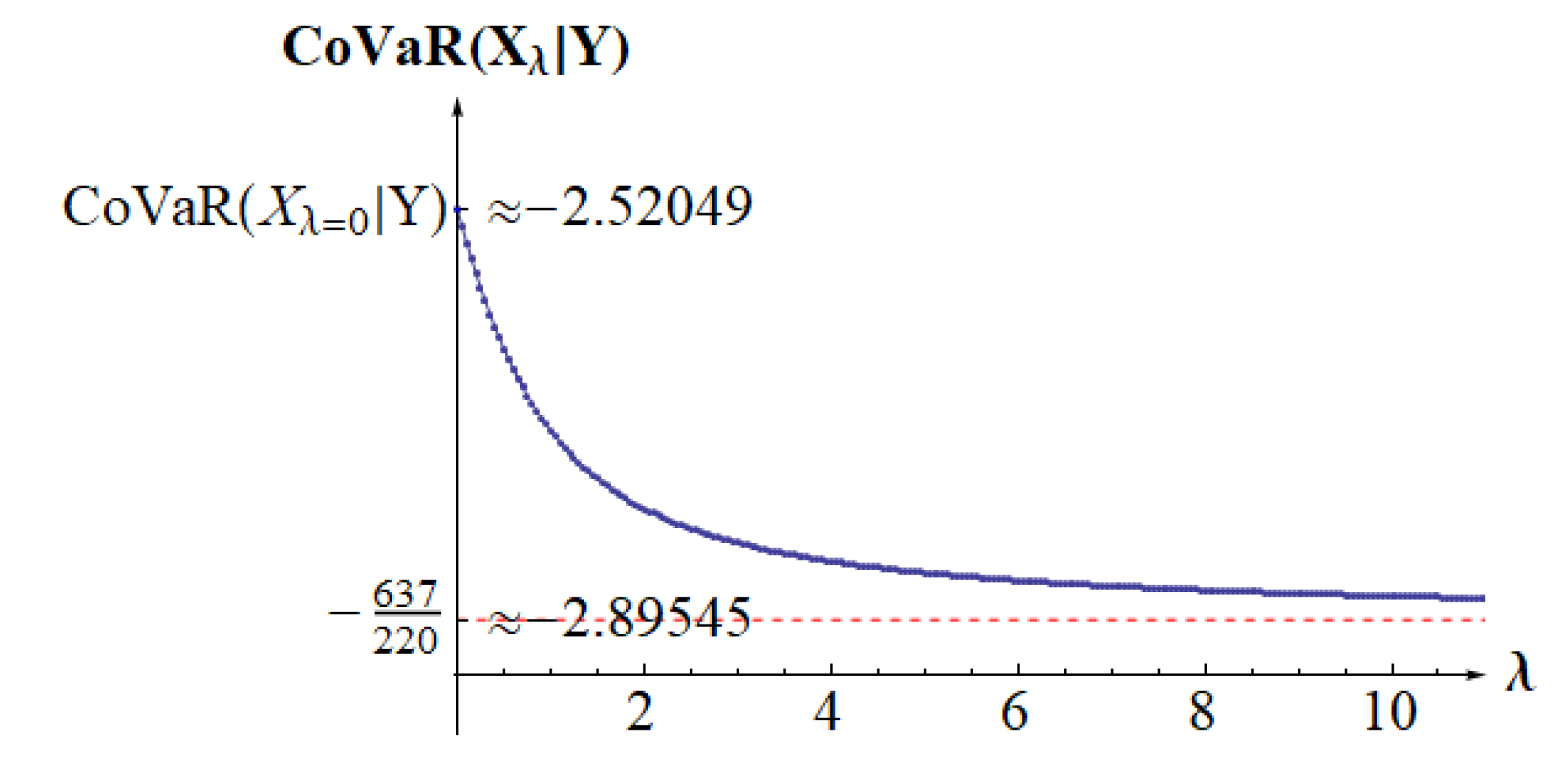
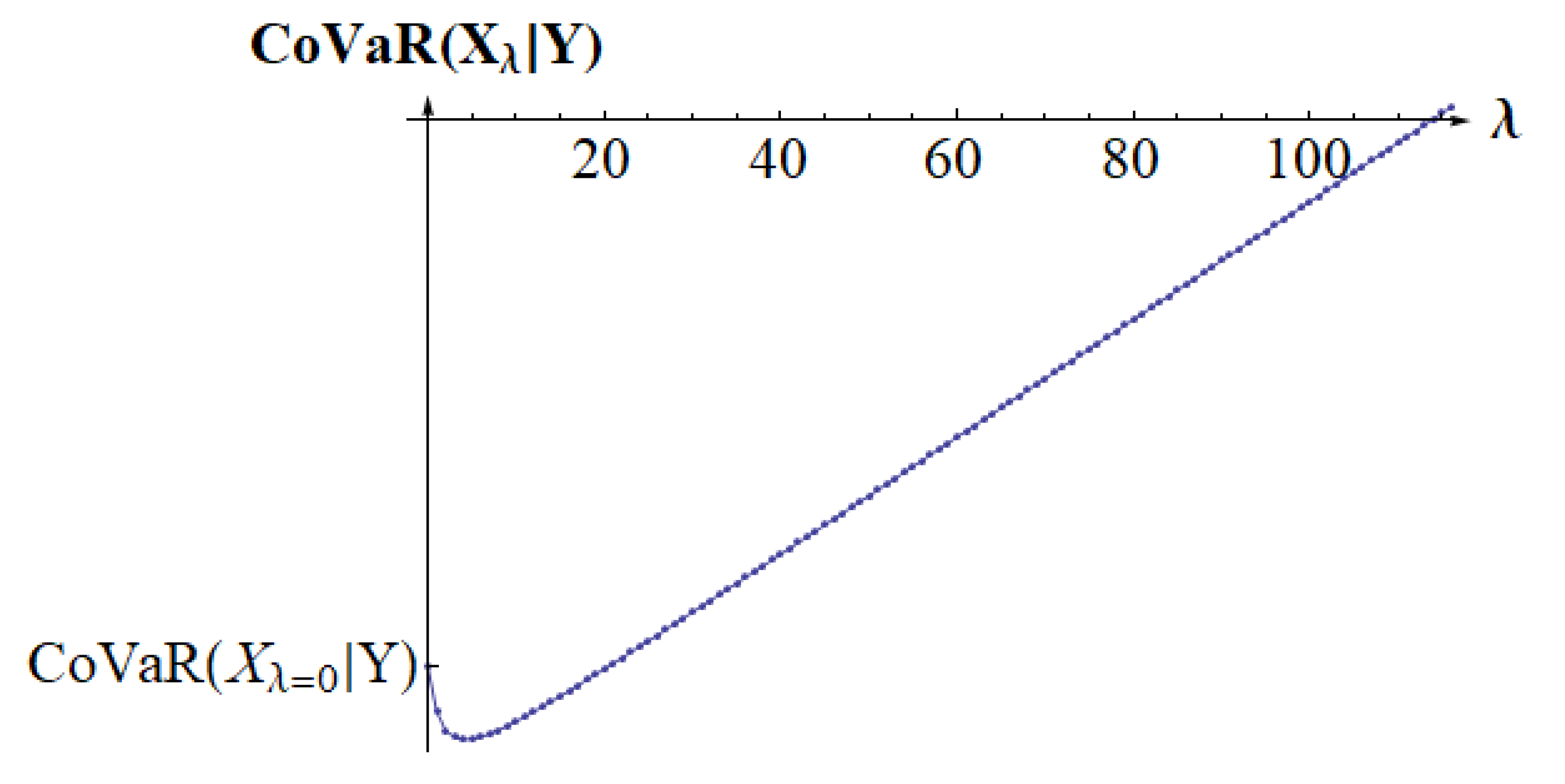
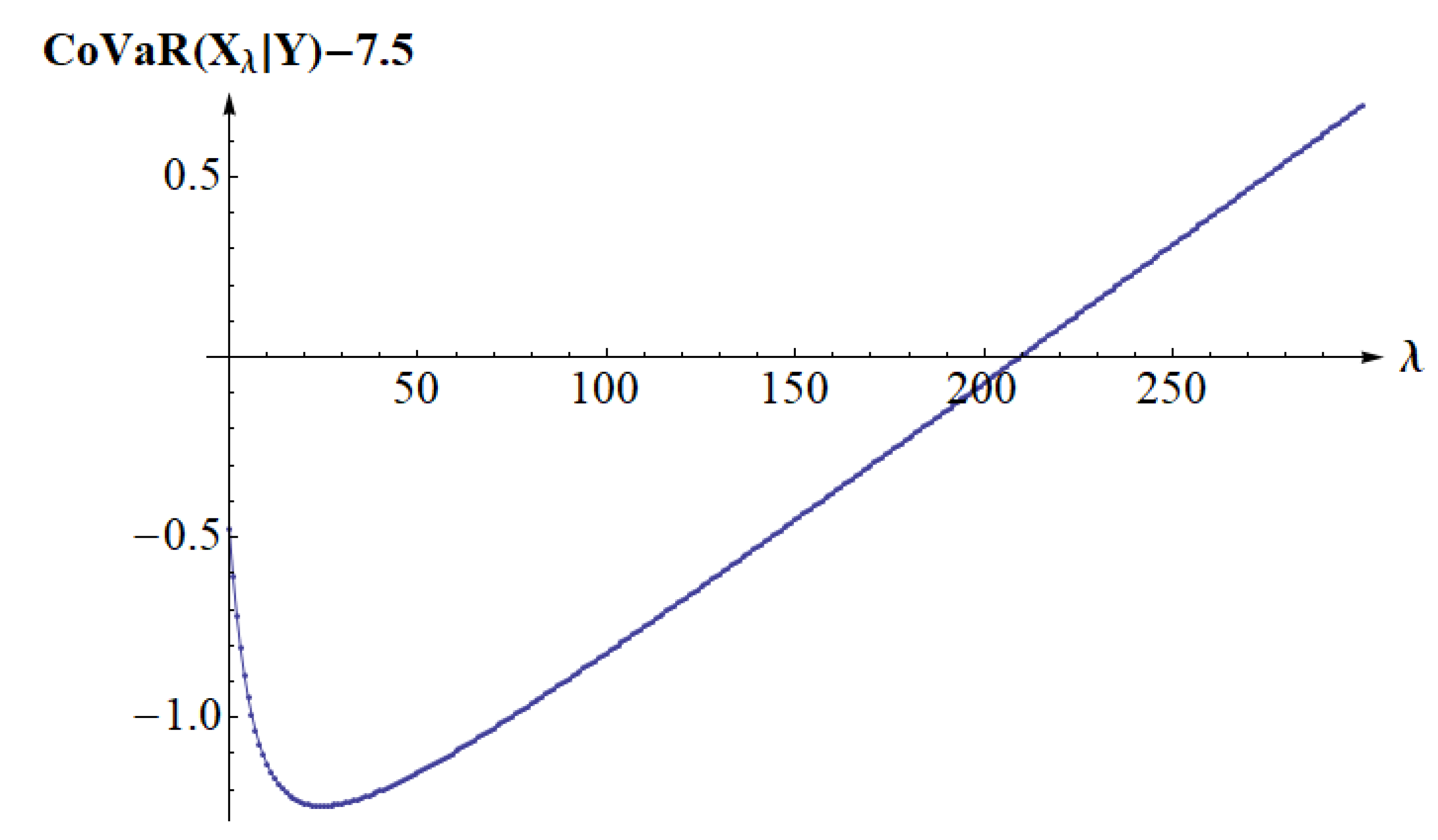
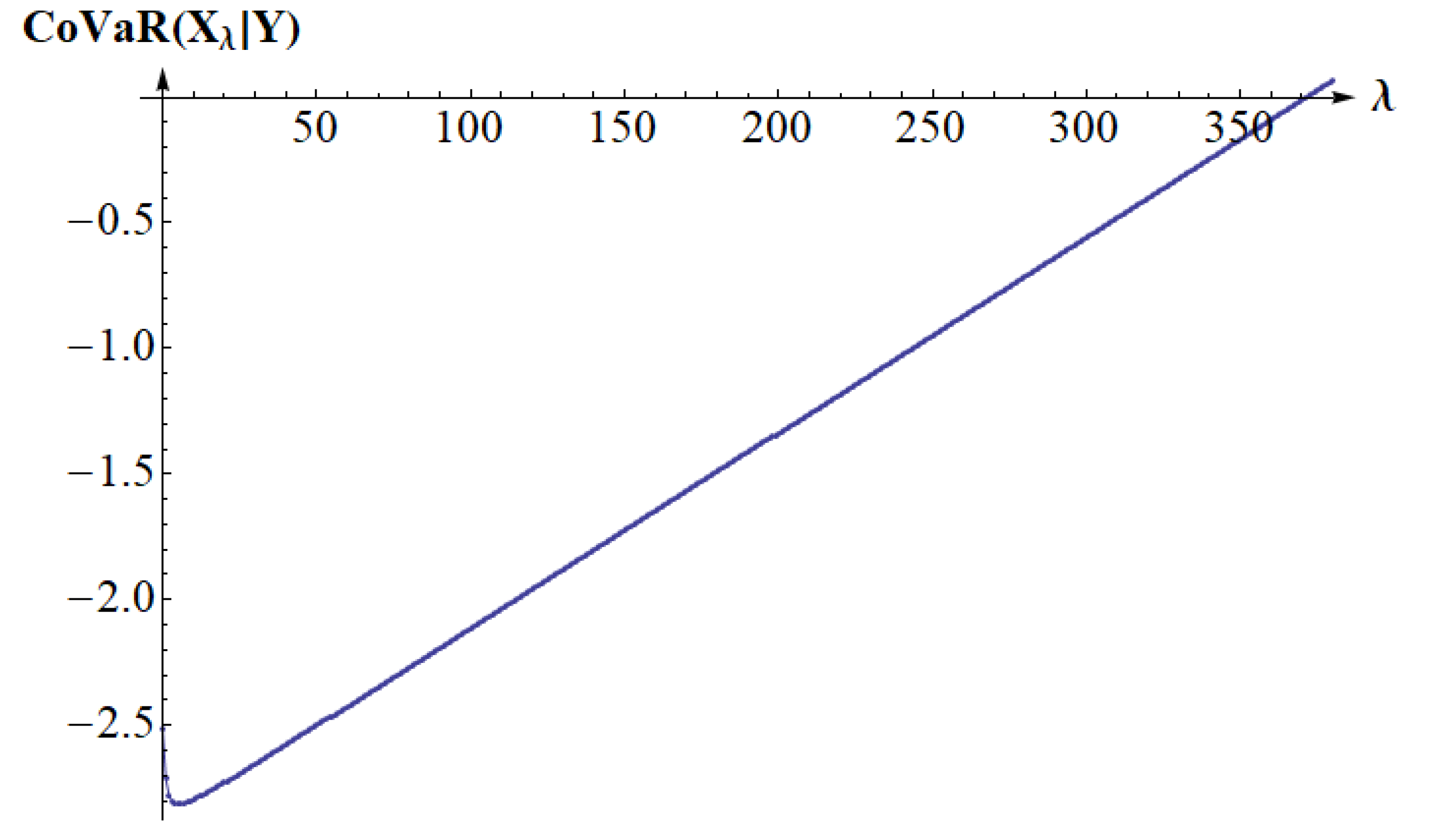
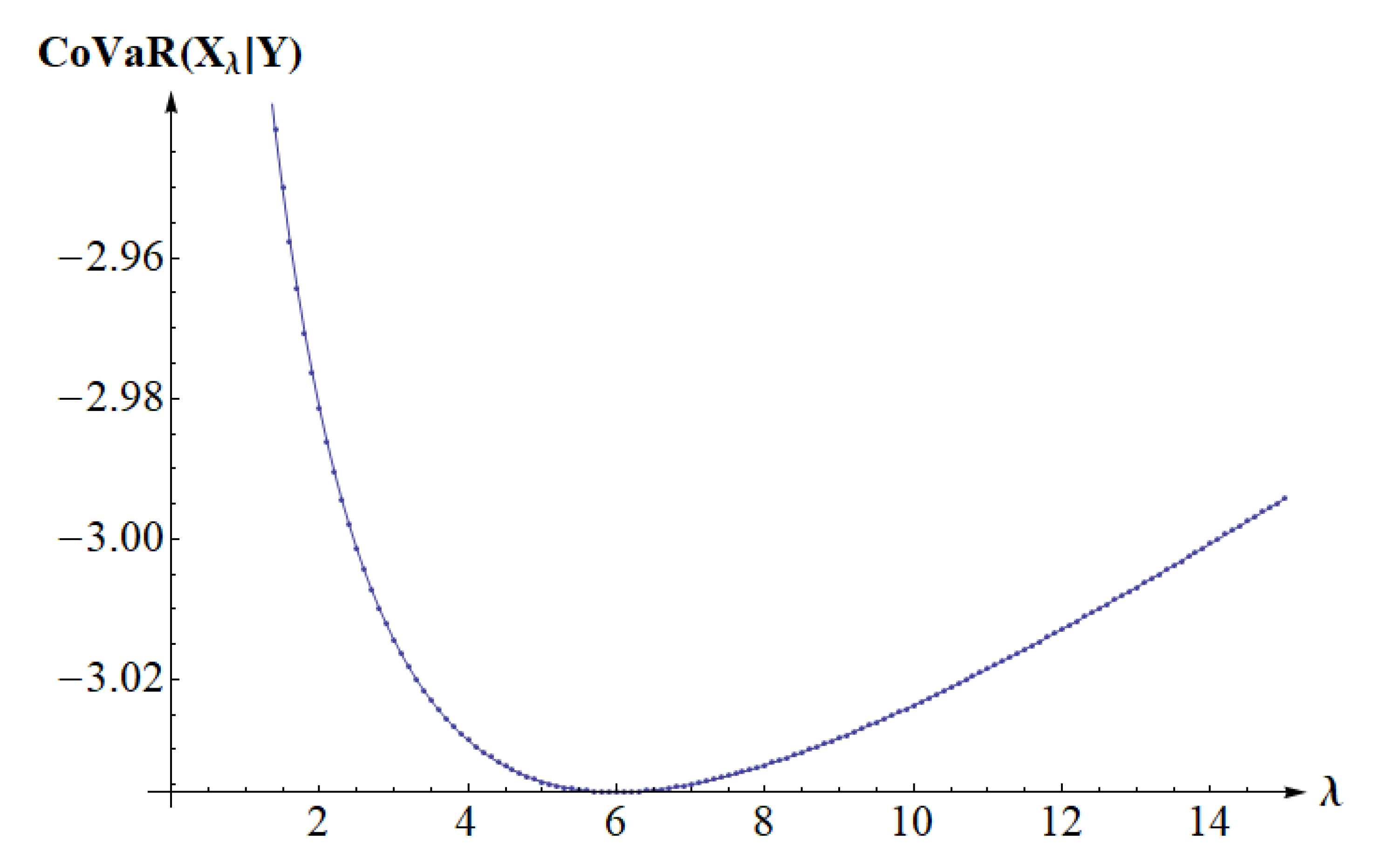
5. Examples
References
- Adrian, T., Brunnermeier, M.K.: CoVaR, The American Economic Review 106.7, 1705-1741 (2016).
- Bernardi, M., Durante, F., Jaworski, P., 2017. Covar of families of copulas. Statistics & Probability Letters 120, 8–17.
- Bernardi, M., Durante, F., Jaworski, P., Petrella, L., Salvadori, G.: Conditional Risk based on multivariate Hazard Scenarios. Stochastic Environmental Research and Risk Assessment 32 (2018) 203-211.
- Cherubini, U., Luciano, E., Vecchiato, W.: Copula Methods in Finance, John Wiley & Sons Ltd 2004.
- Durante, F., Sempi, C.: Principles of copula theory, CRC Press 2016.
- Embrechts, P.: Copulas: a personal view. Journal of Risk and Insurance, 76, 639–650 (2009).
- Föllmer, H., Schied, A.: Stochastic Finance. An Introduction in Discrete Time, de Gruyter, 2nd Edition, 2004.
- Girardi, G., Ergün T.A.: Systemic risk measurement: Multivariate GARCH estimation of CoVar, Journal of Banking & Finance 37, (2013) 3169-3180.
- Hakwa B., Jäger-Ambrozewicz, M., Rüdiger, B.: Analysing systemic risk contribution using a closed formula for conditional Value at Risk through copula. Commun. Stoch. Anal., 9(1):131–158, 2015.
- Jaworski, P.: The limiting properties of copulas under univariate conditioning, In: Copulae in Mathematical and Quantitative Finance, P.Jaworski, F.Durante, W.K.Härdle (Eds.), Springer 2013, pp.129–163.
- Jaworski, P., On the Conditional Value at Risk (CoVaR) for tail-dependent copulas, Dependence Modeling 5 (2017) 1-15.
- Jaworski, P., On the Conditional Value-at-Risk (CoVaR) in copula setting, W: Úbeda Flores, M., de Amo Artero, E., Durante, F., Fernández-Sánchez, J. (Eds.) Copulas and Dependence Models with Applications, Springer, Cham 2017, pp. 95-117.
- Joe, H.: Dependence Modeling with Copulas. Chapman & Hall/CRC, London, 2014.
- Mai, J., Scherer, M., 2012. Simulating Copulas: Stochastic Models, Sampling Algorithms, and Applications. Series in quantitative finance. Imperial College Press.
- Mainik G., Schaanning E.: On dependence consistency of CoVaR and some other systemic risk measures. Stat. Risk Model., 31, 49–77 (2014).
- McNeil, A.J., Frey, R., Embrechts, P.. Quantitative risk management. concepts, techniques and tools. Princeton Series in Finance. Princeton University Press, Princeton, NJ, 2005.
- Meyer, C., 2013. The bivariate normal copula. Communications in Statistics - Theory and Methods 42 (13), 2402–2422.
- Nelsen, R.B.: An introduction to copulas. Springer Series in Statistics. Springer, New York, second edition, 2006.
- Sheppard, W.F., 1900 On the calculation of the double integral expressing normal correlation. Trans. Camb. Phil. Soc., 19, 23-68.
- Zalewska, A., 2018. On peculiarities of covar-based portfolio selection. Applicationes Mathematicae, 181–197.
| 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




