Enhanced Feature Selection via Hierarchical Concept Modeling

1. Introduction

Nowadays, big data are often confronted, and dataset sizes have increased dramatically in applications of classification by machine learning. Feature selection is typically applied in these classification tasks. The aim of feature selection is to improve the predictive performance of classifiers by removing redundant or irrelevant features. A single feature subset to generate a binary classifier tends to have features that are useful for distinguishing these specific classes but useless for distinguishing others [1,2,3]. Feature selection is a common task in applications of pattern recognition, data mining, and machine learning since it can help improve prediction quality, reduce computation time, and allow building more human-understandable models. Thus, it is used in many applications before training a classifier [3]. However, while there are a lot of state-of-the-art approaches for feature selection in standard feature space [4], only a few approaches for feature selection in hierarchical feature space have been proposed in the literature [1,5].

Hierarchical model is one approach to feature selection for enhanced predictive performance of classifiers. It is not only advantageous for identifying the hierarchical model itself but is also helpful for selecting a feature subset for each node [1,5,6,7,8]. Classes in a hierarchical structure have both parent-children relationships and sibling relationships [2,9,10]. Moreover, classes with a parent-children relationship are similar to each other and may share common features for classification, while distinguishing between classes with a sibling relationship may require different features [1,8,11]. The authors developed a method for joint feature selection and hierarchical classifier design using genetic algorithms. Thus, this work focuses on using hierarchical structure in feature selection to improve the predictive performance in classification. In this study, we designed a feature selection algorithm based on the hierarchical information structure.

The hierarchical models were built by using two strategies: bottom-up and top-down. The bottom-up strategy starts by placing each object in its own cluster and then merges these atomic clusters into larger and larger clusters until all of the objects are in a single cluster or until some other termination conditions are satisfied. Later, the top-down strategy does the reverse by starting with all objects in one cluster. It subdivides the cluster into smaller and smaller pieces until each object forms a cluster on its own or until some other termination conditions are met, such as a desired number of clusters or that the distance between the two closest clusters is above a certain threshold [12,13,14]. Thus, this work applied both bottom-up and top-down approaches, which were done with formal concept analysis (FCA) and decision tree, respectively. Both FCA and decision tree approach were considered for feature selection in order to reduce the attribute count while still retaining the efficiency of data classification.

FCA [15,16,17,18], invented by Rudolf Wille in 1982, is a method for data analysis based on concept lattice. It is widely used in information science to describe attributes and objects of information that can be represented in a hierarchical structure. FCA provides relationships of generalization and specialization among concepts in the concept lattice. This method is rarely applied to feature selection in classification or other tasks.This research applied the advantage of being general knowledge through calculation and selection a root node of hierarchical structure. The alternative approach by decision trees uses these powerful and popular tools for classification and prediction. Such classifier has a tree structure, where each node is either a leaf node or a branching decision node [11,19]. This approach is widely used to perform feature selection. The advantages of decision trees are intuitive appeal for knowledge expression, simple implementation, and high classification accuracy. Thus, this work applied both FCA and decision trees to reduce the number of features that need to be collected and also to provide better classification accuracy. Due to the different patterns of selecting general knowledge in both FCA and decision trees in hierarchical concept structure, FCA will be constructed a concept lattice structure based on logic and set theory while decision trees will be built a tree structure based on information gain. Moreover, the decision tree in this study is considered to provide a mathematical selection of the features with the optimization level based on paired-samples t-test. Next, the proposed models were tested and evaluated by using three popular algorithms for classification, namely decision tree, Support Vector Machine (SVM), and Artificial Neural Network (ANN), to assess the predictive performances with the presented approach, using data from the UCI repository.

This article is organized as follows. Section 2 briefly describes the machine learning techniques applied in this work. Section 3 presents the research methodology, followed by experimental results and discussion in section 4. Finally, section 5 concludes the article.

2. Related Works

Feature selection methods have been used for a wide variety of applications [1,2]. Such methods proceed to eliminate unfavorable features that might be noisy, redundant, or irrelevant and could penalize the performance of a classifier [2]. Feature selection contributes thus to reduce the dimensionality of data and to restrict the inputs, which can contain missing values in one or several features [1,4]. The various feature selection methods fall into three main categories: filters, wrappers, and embedded methods [2,3,4,20]. The first category of filter methods selects the features by using weights that indicate correlations between each feature and a class. The largest weights are selected in rank order. The calculated weights may be based on Information gain [1,3,20], Chi-square [21,22], or other saliency measures. The second category is wrapper methods that evaluate feature subsets by directly using a learning algorithm and selecting features based on their impact on the model’s performance [3,20]. While this appears reasonable as a direct approach, it tends to be too expensive computationally. Finally, embedded methods incorporate feature selection within the learning algorithm during the training process [1,2,3]. In prior studies, many feature selection methods were developed to identify the most relevant and informative features from a dataset. Selecting the right set of features can improve model performance, reduce overfitting, enhance interpretability, and speed up the learning process. This study focuses on applying a hierarchical concept model to select the features from available data.

In recent years, feature selection based on a hierarchical information structure has been proposed because of its rational learning inside the structure. [23] proposed a hierarchical feature selection framework by considering the parent-child relationship, sibling relationship, and family relationship. These relationships were modeled and implemented by using a data matrix concept [5]. [13] presented the hierarchical feature selection with subtree based graph regularization by exploring two-way dependence among different classes. [5] designed a feature selection strategy for hierarchical classification based on fuzzy rough sets to compute the lower and upper approximations of classes organized in a class hierarchy. The authors developed an efficient hierarchical feature selection algorithm based on sibling nodes [5]. [24] proposed feature selection framework based on semantic and structural information of labels for hierarchical feature selection by transforming to semantic regularization and adapted the proposed model to a directed acyclic graph case. [25] proposed a robust hierarchical feature to reduce the adverse effects of data outliers and learn relatively robust and discriminative feature subsets for hierarchical classification. All the above mentioned studies assumed specific relationships between categories for hierarchical regularization. However, most of the existing hierarchical feature selection methods are not robust for dealing with the inevitable data outliers, resulting in a serious inter-level error propagation problem in the classification process that follows. Thus, FCA is applied in this current study because the previous experimental studies have shown that FCA is not sensitive to outliers [7]. FCA provides a well-defined mathematical framework to discover implicit and explicit knowledge in an easily understood format by using formal context and a Hasse diagram that clearly represents the concepts’ generalization/specialization relationships. In addition, FCA can construct an informative concept hierarchy providing valuable information on various specific domains. To support this work, [15] also applied FCA method to present a new filter for feature selection, called H-Ratio, which can identify pertinent features from data based on the Shannon entropy, also known as the diversity Shannon index that reflects how many different types there are in a data set to select features without considering classification accuracy. However, the classification accuracy is an important aspect of selection. Thus, this work applied the classification accuracy to formulate for feature selection from concept lattice.

3. The Proposed Models for Feature Selection

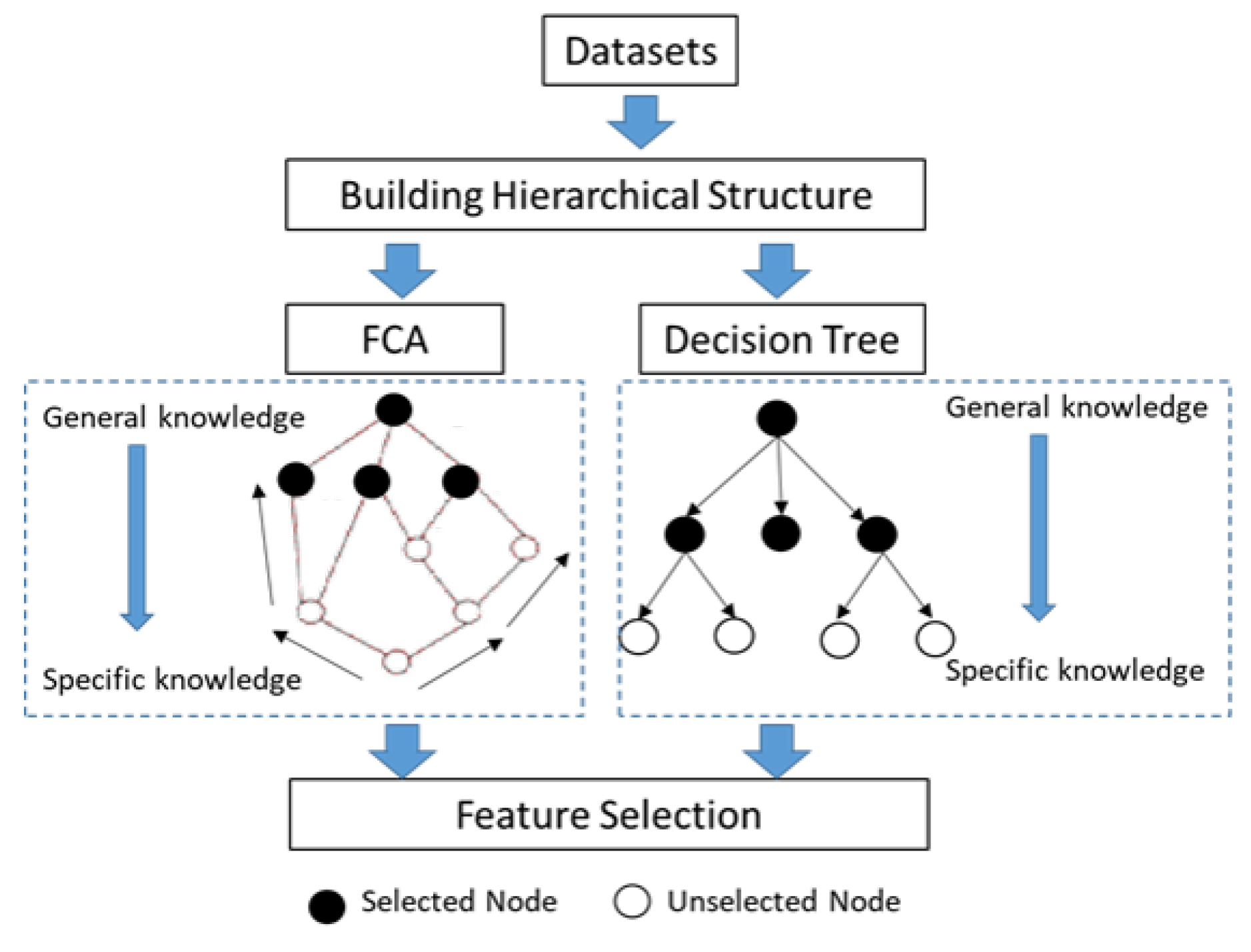
The proposed approaches based on hierarchical models focused on two methods, namely using FCA and DT. FCA and DT were applied to build the hierarchical structures for feature selection from data so that each node in the structure represented a feature (attribute). An overview of the proposed models is depicted in Figure 1.

Initially, the hierarchical structure form was built, where the top node represents general knowledge, whereas the bottom represents specific knowledge. Next, the top node of structure was chosen by considering each level of structure. In this study, we selected a feature for each level of the structure, and then the selected feature was used to represent data for classification in the next step of evaluating the performance.

Afterwards, the relationship between the number count of features (attributes) and classification accuracy was considered. We found that the number of attributes for each level affects classification accuracy at some level. We attempted to optimize the feature selection from the hierarchical structure. Thus, the paired-samples t-test was applied to choose appropriate features for each level. This approach has advantages, including the estimation of mean differences between paired observations and the identification of statistically significant changes in two related measurements. The paired design helps manage individual differences, minimizing the impact of confounding variables, and optimizes data economy by leveraging the paired nature of observations. Furthermore, it serves as an efficient method for testing differences between two related conditions or measurements, offering a straightforward and practical means for comparing means within the same group. We performed feature selection based on a hierarchical structure as follows.

On level l of hierarchical structure, for any $l\in \{1,2,\dots ,k\}$, we defined the total accuracy as follows.

$$TotalAc{c}_l=\sum _{i=1}^n{\displaystyle \frac{Ac{c}_{l,i}}{n}}$$

(1)

where $Ac{c}_{l,i}\in \{0,1\}$ is the $i^{th}$ accuracy on level l of decision tree, and the values 1 and 0 mean that prediction of $Ac{c}_{l,i}$ is true or false, respectively. To find the set of chosen levels, we denoted by $SoCL$ where level 0 is definitely chosen. Next, we consider sequentially the next level of decision tree by using the two-samples z test between total accuracy on level l and $l-1$ defined as

$$Z_{l,l-1}={\displaystyle \frac{TotalAc{c}_l-TotalAc{c}_{l-1}}{\sqrt{\widehat{p}\widehat{q}}\left(\frac{1}{n}+\frac{1}{n}\right)}}$$

$$=\sqrt{{\displaystyle \frac{n}{2\widehat{p}\widehat{q}}}}\left(TotalAc{c}_l-TotalAc{c}_{l-1}\right)$$

(2)

where $\widehat{p}$ = ${\displaystyle \frac{{\sum }_{i=1}^{n}Ac{c}_{l,i}+{\sum }_{i=1}^{n}Ac{c}_{l-1,i}}{n+n}}$ and $\widehat{q}=1-\widehat{p}$ for any $l\in \{1,2,\dots ,k\}$. The level l will be added to set $SoCL$ depending on the level of significance $\alpha$. This means we use $\alpha$ to consider the significant difference between total accuracy of level l and l – 1. If total accuracy of level l is significantly different from total accuracy of level l – 1, we will add l into the set $SoCL$. Otherwise, we do not add l into the set $SoCL$ and stop level finding process. The next table shows some values of significance level $\alpha$ and their corresponding confidence intervals for z.

Table 1. The mapping from $\alpha$ to confidence interval for z

$\mathit{\alpha }$	0.01	0.05	0.1
z	$-2.576\le z\le 2.576$	$-1.96\le Z\le 1.96$	$-1.645\le z\le 1.645$

Table 1. The mapping from $\alpha$ to confidence interval for z

$\mathit{\alpha }$	0.01	0.05	0.1
z	$-2.576\le z\le 2.576$	$-1.96\le Z\le 1.96$	$-1.645\le z\le 1.645$

For example, when we consider the level of significance $\alpha$=0.01, if $|Z_{(l,l-1)}|\le 2.576$, then we add l to the set $SoCL$. Otherwise, l is not added to set $SoCL$, and we stop the process. We denote the set of chosen attributes by $SoCA$. If m is the last level which is added to the set $SoCL$, we have set $SoCL=\{0,1,2,\dots ,m\}$ and set $SoCA={\bigcup }_{i=0}^{m}Att{r}_i$ where $Att{r}_i$ is the set of all attributes on level i. We present the proposed feature selection algorithm using FCA and decision tree, presented as Algorithm 1.

Algorithm 1: Feature selection for FCA and decision tree.

Input    : The training dataset comprises all attributes and n instances.           : Tree in decision tree or concept lattice including k level.           : $\alpha$ and z // for example: $\alpha =0.01,z=[-2.576,2.576]$ Output  : Set of selected attributes ($SoCA$). Method :             1. $SoCL=\left\{0\right\}$, $l=0$             2. $SoCA=\left\{Att{r}_l\right\}$             3. $TotalAcc\left[l\right]={\sum }_{i=1}^n{\displaystyle \frac{Ac{c}_{l,i}}{n}}$ // Accuracy of using selected attributes in level l             4. For $++l$ to k // l=1 to k             5.     $\widehat{p}=({\sum }_{i=1}^{n}Ac{c}_{l,i}+{\sum }_{i=1}^{n}Ac{c}_{l-1,i})/(n+n)$             6.     $\widehat{q}=1-\widehat{p}$             7.     $Z_{l,l-1}=\sqrt{{\displaystyle \frac{n}{2\widehat{p}\widehat{q}}}}\left(TotalAcc\left[l\right]-TotalAcc[l-1]\right)$             8.     If ($|Z_{(l,l-1)}|\le 2.576$)             9.        $SoCL=\left\{0l\right\}$             10.        $SoCA={\bigcup }_{i=0}^{l}Att{r}_i$             11.     Else Break();             12. End For             13. Return ($SoCA$)

4. Research Methodology

4.1. Dataset Description and Tools

This study took all needed datasets from the UCI machine learning repository [26]. These datasets belong to many different fields, such as engineering, social science, and business. Among them, we selected 11 datasets covering many areas for our evaluation. Table 2 shows the different samples of data used. We give also, respectively, the number of attributes, instances, and classes. Moreover, in the final column, we describe the attribute data type in each data set. These data are used to demonstrate the applicability and performance of feature selection. Afterwards, classification is used to evaluate the accuracy when each dataset is randomly split into training and test sets.

This study used the R program for data management and analysis, specifically R-3.5.1 for Windows and RStudio Version 1.1.456. They were used to classify with the classifiers of DT, SVM, and ANN types. We also used Weka software to provide the previous feature selection algorithms compared to our models. The feature selection methods tested were filters methods (Information gain and Chi-square), wrappers methods, and forward selection. In addition, in the proposed model using FCA for feature selection, we applied Concept Explorer (ConExp) [27] programs to generate the hierarchical structure for FCA. The ConExp program has the functionality of creating and editing contexts, generating lattice from contexts, finding the relative attribute that actually occurs in the context, and the basic relationship that is true in the context.

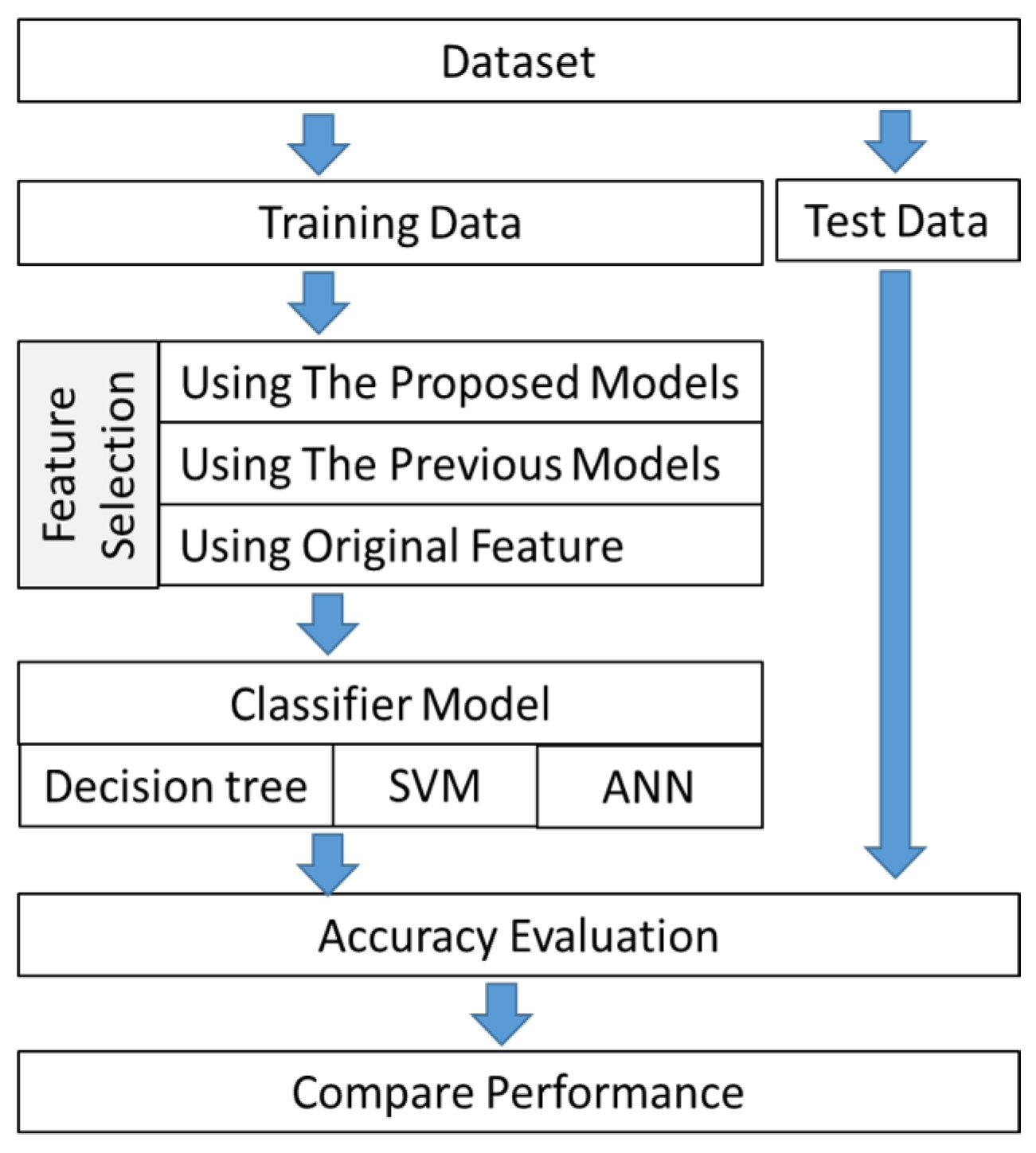
4.2. The Experimental Design

We designed experiments for evaluating the performance in classification tasks. The overall scheme is illustrated in Figure 2.

In these numerical experiments, datasets from the UCI Machine Learning Repository (Asuncion, 2007) were employed, each divided into training and testing groups. The training set was processed feature selection using three methods: the proposed models, prior models, and the original features. Initially, the proposed model involves the utilization of FCA and decision tree within a hierarchical concept model. These structures are created, and significant features are selected, as explained in Section 3. Subsequently, traditional feature selection methods such as IG, CS, FS, and BS are employed to compare the proposed feature selection model and the original features. These conventional methods are widely utilized for feature selection and operate based on filter (e.g., IG and CS) and wrapper (e.g., FS and BS) methods. Finally, the original features are used as a baseline for comparison. Next, the selected feature(s) for each dataset were used to train a classifier, namely DT, SVM, and ANN. These models are popular classifier models. Afterwards, the test data were used to evaluate the classification accuracies of these classifiers. The accuracies served as the performance measures for each model.

Subsequently, the chosen feature(s) for each dataset were employed to train classifiers, specifically DT, SVM, and ANN. These models are well-known in the field of classification. Following the training phase, the test data were utilized to assess the classification accuracies of these classifiers. The accuracies then served as performance metrics for each model.

5. Results and Discussion

5.1. The Original Performance Results

Practically, the datasets in Table 2 were run using 10-fold cross-validation, which is the most used method. For this, each dataset was divided into complementary subsets, performing the analysis on one subset, called the training set, and validating the analysis on the other subset, called the testing set. The results from our experiments for classification accuracy are shown in Table 3.

In this experiment, the input data had not been reduced, instead all original attributes were used for training. In Table 3, the results show the standard classification accuracy for each data set when using DT, SVM, and ANN. Mostly, DT was the superior one. The accuracy results are used as benchmarks for evaluation the feature selection in the next section.

5.2. The Hierarchical Concept Model Performance

This section describes the proposed model for feature selection based on hierarchical concept model by using DT or FCA. Thus, the results will be divided into three parts as follows.

5.2.1. Feature Selection Using Decision Tree

In order to evaluate our models, we used the well-known software RapidMiner Studio to generate a tree structure using the DT algorithm. The datasets in Table 2 were used to create tree structures. Next, we selected the attributes from each level of the tree structure. In this experiment, we selected attributes by filtering from the first to the fifth level of the tree. Table 4 shows the classification accuracy (%) in each level of the decision tree. We compared classification accuracy with our feature selection using DT to the benchmark with original features (without using feature selection at all) in Section 5.1, as shown in Figure 3.

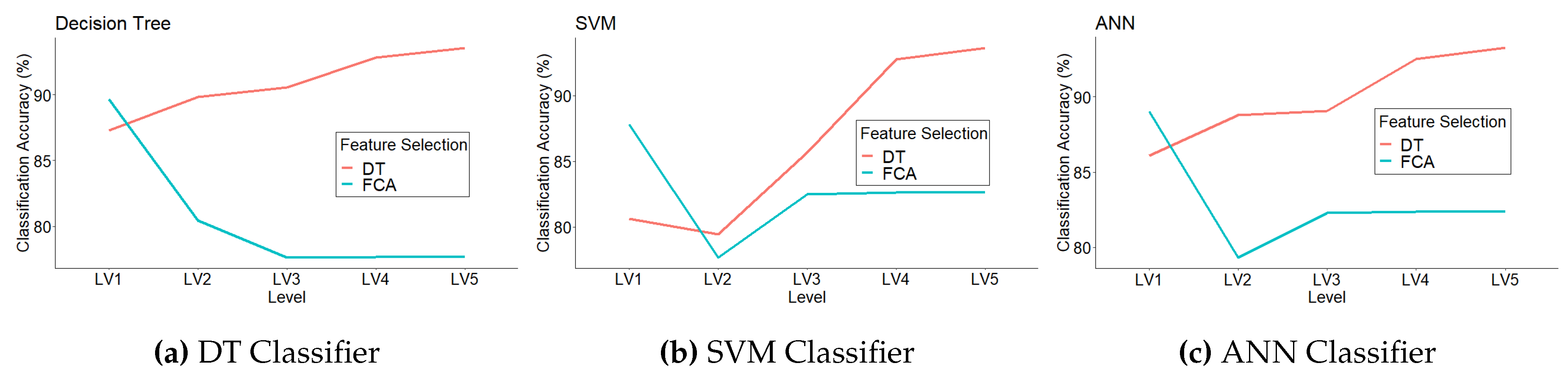
From Figure 3, we see that the classification accuracy did not differ between the original and the proposed models for each level. Indeed, if we add the number of attributes from each level, it leads to a trend of improving accuracy.

5.2.2. Feature Selection Using FCA

The other hierarchical method, FCA, was then applied to generate the hierarchical construct. We applied the ConExp program to build the concept lattice structure. Similarly, we select the attributes from each level of concept lattice from the first to the fifth level. The classification accuracy results are shown in Table 5.

Likewise, we compared classification accuracy of our feature selection using FCA to the benchmark original features (without using feature selection at all) in section 5.1, as shown in Figure 4.

From Figure 4, we see that the classification accuracy is not different between the original and the proposed model at each level. Indeed, if we add the number of attributes from each level, the trend in accuracy is increasing.

From the testing above, we find that the classification accuracy is not different between the original and the proposed model for each level. Thus, we can compare using paired sample t-tests as mentioned in section 3.

On considering the relationship between the number of selected attributes and the average classification accuracy for datasets, as shown in Figure 5, we found that the proposed model using decision tree gave a better classification result than using FCA.

5.2.3. An Example of Feature Selection Optimization

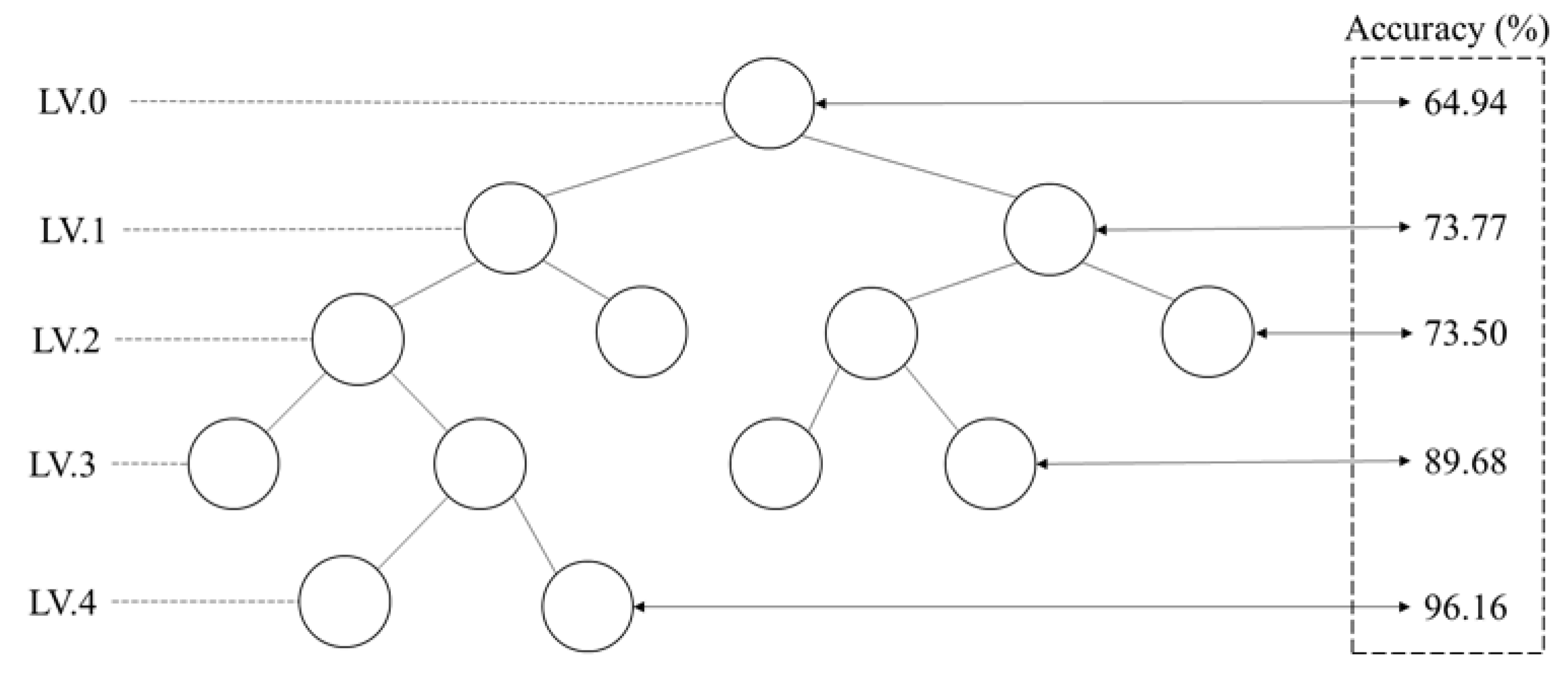
In our feature selection, we select the top node of structure to be representative of dataset. However, the proper selection of relevant attribute leads to an efficient classification. Thus, we experimented with using paired-samples t-test to optimize the selected level. We use the experimental results from Table 4 to demonstrate the proper selection of node attribute in each level. The Dermatology dataset is investigated to show the calculation for selecting attribute in each level of the tree. We assume the hierarchical structure of Dermatology dataset and the classification accuracies shown in Figure 6.

From Figure 6, we can apply the proposed feature selection in an example calculation. The initial attribute node (or root) is selected with an accuracy of 64.94%. Next, we consider the next step for selection or not by using the equation 2 where n= 366, $\widehat{p}$ = ${\displaystyle \frac{{\sum }_{l=i}^{n}Ac{c}_{l,i}+{\sum }_{l=i}^{n}Ac{c}_{l-1,i}}{n+n}}$$={\displaystyle \frac{245+270}{366+366}}=0.704$, $\widehat{q}=1-\widehat{p}=0.296$, thus

$Z_{l,l-1}=\sqrt{{\displaystyle \frac{366}{22\ast 0.704\ast 0.296}}}\left(73.77-64.94\right)=42.18$.

From Table 1, if we consider the level of significance 0.01, if $|Z_{l,l-1}|\le 2.576$, then we select the level 1 (LV.1 in Figure 6). Next, we still consider the next level (LV.2). We calculate $z_{2,1}=-1.61$ and find that this value is less than z in Table 1. Thus, LV.2 is not selected, and we stop the process. Thus, in this structure, we choose attributes from the structure in LV.0 to LV.2.

In addition, we estimate for all datasets which levels should be chosen. We applied the statistical paired-samples t-test to estimate this across all the datasets shown in Table 6. We find that the feature selection from each level depends on the classifier model. Namely, we can use two levels in a decision tree classifier, whereas we should select four levels for using SVM or ANN classifiers.

5.3. The Performances of Prior Feature Selection Approaches

This section evaluates the classification performance of feature selection using IG, CS, FS, and BS. IG and CS algorithms function as filter methods, while FS and BS algorithms operate as wrappers. These algorithms were implemented in the RapidMiner Studio program, representing traditional feature selection methods for comparison with our proposed model. The 10 datasets listed in Table 2 were employed for training and testing through a 10-fold cross-validation approach. The experimental results, presented in Table 7, presented the use of DT, SVM, and ANN as classifiers, with the "No." column indicating the number of selected attributes. The classification accuracies reported in this table will be further compared in the subsequent section.

5.4. Comparison of Performances

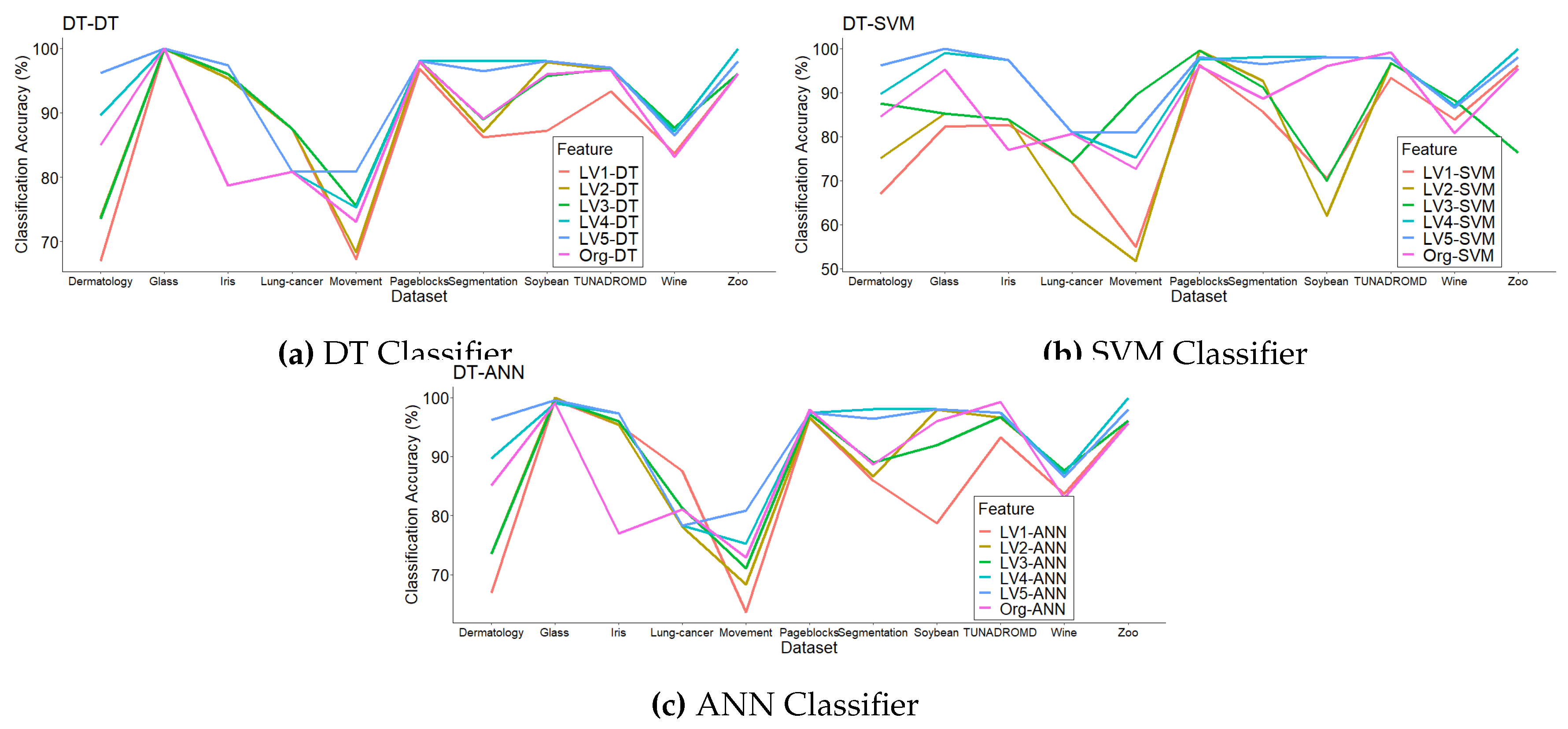
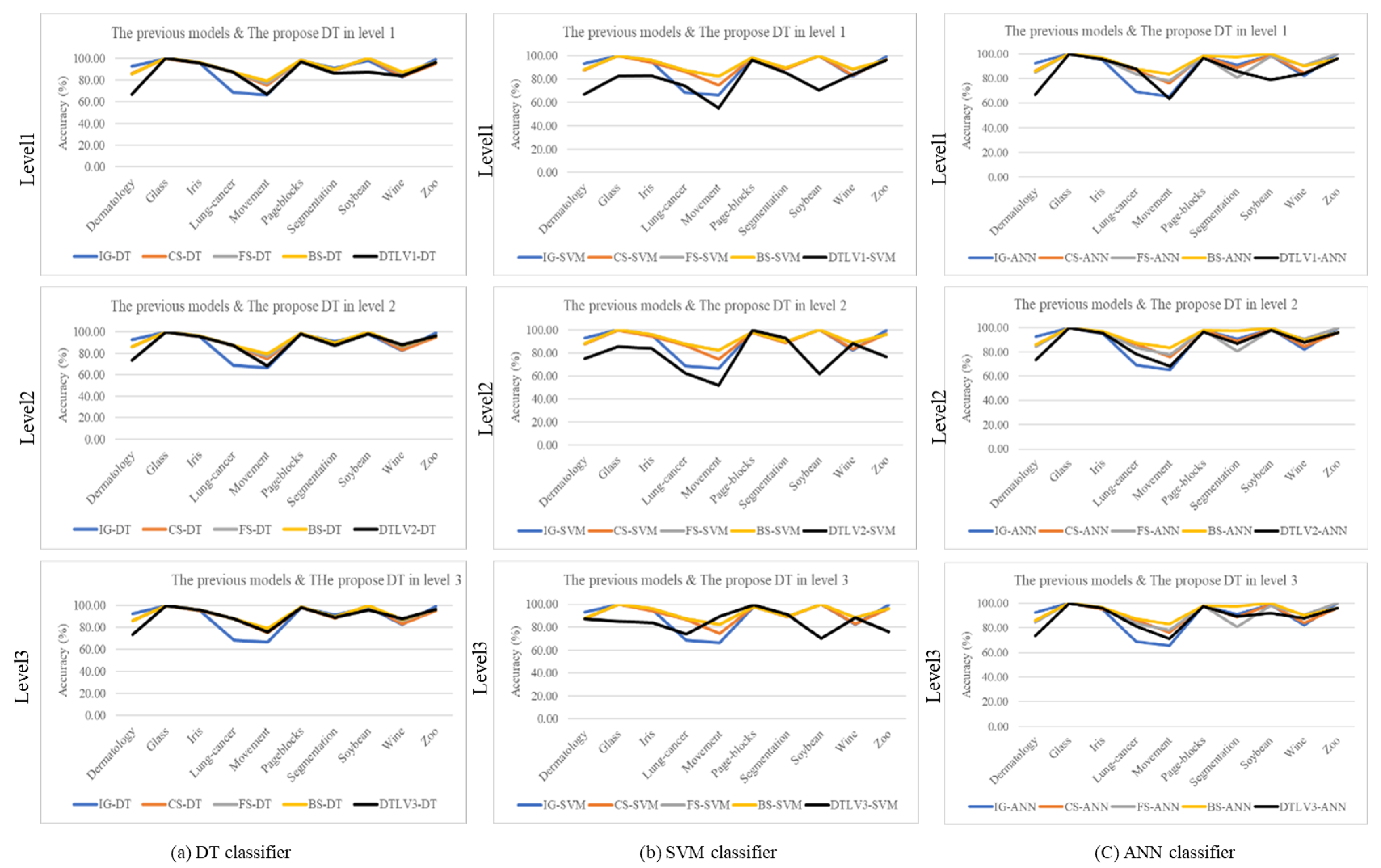
We compared the classification accuracies of our feature selection using Decision Trees in Section 5.2 with others in Section 5.3, as illustrated in Figure 7. The figure depicts the classification performance after utilizing different numbers of attributes at each level (from Level 1 to 3, from top to bottom respectively) for each classification method denoted as Figure 7 (a) to (c), respectively. Detailed data can be found in Tables 4 and 7. From the graphs in each dataset, considering the accuracy of attribute selection at each level, it appears that the performance is relatively consistent with other feature selection methods. For some datasets, the presented method may exhibit superior accuracy from the initial level, such as the Soybean dataset and Segmentation dataset. Conversely, the presented method may have lower accuracy for certain datasets, as observed in the Dermatology dataset.

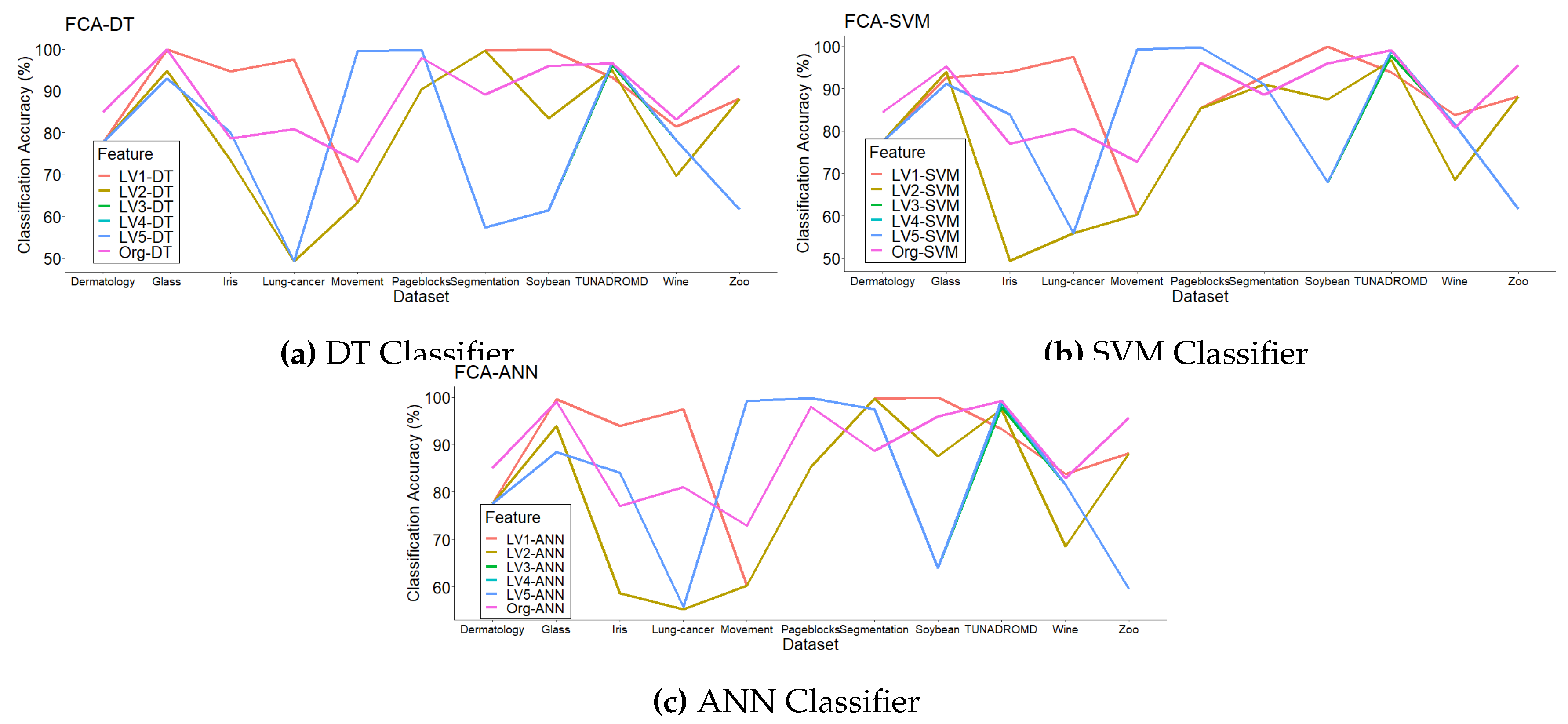
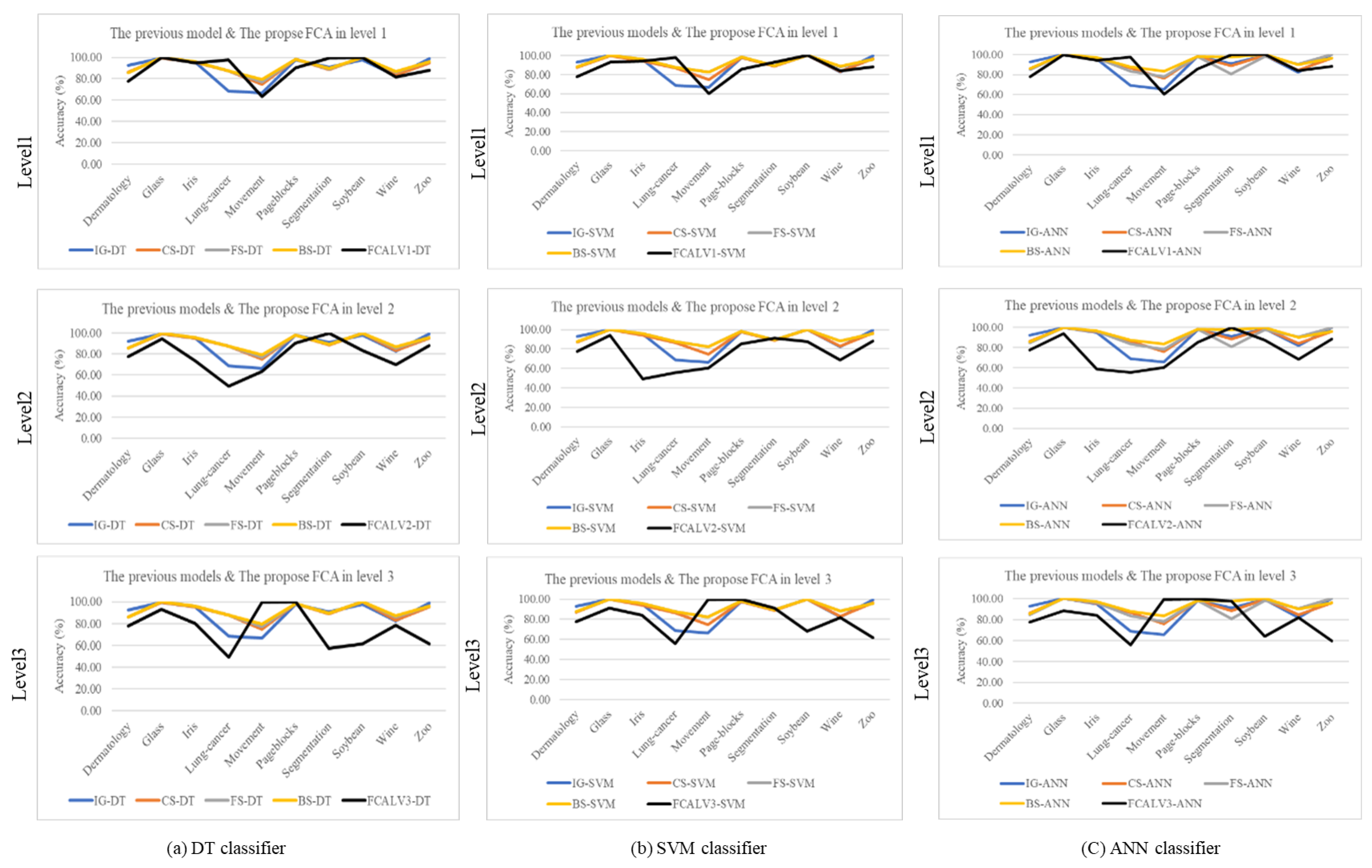
Similarly, we conducted a comparison of the classification accuracy of our models using FCA in Section 5.2 with others in Section 5.3, illustrated in Figure 8. The figure demonstrates the classification performance after employing varying numbers of attributes at each level, with detailed data available in Tables 5 and 7. Upon examining the accuracy trends from this graph, we observe a similar pattern to use the decision tree approach, where some datasets may exhibit comparable performance to other methods, such as the Movement dataset, while others may show comparatively lower classification accuracy.

From above results, the outcomes obtained by employing a hierarchical structure for feature selection before the classification task indicate that it could lead to either favorable or less favorable results. This corresponds to the observed patterns seen in other feature selection methods used for comparison. Importantly, the classification performance of the proposed method does not consistently appear inferior. However, the presented key point in this study is its ability to significantly reduce the number of attributes compared to previous methods.

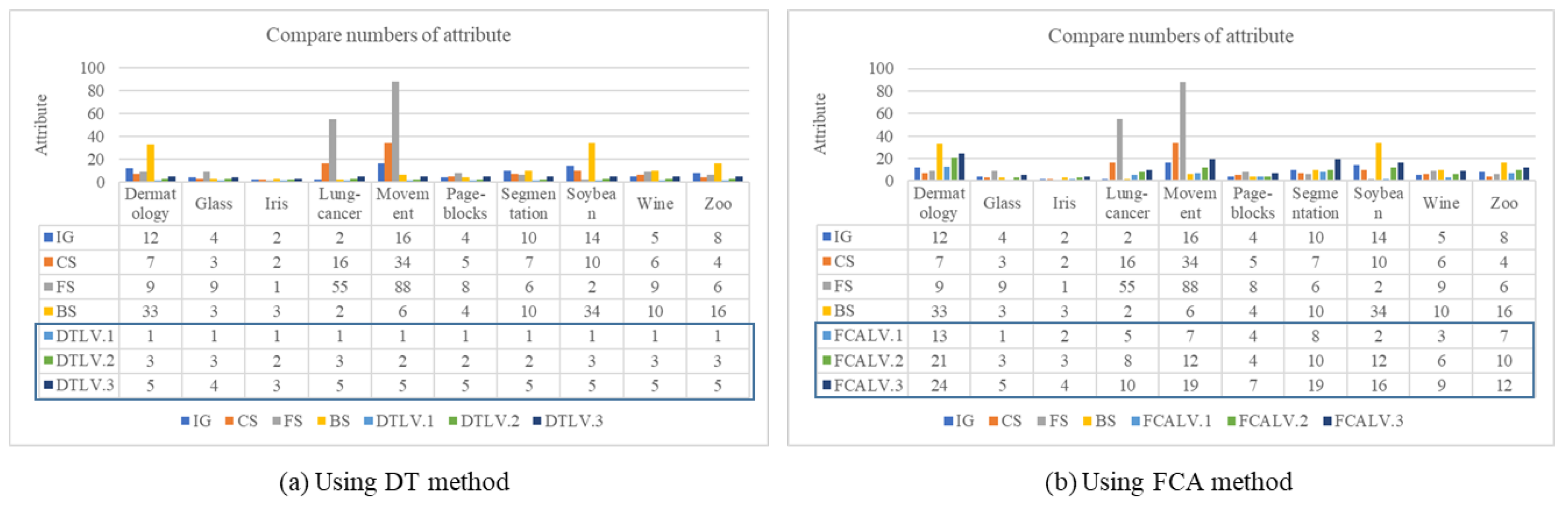
Considering the number count of selected features, the results show clearly that the DT kept less features than the other methods, as shown in Figure 9. This figure will illustrate the number of selected attributes at each level from 1 to 3 in comparison with other methods that exhibit classification performance as shown in Figure 7 and 8 mentioned earlier. Figure 9 (a) displays the count of selected attributes from the decision tree structure, while Figure 9 (b) shows the count of selected attributes from the FCA structure. From as the results, the hierarchical structure using decision tree method can be applied to select the feature for data dimension reduction yields favorable outcomes. This is due to the decision tree’s method, which involves a top-down data entry process using specific filtering and selecting root node. However, FCA produces less satisfactory results due to the creation of a layer-wise structure designed for bidirectional ordering—both from top to bottom and from bottom to top. This may lead to effect of feature selection.

6. Conclusions

Feature selection methods are used in a wide variety of applications. Such methods proceed to eliminate unfavorable features that may be noisy, redundant or irrelevant, as these can penalize the performance of a classifier. Feature selection reduces the dimensionality of data and restricts the inputs to a subset of the original, but the features can have missing values. In this paper, we propose a new feature selection method based on hierarchical concept model to improve the performance of supervised learning. We applied decision tree and FCA to build the hierarchical structures from data to generate knowledge based systems. In these hierarchical structures that embed knowledge, the top and bottom nodes represent general and specific knowledge, respectively. For this reason, we selected the top node of each structure to be representative of the dataset. However, the proper selection of relevant attributes leads to an efficient classification. Thus, we also used paired-samples t-tests to optimize the selected levels in the hierarchical structures. In this study, numerical experiments used available software, RapidMiner Studio and ConExp programs, to generate the hierarchical structures for decision tree and FCA, respectively. Afterwards, the attributes in top node of the obtained structure were selected to use in learning classifier models. Three popular classifier algorithms were used in this study: decision trees, SVM, and ANN. To compare the performances of our feature selection methods with available alternatives: all original features (without using feature selection) and the prior feature selection methods. We used 10 datasets from the UCI Machine Learning Repository for classification. The prior feature selection methods tested were IG, CS, FS, and BS. The results show clearly that the proposed models with DT and FCA gave smaller set of retained attributes than the other methods, while still classification performance remained comparable. In other words, the new approach provided superior data reduction to the least dimensionality without performance sacrifice.