Submitted:
31 October 2024
Posted:
31 October 2024
You are already at the latest version
Abstract
Keywords:
MSC: 62P05; 91B05; 91G05
1. Introduction
| Company name | Types of Insurance | Types of Sanctions |
|---|---|---|
| PT Asuransi Syariah Mubarakah | Life insurance | Revocation of business license |
| PT Asuransi Jiwa Nusantara | Life insurance | Revocation of business license |
| PT Asuransi Jiwa Bumi Asih Jaya | Life insurance | Revocation of business license |
| PT Asuransi Tokio Marine Indonesia | General Insurance (Sharia) | Revocation of business license |
| PT Asuransi Jiwa Bakrie | Life insurance | Revocation of business license |
| PT AXA Life Indonesia | Life insurance | Revocation of business license due to the merger of PT AXA Life Indonesia into PT AXA Financial Indonesia |
| PT Asuransi Himalaya Pelindung | General Insurance | Revocation of business license |
| PT Asuransi Recapital | General Insurance | Revocation of business license |
| PT Asuransi Parolamas | General Insurance | Revocation of business license |
| PT Asuransi Jiwasraya (Persero) | Life insurance | Restructuring and establishing a new company called IFG Life |
| PT Asuransi Jiwa Syariah Bumiputera | Life Insurance (Sharia) | Restrictions on business activities for some business activities |
| PT Asuransi Jiwa Adisarana Wanaartha | Life insurance | Revocation of business license |
| PT Asuransi Cigna | Life insurance | Revocation of business license due to merger between PT Asuransi Cigna and PT Chubb Life Insurance Indonesia |
| PT Asuransi Jiwa Kresna | Life insurance | Revocation of business license |
| PT Asuransi Jiwa Bersama Bumiputera | Life insurance | Special supervision status for the implementation of the company's financial recovery plan |
| PT Asuransi Jiwa Prolife Indonesia | Life insurance | Revocation of business license |
| PT Asuransi Purna Artanugraha | General Insurance | Revocation of business license |
- (a)
- Search for scientific works through databases, using specific keywords.
- (b)
- Manual selection of scientific papers, using the PRISMA (Preferred Reporting Items for Systematic Reviews and Meta-Analyses) flow diagram.
- (c)
- Bibliometric analysis of scientific works selected in point (b), using VOSviewer software.
- (d)
- Gap analysis of scientific works selected in point (b).
- (e)
- The discussion is based on the results of the gap analysis in point (d) and the following proposals for developing a scheme based on needs or social problems in the community.
- RQ1: What are the sharia insurance schemes used in the surplus process modeling?
- RQ2: What are the variables in the surplus process model?
- RQ3: What are the advantages and limitations in modeling the surplus process of each selected scientific work?
- RQ4: What is the form of the proposed development of a scheme based on needs or social problems in the community and a description of the surplus process?
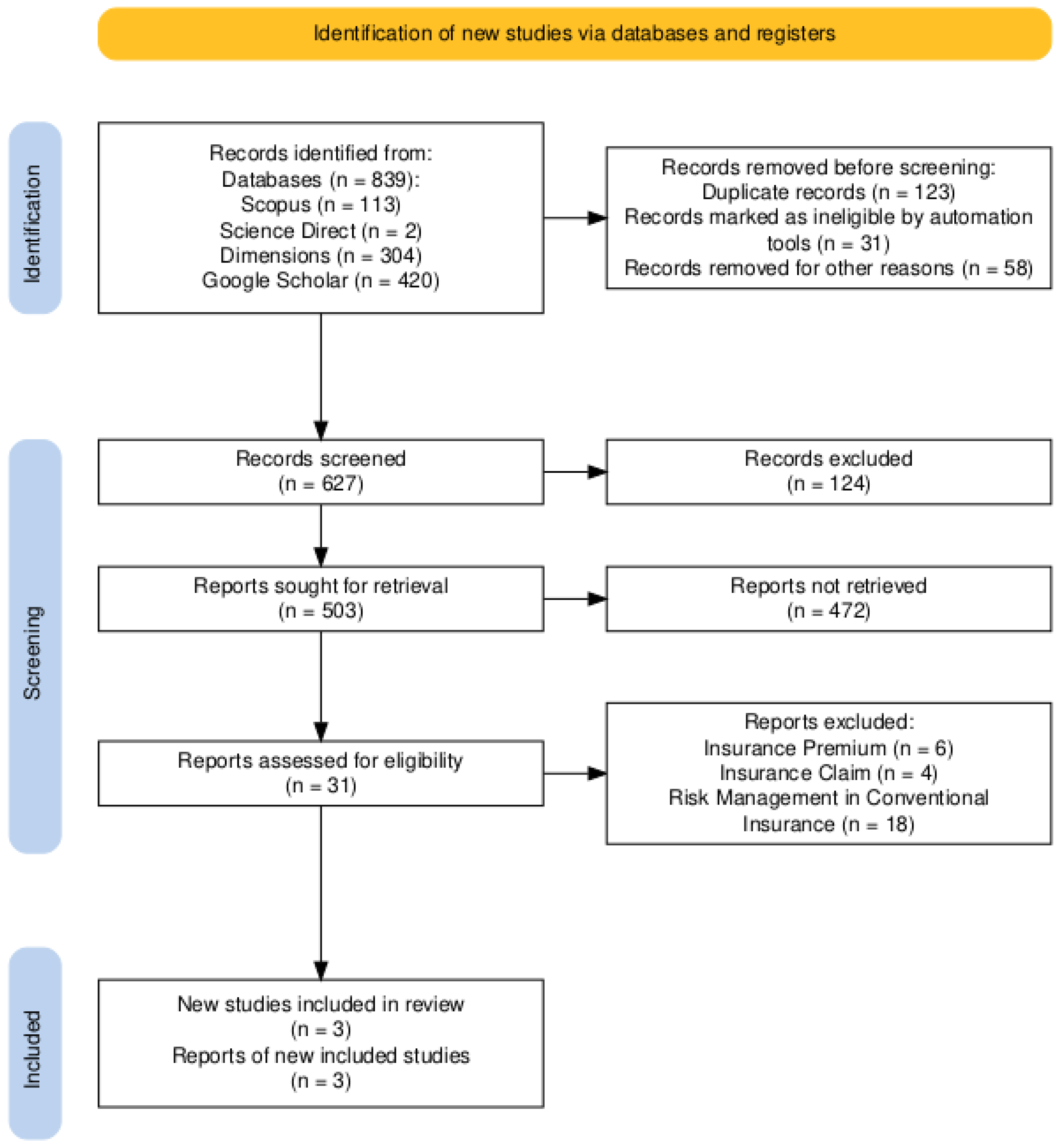
2. Materials and Methods
| Database | Scopus | Science Direct | Dimensions | Google Scholar |
|---|---|---|---|---|
| Amount | 113 | 2 | 304 | 420 |
2.2. Manual Selection of Scientific Papers Using PRISMA Flowcharts
| Reason for Deletion | Scopus | ScienceDirect | Dimensions | Google Scholar |
|---|---|---|---|---|
| Duplication | 1 | 0 | 59 | 63 |
| Language (other than English ) | 0 | 0 | 14 | 17 |
| Islamic law topics | 14 | 0 | 94 | 16 |
| Topic of Islamic banking financial institutions | 17 | 0 | 20 | 21 |
| General topics of sharia insurance and reinsurance | 73 | 2 | 111 | 286 |
| Actuarial in sharia insurance and risk management in conventional insurance | 2 | 0 | 10 | 16 |
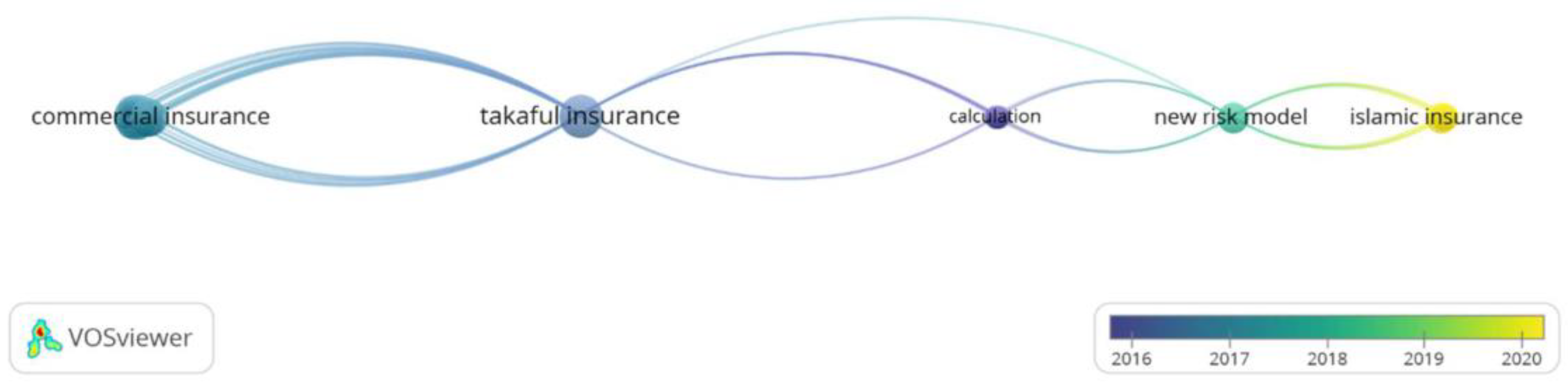
2.2. Bibliometric Analysis of Selected Scientific Works
2.3. Gap Analysis between Selected Scientific Works
| Authors | Sharia insurance scheme |
|---|---|
| Achlak [30] |
Mudharabah scheme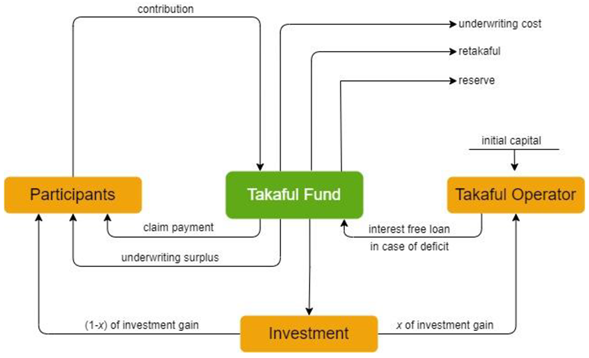
|
| Achlak [30] |
Wakalah Scheme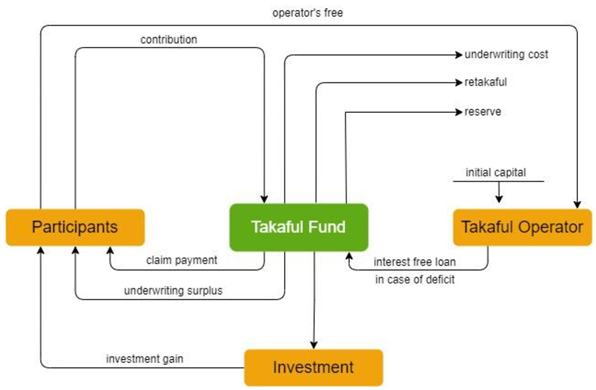
|
| Achlak [30] | Hybrid Scheme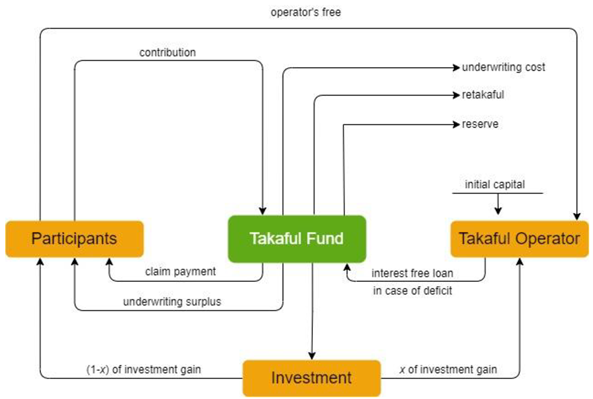
|
| Achlak [30] |
Waqf Scheme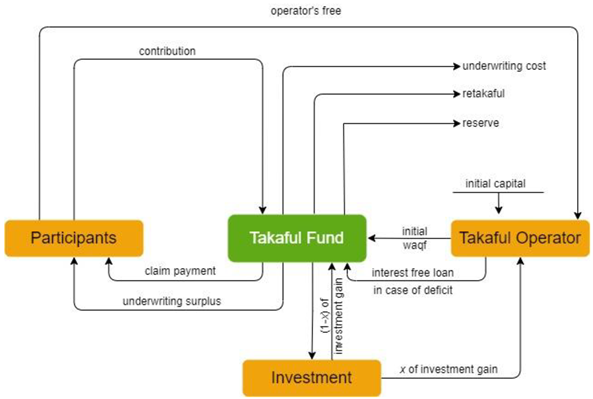
|
| El Hachlaufi and El Msiyah [31] |
Wakalah Scheme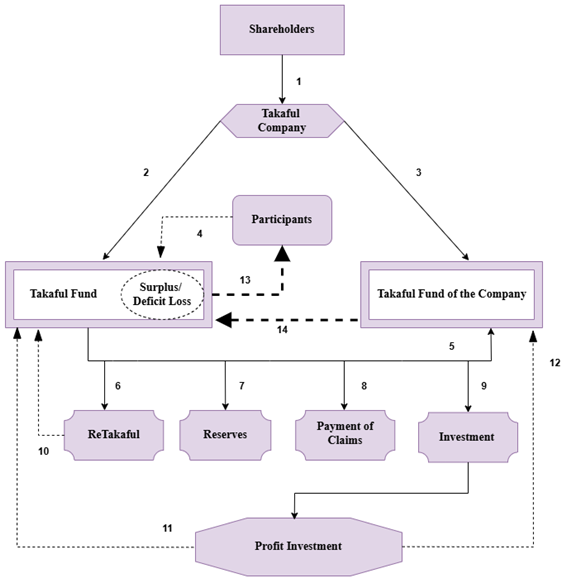
|
| Puspita et al. [32] | Hybrid Scheme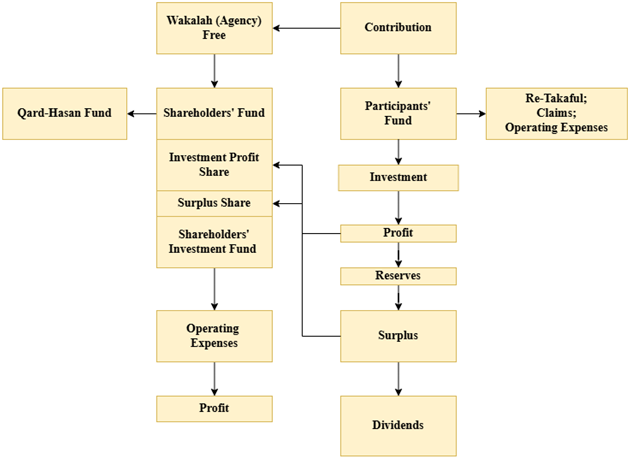
|

| Variables | Kim-Drekic risk model |
Modified Kim-Drekic risk model |
A non-recursive function of the non-stochastic form of the surplus process | Annual surplus for Wakala models | Surplus process for Hybrid-Takaful |
|---|---|---|---|---|---|
| Surplus process | |||||
| Initial surplus (capital) | And ( | ||||
| Premium | |||||
| Deposit | And | - | |||
| Withdrawal from Qard-Hasan | - | - | |||
| Return to Qard-Hasan | - | - | - | - | |
| Withdrawal from investment funds | - | - | - | - | |
| Claim frequency | - | - | |||
| Severity of claim | - | ||||
| Dividend payment | And | - | |||
| Costs | - | - | - | And | - |
| External funds | - | And | |||
| Investment Fund | - | - | - | - |
3. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shiraishi, H. Review of statistical actuarial risk modelling. Cogent Mathematics 2016, 3(1), pp. 1123945. [CrossRef]
- Li, S.; Lu, Y.; Garrido, J. A review of discrete-time risk models. Rev. R. Acad. Cien. Serie A. Mat 2009, 103, pp. 321–337. [CrossRef]
- Lundberg, F. 1. Approximerad framställning af sannolikhetsfunktionen: 2. Återförsäkring af kollektivrisker.; Almqvist &Wiksells, 1903.
- Cramér, H. On the mathematical theory of risk.; Centraltryckeriet, 1930.
- Cramér, H. Collective risk theory: A survey of the theory from the point of view of the theory of stochastic processes.; Nordiska bokhandeln, 1955.
- Bühlmann, H. Mathematical methods in risk theory.; Springer-Verlag: Berlin, Heidelberg, New York, 1970.
- Gerber, H.U. An introduction to mathematical risk theory.; S. S. Huebner Foundation for Insurance Education: Wharton School, University of Pennsylvania, 1979.
- Bowers, N.L.; Gerber, H.U.; Hickman, J.C.; Jones, D.A.; Nesbitt, C.J. Actuarial mathematics, 2nd ed.; Society of Actuaries, 1997.
- Dickson, D.C.M. Insurance risk and ruin, 2nd ed.; Cambridge University Press, 2016. [CrossRef]
- Dufresne, F.; Gerber, H.U. Risk theory for the compound Poisson process that is perturbed by diffusion.; Elsevier, Insurance: Mathematics and Economics 1991, 10(1), pp. 51-59. [CrossRef]
- Huzak, M.; Perman, M.; Šikić, H.; Vondraček, Z. Ruin probabilities for competing claim processes. Journal of Applied Probability 2004, 41(3), pp. 679-690. [CrossRef]
- Andersen, E.S. On the collective theory of risk in case of contagion between claims. Bulletin of the Institute of Mathematics and Its Applications 1957, 12(2), pp. 275-279.
- Dickson, D.C.M.; Hipp, C. On the time to ruin for Erlang(2) risk process. Insurance: Mathematics and Economics 2001, 29(3), pp. 333-344. [CrossRef]
- Gerber, H.U.; Shiu, E.S.W. The time value of ruin in a Sparre Andersen model. North American Actuarial Journal 2005, 9(2), pp. 49-84.
- Willmot, G.E. A Laplace transform representation in a class of renewal queueing and risk processes. Journal of Applied Probability 1999, 36(2), pp. 570–584. [CrossRef]
- Li, S.; Garrido, J. On ruin for the Erlang(n) risk process. Insurance: Mathematics and Economics 2004, 34(3), pp. 391-408. [CrossRef]
- Li, S.; Garrido, J. On a general class of renewal risk process: analysis of the Gerber-Shiu function. Advances in Applied Probability 2005, 37(3), pp. 836-856. [CrossRef]
- Gerber, H.U.; Goovaerts, M.J.; Kaas, R. On the probability and severity of ruin. ASTIN Bulletin: Cambridge University Press, 1987, 17(2), pp. 151-163. [CrossRef]
- Gerber, H.U. Mathematical fun with the compound binomial process. ASTIN Bulletin 1988, 18(2), pp. 161-168. [CrossRef]
- Shiu, E.S.W. The probability of eventual ruin in the compound binomial model. ASTIN Bulletin 1989, 19(2), pp. 179-190. [CrossRef]
- Willmot, G.E. Ruin probabilities in the compound binomial model. Insurance: Mathematics and Economics 1993, 12(2), pp. 133-142. [CrossRef]
- Gerber, H.U.; Shiu, E.S.W. On the time value of ruin. North American Actuarial Journal 1998, 2(1), pp. 48–72. [CrossRef]
- Finetti, B.D. Su un’Impostazione alternativa della teoria collettiva del rischio. Proceedings of the Transactions of the XV International Congress of Actuaries, New York, 1957.
- Gerber, H.U.; Shiu, E.S.W. Optimal dividends: analysis with brownian motion. North American Actuarial Journal 2004, 8(1), pp. 1-20. [CrossRef]
- Gerber, H.U.; Shiu, E.S.W.; Smith, N. Maximizing dividends without bankruptcy. ASTIN Bulletin 2006, 36(1), pp. 5-23. [CrossRef]
- Dickson, D.C.M.; Drekic, S. Optimal dividends under a ruin probability constraint. Annals of Actuarial Science 2006, 1(2), pp. 291-306. [CrossRef]
- Gerber, H.U.; Shiu, E.S.W.; Smith, N. Methods for estimating the optimal dividend barrier and the probability of ruin. Insurance: Mathematics and Economics 2007, 42, pp. 243-254. [CrossRef]
- Avanzi, B. Strategies for dividend distribution: A review. North American Actuarial Journal 2009, 13(2), pp. 217–251. [CrossRef]
- Kim, S.S.; Drekic, S. Ruin analysis of a discrete-time dependent Sparre Andersen model with external financial activities and randomized dividends. Risks 2016, 4(1), pp. 1-15. [CrossRef]
- Achlak, A. Discrete-time surplus process for takaful insurance with multiple threshold levels. Master of Science, Middle East Technical University, 2016.
- El Hachloufi, M.; El Msiyah. Surplus modeling for model wakala of insurance takaful. International Journal of Statistics and Economics 2017, 18(1), pp. 16-26.
- Puspita, D.; Kolkiewicz, A.; Tan, K.S. Discrete time ruin probability for takaful (islamic insurance) with investment and Qard-Hasan (benevolent loan) activities. Journal of Risk and Financial Management 2020, 13(9), pp. 1-24. [CrossRef]
- Cahyandari, R.; Kalfin.; Sukono.; Purwani, S.; Ratnasari, D.; Herawati, T.; Mahdi, S. The development of sharia insurance and its future sustainability in risk management: A systematic literature review. Sustainability 2023, 15(10), pp. 1-23. [CrossRef]
- Delbaen, F.; Haezendonck, J. Classical risk theory in an economic environment. Insurance: Mathematics and Economics 1987, 6(2), pp. 85-116. [CrossRef]
- Cahyandari, R.; Mayaningsih, D.; Sukono. A design of mathematical modelling for the mudharabah scheme in shariah insurance. International Conference on Operations Research, Bogor, Indonesia, 27 August 2016. [CrossRef]
- Cahyandari, R.; Ariany, R.L.; Sukono.; Perkasa, Y.S. The hybrid model algorithm on sharia insurance. International conference on computation in science and engineering, Bandung, Indonesia, 10-12 July 2017. [CrossRef]
- Cahyandari, R.; Awalluddin, A.S.; Wulani, I.; Ariany, R.L.; Rachmawati, T.K.; Setiadji, S.; Sukono. Integration Model Table as an Alternative Presentation of Summary of Illustration Sharia Insurance. The 1st International Conference on Computer, Science, Engineering and Technology, Tasikmalaya, Indonesia, 27-28 November 2018. [CrossRef]
- Cahyandari, R.; Sukono.; Riaman.; Zamri, N. Rancangan inovasi bisnis integrasi wakaf produktif: BUMN holding asuransi. Antologi: transformasi BUMN berbasis holding, seri 1. Unpad Press: Sumedang Jawa Barat, Indonesia, 2024; pp. 207-223.
- Bulinskaya, E.V. New research directions in modern actuarial sciences. International Conference on Modern Problems of Stochastic Analysis and Statistics, Moscow, Rusia, 29 May - 2 June 2016. [CrossRef]
- Bulinskaya, E.V. Discrete time insurance models. Moscow University Mathematics Bulletin 2023, 78, pp. 298-308. [CrossRef]

| Company Insurance | 2018 | 2019 | 2020 | 2021 | 2022 | 2023 | Quarter-1 2024 |
|---|---|---|---|---|---|---|---|
| General Insurance | 76 | 73 | 72 | 71 | 72 | 72 | 72 |
| Life insurance | 59 | 53 | 52 | 53 | 53 | 49 | 49 |
| Reinsurance | 6 | 6 | 6 | 6 | 7 | 7 | 7 |
| Social Security Program | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| Social Insurance for Civil Servants, Police and Military | 3 | 3 | 3 | 3 | 3 | 2 | 2 |
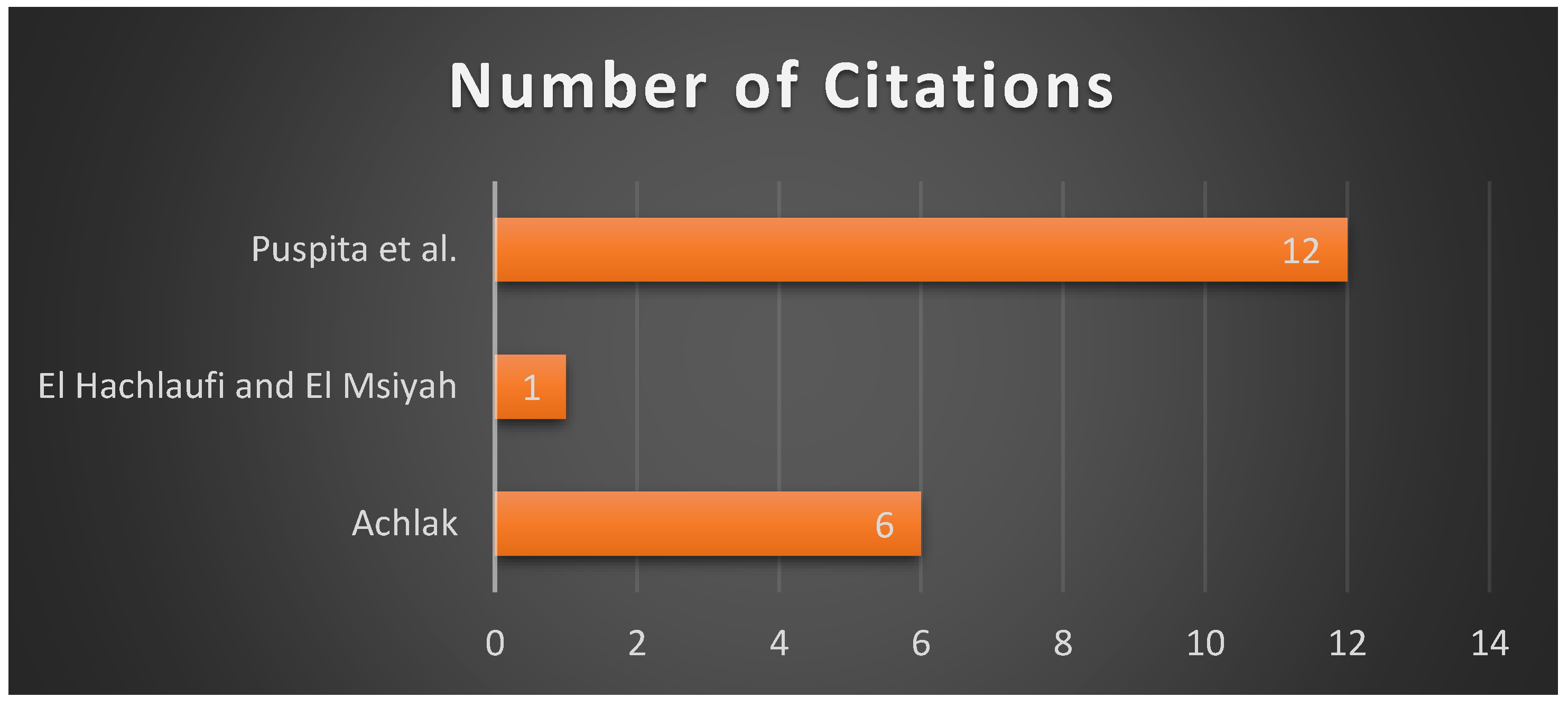
| Authors | Scientific works | Title | Year |
|---|---|---|---|
| Achlak [30] | Book | Discrete-Time Surplus Process for Takaful Insurance with Multiple Threshold Levels | 2016 |
| El Hachlaufi and El Msiyah [31] |
Article | Surplus Modeling for Model Wakala of Insurance Takaful | 2017 |
| Puspita et al. [32] | Article | Discrete-Time Ruin Probability for Takaful (Islamic Insurance) with Investment and Qard-Hasan (Benevolent Loan) Activities | 2020 |
| Principle | Conventional Insurance | Sharia Insurance |
|---|---|---|
| Concept | Risk transfer: an agreement between two or more parties, where the insurer binds itself to the insured by accepting an insurance premium to provide compensation to the insured. |
Risk sharing: a group of people who help each other, guarantee each other and work together by each issuing tabbaru funds for loss insurance, while for life insurance they issue tabbaru funds and savings funds. |
| Contract | Sale and purchase agreement (contract of agreement) |
Tabbaru contract (grant) and tijarah contract (mudharabah, wakalah bil ujroh, mudharabah-musytarakah) |
| Source of Law | Based on human thought and culture. Based on positive law, natural law, and previous examples. | Based on the Word of Allah, Al-Hadith and Ijma Ulama |
| Fund Ownership | The premium funds belong entirely to the company, so the company is free to use and invest them. | Funds from participants, some will belong to the participants, some will be managed by the company as a trustee. |
| Claim Payment Source | Company Account as a consequence of the guarantor towards the insured | Tabbaru accounts are funds belonging to participants |
| Investment | Make investments within the limits of statutory provisions and are not limited to the halal and haram nature of the investments used. | Make investments in accordance with the provisions of the law as long as they do not conflict with Islamic sharia principles. Free from usury and various prohibited investment places |
| Profit | Company owned | Can be shared between the Company and participants in the form of prizes |
| Accounting System | Accrual basis: an accounting process that recognizes events (revenue, increases in assets, liabilities, expenses) that will be received in the future. | Cash basis: recognizing what really exists |
| Sharia Supervisory Board (DPS, Dewan Pengawas Syariah) |
No DPS | There is a DPS to ensure that the business runs in accordance with Islamic sharia principles. |
| Mudharabah | Wakalah | Hybrid | Waqf | |
|---|---|---|---|---|
| Contribution (premium) | ||||
| Operator's fee | ||||
| Underwriting costs | ||||
| Retakaful | ||||
| Reserve | ||||
| Claim payment | ||||
| Underwriting surplus (for participants) |
||||
| Underwriting surplus (for companies) |
||||
| Investment returns: takaful fund (for participants) | ||||
| Investment returns: takaful fund (for companies) | ||||
| Interest-free loan (if deficit) | ||||
| Waqf fund (initial) | ||||
| Initial capital |
| Authors | Model Name | Equation Number |
|---|---|---|
| Achlak [30] | Kim-Drekic risk model | (2) |
| Modified Kim-Drekic risk model | (8) | |
| A non-recursive function of the non-stochastic form of the surplus process | (16) | |
| El Hachloufi dan El Msiyah [31] |
Annual surplus for Wakala model | (21) |
| Puspita et al. [32] | Surplus process for Hybrid-Takaful | (22) |
| Authors | Advantages | Limitations |
|---|---|---|
| Achlak [30] | This research can help companies choose the right business scheme, such as the mudharabah model in the long term produces higher profits along with the increasing amount of external funds. The wakalah model offers stable income for the company. The hybrid model is a combination of mudharabah and wakalah, while the waqf model offers a lower chance of bankruptcy because of the initial waqf capital provided by shareholders through the company. | The model variables still depend on certain assumptions such as claim distribution and management costs are still considered fixed, while in reality they are influenced by many factors, one of which is inflation [34]. The investment level in this study is also still assumed to be fixed, so it does not fully describe the realistic uncertainty in the investment market. |
| El Hachloufi dan El Msiyah [31] |
This study offers better transparency, by separating company funds from participant funds. Company funds are then divided into three parts, namely technical results, financial income and capital management. In addition to transparency, this separation of funds can also reduce the potential for conflict and facilitate the supervision of risk management in accordance with sharia principles. | This research has not used empirical data and case studies, so model validation cannot be carried out and the reliability and accuracy of the research results cannot be known. |
| Puspita et al. [32] | This study offers a hybrid scheme with important innovations in Islamic insurance, namely Qard-Hasan facilities and investment activities. Qard-Hasan facilities can improve financial stability and reduce the risk of corporate bankruptcy in a certain period. Furthermore, the numerical simulations carried out can provide practical insights for corporate risk management in maintaining solvency during a certain period. Furthermore, this study also compares it with conventional schemes so that it can show that the offered Islamic insurance surplus process model has a lower chance of bankruptcy than conventional, especially when the Qard-Hasan lending capacity is high. | This research has not used empirical data from insurance companies. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





