Research on Heterogeneous Network Data Fusion based on Deep Learning

ZHUOHUAN HU; Minghao Liu; Lipeng LIU; Lei Fu; Yu Mao; Xirui Tang

doi:10.20944/preprints202410.2467.v1

Submitted:

29 October 2024

Posted:

30 October 2024

You are already at the latest version

Abstract

The advent of the era of big data has led to the emergence of heterogeneous network data fusion as a prominent area of research. Heterogeneous network data is characterised by multi-modality, multi-source, and high dimensionality, which presents significant challenges for traditional data fusion methods. These methods often encounter difficulties in processing such data, including issues such as information redundancy, data inconsistency, and high computational complexity. This paper proposes a heterogeneous network data fusion model based on a deep neural network. The model employs the Multi-Layer Perceptron (MLP) as its fundamental framework, utilising the deep neural network to facilitate joint feature representation learning on data from disparate modalities. The Adaptive Feature Reconstruction Module enables the model to learn the interrelationships between different modalities and to balance the importance of different modal features in the fusion process in a dynamic manner. Furthermore, we introduce an innovative cross-modal attention mechanism, which is capable of effectively capturing the coupling relationship between deep features in heterogeneous data, thereby enhancing the expressiveness and data fusion efficacy of the model. The experimental results demonstrate that the proposed model markedly enhances the accuracy of classification and regression tasks in comparison to traditional methodologies.

Keywords:

Heterogeneous Network Data

;

Data Fusion

;

Deep Neural Network

;

Cross-Modal Attention Mechanism

Subject:

Computer Science and Mathematics - Artificial Intelligence and Machine Learning

I. Introduction

The rapid development of big data and Internet of Things technologies has resulted in an increase in the prevalence of heterogeneous network data in modern society. Heterogeneous network data is derived from a multitude of sources, including physical sensors, social media platforms, database systems, and Internet of Things (IoT) devices [1]. These data sets are frequently characterised by their multimodality, multi-source nature, and high-dimensionality. The effective fusion and analysis of these heterogeneous data sets can facilitate the exploration of potential correlations and complementarities between the data, while also enhancing the performance of the models in classification, regression, and other data mining tasks [2]. In light of the above, the fusion of heterogeneous network data has been the subject of considerable interest in recent years and has become a prominent area of research within the fields of machine learning and data mining [3].

The conventional heterogeneous data fusion techniques typically employ methodologies such as rule reasoning, matrix factorisation and probability graph models to integrate data of disparate modalities. However, these methods frequently encounter the following challenges when dealing with heterogeneous data [4]: firstly, heterogeneous data often exhibits substantial information redundancy and data noise, and data sources of different modalities may be inconsistent at the physical level, resulting in information conflict and feature mismatch after direct fusion [5].

Subsequently, the high dimensionality and complexity of heterogeneous data make it challenging for traditional methods to effectively cope with the computational complexity and storage overhead, and the model is susceptible to dimensional disasters and overfitting. Thirdly, traditional methods typically necessitate the manual design of feature selection or combination rules [6]. They are deficient in their ability to automatically discern the intricate semantic relationships embedded within the data, and are unable to fully capitalise on the wealth of information encapsulated within multimodal data. In light of these challenges, the urgent need has arisen to develop an efficient and robust heterogeneous data fusion model.

In recent years, deep learning has demonstrated considerable potential in the context of heterogeneous data fusion, due to its robust feature learning and representation capabilities. The deep neural network model is capable of automatically learning high-level feature representations from the data and mining the complex relationships between different modalities, thereby demonstrating superiority in the fusion of large-scale heterogeneous data [7]. Nevertheless, the extant heterogeneous data fusion methods based on deep learning continue to exhibit shortcomings in practical application. These include inconsistent feature expression, insufficient intermodal relationship mining, and inadequate model generalisation and robustness.

This work puts forth a novel heterogeneous network data fusion model founded upon the principles of deep neural networks. The incorporation of an adaptive feature reconstruction module and a cross-modal attention mechanism enables the model to effectively address the issues of inconsistent feature expression and insufficient mining of intermodal relations. Additionally, the incorporation of an adversarial training-based regularisation method enhances the model's stability and generalisation capacity in the presence of noise interference and data distribution alterations.

II. Related Work

Gao et al. [8] undertook a review of the research progress of multimodal data fusion, discussed the limitations of traditional data fusion methods, and proposed the application advantages of deep learning models in multimodal data. This paper compares the applications of various deep learning architectures (such as deep belief networks, stacked autoencoders, convolutional neural networks, and recurrent neural networks) in multimodal data fusion. It also introduces typical cases in cross-modal retrieval, image annotation, and medical-aided diagnosis.

In a recent publication, Liu et al. [9] put forth a novel model, designated as the Deep Multimodal Encoder (DME), which is oriented towards the integration of disparate sensor data. By encoding sensor data and modelling cross-modal feature relationships, the model is able to more effectively capture the intrinsic features of multimodal data, thereby enhancing its generalisation ability and robustness in the fusion process. The experimental results demonstrate that DME exhibits superior performance compared to traditional fusion methods across a range of datasets.

Zhou et al. [10] put forth a multi-source heterogeneous data fusion methodology based on deep learning and demonstrated its efficacy in sensor networks. The authors employed a deep learning model to discern intricate relationships between disparate data sources, and the experimental outcomes substantiate the efficacy of the proposed method in a multitude of sensor data fusion tasks.

III. Methodologies

A. Joint Feature Representation

This work proposed a heterogeneous network data fusion model based on a deep neural network. The model comprises three principal modules: a joint feature representation learning module, an adaptive feature reconstruction module and a cross-modal attention mechanism module. The following section presents the specific mathematical formulas and analysis for each module. The heterogeneous network dataset is composed of

n

modal data, which is denoted as

{X_{1}, X_{2}, \dots, X_{n}}

. Each modality is

X_{i} ϵ R^{m \times d_{i}}

, where

d_{i}

is the feature dimension of the

i

modality and

m

is the number of samples. In order to ensure uniform representation of the features of different modalities, Multi-Layer Perceptron (MLP) pairs are initially employed. Feature extraction and nonlinear transformations are then performed for each modality, denoted as Equation (1)

H_{i} = σ (W_{i} \cdot X_{i} + b_{i}), H_{i} ϵ R^{m \times d_{h}}, i = 1,2, \dots, n,

(1)

where

W_{i} \in R^{d_{i} \times d_{h}}

represents the weight matrix,

b_{i} \in R^{d_{h}}

denotes the bias term,

σ (\cdot)

signifies the nonlinear activation function (such as ReLU), and

d_{h}

refers to the dimension represented by the hidden layer features. The joint feature matrix,

H

, after feature transformation is expressed as Equation (2).

H = {[H}_{1}; H_{2}; \dots; H_{n}] ϵ R^{m \times (n \cdot d_{h})} .

(2)

The joint feature representation matrix integrates the feature information of multimodal data into a more expressive high-dimensional feature space, thereby providing a basis for subsequent feature reconstruction and cross-modal interaction.

The objective of the adaptive feature reconstruction module is to assign suitable weights to the features of different modalities, thereby ensuring a dynamic equilibrium between the relative importance of each modal feature throughout the fusion process. The reconstructed joint features are represented as

\tilde{H}

, which can be expressed as the weighted sum of the modal features and shown in Equation (3).

\tilde{H} = \sum_{i = 1}^{n} α_{i} \cdot H_{i}, \tilde{H} ϵ R^{m \times d_{h}},

(3)

where

α_{i}

represents the weight of the

i

mode, which satisfies

\sum_{i = 1}^{n} α_{i} = 1

. The weight vector

α_{i}

is obtained through the process of adaptive learning, denoted as Equation (4).

α_{i} = \frac{e x p (M L P_{α} (H_{i}))}{\sum_{j = 1}^{n} e x p (M L P_{α} (H_{j}))},

(4)

where

M L P_{α} (\cdot)

is the weight generator, which transforms each modal feature and outputs the weights through a multilayer perceptron. The aforementioned weighting mechanism enables the model to effectively integrate modal information, retain crucial features, and mitigate the impact of superfluous information.

In order to enhance the capacity of the model to interact with heterogeneous data, a cross-modal attention mechanism is incorporated. Firstly, the similarity matrix

A

is calculated between the modal features and shown in Equation (5), where

A_{i, j}

represents the similarity between the modal

i

and the modal

j

.

A_{i, j} = \frac{e x p (H_{i} \cdot H_{j}^{T})}{\sum_{k = 1}^{n} e x p (H_{i} \cdot H_{k}^{T})}, A ϵ R^{n \times n} .

(5)

On the basis of the similarity matrix, a cross-modal weighted summation of the feature

H_{i}

of modal

i

is carried out in order to obtain a new feature representation

H_{i}^{'}

, represented as Equation (6).

H_{i}^{'} = \sum_{j = 1}^{n} A_{i, j} \cdot H_{j}, i = 1,2, \dots, n

(6)

The novel cross-modal feature representation,

H^{'}

, preserves the interactional data between the modalities, thereby facilitating a more accurate representation of the intricate relationships between the diverse modal features within the global feature space.

B. Training and Optimization

In order to enhance the robustness and generalisation capacity of the model, this paper proposes a regularisation method based on adversarial training. This method optimises the parameters of the model by introducing perturbation terms, thereby improving its performance in the context of complex data distributions. The loss functions of the model comprise the loss associated with the basic task (denoted as

L_{t a s k}

) and the loss associated with adversarial training (

L_{a d v}

). The loss associated with the underlying task is typically the intersectional entropy loss inherent to the classification task or the mean squared error inherent to the regression task, denoted as Equation (7).

L_{t a s k} = \frac{1}{m} \sum_{i = 1}^{m} L (f ({\tilde{H}}_{i}), y_{i}),

(7)

where

f ({\tilde{H}}_{i})

represents the prediction output of the model, while

y_{i}

denotes the actual label. In order to introduce adversarial training, the perturbation term

∆

is defined, with a size limited to the

∥ ∆ ∥ \leq ϵ

range. The counter-loss function,

L_{a d v}

, is defined as Equation (8).

L_{a d v} = \frac{1}{m} \sum_{i = 1}^{m} L (f ({\tilde{H}}_{i} + ∆), y_{i}) .

(8)

The final loss function of the model

L

, is the weighted sum of the loss of the underlying task and the adversarial loss and described as Equation (9).

L = L_{t a s k} + λ \cdot L_{a d v},

(9)

note that

λ

represents the weight coefficient of the adversarial loss, which is employed to regulate the influence of the adversarial perturbation on the training of the model.

The objective of adversarial training is to enhance the stability of the model in the presence of heterogeneous data distributions. The specific training process is outlined below: In accordance with the prevailing model parameters, the perturbation term

∆

, which optimises the adversarial loss, is calculated by the following Equation (10).

∆ = ϵ \cdot \frac{\nabla_{\tilde{H}} L (f (\tilde{H}), y)}{∥ \nabla_{\tilde{H}} L (f (\tilde{H}), y) ∥},

(10)

where

\nabla_{\tilde{H}} L

represents the gradient of

\tilde{H}

, as defined by the loss function pair. The perturbation term

∆

is then added to the feature representation

\tilde{H}

in order to calculate the adversarial loss and minimise the final loss function

L

represented as Equation (11).

θ \leftarrow θ - η \cdot \nabla_{θ} L,

(11)

Where the learning rate, represented by the variable

η

and the model parameter, represented by the variable

θ

are of particular interest. The aforementioned adversarial training methods enable the model to retain high stability and accuracy in the presence of noise and perturbation, thereby enhancing its generalisation ability in the context of complex and heterogeneous data distributions.

IV. Experiments

A. Experimental setups

The Heterogeneous Sensor Data Fusion Dataset is a public dataset for multi-source sensor data fusion, designed to solve problems in the fusion of heterogeneous sensor data (such as temperature, humidity, light intensity, etc.). The hidden dimension of the model was 256, the learning rate was set to 0.001, and the Adam optimizer was used for training, with a batch size of 64. A total of 50 epochs were performed for model training, and the ratio of training set to validation set was randomly divided into 8:2 in each epoch.

B. Experimental analysis

In order to evaluate the heterogeneous sensor data fusion model proposed in this paper, we compare it with the following classical methods: the statistical fusion method uses principal component analysis (PCA) to extract the main features, and the traditional machine learning model random forest (RF), which has better performance on low-dimensional data; Deep learning models are stacked with autoencoders (SAEs) to handle complex nonlinear relationships between data.

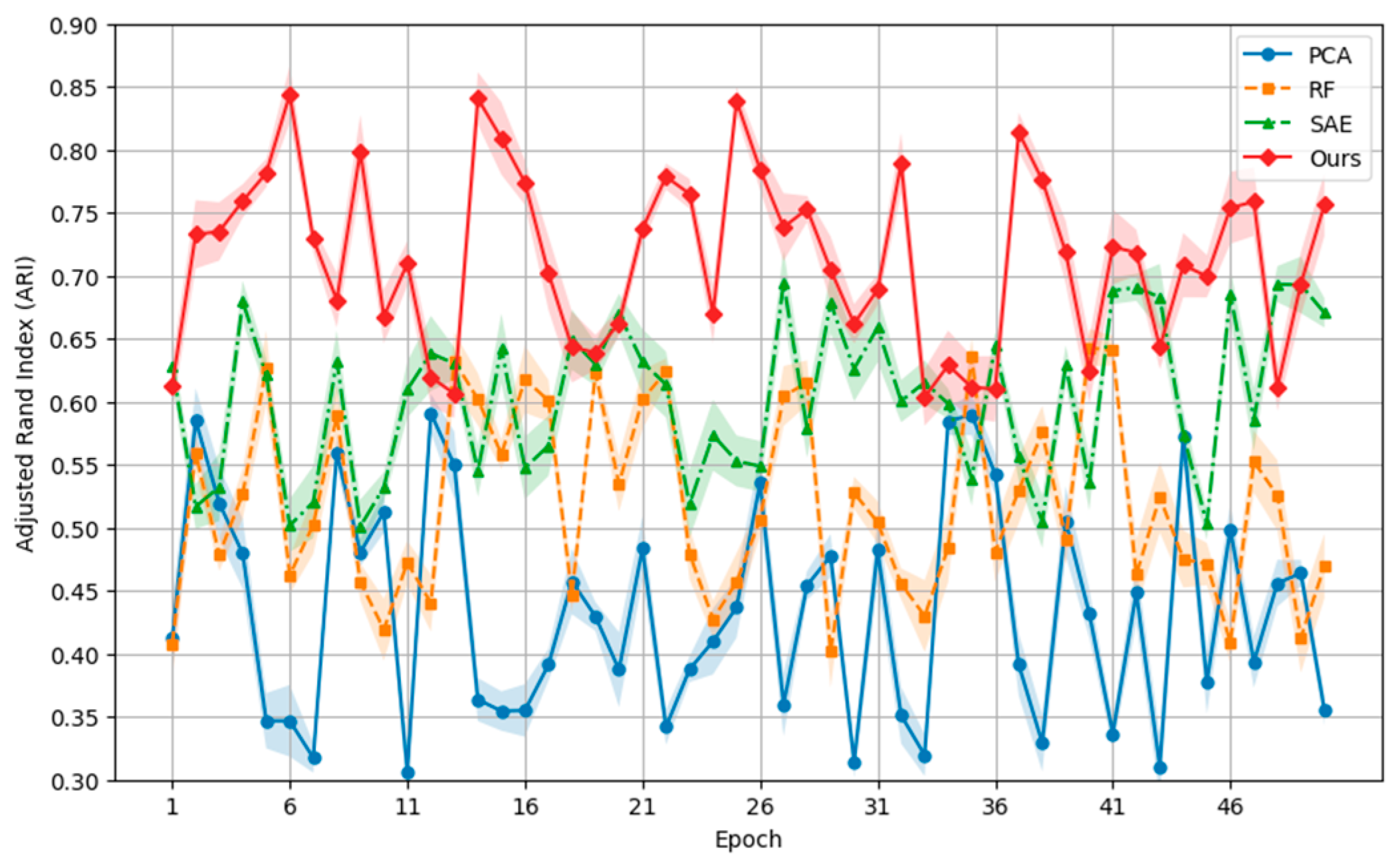
Figure 1 depicts the variation of the adjusted Rand index (ARI) for PCA, RF, SAE, and our proposed method (Ours) under different epochs, with the error ranges for each method represented using shaded areas. It can be observed that the smaller the shaded area, the greater the stability of the method within the interval. Our method (Ours) demonstrates a higher average ARI value and a smaller margin of error, indicating its stability and superiority in addressing heterogeneous data clustering tasks.

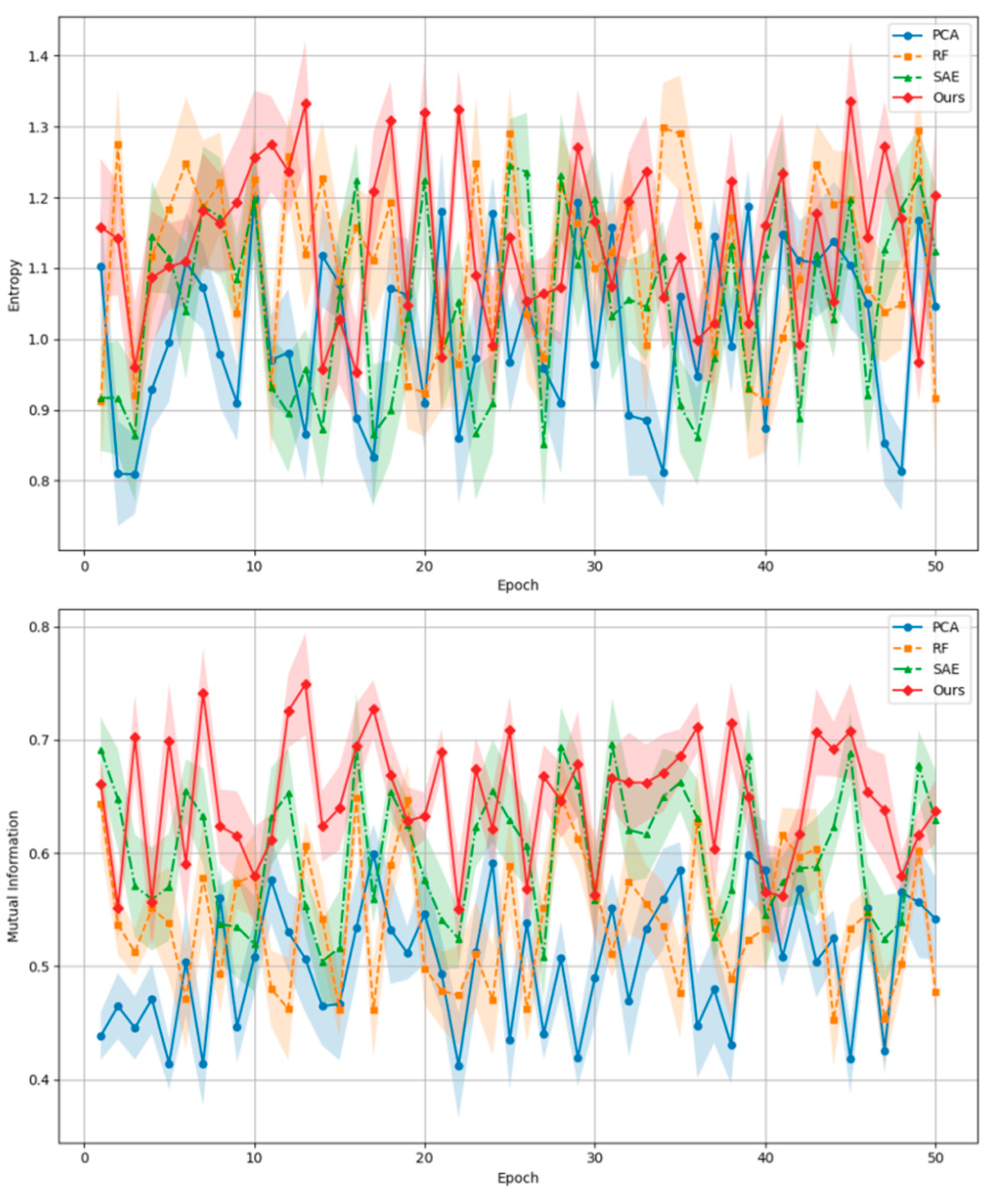
Figure 2 illustrates the experimental comparison of entropy and mutual information for distinct methods (principal component analysis, random forest, sparse autoencoder, and the proposed approach) at each epoch. The diagram employs shaded areas to illustrate the margin of error for each method. The initial graph illustrates the trajectory of information entropy for each method, while the subsequent graph depicts the evolution of mutual information for each method. It can be observed that the proposed method (Ours) exhibits a higher mutual information value and a relatively lower information entropy value in the majority of epochs. This suggests that it is capable of more effectively capturing and retaining essential information within multimodal data, while simultaneously reducing the influence of superfluous information.

We then compared the MIMIC-III (Medical Information Mart for Intensive Care) dataset with the existing Deep multimodal encoders method, which is a large medical dataset containing electronic health records from ICU patients, covering multimodal medical data, including time series, diagnosis, treatment, and other information.

Table 1. Comparison with existing advanced encoders method under novel dataset.

Methods	Deep multimodal encoders	Ours
Adjusted Rand Index (ARI)	0.78	0.85
Mutual Information	1.65	1.75
Entropy	0.60	0.50

V. Conclusions

In conclusion, a heterogeneous network data fusion model based on deep learning is proposed, which effectively improves the performance of multimodal data fusion through an adaptive feature reconstruction module and a cross-modal attention mechanism. Experimental results show that the proposed model is significantly better than traditional methods, such as PCA, Random Forest (RF) and Stacked Autoencoder (SAE), in several evaluation indexes (such as adjusted Rand index, information entropy and mutual information), showing its superiority and stability in complex heterogeneous data fusion tasks. In particular, our method shows strong robustness when dealing with data noise and heterogeneity. Future research can further expand the application scenarios of this model, such as exploring how to better capture the deep interaction between multimodal data in complex systems such as smart cities, medical diagnosis, and environmental monitoring.

References

Zhang, Y., Sheng, M., Liu, X., Wang, R., Lin, W., Ren, P.,... & Song, W. (2022). A heterogeneous multi-modal medical data fusion framework supporting hybrid data exploration. Health Information Science and Systems, 10(1), 22. [CrossRef]
Kashinath, S. A., Mostafa, S. A., Mustapha, A., Mahdin, H., Lim, D., Mahmoud, M. A.,... & Yang, T. J. (2021). Review of data fusion methods for real-time and multi-sensor traffic flow analysis. IEEE Access, 9, 51258-51276. [CrossRef]
Pourghebleh, B., Hekmati, N., Davoudnia, Z., & Sadeghi, M. (2022). A roadmap towards energy-efficient data fusion methods in the Internet of Things. Concurrency and Computation: Practice and Experience, 34(15), e6959. [CrossRef]
Mentasti, S., Barbiero, A., & Matteucci, M. (2024, June). Heterogeneous Data Fusion for Accurate Road User Tracking: A Distributed Multi-Sensor Collaborative Approach. In 2024 IEEE Intelligent Vehicles Symposium (IV) (pp. 1658-1665). IEEE.
Liu, Y., & Liu, Y. (2021). Heterogeneous Network Multi Ecological Big Data Fusion Method Based on Rotation Forest Algorithm. In Big Data Analytics for Cyber-Physical System in Smart City: BDCPS 2020, 28-29 December 2020, Shanghai, China (pp. 632-639). Springer Singapore.
Cai, L., Lu, C., Xu, J., Meng, Y., Wang, P., Fu, X., ... & Su, Y. (2021). Drug repositioning based on the heterogeneous information fusion graph convolutional network. Briefings in bioinformatics, 22(6), bbab319. [CrossRef]
Toldo, M., Maracani, A., Michieli, U., & Zanuttigh, P. (2020). Unsupervised domain adaptation in semantic segmentation: a review. Technologies, 8(2), 35. [CrossRef]
Gao, J., Li, P., Chen, Z., & Zhang, J. (2020). A survey on deep learning for multimodal data fusion. Neural Computation, 32(5), 829-864. [CrossRef]
Liu, Z., Zhang, W., Quek, T. Q., & Lin, S. (2017, March). Deep fusion of heterogeneous sensor data. In 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) (pp. 5965-5969). IEEE.
Zhou, J., & Lei, Y. (2023, January). Multi-source Heterogeneous Data Fusion Algorithm Based on Federated Learning. In International Conference on Soft Computing in Data Science (pp. 46-60). Singapore: Springer Nature Singapore.

Figure 1. Comparison of Adjusted Rand Index (ARI) with Error.

Figure 2. Comparison of Mutual Information and Entropy across Different Methods.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Research on Heterogeneous Network Data Fusion based on Deep Learning

Abstract

Keywords:

Subject:

I. Introduction

II. Related Work

III. Methodologies

A. Joint Feature Representation

B. Training and Optimization

IV. Experiments

A. Experimental setups

B. Experimental analysis

V. Conclusions

References

MDPI Initiatives

Important Links

Subscribe