A PMBM Forward-Backward Smoother for Multiple Extended Targets

1. Problem Formulation

1.1. The Generic Multi-Target Bayesian Forward–Backward Smoother

The extended target states and the measurements are both modelled as RFS. At each time step k, let $x\in {\mathbb{R}}^n$ denote a single extended target state, each target state x is also a random variable. The set of measurements taken at time step k is denoted as $Z_k=\left\{z_1,\dots ,z_n\right\}$, including clutter and target generated measurements. z is the single extended target measurement. The number of targets, i.e. the target set cardinality $|X_k|$, is a time-varying discrete random variable. Y is the smoothed extended target state set.

Let $f_{k\mid k}\left(X_k\mid Z_k\right)$, $f_{k\mid k-1}\left(X_k\mid X_{k-1}\right)$ and $f_k\left(Z_k\mid X_k\right)$ denote the multi-target set density, the multi-target transition density and the multi-target measurement likelihood, respectively. The Bayesian multi-target filter propagates the multi-target posterior density $f_{k-1\mid k-1}\left(X_{k-1}\mid Z_{k-1}\right)$ in time using the Chapman-Kolmogorov prediction equation.

$$\begin{array}{c}\hfill f_{k\mid k-1}\left(X_k\mid Z_{k-1}\right)=\int f_{k\mid k-1}\left(X_k\mid X_{k-1}\right)f_{k-1\mid k-1}\left(X_{k-1}\mid Z_{k-1}\right)\delta X_{k-1}\end{array}$$

(1)

and the Bayesian update formula

$$\begin{array}{c}\hfill f_{k\mid k}\left(X_k\mid Z_k\right)={\displaystyle \frac{f_k\left(Z_k\mid X_k\right)f_{k\mid k-1}\left(X_k\mid Z_{k-1}\right)}{\int f_k\left(Z_k\mid X_k\right)f_{k\mid k-1}\left(X_k\mid Z_{k-1}\right)\delta X_k}}.\end{array}$$

(2)

The generic multi-target Bayesian forward–backward smoother (smoothing recursion) is described as follows

$$\begin{array}{c}\hfill f_{k-1\mid l}\left(X_k\mid Z_k\right)=f_{k-1}\left(X_{k-1}\mid Z_l\right)\int {\displaystyle \frac{f_{k\mid l}\left(Y\mid Z_k\right)f_{k\mid k-1}\left(Y\mid X_{k-1}\right)}{f_{l\mid l-1}\left(Y\mid Z_l\right)}}\delta Y.\end{array}$$

(3)

For simplicity the following notation is adopted throughout this paper:

$$\int f\left(X\right)\delta X=\sum _{n=0}^{\infty }{\displaystyle \frac{1}{n!}}\int f\left(\left\{x_1,\cdots ,x_n\right\}\right)\mathrm{d}{x}_{1:n},〈f,g〉=\int f\left(x\right)g\left(x\right)\mathrm{d}x.$$

1.2. Standard Multi-Target System Models

1.2.1. Multi-Target Dynamic Model

As described in Sec.II A, for the extended target set $X_k=\left\{x_1,\dots ,x_n\right\}$ at time step k, each target $x\in X_k\subseteq {\mathbb{R}}^n$ survives with probability $p_S\left(X\right)$ and moves to a new state with a transition density $g\left(·\mid X\right)$ according to a Markov chain, or dies with probability $1-p_S\left(X\right)$. The multi-target set ${\mathbf{X}}_k$ are the union of the surviving targets and new targets, which are born independently following a Poisson point process (PPP) with intensity ${\lambda }^b\left(·\right)$.

1.2.2. Extended Target Measurement Model

Let $Z_k=Z_c\uplus Z_1\uplus \cdots \uplus Z_n$ be the measurement set, where $Z_c,Z_1,\cdots ,Z_n$ are mutually independent disjoint sets. $Z_c$ modelled as a PPP with intensity ${\lambda }^C\left(·\right)$ is the clutter measurement set. $z\in Z_i$ is the measurement generated by the target $i\left(i=1,\cdots ,n\right)$. Each extended target state $x_k\in X_k$ is either detected with probability $p_D\left(x_k\right)$ or missed with probability $1-p_D\left(x_k\right)$. The extended target measurements are modelled as a PPP rate $\gamma \left(x_k\right)$ and spatial distribution $\phi \left(·\mid x_k\right)$, independent of any other targets and their corresponding generated measurements.

We use the convolution formula for the multiple extended target likelihood density, also known as the conditional extended target measurement set likelihood,

$$\begin{array}{c}\hfill l\left(z\mid x_k\right)=p_D\left(x_k\right)e^{-\gamma \left(x_k\right)}\prod _{z\in Z}\gamma \left(x_k\right)\psi \left(z\mid x_k\right).\end{array}$$

(4)

For an extended target $x_k$, the effective detection probability is the product of the detection probability and the PPP probability density function (PDF), i.e., $p_D\left(x_k\right)\left(1-e^{-\gamma \left(x_k\right)}\right),$ where $\left(1-e^{-\gamma \left(x_k\right)}\right)$ is the Poisson probability of generating at least one measurement. Therefore, the effective probability that the extended target $x_k$ will not be detected is

$$\begin{array}{c}\hfill q_D\left(x_k\right)=1-p_D\left(x_k\right)+p_D\left(x_k\right)e^{-\gamma \left(x_k\right)}.\end{array}$$

(5)

Note that the conditional likelihood (4) for an empty measurement set, $l_{\varnothing }\left(x_k\right)$, is also described by (5) [13].

1.3. PMBM RFS

The PMBM filter developed in recent years is an RFS method defined as a convolution of a PPP intensity for the undetected targets and a MBM density for the detected targets. The PMBM filter is an ETT conjugate prior based on the standard RFS method [10]. The importance of the conjugate prior is that, given the assumed models, we know what the theoretically exact density is and can find computationally tractable approximations [14].

In the PMBM model, the set of targets ${\mathbf{X}}_k$ is a union of two disjoint sets, i.e. $X_k=X_k^u\uplus X_k^d$. The set of undetected targets is denoted $X_k^u$, modelled by PPP. The set of detected targets, denoted $X_k^d$, modelled by MBM. The density of the PMBM set can be described by [13]

$$\begin{array}{cc}\hfill f^{pmbm}\left(X_k\right)& =\sum _{X_k^u\uplus X_k^d=X_k}{f}^p\left(X_k^u\right)f^{mbm}\left(X_k^d\right),\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill f^p\left(X_k^u\right)& =e^{-〈{\lambda }^u;1〉}\prod _{x\in X_k^u}{\lambda }^u\left(x\right),\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill f^{mbm}\left(X_k^d\right)& =\sum _{j\in \mathbb{J}}{\mathcal{W}}^j\sum _{{\uplus }_{i\in {\mathbb{I}}^j}{X}^i=X^d}\prod _{i\in {\mathbb{I}}^j}{f}^{j,i}\left(X_k^i\right).\hfill \end{array}$$

(8)

Therefore, the RFS density of PMBM is entirely determined by the parameters ${\lambda }^u,{\left\{\left({\mathcal{W}}^j,{\left\{\left(r^{j,i},p^{j,i}\right)\right\}}_{i\in {\mathbb{I}}^j}\right)\right\}}_{j\in \mathbb{J}}$.

2. The PMBM Forward-Backward Smoother

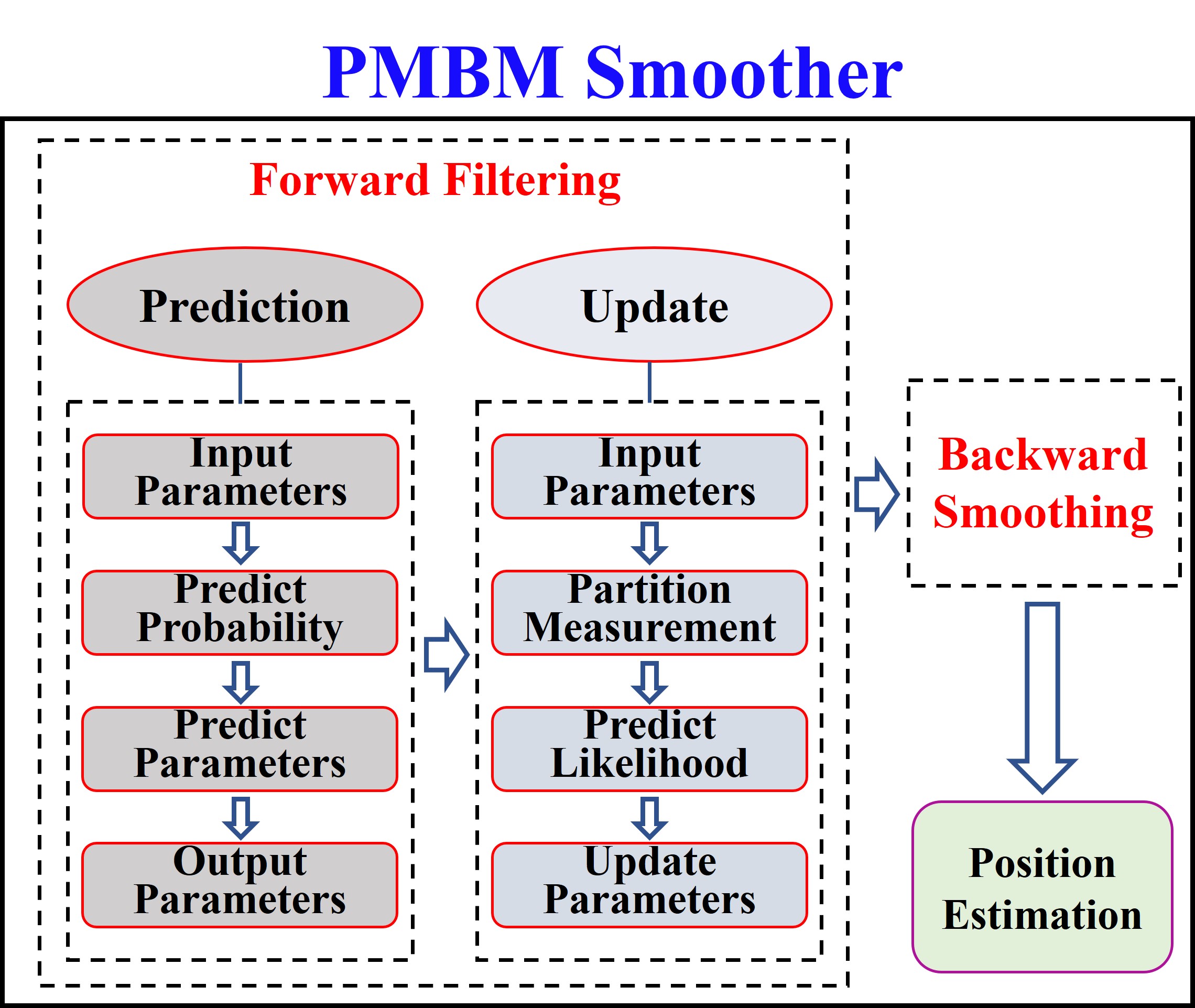
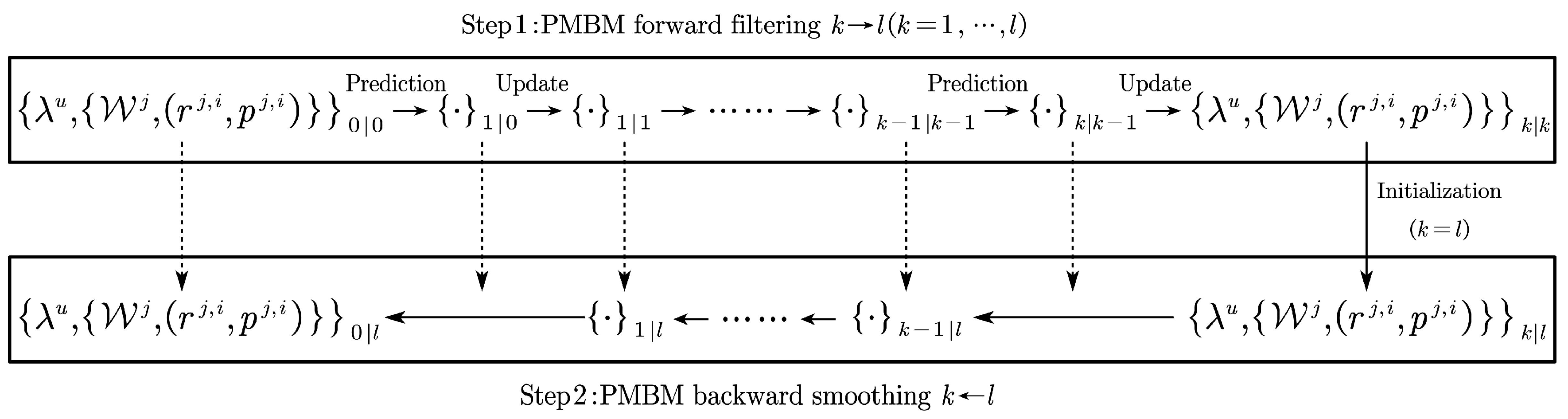
The proposed PMBM forward-backward smoother consists of forward filtering achieved by the PMBM filter recursion, followed by backward smoothing achieved by a parametric updated posterior PMBM density. In this section, we give a representation of the backward smoothing recursion.

2.1. PMBM Forward Filtering

The forward filtering is done by the PMBM filtering recursion. Here the PMBM filtering recursion is omitted, for a more detailed description see [10].

2.2. Backward Smoothing Recursion

After the PMBM filter recursion, the updated PMBM filter density at time k is

$$\begin{array}{c}\hfill f^{pmbm}\left(X_k\mid Z_k\right)=\sum _{X_k^u\uplus X_k^d=X_k}{f}^p\left(X_k^u\right)f^{mbm}\left(X_k^d\right),\end{array}$$

(9)

where

$$\begin{array}{c}\hfill f^p\left(X_k^u\right)=e^{-〈{\lambda }_k^u\left(x\right);1〉}\prod _{x\in X_k^u}{\lambda }_k^u\left(x\right),\end{array}$$

(10)

$$\begin{array}{c}\hfill f^{mbm}\left(X_k^d\right)=\sum _{A\in {\mathcal{A}}^j}{\mathcal{W}}_{A,k}^j\sum _{{\uplus }_{C\in A}{X}^C=X^d}\prod _{C\in A}{f}_C^j\left(X^C\right),\end{array}$$

(11)

$$\begin{array}{c}\hfill {\lambda }_k^u\left(x\right)=q_D\left(x\right){\lambda }_{k\mid k-1}^u\left(x\right),\end{array}$$

(12)

$$\begin{array}{c}\hfill {\mathcal{W}}_{A,k}^j={\displaystyle \frac{{\mathcal{W}}_{k\mid k-1}^j{\prod }_{C\in A}{\mathcal{L}}_C}{{\sum }_{j\in {\mathbb{J}}_{k\mid k-1}}{\sum }_{A\in {\mathcal{A}}^j}{\mathcal{W}}_{k\mid k-1}^j{\prod }_{C\in A}{\mathcal{L}}_C}},\end{array}$$

(13)

where ${\mathcal{A}}^j$ is the space of all data association hypotheses. C is a subset of all data associations A. A data association $A\in {\mathcal{A}}^j$ is an assignment of each measurement in $Z_k$ to a source, either the background (clutter or new target) or one of the existing targets indexed by ${\mathbb{I}}^j$. $q_D\left(x\right)$ is the probability of missed detection. ${\mathcal{L}}_C$ is the likelihood function of the data association C. $f_C^j\left(X^C\right)$ is a Bernoulli density. See [10] for more details.

Given the above updated posterior PMBM density, a set of measurements $Z_k$ and standard multi-target system models, then the PMBM backward smoothing density can be calculated as follows.

$$\begin{array}{c}\hfill f_{k-1\mid l}^{pmbm}\left(X_k\mid Z_k\right)=\sum _{X_k^u\uplus X_k^d=X_k}{f}_{k-1\mid l}^p\left(X_k^u\right)f_{k-1\mid l}^{mbm}\left(X_k^d\right).\end{array}$$

(14)

The detailed implementation of the PMBM smoother is shown in Figure 1.

The Poisson and MBM parts of the backward smoothing are calculated as follows.

2.2.1. PPP

The Poisson part of the backward smoothing can be calculated using the PHD filter smoothing recursion [7], which is given by

$$\begin{array}{cc}\hfill & {\lambda }_{k-1\mid l}^u\left(X\right)={\lambda }_{k-1}^u\left(X\right)\left(1-p_S+p_S〈{\displaystyle \frac{f_{k\mid k-1}\left(Y\mid X\right)}{{\lambda }_{k\mid k-1}^u}},{\lambda }_{k\mid l}^u〉\right),\hfill \end{array}$$

(15)

for a more detailed proof, see [7].

2.2.2. MBM

The Bernoulli part of the backward smoothing can be computed using the Bernoulli filter smoothing recursion [9], which is given by

$$\begin{array}{c}\hfill f_{k-1\mid l}^b\left(X\right)=f_{k-1}^b\left(X\right)\int f_{k\mid k-1}\left(Y\mid X\right){\displaystyle \frac{f_{k\mid l}^b\left(Y\right)}{f_{k\mid k-1}^b\left(Y\right)}}\delta Y.\end{array}$$

(16)

The formula above (16) can be rewritten as

$$\begin{array}{c}\hfill f_{k-1\mid l}^b\sim \left(r_{k-1\mid l},p_{k-1\mid l}\left(x\right)\right),\end{array}$$

(17)

for detailed proof, see [9].

As there are several Bernoulli components in PMBM filtering, we have used

$$\begin{array}{c}\hfill f_{k-1\mid l}^{mb}\sim {\left(r_{k-1\mid l}^{j,i},p_{k-1\mid l}^{j,i}\left(x\right)\right)}_{i\in {\mathbb{I}}^j},\end{array}$$

(18)

where $i\in \mathbb{I}$, $j\in \mathbb{J}$. $\mathbb{I}$ is the index set of the Bernoulli components. $\mathbb{J}$ is the index set of the MBs. The calculation of (18) is the same as that of (17). See [9] for more details. The MBM is composed of several MBs, the smoothing recursion is given by

$$\begin{array}{c}\hfill f_{k-1\mid l}^{mbm}\sim \left\{{\mathcal{W}}_{A,k-1\mid l}^j,{\left(r_{k-1\mid l}^{j,i},p_{k-1\mid l}^{j,i}\left(x\right)\right)}_{i\in {\mathbb{I}}^j}\right\},\end{array}$$

(19)

where ${\left(r_{k-1\mid l}^{j,i},p_{k-1\mid l}^{j,i}\left(x\right)\right)}_{i\in {\mathbb{I}}^j}$ from (18). Next we look at the calculation of ${\mathcal{W}}_{A,k-1\mid l}^j$.

Since the number of data associations is unknown, the number of components in the MBM increases rapidly as more data are observed. Each MB component in the MBM corresponds to a unique global hypotheses. The number of MBs and Bernoulli components is retained in the PMBM prediction. However, due to unknown data association, these two numbers grow in the update, where the more global hypotheses, the more data association weights need to be computed, which may refer to (17a) in [10]. In the PMBM smoothing recursion, we also need to compute weights ${\mathcal{W}}_{A,k-1\mid l}^j$ from four parts according to the data association formed during the filtering process.

For missed detection of PPP

In this part, no data associations have been generated in relation to missed PPP detection or updating the undetected target intensity. Therefore, there is no need to calculate the weight.

For potential targets detected of PPP for the first time

As the MBM filter density is updated in this part, we give expressions for an updated weight for the first measurement cell in the data associations.

$$\begin{array}{c}\hfill {\mathcal{W}}_{A_1,k-1\mid l}^j={\displaystyle \frac{{\mathcal{W}}_{k\mid k-1}^j{\prod }_{C_1\in A_1}{\mathcal{L}}_{C_1}}{{\sum }_{j^{\prime }\in \mathbb{J}}{\sum }_{A_1\in {\mathcal{A}}^{j^{\prime }}}{\mathcal{W}}_{k\mid k-1}^{j^{\prime }}{\prod }_{C_1\in A_1}{\mathcal{L}}_{C_1}}},\end{array}$$

(20)

where ${\mathcal{W}}_{k\mid k-1}^j={\mathcal{W}}_{k-1}^j$, ${\mathcal{W}}_{k\mid k-1}^{j^{\prime }}={\mathcal{W}}_{k-1}^{j^{\prime }}$, ${\mathcal{L}}_{C_1}$ is the likelihood of the first measurement cell, $C_1$ is the first measurement cell corresponding to the data association. $A_1$ is the assignment of measurement cell in Z to new Bernoulli components.

For missed detection of MBM

In this part, we consider the update of the missed detection of the MBM filtering recursion for the second measurement cell in the data associations, so the updated weight is as follows

$$\begin{array}{c}\hfill {\mathcal{W}}_{A_2,k-1\mid l}^j={\displaystyle \frac{{\mathcal{W}}_{k\mid k-1}^j{\prod }_{C_2\in A_2}{\mathcal{L}}_{C_2}}{{\sum }_{j^{\prime }\in \mathbb{J}}{\sum }_{A_2\in {\mathcal{A}}^{j^{\prime }}}{\mathcal{W}}_{k\mid k-1}^{j^{\prime }}{\prod }_{C_2\in A_2}{\mathcal{L}}_{C_2}}},\end{array}$$

(21)

where ${\mathcal{L}}_{C_2}$ is the likelihood of the second measurement cell, $C_2$ is the second measurement cell corresponding to the data association. $A_2$ is the hypotheses of the unassigned measurement cell in Z.

For updated MBM

In this part, we consider the updating of the previous potentially detected targets of the MBM filtering recursion for the third measurement cell in the data associations, so that the updated weight is as follows.

$$\begin{array}{c}\hfill {\mathcal{W}}_{A_3,k-1\mid l}^j={\displaystyle \frac{{\mathcal{W}}_{k\mid k-1}^j{\prod }_{C_3\in A_3}{\mathcal{L}}_{C_3}}{{\sum }_{j^{\prime }\in \mathbb{J}}{\sum }_{A_3\in {\mathcal{A}}^{j^{\prime }}}{\mathcal{W}}_{k\mid k-1}^{j^{\prime }}{\prod }_{C_3\in A_3}{\mathcal{L}}_{C_3}}},\end{array}$$

(22)

where ${\mathcal{L}}_{C_3}$ is the likelihood of the third measurement cell, $C_3$ is the third measurement cell corresponding to the data association. $A_3$ is the assignment of measurement cell in Z to the existing Bernoulli components.

3. Simulation Results

In this section, we evaluate the performance of the proposed algorithm in a scenario over a surveillance area with coalescence, where there are three targets moving randomly and irregularly at a constant speed. The maximum number of global hypotheses considered is $N_h=200$. At each update step, we use ellipsoidal gating with threshold ${\mathrm{\Gamma }}_T=10$ to consider only the relevant measurements for each individual trajectory hypotheses. In the simulation experiment presented here, we focus on comparing the PMBM smoother with the standard PMBM filter. For each filter, 100 Monte Carlo (MC) runs were performed. The Poisson clutter intensity is ${\lambda }^C=10$ and the target detection probability is $P_D=0.90$, the target survival probability is $P_S=0.90$.

Let ${\xi }_k=\left[p_k,v_k\right]\in {\mathbb{R}}^4$ be the kinematic state, where $p_k\in {\mathbb{R}}^2$ is the position of the extended target, $v_k\in {\mathbb{R}}^2$ is the velocity. $l\left(z\mid x\right)=\mathcal{N}\left(z;Hx,R\right)$, where H is the observation matrix and R is the measurement noise covariance matrix, given by respectively

$$H=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\end{array}\right],R={\sigma }_{\epsilon }^2\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right],$$

where ${\sigma }_{\epsilon }=1m$ is the standard deviation of the measurement noise. The Generalised Optimal Sub-pattern Assignment (GOSPA) metric [15] is used to assess performance. The cut-off and order parameters are set to $c=20$ and $p=2$ respectively

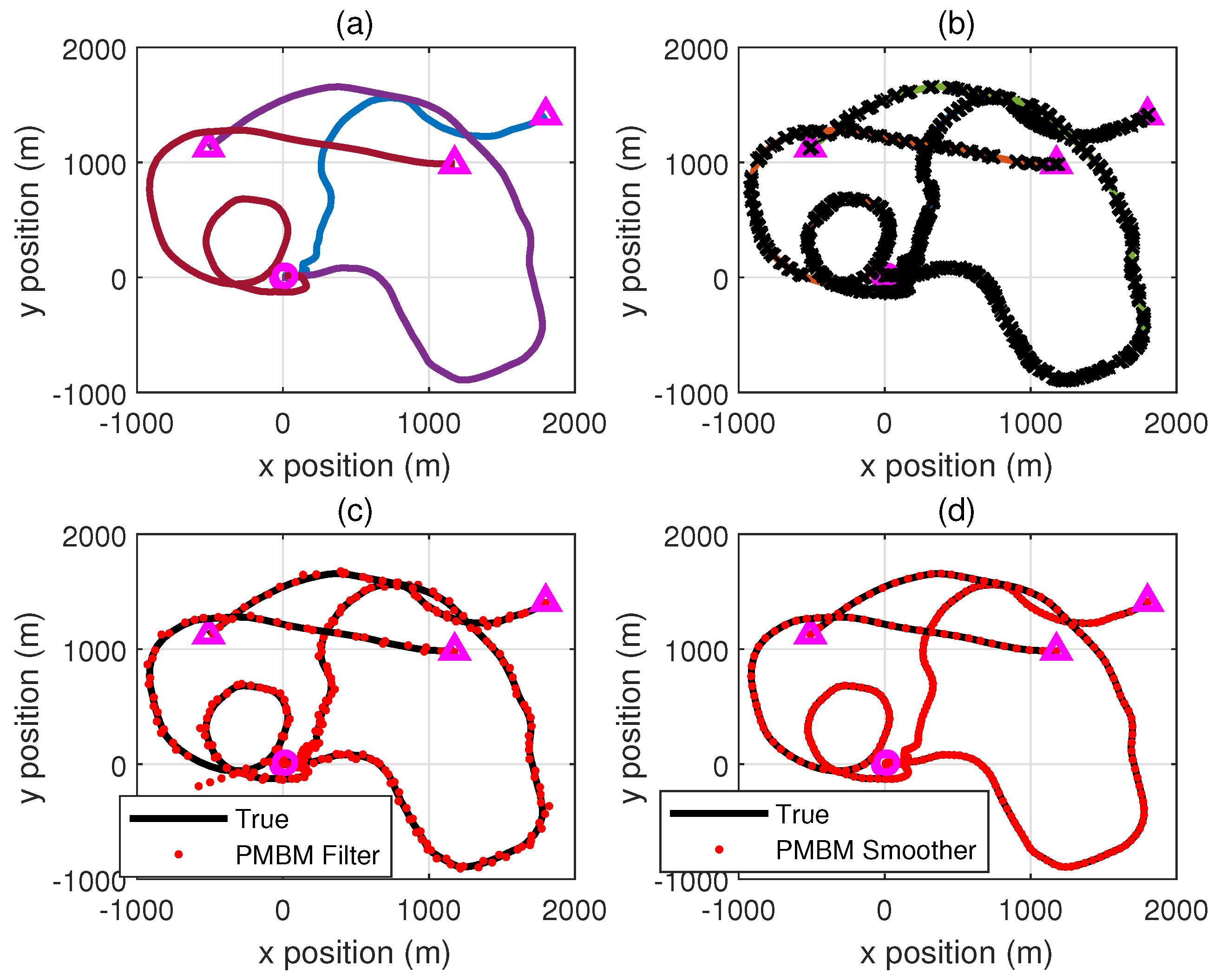
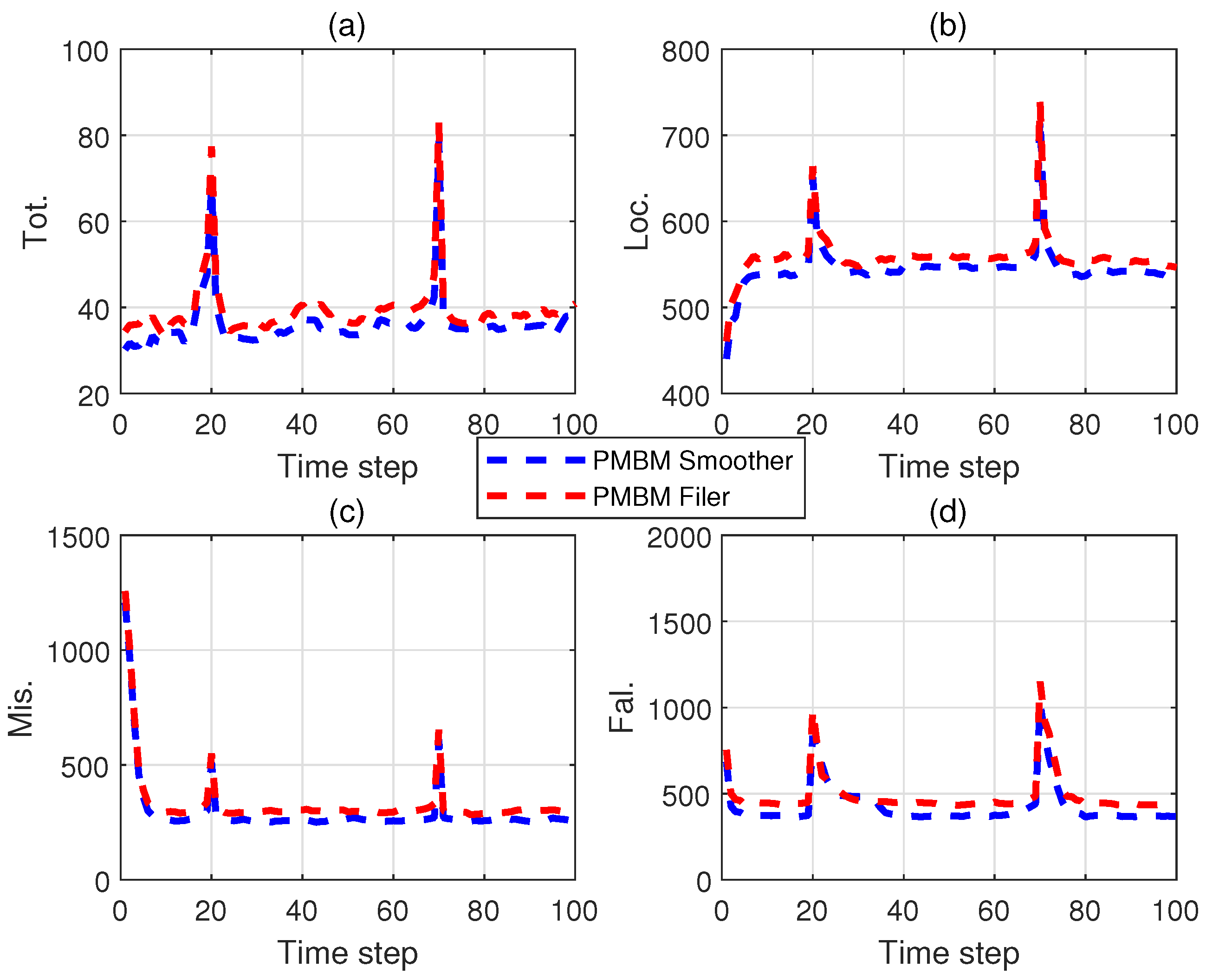
It can be seen from Figure 2 that the PMBM smoother performs much better and more stable compared to the PMBM filter because more measurements are used to produce more effective estimates by delaying the decision time (k) and using data at a later time $l\left(l>k\right)$. The decomposition of the GOSPA errors of the PMBM smoother and the PMBM filter are shown in Figure 3, while the mean computation time per MC is shown in Table 1. It can be seen that the PMBM smoother has the better performance according to the GOSPA errors and stable trajectory estimation. However, the PMBM smoother is generally a more computationally expensive operation, as the mean computation time of the PMBM smoother is slower than that of the PMBM filter, because the PMBM smoother has to perform the third step "smoothing" after "prediction" and "filtering", while the PMBM filter does not. In other words, the PMBM smoother must be computed in reverse order from $k-1$ to 0 with the following PMBM recursive density after "updating" with measurements at a current time k.

4. Conclusion

In this paper, we have presented a PMBM smoother under the RFS framework, which has the advantage of maintaining the tracking accuracy of different positions. The proposed smoother consists of forward propagation of PMBM filter densities followed by backward propagation of an updated PMBM filter density including PPP smoothing and MBM smoothing, respectively. Simulation results have demonstrated the superior performance of the smoother in terms of GOSPA errors and tracking performance compared to the standard PMBM filter.