Submitted:
27 October 2024
Posted:
28 October 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Mathematical Model of Non-Stationary Transport of 1:1 Salt Ions in the Diffusion Layer of the Ion Exchange Membrane
2.1. Diffusion Layer at the Cation-Exchange Membrane (CEM)
2.2. Mathematical Model
2.3. Boundary Conditions
2.4. Initial Conditions ()
3. Characteristic Quantities and Transition to Dimensionless Form
4. Boundary Value Problem for a One-Dimensional Non-Stationary System of Equations of the NPP in Dimensionless Form
5. The Relationship Between the Currents in the Circuit and in the Diffusion Layer
6. Stationary Boundary Value Problem
7. Algorithm for Solving a Non-Stationary Boundary Value Problem
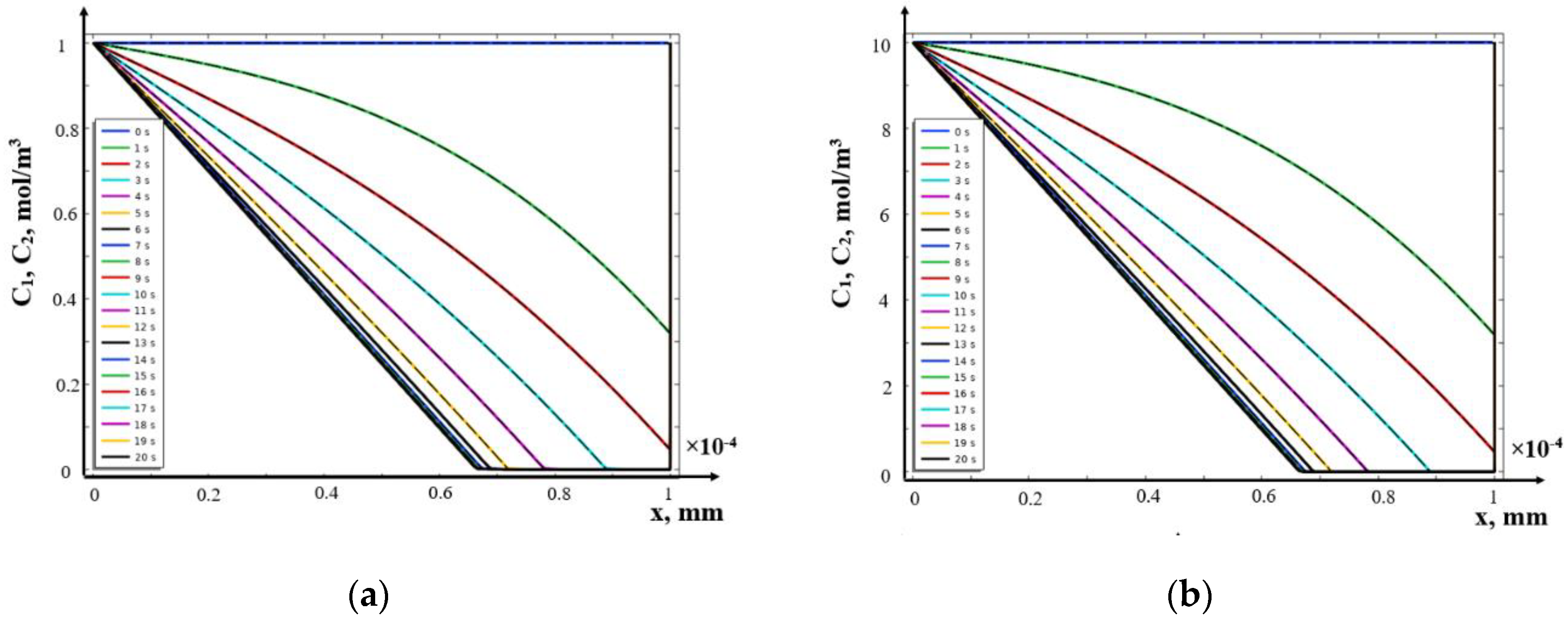
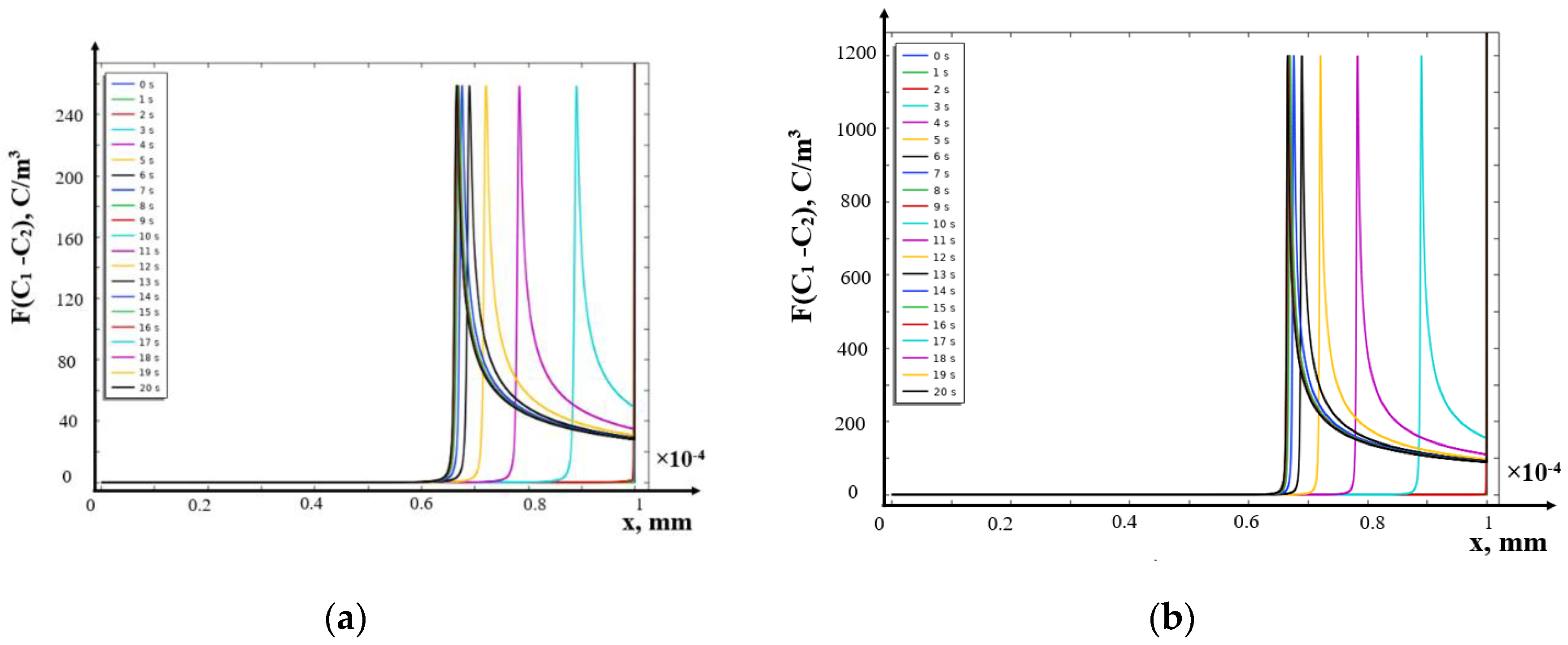
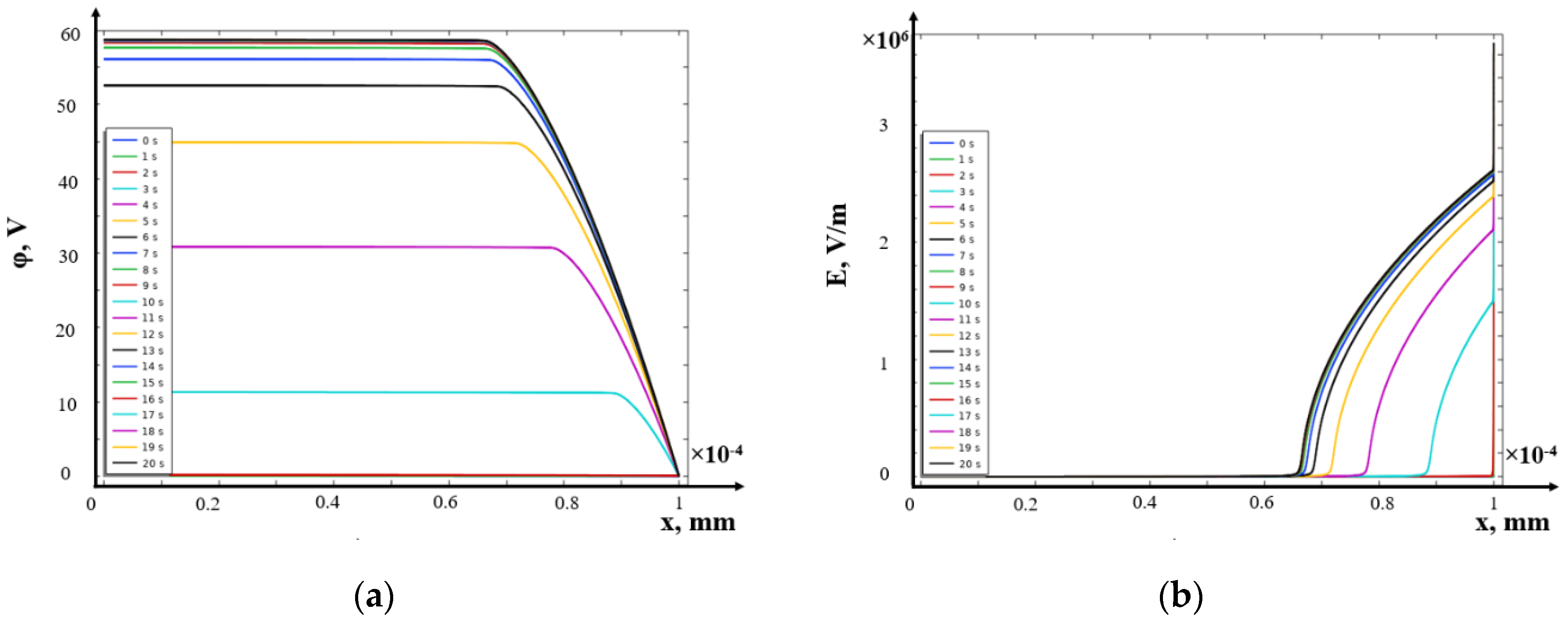
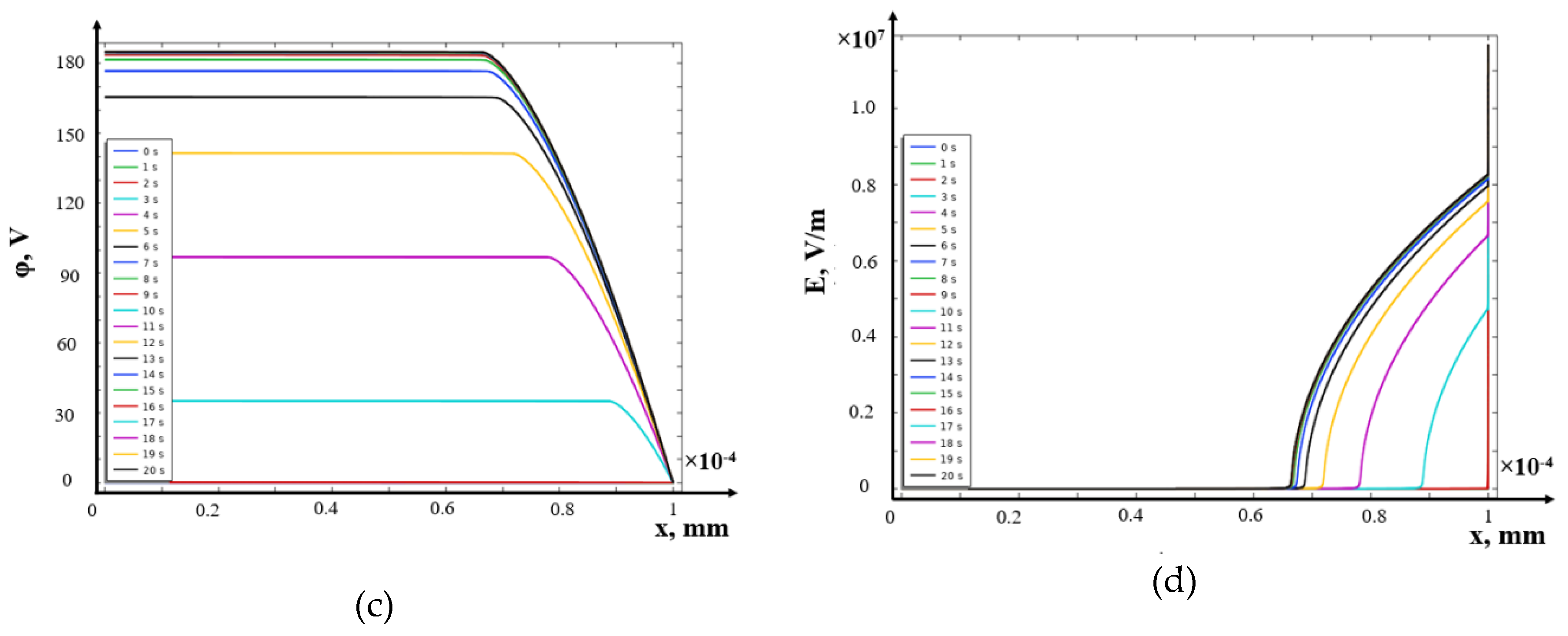

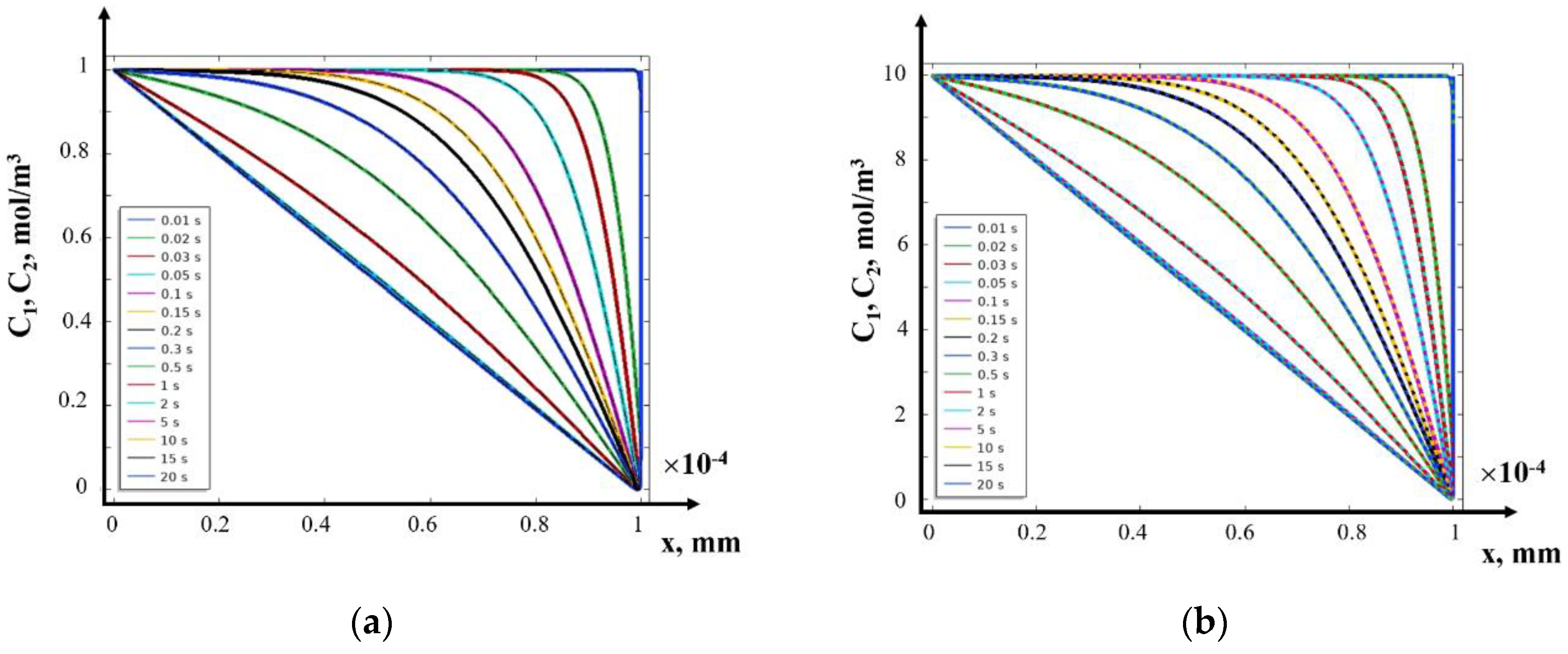
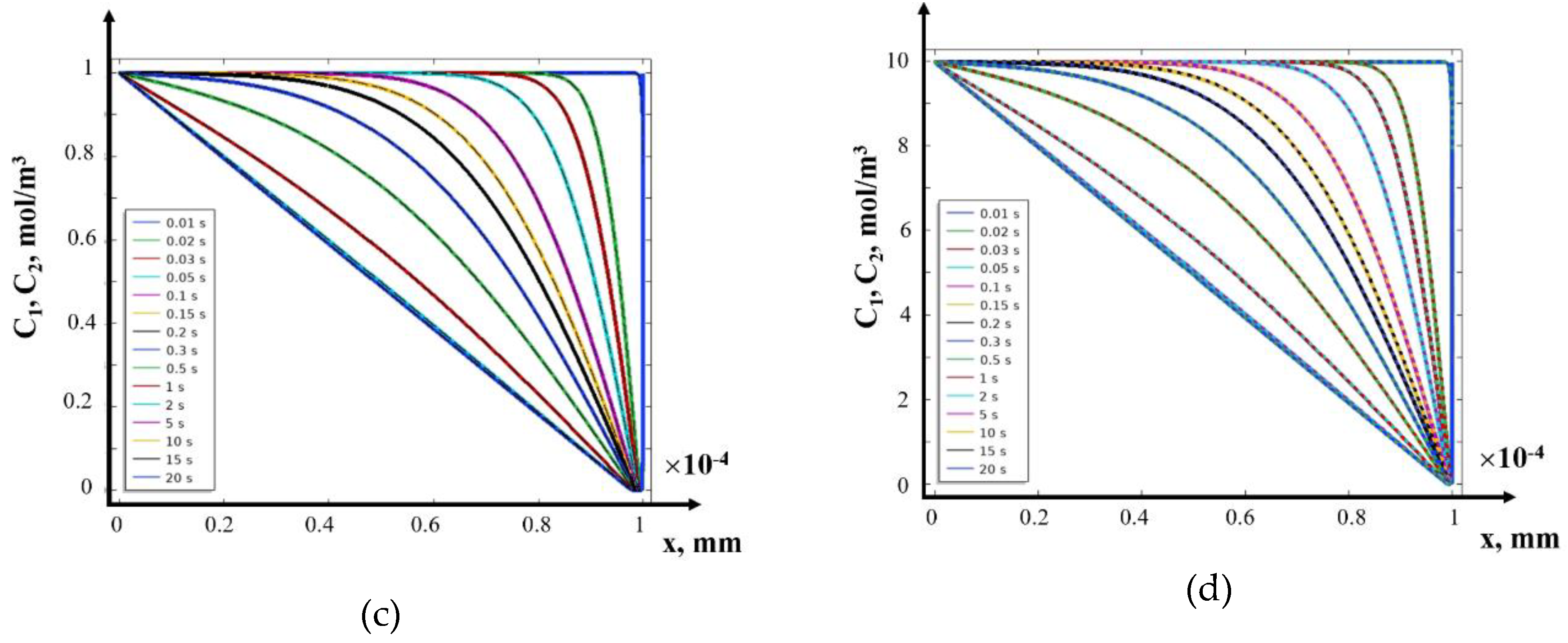
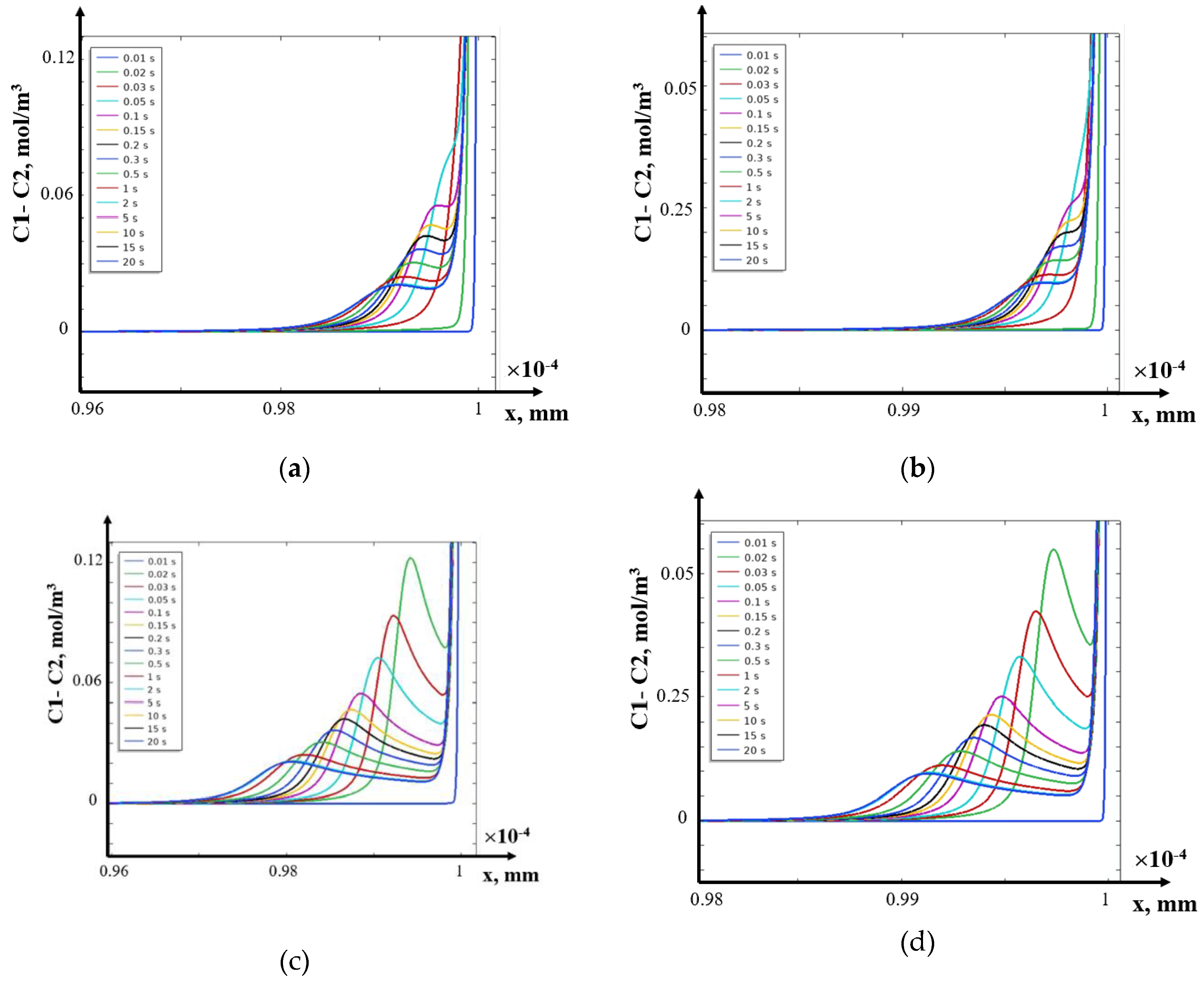
8. Solution in the Field of Electroneutrality
9. Derivation of the Equation for the Potential in the SCR of the CEM
10. Analytical Solution of the Equation for inside the region
11. Reduction of the Equation for in the SCR to an Auxiliary Linear Differential Equation of Parabolic Type
12. Diffusion Layer of an Anion Exchange Membrane (AEM). Derivation of the Equation for the Potential in the SCR at the AEM
13. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Jasielec, J.J. Electrodiffusion Phenomena in Neuroscience and the Nernst–Planck–Poisson Equations. Electrochem 2021, 2, 197–215. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, L.; Zhang, M. Studies on Ionic Flows via Poisson–Nernst–Planck Systems with Bikerman’s Local Hard-Sphere Potentials under Relaxed Neutral Boundary Conditions. Mathematics 2024, 12, 1182. [Google Scholar] [CrossRef]
- Jérôme Cartailler. Asymptotic of Poisson-Nernst-Planck equations and application to the voltage distribution in cellular micro-domains. Analysis of PDEs [math.AP]. Université Pierre et Marie Curie - Paris VI, 2017. English. ffNNT : 2017PA066297ff. fftel-02366969f.
- Sun, L.; Liu, W. Non-localness of Excess Potentials and Boundary Value Problems of Poisson–Nernst–Planck Systems for Ionic Flow: A Case Study. J. Dyn Diff Equat 2018, 30, 779–797. [Google Scholar] [CrossRef]
- Chao, Z.; Xie, D. An improved Poisson-Nernst-Planck ion channel model and numerical studies on effects of boundary conditions, membrane charges, and bulk concentrations. J. Comput. Chem. 2021, 42(27), 1929. [Google Scholar] [CrossRef]
- Liu, H.; Wang, Z. A free energy satisfying discontinuous Galerkin method for one-dimensional Poisson–Nernst–Planck systems. Journal of Computational Physics 2017, 328, 413–437. [Google Scholar] [CrossRef]
- Gwecho, A.; Shu, W. , Mboya, O. and Khan, S. Solutions of Poisson-Nernst Planck Equations with Ion Interaction. Applied Mathematics 2022, 13, 263–281. [Google Scholar] [CrossRef]
- Kumar, P.; Rubinstein, S.M.; Rubinstein, I. and Zaltzman, B. Mechanisms of hydrodynamic instability in concentration polarization. Phys. Rev. Research 2020, 2, 033365. [Google Scholar] [CrossRef]
- Rubinstein, I.; Zaltzman, B. Electroconvection in electrodeposition: Electrokinetic regularization mechanisms of shortwave instabilities. Phys. Rev. Fluids 2024, 9, 053701. [Google Scholar] [CrossRef]
- Lebedev, K.A.; Zabolotsky, V.I.; Vasil’eva, V.I.; Akberova, E.M. Mathematical modelling of vortex structures in the channel of an electrodialysis cell with ion-exchange membranes of different surface morphology. Condensed Matter and Interphases 2022, 24(4), 483–495. [Google Scholar] [CrossRef]
- Nikonenko, V.V.; Kovalenko, A.V.; Urtenov, M.K.; Pismenskaya, N.D.; Han, J.; Sistat, P.; Pourcelly, G. Desalination at overlimiting currents: State-of-the-art and perspectives. Desalination 2014, 342, 85–106. [Google Scholar] [CrossRef]
- Kovalenko, A.V.; Nikonenko, V.V.; Chubyr, N.O.; Urtenov, M.K. Mathematical modeling of electrodialysis of a dilute solution with accounting for water dissociation-recombination reactions. Desalination 2023, 24(4), 483–495. [Google Scholar] [CrossRef]
- Deng, D.; Aouad, W.; Braff, W.A.; Schlumpberger, S.; Suss, M.E.; Bazant, M.Z. Water purification by shock electrodialysis: Deionization, filtration, separation, and disinfection. Desalination 2015, 357, 77–83. [Google Scholar] [CrossRef]
- Tian, H.; Alkhadra, M.A.; Bazant, M.Z. Theory of shock electrodialysis I: Water dissociation and electrosmotic vortices. Journal of Colloid and Interface Science 2021, 589, 606–615. [Google Scholar] [CrossRef] [PubMed]
- Rybalkina, O.; Solonchenko, K.; Chuprynina, D.; Pismenskaya, N.; Nikonenko, V. Effect of Pulsed Electric Field on the Electrodialysis Performance of Phosphate-Containing Solutions. Membranes 2022, 12, 1107. [Google Scholar] [CrossRef]
- Gorobchenko, A.; Mareev, S.; Nikonenko, V. Mathematical Modeling of the Effect of Pulsed Electric Field on the Specific Permselectivity of Ion-Exchange Membranes. Membranes 2021, 11(2), 115. [Google Scholar] [CrossRef]
- Nichka, V.; Mareev, S.; Pismenskaya, N.; Nikonenko, V.; Bazinet, L. Mathematical Modeling of the Effect of Pulsed Electric Field Mode and Solution Flow Rate on Protein Fouling during Bipolar Membrane Electroacidificaiton of Caseinate Solution. Membranes 2022, 12, 193. [Google Scholar] [CrossRef]
- Lemay, N.; Mikhaylin, S.; Mareev, S.; Pismenskaya, N.; Nikonenko, V.; Bazinet, L. How demineralization duration by electrodialysis under high frequency pulsed electric field can be the same as in continuous current condition and that for better performances? Journal of Membrane Science 2020, 603, 117878. [Google Scholar] [CrossRef]
- Mikhaylin, S.; Nikonenko, V.; Pourcelly, G.; Bazinet, L. Intensification of demineralization process and decrease in scaling by application of pulsed electric field with short pulse/pause conditions. Journal of Membrane Science 2014, 468, 389–399. [Google Scholar] [CrossRef]
- Uzdenova, A.M.; Kovalenko, A.V.; Urtenov, M.K.; Nikonenko, V.V. Effect of electroconvection during pulsed electric field electrodialysis. Numerical experiments. Electrochemistry Communications 2015, 51, 1–5. [Google Scholar] [CrossRef]
- Sistat, P.; Huguet, P.; Ruiz, B.; Pourcelly, G.; Mareev, S.A.; Nikonenko, V.V. Effect of pulsed electric field on electrodialysis of a NaCl solution in sub-limiting current regime. Electrochimica Acta 2015, 164, 267–280. [Google Scholar] [CrossRef]
- Karlin, Y.V.; Kropotov, V.N. Electrodialysis separation of Na+ and Ca2+ in a pulsed current mode. Russ. J. Electrochem. 1995, 31(5), 472–476. [Google Scholar]
- Mishchuk, N.A.; Koopal, L.K.; Gonzalez-Caballero, F. Intensification of electrodialysis by applying a non-stationary electric field. Colloids Surf. A: Physicochem. Eng. Asp. 2001, 176(2-3), 195–212. [Google Scholar] [CrossRef]
- Dufton, G.; Mikhaylin, S.; Gaaloul, S.; Bazinet, L. Positive impact of pulsed electric field on lactic acid removal, demineralization and membrane scaling during acid whey electrodialysis. Int. J. Mol. Sci. 2019, 20(4), 797. [Google Scholar] [CrossRef] [PubMed]
- Newman, J. The polarized diffuse double layer. Trans Faraday Soc 1966, 61, 2229–2237. [Google Scholar] [CrossRef]
- Uzdenova, A.M.; Kovalenko, A.V.; Urtenov, M.K.; Nikonenko, V.V. Theoretical Analysis of the Effect of Ion Concentration in Solution Bulk and at Membrane Surface on the Mass Transfer at Overlimiting Currents. Russian Journal of Electrochemistry 2017, 53(11), 1254–1265. [Google Scholar] [CrossRef]
- Urtenov, M.K.; Kovalenko, A.V.; Sukhinov, A.I.; Chubyr, N.O.; Gudza, V.A. Model and numerical experiment for calculating the theoretical current-voltage characteristic in electro-membrane systems. IOP Conference Series: Materials Science and Engineering 2019, 680(1), 012030. [Google Scholar] [CrossRef]
- Uzdenova, A.; Kovalenko, A.; Urtenov, M.; Nikonenko, V. 1D Mathematical Modelling of Non-Stationary Ion Transfer in the Diffusion Layer Adjacent to an Ion-Exchange Membrane in Galvanostatic Mode. Membranes 2018, 8(3), 84. [Google Scholar] [CrossRef]
- Uzdenova, A.; Urtenov, M. Mathematical Modeling of the Phenomenon of Space-Charge Breakdown in the Galvanostatic Mode in the Section of the Electromembrane Desalination Channel. Membranes 2021, 11, 873. [Google Scholar] [CrossRef]
- Uskov, V.I. Asymptotic solution of first-order equation with small parameter under the derivative with perturbed operator. Tambov University Reports. Series: Natural and Technical Sciences 2018, 23(124), 784–796, (In Russian, Abstr. in Engl.).. [Google Scholar] [CrossRef]
- Vasil'eva, A.B.; Butuzov, V.F. Singularly perturbed equations in critical cases. M: −Moscow University, 1978, p.106.
- Doolan, E.R.; Miller, J.J.H.; Schilders, W.H.A. , Uniform Numerical Methods for Problems with Initial and Boundary Layers, Boole Press, Dublin, 1980. 324 p.
- Listovnichy, A.V. Concentration polarization of the ionite membrane-electrolyte solution system in the overlimiting mode. Electrochemistry. 1991, 27, 316–323. [Google Scholar]
- Grafov, B.M.; Chernenko, A.A. The theory of the passage of a direct current through a solution of binary electrolyte. Dokl. Akad. Nauk SSSR 1962, 153, 1110–1113. [Google Scholar]
- Nikonenko, V.V.; Urtenov, M.K. Analysis of electrodiffusion equations in the decomposition form. Russian Journal of Electrochemistry 1996, 32(2), 187–194. [Google Scholar]
- Nikonenko, V.V.; Urtenov, M.K. On a generalization of the electroneutrality condition. Russian Journal of Electrochemistry 1996, 32(2), 195–198. [Google Scholar]
- Kovalenko, S.A.; Urtenov, M.K. Asymptotic solution of the boundary value problem in the diffusion layer for the stationary system of Nernst – Planck – Poisson equations. Prospects of Science. 2024, 6(177), 105–113. [Google Scholar]
- Urtenov, M.; Chubyr, N.; Gudza, V. Reasons for the Formation and Properties of Soliton-Like Charge Waves in Membrane Systems When Using Overlimiting Current Modes. Membranes 2020, 10, 189. [Google Scholar] [CrossRef]
- Fletcher, C.A.J. Computational Techniques for Fluid Dynamics. Springer Verlag; Subsequent edition. 1991, 401 p.
- Ilʹin, A.M. Matching of Asymptotic Expansions of Solutions of Boundary Value Problems. American Mathematical Society. 1992. 281 p.
- Matveev, V.B.; Salle, M.A. Darboux Transformations and Solitons, Springer-Verlag, Berlin, 1991.
- Kudryavtsev, A.G.; Sapozhnikov, O.A. Determination of the exact solutions to the inhomogeneous Burgers equation with the use of the darboux transformation. Acoust. Phys. 2011, 57, 311–319. [Google Scholar] [CrossRef]
- Kushner, A.G.; Matviichuk, R.I. Exact solutions of the Burgers–Huxley equation via dynamics. Journal of Geometry and Physics 2020, 151, 103615. [Google Scholar] [CrossRef]
- Ryskin, N.M.; Trubetskov, D. Nonlinear Waves. 2000. Fizmatlit, Moscow. 296 p.
- Trubetskov, D.I.; McHedlova, E.S.; Anfinogentov, V.G.; Ponomarenko, V.I.; Ryskin, N.M. Nonlinear waves, chaos and patterns in microwave electronic devices. Chaos. 1996, 6(3), 358–367. [Google Scholar] [CrossRef]
| 1 | ionistor (supercapacitor, ultracapacitor, double-layer electrochemical capacitor) is an electrochemical device, a capacitor with an electrolyte, the "plates" of which are a double electric layer at the interface of the electrolyte solution/ion-exchange membrane. The typical capacity of an ionistor is several farads at a nominal voltage of 2-10 volts |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




