Median Based Unit Weibull (MBUW): A New Unit Distribution Properties

Iman Attia

doi:10.20944/preprints202410.1985.v1

Submitted:

24 October 2024

Posted:

25 October 2024

You are already at the latest version

Abstract

A new 2 parameter unit Weibull distribution is defined on the unit interval (0,1). The methodology of deducing its PDF, some of its properties and related functions are discussed. The paper is supplied by many figures illustrating the new distribution and how this can make it illegible to fit a wide range of skewed data. The new distribution holds a name (Attia) as a nickname.

Keywords:

Median Based Unit Weibull (MBUW) distribution

;

new distribution

;

unit distribution

Subject:

Computer Science and Mathematics - Probability and Statistics

Introduction

Waloddi Weibull (Weibull, 1951) was the first to introduce the Weibull distribution. It is one of the famous distributions used to model life data and reliability. It can describe the increasing failure rate cases as well as the decreasing failure rate cases. The exponential distribution is a special case of it, when the shape parameter is one. Rayleigh distribution is another special case of it, when the shape parameter is 2. It can also describe and explain the life expectancy of the elements entailed in the fatigue derived failure and can also evaluate the electron tube reliability and load handling machines. It is used in many fields like medicine, physics, engineering, biology, and quality control. As the distribution does not represent a bathtub or unimodal shapes (Gül, 2023), this enforces many researchers to generalize and transform this distribution in the recent decades. To mention some of these researchers:, (Singla et al., 2012) elucidated beta generalized weibull, (Khan et al., 2017) described in details the transmuted weibull, (Xie et al., 2002) explored the modified weibull, (Lee et al., 2007) clearly explained the beta weibull, (Cordeiro et al., 2010) demonstrated Kumaraswamy weibull, (Silva et al., 2010) expounded beta modified weibull, (Mudholkar & Srivastava, 1993) expatiated the exponentiated weibull, (Zhang & Xie, 2011) interpreted truncated weibull, (Khan & King, 2013) explicated transmuted modified weibull, and (Marshall & Olkin, 1997) handled the extended weibull.

Many distributions were defined on unit interval by many authors. Some of these distributions are:

1): Johnson S_B distribution (Johnson, 1949).
2): Beta distribution (Eugene et al., 2002).
3): Unit Johnson (S_U ) distribution (Gündüz & Korkmaz, 2020).
4): Topp- Leone distribution (Topp & Leone, 1955).
5): Unit Gamma (Consul & Jain, 1971; Grassia, 1977; Mazucheli et al., 2018b; Tadikamalla, 1981).
6): Unit Logistic distribution (Tadikamalla & Johnson, 1982).
7): Kumaraswamy distribution (Kumaraswamy, 1980).
8): Unit Burr-III (Modi & Gill, 2020).
9): Unit modified Burr-III (Haq et al., 2023).
10): Unit Burr-XII (Korkmaz & Chesneau, 2021).
11): Unit-Gompertz (Mazucheli, Maringa, et al., 2019).
12): Unit-Lindely (Mazucheli, Menezes, et al., 2019).
13): Unit-Weibull (Mazucheli et al., 2020).
14): Unit Muth distribution (Maya et al., 2024).

(Mazucheli et al., 2018a) proposed unit Weibull distribution to describe data on the unit interval like the real data he used describing maximum flood level and Petroleum reservoirs data. He proposed a quantile regression model for this unit weibull distribution and found that it sueprexceeded the competing distributions like the beta, Kumaraswamy, Unit Logistic, Simplex, Unit Gamma, Exponentiated Topp-Leone and Extended Arcsine. It has a closed form of the quantile function.

In this paper, another methodology is used to describe a new unit weibull distribution relying on the pdf of the median order statistics of a sample size n=3. The author will discuss the new unit 2 parameter distribution Median based unit Weibull (MBUW) and some of its basic properties. The author gave a nickname for the distribution (Attia) after the name of the author’s grandfather and for his memorial.

The paper is arranged into 2 sections. In Section 1, the author will explain the methodology of obtaining the new distribution. In Section 2, elaboration of its PDF, CDF, Survival function, Hazard function and reversed hazard function will be presented.

Section 1

Methodology

Derivation of the MBUW Distribution

Using the pdf of median order statistics of a sample size=3 and parent distribution Weibull, both the scale parameter alpha and shape parameter beta are positive.

f_{i : n} (x) = \frac{n!}{(i - 1)! (n - i)!} {\{F (x)\}}^{i - 1} {\{1 - F (x)\}}^{n - i} f (x), x > 0 f_{2 : 3} (x) = \frac{3!}{(2 - 1)! (3 - 1)!} {\{F (x)\}}^{2 - 1} {\{1 - F (x)\}}^{3 - 2} f (x), x > 0 F (x) = 1 - e^{{- (\frac{x}{α})}^{β}}, f (x) = {\frac{β}{α} (\frac{x}{α})}^{β - 1} e^{{- (\frac{x}{α})}^{β}}, x > 0, α & β > 0 f_{2 : 3} (x) = 3! {\{1 - e^{\frac{{- x}^{β}}{α^{β}}}\}}^{2 - 1} {\{e^{\frac{{- x}^{β}}{α^{β}}}\}}^{3 - 2} {\frac{β}{α} (\frac{x}{α})}^{β - 1} e^{{- (\frac{x}{α})}^{β}}, x > 0 f_{2 : 3} (x) = \frac{6 β x^{β - 1}}{α^{β}} [1 - e^{\frac{{- x}^{β}}{α^{β}}}] [e^{\frac{- 2 x^{β}}{α^{β}}}], x > 0, α & β > 0 f_{2 : 3} (x) = \frac{6 β x^{β - 1}}{α^{β}} [1 - e^{\frac{{- x}^{β}}{α^{β}}}] [e^{\frac{- 2 x^{β}}{α^{β}}}], x > 0, α & β > 0

Using the following transformation:

l e t y = e^{- x^{β}} - l n (y) = x^{β} {[- l n (y)]}^{\frac{1}{β}} = x \frac{d x}{d y} = {\frac{1}{β} [- l n (y)]}^{\frac{1 - β}{β}} (\frac{- 1}{y})

So the new distribution is the Median Based Unit Weibull (MBUW) Distribution.

Section 2

Some of the Properties of the New Distribution ( MBUW)

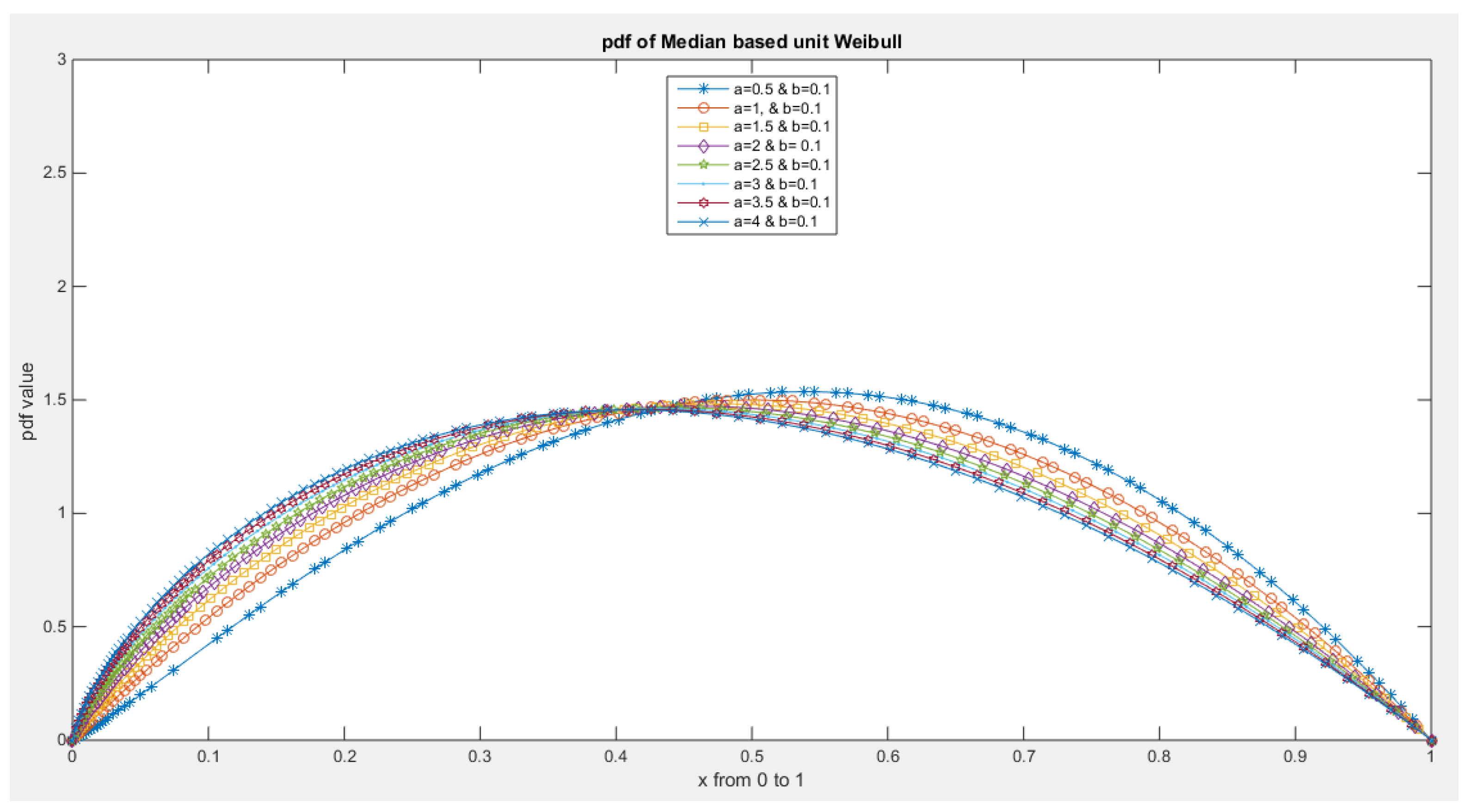
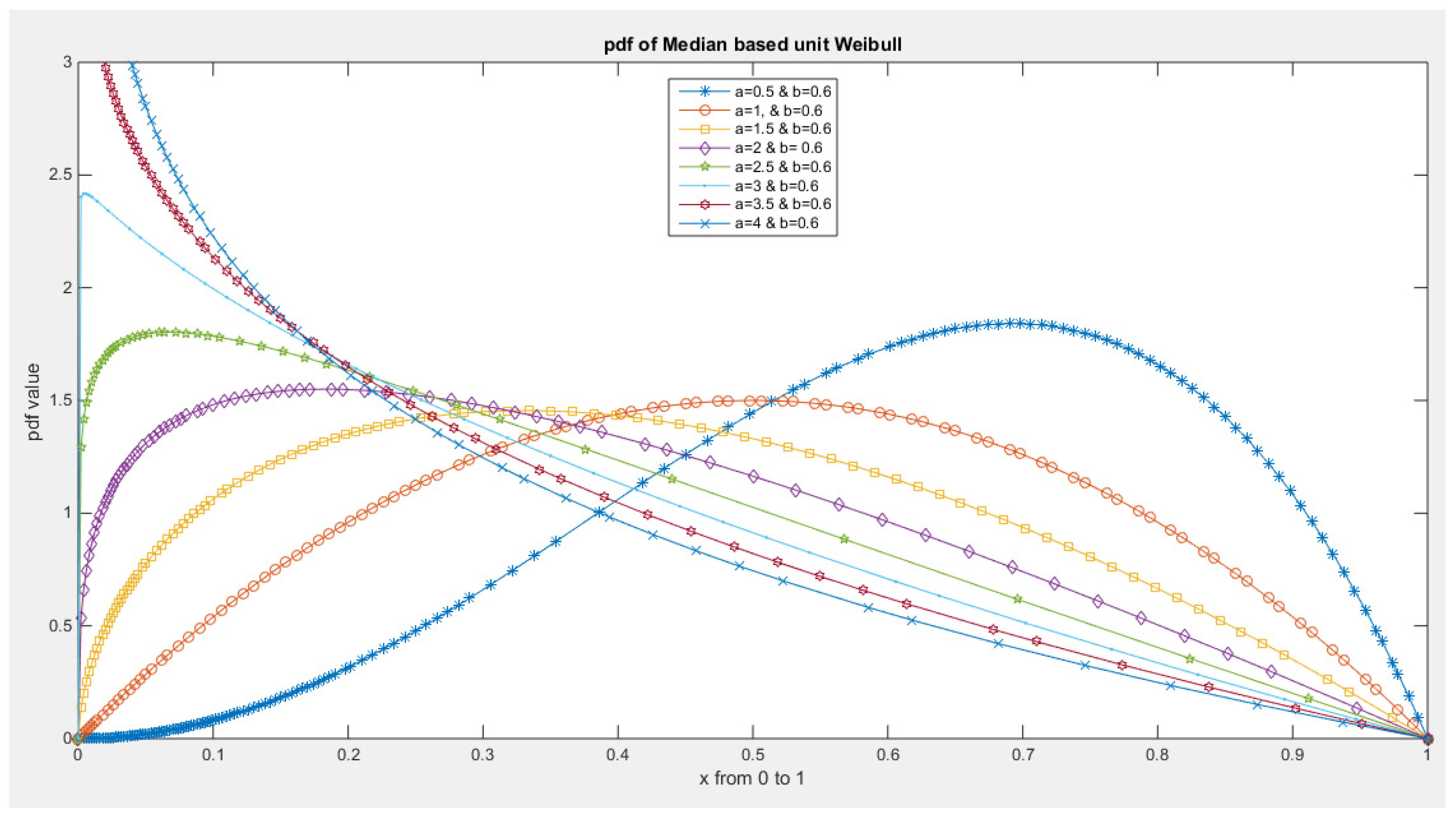
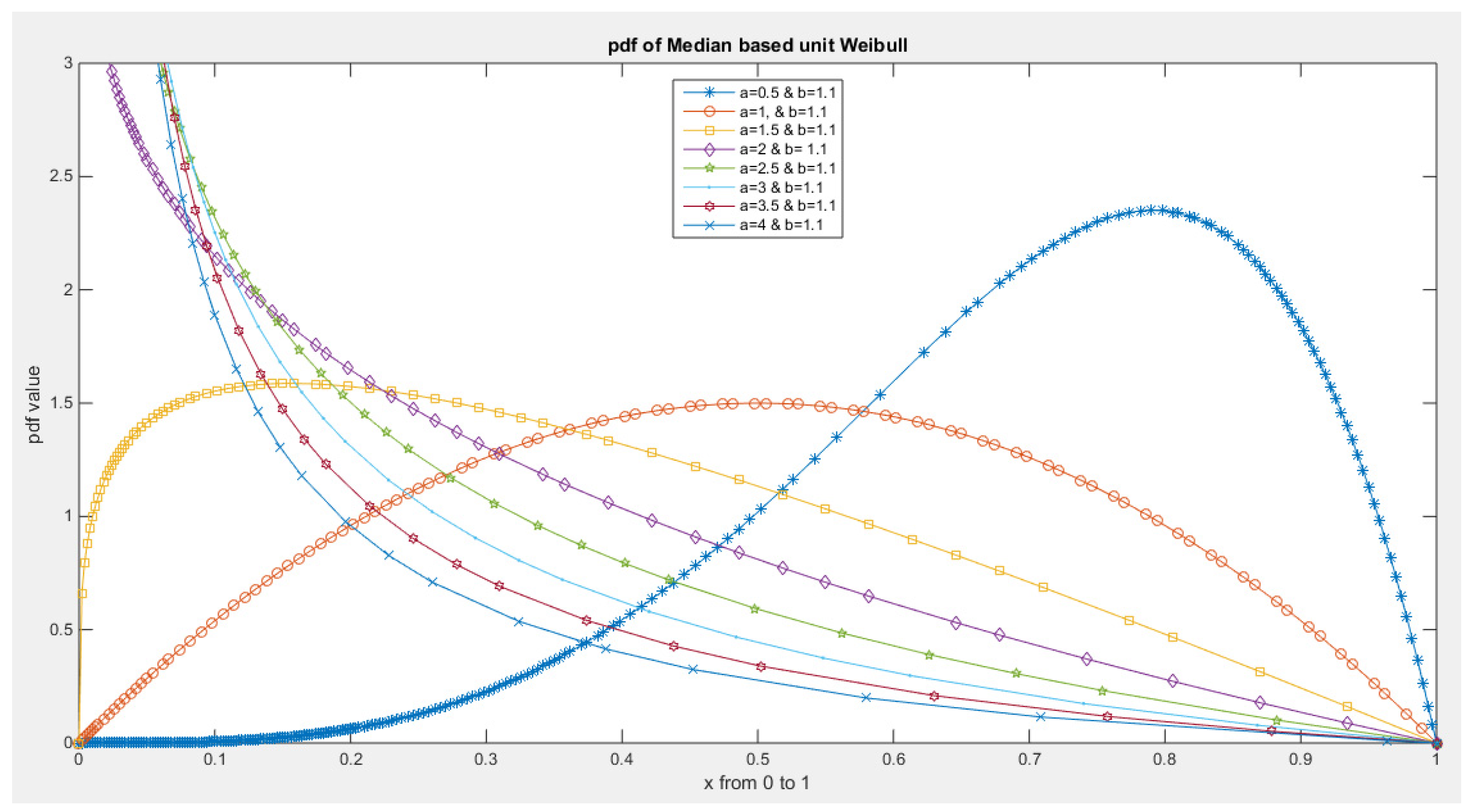
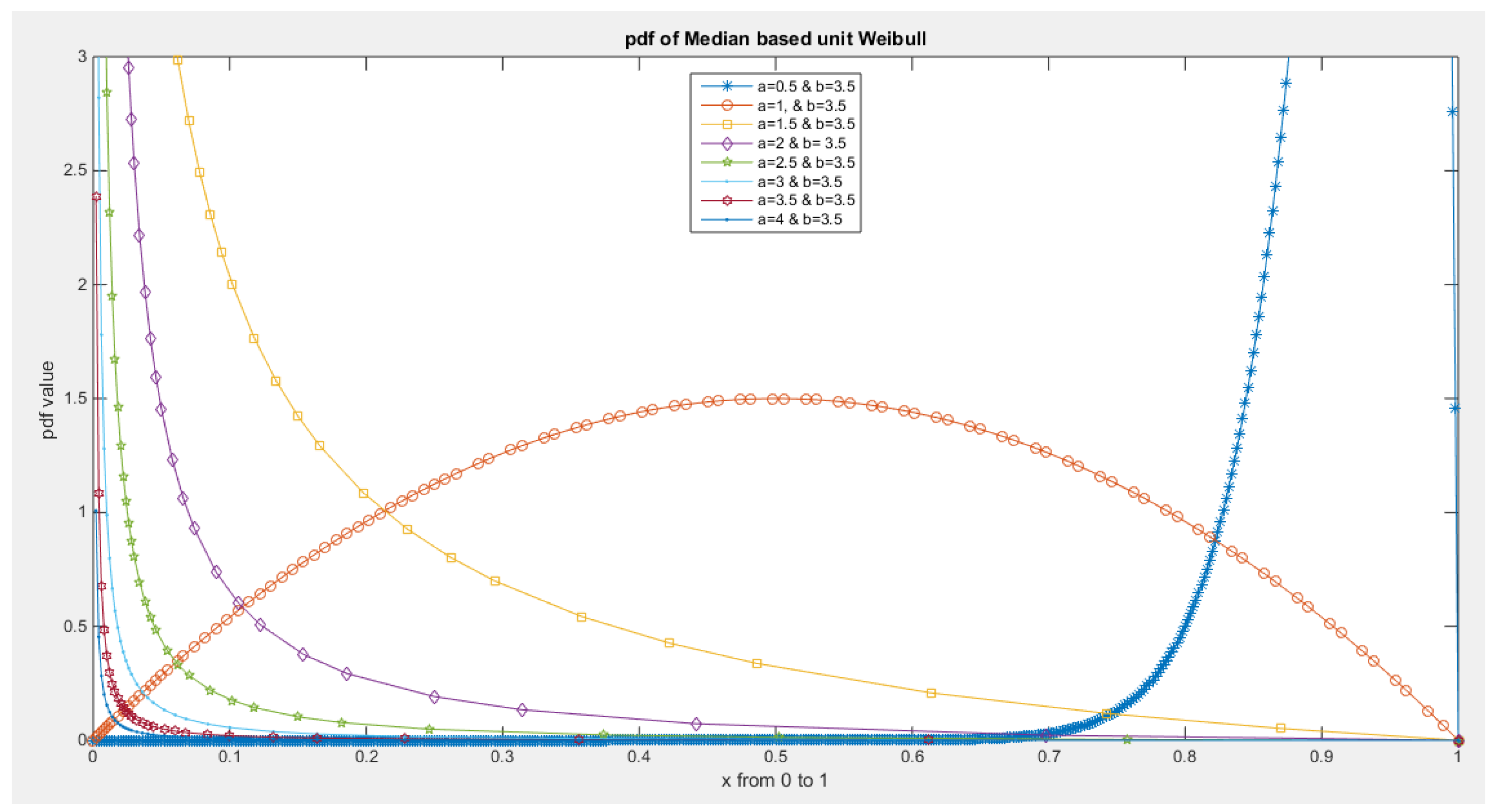
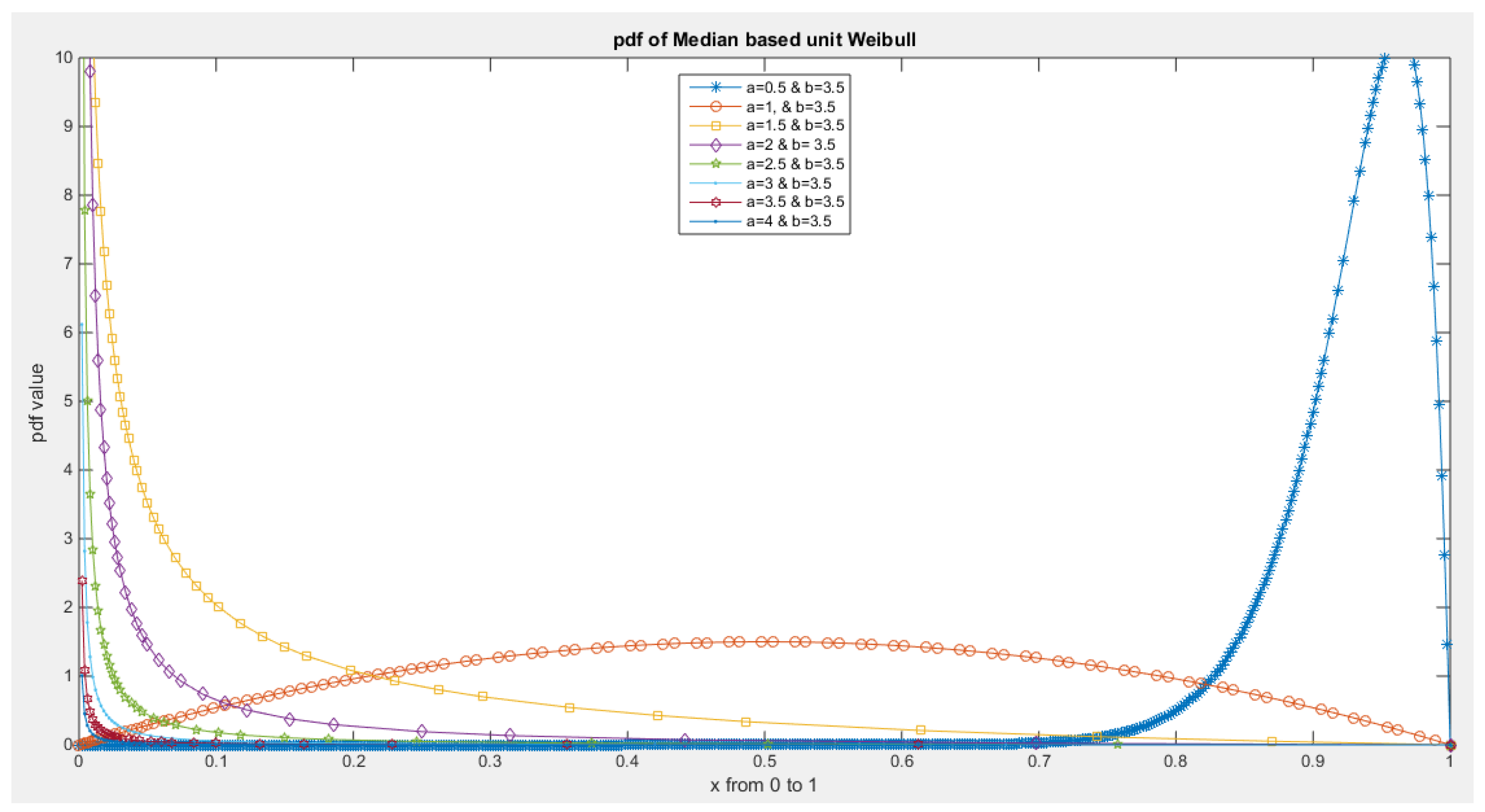
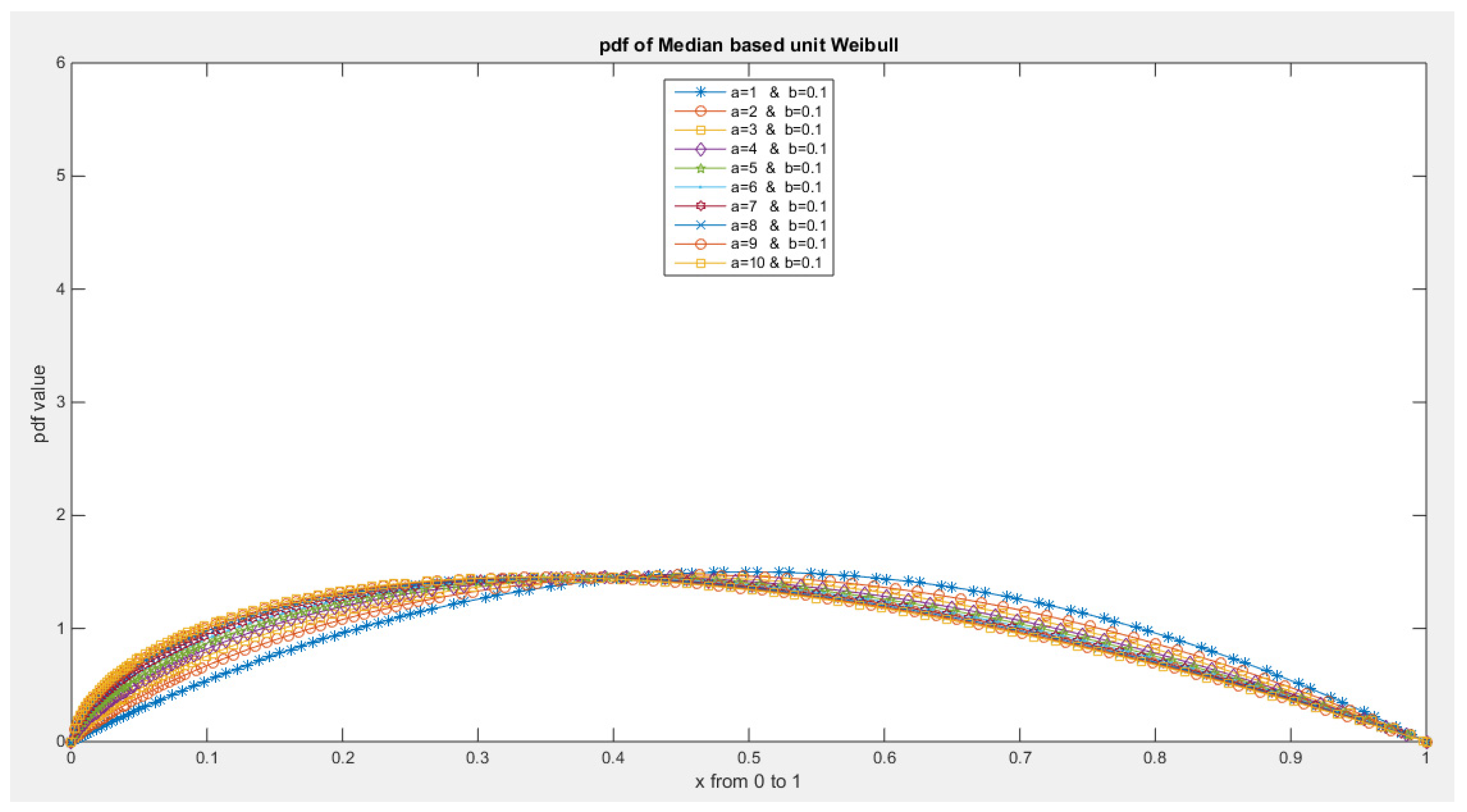
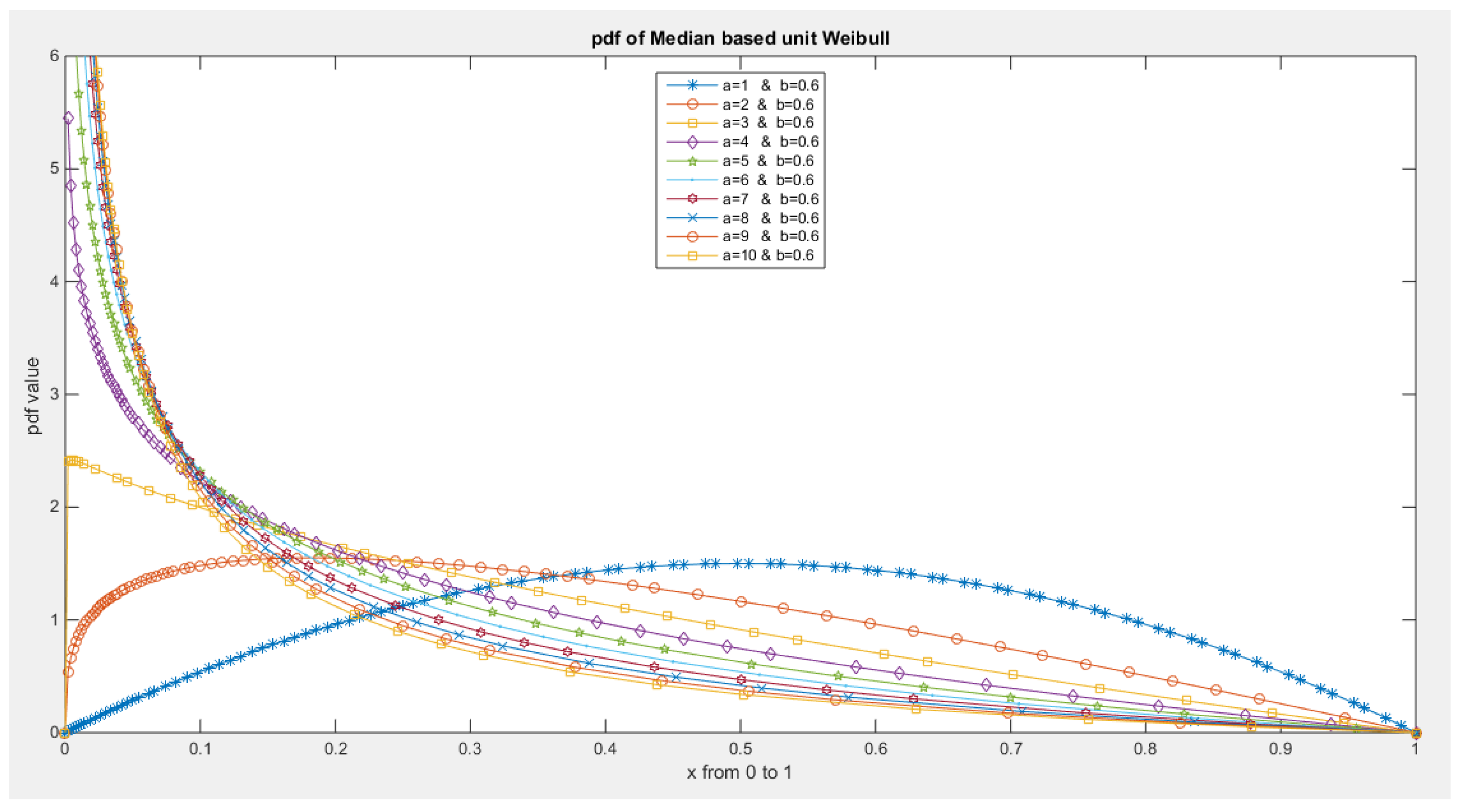
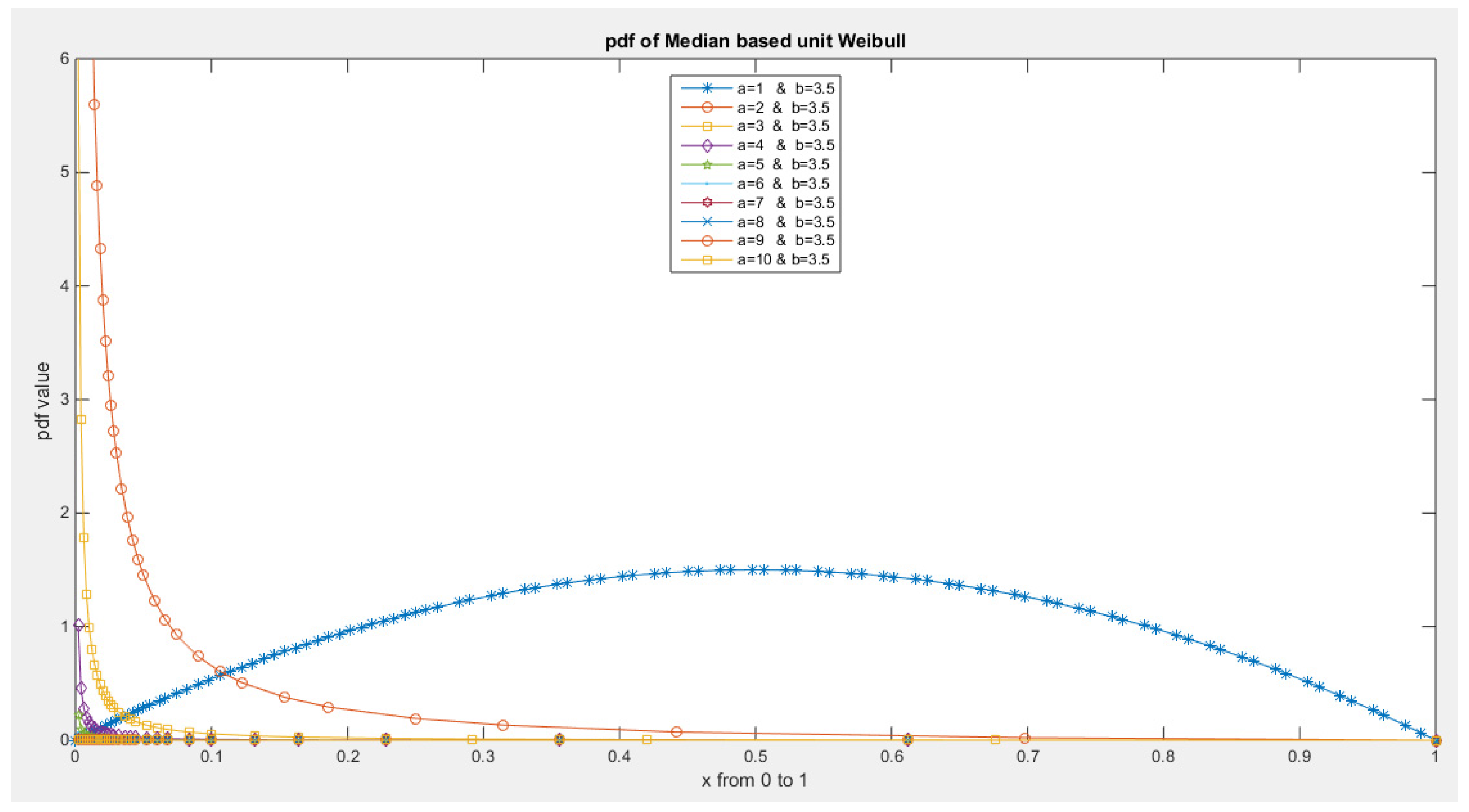
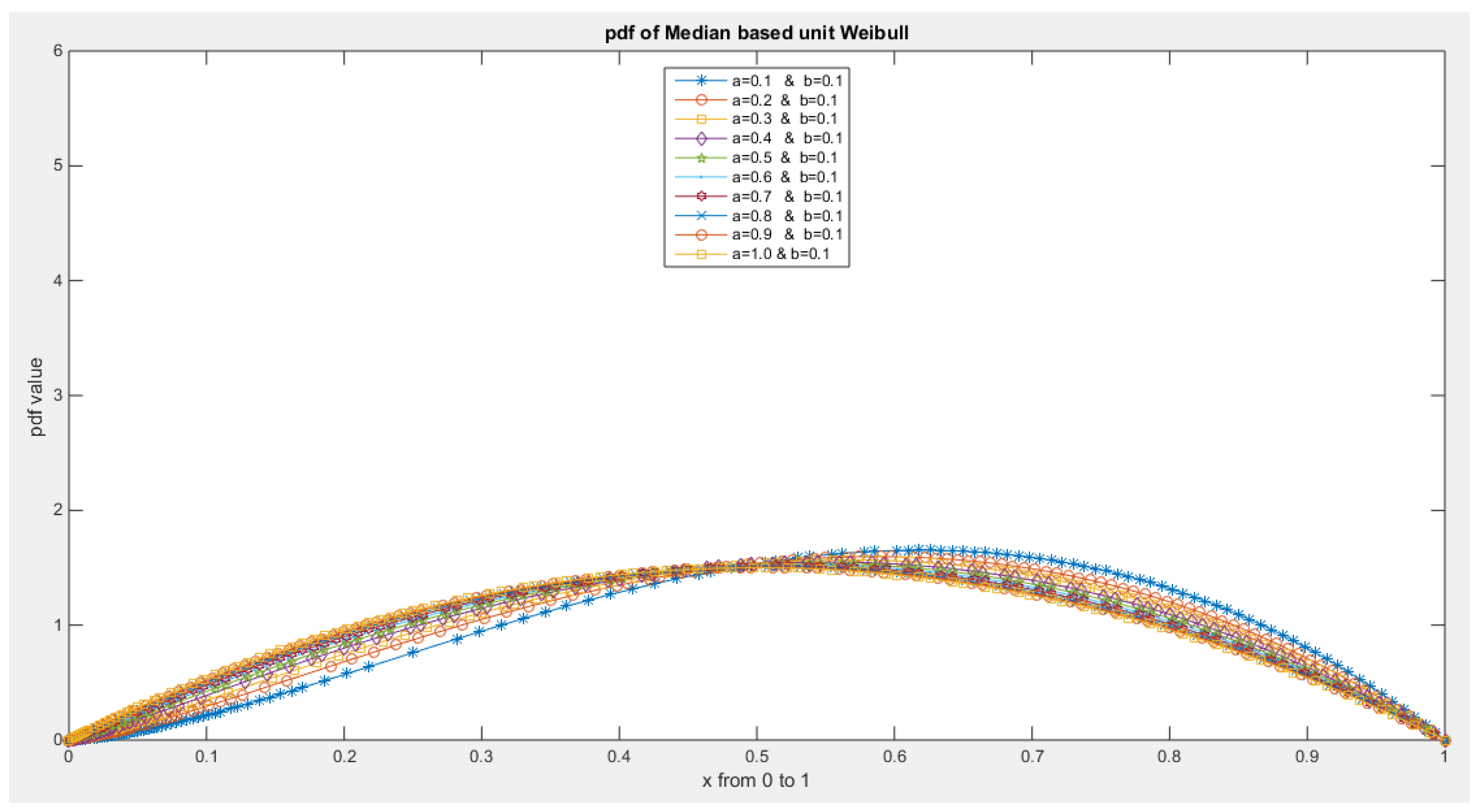
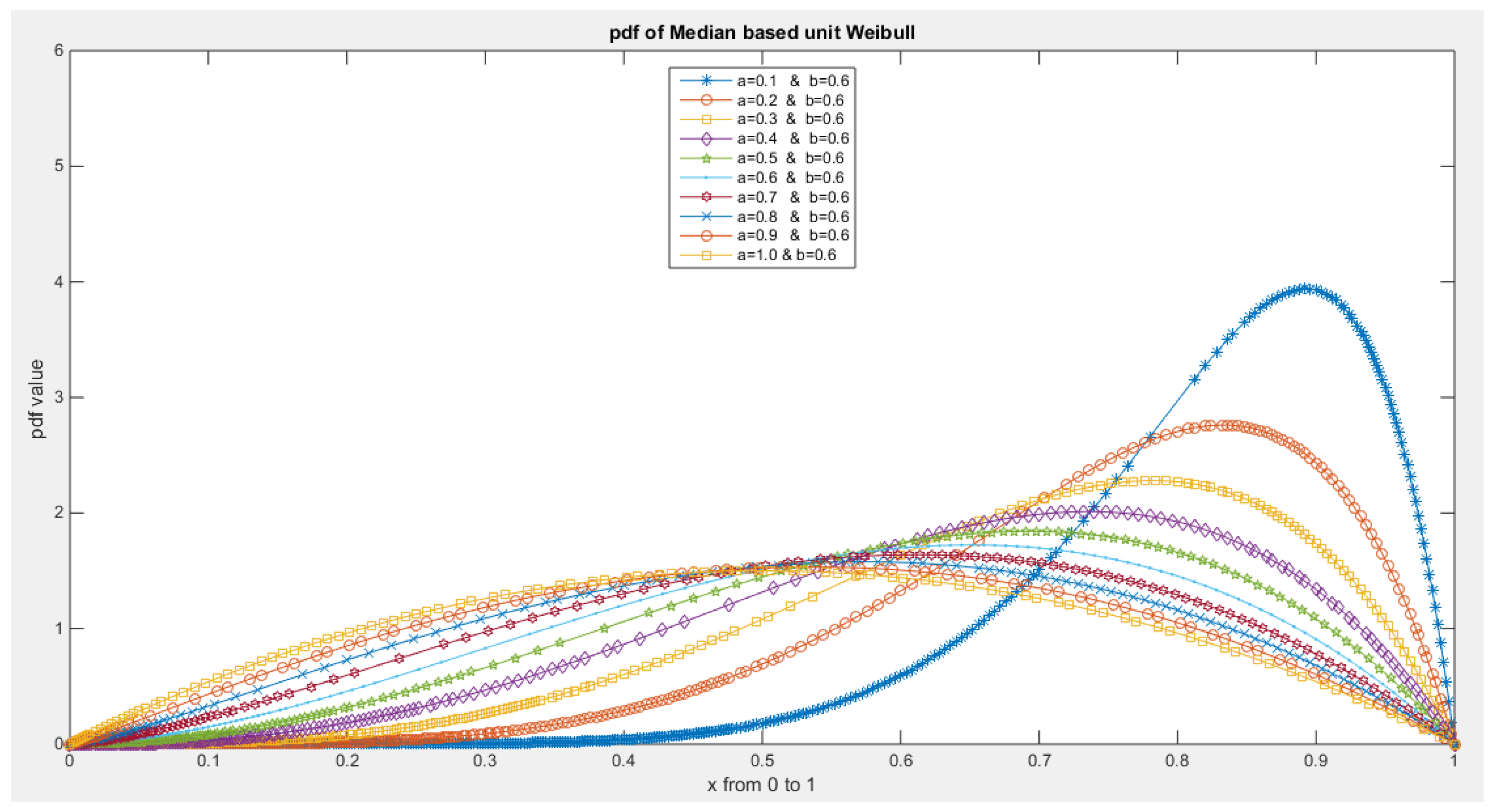
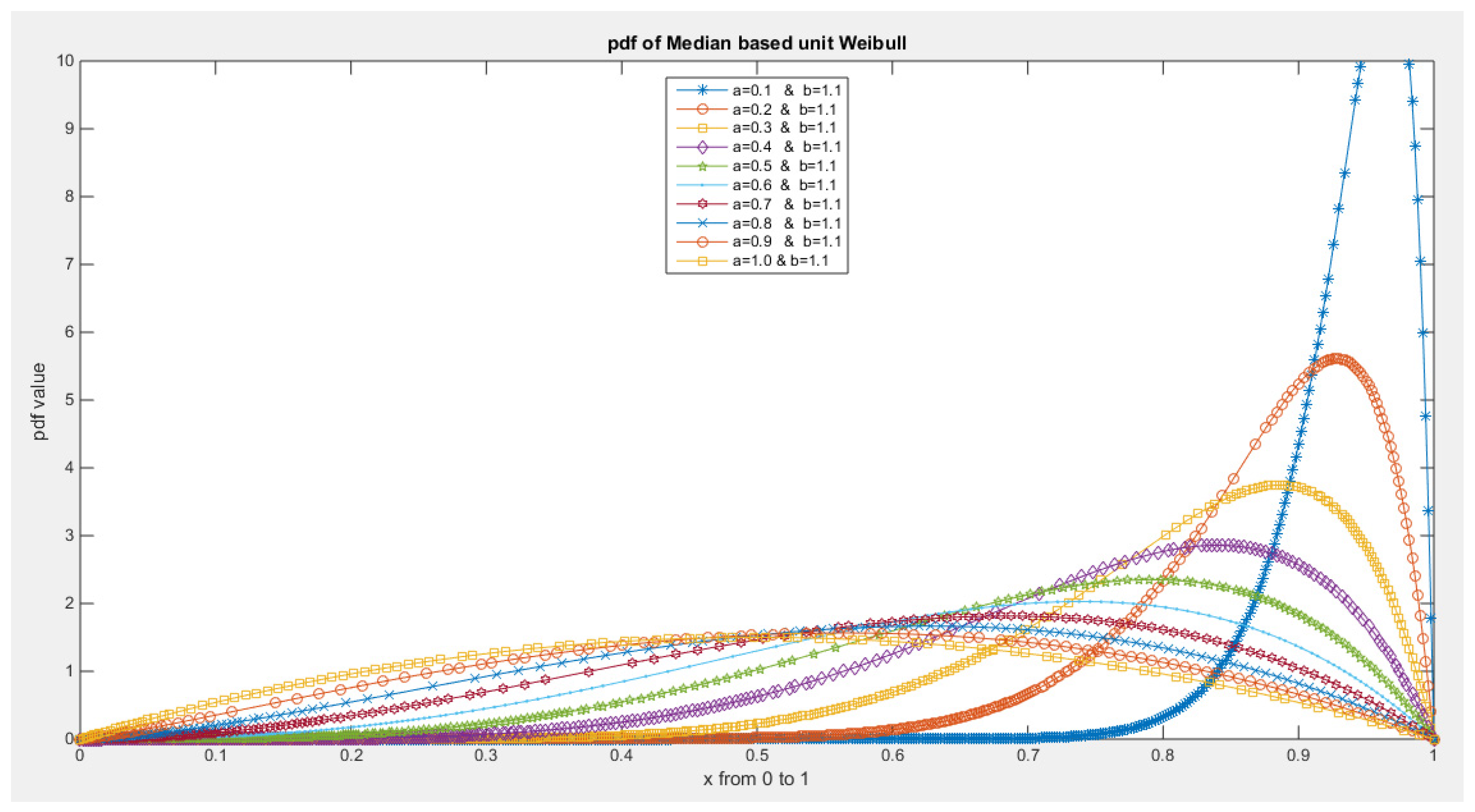
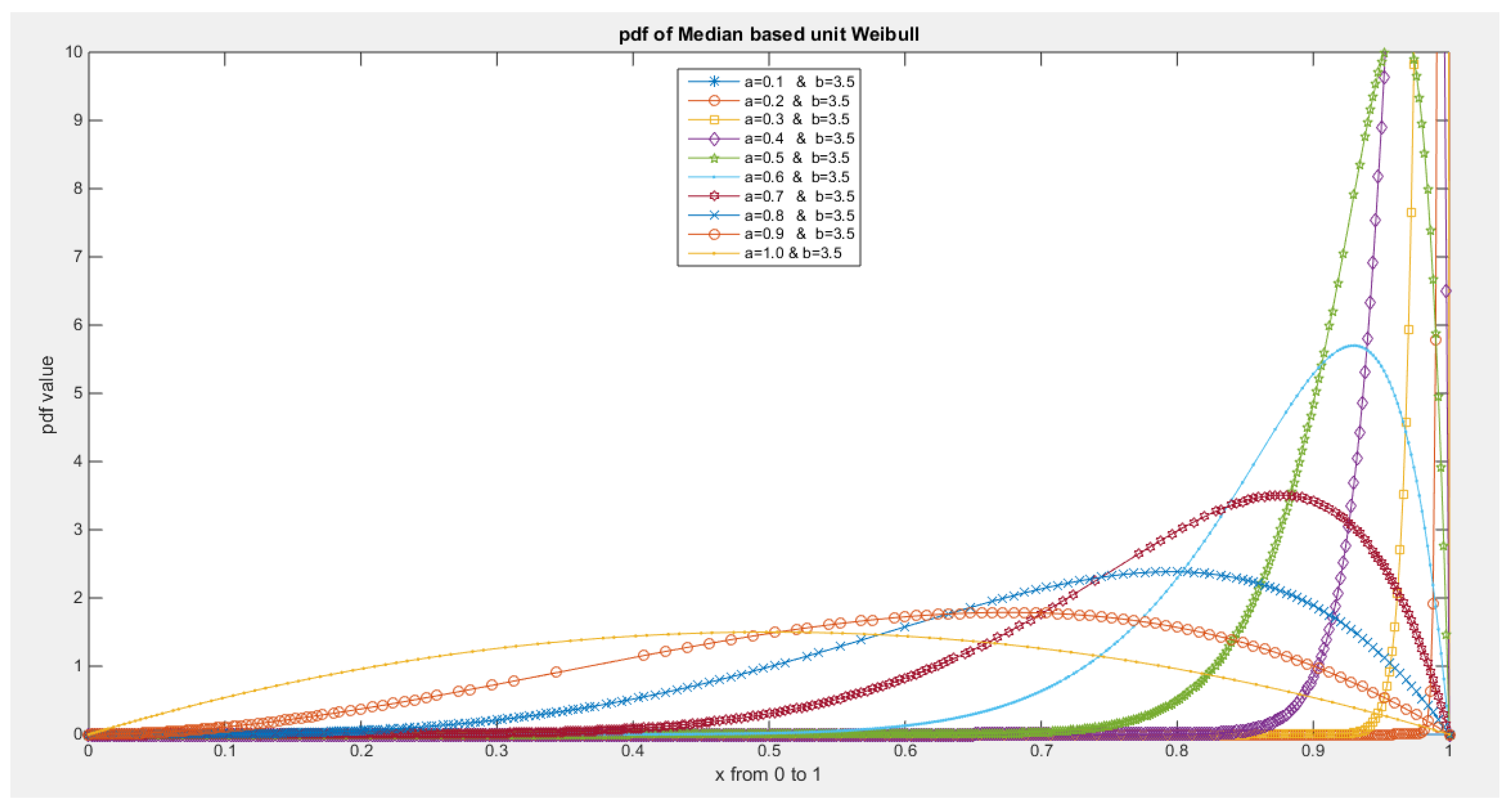
1-: The following is the pdf :

f (y) = \frac{6}{α^{β}} [1 - y^{\frac{1}{α^{β}}}] y^{(\frac{2}{α^{β}} - 1)}, 0 < y < 1, α > 0, β > 0

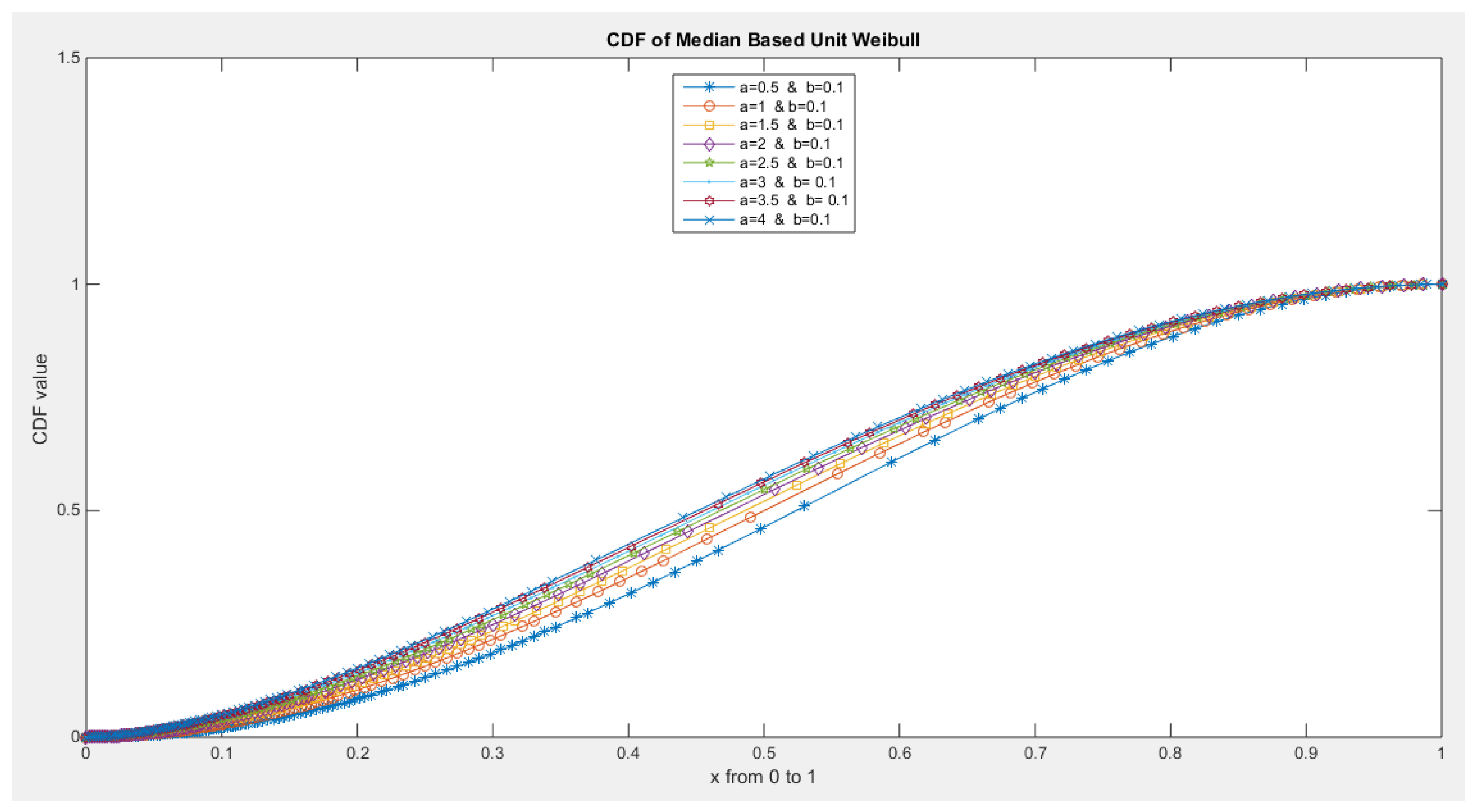
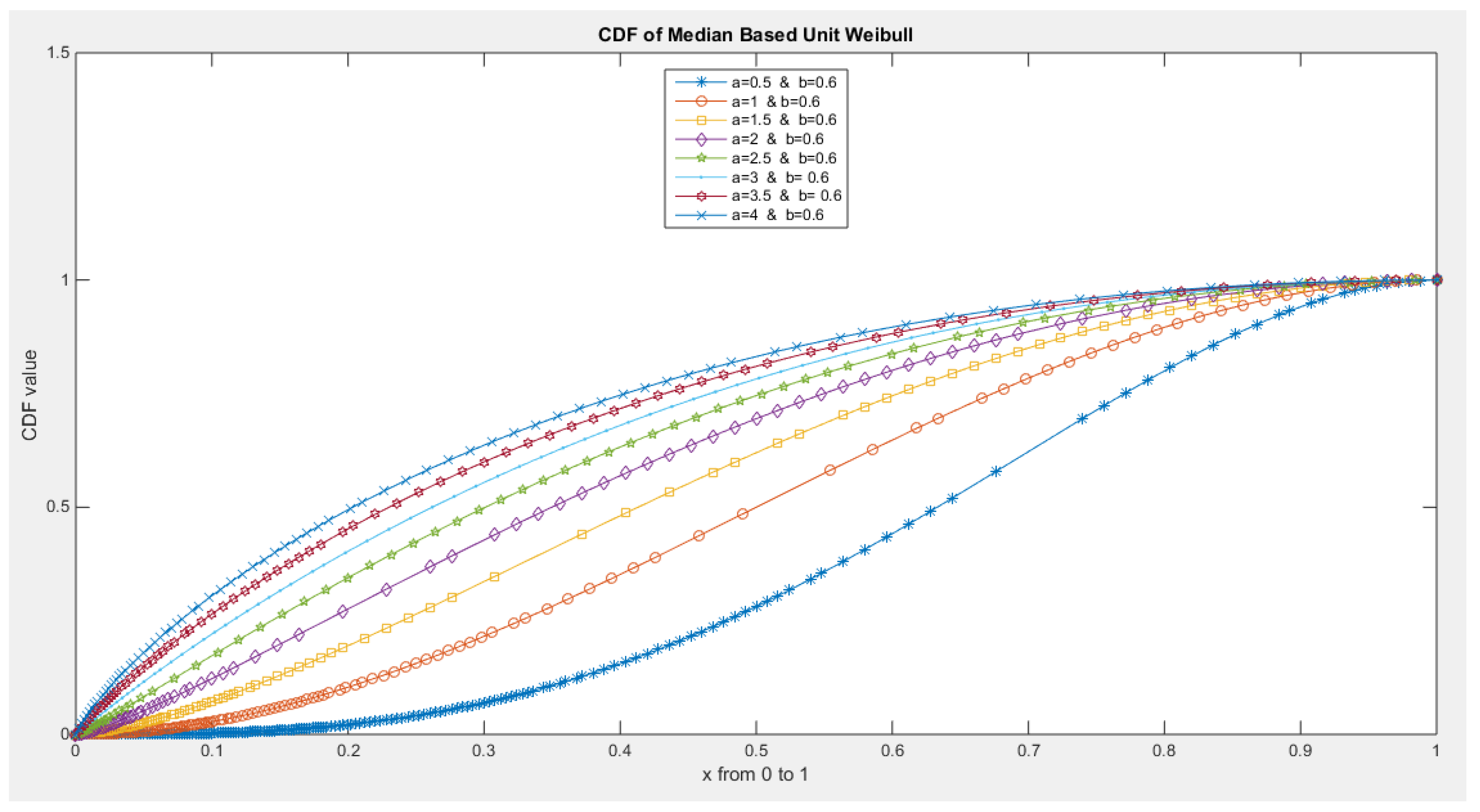
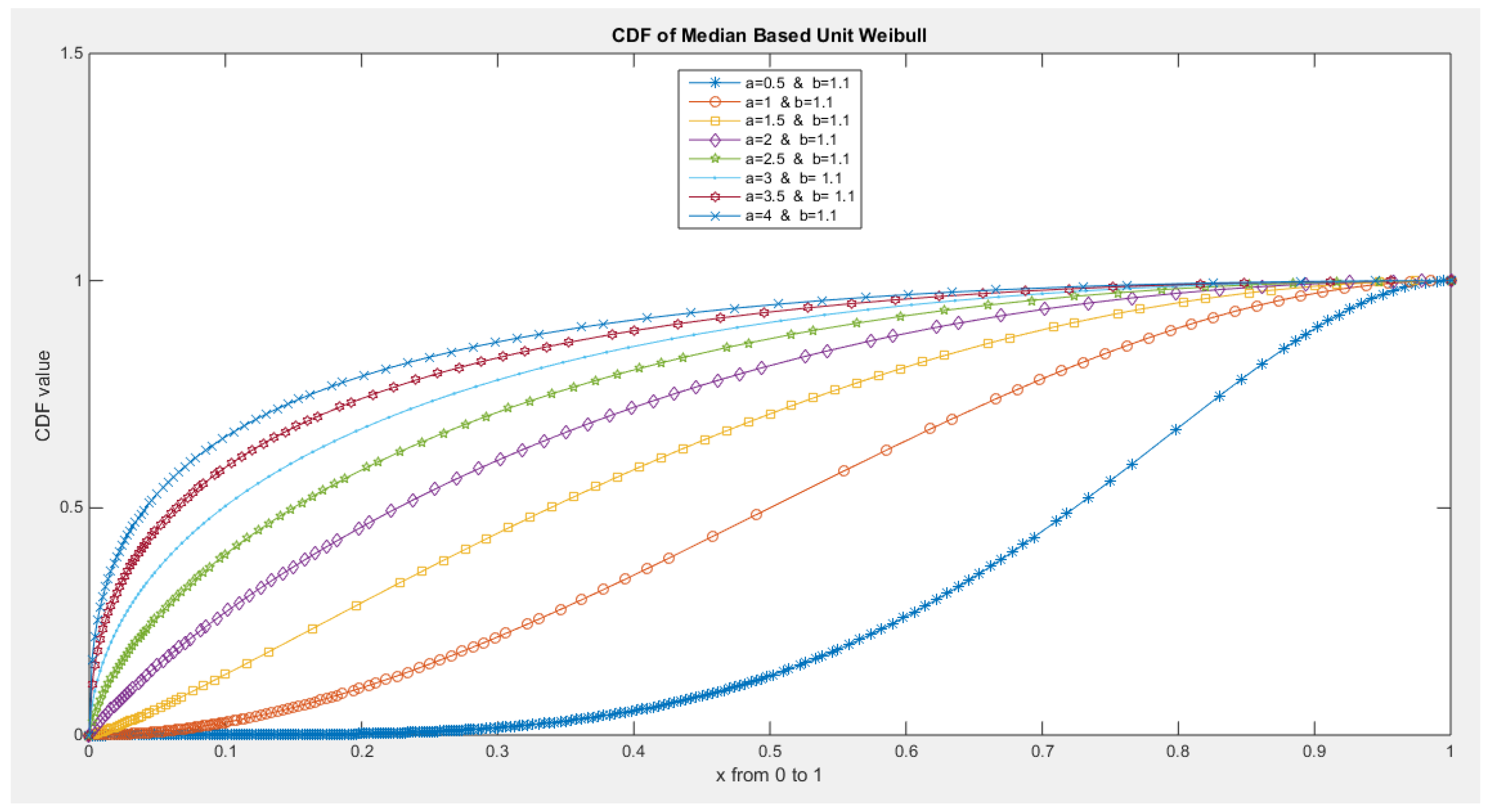
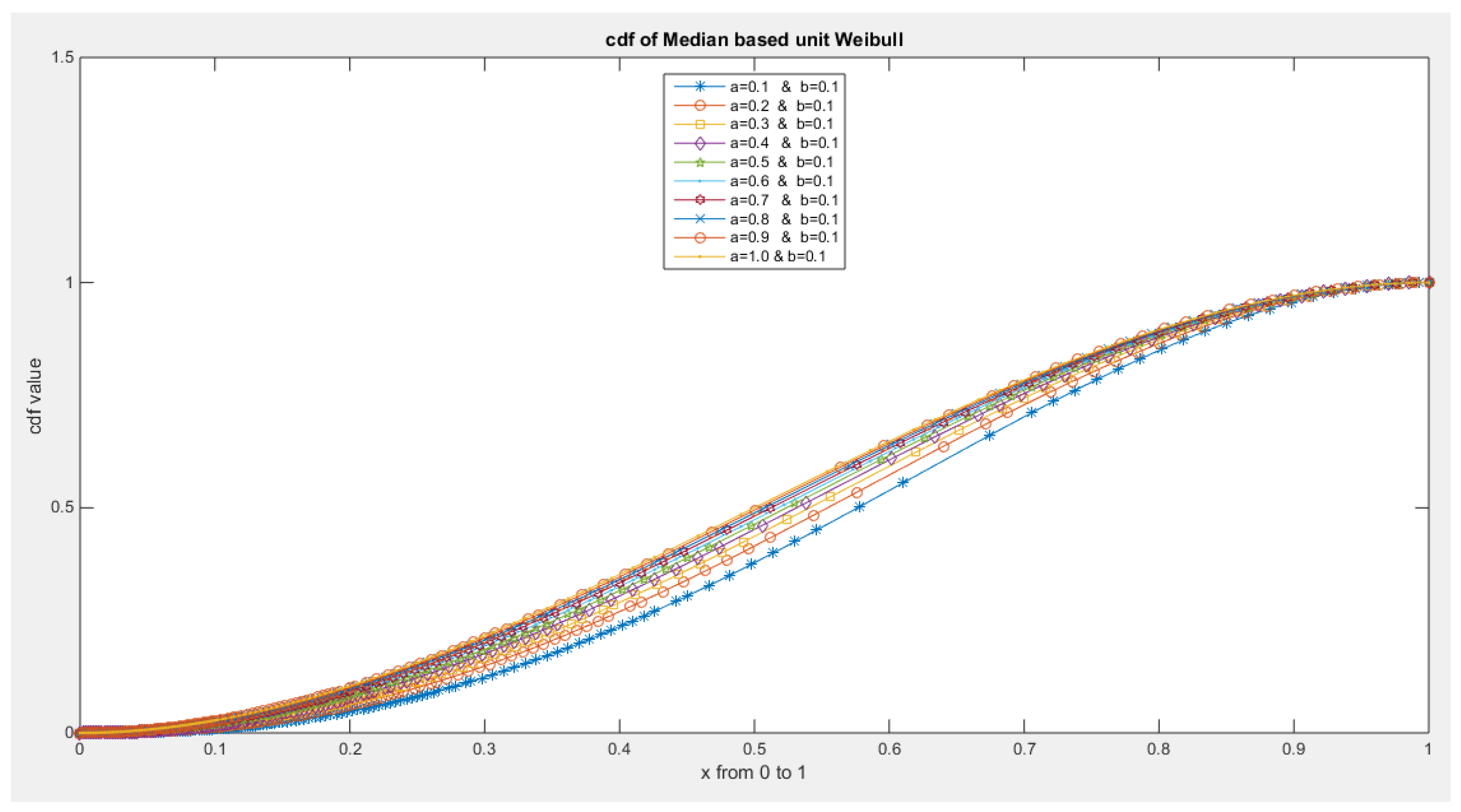
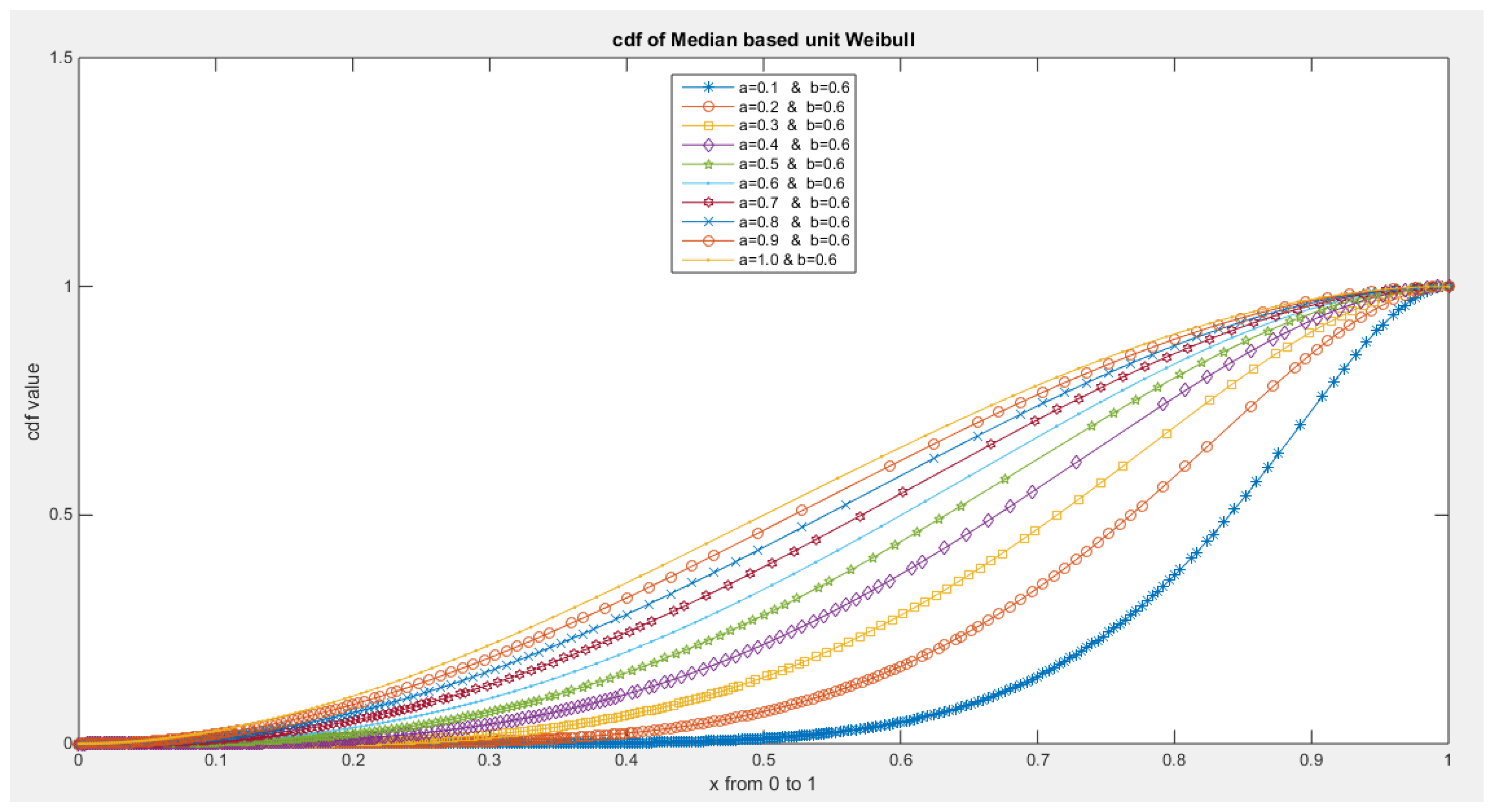
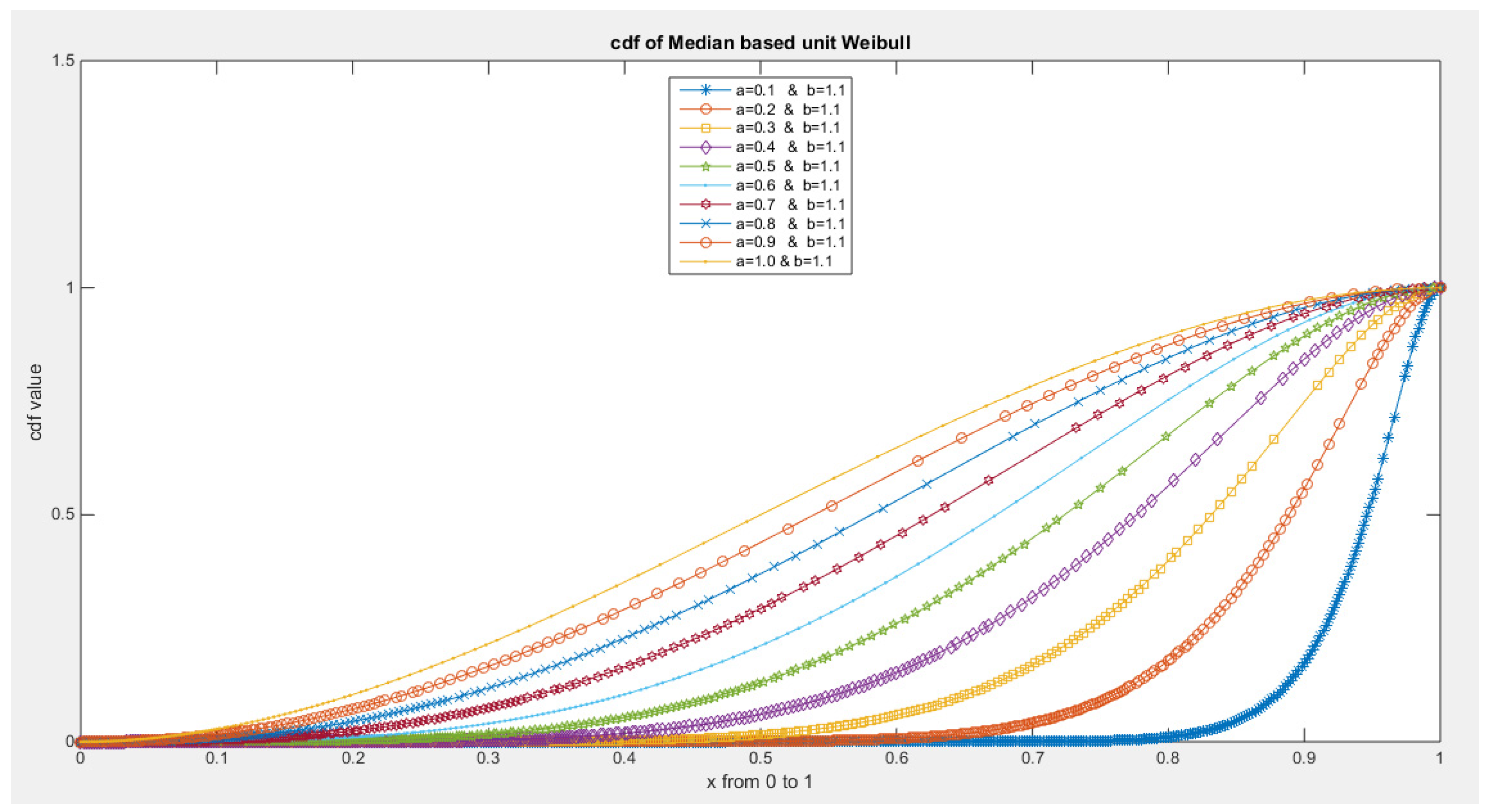
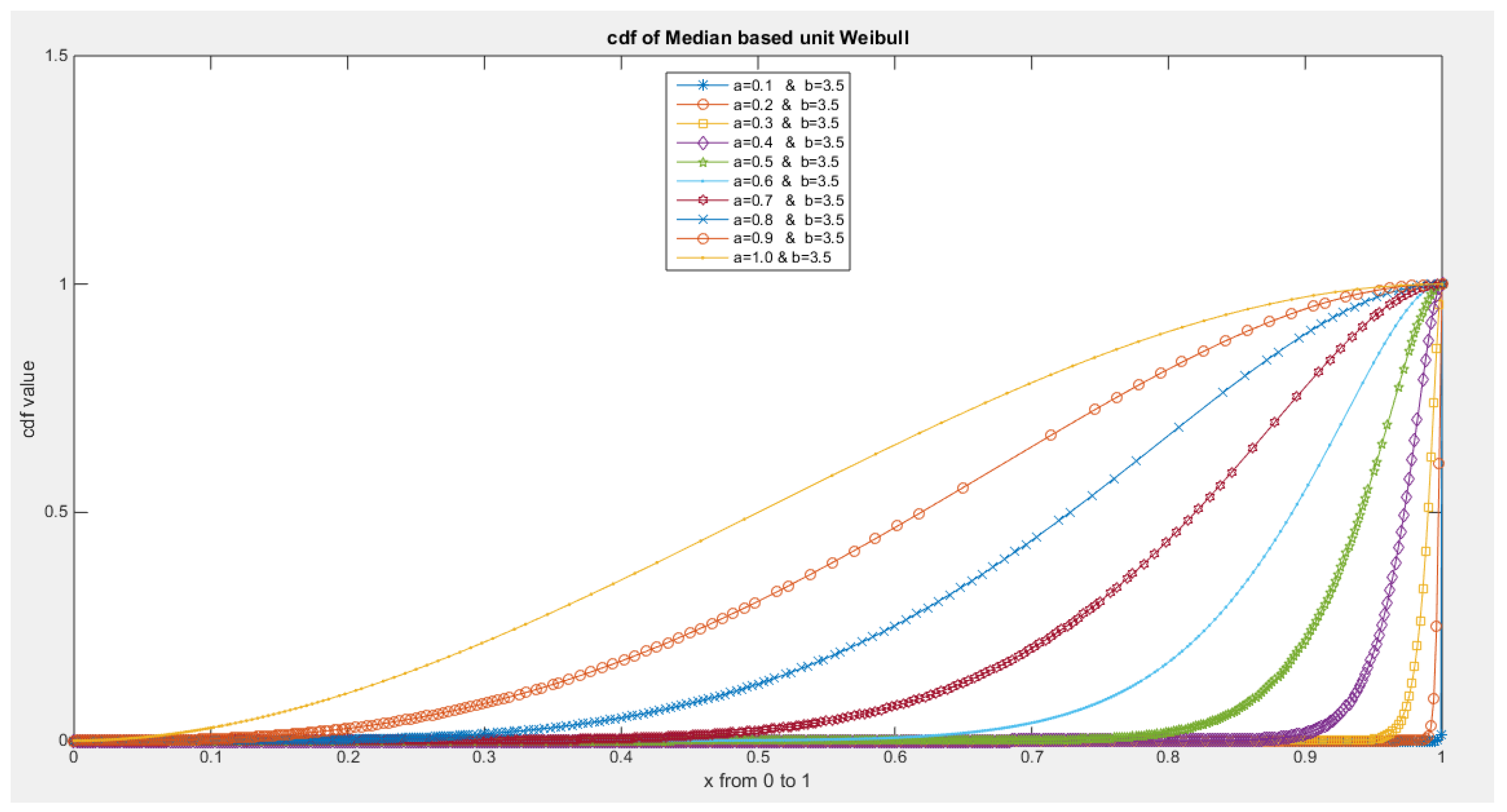
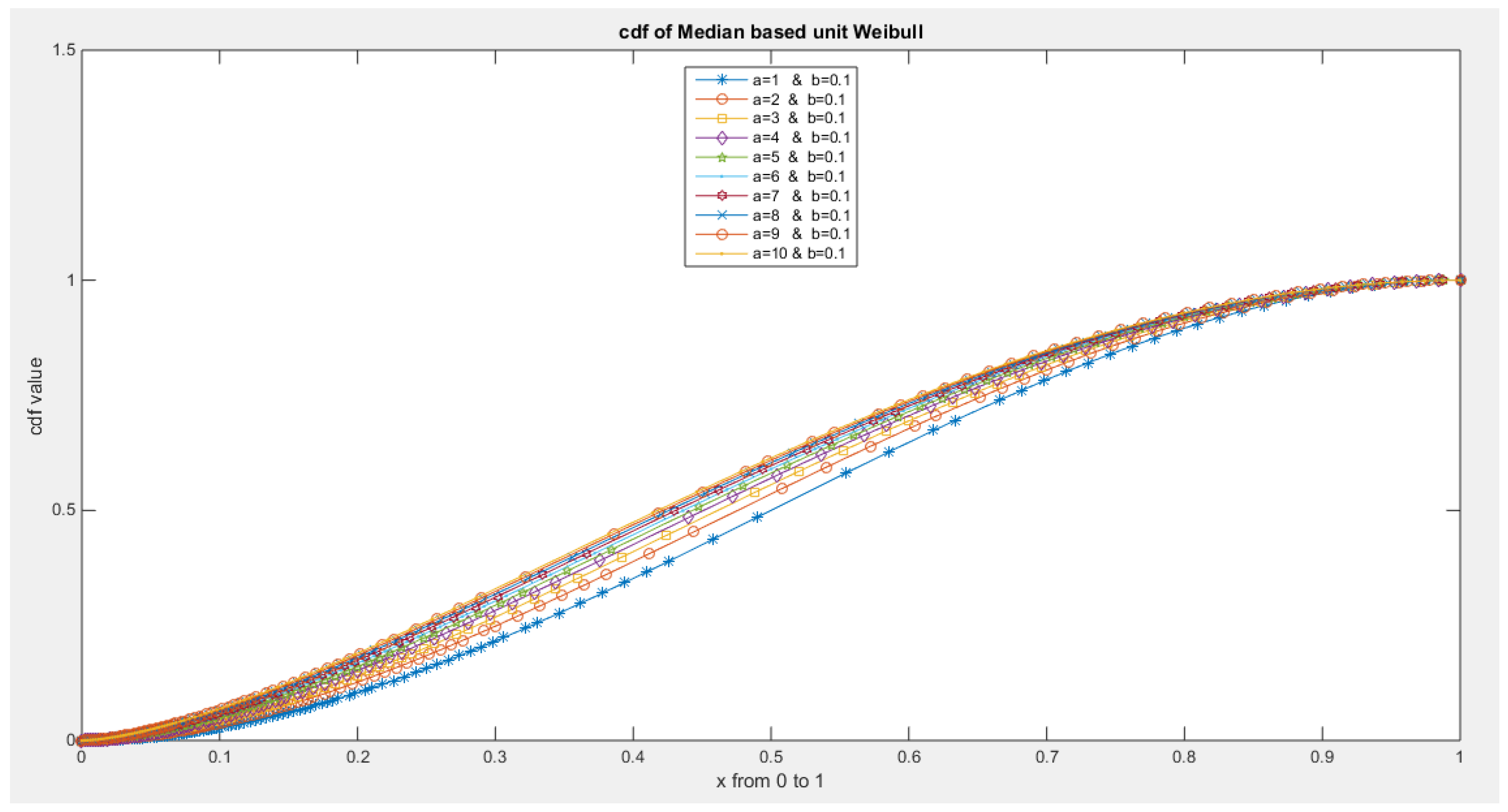
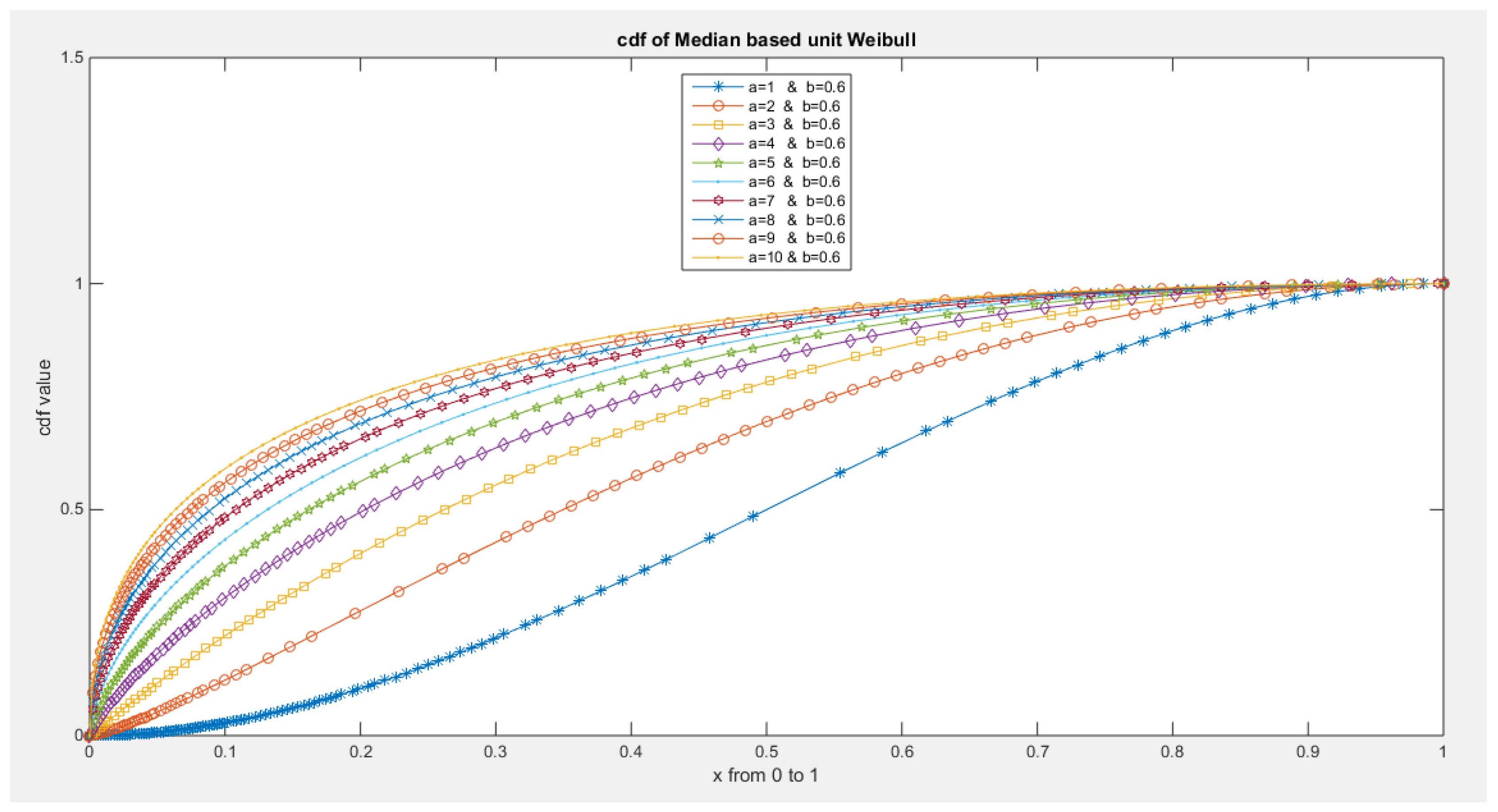
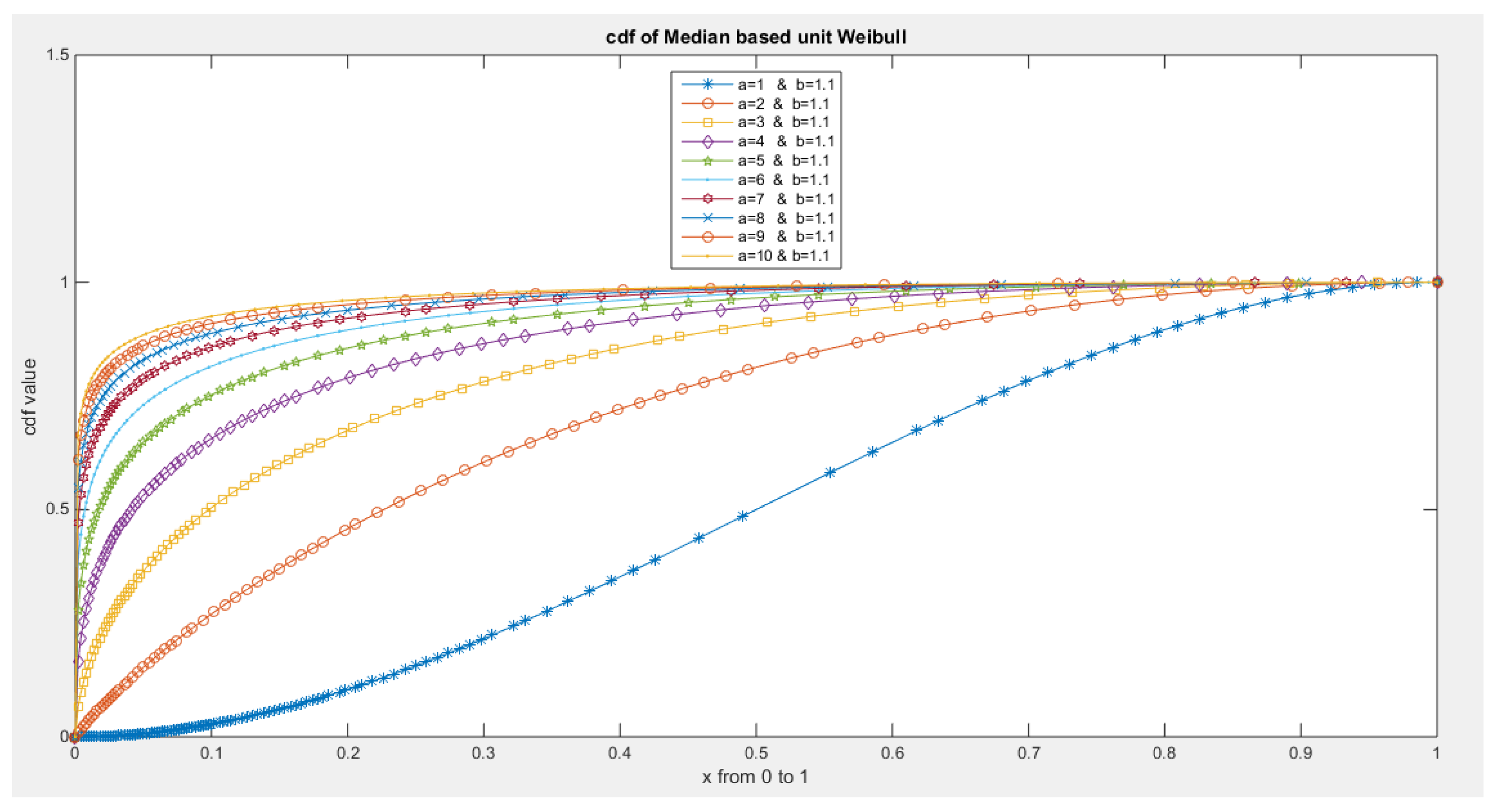
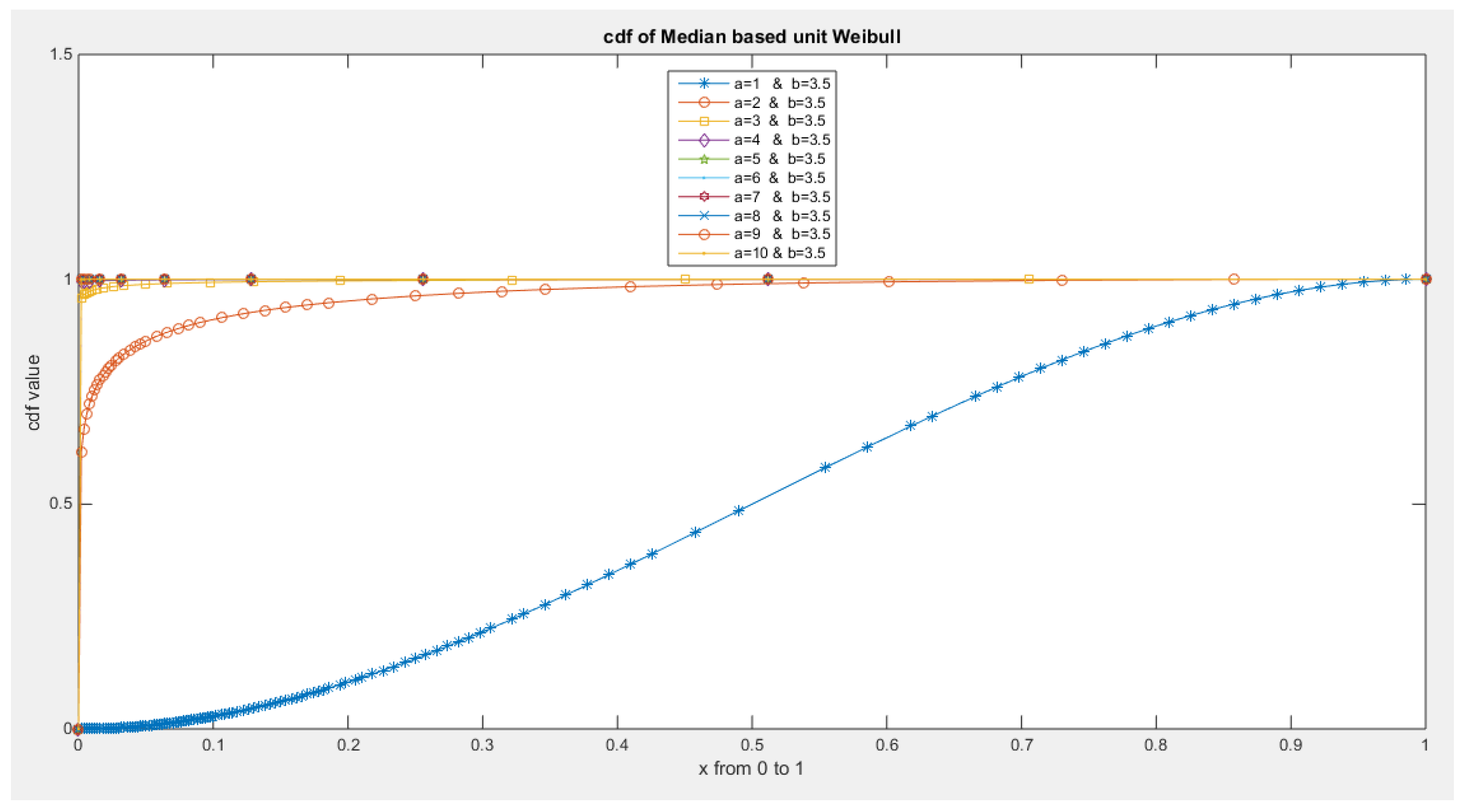
2-: The following is the CDF:

F (y) = {3 y}^{\frac{2}{α^{β}}} - {2 y}^{\frac{3}{α^{β}}}, 0 < y < 1, α > 0, β > 0

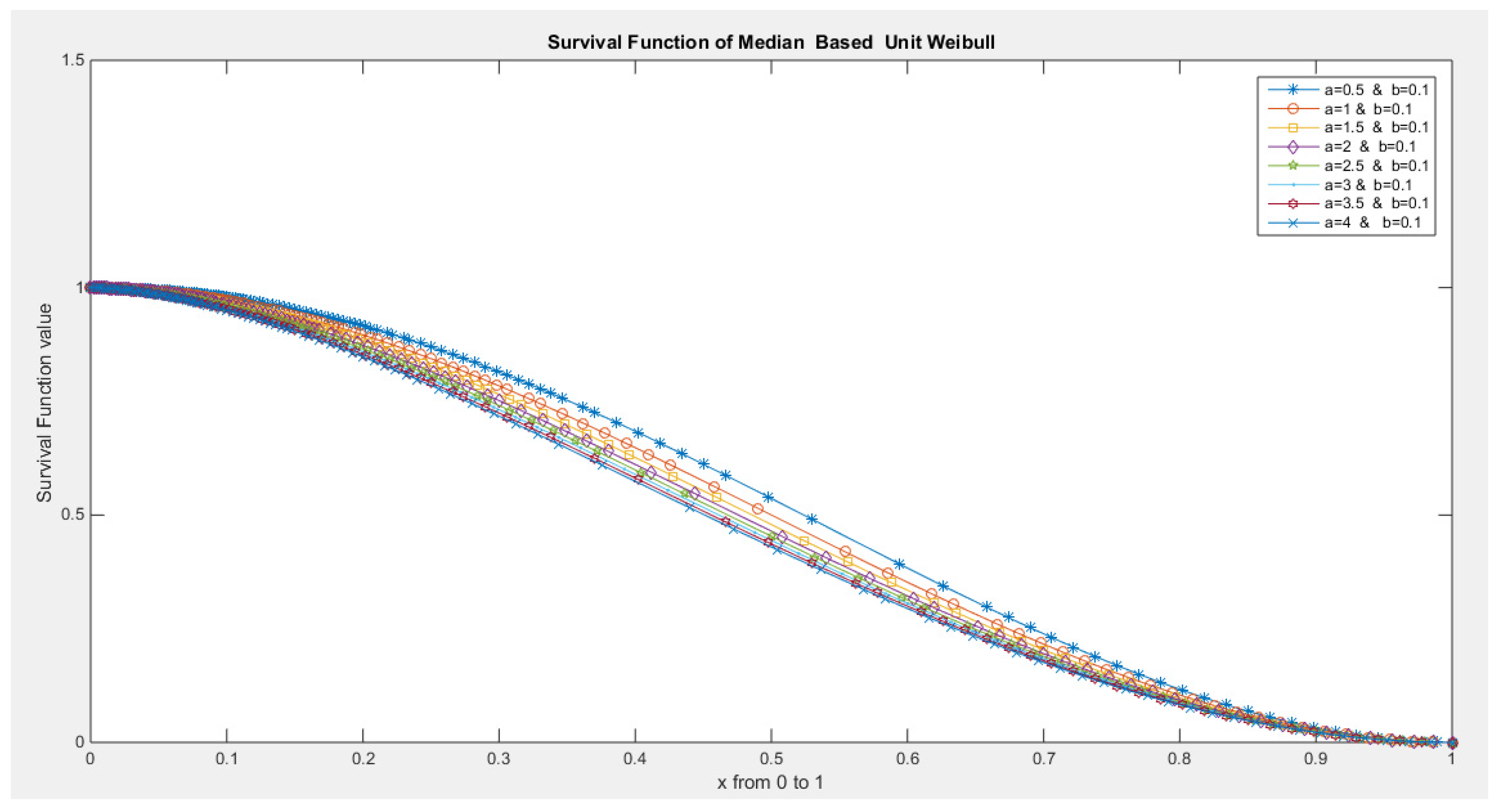
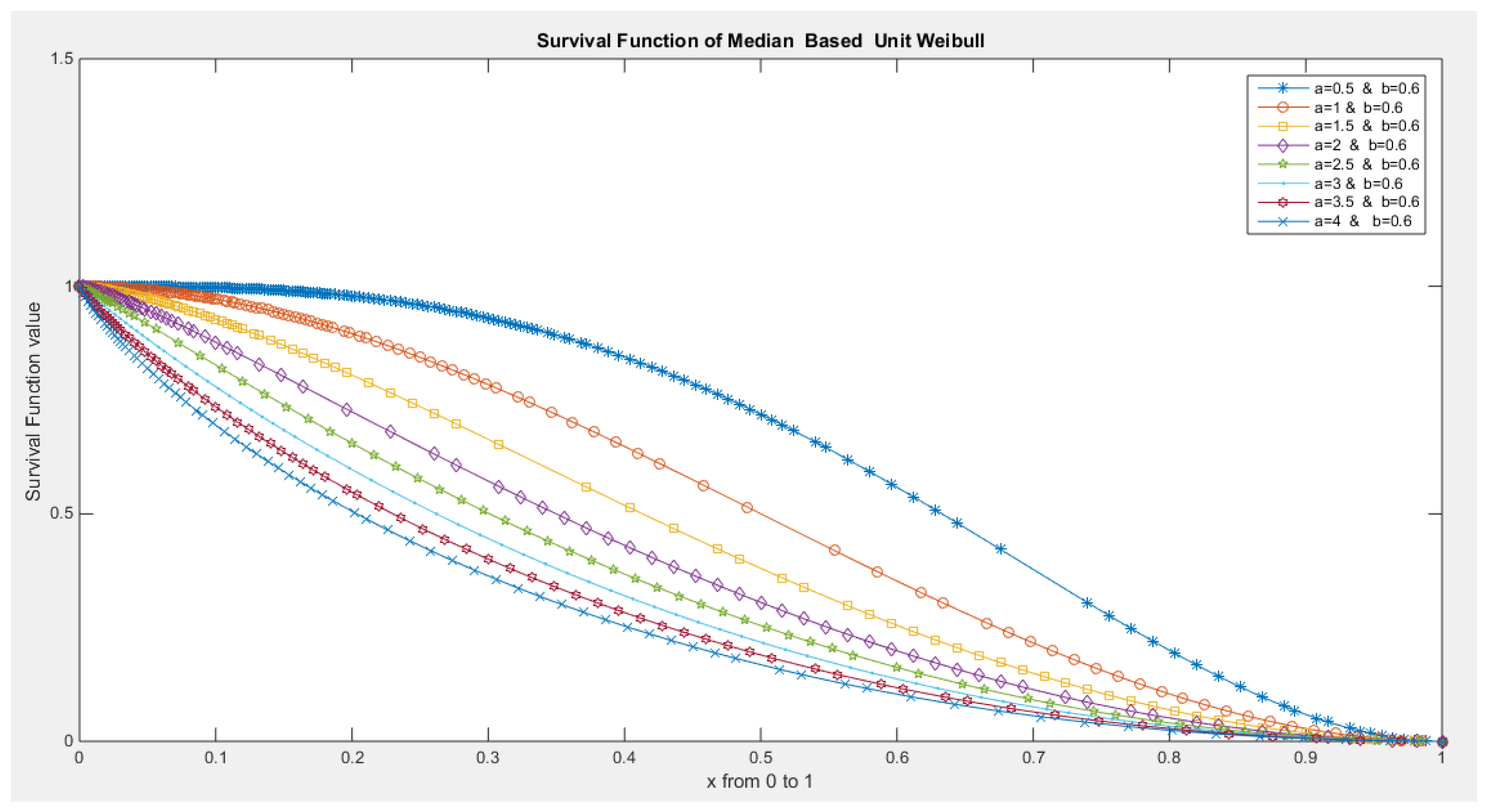
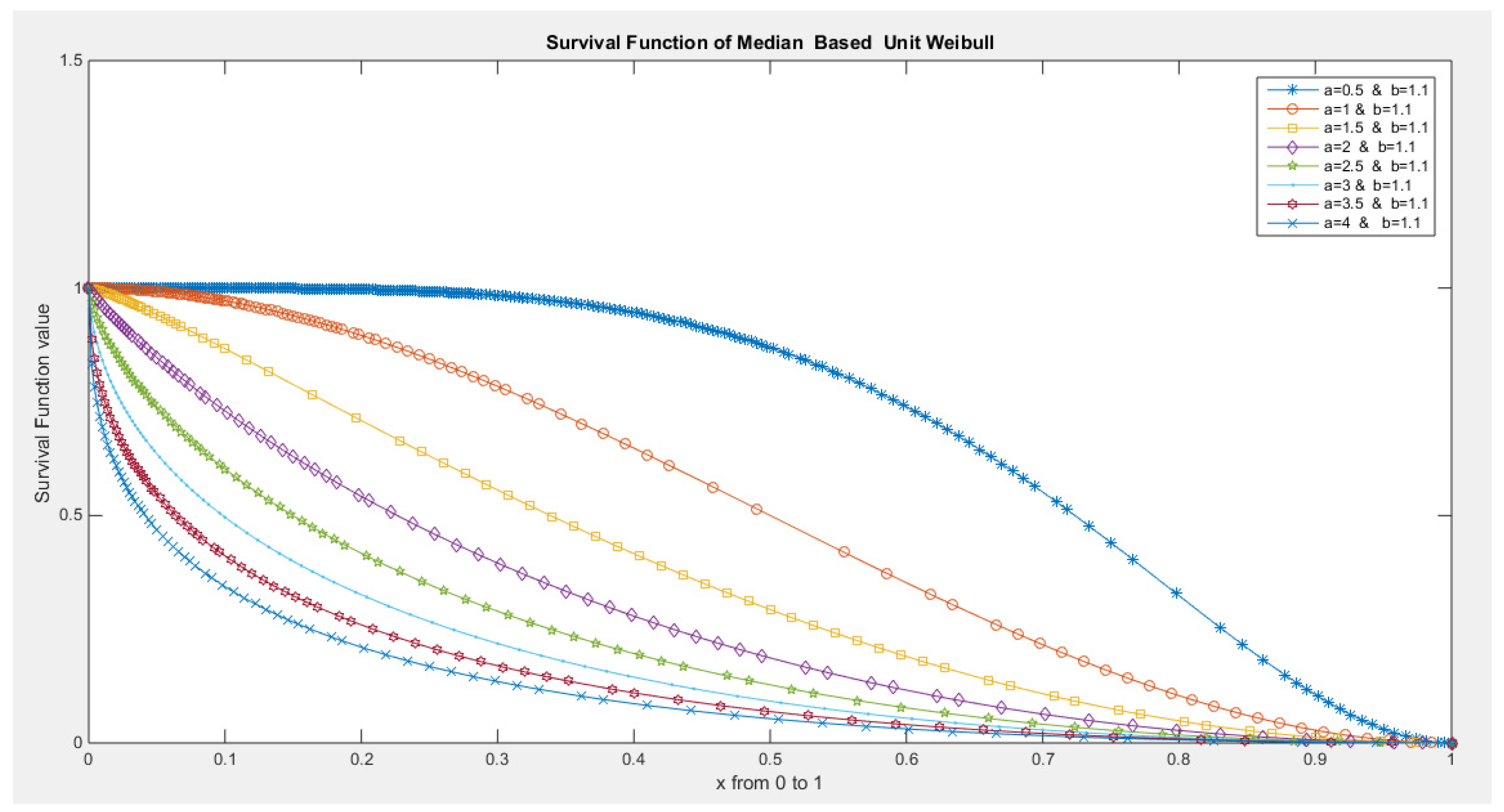
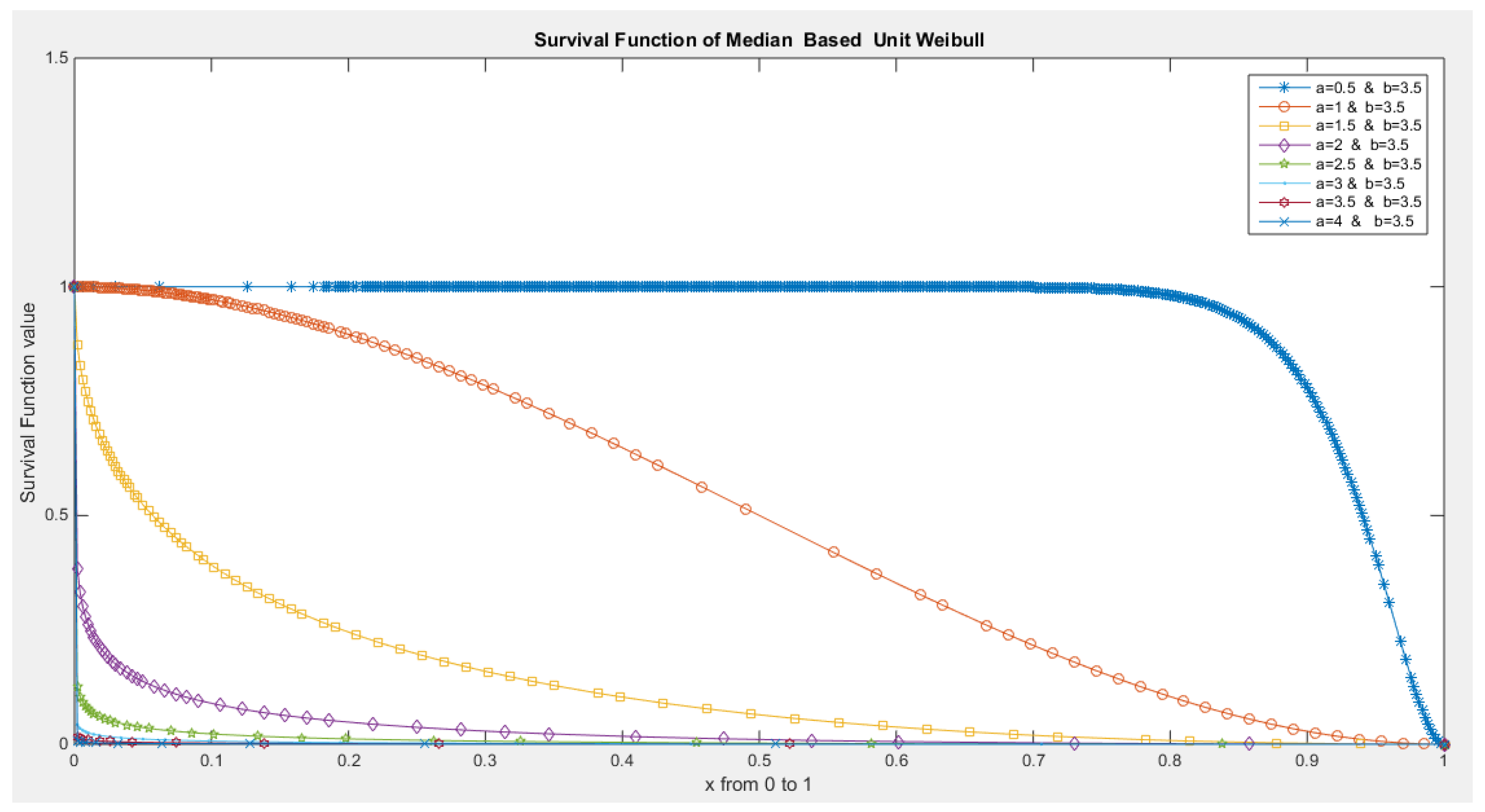
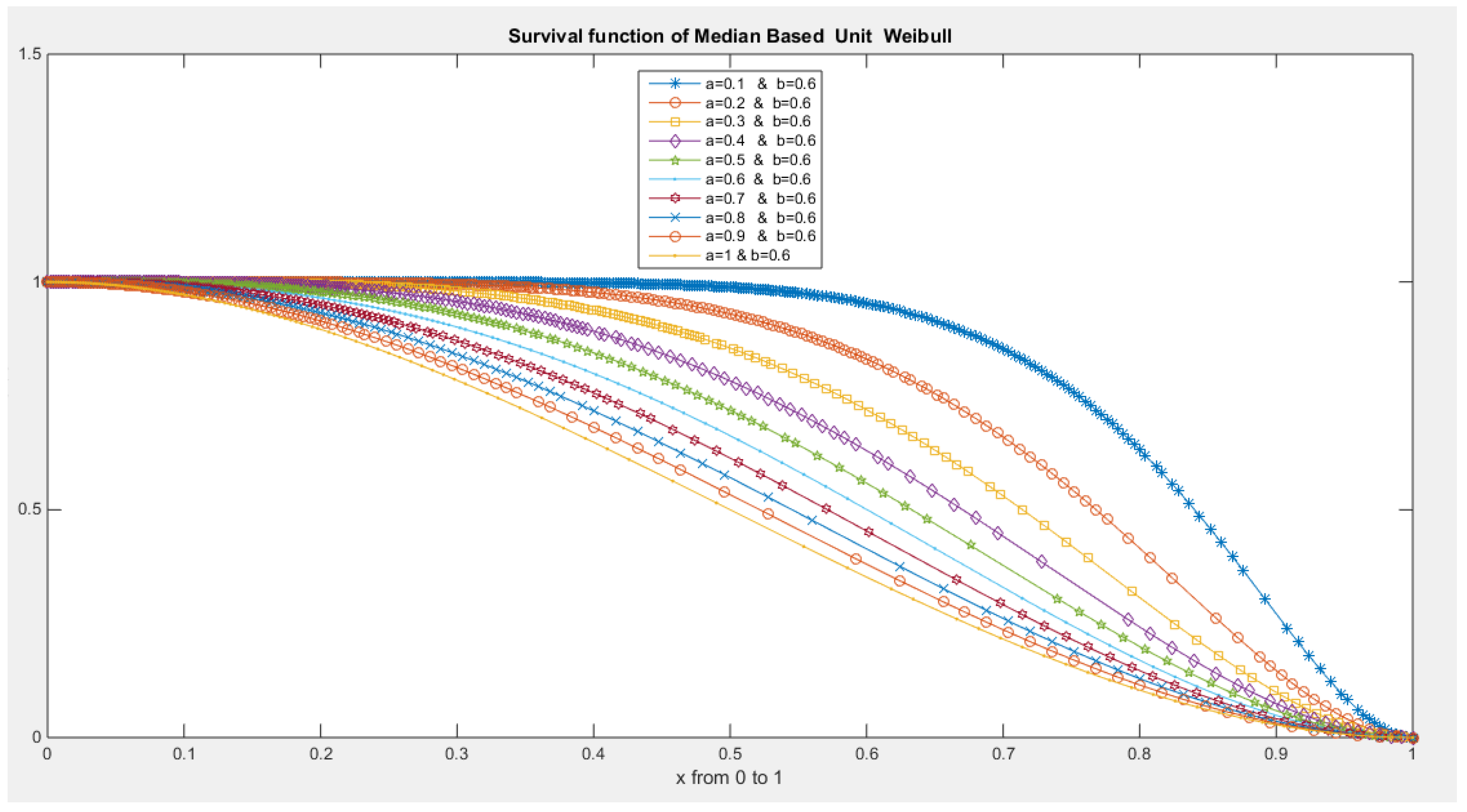
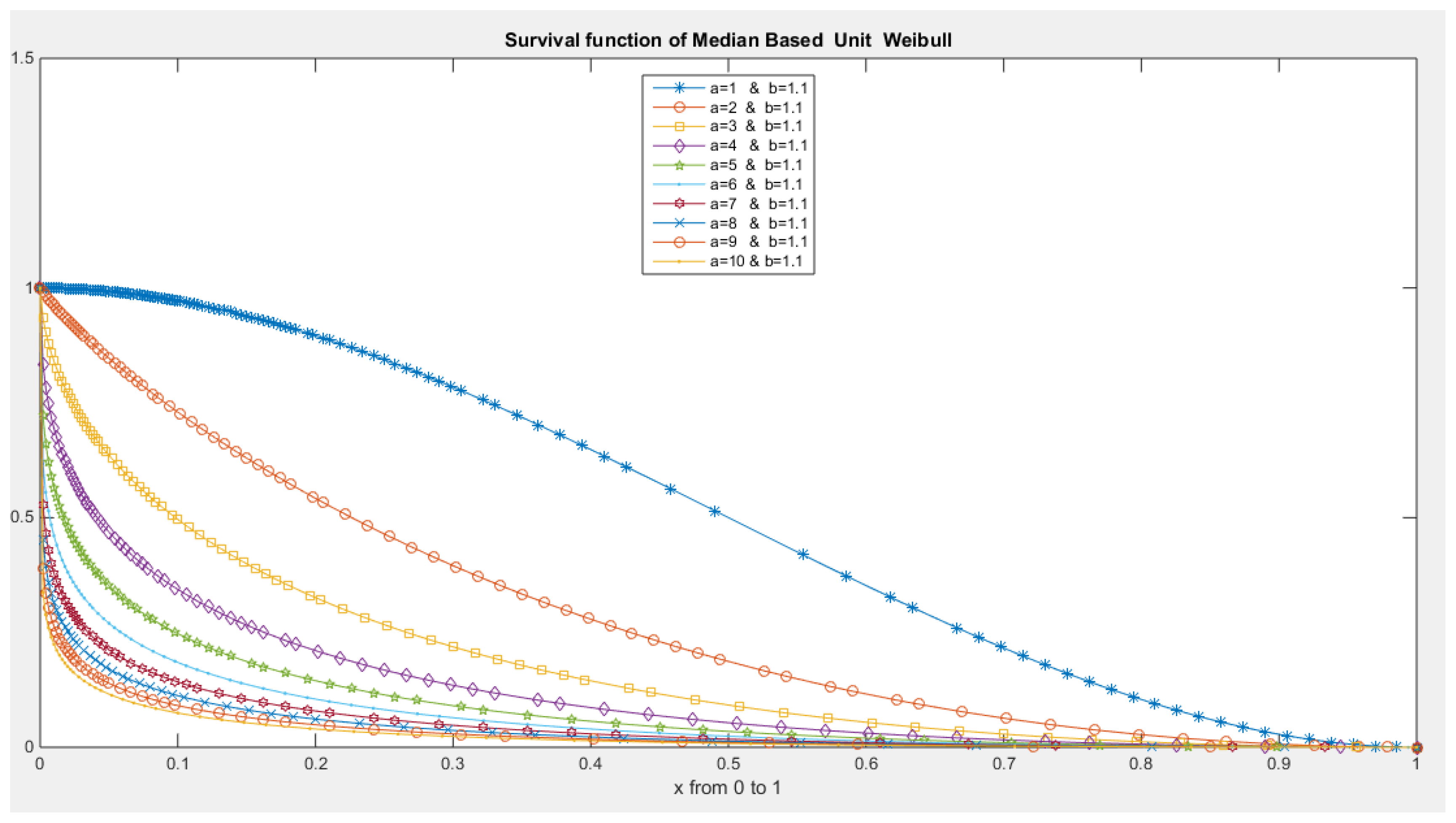
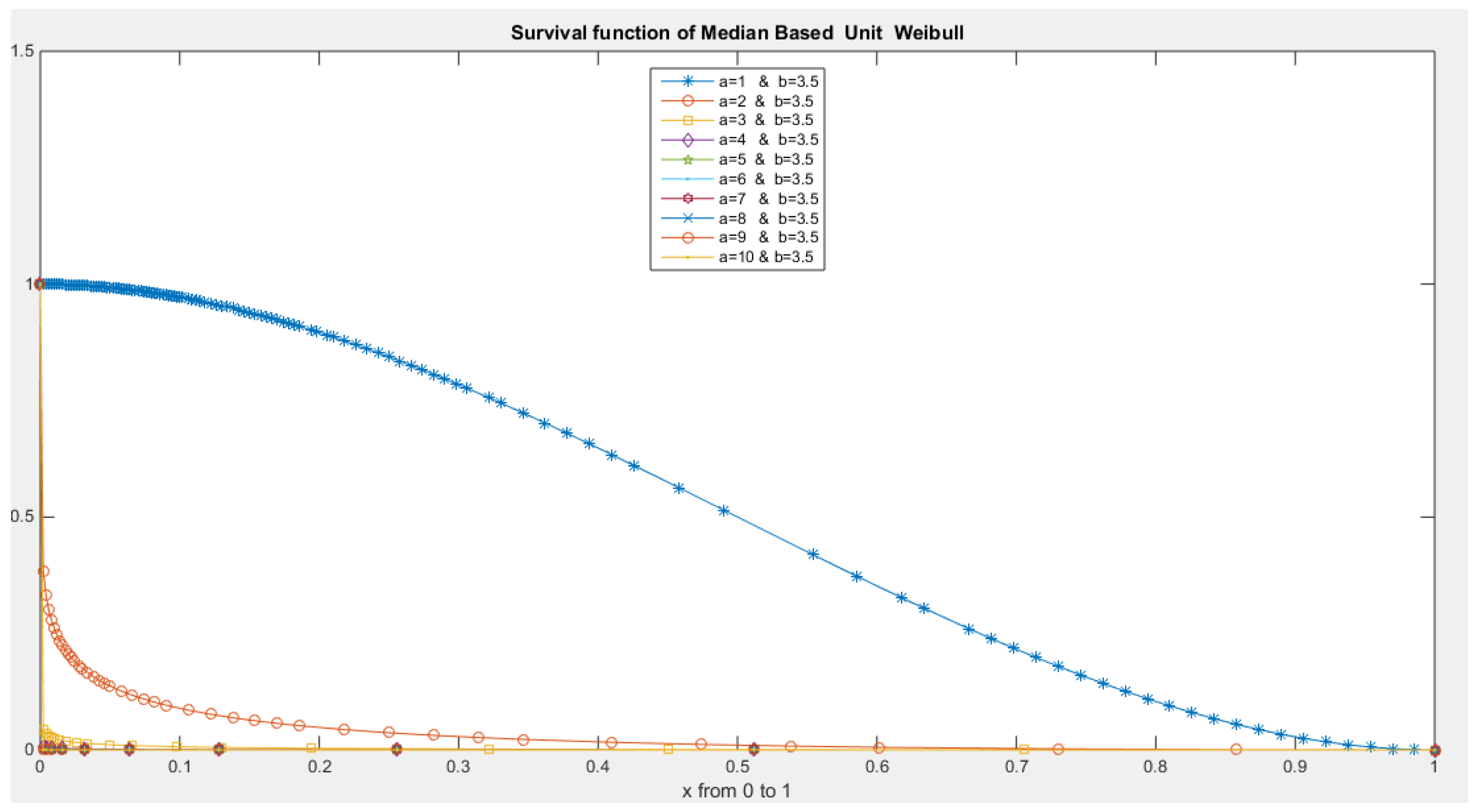
3-: The following is the survival function :

S (y) = 1 - F (Y) = 1 - ({3 y}^{\frac{2}{α^{β}}} - {2 y}^{\frac{3}{α^{β}}}), 0 < y < 1, α > 0, β > 0

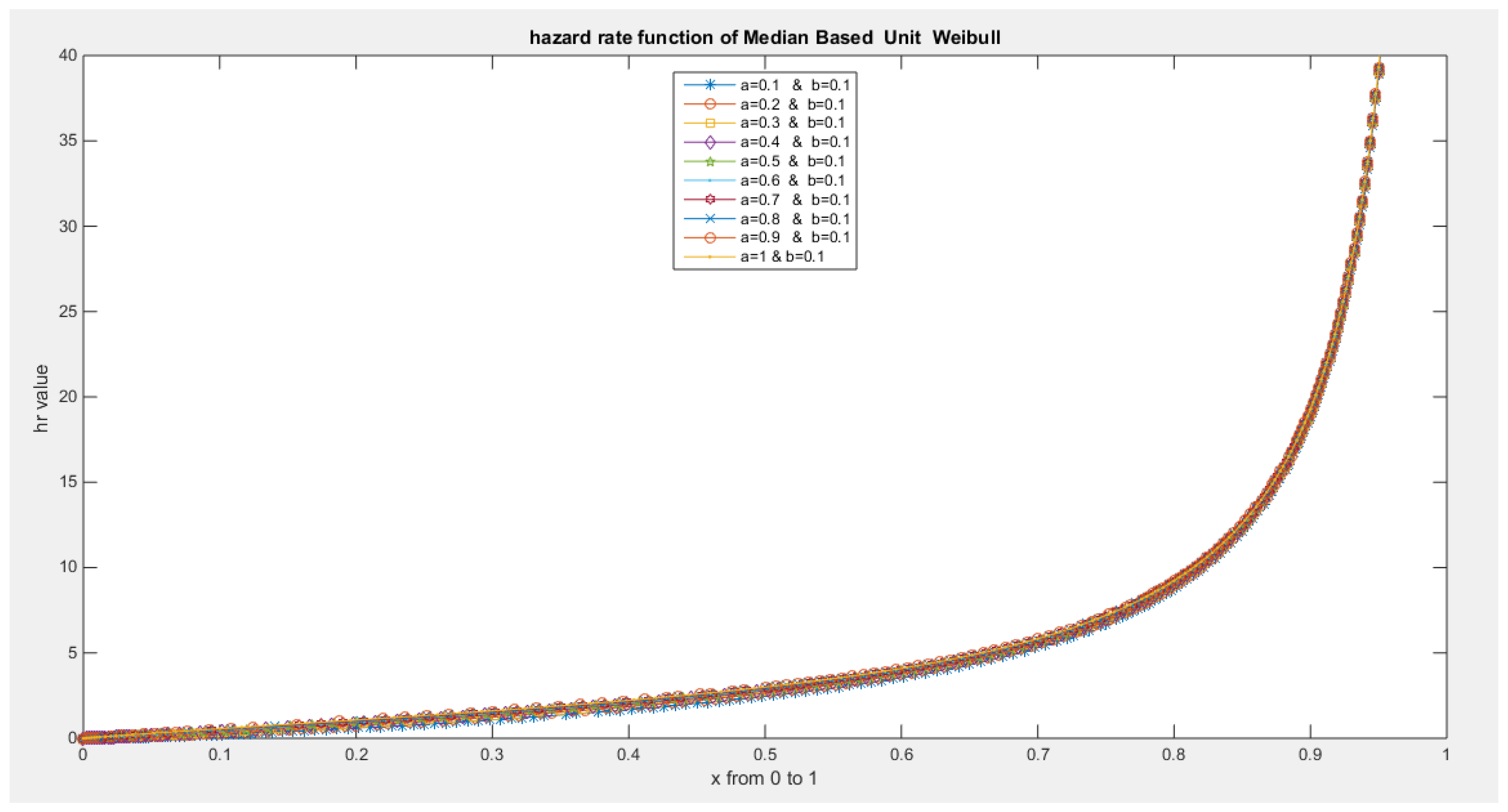
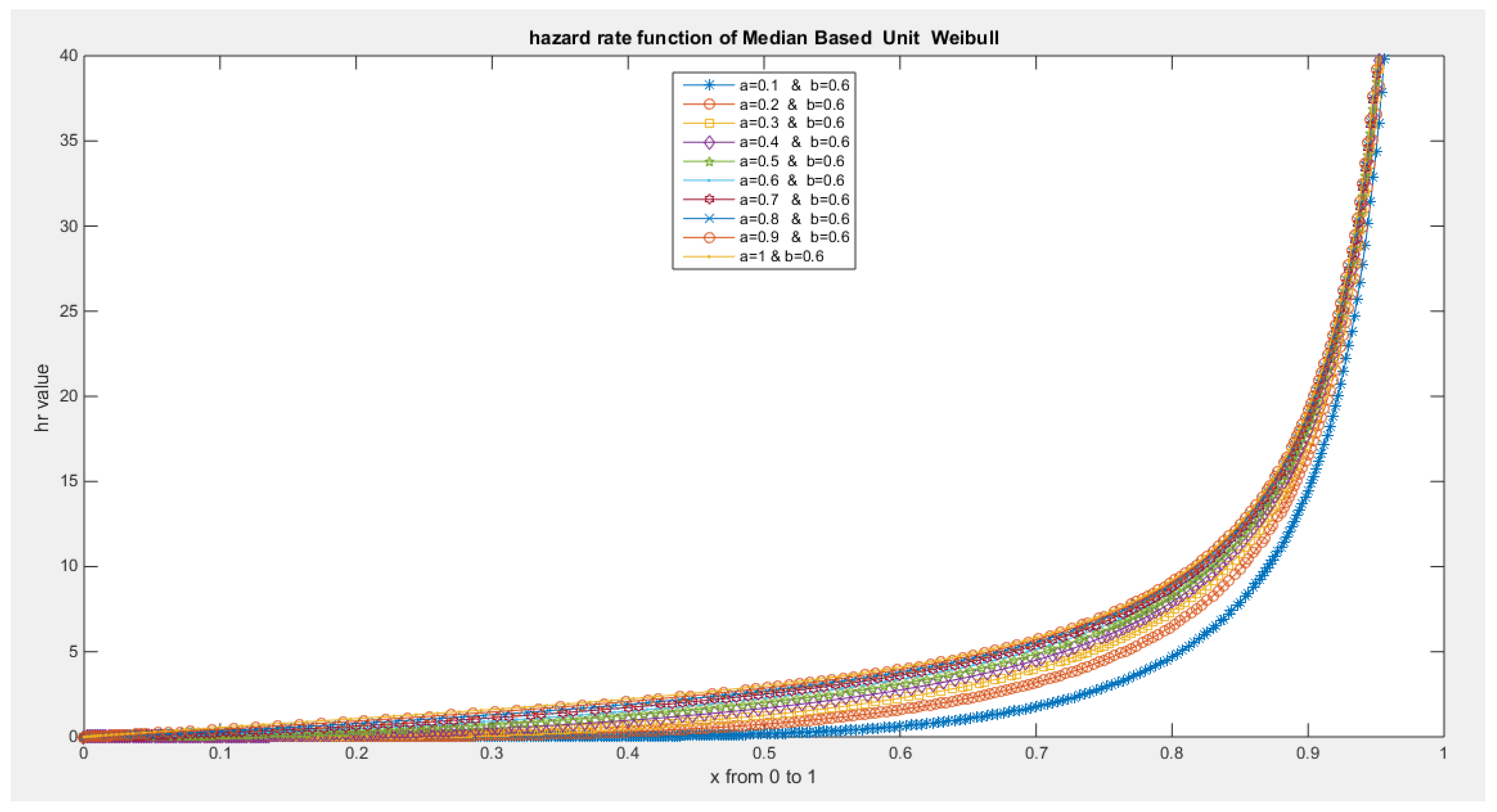
4-: The following is the hazard function (hf) and reversed hazard function (rhf) respectively:

h (y) = \frac{f (y)}{S (y)} = \frac{\frac{6}{α^{β}} (1 - y^{\frac{1}{α^{β}}}) y^{(\frac{2}{α^{β}} - 1)}}{1 - ({3 y}^{\frac{2}{α^{β}}} - {2 y}^{\frac{3}{α^{β}}})}, 0 < y < 1, α > 0, β > 0 r h (y) = \frac{f (y)}{F (y)} = \frac{\frac{6}{α^{β}} (1 - y^{\frac{1}{α^{β}}}) y^{(\frac{2}{α^{β}} - 1)}}{{3 y}^{\frac{2}{α^{β}}} - {2 y}^{\frac{3}{α^{β}}}}, 0 < y < 1, α > 0, β > 0

The following figures, Figure 1, Figure 2, Figure 3 and Figure 4, show the PDF for different values of alpha ( 0.5 , 1, 1.5, 2 , 2.5 , 3 , 3.5 , 4 ) and beta ( 0.1 , 0.6 , 1.1 . 3.5 ):

Figure 1. pdf of Median Based Unit Weibull ( MBUW) distribution, alpha ( 0.5 , 1, 1.5, 2 , 2.5 , 3 , 3.5 , 4 ) and beta ( 0.1) .

Figure 2. pdf of Median Based Unit Weibull ( MBUW) distribution, alpha ( 0.5 , 1, 1.5, 2 , 2.5 , 3 , 3.5 , 4 ) and beta ( 0.6 ).

Figure 3. pdf of Median Based Unit Weibull ( MBUW) distribution, alpha ( 0.5 , 1, 1.5, 2 , 2.5 , 3 , 3.5 , 4 ) and beta ( 1.1).

Figure 4. pdf of Median Based Unit Weibull ( MBUW) distribution, alpha ( 0.5 , 1, 1.5, 2 , 2.5 , 3 , 3.5 , 4 ) and beta ( 3.5)

Figure 5. pdf of Median Based Unit Weibull ( MBUW) distribution, alpha ( 0.5 , 1, 1.5, 2 , 2.5 , 3 , 3.5 , 4 ) and beta ( 3.5), changing vertical scale.

Figure 6. cdf of Median Based Unit Weibull ( MBUW) distribution, alpha ( 0.5 , 1, 1.5, 2 , 2.5 , 3 , 3.5 , 4 ) and beta ( 0.1).

Figure 7. cdf of Median Based Unit Weibull ( MBUW) distribution, alpha ( 0.5 , 1, 1.5, 2 , 2.5 , 3 , 3.5 , 4 ) and beta ( 0.6).

Figure 8. cdf of Median Based Unit Weibull ( MBUW) distribution, alpha ( 0.5 , 1, 1.5, 2 , 2.5 , 3 , 3.5 , 4 ) and beta ( 1.1).

Figure 9. cdf of Median Based Unit Weibull ( MBUW) distribution, alpha ( 0.5 , 1, 1.5, 2 , 2.5 , 3 , 3.5 , 4 ) and beta ( 3.5).

Figure 10. hazard rate of Median Based Unit Weibull ( MBUW) distribution, alpha ( 0.5 , 1, 1.5, 2 , 2.5 , 3 , 3.5 , 4 ) and beta ( 0.1).

Figure 11. hazard rate of Median Based Unit Weibull ( MBUW) distribution, alpha ( 0.5 , 1, 1.5, 2 , 2.5 , 3 , 3.5 , 4 ) and beta ( 0.6).

Figure 12. hazard rate of Median Based Unit Weibull ( MBUW) distribution, alpha ( 0.5 , 1, 1.5, 2 , 2.5 , 3 , 3.5 , 4 ) and beta ( 1.1).

Figure 13. hazard rate of Median Based Unit Weibull ( MBUW) distribution, alpha ( 0.5 , 1, 1.5, 2 , 2.5 , 3 , 3.5 , 4 ) and beta ( 3.5).

Figure 14. Survival function of Median Based Unit Weibull ( MBUW) distribution, alpha ( 0.5 , 1, 1.5, 2 , 2.5 , 3 , 3.5 , 4 ) and beta ( 0.1).

Figure 15. Survival function of Median Based Unit Weibull ( MBUW) distribution, alpha ( 0.5 , 1, 1.5, 2 , 2.5 , 3 , 3.5 , 4 ) and beta ( 0.6).

Figure 16. Survival function of Median Based Unit Weibull ( MBUW) distribution, alpha ( 0.5 , 1, 1.5, 2 , 2.5 , 3 , 3.5 , 4 ) and beta ( 1.1).

Figure 17. Survival function of Median Based Unit Weibull ( MBUW) distribution, alpha ( 0.5 , 1, 1.5, 2 , 2.5 , 3 , 3.5 , 4 ) and beta ( 3.5).

Figure 18. reversed hazard rate of Median Based Unit Weibull ( MBUW) distribution, alpha ( 0.5 , 1, 1.5, 2 , 2.5 , 3 , 3.5 , 4 ) and beta ( 0.1).

Figure 19. reversed hazard rate of Median Based Unit Weibull ( MBUW) distribution, alpha ( 0.5 , 1, 1.5, 2 , 2.5 , 3 , 3.5 , 4 ) and beta ( 0.6).

Figure 20. reversed hazard rate of Median Based Unit Weibull ( MBUW) distribution, alpha ( 0.5 , 1, 1.5, 2 , 2.5 , 3 , 3.5 , 4 ) and beta ( 1.1).

Figure 21. reversed hazard rate of Median Based Unit Weibull ( MBUW) distribution, alpha ( 0.5 , 1, 1.5, 2 , 2.5 , 3 , 3.5 , 4 ) and beta ( 3.5).

Figure 22. : pdf of Median Based Unit Weibull ( MBUW) distribution, alpha ( from 1 to 10 ) and beta ( 0.1).

Figure 23. : pdf of Median Based Unit Weibull ( MBUW) distribution, alpha ( from 1 to 10 ) and beta ( 0.6).

Figure 24. : pdf of Median Based Unit Weibull ( MBUW) distribution, alpha ( from 1 to 10 ) and beta ( 1.1).

Figure 25. : pdf of Median Based Unit Weibull ( MBUW) distribution, alpha ( from 1 to 10 ) and beta ( 3.5).

Figure 26. : pdf of Median Based Unit Weibull ( MBUW) distribution, alpha (from 0.1 to 1) and beta ( 0.1).

Figure 27. : pdf of Median Based Unit Weibull ( MBUW) distribution, alpha (from 0.1 to 1) and beta ( 0.6).

Figure 28. : pdf of Median Based Unit Weibull ( MBUW) distribution, alpha (from 0.1 to 1) and beta ( 1.1).

Figure 29. : pdf of Median Based Unit Weibull ( MBUW) distribution, alpha (from 0.1 to 1) and beta ( 3.5).

Figure 30. : cdf of Median Based Unit Weibull ( MBUW) distribution, alpha (from 0.1 to 1) and beta ( 0.1).

Figure 31. : cdf of Median Based Unit Weibull ( MBUW) distribution, alpha (from 0.1 to 1) and beta ( 0.6).

Figure 32. : cdf of Median Based Unit Weibull ( MBUW) distribution, alpha (from 0.1 to 1) and beta ( 1.1).

Figure 33. : cdf of Median Based Unit Weibull ( MBUW) distribution, alpha (from 0.1 to 1) and beta ( 3.5).

Figure 34. : cdf of Median Based Unit Weibull ( MBUW) distribution, alpha (from 1 to 10) and beta ( 0.1).

Figure 35. : cdf of Median Based Unit Weibull ( MBUW) distribution, alpha (from 1 to 10) and beta ( 0.6).

Figure 36. : cdf of Median Based Unit Weibull ( MBUW) distribution, alpha (from 1 to 10) and beta ( 1.1).

Figure 37. : cdf of Median Based Unit Weibull ( MBUW) distribution, alpha (from 1 to 10) and beta ( 3.5).

Figure 38. : Sf of Median Based Unit Weibull ( MBUW) distribution, alpha (from 0.1 to 1) and beta ( 0.1).

Figure 39. : Sf of Median Based Unit Weibull ( MBUW) distribution, alpha (from 0.1 to 1) and beta ( 0.6).

Figure 40. : Sf of Median Based Unit Weibull ( MBUW) distribution, alpha (from 0.1 to 1) and beta ( 1.1).

Figure 41. : Sf of Median Based Unit Weibull ( MBUW) distribution, alpha (from 0.1 to 1) and beta ( 3.5).

Figure 42. : Sf of Median Based Unit Weibull ( MBUW) distribution, alpha (from 1 to 10) and beta ( 0.1).

Figure 43. : Sf of Median Based Unit Weibull ( MBUW) distribution, alpha (from 1 to 10) and beta ( 0.6).

Figure 44. : Sf of Median Based Unit Weibull ( MBUW) distribution, alpha (from 1 to 10) and beta ( 1.1).

Figure 45. : Sf of Median Based Unit Weibull ( MBUW) distribution, alpha (from 1 to 10) and beta ( 3.5).

Figure 46. : hr of Median Based Unit Weibull ( MBUW) distribution, alpha (from 0.1 to 1) and beta ( 0.1).

Figure 47. : hr of Median Based Unit Weibull ( MBUW) distribution, alpha (from 0.1 to 1) and beta ( 0.6).

Figure 48. : hr of Median Based Unit Weibull ( MBUW) distribution, alpha (from 0.1 to 1) and beta ( 1.1).

Figure 49. : hr of Median Based Unit Weibull ( MBUW) distribution, alpha (from 0.1 to 1) and beta ( 3.5).

Figure 50. : hr of Median Based Unit Weibull ( MBUW) distribution, alpha (from 1 to 10) and beta ( 0.1).

Figure 51. : hr of Median Based Unit Weibull ( MBUW) distribution, alpha (from 1 to 10) and beta ( 0.6).

Figure 52. : hr of Median Based Unit Weibull ( MBUW) distribution, alpha (from 1 to 10) and beta ( 1.1).

Figure 53. : hr of Median Based Unit Weibull ( MBUW) distribution, alpha (from 1 to 10) and beta ( 3.5).

Figure 54. : rhr of Median Based Unit Weibull ( MBUW) distribution, alpha (from 0.1 to 1) and beta ( 0.1).

Figure 55. rhr of Median Based Unit Weibull ( MBUW) distribution, alpha (from 0.1 to 1) and beta ( 0.6).

Figure 56. : rhr of Median Based Unit Weibull ( MBUW) distribution, alpha (from 0.1 to 1) and beta ( 1.1).

Figure 57. : rhr of Median Based Unit Weibull ( MBUW) distribution, alpha (from 0.1 to 1) and beta ( 3.5).

Figure 58. : rhr of Median Based Unit Weibull ( MBUW) distribution, alpha (from 1 to 10) and beta ( 0.1).

Figure 59. : rhr of Median Based Unit Weibull ( MBUW) distribution, alpha (from 1 to 10) and beta ( 0.6).

Figure 60. : rhr of Median Based Unit Weibull ( MBUW) distribution, alpha (from 1 to 10) and beta ( 1.1).

Figure 61. : rhr of Median Based Unit Weibull ( MBUW) distribution, alpha (from 1 to 10) and beta ( 3.5).

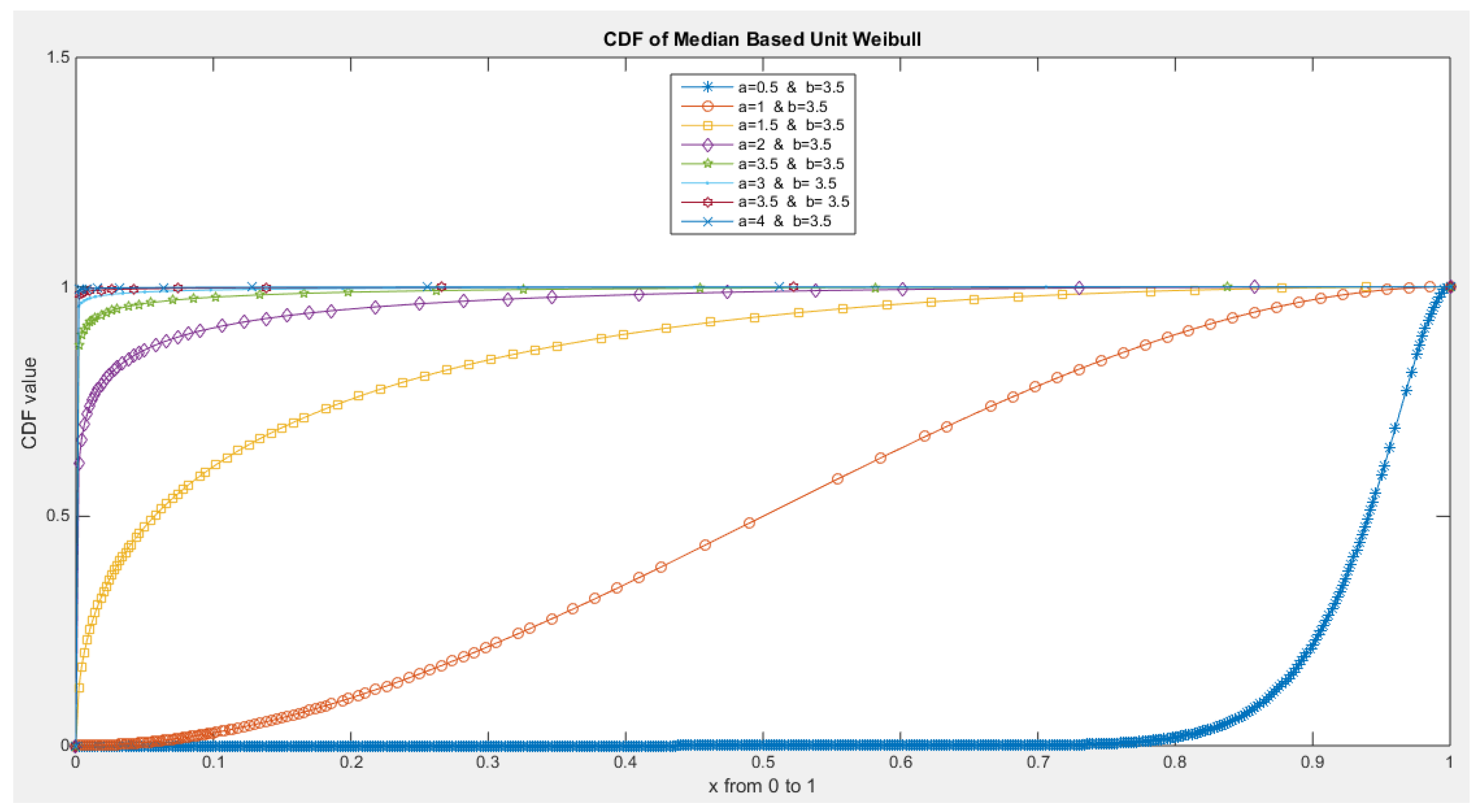
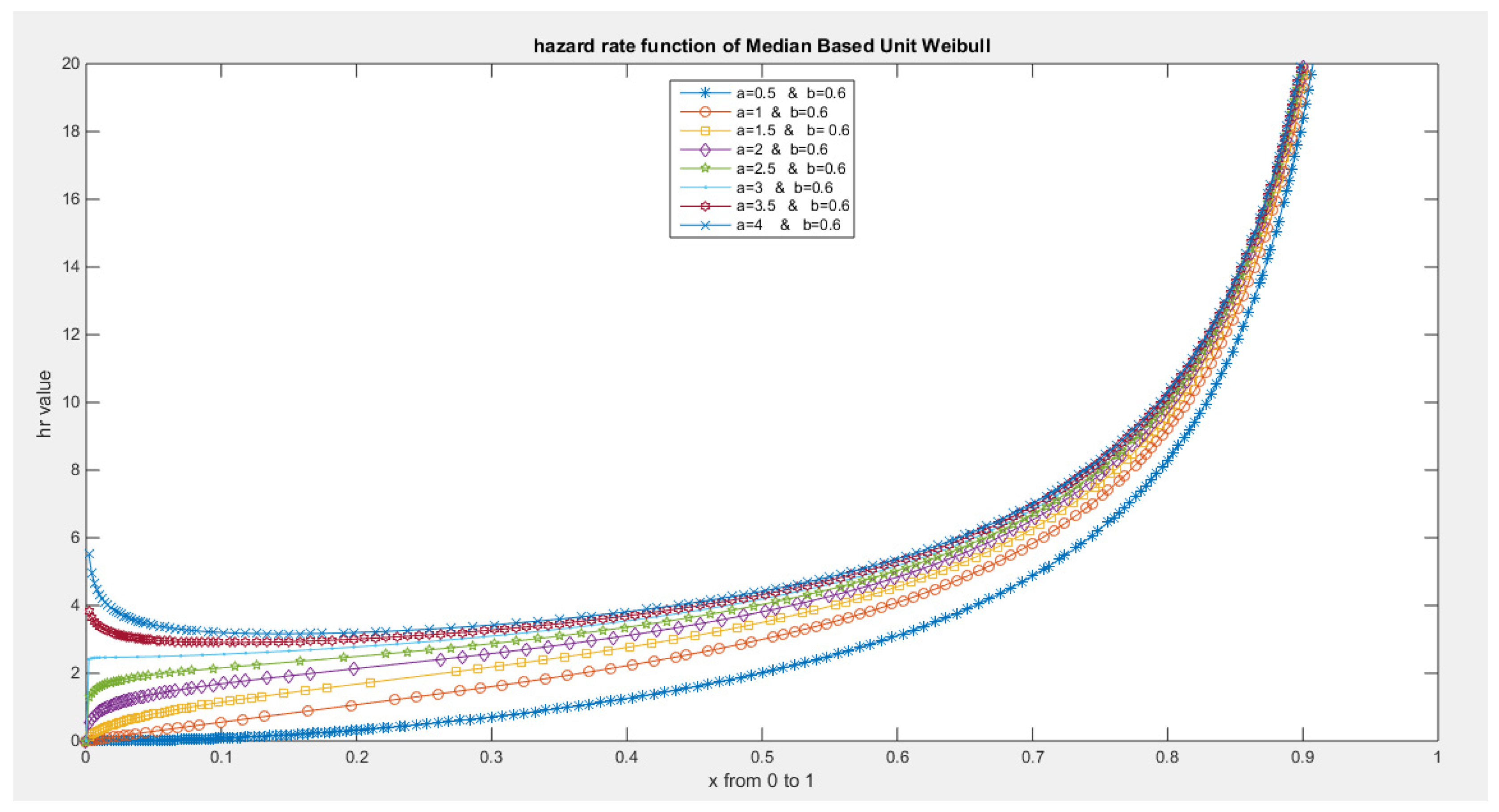
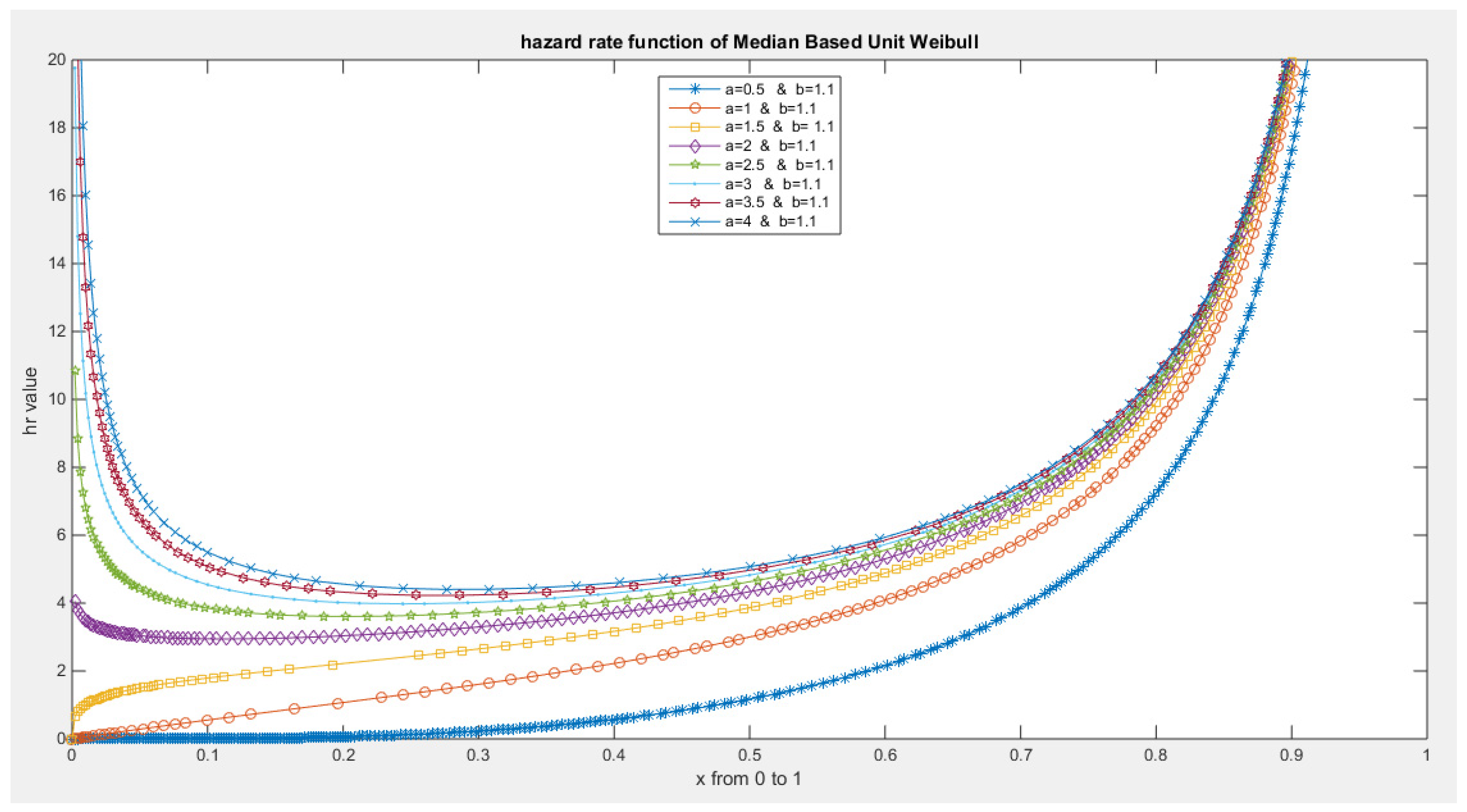
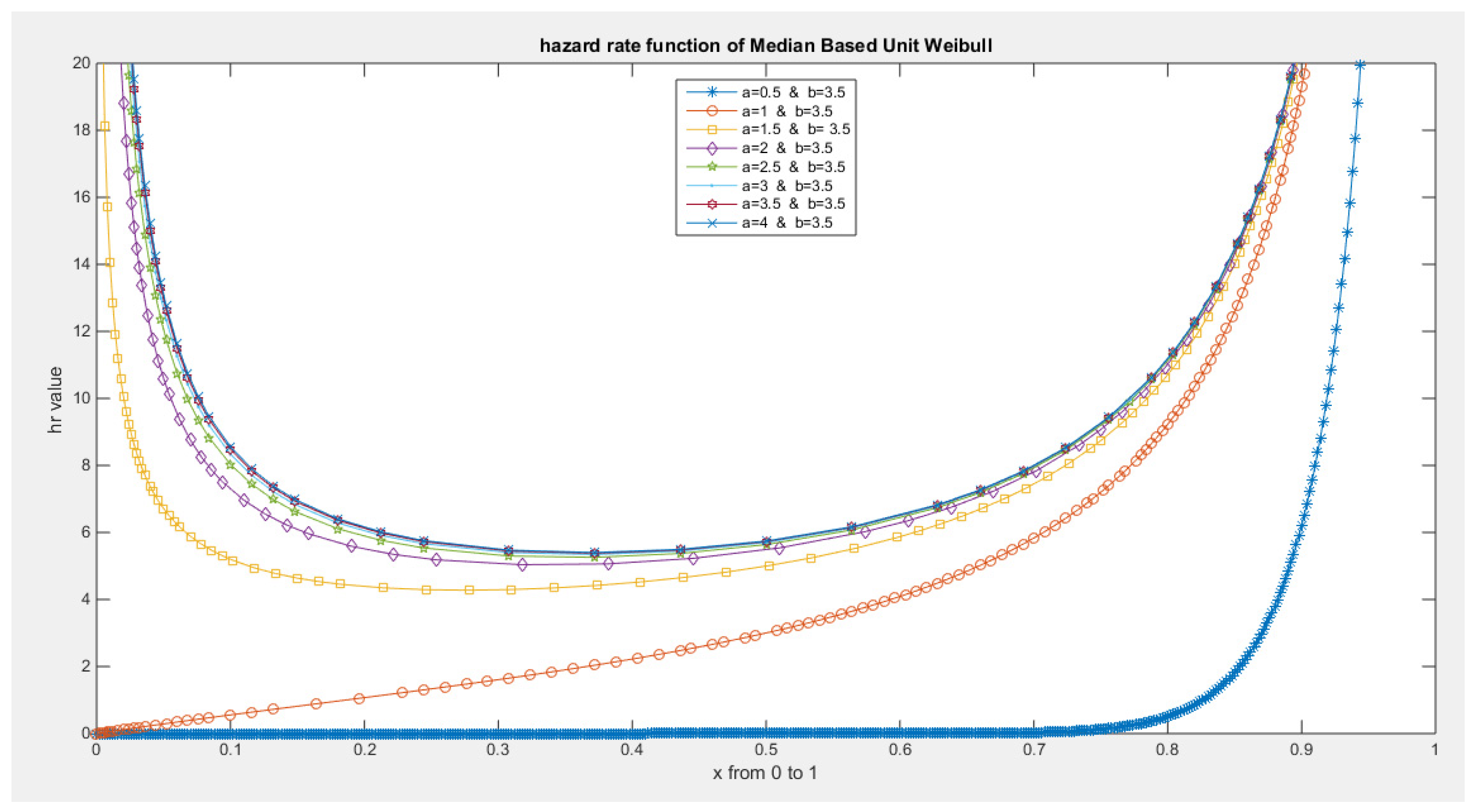
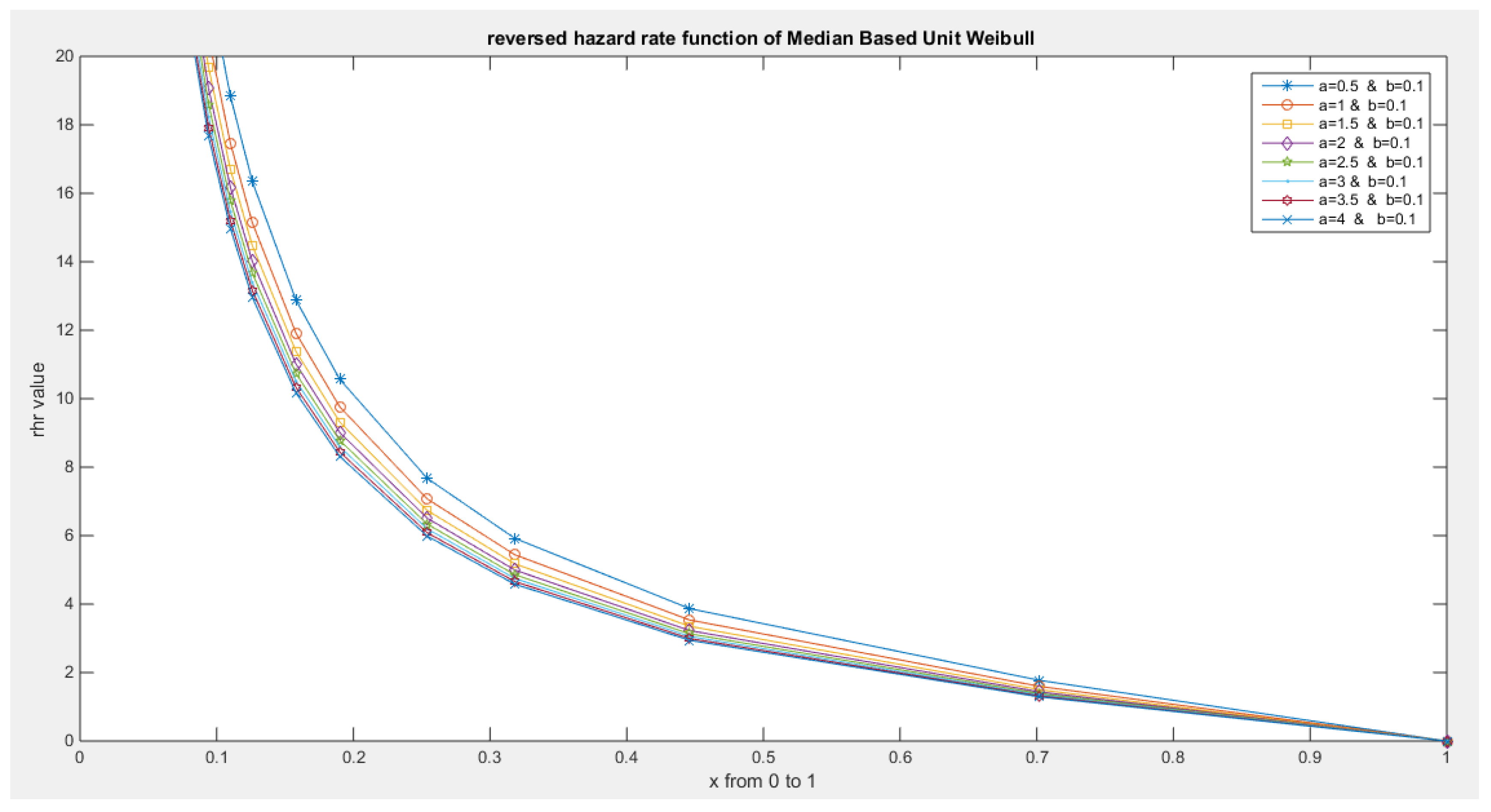
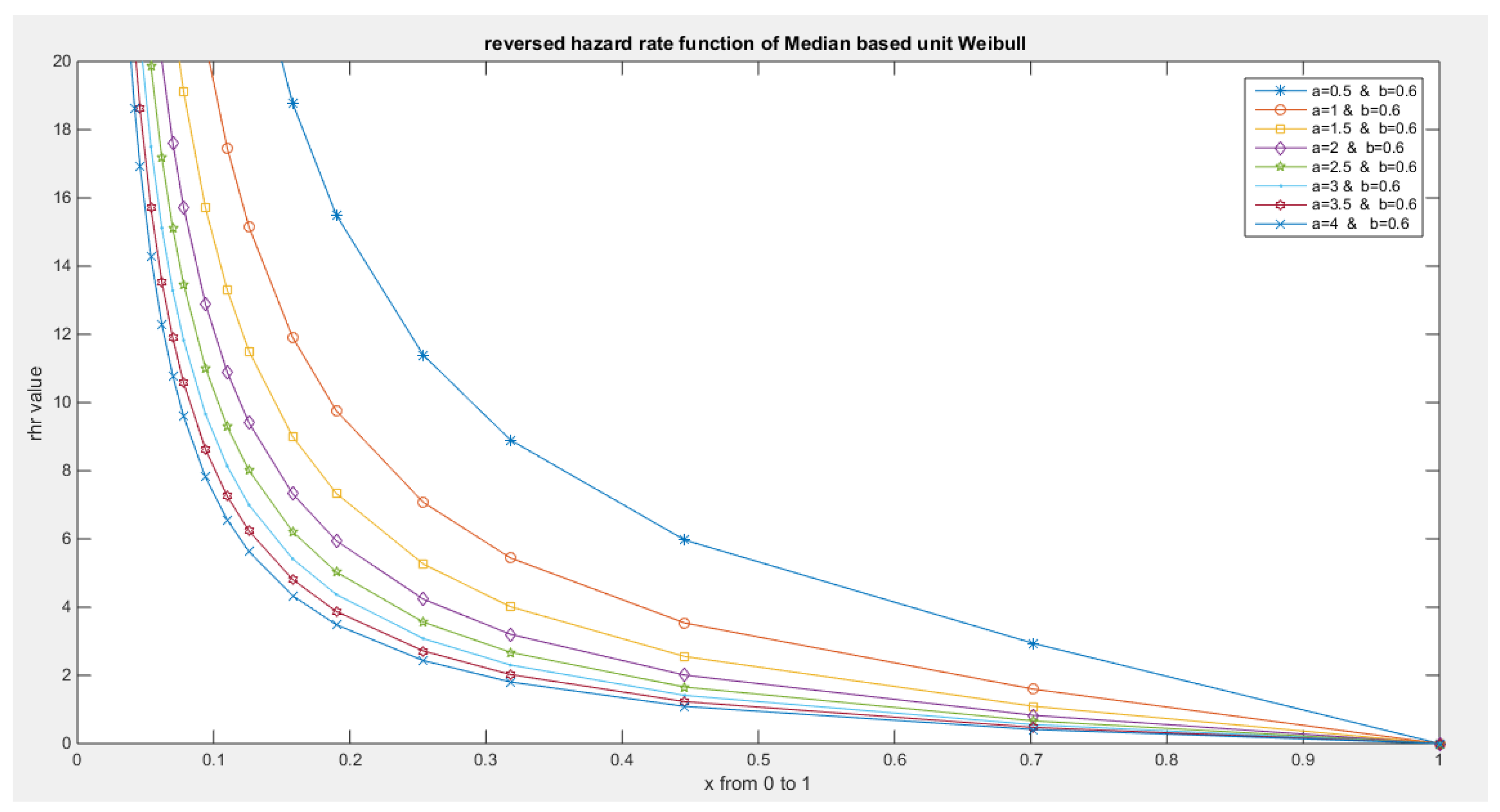
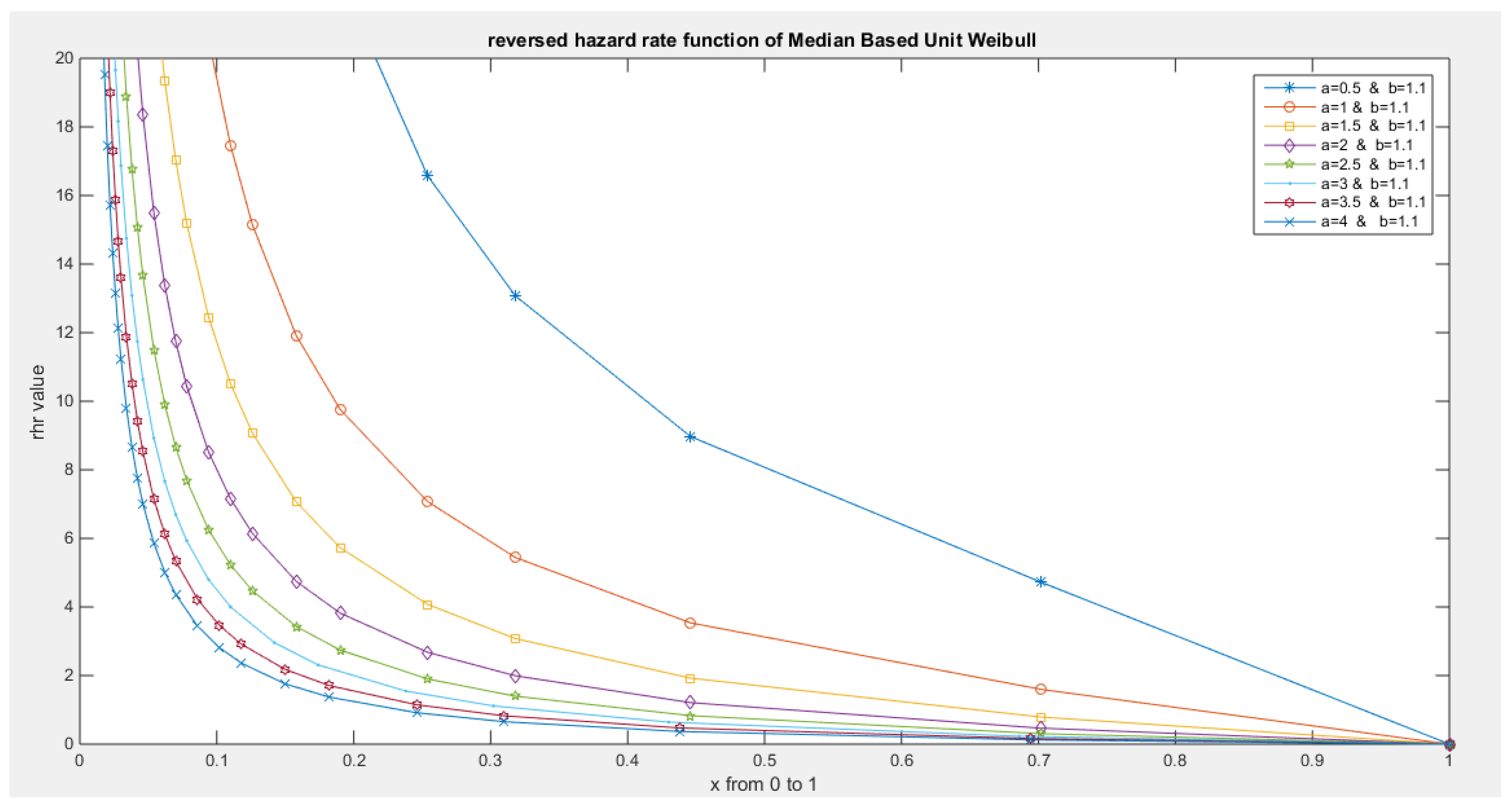
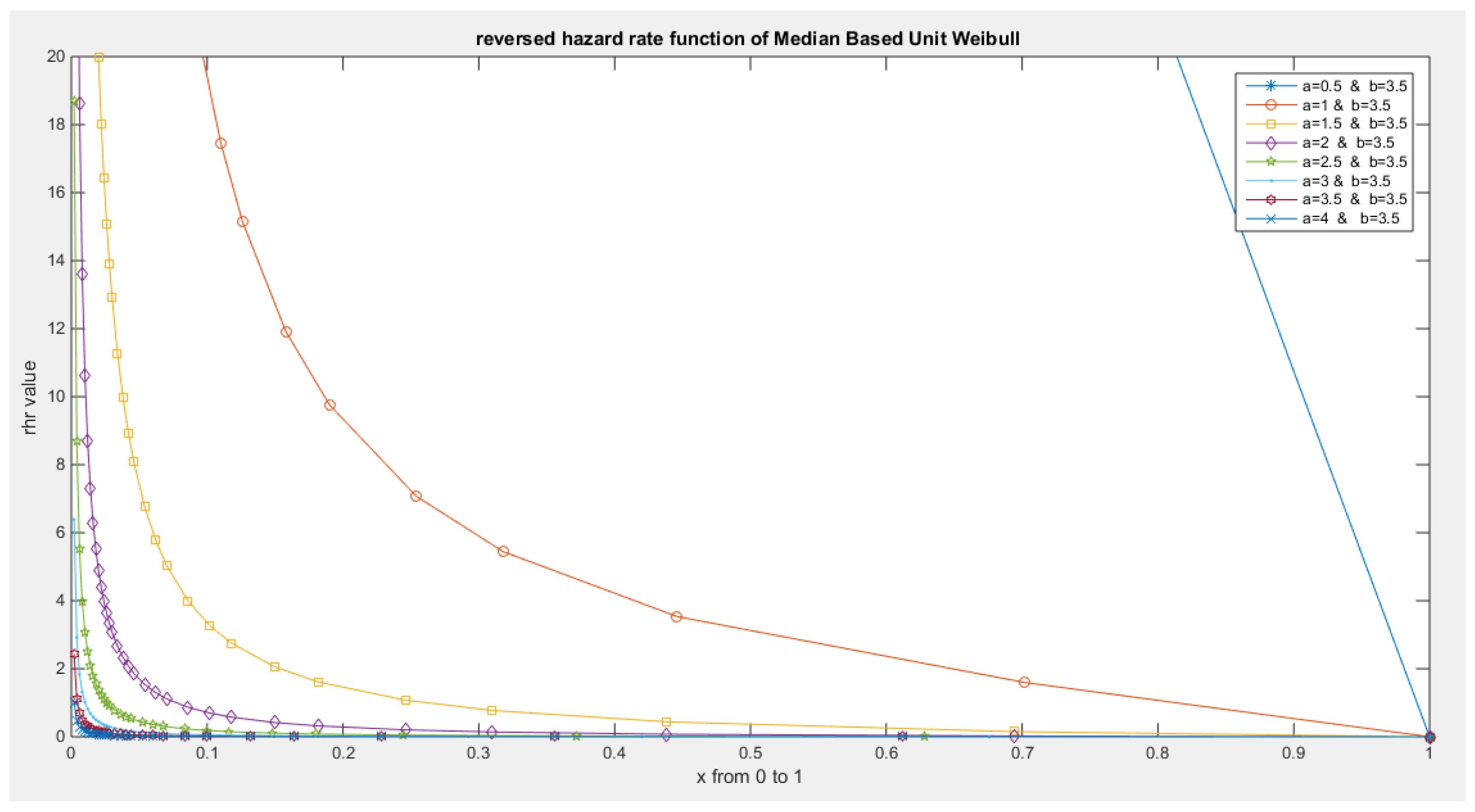
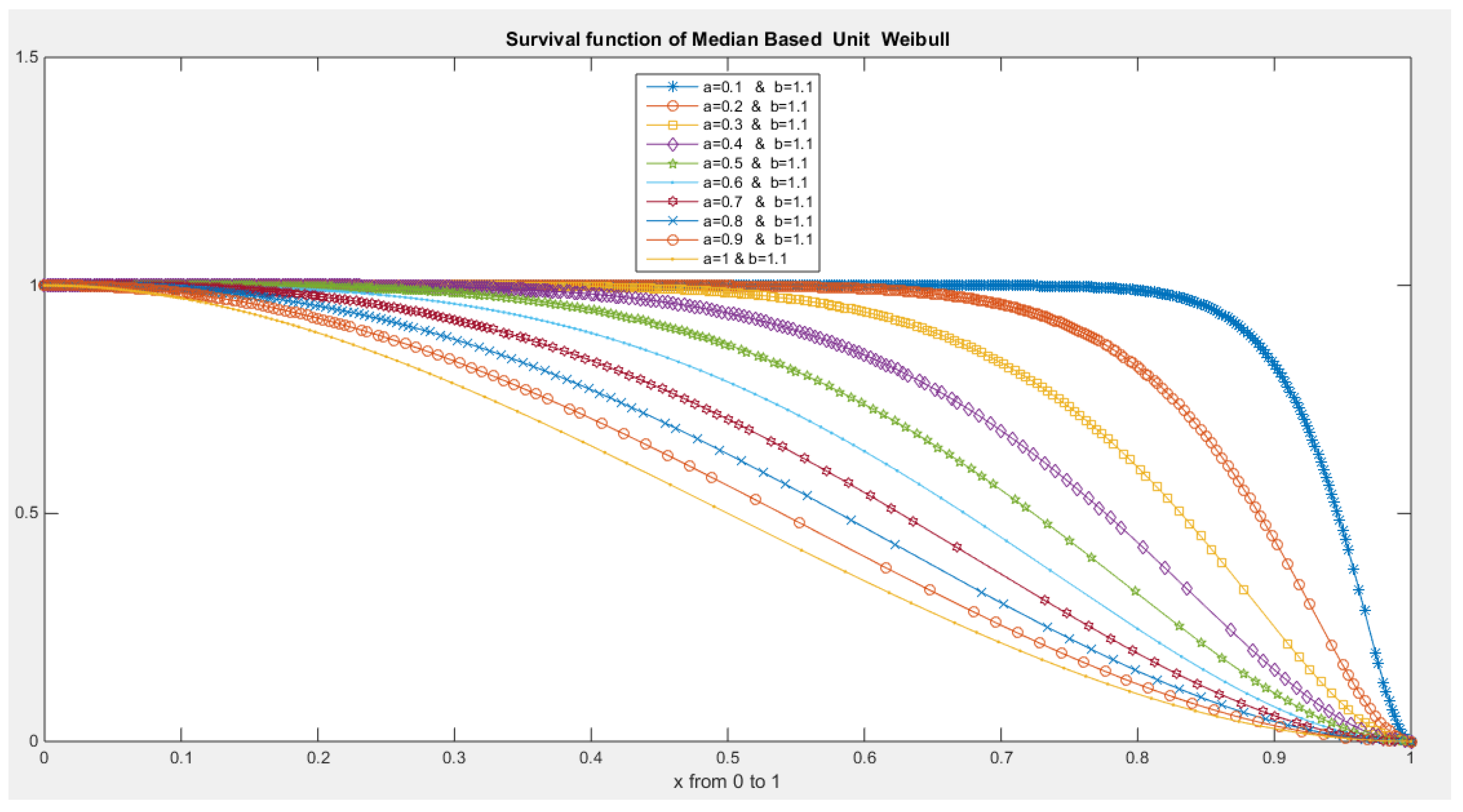
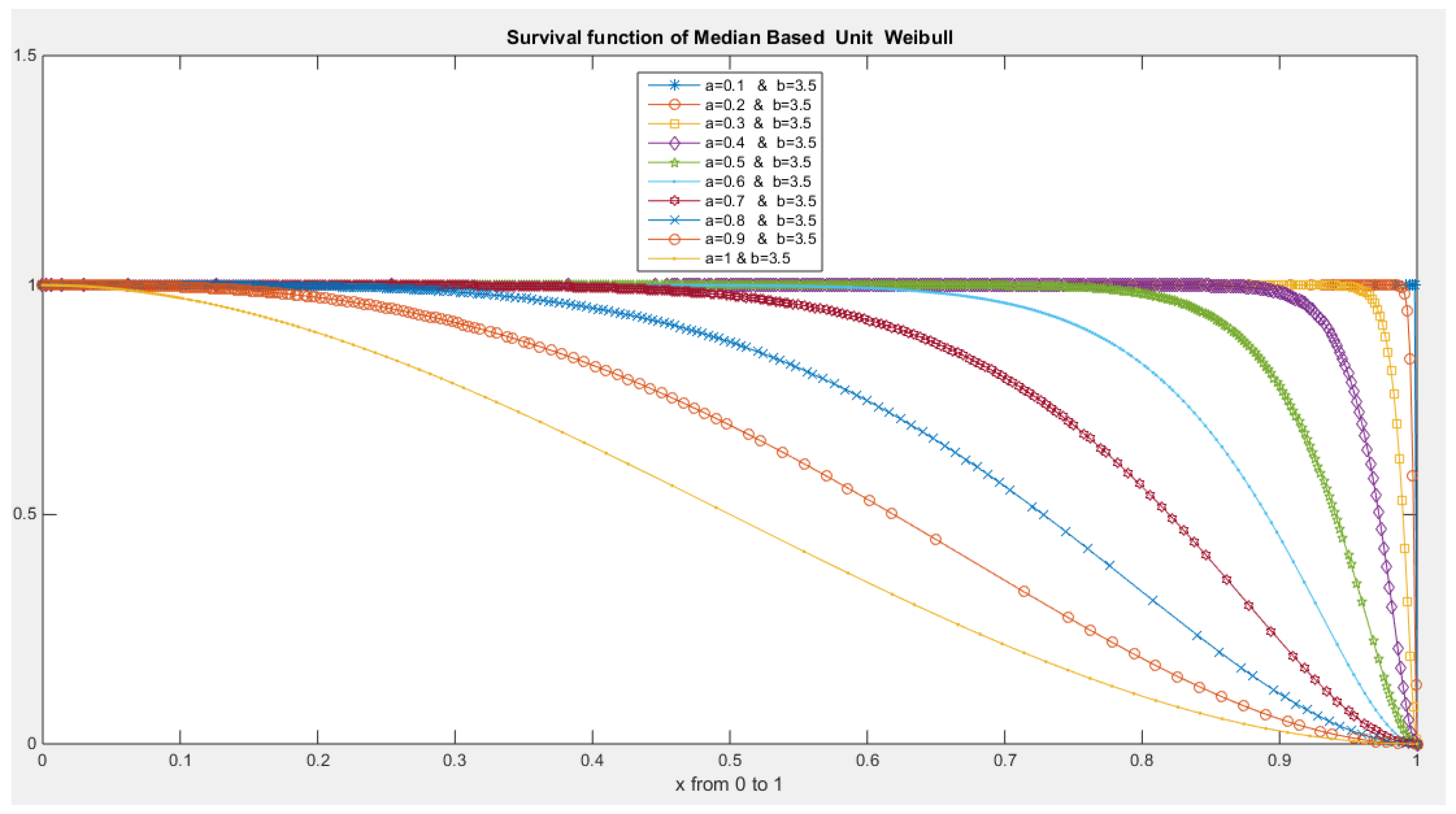
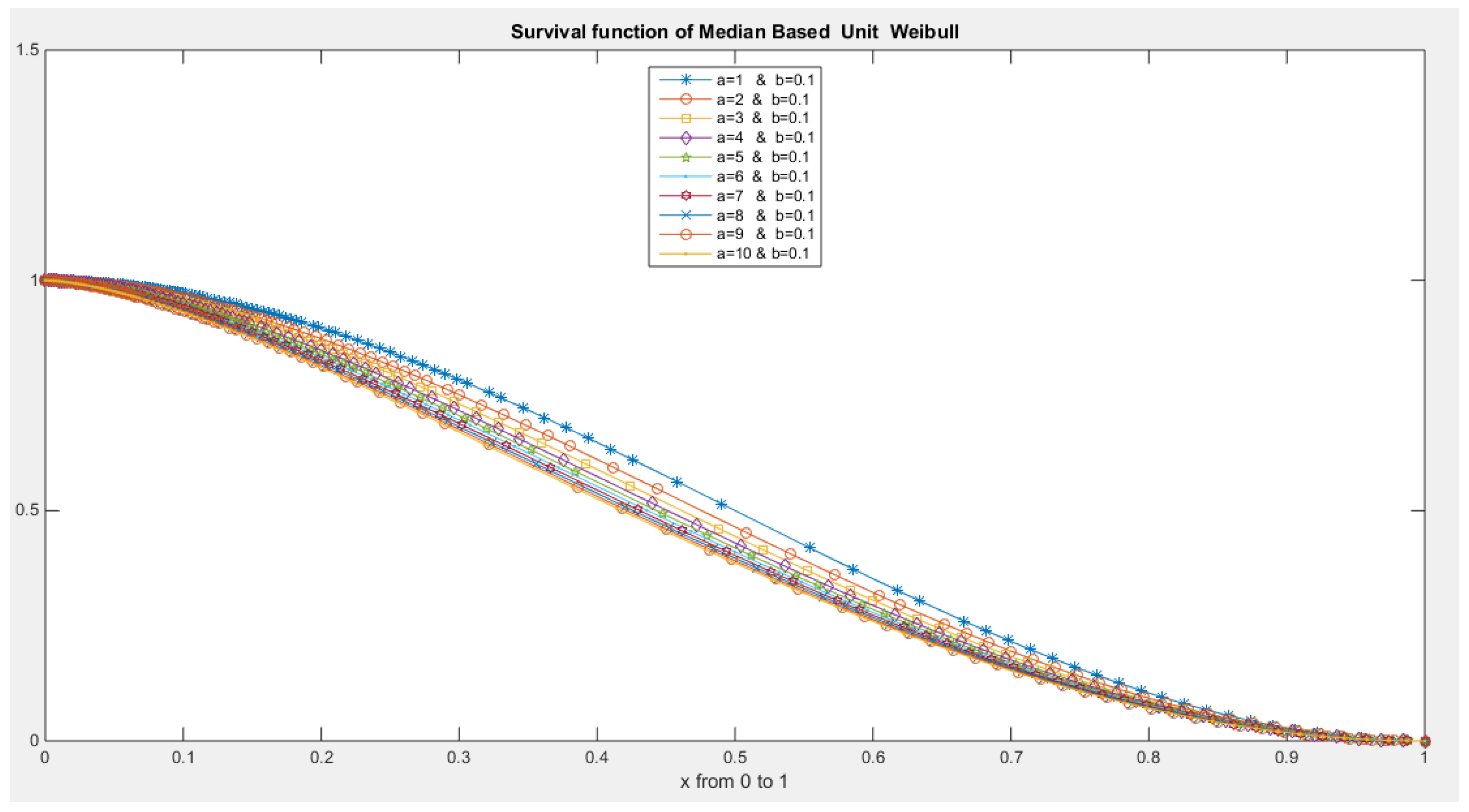
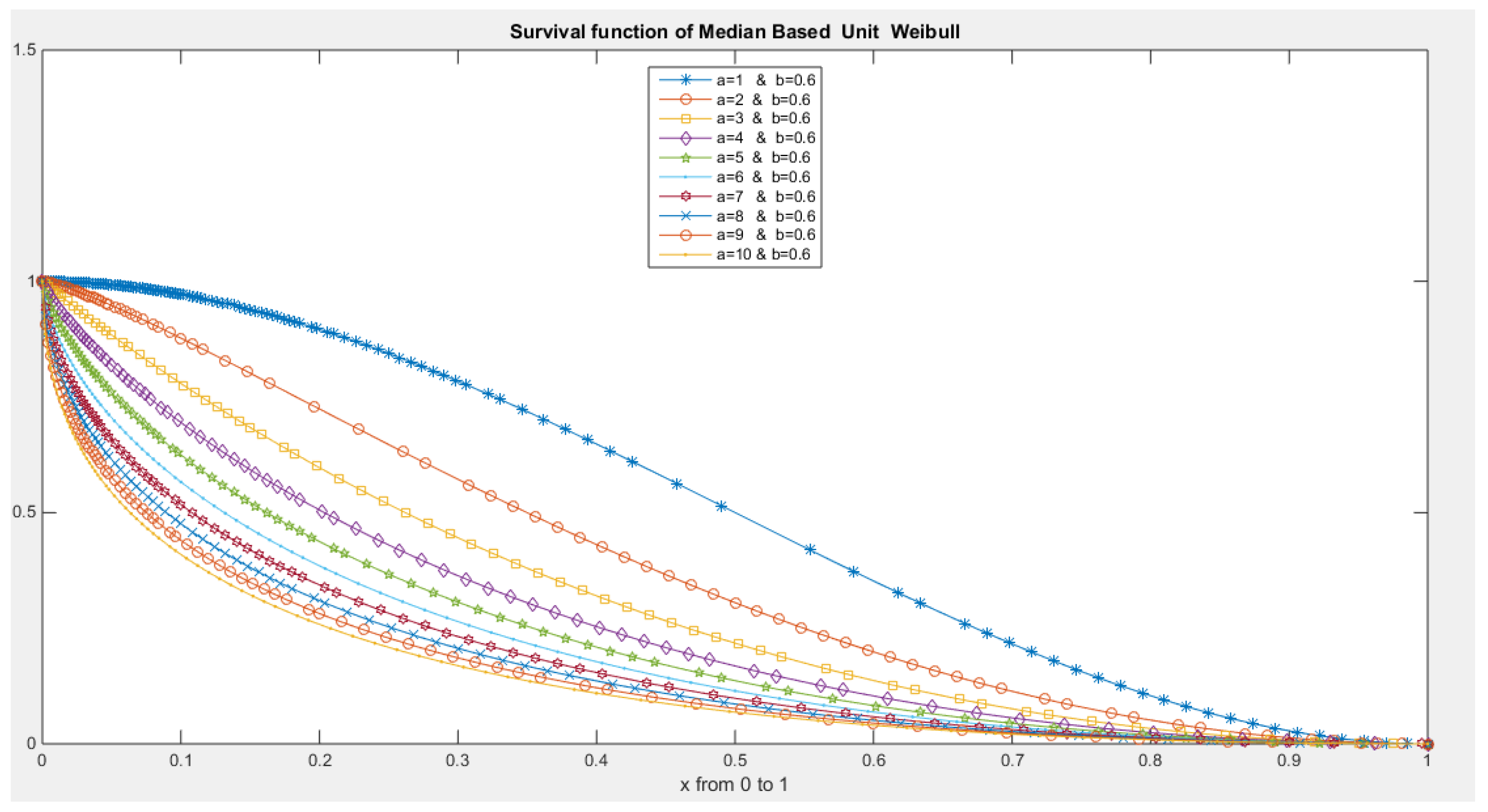
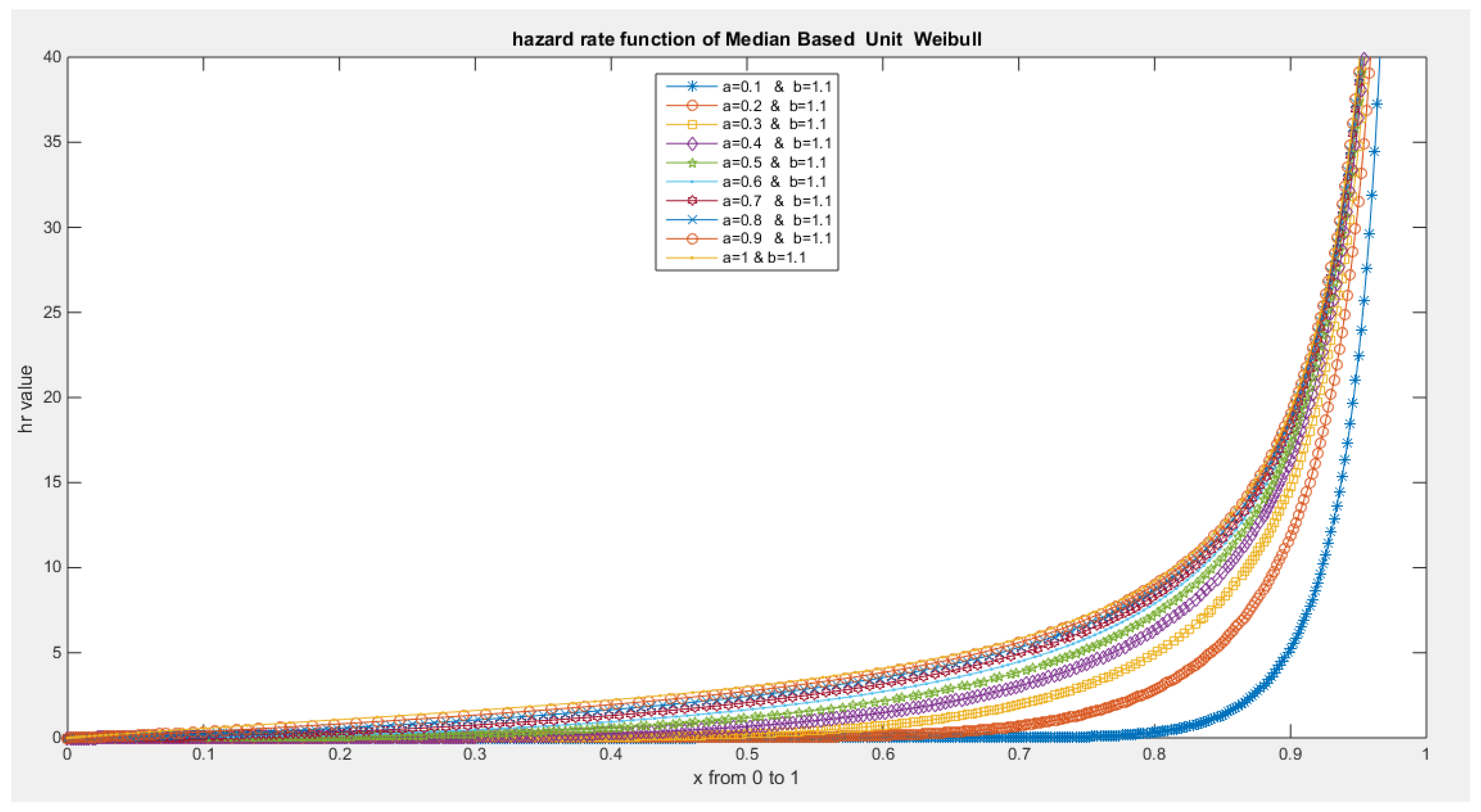
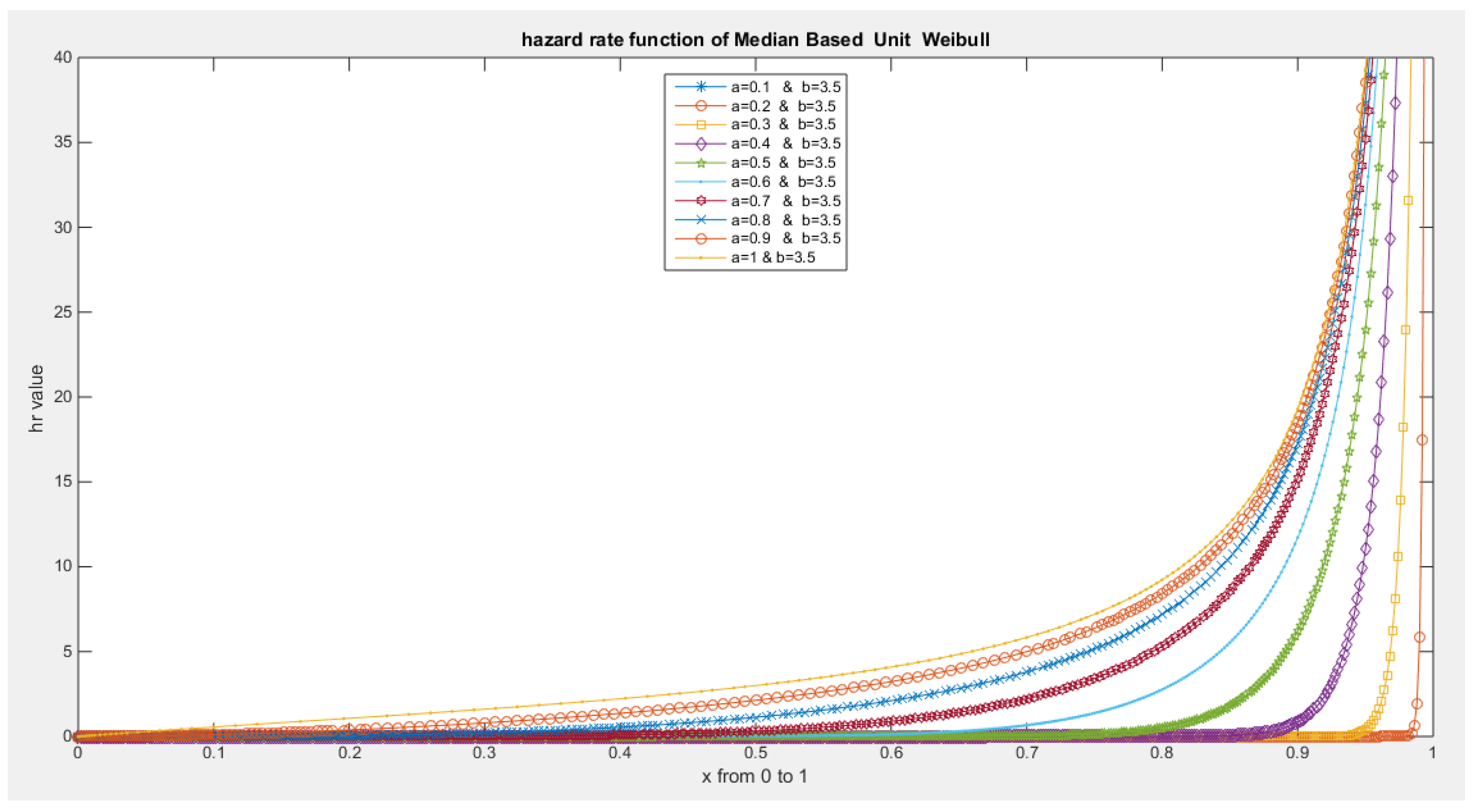
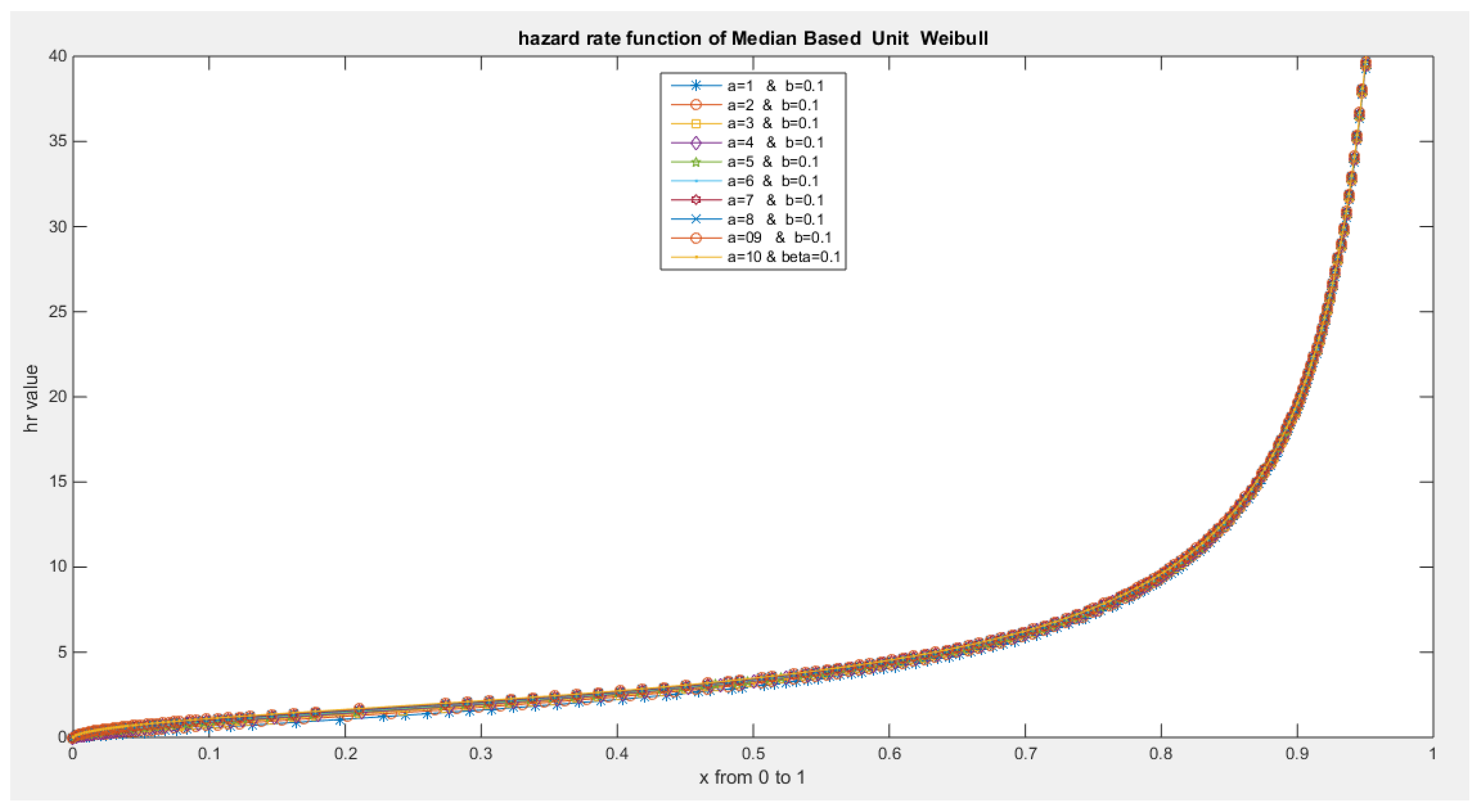
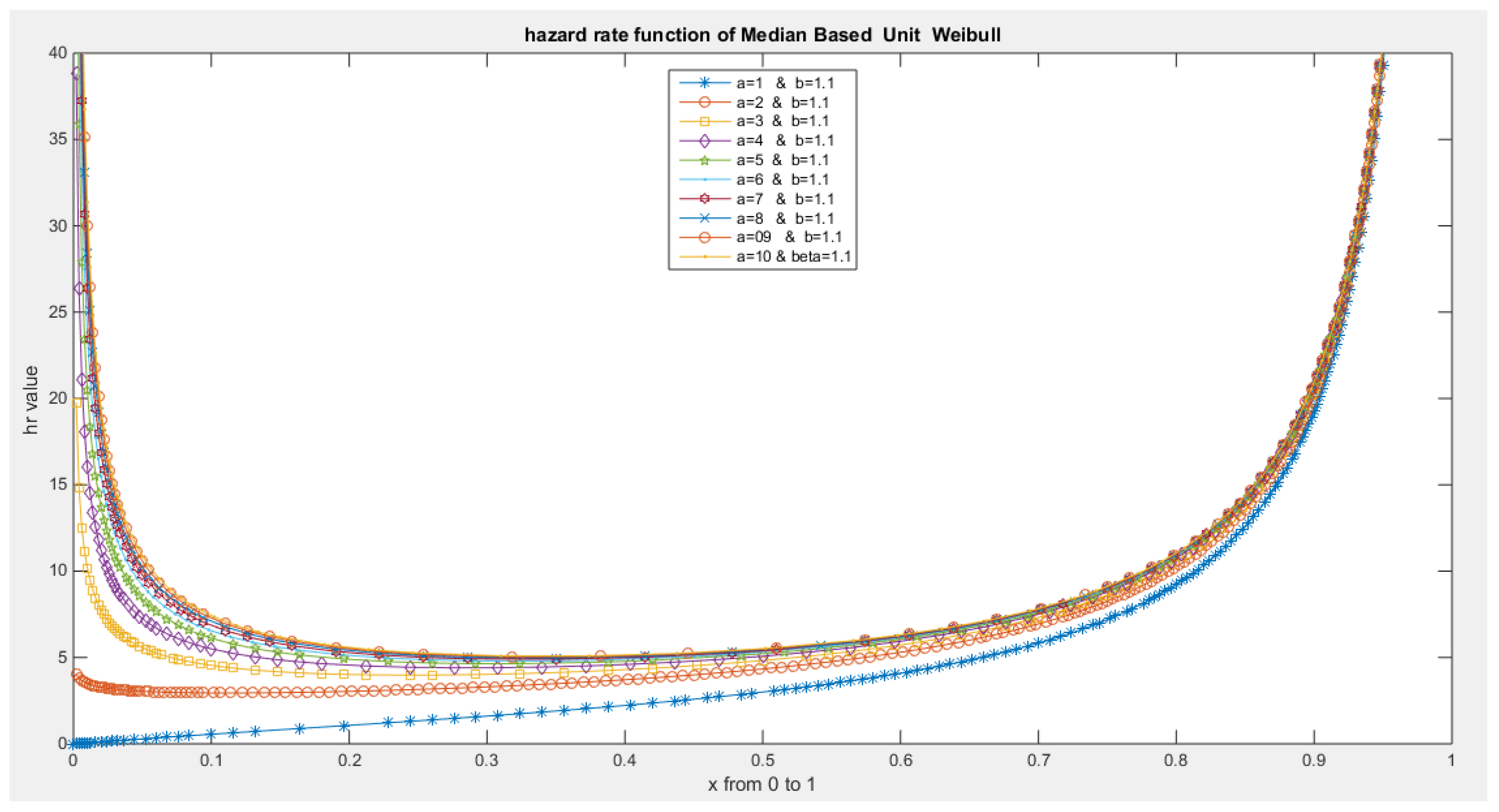
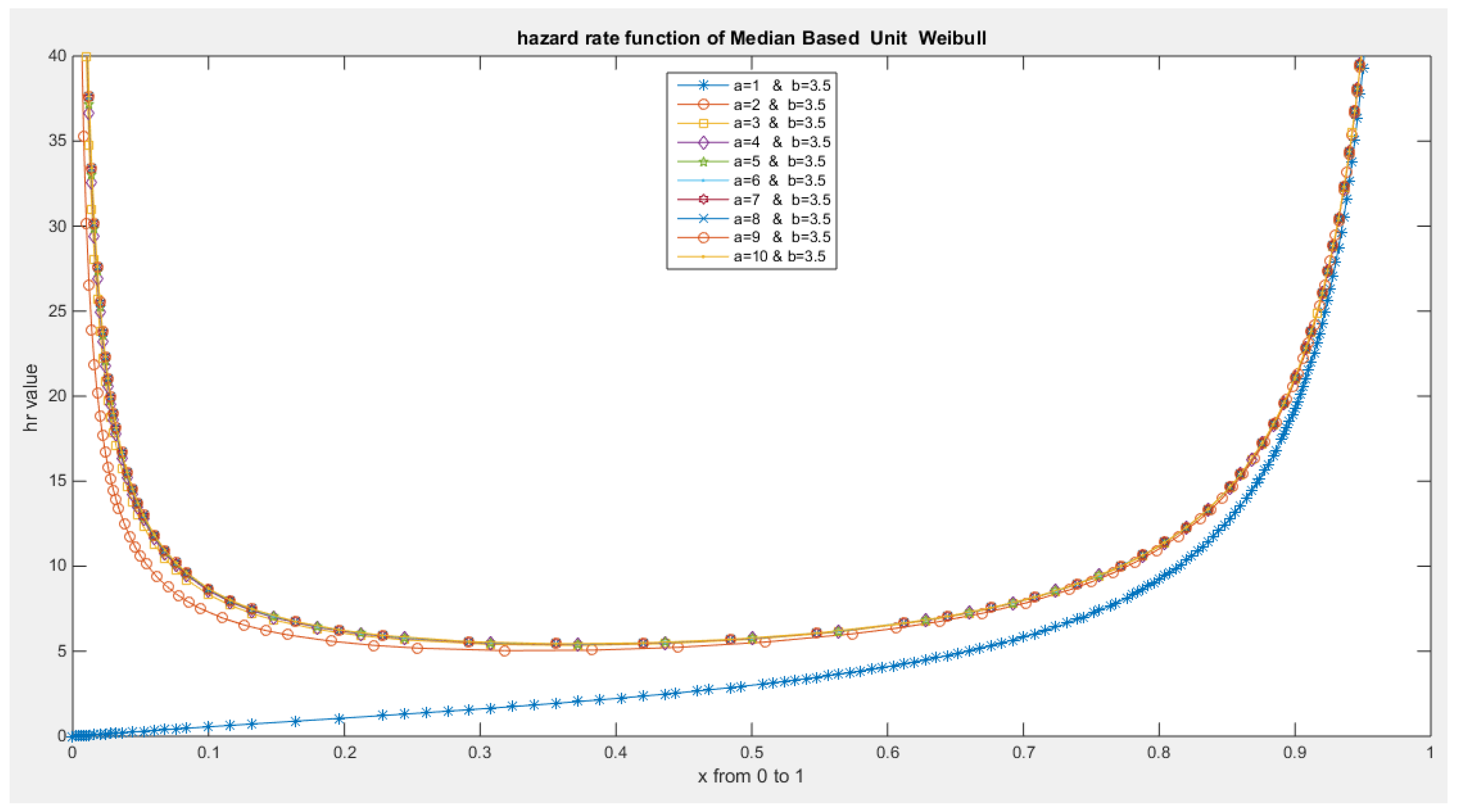
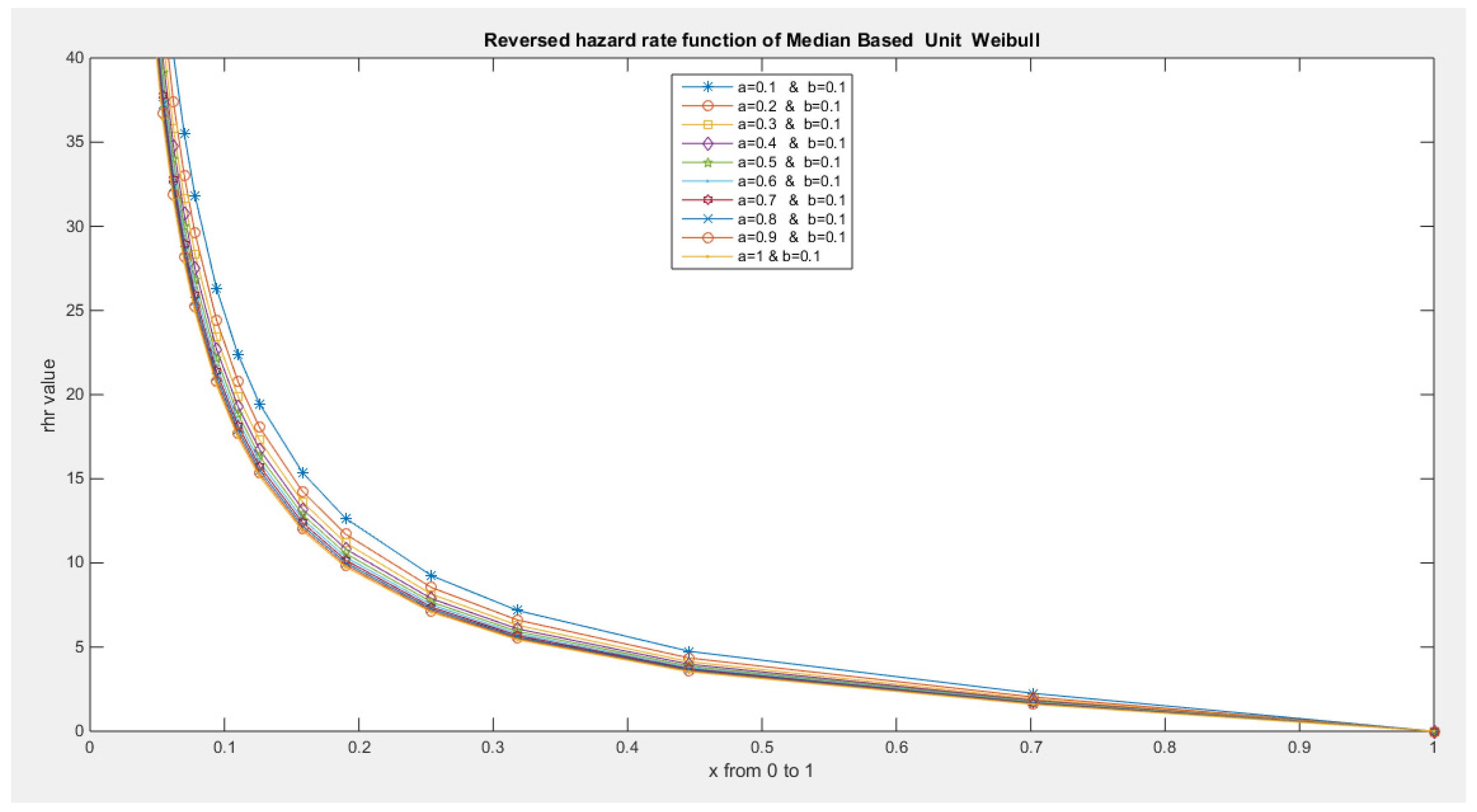
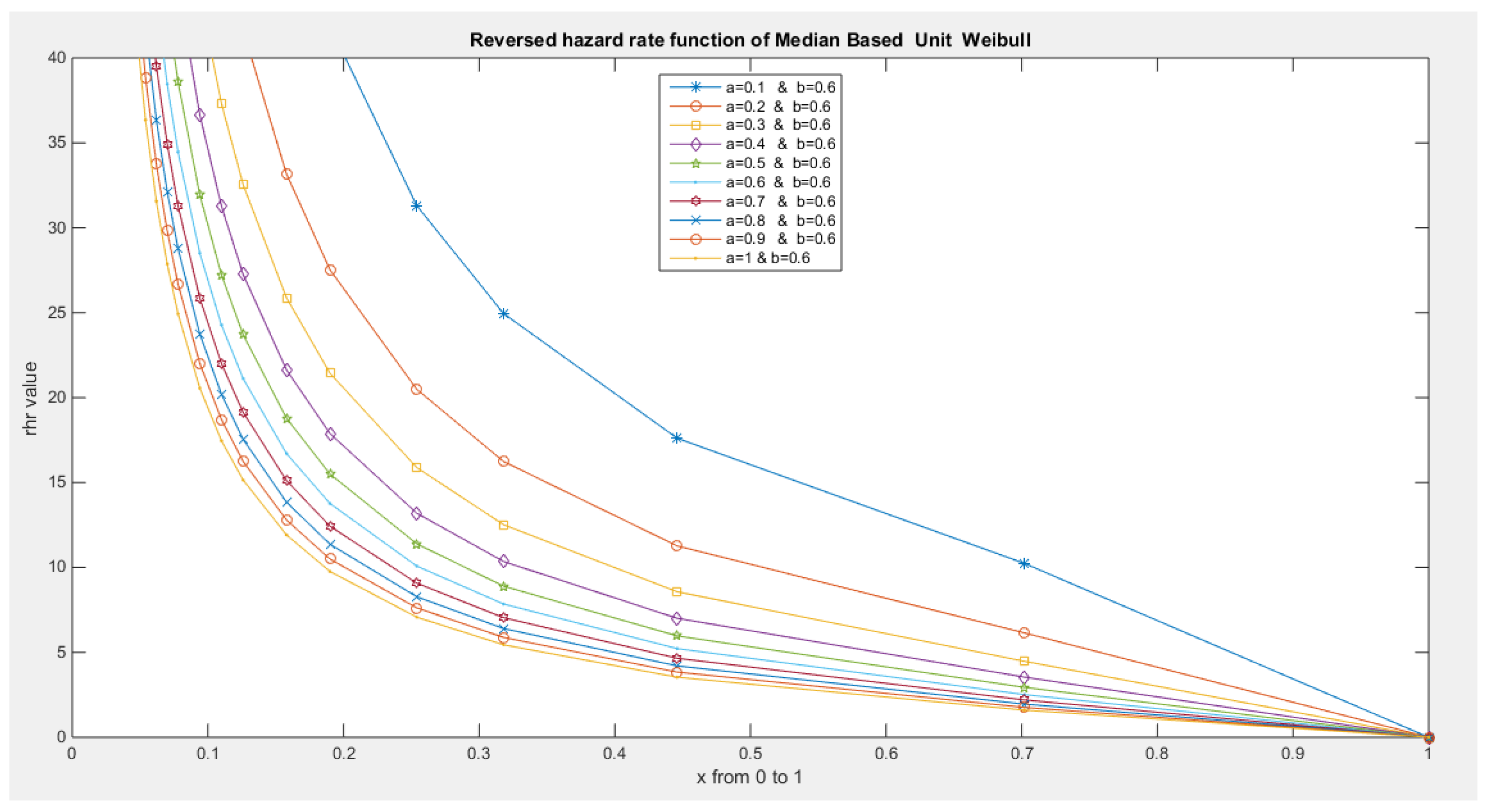
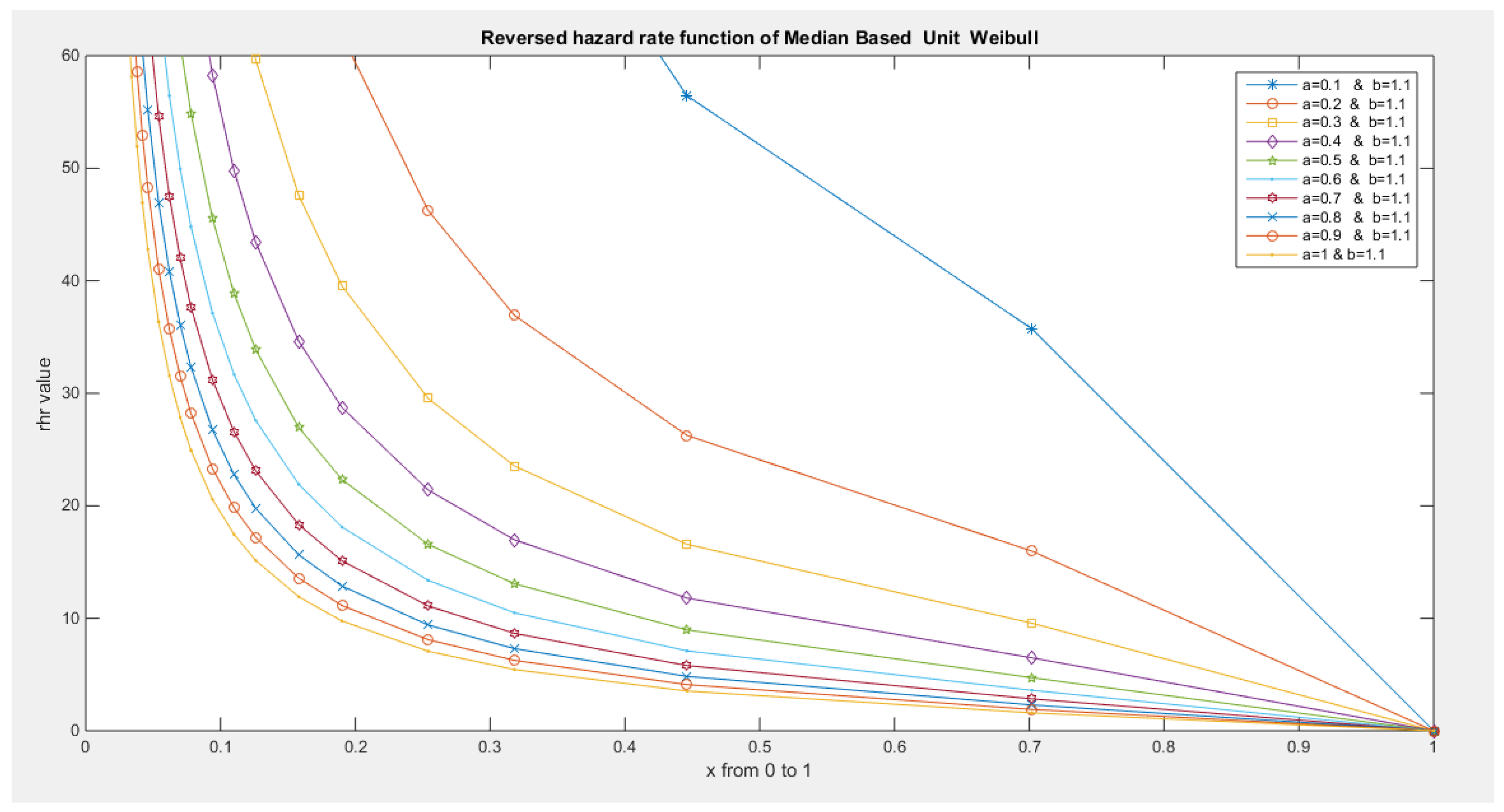
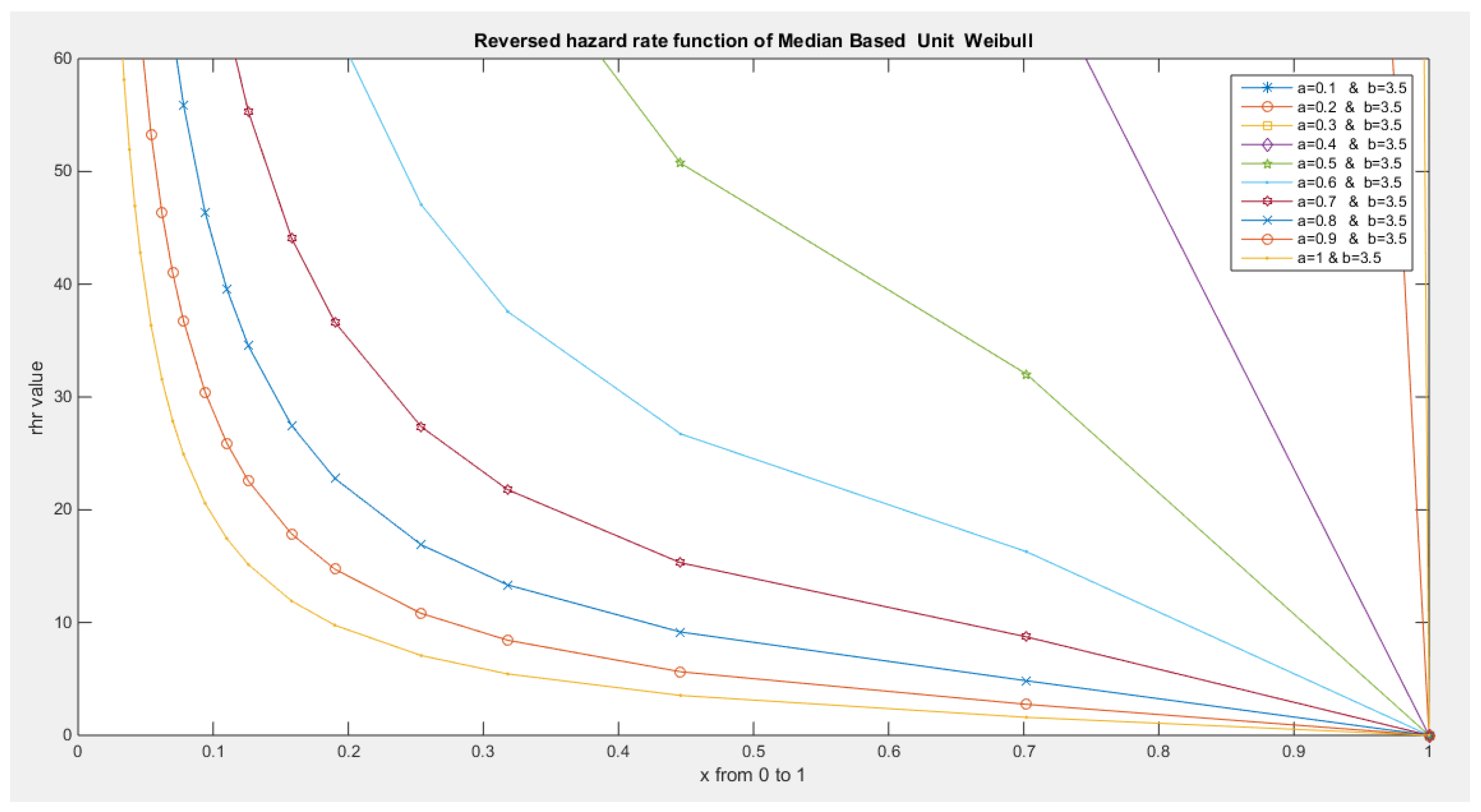
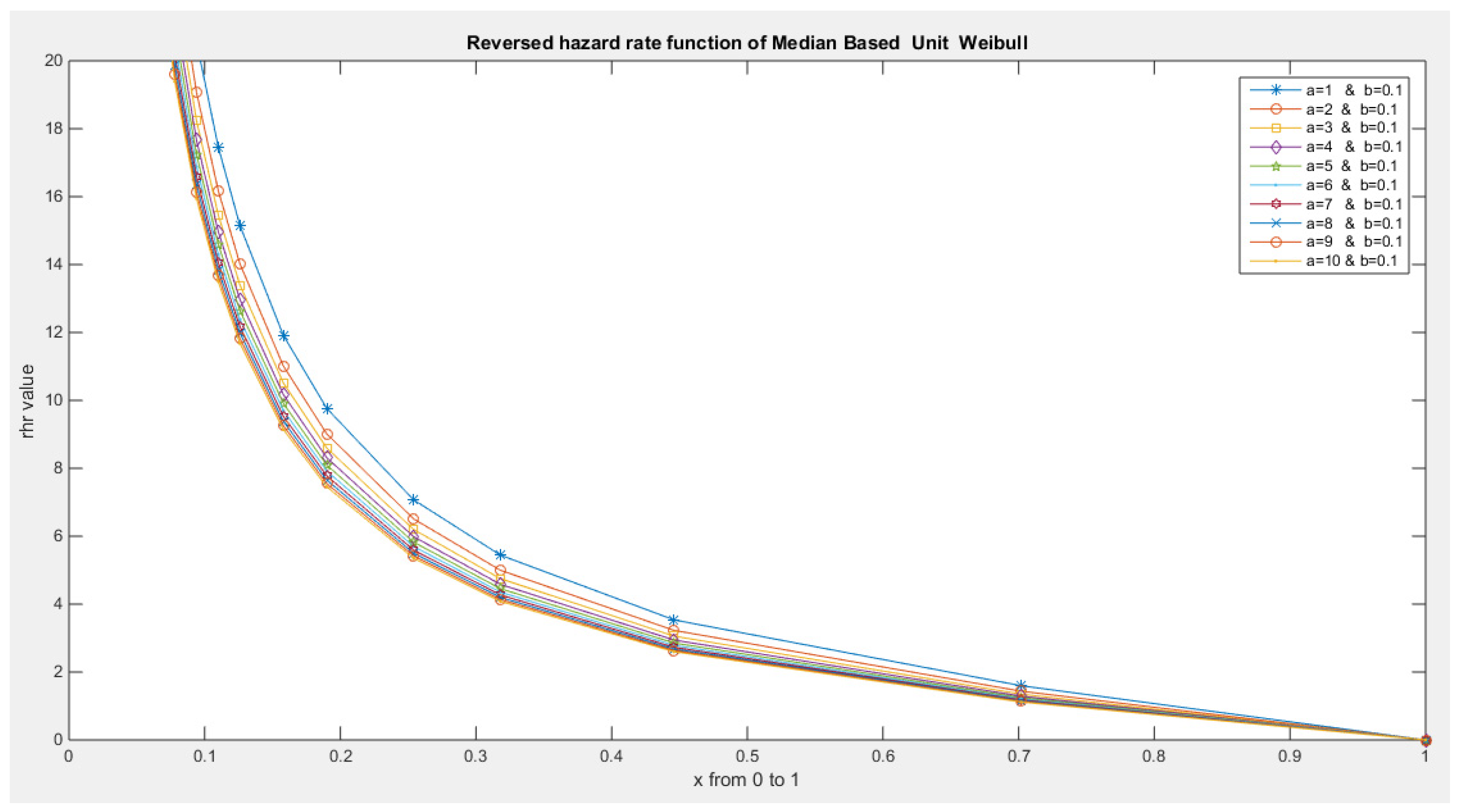
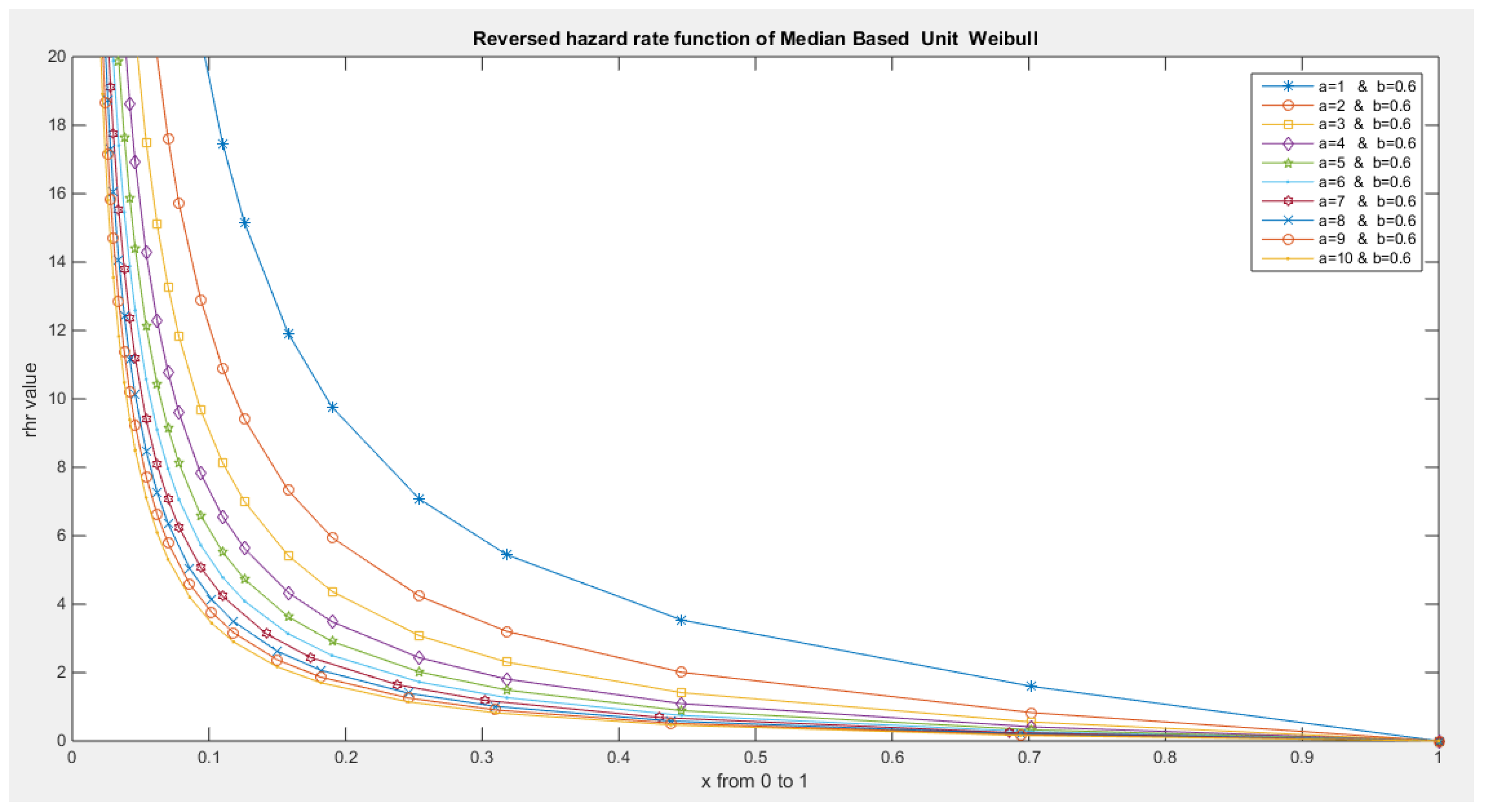
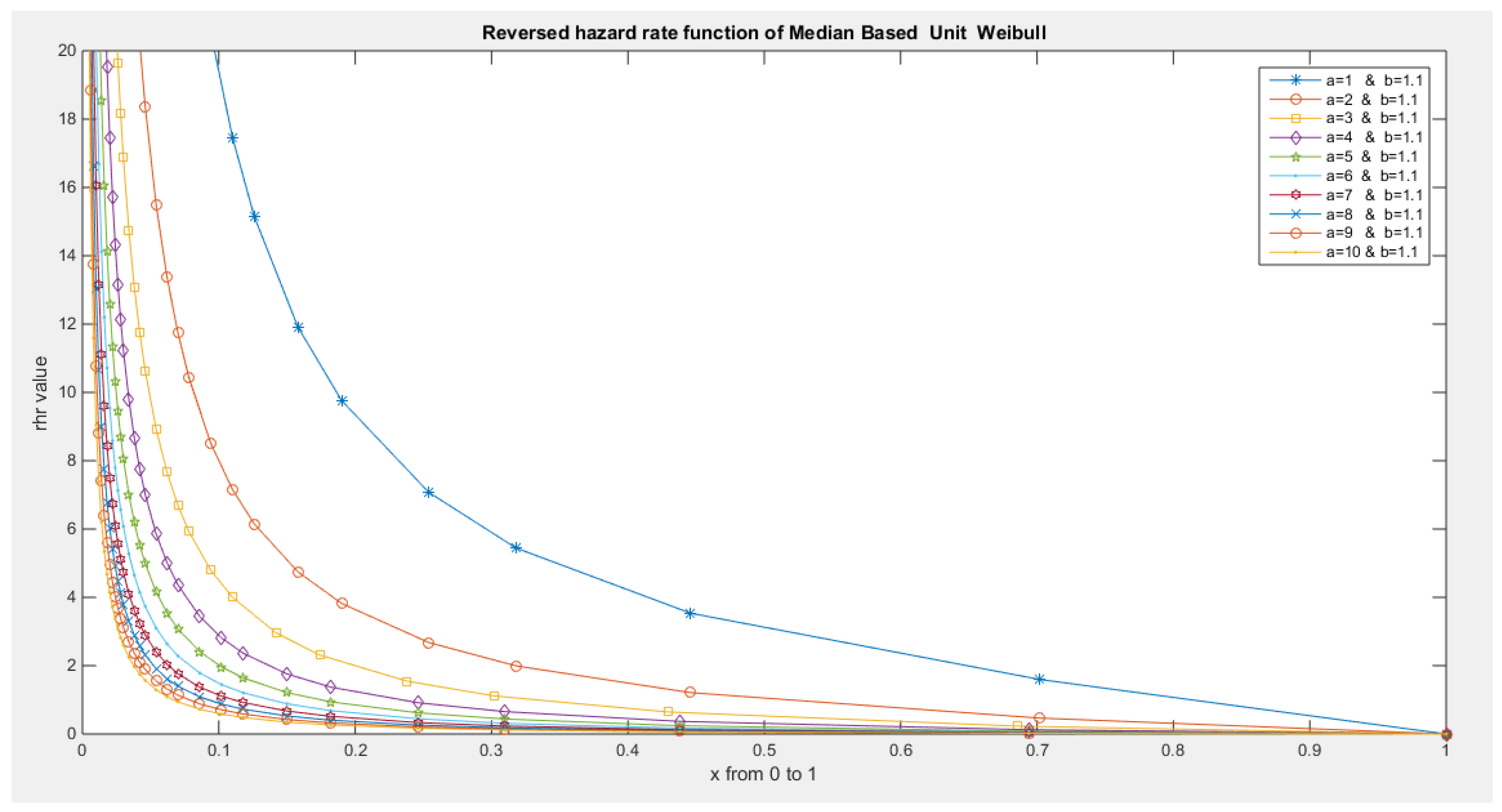
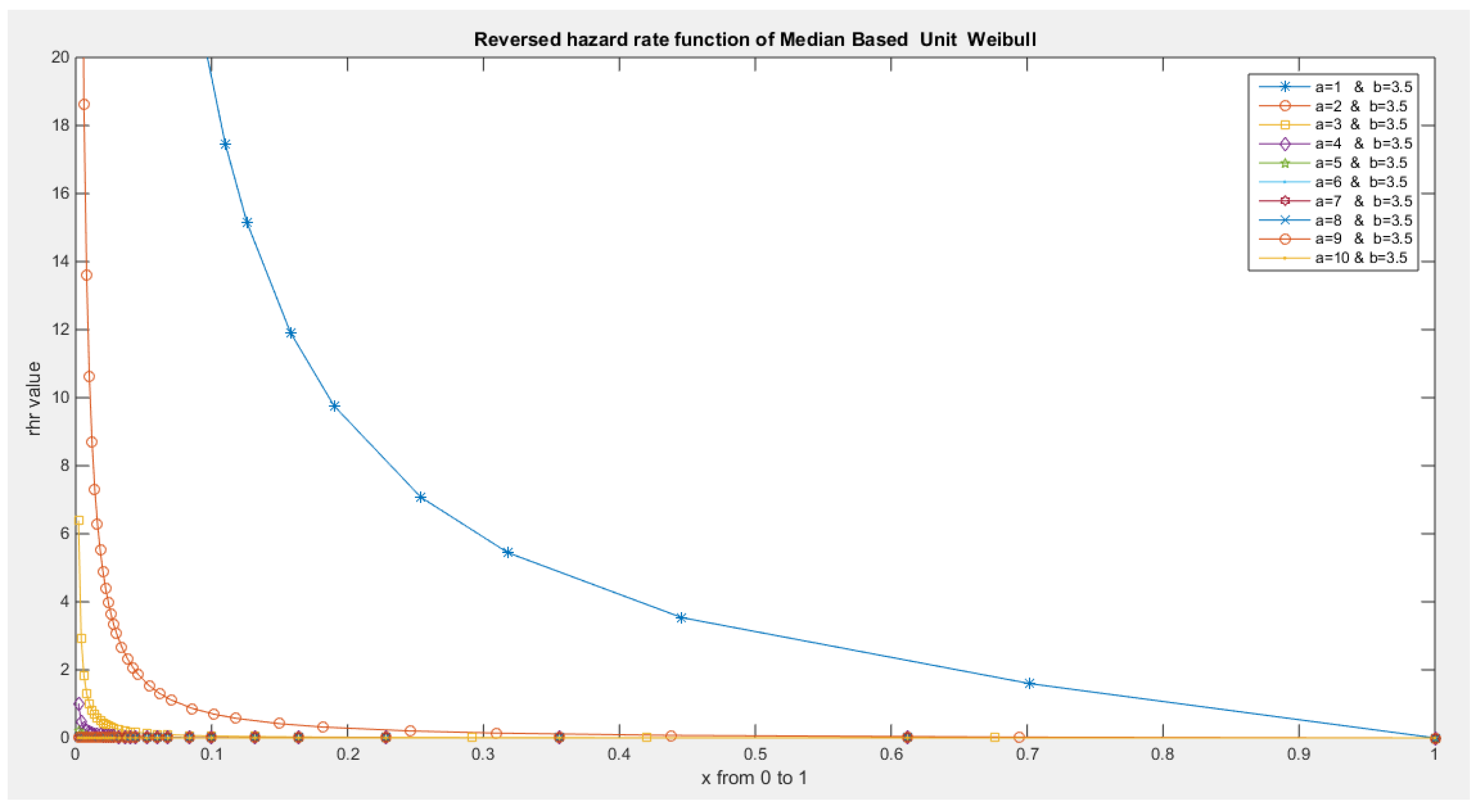
5-: Quantile Function:

u = F (y) = {3 y}^{\frac{2}{α^{β}}} - {2 y}^{\frac{3}{α^{β}}} = - 2 {(y^{\frac{1}{α^{β}}})}^{3} + 3 {(y^{\frac{1}{α^{β}}})}^{2}

The inverse of the CDF is used to obtain y , the real root of this 3rd polynomial function is :

y = F^{- 1} (y) = {\{- . 5 (c o s [\frac{{c o s}^{- 1} (1 - 2 u)}{3}] - \sqrt{3} s i n [\frac{{c o s}^{- 1} (1 - 2 u)}{3}]) + . 5\}}^{α^{β}}

To generate random variable distributed as MBUR:

1-: Generate uniform random variable (0,1): $u ~ u n i f o r m (0,1)$ .
2-: Choose alpha and beta levels
3-: Substitute the above values of u (0,1) and the chosen alpha and beta in the quantile function, to obtain y distributed as $y ~ M B U W (α, β)$

6-: rth Raw Moments:

E (y^{r}) = \frac{6}{(2 + r α^{β}) (3 + r α^{β})} E (y^{r}) = \int_{0}^{1} y^{r} \frac{6}{α^{β}} [1 - y^{\frac{1}{α^{β}}}] y^{(\frac{2}{α^{β}} - 1)} d y E (y) = \frac{6}{(2 + α^{β}) (3 + α^{β})} E (y^{2}) = \frac{6}{(2 + 2 α^{β}) (3 + 2 α^{β})} E (y^{3}) = \frac{6}{(2 + 3 α^{β}) (3 + 3 α^{β})} E (y^{4}) = \frac{6}{(2 + 4 α^{β}) (3 + 4 α^{β})} v a r (y) = E (y^{2}) - {[E (y)]}^{2} v a r (y) = \frac{78 α^{2 β} + 60 α^{3 β} + 6 α^{4 β}}{(6 + 10 α^{β} + 4 α^{2 β}) {(6 + 5 α^{β} + α^{2 β})}^{2}}

7-: Coefficient of Skewness:

E \frac{{(y - μ)}^{3}}{σ^{3}} = \frac{E (y^{3}) - 3 μ E (y^{2}) + 3 μ^{2} E (y) - μ^{3}}{σ^{3}} = \frac{E (y^{3}) - 3 μ [E (y^{2}) - μ E (y)] - μ^{3}}{σ^{3}} = \frac{E (y^{3}) - 3 μ [E (y^{2}) - μ μ] - μ^{3}}{σ^{3}} c o e f f i c i e n t o f s k e w n e s s = \frac{E (y^{3}) - 3 μ σ^{3} - μ^{3}}{σ^{3}} = \frac{E (y^{3}) - μ ({3 σ}^{2} + μ^{2})}{σ^{3}}

8-: Coefficient of Kurtosis:

E \frac{{(y - μ)}^{4}}{σ^{4}} = \frac{E (y^{4}) - 4 μ E (y^{3}) + 6 μ^{2} E (y^{2}) - {3 μ}^{4}}{σ^{4}} = \frac{E (y^{4}) - 4 μ E (y^{3}) + 6 μ^{2} [σ^{2} + μ^{2}] - {3 μ}^{4}}{σ^{4}} = \frac{E (y^{4}) - 4 μ E (y^{3}) + 6 μ^{2} σ^{2} + 6 μ^{4} - {3 μ}^{4}}{σ^{4}} = \frac{E (y^{4}) - 4 μ E (y^{3}) + 6 μ^{2} σ^{2} + 3 μ^{4}}{σ^{4}} = c o e f f i c i e n t o f K u r t o s i s = \frac{E (y^{4}) - 4 μ E (y^{3}) + 3 μ^{2} [{2 σ}^{2} + μ^{4}]}{σ^{4}}

9-: Coefficient of Variation :

C V = \frac{S}{μ}

The following Figures illustrate the graphs for the above coefficients

Figure 62. the variance and different coefficients with alpha ( from 0.1 to 6) & b=0.1.

Figure 63. the variance and different coefficients with alpha ( from 0.1 to 6) & b=0.6.

Figure 64. the variance and different coefficients with alpha ( from 0.1 to 6) & b=1.1.

Figure 64. the variance and different coefficients with alpha ( from 0.1 to 6) & b=3.5.

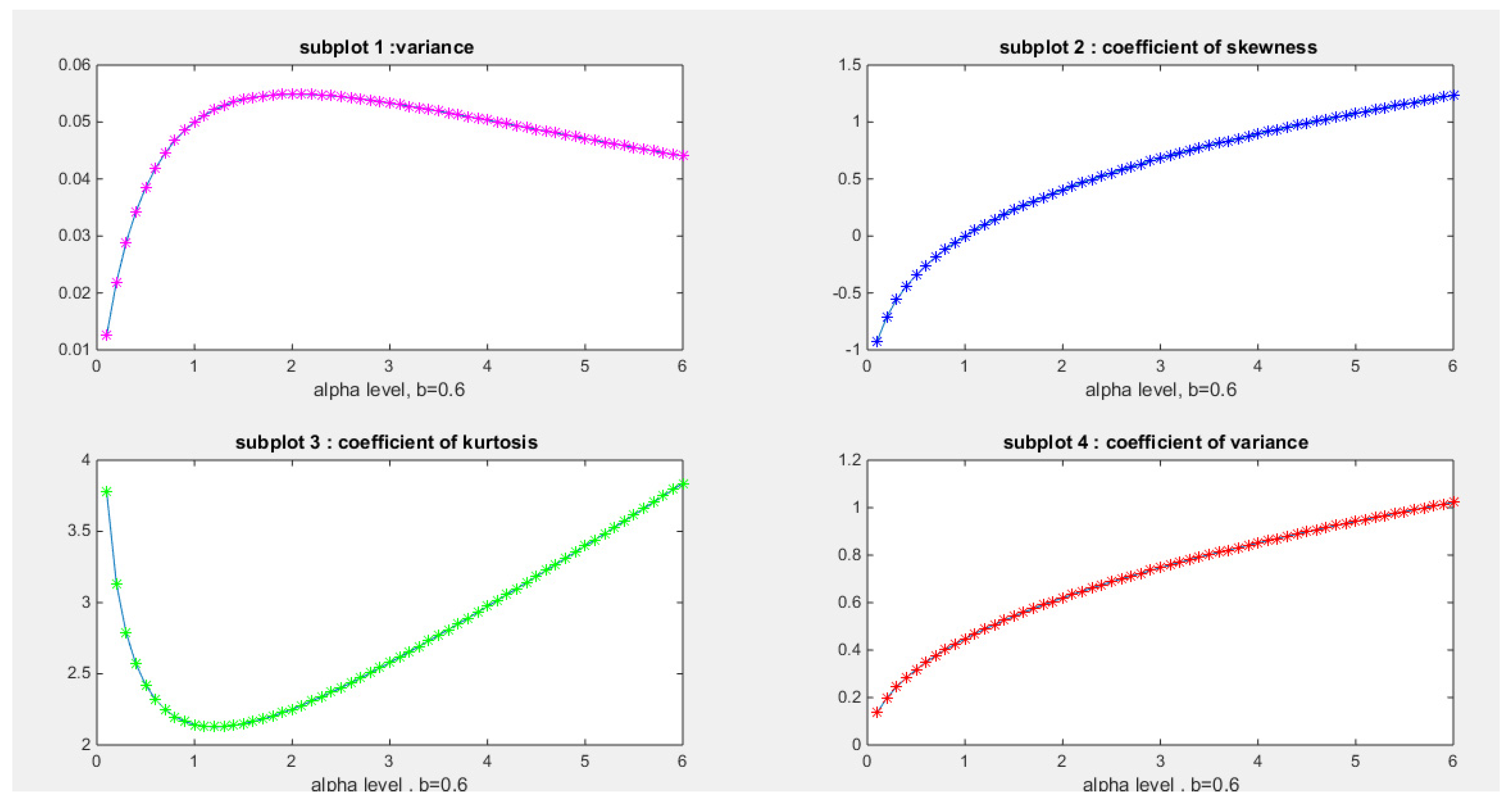
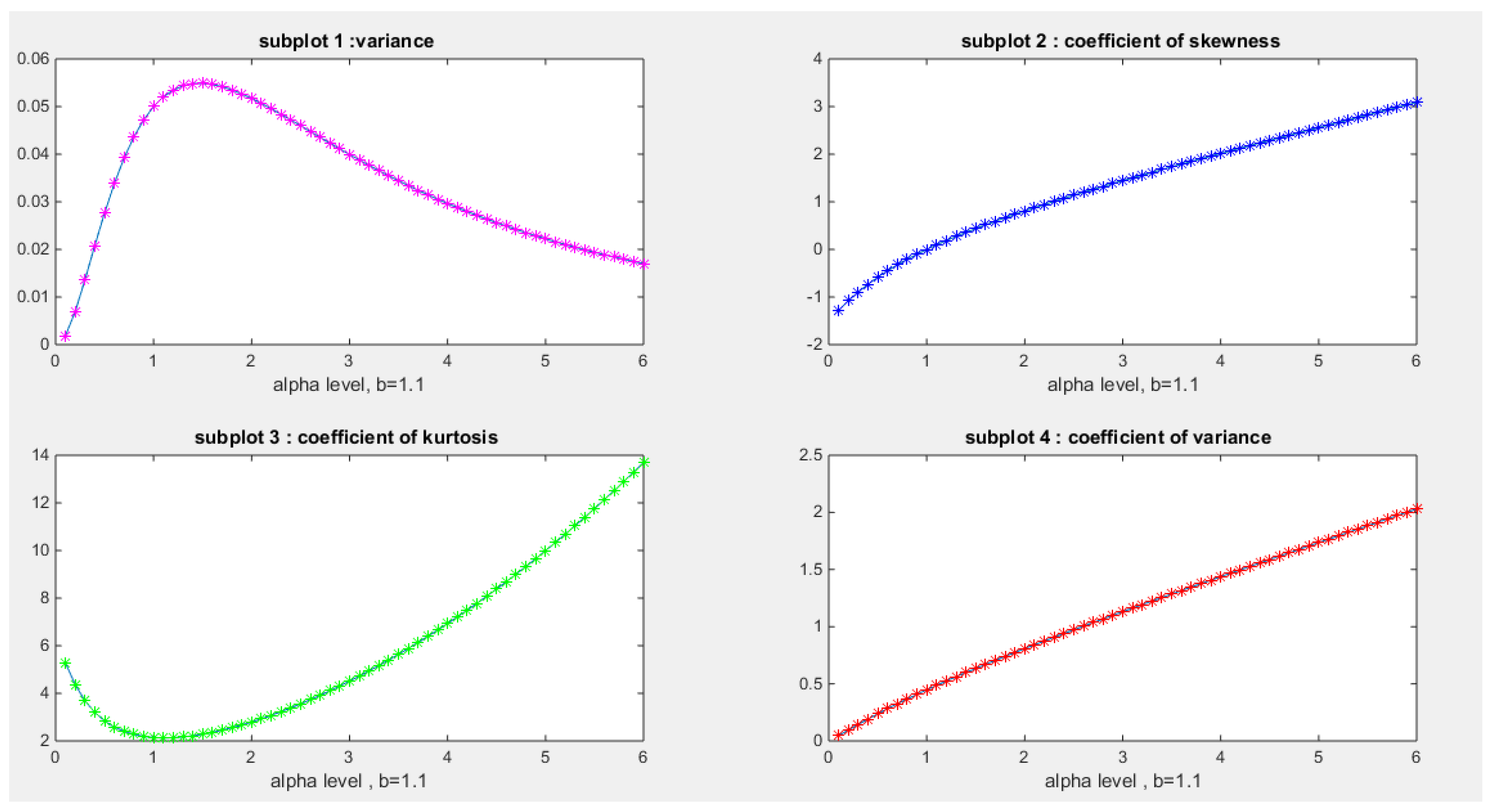
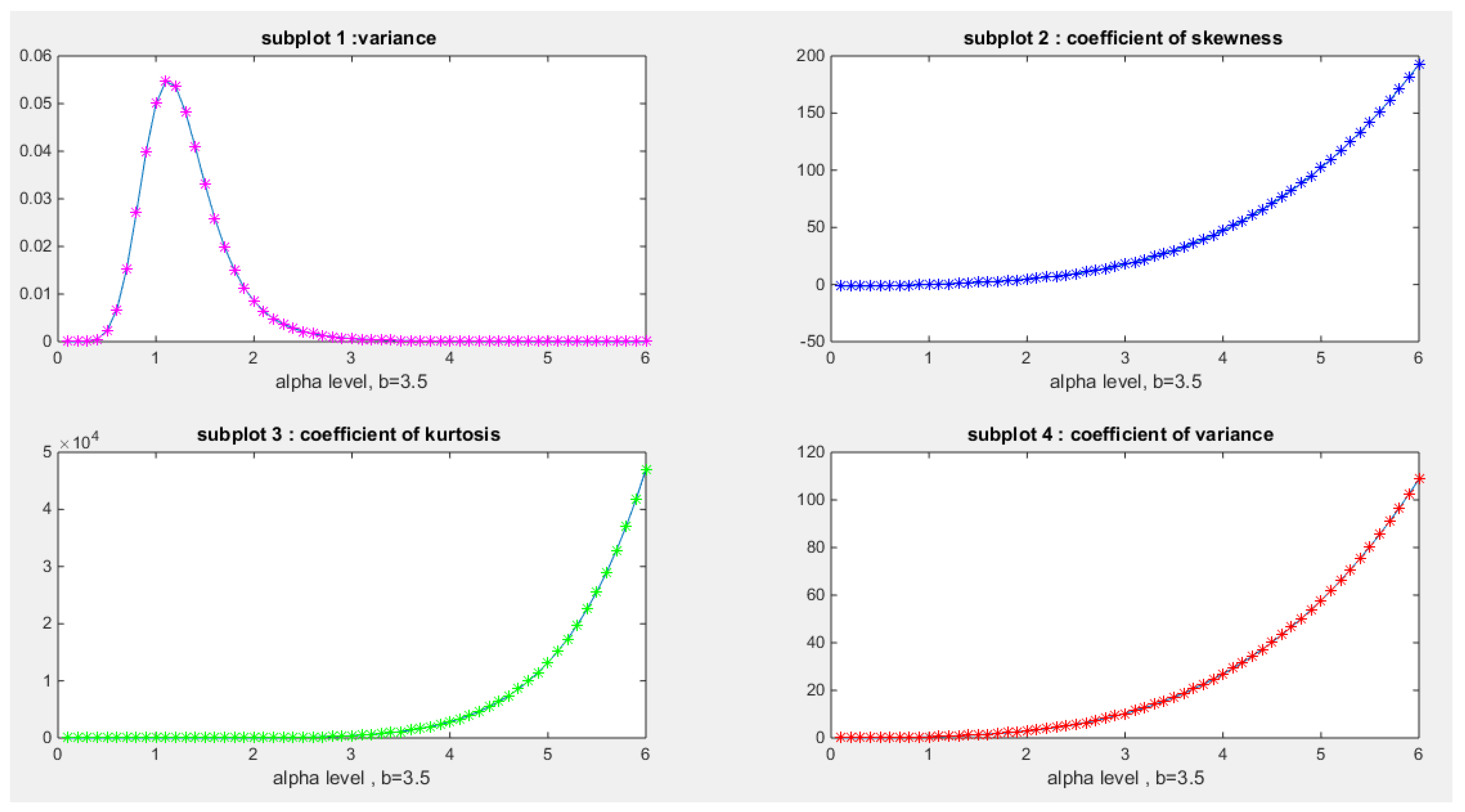
10-: rth incomplete Moments:

E (y^{r} | y < t) = \int_{0}^{t} y^{r} \frac{6}{α^{β}} [1 - y^{\frac{1}{α^{β}}}] y^{(\frac{2}{α^{β}} - 1)} d y E (y) = \frac{6 t^{\frac{2}{α^{β}} + r}}{(2 + r α^{β})} - \frac{6 t^{\frac{3}{α^{β}} + r}}{(3 + r α^{β})}

Conclusion

This new distribution overcomes some of the weaknesses of the weibull distribution as regard lack of bathtub and unimodal shapes. It is also defined over the unit interval, so it can be used to fit proportions and ratios. It has a well closed form of quantile function and this makes it compatible for parametric quantile regression conditioning on the median or any other quantile rather than conditioning on the mean which is not a good candidate to describe central tendency in such highly skewed distribution.

Future Work

The author is working on methods of estimation of this new distribution and for its applications in regression analysis.

Author Contributions

AI carried the conceptualization by formulating the goals, aims of the research article, formal analysis by applying the statistical, mathematical and computational techniques to synthesize and analyze the hypothetical data, carried the methodology by creating the model, software programming and implementation, supervision, writing, drafting, editing, preparation, and creation of the presenting work.

Funding

No funding resource. No funding roles in the design of the study and collection, analysis, and interpretation of data and in writing the manuscript are declared

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable

Data Availability Statement

Not applicable. Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.

Acknowledgement

Not applicable

Conflicts of Interest

The author declares no competing interests of any type.

References

Consul, P. C., & Jain, G. C. (1971). On the log-gamma distribution and its properties. Statistische Hefte, 12(2), 100–106. [CrossRef]
Cordeiro, G. M., Ortega, E. M. M., & Nadarajah, S. (2010). The Kumaraswamy Weibull distribution with application to failure data. Journal of the Franklin Institute, 347(8), 1399–1429. [CrossRef]
Eugene, N., Lee, C., & Famoye, F. (2002). BETA-NORMAL DISTRIBUTION AND ITS APPLICATIONS. Communications in Statistics—Theory and Methods, 31(4), 497–512. [CrossRef]
Grassia, A. (1977). ON A FAMILY OF DISTRIBUTIONS WITH ARGUMENT BETWEEN 0 AND 1 OBTAINED BY TRANSFORMATION OF THE GAMMA AND DERIVED COMPOUND DISTRIBUTIONS. Australian Journal of Statistics, 19(2), 108–114. [CrossRef]
Gül, H. H. (2023). Unit-Weibull Distribution: Different Method of Estimations. Karadeniz Fen Bilimleri Dergisi, 13(2), 547–560. [CrossRef]
Gündüz, S., & Korkmaz, M. Ç. (2020). A New Unit Distribution Based On The Unbounded Johnson Distribution Rule: The Unit Johnson SU Distribution. Pakistan Journal of Statistics and Operation Research, 471–490. [CrossRef]
Haq, M. A. U., Hashmi, S., Aidi, K., Ramos, P. L., & Louzada, F. (2023). Unit Modified Burr-III Distribution: Estimation, Characterizations and Validation Test. Annals of Data Science, 10(2), 415–440. [CrossRef]
Johnson, N. L. (1949). Systems of Frequency Curves Generated by Methods of Translation. Biometrika, 36(1/2), 149–176. [CrossRef]
Khan, M. S., & King, R. (2013). Transmuted Modified Weibull Distribution: A Generalization of the Modified Weibull Probability Distribution. European Journal of Pure and Applied Mathematics, 6(1), 66–88. https://www.ejpam.com/index.php/ejpam/article/view/1606.
Khan, M. S., King, R., & Hudson, I. L. (2017). Transmuted Weibull distribution: Properties and estimation. Communications in Statistics—Theory and Methods, 46(11), 5394–5418. [CrossRef]
Korkmaz, M. Ç., & Chesneau, C. (2021). On the unit Burr-XII distribution with the quantile regression modeling and applications. Computational and Applied Mathematics, 40(1), 29. [CrossRef]
Kumaraswamy, P. (1980). A generalized probability density function for double-bounded random processes. Journal of Hydrology, 46(1–2), 79–88. [CrossRef]
Lee, C., Famoye, F., & Olumolade, O. (2007). Beta-Weibull Distribution: Some Properties and Applications to Censored Data. Journal of Modern Applied Statistical Methods, 6(1), 173–186. [CrossRef]
Marshall, A. W., & Olkin, I. (1997). A New Method for Adding a Parameter to a Family of Distributions with Application to the Exponential and Weibull Families. Biometrika, 84(3), 641–652. https://www.jstor.org/stable/2337585.
Maya, R., Jodrá, P., Irshad, M. R., & Krishna, A. (2024). The unit Muth distribution: Statistical properties and applications. Ricerche Di Matematica, 73(4), 1843–1866. [CrossRef]
Mazucheli et al. (2018a). THE UNIT-WEIBULL DISTRIBUTION AND ASSOCIATED INFERENCE. Journal of Applied Probability and Statisitcs, 13(2), 1–22.
Mazucheli, J., Maringa, A. F., & Dey, S. (2019). Unit-Gompertz Distribution with Applications. Statistica, Vol 79, 25-43 Pages. [CrossRef]
Mazucheli, J., Menezes, A. F. B., & Chakraborty, S. (2019). On the one parameter unit-Lindley distribution and its associated regression model for proportion data. Journal of Applied Statistics, 46(4), 700–714. [CrossRef]
Mazucheli, J., Menezes, A. F. B., & Dey, S. (2018b). Improved maximum-likelihood estimators for the parameters of the unit-gamma distribution. Communications in Statistics—Theory and Methods, 47(15), 3767–3778. [CrossRef]
Mazucheli, J., Menezes, A. F. B., Fernandes, L. B., De Oliveira, R. P., & Ghitany, M. E. (2020). The unit-Weibull distribution as an alternative to the Kumaraswamy distribution for the modeling of quantiles conditional on covariates. Journal of Applied Statistics, 47(6), 954–974. [CrossRef]
Modi, K., & Gill, V. (2020). Unit Burr-III distribution with application. Journal of Statistics and Management Systems, 23(3), 579–592. [CrossRef]
Mudholkar, G. S., & Srivastava, D. K. (1993). Exponentiated Weibull family for analyzing bathtub failure-rate data. IEEE Transactions on Reliability, 42(2), 299–302. IEEE Transactions on Reliability. [CrossRef]
Silva, G. O., Ortega, E. M. M., & Cordeiro, G. M. (2010). The beta modified Weibull distribution. Lifetime Data Analysis, 16(3), 409–430. [CrossRef]
Singla, N., Jain, K., & Kumar Sharma, S. (2012). The Beta Generalized Weibull distribution: Properties and applications. Reliability Engineering & System Safety, 102, 5–15. [CrossRef]
Tadikamalla, P. R. (1981). On a family of distributions obtained by the transformation of the gamma distribution. Journal of Statistical Computation and Simulation, 13(3–4), 209–214. [CrossRef]
Tadikamalla, P. R., & Johnson, N. L. (1982). Systems of frequency curves generated by transformations of logistic variables. Biometrika, 69(2), 461–465. [CrossRef]
Topp, C. W., & Leone, F. C. (1955). A Family of J-Shaped Frequency Functions. Journal of the American Statistical Association, 50(269), 209–219. [CrossRef]
Weibull, W. (1951). A Statistical Distribution Function of Wide Applicability. Journal of Applied Mechanics, 18(3), 293–297. [CrossRef]
Xie, M., Tang, Y., & Goh, T. N. (2002). A modified Weibull extension with bathtub-shaped failure rate function. Reliability Engineering & System Safety, 76(3), 279–285. [CrossRef]
Zhang, T., & Xie, M. (2011). On the upper truncated Weibull distribution and its reliability implications. Reliability Engineering & System Safety, 96(1), 194–200. [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Median Based Unit Weibull (MBUW): A New Unit Distribution Properties

Abstract

Keywords:

Subject:

Introduction

Section 1

Methodology

Derivation of the MBUW Distribution

Section 2

Some of the Properties of the New Distribution ( MBUW)

Conclusion

Future Work

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Acknowledgement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe