Prerpints.org logo
Preprint
Review

This version is not peer-reviewed.

Research Progress on Newton’s Iterative Methods for Nonlinear Equation

Submitted:

21 October 2024

Posted:

22 October 2024

Read the latest preprint version here

Abstract
Reviewed the research progress of Newton’s iterative methods for nonlinear equation. Convergence with second order, third order, fourth order, fifth order, sixth order, seventh order, eighth order and ninth order Newton’s iterative methods are given in turn, and the efficiency index of these iterative methods are analyzed. Numerical experiments show that the convergence process of the three Newton iterative methods, and the results indicate that the convergence of the higher-order Newton’s method can be well demonstrated only when the initial point is close to the root.
Keywords: 
nonlinear equation
;  
Newton’s iteration method
;  
convergence order
;  
efficiency index
;  
initial point
Subject: 
Computer Science and Mathematics  -   Computational Mathematics

1. Introduction

For the nonlinear equation f ( x ) = 0 , f ( x ) is a smooth curve, and has a single root on the open interval I .The classical Newton's method and the modified Newton's method are the most basic methods for solving nonlinear equations. In order to improve the convergence speed, the third, fourth, fifth, sixth, seventh, eighth and ninth order Newton's methods have appeared one after another. For the initial point x 0 , the higher the order of convergence, and the faster the convergence speed. If the nonlinear equations are convergent, the computational complexity also needs to be considered. In general, the higher the order of convergence and the larger the computational workload. Therefore, when constructing a higher-order Newton method, it is necessary to consider both the convergence order and the computational efficiency.
Definition1 Let the sequence x k converge to a , a is single root of the equation f ( x ) = 0 ,denote e k = x k − a . If there exist p ≥ 1 and a constant C ≠ 0 , such that the limit lim k → ∞ e k + 1 e k p = C holds, then the sequence x k is convergent of p order. Here C is the convergence factor and e k + 1 = C e k p + O ( e k p + 1 ) is the error equation. When p = 1 ,the convergence is linear convergence. When p > 1 ,the convergence is superlinear convergence. When p = 2 , the convergence is square convergence.
Definition 2 If the convergence order of an iterative method is p > 1 , and the computational workload for each iteration from x k to x k + 1 is n (the computation numbers of function values and derivative function values), then the efficiency index of this iterative method is E = p n .
There are some Newton's methods for solving nonlinear equations. Following we analyses the convergence order and efficiency index of these Newton's iterative methods.

2. Several Newton’s iterative methods

2.1. Classical Newton’s iterative

The process of classical Newton iteration is as follows:
x k + 1 = x k − f ( x k ) f ′ ( x k ) .  
The classical Newton’s method has a second-order convergence rate, i.e. p = 2 .Each iteration from x k to x k + 1 requires the calculation of the function value f ( x k ) and the derivative function f ′ ( x k ) value. So the computational workload is 2. Therefore, the efficiency index of the classical Newton method is 2 ≈ 1.414 . The second-order convergence can be well reflected when the initial point x 0 is very close to the root a in actual computation.

2.2. Newton's iterative method with third order convergence

Common Newton’s iteration methods with third order convergence are listed in following.
①Euler iterative method
x k + 1 = x k − 2 1 + 1 − 2 L f ( x k ) f ( x k ) f ′ ( x k ) , L f ( x k ) = f ( x k ) f ″ ( x k ) f ′ ( x k ) 2 .
Each iteration from x k to x k + 1 requires the calculation of the function value f ( x k ) , and the derivative function value f ′ ( x k ) , f ″ ( x k ) . So the computational workload is 3, thus the efficiency index of the iteration is 3 3 ≈ 1.442 .
②Halley iterative method
x k + 1 = x k − 2 f ( x k ) f ′ ( x k ) 2 f ′ ( x k ) 2 − f ( x k ) f ″ ( x k ) .
③Chebyshev iteration method
x k + 1 = x k − 1 + 1 2 L f ( x k ) f ( x k ) f ′ ( x k ) , L f ( x k ) = f ( x k ) f ″ ( x k ) f ′ ( x k ) 2 .
Moreover,
y k = x k − f ( x k ) f ′ ( x k ) , x k + 1 = x k − 2 f ( x k ) f ′ ( x k ) + f ′ ( y k ) ,
y k = x k − f ( x k ) f ′ ( x k ) , x k + 1 = x k − f ( x k ) 2 1 f ′ ( x k ) + 1 f ′ ( y k ) ,
y k = x k − f ( x k ) f ′ ( x k ) , x k + 1 = x k − f ( x k ) + f ( y k ) f ′ ( x k ) ,
y k = x k − f ( x k ) f ′ ( x k ) , x k + 1 = x k − f ( x k ) f ′ ( x k + y k 2 ) ,
y k = x k − 2 f ( x k ) 2 f ′ ( x k ) , x k + 1 = x k − 5 f ′ ( x k ) − f ′ ( y k ) 2 f ′ ( x k ) + 2 f ′ ( y k ) f ( x k ) f ′ ( x k ) ,
y k = x k − f ( x k ) 3 f ′ ( x k ) , x k + 1 = x k − f ′ ( x k ) + f ′ ( y k ) 4 f ′ ( x k ) − 2 f ′ ( y k ) f ( x k ) f ′ ( x k ) .  
These are all convergent Newton’s iterations with third order, and the efficiency indices of all these iterative methods are 3 3 ≈ 1.442 . There are a variety of third order convergent Newton’s iterations in the literature [1]. Among them, what is striking is that
x k + 1 = x k − f ( x k ) f ′ ( x k ) − 1 2 x k x k 2 − f ( x k ) f ′ ( x k ) 2 .
The computational workload for each iteration from x k to x k + 1 is 2 (just calculate f ( x k ) , f ′ ( x k ) ). Therefore, the efficiency index of this iteration is 3 2 ≈ 1.732 , which is the best result for the efficiency index of the current third order convergent Newton iteration method.

2.3. Newton's iterative method with fourth order convergence

The classical double Newton’s iterative method
y k = x k − f ( x k ) f ′ ( x k )    ,    x k + 1 = y k − f ( y k ) f ′ ( y k ) .
It has fourth order convergence and its efficiency index is 4 4 ≈ 1.414 .
There is the fourth-order convergent Newton iterative method in the literature [2],
y k = x k − f ( x k ) f ′ ( x k ) , x k + 1 = x k − f ( x k ) f ′ ( x k ) − 2 f ( y k ) f ′ ( x k ) + f ( y k ) f ′ ( y k ) f ′ ( x k ) 2 .
Its efficiency index is 4 4 ≈ 1.414 . In the literature [3], another fourth-order convergent Newton iterative method is given,
y k = x k − f ( x k ) f ′ ( x k ) , x k + 1 = x k − f 2 ( x k ) + f 2 ( y k ) f ′ ( x k ) f ( x k ) − f ( y k ) .
The Jarratt iterative method is an iterative format with fourth-order convergence [4]. Where one iteration requires the calculation of two derivative function values and one function value.The specific forms are as follows.
y k = x k − 2 3 f ( x k ) f ′ ( x k ) x k + 1 = x k − 3 f ′ ( y k ) + f ′ ( x k ) 6 f ′ ( y k ) − 2 f ′ ( x k ) ⋅ f ( x k ) f ′ ( x k )
In the literature [5], an iterative method with fourth-order convergence is presented.
y k = x k − 2 3 f ( x k ) f ′ ( x k ) z k = y k − 1 28 + f ′ ( x k ) 2 294 125 f ′ ( y k ) 2 + 126 125 f ′ ( x k ) 2 f ( x k ) f ′ ( y k ) .
King gave a class of iterative formats with fourth-order convergence in the literature [6].
y k = x k − f ( x k ) f ′ ( x k ) , x k + 1 = x k − f ( x k ) + β f ( y k ) f ( x k ) + ( β − 2 ) f ( y k ) f ( y k ) f ′ ( x k ) .  
where β ∈ R .
The computational efficiency index of the last four iterations is 4 3 ≈ 1.587 , which is the best result for the efficiency index of the current fourth-order convergent Newton’s iteration method.

2.4. Newton's iterative method with fifth order convergence

The variation of the double Newton method
y k = x k − f ( x k ) f ′ ( x k )                                                                             x k + 1 = y k − 1 + f ( y k ) f ( x k ) 2 f ( y k ) f ′ ( y k ) .
has fifth-order convergence.
Ham gave a fifth order convergent Newtonian iterative method in [7]
y k = x k − f ( x k ) f ′ ( x k ) x k + 1 = x k − A f ′ ( y k ) + B f ′ ( x k ) C f ′ ( y k ) + D f ′ ( x k ) ⋅ f ( y k ) f ′ ( x k ) .
Where the parameters A , B , C , D satisfy A + B = C + D , C = B + 2 A , B = 3 A , C + D ≠ 0 .
Xue gave a fifth order convergent Newton iterative method in [8]
y k = x k − f ( x k ) f ′ ( x k ) , z k = x k − f ( x k ) f ′ x k + y k 2 , x k + 1 = z k − f ( z k ) f ′ x k + y k 2 3 f ′ ( x k ) f ′ x k + y k 2 − 2 f ′ ( x k ) 2 .
Liu gave a class of Newton iterative methods with fifth order convergence in [9]
y k = x k − f ( x k ) f ′ ( x k ) , x k + 1 = y k − f ( y k ) f ′ ( y k ) − f 2 ( y k ) f ′ ( x k ) 3 − f ′ ( y k ) f ′ ( x k ) 2 − μ f ( x k ) 2 2 f ′ ( y k ) 3 f ′ ( x k ) f ( x k ) .
Wu gave two Newton iterative methods with fifth order convergence in [10]
y k = x k − 2 f ( x k ) 3 f ′ ( x k ) , z k = x k − 5 f ′ ( x k ) − f ′ ( y k ) 2 f ′ ( x k ) + 2 f ′ ( y k ) f ( x k ) f ′ ( x k ) , x k + 1 = z k − 4 f ( z k ) f ′ ( x k ) + f ′ ( y k ) 22 f ′ ( y k ) f ′ ( x k ) − 11 f ′ ( x k ) 2 − 3 f ′ ( y k ) 2 .
y k = x k − f ( x k ) 3 f ′ ( x k ) , z k = x k − f ′ ( x k ) + f ′ ( y k ) 4 f ′ ( y k ) − 2 f ′ ( y k ) f ( x k ) f ′ ( x k ) , x k + 1 = z k − 2 f ( z k ) 2 f ′ ( y k ) − f ′ ( x k ) 4 f ′ ( y k ) f ′ ( x k ) − 5 f ′ ( x k ) 2 + 3 f ′ ( y k ) 2 .
More fifth-order convergent Newton iteration methods are given in the literature [11,12,13,14,15,16,17].
In recent years, a new fifth order convergent Newton iteration method is presented in the literature [18],
y k = x k − f ( x k ) 2 f ′ ( x k ) , z k = x k − f ( x k ) f ′ ( y k ) , x k + 1 = z k − 2 f ′ ( y k ) − 1 f ′ ( x k ) f ( z k ) .
It is successfully applied to solve linear programming and portfolio optimization.
The computational efficiency index of all these fifth order Newton iterations above is 5 4 ≈ 1.495 , which is the best result of the efficiency index of the current fifth order convergent Newton’s iteration method.

2.5. Newton's iterative method for sixth order convergence

In order to improve the convergence order, Kou [4] et al. constructed a new three-step iterative method as follows.
y k = x k − 2 3 f ( x k ) f ′ ( x k ) z k = x k − J f ( x k ) ⋅ f ( x k ) f ′ ( x k ) , J f ( x k ) = 3 f ′ ( y k ) + f ′ ( x k ) 6 f ′ ( y k ) − 2 f ′ ( x k ) x k + 1 = z k − 2 f ( z k ) 3 2 J f ( x k ) f ′ ( y k ) + 1 − 3 2 J f ( x k ) f ′ ( x k ) .
and proved that the iteration has sixth order convergence.
Chun proposed the Newton iterative methods with sixth order convergence based on the literature [19],
y k = x k − 2 3 f ( x k ) f ′ ( x k ) z k = x k − J f ( x k ) ⋅ f ( x k ) f ′ ( x k ) , J f ( x k ) = 3 f ′ ( y k ) + f ′ ( x k ) 6 f ′ ( y k ) − 2 f ′ ( x k ) x k + 1 = z k − 2 f ( z n ) λ ( z k − x k ) ( z k − y k ) + 3 2 J f ( x k ) f ′ ( y k ) + 1 − 3 2 J f ( x k ) f ′ ( x k ) .
where λ ∈ R , and it is the sixth-order convergence. When λ = 0 , it is the method of the Kou’s method. In the literature [10], Wu gave two Newton’s iterative methods with sixth order convergence in the following,
y k = x k − f ( x k ) f ′ ( x k ) , z k = x k − 2 f ( x k ) f ′ ( x k ) + f ′ ( y k ) , x k + 1 = z k − f ( z k ) f ′ ( x k ) + f ′ ( y k ) 3 f ′ ( y k ) f ′ ( x k ) − f ′ ( x k ) 2 .
y k = x k − f ( x k ) f ′ ( x k ) , z k = x k − f ′ ( x k ) 2 + f ′ ( y k ) 2 f ′ ( x k ) f ′ ( y k ) + f ′ ( y k ) 2 f ( x k ) f ′ ( x k ) , x k + 1 = z k − f ( z k ) f ′ ( y k ) f ′ ( x k ) + f ′ ( y k ) 2 f ′ ( x k ) 2 f ′ ( y k ) − f ′ ( x k ) 3 + f ′ ( y k ) 3 .
another sixth order convergent Newton iterative method is proposed in the literature [20].
y k = x k − f ( x k ) f ′ ( x k ) , z k = y k − ( x k − y k ) f ( x k ) − 2 f ( y k ) f ( y k ) , x k + 1 = z k − ( x k − y k ) f ( x k ) − 2 f ( y k ) f ( z k ) .
The efficiency index of these sixth order Newton iterations above are 6 4 ≈ 1.565 .

2.6. Newton's iterative method with seventh order convergence

Two Newton iterative methods with seventh-order convergence are given by Zheng in the literature [21], one of them is
z k = x k − 1 + 1 2 f ″ ( x k ) f ( x k ) f ′ ( x k ) 2 f ( x k ) f ′ ( x k ) , y k = z k − f ( z k ) f ′ ( x k ) + f ″ ( x k ) ( z k − x k ) , x k + 1 = y k − 2 f ( y k ) f ′ ( z k ) + f ′ ( y k ) .
Its computational efficiency index is 7 7 ≈ 1.320 . Another Newton iterative method with seventh order convergence is
z k = x k − f ( x k ) f ′ ( x k ) , y k = z k − f ′ ( z k ) + 3 f ′ ( x k ) 5 f ′ ( z k ) − f ′ ( x k ) f ( z k ) f ′ ( x k ) , x k + 1 = y k − 2 f ( y k ) f ′ ( z k ) + f ′ ( y k ) .
Its computational efficiency index is 7 6 ≈ 1.383 .
Shno [22] constructed a new three-step iterative method based on the Jarratt iterative method,
y k = x k − 2 3 f ( x k ) f ′ ( x k ) z k = x k − J f ( x k ) ⋅ f ( x k ) f ′ ( x k ) , J f ( x k ) = 3 f ′ ( y k ) + f ′ ( x k ) 6 f ′ ( y k ) − 2 f ′ ( x k ) x k + 1 = z k − f ( z k ) 3 f ( z k ) − f ( x k ) ( z k − x k ) − 2 f ′ ( x k ) + 1 2 f ″ ( x k ) ( z k − x k )
Its computational efficiency index is 7 5 ≈ 1.476 .
Wang [3] gave a Newton iterative method with seventh order convergence using difference quotient in the following form,
y k = x k − f ( x k ) f ′ ( x k ) , z k = x k − f ( x k ) 2 + f ( y k ) 2 f ′ ( x k ) f ( x k ) − f ( y k ) , x k + 1 = z k − f ( z k ) 2 f [ z k , y k ] + f [ z k , x k , x k ] ( z k − y k ) .
Where f [ z k , y k ] , f [ z k , x k , x k ] is the first-order difference quotient and second-order difference quotient, respectively. Its computational efficiency index is 7 4 ≈ 1.627 .
The Newton iterative method with seventh order convergence is given by Kou [23] in the following form,
y k = x k − f ( x k ) f ′ ( x k ) , z k = y k − f ( y k ) f ( x k ) − 2 f ( y k ) ( x k − y k ) , x k + 1 = z k − 1 + f ( y k ) f ( x k ) − 2 f ( y k ) 2 + f ( z k ) f ( y k ) f ( z k ) f ( x k ) .
Whose efficiency index is 7 4 ≈ 1.627 ,which is the best result of the efficiency index of the current seventh order convergent Newton’s iteration method.

2.7. Newton's iterative method with eighth order convergence

The literature [3] gave the Newton’s iterative method with eighth order convergence in the following form,
y k = x k − f ( x k ) f ′ ( x k ) , z k = y k − f ( x k ) 2 + f ( y k ) 2 f ′ ( x k ) f ( x k ) − f ( y k ) , x k + 1 = z k − f ( z k ) f ′ ( z k ) .
Whose efficiency index is 8 5 = 1.516 .
The literature [24] gave the Newton iterative method with eighth order convergence in the following form,
y k = x k − f ( x k ) f ′ ( x k )                                                                                                                                                             z k = y k − f ( x k ) + β f ( y k ) f ( x k ) + ( β − 2 ) f ( y k ) f ( y k ) f ′ ( x k )                                                     x k + 1 = z k − H ( μ k ) f ( z k ) f [ z k , y k ] + f [ z k , x k , x k ] ( z k − y k ) .
Where H ( t ) is a real-valued function and satisfies H ( 0 ) = 1 , H ′ ( 0 ) = 2 , H ″ ( 0 ) < ∞ , β = − 0.5 , μ k = f ( z k ) f ( x k ) , f [ z k , y k ] , f [ z k , x k , x k ] are the first-order difference quotient and the second-order difference quotient, respectively. The function value needs to be evaluated three times at each iteration and its first-order derivative is evaluated once, so the efficiency index of this method is 8 4 = 1.682 .
A class of Newton’s iterative methods with eighth order convergent is given in the literature [25] with efficiency index of 8 4 = 1.682 ,which is the best result for the efficiency index of the current eighth order convergent Newton’s iterative method. More Newton iterative methods with eighth order convergence can be found in the literature [26,27,28].

2.8. Newton's iterative method with ninth order convergence

A Newton’s iteration method with ninth order convergence is in the literature [29] as follows,
y k = x k − f ( x k ) f ′ ( x k ) , z k = y k − 1 + f 2 ( y k ) f 2 ( x k ) f ( y k ) f ′ ( y k ) , x k + 1 = z k − 1 + 2 f 2 ( y k ) f 2 ( x k ) + 2 f ( z k ) f ( y k ) f ( z k ) f ′ ( y k ) .
Whose efficiency index is 9 5 = 1.552 .
The literature [30] constructed a Newton iterative method with ninth order convergence using the difference quotient,
y k = x k − f ( x k ) f ′ ( x k )                                                                                                                                                             z k = y k − 2 f ( y k ) f ′ ( y k ) 2 f ′ ( y k ) 2 − f ( y k ) P f ( x k , y k )                                                     x k + 1 = z k − f ( z k ) f [ z k , y k ] + f [ z k , x k , x k ] ( z k − y k )
Here P f ( x k , y k ) = 2 ( y k − x k ) 2 f ′ ( y k ) + f ′ ( x k ) − 3 f ( y k ) − f ( x k ) y k − x k , f [ z k , y k ] , f [ z k , x k , x k ] are the first-order difference quotient and the second-order difference quotient respectively, and the efficiency index of this method is 9 5 = 1.552 .

3. Efficiency index of the Newton iterative method

Table 1 gives the values of the corresponding functions p n for p taken from 2 to 9 and n taken from 2 to 9.
As pointed out earlier, the higher the order of convergence and the greater the computational cost required. Therefore, both the convergence order and the computational complexity need to be considered when constructing a higher order Newton’s iterative method for solving nonlinear equations. The underlined numbers in Table 1 indicate the best efficiency index that can be achieved when the convergence order is taken from 2 to 9. Whether the efficiency index can theoretically reach 2 needs to be further investigated.

4. Numerical experiments

Following we give two numerical examples to verify the convergence process of Newton's iterative method.
f 1 ( x ) = x 3 + 4 x 2 − 10 = 0 ,
f 2 ( x ) = x 5 + x 4 + 4 x 2 − 20 = 0 .
The root of equation f 1 ( x ) = 0 is a = 1.36523001341409688791373 .
The root of equation f 2 ( x ) = 0 is a = 1.46627907386472267070587 .
Preprints 121862 g002
Figure 1. Image of the function f 1 ( x ) , f 2 ( x ) .
Figure 1. Image of the function f 1 ( x ) , f 2 ( x ) .
Preprints 121862 g002
Three Newton’s iterative methods are used for solving, and the program is written by MATLAB R2009a. In the classical Newton iterative method, we set x ( k + 1 ) − x ( k ) + f ( x ( k ) ) < ε is the termination condition. In the fifth order Newton method [16] and the ninth-order Newton method [29], we set
x ( k + 1 ) − x ( k ) + f ( x ( k ) ) + f ( y ( k ) ) + f ( z ( k ) ) < ε
is the termination condition, where ε = 1 × 10 − 10 .
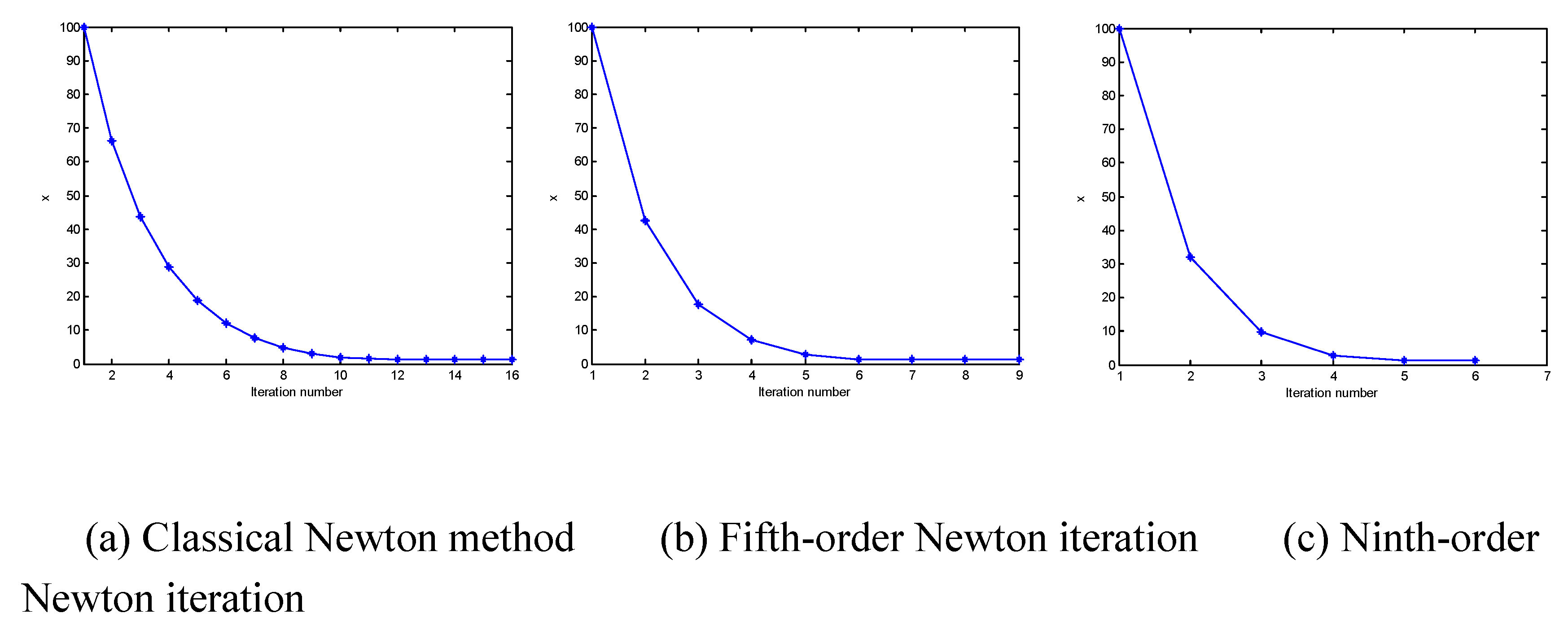
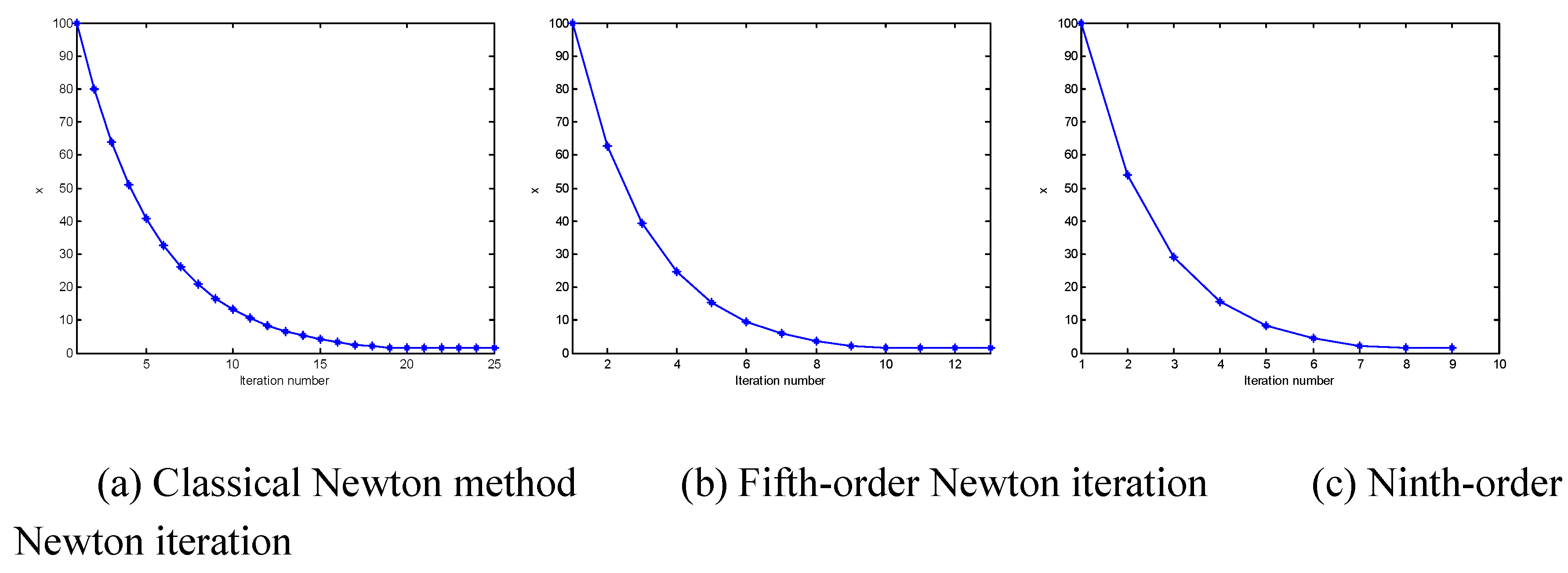
Table 2 gives the calculation results of the three Newton’s iterative methods by taking the different initial points.
As can be seen from Table 2, although the initial points are sometimes far from the roots, three iterative methods are all eventually convergent.
Given the same initial point, the number of ninth order Newton’s iteration is the smallest and the number of classical Newton’s iterations is the largest. Figure 2 and Figure 3 shows the Newton’s iterative process of functions f 1 ( x ) and f 2 ( x ) (the horizontal axis indicates the number of iterations, and the vertical axis indicates the value of x during the iterative process).
More experimental results show that the convergence and convergence speed of various Newton's iterative methods are related to the selection of the initial point. The higher the order of convergence, the greater the computational cost required. Even for the higher-order Newton's iterative method, the higher-order convergence can be well reflected only when the initial point is close to the root.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data used to support the findings of this study are available from the corresponding author upon request.

Acknowledgments

This work is supported by Natural Science Foundation of Shaanxi Province(2024JC-YBMS-014), and the Foundation of Shaanxi University of Technology (SLGNL202409).

Conflicts of Interest

The author declares that there is no conflict of interest regarding the publication of this paper.

References

  1. R. Thukral. New Modification of Newton Method with Third-Order Convergence for Solving Nonlinear Equations of Type f(x)=0[J].American Journal of Computational and Applied Mathematics 2016, 6(1): 14-18.
  2. Chun, C. Iterative methods improving Newton's methods by the decomposition method[J]. Comput.Math. Appl., 2005, 50(10-12): 1559-1568.
  3. Wang Xiao-feng; Shi Dong-yang. A novel and precise seventh-order newton’s iterative method for solving nonlinear equations[J].Journal of Mathematics. 2015(5):1017-1025.
  4. J.Kou,Y.Li,X.Wang,An improvements of the Jarratts method[J].J.Comput.Appl.Math., 2007, 189:1816-1821.
  5. M. Matinfar,M. Aminzadeh.Three-step iterative methods with eighth-order convergence for solving nonlinear equations[J]. Journal of Interpolation and Approximation in Scientific Computing, 2013, (1): 1-11.
  6. R.F. King, A family of fourth order methods for nonlinear equations[J]. SIAM J. Numer. Anal. 10 (1973) 876-879.
  7. Ham Y M, Chun C. A fifth-order iterative method for solving nonlinear equations[J]. Applied Mathematics and Computation, 2007,194 :287-290.
  8. Xue Shuang.Two Families of Newton’s Iteration Methods With Third-Order Convergence[J].Journal of Anhui Normal University(Natural Science). 2013(5):430-436.
  9. Liu Tian-bo, Cai Hua. A Family of Fifth-order Iterative Methods for Solving Nonlinear Equations[J]. Communications in Mathematical Research, 2013, 29(3):255-260.
  10. Wu Jiang.The Research on High-order Iterative Methods for Solving Nonlinear Equations[D].Hangzhou: Hangzhou Normal University,2019.
  11. Ham Y M, Chun C. A fifth-order iterative method for solving nonlinear equations[J]. Applied Mathematics and Computation, 2007,194 :287-290.
  12. Noor M A, Noor K I. Fifth-order iterative methods for solving nonlinear equations[J]. Applied Mathematics & Computation, 2007,188(1):406-410.
  13. Rafiullah, M. A fifth-order iterative method for solving nonlinear equations [J]. Numerical Analysis & Applications, 2011, 4(3):239.
  14. Tian-Bao L, Hua C. A Family of Fifth-order Iterative Methods for Solving Nonlinear Equations[J]. Comm. in Math. Research, 2013,29(3):255-260.
  15. Liu Tian-bo, Cai Hua. A Family of Fifth-order Iterative Methods for Solving Nonlinear Equations[J]. Communications in Mathematical Research, 2013, 29(3):255-260.
  16. Sharma J R, Gupta P. An efficient fifth order method for solving systems of nonlinear equations [J]. Computers & Mathematics with Applications, 2014, 67(3):591-601.
  17. Liang J, Li X, Wu Z, et al. Fifth-Order Iterative Method for Solving Multiple Roots of the Highest Multiplicity of Nonlinear Equation[J]. Algorithms, 2015, 8 (3):656-668.
  18. Foutayeni Y E, Bouanani H E, Khaladi M. An Efficient Fifth-Order Method for Linear Optimization[J]. Journal of Optimization Theory and Applications, 2016, 170(1):189-204.
  19. C.Chun. Some improvements of Jarrett’s method with sixth-order convergence[J].J.Comput.Appl. Math, 2007,190:432-1437.
  20. M. Grau, J.L. Diaz-Barrero. An improvement to Ostrowski root-finding method[J]. Appl. Math. Comput. 2006,173: 450-456.
  21. Zheng Hao, Zhang Yue-qin, Zhang Chuan-lin. Two Variants of Newton’s Iteration Method with Seventh-Order Convergence[J].Journal of Southwest University(Natural Science Edition). 2012(3):32-35.
  22. Shno, O. Ahmed.An improvement of Jarratt method with seventh-order convergence[J]. International Journal of Scientific Research and Innovative Technology,2015,2(5) 97-102.
  23. Kou J, Li Y, Wang X. Some variants of Ostrowski's method with seventh-order convergence [J]. Journal of Computational & Applied Mathematics, 2007, 209(2):153-159.
  24. Bi W, Ren H, Wu Q. Three-step iterative methods with eighth-order convergence for solving nonlinear equations[M]. Journal of Computational and Applied Mathematics,2009, 225:105-112.
  25. Wang Xiao-feng, Zhang Tie.A Family of Optimal Eighth-Order Iterative Methods for Solving Nonlinear Equations[J].Journal of Jilin University(Science Edition). 2013(4):568-572.
  26. Kou Jisheng, Wang Xiuhua, Li Yitian, Some eight-order root-finding three-step methods[J]. Commun. Nonlinear Sci. Numer. Simulat., 2010, 15(3): 536-544.
  27. Thukral R, Petkovic M S. A family of three-point methods of optimal order for solving nonlinear equations[J]. J. Comput. Appl. Math., 2010, 233(9): 2278-2284.
  28. Neta B, Petkovic M S. Construction of optimal order nonlinear solvers using inverse interpolation[J].Appl. Math. Comput., 2010, 217(6): 2448-2455.
  29. Hu Z, Liu G, Tian L. An iterative method with ninth-order convergence for solving nonlinear equations[J]. International Journal of Contemporary Mathematical Sciences, 2011, 6(1-4):17-23.
  30. Al-Subaihi I., A. A ninth-order iterative method free from second derivative for solving nonlinear equations[J]. Int. J. Math. Analysis, 2011, 5(47): 2337-2347.
Preprints 121862 g002
Figure 2. Iteration process f 1 ( x ) = 0 under the initial iteration point x 0 = 100 .
Figure 2. Iteration process f 1 ( x ) = 0 under the initial iteration point x 0 = 100 .
Preprints 121862 g002
Preprints 121862 g003
Figure 3. Iteration process f 2 ( x ) = 0 under the initial iteration point x 0 = 100 .
Figure 3. Iteration process f 2 ( x ) = 0 under the initial iteration point x 0 = 100 .
Preprints 121862 g003
Table 1. Values of the functions p n (p taken from 2 to 9 and n taken from 2 to 9).
Table 1. Values of the functions p n (p taken from 2 to 9 and n taken from 2 to 9).
P n 2 3 4 5 6 7 8 9
2 1.414 1.260 1.189 1.149 1.122 1.104 1.091 1.080
3 1.732 1.442 1.316 1.246 1.201 1.170 1.147 1.130
4 2.000 1.587 1.414 1.320 1.260 1.219 1.189 1.167
5 2.236 1.710 1.495 1.380 1.308 1.258 1.223 1.196
6 2.449 1.817 1.565 1.431 1.348 1.292 1.251 1.220
7 2.646 1.913 1.627 1.476 1.383 1.320 1.275 1.241
8 2.828 2.000 1.682 1.516 1.414 1.346 1.297 1.260
9 3.000 2.080 1.732 1.552 1.442 1.369 1.316 1.277
Table 2. Calculation results of three Newton’s iterative methods.
Table 2. Calculation results of three Newton’s iterative methods.
fi(x) Initial point Number of iterations
Classical Newton iteration Fifth-order Newton iteration Ninth-order Newton iteration
f1(x) 1 5 3 2
10 8 5 3
100 16 9 6
f2(x) 1 6 4 3
10 12 7 4
100 25 13 9
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
bsky
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

Privacy Settings

© 2025 MDPI (Basel, Switzerland) unless otherwise stated