Proof of the Riemann Hypothesis

1. Introduction

This work is only concerned with proving the Riemann Hypothesis ([1]), so it is very short and focuses on the proof only. The Riemann Hypothesis concerns about the Riemann zeta function ([2,3]) which is defined for $\Re \left(z\right)>1$ by the following infinite sum:

$$\begin{array}{cc}\hfill \zeta \left(z\right):& =\sum _{n=1}^{\infty }{\displaystyle \frac{1}{n^z}}=\sum _{n=1}^{\infty }{\displaystyle \frac{1}{e^{zlnn}}}=\sum _{n=1}^{\infty }{\displaystyle \frac{e^{-i(ylnn)}}{n^x}}\hfill \end{array}$$

(1)

Riemann does not refer to analytic continuation of the function $\zeta$ beyond the half plane $\Re \left(z\right)>1.$ Instead, he focuses on finding a formula that applies to all $z.$ First, he derives his formula for ${\displaystyle \zeta \left(z\right)=\sum _{n=1}^{\infty }{n}^{-z}}$ which is valid for every $z:\Re \left(z\right)>0,$ he achieved this by relating the function $\zeta$ to the function ${\displaystyle \Gamma \left(z\right)={\int }_0^{\infty }{t}^{z-1}{e}^{-t}dt}$ with the following relation

$$\begin{array}{cc}\hfill \zeta \left(z\right)& ={\displaystyle \frac{1}{\Gamma \left(z\right)}}{\int }_0^{\infty }{\displaystyle \frac{t^{z-1}}{e^t-1}}dt\hfill \end{array}$$

(2)

Next, Riemann derives his formula to remains valid for all $z$ by the relation

$$\begin{array}{cc}\hfill {\pi }^{-{\displaystyle \frac{z}{2}}}\Gamma \left(({\displaystyle \frac{z}{2}}\right)\zeta \left(z\right)& ={\int }_1^{\infty }\left[t^{{\displaystyle \frac{z}{2}}}+t^{{\displaystyle \frac{1-z}{2}}}\right]{\displaystyle \frac{\psi \left(t\right)}{t}}dt-{\displaystyle \frac{1}{z(1-z)}}\hfill \end{array}$$

(3)

where ${\displaystyle \psi \left(t\right):=\sum _{n=1}^{\infty }{e}^{-\pi n^{2}t}.}$

The functional equation of the zeta function is demonstrated by the fact that the right side of (3) remains unchanged when $z=1-z:$

$$\begin{array}{c}\hfill {\pi }^{{\displaystyle \frac{-z}{2}}}\Gamma \left({\displaystyle \frac{z}{2}}\right)\zeta \left(z\right)={\pi }^{{\displaystyle \frac{-(1-z)}{2}}}\Gamma \left({\displaystyle \frac{1-z}{2}}\right)\zeta (z-1)\end{array}$$

(4)

In the symmetric form of the functional equation, the function ${\pi }^{{\displaystyle \frac{-z}{2}}}\Gamma \left({\displaystyle \frac{z}{2}}\right)\zeta \left(z\right),$ has removable poles at $z=0$ and $z=1,$ Riemann multiplies it by ${\displaystyle \frac{1}{2}}z(z-1)$ and define

$$\xi \left(z\right):={\displaystyle \frac{1}{2}}z(z-1){\pi }^{-{\displaystyle \frac{z}{2}}}\Gamma \left({\displaystyle \frac{z}{2}}\right)\zeta \left(z\right)$$

(5)

2. Main Results

Lemma 1. 

If $z=x+yi$ and $y\ne 0,$ then

I. 

$\overline{\zeta \left(z\right)}=\zeta \left(\overline{z}\right)$ and $\overline{\Gamma \left(z\right)}=\Gamma \left(\overline{z}\right)$

II. 

$\overline{\xi \left(z\right)}=\xi \left(\overline{z}\right)$

III. 

$\xi \left(z\right)=\xi (1-z)$

IV. 

$\overline{\xi \left(z\right)}=\xi (1-\overline{z})$

V. 

If $\xi \left(\right(1-x)+yi)=\xi (x+yi),$ then $x={\displaystyle \frac{1}{2}}$

VI. 

The non-trivial zeros of $\zeta$ is the same the non-trivial zeros of $\xi$

Proof. 

I. First we prove that $\overline{\zeta \left(z\right)}=\zeta \left(\overline{z}\right)$

$$\begin{array}{cc}\hfill \overline{\zeta \left(z\right)}& =\overline{\sum _{n=1}^{\infty }{n}^{-z}}=\overline{\sum _{n=1}^{\infty }{n}^{-x}{e}^{-iylnn}}\hfill \\ \hfill & =\overline{\sum _{n=1}^{\infty }{n}^{-x}cos(ylnn)-i\sum _{n=1}^{\infty }{n}^{-x}sin(ylnn)}\hfill \\ \hfill & =\sum _{n=1}^{\infty }{n}^{-x}cos(ylnn)+i\sum _{n=1}^{\infty }{n}^{-x}sin(ylnn)\hfill \\ \hfill & =\sum _{n=1}^{\infty }{n}^{-x}{e}^{iylnn}=\sum _{n=1}^{\infty }{n}^{-(x-yi)}=\zeta \left(\overline{z}\right)\hfill \end{array}$$

Similarly, we can prove that $\overline{\Gamma \left(z\right)}=\Gamma \left(\overline{z}\right)$

II.

By the definition of $\xi$ and using I., we have

$$\begin{array}{cc}\hfill \overline{\xi \left(z\right)}& =\overline{{\displaystyle \frac{1}{2}}z(z-1){\pi }^{-{\displaystyle \frac{z}{2}}}\Gamma \left({\displaystyle \frac{z}{2}}\right)\zeta \left(z\right)}\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}\overline{z(z-1)}\overline{{\pi }^{-{\displaystyle \frac{z}{2}}}}\overline{\Gamma \left({\displaystyle \frac{z}{2}}\right)}\overline{\zeta \left(z\right)}\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}\overline{z}(\overline{z}-1){\pi }^{-{\displaystyle \frac{\overline{z}}{2}}}\Gamma \left({\displaystyle \frac{\overline{z}}{2}}\right)\zeta \left(\overline{z}\right)=\xi \left(\overline{z}\right)\hfill \end{array}$$

III.

It is obvious from (4) that $\xi \left(z\right)=\xi (1-z)$

IV.

From II. and III., we obtain IV.

VI.

Let $\xi \left(\right(1-x)+yi)=\xi (x+yi).$ By substitute in the definition of $\xi \left(z\right)$ and using (3), we have

$$\begin{array}{cc}\hfill (a-bi){\int }_1^{\infty }\left[t^{{\displaystyle \frac{(1-x)+yi}{2}}}+t^{{\displaystyle \frac{x-yi}{2}}}\right]{\displaystyle \frac{\psi \left(t\right)}{t}}dt& =(a+bi){\int }_1^{\infty }\left[t^{{\displaystyle \frac{x+yi}{2}}}+t^{{\displaystyle \frac{(1-x)-yi}{2}}}\right]{\displaystyle \frac{\psi \left(t\right)}{t}}dt\hfill \end{array}$$

where $a=x^2-y^2-x$ and $b=2xy-y.$

After simplification, we obtain

$$\begin{array}{cc}\hfill & y\left(2x-1\right){\int }_1^{\infty }\left[t^{{\displaystyle \frac{1}{2}}x}-t^{{\displaystyle \frac{1}{2}}(1-x)}\right]cos(ylnt){\displaystyle \frac{\psi \left(t\right)}{t}}dt\hfill \\ \hfill & +\left(x^2-x-y^2\right){\int }_1^{\infty }\left[t^{{\displaystyle \frac{1}{2}}x}-t^{{\displaystyle \frac{1}{2}}(1-x)}\right]sin(ylnt){\displaystyle \frac{\psi \left(t\right)}{t}}dt=0\hfill \end{array}$$

this is true only if $t^{{\displaystyle \frac{1}{2}}x}=t^{{\displaystyle \frac{1}{2}}(1-x)}$ for all $t\ge 1,$ which implies to $x={\displaystyle \frac{1}{2}}.$

VI.

Since ${\pi }^{-{\displaystyle \frac{z}{2}}}$ and $\Gamma \left({\displaystyle \frac{z}{2}}\right)$ have no zeros, then,VI. is verified.

□

Theorem 1. 

If $z=x+yi$ and $y\ne 0,$ then $\xi \left(z\right)$ is real if and only if $x={\displaystyle \frac{1}{2}}.$

Proof. 

First, let $z=x+iy,$$y\ne 0,$ and $\overline{\xi \left(z\right)}=\xi \left(z\right).$ From IV. in Lemma1, $\overline{\xi \left(z\right)}=\xi (1-\overline{z}),$ then $\xi \left(\right(1-x)+yi)=\xi (x+yi)$ From V. in Lemma1, $x={\displaystyle \frac{1}{2}}.$

Second, $\overline{\xi \left({\displaystyle \frac{1}{2}}+yi\right)}=\xi \left(\overline{{\displaystyle \frac{1}{2}}+yi}\right)=\xi \left({\displaystyle \frac{1}{2}}-yi\right)=\xi \left(1-\left({\displaystyle \frac{1}{2}}-yi\right)\right)=\xi \left({\displaystyle \frac{1}{2}}+yi\right)$ this complete the proof. □

Since zero is a real number, then from Theorem 1, we have the following corollary:

Corollary 1. 

All non-trivial zeros $z=x+yi$ of $\xi$ must lie on the critical line $x={\displaystyle \frac{1}{2}}.$

From Lemma 1,VI., we obtain:

Corollary 2.(Riemann Hypothesis) All non-trivial zeros $z=x+yi$ of $\zeta$ must lie on the critical line $x={\displaystyle \frac{1}{2}}.$

In [4] a real function

$$\mathsf{ϝ}\left(y\right):={\displaystyle \frac{{\pi }^{\frac{-iy}{2}}\Gamma \left(\frac{1}{4}+\frac{iy}{2}\right)\zeta \left(\frac{1}{2}+\frac{iy}{2}\right)}{\left|\Gamma \left(\frac{1}{4}+\frac{iy}{2}\right)\right|}}$$

(6)

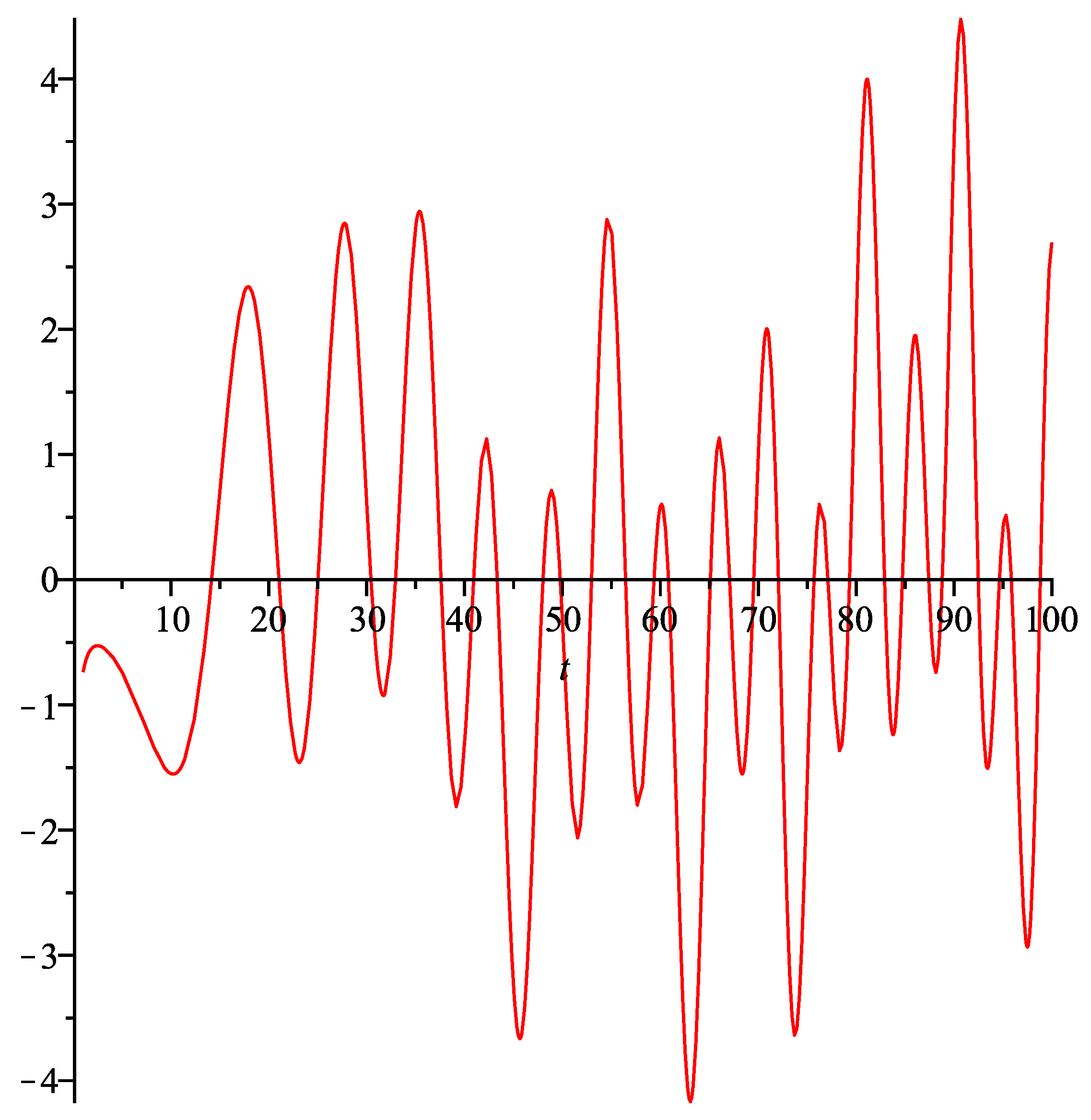
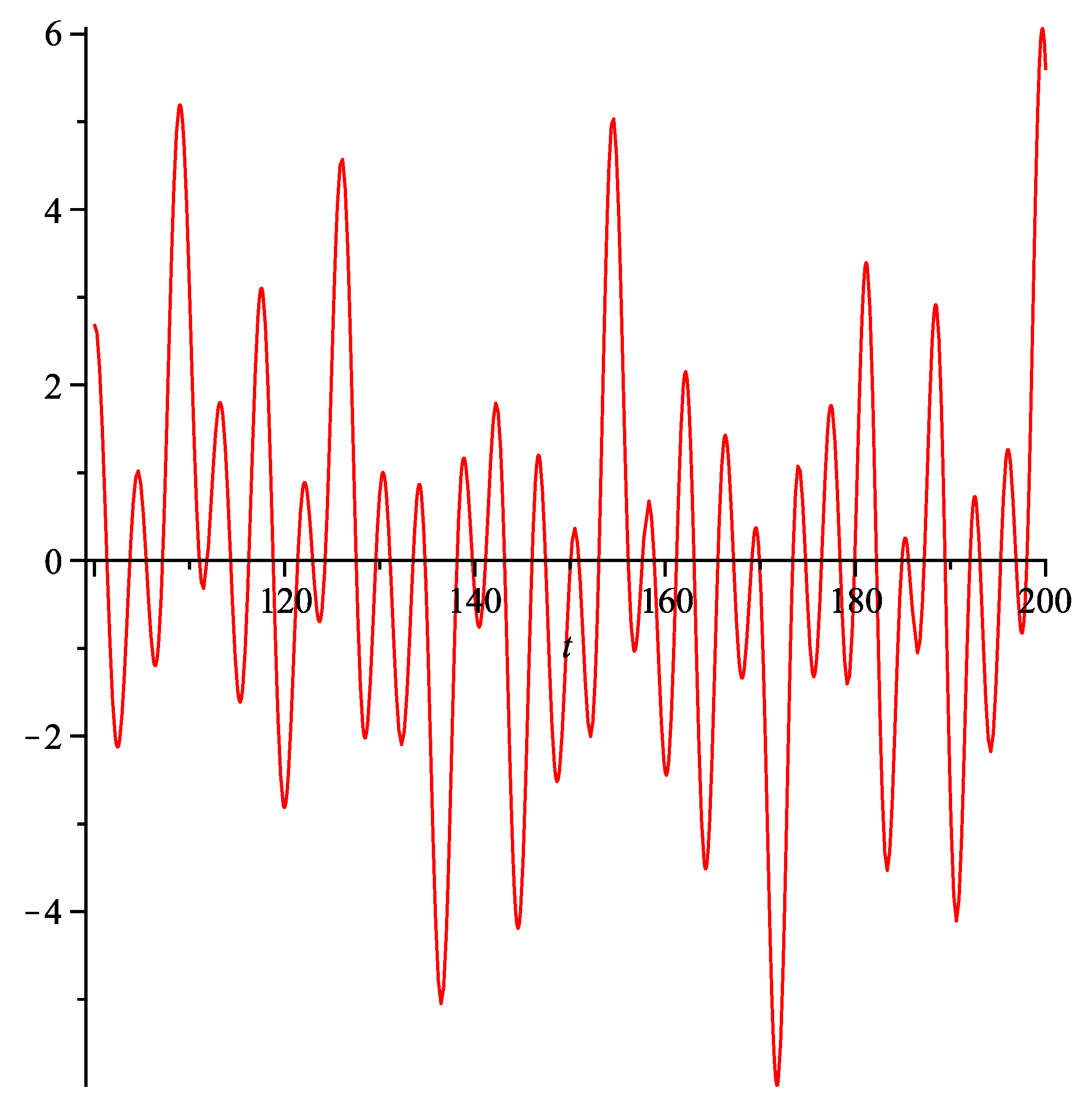
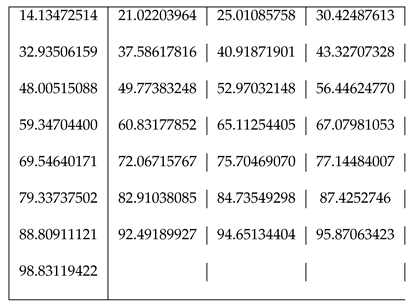
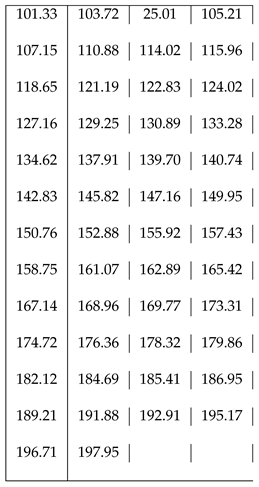
has been constructed. A zero of this function corresponds precisely to the imaginary part of a zero of the zeta function. In this way zeta’s zeros can be plotted (Figure 1 and Figure 2) and calculated (Table 1 and Figure 2).

3. Conclusion

We have proven a very important principle for the function $\xi$ that is "if $z$ is a complex number with nonzero imaginary part, then $\xi \left(z\right)$ is real if and only if $z$ have a real part equal ${\displaystyle \frac{1}{2}}".$ From this principle and the relation between the zeros of $\zeta$ and $\xi$ functions, the Riemann hypothesis have been verified.