Submitted:
20 September 2025
Posted:
23 September 2025
Read the latest preprint version here
Abstract
Keywords:
1. Overview
- Elementary arithmetic.
- −
- ˽ Operations on integers, determination and properties of primes. ( Basic operations, congruence, gcd, lcm, ………..).
- −
- Decomposition of integers into products or sums of primes
- Analytical number theory.
- −
- −
- Algebraic, probabilistic, combinatorial and algorithmic number theories.
- −
- Modular arithmetic.
- −
- Diophantine approximations and equations.
- −
- Arithmetic and algebraic functions.
- −
- Diophantine and number geometry.
- −
- Computational number theory.
2. Definitions Notations and Background
| ● Lagrange-Lemoine-Levy conjecture | (3L) conjecture | (2.17) |
| ● Bachet-Bézout-Goldbach conjecture | (BBG) conjecture | (2.18) |
| ● (Extreme) Goldbach decomponents | (E).G.D | (2.19) |
3. Introduction
- Chen conjecture : For any integer K ≥ 1 there are infinitely many pairs of primes with a difference equal to 2K.
- De Polignac conjecture : Same as Chen, but with consecutive pairs of primes.
- What we know : April 2013, Yitang Zhang [50] demonstrates that the smallest even integer 2K verifying the conjecture is greater than 70 million.
- Either
- Either
4. Theorem (Chen’s Weak or Goldbach(-) Conjecture)
- ►
- Chen(2) is true : 7 - 3 = 4 q = 3 ≤ 4 and p = 7 ≤ 4 x 2 = 8
- ►
- Let’s show
5. Corollary
|
T1(K) = 2K + 3 (T1(K) ; 2K) → (5;2) ; (7 4) ; (11;8) ; (13;10) ; (17;14) ; (19;16) ; (23;20) ; (29;26) ; (29;28);.. T2(K) = 2K + 5 (T2(K) ; 2K) → (7;2) ; (11;6) ; (13;8) ; (17;12) ; (19;14) ; (23;18) ; (29;24) ; (31;26) ; (37;32)................................ T3(K) = 2K + 7 (T3(K) ; 2K) → (11;4) ; (13;6) ; (17;10) ; (19;12) ; (23;16) ; (29;22) ; (31;24) ; (37;30)........... T4(K) = 2K + 11 (T11(K) ; 2K) → (13;2) ; (17;6) ; (19;8) ; (23;12) ; (29;18) ; (31;20) ; (37;26) ; (41;30) ; (43;34)......................... (T13(K) ; 2K) → (17;4) ; (19;6) ; (23;10) ;(29;16) ; (31;18) ; (37;24) ; (41;28) ; (43;30 ; (47;34).......................... ...................................... Tr(K) = 2K + qr (K ∈ ℕ* : Tr(K) and qr are primes) (see Appendix 16) |
- ▶
- () is true (see Appendix 16).
- ▶
- Let’s show: ( r ) ( r + 1)
6. Lemma (Goldbach’s Fundamental Lemma)
7. Principle of Proof
- For any integer n
- If ( 2n - ) is a prime
- Otherwise, if ( 2n - ) is a composite number
- Remark. Using the same method as in Theorem 4, we can the following equivalent property by strong recurrence : For any integer n greater than 48
- ►
- ret(49) is true.
- ►
- The heredity of the property (n) : (n) (n + 1)
8. Theorem (Goldbach Conjecture)
- ▶
- (2) is true : it suffices to choose = = 2 .
- ▶
- Let's show that the property (n) is hereditary : (n) (n + 1)
- If ( 2(n + 1) - ) is a prime
- Otherwise, if ( 2(n+1) - ) is a composite number
- If ( 2n - ) is a prime
- Otherwise, if ( 2n - ) is a composite number
9. Lemma
- ▶
- (2000) is true according to program 13.2 and the table in appendix 14.
- ▶
- For any integer n ≥ 2000 let’s show that (n) is hereditary:
- If (2(n + 1) - ) is a prime
- Otherwise, if ( 2(n + 1) - ) is a composite number
10. Propositions
- A)
- Link between Goldbach conjecture and the fundamental theorem of arithmetic.
|
( p’, q’ ∈ Ƥ │ p’ q’ and P " Q " ) ; then, 2n = P ".Q " = p’ + q’ and p’ - q’ = 2K ln(P ".Q ") = ln(P ") + ln(Q ") = ln(p’ + q’) = ln(p’(1 + )) ≈ ln(p’) + |
|
Examples: ● evalf(solve([90 = x*(1 + ln(96/x)), x < 96], x)); {x = 64.12418697} ; p’ = 67 q’ = 29 ● evalf(solve([1000 = x*(1 + ln(1100/x)), x < 1100], x)); { x = 665.6361412} prevprime(665); 661 isprime(1100 - 661); true ; p’ = 661 q’ = 439 ● evalf(solve([9700 = x*(1 + ln(10000/x)), x < 10000], x)); { x = 7652.697929} prevprime(7652); 7649 isprime(10000 - 7649); true ; p’ = 7649 q’ = 4351 ● evalf(solve([99950 = x*(1 + ln(100000/x)), x < 100000], x)); { x = 96854.43333} a := prevprime(96799); a := 96797 # obtained after 3 or 4 iterations of the command prevprime( ) isprime(100000 - a); true ; p’ = 96799 q’ = 3201 |
- gcd(n, p’)= gcd(n ,2n - p’) = gcd( n ,q’) = gcd(n ,K)= gcd(n,p’.q’) = gcd(n,n² - K²) = 1
- gcd(K,p’) = gcd(K,q’) = gcd(n.K, p’) = gcd( n.K, q’) = 1
- The smallest E.G.D. of 2n is less than the square of its greatest prime factor.
- For any non-zero integer R, the smallest of G.D.’s of R.# is greater than .
- B)
- Method of locating G.D. products ( Difference in squares: N² - K² or decentered dichotomy by geometric mean ( see code RSA , [37]).
| > | ||||
|
n2:= 1000; # To determine two G.D.s of 2n = 1000, we choose two decomponents of a lower integer, m2 and two decomponents of a higher integer, r2 to 2n; we easily calculate m2 < 2n = n2 < r2 and their differences km2 and kr2; then we examine their products which are assumed to preserve order, (if the initial decomponents are well chosen : and ≥ ,( p'. q' = n² - k² ); we then define admissible bounds for k from a = . and b = . . min2 = trunc(evalf(sqrt(n² - b),Digits)) and max2 = trunc(evalf(sqrt(n² - a),Digits)); decomponents of 2n are deduced by iterating the nextprime( ) command from n + min2 , (choose a gap of the order of c.ln²(n) between m2 and r2. |
||||
| pinf := prevprime(735); | pinf := 733 | |||
| qinf := nextprime(17); | qinf := 19 | |||
| psup := nextprime(1050); | psup := 1051 | |||
| qsup := nextprime(29); | qsup := 31 | |||
| m2 := pinf + qinf; | m2 := 752 | |||
| r2 := psup + qsup; | r2 := 1082 | |||
| km2 := pinf - qinf; | km2 := 714 | |||
| kr2 := psup - qsup; | kr2 := 1020 | |||
| a := m2*m2 - km2*km2; | a := 55708 | # a := pinf.qinf | ||
| b := r2*r2 - kr2*kr2; | b := 130324 | # b := psup.qsup | ||
| min2 := trunc(evalf(sqrt(0.25*n2*n2 - b),digits); | min2 := 466 | |||
| max2 := trunc(evalf(sqrt(0.25*n2*n2 - a),digits); | max2 := 485 | |||
| n:= trunc(0.5*n2); | ||||
| em := nextprime(n + min2 - 1); | em := 967 | |||
| nextprime(em); | 971 | |||
| em2 := 0.5*n2 + max2; | em2 := 985.0 | |||
| q := n2 - 971; | q := 29 | |||
| isprime(q); | true | |||
- C)
- Euclidean divisions of 2n by its presumed Goldbach decomponents
- Implementation:
|
3,5,7,11,..... 20 = 3 x 6 + 2 = (3 x 5 + 2) + 3 = 17 + 3 22 = 3 x 7 + 1 = (3 x 6 + 1) + 3 = 19 + 3 24 = 3 x 8 = 5 x 4 + 4 = (5 x 3 + 4) + 5 = 19 + 5 26 = 3 x 8 + 2 = (3 x 7 + 2) + 3 = 23 + 3 28 = 3 x 9 + 1 = (3 x 8 + 1) + 3 = 5 x 5 + 3 = (5 x 4 + 3) + 5 = 23 + 5 30 = 3 x 10 = 5 x 6 = 7 x 4 + 2 = (7 x 3 + 2) + 7 = 23 + 7 32 = 3 x 10 + 2 = (3 x 9 + 2) + 3 = 29 + 3 34 = 3 x 10 + 4 = (3 x 9 + 4) + 3 = 31 + 3 36 = 3 x 12 = 5 x 7 + 1 = (5 x 6 + 1) + 5 = 31 + 5 38 = 3 x 12 + 2 = (3 x 11 + 2) + 3 = 35 + 3 = 5 x 7 + 3 = (5 x 6 + 3) + 5 = 33 + 5 = 7 x 5 + 3 = (7 x 4 + 3) + 7 = 31 + 7 ................................................................................................ 500 = 3 x 166 + 2 = (3 x 165 + 2) + 3 = 497 + 3 = 5 x 100 = 7 x 71 + 3 = (7 x 70 + 3) + 7 = 493 + 7 = 11 x 45 + 5 = (11 x 44 + 5) + 11 = 489 + 11 = 13 x 38 + 6 = (13 x 37 + 6) + 13 = 487 + 13 |
11. Theorem
12. Lemma
- If 2n = 6m then (p ; q) = (6r + 5 ; 6(m - r - 1) + 1) or (6r+1 ; 6(m - 1 - r) + 5)
- If 2n = 6m + 2 then (p ; q) = ( 6r + 1 ; 6(m - r) + 1)
- If 2n = 6m + 4 then (p ; q) = (6r + 5 ; 6(m- 1 - r) + 5)
| p + q mod 6 | 1 | 5 |
| 1 | 2 | 0 |
| 5 | 0 | 4 |
| + mod 30 | 1 | 7 | 11 | 13 | 17 | 19 | 23 | 29 |
| 1 | 2 | 8 | 12 | 14 | 18 | 20 | 24 | 0 |
| 7 | 8 | 14 | 18 | 20 | 24 | 26 | 0 | 6 |
| 11 | 12 | 18 | 22 | 24 | 28 | 0 | 4 | 10 |
| 13 | 14 | 20 | 24 | 26 | 0 | 2 | 6 | 12 |
| 17 | 18 | 24 | 28 | 0 | 4 | 6 | 10 | 16 |
| 19 | 20 | 26 | 0 | 2 | 6 | 8 | 12 | 18 |
| 23 | 24 | 0 | 4 | 6 | 10 | 12 | 16 | 22 |
| 29 | 0 | 6 | 10 | 12 | 16 | 18 | 22 | 28 |
13. Properties
14. Algorithm
14.1. Algorithm Written in Natural Language
|
Inputs: Input four integer variables : k, N, n, P Input : = 2 , = 3 , = 5 , 7 , ................., the first N primes. n ← 3 P = M, R, G, S or T as indicated in paragraph 2 Algorithm body : A) Compute : = Sup( p : p ≤ 2n - 3 ) If = (2n - ) is a prime | |
| ← and ← | (14.1.1) |
|
otherwise B) If is a composite number Let : k = 1 B.1) While + 2k is a composite number assign to k the value k + 1 (k k + 1). return to B1) End while Assign to k the value () Let : | |
| = + 2 and = | (14.1.2) |
|
Assign to n the value n + 1 (nand return to A) End : Outputs for integers less than 104:: Print ( 2n = ● ; 2n - 3 = ● ; = ● ; = ● ; = ● ; = ● ) Outputs for large integers : Print ( 2n - P = ● ; 2n - 3 - P = ● ; - P = ● ; = ● ; = ● ) | |
14.2. Program Written with Maxima Software for 2n Around 101000
14.3. Program Written with Maplesoft Maple for 2n Around 101000
|
G := 10^1000: V := [1, 11, 13, 17, 19, 23, 29]: A := G + 500000: B := A + 59: b:=2: st := time( ): for q from A by 6 to B do # Program modulo 30 .using the results of Lemma 11 Possibility of inverting the two loops or defining three similar structures with s := 0, 1, 2. for s from 0 to 2 do n := q + s + s : b := trunc(0.59b - 20); # Improving computation time: the idea is to recognise that for any integer n large enough there exists a Goldbach decomponent and a successor such that (E):│- │< k.(n) ; this reduces the number of ‘nextprime(●)’ operations which take up the most computing time. ( If G = : Computingtime is around 10 sec for thirty terms );The algorithm can be refined by exploiting frame (E). Cesàro averages can also be used to determine the initial condition for b. t:= 0: R := [[1, 5], [1], [5]]: Q := [[1, 7, 11, 13, 17, 19, 23, 29], [1, 13, 19], [11, 17, 23], [7, 13, 17, 19, 23, 29], [1, 7, 19], [11, 17, 23, 29], [1, 11, 13, 19, 23, 29], [1, 7, 13], [17, 23, 29], [1, 7, 11, 17, 19, 29], [1, 19, 7, 13], [11, 23, 29], [1, 23, 7, 17, 11, 13], [7, 19, 13], [11, 17, 29]]: while t = 0 do . b := nextprime(b + 100); # Additional test possible by improving Lemma 11. (with V mod 30). # Possibility of replacing nextprime with a faster procedure ( see Sainty [37]).( the computation time is greatly reduced by replacing with b:=nextprime(b + k(b,G)), k(b,G) constant around 150 for G=, k(b,G) chosen randomly with the rand procedure or very slowly increasing as a function of b and G ), but in general we don't obtain the E.G.D. but any Goldbach decomponents. e := n - b; K := e mod 6; if K in R[s+1] then if isprime(e) Then t := 1; print(n - G, b, e - G); end if; end if; end do: end do: end do: Computingtime:= time( ) - st; Comments : Possible test with igcd(n , b) = 1 and igcd(n , 2n - b) = 1 (or igcd(n,b.(n-b)) = 1) then isprime(b) and isprime(2n - b) may be faster than nextprime( ), if we can improve the gcd algorithm. RESULTS : G = |
|||
|
b: b:= nextprime(b+rand(100..150)) b:= nextprime(b+100) b:= nextprime(b+150) | |||
|
n - G b n - G - b 500000, 54133, 445867 500002, 40693, 459309 500004, 422393, 77611 500006, 49157, 450849 500008, 222991, 277017 500010, 259451, 240559 500012, 521981, -21969 500014, 622561, -22547 500016, 342929, 157087 500018, 25097, 474921 500020, 95083, 404937 500022, 201821, 298201 500024, 226337, 273687 500026, 255859, 244167 500028, 8147, 491881 500030, 83833, 416197 500032, 43261, 456771 500034, 162251, 337783 500036, 179203, 320833 500038, 12601, 487437 500040, 608471,-108431 500042, 157103, 342939 500044, 145531, 354513 500046, 440303, 59743 500048, 162577, 337471 500050, 258637, 241413 500052, 111791, 388261 500054, 139661, 360393 500056, 126397, 373659 500058, 40739, 459319 500060, 106121, 393939 ComComputtime:= 179.343 sec |
500000, 139387, 360613 500002, 40693, 459309 500004, 731447, -231443 500006, 54139, 445867 500008, 205651, 294357 500010, 100109, 399901 500012, 40693, 459319 500014, 261823, 238191 500016, 82913, 417103 500018, 300889, 199129 500020, 12583, 487437 500022, 233591, 266431 500024, 159871, 340153 500026, 106087, 393939 500028, 608459, -108431 500030, 30347, 469683 500032, 43261, 456771 500034, 201833, 298201 500036, 186859, 313177 500038, 95101, 404937 500040, 121763, 378277 500042, 9029, 491013 500044, 148663, 351381 500046, 304847, 195199 500048, 157109, 342939 500050, 40459, 459591 500052, 8171, 491881 500054, 223037, 277017 500056, 49207, 450849 500058, 301349, 198709 Computtime:= 188.250 sec |
500000, 361069, 138931 500002, 40693, 459309 500004, 535637, -35633 500006, 277789, 222217 500008, 205651, 294357 500010, 138959, 361051 500012, 40693, 459319 500014, 145501, 354513 500016, 198659, 301357 500018, 26309, 473709 500020, 77347, 422673 500022, 160709, 339313 500024, 162553, 337471 500026, 106087, 393939 500028, 263009, 237019 500030, 151813, 348217 500032, 24049, 475983 500034, 400031, 100003 500036, 145037, 354999 500038, 854257, -354219 500040, 121763, 378277 500042, 8161, 491881 500044, 145987, 354057 500046, 304847, 195199 500048, 12611, 487437 500050, 163729, 336321 500052, 100151, 399901 500054, 155291, 344763 500056, 126397, 373659 500058, 208277, 291781 500060, 67547, 432513 Computime:= 163.828 sec |
|
| b:= nextprime(b+rand(150..175)) b:= nextprime(b+rand(140..160)) | |||
| n-G b n-b-G | n-G b n-b-G | ||
| 500000, 139387, 360613 500002, 90481, 409521 500004, 422393, 77611 500006, 145007, 354999 500008, 604339, -104331 500010, 138959, 361051 500012, 221021, 278991 500014, 334843, 165171 500016, 297779, 202237 500018, 167267, 332751 500020, 54577, 445443 500022, 139409, 360613 500024, 336491, 163533 500026, 12589, 487437 500028, 263009, 237019 500030, 145517, 354513 500032, 334861, 165171 500034, 163697, 336337 500036, 318979, 181057 500038, 221047, 278991 500040, 761591, -261551 500042, 178691, 321351 500044, 54601, 445443 500046, 174989, 325057 500048, 84229, 415819 500050, 163729, 336321 500052, 159899, 340153 500054, 155291, 344763 500056, 166183, 333873 500058, 151841, 348217 Computtime:= 174.438 sec |
500000, 112429,-387571 500002, 40693, 459309 500004, 277787, 222217 500006, 82903, 417103 500008, 148627, 351381 500010, 139397, 360613 500012, 40693, 459319 500014, 145501, 354513 500016, 388313, 111703 500018, 258329, 241689 500020, 77347, 422673 500022, 453683, 46339 500024, 67511, 432513 500026, 221197, 278829 500028, 263009, 237019 500030, 112459, 387571 500032, 178681, 321351 500034, 208253, 291781 500036, 274019, 226017 500038, 14071, 485967 500040, 162257, 337783 500042, 361111, 138931 500044, 52903, 447141 500046, 582299, -82253 500048, 8167, 491881 500050, 67537, 432513 500052, 111791, 388261 500054, 126641, 373413 500056, 126397, 373659 500058, 40739, 459319 Computtime:= 138.578 sec |
Record : 116 sec; see in researchgate files PDFGOLDBACHTEST4,10 (For n from G+5000000 to 5000058 by 2), [37]. |
|
| 500000, 9473, 490527 500002, 24019, 475983 500004, 8123, 491881 500006, 9479, 490527 500008, 25087, 474921 500010, 57917, 442093 500012, 8999, 491013 500014, 9001, 491013 500016, 40697, 459319 500018, 9491, 490527 500020, 9007, 491013 500022, 139409, 360613 500024, 9011, 491013 500026, 9013, 491013 500028, 8147, 491881 500030, 26321, 473709 500032, 24049, 475983 500034, 54167, 445867 500036, 57943, 442093 500038, 9511, 490527 500040, 57947, 442093 500042, 8161, 491881 500044, 24061, 475983 500046, 162263, 337783 500048, 8167, 491881 500050, 12613, 487437 500052, 8171, 491881 500054, 9041, 491013 500056, 9043, 491013 500058, 40739, 459319 Computingtime : 343.453 sec G = n - G n - b - G b n - G b n - b - G 40000, 39957, 43 40050, 86117, -46067 40002, 39091, 911 40052, 503, 39549 40004, 39957, 47 40054, 97, 39957 40006, 39549, 457 40056, 89393, -49337 40008, 25369, 14639 40058, 101, 39957 40010, 39957, 53 40060, 103, 39957 40012, 39549, 463 40062, 971, 39091 40014, 17737, 22277 40064, 107, 39957 40016, 39957, 59 40066, 109, 39957 40018, 39957, 61 40068, 977, 39091 40020, 39091, 929 40070, 113, 39957 40022, 39141, 881 40072, 523, 39549 40024, 39957, 67 40074, 983, 39091 40026, 35443, 4583 40076, 16937, 23139 40028, 39957, 71 40078, 937, 39141 40030, 39957, 73 40080, 4637, 35443 40032, 39091, 941 40082, 941, 39141 40034, 35443, 4591 40084, 127, 39957 40036, 39957, 79 40086, 4643, 35443 40038, 39091, 947 40088, 131, 39957 40040, 39957, 83 40090, 541, 39549 40042, 23139, 16903 40092, 4649, 35443 40044, 39091, 953 40094, 137, 39957 40046, 39957, 89 40096, 139, 39957 40048, 39549, 499 40098, 31991, 8107 40100, 1009, 39091 G = n - G b n - b - G 100000, 36529, 63471 100002, 77069, 22933 100004, 22717, 77287 100006, 181873, -81867 100008, 12239, 87769 100010, 4547, 95463 100012, 4549, 95463 100014, 22727, 77287 100016, 59497, 40519 100018, 24847, 75171 100020, 12251, 87769 100022, 12253, 87769 100024, 4561, 95463 100026, 22739, 77287 100028, 22741, 77287 100030, 4567, 95463 100032, 12263, 87769 100034, 36563, 63471 100036, 42649, 57387 100038, 12269, 87769 100040, 23143, 76897 100042, 36571, 63471 100044, 43973, 56071 100046, 4583, 95463 100048, 24877, 75171 100050, 12281, 87769 G = n - G b n - b - G n - G b n - b - G n - G b n - b - G 100000, 31147, 68853 100050, 12611, 87439 100100, 31247, 68853 100002, 309371, -209369 100052, 12613, 87439 100102, 31249, 68853 100104, 105071, -4967 100106, 13649, 86457 100004, 31151, 68853 100054, 13597, 86457 100108, 640669, -540561 100006, 31153, 68853 100056, 105023, -4967 100110, 12671, 87439 100008, 12569, 87439 100058, 12619, 87439 100112, 31259, 68853 100114, 87991, 12123 100116, 122033, -21917 100118, 18379, 81739 100010, 13553, 86457 100060, 54151, 45909 100012, 31159, 68853 100062, 108971, -8909 100014, 108923, -8909 100064, 103091, -3027 100016, 12577, 87439 100066, 87943, 12123 100018, 592237, -492219 100068, 18329, 81739 100020, 104987, -4967 100070, 13613, 86457 100022, 12583, 87439 100072, 31219, 68853 100024, 13567, 86457 100074, 264881, - 100026, 18287, 81739 100076, 12637, 87439 100028, 12589, 87439 100078, 107971, -7893 100030, 31177, 68853 100080, 12641, 87439 100032, 61871, 38161 100082, 76913, 23169 100034, 13577, 86457 100084, 13627, 86457 100036, 31183, 68853 100086, 12647, 87439 100038, 108947, -8909 10038, 108947, -8909 100088, 61927, 38161 100040, 12601, 87439 100090, 13633, 86457 100042, 31189, 68853 100092, 12653, 87439 100044, 457091, -357047 100094, 61933, 38161 100046, 18307, 81739 100096, 87973, 12123 100048, 13591, 86457 100098, 12659, 87439 100120, 31267, 68853 100122, 61961, 38161 100124, 31271, 68853 100126, 13669, 86457 100128, 12689, 87439 100130, 31277, 68853 100132, 76963, 23169 100134, 122051, -21917 100136, 12697, 87439 100138, 13681, 86457 100140, 18401, 81739 100142, 12703, 87439 100144, 13687, 86457 100146, 152993, -52847 100148, 13691, 86457 100150, 13693, 86457 1000000, 35509, 964491 1000002, 113, 999889 1000004, 69193, 930811 1000006, 95233, 904773 1000008, 69197, 930811 1000010, 31873, 968137 1000012, 35521, 964491 1000014, 69203, 930811 1000016, 127, 999889 1000018, 35527, 964491 1000020, 131, 999889 Maple program corrected and improved, (see Sainty [37]). |
|||
15. Appendix
- WATCH OUT !
| 2n 2n - 3 | =2n - | |||||
| 4 1 |
X | X | 2 | 2 | ||
| 6 3 |
3 | 3 | 3 | 3 | ||
| 8 5 |
5 | 3 | 5 | 3 | ||
| 1 10 7 |
7 | 3 | 7 | 3 | ||
| 112 9 |
7 | 5 | 7 | 5 | ||
| 14 11 |
11 | 3 | 11 | 3 | ||
| 16 13 |
13 | 3 | 13 | 3 | ||
| 18 15 |
13 | 5 | 13 | 5 | ||
| 20 17 |
17 | 3 | 17 | 3 | ||
| 22 19 |
19 | 3 | 19 | 3 | ||
| 24 21 |
19 | 5 | 19 | 5 | ||
| 26 23 |
23 | 3 | 23 | 3 | ||
| 28 25 |
23 | 5 | 23 | 5 | ||
| 30 27 |
23 | 7 | 23 | 7 | ||
| 32 29 |
29 | 3 | 29 | 3 | ||
| 34 31 |
31 | 3 | 31 | 3 | ||
| 36 33 |
31 | 5 | 31 | 5 | ||
| 38 35 |
31 | 7 | 31 | 7 | ||
| 40 37 |
37 | 3 | 37 | 3 | ||
| 80 77 |
73 | 7 | 73 | 7 | ||
| 82 79 |
79 | 3 | 79 | 3 | ||
| 84 81 |
79 | 5 | 79 | 5 | ||
| 86 83 |
83 | 3 | 83 | 3 | ||
| 88 85 |
83 | 5 | 83 | 5 | ||
| 90 87 |
83 | 7 | 83 | 7 | ||
| 92 89 |
89 | 3 | 89 | 3 | ||
| 94 91 |
89 | 5 | 89 | 5 | ||
| 96 93 |
89 | 7 | 89 | 7 | ||
|
**98 95 |
89 | 9 | 79 | 19 | ||
| 100 97 |
97 | 3 | 97 | 3 | ||
| 120 117 |
113 | 7 | 113 | 7 | ||
|
**122 119 |
113 | 9 | 109 | 13 | ||
| 124 121 |
113 | 11 | 113 | 11 | ||
| 126 123 |
113 | 13 | 113 | 13 | ||
|
**128 125 |
113 | 15 | 109 | 19 | ||
| 130 127 |
127 | 3 | 127 | 3 | ||
| 132 129 |
127 | 5 | 127 | 5 | ||
| 134 131 |
131 | 3 | 131 | 3 | ||
| 136 133 |
131 | 5 | 131 | 5 | ||
| 138 135 |
131 | 7 | 131 | 7 | ||
| 140 137 |
137 | 3 | 137 | 3 | ||
|
**500 497 |
491 | 9 | 487 | 13 | ||
| 502 499 |
499 | 3 | 499 | 3 | ||
| 504 501 |
499 | 5 | 499 | 5 | ||
| 506 503 |
503 | 3 | 503 | 3 | ||
| 508 505 |
503 | 5 | 503 | 5 | ||
| 510 507 |
503 | 7 | 503 | 7 | ||
| 1000 997 |
997 | 3 | 997 | 3 | ||
| 1002 999 |
997 | 5 | 997 | 5 | ||
| 1004 1001 |
997 | 7 | 997 | 7 | ||
|
**1006 1003 |
997 | 9 | 983 | 23 | ||
| 1008 1005 |
997 | 11 | 997 | 11 | ||
| 1010 1007 |
997 | 13 | 997 | 13 | ||
| 1012 1009 |
1009 | 3 | 1009 | 3 | ||
| 1014 1011 |
1009 | 5 | 1009 | 5 | ||
| 1016 1013 |
1013 | 3 | 1013 | 3 | ||
| 1018 1015 |
1013 | 5 | 1013 | 5 | ||
| 10002 9999 |
9973 | 29 | 9973 | 29 | ||
| 10004 10001 |
9973 | 31 | 9973 | 31 | ||
|
**10006 10003 |
9973 | 33 | 9923 | 83 | ||
|
**10008 10005 |
9973 | 35 | 9967 | 41 | ||
| 10010 10007 |
10007 | 3 | 10007 | 3 | ||
| 10012 10009 |
10009 | 3 | 10009 | 3 | ||
| 10014 10011 |
10009 | 5 | 10009 | 5 | ||
| 10016 10013 |
10009 | 7 | 10009 | 7 | ||
|
**10018 10015 |
10009 | 9 | 10007 | 11 | ||
| 10020 10017 |
10009 | 11 | 10009 | 11 | ||
| 2n - M (2n - 3) - M | - M | = 2n - | - M | |||
| +1000 +997 |
+993 | 7 | +993 | 7 | ||
|
**+1002 +999 |
+993 | 9 | +931 | 71 | ||
| +1004 +1001 |
+993 | 11 | +993 | 11 | ||
| +1006 +1003 |
+993 | 13 | +993 | 13 | ||
|
**+1008 +1005 |
+993 | 15 | +919 | 89 | ||
| +1010 +1007 |
+993 | 17 | +993 | 17 | ||
| +1012 +1009 |
+993 | 19 | +993 | 19 | ||
| +1014 +1011 |
+1011 | 3 | +1011 | 3 | ||
| +1016 +1013 |
+1011 | 5 | +1011 | 5 | ||
| +1018 +1015 |
+1011 | 7 | +1011 | 7 | ||
|
**+1020 +1017 |
+1011 | 9 | +931 | 89 | ||
| 2n - R | (2n - 3) - R | - R | = 2n - | - R | ||
|
**+1000 +997 |
+979 | 21 | +903 | 97 | ||
| +1002 +999 |
+979 | 23 | +979 | 23 | ||
|
**+1004 +1001 |
+979 | 25 | +951 | 53 | ||
|
**+1006 +1003 |
+979 | 27 | +903 | 103 | ||
| +1008 +1005 |
+979 | 29 | +979 | 29 | ||
| +1010 +1007 |
+979 | 31 | +979 | 31 | ||
|
**+1012 +1009 |
+979 | 33 | +951 | 61 | ||
|
**+1014 +1011 |
+979 | 35 | + 781 | 233 | ||
| +1016 +1013 |
+979 | 37 | +979 | 37 | ||
| **+1018 | +1015 | +979 | 39 | +951 | 67 | |
| +1020 | +1017 | +1017 | 3 | +1017 | 3 | |
| 2n - G | (2n - 3) - G | - G | = 2n - | - G | ||
|
**+10000 +9997 |
+9631 | 369 | +7443 | 2557 | ||
|
**+10002 +9999 |
+9631 | 371 | +9259 | 743 | ||
| +10004 +10001 |
+9631 | 373 | +9631 | 373 | ||
|
**+10006 +10003 |
+9631 | 375 | +8583 | 1423 | ||
|
**+10008 + 10005 |
+9631 | 377 | +6637 | 3371 | ||
| +10010 +10007 |
+9631 | 379 | +9631 | 379 | ||
|
**+10012 +10009 |
+9631 | 381 | +8583 | 1429 | ||
| +10014 +10011 |
+9631 | 383 | +9631 | 383 | ||
|
**+10016 +10013 |
+9631 | 385 | +9259 | 757 | ||
|
**+10018 +10015 |
+9631 | 387 | +4491 | 5527 | ||
| +10020 +10017 |
+9631 | 389 | +9631 | 389 | ||
| 2n-S | (2n-3)-S | - S | = 2n - | - S | ||
| **+20000 | +19997 | +18031 | 1969 | +17409 | 2591 | |
| **+20002 | +19999 | +18031 | 1971 | + 17409 | 2593 | |
| +20004 +20001 |
+18031 | 1973 | +18031 | 1973 | ||
| **+20006 | +20003 | +18031 | 1975 | +16663 | 3343 | |
| **+20008 | +20005 | +18031 | 1977 | +16941 | 3067 | |
| +20010 +20007 |
+18031 | 1979 | +18031 | 1979 | ||
| **+20012 | +20009 | +18031 | 1981 | +5671 | 14341 | |
| **+20014 | +20011 | +18031 | 1983 | +4101 | 15913 | |
| **+20016 | +20013 | +18031 | 1985 | +3229 | 16787 | |
| +20018 +20015 |
+18031 | 1987 | +18031 | 1987 | ||
| **+20020 | +20017 | +18031 | 1989 | +16941 | 3079 | |
|
2n-T (2n-3)-T |
-T | = 2n - | ||||
|
**+40000 +39997 |
+29737 | 10263 | +21567 | 18433 | ||
|
**+40002 +39999 |
+29737 | 10265 | + 22273 | 17729 | ||
| +40004 | +40001 | +29737 | 10267 | +29737 | 10267 | |
| **+40006 | +40003 | +29737 | 10269 | +21567 | 18439 | |
| +40008 | +40005 | +29737 | 10271 | +29737 | 10271 | |
| +40010 | + 40007 | +29737 | 10273 | +29737 | 10273 | |
| **+40012 | +40009 | +29737 | 10275 | +10401 | 29611 | |
| **+40014 | +40011 | +29737 | 10277 | -56003 | 96017 | |
| **+40016 | +40013 | +29737 | 10279 | +27057 | 12959 | |
| **+40018 | +40015 | +29737 | 10281 | +25947 | 14071 | |
| **+40020 | +40017 | +29737 | 10283 | +24493 | 15527 | |
16. Appendix
| 7-3=4 | 11-5=6 | 11-3=8 | 13-3=10 | 17-5=12 | 17-3=14 | 19-3=16 | 23-5=18 |
| 23-3=20 | 29-7=22 | 29-5=24 | 29-3=26 | 31-3=28 | 37-7=30 | 37-5=32 | 37-3=34 |
| 41-5=36 | 41-3=38 | 43-3=40 | 47-5=42 | 47-3=44 | 53-7=46 | 53-5=48 | 53-3=50 |
| 59-7=52 | 59-5=54 | 59-3=56 | 61-3=58 | 67-7=60 | 67-5=62 | 67-3=64 | 71-5=66 |
| 71-3=68 | 73-3=70 | 79-7=72 | 79-5=74 | 79-3=76 | 83-5=78 | 83-3=80 | 89-7=82 |
| 89-5=84 | 89-3=86 | 101-13=88 | 97-7=90 | 97-5=92 | 97-3=94 | 101-5=96 | 101-3=98 |
| 103-3=100 | 107-5=102 | 107-3=104 | 109-3=106 | 113-5=108 | 113-3=110 | 131-19=112 | 127-13=114 |
| 127-11=116 | 131-13=118 | 127-7=120 | 127-5=122 | 127-3=124 | 131-5=126 | 131-3=128 | 137-7=130 |
| 137-5=132 | 137-3=134 | 139-3=136 | 149-11=138 | 151-11=140 | 149-7=142 | 149-5=144 | 149-3=146 |
| 151-3=148 | 157-7=150 | 157-5=152 | 157-3=154 | 163-7=156 | 163-5=158 | 163-3=160 | 167-5=162 |
| 167-3=164 | 173-7=166 | 173-5=168 | 173-3=170 | 179-7=172 | 179-5=174 | 179-3=176 | 181-3=178 |
| 191-11=180 | 193-11=182 | 191-7=184 | 191-5=186 | 191-3=188 | 193-3=190 | 197-5=192 | 197-3=194 |
| 199-3=196 | 211-13=198 | 211-11=200 | 233-31=202 | 211-7=204 | 211-5=206 | 211-3=208 | 223-13=210 |
| 229-17=212 | 227-13=214 | 223-7=216 | 223-5=218 | 223-3=220 | 227-5=222 | 227-3=224 | 229-3=226 |
| 233-5=228 | 233-3=230 | 239-7=232 | 239-5=234 | 239-3=236 | 241-3=238 | 251-11=240 | 271-29=242 |
| 251-7=244 | 251-5=246 |
17. Appendix
| Tr(K) | |||||||||||
| = 3 | = 5 | = 7 | = 11 | = 13 | = 17 | = 19 | = 23 | = 29 | = 31 | =37 | |
| 2K = 2 | 5 | 7 | 13 | 19 | 31 | ||||||
| 2K = 4 | 7 | 11 | 17 | 23 | 41 | ||||||
| 2K = 6 | 11 | 13 | 17 | 19 | 23 | 29 | 37 | 43 | |||
| 2K = 8 | 11 | 13 | 19 | 31 | 37 | ||||||
| 2K = 10 | 13 | 23 | 29 | 41 | 47 | ||||||
| 2K = 12 | 17 | 19 | 23 | 29 | 31 | 41 | 43 | ||||
| 2K =14 | 17 | 19 | 31 | 37 | 43 | ||||||
| 2K = 16 | 19 | 23 | 29 | 47 | 59 | ||||||
| 2K = 18 | 23 | 29 | 31 | 37 | 41 | 47 | 61 | ||||
| 2K =20 | 23 | 31 | 37 | 43 | 67 | ||||||
| 2K=22 | 29 | 41 | 53 | ||||||||
| 2K=24 | 29 | 31 | 37 | 41 | 43 | 47 | 53 | 71 | |||
| 2K=26 | 29 | 31 | 37 | 43 | 73 | ||||||
| 2K=28 | 31 | 41 | 47 | 59 | |||||||
| 2K=30 | 37 | 41 | 43 | 47 | 53 | 59 | 61 | ||||
| 2K=32 | 37 | 43 | 61 | 79 | |||||||
| 2K=34 | 37 | 41 | 47 | 53 | |||||||
| 2K=36 | 41 | 43 | 47 | 53 | 59 | 67 | 83 | ||||
| 2K=38 | 41 | 43 | 61 | 67 | |||||||
| 2K=40 | 43 | 47 | 53 | 59 | 71 | ||||||
| 2K=42 | 47 | 53 | 59 | 61 | 71 | 73 | 89 | ||||
| 2K=44 | 47 | 61 | 67 | 73 | |||||||
| 2K=46 | 53 | 59 | |||||||||
| 2K=48 | 53 | 59 | 61 | 67 | 71 | 79 | |||||
| 2K=50 | 53 | 61 | 67 | 73 | 79 | 97 | |||||
| 2K=52 | 59 | 71 | 83 | ||||||||
| 2K=54 | 59 | 61 | 67 | 71 | 73 | 83 | |||||
| 2K=56 | 59 | 61 | 67 | 73 | 79 | ||||||
| 2K=58 | 61 | 71 | 89 | ||||||||
| 2K=60 | 67 | 71 | 73 | 79 | 83 | 89 | |||||
18. Perspectives and Generalizations
- f is strictly increasing on the interval J
- f (3) = 3 and = +
- ▪
- f : x a x + 3 - 3a (a: 0 < a
- ▪
- g : x[ 4 9 ] ( [x] is the integer part of the real x )
- ▪
- h : x + 3
- If Tl2n = (2n + 1 - 2 Wl2n) is a prime
- If Tl2n is a composite number
- Let K and Q be two odd integers prime to each other :
- Let K and Q be two integers of different parity prime to each other :
- GOLDBACH (-) :
- GOLDBACH (+) :
- For any integer n greater than one, there exists two integers KMin and KMax such that the G.D. f 2n are n - K and n + K │ KMin ≤ K ≤ KMax.
19. Conclusions
|
Framing and mean value of the Goldbach comet by functions of the type f : x -> a.x /(x) , ( via AI CLAUDE : to be specified ). |
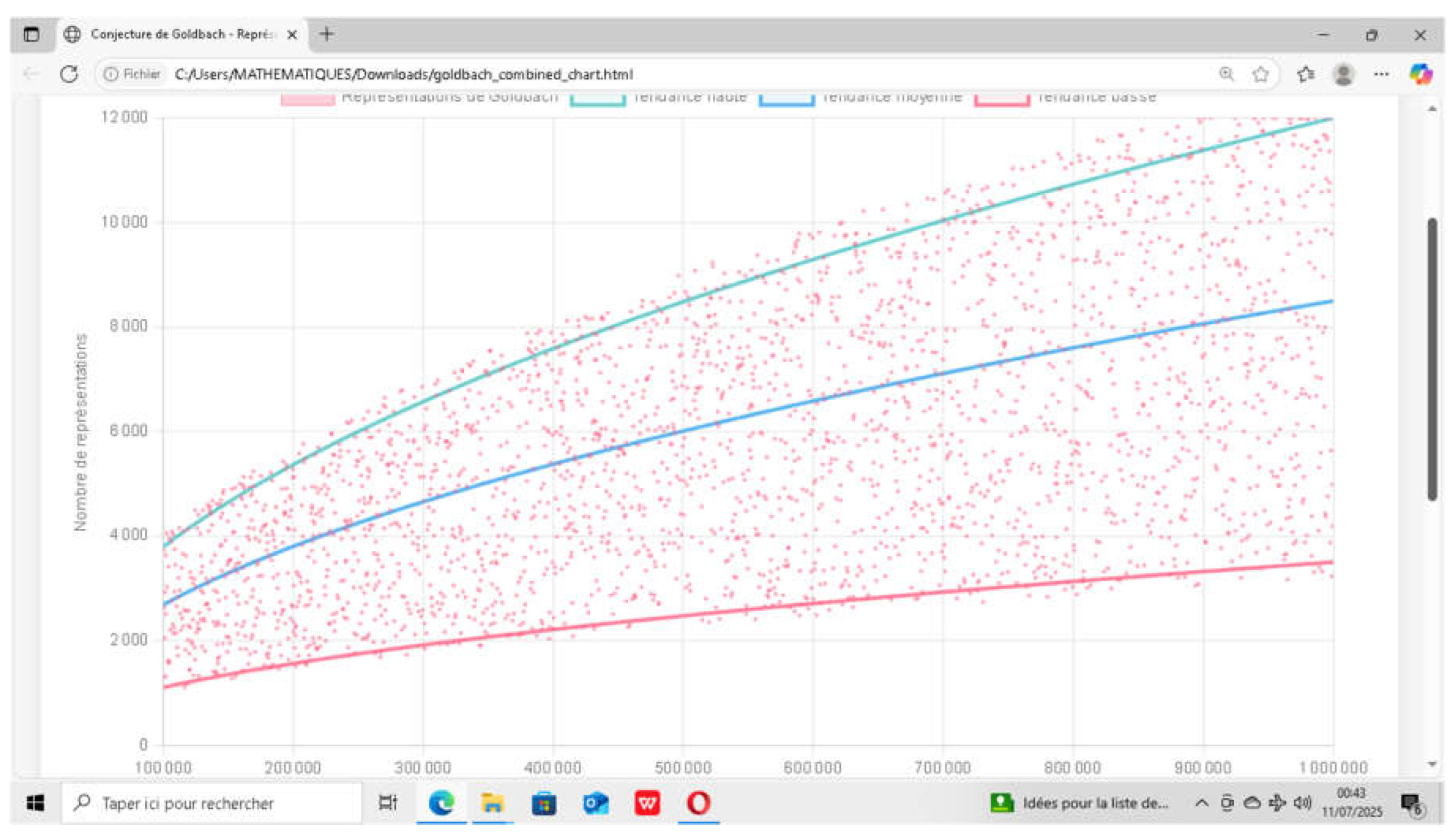
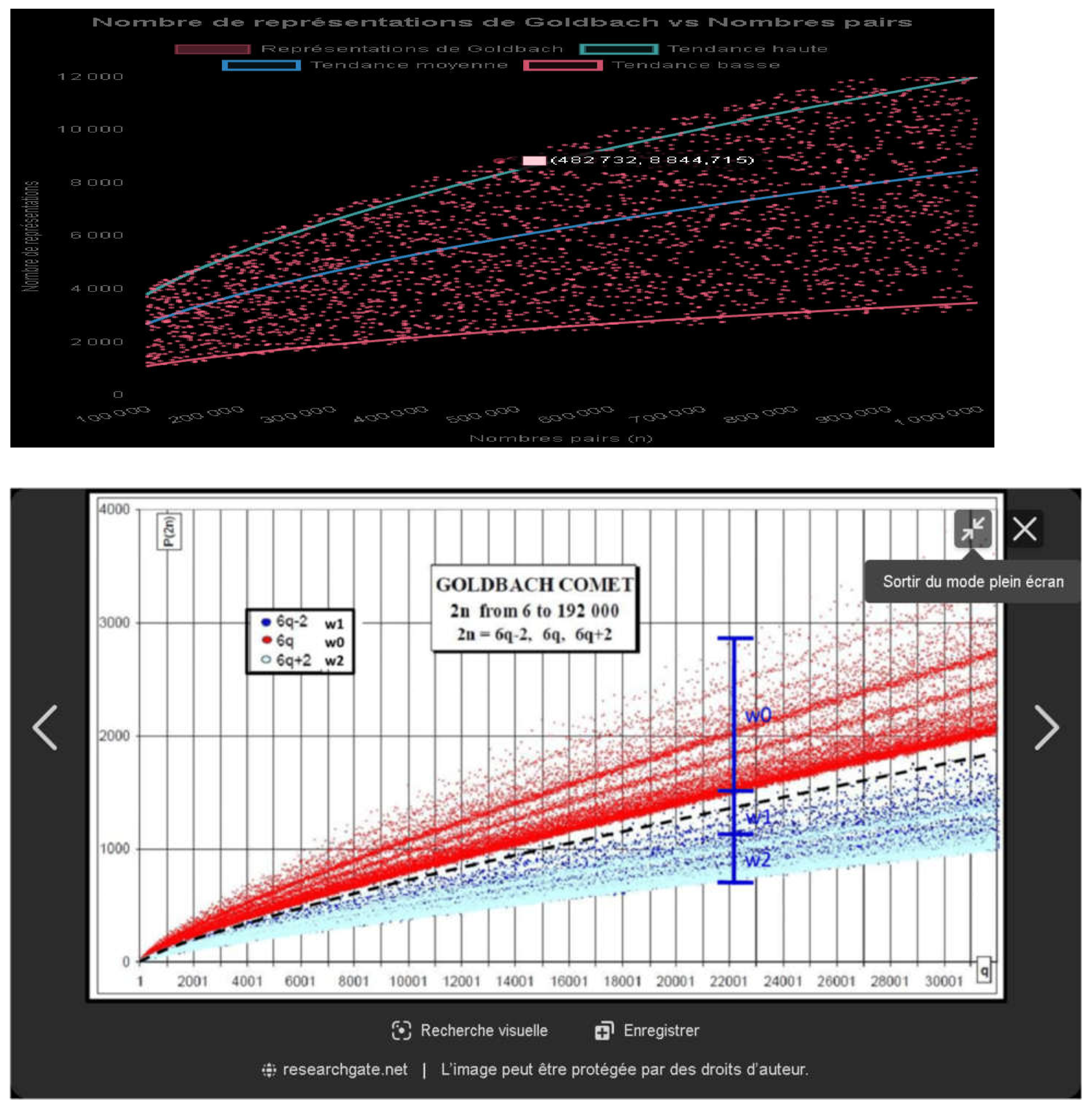
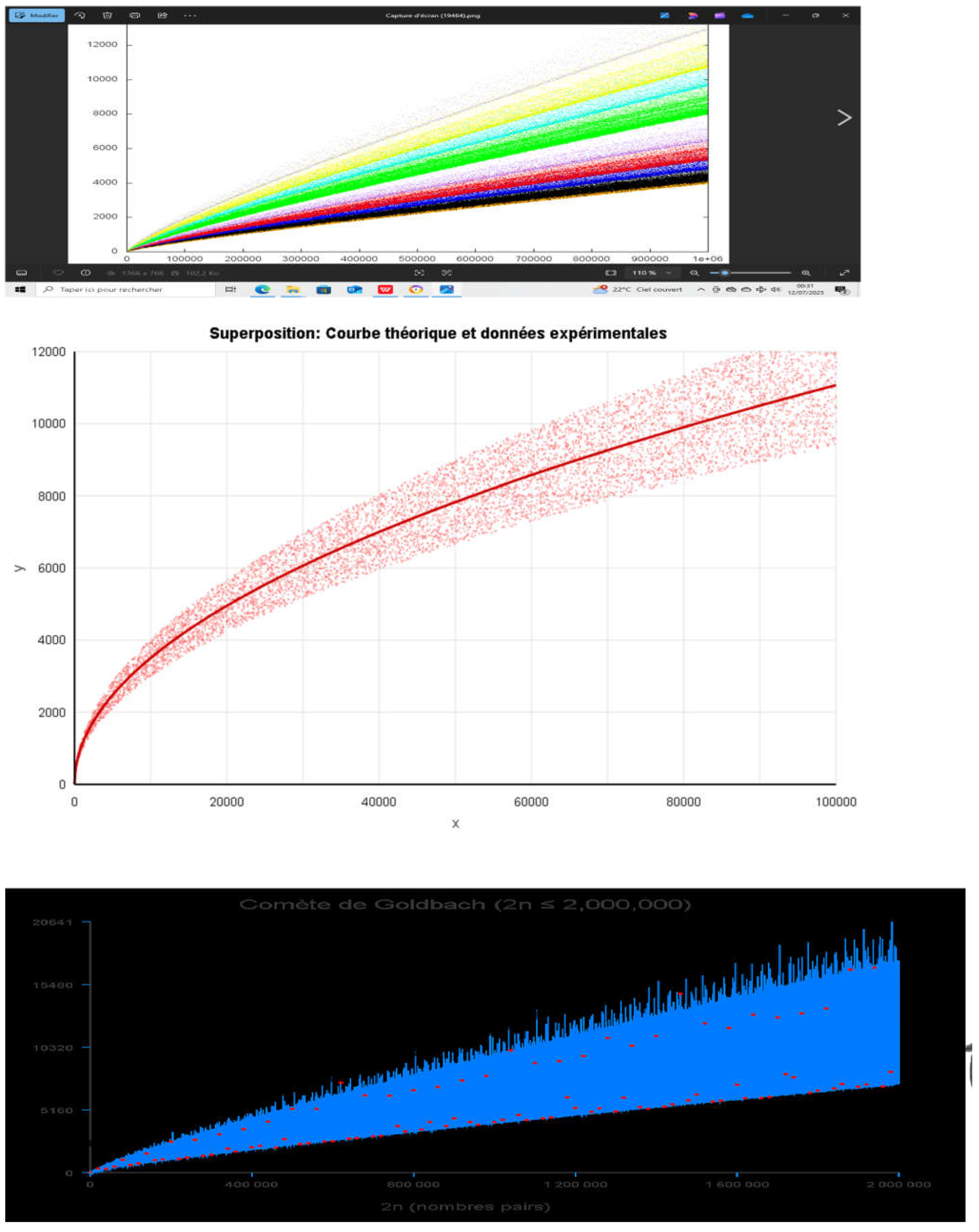
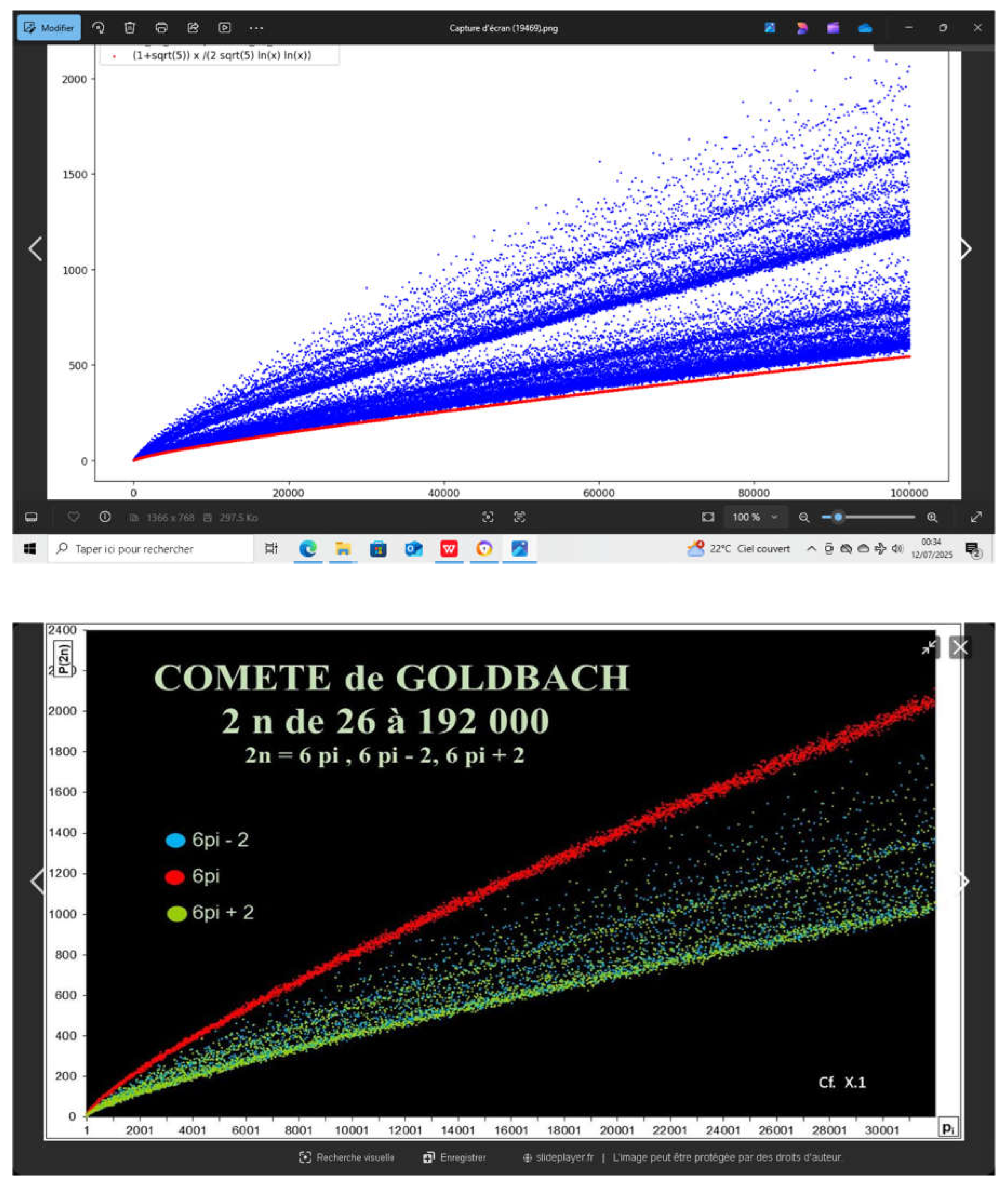
Comments :
- . Therefore, if n is a large even integer and m is a number between 3 and n, the probability that both m and (n - m) are primes is approximately 1/(ln(n).ln(n - m)). Although this heuristic argument is imperfect for several reasons, such as the lack of consideration of correlations between the probabilities of m and (n – m) being primes, it nevertheless indicates that the total number of ways of writing a large even integer n as the sum of two odd primes is approximately proportional to n / (n).
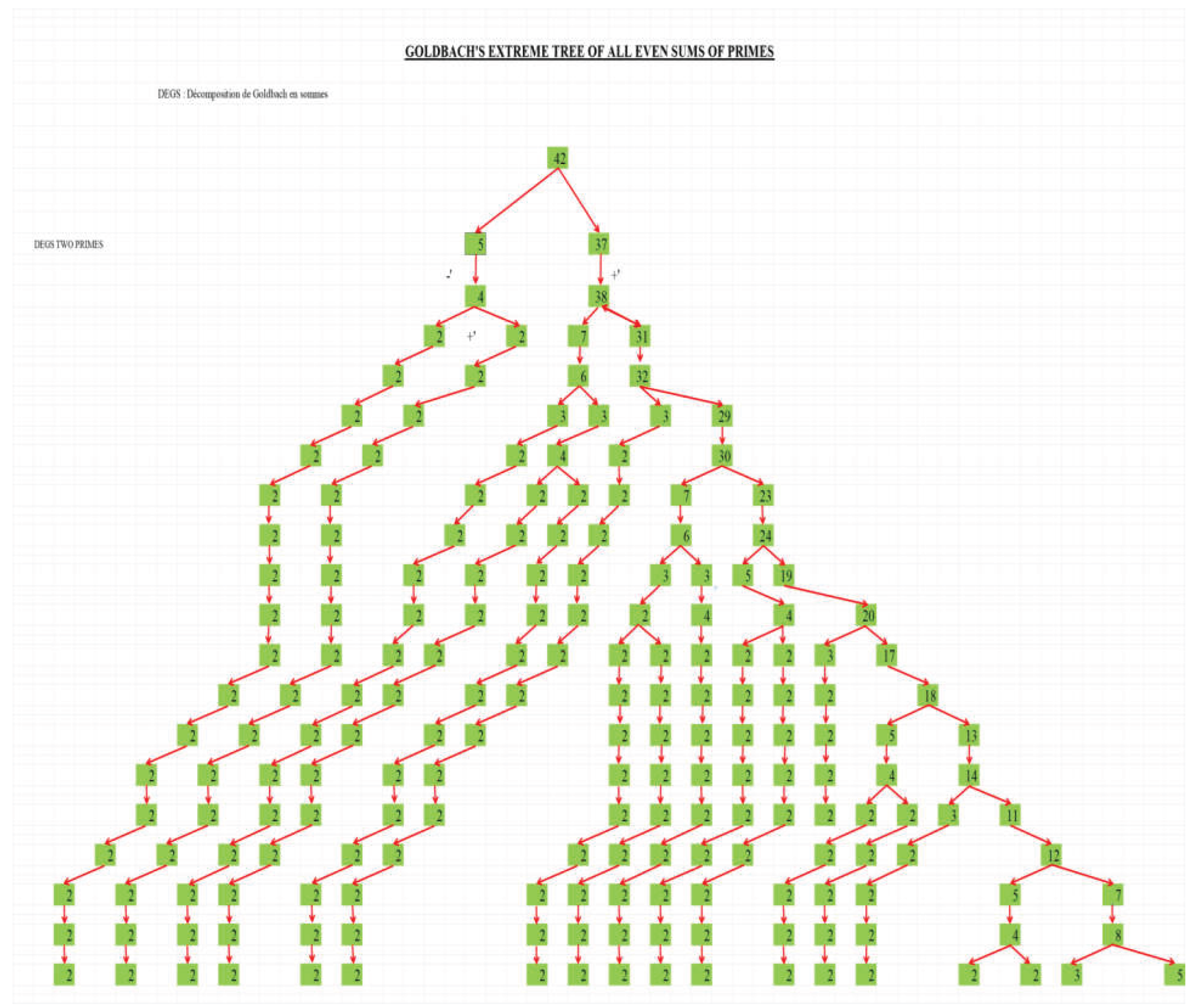
- GRAPHICAL SYNTHESIS
- 2 + 2 + 2 + ... + 2 = 2n. This technique can be used to create new number bases based on primes. Other variations of this tree can be created by adding or subtracting odd integers (other than +1 or -1 ) to the E.G.D. determined at each level.
- Example: ( Draft for 2n = 42 ).
- Goldbach's extreme decomponents tree (parallel algorithm) in even sums of primes.
- Construction rules and properties:
- The tree consists of n levels of k integers 2 ≤ k ≤ n .
- If a level consists of even integers, the next level consists of primes.
- Each line (level) of the tree consists of an ascending sequence of even integers or primes whose sum is 2n.
- The number of 2 for each level is increasing
- The range of the first level is - .
- The ranges of primes levels decrease from - . to 0.
- The range of the last level is 0.
- The range of each level is maximal.
- The integer of the level following a 2 is a 2 .
- The integer of the next level corresponding to a maximum E.G.D. p' is p' + 1 .
- The integer of the next level corresponding to a minimum E.G.D. q' is q' - 1.
- To determine the inverse tree (inverse algorithm), additional rules must be specified in accordance with Goldbach trees of order n less than 2p p ≤ n .
References
- L. Adleman, K. Mc Curley, " Open Problems in Number Theoretic Complexity " , " II. Algorithmic number theory" (Ithaca, NY,1994), 291–322, Lecture Notes in Comput. Sci., 877, Springer, Berlin, (1994).
- C. Axler, “ New Estimates for the nth Prime ” 19.4.2 2 Journal of Integer Sequences, Vol. 22, 30 p., (2019),.
- E. Bombieri, Davenport, " Small differences between prime numbers ", Proc. Roy. Soc. Ser. A293 , pp. 1-18 , (1966). [CrossRef]
- R. C. Baker, Harman, G. " The difference between consecutive primes". Proc. London Math. Soc. (3) 72, 2 (1996), 261–280. [CrossRef]
- R. C. Baker, Harman, G., and Pintz, J. " The difference between consecutive primes ". II. Proc. London Math. Soc. (3) 83, 3 (2001), 532–562. [CrossRef]
- J. Brillhart, D. H. Lehmer & J. L. Selfridge, " New primality criteria and factorizations of 2m ± 1", Math. Comp., vol. 29, no 130, 1975, p. 620-647 (read online [archive]), Th. 4. [CrossRef]
- J. R. Chen, " On the representation of a large even integer as the sum of a prime and the product of at most two primes ". Kexue Tongbao 17 (1966), pp. 385-386 (Chinese) . [CrossRef]
- M. Cipolla, " La determinazione assintotica dell n imo numero primo ", Rend. Acad. Sci. Fis. Mat. Napoli 8(3) (1902).
- H. Cramer, "On the order of magnitude of the difference between consecutive prime numbers", Acta Arithmetica vol. 2 , (1986), p.23-46. [CrossRef]
- N. Dawar, “Lemoine's Conjecture: A Limited Solution Using Computers” , TechRxiv [ Archive online ] (2023). [CrossRef]
- Deshouillers, J.-M.; te Riele, H. J. J.; and Saouter, Y. "New Experimental Results Concerning The Goldbach Conjecture." In Algorithmic Number Theory: Proceedings of the 3rd International Symposium (ANTS-III) held at Reed College, Portland, OR, June 21-25, 1998 (Ed. J. P. Buhler). Berlin: Springer-Verlag, pp. 204-215, 1998. Modélisation, analyse et simulation (MAS), Rapport MAS-R9804, 31 mars 1998.
- P. Dusart, ”About the prime counting function π ” , PhD Thesis. University of Limoges, France, (1998).
- P. Dusart, ’’HDR : Estimations explicites en théorie des nombres’’ , HDR, University of Limoges, France, (2022).
- P. Erdos, "On a new method in elementary number theory which leads to an elementary proof of the prime number theorem", Proc. Natl. Acad. Sci. USA 36, pp. 374-384 (1949). [CrossRef]
- Euclid, (trans. Bernard Vitrac), "Les éléments d'Euclide", Ed. PUF Paris, vol.2, p. 444-446 and p. 339-341, (1994).
- G. G. Filhoa, G.D.G. Jaimea, F.M.de Oliveira Gouveaa, S. Keller Füchter, "Bridging Mathematics and AI: A novel approach to Goldbach’s Conjecture", Contents lists available at ScienceDirect : Measurement: Sensors journal homepage : www.sciencedirect.com/journal.
- A. Granville, "Harald Cramér and the distribution of prime numbers", Scandinavian Actuarial Journal, 1: 12–28,(1995). [CrossRef]
- J. Hadamard, "On the zeros of the function ζ(s) of Riemann". C. R. 122, p.1470-1473 (1896), and "On the distribution of zeros of the function ζ'(s) and its arithmetical consequences". S. M. F. Bull. 24, pp. 199-220 (1896).
- J. Härdig, "Goldbach’s conjecture", Examensarbete i matematik, 15 hp U.U.D.M. Project Report August 2020:37, UPPSALA UNIVERSITET.
- G. H. Hardy, Wright , "An introduction to the Theory of numbers", Oxford : Oxford University Press 621 p. (2008).
- G. H. Hardy, J. E. Littlewood, "Some problems of 'partitio numerorum’" ; III: «On the expression of a number as a sum of primes« (Acta Math. Vol. 44: pp. 1 – 70, (1922) . [CrossRef]
- H. Helfgott, Platt , "The ternary Goldbach conjecture", Gaz. Math. Soc. Math. Fr. 140, pp. 5-18 (2014). "The weak Goldbach conjecture", Gac. R. Soc. Mat. Esp. 16, no. 4, 709-726 (2013). "Numerical verification of the ternary Goldbach conjecture up to 8.875.1030", Exp. Math. 22, n° 4, 406-409 (2013).(arXiv1312.7748, 2013), (to appear in Ann. Math.).
- L. Hodges, "A lesser-known Goldbach conjecture", Math. Mag., 66 (1993): 45–47. [CrossRef]
- H. Iwaniec, Pintz, "Primes in short intervals". Monatsh. Math. 98, pp. 115-143 (1984). [CrossRef]
- J. O. Kiltinen and P. B. Young, "Goldbach, Lemoine, and a Know/Don't Know Problem", Mathematics Magazine, 58(4) (Sep., 1985), p. 195–203. [CrossRef]
- E. Landau, "Handbuch der Lehre von der Verteiligung der Primzahlen", vol. 1 and vol. 2 (1909) , published by Chelsea Publishing Company (1953).
- E. Lemoine, “L’intermédiaire de mathématiciens”, vol. 1, 1894, p. 179, vol. 3, 1896, p. 151.
- H. Levy, “On Goldbach’s conjecture”, Math. Gaz." 47 (1963): 274.
- J. Littlewood , "Sur la distribution des nombres premiers", CRAS Paris, vol. 158, (1914), p. 1869-1875.
- H. Maier, ”Primes in short intervals”. Michigan Math. J., 32(2):221–225, 1985. [CrossRef]
- J. Maynard, "Small gaps between primes", Annals of Mathematics, vol. 181, 2015, p. 383–413 (arXiv 1311.4600), [Submitted on 19 Nov 2013 (v1), last revised 28 Oct 2019 (this version, v3)]. [CrossRef]
- T. R. Nicely, "New maximal prime gaps and first occurrences", Mathematics of Computation, 68 (227): 1311–1315, (1999) . [CrossRef]
- D. Parrochia, "Sur les conjectures de Goldbach forte et faible (quelques remarques historico-épistémologiques)". Preprint submitted on 15 Dec 2023,. HAL Id: hal-04346907 , https://hal.science/hal-04346907v1.
- H. C. De Pocklington, " The determination of the prime or composite nature of large numbers by Fermat's theorem ", Proc. Cambridge Philos. Soc., vol. 18, 1914-1916, p. 29-30.
- O. Ramaré, Saouter, "Short effective intervals containing primes", J. Number theory, 98, No. 1, p..10-33, (2003). [CrossRef]
- [P. Ribenboim," The New Book of Prime Number Records ", Springer, 1996, 3e éd. (read online [archive]), p. 52.
- Ph. Sainty, "Primes frames" , "Primality tests" , "Goldbach decomponents : E.D.G. File S Around 2n = 10S for S = 1, 2, 3,............., 1000", htpps://www.researchgate.net, Internet Archive archive.org and (OEIS) The On-Line Encyclopedia of Integer Sequences, https://oeis.org (to appear).
- Ph. Sainty, "About the strong EULER-GOLDBACH conjecture", Matematicheskie Zametki /Mathematical Notes, In press., hal-03838423, HAL Id:hal-03838423, https://cnrs.hal.science/hal-03838423v1,Submitted on 3 Nov 2022 .
- L. Schnirelmann, "Schnirelmann density", Wikipedia, (on line, internet) and "A proof of the fundamental theorem on the density of sums of sets of positive integers", Annals of Math, 2nd series, vol. 43, no. 3, (1942), pp. 523-527. [CrossRef]
- D. Shanks, "On Maximal Gaps between Successive Primes", Mathematics of Computation, American Mathematical Society, 18 (88): 646–651, (1964). [CrossRef]
- T. O. e Silva, Herzog, Pardi, "Empirical verification of the even Goldbach conjecture and computation of prime gaps up to 4.1018''. Math. Comput. 83, no. 288, pp. 2033-2060 (2014). [CrossRef]
- Z-W. Sun, "On sums of primes and triangular numbers" » [archive], arXiv, 2008 (arXiv 0803.3737). [CrossRef]
- T. Tao, "Every odd number greater than 1 is the sum of at most five primes", Math. Comput. 83, no. 286, p.997-1038(2014). [CrossRef]
- P. Tchebychev, "Mémoire sur les nombres premiers" J. math. pures et appliquées, 1ère série, t.17, p. 366-390 et p. 381-382, (1852).
- C.- J. de La Vallée-Poussin, "Recherches analytiques sur la théorie des nombres premiers", Brux. S. sc. 21 B, pp. 183-256, 281-362, 363-397, vol.21 B, pp. 351-368, (1896).
- D. Vella-Chemla, "Calculs au sujet de la conjecture de Goldbach à l’aide du logiciel gb-tools" , 31.8.2020, 123dok FR ,https://123dok.net › document, "Conjecture de Goldbach : La tete dans les nombres", Freehttp://denise.vella.chemla.free.fr notesnp.
- A. Vinogradov, "Representation of an odd number as a sum of three primes". Dokl. Akad.Nauk. SSR, 15:291-294, (1937).
- E.W. Weisstein, "Levy's Conjecture" » [archive], sur MathWorld , CRC Concise Encyclopédie de mathématiques (CRC Press, ), 733-4, (1999).
- M. S. Chin Woon, "On Partitions of Goldbach’s Conjecture" DPMMS, arXiv : math/ 0010027v2 [math.GM 4 Oct 2000] . [CrossRef]
- Y. Zhang, "Bounded gaps between primes", Ann. Math. (2) 179, no. 3, pp.1121-1174 (2014). [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).



