Proof of the Binary Goldbach Conjecture

1. Overview

Number theory " the queen of mathematics " studies the structures and properties defined on integers and primes (Euclid [13], Hadamard [15], Hardy and Wright [16], Landau [22], Tchebychev [35]). Numerous problems have been raised and conjectures made, the statements of which are often simple but very difficult to prove. These main components include

● Elementary arithmetic . Determination and properties of primes, operations on integers

(basic operations, congruence, gcd, lcm, ).

Decomposition of integers into products or sums of primes

(fundamental theorem of arithmetic, decomposition of large numbers, cryptography and Goldbach's conjecture).

● Analytical number theory . Distribution of primes (Prime Number Theorem,

Hadamard [15], De la Vallée-Poussin [36], Littlewood [25] and Erdos [12], the Riemann hypothesis,.....).

Gaps between consecutive primes (Bombieri,Davenport [3], Cramer [8], Baker,Harmann,Iwaniec, Pintz [4],[5],[20], Granville [14], Maynard [27], Tao [34], Shanks [30], Tchebychev [35] and Zhang [39]).

● Algebraic, probabilistic, combinatorial and algorithmic number theories . Modular arithmetic,

diophantine approximations, equations, arithmetic functions and algebraic, diophantine and

number geometry.

2. Definitions Notations and Background

The integers n, k, p, q, r,……..... used in this article are always positive.(2.1)

The symbol ‘‘ / ‘’ means " in relation to". (2.2)

Let $\mathcal{P}$be the infinite set of positive primes $p_k$(called simply primes) (2.3)

($p_1$ = 2 ; $p_2$ = 3 ; $p_3$= 5 ; $p_4$= 7 ; $p_5$ = 11 ; $p_6$ = 13 ; .........)

For any integer K ≥ 1${\mathcal{P}}_K$ = { p ∈ $\mathcal{P}$: p ≤ 2K } (2.4)

The writing of large numbers (see appendix 12) is simplified using the following constants

M = ${10}^9$ ; R = 4.${10}^8$ ; G = ${10}^{100}$ ; S = ${10}^{500}$ ; T = 10 ¹⁰⁰⁰ (2.5)

ln(x) denotes the neperian logarithm of the real x > 0

Let ($W_{2n})$ be the sequence of primes defined by

∀ n ∈ ℕ + 3 $W_{2n}$ = Sup(p ∈ $\mathcal{P}$ : p ≤ 2n - 3) (2.6)

Any sequence denoted by ($G_{2n})$ = ($U_{2n};V_{2n}$) verifying (2.6.1) is called a Goldbach sequence.

∀ n ∈ ℕ + 2$U_{2n}$ ,$V_{2n}$ ∈ $\mathcal{P}$ and$U_{2n}$ + $V_{2n}$ = 2n(2.7)

$U_{2n}$ and $V_{2n}$ are also known as " Goldbach decomponents ".

Iwaniec,Pintz [20] have shown that for a sufficiently large integer n there is always a prime

between n − $n^{23/42}$ and n . Baker,Harman [4],[5] concluded that there is a prime in the interval

[ n ; n + o ($n^{0.525}\left)\right].$ Thus this results provides an increase of the gap between two consecutive primes $p_k$and $p_{k+1}$of the form

$\forall$ $\epsilon$ > 0 $\exists$ $k_{\epsilon }$ ∈${\mathbb{N}}^{\mathrm{*}}$ / ∀ k ∈ ℕ k ≥ $k_{\epsilon }{p}_{k+1}$ - $p_k$ < $\epsilon .p_k^{0.525}$(2.8)

The results obtained on the Cramer-Granville-Maier-Nicely conjecture [1],[3],[8],[14],[26],[28] imply the following majorization.

For any real c > 2 and for any integer k ≥ 500

$p_{k+1}$ - $p_k$ ≤ 0.7 ${\mathrm{l}\mathrm{n}}^{\mathrm{c}}$($p_k$) (with probability one) (2.9)

3. Introduction

Chen [6], Hardy,Littlewood [17], Hegfollt,Platt [18], Ramaré,Saouter [29], Tao [34],

Tchebychev [35] and Vinogradov [37] have taken important steps and obtained promising results on the Goldbach conjecture (Any integer n ≥ 2 is the mean arithmetic of two primes).

Indeed, Helfgott,Platt [18] proved the weak Goldbach conjecture in 2013.

Silva,Herzog,Pardi [32] held the record for calculating the terms of Goldbach sequences after determining pairs of primes ($U_{2n};V_{2n})$ verifying

∀ n ∈ ℕ / 4 ≤ 2n ≤ 4.10¹⁸ $U_{2n}$ + $V_{2n}$ = 2n (3.1)

In previous research work there is no explicit construction of recurrent Goldbach sequences. In this article two sequences of primes are developed using a simple, efficient and « located » algorithm to compute for any integer n $\ge 3$ by successive iterations any term $U_{2n}$ and $V_{2n}$ .

Using Maxima scientific software on a personal computer Silva's record is broken and

the values 2n = 10⁵⁰⁰ and even 2n = 10¹⁰⁰⁰ are reached. The binary Goldbach conjecture can be established on the same principle by recurrence by using the weak Chen or Goldbach(-) conjecture

(any even integer greater than three is the difference of two primes) demonstrated in Teorem 4.

● Remark.

1. Chen conjecture: For any integer K ≥ 1 there are infinitely many pairs of primes with a difference equal to 2K.

2. Polignac conjecture : Same as Chen, but with consecutive pairs of primes.

3.What we know :

April 2013, Yitang Zhang [39] demonstrates that the smallest even integer 2K verifying

the conjecture is greater than 70 million.

In 2014, James Maynard [27] then Terence Tao [34] lowered this limit to 246.

We validate weak Chen or Goldbach(-) conjecture by verifying directly in the prime number tables that all even gaps from 2 to 246 are possible between primes.

In addition, the Lagrange-Lemoine-Lévy conjectures [9],[19],[21],[26],[28],[33],[38] and its generalization called ‘’ Bezout-Goldbach « conjecture’ are validated.

Using case disjunction reasoning we construct two recurrent sequences of primes ($V_{2n}$) and ($U_{2n}$)

according to the sequence ($W_{2n})$ by the following process

For any integer n ≥ 2

$U_4$ = 2 and $V_4$= 2 (3.2)

Let n ∈ ℕ + 3

● Either

(2n - $W_{2n}$) is a prime

then $V_{2n}$ and $U_{2n}$ are defined directly in terms of $W_{2n}$ .

● Either

(2n - $W_{2n}$) is a composite number

then $V_{2n}$ and $U_{2n}$are determined from the previous terms of the sequence ($G_{2n})$.

4. Theorem (Weak Chen or Goldbach(-) conjecture)

∀ K ∈ ℕ* $\exists$ p , q ∈ $\mathcal{P}$ /

p - q = 2K3 ≤ q ≤ 2K and 3 + 2K ≤ p ≤ 4K if K ≥ 2 (4.1)

Practical method on some examples:

First of all (5 - 3 = 2), then we begin the process at (7 - 3 = 4), we will select the smallest primes for which the difference is precisely 6 (11 - 5 = 6) then 8 (11 - 3 = 8)

then 10 (13 - 3 = 10),......... then 2K , then 2(K + 1) (demonstration established by strong recurrence, by the asurd and return).

All pairs of Goldbach(-) decomponents obtained by this method for K between 2 and 123 are listed in the table in Appendix 13.

Proof . The proof is established by strong recurrence on K . Let ${\mathcal{P}}_{Chen}$(K) be the following property

« ∀ K ∈ ℕ* $\exists$ p, q ∈ $\mathcal{P}$ / p - q = 2K3 ≤ q ≤ 2K and 2K + 3 ≤ p ≤ 4K «(4.2)

►${\mathcal{P}}_{Chen}$ (2) is true : 7 - 3 = 4 ; q = 3 ≤ 4 and p = 7 ≤ 4 x 2 = 8

► Let’s show

∀ M ∈ ℕ / M ≤ K then ${\mathcal{P}}_{Chen}$ (M) $⟹$ ${\mathcal{P}}_C$ (K + 1)

We reason through the absurd

∀ p , q ∈ ${\mathcal{P}}_K$ / p ≥ q ; ∀ h, m ∈ ℕ / p + 2h , q + 2m ∈ $\mathcal{P}$we assume that

p + 2h - q - 2m ≠ 2(K + 1)

Therefore

p - q ≠ 2(K + 1 - h + m).

You can always choose (h ≥ m and h - m ≤ K + 1).

However the strong recurrence hypothesis asserts that

∀ M ∈ ℕ / M ≤ K $\exists$ p, q ∈ $\mathcal{P}$ / p - q = 2M(4.3)

By choosing M = K + 1 - h + m

t$\mathrm{h}\mathrm{i}\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{c}\mathrm{t}\mathrm{s}$ (4.3).

So

$\exists$ h,m ∈ ℕ / p + 2h - q - 2m = 2(K + 1) (p, p+2h, q, q+2m ∈ $\mathcal{P}$ : h ≥ m and h - m ≤ K + 1) (4.4)

Thus validating the heredity of property ${\mathcal{P}}_{Chen}$ (K).

The property ${\mathcal{P}}_{Chen}$ (K) is therefore true. As a result Goldbach(-)’s conjecture is validated.

5. Corollary

Let ${(R}_{2K}$) and ${(Q}_{2K}$) two sequences of primes determined by

$R_{2K}$ = Inf (p ∈ $\mathcal{P}$: p - 2K ∈ $\mathcal{P})$ and $Q_{2K}$= Inf (p ∈ $\mathcal{P}$: 2K + p ∈ $\mathcal{P}$) = $R_{2K}$ - 2K (5.1)

They are defined for any integer K ∈ $\mathbb{N}$* and satisfy

(5.1) lim $R_{2K}$ = +$\mathrm{\infty }$(5.2) ${\forall K\in {\mathbb{N}}^{\mathrm{*}}R}_{2K}$, $Q_{2K}$∈ $\mathcal{P}$and $R_{2K}$ - $Q_{2K}$ = 2K

(5.3) For any integer K / 2 ≤ K ≤ 163 ≤ $Q_{2K}$≤ 2K and 2K + 3 ≤ $R_{2K}$ ≤ 4K

(5.4) For any integer K ≥ 16

3 ≤ $Q_{2K}$≤ 2${\left(2K\right)}^{0.525}$ and 2K + 3 ≤ $R_{2K}$ ≤ 2K + ${\left(2K\right)}^{0.525}$Proof. According to the previous theorem, the sequences ($R_{2K}$) and ${(Q}_{2K}$) are defined by

strong recurrence and finite descent.

(5.1) $R_{2K}$ ≥ 2K ⇒ lim $R_{2K}$ = +$\mathrm{\infty }$(5.2) By construction, these sequences thus verify $R_{2K}$ - $Q_{2K}$ = 2K

(5.3) The term-to-term property can be verified directly by examining the sequence proposed above.

(5.4) This property is verified up to 2K = 246 by calculations on the previous list.

We prove this result by recurrence

First of all we order the Goldbach(-) decomponents at a fixed prime Q,

so as to obtain the estimate (5.4) more easily.

We examine the following sequences of primes (PQ(K)).

P3(K) = 2K + 3

(P3(K) ; 2K) → (5;2);(7;4);(11;8);(13;10);(17;14);(19;16);(23;20);(29;26);(29;28);..........

P5(K) = 2K + 5

(P5(K) ; 2K) → (7;2);(11;6);(13;8);(17;12);(19;14);(23;18);(29;24);(31;26);(37;32)........

P7(K) = 2K + 7

(P7(K) ; 2K) → (11;4);(13;6);(17;10);(19;12);(23;16);(29;22);(31;24);(37;30)...........

P11(K) = 2K + 11

(P11(K) ; 2K) → (13;2);(17;6);(19;8);(23;12);(29;18);(31;20);(37;26);(41;30);(43;34)......

(P13(K) ; 2K) → (17;4);(19;6);(23;10);(29;16);(31;18);(37;24);(41;28);(43;30);(47;34)......

PQ(K) = 2K + Q (K ∈ ${\mathbb{N}}^{*}$: PQ(K) and Q are primes)

(see the table in Appendix 14)

For any integer K satisfying 2${\left(2K\right)}^{0.525}$ > Q the property holds for PQ(K).

Therefore it is generally validated for all K > 15, since we obtain all possible cases of

Chen's weak conjecture starting with P3(K), then P5(K), then P7(K) ...... for 2${\left(2K\right)}^{0.525}$ ≤ Q .

(can be proved by strong recurrence using the same method as inTheorem 4 by “finite descent»).

Let $c_p$ = ${\displaystyle \frac{40}{21}}$ and Pr(K) be the following property

« For any integer M < ${\left(0.5Q_K\right)}^{c_p}$, there exists at least a prime Q < $Q_K$ such that

2 M + Q is a prime «

▶ Pr(15) is true (see Appendix 14).

▶ Let’s show : Pr(K) ⇒ Pr(K + 1)

$Q_{K+1}$ ≤ $Q_K$ + $Q_K^{0.525}$It is assumed thatM /

$P_{K+1}$ - $Q_{K+1}$ ≠ 2M M < ${\left(0.5Q_{K+1}\right)}^{c_p}{P}_{K+1}$ = p + 2h and $Q_{K+1}$ = q +2s

then

p - q ≠ 2(M + s - h)

which is impossible according to the hypothesis of strong recurrence since

2(M + s - h) is less than ${\left(0.5Q_K\right)}^{c_p}$ and that all primes p, q satisfy the recurrence hypothesis.

We deduce that Pr(K) ⇒ Pr(K + 1)

Thus the property (5.4) is true.

6. Principle of Proof

To determine pairs of primes that verify Goldbach’s conjecture three sequences of primes

($W_{2n}),(V_{2n}$), ($U_{2n})$ are defined and they verify the following properties

lim $V_{2n}$ = +$\mathrm{\infty }.$ (6.1)

(6.2) ∀ n ∈ ℕ + 2$V_{2n}$is defined as a function of $W_{2n}$ = Sup(p ∈ Ƥ : p ≤ 2n - 3)

(6.3) ($W_{2n}$) is an increasing sequence of primes that contains all primes except $p_1$ = 2

(6.4) lim $W_{2n}=+\mathrm{\infty }$(6.5) ($U_{2n}$) is a complementary sequence of negligible primes with respect to 2n

(6.6) For any integer n $\ge 3$● If (2n - ${\mathit{W}}_{2\mathit{n}}$) is a prime

then $V_{2n}$ and $U_{2n}$ are defined by

(6.7) $V_{2n}$ = $W_{2n}$ and $U_{2n}$= 2n - $W_{2n}$● Otherwise, if (2n - ${\mathit{W}}_{2\mathit{n}}$) is a composite number

we search for two previous terms of the sequence ($G_{2n}$), $U_{2(n-k)}$₎ and $V_{2(n-k)}$ satisfying the following conditions

(6.8) $U_{2(n-k)}$, $V_{2(n-k)}$ and $U_{2(n-k)}$ + 2k are primes $U_{2\left(n-k\right)}$ + $V_{2\left(n-k\right)}$ = 2(n - k)

which is always possible (see Theorem 4)

So by setting

(6.9) $V_{2n}$ = $V_{2(n-k)}$ and $U_{2n}$ = $U_{2(n-k)}$+ 2k

two new primes $V_{2n}$ and $U_{2n}$ satisfying (4.10) are generated .

(6.10) $U_{2n}$ + $V_{2n}$ = 2n

This process is then repeated incrementing n by one unit (n → n + 1).

7. Theorem

There exists a recurrent sequence ($G_{2n}$) = ($U_{2n};V_{2n})$ of primes satisfying the following conditions.

For any integer n ≥ $2$$U_{2n}$ ,$V_{2n}$ $\mathsf{ϵ}$ $\mathcal{P}$ and $U_{2n}$ + $V_{2n}$ = 2n(7.1)

(Any integer n ≥ $2$ is the mean arithmetic of two primes)

An algorithm can be used to explicitly compute any term $U_{2n}$and $V_{2n}$ . (7.2)

Proof .

□ FIRST METHOD :

For any integer n $\ge 3$● If (2n - ${\mathit{W}}_{2\mathit{n}}$) is a prime

then $V_{2n}$ and $U_{2n}$ are defined by

(7.3) $V_{2n}$ = $W_{2n}$ and $U_{2n}$= 2n - $W_{2n}$● Otherwise, if (2n - ${\mathit{W}}_{2\mathit{n}}$) is a composite number

we use the previous terms of the sequence ($G_{2n}$).

For any integer q such that 1 ≤ q ≤ n - 3 we have

3 ≤ $U_{2(n-q)}$ ≤ n .

Then, there exists an integer k / 1 ≤ k ≤ n - 3 following the Bertrand principle and Theorem 4

since all primes smaller than 2k are represented by $U_{2(n-j)}$ , (if there were no such primes, we would have a contradiction with the Theorem 4 , even if it means transforming the indexing of the sequence ($U_{2n})$ . In fact, in an equivalent way we can copy the proof of Teorem 4 by performing a similar strong recurrence “ finite descent return and absurd ” directly on the set { }$U_{2(r-j)}$).

such that

(7.4) $R_{2n}$ = $U_{2(n-k)}$ + 2k ∈ Ƥ

The smallest integer k / $R_{2n}$∈ Ƥ is denoted by $k_n$ .

So

(7.5) $U_{2n}$ = $U_{2\left(n-k_n\right)}$ + 2$k_n$ and$V_{2n}$ = $V_{2\left(n-k_n\right)}$(These two terms are primes)

In the previous steps two primes $U_{2\left(n-k_n\right)}$ and $V_{2\left(n-k_n\right)}$whose sum is equal to 2(n - $k_n$) were

determined.

(7.6) $U_{2\left(n-k_n\right)}$ + $V_{2\left(n-k_n\right)}$ = 2(n -$k_n$)

By adding the term $k_n$ to each member of the equality (5.6), it follows

(7.7) $U_{2\left(n-k_n\right)}$ + 2$k_n$ + $V_{2\left(n-k_n\right)}$= 2(n - $k_n$) + 2$k_n$(7.8) $\iff$ [$U_{2\left(n-k_n\right)}$ + 2$k_n$] + $V_{2\left(n-k_n\right)}$ = 2n

(7.9)$\iff U_{2n}$ + $V_{2n}$ = 2n

Finally for any integer n ≥ 3 this algorithm determines two sequences of primes ($U_{2n}$) and ($V_{2n}$)

verifying Goldbach's conjecture.

□ SECOND METHOD :

The proof can be made using the following strong recurrence principle.

Let P(n) be the property defined for any integer n ≥ 2 by

P(n) : “ For any integer p satisfying 2 ≤ p ≤ n there exists two primes$U_{2p}$ and $V_{2p}$ such their sum is equal to 2p “ .

(∀ p ∈ ℕ / 2 ≤ p ≤ n $U_{2p}$ ,$V_{2p}$ $\mathsf{ϵ}$ $\mathcal{P}$ and $U_{2p}$ + $V_{2p}$ = 2p)

Let's show by strong recurrence that P(n) is true for any integer n ≥ 2

a) P(2) is true : it suffices to choose $U_4$ = $V_4$ = 2 .

b) Let's show that the property P(n) is hereditary i.e ∀ k ∈ ℕ + 2P(n) $\Rightarrow$ $\mathrm{P}$(n+ 1)

Assume property P(n) is true,

● If (2(n + 1) - ${\mathit{W}}_{2(\mathit{n}+1)}$) is a prime

then $V_{2(n+1)}$ and $U_{2(n+1)}$ are defined by

$V_{2(n+1)}$ = $W_{2(n+1)}$ and$U_{2(n+1)}$= 2(n+1) - $W_{2(n+1)}$ (7.10)

● Otherwise, if (2(n+1) - ${\mathit{W}}_{2(\mathit{n}+1)}$) is a composite number

there exists an integer k to obtain two terms $U_{2(n+1-k)}$₎ and $V_{2(n+1-k)}$ satisfying the following

conditions

(7.11) $U_{2(n+1-k)}$, $V_{2(n+1-k)}$ and $U_{2(n+1-k)}$ + 2k are primes $U_{2\left(n+1-k\right)}$ + $V_{2\left(n+1-k\right)}$ = 2(n +1- k)

(which is always possible : see FIRST METHOD and Theorem 4).

Thus by setting

(7.12) $V_{2(n+1)}$ = $V_{2(n+1-k)}$ and $U_{2(n+1)}$ = $U_{2(n+1-k)}$+ 2k

Two new primes $V_{2(n+1)}$ and $U_{2(n+1)}$ satisfying ($U_{2(n+1)}$ + $V_{2(n+1)}$ = 2(n + 1)) are generated.

It follows that P(n + 1) is true. Then the property P(n) is hereditary (P(n) => P(n + 1)).

Therefore for any integer n ≥ 2 the property P(n) is true.

it follows

$\forall$ n ∈ ℕ+2there are two primes $U_{2n}$ and $V_{2n}$ and such their sum is 2n : ($U_{2n}$ + $V_{2n}$ = 2n)

8. Lemma

The sequence ($U_{2n})$ verifies the following majorization

For any integer n ≥ 65

(8.1) $U_{2n}$ ≤ (2${n)}^{0.55}$Proof . According to the programm 11.2 and appendix 12 the majorization (8.1) is verified

For any integer n such that 65 ≤ n ≤ 2000 . For any integer n > 2000 the proof is established by recurrence. For this purpose let P1(n) be the following property

(8.2) P1(n) : “ There exists a strictly increasing sequence of positive numbers ($C_n$) such that

$U_{2n}$ ≤ $C_n{\left(2n\right)}^{0.525}$ “ .

P1(2000) is true according to program 11.2 and the table in appendix 12.

For any integer n ≥ 2000 let’s show that P1(n) is hereditary i.e P1(n) ⇒ P1(n + 1).

Assume that P1(n) is true : then

● If (2(n + 1) - ${\mathit{W}}_{2(\mathit{n}+1)}$) is a prime

then $V_{2(n+1)}$ and $U_{2(n+1)}$ are defined by

(8.3) $V_{2(n+1)}$ = $W_{2(\mathrm{n}+1)}$ and $U_{2(n+1)}$= 2(n + 1) - $W_{2(n+1)}$According to the results in [4],[5],[20] there is a constant K > 0 such that

(n + 1) - K .${\left[2\right(n+1\left)\right]}^{0.525}$ < $W_{2(n+1)}$ < 2(n + 1)

⇒ $U_{2(n+1)}$ < K ${.\left[2\right(n+1\left)\right]}^{0.525}$⇒ $U_{2(n+1)}$ ≤ $C_{n+1}{.\left[2\right(n+1\left)\right]}^{0.525}$● Otherwise, if (2(n + 1) - ${\mathit{W}}_{2(\mathit{n}+1)}$) is a composite number

(8.4)$\exists$ p ∈ ${\mathbb{N}}^{\mathrm{*}}$/ $U_{2(n+1)}$ = $U_{2(n+1-p)}$ + 2p

According to [4],[5],[18] the smallest integer p defined in (6.4) verifies

(8.5) 2p < K.[ ${U_{2(n+1-p)}]}^{0.525}$ and $U_{2(n+1-p)}$ < $C_{n+1-p}{.\left[2\right(n+1-p\left)\right]}^{0.525}$It follows

$U_{2(n+1)}$ < K .$C_{n+1-p}^{0.525}{.\left[2\right(n+1-p\left)\right]}^{0.275625}$ + $C_{n+1-p}{.\left[2\right(n+1-p\left)\right]}^{0.525}$Then

(8.6) $U_{2(n+1)}$ < $C_{n+1}.[{2(n+1)]}^{0.525}$and by setting $C_n$ = ${\left(2n\right)}^{0.025}$It follows

(8.7) $U_{2(n+1)}$ < ${\left[2\right(n+1\left)\right]}^{0.55}$P1(n + 1) is true then P1(n) is hereditary.

So for any integer n ≥ 2000 the property P1(n) is true.

(The inequality (6.7) is verified with the aid of the software Maple studying the functions of the type f : x $\to$ a ${.x}^{0.275625}$ + b . $x^{0.525}$ increased by g : x $\to$ $x^{0.55}$ a and b being two strictly positive real parameters).

● Remark. A more precise estimate can be obtained using the Cipolla or Axler frames [7],[2].

9. Theorem

For any integer n $\ge$ 3 it is easy to check

(9.1) ($W_{2n}$) is a positive increasing sequence of primes.

(9.2) { $W_{2n}$ : n $\in$ IN + 3 } $\cup \left\{2\right\}$ = $\mathcal{P}$(9.3) lim $W_{2n}$ = +oo

(9.4) ($U_{2n}$) and ($V_{2n}$) are sequences of primes and the set {($U_{2k}$) : k ≤ n} contains all primes less than ln(n)

(9.5) n $\le$ $V_{2n}$ ≤ $W_{2n}$(9.6) 3$\le {2n-W_{2n}\le U}_{2n}\le$n

(9.7) lim $V_{2n}$ = +oo

Proof .

(9.1) For any integer n ≥ 2 ${\mathcal{P}}_n\subset {\mathcal{P}}_{n+1}$ .Therefore, $W_{2n}$ ≤ $W_{2(n+1)}$. So the sequence ($W_{2n}$)

is increasing.

(9.2) Any prime except $p_1$ = 2 is odd, hence the result.

(9.3) lim $W_{2n}$ = lim $p_k$ = +oo

(9.4) By definition $V_{2n}$ = $W_{2n}$ or there exits an integer k ≤ n - 2 such that $V_{2n}$ = $V_{2(n-k)}$ ;

so the terms of the sequence ($V_{2n)}$) are primes.

(9.5) According to Lemma 6, for any integer n ≥ 65

$U_{2n}$ < ${\left(2n\right)}^{0.55}$therefore

$U_{2n}$ < ${\left(2n\right)}^{0.55}$ < n

and

$V_{2n}$ = 2n - $U_{2n}$ > 2n - n > n

For any integer n / 3 ≤ n ≤ 65 verification is carried out according to the computer program in paragraph 11.2 and the table in appendix 12.

we can also see that by construction $V_{2n}$ ≥ $U_{2n}$ because if we assume the opposite then $V_{2n}$ is not the largest prime number verifying ${\displaystyle \frac{1}{2}}$ ($U_{2n}$ + $V_{2n}$) = n .

So

$V_{2n}$ ≥ n

(9.6) According to (9.5) n $\le$ $V_{2n}$ ⇒ $U_{2n}$ = 2n - $V_{2n}$ ≤ 2n - n ≤ n

therefore

$V_{2n}$ ≤ $W_{2n}$ ⇒ 2n - $W_{2n}$ ≤ 2n - $V_{2n}$ = $U_{2n}$(9.7) By (9.5) for any integer n ≥ 2 : n $\le$ $V_{2n}$so

lim $V_{2n}$ = +oo .

10. Remarks

10.1 For any integer k ≥ 2 there are infinitely many integers n such that $U_{2n}$ = $p_k$.

10.2 $V_{2n}$ ~ 2n for (n $\to$ +oo) .

10.3 For any sufficiently large integer n / n ≥ 5000

$U_{2n}$ $\ll V_{2n}$andlim (${\displaystyle \frac{U_{2n}}{V_{2n}}}$) = 0.

10.4 The smallest integer n such that

$U_{2n}\ne$2n -$W_{2n}$ is obtained for n = 49 and $G_{98}$= (79 ; 19).

(This type of terms increases in the Goldbach sequence ($G_{2n})$ as n increases in the sense of the Schnirelmann density and there are an infinite number of them; their proportion per interval can be computed using the results given in [29]).

10.5 If q is an odd integer greater than four we could generalize this algorithm with sequences (${W\text{'}}_{2n}$)

defined by

(10.5.1) $\forall$ n ∈ $\mathbb{N}$/ n ≥ ${\displaystyle \frac{(q+3)}{2}}$ ${W\mathrm{\text{'}}}_{2n}$ = Sup(p ∈ $\mathcal{P}$: p ≤ 2n - q)

Other Goldbach’s sequences $\left({G\text{'}}_{2n}\right)$ independent of ($G_{2n})$are thus generated.

10.6 The sequence ($G_{2n}$) is ‘‘extremal’’ in the sense that for any integer n$\ge 2V_{2n}$ and $U_{2n}$ are the largest and smallest possible primes such that $U_{2n}$ + $V_{2n}$ = 2n.

10.7 The Cramer-Granville-Maier-Nicely conjecture [8],[14],[19],[21],[23],[24],[26],[28],[33]

is verified with probability one. It leads to the following majorization

For any integer p ≥ 500

(10.7.1) $U_{2p}$ ≤ 0.7 [${\mathrm{l}\mathrm{n}\left(2p\right)]}^{(2.2-{\displaystyle \frac{1}{p}})}$(with probability one)

The proof is similar to that of lemma 8 and is validated by the studying functions of the type

f : x $\to$ a .g (x) + b${\left[\mathrm{l}\mathrm{n}\right(g\left(x\right)\left)\right]}^c$(a,b > 0 ; c > 2) with

g : x $\to$ 0.7 [l${\mathrm{n}\left(x\right)]}^{(c-{\displaystyle \frac{1}{x}})}$ and h : x $\to$ 0.7${\left[\mathrm{l}\mathrm{n}\right(x\left)\right]}^{(2.2-{\displaystyle \frac{1}{x}})}$ using Maple software.

● Remark. A better estimate can be obtained via [26],[28],[30] .

10.8 According to Bombieri [3] and using the same method as in the proof of Lemma 8,

on average, we obtain the following estimate of $U_{2n}$(10.8.1) $\forall$ $\epsilon$ > 0 $U_{2n}$ = O (${\mathrm{l}\mathrm{n}}^{1.3+\epsilon }(2n$)) (on average)

11. Algorithm

11.1. Algorithm Written in Natural Language

Inputs :

Input four integer variables : k, N, n, P

Input : $p_1$= 2 , $p_2$= 3 , $p_3$ = 5 , $p_4=$ 7 , ................., $p_N$ the first N primes.

: n = 3

: P = M, R, G, S or T as indicated in paragraph 2

Algorithm body :

Compute : $W_{2n}$ = Sup(p $\in$ $\mathcal{P}$ : p ≤ 2n - 3)

If ${\mathit{T}}_{2\mathit{n}}$= (2n - ${\mathit{W}}_{2\mathit{n}}$) is a prime

Let :

(11.1.1)$U_{2n}$ = $T_{2n}$ and $V_{2n}$ = $W_{2n}$otherwise

If ${\mathit{T}}_{2\mathit{n}}$ is a composite number

Let : k = 1

B.1) While $U_{2\left(n-k\right)}$ + 2k is a composite number

assign to k the value k + 1 (k $\to$ k + 1).

return to B1)

End while

Assign to k the value $k_n$ (k $\to k_n$)

(11.1.2) Let :

$U_{2n}$ = $U_{2\left(n-k_n\right)}$ + 2$k_n$ and $V_{2n}$ = $V_{2\left(n-k_n\right)}$Assign to n the value n + 1 (n$\to n+1$ and return to A)

End :

Outputs for integers less than ${10}^{4:}:$Print (2n = ● ; 2n - 3 = ● ; $W_{2n}$ = ● ; $T_{2n}$ = ● ; $V_{2n}$ = ● ; $U_{2n}$ = ●)

Outputs for large integers :

Print (2n - P = ● ; 2n - 3 - P = ● ; $W_{2n}$ - P = ● ; $T_{2n}$ = ● ; ${V_{2n}-P=\mathrm{●};U}_{2n}$ = ●)

11.2. Program Written with Maxima Software for 2n = ${10}^{500}$

n1 : 10**500 ; for n :5*10**499 + 10000 thru 5*10**499 + 10010 do

(a :2*n , c :a - 3 , test : 0 , b : prev_prime(a - 1) ,d :a - b ,

if primep(d)

then print(a - n1 , c - n1 , b - n1 , d , b - n1 , d)

else (

while test = 0 do

(e :a - c , if (primep(c) and primep(e))

then (test:1 , print(a - n1 , b - n1 , d , c - n1 , e ," ** "))

else (test : 0 , c : c - 2))) ;

12. Appendix

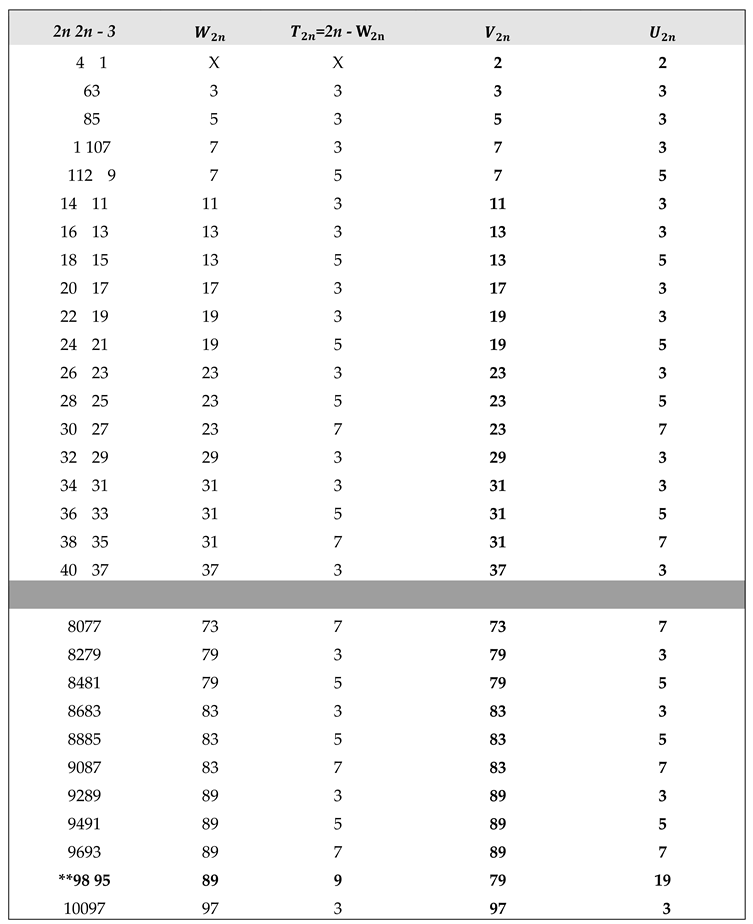
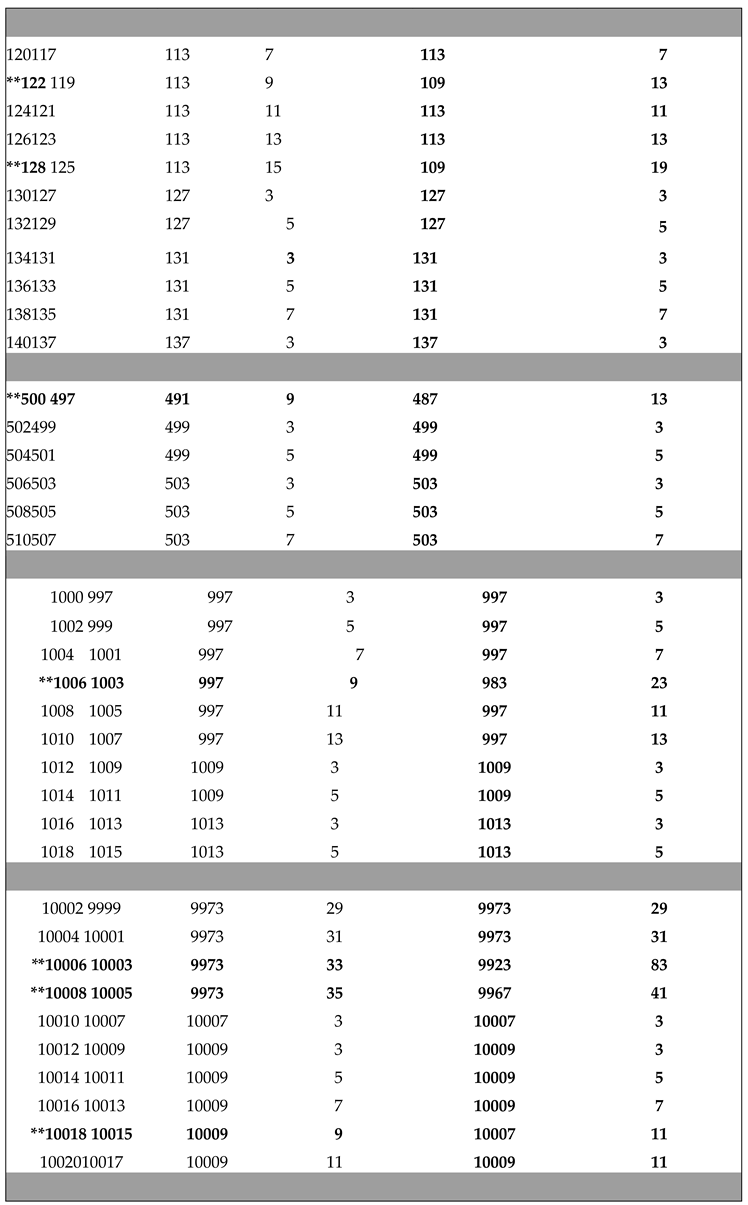
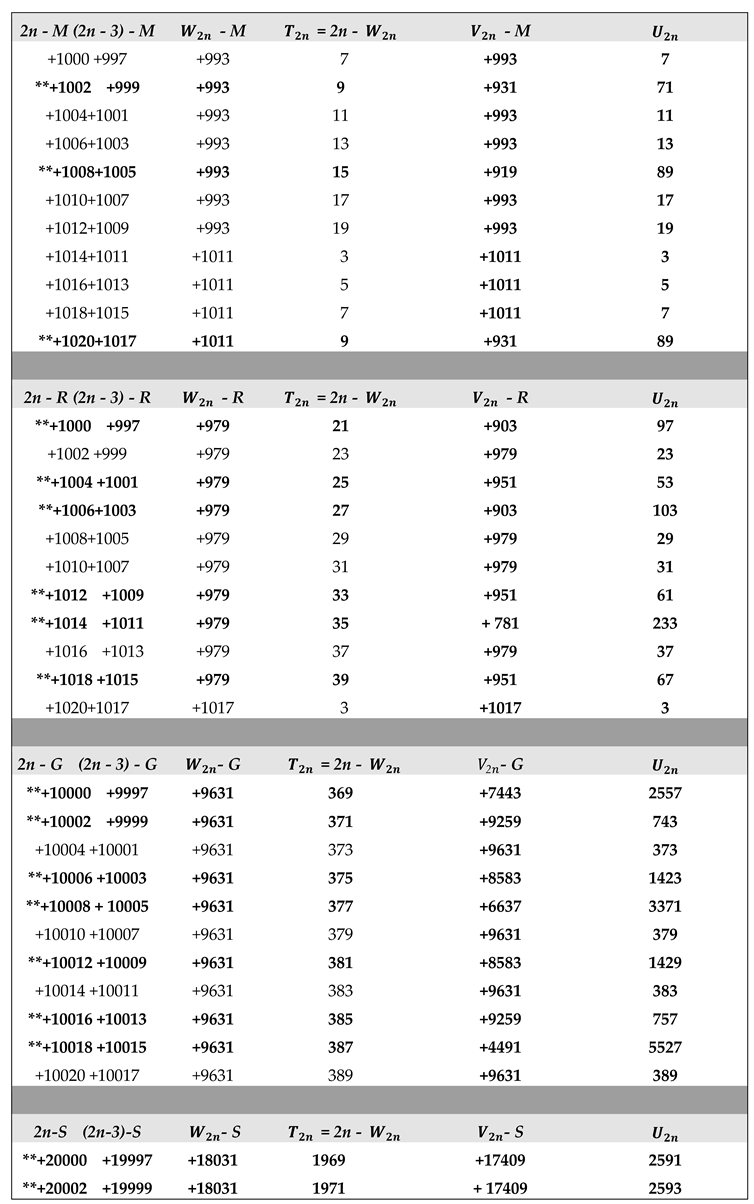
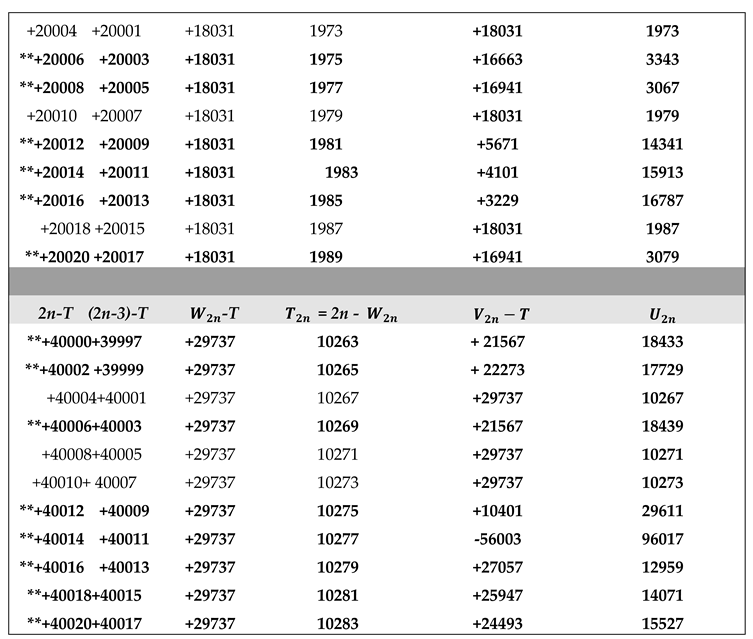
Application of Algorithm 11 : Table of ${\mathit{U}}_{2\mathit{n}}$and ${\mathit{V}}_{2\mathit{n}}$ terms of the Goldbach sequence (${\mathit{G}}_{2\mathit{n}}$) computed from program 11.2 (2 ≤ 2n ≤ ${10}^{1000}$ + 4020).

The ** sign in the table below indicates the results given by the algorithm 11 in case B) of return to the previous terms of the sequence ($G_{2n})$. WATCH OUT ! For large integers n (2n >${10}^9$ for example), to simplify the display of large numbers the results are entered as follows

2n - P , (2n - 3) - P ,${\mathit{W}}_{2\mathit{n}}$ - P , ${\mathit{T}}_{2\mathit{n}}$, ${\mathit{V}}_{2\mathit{n}}$- P and ${\mathit{U}}_{2\mathit{n}}$with

P = M, R, G, S, orTconstants defined in (2.3)

13. Appendix

7-3=4	11-5=6	11-3=8	13-3=10	17-5=12	17-3=14	19-3=16	23-5=18
23-3=20	29-7=22	29-5=24	29-3=26	31-3=28	37-7=30	37-5=32	37-3=34
41-5=36	41-3=38	43-3=40	47-5=42	47-3=44	53-7=46	53-5=48	53-3=50
59-7=52	59-5=54	59-3=56	61-3=58	67-7=60	67-5=62	67-3=64	71-5=66
71-3=68	73-3=70	79-7=72	79-5=74	79-3=76	83-5=78	83-3=80	89-7=82
89-5=84	89-3=86	101-13=88	97-7=90	97-5=92	97-3=94	101-5=96	101-3=98
103-3=100	107-5=102	107-3=104	109-3=106	113-5=108	113-3=110	131-19=112	127-13=114
127-11=116	131-13=118	127-7=120	127-5=122	127-3=124	131-5=126	131-3=128	137-7=130
137-5=132	137-3=134	139-3=136	149-11=138	151-11=140	149-7=142	149-5=144	149-3=146
151-3=148	157-7=150	157-5=152	157-3=154	163-7=156	163-5=158	163-3=160	167-5=162
167-3=164	173-7=166	173-5=168	173-3=170	179-7=172	179-5=174	179-3=176	181-3=178
191-11=180	193-11=182	191-7=184	191-5=186	191-3=188	193-3=190	197-5=192	197-3=194
199-3=196	211-13=198	211-11=200	233-31=202	211-7=204	211-5=206	211-3=208	223-13=210
229-17=212	227-13=214	223-7=216	223-5=218	223-3=220	227-5=222	227-3=224	229-3=226
233-5=228	233-3=230	239-7=232	239-5=234	239-3=236	241-3=238	251-11=240	271-29=242
251-7=244	251-5=246

14. Appendix

(PQ(K) ; 2K)

Q= 3	Q= 5	Q= 7	Q= 11	Q= 13	Q= 17	Q= 19	Q= 23	Q= 29	Q= 31
5;2	7;2		13;2		19;2			31;2
7;4		11;4		17;4		23;4
	11;6	13;6	17;6	19;6	23;6		29;6		37;6
11;8	13;8		19;8				31;8	37;8
13;10				23;10		29;10			41;10
	17;12	19;12	23;12		29;12	31;12		41;12	43;12
17;14	19;14				31;14		37;14	43;14
19;16		23;16		29;16					47;16
	23;18		29;18	31;18		37;18	41;18	47;18
23;20			31;20		37;20		43;20
		29;22				41;22			53;22
	29;24	31;24		37;24	41;24	43;24	47;24	53;24
29;26	31;26		37;26		43;26
31;28				41;28		47;28			59;28
		37;30	41;30	43;30	47;30		53;30	59;30	61;30
	37;32		43;32					61;32
37;34		41;34		47;34		53;34
	41;36	43;36	47;36		53;36		59;36		67;36
41;38	43;38						61;38	67;38
43;40		47;40		53;40		59;40			71;40
	47;42		53;42		59;42	61;42		71;42	73;42
47;44					61;44		67;44	73;44
		53;46		59;46
	53;48		59;48	61;48		67;48	71;48		79;48
53;50			61;50		67;50		73;50	79;50
		59;52				71;52			83;52
	59;54	61;54		67;54	71;54	73;54		83;54
59;56	61;56		67;56		73;56		79;56
61;58				71;58					89;58
		67;60	71;60	73;60		79;60	83;60	89;60

15. Perspectives and Generalizations

15.1 Other Goldbach sequences (${G\text{'}}_{2n}$) and (${G"}_{2n}$) independent of $\left(G_{2n}\right)$ may be studied using the increasing sequences of primes (${W\text{'}}_{2n}),\left(\mathrm{s}\mathrm{e}\mathrm{e}10.5\right)$ and (${W"}_{2n}$) defined by

For any integer n $\ge 3$${W"}_{2n}$ = Sup(p$\mathsf{ϵ}\mathcal{P}:p\le$ f (n))

f is a function defined on the interval I = [3 ; +$\mathrm{\infty }$[ and satisfying the following conditions

● f is strictly increasing on the interval I

● f (3) = 3 and $\underset{x\to +\infty }{\lim }f\left(x\right)$ = +$\mathrm{\infty }$● $\forall x\mathsf{ϵ}If\left(x\right)\le 2x-3$For example, one of the following functions defined on I can be selected.

□ f : x $\to$a x + 3 - 3a(a$\in \mathbb{R}$ : 0 < a$\le 2)$□ g : x$\to$[ 4$\sqrt{3x}-$9 ] ([ x ] is the integer part of the real number x)

□ h : x $\to 6\mathrm{l}\mathrm{n}\left({\displaystyle \frac{x}{3}}\right)$ + 3

15.2 Using this method it would be interesting to study the Schnirelmann density [31] of primes

3 , 5 , 7, 11 ,........ ... in the sequence ($U_{2n}$) on variable intervals .

15.3 It is possible to exceed the values shown in the table of 2n = ${10}^{1000}$ by perfecting this algorithm starting from n , exploiting the fact that one of Goldbach's decomponents can be chosen

equal to 12p + 1,

(the set of Goldbach decomponents consists of primes of the form 6p +/- 1) using Cipolla-Axler-Dusart type functions [2],[7],[10],[11] to better identify the terms of ($G_{2n}),\mathrm{u}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{u}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{s}$a$\mathrm{n}\mathrm{d}\mathrm{m}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{e}\mathrm{f}\mathrm{f}\mathrm{i}\mathrm{c}\mathrm{i}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{s}\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{w}\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{s}$ Maple.

15.4 Diophantine equations and conjectures of the same nature (Lagrange-Lemoine-Levy conjecture [9],[19],[21],[23],[24],[33]) can be processed using similar reasoning and algorithms.

1) To validate the Lagrange_Lemoine-Levy conjecture we study the following sequences of primes

(W$l_{2n}$), (${Vl}_{2n})\mathrm{a}\mathrm{n}\mathrm{d}$ (${Ul}_{2n})\mathrm{d}\mathrm{e}\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{d}\mathrm{b}\mathrm{y}$$\mathrm{F}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{y}\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{g}\mathrm{e}\mathrm{r}n\ge 3{Wl}_{2n}$= Sup(p $\mathsf{ϵ}\mathcal{P}:p\le n-1)$● If ${Tl}_{2n}$= (2n + 1 - 2 ${Wl}_{2n}$) is a prime

then let

${Vl}_{2n}$= ${Wl}_{2n}$ and ${Ul}_{2n}$= ${Tl}_{2n}$● If ${Tl}_{2n}$ is a composite number

then there exists an integer k / 1 $\le k\le n-3$such hat

${Ul}_{2\left(n-k\right)}$ + 2k is a prime

then let

${Vl}_{2n}$= ${Vl}_{2\left(n-k\right)}$ and ${Ul}_{2n}$=${Ul}_{2\left(n-k\right)}$+ 2k

Using the same type of reasoning a generalization called «Bezout-Goldbach conjecture» of the following form can be validated

● Let K and Q be two odd integers prime to each other :

For any integer n / 2n$\ge 3$(K + Q) there exist two primes ${Ub}_{2n}$ and ${Vb}_{2n}$ verifying

K . ${Ub}_{2n}$ + Q. ${Vb}_{2n}$ = 2n

● Let K and Q be two integers of different parity prime to each other :

For any integer n such that 2n $\ge 3$(K + Q) there are two primes ${Ub}_{2n}$ and ${Vb}_{2n}$ verifying

K ${.Ub}_{2n}$ + Q .${Vb}_{2n}$ = 2n + 1.

15.5 Remark

GOLDBACH(-) :

$R_{2K}$ = Inf (p ∈ $\mathcal{P}$ : p - 2K ∈ $\mathcal{P})$ and $Q_{2K}$= Inf (p ∈ $\mathcal{P}$: 2K + p ∈ $\mathcal{P})$ = $R_{2K}$ - 2K

GOLDBACH(+) :

$V_{2K}$ = Sup (p ∈ $\mathcal{P}$: 2K - p ∈ $\mathcal{P})$ and $U_{2K}$= Inf (p ∈ $\mathcal{P}$ : 2K - p ∈ $\mathcal{P}$) = 2K - $V_{2K}$(Is it possible to envisage a symmetry in the Goldbach triangle parametrized by arithmetic sequences between the representations of primes and even integers ?)

16. Conclusions

16.1 A recurrent and explicit Goldbach sequence ($G_{2n}$) = ($U_{2n}$; $V_{2n}$) verifying

$\forall$ n ∈ $\mathbb{N}+2U_{2n}$ and $V_{2n}$ are primes $\mathrm{a}\mathrm{n}\mathrm{d}{U}_{2n}$ +$V_{2n}$= 2n

has been developed using an simple and efficient "located" algorithm.

16.2 The record of Silva [29] is beaten on a personal computer and ten Goldbach decomponents

$U_{2n}$ and $V_{2n}$ are obtained for values of the order 2n =${10}^{1000}$ for a computation time of less than

three hours.

16.3 For a given integer n ≥ 49 the evaluation of the terms $U_{2n}$ and $V_{2n}$ does not require the computing of all previous terms $U_{2k}$ and $V_{2k}$ / 1 $\le$k < n - 1 . We just need to know the primes $p_l$ and $V_{2r}$such that

(16.3.1) $p_l$ ≤ 7.${\mathrm{l}\mathrm{n}}^{1.3}\left(2n\right)$ and 2n - 7.${\mathrm{l}\mathrm{n}}^{1.3}$(2n) ≤ $V_{2r}$≤ 2n (on average)

This property allows quick computing of $U_{2n}$ and $V_{2n}$ .

16.4 Therefore the Lagrange-Lemoine-Levy and the binary Goldbach(- & +) conjectures,

« Any even integer greater than three is the sum and difference of two primes » are true.

In fact, these two conjectures are intertwined.