1. Introduction
Whale songs are frequently recorded on the hydrophones of the International Monitoring System (IMS) hydroacoustic network of the Comprehensive Nuclear-Test-Ban Treaty Organization (CTBTO) [
1]. The larger whales, such as blue whales —
Balaenoptera musculus — and fin whales —
Balaenoptera physalus —, emit acoustic energy in the [15-50] Hz frequency range [
3], which can be used to assess the suitability of simple ocean-acoustic wave propagation models to estimate the location of the whales. A lot is unknown about whale vocalization (acoustic signal emitted by whales). Such questions as: the depth at which they emit the sound; if they emit the sound when only at certain depths; the depth-dependent interference of the direct signal with the surface reflection; the possible frequency — and depth — dependent radiation pattern of the acoustic emission, etc. Attempts have been made to estimate the range from the in-water hydrophone IMS stations at which the signals are recorded. Even far ranges are considered in these attempts as it is well known that acoustic energy can travel very efficiently if it is guided in the Sound Fixing and Ranging (SOFAR) channel [
4].
The locations of all IMS stations [
2], including the hydroacoustic stations, are openly available. Five of the six in-water hydrophone IMS stations consist of pairs of triplets of hydrophones close to oceanic islands. These island stations have one triplet deployed to the north and the other to the south of the island with hydrophone deployment depths close to the generally considered depth of the SOFAR channel of 700 m to 1000 m. This hydrophone depth provides excellent detections of hydro-acoustic signals originating from very far distances of thousands of kilometers if trapped in the SOFAR channel. The acquisition system of the hydrophones has a sampling frequency of 250 Hz. A filter is applied to the data compensating for the system response that makes the data above 100 Hz difficult to use as calibrated data. Less relevant to the study in this paper, the acquisition system also has limitation on the lower frequency end. This still allows recordings of signals almost undisturbed between 1 and 100 Hz. This bandwidth is mandated by Member States of the CTBTO [
1] as specifications for the IMS hydrophones in the Operational Manual for Hydroacoustic Stations developed as required by the CTBT Treaty.
Previous works were concerned with whale tracking methods for basic understanding of animal behavior and mitigation of seismic air gun surveys on the animals. Methods have been developed to estimate the depth of a diving sperm whale —
Physeter macrocephalus— from the time difference between the direct arrival and the surface reflection, using two or three elements vertical or horizontal hydrophone arrays [
5]. Triangulation has been used to track the diving behavior of bowhead whales —
Balaena mysticetus — in the noisy environment of a seismic air gun survey [
5]. In both these examples, the signals emitted by the animal cover higher frequencies ([5-20] kHz and short duration < 25 ms) for sperm whales, and [0.2-2] kHz for bowhead whales). These higher frequencies are above the useful frequency range of the IMS hydrophones, and the present work studies signals emitted by likely fin whales, at frequencies below 0.1 kHz. Whale tracking has also been used to compare the source level of fin whale signals recorded at an in-water hydrophone location in the Pacific Ocean and an Ocean Bottom Seismometer (OBS) in the Atlantic Ocean [
7]. Parabolic equation modeling is the central tool used to derive the source level of fin whales in the two regions [
8].
Other works do not specifically track whales but rather use characteristics of their calls and spatial and temporal statistics of the calls, for instance to get information on the population of blue whales in the southeast Indian Ocean and southwest Pacific Ocean [
9]. Temporal statistics have put in evidence that the dominant frequency of pygmy blue whales decreases with time over a period of 8 years [
10], and that their range of detectability is between 50 km and 200 km from the HA01 triplet [
11]. A range estimate of up to several tens of kilometers from the northern triplet of HA08 for blue whales in the Chagos archipelago in the Indian Ocean, was obtained using a method based on two parameters: back-azimuth estimates using the signals on the three hydrophones and amplitude decay estimates [
12]. At these distances, based on modeling up to signal propagation ranges of 250 km, the amplitude of the whale signal decays roughly like the inverse of the square root of the distance to the hydrophone, as expected from a cylindrical geometrical spreading. The blue whale calls were detected in records from January 2003 with a Short-Term Average/Long-Term Average (STA/LTA) method using a ratio threshold of 2.5.
At closer range, it is possible to make the assumption that the whale is close to the surface (whale depth is assumed to be zero) and then use the differences in the times of arrivals between the three hydrophones to estimate a location. At further ranges, only the direction of the incoming signals is available. A grid-search method was used to trace the path of a likely fin whale crossing the waters above hydrophone station HA01, Cape Leeuwin, Australia [
13]. In that work, the authors tracked the movement of the whale through the three hydrophones using the direct arrival from the whale signal. They also observed multiple scattered energetic arrivals — one directly from the ocean bottom, another from the sea surface after reflection from the ocean bottom — as the whale position was close to being in the area directly above the hydrophones. Similar multiple scattered arrivals from the ocean bottom and sea surface had previously been observed in bottom-moored hydrophones in the Southern Ocean [
14]. In addition to water multiple reflections, crustal reflections were observed from fin whale calls recorded on ocean bottom seismometers in the straights of Juan de Fuca, between the USA and Canada [
15].
Tagged animal studies on fin and blue whales [
16] have been conducted and show some variability in the swimming depth of a fin whale between very shallow depth (10 m) and up to nearly 300 m. A deeper dive may occur amidst shallower ones. At shallow depths of vocalization of a fin whale, somewhere between the sea surface and 300 m depth, it may be difficult to differentiate in time between the direct path from the animal to the hydrophone, and the reflection from the sea surface. In [
13], a double peak in the autocorrelation and envelope of the first arrival may hint at this sea surface reflection. An elaborate approach [
17] based on modeling Lloyd’s mirror effect [
18] estimated the depth of vocalizing fin whales using the hydrophone and vertical component seismometer channels of Ocean Bottom Seismometers (OBS) and estimated a depth of 72 m in one of the examples. A shallow depth of 15 m was also estimated, for an individual fin whale localization, based on the modeling of travel times of multiple bottom and surface reflections, at the three hydrophones of the southern triplet of IMS hydroacoustic station HA11 [
19].
The purpose of the paper is to track and locate whales emitting low-frequency sound, such as blue whales, fin whales, and recorded on the existing deployed hydro acoustic network of the IMS sensor network. Because of the frequency bandwidth of the recordings, it is a challenge to separate arrivals in the time domain when they are close together, as is the case for the direct arrival and the surface reflection if the animal is close to the surface. It may be possible to gain information in the frequency domain, together with the three distances to the hydrophones, i.e., the Lloyd´s mirror where the separation of fringes at a particular frequency depends on the distance of the source to the sea surface. The advantages of the IMS network are its quality, thanks to the calibration of the data, its spatial coverage, continuous acquisition system, and potential for automatic processing, for instance detecting specific features in the signal. In the present work, data processing and location methods are applied to a data set recorded at the same hydrophone triplet H11, on 19 and 20 February 2024. A fin whale passed close to the triplet, similarly to the 26 July 2017 at HA01 [
13], and the multiple passages at HA11, between 2010 and 2022 [
19].
After finding that a method purely based on cross-correlation to measure the time delays of the signal arrival time at different hydrophones — or Time Differences of Arrival (TDOA) — is inappropriate because of the presence of strong bottom and sea surface reflections, a method based on time pick differences combined with cross-correlation is presented and found to be appropriate for the case of this data set where the animal is close to the hydrophone triplet. A grid-search localization method is then presented and applied with the TDOAs as input.
A further contribution of this work is to take advantage of the passage of the whale close to two of the hydrophones to estimate its vocalization depth when above the hydrophones. It is assumed that the amplitudes decay linearly with (one over distance law) distance from the source when in the vicinity of the hydrophones, specifically within 1.5 km from the center of the hydrophone triplet. This is equivalent to the inverse square law of energy for a point source in free space. Energy is the square of the amplitude. It is also assumed that the amplitudes of the signals are spherically symmetrical and do not depend on the direction of motion of the whale.
4. Discussion
Waveforms originating from what is assumed to be vocalizing fin whales recorded on the IMS hydro acoustics station HA11S have been presented and analyzed to estimate optimal locations of the whales from the TDOAs between hydrophones. The waveforms recorded for each whale call on each hydrophone are rendered complex by the presence of the water surface reflection and multiple water bottom reflections when the whale is in the close vicinity of the triplet of hydrophones. This leads to issues with methods based purely on waveform cross-correlation such as the progressive multi-channel cross-correlation (PMCC) method [
26], when the vocalization happens close to the hydrophone. Some reflections are as energetic as the first, direct arrival, causing confusion as to which peak in the cross-correlation functions are to be used. To counter this issue, a hybrid method was presented that avoids the ambiguity of pure cross-correlation methods yet takes advantage of its precise estimate of TDOAs. The measurement of amplitudes is likely affected by the multiplicity of the arrivals, and perhaps a more sophisticated method than the one used in this study could be used to pick the amplitude of the first arrival with confidence, rather than assuming it will be the highest value of amplitude within a six second segment.
The results presented in this paper regarding the depth of the vocalizations rely on the accuracy of the published depth of the hydrophones. It should be possible to extract the waveform of the source signal by assuming a spectral shape, pitch variation, and minimum phase for each of the A and B types of call, using wavelet deconvolution techniques from the seismic exploration industry [
27]. Waveform modeling using a method that identifies individual arrivals, such as simple ray methods, should then become feasible, leading to estimations of the reflection coefficients, more exact whale depths estimates, and verification of the hydrophone depths.
It is likely that there are in fact differences of possibly up to a few tens of meters between the depths of the three hydrophones, as the mooring cable lengths were pre-established during deployment, but the exact water depth at which the hydrophones were dropped is likely to have deviated from the depth of the target locations, even though a very precise bathymetry was acquired before the deployment. The deployment of the hydrophones is a complex operation with a large surface vessel trying to maintain position while kilometers long cable is deployed to the bottom of the ocean. Analysis of the amplitudes of the signals exploited in this work points to a possible need for either correcting the S3 location to a point further from S1 and S2. A possible explanation for the discrepancies observed in the residuals in
Figure 10b is that the S3 hydrophone’s position is not correct and that it is located further away from the S1-S2 line than the coordinates used in this study indicate. Testing this hypothesis for a point located as shown on
Figure 12d as S3’, it is found that the constant bias is indeed removed from the distribution for point S3’ at coordinates (-2.04 km, -1.96 km, S3 hydrophone depth unchanged) on the S1-S3 line at a distance 1.4 times larger than the distance S1-S3.
The standard deviation of residuals after moving the location of S3 to S3’ is higher than when a constant bias correction on S3 amplitudes is applied. One also has to keep in mind that the calculation of the vocalization locations itself depends on the location of S3, and that these locations have not been updated in this work before re-calculating the residuals.
Another possibility for the lack of consistency of the relative ratios of amplitudes and distances between S1 and S3 is that a calibration correction of the hydrophone at S3 is needed. A simple study of a large number of horizontally propagating signals recorded at the triplet should be able to confirm or infirm a calibration issue.
In analyzing the amplitude of the signals, the assumption was made that the source of sound is spherically symmetrical, with no azimuthally or vertically dependent radiation pattern. It may be possible, in a more refined analysis, to use the direction of motion of the whale as a substitute for the position of the animal and detect any variation in the strength of the signal depending on the position of the receiver with respect to the whale and its front to rear axis
An inversion problem using both amplitudes and delay residuals to estimate potential corrections to the hydrophone locations may be possible if a very large number of calls are collected. It would be beneficial to search the data for additional similar sequences, providing better coverage especially close to the S3 hydrophone.
5. Conclusions
The sequence of calls studied in this work has a long duration and the tracks followed by the whale allow for good coverage of the area directly above the triplets. It was shown that using the amplitude ratios of the signal at two different hydrophones, when the source is in the near field, less than 1.5 km horizontally from the center of the triplet, can be of interest. The amplitude ratios between S1 and S2 confirm that amplitudes follow the expected decay rule of being inversely proportional to the distance between source and receiver. This is however not the case for the amplitude ratios between S1 and S3. Several hypotheses may explain this, including that the relative location of S3 with respect to S1 and S2 needs to be corrected. Another possibility is that the amplitude radiation pattern of the calls is not isotropic, and there is a need to account for amplitudes decaying with the angle between the source-receiver line and the direction of propagation of the whale. Further collection of similar data with increased coverage may resolve which hypothesis explains the data best.
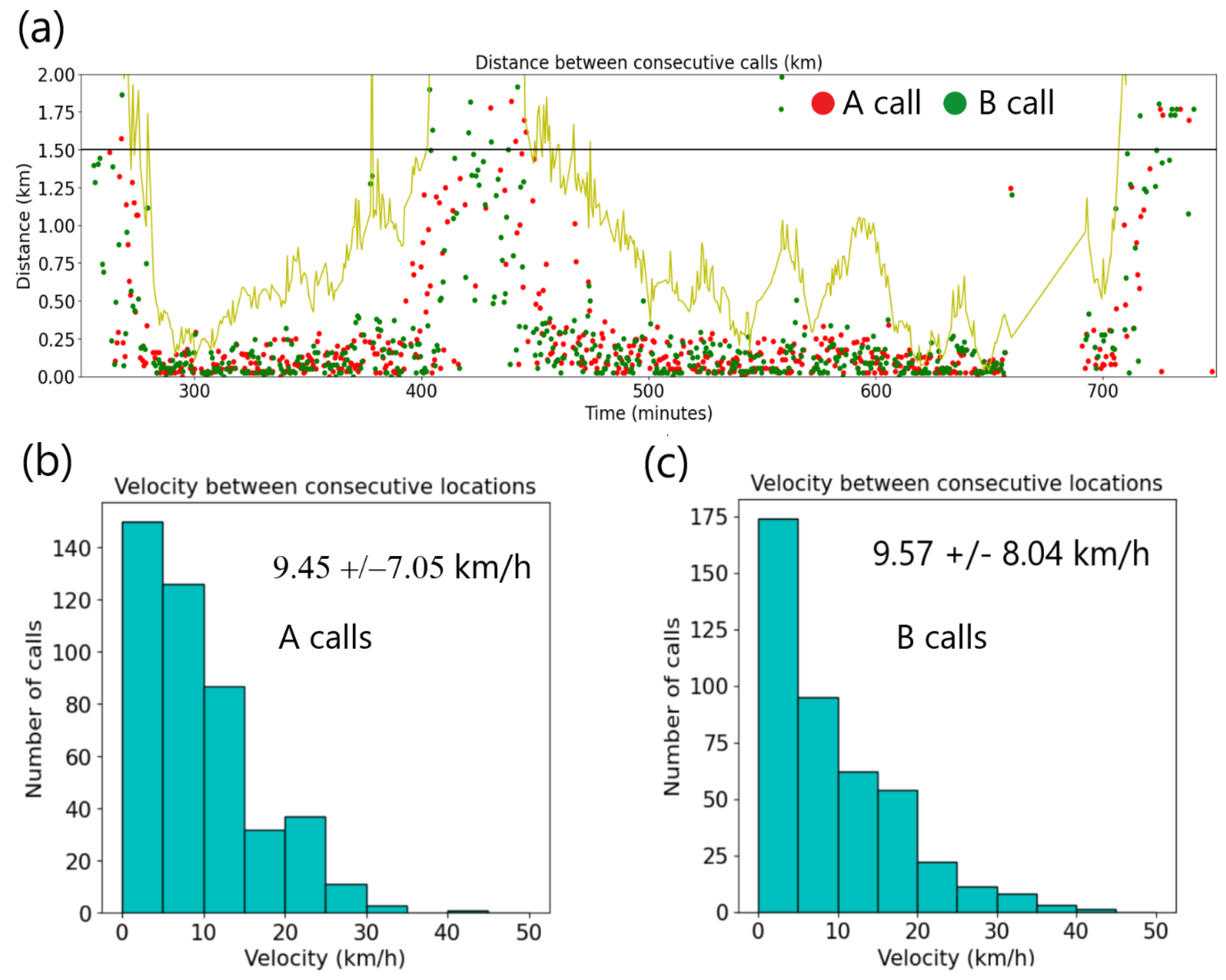
The estimated average swimming speed of the whale between A calls is 9.45 ± 7.05 km/h, and 9.57 ± 8.04 km/h between B calls. This is obtained when the cetacean is located less than 1.5 km from the center of the triplet, where locations and therefore distances swum are more accurately determined. The swim speed estimate is compatible with what is known about the maximum speed of 37 km/h (20 knots) for these cetaceans [
3].
Given the very close relationship between the locations and relative amplitudes of A and B calls, it is expected that either the source of the calls is a single animal, at least in contiguous periods of time, or if they are from two distinct animals, their relationship must be quite symbiotic. A different conclusion was reached by the authors of [
19], on very similar data from February 2019, also from HA11S. They concluded that A and B calls originated from two different animals. Our analysis could be repeated on the data set they used, with the addition of an analysis of the amplitudes in addition to the TDOAs and this will be the object of future work to attempt to resolve these differing interpretations.
According to [
28], both triplets at HA11 were deployed around a seamount. It may not be a coincidence but rather directed by foraging around that seamount that initially, as shown on
Figure 7, the whale appears to head towards the seamount and to slow down around it.
As a general conclusion amplitude may be a source of information additional to the travel times provided that sensor locations are estimated within a few meters and that more is known about the radiation pattern of the acoustic sources.
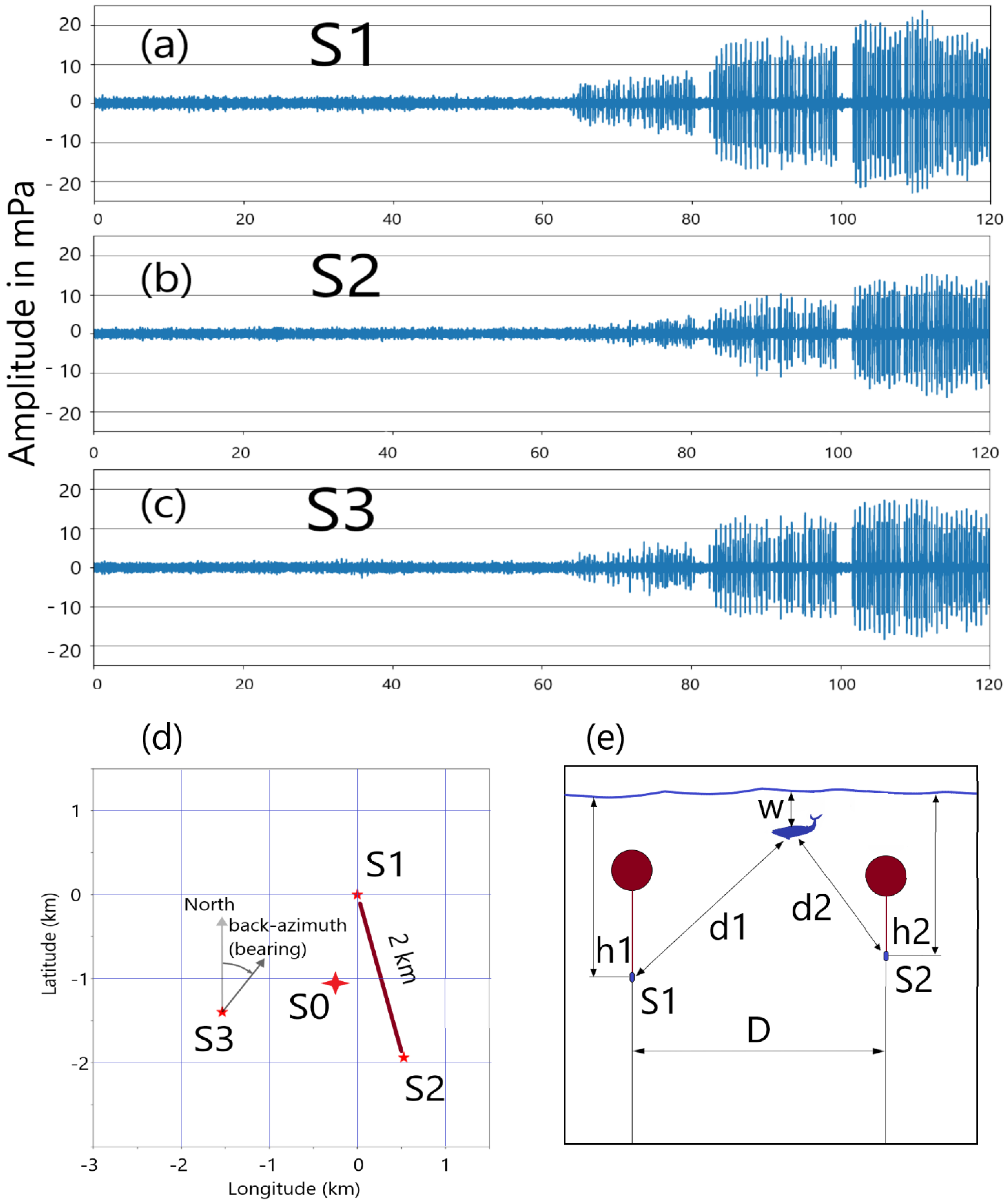
Figure 1.
(a), (b), and (c) show two hours of unfiltered hydrophone data starting at 21:00 UTC on 19 February 2024 for, respectively, the S1, S2, and S3 hydrophones. At the one-hour mark approximately, frequent (approximately once every 25 seconds) impulsive signals are visible and increasing in amplitude towards the end of the section. The amplitudes are in mPa, and the horizontal lines are the -10, -20, 10, and 20 mPa levels. (d) Basic map with the S1 hydrophone being the origin of the local horizontal coordinate system. S0 marks the center of the triplet and the arrow next to S3 shows how the back-azimuth is measured from the North. The latitude and longitude differences are in kilometers. The absolute latitude and longitude of the S1 hydrophone are respectively 15.50827 degrees North and 166.700272 degrees East. (e) Vertical geometry in a cross-section including S1 and S2 and defines parameters used in the text. The whale may or may not be in the same plane as S1 and S2.
Figure 1.
(a), (b), and (c) show two hours of unfiltered hydrophone data starting at 21:00 UTC on 19 February 2024 for, respectively, the S1, S2, and S3 hydrophones. At the one-hour mark approximately, frequent (approximately once every 25 seconds) impulsive signals are visible and increasing in amplitude towards the end of the section. The amplitudes are in mPa, and the horizontal lines are the -10, -20, 10, and 20 mPa levels. (d) Basic map with the S1 hydrophone being the origin of the local horizontal coordinate system. S0 marks the center of the triplet and the arrow next to S3 shows how the back-azimuth is measured from the North. The latitude and longitude differences are in kilometers. The absolute latitude and longitude of the S1 hydrophone are respectively 15.50827 degrees North and 166.700272 degrees East. (e) Vertical geometry in a cross-section including S1 and S2 and defines parameters used in the text. The whale may or may not be in the same plane as S1 and S2.
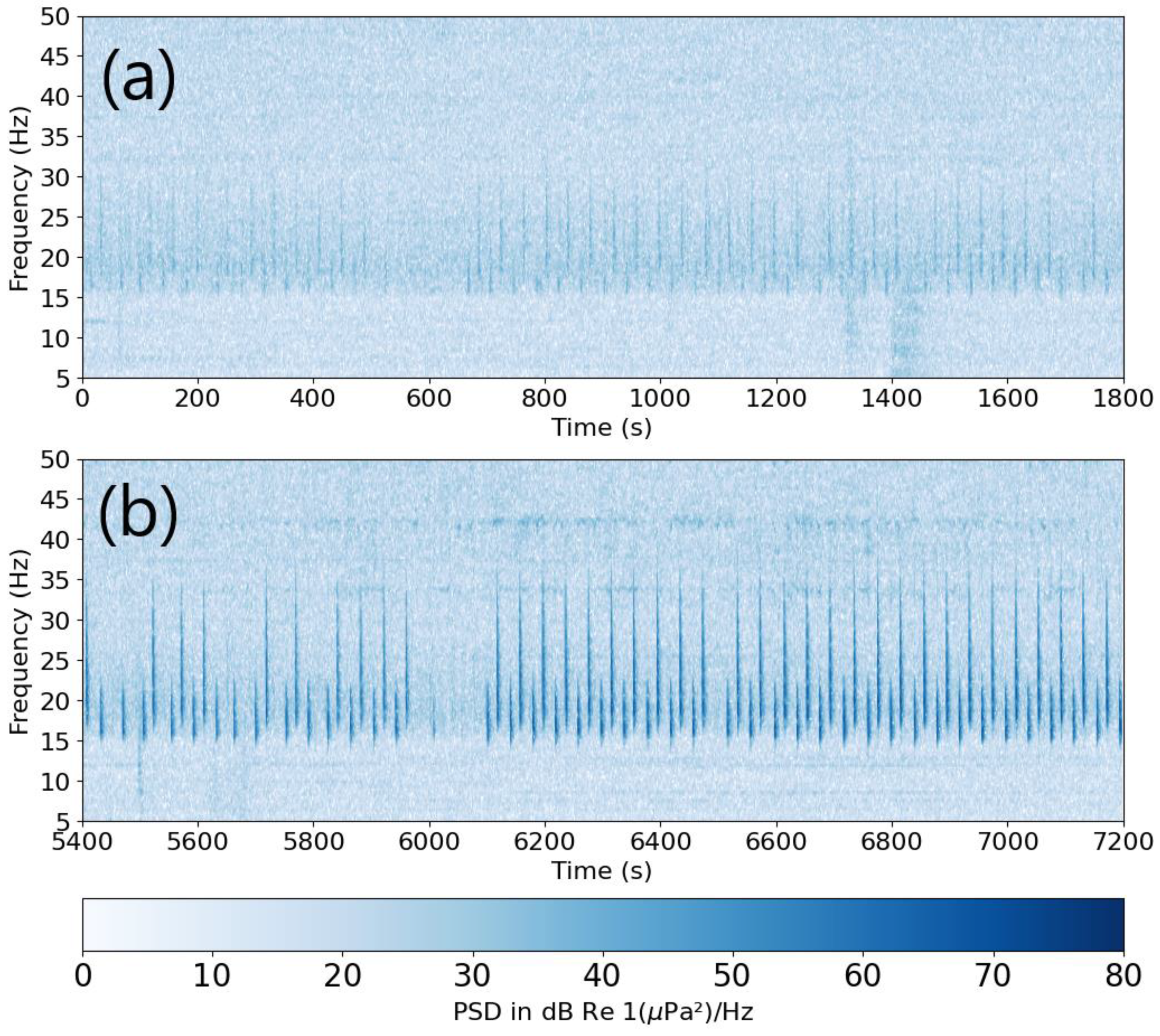
Figure 2.
Spectrograms of the first 30 minutes (a), and the last 30 minutes (b) of the two hours of waveforms for S2 shown on
Figure 1. An FFT length of 1024 points with 512 points overlap was used to compute the whole spectrogram over the 7200 s. The first 30 minutes and last 30 minutes were then windowed. The Nyquist frequency is 125 Hz. The frequency resolution is 0.244 Hz (512 intervals in [0-125] Hz) and the time resolution is 2.05 s.
Figure 2.
Spectrograms of the first 30 minutes (a), and the last 30 minutes (b) of the two hours of waveforms for S2 shown on
Figure 1. An FFT length of 1024 points with 512 points overlap was used to compute the whole spectrogram over the 7200 s. The first 30 minutes and last 30 minutes were then windowed. The Nyquist frequency is 125 Hz. The frequency resolution is 0.244 Hz (512 intervals in [0-125] Hz) and the time resolution is 2.05 s.
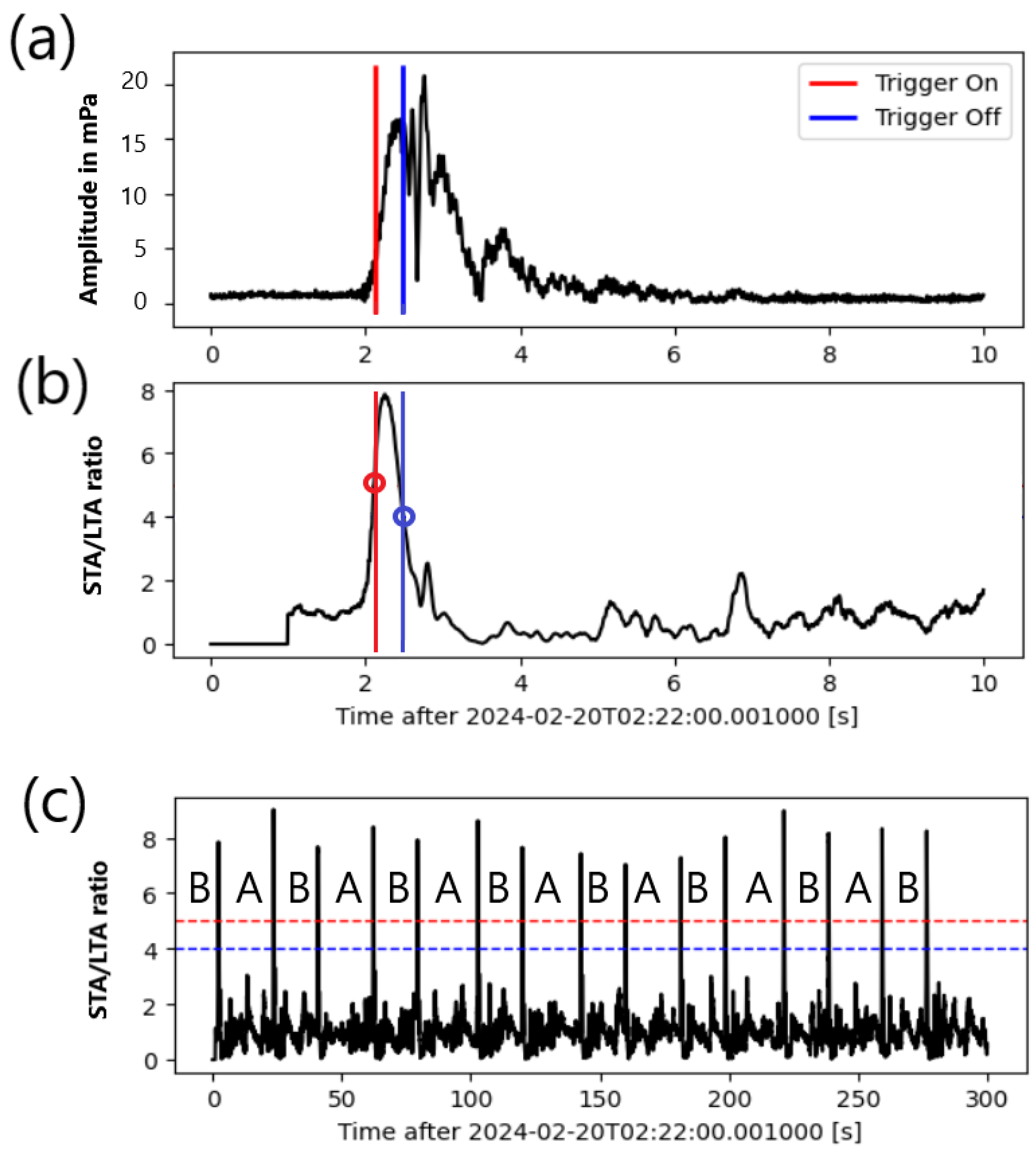
Figure 3.
Illustration of the STA/LTA detection method on a 10 second interval with a single call at S1. (a) envelope of the first signal with red and blue timelines to show respectively the trigger-on and trigger-off times. (b) STA/LTA function of the first signal. In addition to the timelines showing the trigger-on and trigger-off, the circle markers show their respective threshold values of 5 and 4 (c) STA/LTA of the envelope of the five-minute interval with fifteen calls. Each call is labelled A or B according to its center frequency. The red and blue horizontal dotted lines show the trigger-on and trigger-off thresholds.
Figure 3.
Illustration of the STA/LTA detection method on a 10 second interval with a single call at S1. (a) envelope of the first signal with red and blue timelines to show respectively the trigger-on and trigger-off times. (b) STA/LTA function of the first signal. In addition to the timelines showing the trigger-on and trigger-off, the circle markers show their respective threshold values of 5 and 4 (c) STA/LTA of the envelope of the five-minute interval with fifteen calls. Each call is labelled A or B according to its center frequency. The red and blue horizontal dotted lines show the trigger-on and trigger-off thresholds.
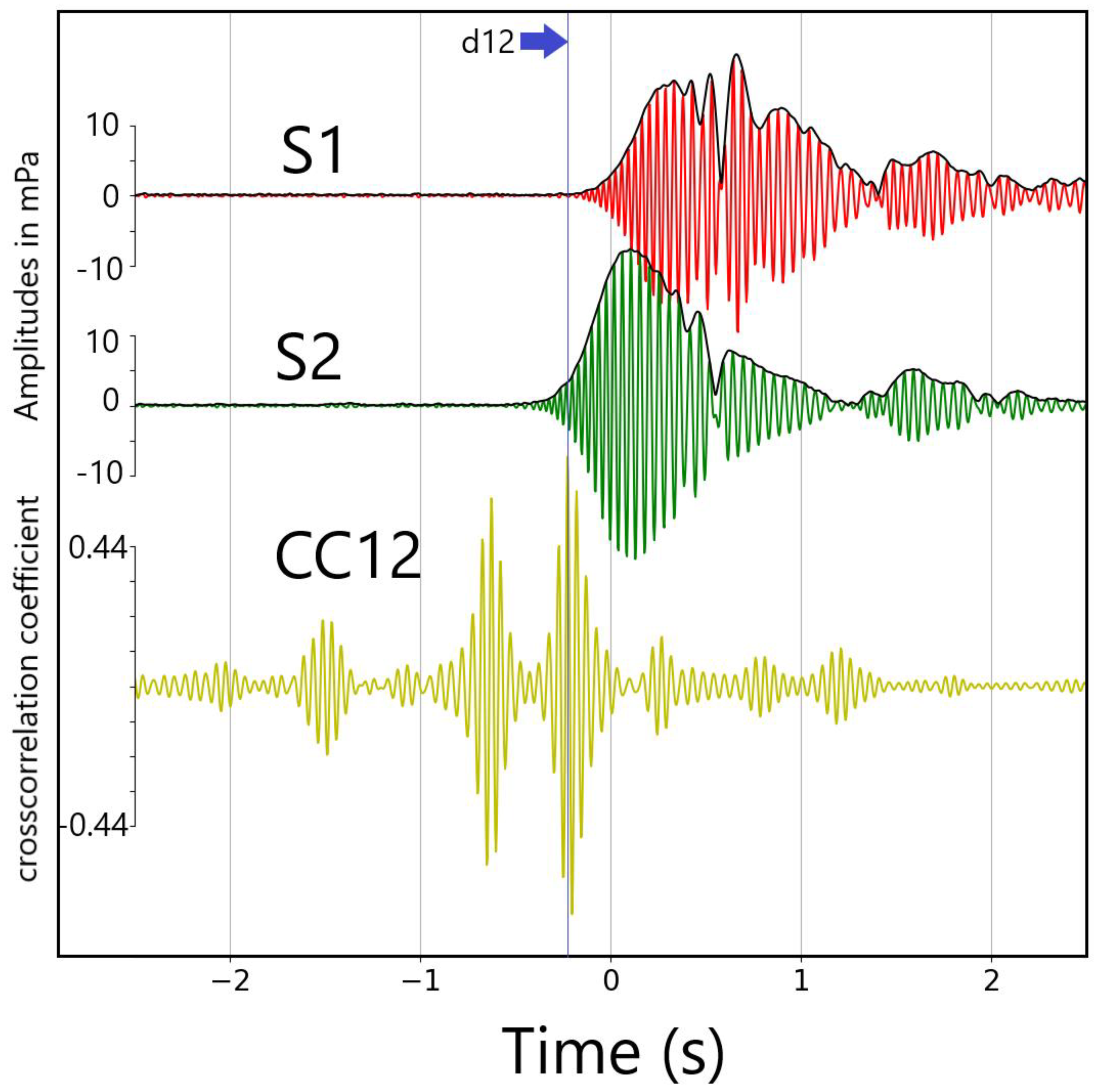
Figure 4.
Traces S1, S2, and their cross-correlation function CC12 for the call shown in
Figure 3. The zero on the time axis is the time of the STA/LTA pick on S1. The maximum value of the CC12 cross-correlation is 0.73 for a time shift of -0.23 s, emphasized by the thin blue line marked d12.
Figure 4.
Traces S1, S2, and their cross-correlation function CC12 for the call shown in
Figure 3. The zero on the time axis is the time of the STA/LTA pick on S1. The maximum value of the CC12 cross-correlation is 0.73 for a time shift of -0.23 s, emphasized by the thin blue line marked d12.
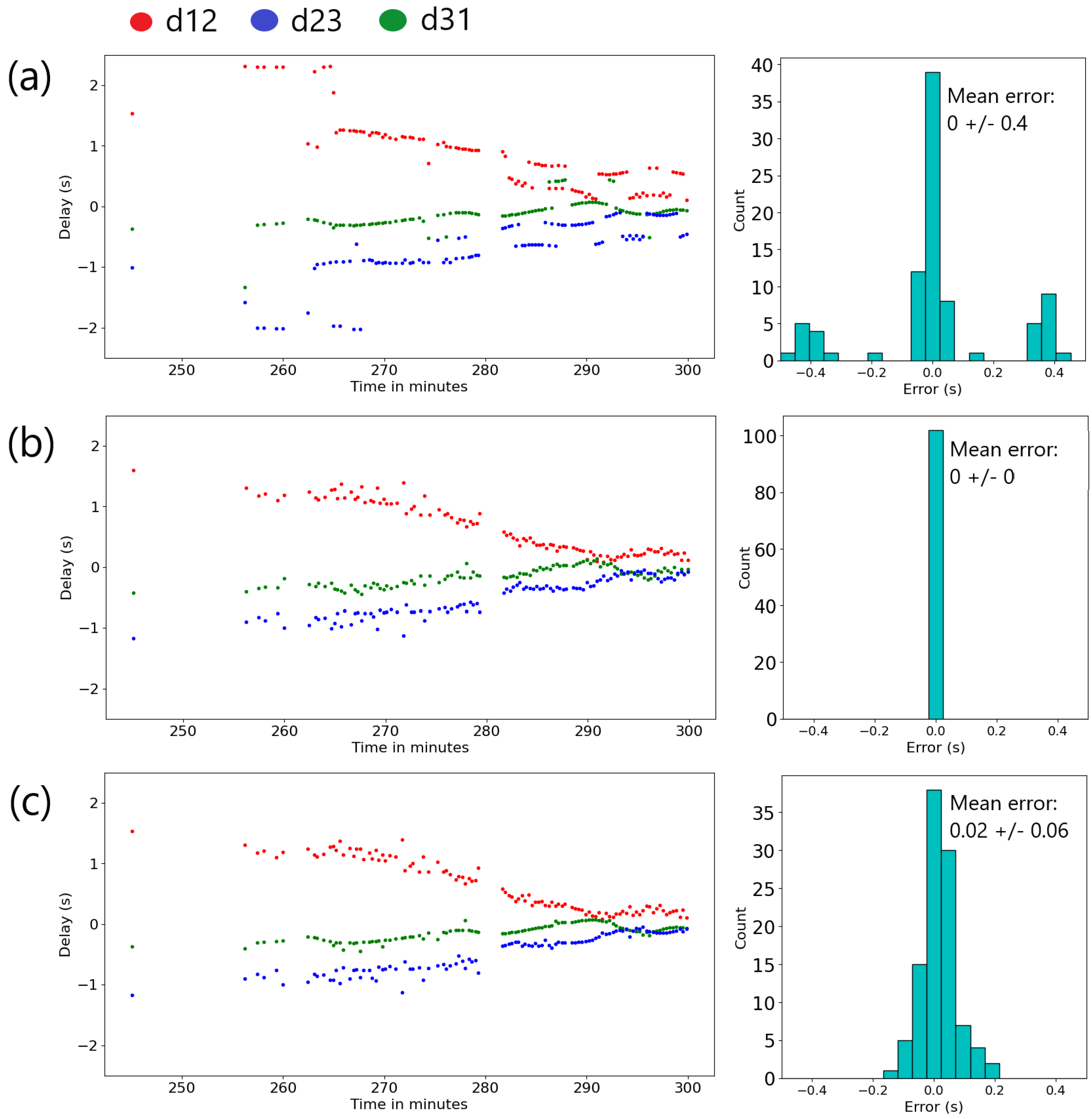
Figure 5.
Panel (a) shows the results of picking TDOAs based on method 1 (cross-correlation), and panel (b) is based on method 2 (STA/LTA picks only). Panel (c) shows the result of improved method 2, obtained by adjusting (b) with cross-correlation values when TDOAs obtained with the two different methods are within a tenth of a second of each other. Red dots are the delays (d12 or cd12) between S1 and S2, the green dots, the TDOAs (d31 or cd31) between S1 and S3, and the blue dots are the TDOAs between S2 and S3 (d23 or cd23). On the right of each panel is a histogram of the errors estimated from the difference between the measured TDOAs e=(d12+d23+d31) which should theoretically be zero.
is called the closure and is described in detail in [
26].
Figure 5.
Panel (a) shows the results of picking TDOAs based on method 1 (cross-correlation), and panel (b) is based on method 2 (STA/LTA picks only). Panel (c) shows the result of improved method 2, obtained by adjusting (b) with cross-correlation values when TDOAs obtained with the two different methods are within a tenth of a second of each other. Red dots are the delays (d12 or cd12) between S1 and S2, the green dots, the TDOAs (d31 or cd31) between S1 and S3, and the blue dots are the TDOAs between S2 and S3 (d23 or cd23). On the right of each panel is a histogram of the errors estimated from the difference between the measured TDOAs e=(d12+d23+d31) which should theoretically be zero.
is called the closure and is described in detail in [
26].
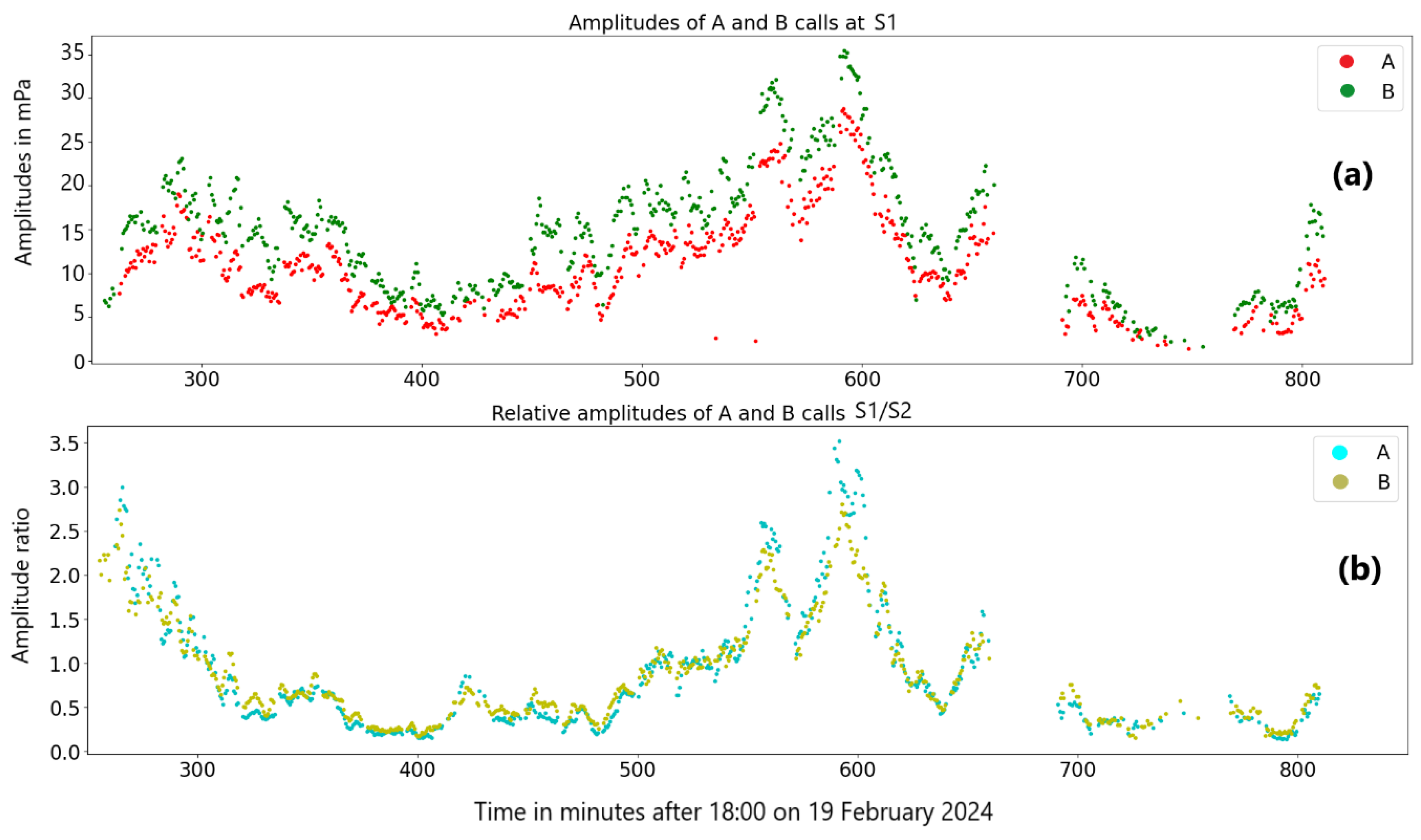
Figure 6.
(a) Illustration of the amplitude differences between A and B types of calls. The amplitude measure for type B is consistently higher than for type A. The amplitude scale is in mPa. (b) Shows the consistency of the relative amplitudes for types A and B, in this case amplitude at S1 divided by amplitude at S2.
Figure 6.
(a) Illustration of the amplitude differences between A and B types of calls. The amplitude measure for type B is consistently higher than for type A. The amplitude scale is in mPa. (b) Shows the consistency of the relative amplitudes for types A and B, in this case amplitude at S1 divided by amplitude at S2.
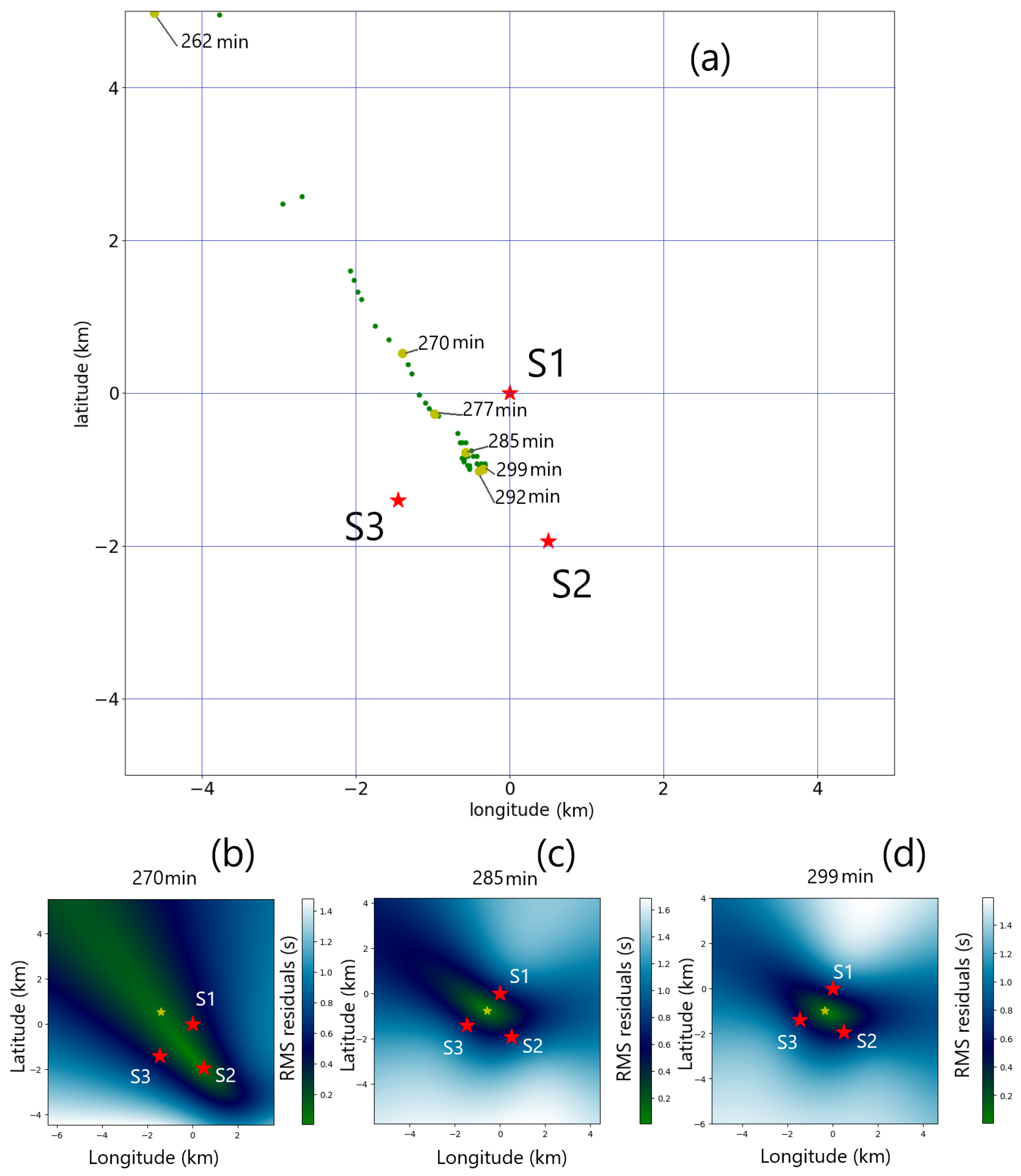
Figure 7.
Panel (a) is a map showing the location of all A calls (small green dots) detected during the two-hour interval shown on
Figure 1. Six of the calls are shown with larger yellow dots and labeled in minutes, corresponding to the detection time on S1 after 18:00 UTC on 19 February 2024, and show the progression of the whale from the northwest of the triplet to its center. The red stars are the locations of the hydrophones. Panel (b) to (d) are the surfaces of the time delay residuals at the time indicated. The yellow star shows the location of the minimum of the RMS of delay residuals for the three specific calls. Note that panels (b) to (d) show ten-kilometers squares centered on the yellow star.
Figure 7.
Panel (a) is a map showing the location of all A calls (small green dots) detected during the two-hour interval shown on
Figure 1. Six of the calls are shown with larger yellow dots and labeled in minutes, corresponding to the detection time on S1 after 18:00 UTC on 19 February 2024, and show the progression of the whale from the northwest of the triplet to its center. The red stars are the locations of the hydrophones. Panel (b) to (d) are the surfaces of the time delay residuals at the time indicated. The yellow star shows the location of the minimum of the RMS of delay residuals for the three specific calls. Note that panels (b) to (d) show ten-kilometers squares centered on the yellow star.
Figure 8.
(a) Distances between consecutive calls of the same type based on locations derived from the TDOAs for the A and B calls. The red dots correspond to the A calls and the green dots to the B calls. The yellow line shows the distance from the B calls to the center of the triplet. Since the A and B calls are close to each other, the line derived from the A calls would be similar. The solid black indicates 1.5 km. (b) shows the histogram of estimated speed between two consecutive A calls when inside the 1.5 km line for the two different calls (c) shows the histograms of velocity estimates between consecutive B calls.
Figure 8.
(a) Distances between consecutive calls of the same type based on locations derived from the TDOAs for the A and B calls. The red dots correspond to the A calls and the green dots to the B calls. The yellow line shows the distance from the B calls to the center of the triplet. Since the A and B calls are close to each other, the line derived from the A calls would be similar. The solid black indicates 1.5 km. (b) shows the histogram of estimated speed between two consecutive A calls when inside the 1.5 km line for the two different calls (c) shows the histograms of velocity estimates between consecutive B calls.
Figure 9.
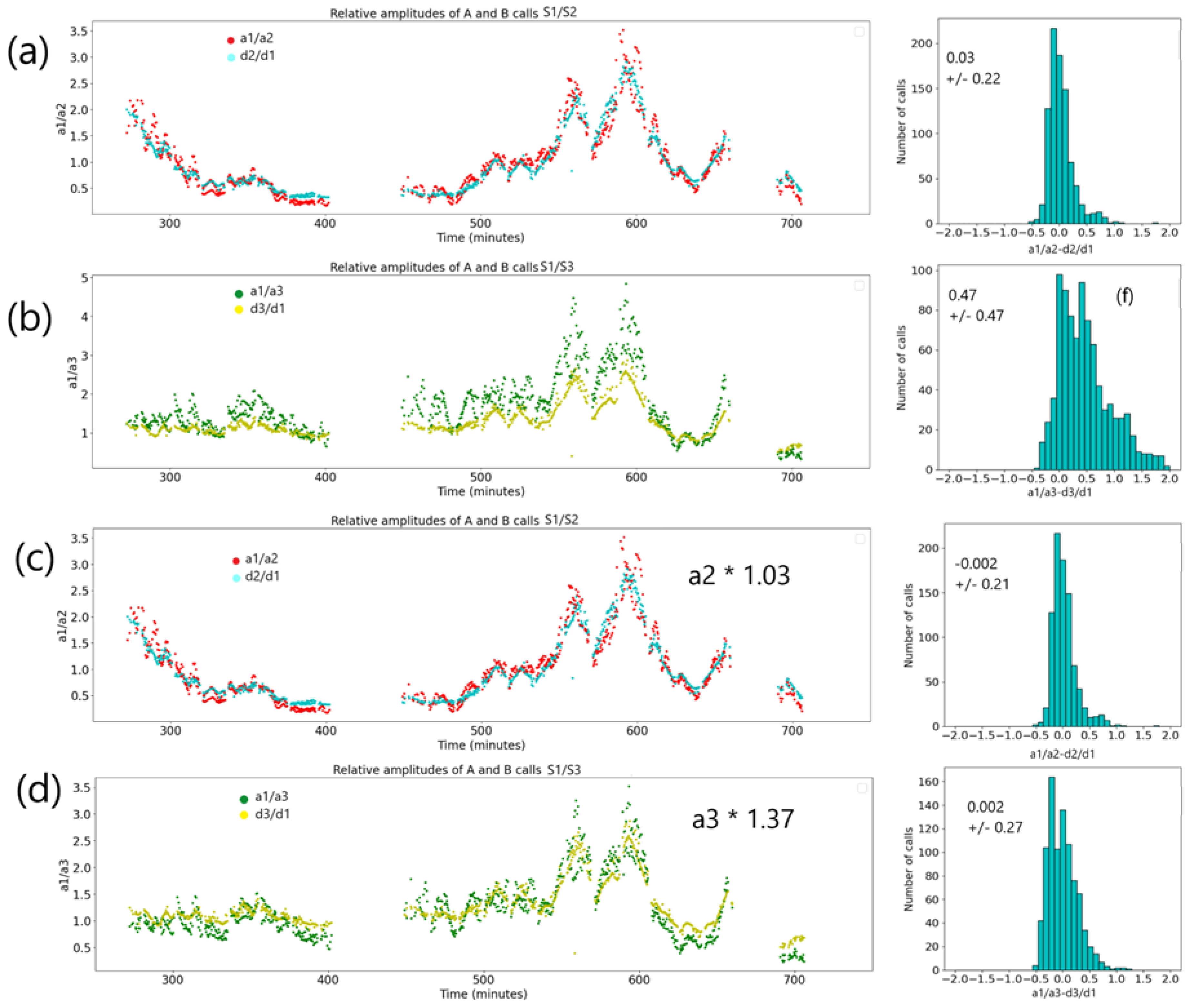
Relative measured amplitudes a1/a2 (a) and a1/a3 (b) displayed as a function of time when the call location is within 1.5 km of the triplet center. The scale is in minutes from 18:00 on 19 February 2024. For comparison, the distance ratios d2/d1 and d3/d1 are displayed on the same graphs. When a constant bias of 1.03 and 1.37 are applied to respectively a2 and a3, the graphs are displayed in (c) and (d). The histograms of the residuals (a1/a2-d2/d1) and (a1/a3-d3/d1) corresponding to each time series are shown to the right of each time series along with their mean and standard deviation.
Figure 9.
Relative measured amplitudes a1/a2 (a) and a1/a3 (b) displayed as a function of time when the call location is within 1.5 km of the triplet center. The scale is in minutes from 18:00 on 19 February 2024. For comparison, the distance ratios d2/d1 and d3/d1 are displayed on the same graphs. When a constant bias of 1.03 and 1.37 are applied to respectively a2 and a3, the graphs are displayed in (c) and (d). The histograms of the residuals (a1/a2-d2/d1) and (a1/a3-d3/d1) corresponding to each time series are shown to the right of each time series along with their mean and standard deviation.
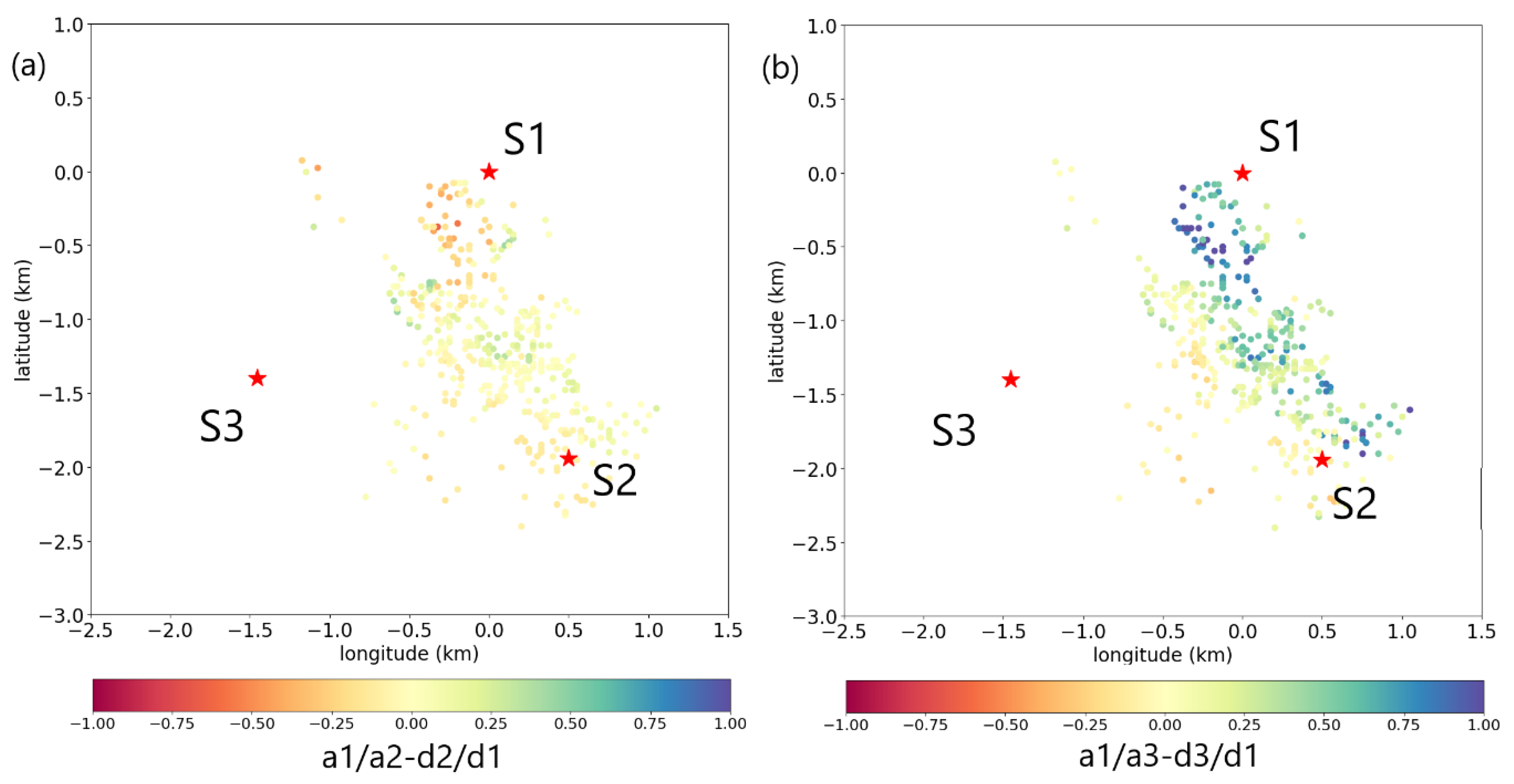
Figure 10.
Spatial mapping of residuals a1/a2-d2/d1 (a) and a1/a3-d3/d1 (b). Note the higher amplitudes of the residuals in (b), which a plane sloping from the S1-S2 line towards S3 would fit.
Figure 10.
Spatial mapping of residuals a1/a2-d2/d1 (a) and a1/a3-d3/d1 (b). Note the higher amplitudes of the residuals in (b), which a plane sloping from the S1-S2 line towards S3 would fit.
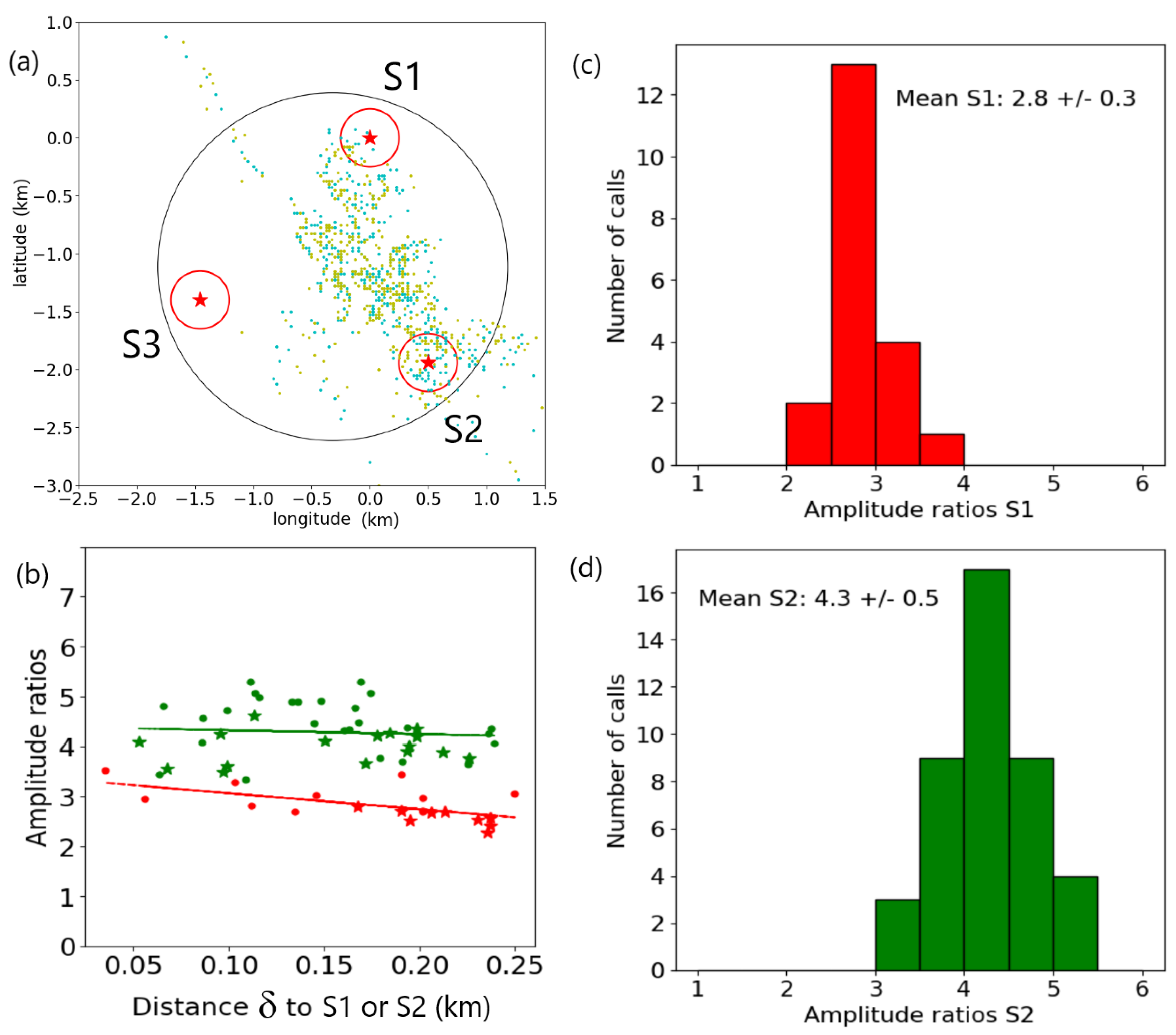
Figure 11.
(a) Map of all calls analyzed in the study. 597 A calls are in cyan, 600 B calls in yellow. The large circle is centered in the middle of the triplet and has a radius of 1.5 km. The small red circles are centered on each hydrophone and have a radius of 250 m. (b) Amplitude ratios a1/a2 in red, and a2/a1 in green, displayed as a function of distance for calls within 250 m of the hydrophones. (c) Histogram of the amplitude ratios a1/a2 for calls close to S1. (d) Histogram of the amplitude ratios a2/a1 for calls close to S2.
Figure 11.
(a) Map of all calls analyzed in the study. 597 A calls are in cyan, 600 B calls in yellow. The large circle is centered in the middle of the triplet and has a radius of 1.5 km. The small red circles are centered on each hydrophone and have a radius of 250 m. (b) Amplitude ratios a1/a2 in red, and a2/a1 in green, displayed as a function of distance for calls within 250 m of the hydrophones. (c) Histogram of the amplitude ratios a1/a2 for calls close to S1. (d) Histogram of the amplitude ratios a2/a1 for calls close to S2.
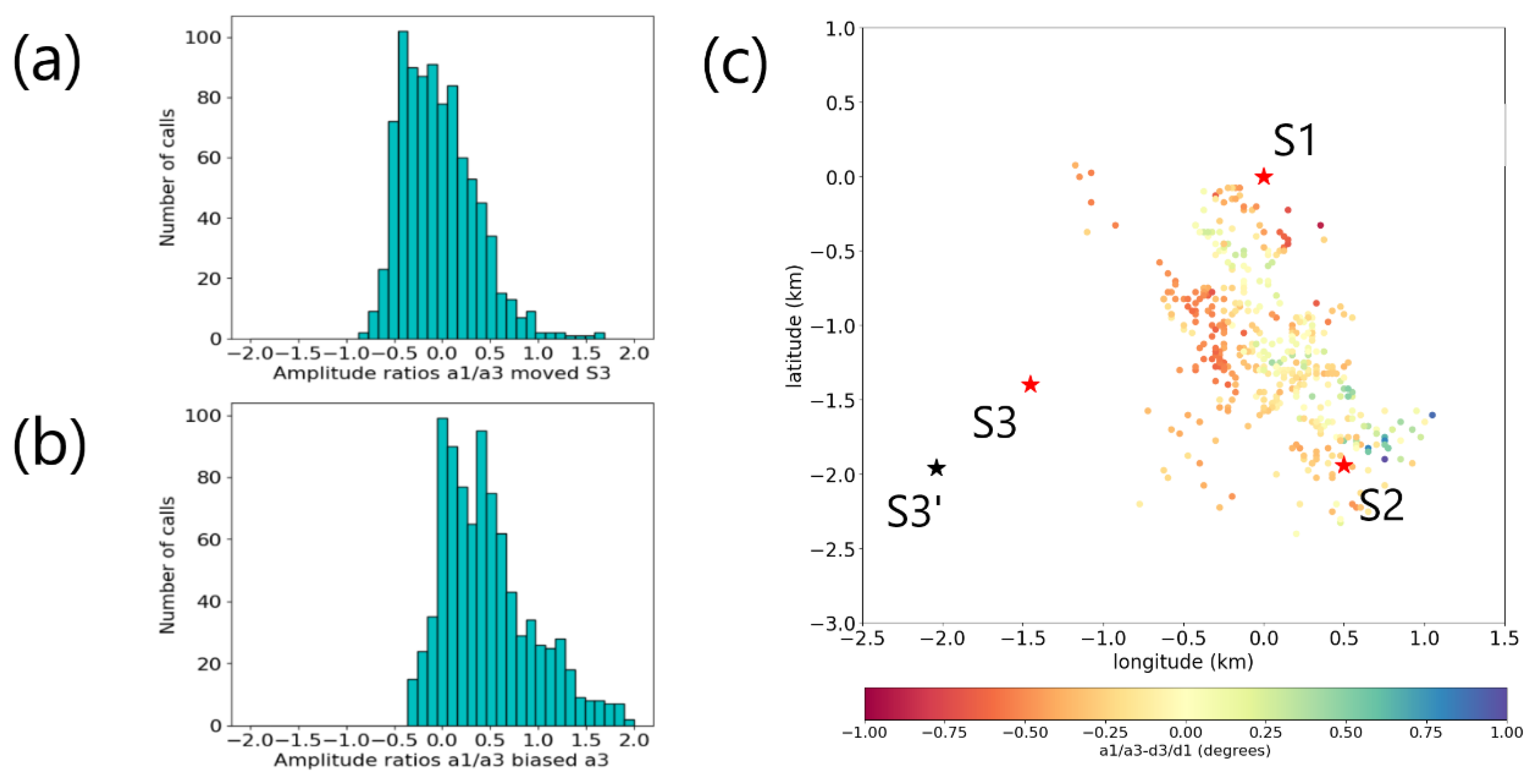
Figure 12.
(a) Histogram of the a1/a3-d3/d1 residuals with moved S3’ (top). (b) Histogram of the a1/a3-d3/d1 residuals with original S3 (bottom). (c) Spatial mapping of residuals a1/a3-d3/d1 when S3 is moved to S3’.
Figure 12.
(a) Histogram of the a1/a3-d3/d1 residuals with moved S3’ (top). (b) Histogram of the a1/a3-d3/d1 residuals with original S3 (bottom). (c) Spatial mapping of residuals a1/a3-d3/d1 when S3 is moved to S3’.
Table 1.
Basic geometry parameters for HA11S triplet. The water depth is 1174 m.
Table 1.
Basic geometry parameters for HA11S triplet. The water depth is 1174 m.
| Hydrophone |
Identifier |
Latitude
Longitude*
(decimal degree) |
Latitude
Longitude
(km from S1) |
Depth
(m) |
| H11S1 |
S1 |
18.50827
166.700272 |
0.000
0.000 |
h1 |
739**
750* |
| H11S2 |
S2 |
18.49082
166.705002 |
-1.939
0.498 |
h2 |
739**
742* |
| H11S3 |
S3 |
18.49568
166.686462 |
-1.399
-1.455 |
h3 |
739**
724* |
Table 2.
Vocalization depths estimates when the whale is above S1 or S2.
Table 2.
Vocalization depths estimates when the whale is above S1 or S2.
| Hydrophone |
Amplitude ratios |
h1 = 739 m
h2 = 739 m |
h1 = 750 m
h2 = 742 m |
| S1 |
r1 = 2.8 |
w1 = 28 m |
w1 = 51 m |
| r1 = 3.4 |
w1 = 167 m |
w1 = 191 m |
| S2 |
r2 = 4.3 |
w2 = 295 m |
w2 = 284 m |
| r2 = 4.4 |
w2 = 305 m |
w2 = 295 m |