Solvability of a Boundary Value Problem for One-Dimensional Motion of a Granular Matter

1. Introduction

Granular material is the assembly of large amount of discrete solid particles. The particles of this matter can be homogeneous or heterogeneous in material, size and shape, and it can be in an elastic or plastic state and have varying degrees of strength. Typically, the spaces between particles are filled with air or water, so granular flow represents a multiphase process. However, if particles are close-packed or the density of particles significantly exceeds the intergranular fluid or gas, then only the particles will be essential in momentum transfer in the matter, and not the fluid (gas) or interaction between the fluid (gas) and particles. Thus the intergranular fluid (gas) may not be taken into account in this case. Granular material mostly gets into this category and therefore can be considered as a dispersed single-phase rather than a multiphase mixture.

Granular materials can behave like elastic-plastic solids, viscous fluids, and even "granular gases" under various external influences. This diversity of granular media modes of behavior explains the existence of different approaches for its description [1,2]:

• Microscopic models and molecular dynamics simulations;
• Statistical mechanics kinetic theory;
• Phenomenological model and continuum models.

Works [2,3,4,5,6,7,8] present studies on the granular media mechanics. Applied problems of granular media mechanics, associated with mining engineering are considered in [2]. The connection between granular mechanics and plasticity theory, geological mechanics, synergetics and other branches of science is shown. The paper indicates the existence of two ways in the development of mathematical models of granular material: the first - continuum modeling in the context of continuum mechanics and the second - discrete modeling in the context of discrete element method (DEM), for example. Granular media are standing at intermediate position between viscous fluids and solids (elastic or plastic). One of the problems of granular material mechanics is formulation of closed equations systems, simulating the deformation processes of such materials. [3] gives the experiments of sand deformation of different sizes, which shown that the main axes of stress tensor are deviate from the strain tensor axes. Unlike viscous fluids, granular materials are not sensitive to strain rate, so the internal stresses of packing derived to a stationary condition remain unchanged. Some technological processes in mining and the chemical industry are associated with deformation of granular materials under gas filtration conditions. Paper [4] presents an experimental set for study of the structural behavior of granular medium in shear with an air filtration flow influence without the occurrence of fluidization. The air flow during deformation of the stationary packing of particles causes softening of the material, associated with the decrease of normal and shearing stresses and a porosity increase. Work [5] investigates the stress state of a granular conical embankment. The results of experiments show that the embankment foundation stresses after formation have underestimated values in the center of its hollow above the apex. The reason of its weak growth is the multi-tier "arch structure" which can collapse by weak vibrations. The DEM-based numerical calculations confirm the experimental data. In [6] the uniform shear of a granular sample based on the DEM is considered. Usage opportunity of the numerical results for continuous models formulation is presented. Work [7] presents a DEM based numerical research of the whirling motion of a granular material in a bounded domain. In [8] the 2D problem of unidirectional mass transfer in a granular medium caused by a combined loading with continuous rotation of the strain tensor main axes. To describe this phenomenon a hypoplastic model of a granular material and a resemblance model of an incompressible fluid are used. For both models the deformation kinematics calculations are performed and the results obtained were compared with experimental data. It is shown that the models qualitatively describe the deformation process and the unidirectional mass transfer effect which are observed in experiments.

In many physical processes the granular materials are behave like liquid, thus the transition to hydrodynamic description of these materials is an important question for the flowability study [9,10,11,12,13,14,15,16,17,18,19]. At the moment, a lot of studies of flowability dedicated to the description of its behavior using continuum theories were performed [17,20,21,22,23]. A research of the granular medium motion in a vertically shaken opened container shown that experimental and numerical results can be explained using the hydrodynamics theory [24]. The hydrodynamic model is structurally close to the viscous gas equations system [25] with the dependence of viscosity on density. The solvability issues for related models are considered in [27,28,29,30,31]. The most common numerical methods for similar problems are given in [32,33,34].

This paper proves the solvability of an initial boundary-value problem for the equations of one-dimensional non-stationary isothermal and non-isothermal motion of granular material. The viscosity depends on density and temperature, and the pressure is the interpolation form of VanderWaals state equation. A numerical study of a model of one-dimensional isothermal motion of granular medium is presented. A difference scheme based on finite-difference approximation is proposed to obtain a numerical solution.

Let’s introduce the necessary notations. Let ${\left|\right|f\left|\right|}_{q,\Omega }=(\underset{\Omega }{\int }{\left|f\left(x\right)\right|}^q{dx)}^{1/q}$, ${\left|\right|u\left|\right|}_{q,r,Q_T}=$

$=(\underset{0}{\overset{T}{\int }}(\underset{\Omega }{\int }{|u(x,t)}^q{dx\left|\right)}^{r/q}{)}^{1/r}$ are the norm functions in Lebesgue’s spaces $L_q(\Omega )$, $L_{q,r}\left(Q_T\right)$, where $r,q\in [1,\infty ]$. We assume $\left|\right|·{\left|\right|}_q=\left|\right|·{\left|\right|}_{q,\Omega },\left|\right|·\left|\right|=\left|\right|·{\left|\right|}_{2,\Omega }$ for brevity. Also we use Sobolev’s spaces $W_p^l(\Omega )$, where l is natural, $1\le p\le \infty$, with the norm ${\left|\right|u\left|\right|}_{W_p^l(\Omega )}={\left|\right|u\left|\right|}_{p,\Omega }^{\left(l\right)}=$

$={\displaystyle \sum _{\left|\alpha \right|=0}^l}{\displaystyle \sum _{\left(\alpha \right)}}\left|\right|D_x^{\alpha }u{\left|\right|}_{L_p(\Omega )}$, where ${\displaystyle \sum _{\left(\alpha \right)}}$ means summing $\left|\alpha \right|={\alpha }_1+...+{\alpha }_n$ [25].

2. Setting up the problem and formulation of the main result

We consider a motion of a shallow, vertically shaken granular bed. The differential equations system, simulating the one-dimensional non-isothermal motion of a granular matter consists of mass, momentum and energy equations [24]:

$${\displaystyle \frac{\partial \left(mn\right)}{\partial t}}+{\displaystyle \frac{\partial \left(mnu\right)}{\partial x}}=0,$$

$$mn\left({\displaystyle \frac{\partial u}{\partial t}}+u{\displaystyle \frac{\partial u}{\partial x}}\right)=mng-{\displaystyle \frac{\partial p}{\partial x}}+{\displaystyle \frac{\partial }{\partial x}}\left([2\mu +\lambda ]{\displaystyle \frac{\partial u}{\partial x}}\right),$$

$$n\left({\displaystyle \frac{\partial T}{\partial t}}+u{\displaystyle \frac{\partial T}{\partial x}}\right)={\displaystyle \frac{\partial }{\partial x}}\left(\kappa {\displaystyle \frac{\partial T}{\partial x}}\right)-p{\displaystyle \frac{\partial u}{\partial x}}-I.$$

Here $(x,t)$ - Euler’s coordinates; n - number density; m - mass of a particle; u - velocity; p - pressure, $\mu$ - shear viscosity; $\lambda$ - second viscosity; g - gravity acceleration; T - granular temperature, determined by vibrations of particles’ mean velocity, i.e. $1/2k_{B}T=1/2m(<u^2>-<u{>}^2)$, where $k_B$ is the Boltzmann’s constant; I is the dissipative term due to the inelastic particle collisions; $\kappa$ is the heat conductivity coefficient. . In the applications we use the following relations [35,36,37]:

$$p(n,T)=nT{\displaystyle \frac{n_c+n}{n_c-n}},\lambda (n,T)=-2/3\mu (n,T),\mu (n,T)=m\kappa Pr,$$

$$\kappa (n,T)={\displaystyle \frac{n{(\alpha l+d)}^2}{l}}\sqrt{{\displaystyle \frac{}{}}}Tm,I(n,T)={\displaystyle \frac{\epsilon }{l{\gamma }_c}}nT\sqrt{{\displaystyle \frac{}{}}}Tm.$$

Here $n_c$ is the number density of a hexagonal close-packed crystal; d - diameter of the particles; $l={\displaystyle \frac{n_c-n}{\sqrt{8}nd(n_c-an)}}$ - is the mean free path, where $a=1-\sqrt{3/8}$ [35]; $Pr$ is the Prandtl number; $\epsilon =(1-e^2)$ - inelasticity parameter [24], $e\approx 0,9$ is the normal restitution coefficient; $\alpha =0,6$ and ${\gamma }_c=2,26$ are constants from [35,37] respectively. Assuming that the flow density $\rho (x,t)$ equals $mn$ [11], we obtain the Navier-Stokes equations

$${\displaystyle \frac{\partial \rho }{\partial t}}+{\displaystyle \frac{\partial \left(\rho u\right)}{\partial x}}=0,$$

(1)

$$\rho \left({\displaystyle \frac{\partial u}{\partial t}}+u{\displaystyle \frac{\partial u}{\partial x}}\right)=\rho g-{\displaystyle \frac{\partial p}{\partial x}}+{\displaystyle \frac{\partial }{\partial x}}\left([2\mu +\lambda ]{\displaystyle \frac{\partial u}{\partial x}}\right),$$

(2)

$${\displaystyle \frac{\rho }{m}}\left({\displaystyle \frac{\partial T}{\partial t}}+u{\displaystyle \frac{\partial T}{\partial x}}\right)={\displaystyle \frac{\partial }{\partial x}}\left(\kappa {\displaystyle \frac{\partial T}{\partial x}}\right)-p{\displaystyle \frac{\partial u}{\partial x}}-I,$$

(3)

which can be solved in the $Q_T=\Omega \times (0,T)$, $\Omega =(0,L)$ domain with the initial-boundary conditions

$${\left.u\right|}_{t=0}=u^0\left(x\right),{\left.T\right|}_{t=0}=T^0\left(x\right),{\left.\rho \right|}_{t=0}={\rho }^0\left(x\right),$$

$${\left.u\right|}_{x=0}={\left.u\right|}_{x=1}=0,{\left.{\displaystyle \frac{\partial T}{\partial x}}\right|}_{x=0}={\left.{\displaystyle \frac{\partial T}{\partial x}}\right|}_{x=1}=0.$$

(4)

For the proof of problem (1) – (4) in a short period it is convenient to use another independent variables, namely Lagrange coordinates. Let $y=y(\zeta ,x,t)$ – is the solution of Cauchy problem: ${\displaystyle \frac{\partial y}{\partial \zeta }}{=u(y,\zeta ),y|}_{\zeta =t}=x$. Assume ${\xi =y(\zeta ,x,t)|}_{\zeta =0}$ and consider $\xi$ and t variables as new. Then, $\rho (\xi ,t)={\rho }^0\left(\xi \right)J(\xi ,t)$, where $J(\xi ,t)={\displaystyle \frac{\partial \xi }{\partial x}}$ - is the transition Jacobian [25]. Turning into mass Lagrangian variables $(\overline{x},t)$ from $(\xi ,t)$ with the rule ${\rho }^0\left(\xi \right)d\xi =d\overline{x},\overline{x}\left(\xi \right)=\underset{0}{\overset{\xi }{\int }}{\rho }^0\left(\eta \right)d\eta \in [0,L]$ and designate $\overline{x}$ as x, we obtain

$${\displaystyle \frac{\partial \rho }{\partial t}}+{\rho }^2{\displaystyle \frac{\partial u}{\partial x}}=0,$$

(5)

$${\displaystyle \frac{\partial u}{\partial t}}={\displaystyle \frac{\partial }{\partial x}}\left({\displaystyle \frac{4}{3}}\mu \rho {\displaystyle \frac{\partial u}{\partial x}}\right)-{\displaystyle \frac{\partial p}{\partial x}}+g,2\mu +\lambda =[\lambda =-{\displaystyle \frac{2}{3}}\mu ]={\displaystyle \frac{4}{3}}\mu .$$

(6)

$${\displaystyle \frac{1}{m}}{\displaystyle \frac{\partial T}{\partial t}}={\displaystyle \frac{\partial }{\partial x}}\left(\kappa \rho {\displaystyle \frac{\partial T}{\partial x}}\right)-p{\displaystyle \frac{\partial u}{\partial x}}-{\displaystyle \frac{1}{\rho }}I.$$

(7)

The initial-boundary conditions are

$${\left.u\right|}_{t=0}=u^0\left(x\right),{\left.\rho \right|}_{t=0}={\rho }^0\left(x\right),{\left.T\right|}_{t=0}=T^0\left(x\right),$$

$${\left.u\right|}_{x=0}={\left.u\right|}_{x=L}=0,{\left.{\displaystyle \frac{\partial T}{\partial x}}\right|}_{x=0}={\left.{\displaystyle \frac{\partial T}{\partial x}}\right|}_{x=L}=0.$$

(8)

In (5)-(7) we use the following dimensionless relations (see Appendix A):

$$x^{\prime }={\displaystyle \frac{x}{x_1}},t^{\prime }={\displaystyle \frac{t}{t_1}},u^{\prime }={\displaystyle \frac{u}{u_1}},{\rho }^{\prime }={\displaystyle \frac{\rho }{m{n}_c}},T^{\prime }={\displaystyle \frac{T}{T_0}},l^{\prime }={\displaystyle \frac{l}{l_1}},$$

where $x_1=\underset{0}{\overset{L}{\int }}{\rho }^0\left(\xi \right)d\xi =m{n}_{c}d$, $l_1=d$,$t_1={\displaystyle \frac{d\sqrt{m}}{{\sqrt{T}}_0}}$, $u_1={\displaystyle \frac{{\sqrt{T}}_0}{\sqrt{m}}}$, $p({\rho }^{\prime },T^{\prime })=n_c{T}_0{p}^{\prime },$$\kappa ({\rho }^{\prime },T^{\prime })=n_{c}d\sqrt{{\displaystyle \frac{T_0}{m}}}{\kappa }^{\prime },$$\mu ({\rho }^{\prime },T^{\prime })=m\kappa Pr=m{n}_{c}d\sqrt{{\displaystyle \frac{T_0}{m}}}{\mu }^{\prime },$$T_0\propto m{\left(af\right)}^2$ is the given granular temperature at the bottom of container, amplitude a and frequency f are generated by a shaking table, where the container partially filled with beads is located. Therefore, the range of $x^{\prime }$ is a unit segment [0,1]and the system (5)–(7) becomes (primes omitted):

$${\displaystyle \frac{\partial \rho }{\partial t}}+{\rho }^2{\displaystyle \frac{\partial u}{\partial x}}=0,$$

(9)

$${\displaystyle \frac{\partial u}{\partial t}}={\displaystyle \frac{\partial }{\partial x}}\left({\displaystyle \frac{4}{3}}\mu \rho {\displaystyle \frac{\partial u}{\partial x}}\right)-{\displaystyle \frac{\partial p}{\partial x}}+G,$$

(10)

$${\displaystyle \frac{\partial T}{\partial t}}={\displaystyle \frac{\partial }{\partial x}}\left(\kappa \rho {\displaystyle \frac{\partial T}{\partial x}}\right)-p{\displaystyle \frac{\partial u}{\partial x}}-{\displaystyle \frac{1}{\rho }}I,$$

(11)

where $G={\displaystyle \frac{mdg}{T_0}}$ is the dimensionless term, which contains the dimensionless shaking strength $S={\displaystyle \frac{T_0}{mgd}}={\displaystyle \frac{a^2{\omega }^2}{gd}}(\omega =2\pi f)$ - it is the ratio of kinetic energy, inserted into the system by the vibrating bottom and the potential energy associated with the particle diameter

The initial and boundary conditions are as follows:

$${\left.u\right|}_{t=0}=u^0\left(x\right),{\left.\rho \right|}_{t=0}={\rho }^0\left(x\right),{\left.u\right|}_{x=0}={\left.u\right|}_{x=1}=0,$$

(12)

$${\left.T\right|}_{t=0}=T^0\left(x\right),{\left.{\displaystyle \frac{\partial T}{\partial x}}\right|}_{x=0}={\left.{\displaystyle \frac{\partial T}{\partial x}}\right|}_{x=1}=0.$$

(13)

We formulate the following results of this work.

Definition 1. A generalized solution of the problem (9) – (13) is the set of functions $\left(u\right(x,t)$, $\rho (x,t)$, $T(x,t))$ from the following spaces:

$$\rho \in L_{\infty }(0,T;W_2^1(\Omega )),$$

$$(u,T)\in L_{\infty }(0,T;W_2^1(\Omega ))\cap L_2(0,T;W_2^2(\Omega )),$$

$$({\displaystyle \frac{\partial \rho }{\partial t}},{\displaystyle \frac{\partial u}{\partial t}},{\displaystyle \frac{\partial T}{\partial t}})\in L_2\left(Q_T\right),\Omega =(0,1),Q_T=\Omega \times (0,T),$$

which satisfy equations (9) – (11) and inequations $0<\rho (x,t)<1,0<T(x,T)<\infty$ almost everywhere in $Q_T$ and take the given boundary and initial values in the matter of traces of functions from specified classes.

Theorem 1. 

Let problem (9), (10), (12) comply the following smoothness conditions:

$$(u^0,{\rho }^0)\in W_2^1(\Omega ),u^0\left(0\right)=u^0\left(1\right)=0.$$

Let the functions $p\left(\rho \right)$, $\kappa \left(\rho \right)$ and their derivatives are continuous up to the second order for $\varrho (x,t)\in (0,1)$ and satisfy as follows:

$$k_0^{-1}{\rho }^{q_1}{(1-\rho )}^{q_2}{(1-a\rho )}^{q_3}\le \kappa \left(\rho \right)\le k_0{\rho }^{q_4}{(1-\rho )}^{q_5}{(1-a\rho )}^{q_6},$$

$$k_0^{-1}{\rho }^{q_7}{(1+\rho )}^{q_8}{(1-\rho )}^{q_9}\le p\left(\rho \right)\le k_0{\rho }^{q_{10}}{(1+\rho )}^{q_{11}}{(1-\rho )}^{q_{12}},$$

$$\left|\right(\kappa {\left(\rho \right)}_{\rho }^{\prime }|\le k_0{\rho }^{q_{13}}{(1-\rho )}^{q_{14}}{(1-a\rho )}^{q_{15}},$$

$$\left|\right(p{\left(\rho \right)}_{\rho }^{\prime }|\le k_0{\rho }^{q_{16}}{(1+\rho )}^{q_{17}}{(1-\rho )}^{q_{18}},$$

where $k_0=const>0$, $q_1,\dots ,q_{18}$ are fixed real parameters. If the following conditions are satisfied

$$0<b_0\le {\rho }^0\left(x\right)\le B_0<1,x\in \overline{\Omega },$$

(14)

where $b_0$, $B_0$ are known positive constants, then there is a small enough value $t_0\in (0,T)$, such that for every $t\le t_0$ a generalized solution $\rho (x,t)$, $u(x,t)$ exists for the problem (9), (10), (12).

Theorem 2. 

Let problem (9) – (13) comply the following smoothness conditions:

$$(u^0,{\rho }^0,T^0)\in W_2^1(\Omega ),g\in L_2(0,T;W_2^1(\Omega ))$$

and the matching conditions $u_i^0{\mid }_{x=0,x=1}={\displaystyle \frac{\partial T^0}{\partial x}}{\mid }_{x=0,x=1}=0$. Let functions $p(\rho ,T)$, $\kappa (\rho ,T)$, $I(\rho ,T)$ and their derivatives up to the second order are continuous for $\rho (x,t)\in (0,1)$ and satisfy as follows:

$$k_0^{-1}{\rho }^{q_{19}}{(1-\rho )}^{q_{20}}{(1-a\rho )}^{q_{21}}{\left|T\right|}^{q_{22}}\le \kappa (\rho ,T)\le k_0{\rho }^{q_{23}}{(1-\rho )}^{q_{24}}{(1-a\rho )}^{q_{25}}{\left|T\right|}^{q_{26}},$$

$$k_0^{-1}{\rho }^{q_{27}}{(1+\rho )}^{q_{28}}{(1-\rho )}^{q_{29}}{\left|T\right|}^{q_{30}}\le p(\rho ,T)\le k_0{\rho }^{q_{31}}{(1+\rho )}^{q_{32}}{(1-\rho )}^{q_{33}}{\left|T\right|}^{q_{34}},$$

$$k_0^{-1}{\rho }^{q_{35}}{(1-\rho )}^{q_{36}}{(1-a\rho )}^{q_{37}}{\left|T\right|}^{q_{38}}\le I(\rho ,T)\le k_0{\rho }^{q_{39}}{(1-\rho )}^{q_{40}}{(1-a\rho )}^{q_{41}}{\left|T\right|}^{q_{42}},$$

$$\left|\right(\kappa {(\rho ,T)}_{\rho }^{\prime }|\le k_0{\rho }^{q_{43}}{(1-\rho )}^{q_{44}}{(1-a\rho )}^{q_{45}}|T{|}^{q_{46}},$$

$$\left|\right(\kappa {(\rho ,T)}_T^{\prime }|\le k_0{\rho }^{q_{47}}{(1-\rho )}^{q_{48}}{(1-a\rho )}^{q_{49}}|T{|}^{q_{50}},$$

$$\left|\right(p{(\rho ,T)}_{\rho }^{\prime }|\le k_0{\rho }^{q_{51}}{(1+\rho )}^{q_{52}}{(1-\rho )}^{q_{53}}|T{|}^{q_{54}},$$

$$\left|\right(p{(\rho ,T)}_T^{\prime }|\le k_0{\rho }^{q_{55}}{(1+\rho )}^{q_{56}}{(1-\rho )}^{q_{57}}|T{|}^{q_{58}},$$

$$\mid p{(\rho ,T)}_{\rho \rho }^{\prime \prime }\mid \le k_0{\rho }^{q_{59}}{(1+\rho )}^{q_{60}}{(1-\rho )}^{q_{61}}{\left|T\right|}^{q_{62}},$$

$$\mid p{(\rho ,T)}_{\rho T}^{\prime \prime }\mid \le k_0{\rho }^{q_{63}}{(1+\rho )}^{q_{64}}{(1-\rho )}^{q_{65}}{\left|T\right|}^{q_{66}},$$

$$\mid p{(\rho ,T)}_{TT}^{\prime \prime }\mid \le k_0{\rho }^{q_{67}}{(1+\rho )}^{q_{68}}{(1-\rho )}^{q_{69}}{\left|T\right|}^{q_{70}},$$

where $k_0=const>0$, $q_{19},...,q_{70}$ are fixed real parameters.

If conditions (14) and

$$0<b_1\le T^0\left(x\right)\le B_1<\infty ,x\in \overline{\Omega },$$

(15)

where $b_0$, $B_0$, $b_1$, $B_1$ are known positive constants, then there is a small enough value $t_0\in (0,T)$, such that for every $t\le t_0$ a generalized solution $\rho (x,t)$, $u(x,t)$, $T(x,t)$ exists for the problem (9) – (13).

3. Local solvability of the isothermal problem

We will find a local generalized solution as a limit of approximate solutions $({\rho }^n,u^n)$, where $u^n$ are expressed as a finite sum:

$$u^n(x,t)=\sum _{i=1}^n{u}_i^n\left(t\right)sin\left(\pi ix\right),$$

with unknown coefficients $u_i^n\left(t\right)$, $i=1,2,...,n$. To define these coefficients we require (10) be satisfied approximately:

$$\underset{0}{\overset{1}{\int }}\left[{\displaystyle \frac{\partial u^n}{\partial t}}-{\displaystyle \frac{\partial }{\partial x}}\left({\displaystyle \frac{4}{3}}{\mu }^n{\rho }^n{\displaystyle \frac{\partial u^n}{\partial x}}\right)+{\displaystyle \frac{\partial p}{\partial x}}-G\right]sin\left(\pi ix\right)dx=0.$$

(16)

The function ${\rho }^n(x,t)$ will be determined from a solution of:

$${\displaystyle \frac{\partial {\rho }^n}{\partial t}}+{\left({\rho }^n\right)}^2{\displaystyle \frac{\partial u^n}{\partial x}}=0,{\left.{\rho }^n\right|}_{t=0}={\rho }^0\left(x\right).$$

(17)

From (17) we obtain the following relation for ${\rho }^n(x,t)$:

$${\rho }^n(x,t)={\rho }^0\left(x\right){\left[1+{\rho }^0\left(x\right)\underset{0}{\overset{t}{\int }}{\displaystyle \frac{\partial u^n}{\partial x}}(x,\tau )d\tau \right]}^{-1}.$$

(18)

Unknown coefficients $u_i^n\left(t\right)$ are found from the Cauchy problem solution for the ordinary differential system:

$${\displaystyle \frac{d{u}_i^n}{dt}}={\Phi }_i^n(u_1^n,...,u_n^n;{\rho }^n),{\Phi }_i^n=2\underset{0}{\overset{1}{\int }}\left({\displaystyle \frac{\partial }{\partial x}}\left({\displaystyle \frac{4}{3}}{\mu }^n{\rho }^n{\displaystyle \frac{\partial u^n}{\partial x}}\right)-{\displaystyle \frac{\partial p^n}{\partial x}}+G\right)sin\left(\pi ix\right)dx,$$

(19)

and $u^n(x,t)={\displaystyle {\sum }_{i=1}^n}{u}_i^n\left(t\right)sin\left(\pi ix\right)$, ${\rho }^n(x,t)$ is determined by (18). Initial conditions for (19) will find from a sine expansion in the Fourier series of the initial functions $u^0\left(x\right)$:

$$u_i^n\left(0\right)=u_i^0\equiv 2\underset{0}{\overset{1}{\int }}{u}^0\left(x\right)sin\left(\pi ix\right)dx,i=1,...,n.$$

(20)

Thus, the generalized solution $(u^n,{\rho }^n)$ satisfies the Cauchy problem (19), (20), the local solvability of this problem follows from Cauchy - Picard theorem for each fixed n for an ordinary differential system [38].

We indicate a value for $t_0$, for which the problem given is solvable for every n on $[0,t_0]$. Another condition of which an interval quantity of $t_0$, is chosen associated with the requirement of positivity for ${\rho }^n(x,t)$. Because $0<b_0\le {\rho }^0\left(x\right)<B_0<1$, we demand that the following relations be satisfied for ${\rho }^n(x,t)$

$$0<{\displaystyle \frac{b_0}{2}}\le {\rho }^n(x,t)\le {\displaystyle \frac{1+B_0}{2}}<1,$$

(21)

for every n and with $x\in [0,1],t\in [0,t_0]$. Besides, from (18) and (21) we obtain

$$|{\rho }_x^n|\le C(1+\underset{0}{\overset{t}{\int }}|u_{xx}^n\left|d\tau \right).$$

(22)

Lemma 1. 

There is a value $t_0>0$ such that for all n on the interval $[0,t_0]$ the solution $u^n$ to problem (19), (20) satisfies the following estimate

$$\underset{0\le t\le t_0}{max}\left|\right|u_x^n{\left(t\right)\left|\right|}^2+\underset{0}{\overset{t_0}{\int }}\left|\right|u_{xx}^n{\left|\right|}^2+\left|\right|u_t^n{\left|\right|}^{2}dt\le N_1.$$

Proof 

(Proof).

$$z_n\left(t\right)=\left|\right|u^n{\left(t\right)\left|\right|}^2+\left|\right|u_x^n\left(t\right){\left|\right|}^2+\beta \left(\underset{0}{\overset{t}{\int }}\left|\right|u_{xx}^n\left(\tau \right){\left|\right|}^{2}d\tau \right),$$

where the real parameter $\beta \in (0,1)$ will be designated later. Multiply each equation of (16) by $u_i^n\left(t\right)$, sum over i from 1 to n and integrate over x from 0 to 1. We obtain the following equality

$${\displaystyle \frac{1}{2}}{\displaystyle \frac{d}{dt}}\underset{0}{\overset{1}{\int }}{\left(u^n\right)}^{2}dx+\underset{0}{\overset{1}{\int }}{\rho }^n{\left(u_x^n\right)}^2{\displaystyle \frac{4}{3}}\mu \left({\rho }^n\right)dx=-\underset{0}{\overset{1}{\int }}{u}^n{\displaystyle \frac{\partial p\left({\rho }^n\right)}{\partial x}}dx+\underset{0}{\overset{1}{\int }}{u}^{n}Gdx.$$

(23)

We show that from (23) follows estimate

$${\displaystyle \frac{d}{dt}}\left|\right|u^n{\left(t\right)\left|\right|}^2+{\displaystyle \frac{8}{3}}{\nu }_0\left|\right|u_x^n{\left|\right|}^2\le C\left(z_n\left(t\right)+{\left|\right|G\left(t\right)\left|\right|}^2\right).$$

(24)

Functions ${\displaystyle \frac{{\rho }^n}{1-{\rho }^n}}$; ${\displaystyle \frac{1+{\rho }^n}{1-{\rho }^n}}$; ${\displaystyle \frac{{\rho }^n(1+{\rho }^n)}{{(1-{\rho }^n)}^2}}$ are uniformly bounded over n for all ${\rho }^n\in (0,1)$ by virtue of (21). Estimate the terms on the right part of (23) taking into account (22)

$$|\underset{0}{\overset{1}{\int }}{u}^n{\displaystyle \frac{\partial p\left({\rho }^n\right)}{\partial x}}dx|=|\underset{0}{\overset{1}{\int }}{u}^n{\left(p\left({\rho }^n\right)\right)}_{{\rho }^n}^{\prime }{\rho }_x^{n}dx|\le C\underset{0}{\overset{1}{\int }}\left|u^n{\rho }_x^n\right|dx\le$$

$$\le C\left|\right|u^n\left|\right|\left|\right|{\rho }_x^n\left|\right|\le C\left(\right||u^n{\left(t\right)\left|\right|}^2+\left|\right|{\rho }_x^n{\left(t\right)\left|\right|}^2)\le C{z}_n\left(t\right),$$

$$|\underset{0}{\overset{1}{\int }}{u}^{n}Gdx|\le C\underset{0}{\overset{1}{\int }}|u^{n}G|dx\le C||u^n\left|\right|\left|\right|G\left(t\right)\left|\right|\le C\left(\right||u^n{\left(t\right)\left|\right|}^2+{\left|\right|G\left(t\right)\left|\right|}^2)\le C(z_n\left(t\right)+{\left|\right|G\left(t\right)\left|\right|}^2).$$

Here and further on C is a positive constant which is not depend on n. Because $\mu \left({\rho }^n\right){\rho }^n\ge {\nu }_0\equiv k_0^{-1}{\left({\displaystyle \frac{b_0}{2}}\right)}^{q_1+1}{\left({\displaystyle \frac{1-B_0}{2}}\right)}^{q_2}{\left(1-{\displaystyle \frac{a(1+B_0)}{2}}\right)}^{q_3},$ then follows inequality (24).

Each of equations (16) is multiplied by ${\left(i\pi \right)}^2{u}_i^n\left(t\right)$ and is summed over i from 1 to n. Considering the equality ${\displaystyle {\sum }_{i=1}^n}{u}_i^n{\left(i\pi \right)}^{2}sin\left(i\pi x\right)=-u_{xx}^n$ we obtain

$${\displaystyle \frac{1}{2}}{\displaystyle \frac{d}{dt}}\underset{0}{\overset{1}{\int }}{\left(u_x^n\right)}^{2}dx+{\displaystyle \frac{4}{3}}\underset{0}{\overset{1}{\int }}\mu \left({\rho }^n\right){\rho }^n{\left(u_{xx}^n\right)}^{2}dx=-{\displaystyle \frac{4}{3}}\underset{0}{\overset{1}{\int }}{u}_{xx}^n{\left(\mu \left({\rho }^n\right)\right)}_x^{\prime }{\rho }^n{u}_x^{n}dx-$$

$$-{\displaystyle \frac{4}{3}}\underset{0}{\overset{1}{\int }}{u}_{xx}^n\mu \left({\rho }^n\right){\rho }_x^n{u}_x^{n}dx+\underset{0}{\overset{1}{\int }}{u}_{xx}^n{\displaystyle \frac{\partial p\left({\rho }^n\right)}{\partial x}}dx+\underset{0}{\overset{1}{\int }}{u}_{xx}^{n}Gdx.$$

(25)

Show, that (25) implied the estimate

$${\displaystyle \frac{d}{dt}}\left|\right|u_x^n{\left|\right|}^2+{\displaystyle \frac{8}{3}}{\nu }_0\left|\right|u_{xx}^n{\left|\right|}^2\le {\displaystyle \sum _{i=1}^4}{\epsilon }_i\left|\right|u_{xx}^n{\left|\right|}^2+C(z_n\left(t\right)+z_n^3\left(t\right)+{\left|\right|G\left(t\right)\left|\right|}^2).$$

(26)

Functions ${\rho }^n{\mu }_{{\rho }^n}^{\prime };\mu \left({\rho }^n\right);p_{{\rho }^n}^{\prime }$ are uniformly bounded over n for all ${\rho }^n\in (0,1)$ by virtue of (21). Estimate the terms on the right part of (25) taking into account (22)

$$|\underset{0}{\overset{1}{\int }}{u}_{xx}^n{\left(\mu \left({\rho }^n\right)\right)}_x^{\prime }{\rho }^n{u}_x^{n}dx|=|\underset{0}{\overset{1}{\int }}{u}_{xx}^n{\rho }^n{u}_x^n{\mu }_{{\rho }^n}^{\prime }·{\rho }_x^{n}dx|\le C\underset{0}{\overset{1}{\int }}|u_{xx}^n\left|\right|{\rho }_x^n\left|\right|u_x^n|dx\le$$

$$\le C\underset{0\le x\le 1}{max}|u_x^n(x,t)|\underset{0}{\overset{1}{\int }}|u_{xx}^n\left|\right|{\rho }_x^n|dx\le C||u_x^n{\left|\right|}^{1/2}\left|\right|u_{xx}^n{\left|\right|}^{1/2}\left|\right|u_{xx}^n\left|\right|\left|\right|{\rho }_x^n\left|\right|=$$

$$=C\left|\right|u_x^n{\left|\right|}^{1/2}\left|\right|u_{xx}^n{\left|\right|}^{3/2}\left|\right|{\rho }_x^n\left|\right|\le {\epsilon }_1\left|\right|u_{xx}^n{\left|\right|}^2+{\displaystyle \frac{C}{{\epsilon }_1}}\left(\left|\right|u_x^n{\left|\right|}^2\left|\right|{\rho }_x^n{\left|\right|}^4\right)\le$$

$$\le {\epsilon }_1\left|\right|u_{xx}^n\left|\right|+{\displaystyle \frac{C}{{\epsilon }_1}}\left(\right||u_x^n{\left|\right|}^6+\left|\right|{\rho }_x^n{\left|\right|}^6)\le {\epsilon }_1\left|\right|u_{xx}^n{\left|\right|}^2+{\displaystyle \frac{C}{{\epsilon }_1}}{z}_n^3\left(t\right),$$

$$|\underset{0}{\overset{1}{\int }}{u}_{xx}^n\mu \left({\rho }^n\right){\rho }_x^n{u}_x^{n}dx|\le C\underset{0}{\overset{1}{\int }}|u_{xx}^n\left|\right|{\rho }_x^n\left|\right|u_x^n|dx\le {\epsilon }_2\left|\right|u_{xx}^n{\left|\right|}^2+{\displaystyle \frac{C}{{\epsilon }_2}}{z}_n^3\left(t\right),$$

$$|\underset{0}{\overset{1}{\int }}{u}_{xx}^n{\displaystyle \frac{\partial p\left({\rho }^n\right)}{\partial x}}dx|=\underset{0}{\overset{1}{\int }}|u_{xx}^n{p}_{{\rho }^n}^{\prime }·{\rho }_x^{n}dx|\le C\underset{0}{\overset{1}{\int }}|u_{xx}^n\left|\right|{\rho }_x^n|dx\le C||u_{xx}^n\left|\right|\left|\right|{\rho }_x^n\left|\right|\le$$

$$\le {\epsilon }_3\left|\right|u_{xx}^n{\left|\right|}^2+{\displaystyle \frac{C}{{\epsilon }_7}}\left|\right|{\rho }_x^n{\left|\right|}^2\le {\epsilon }_3\left|\right|u_{xx}^n{\left|\right|}^2+C{z}_n\left(t\right),$$

$$|\underset{0}{\overset{1}{\int }}{u}_{xx}^{n}Gdx|\le C\underset{0}{\overset{1}{\int }}|u_{xx}^{n}G|dx\le C||u_{xx}^n\left|\right|\left|\right|G\left(t\right)\left|\right|\le {\epsilon }_4\left(\right||u_{xx}^n{\left(t\right)\left|\right|}^2+{\displaystyle \frac{C}{{\epsilon }_4}}{\left|\right|G\left(t\right)\left|\right|}^2.$$

Thus we obtain the inequality (26).

Let’s add up (24) and (26)

$${\displaystyle \frac{d}{dt}}\left(\right||u^n{\left(t\right)\left|\right|}^2+\left|\right|u_x^n{\left(t\right)\left|\right|}^2)+{\displaystyle \frac{8}{3}}{\nu }_0\left|\right|u_{xx}^n{\left(t\right)\left|\right|}^2+{\displaystyle \frac{8}{3}}{\nu }_0\left|\right|u_x^n\left(t\right){\left|\right|}^2\le$$

$$\le {\displaystyle \sum _{i=1}^4}{\epsilon }_i\left|\right|u_{xx}^n{\left|\right|}^2+C(z_n\left(t\right)+z_n^3\left(t\right)+{\left|\right|G\left(t\right)\left|\right|}^2)$$

and choose ${\epsilon }_1-{\epsilon }_4$ from the condition ${\displaystyle \sum _{i=1}^4}{\epsilon }_i={\displaystyle \frac{8}{3}}{\nu }^0-\beta$ (if ${\nu }^0\le 1$, then assume $\beta ={\nu }^0/2$ and choose ${\epsilon }_1-{\epsilon }_4$ from ${\displaystyle \sum _{i=1}^4}{\epsilon }_i={\displaystyle \frac{8}{3}}{\nu }^0-{\displaystyle \frac{{\nu }^0}{2}}={\displaystyle \frac{13{\nu }^0}{2}}$; if ${\nu }^0>1$, then $\beta =1/2$ and choose ${\epsilon }_1-{\epsilon }_4$ from ${\displaystyle \sum _{i=1}^4}{\epsilon }_i={\displaystyle \frac{8}{3}}{\nu }^0-1/2)$. Then the last inequality can be written in differential form

$${\displaystyle \frac{d{z}_n\left(t\right)}{dt}}\le C(z_n^3\left(t\right)+{\left|\right|G\left(t\right)\left|\right|}^2),$$

(27)

where C is not depend on n. From (27) it follows that it follows that $z_n\left(t\right)$ is uniformly bounded in n for all $t\le t_0$, where

$$t_0<{\displaystyle \frac{1}{C}}(z^n\left(0\right)+C\underset{0}{\overset{T}{\int }}{\left|\right|G\left(\tau \right)\left|\right|}^2{d\tau )}^{-2}.$$

With this choice of $t_0$ it follows from (27) that for all n the following inequality is valid

$$\underset{0\le t\le t_0}{max}\left|\right|u_x^n{\left(t\right)\left|\right|}^2+\underset{0}{\overset{t_0}{\int }}\left|\right|u_{xx}^n{\left|\right|}^{2}dt\le N$$

(28)

within dependent of n constant N.

Now we return to (21). It is easy to receive from inequality (18) as follows

$${\displaystyle \frac{b_0}{1+2^{1/2}{B}_0{N}^{1/2}{t}_0^{3/4}}}\le {\rho }^n(x,t)\le {\displaystyle \frac{B_0}{1-2^{1/2}{B}_0{N}^{1/2}{t}_0^{3/4}}},$$

where N is the constant of (28). If we choose

$$t_0\le min({\left({\displaystyle \frac{1-B_0}{(1+B_0)2^{1/2}{B}_0{N}^{1/2}}}\right)}^{4/3},{\displaystyle \frac{1}{C}}(z^n\left(0\right)+C\underset{0}{\overset{T}{\int }}\left|\right|G\left(\tau \right){\left|\right|}^{2}d\tau {)}^{-2}),$$

then the inequalities (21) and (28) are satisfied for $x\in [0,1]$ and $t\in [0,t_0]$.

Each equation of (16) is multiplied by ${\left(u_i^n\left(t\right)\right)}_t^{\prime }$ and summed over i from 1 to n.

$$\underset{0}{\overset{1}{\int }}{\left(u_t^n\right)}^{2}dx-{\displaystyle \frac{4}{3}}\underset{0}{\overset{1}{\int }}{\left(\mu \left({\rho }^n\right){\rho }^n{u}_x^n\right)}_x{u}_t^{n}dx+\underset{0}{\overset{1}{\int }}{u}_t^n{p}_x\left({\rho }^n\right)dx-\underset{0}{\overset{1}{\int }}{u}_t^{n}Gdx=0.$$

Consider the second term

$${\displaystyle \frac{4}{3}}\underset{0}{\overset{1}{\int }}{\left(\mu \left({\rho }^n\right){\rho }^n{u}_x^n\right)}_x{u}_t^{n}dx={\displaystyle \frac{4}{3}}\underset{0}{\overset{1}{\int }}{\left(\mu \left({\rho }^n\right){\rho }^n{u}_x^n{u}_t^n\right)}_{x}dx-{\displaystyle \frac{4}{3}}\underset{0}{\overset{1}{\int }}\mu \left({\rho }^n\right){\rho }^n{u}_x^n{u}_{tx}^{n}dx.$$

Then we obtain

$$\underset{0}{\overset{1}{\int }}{\left(u_t^n\right)}^{2}dx+{\displaystyle \frac{4}{3}}\underset{0}{\overset{1}{\int }}\mu \left({\rho }^n\right){\rho }^n{u}_x^n{u}_{tx}^{n}dx+\underset{0}{\overset{1}{\int }}{u}_t^n{p}_x\left({\rho }^n\right)dx-\underset{0}{\overset{1}{\int }}{u}_t^{n}Gdx=0.$$

Functions ${\rho }^n,\mu \left({\rho }^n\right)$ are uniformly bounded over n for all ${\rho }^n\in (0,1)$ due to (21). Estimate the last $\left|\right|{\rho }_x^n\left(t\right)\left|\right|\le C(1+(\underset{0}{\overset{t}{\int }}\left|\right|u_{xx}^n{\left|\right|}^{2}d\tau {)}^{{\displaystyle \frac{1}{2}}})$ two assuming

$$|\underset{0}{\overset{1}{\int }}{u}_t^n{p}_x\left({\rho }^n\right)dx|\le \underset{0}{\overset{1}{\int }}|u_t^n{p}_{{\rho }^n}{\rho }_x^n|dx\le C\underset{0}{\overset{1}{\int }}|u_t^n\left|\right|{\rho }_x^n|dx\le$$

$$\le C\left|\right|u_t^n\left(t\right)\left|\right|\left|\right|{\rho }_x^n\left(t\right)\left|\right|\le {\epsilon }_5\left|\right|u_t^n{\left|\right|}^2+{\displaystyle \frac{C}{{\epsilon }_5}}\left|\right|{\rho }_x^n{\left|\right|}^2,$$

$$|\underset{0}{\overset{1}{\int }}{u}_t^{n}Gdx|\le \underset{0}{\overset{1}{\int }}|u_t^n\left|\right|G|dx\le C\left|\right|u_t^n\left(t\right)\left|\right|\left|\right|G\left|\right|\le {\epsilon }_6\left|\right|u_t^n{\left|\right|}^2+{\displaystyle \frac{C}{{\epsilon }_6}}{\left|\right|G\left|\right|}^2.$$

Choosing ${\epsilon }_5+{\epsilon }_6={\displaystyle \frac{1}{3}}$ we obtain the following estimate

$$\underset{0}{\overset{1}{\int }}{\left(u_t^n\right)}^{2}dx+{\nu }_0\underset{0}{\overset{1}{\int }}{\left(u_x^n\right)}_t^{2}dx\le {\displaystyle \frac{C}{{\epsilon }_5}}\left|\right|{\rho }_x^n{\left|\right|}^2+{\displaystyle \frac{C}{{\epsilon }_6}}{\left|\right|G\left|\right|}^2.$$

(29)

Taking into account (21) and (28) we deduce the estimate

$$\underset{0}{\overset{t_0}{\int }}\left|\right|u_t^n{\left|\right|}^{2}dt\le N_2.$$

(30)

From (28) and (30) follows the estimate specified in Lemma 1. Lemma 1 is proven.

The estimate of Lemma 1 and (21) allows us to select a converging sequence from subsequences $\left\{{\rho }^n\right\}$,and $\left\{u^n\right\}$. The passage to the limit in (16) and (17) shows that the limit functions of $\rho$ and u gives a generalized solution on the interval [$0,t_0$]. Theorem 1 is proved. □

4. Local solvability of the non-isothermal problem

It is worthy to note that the presence of $g(x,t)$ in equation (10) does not introduce any fundamental difficulties into further research, if $g(x,t)$ is sufficiently smooth. There fore we restrict to the case of $g=0$ for brevity.

We will search for a local generalized solution as a limit of approximate solutions $({\rho }^n,u^n,T^n)$, where $u^n$ and $T^n$ are expressed as the finite sums:

$$u^n(x,t)={\displaystyle \sum _{i=1}^n}{u}_i^n\left(t\right)sin\left(\pi ix\right),T^n(x,t)={\displaystyle \sum _{j=1}^n}{T}_j^n\left(t\right)cos\left(\pi jx\right),$$

with unknown coefficients $u_i^n\left(t\right)$, $i=1,2,...,n$ and $T_j^n\left(t\right)$, $j=0,1,...,n$. To determine these coefficients we require that (10) and (11) be satisfied approximately:

$$\underset{0}{\overset{1}{\int }}\left[{\displaystyle \frac{\partial u^n}{\partial t}}-{\displaystyle \frac{\partial }{\partial x}}\left({\displaystyle \frac{4}{3}}\mu ({\rho }^n,T^n){\rho }^n{\displaystyle \frac{\partial u^n}{\partial x}}\right)+{\displaystyle \frac{\partial p({\rho }^n,T^n)}{\partial x}}\right]sin\left(\pi ix\right)dx=0;$$

(31)

$$\underset{0}{\overset{1}{\int }}\left[{\displaystyle \frac{\partial T^n}{\partial t}}-{\displaystyle \frac{\partial }{\partial x}}\left(\kappa ({\rho }^n,T^n){\rho }^n{\displaystyle \frac{\partial T^n}{\partial x}}\right)+p({\rho }^n,T^n){\displaystyle \frac{\partial u^n}{\partial x}}+{\displaystyle \frac{1}{{\rho }^n}}I({\rho }^n,T^n)\right]cos\left(\pi ix\right)dx=0.$$

(32)

We will search for ${\rho }^n(x,t)$ as a solution of the problem (17) and it has the form of (18). Another condition of which an interval quantity of $t_0$is chosen associated with the requirement of positivity for ${\rho }^n(x,t)$ and $T^n(x,t)$. The inequalities (14) and (15) are satisfy ${\rho }^0\left(x\right)$ and $T^0\left(x\right)$), respectively. We require the relations (21) be satisfied in (18)and for $T^n(x,t)$ the following relations

$$0<{\displaystyle \frac{b_1}{2}}\le T^n(x,t)\le 2B_1<\infty ,$$

(33)

for all n and for $x\in [0,1],t\in [0,t_0]$. Moreover, the inequality (22) is true.

Unknown coefficients $u_i^n\left(t\right)$ and $T_j^n\left(t\right)$ are found from the Cauchy problem’s solution for the ordinary differential system:

$$\left\{\begin{array}{c}{\displaystyle \frac{d{u}_i^n}{d{t}_n}}={\Phi }_i^n(u_1^n,...,u_n^n;T_0^n,T_1^n,...,T_n^n,{\rho }^n),\hfill \\ {\displaystyle \frac{d{T}_j^n}{d{t}_n}}={\lambda }_j{\Psi }_j^n(u_1^n,...,u_n^n;T_0^n,T_1^n,...,T_n^n,{\rho }^n),\hfill \end{array}\right.$$

(34)

where ${\lambda }_0=1$, ${\lambda }_j=2$, $j=1,2,\dots n$,

$${\Phi }_i^n=2\underset{0}{\overset{1}{\int }}\left({\displaystyle \frac{\partial }{\partial x}}\left({\displaystyle \frac{4}{3}}\mu ({\rho }^n,T^n){\rho }^n{\displaystyle \frac{\partial u^n}{\partial x}}\right)-{\displaystyle \frac{\partial p({\rho }^n,T^n)}{\partial x}}\right)sin\left(\pi ix\right)dx,$$

$${\Psi }_j^n=\underset{0}{\overset{1}{\int }}\left({\displaystyle \frac{\partial }{\partial x}}\left(\kappa ({\rho }^n,T^n){\rho }^n{\displaystyle \frac{\partial T^n}{\partial x}}\right)-p({\rho }^n,T^n){\displaystyle \frac{\partial u^n}{\partial x}}-{\displaystyle \frac{1}{{\rho }^n}}I({\rho }^n,T^n)\right)cos\left(\pi jx\right)dx,$$

and $u^n(x,t)={\displaystyle {\sum }_{i=1}^n}{u}_i^n\left(t\right)sin\left(\pi ix\right),T^n(x,t)={\displaystyle {\sum }_{j=1}^n}{T}_j^n\left(t\right)cos\left(\pi jx\right)$, ${\rho }^n$ are determined from (18). Initial conditions for (34) we will find from sine and cosine expansions in the Fourier series of the initial functions $u^0\left(x\right)$ and $T^0\left(x\right)$, respectively:

$$u_i^n\left(0\right)=u_i^0\equiv 2\underset{0}{\overset{1}{\int }}{u}^0\left(x\right)sin\left(\pi ix\right)dx,i=1,...,n;$$

$$T_j^n\left(0\right)=T_j^0\equiv 2\underset{0}{\overset{1}{\int }}{T}^0\left(x\right)cos\left(\pi jx\right)dx,j=1,...,n,T_0^n\left(0\right)=\underset{0}{\overset{1}{\int }}{T}^0\left(x\right)dx.$$

The local solvability of (34) follows from Cauchy - Picard theorem for each fixed n for ordinary differential systems. Now we will indicate such a value $t_0$ for which the problem given is solvable for each n on $[0,t_0]$. It is enough to obtain uniform estimates in n for $u_i^n$ and $T_j^n$. Let

$$I=\left\{\begin{array}{c}I,T>0\hfill \\ 0,T<0\hfill \end{array}\right.and\kappa =\left\{\begin{array}{c}\kappa ,T>0\hfill \\ 0,T<0.\hfill \end{array}\right.$$

Each equation of (31) we multiply by $u_i^n\left(t\right)$, sum over i from 1 to n and integrate over x from 0 to 1. We obtain the following expression

$$\underset{0}{\overset{1}{\int }}(u^n{u}_t^n-{\displaystyle \frac{4}{3}}{\left(\mu ({\rho }^n,T^n){\rho }^n{u}_x^n\right)}_x{u}^n+u^n{p}_x({\rho }^n,T^n))dx=0.$$

Then we add this to equation (32) with $j=0$

$$\underset{0}{\overset{1}{\int }}(T_t^n-{\left(\kappa ({\rho }^n,T^n){\rho }^n{T}_x^n\right)}_x+p({\rho }^n,T^n)u_x^n+{\displaystyle \frac{1}{{\rho }^n}}I({\rho }^n,T^n))dx=0,$$

and obtain

$$\underset{0}{\overset{1}{\int }}(u^n{u}_t^n-{\displaystyle \frac{4}{3}}{\left(\mu ({\rho }^n,T^n){\rho }^n{u}_x^n\right)}_x{u}^n+u^n{p}_x({\rho }^n,T^n)+T_t^n-$$

$$-{\left(\kappa ({\rho }^n,T^n){\rho }^n{T}_x^n\right)}_x+p({\rho }^n,T^n)u_x^n+{\displaystyle \frac{1}{{\rho }^n}}I({\rho }^n,T^n))dx=0.$$

Rewrite the last equation accounting ${\left(u^n\right)}_t^2=2u^n{u}_t^n$, ${\left({\mu }^n{\rho }^n{u}^n{u}_x^n\right)}_x={\left({\mu }^n{\rho }^n{u}_x^n\right)}_x{u}^n++{\mu }^n{\rho }^n{\left(u_x^n\right)}^2$, $u^n{p}_x({\rho }^n,T^n)+p({\rho }^n,T^n)u_x^n={\left(p({\rho }^n,T^n)u^n\right)}_x$

$$\underset{0}{\overset{1}{\int }}\left({\displaystyle \frac{1}{2}}{\left(u^n\right)}_t^2+T_t^n+{\displaystyle \frac{4}{3}}\left(\mu ({\rho }^n,T^n){\rho }^n{\left(u_x^n\right)}^2\right)+{\displaystyle \frac{1}{{\rho }^n}}I({\rho }^n,T^n)\right)dx=0.$$

Integrate the last equation over t and we will get

$$\underset{0}{\overset{1}{\int }}\left({\displaystyle \frac{1}{2}}{\left(u^n\right)}^2+T^n\right)dx+\underset{0}{\overset{t}{\int }}\underset{0}{\overset{1}{\int }}\left({\displaystyle \frac{4}{3}}\left(\mu ({\rho }^n,T^n){\rho }^n{\left(u_x^n\right)}^2\right)+{\displaystyle \frac{1}{{\rho }^n}}I({\rho }^n,T^n)\right)dxd\tau =$$

$$=\underset{0}{\overset{1}{\int }}\left({\displaystyle \frac{1}{2}}{\left(u^0\left(x\right)\right)}^2+T^0\left(x\right)\right)dx$$

Thus, the following estimate has the form

$${\displaystyle \frac{1}{2}}\Vert u^n{\Vert }_{2,\Omega }^2+\Vert T^n{\Vert }_{1,\Omega }\le {\displaystyle \frac{1}{2}}\Vert u^0{\left(x\right)\Vert }_{2,\Omega }^2+{\Vert T^0\left(x\right)\Vert }_{1,\Omega }\equiv N_3.$$

(35)

Lemma 2. 

There is a value $t_0>0$ exists, such that for all n on interval $[0,t_0]$ the following estimates are satisfy the solutions $u^n$ and $T^n$ of problem (34)

$$0<{\displaystyle \frac{b_0}{2}}\le {\rho }^n(x,t)\le {\displaystyle \frac{B_0+1}{2}}<1,x\in [0,1],t\in [0,t_0],$$

$$\underset{0\le t<t_0}{max}\left|\right|u_x^n\left(t\right){\left|\right|}^2+\underset{0}{\overset{t_0}{\int }}\left(\left|\right|u_{xx}^n{\left|\right|}^2+{\Vert u_t^n\Vert }^2\right)dt\le N_4,$$

(36)

$$\underset{0\le t\le t_0}{max}\left|\right|T_x^n\left(t\right){\left|\right|}^2+\underset{0}{\overset{t_0}{\int }}\left(\left|\right|T_{xx}^n{\left|\right|}^2+{\Vert T_t^n\Vert }^2\right)dt\le N_5.$$

(37)

Proof. 

We assume

$$z_n\left(t\right)=\left|\right|u^n{\left(t\right)\left|\right|}^2+\left|\right|T^n{\left(t\right)\left|\right|}^2+\left|\right|u_x^n{\left(t\right)\left|\right|}^2+\left|\right|T_x^n{\left|\right|}^2+\gamma \underset{0}{\overset{t}{\int }}\left(\right||u_{xx}^n{\left(\tau \right)\left|\right|}^2+\left|\right|T_{xx}^n\left(\tau \right){\left|\right|}^{2}d\tau ,$$

where the real parameter $\gamma \in (0,1)$ will be indicated later. Each equation of (31) we multiply by $u_i^n\left(t\right)$, sum over i from 1 to n and integrate over x from 0 to 1. Then we obtain as follows:

$${\displaystyle \frac{1}{2}}{\displaystyle \frac{d}{dt}}\underset{0}{\overset{1}{\int }}{\left(u^n\right)}^{2}dx+{\displaystyle \frac{4}{3}}\underset{0}{\overset{1}{\int }}\left({\rho }^n{\left(u_x^n\right)}^2\mu ({\rho }^n,T^n)\right)dx=-\underset{0}{\overset{1}{\int }}\left(u^n{\displaystyle \frac{\partial p({\rho }^n,T^n)}{\partial x}}\right)dx.$$

(38)

We will show that and estimate follows from (38)

$${\displaystyle \frac{d}{dt}}\left|\right|u^n{\left(t\right)\left|\right|}^2+{\displaystyle \frac{8}{3}}{\nu }_0\left|\right|u_x^n{\left|\right|}^2\le C\left(z_n\left(t\right)+z_n^2\left(t\right)\right).$$

(39)

The right part of (38) we will present in the form of functions $p_{{\rho }^n},p_{T^n}$, which are uniformly bounded over n due to (21) for all ${\rho }^n\in (0,1)$, and accounting $\left|\right|{\rho }_x^n\left(t\right)\left|\right|\le C(1+(\underset{0}{\overset{t}{\int }}\left|\right|u_{xx}^n{\left|\right|}^{2}d\tau {)}^{{\displaystyle \frac{1}{2}}})$

$$|\underset{0}{\overset{1}{\int }}{u}^n{\displaystyle \frac{\partial p({\rho }^n,T^n)}{\partial x}}dx|\le \mid \underset{0}{\overset{1}{\int }}{u}^n{p}_{{\rho }^n}{\rho }_x^{n}dx\mid +\mid \underset{0}{\overset{1}{\int }}{u}^n{p}_{T^n}{T}_x^{n}dx\mid =A_1+A_2.$$

$$A_1\le C\underset{0}{\overset{1}{\int }}\mid {\rho }_x^n{u}^n\mid dx\le C\Vert {\rho }_x^n\Vert \Vert u^n\Vert \le {\epsilon }_7\Vert u^n{\Vert }^2+{\displaystyle \frac{C}{{\epsilon }_7}}{\Vert {\rho }_x^n\Vert }^2,$$

$$A_2\le C\underset{0}{\overset{1}{\int }}\mid T_x^n{u}^n\mid dx\le C\Vert T_x^n\Vert \Vert u^n\Vert \le {\epsilon }_8\Vert T_x^n{\Vert }^2+{\displaystyle \frac{C}{{\epsilon }_8}}{\Vert u^n\Vert }^2.$$

Here and further, C is a positive constant, which does not depend on n. We derive the equality (39), since $\mu \left({\rho }^n\right){\rho }_n\ge {\nu }_0\equiv k_0^{-1}{\left({\displaystyle \frac{b_0}{2}}\right)}^{q_{19}+1}{\left({\displaystyle \frac{1-B_0}{2}}\right)}^{q_{20}}{\left(1-{\displaystyle \frac{a(1+B_0)}{2}}\right)}^{q_{21}}{\left({\displaystyle \frac{b_1}{2}}\right)}^{q_{22}}$.

Each equation of (31) is multiplied by ${\left(i\pi \right)}^2{u}_i^n\left(t\right)$, summed over i from 1 to n and integrated over x from 0 to 1. Taking into account this expression ${\displaystyle {\sum }_{i=1}^n}{u}_i^n{\left(i\pi \right)}^{2}sin\left(i\pi x\right)=-u_{xx}^n$ we obtain

$${\displaystyle \frac{1}{2}}{\displaystyle \frac{d}{dt}}\underset{0}{\overset{1}{\int }}{\left(u_x^n\right)}^{2}dx+{\displaystyle \frac{4}{3}}\underset{0}{\overset{1}{\int }}\mu ({\rho }^n,T^n){\rho }^n{\left(u_{xx}^n\right)}^{2}dx=-{\displaystyle \frac{4}{3}}\underset{0}{\overset{1}{\int }}{u}_{xx}^n{\left(\mu ({\rho }^n,T^n)\right)}_x^{\prime }{\rho }^n{u}_x^{n}dx-$$

$$-{\displaystyle \frac{4}{3}}\underset{0}{\overset{1}{\int }}{u}_{xx}^n\mu ({\rho }^n,T^n){\rho }_x^n{u}_x^{n}dx+\underset{0}{\overset{1}{\int }}{u}_{xx}^n{\displaystyle \frac{\partial p({\rho }^n,T^n)}{\partial x}}dx.$$

(40)

We will show that from (40) the estimate follows

$${\displaystyle \frac{d}{dt}}\left|\right|u_x^n{\left|\right|}^2+{\displaystyle \frac{8}{3}}{\nu }_0\left|\right|u_{xx}^n{\left|\right|}^2\le {\displaystyle \sum _{i=9}^{13}}{\epsilon }_i\left|\right|u_{xx}^n{\left|\right|}^2+C(z_n\left(t\right)+z_n^3\left(t\right)).$$

(41)

Functions ${\rho }^n{\mu }_{{\rho }^n};{\rho }^n{\mu }_{T^n};\mu ({\rho }^n,T^n);p_{T^n};p_{{\rho }^n}$ are uniformly bounded over n due to (21) for all ${\rho }^n\in (0,1)$. The first term of the right part of (40) we estimate as follows

$$\mid \underset{0}{\overset{1}{\int }}{u}_{xx}^n{\left(\mu ({\rho }^n,T^n)\right)}_x^{\prime }{\rho }^n{u}_x^{n}dx\mid =\mid \underset{0}{\overset{1}{\int }}({\mu }_{{\rho }^n}{\rho }_x^n+{\mu }_{T^n}{T}_x^n){\rho }^n{u}_x^n{u}_{xx}^{n}dx\mid \le$$

$$\le \mid \underset{0}{\overset{1}{\int }}{\mu }_{{\rho }^n}{\rho }_x^n{\rho }^n{u}_x^n{u}_{xx}^{n}dx\mid +\mid \underset{0}{\overset{1}{\int }}{\mu }_{T^n}{T}_x^n{\rho }^n{u}_x^n{u}_{xx}^{n}dx\mid =A_3+A_4,$$

$$A_3=C\underset{0}{\overset{1}{\int }}\mid {\rho }_x^n{u}_x^n{u}_{xx}^n\mid dx\le C\underset{0\le x\le 1}{max}|u_x^n(x,t)|\underset{0}{\overset{1}{\int }}|u_{xx}^n\left|\right|{\rho }_x^n|dx\le$$

$$\le {\epsilon }_9\Vert u_{xx}^n{\Vert }^2+{\displaystyle \frac{C}{{\epsilon }_9}}(\Vert u_x^n{\Vert }^6+\Vert {\rho }_x^n{\Vert }^6)\le {\epsilon }_9{\Vert u_{xx}^n\Vert }^2+{\displaystyle \frac{C}{{\epsilon }_9}}{z}_n^3\left(t\right),$$

$$A_4=C\underset{0}{\overset{1}{\int }}\mid T_x^n{u}_x^n{u}_{xx}^n\mid dx\le {\epsilon }_{10}\Vert u_{xx}^n{\Vert }^2+{\displaystyle \frac{C}{{\epsilon }_{10}}}(\Vert u_x^n{\Vert }^6+\Vert T_x^n{\Vert }^6)\le {\epsilon }_{10}{\Vert u_{xx}^n\Vert }^2+{\displaystyle \frac{C}{{\epsilon }_{10}}}{z}_n^3\left(t\right).$$

The second term of the right part of (40) we estimate analogically to $A_3$

$$\mid \underset{0}{\overset{1}{\int }}{u}_{xx}^n\mu ({\rho }^n,T^n){\rho }_x^n{u}_x^{n}dx\mid \le {\epsilon }_{11}\Vert u_{xx}^n{\Vert }^2+{\displaystyle \frac{C}{{\epsilon }_{11}}}(\Vert u_x^n{\Vert }^6+\Vert {\rho }_x^n{\Vert }^6)\le {\epsilon }_{11}{\Vert u_{xx}^n\Vert }^2+{\displaystyle \frac{C}{{\epsilon }_{11}}}{z}_n^3\left(t\right).$$

The last term of the right part of (40) we represent as

$$\underset{0}{\overset{1}{\int }}{u}_{xx}^n{\displaystyle \frac{\partial p({\rho }^n,T^n)}{\partial x}}=\underset{0}{\overset{1}{\int }}{u}_{xx}^n\left(p_{{\rho }^n}{\rho }_x^n+p_{T^n}{T}_x^n\right)dx=\underset{0}{\overset{1}{\int }}{u}_{xx}^n{p}_{{\rho }^n}{\rho }_x^{n}dx+\underset{0}{\overset{1}{\int }}{u}_{xx}^n{p}_{T^n}{T}_x^{n}dx=A_5+A_6,$$

$$A_5\le C\underset{0}{\overset{1}{\int }}\mid u_{xx}^n{\rho }_x^n\mid dx\le {\epsilon }_{12}\Vert u_{xx}^n{\Vert }^2+{\displaystyle \frac{C}{{\epsilon }_{12}}}\Vert {\rho }_x^n{\Vert }^2\le {\epsilon }_{12}{\Vert u_{xx}^n\Vert }^2+{\displaystyle \frac{C}{{\epsilon }_{12}}}{z}_n\left(t\right),$$

$$A_6\le C\underset{0}{\overset{1}{\int }}\mid u_{xx}^n{T}_x^n\mid dx\le {\epsilon }_{13}\Vert u_{xx}^n{\Vert }^2+{\displaystyle \frac{C}{{\epsilon }_{13}}}\Vert T_x^n{\Vert }^2\le {\epsilon }_{13}{\Vert u_{xx}^n\Vert }^2+{\displaystyle \frac{C}{{\epsilon }_{13}}}{z}_n\left(t\right).$$

Therefore, we obtain (41).

Now we establish the necessary estimates for $T^n(x,t)$. Each equation of (32) is multiplied by $T_j^n\left(t\right)$ and summed over j from 0 to n. We obtain the following equation

$${\displaystyle \frac{1}{2}}{\displaystyle \frac{d}{dt}}\underset{0}{\overset{1}{\int }}{\left(T^n\right)}^{2}dx+\underset{0}{\overset{1}{\int }}\kappa ({\rho }^n,T^n){\rho }^n{\left(T_x^n\right)}^{2}dx=-\underset{0}{\overset{1}{\int }}{T}^{n}p({\rho }^n,T^n){\displaystyle \frac{\partial u^n}{\partial x}}dx-\underset{0}{\overset{1}{\int }}{T}^n{\displaystyle \frac{1}{{\rho }^n}}I({\rho }^n,T^n)dx.$$

(42)

We show that the following estimate comes from (42)

$${\displaystyle \frac{d}{dt}}\left|\right|T^n{\left|\right|}^2+2{\nu }_0\left|\right|T_x^n{\left|\right|}^2\le C\left(z_n\left(t\right)\right).$$

(43)

Functions $p({\rho }^n,T^n);{\displaystyle \frac{1}{{\rho }^n}}I({\rho }^n,T^n)$ are uniformly bounded over n due to (21) for all ${\rho }^n\in (0,1)$. Estimate each term of the right part

$$\underset{0}{\overset{1}{\int }}{T}^{n}p({\rho }^n,T^n){\displaystyle \frac{\partial u^n}{\partial x}}dx\le C\underset{0}{\overset{1}{\int }}\left|T^n{\displaystyle \frac{\partial u^n}{\partial x}}\right|dx\le C\left(\Vert T^n{\Vert }^2+{\Vert {\displaystyle \frac{\partial u^n}{\partial x}}\Vert }^2\right)\le C{z}_n\left(t\right)$$

$$\underset{0}{\overset{1}{\int }}{\displaystyle \frac{1}{{\rho }^n}}{T}^n{I}^{n}dx\le C\underset{0}{\overset{1}{\int }}|T^n|dx\le C\Vert T^n{\Vert }^2\le C{z}_n\left(t\right).$$

Because $\kappa ({\rho }^n,T^n){\rho }^n\ge {\nu }_0\equiv k_0^{-1}{\left({\displaystyle \frac{b_0}{2}}\right)}^{q_{19}+1}{\left({\displaystyle \frac{1-B_0}{2}}\right)}^{q_{20}}{\left(1-{\displaystyle \frac{a(1+B_0)}{2}}\right)}^{q_{21}}{\left({\displaystyle \frac{b_1}{2}}\right)}^{q_{22}},$ so we get to the (43).

Then, each equation of (32) is multiplied by ${\left({\pi }_j\right)}^2{T}_j^n\left(t\right)$ and summed it over j from 0 to n. Considering the equation ${\displaystyle {\sum }_{j=1}^n}{\left({\pi }_j\right)}^2{T}_j^n\left(t\right)cos\left({\pi }_{j}x\right)=-T_{xx}^2$, we obtain

$${\displaystyle \frac{1}{2}}{\displaystyle \frac{d}{dt}}\underset{0}{\overset{1}{\int }}{\left(T_x^n\right)}^{2}dx+\underset{0}{\overset{1}{\int }}\kappa ({\rho }^n,T^n){\rho }^n{\left(T_{xx}^n\right)}^{2}dx=-\underset{0}{\overset{1}{\int }}{T}_{xx}^n{\kappa }_x({\rho }^n,T^n){\rho }^n{T}_x^{n}dx-$$

$$-\underset{0}{\overset{1}{\int }}{T}_{xx}^n\kappa ({\rho }^n,T^n){\rho }_x^n{T}_x^{n}dx+\underset{0}{\overset{1}{\int }}{T}_{xx}^{n}p({\rho }^n,T^n){\displaystyle \frac{\partial u^n}{\partial x}}dx+\underset{0}{\overset{1}{\int }}{T}_{xx}^n{\displaystyle \frac{1}{{\rho }^n}}I({\rho }^n,T^n)dx.$$

(44)

Since the functions ${\left(\kappa ({\rho }^n,T^n)\right)}_{{\rho }^n}^{\prime }·{\rho }^n;{\left(\kappa ({\rho }^n,T^n)\right)}_{T^n}^{\prime }·{\rho }^n;\kappa ({\rho }^n,T^n);p({\rho }^n,T^n){\displaystyle \frac{1}{{\rho }^n}}I({\rho }^n,T^n)$ are uniformly bounded over n for all ${\rho }^n\in (0,1)$, we estimate the terms on the right side of (44) considering the inequalities of (21) and Cauchy $\forall {\epsilon }_i>0$, $i=14-18$. The first term of (44) is represented as

$$\underset{0}{\overset{1}{\int }}{T}_{xx}^n{\kappa }_x({\rho }^n,T^n){\rho }^n{T}_x^{n}dx=\underset{0}{\overset{1}{\int }}{T}_{xx}^n{\rho }^n{T}_x^n\left({\left(\kappa \right)}_{{\rho }^n}^{\prime }·{\rho }_x^n+{\left(\kappa \right)}_{T^n}^{\prime }·T_x^n\right)dx=$$

$$=\underset{0}{\overset{1}{\int }}{T}_{xx}^n{\rho }^n{T}_x^n{\left(\kappa \right)}_{{\rho }^n}^{\prime }{\rho }_x^{n}dx+\underset{0}{\overset{1}{\int }}{T}_{xx}^n{\rho }^n{\left(T_x^n\right)}^2{\left(\kappa \right)}_{T^n}^{\prime }dx=A_7+A_8.$$

$$A_7=\underset{0}{\overset{1}{\int }}{T}_{xx}^n{\rho }^n{T}_x^n{\left(\kappa \right)}_{{\rho }^n}^{\prime }{\rho }_x^{n}dx\le C\underset{0}{\overset{1}{\int }}|T_{xx}^n\left|\right|{\rho }_x^n\left|\right|T_x^n|dx\le C\underset{0\le x\le 1}{max}|T_x^n(x,t)|\underset{0}{\overset{1}{\int }}|T_{xx}^n\left|\right|{\rho }_x^n|dx\le$$

$$\le C\left|\right|T_x{\left|\right|}^{1/2}\left|\right|T_{xx}^n{\left|\right|}^{3/2}\left|\right|{\rho }_x^n\left|\right|\le {\epsilon }_{14}\left|\right|T_{xx}^n{\left|\right|}^2+{\displaystyle \frac{C}{{\epsilon }_{14}}}\left(\left|\right|T_x^n{\left|\right|}^2\left|\right|{\rho }_x^n{\left|\right|}^4\right)\le$$

$$\le {\epsilon }_{14}\left|\right|T_x^n{\left|\right|}^2+{\displaystyle \frac{C}{{\epsilon }_{14}}}\left(\left|\right|T_x^n{\left|\right|}^6+\left|\right|{\rho }_x^n{\left|\right|}^6\right)\le {\epsilon }_{14}\left|\right|T_x^n{\left|\right|}^2{\displaystyle \frac{C}{{\epsilon }_{14}}}{z}_n^3\left(t\right).$$

The following estimate for $A_8$ is true:

$$A_8=\underset{0}{\overset{1}{\int }}{T}_{xx}^n{\rho }^n{\left(T_x\right)}^2{\left(\kappa \right)}_{T^n}^{\prime }dx\le C\underset{0}{\overset{1}{\int }}|T_{xx}^n\left|\right|T_x^n{|}^{2}dx\le C\underset{0\le x\le 1}{max}|T_x^n|\underset{0}{\overset{1}{\int }}|T_{xx}^n\left|\right|T_x^n|dx\le$$

$$\le C\left|\right|T_{xx}^n{\left|\right|}^{3/2}\left|\right|T_x^n{\left|\right|}^{3/2}\le {\epsilon }_{15}\left|\right|T_{xx}^n{\left|\right|}^2+{\displaystyle \frac{C}{{\epsilon }_{15}}}\left|\right|T_x^n{\left|\right|}^6\le {\epsilon }_{15}\left|\right|T_{xx}^n{\left|\right|}^2+{\displaystyle \frac{C}{{\epsilon }_{15}}}{z}_n^3\left(t\right).$$

The rest term of the right side of (44) are estimated as follows:

$$\underset{0}{\overset{1}{\int }}{T}_{xx}^n\kappa ({\rho }^n,T^n){\rho }_x^n{T}_x^{n}dx\le C\underset{0}{\overset{1}{\int }}|T_{xx}^n\left|\right|{\rho }_x^n\left|\right|T_x^n|dx\le {\epsilon }_{16}\left|\right|T_{xx}^n{\left|\right|}^2+{\displaystyle \frac{C}{{\epsilon }_{16}}}{z}_n^3\left(t\right),$$

$$\underset{0}{\overset{1}{\int }}{T}_{xx}^{n}p({\rho }^n,T^n){\displaystyle \frac{\partial u^n}{\partial x}}dx\le C\underset{0}{\overset{1}{\int }}|T_{xx}^n\left|\right|{\displaystyle \frac{\partial u^n}{\partial x}}|dx\le C||T_{xx}^n\left|\right|\left|\right|u_x^n\left|\right|\le$$

$$\le {\epsilon }_{17}\left|\right|T_{xx}^n{\left|\right|}^2+{\displaystyle \frac{C}{{\epsilon }_{17}}}\left|\right|u_x^n{\left|\right|}^2\le {\epsilon }_{17}\left|\right|T_{xx}^n{\left|\right|}^2+{\displaystyle \frac{C}{{\epsilon }_{17}}}{z}_n\left(t\right),$$

$$\underset{0}{\overset{1}{\int }}{T}_{xx}^n{\displaystyle \frac{1}{{\rho }^n}}I({\rho }^n,T^n)dx\le C\underset{0}{\overset{1}{\int }}|T_{xx}^n|dx\le {\epsilon }_{18}\left|\right|T_{xx}^n{\left|\right|}^2.$$

We obtain this inequality

$${\displaystyle \frac{d}{dt}}\left|\right|T_x^n{\left|\right|}^2+2{\nu }_0\left|\right|T_{xx}^n{\left|\right|}^2\le {\displaystyle \sum _{i=14}^{18}}{\epsilon }_i\left|\right|T_{xx}^n{\left|\right|}^2+C(z_n\left(t\right)+z_n{\left(t\right)}^3).$$

(45)

Summing inequalities (39), (41), (43), (45) we get

$$\begin{array}{c}\hfill {\displaystyle \frac{d}{dt}}\left(\left|\right|u^n{\left(t\right)\left|\right|}^2+\left|\right|u_x^n{\left(t\right)\left|\right|}^2+\left|\right|T^n{\left(t\right)\left|\right|}^2+\left|\right|T_x^n\left(t\right){\left|\right|}^2\right)+{\displaystyle \frac{8}{3}}{\nu }_0\left|\right|u_x^n{\left|\right|}^2+{\displaystyle \frac{8}{3}}{\nu }_0\left|\right|u_{xx}^n{\left|\right|}^2+\\ \hfill +2{\nu }_0\left|\right|T_x^n{\left|\right|}^2+2{\nu }_0\left|\right|T_{xx}^n{\left|\right|}^2\le {\displaystyle \sum _{i=9}^{13}}{\epsilon }_i\left|\right|u_{xx}^n{\left|\right|}^2+{\displaystyle \sum _{i=14}^{18}}{\epsilon }_i\left|\right|T_{xx}^n{\left|\right|}^2+C(z_n\left(t\right)+z_n^3\left(t\right)),\end{array}$$

(46)

and choose ${\displaystyle \sum _{i=9}^{13}}{\epsilon }_i={\displaystyle \frac{8}{3}}{\nu }^0-\gamma$, (if ${\nu }^0\le 1$, then assume $\gamma ={\nu }^0/2$ and choose ${\displaystyle \sum _{i=9}^{13}}{\epsilon }_i$ from ${\displaystyle \sum _{i=1}^4}{\epsilon }_i={\displaystyle \frac{8}{3}}{\nu }^0-{\displaystyle \frac{{\nu }^0}{2}}={\displaystyle \frac{13{\nu }^0}{6}}$; if ${\nu }^0>1$, then $\gamma =1/2$ and choose ${\displaystyle \sum _{i=9}^{13}}{\epsilon }_i$ from ${\displaystyle \sum _{i=1}^4}{\epsilon }_i={\displaystyle \frac{8}{3}}{\nu }^0-1/2)$, and ${\displaystyle \sum _{i=14}^{18}}{\epsilon }_i=2{\nu }^0-\gamma$, (if ${\nu }^0\le 1$, then we assume that$\gamma ={\nu }^0/2$ and ${\displaystyle \sum _{i=9}^{13}}{\epsilon }_i$ choose from the condition ${\displaystyle \sum _{i=1}^4}{\epsilon }_i=2{\nu }^0-{\displaystyle \frac{{\nu }^0}{2}}={\displaystyle \frac{3{\nu }^0}{2}}$; if ${\nu }^0>1$, then assume $\gamma =1/2$ and ${\displaystyle \sum _{i=9}^{13}}{\epsilon }_i$ choose from the condition ${\displaystyle \sum _{i=1}^4}{\epsilon }_i=2{\nu }^0-1/2)$. The ratio (46) may be represented as differential inequality

$${\displaystyle \frac{d{z}_n\left(t\right)}{dt}}\le C{z}_n^3\left(t\right),$$

(47)

where C constant doesn’t depend on n. The uniform bounded ness $z_n\left(t\right)$ over n follows of (47) for all $t\le t_0$, where

$$t_0<{\displaystyle \frac{1}{C{z}_n^2\left(0\right)}}$$

The choice of $t_0$ satisfies the inequality for any n, as it follows from (47)

$$\underset{0\le t<t_0}{max}\left|\right|u_x^n{\left(t\right)\left|\right|}^2+\underset{0\le t<t_0}{max}\left|\right|T_x^n\left(t\right){\left|\right|}^2+\underset{0}{\overset{t_0}{\int }}\underset{0}{\overset{1}{\int }}\left(\left|\right|u_{xx}^n{\left|\right|}^2+\left|\right|T_{xx}^n{\left|\right|}^2\right)dxdt\le N_6,$$

(48)

with constant $N_6$ which is independent of n. Multiply the equation (31) by ${\left(u_i^n\left(t\right)\right)}_t^{\prime }$, sum over i from 1 to n and integrate over x from 0 to 1. The following equation we get:

$$\underset{0}{\overset{1}{\int }}\left({\left(u_t^n\right)}^2-{\displaystyle \frac{4}{3}}{\left(\mu ({\rho }^n,T^n){\rho }^n{u}_x^n\right)}_x{u}_t^n+u_t^n{p}_x({\rho }^n,T^n)\right)dx=0.$$

(49)

Consider the second term

$${\displaystyle \frac{4}{3}}{\left(\mu ({\rho }^n,T^n){\rho }^n{u}_x^n\right)}_x{u}_t^n={\displaystyle \frac{4}{3}}{\left(\mu ({\rho }^n,T^n){\rho }^n{u}_x^n{u}_t^n\right)}_x-{\displaystyle \frac{4}{3}}\mu ({\rho }^n,T^n){\rho }^n{u}_x^n{u}_{tx}^n=$$

$$={\displaystyle \frac{4}{3}}{\left(\mu ({\rho }^n,T^n){\rho }^n{u}_x^n{u}_t^n\right)}_x-{\displaystyle \frac{2}{3}}\mu ({\rho }^n,T^n){\rho }^n{\left(u_x^n\right)}_t^2.$$

Then (49) represents as

$$\underset{0}{\overset{1}{\int }}{\left(u_t^n\right)}^{2}dx+{\displaystyle \frac{2}{3}}\underset{0}{\overset{1}{\int }}\mu ({\rho }^n,T^n){\rho }^n{\left(u_x^n\right)}_t^{2}dx+\underset{0}{\overset{1}{\int }}{u}_t^n(p_{{\rho }^n}({\rho }^n,T^n){\rho }_x^n+p_{T^n}({\rho }^n,T^n)T_x^n)dx=0.$$

Since the functions $p_{{\rho }^n}({\rho }^n,T^n),p_{T^n}({\rho }^n,T^n)$ are uniformly bounded over n for all ${\rho }^n\in (0,1)$ due to (21), we estimate the third term of the last equation.

$$\mid \underset{0}{\overset{1}{\int }}{u}_t^n{p}_{{\rho }^n}({\rho }^n,T^n){\rho }_x^{n}dx\mid \le C\underset{0}{\overset{1}{\int }}\mid {\rho }_x^n{u}_t^n\mid dx\le {\epsilon }_{19}\Vert u_t^n{\Vert }^2+{\displaystyle \frac{C}{{\epsilon }_{19}}}{\Vert {\rho }_x^n\Vert }^2,$$

$$\mid \underset{0}{\overset{1}{\int }}{u}_t^n{p}_{T^n}({\rho }^n,T^n)T_x^{n}dx\mid \le C\underset{0}{\overset{1}{\int }}\mid u_t^n{T}_x^n\mid dx\le {\epsilon }_{20}\Vert u_t^n{\Vert }^2+{\displaystyle \frac{C}{{\epsilon }_{20}}}{\Vert T_x^n\Vert }^2.$$

We obtain this

$$\underset{0}{\overset{1}{\int }}{\left(u_t^n\right)}^{2}dx+{\displaystyle \frac{2}{3}}{\nu }_0\underset{0}{\overset{1}{\int }}\mu ({\rho }^n,T^n){\rho }^n{\left(u_x^n\right)}_t^{2}dx\le {\displaystyle \sum _{i=19}^{20}}{\epsilon }_i\Vert u_t^n{\Vert }^2+{\displaystyle \frac{C}{{\epsilon }_{19}}}\Vert {\rho }_x^n{\Vert }^2+{\displaystyle \frac{C}{{\epsilon }_{20}}}{\Vert T_x^n\Vert }^2,$$

choosing ${\displaystyle \sum _{i=19}^{20}}{\epsilon }_i=1/3$ and by virtue of the estimate (48) we have

$${\displaystyle \frac{2}{3}}\underset{0}{\overset{1}{\int }}{\left(u_t^n\right)}^{2}dx+{\displaystyle \frac{2}{3}}{\nu }_0\underset{0}{\overset{1}{\int }}{\left(u_x^n\right)}_t^{2}dx\le ({\displaystyle \frac{C}{{\epsilon }_{19}}}\Vert {\rho }_x^n{\Vert }^2+{\displaystyle \frac{C}{{\epsilon }_{20}}}\Vert T_x^n{\Vert }^2)\le ({\displaystyle \frac{C}{{\epsilon }_{19}}}+{\displaystyle \frac{C}{{\epsilon }_{20}}})N_6\equiv N_7.$$

Integrate over t the last inequality

$$\underset{0}{\overset{t_0}{\int }}{\Vert u_t^n\Vert }^{2}dt\le N_8$$

(50)

Summing (48) and (50) we obtain the estimate (36)

$$\underset{0\le t<t_0}{max}\left|\right|u_x^n\left(t\right){\left|\right|}^2+\underset{0}{\overset{t_0}{\int }}\left(\left|\right|u_{xx}^n{\left|\right|}^2+{\Vert u_t^n\Vert }^2\right)dt\le N_4.$$

Now we multiply the equation (32) by ${\left(T_j^n\left(t\right)\right)}_t^{\prime }$, sum it over j from 0 to n and integrate over x from 0 to 1. The following equality we get

$$\underset{0}{\overset{1}{\int }}{\left(T_t^n\right)}^{2}dx+{\displaystyle \frac{{\nu }_0}{2}}\underset{0}{\overset{1}{\int }}{\left({\left(T_x^n\right)}^2\right)}_{t}dx+\underset{0}{\overset{1}{\int }}p({\rho }^n,T^n)T_t^n{u}_x^{n}dx+\underset{0}{\overset{1}{\int }}{\displaystyle \frac{1}{{\rho }^n}}{T}_t^{n}I({\rho }^n,T^n)dx=0.$$

Then we estimate the last two terms of the equality obtained taking into account this inequality

$\mid T^n\mid \le \mid \underset{0}{\overset{1}{\int }}{T}^{n}dx\mid +\Vert T_x^n\Vert$ and estimates (35) and (48)

$$\mid \underset{0}{\overset{1}{\int }}p({\rho }^n,T^n)T_t^n{u}_x^{n}dx\mid \le C\underset{0}{\overset{1}{\int }}\mid T^n{T}_t^n{u}_x^n\mid dx\le (N_3+\Vert T_x^n\Vert )\Vert T_t^n\Vert \Vert u_x^n\Vert \le$$

$$\le {\epsilon }_{21}\Vert T_t^n{\Vert }^2+{\displaystyle \frac{C}{{\epsilon }_{21}}}(N_3+\Vert T_x^n{\Vert )}^2\Vert u_x^n{\Vert }^2\le {\epsilon }_{21}{\Vert T_t^n\Vert }^2+{\displaystyle \frac{C}{{\epsilon }_{21}}}(N_3^2+N_6)N_6,$$

$$\mid \underset{0}{\overset{1}{\int }}{\displaystyle \frac{1}{{\rho }^n}}{T}_t^{n}I({\rho }^n,T^n)dx\mid \le C\underset{0}{\overset{1}{\int }}\mid T_t^n\mid dx\le {\epsilon }_{22}{\Vert T_t^n\Vert }^2.$$

Therefore the following estimate is satisfied

$$\underset{0}{\overset{1}{\int }}{\left(T_t^n\right)}^{2}dx+{\displaystyle \frac{{\nu }_0}{2}}\underset{0}{\overset{1}{\int }}{\left({\left(T_x^n\right)}^2\right)}_{t}dx\le {\displaystyle \sum _{i=21}^{22}}{\epsilon }_i{\Vert T_t^n\Vert }^2+{\displaystyle \frac{C}{{\epsilon }_{21}}}(N_3^2+N_6)N_6,$$

choosing ${\displaystyle \sum _{i=21}^{22}}{\epsilon }_i=1/2$ we have

$$\Vert T_t^n{\Vert }^2+{\nu }_0\underset{0}{\overset{1}{\int }}{\left({\left(T_x^n\right)}^2\right)}_{t}dx\le {\displaystyle \frac{C}{{\epsilon }_{21}}}(N_3^2+N_6)N_6\equiv N_9.$$

Integrate over t the last inequality

$$\underset{0}{\overset{t_0}{\int }}{\Vert T_t^n\Vert }^{2}dt\le N_{10}$$

(51)

Add up (48) and (51) we obtain the estimate (37)

$$\underset{0\le t\le t_0}{max}\left|\right|T_x^n\left(t\right){\left|\right|}^2+\underset{0}{\overset{t_0}{\int }}\left(\left|\right|T_{xx}^n{\left|\right|}^2+{\Vert T_t^n\Vert }^2\right)dt\le N_5.$$

Let’s return now to the inequalities of (21). From (18) we have

$${\displaystyle \frac{m_0}{1+2^{1/2}{B}_0{N}_4^{1/2}{t}_0^{3/4}}}\le {\rho }^n(x,t)\le {\displaystyle \frac{M_0}{1-2^{1/2}{B}_0{N}_4^{1/2}{t}_0^{3/4}}}.$$

If we choose

$$t_0\le {\left({\displaystyle \frac{1-B_0}{(1+M_0)\sqrt{2}{B}_0{N}_4^{1/2}}}\right)}^{4/3},$$

then this inequality is satisfied

$$0<{\displaystyle \frac{b_0}{2}}\le {\rho }^n(x,t)\le {\displaystyle \frac{B_0+1}{2}}<1,x\in [0,1],t\in [0,t_0].$$

Lemma 2 is proven. □

A-priori estimates for derivatives. Using the obtained estimates we can get estimates of strict positivity for $T^n(x,t)$. It follows directly from the equation (9):

$$\underset{0\le t\le t_0}{max}\left|\right|{\rho }_t^n\left(t\right){\left|\right|}^2\le N_{11}.$$

(52)

Differentiate with respect to x the equation (9) and obtain

$${\rho }_{tx}^n\left(t\right)=-({\left({\rho }^n\right)}^2{u}_{xx}^n+2{\rho }^n{\rho }_x^n{u}_x^n),$$

square it

$${\left({\rho }_{tx}^n\left(t\right)\right)}^2={({\left({\rho }^n\right)}^2{u}_{xx}^n+2{\rho }^n{\rho }_x^n{u}_x^n)}^2\le 2{\left({\rho }^n\right)}^4{\left(u_{xx}^n\right)}^2+4{\left({\rho }^n\right)}^2{\left({\rho }_x^n\right)}^2{\left(u_x^n\right)}^2.$$

Integrate the last inequality over x from 0 to 1 and over t from 0 to $t_0$

$$\underset{0}{\overset{t_0}{\int }}\underset{0}{\overset{1}{\int }}{\left({\rho }_{tx}^n\left(t\right)\right)}^{2}dxdt\le \underset{0}{\overset{t_0}{\int }}\underset{0}{\overset{1}{\int }}2{\left({\rho }^n\right)}^4{\left(u_{xx}^n\right)}^{2}dxdt+\underset{0}{\overset{t_0}{\int }}\underset{0}{\overset{1}{\int }}4{\left({\rho }^n\right)}^2{\left({\rho }_x^n\right)}^2{\left(u_x^n\right)}^{2}dxdt.$$

Then estimate each term of the right part considering (21) and (38). We obtain

$$\underset{0}{\overset{t_0}{\int }}\underset{0}{\overset{1}{\int }}2{\left({\rho }^n\right)}^4{\left(u_{xx}^n\right)}^{2}dxdt\le C\underset{0}{\overset{t_0}{\int }}\underset{0}{\overset{1}{\int }}{\left(u_{xx}^n\right)}^{2}dxdt=C\underset{0}{\overset{t_0}{\int }}{\Vert u_{xx}^n\Vert }^{2}dt\le C{N}_4,$$

$$\underset{0}{\overset{t_0}{\int }}\underset{0}{\overset{1}{\int }}4{\left({\rho }^n\right)}^2{\left({\rho }_x^n\right)}^2{\left(u_x^n\right)}^{2}dxdt\le C\underset{0}{\overset{t_0}{\int }}\underset{0}{\overset{1}{\int }}{\left({\rho }_x^n\right)}^2{\left(u_x^n\right)}^{2}dxdt\le C\underset{0}{\overset{t_0}{\int }}\underset{0\le x\le 1}{max}{\left(u_x^n\right)}^2\underset{0}{\overset{1}{\int }}{\left({\rho }_x^n\right)}^{2}dxdt\le$$

$$\le C(1+N_4)\underset{0}{\overset{t_0}{\int }}{\Vert u_{xx}^n\Vert }^{2}dt\le C(1+N_4)N_4\equiv N_{12}.$$

Therefore, the following estimate is true

$$\underset{0}{\overset{t_0}{\int }}{\Vert {\rho }_{tx}^n\left(t\right)\Vert }^{2}dt\le C{N}_4+N_{12}\equiv N_{13}.$$

(53)

Differentiate the equality (31) with respect to t and obtain

$$\underset{0}{\overset{1}{\int }}{\left[{\displaystyle \frac{\partial u^n}{\partial t}}-{\displaystyle \frac{\partial }{\partial x}}\left({\displaystyle \frac{4}{3}}\mu ({\rho }^n,T^n){\rho }^n{\displaystyle \frac{\partial u^n}{\partial x}}\right)+{\displaystyle \frac{\partial p({\rho }^n,T^n)}{\partial x}}\right]}_t^{\prime }sin\left(\pi ix\right)dx=$$

$$=\underset{0}{\overset{1}{\int }}[u_{tt}^n-{\displaystyle \frac{4}{3}}({\mu }_x({\rho }^n,T^n){\rho }^n{u}_x^n+\mu ({\rho }^n,T^n){\rho }_x^n{u}_x^n+$$

$$+\mu ({\rho }^n,T^n){\rho }^n{u}_{xx}^n{)}_t^{\prime }+p_{xt}({\rho }^n,T^n)]sin\left(\pi ix\right)dx=$$

$$=\underset{0}{\overset{1}{\int }}[u_{tt}^n-{\displaystyle \frac{4}{3}}({\left({\mu }_t({\rho }^n,T^n){\rho }^n{u}_x^n\right)}_x^{\prime }+{\left(\mu ({\rho }^n,T^n){\rho }_t^n{u}_x^n\right)}_x^{\prime }+$$

$$+{\left(\mu ({\rho }^n,T^n){\rho }^n{u}_{tx}^n\right)}_x^{\prime })+p_{xt}({\rho }^n,T^n)]sin\left(\pi ix\right)dx=0$$

The last equality is multiplied by ${\left(u_i^n\left(t\right)\right)}_t^{\prime }$, summed over i from 1 to n and integrated over x from 0 to 1. The following equality is obtained

$$\underset{0}{\overset{1}{\int }}[u_{tt}^n{u}_t^n-{\displaystyle \frac{4}{3}}{u}_t^n({\left({\mu }_t({\rho }^n,T^n){\rho }^n{u}_x^n\right)}_x^{\prime }+{\left(\mu ({\rho }^n,T^n){\rho }_t^n{u}_x^n\right)}_x^{\prime }+$$

$$+{\left(\mu ({\rho }^n,T^n){\rho }^n{u}_{tx}^n\right)}_x^{\prime })+u_t^n{p}_{xt}({\rho }^n,T^n)]dx=0.$$

Notice, that $u_t^n{\left({\mu }_t({\rho }^n,T^n){\rho }^n{u}_x^n\right)}_x={\left(u_t^n{\mu }_t({\rho }^n,T^n){\rho }^n{u}_x^n\right)}_x-u_{tx}^n\left({\mu }_t({\rho }^n,T^n){\rho }^n{u}_x^n\right)$, then

$$\underset{0}{\overset{1}{\int }}{u}_t^n{\left({\mu }_t({\rho }^n,T^n){\rho }^n{u}_x^n\right)}_{x}dx=\underset{0}{\overset{1}{\int }}{\left(u_t^n{\mu }_t({\rho }^n,T^n){\rho }^n{u}_x^n\right)}_{x}dx-\underset{0}{\overset{1}{\int }}{u}_{tx}^n\left({\mu }_t({\rho }^n,T^n){\rho }^n{u}_x^n\right)dx=$$

$$=u_t^n{\mu }_t({\rho }^n,T^n){\rho }^n{u}_x^n{\mid }_0^1-\underset{0}{\overset{1}{\int }}{u}_{tx}^n\left({\mu }_t({\rho }^n,T^n){\rho }^n{u}_x^n\right)dx=$$

$$={\left[{\left(u_i^n\left(t\right)\right)}_t^{\prime }sin\left(\pi ix\right){\mu }_t({\rho }^n,T^n){\rho }^n{u}_i^n\left(t\right)\left(\pi i\right)cos\left(\pi ix\right)\right]}_0^1-\underset{0}{\overset{1}{\int }}{u}_{tx}^n\left({\mu }_t({\rho }^n,T^n){\rho }^n{u}_x^n\right)dx=$$

$$=-\underset{0}{\overset{1}{\int }}{u}_{tx}^n\left({\mu }_t({\rho }^n,T^n){\rho }^n{u}_x^n\right)dx.$$

Analogically if we reveal the third and fourth terms it follows

$${\displaystyle \frac{1}{2}}\underset{0}{\overset{1}{\int }}{\left({\left(u_t^n\right)}^2\right)}_{t}dx+{\displaystyle \frac{4}{3}}\underset{0}{\overset{1}{\int }}{\left(u_{tx}^n\right)}^2\mu ({\rho }^n,T^n){\rho }^{n}dx=$$

$$=-{\displaystyle \frac{4}{3}}\underset{0}{\overset{1}{\int }}{u}_{tx}^n{\mu }_t({\rho }^n,T^n){\rho }^n{u}_x^{n}dx-{\displaystyle \frac{4}{3}}\underset{0}{\overset{1}{\int }}{u}_{tx}^n\mu ({\rho }^n,T^n){\rho }_t^n{u}_x^{n}dx-\underset{0}{\overset{1}{\int }}{u}_t^n{p}_{xt}({\rho }^n,T^n)dx.$$

Now we estimate the right part of the last inequality

$$\mid \underset{0}{\overset{1}{\int }}{u}_{tx}^n{\mu }_t({\rho }^n,T^n){\rho }^n{u}_x^{n}dx\mid =\mid \underset{0}{\overset{1}{\int }}({\mu }_{{\rho }^n}{\rho }_t^n+{\mu }_{T^n}{T}_t^n)u_{tx}^n{\rho }^n{u}_x^{n}dx\mid =$$

$$=\mid \underset{0}{\overset{1}{\int }}{\mu }_{{\rho }^n}{\rho }_t^n{u}_{tx}^n{\rho }^n{u}_x^{n}dx\mid +\mid \underset{0}{\overset{1}{\int }}{\mu }_{T^n}{T}_t^n{u}_{tx}^n{\rho }^n{u}_x^{n}dx\mid =A_9+A_{10}.$$

Since the functions ${\mu }_{{\rho }^n},{\mu }_{T^n}$ are uniformly bounded over n due to (21) for all ${\rho }^n\in (0,1)$, then

$$A_9\le C\underset{0}{\overset{1}{\int }}\mid {\rho }_t^n{u}_{tx}^n{\rho }^n{u}_x^n\mid dx\le C\underset{0\le x\le 1}{max}\mid u_x^n\mid \underset{0}{\overset{1}{\int }}\mid {\rho }_t^n\mid \mid u_{tx}^n\mid dx\le C\Vert u_{xx}^n\Vert \Vert {\rho }_t^n\Vert \Vert u_{tx}^n\Vert \le$$

$$\le C\underset{0\le t\le t_0}{max}\Vert {\rho }_t^n\Vert \Vert u_{xx}^n\Vert \Vert u_{tx}^n\Vert \le C{N}_9\Vert u_{xx}^n\Vert \Vert u_{tx}^n\Vert \le {\epsilon }_{23}\Vert u_{tx}^n{\Vert }^2+{\displaystyle \frac{C}{{\epsilon }_{23}}}\Vert u_{xx}^n\Vert ,$$

$$A_{10}\le C\underset{0}{\overset{1}{\int }}\mid T_t^n{u}_{tx}^n{\rho }^n{u}_x^n\mid dx\le C\underset{0\le x\le 1}{max}\mid u_x^n\mid \Vert T_t^n\Vert \Vert u_{tx}^n\Vert \le$$

$$\le C\Vert u_x^n{\Vert }^{1/2}\Vert u_{xx}^n{\Vert }^{1/2}\Vert T_t^n\Vert \Vert u_{tx}^n\Vert \le {\epsilon }_{24}\Vert u_{tx}^n{\Vert }^2\Vert u_x^n\Vert +{\displaystyle \frac{C}{{\epsilon }_{24}}}\Vert T_t^n{\Vert }^2\Vert u_{xx}^n\Vert \le$$

$$\le {\epsilon }_{24}{N}_4^{1/2}\Vert u_{tx}^n{\Vert }^2+{\displaystyle \frac{C}{{\epsilon }_{24}}}\Vert T_t^n{\Vert }^2\Vert u_{xx}^n\Vert ,$$

$$\mid \underset{0}{\overset{1}{\int }}{u}_{tx}^n\mu ({\rho }^n,T^n){\rho }_t^n{u}_x^{n}dx\mid \le C\underset{0}{\overset{1}{\int }}\mid u_{tx}^n{\rho }_t^n{u}_x^n\mid dx\le \underset{0\le x\le 1}{max}\mid u_x^n\mid \Vert {\rho }_t^n\Vert \Vert u_{tx}^n\Vert \le$$

$$\le C\Vert u_{xx}^n\Vert \underset{0\le t\le t_0}{max}\Vert {\rho }_t^n\Vert \Vert \Vert u_{tx}^n\Vert \le C{N}_{11}\Vert u_{xx}^n\Vert \Vert u_{tx}^n\Vert \le {\epsilon }_{25}\Vert u_{tx}^n{\Vert }^2+{\displaystyle \frac{C}{{\epsilon }_{25}}}{\Vert u_{xx}^n\Vert }^2,$$

$$\mid \underset{0}{\overset{1}{\int }}{u}_t^n{p}_{xt}({\rho }^n,T^n)dx\mid \le \mid \underset{0}{\overset{1}{\int }}{u}_t^n{(p_{{\rho }^n}{\rho }_x^n+p_{T^n}{T}_x^n)}_t^{\prime }dx\mid \le$$

$$\le \mid \underset{0}{\overset{1}{\int }}{u}_t^n(p_{{\rho }^n{\rho }^n}^{\prime \prime }{\rho }_x^n{\rho }_t^n+p_{{\rho }^n{T}^n}^{\prime \prime }{\rho }_x^n{T}_t^n+p_{{\rho }^n}{\rho }_{tx}^n+p_{T^n{T}^n}^{\prime \prime }{T}_t^n{T}_x^n+p_{T^n{\rho }^n}^{\prime \prime }{\rho }_t^n{T}_x^n+p_{T^n}{T}_{tx}^n)dx\mid .$$

Since the functions $p_{{\rho }^n{\rho }^n}^{\prime \prime },p_{{\rho }^n{T}^n}^{\prime \prime },p_{{\rho }^n}^{\prime },p_{T^n{T}^n}^{\prime \prime },p_{T^n}^{\prime }$ are uniformly bounded over n due to (21) for all ${\rho }^n\in (0,1)$, we estimate each term of the last inequality

$$\mid \underset{0}{\overset{1}{\int }}{p}_{{\rho }^n}{\rho }_{tx}^n{u}_t^{n}dx\mid \le C\underset{0}{\overset{1}{\int }}\mid {\rho }_{tx}^n\mid \mid u_t^n\mid dx\le C\Vert u_t^n\Vert \Vert {\rho }_{tx}^n\Vert \le {\epsilon }_{26}\Vert u_t^n{\Vert }^2+{\displaystyle \frac{C}{{\epsilon }_{26}}}{\Vert {\rho }_{tx}^n\Vert }^2,$$

$$\mid \underset{0}{\overset{1}{\int }}{p}_{T^n}{T}_{tx}^n{u}_t^{n}dx\mid \le C\underset{0}{\overset{1}{\int }}\mid T_{tx}^n\mid \mid u_t^n\mid dx\le C\Vert u_t^n\Vert \Vert T_{tx}^n\Vert \le {\epsilon }_{27}\Vert T_{xt}^n{\Vert }^2+{\displaystyle \frac{C}{{\epsilon }_{27}}}{\Vert u_t^n\Vert }^2,$$

$$\mid \underset{0}{\overset{1}{\int }}{u}_t^n{p}_{{\rho }^n{\rho }^n}^{\prime \prime }{\rho }_x^n{\rho }_t^{n}dx\mid \le C\underset{0}{\overset{1}{\int }}\mid u_t^n{\rho }_x^n{\rho }_t^n\mid dx\le C\underset{0}{\overset{1}{\int }}\mid u_t^n{\rho }_x^n{\left({\rho }^n\right)}^2{u}_x^n\mid dx\le C\underset{0}{\overset{1}{\int }}\mid u_t^n{\rho }_x^n{u}_x^n\mid dx\le$$

$$\le C\underset{0\le x\le 1}{max}\mid u_x^n\mid \Vert u_t^n\Vert \Vert {\rho }_x^n\Vert \le C{N}_4^{1/2}\Vert u_{xx}^n\Vert \Vert u_t^n\Vert \le {\epsilon }_{28}\Vert u_t^n{\Vert }^2+{\displaystyle \frac{C}{{\epsilon }_{28}}}{\Vert u_{xx}^n\Vert }^2,$$

$$\mid \underset{0}{\overset{1}{\int }}{p}_{{\rho }^n{T}^n}^{\prime \prime }{\rho }_x^n{T}_t^n{u}_t^{n}dx\mid \le C\underset{0}{\overset{1}{\int }}\mid T_t^n{u}_t^n\mid dx\le {\epsilon }_{29}\Vert u_t^n{\Vert }^2+{\displaystyle \frac{C}{{\epsilon }_{29}}}{\Vert T_t^n\Vert }^2,$$

$$\mid \underset{0}{\overset{1}{\int }}{p}_{T^n{T}^n}^{\prime \prime }{T}_t^n{T}_x^n{u}_t^{n}dx\mid \le C\underset{0}{\overset{1}{\int }}\mid T_t^n{T}_x^n{u}_t^n\mid dx\le C\underset{0\le x\le 1}{max}\mid T_x^n\mid \Vert T_t^n\Vert \Vert u_t^n\Vert \le$$

$$\le C\Vert T_x^n{\Vert }^{1/2}\Vert T_{xx}^n{\Vert }^{1/2}\Vert T_t^n\Vert \Vert u_t^n\Vert \le {\epsilon }_{30}\Vert u_t^n{\Vert }^2\Vert T_{xx}^n\Vert +{\displaystyle \frac{C}{{\epsilon }_{30}}}\Vert T_t^n{\Vert }^2\Vert T_x^n\Vert ,$$

$$\mid \underset{0}{\overset{1}{\int }}{p}_{T^n{\rho }^n}^{\prime \prime }{\rho }_t^n{T}_x^n{u}_t^{n}dx\mid \le C\underset{0}{\overset{1}{\int }}\mid {\rho }_t^n{T}_x^n{u}_t^n\mid dx\le C\underset{0\le x\le 1}{max}\mid T_x^n\mid \Vert {\rho }_t^n\Vert \Vert u_t^n\Vert \le$$

$$\le C\underset{0\le t\le t_0}{max}\Vert {\rho }_t^n\Vert \Vert T_{xx}^n\Vert \Vert u_t^n\Vert \le C{N}_{11}\Vert T_{xx}^n\Vert \Vert u_t^n\Vert \le {\epsilon }_{31}\Vert u_t^n{\Vert }^2+{\displaystyle \frac{C}{{\epsilon }_{31}}}{\Vert T_{xx}^n\Vert }^2.$$

Then,

$${\displaystyle \frac{1}{2}}\underset{0}{\overset{1}{\int }}{\left({\left(u_t^n\right)}^2\right)}_{t}dx+{\displaystyle \frac{4}{3}}{\nu }_0\underset{0}{\overset{1}{\int }}{\left(u_{tx}^n\right)}^{2}dx\le$$

$$\le {\displaystyle \sum _{i=23}^{25}}{\epsilon }_i\Vert u_{tx}^n{\Vert }^2+{\epsilon }_{27}\Vert T_{xt}^n{\Vert }^2+{\Vert u_{xx}^n\Vert }^2({\displaystyle \frac{C}{{\epsilon }_{23}}}+{\displaystyle \frac{C}{{\epsilon }_{25}}}+{\displaystyle \frac{C}{{\epsilon }_{28}}})+$$

$$+\Vert T_t^n{\Vert }^2({\displaystyle \frac{C}{{\epsilon }_{24}}}\Vert u_{xx}^n\Vert +{\displaystyle \frac{C}{{\epsilon }_{29}}}+{\displaystyle \frac{C}{{\epsilon }_{30}}}\Vert T_x^n\Vert )+$$

$$+\Vert u_t^n{\Vert }^2({\epsilon }_{26}+{\displaystyle \frac{C}{{\epsilon }_{27}}}+{\epsilon }_{28}+{\epsilon }_{29}+{\epsilon }_{30}\Vert T_{xx}^n\Vert +{\epsilon }_{31})+{\displaystyle \frac{C}{{\epsilon }_{26}}}\Vert {\rho }_{xt}^n{\Vert }^2+{\displaystyle \frac{C}{{\epsilon }_{31}}}{\Vert T_{xx}^n\Vert }^2.$$

Integrate over t and apply the estimates (36), (37) and(53), we obtain

$${\displaystyle \frac{1}{2}}\underset{0\le t\le t_0}{max}\Vert u_t^n{\Vert }^2+{\displaystyle \frac{4}{3}}{\nu }_0\underset{0}{\overset{t_0}{\int }}\Vert u_{tx}^n{\Vert }^{2}dt\le {\displaystyle \sum _{i=23}^{25}}{\epsilon }_i\underset{0}{\overset{t_0}{\int }}\Vert u_{tx}^n{\Vert }^{2}dt+{\epsilon }_{27}\underset{0}{\overset{t_0}{\int }}{\Vert T_{xt}^n\Vert }^{2}dt+$$

$$+N_4({\displaystyle \frac{C}{{\epsilon }_{23}}}+{\displaystyle \frac{C}{{\epsilon }_{25}}}+{\displaystyle \frac{C}{{\epsilon }_{28}}})+\underset{0}{\overset{t_0}{\int }}\Vert T_t^n{\Vert }^2({\displaystyle \frac{C}{{\epsilon }_{24}}}\Vert u_{xx}^n\Vert +{\displaystyle \frac{C}{{\epsilon }_{29}}}+{\displaystyle \frac{C}{{\epsilon }_{30}}}\Vert T_x^n\Vert )dt+$$

(54)

$$+\underset{0}{\overset{t_0}{\int }}\Vert u_t^n{\Vert }^2({\epsilon }_{26}+{\displaystyle \frac{C}{{\epsilon }_{27}}}+{\epsilon }_{28}+{\epsilon }_{29}+{\epsilon }_{30}\Vert T_{xx}^n\Vert +{\epsilon }_{31})dt+N_{12}{\displaystyle \frac{C}{{\epsilon }_{26}}}+N_5{\displaystyle \frac{C}{{\epsilon }_{31}}}.$$

Differentiate the equality (32) by t, we get

$$\underset{0}{\overset{1}{\int }}[T_{tt}^n-{({\kappa }_x({\rho }^n,T^n){\rho }^n{T}_x^n+\kappa ({\rho }^n,T^n){\rho }_x^n{T}_x^n+\kappa ({\rho }^n,T^n){\rho }^n{T}_{xx}^n)}_t^{\prime }+$$

$$+p_t({\rho }^n,T^n)u_x^n+p({\rho }^n,T^n)u_{xt}^n+{\left({\displaystyle \frac{1}{{\rho }^n}}\right)}_{t}I({\rho }^n,T^n)+{\displaystyle \frac{1}{{\rho }^n}}{I}_t({\rho }^n,T^n)]cos\left(\pi jx\right)dx=0.$$

The last equality is multiplied by ${\left(T_j^n\left(t\right)\right)}_t^{\prime }$, summed over j from 0 to n. We obtain this equation

$$\underset{0}{\overset{1}{\int }}[T_{tt}^n{T}_t^n-T_t^n{({\kappa }_x({\rho }^n,T^n){\rho }^n{T}_x^n+\kappa ({\rho }^n,T^n){\rho }_x^n{T}_x^n+\kappa ({\rho }^n,T^n){\rho }^n{T}_{xx}^n)}_t^{\prime }+$$

$$+T_t^n{p}_t({\rho }^n,T^n)u_x^n+T_t^{n}p({\rho }^n,T^n)u_{xt}^n+T_t^n{\left({\displaystyle \frac{1}{{\rho }^n}}\right)}_{t}I({\rho }^n,T^n)+T_t^n{\displaystyle \frac{1}{{\rho }^n}}{I}_t({\rho }^n,T^n)]dx=0.$$

Consider separately

$${({\kappa }_x({\rho }^n,T^n){\rho }^n{T}_x^n+\kappa ({\rho }^n,T^n){\rho }_x^n{T}_x^n+\kappa ({\rho }^n,T^n){\rho }^n{T}_{xx}^n)}_t^{\prime }=$$

$$={\kappa }_{xt}({\rho }^n,T^n){\rho }^n{T}_x^n+{\kappa }_x({\rho }^n,T^n){\rho }_t^n{T}_x^n+{\kappa }_x({\rho }^n,T^n){\rho }^n{T}_{xt}^n+$$

$$+{\kappa }_t({\rho }^n,T^n){\rho }_x^n{T}_x^n+\kappa ({\rho }^n,T^n){\rho }_{xt}^n{T}_x^n+\kappa ({\rho }^n,T^n){\rho }_x^n{T}_{xt}^n+$$

$$+{\kappa }_t({\rho }^n,T^n){\rho }^n{T}_{xx}^n+\kappa ({\rho }^n,T^n){\rho }_t^n{T}_{xx}^n+\kappa ({\rho }^n,T^n){\rho }^n{T}_{xxt}^n,$$

and notice

$${\left({\kappa }_t({\rho }^n,T^n){\rho }^n{T}_x^n\right)}_x^{\prime }={\kappa }_{xt}({\rho }^n,T^n){\rho }^n{T}_x^n+{\kappa }_t({\rho }^n,T^n){\rho }_x^n{T}_x^n+{\kappa }_t({\rho }^n,T^n){\rho }^n{T}_{xx}^n,$$

$${\left(\kappa ({\rho }^n,T^n){\rho }_t^n{T}_x^n\right)}_x^{\prime }={\kappa }_x({\rho }^n,T^n){\rho }_t^n{T}_x^n+\kappa ({\rho }^n,T^n){\rho }_{xt}^n{T}_x^n+\kappa ({\rho }^n,T^n){\rho }_t^n{T}_{xx}^n$$

$${\left(\kappa ({\rho }^n,T^n){\rho }^n{T}_{xt}^n\right)}_x^{\prime }={\kappa }_x({\rho }^n,T^n){\rho }^n{T}_{xt}^n+\kappa ({\rho }^n,T^n){\rho }_x^n{T}_{xt}^n++\kappa ({\rho }^n,T^n){\rho }^n{T}_{xxt}^n.$$

Thus, the last equation can be represented as follows

$$\underset{0}{\overset{1}{\int }}[T_{tt}^n{T}_t^n-T_t^n{\left({\kappa }_t({\rho }^n,T^n){\rho }^n{T}_x^n\right)}_x^{\prime }-T_t^n{\left(\kappa ({\rho }^n,T^n){\rho }_t^n{T}_x^n\right)}_x^{\prime }-T_t^n{\left(\kappa ({\rho }^n,T^n){\rho }^n{T}_{xt}^n\right)}_x^{\prime }+$$

$$+T_t^n{p}_t({\rho }^n,T^n)u_x^n+T_t^{n}p({\rho }^n,T^n)u_{xt}^n+T_t^n{\left({\displaystyle \frac{1}{{\rho }^n}}\right)}_{t}I({\rho }^n,T^n)+T_t^n{\displaystyle \frac{1}{{\rho }^n}}{I}_t({\rho }^n,T^n)]dx=0.$$

The second term can be expressed in the following form

$$T_t^n{\left({\kappa }_t({\rho }^n,T^n){\rho }^n{T}_x^n\right)}_x^{\prime }={\left(T_t^n{\kappa }_t({\rho }^n,T^n){\rho }^n{T}_x^n\right)}_x^{\prime }-T_{xt}^n\left({\kappa }_t({\rho }^n,T^n){\rho }^n{T}_x^n\right).$$

Then,

$$\underset{0}{\overset{1}{\int }}{T}_t^n{\left({\kappa }_t({\rho }^n,T^n){\rho }^n{T}_x^n\right)}_x^{\prime }dx=\left(T_t^n{\kappa }_t({\rho }^n,T^n){\rho }^n{T}_x^n\right){\mid }_0^1-\underset{0}{\overset{1}{\int }}{T}_{xt}^n\left({\kappa }_t({\rho }^n,T^n){\rho }^n{T}_x^n\right)dx=$$

$$=\left({\left(T_j^n\left(t\right)\right)}_{t}cos\left(\pi jx\right){\kappa }_t({\rho }^n,T^n){\rho }^n{T}_j^n\left(t\right)(-\pi j)sin\left(\pi jx\right)\right){\mid }_0^1-\underset{0}{\overset{1}{\int }}{T}_{xt}^n\left({\kappa }_t({\rho }^n,T^n){\rho }^n{T}_x^n\right)dx=$$

$$=-\underset{0}{\overset{1}{\int }}{T}_{xt}^n\left({\kappa }_t({\rho }^n,T^n){\rho }^n{T}_x^n\right)dx.$$

The third and fourth terms are reformed analogically and we obtain

$${\displaystyle \frac{1}{2}}\underset{0}{\overset{1}{\int }}{\left(T_t^n\right)}^{2}dx+\underset{0}{\overset{1}{\int }}\kappa ({\rho }^n,T^n){\rho }^n{\left(T_{xt}^n\right)}^{2}dx=-\underset{0}{\overset{1}{\int }}{T}_{xt}^n{\kappa }_t({\rho }^n,T^n){\rho }^n{T}_x^{n}dx-$$

$$-\underset{0}{\overset{1}{\int }}{T}_{xt}^n\kappa ({\rho }^n,T^n){\rho }_t^n{T}_x^{n}dx+$$

$$+\underset{0}{\overset{1}{\int }}{T}_t^n{p}_t({\rho }^n,T^n)u_x^{n}dx+\underset{0}{\overset{1}{\int }}{T}_t^{n}p({\rho }^n,T^n)u_{xt}^{n}dx+\underset{0}{\overset{1}{\int }}{T}_t^n{\left({\displaystyle \frac{1}{{\rho }^n}}\right)}_{t}I({\rho }^n,T^n)dx+$$

$$+\underset{0}{\overset{1}{\int }}{T}_t^n{\displaystyle \frac{1}{{\rho }^n}}{I}_t({\rho }^n,T^n)dx.$$

Now estimate the right part of the equality obtained

$$\mid \underset{0}{\overset{1}{\int }}{T}_{xt}^n{\kappa }_t({\rho }^n,T^n){\rho }^n{T}_x^{n}dx\mid =\mid \underset{0}{\overset{1}{\int }}({\kappa }_{{\rho }^n}{\rho }_t^n+{\kappa }_{T^n}{T}_t^n){\rho }^n{T}_x^n{T}_{xt}^{n}dx\mid =$$

$$=\mid \underset{0}{\overset{1}{\int }}{\kappa }_{{\rho }^n}{\rho }_t^n{\rho }^n{T}_x^n{T}_{xt}^{n}dx\mid +\mid \underset{0}{\overset{1}{\int }}{\kappa }_{T^n}{T}_t^n{\rho }^n{T}_x^n{T}_{xt}^{n}dx\mid =A_{11}+A_{12}.$$

The functions ${\kappa }_{{\rho }^n},{\kappa }_{T^n},{\rho }^n$ are uniformly bounded over n due to (21) for all ${\rho }^n\in (0,1)$, therefore

$$A_{11}=C\underset{0}{\overset{1}{\int }}\mid {\rho }_t^n{T}_x^n{T}_{xt}^n\mid dx\le C\underset{0\le x\le 1}{max}\mid T_x^n\mid \Vert {\rho }_t^n\Vert \Vert T_{xt}^n\Vert \le {\epsilon }_{32}\Vert T_{xt}^n{\Vert }^2+{\displaystyle \frac{C}{{\epsilon }_{32}}}{\Vert T_{xx}^n\Vert }^2,$$

$$A_{12}=C\underset{0}{\overset{1}{\int }}\mid T_t^n{T}_x^n{T}_{xt}^n\mid dx\le C\underset{0\le x\le 1}{max}\mid T_x^n\mid \Vert T_t^n\Vert \Vert T_{xt}^n\Vert \le$$

$$\le C\Vert T_x^n{\Vert }^{1/2}\Vert T_{xx}^n{\Vert }^{1/2}\Vert T_t^n\Vert \Vert T_{xt}^n\Vert \le {\epsilon }_{33}\Vert T_{xt}^n{\Vert }^2\Vert T_x^n\Vert +{\displaystyle \frac{C}{{\epsilon }_{33}}}\Vert T_t^n{\Vert }^2\Vert T_{xx}^n\Vert \le$$

$$\le {\epsilon }_{33}{N}_5^{1/2}\Vert T_{xt}^n{\Vert }^2+{\displaystyle \frac{C}{{\epsilon }_{33}}}\Vert T_t^n{\Vert }^2\Vert T_{xx}^n\Vert ,$$

$$\mid \underset{0}{\overset{1}{\int }}{T}_{xt}^n\kappa ({\rho }^n,T^n){\rho }_t^n{T}_x^{n}dx\mid \le C\underset{0}{\overset{1}{\int }}\mid T_{xt}^n{\rho }_t^n{T}_x^n\mid dx\le C\underset{0\le x\le 1}{max}\mid T_x^n\mid \Vert {\rho }_t^n\Vert \Vert T_{xt}^n\Vert \le$$

$$\le C\underset{0\le t\le t_0}{max}\Vert {\rho }_t^n\Vert \Vert T_{xx}^n\Vert \Vert T_{xt}^n\Vert \le C{N}_{11}\Vert T_{xx}^n\Vert \Vert T_{xt}^n\Vert \le {\epsilon }_{34}\Vert T_{xt}^n{\Vert }^2+{\displaystyle \frac{C}{{\epsilon }_{34}}}{\Vert T_{xx}^n\Vert }^2,$$

$$\mid \underset{0}{\overset{1}{\int }}{T}_t^n{p}_t({\rho }^n,T^n)u_x^{n}dx\mid =\mid \underset{0}{\overset{1}{\int }}(p_{{\rho }^n}{\rho }_t^n+p_{T^n}{T}_t^n)T_t^n{u}_x^{n}dx\mid =$$

$$=\mid \underset{0}{\overset{1}{\int }}{p}_{{\rho }^n}{\rho }_t^n{T}_t^n{u}_x^{n}dx\mid +\mid \underset{0}{\overset{1}{\int }}{p}_{T^n}{T}_t^n{T}_t^n{u}_x^{n}dx\mid =A_{13}+A_{14}.$$

Since the functions $p_{{\rho }^n},p_{T^n}$ are uniformly bounded over n by virtue of (21) for all ${\rho }^n\in (0,1)$, then

$$A_{13}\le C\underset{0}{\overset{1}{\int }}\mid {\rho }_t^n{T}_t^n{u}_x^n\mid dx\le C\underset{0\le x\le 1}{max}\mid u_x^n\mid \Vert {\rho }_t^n\Vert \Vert T_t^n\Vert \le$$

$$\le \underset{0\le t\le t_0}{max}\Vert {\rho }_t^n\Vert \Vert u_{xx}^n\Vert \Vert T_t^n\Vert \le {\epsilon }_{35}\Vert T_t^n{\Vert }^2+{\displaystyle \frac{C}{{\epsilon }_{35}}}{\Vert u_{xx}^n\Vert }^2,$$

$$A_{14}\le C\underset{0}{\overset{1}{\int }}\mid T_t^n{T}_t^n{u}_x^n\mid dx\le C\underset{0\le x\le 1}{max}\mid u_x^n\mid \Vert T_t^n{\Vert }^2\le C\Vert T_t^n{\Vert }^2\Vert u_{xx}^n\Vert .$$

The functions ${\rho }^n{\displaystyle \frac{1+{\rho }^n}{1-{\rho }^n}}$ are uniformly bounded over n due to (21) for all ${\rho }^n\in (0,1)$, taking into account the inequality $\mid T^n\mid \le \mid \underset{0}{\overset{1}{\int }}{T}^{n}dx\mid +\Vert T_x^n\Vert$ and estimate (48) we get

$$\mid \underset{0}{\overset{1}{\int }}{T}_t^{n}p({\rho }^n,T^n)u_{xt}^{n}dx\mid \le C\underset{0}{\overset{1}{\int }}\mid T^n{T}_t^n{u}_{xt}^n\mid dx\le C(N_3+\Vert T_x^n\Vert )\Vert T_t^n\Vert \Vert u_{xt}^n\Vert \le$$

$$\le {\epsilon }_{36}\Vert u_{xt}^n{\Vert }^2+{\displaystyle \frac{C}{{\epsilon }_{36}}}(N_3+\Vert T_x^n{\Vert )}^2\Vert T_t^n{\Vert }^2\le {\epsilon }_{36}\Vert u_{xt}^n{\Vert }^2+{\displaystyle \frac{C}{{\epsilon }_{36}}}(N_3^2+N_6){\Vert T_t^n\Vert }^2.$$

We use (9) to estimate the fifth term

$$\mid \underset{0}{\overset{1}{\int }}{T}_t^n{\left({\displaystyle \frac{1}{{\rho }^n}}\right)}_{t}I({\rho }^n,T^n)dx\mid \le C\underset{0}{\overset{1}{\int }}\mid T_t^n{u}_x^n\mid dx\le {\epsilon }_{37}\Vert T_t^n{\Vert }^2+{\displaystyle \frac{C}{{\epsilon }_{37}}}\Vert u_x^n{\Vert }^2\le {\epsilon }_{37}{\Vert T_t^n\Vert }^2+{\displaystyle \frac{C{N}_4}{{\epsilon }_{37}}},$$

$$\mid \underset{0}{\overset{1}{\int }}{T}_t^n{\displaystyle \frac{1}{{\rho }^n}}{I}_t({\rho }^n,T^n)dx\mid =\mid \underset{0}{\overset{1}{\int }}{T}_t^n{\displaystyle \frac{1}{{\rho }^n}}(I_{{\rho }^n}{\rho }_t^n+I_{T^n}{T}_t^n)dx\mid =$$

$$=\mid \underset{0}{\overset{1}{\int }}{T}_t^n{\displaystyle \frac{1}{{\rho }^n}}{I}_{{\rho }^n}{\rho }_t^{n}dx\mid +\mid \underset{0}{\overset{1}{\int }}{T}_t^n{\displaystyle \frac{1}{{\rho }^n}}{I}_{T^n}{T}_t^{n}dx\mid =A_{15}+A_{16}.$$

Since the functions ${\displaystyle \frac{1}{{\rho }^n}}{I}_{{\rho }^n},{\displaystyle \frac{1}{{\rho }^n}}{I}_{T^n}$ are uniformly bounded over n by virtue of (21) for all ${\rho }^n\in (0,1)$, then we have

$$A_{15}\le C\underset{0}{\overset{1}{\int }}\mid T_t^n{\rho }_t^n\mid dx\le C\Vert T_t^n\Vert \Vert {\rho }_t^n\Vert \le C\underset{0\le t\le t_0}{max}\Vert {\rho }_t^n\Vert \Vert T_t^n\Vert \le$$

$$\le C{N}_{11}\Vert T_t^n\Vert \le {\epsilon }_{38}{\Vert T_t^n\Vert }^2,$$

$$A_{16}\le C\underset{0}{\overset{1}{\int }}{\left(T_t^n\right)}^{2}dx\le C{\Vert T_t^n\Vert }^2.$$

Therefore,

$${\displaystyle \frac{1}{2}}\underset{0}{\overset{1}{\int }}{\left(T_t^n\right)}^{2}dx+\underset{0}{\overset{1}{\int }}\kappa ({\rho }^n,T^n){\rho }^n{\left(T_{xt}^n\right)}^{2}dx\le {\displaystyle \sum _{i=32}^{34}}{\epsilon }_i\Vert T_{xt}^n{\Vert }^2+{\epsilon }_{36}{\Vert u_{xt}^n\Vert }^2+$$

$$+\Vert T_t^n{\Vert }^2({\displaystyle \frac{C}{{\epsilon }_{33}}}\Vert T_{xx}^n\Vert +{\epsilon }_{35}+C\Vert u_{xx}^n\Vert +{\displaystyle \frac{C}{{\epsilon }_{36}}}+{\epsilon }_{37}+{\epsilon }_{38}+C)+$$

$$+\Vert T_{xx}^n{\Vert }^2({\displaystyle \frac{C}{{\epsilon }_{32}}}+{\displaystyle \frac{C}{{\epsilon }_{34}}})+{\Vert u_{xx}^n\Vert }^2{\displaystyle \frac{C}{{\epsilon }_{35}}}+{\displaystyle \frac{C{N}_4}{{\epsilon }_{37}}},$$

Now, integrate this over t, we obtain

$${\displaystyle \frac{1}{2}}\underset{0\le t\le t_0}{max}\Vert T_t^n{\Vert }^2+{\nu }_0\underset{0}{\overset{t_0}{\int }}\Vert T_{xt}^n{\Vert }^{2}dt\le {\displaystyle \sum _{i=32}^{34}}{\epsilon }_i\underset{0}{\overset{t_0}{\int }}\Vert T_{xt}^n{\Vert }^{2}dt+{\epsilon }_{36}\underset{0}{\overset{t_0}{\int }}{\Vert u_{xt}^n\Vert }^{2}dt+$$

$$+\underset{0}{\overset{t_0}{\int }}\Vert T_t^n{\Vert }^2({\displaystyle \frac{C}{{\epsilon }_{33}}}\Vert T_{xx}^n\Vert +{\epsilon }_{35}+C\Vert u_{xx}^n\Vert +{\displaystyle \frac{C}{{\epsilon }_{36}}}+{\epsilon }_{37}+{\epsilon }_{38}+C)dt+N_{14}.$$

(55)

Adding up (54) and (55)

$${\displaystyle \frac{1}{2}}\underset{0\le t\le t_0}{max}\Vert u_t^n{\Vert }^2+{\displaystyle \frac{1}{2}}\underset{0\le t\le t_0}{max}\Vert T_t^n{\Vert }^2+{\displaystyle \frac{4}{3}}{\nu }_0\underset{0}{\overset{t_0}{\int }}\Vert u_{tx}^n{\Vert }^{2}dt+{\nu }_0\underset{0}{\overset{t_0}{\int }}{\Vert T_{xt}^n\Vert }^{2}dt\le$$

$$\le ({\displaystyle \sum _{i=23}^{25}}{\epsilon }_i+{\epsilon }_{36})\underset{0}{\overset{t_0}{\int }}\Vert u_{tx}^n{\Vert }^{2}dt+({\displaystyle \sum _{i=32}^{34}}{\epsilon }_i+{\epsilon }_{27})\underset{0}{\overset{t_0}{\int }}{\Vert T_{xt}^n\Vert }^{2}dt+$$

$$+N_{15}\underset{0}{\overset{t_0}{\int }}\Vert T_t^n{\Vert }^2(\Vert u_{xx}^n\Vert +\Vert T_{xx}^n\Vert +\Vert T_x^n\Vert )dt+N_{16}\underset{0}{\overset{t_0}{\int }}\Vert u_t^n{\Vert }^2\Vert T_{xx}^n\Vert dt+N_{17}.$$

Now we choose ${\displaystyle \sum _{i=23}^{25}}{\epsilon }_i+{\epsilon }_{36}={\displaystyle \frac{5{\nu }_0}{6}}$ and $\sum _{i=32}^{34}{\epsilon }_i+{\epsilon }_{27}={\displaystyle \frac{{\nu }_0}{2}}$, then the last inequality has the form

$$\underset{0\le t\le t_0}{max}\Vert u_t^n{\Vert }^2+\underset{0\le t\le t_0}{max}\Vert T_t^n{\Vert }^2+{\nu }_0(\underset{0}{\overset{t_0}{\int }}(\Vert T_{xt}^n{\Vert }^2+\Vert u_{xt}^n{\Vert }^2)dt\le$$

$$+N_{15}\underset{0}{\overset{t_0}{\int }}\Vert T_t^n{\Vert }^2(\Vert u_{xx}^n\Vert +\Vert T_{xx}^n\Vert +\Vert T_x^n\Vert )dt+N_{16}\underset{0}{\overset{t_0}{\int }}\Vert u_t^n{\Vert }^2\Vert T_{xx}^n\Vert dt+N_{17}.$$

Let $y\left(t\right)=\Vert u_t^n{\Vert }^2+{\Vert T_t^n\Vert }^2$. Therefore, the last inequality can be represented in the following form

$${\displaystyle \frac{dy}{dt}}\le C+y\left(t\right)(\Vert u_{xx}^n\Vert +\Vert T_{xx}^n\Vert +\Vert T_x^n\Vert ).$$

From Gronwall’s lemma we obtain

$$y\left(t\right)\le e^{\underset{0}{\overset{t_0}{\int }}(\Vert u_{xx}^n\Vert +\Vert T_{xx}^n\Vert +\Vert T_x^n\Vert )dt}(y\left(0\right)+\underset{0}{\overset{t_0}{\int }}{e}^{-\underset{0}{\overset{\tau }{\int }}(\Vert u_{xx}^n\Vert +\Vert T_{xx}^n\Vert +\Vert T_x^n\Vert )ds}dt),$$

thus, $y\left(t\right)$ is bounded. Then

$$\underset{0\le t\le t_0}{max}\Vert u_t^n{\Vert }^2+\underset{0\le t\le t_0}{max}\Vert T_t^n{\Vert }^2+{\nu }_0(\underset{0}{\overset{t_0}{\int }}(\Vert T_{xt}^n{\Vert }^2+\Vert u_{xt}^n{\Vert }^2)dt\le N_{18}.$$

Let $\omega (x,t)=T_t^n+\underset{0}{\overset{1}{\int }}{T}_t^{n}dx$ , for which the equality holds $\underset{0}{\overset{1}{\int }}\omega (x,t)dx=0$, , therefore, there is a point $a\left(t\right)$ exists, such that $\omega \left(a\right(t),t)=0$. Then

$$\omega (x,t)=\omega (a\left(t\right),t)+\underset{a\left(t\right)}{\overset{x}{\int }}{\omega }_y(y,t)dy,$$

$$T_t^n-\underset{0}{\overset{1}{\int }}{T}_t^{n}dx=\underset{a\left(t\right)}{\overset{x}{\int }}{T}_{ty}^{n}dy,$$

$$T_t^n=\underset{0}{\overset{1}{\int }}{T}_t^{n}dx+\underset{a\left(t\right)}{\overset{x}{\int }}{T}_{ty}^{n}dy,$$

$$\mid T^n(x,t)-T^n(x,0)\mid =\mid \underset{0}{\overset{t}{\int }}{T}_{\tau }^{n}d\tau \mid =\mid \underset{0}{\overset{t}{\int }}(\underset{0}{\overset{1}{\int }}{T}_{\tau }^{n}dx+\underset{a\left(t\right)}{\overset{x}{\int }}{T}_{\tau y}^{n}dy)d\tau \mid \le$$

$$\le \mid \underset{0}{\overset{t}{\int }}\underset{0}{\overset{1}{\int }}{T}_{\tau }^{n}dxd\tau \mid +\mid \underset{0}{\overset{t}{\int }}\underset{a\left(t\right)}{\overset{x}{\int }}{T}_{\tau y}^{n}dyd\tau \mid \le \underset{0}{\overset{t_0}{\int }}\underset{0}{\overset{1}{\int }}\mid T_t^n\mid dxdt+\underset{0}{\overset{t_0}{\int }}\underset{0)}{\overset{1}{\int }}\mid T_{ty}^n\mid dxdt\le$$

$$\le \underset{0}{\overset{t_0}{\int }}\Vert T_t^n\Vert dt+\underset{0}{\overset{t_0}{\int }}\Vert T_{tx}^n\Vert dt\le N_5^{1/2}{t}_0^{1/2}+N_{18}^{1/2}{t}_0^{1/2}\le N_{19}{t}_0^{1/2}.$$

And then

$$\mid T^n(x,t)-T^n(x,0)\mid =\mid T^n(x,t)-T^0\left(x\right)\mid \le N_{19}{t}_0^{1/2},$$

$$T^0-N_{19}{t}_0^{1/2}\le T^n(x,t)\le T^0+N_{19}{t}_0^{1/2}.$$

That means if we choose $t_0\le {\left({\displaystyle \frac{b_1}{2N_{19}}}\right)}^2$ the following inequality will hold

$$0<{\displaystyle \frac{b_1}{2}}\le T^n(x,t)\le 2B_1<\infty .$$

Choosing $t_0=min\{{\left({\displaystyle \frac{b_1}{2N_{19}}}\right)}^2;{\left({\displaystyle \frac{1-B_0}{(1+M_0)\sqrt{2}{B}_0{N}_4^{1/2}}}\right)}^{4/3}\}$, we obtain inequalities (21) and (33) respectively, for $x\in [0,1],t\in [0,t_0]$.

The estimates (21), (33) and (36), (37) allow us to select converging subsequences from the sequences $\left\{{\rho }^n\right\},\left\{u^n\right\},\left\{T^n\right\}$. Passing to the limit in the equalities (17), (18), (31) and (32) shows that the limit functions $\rho ,u,T$ give a generalized solution on the interval [$0,t_0$]. Theorem 2 is proven.

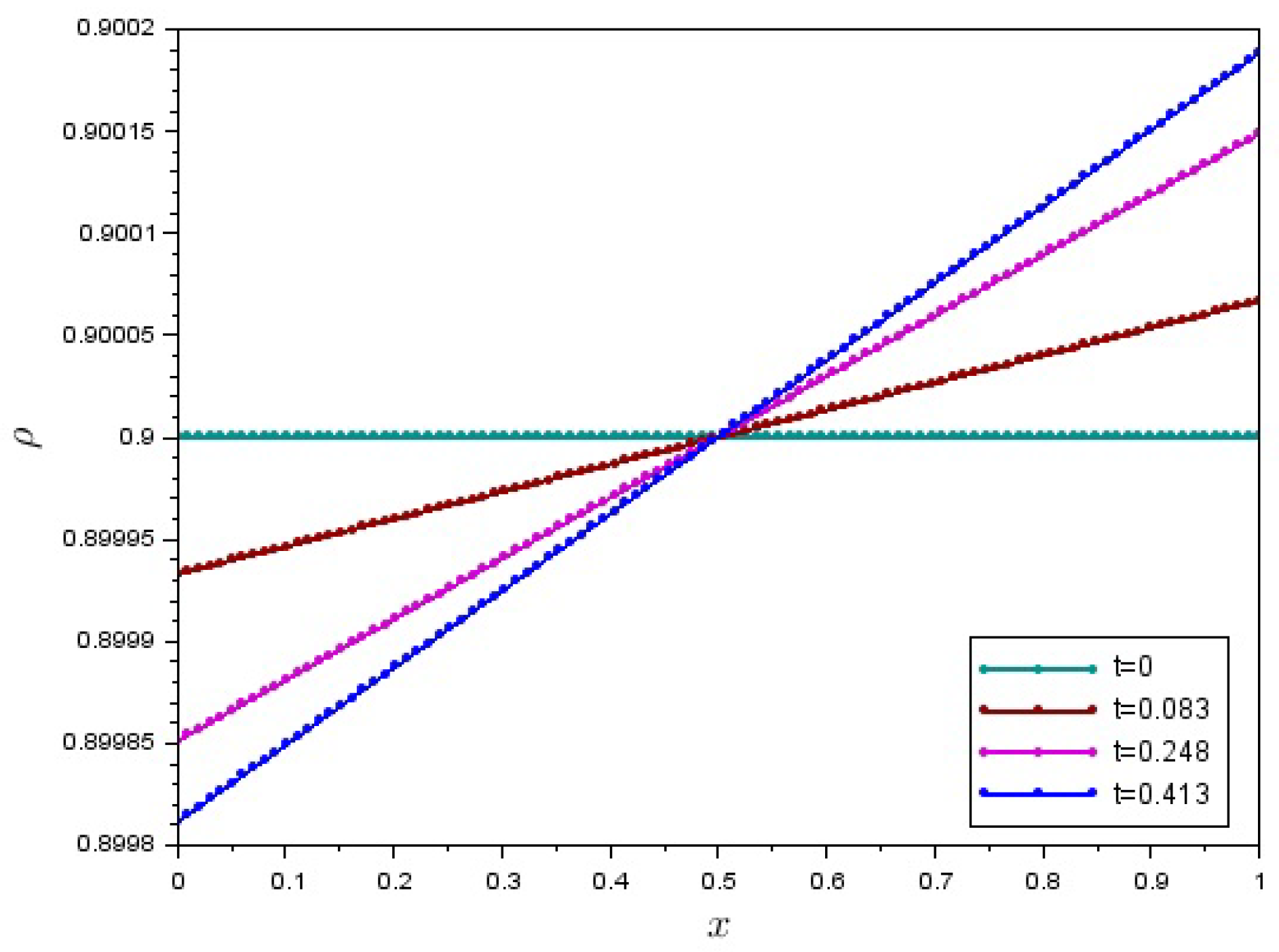
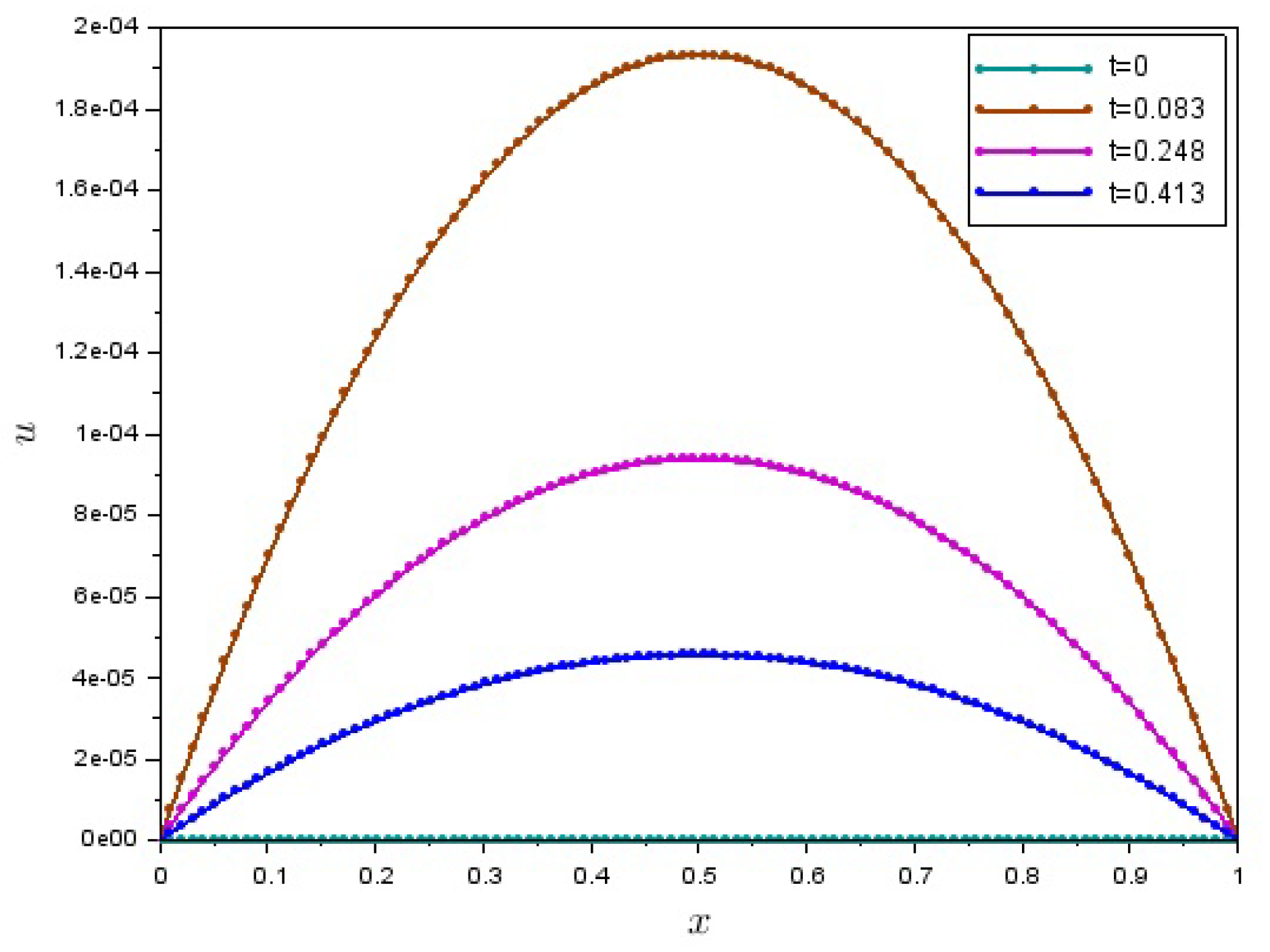
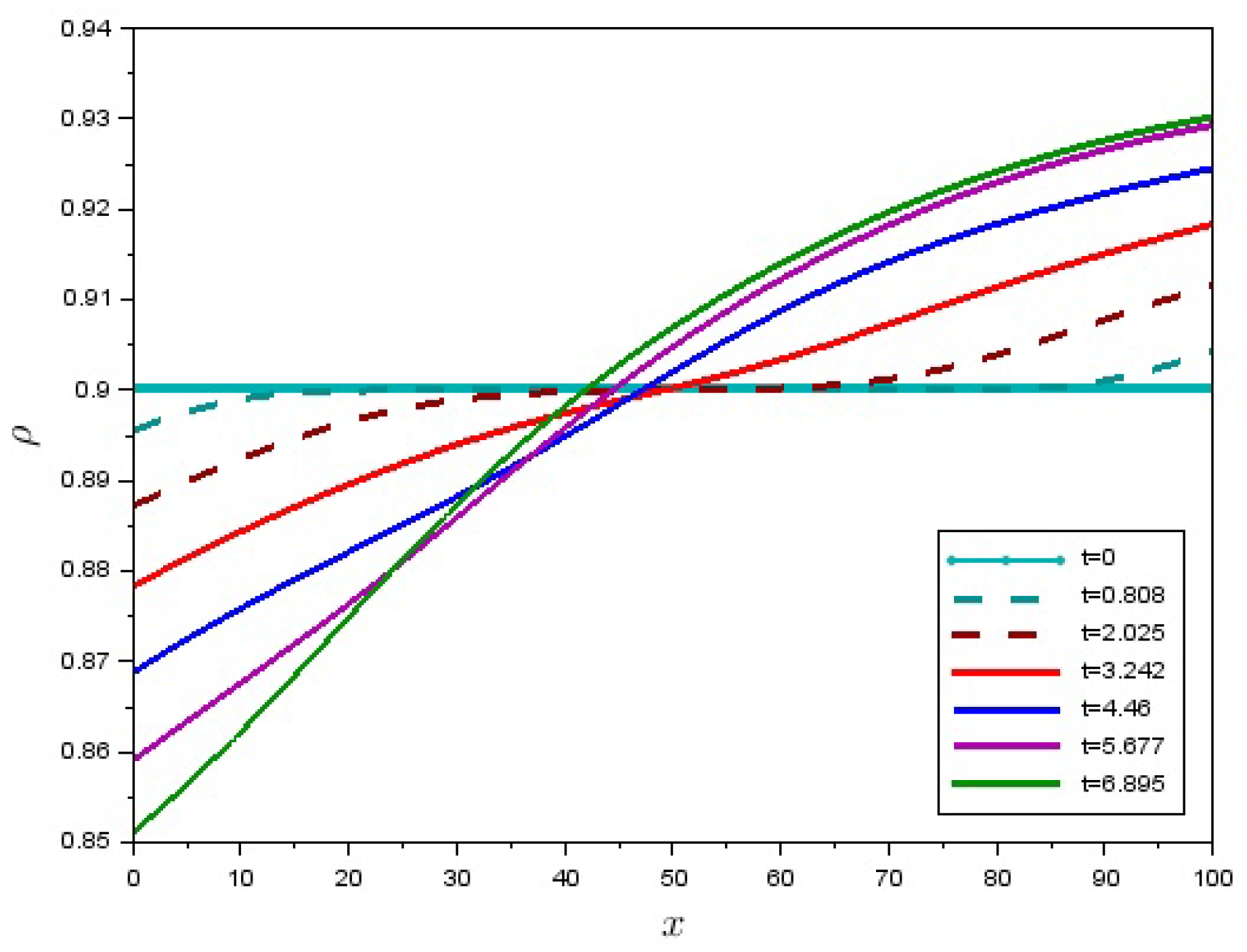
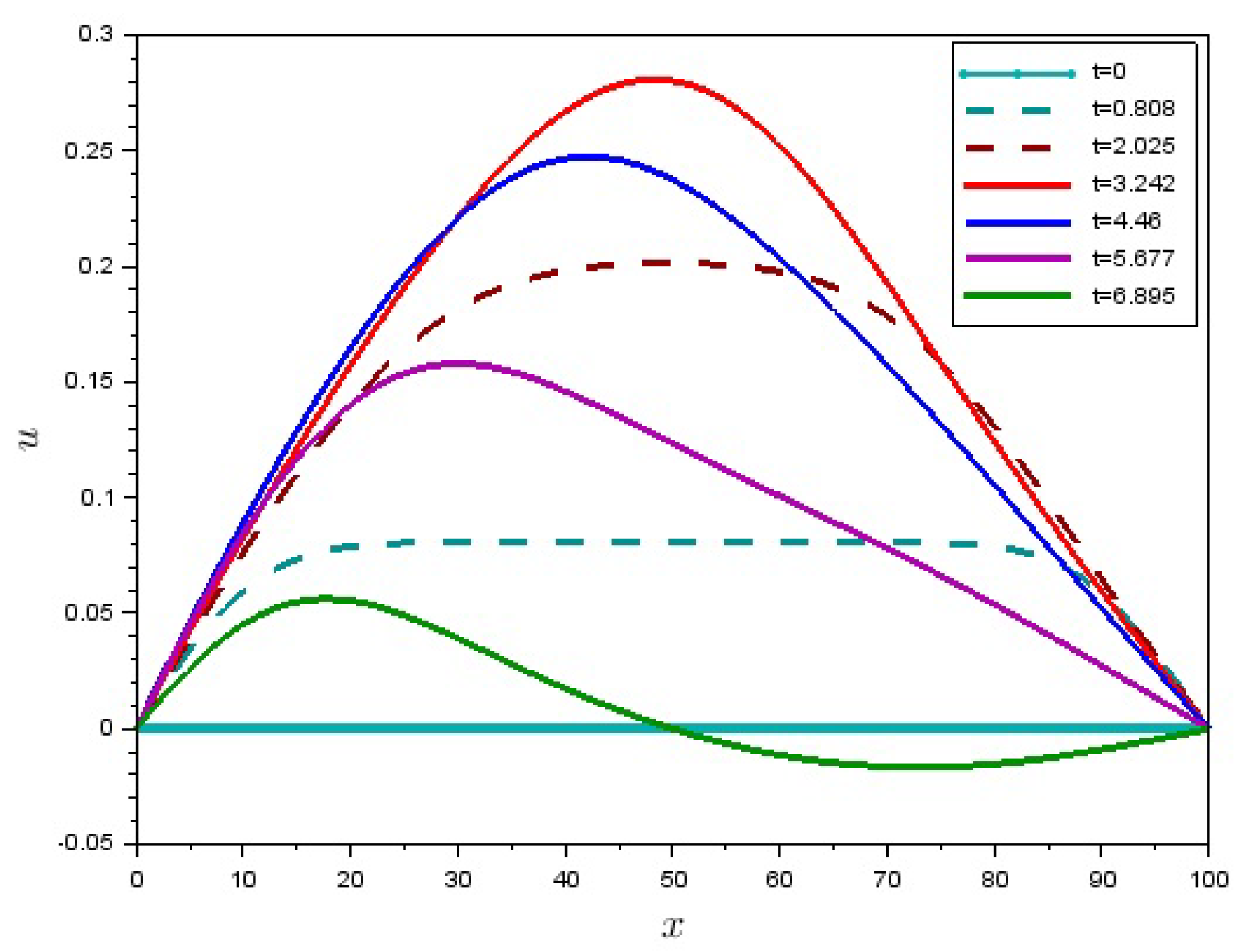
5. Numerical Solution of a Boundary-Value Problem for One-Dimensional Motion of a Granular Matter

We consider a numerical solution for the formulated problem, based on the finite difference approximation. Rewrite the one-dimensional equations system (7) and (8) in the following form:

$${\displaystyle \frac{\partial u}{\partial t}}=L_{u}u+f_u,{\displaystyle \frac{\partial \rho }{\partial t}}=L_{\rho }\rho .$$

(56)

The differential operators $L_u$, $L_{\rho }$ and right part $f_u$ have the form:

$$L_u={\displaystyle \frac{\partial }{\partial x}}\left({\displaystyle \frac{4}{3}}\mu \rho {\displaystyle \frac{\partial u}{\partial x}}\right),L_{\rho }={\rho }^2{\displaystyle \frac{\partial u}{\partial x}},f_u=G-{\displaystyle \frac{\partial p}{\partial x}}.$$

A solution of the problem is carried out by using the finite-difference method on the spatiotemporal mesh:

$$x_i=(i-1)h,t_n=(n-1)\tau ,$$

where $h={\displaystyle \frac{M}{N_x-1}}$ ) is the spatial coordinate step, $\tau$ is the temporal step, $i=1,2,\dots ,N_x$, $n=1,2,\dots ,N_t$. We introduce designations for the required functions in mesh points:

$$\rho (x_i,t_n)={\rho }_i^n,u(x_i,t_n)=u_i^n.$$

Derivatives with respect to spatial variables are written in central differences: ${\displaystyle \frac{\partial u}{\partial x}}\sim {\displaystyle \frac{u_{i+1}-u_{i-1}}{2h}}$, temporal derivatives are approximated with right differences: ${\displaystyle \frac{\partial u}{\partial t}}\sim {\displaystyle \frac{u^{n+1}-u_n}{\tau }}$ (formulas for density are similar).

The difference scheme which approximates the equations of (56) is represented as:

$$(E-\tau {\tilde{L}}_u)u^{n+1}=u_i^n+\tau {\tilde{f}}_u^n,$$

(57)

$${\rho }_i^{n+1}={\rho }_i^n+\tau {\tilde{L}}_{\rho }{\rho }^n.$$

(58)

E is the unity operator here, $Eu=u$.

The difference operators ${\tilde{L}}_u$, ${\tilde{L}}_{\rho }$ are approximate their corresponding to them differential operators as follows:

$${\tilde{L}}_u{u}^{n+1}={\displaystyle \frac{4}{3}}{\displaystyle \frac{1}{h^2}}\left({\left(\mu \rho \right)}_{i-1/2}^n{u}_{i-1}^{n+1}-({\left(\mu \rho \right)}_{i-1/2}^n+{\left(\mu \rho \right)}_{i+1/2}^n)u_i^{n+1}+{\left(\mu \rho \right)}_{i+1/2}^n{u}_{i+1}^{n+1}\right),$$

$${\tilde{L}}_{\rho }{\rho }^n=-{\left({\rho }_i^n\right)}^2{\displaystyle \frac{u_{i+1}^{n+1}-u_{i-1}^{n+1}}{2h}}.$$

Difference operator of the right side of ${\tilde{f}}_u$ is represented as:

$${\tilde{f}}_u=G-{\displaystyle \frac{p_{i+1}^n-p_{i-1}^n}{2h}}.$$

The values with fractional subscripts are defined as:

$${\left(\mu \rho \right)}_{i-1/2}^n={\displaystyle \frac{{\left(\mu \rho \right)}_i^n+{\left(\mu \rho \right)}_{i-1}^n}{2}},{\left(\mu \rho \right)}_{i+1/2}^n={\displaystyle \frac{{\left(\mu \rho \right)}_{i+1}^n+{\left(\mu \rho \right)}_i^n}{2}}.$$

The differencing scheme (57), (58) approximates the differential system (56) on smooth functions of order $O(\tau +h^2)$.

We propose the following realization of numerical calculations. At first iteration, nodal velocity values are calculated at $(n+1)$ time step using values of the sought functions, found at the previous time step. For that, the difference equations of (57) are reduced to a system of linear algebraic equations which makes possible to use the Tridiagonal Matrix method:

$$-c_i{u}_{i-1}^{n+1}+a_i{u}_i^{n+1}-b_i{u}_{i+1}^{n+1}=f_i,i=2,3,\dots N_x-1,$$

$$u_1^{n+1}=0,u_{N_x}^{n+1}=0.$$

Here

$$a_i=1+{\displaystyle \frac{4}{3}}{\displaystyle \frac{\tau }{h^2}}\left({\left(\mu \rho \right)}_{i-1/2}^n+{\left(\mu \rho \right)}_{i+1/2}^n\right),$$

$$b_i={\displaystyle \frac{4}{3}}{\displaystyle \frac{\tau }{h^2}}{\left(\mu \rho \right)}_{i+1/2}^n,c_i={\displaystyle \frac{4}{3}}{\displaystyle \frac{\tau }{h^2}}{\left(\mu \rho \right)}_{i-1/2}^n,$$

$$f_i=u_i^n+\tau \left(G-{\displaystyle \frac{p_{i+1}^n-p_{i-1}^n}{2h}}\right).$$

second iteration, nodal density values are calculated at the $(n+1)$ time step using the explicit difference scheme (58). It is proposed to obtain the density values at boundary nodes for $i=1$ and $i=N$ by extrapolation from the two nearest nodes.

Numerical calculations were carried out in the case of the dimensionless problem formulation. The $Ox$ axis is vertically directed and coincides with the gravity force. The initial values of density and velocity are set $u^0=0$, ${\rho }^0=0,9$, $G=1/10$. The variable x varies from 0 (upper bound) to $M={\rho }^0\tilde{L}$ (bottom line), where $\tilde{L}=1$.

Figure 1 and Figure 2 show the density and velocity profiles at different time moments, where the $Ox$ axis is understood in Euler variables. The calculations showed that the density increases at the bottom and decrease sat the top.

Figure 3 and Figure 4 present the density and velocity profiles at different time moments, the values on the $Ox$ axis correspond to Euler variables, $\tilde{L}=100$.

6. Conclusions

The Theorems on the local solvability of isothermal and non-isothermal problems for one-dimensional motion of a granular material are proved. The numerical solution based on the finite difference approximation is obtained.