Security Proof of SSSD Protocols Built on Top of SMC Protocol

1. Introduction

In recent years, SMC protocol has witnessed significant advancements in its ability to facilitate privacy-preserving computations across distributed networks. Among the various applications of SMC, one particularly compelling area of exploration has been the development of secure protocols for SSSD computations. These protocols hold immense promise for ensuring the confidentiality and integrity of data in scenarios where sensitive information, such as network graphs or distance metrics, needs to be computed collaboratively while preserving individual privacy. Additionally, recent developments in privacy-preserving computations over the Sharemind SMC platform [1,2] have emerged various methods and techniques applied to diverse fields, including data mining [3], genotyping [4,5], minimum spanning tree [6] and forest [7] problems, logic programming [8,9], and statistical data analysis [10,11]. In alignment with this progress, our proposed protocols, detailed in this paper, are also implemented over the Sharemind SMC platform, contributing to the growing body of research in secure and privacy-preserving computations.

In recent years, there has been substantial growth in research endeavors dedicated to developing pioneering shortest-path protocols designed for utilization on SMC platforms. These protocols have been intricately designed to cater to a broad spectrum of scenarios, each distinguished by unique graph characteristics encompassing variations in size and structure. Among these innovative protocols are the Bellman-Ford and Dijkstra protocols [12], renowned for their efficiency in traversing sparse and dense graphs, respectively, and specialized methodologies such as radius-stepping [13] and Breadth-First Search (BFS) [14], meticulously engineered to meet the computational requirements of spatial, dense, and planar graphs. In [15], a parallel algorithm based on Algebraic Path Computation (APC) is proposed, significantly improving the efficiency of privacy-preserving SSSD calculations compared to classical SSSD algorithms. The SSSD protocols are built upon optimized versions of combinatorial and classical algorithms, facilitated by parallel Single-Instruction-Multiple-Data (SIMD) frameworks, which have been implemented using the SecreC high-level language [16]. Notably, SecreC is a language designed with a focus on security, specifically tailored for privacy-preserving computations. Furthermore, these protocols benefit from utilizing a parallel oblivious reading subroutine developed by Laud [17].

Abstractions play a vital role in advancing complex cryptographic protocols like SMC by allowing for the deduction of both functional and non-functional properties of the results. An essential abstraction in the context of secure multiparty computation is the Arithmetic Black Box (ABB) [18], which provides a means to describe more intricate privacy-preserving computations without delving into the intricacies of the protocols governing primitive operations involving private data. The ABB functions as an ideal functionality in the framework of Universal Composability (UC) [19], while its corresponding real functionality comprises the concrete protocol implementations for individual operations involving private data [20].

The focus of this paper revolves around an in-depth examination and analysis of the security and privacy aspects pertaining to the integration of the SSSD protocol supported by the ABB. Additionally, we explore the construction of the SSSD protocol on top of SMC within the framework of Universal Composability. It is imperative that we ensure the security of the SSSD protocol when built upon SMC protocols, guaranteeing that the security properties remain robust and unaffected by advancements in SSSD algorithms. The incorporation of the SIMD approach in the development of these algorithms aims to mitigate round complexity in computations implemented atop SMC protocols.

These pioneering advancements represent significant strides in secure computations, offering tailored solutions for diverse real-world scenarios where privacy-preserving shortest-path computations are imperative. This combined introduction provides an overview of the significance of SMC in preserving privacy, particularly in the context of SSSD computations, and highlights the relevance of this work in the broader landscape of privacy-preserving computations over the Sharemind SMC platform.

2. Materials and Methods

2.1. Secure Multiparty Computation

Secure multiparty computation (SMC/MPC) stands as a cryptographic protocol enabling a group of n participants, denoted as ${\mathcal{P}}_1$,…, ${\mathcal{P}}_n$, to collaboratively compute a function $(y_1,\dots ,y_n)=\mathcal{F}(x_1,\dots ,x_n)$, where each party ${\mathcal{P}}_i$ submits their respective input $x_i$ and receives their output $y_i$ [23]. Critically, this protocol ensures that the individual party, $\left\{{\mathcal{P}}_i\right\}$, gains no additional knowledge beyond their input $x_i$ and output $y_i$, and any information derivable from them, considering the publicly known description of the function $\mathcal{F}$. To extend this privacy guarantee, a concept of a downwards closed set emerges, encompassing subsets of $\{1,\dots ,n\}$. For any such subset I within this set, the coalition of parties ${\left\{{\mathcal{P}}_i\right\}}_{i\in I}$ is precluded from acquiring any supplementary information beyond their respective inputs ${\left(x_i\right)}_{i\in I}$ and outputs ${\left(y_i\right)}_{i\in I}$ during executing the computation of $\mathcal{F}$.

Generic protocols for secure multiparty computation effectively translate a computational task, typically represented as a boolean or arithmetic circuit, into a cryptographic protocol [24,25,26]. Diverse approaches exist for executing the circuit or program representing the function $\mathcal{F}$ while preserving privacy. These methods include garbled circuits [24], homomorphic encryption [27,28], or secret sharing [29,30,31] each offering different security assurances against both passive and active adversaries [32]. The secret sharing approach, specifically, accommodates adversaries capable of corrupting a fraction of the total n computation parties, denoted as $\left\{{\mathcal{P}}_n\right\}$, with the threshold parameter t varying depending on the adversary’s protocol ${\Pi }^{\prime }$. In cases involving a passive adversary, security is achieved when the number of computation parties corrupted, t, is less than n/2. For an active adversary, security holds when t is less than n/3.

A passive adversary, also known as a semi-honest adversary, corrupts computation parties $\left\{{\mathcal{P}}_i\right\}$ but adheres faithfully to the protocol’s execution steps to gain additional insight into other computation parties’ messages. In the semi-honest model, a protocol $\Pi$ is considered secure if the entirety of the computations $(y_1,\dots ,y_n)=\mathcal{F}(x_1,\dots ,x_n)$ performed by a party ${\mathcal{P}}_i$ within $\Pi$ can only be inferred from their input $x_i$ and output $y_i$.

In contrast, a malicious adversary can persuade corrupted parties $\left\{{\mathcal{P}}_i\right\}$ to deviate arbitrarily from the prescribed protocol ${\Pi }^{\prime }$ to compromise the overall security of protocol $\Pi$. This malicious adversary shares certain characteristics with semi-honest adversaries, enabling them to learn information about computation parties’ messages $\left\{{\mathcal{P}}_i\right\}$ and take actions that could jeopardize security. Importantly, malicious adversaries have more advanced capabilities, such as message alteration, manipulation, and the arbitrary creation of messages for computation parties $\left\{{\mathcal{P}}_i\right\}$. The concept of universal composability in SMC is introduced to establish a comprehensive framework for analyzing cryptographic protocols with robust security properties [19,33]. This framework provides a generalized and rigorous approach to assessing the security and integrity of SMC protocols in a broader context.

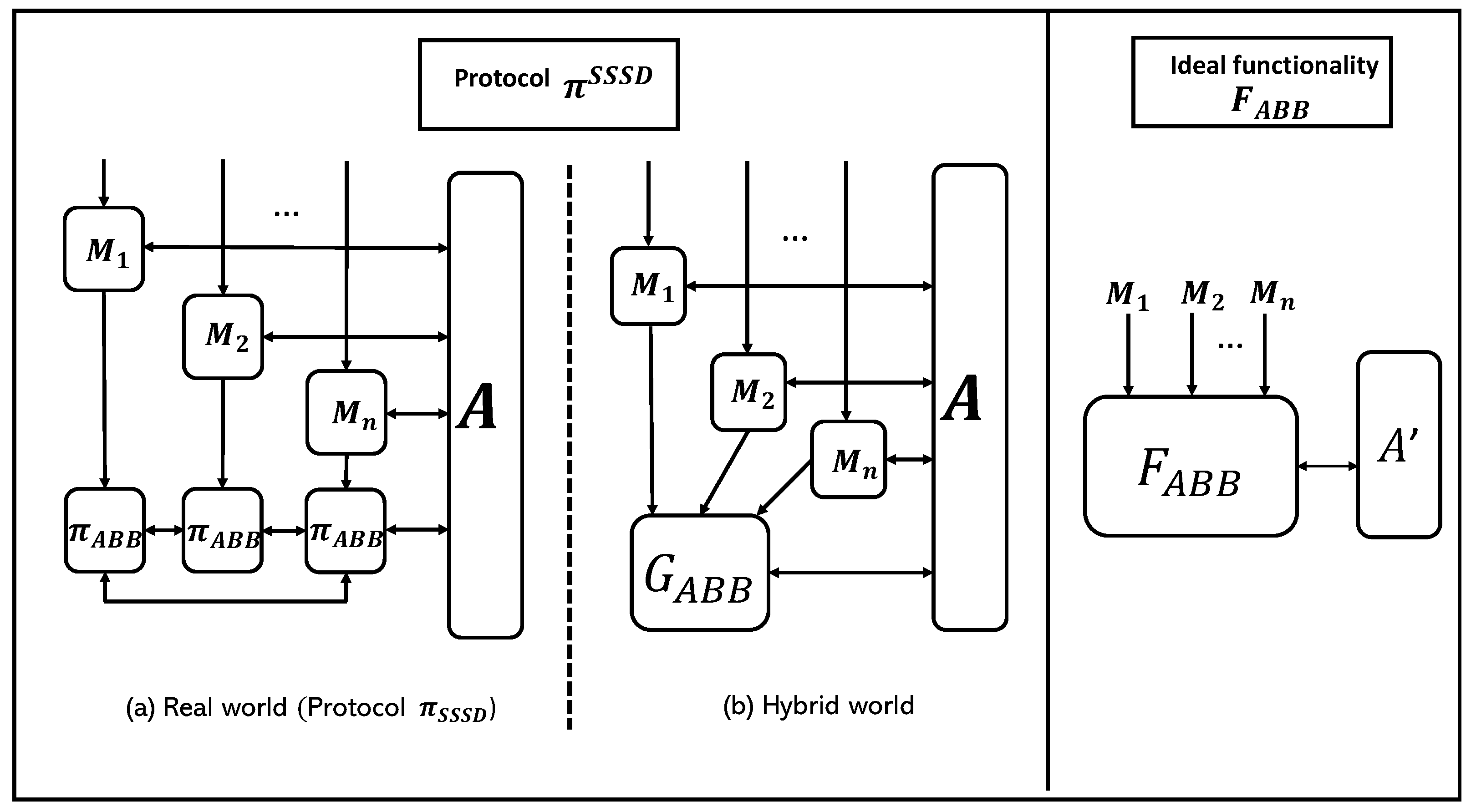
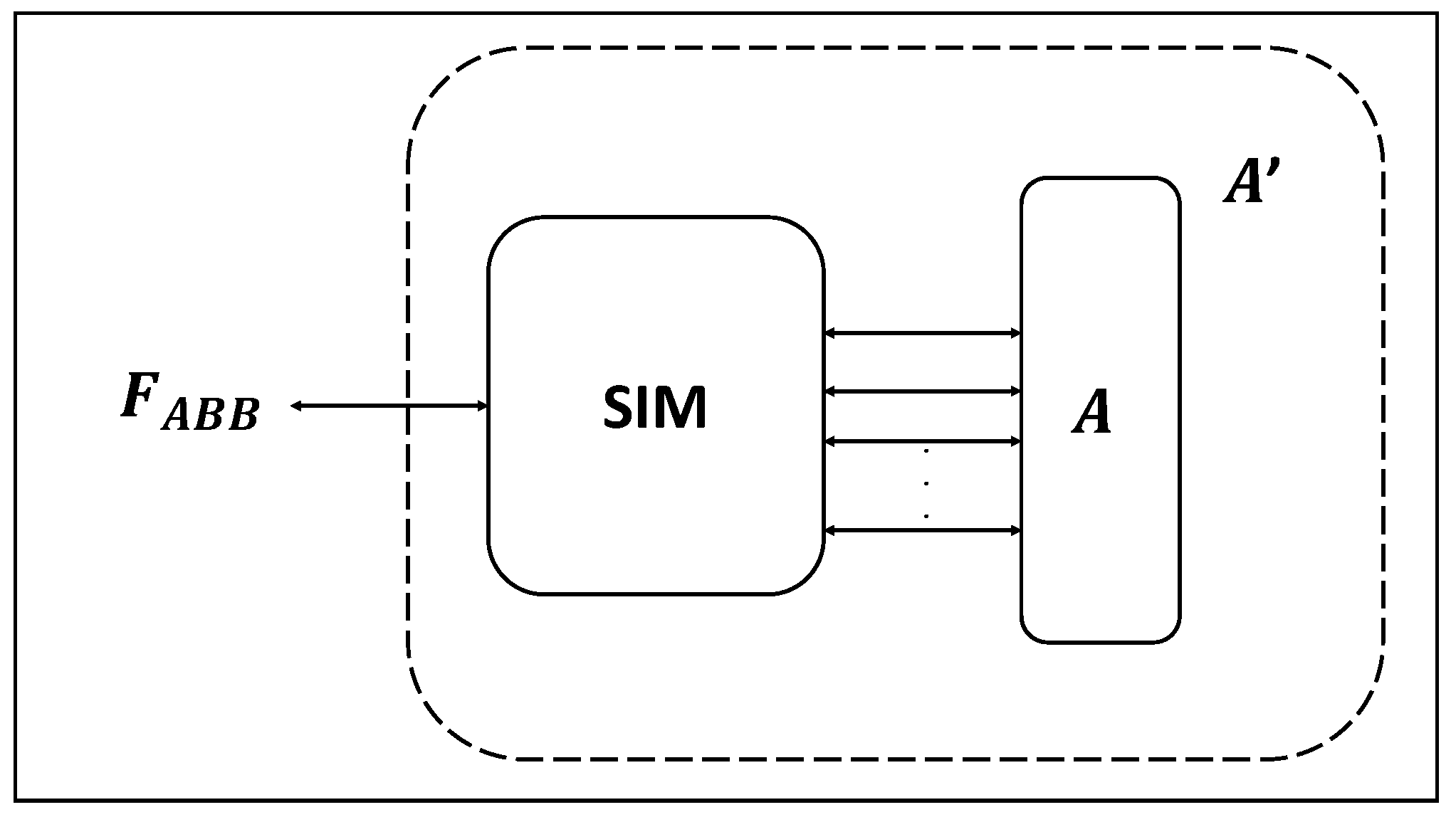
2.1.1. Universal Composability

The Universal Composability (UC) framework revolves around interconnected Turing machines operating concurrently and exchanging information among themselves, including the adversarial Turing machines — the adversary $\mathcal{A}$ and the environment $\mathcal{Z}$. According to this framework, secure implementation occurs when one set of Turing machines can securely emulate the behavior of another set, meaning that any possible view (determined by the choice of $\mathcal{A}$) of $\mathcal{Z}$ running in parallel with the first set of machines is also achievable when running in parallel with the second set of machines.

The true strength of this framework lies in its composition theorem. Suppose that in the context of the UC framework, a protocol $\Pi$ securely implements an ideal functionality $\mathcal{G}$ in the $\mathcal{F}$-hybrid model, meaning that the Turing machines comprising $\Pi$ have access to an ideal functionality $\mathcal{F}$. Suppose another protocol, $\Xi$, securely implements functionality $\mathcal{F}$. In that case, the composition of $\Pi$ and $\Xi$, achieved by combining each protocol party’s Turing machine from $\Pi$ with their corresponding machine in $\Xi$, securely implements $\mathcal{G}$.

In the ideal world, computation parties ${\mathcal{P}}_i$ confidentially transmit their private inputs $x_i$ to a trusted party, ${\mathcal{T}}_p$, for the computation of functionality $\mathcal{F}$. Each party possesses its private input, $x_i\in \{x_1,x_2,\dots ,x_n\}$, which they send to ${\mathcal{T}}_p$ for secure computation of $\mathcal{F}$$(x_1,x_2,\dots ,x_n)$. Subsequently, the results $(y_1,y_2,\dots ,y_n)$ are returned to the parties $P_i$. It’s important to note that every party knows their own $x_i$, and learns their individual output $y_i$, but does not gain knowledge of other parties’ $x_j$ and $y_j$. When an adversary, $\mathcal{A}$, attempts to breach the ideal world, they can only exert control over the computation parties$\left\{{\mathcal{P}}_i\right\}$, not the trusted party ${\mathcal{T}}_p$.

In the real world, the trusted party ${\mathcal{T}}_p$ is absent, and the ideal world with its trusted party ${\mathcal{T}}_p$ is used solely as a benchmark for evaluating the security of actual protocols. Instead of ${\mathcal{T}}_p$, the real world employs a protocol $\Pi$ for parties to communicate with one another while securely computing function $\mathcal{F}$. In this scenario, computation parties execute protocol $\Pi$, transmitting their private inputs $\{x_1,x_2,\dots ,x_n\}$ to function $\mathcal{F}$ and receiving their private outputs $\{y_1,y_2,\dots ,y_n\}$. An adversary $\mathcal{A}$ may corrupt the computation parties $\left\{{\mathcal{P}}_i\right\}$, causing them to either deviate arbitrarily from their expected behavior or adhere to the protocol $\Pi$. The protocol $\Pi$ is deemed secure if adversary $\mathcal{A}$ cannot achieve any outcome in the real world that cannot also be achieved by a corresponding adversary ${\mathcal{A}}^{\prime }$ in the ideal world.

2.1.2. Arithmetic Black Box

The Arithmetic Black Box (ABB) represents an ideal functionality, referred to as ${\mathcal{F}}_{\mathcal{ABB}}$, designed for performing computations involving private data. ${\mathcal{F}}_{\mathcal{ABB}}$ enables participants to securely store their confidential information, execute operations based on user instructions, and furnish specific values to users upon request, provided a sufficient number of users make such requests.

For instance, suppose a party initiates a command, $\mathbf{store}\left(v\right)$ instructing the ideal functionality to perform a calculation, with v representing a certain value. ${\mathcal{F}}_{\mathcal{ABB}}$ receives and securely stores this value v while assigning it a unique identifier, denoted as h by creating a pairing of $(h,v)$. Subsequently, ${\mathcal{F}}_{\mathcal{ABB}}$ distributes h to all participating parties. To perform computations without disclosing intermediate results, the ABB awaits a command, such as $(\mathsf{perform},op,h_1,\dots ,h_k$) from all participating computation parties or a sufficient number thereof. It then retrieves the values $v_1,\dots ,v_k$ associated with the respective handles $h_1,\dots ,h_k$, applies the specified operation $op$ to these values, yielding a result v which it stores under a new handle h. This h is then returned to all participating parties. To access a value stored under a particular handle h, all participating parties must issue the command, $\mathbf{declassify}\left(\mathbf{h}\right)$ to the ABB. In response, the ABB looks up the pair $(h,v)$ and provides the value v [18].

It is important to note that the ideal functionality ${\mathcal{F}}_{\mathcal{ABB}}$ forwards commands from parties ${\mathcal{P}}_1$, ⋯, ${\mathcal{P}}_n$ to the adversary, excluding sensitive input values that are part of a command. Additionally, the adversary receives the fresh handles created by the ABB and the results of declassification.

2.1.3. Sharmind Protocols Set

This study is predicated on the premise that the ABB functionality is realized through the Sharemind protocol set [2]. Within this context, we operate under the assumption that the ABB encompasses a spectrum of operations. These operations encompass logical manipulations involving private booleans, arithmetic operations on private n-bit integers across varying bit lengths n, conversions between different data types, the ability to sort private values, assignment of private values, and the capacity for classifying and declassifying data between the realms of public and private. Furthermore, this ABB framework accommodates operations related to private read and write for private vectors using private indices, all of which can be efficiently performed in a SIMD fashion. Notably, analogous operations are available in alternative protocol implementations such as the SPDZ [21] protocol set, characterized by its security provisions against active adversaries.

2.2. Graphs

A graph is a mathematical structure comprising of a set of vertices denoted as V, which are connected in various ways by edges from the set E. These edges can also possess values describing the distance or weight. A graph can take on different forms; it can be directed, meaning that edges have a specific direction between vertices, or can be undirected, allowing for connections in both directions. Let’s denote a directed weighted graph as $G=(V,E)$, where the vertex set is $V=\{0,1,2,\dots ,n-1\}$, and the set of directed weighted edges is $E\subseteq V\times V$. Each edge $e\in E$ is assigned a weight $w\left(e\right)$∈ the set of real numbers $\mathbb{R}$.

When it comes to representing a graph $G=(V,E)$ in computer memory, there are two common approaches. The first is the adjacency matrix, which takes the form of a $\left|V\right|\times \left|V\right|$ matrix, where the entry in the u-th row and v-th column represents the weight $w(u,v)$ of the edge between vertices u and v. This representation has ${\left|V\right|}^2$ entries and is often referred to as the dense representation. Conversely, the adjacency list representation provides, for each vertex $u\in V$, a list of pairs $(v_1,w_1),(v_2,w_2),\dots ,(v_k,w_k)$, where $(u,v_1),(u,v_2),\dots ,(u,v_k)$ are all the edges in G that originate from vertex u, and $w_i=w(u,v_i)$. This representation has O(|E|) entries and is called the sparse representation. When the number of edges $\left|E\right|$ is significantly smaller than ${\left|V\right|}^2$, the sparse representation occupies less memory, and algorithms designed for it often exhibit improved efficiency [34].

Graphs, or an infinite family of graphs, can be categorized as sparse if the number of edges is “proportional” to the number of vertices, denoted as $\left|E\right|=O\left(\right|V\left|\right)$. Conversely, a graph is considered dense when $\left|E\right|=\omega \left(\right|V\left|\right)$, signifying a high edge-to-vertex ratio. Furthermore, a graph is planar if it can be represented in a plane without edge crossings outside the vertices. For planar graphs, Euler’s formula relates the numbers of edges, vertices, and faces in its drawing, establishing that $\left|E\right|\le 3\left|V\right|-6$ [35].

2.2.1. Shortest Path

A path denoted as $\delta (u,v)$ from a source vertex u to a target vertex v within the graph G is defined as a finite sequence of vertices $u=v_0,v_1,\dots ,v_n=v$, where there exists an edge $(v_{i-1},v_i)\in E$ for all $i\in \{1,\dots ,n\}$.

The shortest path between two vertices, $\delta (u,v)$, within a graph G is a path that possesses the minimum total sum of weights ${\sum }_{i=1}^{n}w(v_{i-1},v_i)$ among all possible paths from the source vertex u to target vertex v, shortest distance from u to v is [36]:

$$w(u,v)=\left\{\begin{array}{cc}mi{n}_p\left\{w\left(p\right)\right\},\hfill & \mathrm{if}\mathrm{there}\mathrm{exists}\mathrm{a}\mathrm{path}p=\delta (u,v)\hfill \\ \infty ,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

The shortest path problem involves discovering a path between two vertices within a graph denoted as $G=(V,E)$ where the sum of edge weights, represented as $w\left(e\right)\in R$, from vertex u to vertex v is minimized. This problem holds significant importance in the realms of combinatorial and algebraic graph theories, as it involves crucial trade-offs between computation and communication costs that make certain algorithms more suitable for specific scenarios.

In the context of small to medium-sized graphs, finding the shortest distances from a single source vertex can be achieved by employing classical sequential algorithms such as Dijkstra [38], Bellman-Ford [37], or Thorup [39]. Dijkstra’s algorithm operates effectively with non-negative edge weights, whereas Bellman-Ford handles graphs with some negative weights. Bellman-Ford’s time complexity is $\mathcal{O}\left(nm\right)$ for general graphs, where n represents the number of vertices, and m denotes the number of weighted edges in the graph G. The time complexity of Dijkstra’s algorithm is $\mathcal{O}\left(n^2\right)$ in the adjacency matrix representation of G, and $\mathcal{O}(mlogn)$ in the adjacency list representation when utilizing a binary heap.

While some sequential algorithms may exhibit poor worst-case performance, they can perform adequately for certain types of graphs. However, processing larger graphs often necessitates the use of parallel algorithms. Notable parallel algorithms for solving the single-source shortest path problem include the $\Delta$-Stepping [40] and Radius-Stepping [41] algorithms. The $\Delta$-Stepping algorithm adjusts tentative distances of vertices multiple times during edge relaxation until all tentative distances are finalized; it is referred to as a label-correcting algorithm. In contrast, the Radius-Stepping algorithm addresses a limitation of the $\Delta$-Stepping approach by providing a provable upper bound on the number of steps. The average time complexity of the $\Delta$-Stepping algorithm is $\mathcal{O}(nlogn+m)$, while it is $\mathcal{O}(mlogn)$ for the Radius-Stepping algorithm.

Shortest paths can also be computed using non-traditional algorithms, such as search algorithms like Breadth-First Search, and alternative techniques like Algebraic Path Computation. The algebraic path problem employs a distinctive approach based on a specialized algebraic structure known as a closed semiring. Additionally, this problem addresses various graph-related challenges beyond algebraic paths [42].

2.3. Bellman-Ford Protocols on Top of MPC

In [12], two privacy-preserving Bellman-Ford protocols were designed for sparse graphs. Both versions of these protocols share a similar main program structure, with the primary distinction lying in the parallel algorithm used in the PefixMin2 subroutines. The Bellman-Ford algorithm, which iteratively updates edges in a graph, can be executed in a privacy-preserving manner using a Sharemind-inspired ABB. This approach is suitable for sparse graph representations involving public values n (vertices) and m (edges), along with private vectors $〚\overrightarrow{S}〛$, $〚\overrightarrow{T}〛$, and $〚\overrightarrow{W}〛$, containing information about edge start and end vertices and their weights. Importantly, this representation maintains privacy by concealing the graph structure, including vertex degrees, while allowing for efficient computation.

The algorithm described in Algorithm 1 computes distances from a designated starting vertex s. Subroutines in Algorithm 2 and Algorithm 4 support this process. When the initial requirements specified in Algorithm 1 are not met, a privacy-preserving solution can be achieved by adding extra edges to the graph, increasing the lengths of $〚\overrightarrow{S}〛$, $〚\overrightarrow{T}〛$, and $〚\overrightarrow{W}〛$, and sorting the inputs based on $〚\overrightarrow{T}〛$. This approach introduces challenges in edge relaxation since it involves locating private values such as $D\left(S\right[i\left]\right)$. However, the algorithm can leverage parallel reading subroutines because it relaxes all edges concurrently. To streamline these operations, the prepareRead routine is invoked once at the start, with subsequent iterations utilizing the more efficient performRead routine.

Algorithm 1: Privacy-preserving Bellman-Ford, main program

The algorithm then calculates $〚\overrightarrow{b}〛$, representing the sum of the current distance from the starting vertex of an edge and the length of that edge. When computing sums $b\left[i\right]=D\left[S\right[i\left]\right]+W\left[i\right]$, the value $D\left[T\right[i\left]\right]$ must be updated if it is smaller than any other $b\left[j\right]$ where $T\left[i\right]=T\left[j\right]$. Thanks to a loop edge of length 0 at the starting vertex, this process is simplified as it eliminates the need to consider the old value of $D\left[T\right[i\left]\right]$ during updates. These updates align naturally with parallel writing, where concurrent writes to the same location prioritize the smallest value.

Algorithm 1 focuses on improving the efficiency of parallel reading updates, with particular attention to unchanging indices across iterations. The approach starts by initially calculating the minimum distances for all vertices without considering specific edge endpoints. It utilizes the sorted nature of vector $〚\overrightarrow{T}〛$ to group edges that end at the same vertex into a single segment within vector $〚\overrightarrow{b}〛$. For each of these segments, the minimum distance is computed and stored in vector $〚\overrightarrow{c}〛$, positioned at an index corresponding to the last vertex of that segment. Retrieval of this value is facilitated by employing another performRead operation, with the read indices stored in vector $〚\overrightarrow{Z}〛$. The process of minimizing distances for segments with private start and end points is accomplished through prefix computation, applying an associative operation similar to determining the minimum value.

Algorithm 2: PrefixMin2 (version 1)

This approach combines vectors $\overrightarrow{T}$ and $\overrightarrow{b}$, computes prefix-min2, and results in pairs where the first components represent $\overrightarrow{T}$, and the second components indicate prefix-minima for corresponding segments in $\overrightarrow{b}$. Using the efficient Ladner-Fisher parallel prefix computation method [43], Algorithm 2 computes privacy-preserving prefix-min2. This process is simplified because the $\overrightarrow{T}$-component remains constant, yielding a list of second components. Our ABB supports all the operations required in Algorithm 2.

The process of computing vector $〚\overrightarrow{Z}〛$ for marking segment ends in $〚\overrightarrow{T}〛$ (Algorithm 3) follows standard steps. Initially, we create an index vector $〚\overrightarrow{b}〛$ with m elements, where n elements are true. To enhance privacy, we apply a random permutation to $〚\overrightarrow{b}〛$ using the apply-routine, associating each element with an index i in the original sorted vector $〚\overrightarrow{v}〛$. After this permutation, we convert the result from private to public using the declassify routine, resulting in a randomized Boolean vector of length m with precisely n true elements. This distribution can be predicted based solely on n and m without needing $〚\overrightarrow{b}〛$. Importantly, this declassification step doesn’t compromise the privacy of our SSSD algorithm. Detecting shortest paths becomes challenging when dealing with graphs containing negative-length cycles, as such cycles can make any path appear cheaper. To address this, Algorithm 1 could be modified to identify negative cycles by performing an additional iteration of its main loop and checking for changes in $〚\overrightarrow{D}〛$ during this extra iteration.

Algorithm 3: GenIndicesVector

Algorithm 4: prefixMin2 (version 2)

Nevertheless, there are various trade-offs available between communication and round complexity. To explore these trade-offs, the authors in [12] also implemented the prefixMin2 method using the Hillis-Steele parallel prefix computation approach [44]. This alternative implementation is outlined in Algorithm 4. It effectively conveys that the second version of the Bellman-Ford protocol is created by replacing the call in Algorithm 1 with a different implementation. Algorithm 4 consists of a single loop executed $\mathcal{O}(logn)$ times. The round complexity for each iteration is the sum of the round complexities for finding the minimum and performing an oblivious choice. The primary contributor to complexity is finding the minimum, while the oblivious choice necessitates only a single round of communication. In comparison to Algorithm 2, this approach reduces round complexity by approximately half. However, it increases data volume usage by around a factor of $\mathcal{O}(logn)$.

3. Results

3.1. Security of Protocols Built on Top of ABB

Recently, novel protocols and related algorithms for privacy-preserving SSSD computations have been introduced. These protocols are designed to handle input data structured in a confidential manner, which can be presented either in the form of an adjacency matrix or through the utilization of three private vectors. Notably, these protocols are grounded on a universally composable ABB framework. It is crucial to highlight that the privacy-preserving nature of protocols built on top of ABB hinges on the absence of declassification operations. In this context, declassification pertains to converting private data into public data. When no declassification operations are involved, the protocols inherently maintain their privacy-preserving characteristics. Furthermore, when these protocols are combined with an SMC protocol set, serving as a secure implementation of the ABB, the resultant composition inherits the security and privacy properties of the underlying protocol set, as demonstrated in prior research [18].

However, it is imperative to acknowledge that the proposed SSSD protocols contain declassification operations. Consequently, unintended information leakage occurs in certain instances, notably with the inadvertent disclosure of the number of iterations in algorithms such as Algorithm 2 in [13], Algorithms 1 and 2 in [14]. Additionally, in specific versions of Dijkstra’s protocol, specifically, Algorithm 5 in [12] and Algorithm 9 in [45], unintentional revelation transpires as the identities of source vertices s and start-point edges u become apparent due to masking through permutation. Nonetheless, asserting the following security theorem is prudent despite these inadvertent disclosures. Nonetheless, we can formulate the ensuing security theorem as follows:

Theorem 1. 

If our SMC protocol set effectively implements an ABB for a group of k computing parties, providing security against an active or passive adversary who can corrupt up to t computing parties, then an active or passive adversary concurrently participating with k parties executing any of the abovementioned SSSD protocols alongside this SMC protocol set for private computations, with the ability to corrupt a maximum of t parties, will gain no insight into the inputs of the protocol beyond the graph’s number of vertices and edges and the initial vertex s.

Proof of Theorem 1. 

It is imperative to devise a simulator capable of emulating the adversary’s perspective in both the ideal and real-world scenarios. Within this simulator, an emulation of the Arithmetic Black Box’s ideal functionality is operational. In the context of the ideal world, the adversary’s access is restricted to solely two pieces of information, namely n representing the total number of vertices and s designating the source vertex. Conversely, in the real-world context, when multiple computation parties succumb to compromise, the adversary’s purview extends to encompass several additional components, which encompass:

• The input parameters, encompassing n (denoting the quantity of vertices) and s (indicating the source vertex).
• The handles to private values, identified within variables denoted as $〚·〛$ in the algorithm, regardless of whether these values manifest as individual elements, vectors, or an adjacency matrix.
• Declassified values, which may assume the form of integer values, individual elements, or complete vectors.
• In scenarios wherein the adversary assumes an active role, they gain insight into the ABB’s responses to efforts by the corrupted parties to deviate from the prescribed SSSD protocol.

The composition theorem within the universal composability framework addresses the observations made by the real-world adversary, which occur through compromised parties during the execution of SMC protocols implementing the ABB. Additionally, it accounts for the ramifications of any deviations from these protocols by the compromised parties.

In the ideal-world scenario, the adversary provides the simulator with the parameters n and s. Notably, the values associated with the handles (in contrast to those they reference within the ABB) are publicly accessible, enabling the simulator to derive these values. Furthermore, the simulator actively monitors and records the instructions transmitted to the ABB by all k parties. It also acquires knowledge regarding any instances of misconduct by corrupted parties deviating from the SSSD protocol and its associated subroutines while also tracking the responses of the ABB.

Within the SSSD protocols, the declassified values can pertain to either the number of iterations n or to the identities of the source vertices s of edges. In algorithms that employ the declassification of source vertices, an initial step involves the random permutation of vertices. This permutation is conducted as an essential preprocessing step while maintaining the privacy of the permutation itself, thereby preventing visibility to potential adversaries. Consequently, the sequence in which vertices are selected for relaxation, specifically their inclusion in the set M within the primary loop, is inherently randomized.

To simulate declassified values for the source vertices, the simulator Sim employs a random permutation technique on the range of integers from 0 to $n-1$. Subsequently, these values can be disclosed either as a single vector during the declassification process, as indicated in line 7 of Algorithm 5 in [12], or divulged individually one by one during declassification, as illustrated in line 15 of Algorithm 5. Alternatively, the simulator can release them as vectors, where each vector is disclosed incrementally, such as during the declassification process in line 16 of Algorithm 9 in [45].

In an algorithm where the declassification of the number of iterations n is performed, it is noteworthy that the outcomes of the algorithms do not straightforwardly derive from the publicly available graph parameters. A practical approach to mitigate this information leakage involves empirically establishing an upper bound on the iterations. By consistently executing a minimum number of iterations equal to this determined upper bound in such algorithms, it becomes possible to minimize this information disclosure effectively. This approach preserves the benefits of iteration, ensuring the process continues only as long as significant changes occur while simultaneously enhancing privacy.

The number of iterations n required is contingent upon a multitude of parameters, incorporating the underlying structure of the graph G, the potential influence of radii r considerations within the radius-stepping protocol, and the volumetric composition of edges, particularly relevant in protocols like BFS. A noteworthy illustration lies in the case of the UBFS protocol when applied to a densely interconnected graph. In such scenarios, the algorithm showcases a constant round complexity, culminating in termination after a singular iteration, as extensively expounded upon in BFS protocol. Consequently, the inadvertent disclosure of the iteration count remains bereft of practical significance, for it fails to endow the adversary with any discernible insights into the intricacies of the computational process. □

3.2. Detailed Security Proof for Privacy-Preserving Bellman-Ford

The process of computing the SSSD on the foundation of SMC protocol inherently upholds privacy, as it refrains from declassifying any private data. Nevertheless, we employ declassification exclusively reserved for permuted private data. Within the realm of the Universal Composability security definition, composability stands out as a pivotal feature. This attribute empowers developers to construct expansive privacy-preserving applications and allows researchers to introduce novel operations into the ABB. While the fundamental ABB operations encompass arithmetic and logical functions, discussions regarding comparisons and permutations can be found in Section 2.2 of [12]. Notably, other scholars have expanded the ABB’s repertoire to incorporate innovative operations, such as sorting [46,47], and private read/write, as discussed in [17], which predominantly feature in various research contributions within the scope of [12].

Based on these contributions, we postulate the existence of an implementation denoted as $\Xi$, which securely realizes the ideal functionality ${\mathcal{G}}_{ABB}$ for ABB, which caters to n computation parties. This secure implementation is equipped to facilitate the following operations:

• Arithmetic. The arithmetic operations, encompassing addition and multiplication, necessitate the provision of two handles, each corresponding to integers. Subsequently, these operations yield a handle to an integer, given that both input integers are private.
• Comparison. The comparison operations, encompassing "less than" (<), "less or equal than" (≤), "equal to" (==), and "not equal to" (≠), among others, necessitate two handles corresponding to integers (or floating-point values). These operations yield a handle to a Boolean value. It is worth noting that for the "equal to" (==) and "not equal to" (≠) operations, the input data may also include Boolean values.
• Logic. The logical operation on private vectors is employed using the "choose" function denoted as $\mathsf{choose}$ ($〚\overrightarrow{a}〛$, $〚\overrightarrow{x}〛$, $〚\overrightarrow{y}〛$). It is imperative to note that $〚\overrightarrow{a}〛$, $〚\overrightarrow{x}〛$, and $〚\overrightarrow{y}〛$ all represent vectors of handles. The outcome of this operation is a vector of handles, directing to elements within either $〚\overrightarrow{x}〛$ or $〚\overrightarrow{y}〛$, contingent upon the specific values that the elements within $〚\overrightarrow{a}〛$ point to. It is pertinent to mention that the data type of the vectors $〚\overrightarrow{x}〛$ and $〚\overrightarrow{y}〛$ can encompass integers, floating-point values, and Booleans, all of which are exclusively accessible via handles. Furthermore, it is noteworthy that the results derived from the choose operation are exclusively of Boolean type, similarly accessible solely through handles.
• Declassification. This operation entails declassifying private data, making it publicly accessible. The input data for this operation comprises private integers denoted as $〚\overrightarrow{y}〛$—a vector of handles. The output, in turn, consists of a public vector of integers represented as x.
• Sorting. This operation takes private integers as input values, residing within vector $〚\overrightarrow{x}〛$. The operation’s outcome consists of sorted private integers stored in the private vector $〚\overrightarrow{y}〛$. The sorted vector comprises handles to values, reflecting the result of sorting the vector of values referenced by handles within $〚\overrightarrow{x}〛$.
• Random permutation. This operation is designed to generate a private permutation of n elements randomly. It takes a public integer n as input and yields a private permutation denoted as $〚\sigma 〛$ via a handle. Subsequently, this permutation can be applied to a private vector $〚\overrightarrow{v}〛$ using the operation $\mathsf{apply}$($〚\sigma 〛$,$〚\overrightarrow{v}〛$), resulting in a private vector $〚\overrightarrow{w}〛$. Specifically, for all i∈$\{1,\dots ,n\}$, $w_i=v_{\sigma }\left(i\right)$. Furthermore, it is feasible to apply the inverse of $\sigma$ to v using the operation $\mathsf{unApply}$($〚\sigma 〛$,$〚\overrightarrow{v}〛$).
• prepareRead and performRead. This operation facilitates the retrieval of data from a vector using a private index. The reading process involves the application of the performRead-operation, which takes two arguments: an integer vector $〚\overrightarrow{v}〛$ of length n and a second argument derived from prepareRead(n, $〚\overrightarrow{y}〛$), where $〚\overrightarrow{y}〛$ represents the indices of the m elements intended for retrieval. Subsequently, this operation yields a private vector $〚\overrightarrow{w}〛$ of length m via a handle. The length of $〚\overrightarrow{v}〛$ corresponds to the first argument used in prepareRead, while the second argument of performRead is the output of prepareRead. It is crucial to note that if these conditions are not met, the behavior of ${\mathcal{F}}_{ABB}$ may be arbitrary. The return value of the performRead-operation is a handle referencing a private vector of integers. The vector within the return value is denoted as $〚\overrightarrow{w}〛$, and each element is represented by $w_i$ = $v_{y_i}$.

We employ the composition theory, as outlined in [33], to introduce a new operation, SSSD, into the set of supported ABB operations. The implementation of SSSD atop the ABB framework is delineated through four primary protocols with their versions, which are detailed below:

• Privacy-preserving Dijkstra protocol (Algorithm 5 in [12]).
• Privacy-preserving Bellman-ford protocol (Algorithm 1).
• Privacy-preserving Radius-stepping protocol (Algorithm 2 in [13]).
• Privacy-preserving Breadth-first search protocol (Algorithm 3 in [14]).

These protocols exhibit distinct characteristics concerning the types of graphs they handle, relaxation procedures, and the structure of private input data. For the sake of a comprehensive security analysis, we have chosen to provide detailed security proof for the Bellman-Ford protocol. This choice is motivated by utilizing the four proposed protocols’ most intriguing privacy-preserving computation subroutines (e.g., prefixMin2, as presented in Algorithms 2 and 4).

The new operation, SSSD, takes handles that point to the locations of edges and their corresponding weights, following the definition of Bellman-Ford. It then returns handles that point to the distances of vertices from the source vertex s. We will now introduce a secure implementation of an ABB Framework, denoted as ${\mathcal{F}}_{ABB}$ (for n parties). This ${\mathcal{F}}_{ABB}$ not only supports all the operations of ${\mathcal{G}}_{ABB}$ but also extends its functionality to include the SSSD operation. The intricate details about the inputs and outputs of the SSSD operation are outlined as follows:

• Upon receiving inputs from all honest computing parties (${\mathcal{P}}_i$, for $i\in \{1,\dots ,n\}$), these parties abstain from performing any computations themselves. Instead, their role involves exclusively providing inputs to and receiving outputs from either the machines ${\mathcal{M}}_1$,…,${\mathcal{M}}_n$ or the ideal functionality ${\mathcal{F}}_{ABB}$. In the context of the SSSD operation facilitated by Bellman-Ford and supported by ${\mathcal{F}}_{ABB}$, when all honest parties collectively initiate the SSSD operation, they do so with specified arguments: $〚\overrightarrow{S}〛$, $〚\overrightarrow{T}〛$, $〚\overrightarrow{W}〛$, s, and N. Here, $〚\overrightarrow{S}〛$ and $〚\overrightarrow{T}〛$ represent the locations of the edges, $〚\overrightarrow{W}〛$ signifies the weights of said edges, s denotes the source vertex, and N corresponds to the total number of vertices. Subsequently, ${\mathcal{F}}_{ABB}$ completes the SSSD computation and furnishes the outcome as a vector of handles to each participating computing party. These handles serve as pointers to the shortest distances from the source vertex s. Notably, the length of the returned vector is equal to N. It is essential to highlight that the ideal functionality ${\mathcal{F}}_{ABB}$ maintains ongoing communication with the adversary $\mathcal{A}$, ensuring they are apprised of the ongoing computations, as elaborated in Sec Section 2.1.2.
• Upon completion of their computations, each honest computing party ${\mathcal{P}}_i$ transmits their respective SSSD results to the corresponding party ${\mathcal{P}}^{\prime }$. These results manifest as a vector denoting the shortest distances from the single source vertex s to all vertices, represented as $〚\overrightarrow{T}〛$.

Theorem 2. 

There exists a protocol ${\Pi }^{SSSD}$ that securely implements the functionality ${\mathcal{F}}_{ABB}$ in the ${\mathcal{G}}_{ABB}$-hybrid model. The implementation inherits the security model (number and kind of tolerated corruptions among the parties) of any implementation ${\pi }_{ABB}$ of ${\mathcal{G}}_{ABB}$.

Proof of Theorem 2. 

The protocol ${\Pi }^{SSSD}$ is a composition of machines denoted as ${\mathcal{M}}_1$ to ${\mathcal{M}}_n$. In cases where ${\mathcal{M}}_1$ to ${\mathcal{M}}_n$ receive a command other than SSSD, they will transmit this command to ${\mathcal{G}}_{ABB}$, see Figure 1. However, when ${\mathcal{M}}_1$ to ${\mathcal{M}}_n$ receive an SSSD command, they will adhere to the procedures outlined in Algorithm 1, including the subroutines in Algorithms 2 and 3. This entails the invocation of ${\mathcal{G}}_{ABB}$ operations in the sequence prescribed by Algorithm 1-3.

To demonstrate that the security of the composition involving ${\mathcal{M}}_1$ to ${\mathcal{M}}_n$ and ${\mathcal{G}}_{ABB}$ is at least at least as secure as ${\mathcal{F}}_{ABB}$, we will introduce a simulator. This simulator is designed to map any actions taken by an adversary targeting the actual system (in the hybrid world) into actions directed towards ${\mathcal{F}}_{ABB}$, see Figure 2. This mapping ensures that parties ${\mathcal{P}}_1$ to ${\mathcal{P}}_n$ remain oblivious to any distinctions between the two scenarios.

The simulator $Sim$ operates as an intermediary component positioned between the ideal functionality ${\mathcal{F}}_{ABB}$ and a real adversary $\mathcal{A}$, who anticipates interacting with Turing machines ${\mathcal{M}}_1$ to ${\mathcal{M}}_n$ and ${\mathcal{G}}_{ABB}$. $Sim$ receives from ${\mathcal{F}}_{ABB}$ the commands that the computational parties ${\mathcal{M}}_1$ to ${\mathcal{M}}_n$ submitted to it. The simulator translates them for $\mathcal{A}$ as follows:

• If the command is non-SSSD in nature, $Sim$ relays it to $\mathcal{A}$ as a message that came from ${\mathcal{G}}_{ABB}$.
• If the command originates from ${\mathcal{M}}_1$ to ${\mathcal{M}}_n$ and pertains to SSSD, then $Sim$ relays an SSSD command from each machine ${\mathcal{M}}_1$ to ${\mathcal{M}}_n$ to the adversary $\mathcal{A}$. Additionally, $Sim$ sends a series of commands to $\mathcal{A}$, as if they came from ${\mathcal{G}}_{ABB}$. These commands correspond to the commands that ${\mathcal{G}}_{ABB}$ receives in order to run the Algorithms 1–3.

This orchestration allows for the seamless translation of commands and maintains the appropriate communication flow within the system.

The simulator is tasked with the simulation of ${\mathcal{G}}_{ABB}$. The primary objective is to create an illusion of an adversary-free environment in which adversary $\mathcal{A}$ believes it interacts with the components of the protocol ${\Pi }^{SSSD}$. It is important to note that the simulator is unaware of the actual sensitive input values that ${\mathcal{G}}_{ABB}$ operates on, since ${\mathcal{F}}_{ABB}$ does not relay this information to the simulator. Consequently, the simulator operates an internal copy of ${\mathcal{G}}_{ABB}$ with arbitrary placeholder values. However, in scenarios where parties ${\mathcal{P}}_1$ to ${\mathcal{P}}_n$ request the declassification of specific information from ${\mathcal{F}}_{ABB}$, the simulator gains access to these declassified values. At this juncture, the simulator can replace these values with the correct ones and transmit them to adversary $\mathcal{A}$ through the ${\mathcal{G}}_{ABB}$ –> $\mathcal{A}$ channel.

The declassification command serves as a mechanism for parties to access the actual data through the use of a handle. Notably, a declassification command is integrated into step 5 of Algorithm 3. It is imperative to emphasize that ${\mathcal{F}}_{ABB}$’s proper functioning depends on receiving identical instructions from all participating computing parties within the same ${\mathcal{G}}_{ABB}$ context.

We see that step 5 of Algorithm 3 declassifies a vector of booleans that has been constructed in this and previous steps, starting from a private vector $〚\overrightarrow{v}〛$ of length m. The vector $\overrightarrow{v}$ is sorted, and the values occurring in it are all between 0 and $(n-1)$, with each value in this range occurring at least once. Hence it is publicly known that the boolean vector $〚\overrightarrow{b}〛$ constructed in step 3 of Algorithm 3 contains exactly n values “true” among its m entries, while the positions of “true” values are private. The subsequent random permutation results in a boolean vector $\overrightarrow{c}$ with n values “true” and $(n-m)$ values “false”, where the locations of these values are permuted. Hence the distribution of the vector $\overrightarrow{c}$ only depends on the public parameters and $Sim$ is able to simulate its value being made available to $\mathcal{A}$. Indeed, at this point of execution, where $\mathcal{A}$ expects to see the value of $\overrightarrow{c}$, the simulator $Sim$ generates a uniformly randomly distributed boolean vector of length m with exactly n entries “true”, and sends it to $\mathcal{A}$. As the simulation is possible, we have determined that this declassification step within Algorithms 1–3 does not compromise the privacy of our SSSD Bellman-Ford protocol. □

4. Discussion

In this research, we have delved into the critical realm of SMC and its application in the realm of SSSD protocols. Our primary objective was to establish the security and privacy guarantees of SSSD protocols when implemented on top of SMC protocols. To achieve this, we introduced a series of SSSD protocols tailored to diverse scenarios, each designed to tackle the unique challenges of different graph structures and computation scenarios. These protocols form the foundation of our study, allowing us to thoroughly investigate the security implications of leveraging SMC for private computation.

Our research has led to two significant theorems that provide strong assurances of security and privacy in the context of SSSD protocols over SMC. The first theorem establishes that the composition of SMC protocols implementing an ABB with the SSSD operation results in a system that preserves the privacy of private data. This theorem underscores the practicality of utilizing SMC to perform complex computations while safeguarding data confidentiality. The second theorem extends the security guarantees to cover scenarios involving both active and passive adversaries, thereby enhancing the robustness of the SSSD protocols. We have meticulously proven these theorems, considering various parameters and potential attacks, ensuring the validity and reliability of our security claims. It is important to note that the Sharemind system is secure against a single passively corrupted party. Furthermore, we have introduced a simulator that bridges the gap between the real-world execution of our SSSD protocols and the ideal functionality of an ABB. This simulator is crucial in demonstrating the security of our protocols and ensuring that they meet the rigorous standards set forth by the universal composability framework.

In conclusion, our research has not only contributed a set of secure SSSD protocols for various scenarios but has also provided comprehensive security proofs and simulations to validate the robustness of our approach. Our findings lay the groundwork for developing privacy-preserving applications in diverse domains, enabling researchers and practitioners to harness the power of secure multi-party computation for complex tasks while maintaining the highest data security standards.

As we move forward, further exploration into this intersection of SMC and SSSD promises to unlock new possibilities for secure and private computation, paving the way for innovative solutions in an increasingly interconnected and data-driven world.