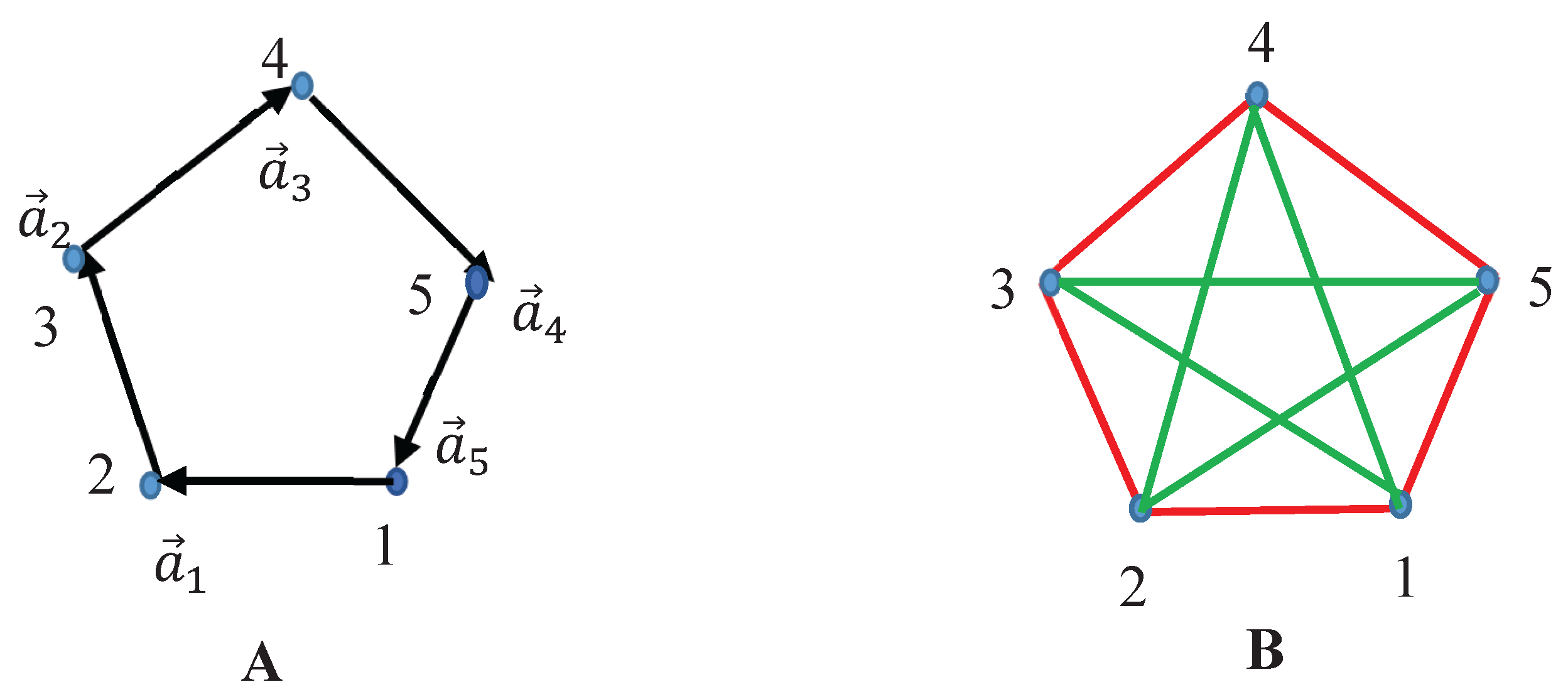1. Introduction
In this paper we consider Ramsey graphs emerging from vector fields. In its general meaning Ramsey theory refers to any mathematical problem which states that a structure of a given kind is guaranteed to contain a well-defined substructure. The classical problem in Ramsey theory is the so-called “party problem”, which asks the minimum number of guests denoted
R(m,n) that must be invited so that at least
m will know each other, or at least n will not know each other (i.e., there exists an independent set of order
n [
1,
2,
3,
4,
5]). When Ramsey theory is re-shaped in the notions of the graph theory, it states that any structure will necessarily contain an interconnected substructure [
4,
5,
6,
7]. The Ramsey theorem, in its graph-theoretic forms, states that one will find monochromatic cliques in any edge color labelling of a sufficiently large complete graph [
4,
5,
6,
7]. In our paper we address the Ramsey graphs emerging from vector fields, including graphs generated by the infinite/countable sets of vectors.
2. Ramsey Graphs Generated by Vector Fields
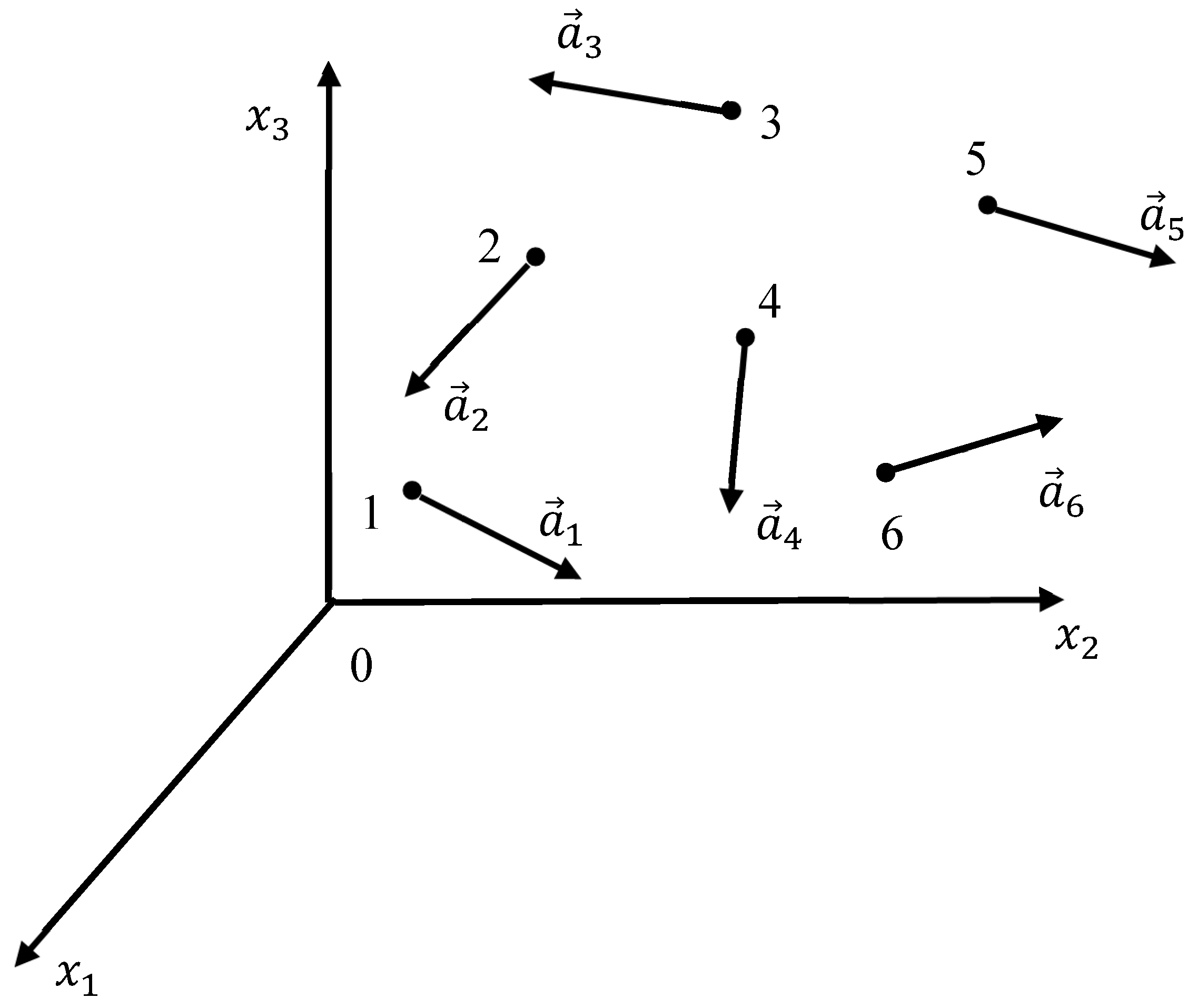
Consider vector field defined on
. Consider sets of six points
and six vectors related to these points
depicted in
Figure 1. Uppercase letters denote the coordinates of the points in
Origin of the vectors
is related to the points
) (actually, the vectors are seen as sliding ones, and the location of their origin is not important);
; lowercase letters denote the coordinates of the vectors (again, seen as sliding vectors). We define the set
as the set of vectors generating the complete bi-colored graph. Vectors
we denote as the “generators” of the Ramsey graph. The graph is built according to the following procedure. Points
serve as the vertices of the graph.
Vertices numbered i and j are connected with the red link, when Equation 1 takes place:
(1)
And, correspondingly, the vertices numbered i and j are connected with the green link, when Equation (2) occurs:
(2)
It is easily seen, that the exact location of the vectors/generators is not important, when the coloring procedure defined by Equations (1) and (2) is adopted. Vectors/generators themselves may be considered as the vertices of the graph. Vectors are “acquainted” each with another and they are connected with the red link, when Equation (1) takes place, and vectors are “not acquainted” each with another, and they are connected with the green link, when Equation (2) is true. The aforementioned procedure gives rise to the complete, bi-colored, Ramsey graph. Consider that the scalar product of vectors is independent of the system of coordinates; thus, the suggested coloring procedure defined by Equations (1) and (2) is invariant relatively to rotation/translations of frames.
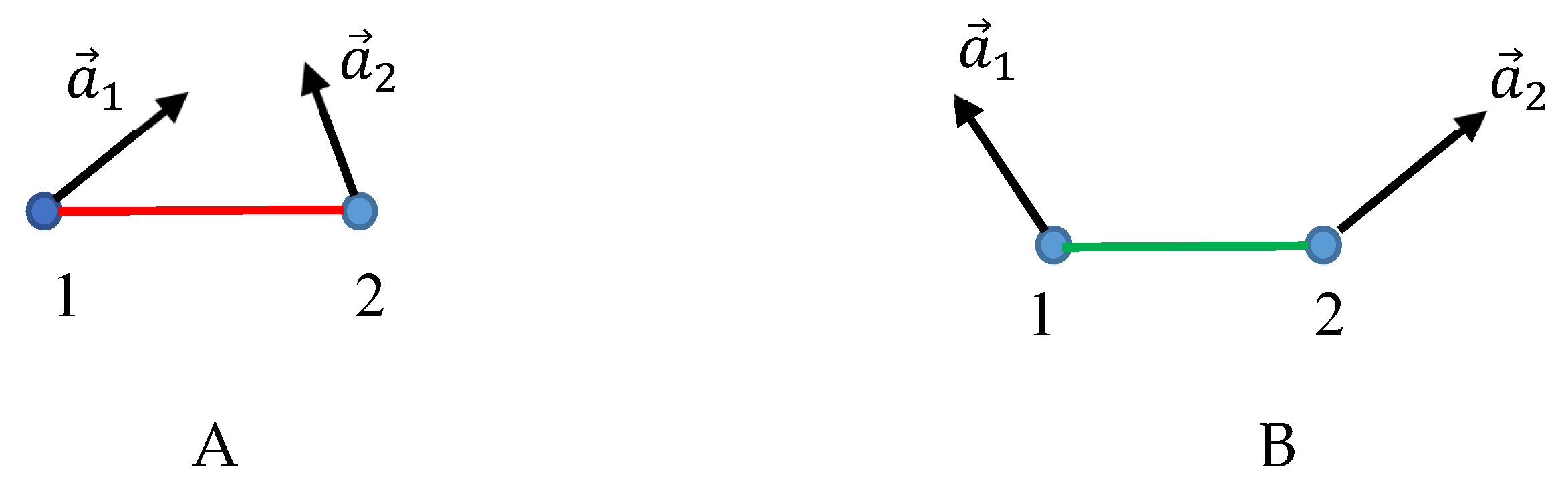
Let us illustrate the introduced procedure with
Figure 2, demonstrating two vectors
and
, belonging to the same plane. Sketch
A depicts the situation, where points “1” and “2” are connected with the red link, i.e.,
takes place; whereas, sketch
B depicts the situation, where points “1” and “2” are connected with the green link, i.e.,
takes place
The aforementioned mathematical procedure gives rise to the bi-colored, complete, Ramsey graph, such as that depicted in
Figure 3, supplied as an example.
According to the Ramsey theorem, this graph should necessarily contain at least one monochromatic (mono-colored triangle); due to the:
. Indeed, we recognize in
Figure 3 the green subgraph, labeled “345”; whereas, the triangles “123”, “124”,”125”, “126”, “136”, “146” ,”156”, “236”, “246” and “256” are monochromatic red ones.
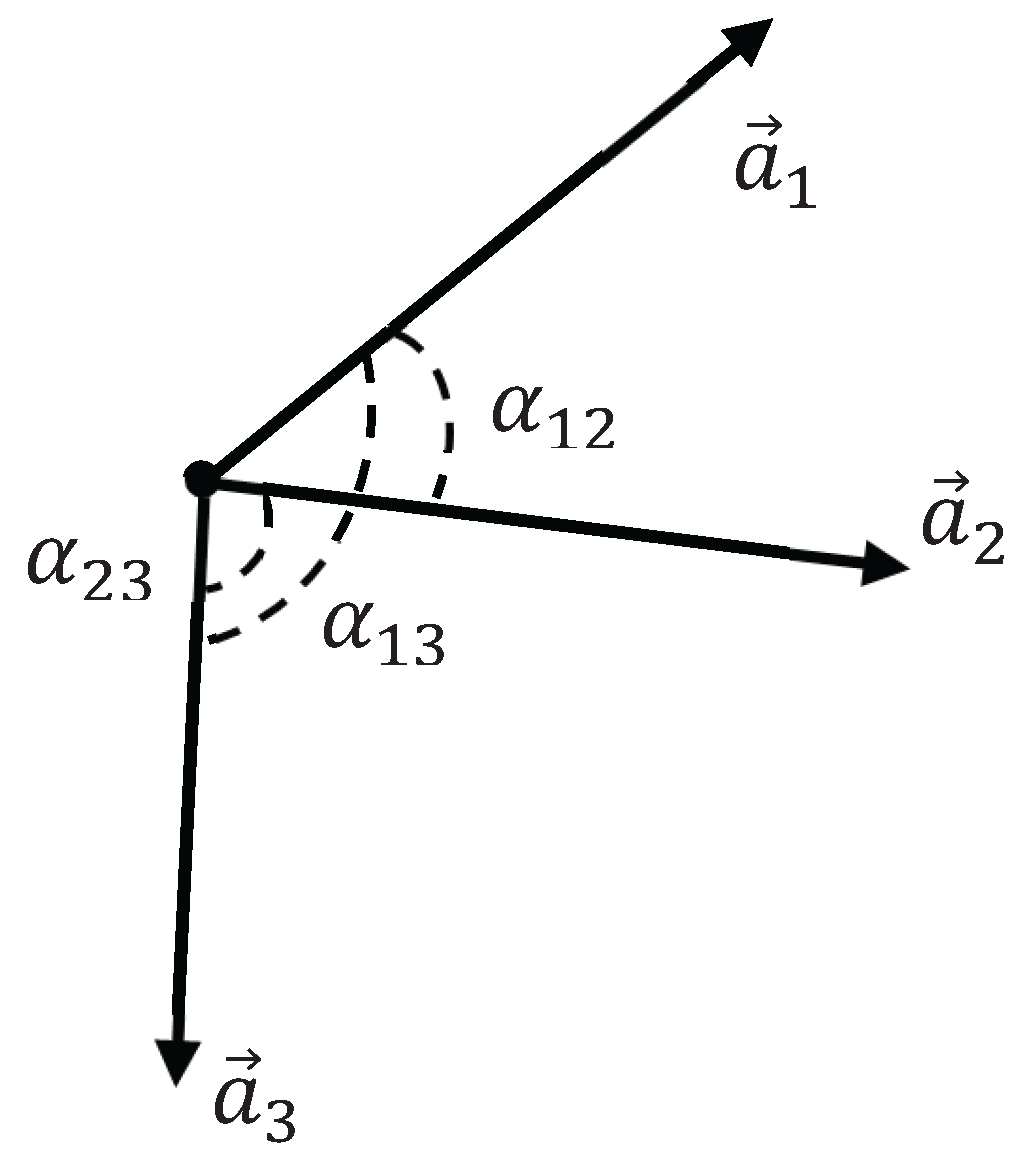
It should be emphasized that the introduced procedures of coloring, defined by Equations (1) and (2) are not transitive. In other words, if:
and
is assumed, it is not necessarily that:
. Let us illustrate this. Consider the planar system of vectors
, depicted in
Figure 4. Angles
are shown in
Figure 4. We adopt
, however
. Thus,
and
takes place. However,
is true (see
Figure 4). Thus, the introduced procedure of coloring of the graph edges is not transitive. The green-colored relation between the vectors/generators is also non-transitive; namely, if:
and
is assumed, it is not necessarily that:
This is important, due to the fact that the transitive Ramsey numbers are different from the non-transitive ones [
8,
9]. The situation is changed for 1D systems of vectors and discussed below in
Section 6.
It is also should be stressed, that only directions of the generating vectors are important; the generating vectors may be considered as the unit ones. We finally come to following theorem.
Theorem: Consider set of the six vectors defined on Vectors are taken as the vertices of the graph. Vertices are connected with the red link, if: takes place, and they are connected with the green link if: The graph contains at least one monochromatic triangle.
Assume, that actually we revealed the red triangle, built of the vertices numbered i, k and l. Thus, according to Equation (1) we have: ; and also . Hence, we derive for the “red” triangles: and also . The extension of this result for the “green” triangles is trivial.
3. Ramsey Graph Generated by the Ring-Like Systems of Generating Vectors
It will be instructive to demonstrate the introduced procedure of formation of bi-colored graphs with the ring-like system of generating vectors depicted in Figure 5A. Five generating vectors form 2D pentagon (in principle the ring-like systems of vectors may be 3D ones) . In this specific case, Equation 5 is true:
(5)
The bi-colored graph generated by the vectors according to Equations (1) and (2) is shown in Figure 5B. The coloring of the graph follows Equations (1) and (2). Five generating vectors serve as the vertices of the Ramsey graph.
Complete bi-colored graph shown in
Figure 5B does not contain any mono-colored triangle. Indeed, the Ramsey number
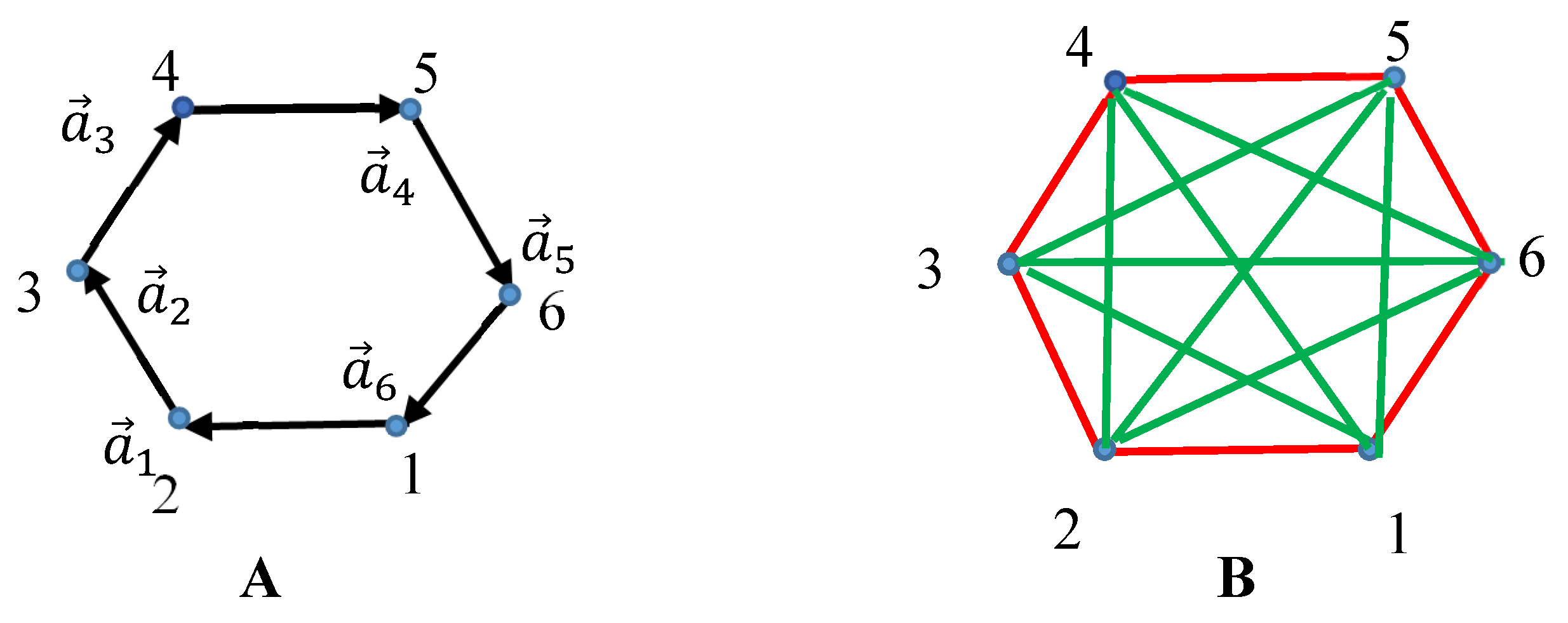
Now, consider the complete bi-colored graph generated by the ring-like system of six vectors
forming hexagon, shown in
Figure 6A. The bi-colored, complete Ramsey graph generated by the vectors
according to Eqs. 1-2, is shown in
Figure 6B. Again,
is true.
According to the Ramsey Theorem this guarantees presence of at least one mono-colored triangle in the graph, presented in Figure 6B. Indeed, triangles “135” and “246” appearing in Figure 6B are green ones.
The suggested procedure is easily generalized for an arbitrary number of generating vectors. However, calculation of the large Ramsey numbers remains an unsolved problem.
4. Extension for the Infinite Sets of Vectors
Consider infinite, however countable set of vectors
. This set generates infinite bi-colored graph, if vectors
serve as vertices and coloring of the links is defined by Equation (1) and Equation (2). According to the infinite Ramsey theorem there must be necessarily present an infinite monochromatic clique in the aforementioned graph (a clique of the undirected graph is a subset of vertices of the graph every two distinct vertices in the clique are adjacent) [
10].
5. Discussion and Applications
The procedure enabling converting of the system of vectors into the bi-colored, complete graph is suggested. The vectors serve as the vertices of the graph. The dual relations between vectors are prescribed by the sign of their scalar product. The suggested coloring procedure defined by Eqs. 1-2 is invariant relatively to rotation/translation of frames. The suggested procedure is applicable for a broad diversity of vector fields. The vectors may represent, for example, velocities or accelerations of the moving particles. Thus, the Ramsey theory imposes non-obvious restrictions on the orientation of these vectors, demanding appearance of mono-colored structures within the graphs generated by the vectors.
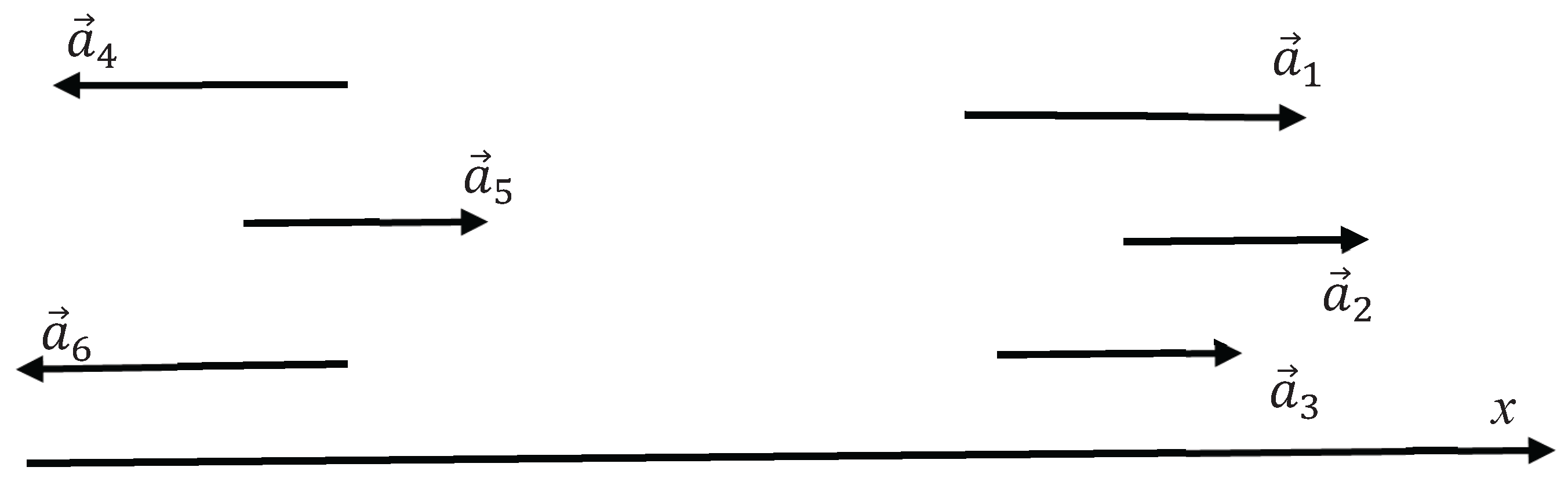
6. The Particular Case of 1D Vector Systems
Now consider the particular, however important, case of the 1D vector systems in which vectors are parallel or anti-parallel each to other. In this situation
when the vectors are parallel (this corresponds to the red link), and
when the vectors are anti-parallel (this corresponds to the green link). One more essential change should be emphasized: if
and
takes place, necessarily
is true, thus the “red” relation is transitive (see the triad of vectors
in
Figure 7). Contrastingly: if
and
takes place, necessarily
is true (see the triad of vectors
in
Figure 7). Thus, the “red” relation between the vectors is transitive; whereas the “green” relation is intransitive. Let us demonstrate this property with the following logical example, involving three groups of experts, labeled “
A”, “
B” and “
C” correspondingly. Consider the situation when group of experts “
A” recognizes group “
B”, and group “
B” recognizes group “C”, but group “
A” does not recognize group “
C”. In this case, the recognition relation among the expert groups is defined as “intransitive”. This is exactly the situation inherent for the triad of vectors
depicted in
Figure 7
We came to a very important conclusion: the change in the dimensionality of the system may change in the logical interrelations between the objects. The regular Ramsey numbers become irrelevant for the 1D situation illustrated with Figure 7. Now we are working for the extension of suggested Ramsey approach to matrices.
7. Conclusions
We suggested the Ramsey approach to the vectors fields. Set of vectors defined on are considered as the vertices of the bi-colored complete graph. Following coloring procedure of the graph is suggested: vertices numbered i and j are linked with the red edge if takes place; and they are linked, in turn, with the green edge if is true. This procedure gives rise to the complete, bi-color graph. Graph generated by six vectors inevitably contains the monochromatic triangle: the Ramsey number The coloring procedure is insensitive to the rotations/translations of the axes. Ring-like and infinite/countable sets of generating vectors are addressed. Applications of the graphs emerging from the vector fields are discussed. Switching to 1D sets of parallel vectors changes the logic of the relations between the vectors. The relations became transitive/intransitive in the 1D systems of vectors.
Data Availability Statement
No data was used for the research described in the article.
Acknowledgments
The author is thankful to Nir Shvalb for useful discussions.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- F. P. Ramsey, On a Problem of Formal Logic. In: Gessel, I., Rota, GC. (eds) Classic Papers in Combinatorics. Modern Birkhäuser Classics. Birkhäuser Boston, 2009, pp. 264-286.
- R. L. Graham, B. L. Rothschild, J. H. Spencer, Ramsey theory, 2nd ed., Wiley-Interscience Series in Discrete Mathematics and Optimization, John Wiley & Sons, Inc., New York, A Wiley-Interscience Publication, 1990, pp. 10-110.
- M. Di Nasso, I. Goldbring, M. Lupini, Nonstandard Methods in Combinatorial Number Theory, Lecture Notes in Mathematics, vol. 2239, Springer-Verlag, Berlin, 2019.
- M. Katz, J. Reimann, Introduction to Ramsey Theory: Fast Functions, Infinity, and Metamathematics, Student Mathemati-cal Library Volume: 87; 2018; pp. 1-34.
- D. Conlon, J. Fox, B. Sudakov, Recent developments in graph Ramsey theory, Surveys in Combinatorics, 424 (2015) 49-118.
- F. D. Dubo, Stein M. On the Ramsey number of the double star, Discrete Mathematics, 348 (1) (2025) 114227.
- X. Hu, Q. Li, Ramsey numbers and a general Erdős-Rogers function, Discrete Mathematics, 347 (12) (2024) 114203.
- S. A. Choudum, B Ponnusamy, Ramsey numbers for transitive tournaments, Discrete Mathematics 206 (1999) 119–129.
- N. Shvalb, M. Frenkel, S. Shoval, Ed. Bormashenko, A Note on the Geometry of Closed Loops, Mathematics 11(8) (2023) 1960.
- Soifer A, 2009 From Pigeonhole Principle to Ramsey Principle. In: The Mathematical Coloring Book. Springer, New York, NY, pp. 263‐265.
Figure 1.
Six vectors defined on .
Figure 1.
Six vectors defined on .
Figure 2.
The coloring procedure is illustrated. Vectors and , belong to the same plane. A. . Points “1” and “2” are connected with the red link. B. . Points “1” and “2” are connected with the green link.
Figure 2.
The coloring procedure is illustrated. Vectors and , belong to the same plane. A. . Points “1” and “2” are connected with the red link. B. . Points “1” and “2” are connected with the green link.
Figure 3.
Bi-colored, complete graph generated by the vectors , and colored according to the Eqs. 1-2 is depicted. Vectors are the vertices of the graph. The coloring of the edges is carried out as follows: , , , , , , is true (see Equation 1). is true (see Equation (2)).
Figure 3.
Bi-colored, complete graph generated by the vectors , and colored according to the Eqs. 1-2 is depicted. Vectors are the vertices of the graph. The coloring of the edges is carried out as follows: , , , , , , is true (see Equation 1). is true (see Equation (2)).
Figure 4.
Triad of planar vectors is depicted. It is adopted: , however . Thus, and takes place. However, is true. The procedure of coloring of links defined by Equation 1 is non-transitive.
Figure 4.
Triad of planar vectors is depicted. It is adopted: , however . Thus, and takes place. However, is true. The procedure of coloring of links defined by Equation 1 is non-transitive.
Figure 5.
Ramsey complete bi-colored graph emerging from the system of five generating vectors forming pentagon. A. generating vectors are depicted. B. Complete bi-colored graph emerging from the system of generating vectors Eqs. 1-2 establish the green-red coloring of the graph. No monochromatic triangle is recognized.
Figure 5.
Ramsey complete bi-colored graph emerging from the system of five generating vectors forming pentagon. A. generating vectors are depicted. B. Complete bi-colored graph emerging from the system of generating vectors Eqs. 1-2 establish the green-red coloring of the graph. No monochromatic triangle is recognized.
Figure 6.
Ramsey complete bi-colored graph emerging from the system of six generating vectors forming hexagon. A. generating vectors, forming a ring are depicted. B. Complete bi-colored graph emerging from the system of generating vectors Eqs. 1-2 establish the green-red coloring of the graph. Triangles “135” and “246” are monochromatic.
Figure 6.
Ramsey complete bi-colored graph emerging from the system of six generating vectors forming hexagon. A. generating vectors, forming a ring are depicted. B. Complete bi-colored graph emerging from the system of generating vectors Eqs. 1-2 establish the green-red coloring of the graph. Triangles “135” and “246” are monochromatic.
Figure 7.
1D system of vectors is depicted. and takes place, implying ; and takes place, implying .
Figure 7.
1D system of vectors is depicted. and takes place, implying ; and takes place, implying .
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).