Submitted:
12 September 2024
Posted:
12 September 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
- (1)
- Extended Euclidean Algorithm (EEA) without using divisions.
- (2)
- Using Fermat’s Little Theorem [1]: .
2. ECC and Modular Inversion Algorithms
2.1. Elliptic Curve Cryptography
2.2. Point Addition and Point Doubling
2.2.1. Point Addition
| Algorithm 1 PA (P, Q, m, a) (Point Addition in Affine Coordinates). |
|
inputs: Points and ; m and a in
output:
begin
1 , , , ,
2 if return Q /* */
3 if return P /* */
4 if
5 if return /* */
6 else return PD (P, m, a) /* */
7
8
9
10 return /* */
end
|
2.2.2. Point Doubling
| Algorithm 2 PD (P, m, a) (Point Doubling in Affine Coordinates). |
|
inputs: Point ; m and a in
output:
begin
1 , ,
2 if return /* vertical tangent */
3
4
5
6 return /* */
end
|
2.3. Modular Inversion Algorithms











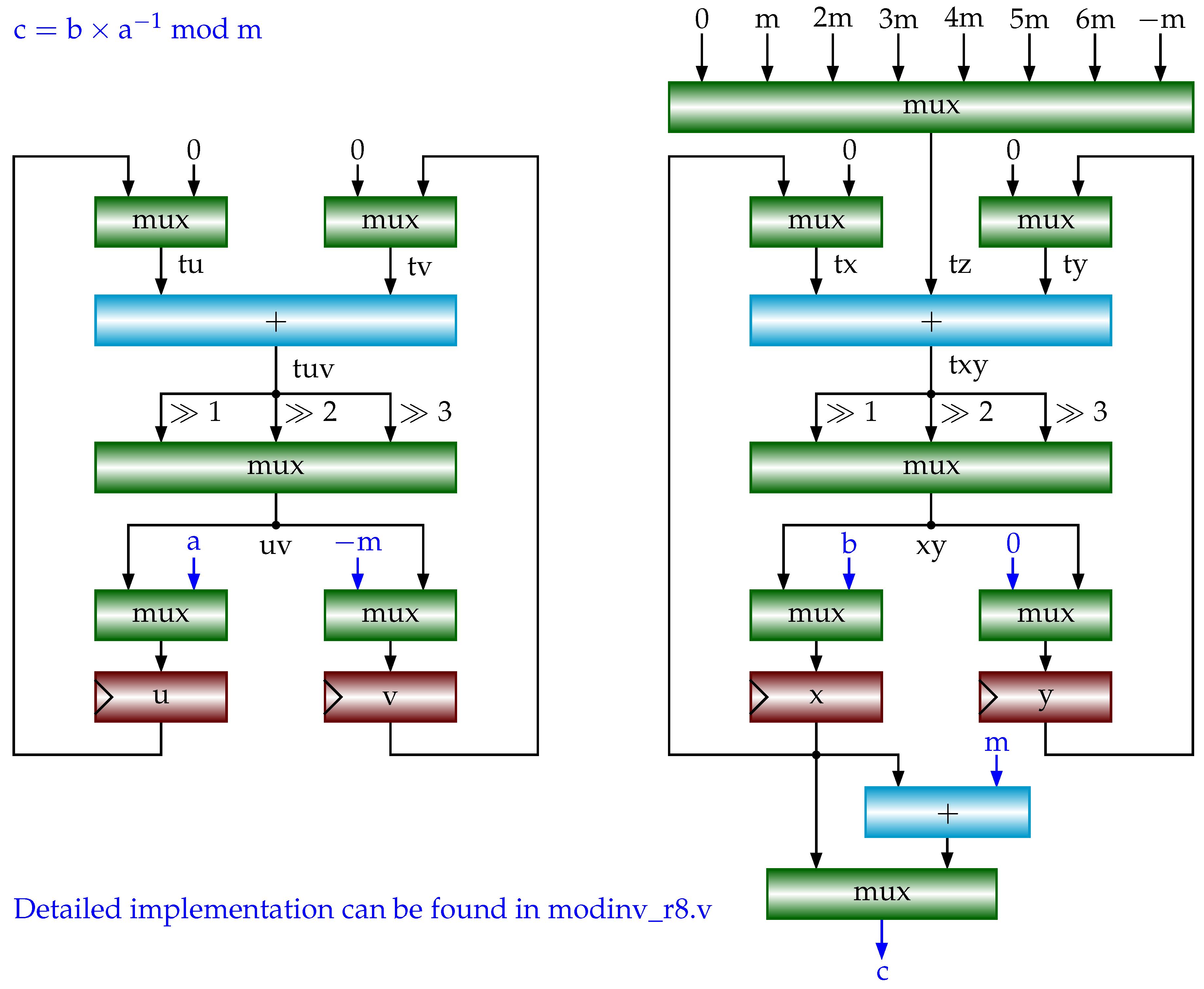
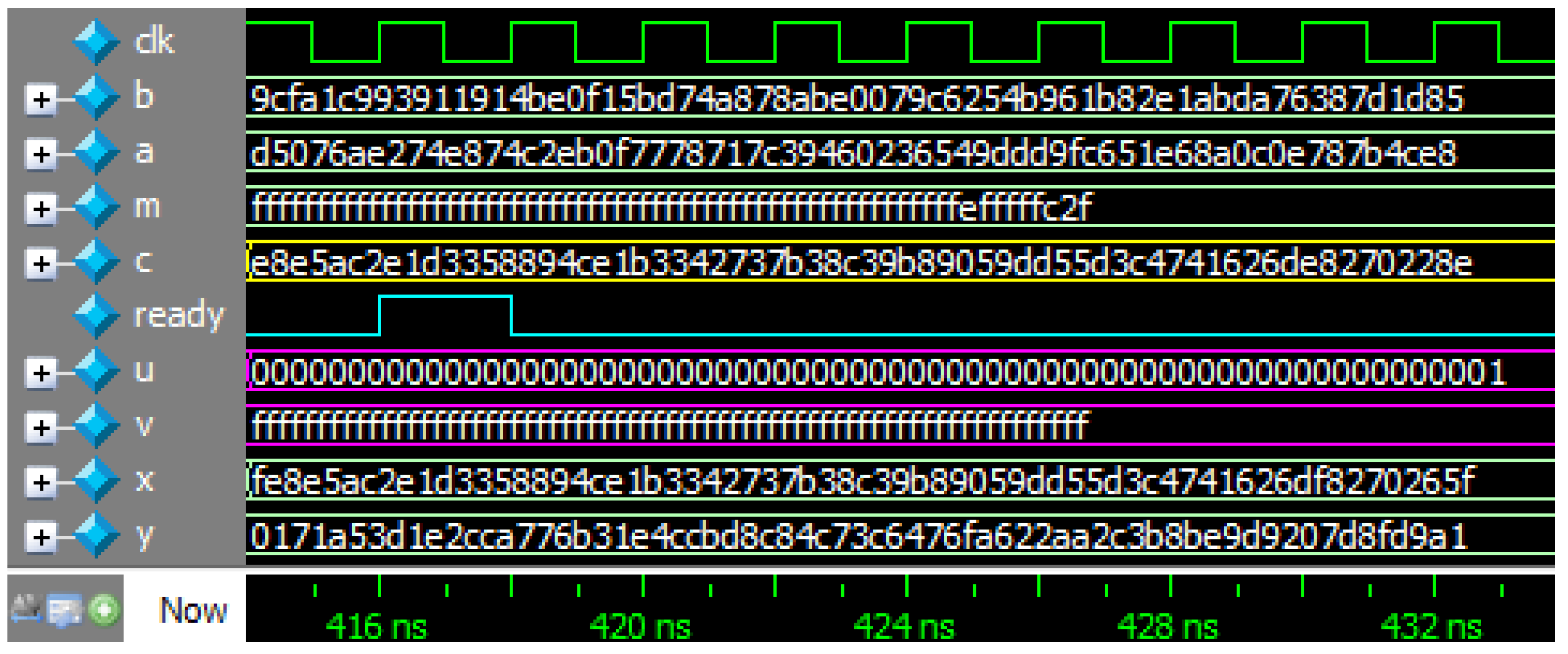
3. Proposed Radix-8 Modular Inversion Algorithm and its Performance

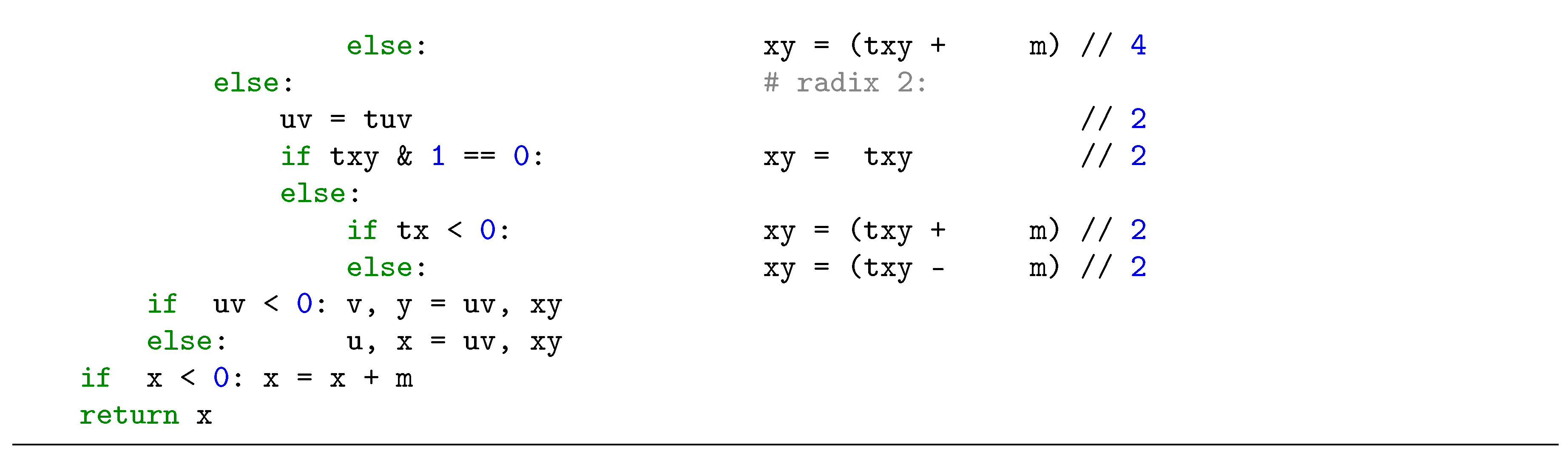
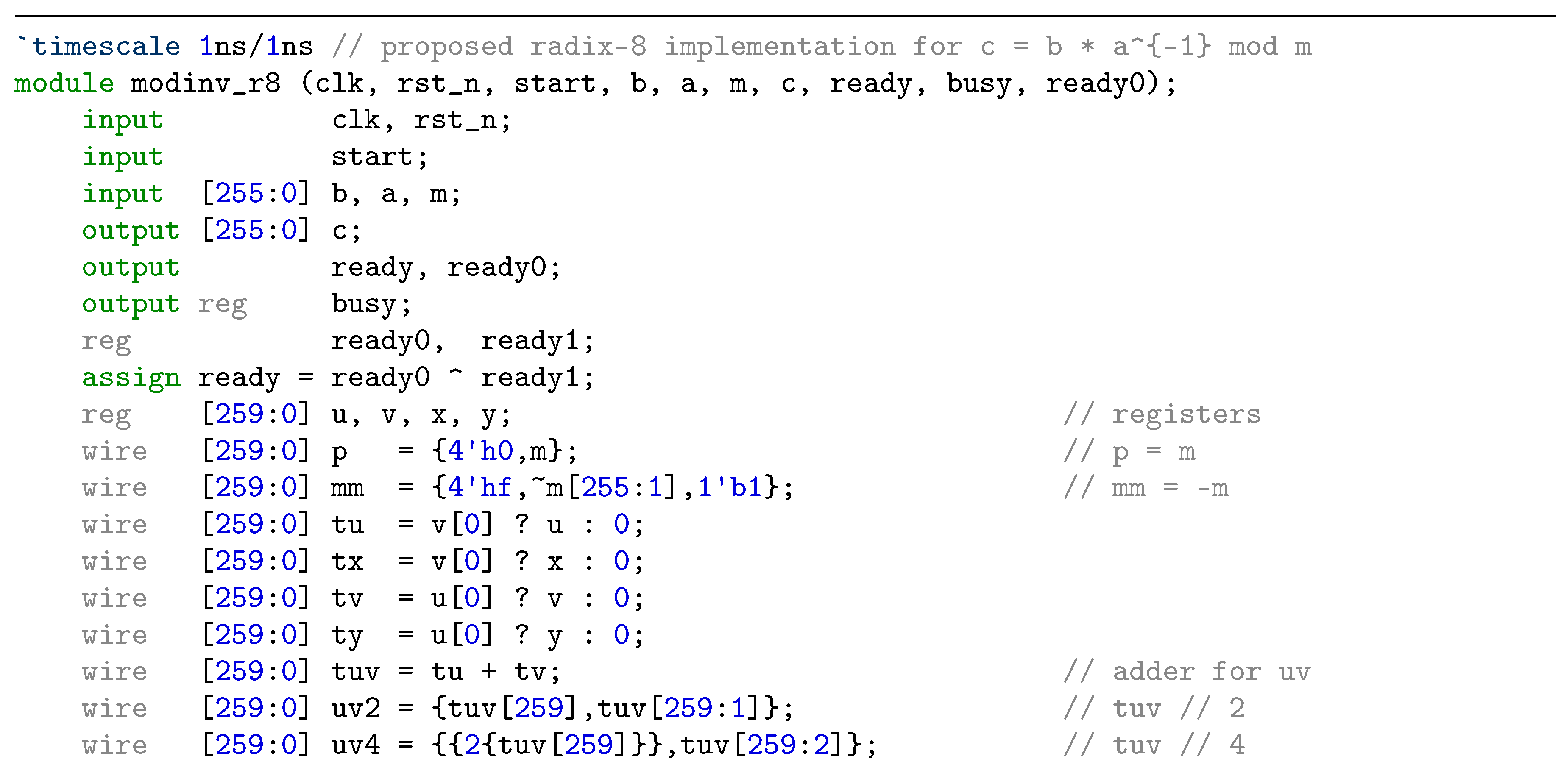


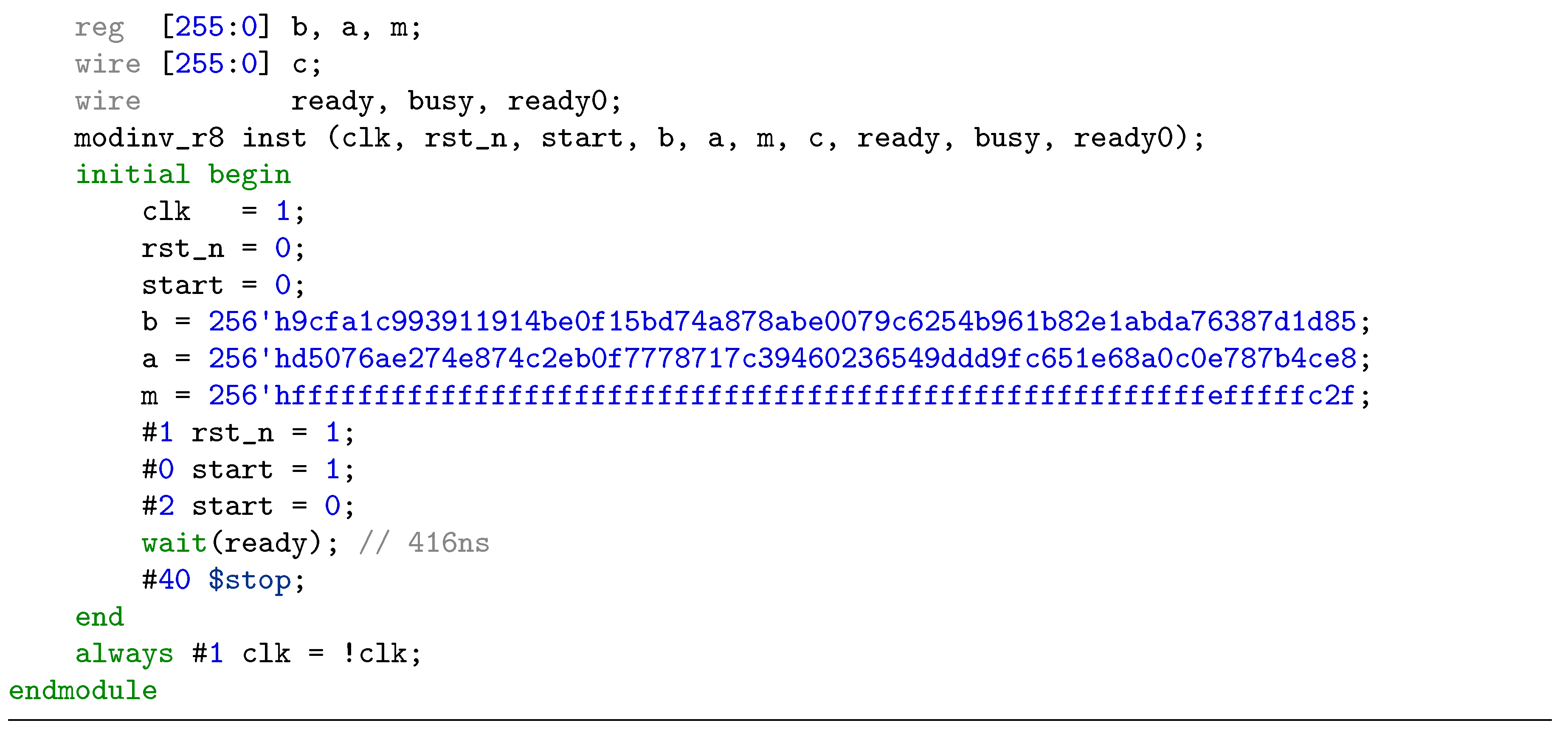
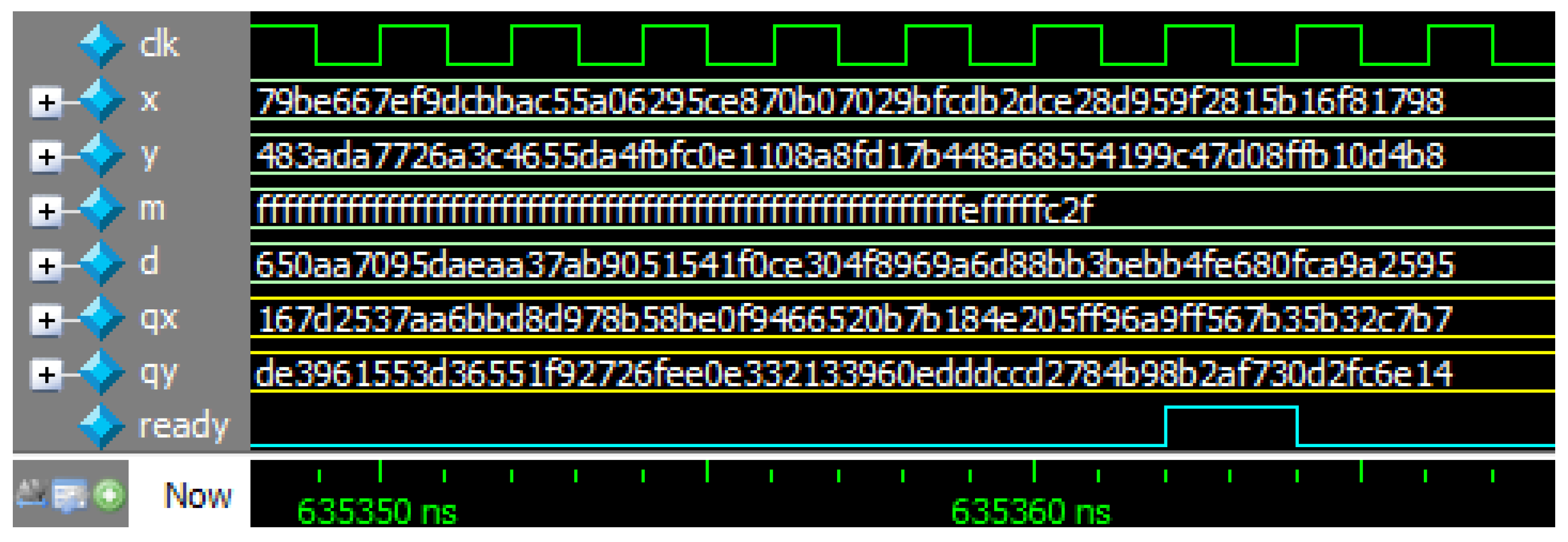
4. ECC Implementation with Proposed Modular Inversion Algorithm
| Algorithm 3 ScaMul (d, P, m, a) (Scalar Point Multiplication in Affine Coordinates). |
|
inputs: and point ; m and a in
output:
begin
1 , , /* and */
2 while to
3 if
4 PA (Q, R, m, a) /* (Algorithm 1) */
5 PD (R, m, a) /* (Algorithm 2) */
6
7 endwhile
8 return Q /* */
end
|



5. Conclusions
References
- Burton, D. The History of Mathematics / An Introduction (7th ed.); McGraw-Hill, 2011. [CrossRef]
- Hankerson, D.; Menezes, A.; Vanstone, S. Guide to Elliptic Curve Cryptography; Springer-Verlag: New York Inc, 2004. [Google Scholar] [CrossRef]
- Hossain, M.S.; Kong, Y. High-Performance FPGA Implementation of Modular Inversion over F_256 for Elliptic Curve Cryptography. 2015 IEEE International Conference on Data Science and Data Intensive Systems, 2015, pp. 169–174. [CrossRef]
- Daly, A.; Marnane, W.; Kerins, T.; Popovici, E. Division in GF(p) for Application in Elliptic Curve Cryptosystems on Field Programmable Logic. In New Algorithms, Architectures and Applications for Reconfigurable Computing; Springer US: Boston, MA, 2005; pp. 219–229. [CrossRef]
- Mrabet, A.; El-Mrabet, N.; Bouallegue, B.; Mesnager, S.; Machhout, M. An efficient and scalable modular inversion/division for public key cryptosystems. 2017 International Conference on Engineering & MIS (ICEMIS), 2017, pp. 1–6. [CrossRef]
- Chen, C.; Qin, Z. Fast Algorithm and Hardware Architecture for Modular Inversion in GF(p). 2009 Second International Conference on Intelligent Networks and Intelligent Systems, 2009, pp. 43–45. [CrossRef]
- Choi, P.; Lee, M.K.; Kong, J.T.; Kim, D.K. Efficient Design and Performance Analysis of a Hardware Right-shift Binary Modular Inversion Algorithm in GF(p). Journal of Semiconductor Technology and Science 2017, 17, 425–437. [Google Scholar] [CrossRef]
- Wang, D.; Lin, Y.; Hu, J.; Zhang, C.; Zhong, Q. FPGA Implementation for Elliptic Curve Cryptography Algorithm and Circuit with High Efficiency and Low Delay for IoT Applications. Micromachines 2023, 14, 1–15, https://www.mdpi.com/2072-666X/14/5/1037, doi:10.3390/mi14051037. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; Dai, Z.; Li, W.; Chen, T. An Efficient ASIC Implementation of Public Key Cryptography Algorithm SM2 Based on Module Arithmetic Logic Unit. 2019 IEEE 13th International Conference on ASIC (ASICON), 2019, pp. 1–4. [CrossRef]
- Yan, X.; Li, S. Modified modular inversion algorithm for VLSI implementation. 2007 7th International Conference on ASIC, 2007, pp. 90–93. [CrossRef]
- Dong, X.; Zhang, L.; Gao, X. An Efficient FPGA Implementation of ECC Modular Inversion over F256. Proceedings of the 2nd International Conference on Cryptography, Security and Privacy, 2018, pp. 29–33. [CrossRef]
- Koblitz, N. Elliptic curve cryptosystems. Mathematics of Computation 1987, 48, 203–209, https://www.ams.org/journals/mcom/1987-48-177/S0025-5718-1987-0866109-5/S0025-5718-1987-0866109-5.pdf. [Google Scholar] [CrossRef]
- Miller, V.S. Use of Elliptic Curves in Cryptography. Advances in Cryptology — CRYPTO ’85 Proceedings; Springer Berlin Heidelberg: Berlin, Heidelberg, 1986; pp. 417–426, https://link.springer.com/content/pdf/10.1007/3-540-39799-X_31.pdf?pdf=inline%20link. [Google Scholar]
- Certicom_Corp. Standards for Efficient Cryptography. SEC 2: Recommended Elliptic Curve Domain Parameters; http://www.secg.org/sec2-v2.pdf, 2010.
- Barker, E.; Chen, L.; Roginsky, A.; Vassilev, A.; Davis, R. SP 800-56A Rev. 3, Recommendation for Pair-Wise Key-Establishment Schemes Using Discrete Logarithm Cryptography; National Institute of Standards and Technology, 2018. https://nvlpubs.nist.gov/nistpubs/SpecialPublications/NIST.SP.800-56Ar3.pdf.
- Li, Y.; Chu, W. Shift-Sub Modular Multiplication Algorithm and Hardware Implementation for RSA Cryptography. 17th International Conference on Information Assurance and Security, Lecture Notes in Networks and Systems; Springer: Cham, 2021; pp. 541–552. [Google Scholar] [CrossRef]
- Li, Y. Hardware Implementations of Elliptic Curve Cryptography Using Shift-Sub Based Modular Multiplication Algorithms. Cryptography 2023, 7, 1–29. [Google Scholar] [CrossRef]
| Expose an elliptic curve and a point P on the elliptic curve to the world | |
| Alice | Bob |
| Generate a secret | Generate a secret |
| Calculate | Calculate |
| Expose | Expose |
| Get from Bob | Get from Alice |
| Calculate | Calculate |
| Use x of as the key | Use x of as the key |
| i | u | v | x | y | q | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 3 | = | a | 11 | = | m | 1 | = | b | 0 | q | = | |||
| 0 | u | = | v | v | = | x | = | y | y | = | |||||
| 1 | 0 | = | |||||||||||||
| 1 | 11 | = | v | 3 | = | 0 | = | y | 1 | = | |||||
| 2 | 3 | = | |||||||||||||
| 2 | 3 | = | v | 2 | = | 1 | = | y | = | ||||||
| 3 | 1 | = | |||||||||||||
| 3 | 2 | = | v | 1 | = | = | y | 4 | = | ||||||
| 4 | 2 | = | |||||||||||||
| 4 | 1 | = | v | 0 | = | 4 | = | y | = | ||||||
| End | u | = | 1 | v | = | 0 | x | = | 4 | ||||||
| m | Comment | |||||
|---|---|---|---|---|---|---|
| 000 | xx1 | |||||
| 100 | xx1 | 100 | ||||
| 010 | x01 | 010 | ||||
| 110 | x11 | 110 | ||||
| 010 | x11 | 110 | ||||
| 110 | x01 | 010 | ||||
| 001 | 001 | |||||
| 011 | 011 | |||||
| 101 | 101 | |||||
| 111 | 111 | |||||
| 001 | 101 | 010 | 111 | |||
| 011 | 111 | 110 | 101 | |||
| 101 | 001 | 010 | 011 | |||
| 111 | 011 | 110 | 001 | |||
| 001 | 111 | |||||
| 011 | 101 | |||||
| 101 | 011 | |||||
| 111 | 001 | |||||
| 001 | 011 | 110 | 001 | |||
| 011 | 001 | 010 | 011 | |||
| 101 | 111 | 110 | 101 | |||
| 111 | 101 | 010 | 111 |
| m | Comment | |||
|---|---|---|---|---|
| 00 | x1 | |||
| 10 | x1 | 10 | ||
| 01 | 01 | |||
| 11 | 11 | |||
| 01 | 11 | |||
| 11 | 01 |
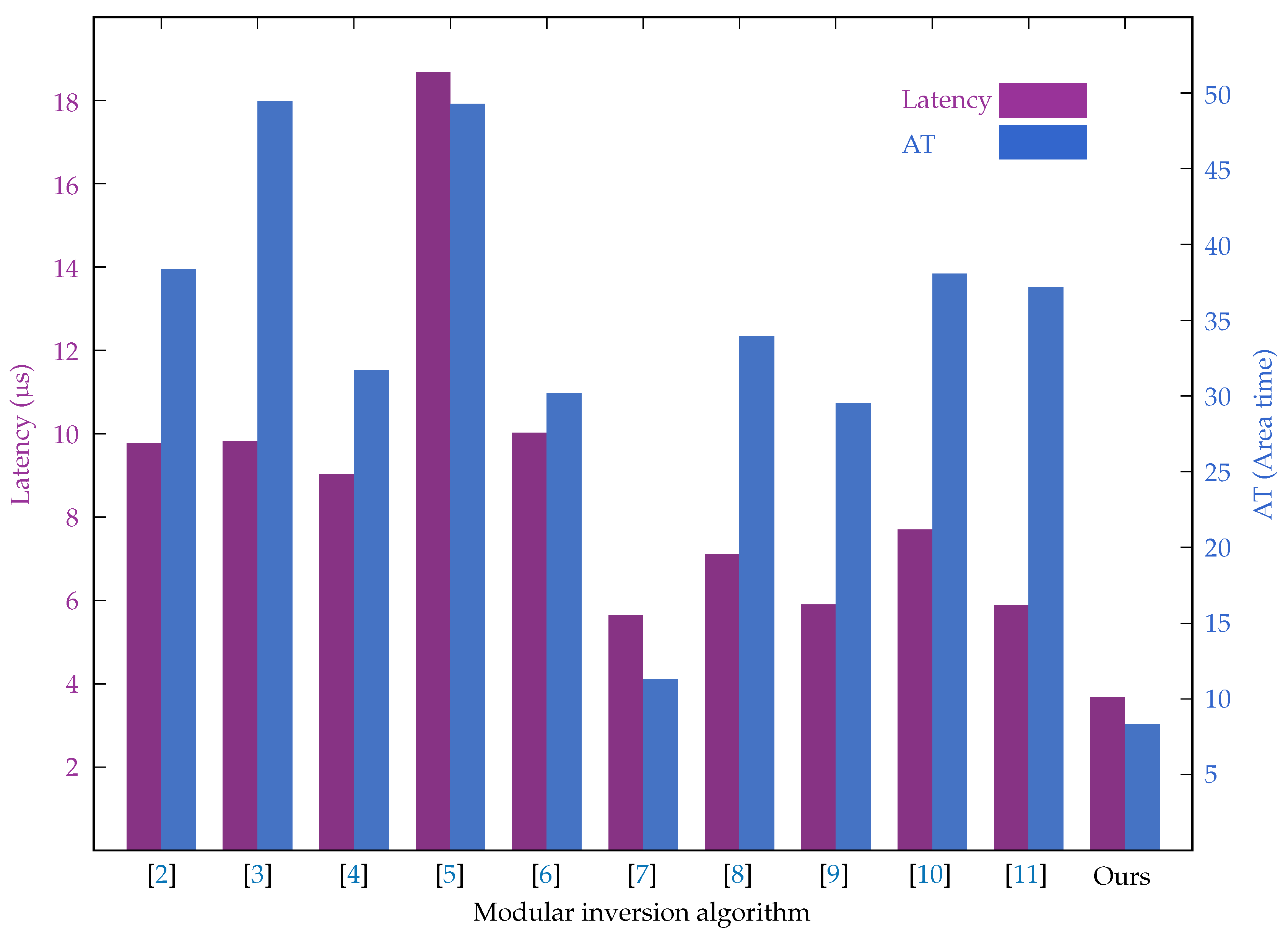
| Algorithm | Cycles | Freq.(MHz) | Latency(s) | ALMs | Registers | AT |
|---|---|---|---|---|---|---|
| [1] | 66264 | 57.54 | 1151.63 | 2004 | 2775 | 5503.66 |
| [2] | 534 | 54.66 | 9.77 | 2619 | 1302 | 38.31 |
| [3] | 535 | 54.52 | 9.81 | 3735 | 1303 | 49.42 |
| [4] | 358 | 39.73 | 9.01 | 2474 | 1038 | 31.64 |
| [5] | 1205 | 64.55 | 18.67 | 1596 | 1043 | 49.26 |
| [6] | 723 | 72.21 | 10.01 | 1968 | 1042 | 30.13 |
| [7] | 358 | 63.60 | 5.63 | 959 | 1037 | 11.24 |
| [8] | 423 | 59.56 | 7.10 | 3475 | 1303 | 33.92 |
| [9] | 356 | 60.43 | 5.89 | 3950 | 1057 | 29.50 |
| [10] | 423 | 54.99 | 7.69 | 3644 | 1303 | 38.05 |
| [11] | 334 | 56.93 | 5.87 | 5276 | 1057 | 37.15 |
| Ours | 208 | 56.71 | 3.67 | 1227 | 1037 | 8.30 |
| Weight | Point addition | Point doubling | |
|---|---|---|---|
| Initial | |||
| 1 | |||
| 2 | |||
| 4 | |||
| 8 | |||
| 16 |
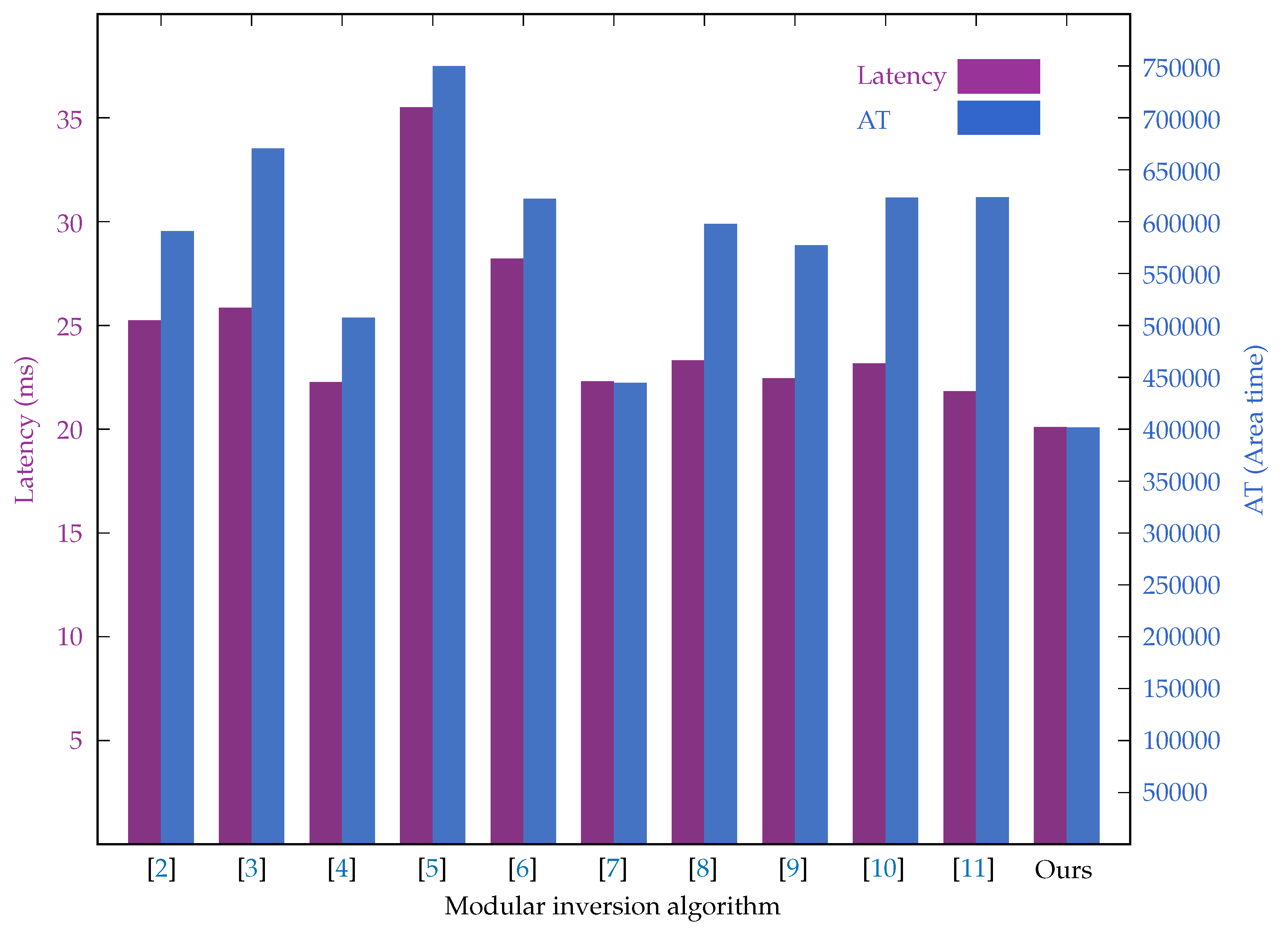
| Algorithm | Cycles | Freq.(MHz) | Latency(ms) | ALMs | Registers | AT |
|---|---|---|---|---|---|---|
| [2] | 402145 | 15.94 | 25.23 | 15043 | 8355 | 590300.42 |
| [3] | 402400 | 15.58 | 25.83 | 17585 | 8355 | 669977.92 |
| [4] | 357262 | 16.06 | 22.25 | 14975 | 7821 | 507107.38 |
| [5] | 570142 | 16.07 | 35.48 | 13292 | 7834 | 749522.08 |
| [6] | 455425 | 16.15 | 28.20 | 14211 | 7831 | 621577.58 |
| [7] | 356878 | 16.01 | 22.29 | 12114 | 7820 | 444347.67 |
| [8] | 372127 | 15.98 | 23.29 | 17292 | 8353 | 597196.30 |
| [9] | 352761 | 15.72 | 22.44 | 17841 | 7860 | 576737.31 |
| [10] | 372127 | 16.08 | 23.14 | 18548 | 8355 | 622595.32 |
| [11] | 346194 | 15.88 | 21.80 | 20716 | 7859 | 622952.99 |
| Ours | 317681 | 15.82 | 20.08 | 12157 | 7824 | 401237.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




