A Consistent Approach to Modeling Quantum Observers

David Ring

doi:10.20944/preprints202408.1517.v1

Preprint

Article

A Consistent Approach to Modeling Quantum Observers

This version is not peer-reviewed.

David Ring^*

This version is not peer-reviewed.

Downloads

121

Views

Comments

Submitted:

20 August 2024

Posted:

21 August 2024

Read the latest preprint version here

A peer-reviewed article of this preprint also exists.

Abstract

Quantum observers, agents whose entanglement with a measured system may remain coherent, are analyzed in a consistent approach. Thought experiments, including one by Deutsch and one by Frauchiger and Renner, are discussed and modeled using quantum circuits. Terminology is suggested which helps avoid contradictions.

Keywords:

quantum mechanics

;

quantum measurement

;

quantum foundations

;

quantum computers

;

quantum circuits

Subject:

Physical Sciences - Quantum Science and Technology

1. Introduction

Quantum theory was originally formulated explicitly assuming two regimes, a quantum world of microscopic phenomena and a classical world of macroscopic objects and observers. The Copenhagen interpretation postulated a collapse mechanism to transition a quantum superposition into a classical single-result reality.

Ordinary computers do not challenge this separation, as their computational states do not interfere. But the advent of quantum computation brings the measurement problem into direct relevance. Quantum observers may become entangled with quantum systems and their very thoughts may exist in superposition.

When such an agent makes an observation, should her knowledge and logic obey the rigid rules of classical logic, or the more etherial rules of quantum mechanics? We might expect the answer to depend on the specific mechanism governing the transition from the multiple possibilities of a superposition to the single possibility of a measurement, but with reasonable assumptions we can analyze observation states without such detailed knowledge.

We will clarify the conditions under which quantum observers can make deductions, and propose terminology which will help avoid contradictions. We will also present quantum circuit models which can experimentally test these ideas today.

Other authors have approached this subject with an aim to categorize interpretations of quantum theory. Most of these analyses include an assumption called Absoluteness of Observed Events (AOE). It should not be surprising that quantum observers challenge this assumption.

One analysis by Frauchiger and Renner [1] (FR) stands out by not including AOE in its assumptions, at least not explicitly1. The analysis predicts certain agents will make statements which are subsequently shown to be false. Rather than questioning the validity of their agents’ reasoning, they instead question the logical consistency of quantum theory itself. We will correct the agents’ reasoning so that all agent statements are both true and consistent.

2. Observation States

When an observation takes place, the combined state of system, apparatus, and observer becomes correlated. In the case of a quantum observer, the three components may be tightly coupled and/or coherent and the lines of separation between the components may be blurred. For our purposes we will separate the observer’s memory and conclusions from the rest. The former we will call her knowledge, and the latter the context. The context may include other observers and their knowledge.

We consider three types of post observation states: entangled, siloed, and collapsed. The density operator for an entangled observation result may be written

ρ_{e} = \sum_{a b} ρ_{a b} \otimes | a 〉 〈 b |

(1)

where

ρ_{a b}

operates in the context Hilbert space, and a and b index the distinguishable results of the observation in the knowledge Hilbert space. For simplicity we assume the knowledge basis is not degenerate. Even with off diagonal terms, expression (1) may describe a product state where the knowledge state is not a basis vector. This, by definition, is not entangled. Nevertheless we will analyze it as if it were an entangled state. The term pseudo-entangled may be used. In all of our thought experiments the initial state will be pure, but that is not a requirement.

If instead the off diagonal components are zero, we have a siloed correlation:

ρ_{s} = \sum_{a} ρ_{a} \otimes | a 〉 〈 a | .

(2)

This is a mixed state and may be considered an incoherent superposition. Evolving a pure state to a mixed state requires loss of information. A loss of “which-way” information [2] is sufficient to guarantee off diagonal components are zero [3].

If quantum collapse occurs, a projection operator

Π_{a} = I \otimes | a 〉 〈 a |

(3)

is applied and we have a collapsed state:

ρ_{c} = N_{a} ρ_{a} \otimes | a 〉 〈 a |,

(4)

where a normalization

N_{a}

is added because the projection operator changes the trace.

If an observation results in a siloed state or a collapsed state we will call it a measurement. Otherwise we call it an observational entanglement.

ρ_{s}

and

ρ_{c}

are equivalent under unitary evolution in the sense that no future experiment can distinguish them. There is no analogous equivalence between the unitary evolution of entangled states and collapsed states, so it is wrong to apply (3) to the former. Nevertheless, we will consider the possibility that some non-unitary physical process can evolve an entangled observation result into a collapsed state. We will insist however that for each observation, whether measurement occurs or not is determined by the experimental setup.

3. Remeasurement

Deutsch was the first to analyse quantum observers with some rigor. He proposed a thought experiment [4] that would have a different result in a unitary universe as opposed to a universe where collapse occurs. A spin is prepared pointing along the positive x-axis. It passes through a Stern Gerlach magnet aligned along the z-axis and an agent’s sense organ before being deposited in a storage ring. The agent records the completion of the observation, but not which result was seen. This is reminiscent of the Wigner’s Friend [5] argument, where the agent could be asked how she felt about her observation. Then the reverse Hamiltonian is applied, pulling the spin out of the storage ring, erasing the agent’s knowledge, and possibly restoring the original prepared spin state. The completion record is somewhat of a red herring, since it is (ideally) always set, and if the reverse Hamiltonian includes it, it will also be erased. In fact, the agent may have no way to know the experiment has even been performed.

If the spin is then measured along the x-axis, the result will depend on whether collapse occurred. If collapse occurs, either result will happen. Otherwise only the prepared state will be seen. Thus the experiment can distinguish the two models.

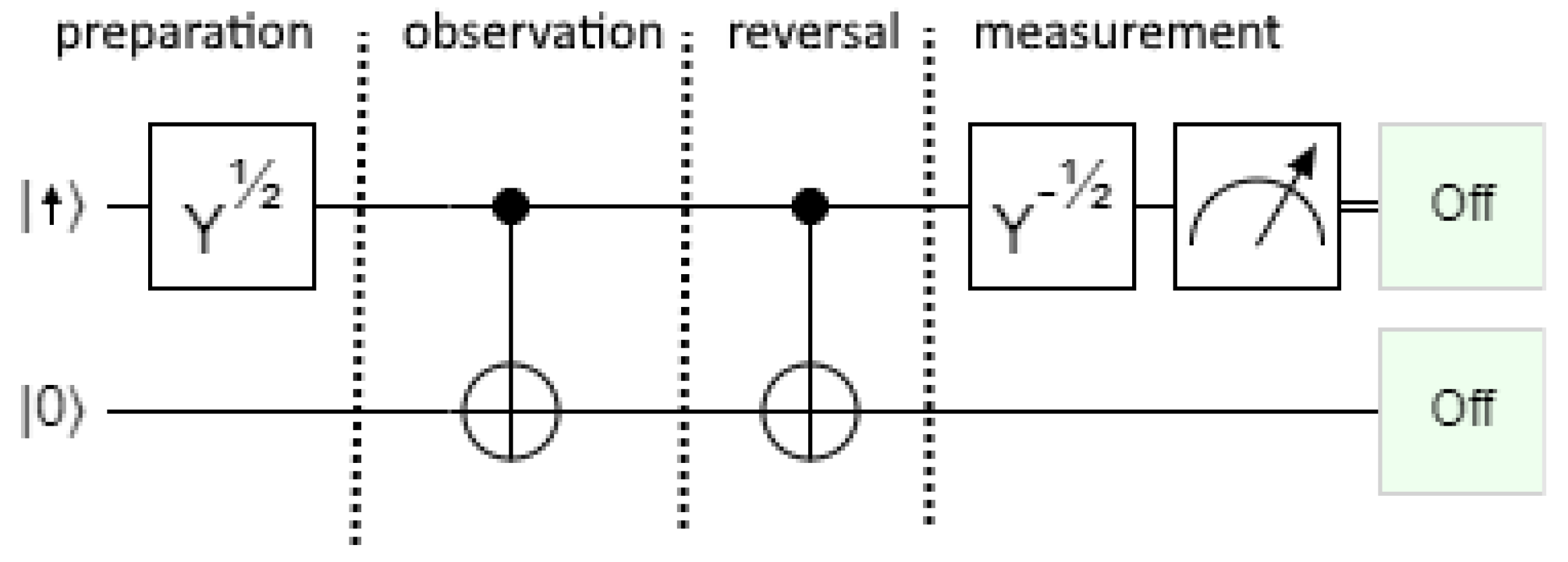
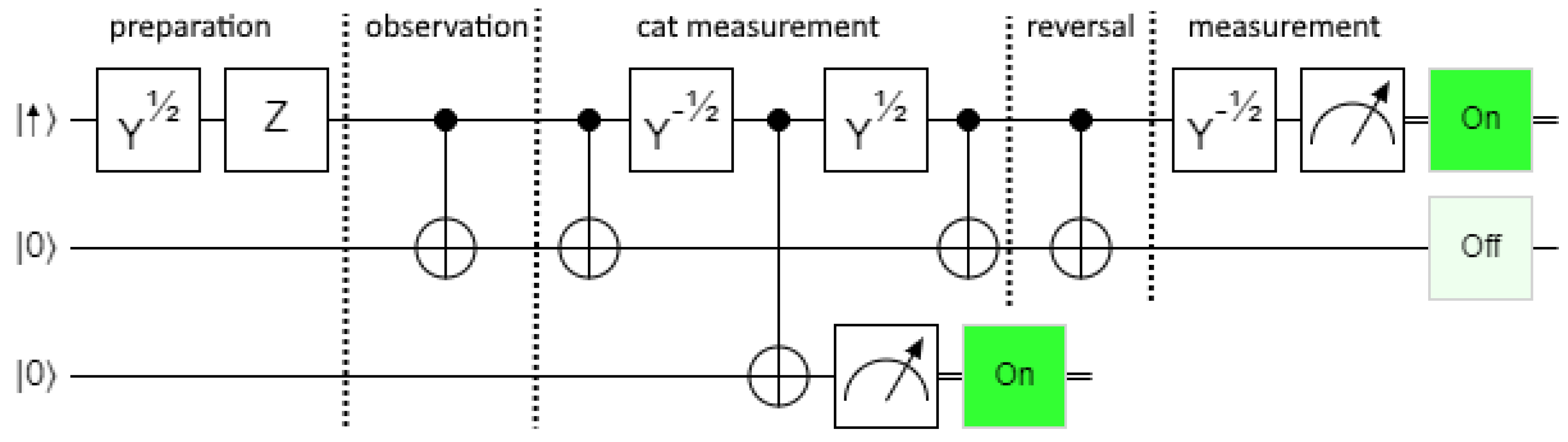
We can demonstrate this using the quantum circuit in Figure 1 2. The first line is a qbit representing a spin system. A

| 0 〉

state may be thought of as a spin pointing along the +z-axis, but we will usually represent spin system states with direction arrows and knowledge and computation qbits with 0’s and 1’s. In order to prepare the spin pointing along the +x-axis, a

Y^{1 / 2}

gate is applied, rotating the spin by

π / 2

radians. The second line represents the agent’s knowledge. The spin is observed using a CNOT gate. The spin and the agent’s memory are now entangled in a state

(| ↑ 0 〉 + | ↓ 1 〉) / \sqrt{2}

. At this point we could say the agent has knowledge of the spin’s z-component, but the knowledge is different in the two components of the superposition. We call this virtual knowledge.

The observation can be reversed using a second CNOT gate. This erases the agent’s virtual knowledge and restores the prepared spin state (

| \to 〉

). We can then measure the spin’s x component by rotating it with a

Y^{- 1 / 2}

gate and applying a measurement gate. In Figure 1 the measurement is successful: “off” (

= | 0 〉

) implies the spin was prepared as

| \to 〉

. For this quantum circuit at least, observational entanglement does not provoke collapse. There is no reason to believe Deutsch’s experiment would behave any differently. Given the ease with which quantum circuits can be constructed and tested today, we should feel confident that observational entanglement alone is not sufficient to cause collapse. The author considers this prediction and verification to be one of the most significant and underappreciated results in the last half century of Physics.

4. Virtual Knowledge

We could allow our agents to parse and emit english sentences encoded in classical bits or qbits that they know will be either 0 or 1. But it is generally simpler to represent statements with a single qbit. This is similar in spirit to the controversial “grandmother cells” in neuroscience [6]. The meaning of the qbit is encoded in reasoning circuits that we do not attempt to model here. The details do not affect our results because reversal of unitary circuits is straightforward. In the observation step of Figure 1 the agent could set her memory to

| 1 〉

to represent the statement “in my branch the spin is down”. This statement applies to the component/branch of the superposition state in which the agent is making that statement. The qualification “in my branch” is necessary. Without it the statement would be false. The spin is not in fact in a ‘down’ state.

The meaning of the qualification is relatively clear here but later we will find it insufficiently rigorous. We therefore define a branch as a synonym for a knowledge projection. Starting from the general state (1), the knowledge projection is given by acting with the projector (3) giving (4). Note that the knowledge projection after a single entanglement observation is identical to the state that would have occured if the observation was instead a measurement with associated collapse.

Bear in mind that quantum logic processing is in general designed around a particular basis, often called the computation basis. As an example: the entangled state in Figure 1,

(| ↑ ↑ 〉 + | ↓ ↓ 〉) / \sqrt{2}

, can also be written

(| \to \to 〉 + | \leftarrow \leftarrow 〉) / \sqrt{2}

. Consider an english language multi-qbit virtual knowledge register deduced by the agent. The register holds a 5 character string with possible values “___up”, “_down”, “_left”, and “right”. If in one basis, the last character is absolutely ‘t’, it cannot be ‘p’ or ‘n’ in another basis.

5. Terminology

When discussing quantum observers, we will use the following terminology:

Entanglement - An entangled correlation. A condition/evolution where an agent is/becomes coherently correlated with a system. If the state is a product state, the term pseudo-entangled may be used.
Measurement - An evolution where an agent becomes incoherently correlated with a system. If a collapse projection is applied, we can say that only one result “actually” occurred.
Observation - An evolution that is either entanglement or measurement.
Knowledge projection - The state formed by projecting to a particular knowledge state. Also called a branch.
Absolute Knowledge - Information that is true about the actual physical state.
Virtual Knowledge - Information that is true in its own branch but not in others.

Note that “absolute” and “virtual” do not distinguish whether the information is known to all branches.

If the procedures for an experiment and the initial pure state are provided to the agents, as we will usually assume, then the entire evolution of the quantum state will be available for deduction as absolute knowledge, including other agents’ virtual thoughts. But explicit recursive reasoning, such as “I know that I know...” or “I know that she knows that I know...”, is limited by available memory.

6. Multiple Agents

Given that agents can store and process virtual knowledge, it should be possible for them to reason about other agents. We will construct explicit examples using quantum circuits. We will not attempt to develop general intelligence, but rather find simple circuits that solve particular problems.

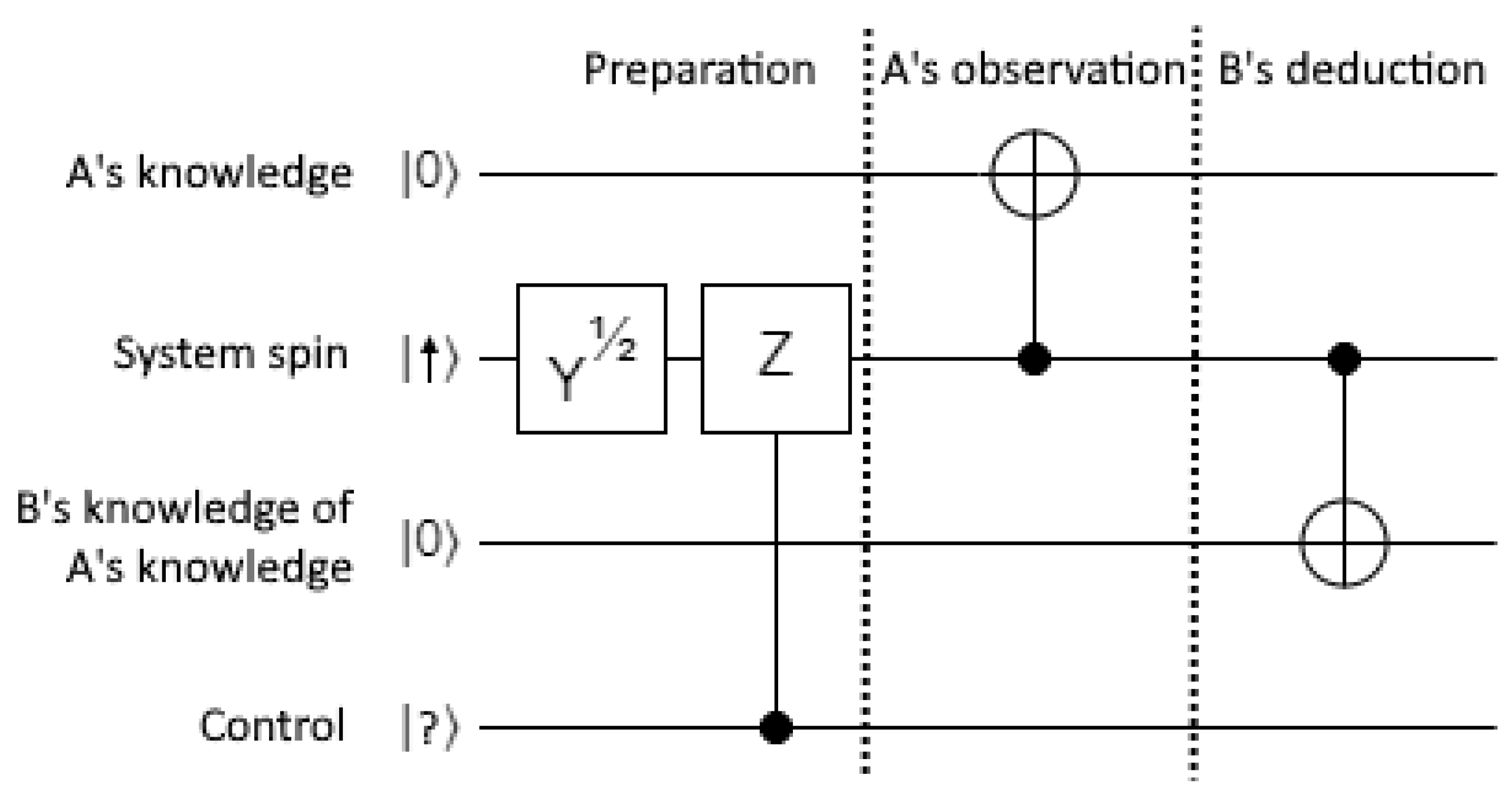
Figure 2 models a spin system and two agents. The spin is prepared based on a control bit which is set to 0 or 1 in each run by the experimenter. The prepared spin is in a state

| \to 〉

| \leftarrow 〉

, depending on whether the Z gate is applied. The agents do not know which state is prepared. The first agent, Alice, interacts with the system and gains virtual knowledge that the spin is ‘up’ and also that it is ‘down’. The second agent, Bob, interacts with the system in order to deduce virtual knowledge that Alice saw ‘up’ and that she saw ‘down’. The final state is one of

\begin{matrix} | R 〉 = (| ↑ 00 〉 + | ↓ 11 〉) / \sqrt{2} \\ | L 〉 = (| ↑ 00 〉 - | ↓ 11 〉) / \sqrt{2} \end{matrix}

(5)

where the states on the left are labeled by the x component of the original prepared spin, and each ket on the right is labeled by 1) the z component of the system spin, 2) Alice’s virtual knowledge (eg. 1 means the system spin is ‘down’), and 3) Bob’s knowledge of Alice’s knowledge. We can read off that all the virtual knowledge is valid since each ket is fully aligned regardless of which spin state was prepared.

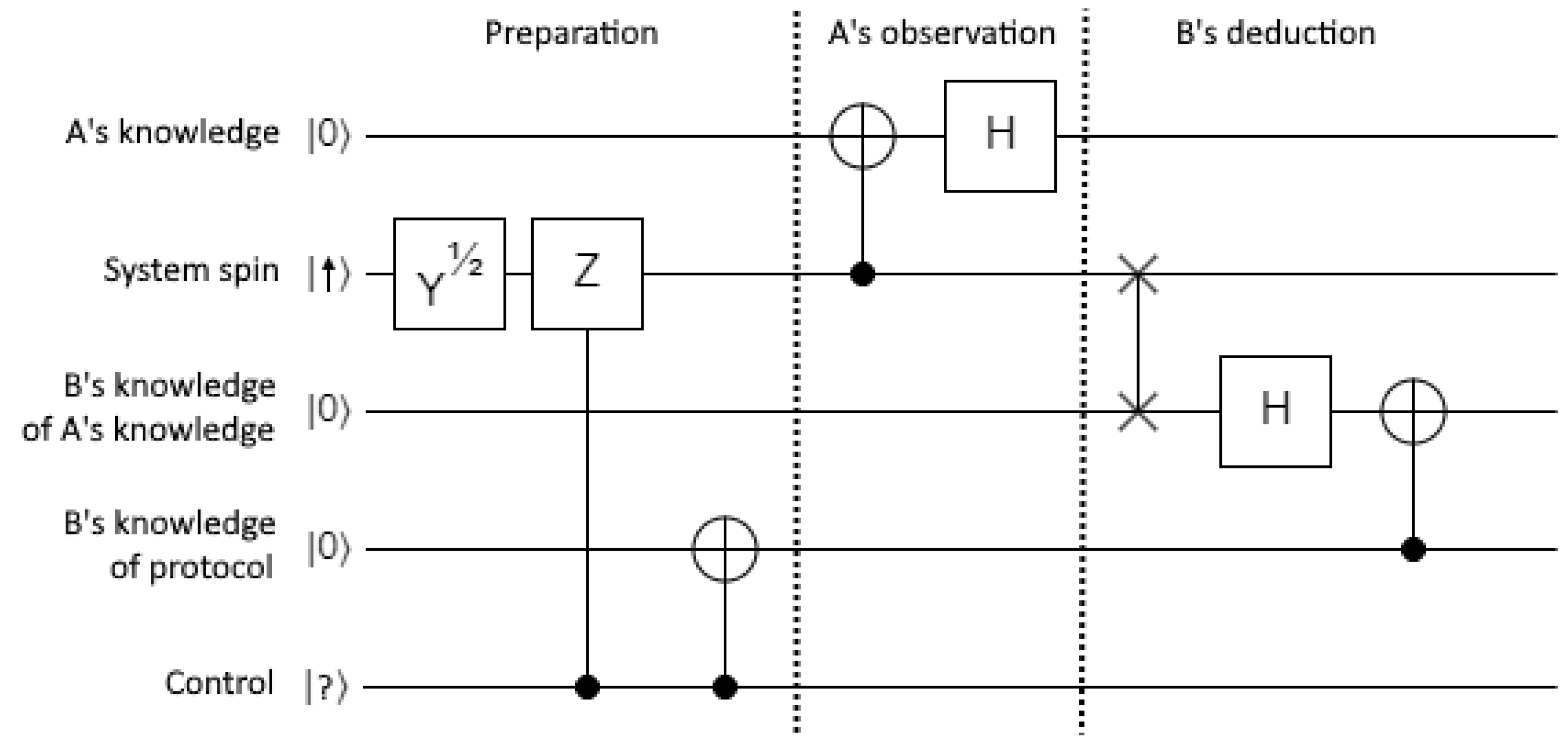
In Figure 3, Alice tries to prevent Bob from learning her knowledge. She applies a Hadamard gate before recording her observation. Bob can still perform the deduction if he has information about the experimental protocol. He first interacts with the system using a swap gate. Note that this is a destructive process, the system is left in a fixed reference state

| ↑ 〉

. He then applies his own Hadamard. Finally, he applies a CNOT gate to flip his virtual knowledge in the case where he knows the Z gate was applied. The final state is

| R^{'} 〉 = | L^{'} 〉 = (| ↑ 00 〉 - | ↑ 11 〉) / \sqrt{2} .

(6)

Bob has successfully deduced Alice’s knowledge.

Without the extra protocol knowledge it is impossible for Bob to deduce Alice’s knowledge. Consider the state after Alice’s observation and Hadamard but before Bob’s deduction. Using the same three-part notation as above, it is one of

\begin{matrix} | R 〉 = (| \to 00 〉 + | \leftarrow 10 〉) / \sqrt{2} \\ | L 〉 = (| \leftarrow 00 〉 + | \to 10 〉) / \sqrt{2} . \end{matrix}

(7)

These states can be swapped by applying a NOT gate to Alice’s knowledge. If Bob manages to get his virtual knowledge aligned with Alice’s in the case that Z is not applied, his knowledge would be exactly wrong in the case Z is applied. Whatever logic circuitry he used to make his deduction would be incorrect.

These circuits are deliberately trivial. A real quantum intelligence would perform the observation, but would have more complex circuitry. The knowledge register would need more qbits to provide context and to distinguish a register of value 0 from an unset register. Knowledge might be represented more abstractly, for example by phases rather than simple register values. Nevertheless a quantum intelligence is a universal computer, and if it is logically possible for us to deduce virtual knowledge from information available to an agent, then a circuit can be designed to perform the same deduction. In the previous example, it is not logically possible for Bob to deduce Alice’s knowledge from supplied information since an experimenter’s choice can invalidate any such knowledge.

7. Cat Measurements and Complementarity

The combination of reversal and measurement in Figure 1 is an example of what is sometimes called a “cat measurement”. The name comes from the idea of proving Schrödinger’s cat is in a superposition by measuring the entire cat coherently. In our case the experimenter is measuring the entire laboratory including system and observer.

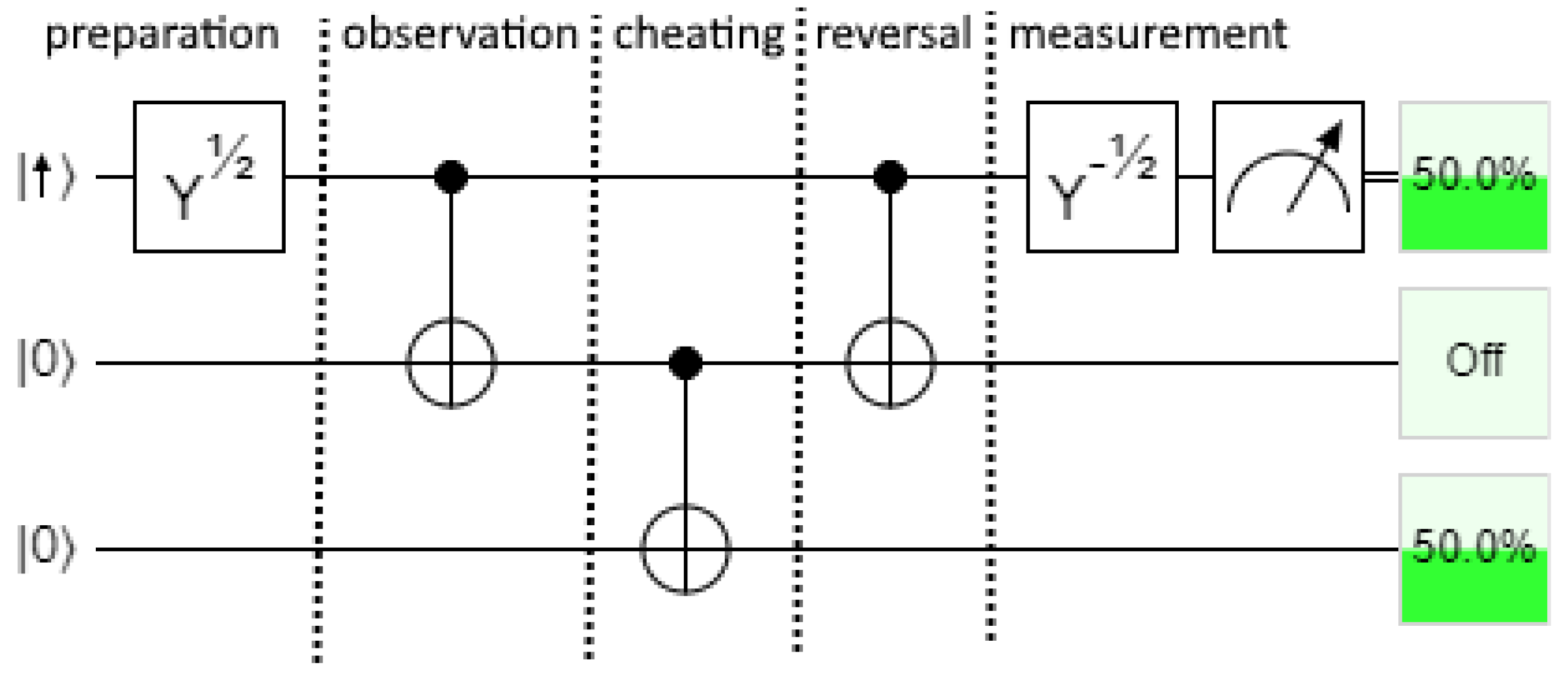
Cat measurements are often used in thought experiments to measure in a complementary basis. This requires the observer’s memory to be erased. Figure 4 represents an attempt by a second observer to cheat and find out both the x-component and z-component of the prepared spin. An additional CNOT gate is used to copy the observation result before reversing the observation. In this case the measurement fails: either result is possible.

It matters what information is copied. In Figure 5 the second agent performs a cat measurement to learn what the x-axis measurement result will be. Both measurements result in “on”, meaning the spin was prepared pointing along the -x-axis. If the Z gate is removed, both measurements will result in “off”, meaning the spin was prepared pointing along the +x-axis.

8. Retrospections and Predictions

Consider the “reversal” circuit in Figure 1. Between the two CNOT gates, the agent is in a superposition of knowing the system spin is up and knowing it is down. This is virtual knowledge. If the agent wrongly treats her knowledge as absolute, she may deduce, in each branch, statement S: “the x-axis measurement has a 50% chance of being

- ℏ / 2

” (this would show as “50.0%” in the circuit diagram). A correct virtual knowledge statement might be “in my branch, S is true”. In reality, the two components of the superposition interfere, and that value never occurs. This is important enough to deserve a name. We will call it the virtual promotion fallacy: virtual knowledge is wrongly promoted to absolute. In this case, S is true in all branches and yet S is absolutely false. Virtual knowledge cannot be trusted, especially when it comes to measurement predictions.

On the other hand, if the first

Y^{1 / 2}

gate is optional (decided in each run by the experimenter), it is possible for the agent to deduce in one of the two branches that the gate has been applied. This is absolute retrospective knowledge that is only available in one branch, and its statement does not need the branch qualification. That agent-branch can then be certain the measurement will be “off”. This is a special case where a quantum agent with partial knowledge is able to make an absolute measurement prediction. Bear in mind that this example assumes the unitary operations comprising the agent’s logic will be reversed and the conclusion forgotten before the second CNOT gate is applied. Otherwise we need to apply something like the “cheating” circuit.

9. Frauchiger and Renner

Perhaps the easiest way to lose one’s way with quantum observers is to treat virtual knowledge as absolute. This is understandable, as physicists are trained from the first few lessons of quantum mechanics to apply a projection operator during measurement. It is natural, but wrong, to extend this intution to the case where an agent is entangled with the system, but has not completed a measurement.

As an example, Frauchiger and Renner (FR) derive a contradiction by applying three deduction rules labeled (Q), (C), and (S) to a cleverly designed thought experiment [1]. They argue that any consistent quantum theory must therefore violate at least one of these rules. What is disturbing is that all three rules are apparently true.

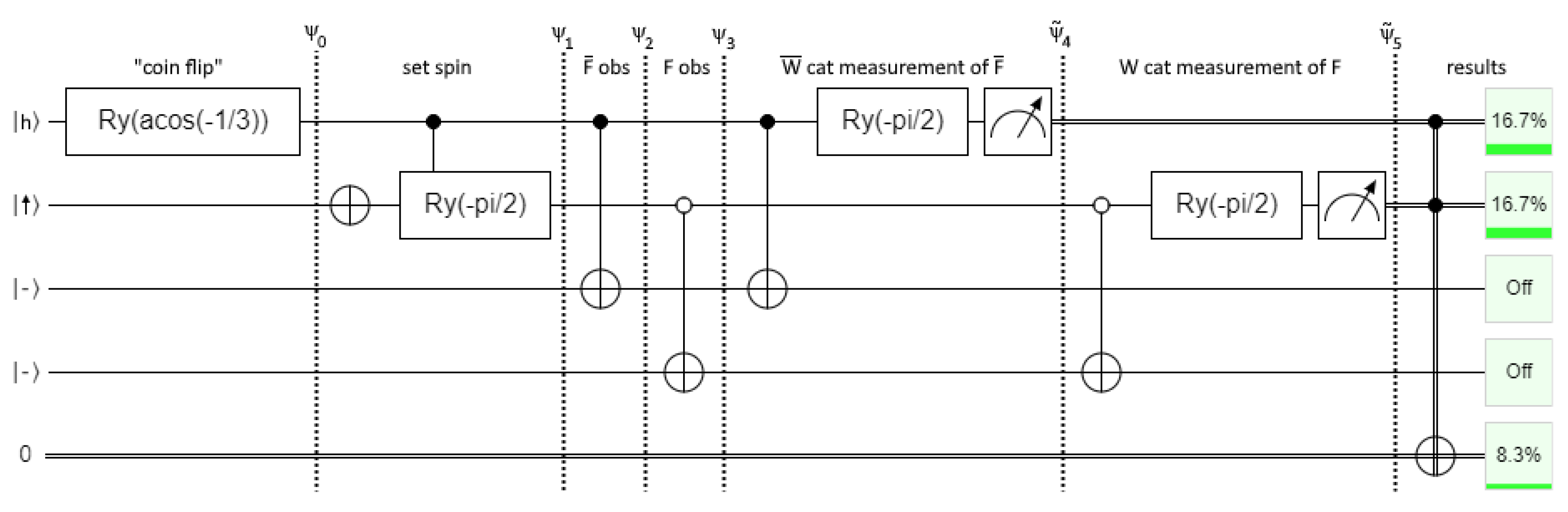
The scenario is somewhat intricate, and we will not reproduce all of it here. We recommend the reader have a copy of their paper handy. The experiment involves four agents. The observations of two of the agents,

\bar{F}

and F, are entanglements, rather than measurements. Agents

\bar{W}

and W perform cat measurements. All agents are aware of the experimental protocol including the fact that the “coin flip” is a superposition.

The relevant states are listed in Table 1. The experiment proceeds as follows.

The state is prepared as

| ψ_{0} 〉

\bar{F}

observes the “coin”. If h is observed she sets the spin to ↓. Otherwise she sets the spin to → leading to

| ψ_{1} 〉

. In the latter case she also flips her knowledge qbit to indicate her belief in statement

S_{\bar{F}}

, leading to

| ψ_{2} 〉

F observes the spin. If it is ‘up’ she flips her knowledge qbit to indicate her belief in statement

S_{F}

, leading to

| ψ_{3} 〉

\bar{W}

cat measures

\bar{F}

. On some runs he gets result

\bar{o k}

, leading to state

| ψ_{4} 〉

W cat measures F. On some runs he gets result

o k

, leading to state

| ψ_{5} 〉

This procedure is modeled in Figure 6. Note that the cat measurements in Figure 6 are not projective measurements3. We are only really interested in the

\bar{f a i l} / \bar{o k}

and

f a i l / o k

results so this does not affect the discussion. The post measurement states become

{\tilde{ψ}}_{4}

and

{\tilde{ψ}}_{5}

, but they are still correlated with

\bar{o k}

and

o k

in the “meter” Hilbert space. It is staightforward to modify the circuit to perform a projective cat measurement using the technique of Figure 5 but it adds unnecessary complexity.

Not included are the agents’ reasoning circuits, and with them their understanding of their statement qbits

S_{\bar{F}}

and

S_{F}

. If the agents are reasoning correctly, statement

S_{\bar{F}}

might reference the knowledge projection

| ψ_{2}^{'} 〉

: “I have observed t. The current state is

| ψ_{2} 〉

. If the state were instead

| ψ_{2}^{'} 〉

, then W’s measurement would result in ‘fail’”. Or she could reason: “as one component of a superposition, I have observed t. When W performs his physical measurement, he will observe ‘fail’ with a probability that depends on the amplitudes of the superposition”. Statement

S_{F}

could be: “I have observed ↑. The current state is

| ψ_{3} 〉

. If the state were instead

| ψ_{3}^{'} 〉

, then

\bar{F}

has recorded her belief in

S_{\bar{F}}

, which says that if the state were instead

| ψ_{2}^{'} 〉

, then W’s measurement would result in ‘fail’“.

As pointed out by Araujo [7] and Baumann [8], the agents in FR do not reason correctly. For example, in the branch where

\bar{F}

observes t, she states without qualification “I am certain that W will observe

w =

fail at time n:31”.

\bar{F}

fell victim to the virtual promotion fallacy. FR goes on to show that in fact W can measure “ok” in some runs, thus proving

\bar{F}

’s statement to be false. They do not address this discrepancy directly. Instead they use

\bar{F}

’s statement in a chain of deduction using (Q), (C), and (S) to arrive at a contradiction. They then describe which of these deduction rules are violated in each of various interpretations of Quantum Mechanics. In fact there is nothing wrong with (Q), (C), and (S). (Q) is correct when applied to a state, rather than a component of a superposition. (C) and (S) are correct when their premises are correct. It is

\bar{F}

’s false statement which causes the contradiction.

Other authors have constructed similar no-go theorems [9,10,11,12,13], but all of these explicitly include an assumption sometimes called Absoluteness of Observed Events (AOE). The author is not aware of a rigorous definition of this assumption, but we take it to mean that for every run of a thought experiment, there exists an assignment of results for all observations that is, in some sense, internally consistent. The FR scenario does seem to lead to contradictions for any assignment of observation results, and we consider these no-go theorems to be strong arguments for abandoning AOE.

10. Conclusions

Quantum observers can process logic in superposition such that knowledge is different in different branches. We call this virtual knowledge to distinguish it from absolute knowledge which is true for the entire state. Simple deduction scenarios, including ones with multiple agents, can be modeled on quantum computers using today’s technology. There are potential pitfalls. Deductions are limited when only partial information is available, and conclusions may be wrong if wrong information is supplied. When represented in English, virtual knowledge should be identified as such to help avoid contradictions. Measurements require special treatment. It is important to distinguish measurement from entanglement. Deducing the results of measurements from virtual knowledge is possible only in special cases since multiple branches can interfere. Nevertheless, with care, quantum observers can make consistent deductions, including about the virtual knowledge of other agents.

Funding

This research received no external funding.

Conflicts of Interest

The author declares no conflict of interest.

References

Frauchiger, D.; Renner, R. Quantum theory cannot consistently describe the use of itself. Nature Communications 2018, 9, 3711. [Google Scholar] [CrossRef] [PubMed]
Feynman, R.; Leighton, R.; Sands, M. The Feynman Lectures on Physics; Pearson/Addison-Wesley, 2006; chapter 3.1. [Google Scholar]
Ring, D. Quantum Collapse in an Isolated Laboratory. Preprints 2024. [Google Scholar] [CrossRef]
Deutsch, D. Quantum theory as a universal physical theory. International Journal of Theoretical Physics 1985, 24, 1–41. [Google Scholar] [CrossRef]
Wigner, E.P. Remarks on the Mind-Body Question. In The Scientist Speculates : An Anthology of Partly-Baked Ideas; Good, I.J.; J., M.A.; M., S.J., Eds.; London: Heinemann, 1962. [Google Scholar]
Connor, C.E. Friends and grandmothers. Nature 2005, 435, 1036–1037. [Google Scholar] [CrossRef] [PubMed]
Araujo, M. The Flaw in Frauchiger and Renner’s Argument. 2018. Available online: https://mateusaraujo.info/2018/10/24/the-flaw-in-frauchiger-and-renners-argument (accessed on 5 May 2024).
Baumann, V.; Hansen, A.; Wolf, S. The measurement problem is the measurement problem is the measurement problem. arXiv 2016, arXiv:1611.01111. [Google Scholar]
Healey, R. Quantum Theory and the Limits of Objectivity. Foundations of Physics 2018, 48, 1568–1589. [Google Scholar] [CrossRef]
Bong, K.W.; Utreras-Alarcón, A.; Ghafari, F.; Liang, Y.C.; Tischler, N.; Cavalcanti, E.G.; Pryde, G.J.; Wiseman, H.M. A strong no-go theorem on the Wigner’s friend paradox. Nature Physics 2020, 16, 1199–1205. [Google Scholar] [CrossRef]
Haddara, M.; Cavalcanti, E.G. A possibilistic no-go theorem on the Wigner’s friend paradox. New Journal of Physics 2023, 25, 093028. [Google Scholar] [CrossRef]
Leegwater, G. When Greenberger, Horne and Zeilinger Meet Wigner’s Friend. Foundations of Physics 2022, 52, 68. [Google Scholar] [CrossRef]
Ormrod, N.; Barrett, J. A no-go theorem for absolute observed events without inequalities or modal logic. arXiv 2022, arXiv:2209.03940. [Google Scholar]

1	An unpublished version of FR did include a version of that assumption
2	All figures in this paper were produced and simulated using Quirk: https://algassert.com/quirk
3	also called repeatable or von Neumann measurements

Figure 1. Reversal of an observation. The first line is a qbit representing a spin system. The second line represents the agent’s knowledge. The spin is observed and the agent knows the spin is ‘up’ and also that it is ‘down’. The observation is reversed, erasing the agent’s knowledge and allowing a different measurement to be performed.

Figure 2. Simple virtual deduction. The experimenter uses a control bit to prepare a system spin. Alice observes the system and records its z-axis values in a qbit register as virtual knowledge. Bob inspects the system to determine Alice’s virtual knowledge. He is able to correctly deduce virtual knowledge of Alice’s virtual knowledge even though neither agent knows whether the Z gate has been applied.

Figure 3. Virtual deduction with protocol knowledge. The experimenter prepares the spin and informs Bob using a CNOT gate. Alice processes her observation before recording her virtual knowledge. Bob is able to deduce her virtual knowledge using absolute knowledge of the experimental protocol. Without protocol knowledge, it is impossible for Bob to deduce Alice’s knowledge.

Figure 4. Attempted cheating. If we try to cheat and copy the z-axis observation result before the reversal the x-axis measurement fails.

Figure 5. Not cheating. It is possible to “cat measure” in a basis consistent with another measurement.

Figure 6. The FR experiment. The four qbits are h/t, ↑/↓, -/

S_{\bar{F}}

, and -/

S_{F}

. Rotation gates are used because a controlled

Y^{- 1 / 2}

introduces an undesirable phase. After the cat measurements, the first two qbits are repurposed for measurement results

\bar{f a i l} / \bar{o k}

and

f a i l / o k

respectively. The classical bit will be true if both measurements are true (

\bar{o k}

and

o k

Figure 6. The FR experiment. The four qbits are h/t, ↑/↓, -/

S_{\bar{F}}

, and -/

S_{F}

. Rotation gates are used because a controlled

Y^{- 1 / 2}

introduces an undesirable phase. After the cat measurements, the first two qbits are repurposed for measurement results

\bar{f a i l} / \bar{o k}

and

f a i l / o k

respectively. The classical bit will be true if both measurements are true (

\bar{o k}

and

o k

Table 1. Experimental states relevant to FR. Each

ψ

is a vector in the 4 qbit Hilbert space.

| - 〉 \equiv | 0 〉

indicates the agent records no statement, while

| S_{\bar{F}} 〉 \equiv | 1 〉

| S_{F} 〉 \equiv | 1 〉

indicate the respective agent has recorded her statement.

Table 1. Experimental states relevant to FR. Each

ψ

is a vector in the 4 qbit Hilbert space.

| - 〉 \equiv | 0 〉

indicates the agent records no statement, while

| S_{\bar{F}} 〉 \equiv | 1 〉

| S_{F} 〉 \equiv | 1 〉

indicate the respective agent has recorded her statement.

$\| ψ_{0} 〉$	$= (\| h - ↑ - 〉 + \sqrt{2} \| t - ↑ - 〉) / \sqrt{3}$
$\| ψ_{1} 〉$	$= (\| h - ↓ - 〉 + \| t - ↓ - 〉 + \| t - ↑ - 〉) / \sqrt{3}$
$\| ψ_{2} 〉$	$= (\| h - ↓ - 〉 + \| t S_{\bar{F}} ↓ - 〉 + \| t S_{\bar{F}} ↑ - 〉) / \sqrt{3}$
$\| ψ_{2}^{'} 〉$	$= (\| t S_{\bar{F}} ↓ - 〉 + \| t S_{\bar{F}} ↑ - 〉) / \sqrt{2}$
$\| ψ_{3} 〉$	$= (\| h - ↓ - 〉 + \| t S_{\bar{F}} ↓ - 〉 + \| t S_{\bar{F}} ↑ S_{F} 〉) / \sqrt{3}$
	$= (2 \| \bar{f a i l} ↓ - 〉 + \| \bar{f a i l} ↑ S_{F} 〉 - \| \bar{o k} ↑ S_{F} 〉) / \sqrt{6}$
$\| ψ_{3}^{'} 〉$	$= \| t S_{\bar{F}} ↑ S_{F} 〉$
$\| ψ_{4} 〉$	$= - \| \bar{o k} ↑ S_{F} 〉$
	$= (\| \bar{o k} o k 〉 - \| \bar{o k} f a i l 〉) / \sqrt{2}$
$\| {\tilde{ψ}}_{4} 〉$	$= - \| t - ↑ S_{F} 〉$
$\| ψ_{5} 〉$	$= \| \bar{o k} o k 〉$
$\| {\tilde{ψ}}_{5} 〉$	$= \| t - ↓ - 〉$
$\| o k 〉$	$= (\| ↓ - 〉 - \| ↑ S_{F} 〉) / \sqrt{2}$
$\| f a i l 〉$	$= (\| ↓ - 〉 + \| ↑ S_{F} 〉) / \sqrt{2}$
$\| \bar{o k} 〉$	$= (\| h - 〉 - \| t S_{\bar{F}} 〉) / \sqrt{2}$
$\| \bar{f a i l} 〉$	$= (\| h - 〉 + \| t S_{\bar{F}} 〉) / \sqrt{2}$

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

121

Views

Comments

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

$\| ψ_{0} 〉$	$= (\| h - ↑ - 〉 + \sqrt{2} \| t - ↑ - 〉) / \sqrt{3}$
$\| ψ_{1} 〉$	$= (\| h - ↓ - 〉 + \| t - ↓ - 〉 + \| t - ↑ - 〉) / \sqrt{3}$
$\| ψ_{2} 〉$	$= (\| h - ↓ - 〉 + \| t S_{\bar{F}} ↓ - 〉 + \| t S_{\bar{F}} ↑ - 〉) / \sqrt{3}$
$\| ψ_{2}^{'} 〉$	$= (\| t S_{\bar{F}} ↓ - 〉 + \| t S_{\bar{F}} ↑ - 〉) / \sqrt{2}$
$\| ψ_{3} 〉$	$= (\| h - ↓ - 〉 + \| t S_{\bar{F}} ↓ - 〉 + \| t S_{\bar{F}} ↑ S_{F} 〉) / \sqrt{3}$
	$= (2 \| \bar{f a i l} ↓ - 〉 + \| \bar{f a i l} ↑ S_{F} 〉 - \| \bar{o k} ↑ S_{F} 〉) / \sqrt{6}$
$\| ψ_{3}^{'} 〉$	$= \| t S_{\bar{F}} ↑ S_{F} 〉$
$\| ψ_{4} 〉$	$= - \| \bar{o k} ↑ S_{F} 〉$
	$= (\| \bar{o k} o k 〉 - \| \bar{o k} f a i l 〉) / \sqrt{2}$
$\| {\tilde{ψ}}_{4} 〉$	$= - \| t - ↑ S_{F} 〉$
$\| ψ_{5} 〉$	$= \| \bar{o k} o k 〉$
$\| {\tilde{ψ}}_{5} 〉$	$= \| t - ↓ - 〉$
$\| o k 〉$	$= (\| ↓ - 〉 - \| ↑ S_{F} 〉) / \sqrt{2}$
$\| f a i l 〉$	$= (\| ↓ - 〉 + \| ↑ S_{F} 〉) / \sqrt{2}$
$\| \bar{o k} 〉$	$= (\| h - 〉 - \| t S_{\bar{F}} 〉) / \sqrt{2}$
$\| \bar{f a i l} 〉$	$= (\| h - 〉 + \| t S_{\bar{F}} 〉) / \sqrt{2}$

A Consistent Approach to Modeling Quantum Observers

Abstract

Keywords:

Subject:

1. Introduction

2. Observation States

3. Remeasurement

4. Virtual Knowledge

5. Terminology

6. Multiple Agents

7. Cat Measurements and Complementarity

8. Retrospections and Predictions

9. Frauchiger and Renner

10. Conclusions

Funding

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe