Submitted:
31 July 2024
Posted:
01 August 2024
Read the latest preprint version here
Abstract
Keywords:
1. Introduction
1.1. A Characteristic Geometric Inconsistency-On Basepoint Operations
1.1.1. Geometric Foundations
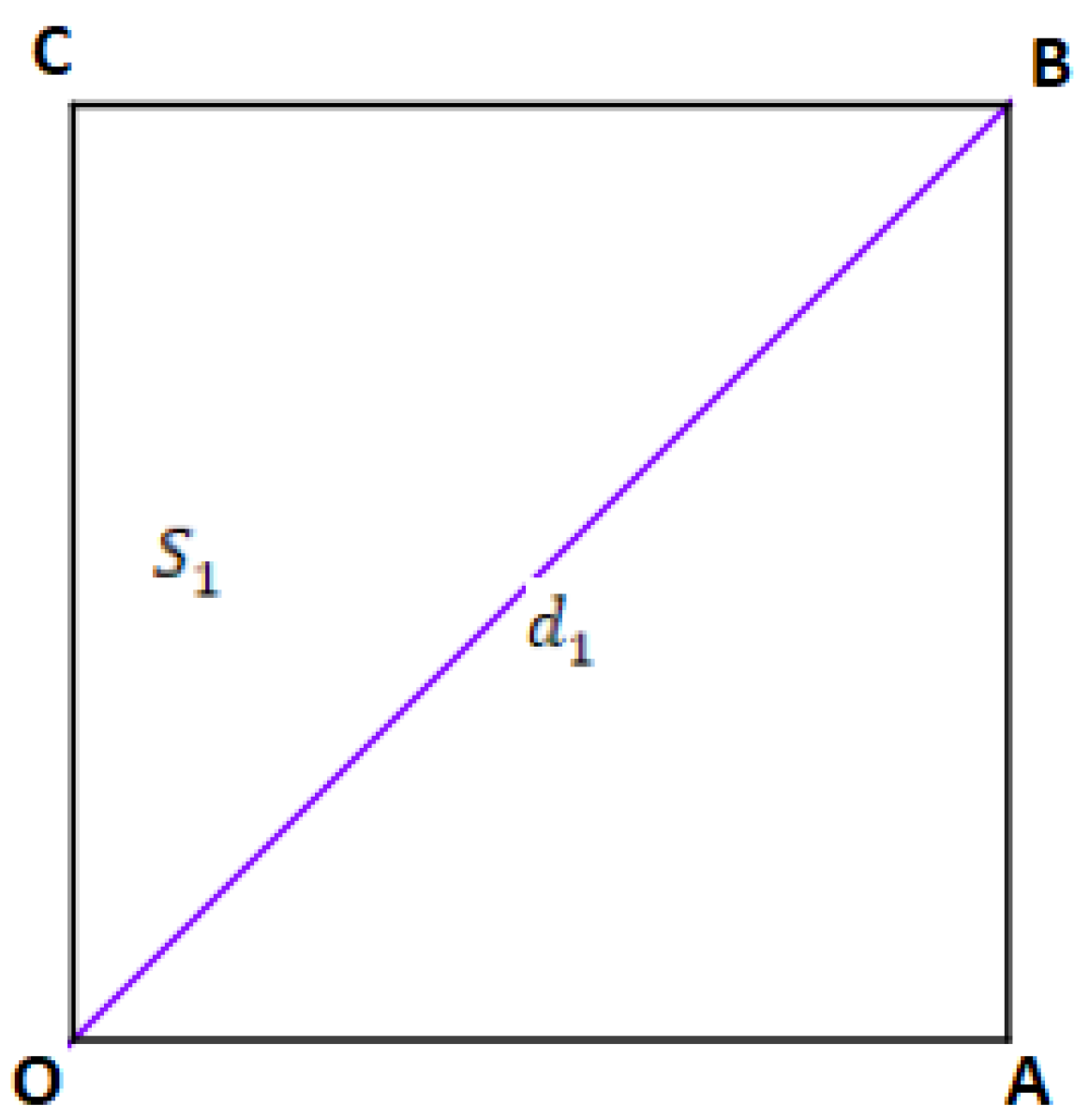
- Construct a line from the point to the point .
- Construct the square of side-lengths , and vertices , , and .
- Construct the diagonal , between the points vertices and .
- The result is depicted in Figure 1.
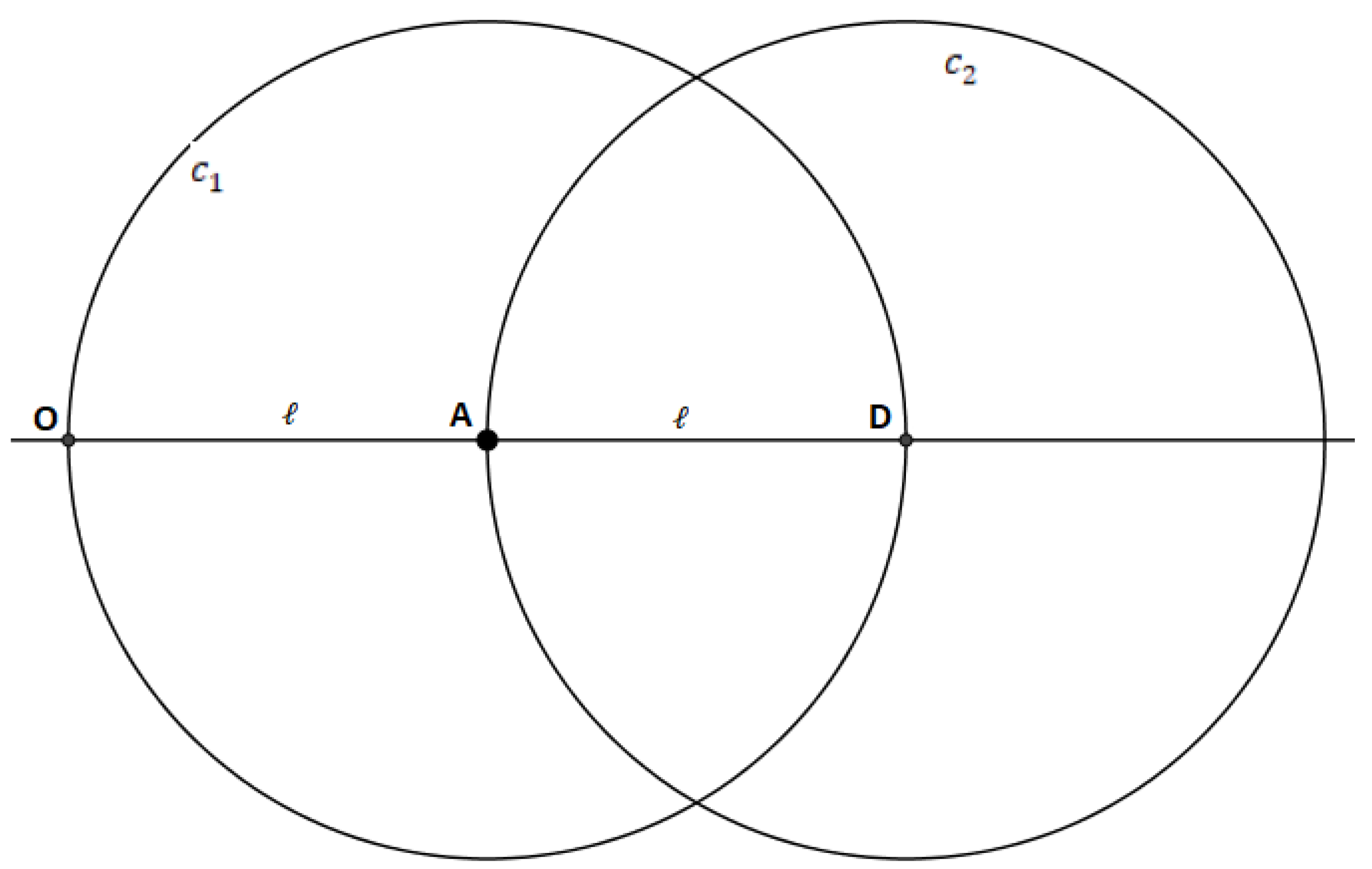
- Construct a circle with radius , centered at the point .
- Construct a circle with radius , centered tat the point .
- Output .
- The circle intersects the line through the point .
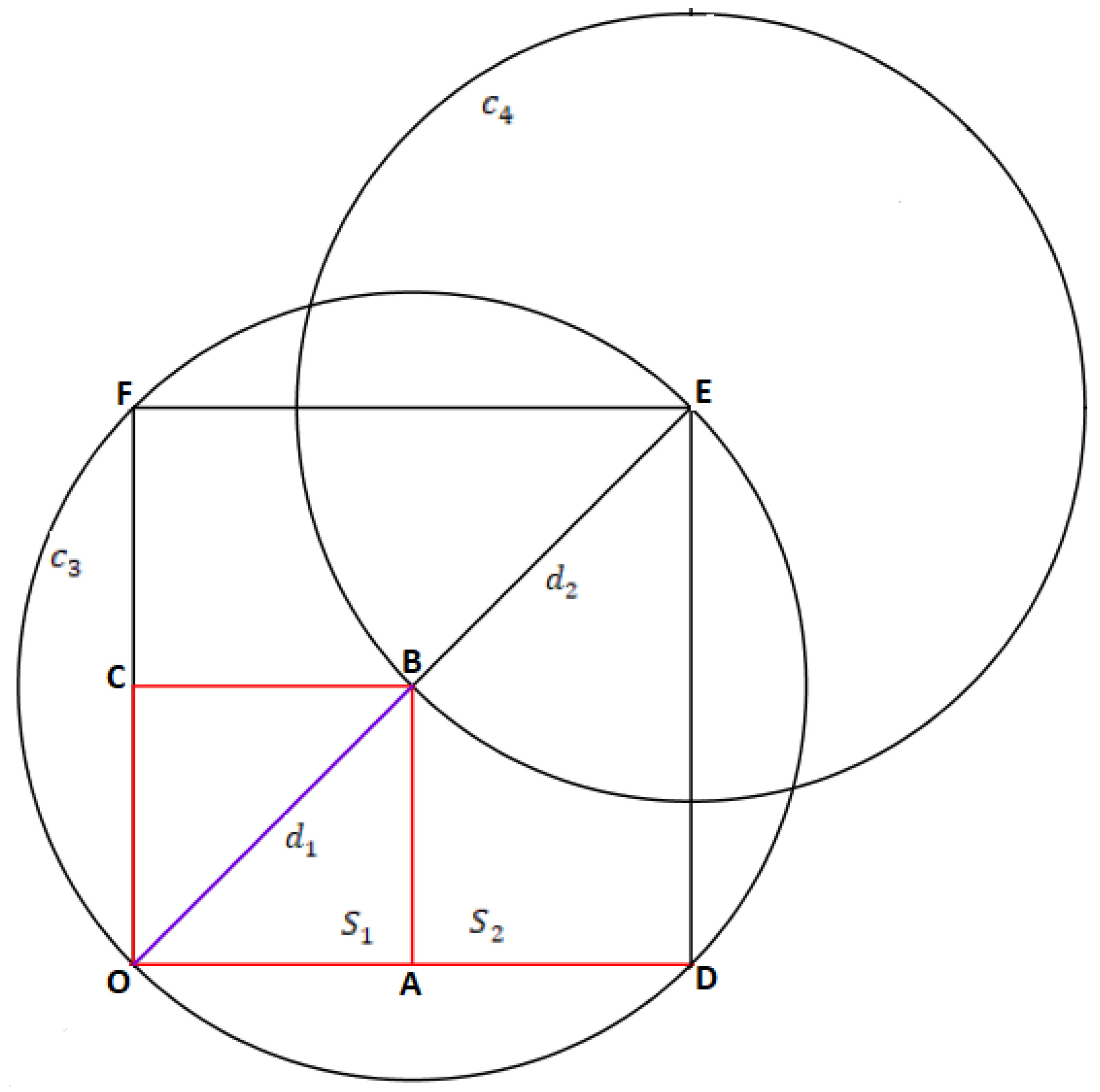
- Construct a square with side-lengths and vertices , , and .
- Construct the diagonal between the points and .
- Construct circle with radius , centered at the point .
- Construct circle with radius , centered at the point .
- Construct a base square face ), with side-lengths .
- Construct the plane ) parallel to ).
- Construct the vertical to and perpendicular edges on ); , , and .
- Output the cube , ).
2. Limitations of the Modern Angles Trisection Impossibility Proof
2.1. Non-Adherence to Euclidean Geometry. In objection to its Euclidean geometric validity, this paper assert that the modern angles non-trisectability impossibility proof does not adhere to Euclidean geometric structure.
2.2. Inadequate Euclidean Logical Structure. The primary limitation of the existing modern impossibility proof (the non-trisectability non-Euclidean impossibility proof [17]) lies in its lack of detailed understanding and equivalence to established impossibility proofs within the Euclidean geometric system [18]. A careful examination reveals that the modern angles trisection impossibility logical structure relies on negating a universal statement to an existential statement. This logical methodic approach pose one of the serious misconceptions exhibited in translating the angles trisection problem from its inherent geometric formulation to a anti-Euclid formulation; regarding what the geometric desires is, for the angles trisectionng problem. We assert that these misconceptions and the inherent logical structural flaws exhibited in the modern non-Euclidean proof of the angles non-trisctability impossibility is not permissible for a Euclidean geometric proof, at least.2.3. Contrasting Modern and Traditional Approaches to Angle Trisection Impossibility
2.3.1. Universal Statement Negation in Angle Trisection Proofs
2.3.2. Universal Statement Negation in Incommensurability Proofs
2.3.3. Contrasting Universal Negation in Angle Trisection and Incommensurability Proofs
3. The Euclidean Approach to Angles Trisection Impossibility Proof
3.1. The Main Result
- a.
- A straight line segment can be drawn between any two points.
- b.
- A circle can be drawn with any center and radius.
- c.
- All right angles are congruent.
- d.
- Two lines intersect at a point, forming vertical angles that are congruent.
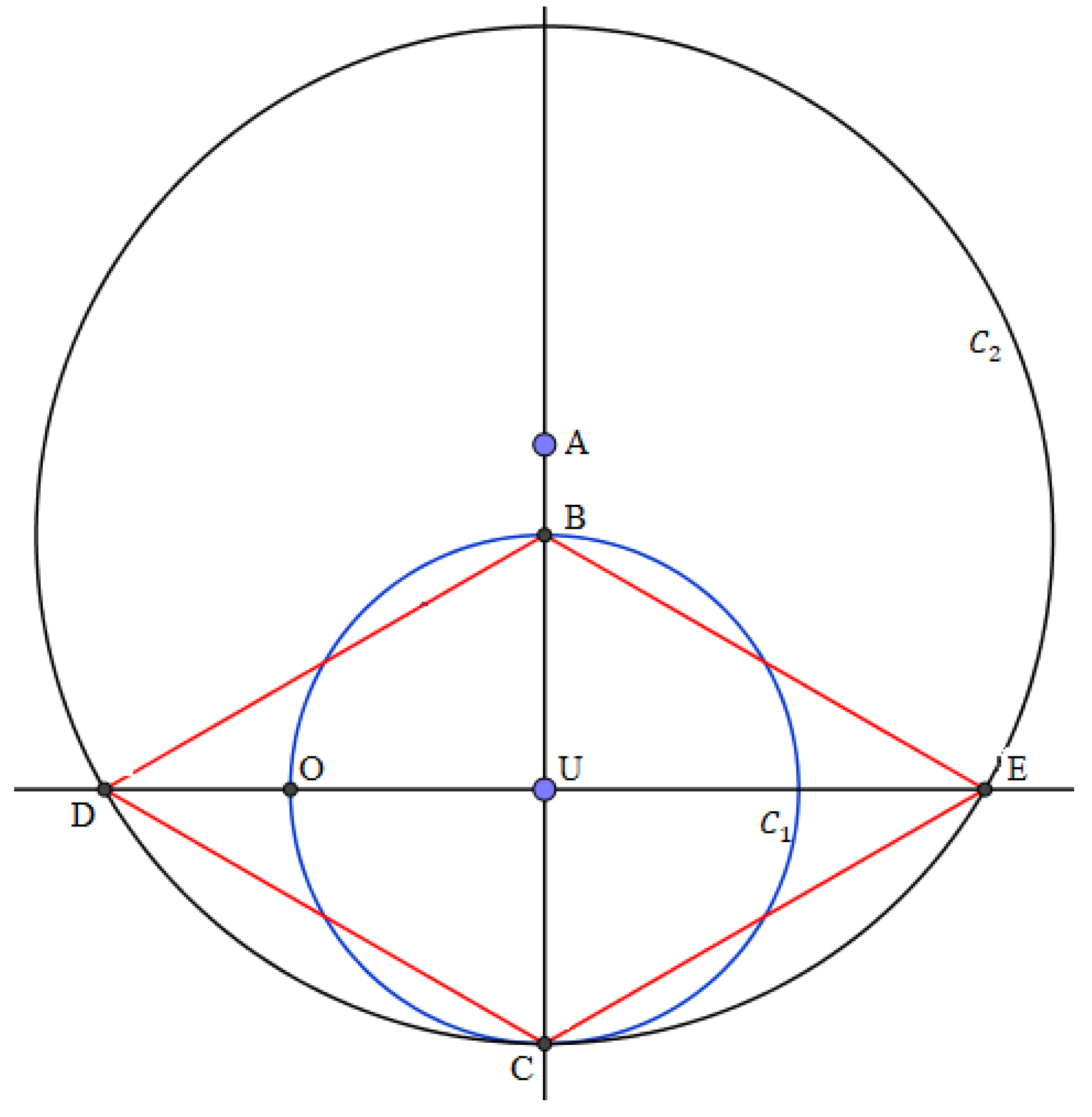
- Start with a right angle formed by two intersecting lines, and , where is horizontal and , is vertical.
- Construct a circle centered at the point with radius .
- Mark the points of intersection of the circle with the vertical line as point and point .
- Construct a circle centered at the point with radius .
- Let the points of intersection of this circle with the horizontal line be the point and the point .
- Construct the extension of the straight line through the points and to form the trisection angle, as depicted in figure (1).
- By construction, the angles; and are straight angles, which means and are congruent.
- The angles; and are right angle, and by , all right angles are congruent.
- Conversely, implies also that all congruent angles are right angles.
- This implies that the angles; and , and the angles; and are right angles.
4. Discussions
4.1. Consequential Inconsistencies within Euclidean Geometry, a Shared Perspective
4.2. Universal Perspective on Traditional vs. Modern Angle Trisection Proofs
4.3. Questioning the Need for a General Proof
4.4. Broader Implications
4.5. Significance of the Provided Angles Trisection Impossibility Proof
5. Conclusions
Conflicts of Interest
References
- Ostermann and G. Wanner, Geometry by Its History. in Undergraduate Texts in Mathematics. Berlin, Heidelberg: Springer Berlin Heidelberg, 2012. [CrossRef]
- S. Yadav and M. Mohan, Eds., Ancient Indian Leaps into Mathematics. Boston, MA: Birkhäuser Boston, 2011. [CrossRef]
- A History of Chinese Mathematics. Springer Berlin Heidelberg, 1997. [CrossRef]
- J. Scriba and P. Schreiber, 5000 Years of Geometry: Mathematics in History and Culture. Basel: Springer Basel, 2015. [CrossRef]
- Heath, Thomas L, The Thirteen Books of Euclid’s Elements, translated from the text of Heiberg, with introduction and commentary, 2nd ed., vol. 3 vols. Cambridge (available in Dover reprint): University Press, 1926.
- F. Borceux, “Euclid’s Elements,” in An Axiomatic Approach to Geometry, Cham: Springer International Publishing, 2014, pp. 43–110. [CrossRef]
- R. Trudeau, “Euclidean Geometry,” 2001, pp. 22–105. [CrossRef]
- K. M. Alex, “The Angle Trisection Solution (A Compass-Straightedge (Ruler) Construction),” J. Adv. Math., vol. 13, no. 4, pp. 7308–7332, Aug. 2017. [CrossRef]
- Kimuya M Alex, “The Possibility of Angle Trisection (A Compass-Straightedge Construction) Kimuya M Alex,” J. Math. Syst. Sci., vol. 7, no. 1, Jan. 2017. [CrossRef]
- M. Ben-Ari, “Trisection of an Angle,” in Mathematical Surprises, Cham: Springer International Publishing, 2022, pp. 11–28. [CrossRef]
- R. Hartshorne, “Teaching Geometry According to Euclid.,” 2000.
- M. Kimuya and S. M. Karanja, “The Incompatibility between Euclidean Geometry and the Algebraic Solutions of Geometric Problems,” Eur. J. Math. Stat., vol. 4, no. 4, Art. no. 4, Jul. 2023. [CrossRef]
- G. E. Martin, “Euclid’s Elements,” in The Foundations of Geometry and the Non-Euclidean Plane, in Undergraduate Texts in Mathematics., New York, NY: Springer New York, 1975, pp. 121–130. [CrossRef]
- M. H. P. Shad, “Angle Trisection:,” J. Adv. Math., vol. 17, pp. 165–231, Sep. 2019. [CrossRef]
- Ostermann and G. Wanner, “The Elements of Euclid,” in Geometry by Its History, A. Ostermann and G. Wanner, Eds., in Undergraduate Texts in Mathematics. , Berlin, Heidelberg: Springer, 2012, pp. 27–59. [CrossRef]
- J. Avigad, E. DEAN, and J. Mumma, “A Formal System for Euclid’S Elements,” Rev. Symb. Log., vol. 2, pp. 700–768, Dec. 2009. [CrossRef]
- Pierre Laurent Wantzel, “Recherches sur les moyens de reconnaitre si un problème de géométrie peut se résoudre avec la règle et le compass,” Journal de Mathematiques pures et appliques, vol. 2, pp. 366–372, 1837.
- M. Panza, “Rethinking geometrical exactness,” Hist. Math., vol. 38, no. 1, pp. 42–95, Feb. 2011. [CrossRef]
- Crippa, “IMPOSSIBILITY RESULTS: FROM GEOMETRY TO ANALYSIS,” phdthesis, Univeristé Paris Diderot Paris 7, 2014. Accessed: Feb. 02, 2021. [Online]. Available: https://hal.archives-ouvertes.fr/tel-01098493.
- J. Barbeau, “Incommensurability Proofs: A Pattern That Peters Out,” Math. Mag., vol. 56, no. 2, pp. 82–90, 1983. [CrossRef]
- “Euclid’s Elements, Book II, Proposition 10.” Accessed: Jun. 29, 2023. [Online]. Available: http://aleph0.clarku.edu/~djoyce/elements/bookII/propII10.html.
- B. Surányi, “Predicates, Negative Quantifiers and Focus: Specificity and Quantificationality of N-Words,” vol. 68, 2007, pp. 255–285. [CrossRef]
- S. Gennari and M. MacDonald, “Acquisition of Negation and Quantification: Insights From Adult Production and Comprehension,” Lang. Acquis. - LANG Acquis., vol. 13, Apr. 2006. [CrossRef]
- M. Beeson, J. Narboux, and F. Wiedijk, “Proof-checking Euclid,” Ann. Math. Artif. Intell., vol. 85, no. 2, pp. 213–257, Apr. 2019. [CrossRef]
- “Euclid’s Elements, Introduction.” Accessed: Jun. 29, 2023. [Online]. Available: https://mathcs.clarku.edu/~djoyce/elements/elements.html.
- D. Crippa, “IMPOSSIBILITY RESULTS: FROM GEOMETRY TO ANALYSIS,” phdthesis, Univeristé Paris Diderot Paris 7, 2014. Accessed: Sep. 05, 2020. [Online]. Available: https://hal.archives-ouvertes.fr/tel-01098493.
- Borceux, An Axiomatic Approach to Geometry: Geometric Trilogy I. Cham: Springer International Publishing, 2014. [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).



