Prerpints.org logo
Preprint
Article

Tailoring Deep Learning for Real-Time Brain-Computer Interfaces: From Offline Models to Calibration-Free Online Decoding

This version is not peer-reviewed.

Submitted:

29 July 2024

Posted:

30 July 2024

Read the latest preprint version here

Abstract
The success of deep learning (DL) in offline brain-computer interfaces (BCIs) has not yet translated into efficient online applications. This is due to two limiting factors: the need for large amounts of training data in DL and the fact that current DL solutions are primarily developed for offline decoding. To enable real-time decoding, even across subjects without calibration data, we first introduce a novel method real-time adaptive pooling (RAP) to tune existing offline DL models towards online decoding by modifying the pooling layers. To reduce the amount of training data required, our approach leverages different levels of domain adaptation. We show how different settings enable different adaptation solutions. Our results demonstrate that our approach is both powerful and can be calibration-free, providing a robust and practical solution for real-time BCI applications. These findings pave the way for the development of co-adaptive and highly efficient DL-based BCI systems.
Keywords: 
Motor imagery
;  
Electroencephalography
;  
Deep Learning
;  
Online decoding
;  
Domain adaptation
;  
Calibration-free
;  
Mutual learning
Subject: 
Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Brain-computer interfaces (BCIs) enable direct communication between the human brain and external devices. As technology advances, the range of applications for BCIs spans from medical rehabilitation to enhancing human-computer interaction and entertainment [1]. One common method to control a BCI is through the motor imagery (MI) paradigm. MI BCIs are particularly utilized as a rehabilitation strategy for post-stroke patients, helping in the recovery of affected limbs [2,3]. During MI the user imagines the movement of a body part without actual physical execution. This process of imagination shares neural mechanisms with the actual execution [4], which makes MI BCIs especially suited for motor recovery in chronic stroke patients. Specifically, during MI, the power of the μ and β rhythm measured over the sensorimotor area of the brain decreases (event related de-synchronization) and recovers after MI (event related synchronization).
BCIs in general, but especially MI BCIs are (initially) difficult to operate for inexperienced users as they rely on the endogenous modulation of brain rhythms [5] instead of external stimuli. Consequently, a large percentage of users is not able to control a BCI, a problem known as BCI inefficiency [6,7]. [6,7] split BCI users into different groups based on their performances and recommend different solutions for each group to improve their performance. These recommendations include using a better decoder (which is able to extract more complex features), employing adaptive decoders to circumvent distribution shifts and longer/better user training.
User learning is especially important as there are users that exhibit promising brain modulation during the initial screening but then fail to elicit the proper signals during MI [7]. In other words, among the users considered as inefficient, there are users which have the potential to efficiently control a BCI. Encouragingly, research indicates that BCI usage is a learnable skill [8,9,10,11,12,13] where users are able to improve their performance and brain modulation [14] through longitudinal training. A crucial part of learning or mastering any skill is the guidance and feedback received during or after the execution [15]. BCIs that provide feedback to the user are referred to as closed-loop or online BCIs whereas BCIs without feedback are termed open-loop or offline BCIs. Apart from enabling self-regulation and user learning, closed-loop BCIs also increase the attention and motivation of participants during BCI usage [12,16]. Concisely, delivering feedback is an indispensable cornerstone of BCIs.
To date, closed-loop systems mostly employ traditional methods such as Common Spatial Patterns (CSP) combined with Linear Discriminant Analysis (LDA) or Support Vector Machine (SVM) classifiers [17]. This is contrary to the trends in single-trial/offline decoding, where deep learning has predominantly overtaken traditional methods [18]. Deep learning models, especially convolutional neural networks (CNNs), exhibit superior performance by implicitly learning complex distinctive features directly from data. However, how these superior offline performances of deep learning models can be translated to online decoding is almost entirely unaddressed in the literature.
[19,20] validated the general feasibility of deep learning for online control by employing long windows as in single-trial decoding to control a robotic arm. In [19] the arm was moved at the end of the trial, whereas the approach of [20] is closer to continuous online control as they use sliding windows ( 4 s length, 0.5   s shift). While both studies prove that deep learning based decoders are generally useful for control, their settings are not suited for continuous feedback as the window size is too long and the update frequency too low.
In other studies [21,22,23] small sliding windows ( 0.5   s - 1 s ) were used to continuously control virtual reality feedback or the position of a cursor. [21] developed a new CNN while [22,23] used modified versions of ShallowNet [24] and EEGNet [25] as decoding architectures which are among the most popular offline decoding models.
We hypothesize that there are two primary factors contributing to the limited literature on DL models for closed-loop decoding. Firstly, as DL models are mostly developed to classify whole trials it is unclear how to properly use them for shorter sequences (e.g., sliding windows). Secondly, DL models require substantial amounts of training data, and since closed-loop decoders are typically trained individually for each subject, the burden of offline calibration needed for each subject would be overwhelming.
We solve the first problem by proposing a new method called real-time adaptive pooling (RAP) that modifies existing offline deep learning models towards online decoding. As RAP tailors the deep learning model towards the specific online decoding requirements (short window size, high update frequency), our model is able to decode multiple consecutive windows at once which reduces the computational demand by a large factor. RAP allows re-using intermediate outputs of the network and therefore effectively exploits the continuous and overlapping nature of sliding windows. This is important because although sliding windows enable continuous control, they introduce a larger computational demand per trial. For short windows and high update frequencies, i.e., a high overlap between consecutive windows, the number of windows per trial increases. This would result in more forward passes and consequently a larger computational demand per trial if each window would be decoded individually.
The second limiting factor mentioned above is the large amount of training data required. The straight-forward solution of just recording more calibration data for each subject is time-consuming and would burden, fatigue or bore the user over time due to the non-interactive (without feedback) recording procedure. Consequently, even if one opts to record extensive calibration data per subject, the quality of the recorded data would likely be compromised.
An alternative approach to tackle this issue is to leverage existing data collected from other subjects to train a cross-subject decoder. As the number of subjects increases, the amount of data required per individual subject decreases. Additionally, a cross-subject decoder is able to immediately provide feedback to facilitate user learning without the need for an open-loop calibration phase.
However, despite deep learning having the ability to generalize across domains to a certain extent when trained on multiple domains, cross-subject models still underperform their within-subject counterparts (if there is enough subject-specific data). This is because of the domain shift between the training and test data, which arises from the different EEG patterns exhibited by different individuals. Solutions mitigating such shifts are categorized as domain adaptation methods. In the context of domain adaptation, the training data is often referred to as source data/domain and the test data is referred to as target data/domain. Depending on the setting and the availability of target data, different solutions such as supervised few-shot learning, unsupervised domain adaptation (UDA) and online test-time adaptation (OTTA) are possible.
In this work we will investigate how different domain adaptation techniques can be used to adapt a pre-trained cross-subject model towards a specific target subject. Compared to the typically employed within-subject decoders that are trained once with subject-specific training data, our method has multiple advantages. It can be 1) calibration-free and is therefore able to immediately provide feedback to facilitate user learning without a dedicated calibration for the target user. Through the usage of a cross-subject model we also 2) eliminate the risk of building a subject-specific decoder based on bad data that would potentially hamper subsequent user learning [26]. Further, the domain adaptation part of our framework allows the model to 3) evolve from a generic model towards a user-specific model. Through the continuous adaptation during OTTA, the decoder can also adapt to behavioral changes within the user which enables mutual learning of user and decoder.

2. Materials and Methods

2.1. Datasets

We employ the large EEG Database [27] published by Dreyer et al. in 2023 and the OpenBMI dataset [5] published by Lee et al. in 2019. In this section we will briefly present both datasets.
The Dreyer2023 dataset contains motor imagery EEG data from 87 subjects. The participants were asked to imagine movements of the right or left hand during the trials. The EEG montage consists of 27 scalp electrodes distributed over the motor cortex. We exclude 8 subjects due to artifacts and missing data, yielding effectively 79 subjects.
For each subject a total of 240 trials were recorded. The trials were recorded in 6 runs with 40 trials per run. During the first two runs, sham feedback was provided to familiarize the user with the visual feedback during the closed-loop phase. With the trials from the first two runs, an algorithm consisting of CSP and LDA was trained. This algorithm delivered the feedback during the last 4 runs.
Each trial lasts a total of 8 seconds and the trial structure is visualized in Figure 1. After an initial fixation cross and an auditory signal, the cue is presented for 1.25 seconds followed by 3.75 seconds of feedback. Since [27] used a sliding window of one second with an update frequency of 16 Hz and provided feedback from 4.25   s after trial onset, we use the data from 3.25   s - 8 s after trial onset for classification which yields an effective trial length of 4.75 seconds. This results in ( 4.75 s − 1 s ) · 16 Hz + 1 = 61 windows per trial. Due to the update frequency of 16 Hz consecutive windows have a 15 16 = 93.75 % overlap.
For preprocessing, we employ a 5 Hz - 35 Hz bandpass filter as in [27] for all subjects and downsample the data from 512 Hz to 256 Hz .
The Lee2019 dataset contains EEG data from 54 subjects performing the same binary classification task as in [27] recorded with 62 electrodes of which the 20 sensors above the motor cortex were selected. The dataset is divided in an offline and an online session, each containing a total of 100 trials per subject. Similarly to the Dreyer2023 dataset, a combination of CSP and LDA was used to provide the visual feedback during the closed-loop phase. No (sham) feedback was provided during the offline session.
Each trial lasts a total of 7 seconds, with 3 seconds of fixation followed by 4 seconds of MI. The cue was present during the whole 4 seconds of imagery and the feedback was indicated by the position of a small cross within the arrow used for the cue. As [5] originally uses a relatively slow online setting ( 1.5   s window, 2 Hz update frequency) and further cropped their trials to a length of 2.5   s , we decided to take over the setting from [27] to have a more challenging task as well as better comparability between the datasets. Starting from 0.25   s after the cue onset, this yields trial lengths of 3.75   s and results in 45 windows per trial.
For preprocessing, we employ a 8 Hz - 30 Hz bandpass filter as in [5] for all subjects and downsample the data from 1000 Hz to 256 Hz .

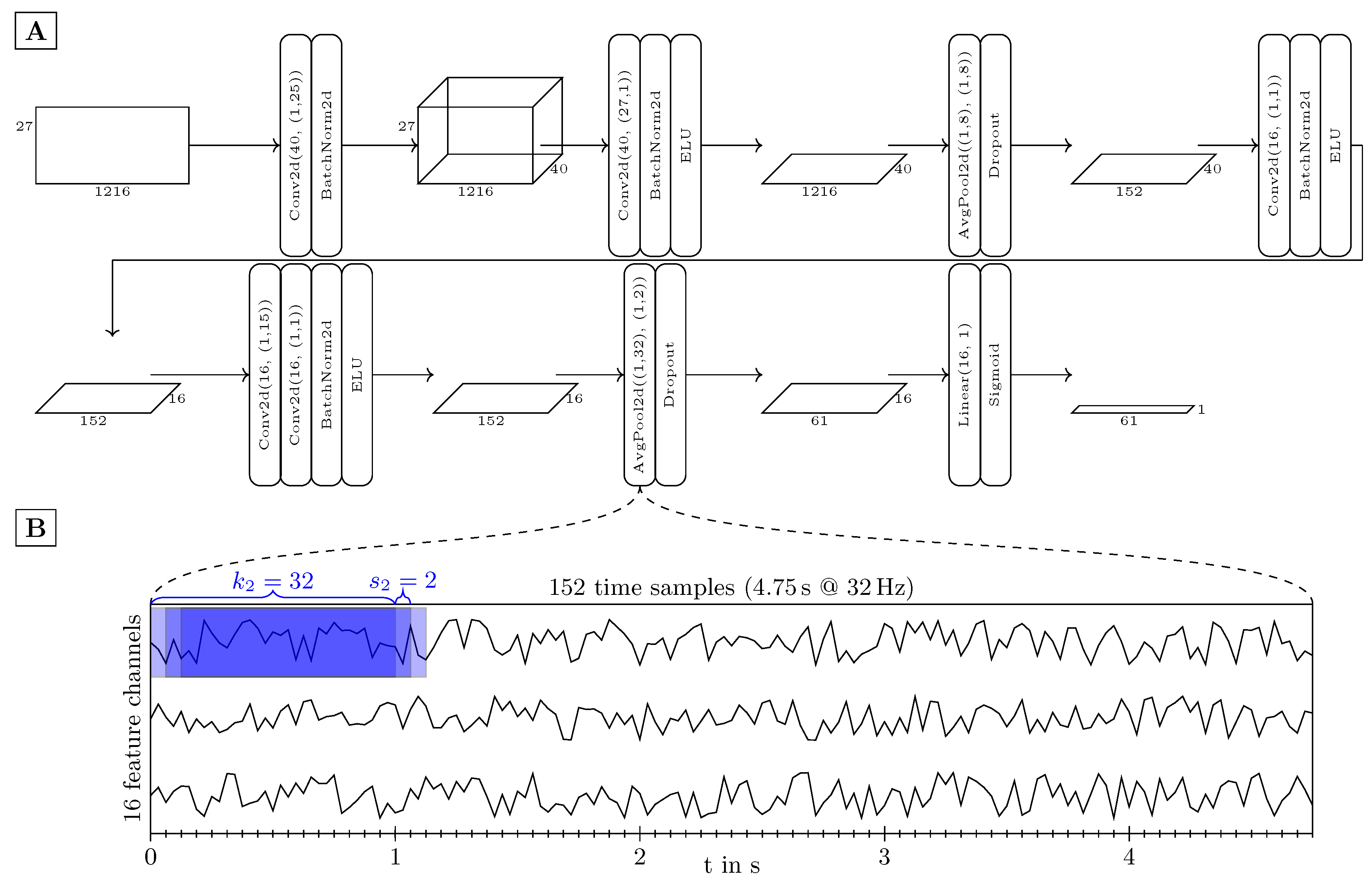
2.2. Model Architecture

There is a vast number of different deep learning architectures in BCI decoding [18] and a huge effort is spend on creating increasingly complex architectures [28]. However, shallow CNNs have shown to perform on a similar level across different datasets while keeping a lower computational complexity [23,28,29]. Therefore, we will employ BaseNet [29], a modern evolution of the popular shallow architectures EEGNet [25] and ShallowNet [24] to showcase our method. The main contributions of this paper are the proposed real-time pooling adaptation (RAP) method and the various domain adaptation techniques to enable cross-subject generalization. These ideas are applicable to any convolutional architecture that employs pooling layers.
As discussed previously, current deep learning models are rarely employed for online decoding [17]. We argue that this is in part due to the unclear process of transitioning from offline to online models, as well as the increased computational complexity associated with using sliding windows. Solving both issues, we will propose a simple yet effective parameter-free method RAP to tune existing offline models towards online decoding whilst keeping the computational complexity close to single-trial decoding. We briefly sketched this idea in a previous short conference paper [30].
As online decoding needs a high update frequency (e.g., 16 Hz ) to provide continuous feedback, there is a high overlap between consecutive windows (e.g., 15 16 for a 1 s window). This overlap is also present in the intermediate layers of a deep learning model as previously stated in [24]. In [24], a ’cropped training’ strategy is used to stabilize the training of a model for offline decoding. Its idea is to decode, instead of one single trial, multiple smaller sliding windows within one trial to increase the number of training samples. As a separate decoding of multiple overlapping windows results in additional computational load, groups of neighboring windows are decoded together and the intermediate outputs are reused.
We employ a somewhat similar strategy, but match it with the online decoding requirements. Specifically, we tune the kernel lengths k i and stride lengths s i of the pooling layers in a model. As this method is applicable to any CNN, we will present our approach for the general case of P pooling layers. The first P − 1 pooling layers are used to downsample the original input from a sampling frequency f s to an intermediate frequency f inter .
f inter = f s ∏ i = 1 P − 1 k i , k i = s i ∀ i ≤ P − 1
The values of k i and s i can be chosen arbitrarily as long as the resulting intermediate frequency f inter is equal to the update frequency f u or an integer multiple of it. For BaseNet ( P = 2 ), we use f s = 256 Hz , k 1 = s 1 = 8 and consequently f inter = 32 Hz (compare Figure 2). For models with only one pooling layer, the downsampling stage would be dropped and f inter = f s .
The last pooling layer P is used to extract overlapping sliding windows which fulfill the requirements of the online application (window length T w in seconds and update frequency f u in Hertz). The kernel size k P is chosen based on the window length T w whereas the stride s P depends on the update frequency f u .
k P = f inter · T w , s P = f inter f u
For BaseNet and our datasets, k 2 = 32 , s 2 = 2 and f u = 16 Hz . The extraction of the overlapping sliding windows through the last pooling layer is visualized in Figure 2B for the Dreyer2023 dataset.
By re-parameterizing the pooling layers in this manner, any model acquires the ability to decode both individual windows and ensembles of consecutive windows. Importantly, the model always outputs a prediction vector with the length equal to the number of windows W, regardless of the number of consecutive windows decoded jointly. Thus for any input X with time length T = T w + ( W − 1 ) · 1 f u in seconds:
y = f ( X ) ∈ R W ; X ∈ R C × T · f s ; W = ( T − T w ) · f u + 1
Due to the padding properties of convolutional layers, decoding a window jointly with other windows yields a slightly different output than decoding it individually. As joint decoding is only used for training and each window is decoded individually during inference, these minor effects at the window edges do not influence the test result and are thus negligible.
Decoding all windows of one trial of length T t jointly is computationally efficient and requires the calculation of T t · f s samples. Decoding all W windows of length T w individually requires the calculation of W · T w · f s samples. Hence the gain in speed or the reduction of computational complexity (in the convolutional layers) of joint decoding is given by
T w T t · W
For our datasets and setting ( T t = 4.75 s / 3.75 s , T w = 1 s , f u = 16 Hz ), this corresponds to factors of ∼ 12.84 and 12 respectively. The computational gain of joint decoding is also visualized in Figure 3 for different trial and window lengths.
Decoding all windows of each trial jointly additionally provides us with the possibility to define a loss function over all windows of one trial. Specifically, we average the predictions of all windows of one trial before backpropagation to stabilize training. For a batch of B trials and W windows per trial, the loss function is given by
L = 1 B ∑ i = 1 B l ( y i , 1 W ∑ j = 1 W y ^ i , j ) ; l ( y , y ^ ) = − ( y · log ( y ^ ) + ( 1 − y ) · log ( 1 − y ^ ) )
with trial labels y i and window predictions y ^ i , j . Importantly, this stabilization only works if there is a constant label y i throughout the whole trial, which is the case for our datasets.

2.3. Training

2.3.1. Data Split

Generally speaking, there are two main settings to train BCI models, one is the within-subject setting, the other one is the cross-subject setting. As both datasets have a slightly different structure, we will use the terms offline (first two runs in the Dreyer2023 dataset, first session in the Lee2019 dataset) and online data (last four runs in the Dreyer2023 dataset, second session in the Lee2019 dataset) in the following to explain the data splits.
Within-subject: We train one model per subject on the offline data and test the model on the online data of the same subject. We repeat this process for every subject and report the average and standard deviation between the subjects.
Cross-subject: We train our models in a leave-one-subject-out cross-subject setting. This means that we train one model per subject using the offline data of the remaining 78/53 subjects. In the domain adaptation context we refer to these 78/53 subjects used for training as source subjects. The subject used for testing is called the target subject. Independent of the domain adaptation setting used, we always report the test accuracy on the online data of the target subject which is not used in training at all. We repeat this process for every subject and report the average and standard deviation between the subjects.
The cross-subject data split resembles a realistic scenario, where a small amount of data from a large number of subjects is available at the beginning of a study. Afterwards, the online BCI usage, user training and model adaptation can be highly individual.

2.3.2. Training Procedure

We train all models with the training procedure described in [29] for both data splits. We use an Adam optimizer with a learning rate of 10 − 3 and train each model for 100 epochs using a learning rate scheduler with 20 warmup epochs. As the training process is stochastic (e.g., subject selection, data shuffling, weight initialization and dropout), we train each model for five different random seeds and report the average of these five runs. The complete source code is available at https://github.com/martinwimpff/eeg-online.

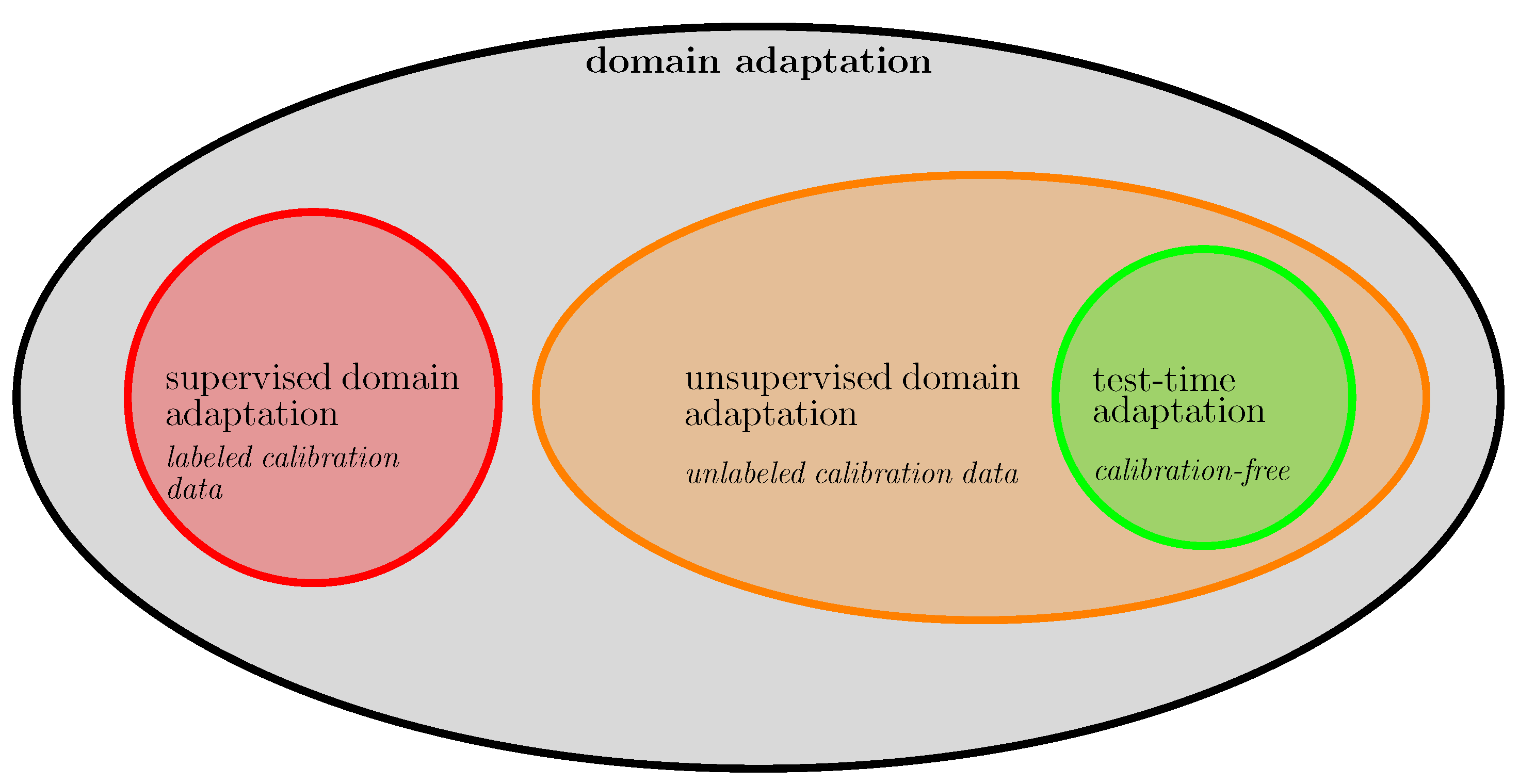
2.4. Transfer Learning and Domain Adaptation

Transfer learning (TL) typically involves utilizing knowledge or data from a source domain to solve a task in the target domain. This approach reduces the amount of target data needed to address the target task [31,32]. Within TL, a key distinction exists between domain generalization (DG) and domain adaptation (DA) [33]. In DG, the target domain is unknown, so the source decoder must generalize to any domain. Conversely, in DA, the target domain is known, and the source decoder is specifically adapted to this particular domain. For our cross-subject setting, both aspects are important. DG ensures that the initially trained cross-subject decoder has a certain generalization capability and immediately provides good feedback to the user without any target data (zero-shot). This starting point is especially important for subjects who initially have problems to elicit the proper brain signals [26,34]. DA on the other hand adapts the initial decoder towards the target subject as target data becomes accessible to mitigate the domain shift and to improve the performance. In the following, we will first formally describe our TL setting and the domain shift we face, followed by a detailed description of the different domain adaptation approaches.
For the cross-subject setting, the source domain consists of N − 1 source subjects with N s labeled source trials { [ ( X s i , j , y s i , j ) ] j = 1 N s } i = 1 N − 1 per subject. Depending on the domain adaptation setting, there are either N t labeled target trials { ( X t , j , y t , j ) } j = 1 N t or N t unlabeled target trials { ( X t , j ) } j = 1 N t available for calibration. In the calibration-free setting there are neither labeled nor unlabeled target trials available and hence N t = 0 [31].
Formally, a domain comprises a feature space X and a corresponding marginal probability distribution P ( X ) with X ∈ X . A task includes a label space Y , a corresponding marginal probability distribution P ( y ) with y ∈ Y , a conditional probability distribution P ( y | X ) and a prediction function f ( X ) [31].
This opens up many possible TL settings, e.g., cross-dateset settings where the feature spaces of two domains [35,39] or the label spaces [37] can be different. However, in this work we consider the case where the acquisition setup as well as the task is consistent across subjects, hence they share a common feature and label space. What differs between the subjects is their marginal distribution P ( X ) as well as the conditional distribution P ( y | X ) . This is considered the most common TL setting in BCI decoding [31]. To enhance the applicability of our investigation, we additionally introduce a constraint to preserve the privacy of the source subjects. Specifically, we restrict the domain adaptation solutions to be source-free, meaning that the source data is not available during the domain adaptation process [40,41,42,43,44,45].
Since there is a large number of different approaches in DA, we will provide a simplified but clear categorization of the most common source-free DA methods from a data availability perspective. This simple categorization is visualized in Figure 4. We distinguish between labeled calibration data, unlabeled calibration data and no calibration data, which yields the categories supervised DA, unsupervised DA and online test-time adaptation (OTTA), respectively. This distinction makes sense for motor imagery as (subject-specific) calibration data is not always available. If calibration data was previously recorded, it can be labeled or unlabeled, e.g., in the case of voluntary imagined movements. To achieve the best performance possible, the available data should be exploited as good as possible. In the following sections we will shortly describe the different scenarios and how we use the datasets to investigate them.
Supervised domain adaptation: Both datasets contain offline and online data, with the latter used for testing as stated previously. The remaining offline data is the subject-specific calibration data. In this setting, we use the calibration data to finetune the model towards the target subject in a supervised fashion. This procedure is also termed supervised few-shot learning or supervised finetuning/calibration and is the most common domain adaptation method [32]. Previous works can be generally divided into source-free finetuning [23,28,35,37,46,47,48,49] and solutions where source and target data are used jointly [50,51,52,53].
Unsupervised domain adaptation: The data split remains the same as in the previous setting, but with the key difference that the labels of the subject-specific data are not available. This setting is sometimes also called unsupervised few-shot learning or unsupervised offline finetuning/calibration. This setting has also already been widely explored in the literature. While the distinction between source-free [39,43,47,54,55,57] approaches and solutions using the source data during adaptation [36,49,57,59] can still be made, the characteristics between different approaches are generally more diverse than in the supervised setting.
Online test-time adaptation: This setting is calibration-free and therefore only exploits the incoming stream of unlabeled test data (the online data of the target subject) for adaptation. Sometimes, an adaption buffer containing previous samples is built online to adapt the model on the fly. This setting is relatively unexplored in the BCI context [26,41,44,45]. [41] performs seizure prediction while [26,44,45] perform motor imagery decoding with [26] using traditional methods and [44,45] employing deep learning.

2.5. Alignment

Alignment is among the easiest and hence most common approaches to mitigate distribution shifts and there are basically two variants of alignment, Euclidean alignment (EA) [28,43,44,47,51,54,57,59,60] and Riemannian alignment (RA) [43,55,59,61,62,63]. The idea of alignment is to compute a reference state per domain and then to re-center the data from each domain based on this reference state. The underlying assumption is that the re-centered brain activity between domains is similar, i.e., the difference between domains lies (predominantly) in the reference state [63].
A reference covariance matrix is computed by either taking the Euclidean mean (arithmetic mean) or the Riemannian mean (geometric mean) of all N S covariance matrices of the input trials X s i , j ∈ R C × T t · f s in one domain i with δ being the Riemannian distance:
R ¯ i E A = 1 N S ∑ j = 1 N S X s i , j · X s i , j T ; R ¯ i R A = arg min R ∑ j = 1 N S δ 2 ( R , X s i , j · X s i , j T )
The major disadvantage of the Riemannian mean R ¯ i R A is that it has no closed form solution and hence the mean has to be computed iteratively. The advantage of RA is that the geometric mean is less susceptible to outliers compared to the arithmetic mean.
The alignment of the trials is similar between EA and RA. After alignment, the (arithmetic or geometric) mean covariance matrix of each domain equals the identity matrix as demonstrated in [60].
X ˜ s i , j E A / R A = R ¯ i E A / R A , − 1 / 2 · X s i , j ; 1 N S ∑ j = 1 N S X ˜ s i , j E A · X ˜ s i , j E A , T = R ¯ i E A , − 1 / 2 R ¯ i E A R ¯ i E A , − 1 / 2 = I
One remaining issue of alignment is the need of a reference state for each new domain. Consequently, unlabeled calibration data is necessary. However, there has been work investigating the use of online estimators for the reference state that only work with the incoming stream and update the reference state accordingly [26,44,45,60,61,63]. The approaches mainly differ in how they weight the incoming samples (e.g., equal [26,44,61], linear [63] or exponential [45]) and how many samples they use to compute the reference state, i.e., using an adaptation buffer [45,60] or not.
As our primary benchmarking method [26] uses equal weighting and no adaptation buffer for their online setting, we will match this for comparability.

2.6. Adaptive Batch Normalization

Adaptive Batch Normalization (AdaBN) [64] is a simple yet very effective DA strategy that changes the statistics in all Batch Normalization (BN) layers of a model to adapt to a new domain.
Generally, BN addresses the internal covariate shifts during training by normalizing the data within the model to speed up convergence and stabilize training. During training, each BN layer normalizes each batch by using the batch statistics. Additionally, each BN layer keeps an exponential moving average of the training statistics (i.e., mean μ S and variance σ S 2 ). During inference, these training statistics are then used to normalize the test samples.
However, if there is a distribution shift between training and inference, this normalization fails, i.e., the data is no longer normalized to zero mean and unit variance and hence the performance drops. AdaBN solves this problem by replacing the source statistics μ S and σ S 2 by target statistics μ T and σ T 2 . As with alignment, unlabeled target data is necessary for AdaBN to collect the target BN statistics but there are also online estimators [65]. In BCI decoding, both offline [36,39,47,55,57] and online approaches [41,42,44,45,54] have been used.
For the online setting, we will update the initial source statistics after every window x from the target data using a small momentum α = 0.001 .
μ i = ( 1 − α ) · μ i − 1 + α · E [ x ] ; μ 0 = μ S
σ i 2 = ( 1 − α ) · σ i − 1 2 + α · Var [ x ] ; σ 0 2 = σ S 2

2.7. Entropy Minimization

Entropy minimization (EM) is a popular way to update the model parameters via an unsupervised loss function. The entropy H ( x ) for C classes is negatively correlated with the confidence of a model such that the entropy of a very confident model is low and vice versa.
H ( x ) = − ∑ c = 1 C p c ( x ) · log ( p c ( x ) ) , H max ( x ) = log ( C ) | p c ( x ) = 1 C ∀ c ∈ [ 1 , C ]
As a high confidence also correlates with a higher accuracy, the entropy can be exploited as a loss function for unsupervised domain adaptation [43,44,45]. One important aspect of EM, however, is that the predictions have to be reliable enough to use EM. Otherwise the adaptation reinforces existing model errors. There are more sophisticated DA techniques such as mean teachers [66] and certainty weighting [67], however, these approaches need longer adaptation periods and are thus not applicable to our datasets.

3. Results

3.1. Benchmark Method

We selected the adaptive Riemannian framework from [26] as our primary benchmark as it is a very recent publication that employs traditional machine learning, is adaptive in different data settings (both unsupervised and supervised) and was originally presented in a very similar setting to ours, making it a competitive and comparable choice for our approach.
Specifically, [26] uses a minimum distance to mean (MDM) Riemannian geometry classifier that uses RA by default, always requiring unlabeled target data, thereby categorizing it as unsupervised domain adaptation. Additionally, they introduced an online RA estimator termed Generic Recentering (GR) and a supervised finetuning strategy named Personally Adjusted Recentering (PAR). This results in one method for each calibration data setting: RiemannMDM+PAR for supervised finetuning, RiemannMDM for unsupervised finetuning, and RiemannMDM+GR for online adaptation.

3.2. Evaluation Metrics

Our most important metric is the trial-wise accuracy (TAcc) from [27]. We average the prediction probabilities of all windows of each trial and check whether the mean prediction equals the correct label. Through the averaging, more confident predictions are favored. Additionally, we also provide the trial-wise accuracy without averaging which we call unaveraged trial-wise accuracy (uTAcc). Further, we provide the window-wise accuracy (WAcc), i.e., the percentage of windows classified correctly. To compare our methods, we perform one-sided paired t-tests between the trial-wise accuracies.

3.3. Within-Subject

The results of the within-subject experiments are displayed in Table 1. Two main observations can be made for the within-subject setting. Firstly, for both datasets, RiemannMDM shows significantly better results than our method. Secondly, while the average accuracy of RiemannMDM is higher, the variance between subjects is also higher. Due to the significant differences in average performance for the Dreyer2023 dataset, we conducted an additional ablation study to examine the impact of training data quantity on the results. Although both decoders generally benefit from increased training data, BaseNet shows a larger improvement (see Appendix A.1).

3.4. Cross-Subject

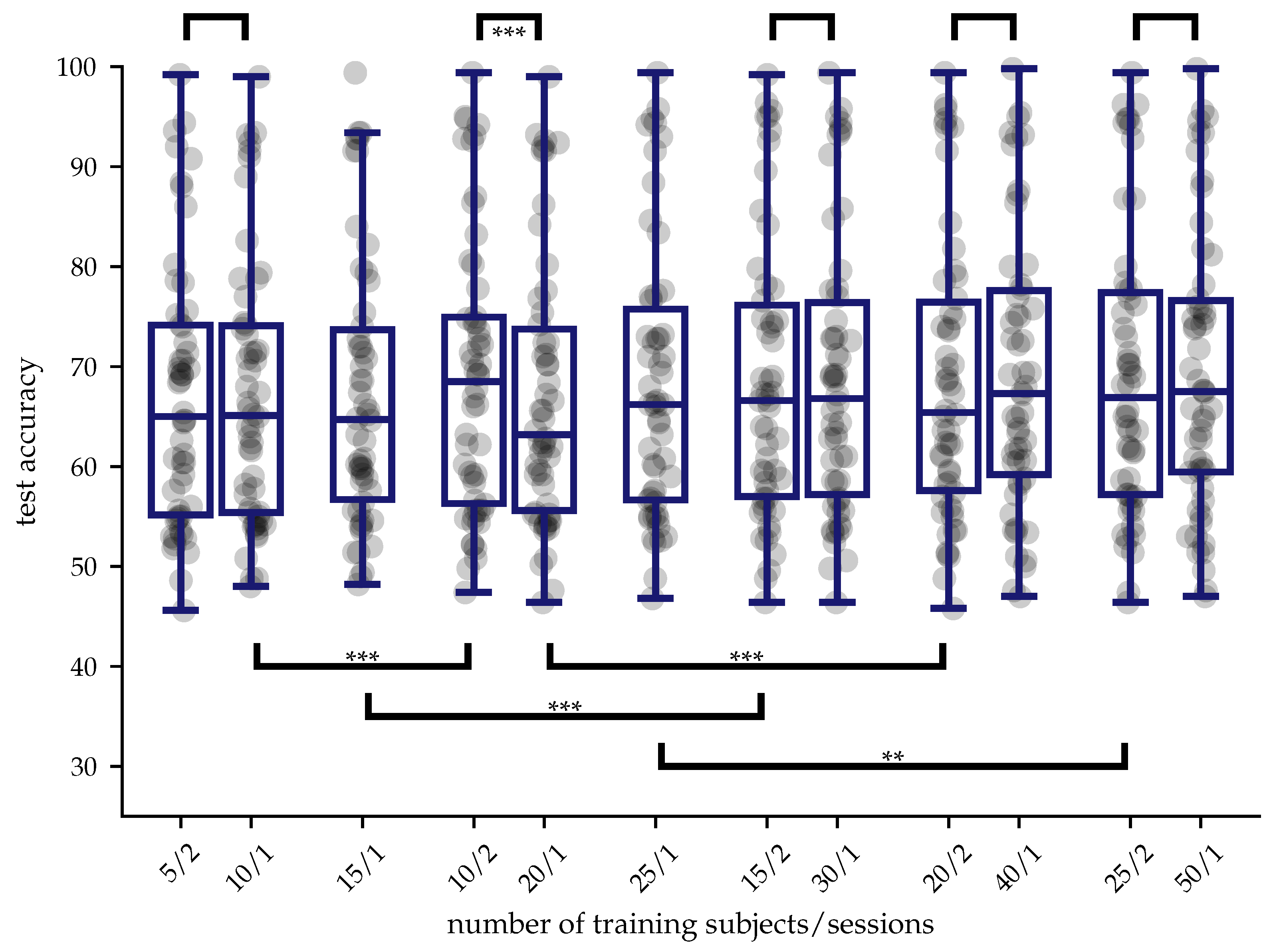
3.4.1. Amount and Diversity of Training Data

To investigate the behavior of our method for the cross-subject setting under different data compositions, we trained BaseNet for different amounts of training subjects (randomly picked) and runs/sessions (sequentially picked, e.g., 4 runs equals picking the first four runs). The results are shown in Figure 5 and Figure 6 for the Dreyer2023 datset and the Lee2019 dataset, respectively. We performed statistical tests between compositions with the same total amount of training data but different amounts of training subjects (above the boxplots) as well as between different amounts of training data using the same number of subjects (below the boxplots). For both datasets, increasing the number of runs/sessions per subject improves the final performance. The impact of subject diversity yields two different outcomes. In the Dreyer2023 dataset, given the same amount of training data, increasing the number of subjects almost always produces significantly better results compared to increasing the number of runs per subject. Conversely, for the Lee2019 dataset, this pattern does not hold. Performance remains quite similar regardless of the composition, and for one instance with 2000 trials, increasing the number of sessions per subject even leads to significantly better performance.

3.4.2. Domain Adaptation Settings

The cross-subject results under different DA settings are shown in Table 2 and Table 3 for the Dreyer2023 dataset and the Lee2019 dataset, respectively. Based on the different DA settings (compare Figure 4), we separate our results in three section and compare them to the corresponding benchmark method from [26].
For the supervised finetuning and the unsupervised finetuning setting, BaseNet performs significantly better than the corresponding benchmark method regardless of the dataset and the specific DA setting. However, for the Lee2019 dataset, using alignment deteriorates the performance compared to using no alignment.
In contrast, for the online setting, alignment does work very well for both datasets. Compared to the benchmark, our results for the Dreyer2023 dataset are better for almost every DA method (except RA), but the differences are not significant (EA: p = 0.25 , AdaBN: p = 0.42 , EA+AdaBN: p = 0.17 , RA+AdaBN: p = 0.08 ). For the Lee2019 dataset, all DA methods except AdaBN ( p = 0.32 ) are significantly better than the benchmark method.
The unaveraged trial-wise accuracy is generally only slightly lower than the trial-wise accuracy, indicating that there are not many windows with a high confidence. The window-wise accuracy is lower than the trial-wise as expected.

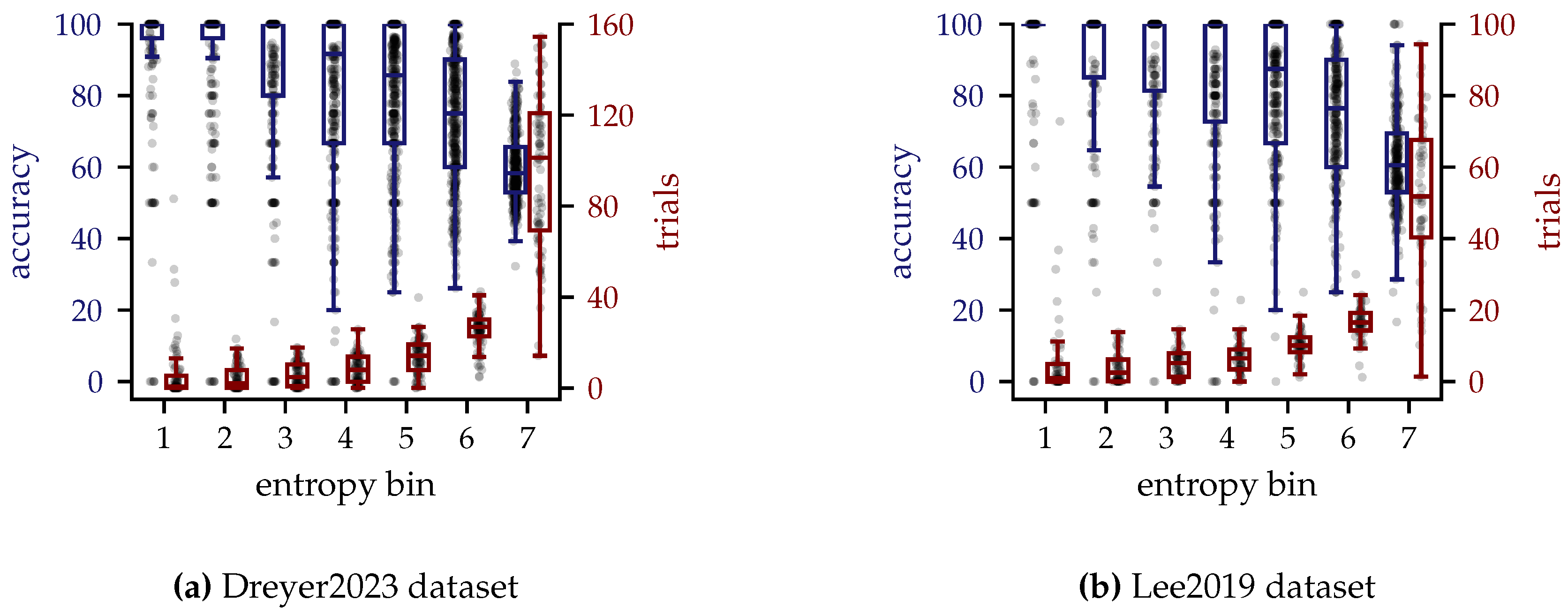
3.4.3. Entropy

As mentioned earlier, entropy minimization can be an effective unsupervised loss function to perform DA. Consequently, we tried to adapt the parameters of BaseNet via EM. However, the results after adaptation were far below the results before adaptation or (for very low learning rates) at the level of AdaBN. To explain the reason for this result, we investigate the confidence of our source model in Figure 7. To do so, we binned the trials according to their entropy and plotted the accuracy per bin in blue as well as the number of trials per bin in red. Figure 7 shows two effects. First, the entropy increases with a decreasing accuracy as expected. Second, most of the trials are in the the last entropy bin. Unfortunately, many of the trials in the last bin are not reliable (low accuracy) and therefore are a bad label for the domain adaptation. This explains the underwhelming results of EM.

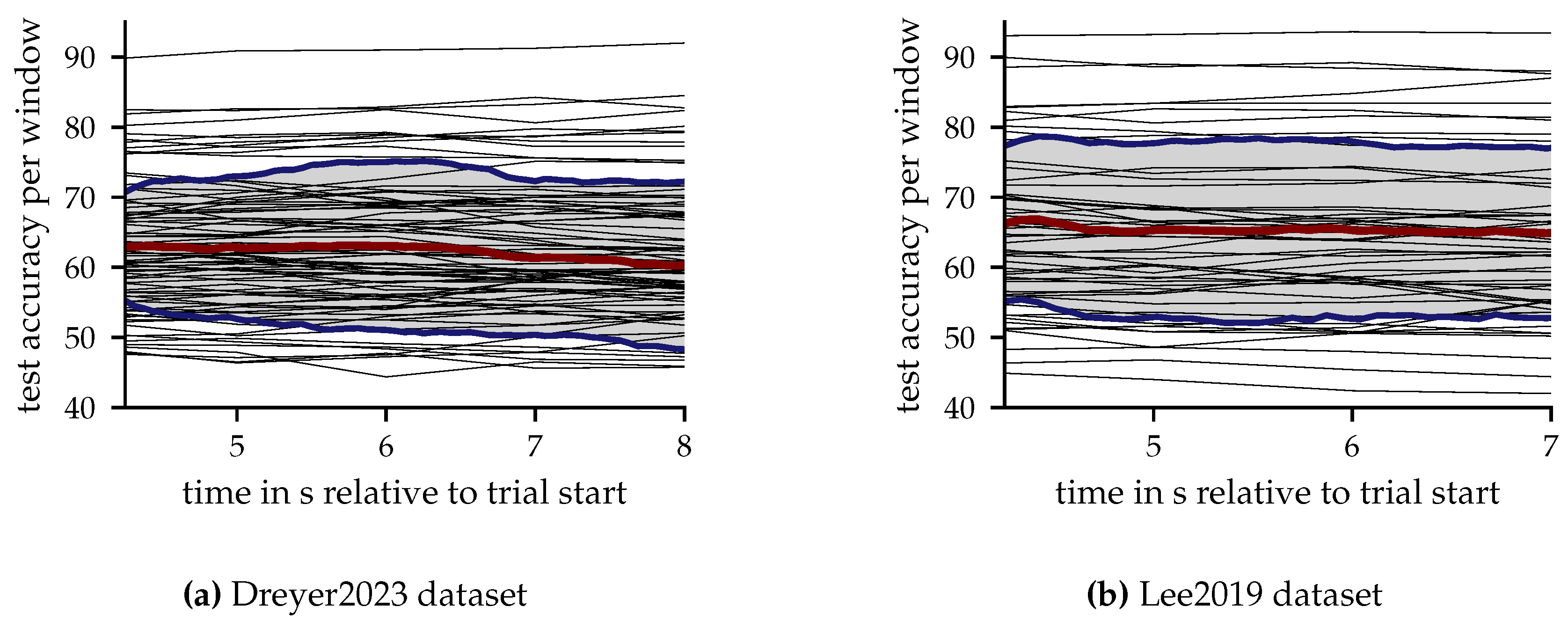
3.4.4. Results per Window

Another important aspect of online decoding is the performance throughout a trial to check whether a subject is able to perform MI long enough. Figure 8 shows the window-wise accuracy over time. Generally, the accuracy is pretty stable over time, with only a slight decrease over time. This means that firstly, the subject is able to perform the MI long enough and, secondly, our model does not have any boundary effects due to padding, cueing or joint decoding during training.
To validate computational feasibility, we measured the inference time for a single window on a CPU (Intel i7-1195G7 with 4 cores). The results showed that BaseNet had an inference time of 2.15   m s , while RiemannMDM achieved 0.5   m s . These times indicate that both algorithms are suitable for online decoding.

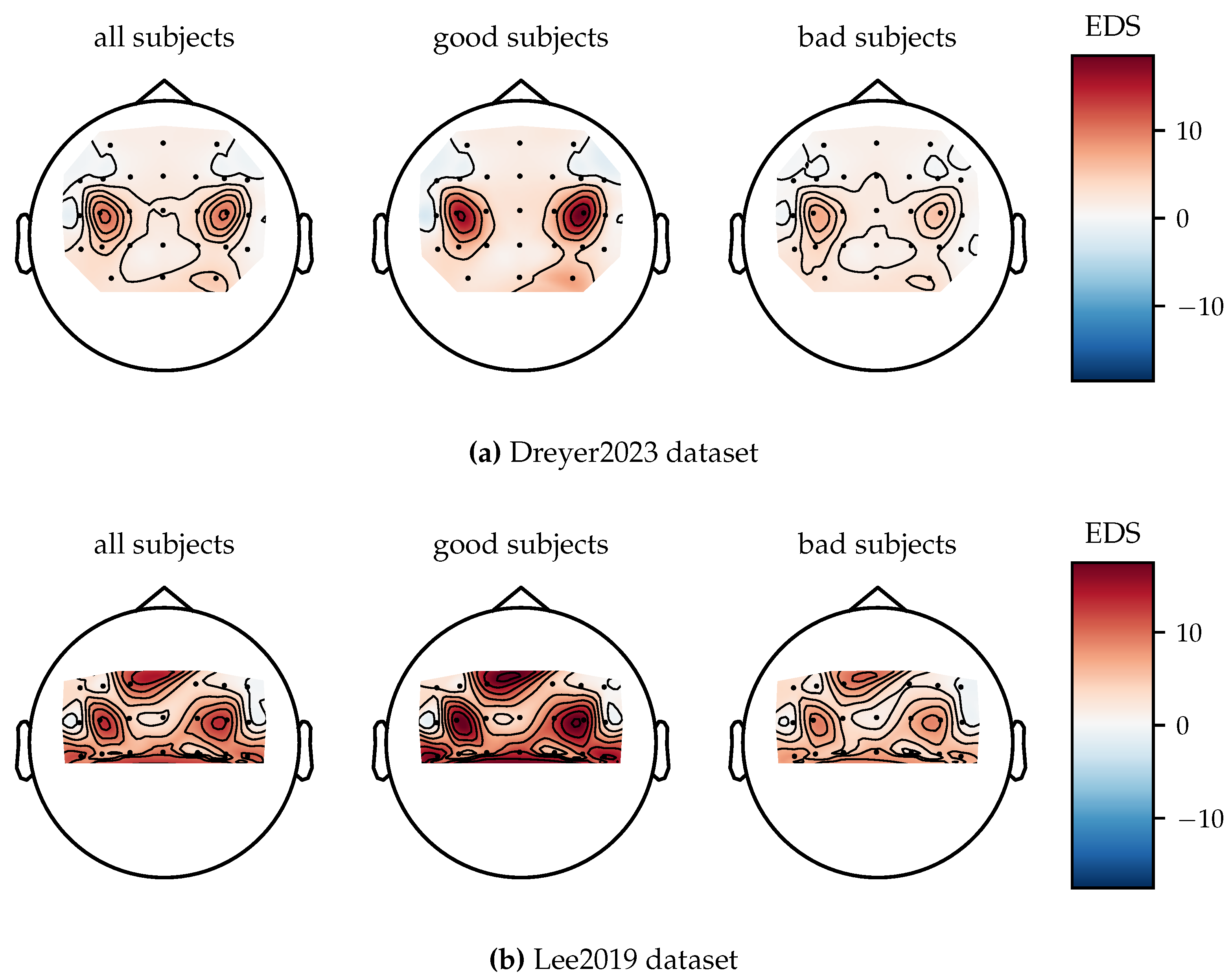
3.4.5. Spatial Patterns

To validate our results, we employ the electrode discriminancy score (EDS) from [26]. The EDS calculates the difference between the initial accuracy and the accuracy if one electrode is dropped (i.e., set to zero) during inference. Thus, a high EDS indicates a significant performance drop when that sensor is removed. The results are presented in Figure 9. For both datasets, the C3 and C4 electrode yield the highest EDS. For the Lee2019 other sensors such as the FC1 electrode and the sensors in the central parietal region of the cortex additionally exhibit high EDS.

4. Discussion

The results show that our proposed method is an effective approach to tune existing DL models towards online BCI MI decoding. In the following sections, we will discuss the prerequisites regarding data availability and data composition as well as the differences between the DA approaches and the general limitations of our investigation.

4.1. Data Availability and Data Composition

Generally, data availability and composition dictate the overall training strategy. If there is insufficient data from other subjects to train a cross-subject decoder, a within-subject decoder using subject-specific data must be trained. In this case, a poor generalization of this decoder to other subjects is highly expected. Additionally, the cognitive and physical demands placed on the subject during data acquisition impact the volume of subject-specific data that can be collected. This, in turn, influences the selection of the appropriate decoding algorithm. For low amounts of data, traditional machine learning methods such as RiemannMDM from [26] or combinations of CSP and LDA are the better choice over DL solutions for within-subject BCI MI decoding as evidenced by Table 1. As more data becomes available, training within-subject DL models starts to get useful (see Appendix A.1).
If there is enough data from other subjects, training in a cross-subject setting becomes feasible. This setting is advantageous for DL as the increased data volume typically enables DL models to exhibit better performances as shown in Figure 5 and Figure 6. The influence of the composition of data (i.e., how many subjects and how many runs/sessions per subject are available) is more complex. Generally, a high subject diversity improves the performance as evidenced by [28] and our experiments on the Dreyer2023 dataset. For the Lee2019 dataset on the other hand, we observed that the composition of subjects and sessions has almost no influence on the final performance. We explain this by the domain shift introduced between offline and online session. Firstly, the sessions of the Lee2019 dataset were recorded on different days, and secondly, unlike the Dreyer2023 routine, there was no sham feedback during the offline sessions. These two aspects might influence the results in Figure 6. The additional sessions introduce some data diversity compared to the additional data coming from the same session as in the Dreyer2023 dataset. Further, the domain shift between offline and online session in terms of recording procedure (i.e., visual feedback) [11] could be reduced through the inclusion of online sessions in the training data. We added a small ablation in Appendix A.2 to further investigate this and found indications that the domain shift between offline and online is relevant for the Lee2019 dataset but without significance ( p = 0.255 ).
Besides the domain shift between offline and online data, there also exists an even bigger domain shift between the data from the source subjects and the data from the target subject due to the large subject-to-subject differences that are naturally present in any EEG recording. These domain shifts can be mitigated through the usage of different DA strategies depending on the availability of target data.

4.2. Domain Adaptation

As mentioned previously, the feasibility of certain DA strategies depends on the availability of target data. Using DL, supervised fine-tuning is the most effective strategy for the Dreyer2023 dataset, followed by online adaption. This effectiveness is likely due to the minimal domain shift between calibration and test data, enabling successful fine-tuning with offline data. For the traditional ML approach on the other hand, the online adaptation strategy yields the best results followed by supervised and unsupervised fine-tuning, between which no differences are observed.
For the Lee2019 dataset, the same observations can be made for the traditional methods. However, the supervised and unsupervised fine-tuning approaches for BaseNet generally underperform the source performance, when alignment is used. This can probably also be attributed to the shift between offline and online data discussed previously. Notably, this dataset shows large improvements through online adaptation, further supporting our previous assumptions about the domain shift between the offline and online data. BaseNet using online alignment and online AdaBN improves the initial source performance by 4.5 % and RiemannMDM+GR outperforms RiemannMDM and RiemannMDM+PAR by over 6 % . Comparing the results from Table 2 and Table 3, the performance improvement of the online adaptation is remarkably larger for the Lee2019 dataset than for the Dreyer2023 dataset, i.e., the online adaptation helps to overcome the stronger inter-session domain shift in Lee2019.
Despite having the lowest data requirements regarding target data (calibration-free), the online adaptation methods yield excellent results for both datasets and both approaches (i.e., traditional methods and DL solutions). This supports the upcoming research of online adaptation methods for BCI MI decoding [26,44,45]. Unexpected domain shifts can occur during inference, regardless of how well a BCI is designed (e.g., due to electrode movement or changes in user behavior). Therefore, it is advisable to use online adaptation methods rather than offline adaptation methods. Additionally, online adaptation supports calibration-free BCI usage, allowing for instant user learning and thus promoting an immediate process of continuous mutual learning between the user and the decoder.

4.3. Limitations

The most important limitation of our study is that despite investigating online adaptation, our experiments were conducted on previously recorded datasets and are thus only pseudo-online. Since we performed an offline study, we did not investigate the translation of model predictions into feedback signals. Both online decoder adaptation and the specific feedback signal likely influence user behavior, which could either deteriorate or improve performance further. In other words, true closed-loop experiments are required in a future study to explore the mutual influence of online decoder adaptation and behavioral change of the user.
Furthermore, the online adaptation time is fixed (i.e., the same number of online trials is available for all subjects) and relatively short. Consequently, we cannot accommodate user-specific needs, such as longer learning periods [12]. Due to the short training time per user (few trials, one session), our methods still need to be evaluated for their effectiveness concerning long-term changes within individual users.
Lastly, averaging the predictions of all windows within one trial only works for discrete MI paradigms (i.e., one task throughout the whole trial).

5. Conclusions

In conclusion, our method RAP, which tailors existing offline DL models for online decoding, demonstrates promising results in enhancing online BCI applications. By leveraging domain adaptation techniques, we effectively reduce the data requirements, making our approach both powerful and potentially calibration-free. Our experiments, conducted on a total of 133 subjects, reveal that online adaptation, despite having the lowest target data requirements, yields the best overall results. These findings underscore the potential of our method for practical real-time BCI applications and pave the way for developing co-adaptive, highly efficient DL-based BCI systems. However, to fully understand the effects of model adaptation on user adaptation and long-term changes, an online BCI study is necessary.

Author Contributions

Conceptualization, M.W.; methodology, M.W.; software, M.W.; validation, M.W., J.Z. and B.Y.; formal analysis, M.W.; investigation, M.W.; resources, M.W.; data curation, M.W.; writing—original draft preparation, M.W.; writing—review and editing, M.W., J.Z. and B.Y.; visualization, M.W.; supervision, B.Y.; project administration, B.Y.; funding acquisition, B.Y. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Quantum Human Machine Interfaces (QHMI) project within the QSens - Quantum Sensors of the Future Cluster grant number 03ZU1110DC. The APC was funded by the Institute of Signal Processing and System Theory, University of Stuttgart.

Data Availability Statement

The large EEG database from [27] is freely available at zenodo https://zenodo.org/records/8089820. The OpenBMI dataset from [5] is freely available at GigaDB http://gigadb.org/dataset/100542 (both accessed on 19 July 2024).

Conflicts of Interest

The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

Appendix A

Appendix A.1. Within-Subject

To investigate how the amount of training data influences the results for the within-subject setting, we trained the algorithms on the Dreyer2023 dataset and varied the amount of runs used for training. All runs were tested on the data from the last run. The results are displayed in Figure A1.
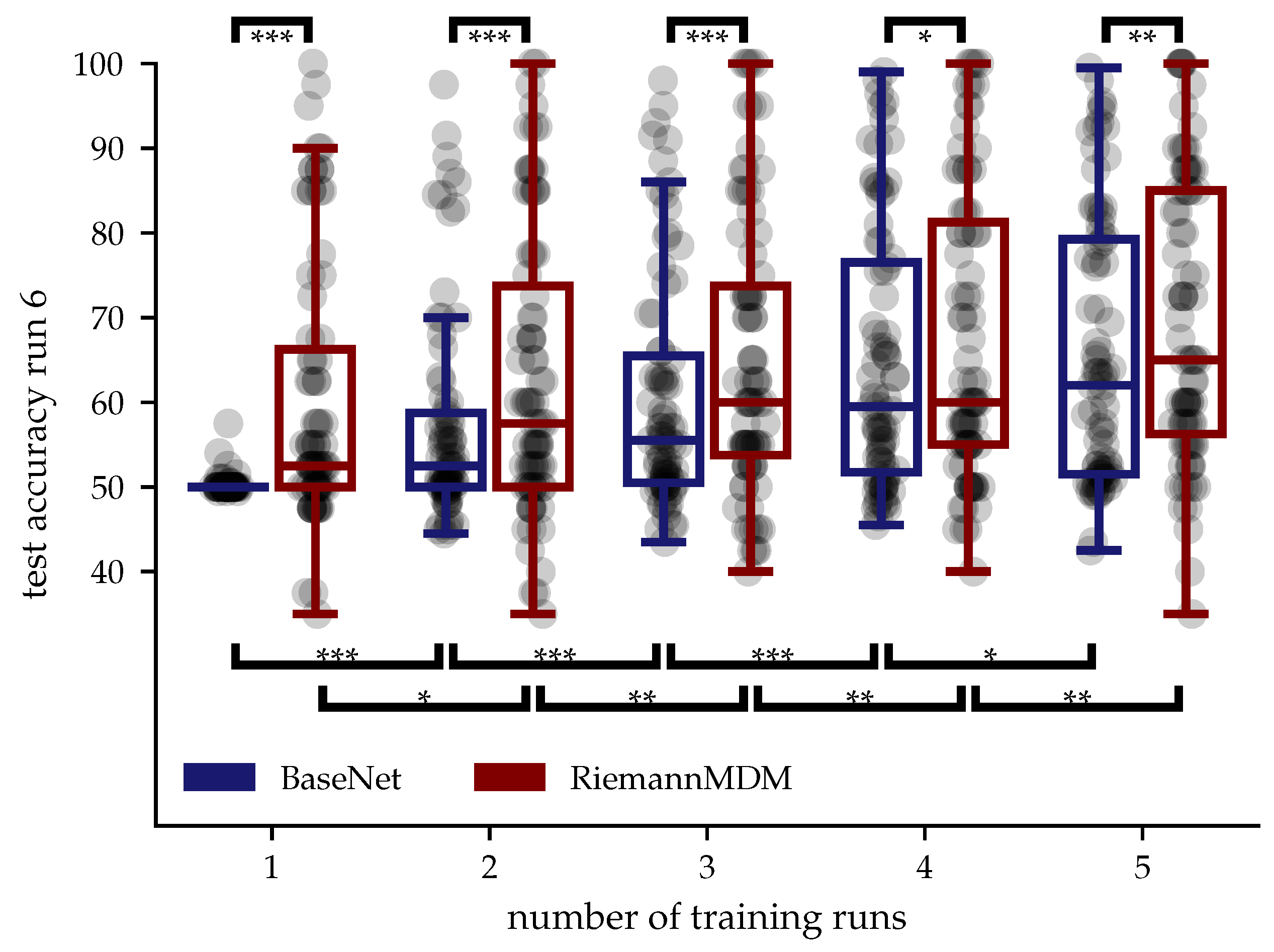
Preprints 113707 g0a1
Figure A1. Within-subject results for Dreyer2023 and different amounts of training data. Each dot resembles a subject, the stars within the brackets resemble the different significance levels (p<0.05(*), p<0.01(**) and p<0.001(***)) when comparing two experiments connected by that bracket.
Figure A1. Within-subject results for Dreyer2023 and different amounts of training data. Each dot resembles a subject, the stars within the brackets resemble the different significance levels (p<0.05(*), p<0.01(**) and p<0.001(***)) when comparing two experiments connected by that bracket.
Preprints 113707 g0a1

Appendix A.2. Domain Shift between Offline and Online Data

Besides the domain shift introduced due to subject variability, there is an additional domain shift between the offline and online data. The results in Table 3 as well as the different recording procedure (two sessions, offline without any feedback) indicate that the domain shift between offline and online data is higher for the Lee2019 dataset than for the Dreyer2023 dataset. To investigate this, we trained BaseNet on the online data of the source subjects and compared the results to training on the offline data. The results in Table A1 show little difference and even a small deterioration for the Dreyer2023 dataset and a small but not significant ( p = 0.255 ) improvement for the Lee2019 dataset when trained on the online data. This indicates a higher domain shift between the offline and online data for the Lee2019 dataset than for the Dreyer2023 dataset.
Table A1. Domain shift between offline and online runs/sessions. Results above double line are for the Dreyer2023 dataset, results below are for the Lee2019 dataset.
Table A1. Domain shift between offline and online runs/sessions. Results above double line are for the Dreyer2023 dataset, results below are for the Lee2019 dataset.
Method training runs TAcc(%) uTacc(%) WAcc(%)
BaseNet 1 + 2 67.80 ± 13.80 67.22 ± 13.56 62.23 ± 10.43
BaseNet 3 + 4 67.61 ± 13.93 67.16 ± 13.85 62.34 ± 10.44
BaseNet 5 + 6 67.56 ± 14.61 67.10 ± 14.41 62.22 ± 10.66
training sessions
BaseNet 1 70.36 ± 14.35 69.73 ± 14.43 65.08 ± 11.84
BaseNet 2 70.74 ± 14.25 70.50 ± 14.12 65.76 ± 11.44

References

  1. Peksa, J. & Mamchur, D. State-of-the-Art on Brain-Computer Interface Technology. Sensors. 23, 6001 (2023). [CrossRef]
  2. Cervera, M., Soekadar, S., Ushiba, J., Millán, J., Liu, M., Birbaumer, N. & Garipelli, G. Brain-computer interfaces for post-stroke motor rehabilitation: a meta-analysis. Annals Of Clinical And Translational Neurology. 5, 651-663 (2018). [CrossRef]
  3. Soekadar, S., Witkowski, M., Mellinger, J., Ramos, A., Birbaumer, N. & Cohen, L. ERD-based online brain-machine interfaces (BMI) in the context of neurorehabilitation: optimizing BMI learning and performance. IEEE Transactions On Neural Systems And Rehabilitation Engineering. 19, 542-549 (2011). [CrossRef]
  4. Decety, J. The neurophysiological basis of motor imagery. Behavioural Brain Research. 77, 45-52 (1996).
  5. Lee, M., Kwon, O., Kim, Y., Kim, H., Lee, Y., Williamson, J., Fazli, S. & Lee, S. EEG dataset and OpenBMI toolbox for three BCI paradigms: An investigation into BCI illiteracy. GigaScience. 8, giz002 (2019). [CrossRef]
  6. Sannelli, C., Vidaurre, C., Müller, K. & Blankertz, B. A large scale screening study with a SMR-based BCI: Categorization of BCI users and differences in their SMR activity. PloS One. 14, e0207351 (2019). [CrossRef]
  7. Zhang, R., Li, F., Zhang, T., Yao, D. & Xu, P. Subject inefficiency phenomenon of motor imagery brain-computer interface: Influence factors and potential solutions. Brain Science Advances. 6, 224-241 (2020).
  8. Perdikis, S., Tonin, L., Saeedi, S., Schneider, C. & Millán, J. The Cybathlon BCI race: Successful longitudinal mutual learning with two tetraplegic users. PLoS Biology. 16, e2003787 (2018).
  9. Korik, A., McCreadie, K., McShane, N., Du Bois, N., Khodadadzadeh, M., Stow, J., McElligott, J., Carroll, Á. & Coyle, D. Competing at the Cybathlon championship for people with disabilities: long-term motor imagery brain–computer interface training of a cybathlete who has tetraplegia. Journal Of NeuroEngineering And Rehabilitation. 19, 95 (2022).
  10. McFarland, D. & Wolpaw, J. Brain–computer interface use is a skill that user and system acquire together. PLoS Biology. 16, e2006719 (2018). [CrossRef]
  11. Shenoy, K. & Carmena, J. Combining decoder design and neural adaptation in brain-machine interfaces. Neuron. 84, 665-680 (2014). [CrossRef]
  12. Orsborn, A., Moorman, H., Overduin, S., Shanechi, M., Dimitrov, D. & Carmena, J. Closed-loop decoder adaptation shapes neural plasticity for skillful neuroprosthetic control. Neuron. 82, 1380-1393 (2014). [CrossRef]
  13. Sitaram, R., Ros, T., Stoeckel, L., Haller, S., Scharnowski, F., Lewis-Peacock, J., Weiskopf, N., Blefari, M., Rana, M., Oblak, E. & Others Closed-loop brain training: the science of neurofeedback. Nature Reviews Neuroscience. 18, 86-100 (2017).
  14. Kober, S., Witte, M., Ninaus, M., Neuper, C. & Wood, G. Learning to modulate one’s own brain activity: the effect of spontaneous mental strategies. Frontiers In Human Neuroscience. 7 pp. 695 (2013). [CrossRef]
  15. Gaume, A., Vialatte, A., Mora-Sánchez, A., Ramdani, C. & Vialatte, F. A psychoengineering paradigm for the neurocognitive mechanisms of biofeedback and neurofeedback. Neuroscience & Biobehavioral Reviews. 68 pp. 891-910 (2016). [CrossRef]
  16. Mladenović, J., Mattout, J. & Lotte, F. A generic framework for adaptive EEG-based BCI training and operation. Brain–Computer Interfaces Handbook. pp. 595-612 (2018).
  17. Vavoulis, A., Figueiredo, P. & Vourvopoulos, A. A Review of Online Classification Performance in Motor Imagery-Based Brain-Computer Interfaces for Stroke Neurorehabilitation. Signals. 4, 73-86 (2023). [CrossRef]
  18. Craik, A., He, Y. & Contreras-Vidal, J. Deep learning for electroencephalogram (EEG) classification tasks: a review. Journal Of Neural Engineering. 16, 031001 (2019). [CrossRef]
  19. Tayeb, Z., Fedjaev, J., Ghaboosi, N., Richter, C., Everding, L., Qu, X., Wu, Y., Cheng, G. & Conradt, J. Validating deep neural networks for online decoding of motor imagery movements from EEG signals. Sensors. 19, 210 (2019). [CrossRef]
  20. Jeong, J., Shim, K., Kim, D. & Lee, S. Brain-controlled robotic arm system based on multi-directional CNN-BiLSTM network using EEG signals. IEEE Transactions On Neural Systems And Rehabilitation Engineering. 28, 1226-1238 (2020). [CrossRef]
  21. Karácsony, T., Hansen, J., Iversen, H. & Puthusserypady, S. Brain computer interface for neuro-rehabilitation with deep learning classification and virtual reality feedback. Proceedings Of The 10th Augmented Human International Conference 2019. pp. 1-8 (2019).
  22. Stieger, J., Engel, S., Suma, D. & He, B. Benefits of deep learning classification of continuous noninvasive brain–computer interface control. Journal Of Neural Engineering. 18, 046082 (2021). [CrossRef]
  23. Forenzo, D., Zhu, H., Shanahan, J., Lim, J. & He, B. Continuous tracking using deep learning-based decoding for noninvasive brain–computer interface. PNAS Nexus. 3, pgae145 (2024).
  24. Schirrmeister, R., Springenberg, J., Fiederer, L., Glasstetter, M., Eggensperger, K., Tangermann, M., Hutter, F., Burgard, W. & Ball, T. Deep learning with convolutional neural networks for EEG decoding and visualization. Human Brain Mapping. 38, 5391-5420 (2017).
  25. Lawhern, V., Solon, A., Waytowich, N., Gordon, S., Hung, C. & Lance, B. EEGNet: a compact convolutional neural network for EEG-based brain-computer interfaces. Journal Of Neural Engineering. 15, 056013 (2018). [CrossRef]
  26. Kumar, S., Alawieh, H., Racz, F., Fakhreddine, R. & Millán, J. Transfer learning promotes acquisition of individual BCI skills. PNAS Nexus. 3, pgae076 (2024).
  27. Dreyer, P., Roc, A., Pillette, L., Rimbert, S. & Lotte, F. A large EEG database with users’ profile information for motor imagery brain-computer interface research. Scientific Data. 10, 580 (2023). [CrossRef]
  28. Sartzetaki, C., Antoniadis, P., Antonopoulos, N., Gkinis, I., Krasoulis, A., Perdikis, S. & Pitsikalis, V. Beyond Within-Subject Performance: A Multi-Dataset Study of Fine-Tuning in the EEG Domain. 2023 IEEE International Conference On Systems, Man, And Cybernetics (SMC). pp. 4429-4435 (2023).
  29. Wimpff, M., Gizzi, L., Zerfowski, J. & Yang, B. EEG motor imagery decoding: A framework for comparative analysis with channel attention mechanisms. Journal Of Neural Engineering. (2024). [CrossRef]
  30. Wimpff, M., Zerfowski, J. & Yang, B. Towards calibration-free online EEG motor imagery decoding using Deep Learning. ESANN 2024 Proceedings (2024), accepted.
  31. Wu, D., Jiang, X. & Peng, R. Transfer learning for motor imagery based brain–computer interfaces: A tutorial. Neural Networks. 153 pp. 235-253 (2022).
  32. Ko, W., Jeon, E., Jeong, S., Phyo, J. & Suk, H. A survey on deep learning-based short/zero-calibration approaches for EEG-based brain–computer interfaces. Frontiers In Human Neuroscience. 15 pp. 643386 (2021).
  33. Kostas, D. & Rudzicz, F. Thinker invariance: enabling deep neural networks for BCI across more people. Journal Of Neural Engineering. 17, 056008 (2020). [CrossRef]
  34. Sultana, M., Reichert, C., Sweeney-Reed, C. & Perdikis, S. Towards Calibration-Less BCI-Based Rehabilitation. 2023 IEEE International Conference On Metrology For EXtended Reality, Artificial Intelligence And Neural Engineering (MetroXRAINE). pp. 11-16 (2023).
  35. Han, J., Wei, X. & Faisal, A. EEG decoding for datasets with heterogenous electrode configurations using transfer learning graph neural networks. Journal Of Neural Engineering. 20, 066027 (2023). [CrossRef]
  36. Jiménez-Guarneros, M. & Gómez-Gil, P. Custom Domain Adaptation: A new method for cross-subject, EEG-based cognitive load recognition. IEEE Signal Processing Letters. 27 pp. 750-754 (2020).
  37. He, H. & Wu, D. Different set domain adaptation for brain-computer interfaces: A label alignment approach. IEEE Transactions On Neural Systems And Rehabilitation Engineering. 28, 1091-1108 (2020). [CrossRef]
  38. Han, J., Wei, X. & Faisal, A. EEG decoding for datasets with heterogenous electrode configurations using transfer learning graph neural networks. Journal Of Neural Engineering. 20, 066027 (2023). [CrossRef]
  39. Gu, X., Han, J., Yang, G. & Lo, B. Generalizable Movement Intention Recognition with Multiple Heterogeneous EEG Datasets. 2023 IEEE International Conference On Robotics And Automation (ICRA). pp. 9858-9864 (2023).
  40. Ju, C., Gao, D., Mane, R., Tan, B., Liu, Y. & Guan, C. Federated transfer learning for EEG signal classification. 2020 42nd Annual International Conference Of The IEEE Engineering In Medicine & Biology Society (EMBC). pp. 3040-3045 (2020).
  41. Mao, T., Li, C., Zhao, Y., Song, R. & Chen, X. Online test-time adaptation for patient-independent seizure prediction. IEEE Sensors Journal. (2023).
  42. Wang, K., Yang, M., Li, C., Liu, A., Qian, R. & Chen, X. Privacy-Preserving Domain Adaptation for Intracranial EEG Classification via Information Maximization and Gaussian Mixture Model. IEEE Sensors Journal. (2023). [CrossRef]
  43. Xia, K., Deng, L., Duch, W. & Wu, D. Privacy-preserving domain adaptation for motor imagery-based brain-computer interfaces. IEEE Transactions On Biomedical Engineering. 69, 3365-3376 (2022). [CrossRef]
  44. Li, S., Wang, Z., Luo, H., Ding, L. & Wu, D. T-TIME: Test-time information maximization ensemble for plug-and-play BCIs. IEEE Transactions On Biomedical Engineering. (2023).
  45. Wimpff, M., Döbler, M. & Yang, B. Calibration-free online test-time adaptation for electroencephalography motor imagery decoding. 2024 12th International Winter Conference On Brain-Computer Interface (BCI). pp. 1-6 (2024).
  46. Guetschel, P. & Tangermann, M. Transfer Learning between Motor Imagery Datasets using Deep Learning–Validation of Framework and Comparison of Datasets. ArXiv Preprint ArXiv:2311.16109. (2023).
  47. Ouahidi, Y., Gripon, V., Pasdeloup, B., Bouallegue, G., Farrugia, N. & Lioi, G. A Strong and Simple Deep Learning Baseline for BCI MI Decoding. ArXiv Preprint ArXiv:2309.07159. (2023).
  48. Xie, Y., Wang, K., Meng, J., Yue, J., Meng, L., Yi, W., Jung, T., Xu, M. & Ming, D. Cross-dataset transfer learning for motor imagery signal classification via multi-task learning and pre-training. Journal Of Neural Engineering. 20, 056037 (2023). [CrossRef]
  49. Xu, Y., Huang, X. & Lan, Q. Selective cross-subject transfer learning based on riemannian tangent space for motor imagery brain-computer interface. Frontiers In Neuroscience. 15 pp. 779231 (2021). [CrossRef]
  50. An, S., Kim, S., Chikontwe, P. & Park, S. Few-shot relation learning with attention for EEG-based motor imagery classification. 2020 IEEE/RSJ International Conference On Intelligent Robots And Systems (IROS). pp. 10933-10938 (2020).
  51. Junqueira, B., Aristimunha, B., Chevallier, S. & Camargo, R. A systematic evaluation of Euclidean alignment with deep learning for EEG decoding. Journal Of Neural Engineering. (2024). [CrossRef]
  52. Liu, S., Zhang, J., Wang, A., Wu, H., Zhao, Q. & Long, J. Subject adaptation convolutional neural network for EEG-based motor imagery classification. Journal Of Neural Engineering. 19, 066003 (2022). [CrossRef]
  53. Duan, T., Chauhan, M., Shaikh, M., Chu, J. & Srihari, S. Ultra Efficient Transfer Learning with Meta Update for Continuous EEG Classification Across Subjects.. Canadian Conference On AI. (2021).
  54. Ouahidi, Y., Lioi, G., Farrugia, N., Pasdeloup, B. & Gripon, V. Unsupervised Adaptive Deep Learning Method For BCI Motor Imagery Decoding. ArXiv Preprint ArXiv:2403.15438. (2024).
  55. Xu, L., Ma, Z., Meng, J., Xu, M., Jung, T. & Ming, D. Improving transfer performance of deep learning with adaptive batch normalization for brain-computer interfaces. 2021 43rd Annual International Conference Of The IEEE Engineering In Medicine & Biology Society (EMBC). pp. 5800-5803 (2021).
  56. Gu, X., Han, J., Yang, G. & Lo, B. Generalizable Movement Intention Recognition with Multiple Heterogeneous EEG Datasets. 2023 IEEE International Conference On Robotics And Automation (ICRA). pp. 9858-9864 (2023).
  57. Bakas, S., Ludwig, S., Adamos, D., Laskaris, N., Panagakis, Y. & Zafeiriou, S. Latent Alignment with Deep Set EEG Decoders. ArXiv Preprint ArXiv:2311.17968. (2023).
  58. Zhuo, F., Zhang, X., Tang, F., Yu, Y. & Liu, L. Riemannian transfer learning based on log-Euclidean metric for EEG classification. Frontiers In Neuroscience. 18 pp. 1381572 (2024). [CrossRef]
  59. Zhang, W. & Wu, D. Manifold embedded knowledge transfer for brain-computer interfaces. IEEE Transactions On Neural Systems And Rehabilitation Engineering. 28, 1117-1127 (2020). [CrossRef]
  60. He, H. & Wu, D. Transfer learning for brain–computer interfaces: A Euclidean space data alignment approach. IEEE Transactions On Biomedical Engineering. 67, 399-410 (2019). [CrossRef]
  61. Xu, L., Xu, M., Ke, Y., An, X., Liu, S. & Ming, D. Cross-dataset variability problem in EEG decoding with deep learning. Frontiers In Human Neuroscience. 14 pp. 103 (2020). [CrossRef]
  62. Zoumpourlis, G. & Patras, I. Motor imagery decoding using ensemble curriculum learning and collaborative training. 2024 12th International Winter Conference On Brain-Computer Interface (BCI). pp. 1-8 (2024).
  63. Zanini, P., Congedo, M., Jutten, C., Said, S. & Berthoumieu, Y. Transfer learning: A Riemannian geometry framework with applications to brain–computer interfaces. IEEE Transactions On Biomedical Engineering. 65, 1107-1116 (2017). [CrossRef]
  64. Li, Y., Wang, N., Shi, J., Liu, J. & Hou, X. Revisiting batch normalization for practical domain adaptation. ArXiv Preprint ArXiv:1603.04779. (2016). [CrossRef]
  65. Schneider, S., Rusak, E., Eck, L., Bringmann, O., Brendel, W. & Bethge, M. Improving robustness against common corruptions by covariate shift adaptation. Advances In Neural Information Processing Systems. 33 pp. 11539-11551 (2020).
  66. Döbler, M., Marsden, R. & Yang, B. Robust mean teacher for continual and gradual test-time adaptation. Proceedings Of The IEEE/CVF Conference On Computer Vision And Pattern Recognition. pp. 7704-7714 (2023).
  67. Marsden, R., Döbler, M. & Yang, B. Universal test-time adaptation through weight ensembling, diversity weighting, and prior correction. Proceedings Of The IEEE/CVF Winter Conference On Applications Of Computer Vision. pp. 2555-2565 (2024).
Preprints 113707 g001
Figure 1. Trial structure for the Dreyer2023 dataset [27]. Each trial starts with a fixation cross, followed by a short auditory signal. The cue occurs after 3 seconds and is present for 1.25 seconds. The cue is followed by a 3.75 second feedback phase. Between the trials a black screen is displayed for 1.5 - 3.5 seconds.
Figure 1. Trial structure for the Dreyer2023 dataset [27]. Each trial starts with a fixation cross, followed by a short auditory signal. The cue occurs after 3 seconds and is present for 1.25 seconds. The cue is followed by a 3.75 second feedback phase. Between the trials a black screen is displayed for 1.5 - 3.5 seconds.
Preprints 113707 g001
Preprints 113707 g002
Figure 2. A) BaseNet architecture and output dimensions for the Dreyer2023 dataset. Layer names are specified following the PyTorch API conventions. For Conv2d layers, the first value indicates the number of filters, and the tuple represents the kernel size. In the pooling layers, the first tuple indicates the kernel size, while the second tuple specifies the stride. B) Visualization of the sliding window extraction in the second pooling layer of BaseNet.
Figure 2. A) BaseNet architecture and output dimensions for the Dreyer2023 dataset. Layer names are specified following the PyTorch API conventions. For Conv2d layers, the first value indicates the number of filters, and the tuple represents the kernel size. In the pooling layers, the first tuple indicates the kernel size, while the second tuple specifies the stride. B) Visualization of the sliding window extraction in the second pooling layer of BaseNet.
Preprints 113707 g002
Preprints 113707 g003
Figure 3. Computational gain of joint decoding for f u = 16 Hz and different trial lengths T t and window lengths T w .
Figure 3. Computational gain of joint decoding for f u = 16 Hz and different trial lengths T t and window lengths T w .
Preprints 113707 g003
Preprints 113707 g004
Figure 4. Simplified overview of the domain adaptation landscape. Italic text specifies requirements regarding calibration data.
Figure 4. Simplified overview of the domain adaptation landscape. Italic text specifies requirements regarding calibration data.
Preprints 113707 g004
Preprints 113707 g005
Figure 5. Cross-subject results for the Dreyer2023 dataset for different data compositions. Each dot resembles a subject, the stars within the brackets resemble the different significance levels (p<0.05(*), p<0.01(**) and p<0.001(***)) when comparing two experiments connected by that bracket.
Figure 5. Cross-subject results for the Dreyer2023 dataset for different data compositions. Each dot resembles a subject, the stars within the brackets resemble the different significance levels (p<0.05(*), p<0.01(**) and p<0.001(***)) when comparing two experiments connected by that bracket.
Preprints 113707 g005
Preprints 113707 g006
Figure 6. Cross-subject results for the Lee2019 dataset for different data compositions. Each dot resembles a subject, the stars within the brackets resemble the different significance levels (p<0.05(*), p<0.01(**) and p<0.001(***)) when comparing two experiments connected by that bracket.
Figure 6. Cross-subject results for the Lee2019 dataset for different data compositions. Each dot resembles a subject, the stars within the brackets resemble the different significance levels (p<0.05(*), p<0.01(**) and p<0.001(***)) when comparing two experiments connected by that bracket.
Preprints 113707 g006
Preprints 113707 g007
Figure 7. Accuracy and samples per entropy bin for BaseNet (width of each bin equals 0.1, starting from 0). Each black dot resembles one subject. The trials are averaged over the seeds but the accuracies are filtered, i.e., accuracies where no trials were in the entropy bin are removed and thus no averaging can be performed.
Figure 7. Accuracy and samples per entropy bin for BaseNet (width of each bin equals 0.1, starting from 0). Each black dot resembles one subject. The trials are averaged over the seeds but the accuracies are filtered, i.e., accuracies where no trials were in the entropy bin are removed and thus no averaging can be performed.
Preprints 113707 g007
Preprints 113707 g008
Figure 8. Accuracies per window. Each black line indicates one subject, the red line corresponds to the average and the blue lines correspond to the average ± standard deviation.
Figure 8. Accuracies per window. Each black line indicates one subject, the red line corresponds to the average and the blue lines correspond to the average ± standard deviation.
Preprints 113707 g008
Preprints 113707 g009
Figure 9. Topoplots of the EDS scores for BaseNet and both datasets. Good subjects have a TAcc > 70%, bad subjects yield a performance below or equal to this threshold.
Figure 9. Topoplots of the EDS scores for BaseNet and both datasets. Good subjects have a TAcc > 70%, bad subjects yield a performance below or equal to this threshold.
Preprints 113707 g009
Table 1. Within-subject results. Results above the double line are for the Dreyer2023 dataset, below are for the Lee2019 dataset. The stars after the method indicate the different significance levels (p<0.05(*), p<0.01(**) and p<0.001(***)) compared to BaseNet.
Table 1. Within-subject results. Results above the double line are for the Dreyer2023 dataset, below are for the Lee2019 dataset. The stars after the method indicate the different significance levels (p<0.05(*), p<0.01(**) and p<0.001(***)) compared to BaseNet.
Method TAcc(%) uTacc(%) WAcc(%)
RiemannMDM*** 63.10 ± 14.79 62.57 ± 14.50 60.03 ± 11.52
BaseNet 57.60 ± 11.60 57.30 ± 11.23 56.02 ± 8.76
RiemannMDM* 62.46 ± 15.15 62.09 ± 14.79 60.52 ± 13.11
BaseNet 60.15 ± 12.59 59.14 ± 12.36 58.32 ± 10.76
Table 2. Dreyer2023 dataset cross-subject experiments. The stars after the method indicate the different significance levels (p<0.05(*), p<0.01(**) and p<0.001(***)) compared to the benchmark method in the same setting.
Table 2. Dreyer2023 dataset cross-subject experiments. The stars after the method indicate the different significance levels (p<0.05(*), p<0.01(**) and p<0.001(***)) compared to the benchmark method in the same setting.
Method TAcc(%) uTacc(%) WAcc(%)
BaseNet 67.80 ± 13.80 67.22 ± 13.56 62.23 ± 10.43
supervised RiemannMDM+PAR 67.35 ± 15.22 66.77 ± 14.95 62.99 ± 11.17
BaseNet*** 70.23 ± 14.37 69.84 ± 14.21 63.74 ± 10.95
BaseNet+EA*** 71.82 ± 15.30 71.60 ± 15.18 65.67 ± 11.92
BaseNet+RA*** 71.84 ± 15.30 71.71 ± 15.14 65.76 ± 11.95
unsupervised RiemannMDM 67.37 ± 15.17 66.74 ± 14.91 62.97 ± 11.16
BaseNet+EA*** 69.56 ± 14.87 69.22 ± 14.71 63.43 ± 10.92
BaseNet+RA*** 69.88 ± 14.95 69.56 ± 14.81 63.63 ± 11.04
BaseNet+AdaBN* 69.21 ± 14.65 68.86 ± 14.41 62.61 ± 10.60
BaseNet+EA+AdaBN*** 69.51 ± 14.62 69.14 ± 14.46 63.29 ± 10.73
BaseNet+RA+AdaBN*** 69.77 ± 14.59 69.37 ± 14.53 63.46 ± 10.79
online RiemannMDM+GR 69.31 ± 14.75 68.58 ± 14.31 63.48 ± 11.28
BaseNet+EA 69.72 ± 14.44 69.43 ± 14.28 63.32 ± 10.72
BaseNet+RA 69.28 ± 14.31 69.06 ± 14.13 63.26 ± 10.79
BaseNet+AdaBN 69.46 ± 14.17 68.96 ± 13.99 62.32 ± 10.38
BaseNet+EA+AdaBN 70.00 ± 14.20 69.80 ± 14.02 63.07 ± 10.31
BaseNet+RA+AdaBN 70.25 ± 14.04 70.05 ± 13.86 63.29 ± 10.37
Table 3. Lee2019 cross-subject experiments. The stars after the method indicate the different significance levels (p<0.05(*), p<0.01(**) and p<0.001(***)) compared to the benchmark method in the same setting.
Table 3. Lee2019 cross-subject experiments. The stars after the method indicate the different significance levels (p<0.05(*), p<0.01(**) and p<0.001(***)) compared to the benchmark method in the same setting.
Method TAcc(%) uTacc(%) WAcc(%)
BaseNet 70.36 ± 14.35 69.73 ± 14.43 65.08 ± 11.84
supervised RiemannMDM+PAR 65.06 ± 12.72 64.72 ± 12.99 62.63 ± 10.46
BaseNet*** 71.32 ± 14.41 70.70 ± 14.15 65.79 ± 12.05
BaseNet+EA*** 70.32 ± 14.99 69.91 ± 14.85 66.01 ± 12.50
BaseNet+RA*** 70.90 ± 15.09 70.61 ± 14.96 66.46 ± 12.66
unsupervised RiemannMDM 65.04 ± 12.74 64.67 ± 12.97 62.60 ± 10.42
BaseNet+EA*** 69.07 ± 14.63 68.77 ± 14.34 65.23 ± 11.86
BaseNet+RA*** 69.46 ± 14.98 69.28 ± 14.91 65.54 ± 12.29
BaseNet+AdaBN*** 70.87 ± 14.01 70.52 ± 13.96 65.30 ± 11.67
BaseNet+EA+AdaBN*** 69.29 ± 14.98 68.89 ± 14.87 65.30 ± 12.05
BaseNet+RA+AdaBN*** 69.66 ± 14.87 69.39 ± 14.80 65.57 ± 12.29
online RiemannMDM+GR 71.39 ± 12.52 71.09 ± 12.02 66.30 ± 10.24
BaseNet+EA* 73.57 ± 13.44 73.12 ± 13.15 67.51 ± 11.22
BaseNet+RA* 73.29 ± 13.37 72.99 ± 13.24 67.19 ± 11.47
BaseNet+AdaBN 71.93 ± 13.76 71.27 ± 13.69 65.26 ± 11.43
BaseNet+EA+AdaBN*** 74.85 ± 12.34 74.37 ± 12.45 67.54 ± 10.75
BaseNet+RA+AdaBN*** 74.99 ± 12.74 74.80 ± 12.59 67.87 ± 10.98
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

279

Views

183

Comments

0

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

Email

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated