Non-local Problems for the Fractional Order Diffusion Equation and the Degenerate Hyperbolic Equation

1. Introduction

Fractional partial differential equations can arise in the mathematical modeling of physical media with fractal geometry [1]. Boundary value problems for the fractional order diffusion equation were studied in [2,3,4,5,6]. In [7] a certain family of generalized derived Riemann–Liouville operators $D_{a+}^{\alpha ,\beta }$ of orders $\alpha$ and $\beta$ was studied. Applications of this operator are given in [8]. In [9] the unique solvability of the problem for the Riemann–Liouville partial fractional derivative equation with a boundary condition containing a generalized fractional integro-differentiation operator was investigated. The problem in which the boundary condition contains a linear combination of generalized fractional operators with a hyper-geometric Gaussian function for a mixed type equation with the partial fractional Riemann–Liouville derivative was studied in [10]. The nonlocal boundary value problem for a mixed type equation with the Riemann–Liouville fractional partial derivative was studied in [11]. A non-local boundary value problem for Gellerstedt equation with singular coefficient in an unbounded domain was investigated in [12].

The article’s research plan is structured as follows. Section 1 provides information about the problem under study and provides relevant links to articles. Section 2 provides the problem statement. Section 3 provides the main results: the issues of existence and uniqueness of the solution are investigated. Section 4 provides the statement of the proposed problem in a particular case, and Section 5 provides the methodology for solving this problem with its visualization.

2. Formulation of a Problem

We consider the equation

$$\left\{\begin{array}{c}{u}_{xx}-D_{0,y}^{\gamma }u=0,\gamma \in (0,1),y>0,\hfill \\ -{(-y)}^m{u}_{xx}+u_{yy}+{\displaystyle \frac{{\alpha }_0}{{(-y)}^{1-\frac{m}{2}}}}{u}_x+{\displaystyle \frac{{\beta }_0}{y}}{u}_y=0,y<0,\hfill \end{array}\right.$$

(1)

where $D_{0,y}^{\gamma }$ is the Riemann–Liouville fractional derivative of order $\gamma (0<\gamma <1)$ of $u(x,y)$ [13]

$$\left(D_{0,y}^{\gamma }u\right)(x,y)={\displaystyle \frac{\partial }{\partial y}}{\displaystyle \frac{1}{\Gamma (1-\gamma )}}\underset{0}{\overset{y}{\int }}{\displaystyle \frac{u(x,t)dt}{{(y-t)}^{\gamma }}},0<\gamma <1,y>0,$$

In (1) $m,{\alpha }_0,{\beta }_0$ are some real numbers satisfying conditions $m>0,|{\alpha }_0|<{\displaystyle \frac{m+2}{2}}$, $-{\displaystyle \frac{m}{2}}<{\beta }_0<1$.

The equation (1) is considered in domain $D=D^{+}\cup D^{-}\cup J$, where $D^{+}$ is the half-plane $y>0$, $D^{-}$ is the finite region of the fourth quadrant of the plane, limited by the characteristics

$$OC:x-{\displaystyle \frac{2}{m+2}}{(-y)}^{{\displaystyle \frac{m+2}{2}}}=0,BC:x+{\displaystyle \frac{2}{m+2}}{(-y)}^{{\displaystyle \frac{m+2}{2}}}=1$$

equations (1) coming from points $O(0,0)$, $B(1,0)$ and intersecting at point $C\left({\displaystyle \frac{1}{2}},-{\left({\displaystyle \frac{m+2}{4}}\right)}^{{\displaystyle \frac{2}{m+2}}}\right)$ and the segment $OB$ of the straight line $y=0$.

Let’s introduce the notation: $J=(0,1)$ is the unit interval of the line $y=0$, ${\Theta }_0\left(x\right)=\left({\displaystyle \frac{x}{2}},-{\left({\displaystyle \frac{m+2}{4}}x\right)}^{{\displaystyle \frac{2}{m+2}}}\right)$ is the intersection point of the characteristic of equation (1) coming from the point $(x,0)\in J$ with the characteristic $OC$.

$\left(I_{0+}^{\mu ,\rho ,\eta }f\right)\left(x\right)$ is a generalized fractional integro-differentiation operator with a hypergeometric Gauss function $F(a,b,c;z)$ introduced by M.Saigo [14] and having the form for real $\mu ,\rho ,\eta$ and $x>0$

$$\left(I_{0+}^{\mu ,\rho ,\eta }f\right)\left(x\right)=\left\{\begin{array}{c}{\displaystyle \frac{x^{-\mu -\rho }}{\Gamma \left(\mu \right)}}\underset{0}{\overset{x}{\int }}{(x-t)}^{\mu -1}F\left(\mu +\rho ,-\eta ;\mu ;1-{\displaystyle \frac{t}{x}}\right)f\left(t\right)dt,\mu >0,\hfill \\ {\left({\displaystyle \frac{d}{dx}}\right)}^n\left(I_{0+}^{\mu +n,\rho -n,\eta -n}f\right)\left(x\right),\mu \le 0,n=[-\mu ]+1.\hfill \end{array}\right.$$

(2)

in particular

$$\left(I_{0+}^{0,0,\eta }f\right)\left(x\right)=f\left(x\right),$$

(3)

Note that if $\mu >0$, then the formulas are valid

$$\left(I_{0+}^{\mu ,-\mu ,\eta }f\right)\left(x\right)=\left(I_{0+}^{\mu }f\right)\left(x\right),\left(I_{0+}^{-\mu ,\mu ,\eta }f\right)\left(x\right)=\left(D_{0+}^{\mu }f\right)\left(x\right),$$

(4)

where $\left(I_{0+}^{\mu }f\right)\left(x\right)$ and $\left(D_{0+}^{\mu }f\right)\left(x\right)$ are fractional Riemann–Liouville integration and differentiation operators of the order $\mu >0$ [13];

$$\left(I_{0+}^{\mu }f\right)\left(x\right)={\displaystyle \frac{1}{\Gamma \left(\mu \right)}}\underset{0}{\overset{x}{\int }}{(x-t)}^{\mu -1}f\left(t\right)dt,\mu >0,x>0,$$

$$\left(D_{0+}^{\mu }f\right)\left(x\right)={\left({\displaystyle \frac{d}{dx}}\right)}^n{\displaystyle \frac{1}{\Gamma (n-\mu )}}\underset{0}{\overset{x}{\int }}{(x-t)}^{n-\mu -1}f\left(t\right)dt,\mu >0,n=\left[\mu \right]+1.$$

(5)

Problem A. Find a solution $u(x,y)$ of the equation (1) in domain D satisfying the boundary conditions

$$y^{1-\gamma }{u|}_{y=0}=0,(-\infty <x\le 0,1\le x<\infty ),$$

(6)

$$A_1{x}^{1+b-\alpha -\beta }\left(I_{0+}^{a,b,-a-\alpha }{t}^{{ }^{\alpha +\beta -1}}u\left[{\Theta }_0\left(t\right)\right]\right)\left(x\right)+A_2\left(I_{0+}^{a+\alpha ,0,\beta -1-a-b}u(t,0)\right)=g\left(x\right),(x\in J)$$

(7)

and the transmission conditions

$$\underset{y\to 0-}{lim}u(x,y)=c\left(x\right)\underset{y\to 0+}{lim}{y}^{1-\gamma }u(x,y),\forall x\in \overline{J},$$

(8)

$$\underset{y\to 0-}{lim}{(-y)}^{{\beta }_0}{u}_y(x,y)=d\left(x\right)\underset{y\to 0+}{lim}{y}^{1-\gamma }{\left(y^{1-\gamma }u(x,y)\right)}_y,\forall x\in J,$$

(9)

Here $\alpha ={\displaystyle \frac{m+2({\beta }_0+{\alpha }_0)}{2(m+2)}},\beta ={\displaystyle \frac{m+2({\beta }_0-{\alpha }_0)}{2(m+2)}},$ $0<\alpha <{\displaystyle \frac{1}{2}},0<\beta <{\displaystyle \frac{1}{2}},$$a>max\{-\alpha ,1-\beta \}$, $A_1,A_2$ are valid constants, $g\left(x\right),c\left(x\right),d\left(x\right)$ are given functions such that

$$g\left(x\right)\in C^1\left(\overline{J}\right)\cap C^2\left(J\right),c\left(x\right),d\left(x\right)\in C^2\left(\overline{J}\right)\cap C^3\left(J\right),c\left(x\right)d\left(x\right)>0,{\displaystyle \frac{d^2}{d{x}^2}}\left[c\left(x\right)d\left(x\right)\right]\le 0.$$

(10)

Note that non-local boundary value problems for Equation (1) in unbounded and bounded domains are studied in [15,16].

We will look for a solution to the $u(x,y)$ problem in the class of doubly differentiable functions in domain of D such that

$$y^{1-\gamma }u(x,y)\in C\left({\overline{D}}^{+}\right),u(x,y)\in C\left({\overline{D}}^{-}\right),$$

$$y^{1-\gamma }{\left(y^{1-\gamma }u(x,y)\right)}_y\in C(D^{+}\cup \{(x,y):0<x<1,y=0\}),$$

$$u_{xx}\in C(D^{+}\cup D^{-}),u_{yy}\in C\left(D^{-}\right).$$

3. Main Results

3.1. Uniqueness of the Solution of the Problem

Theorem 1. 

Let $A_1\le 0$, $A_2>0,$ $c\left(x\right)d\left(x\right)>0,{\displaystyle \frac{d^2}{d{x}^2}}\left(c\left(x\right)d\left(x\right)\right)\le 0.$ Then problem A, has only a trivial solution.

Proof of Theorem 1. 

Let’s introduce the following notation

$$\underset{y\to 0+}{lim}{y}^{1-\gamma }u(x,y)={\tau }_1\left(x\right),\underset{y\to 0-}{lim}u(x,y)={\tau }_2\left(x\right),$$

(11)

$$\underset{y\to 0+}{lim}{y}^{1-\gamma }{\left(y^{1-\gamma }u(x,y)\right)}_y={\nu }_1\left(x\right),\underset{y\to 0-}{lim}{(-y)}^{{\beta }_0}{u}_y(x,y)={\nu }_2\left(x\right).$$

(12)

It is known [17] that the solution of equation (1) in domain $D^{+}$ satisfies the condition (6) and the condition

$$\underset{y\to 0+}{lim}{y}^{1-\gamma }u(x,y)={\tau }_1\left(x\right),\forall x\in \overline{J}$$

(13)

is given by the formula

$$u(x,y)=\underset{0}{\overset{1}{\int }}G(x,y,t){\tau }_1\left(t\right)dt,$$

(14)

where $G(x,y,t)={\displaystyle \frac{\Gamma \left(\gamma \right)}{2}}{y}^{{\displaystyle \frac{\gamma }{2}}-1}{e}_{1,{\displaystyle \frac{\gamma }{2}}}^{1,{\displaystyle \frac{\gamma }{2}}}\left(-|x-t|y^{-{\displaystyle \frac{\gamma }{2}}}\right),$ $e_{1,{\displaystyle \frac{\gamma }{2}}}^{1,{\displaystyle \frac{\gamma }{2}}}\left(z\right)=\sum _{k=0}^{\infty }{\displaystyle \frac{z^k}{k!\Gamma \left(\frac{(1-k)\gamma }{2}\right)}}$ is a Wright type function [17].

It is also known [18] that the functional relation between ${\tau }_1\left(x\right)$ and ${\nu }_1\left(x\right)$, brought from the parabolic part of $D^{+}$ to the line $y=0$, has the form

$${\nu }_1\left(x\right)={\displaystyle \frac{1}{\Gamma (1+\gamma )}}{\tau }_1^{\prime \prime }\left(x\right).$$

(15)

Let’s find the ratio between ${\tau }_2\left(x\right)$ and ${\nu }_2\left(x\right)$ brought to the line $y=0$ from the hyperbolic part $D^{-}$ of domain D.

The solution of the modified Cauchy problem, in domain $D^{-}$, has the form [15]

$$u(x,y)={\gamma }_1\underset{0}{\overset{1}{\int }}{\tau }_2\left(x+{\displaystyle \frac{2}{m+2}}(2t-1){(-y)}^{{\displaystyle \frac{m+2}{2}}}\right)t^{\beta -1}{(1-t)}^{\alpha -1}dt+$$

$$+{\gamma }_2{(-y)}^{1-{\beta }_0}\underset{0}{\overset{1}{\int }}{\nu }_2\left(x+{\displaystyle \frac{2}{m+2}}(2t-1){(-y)}^{{\displaystyle \frac{m+2}{2}}}\right)t^{-\alpha }{(1-t)}^{-\beta }dt,$$

(16)

where ${\gamma }_1={\displaystyle \frac{\Gamma (\alpha +\beta )}{\Gamma \left(\alpha \right)\Gamma \left(\beta \right)}},{\gamma }_2=-{\displaystyle \frac{2\Gamma (1-\alpha -\beta )}{(m+2)\Gamma (1-\alpha )\Gamma (1-\beta )}}.$

Using the formula (16) and the ratio (2) we have

$$u\left[{\Theta }_0\left(x\right)\right]={\gamma }_1\Gamma \left(\alpha \right)\left(I_{0+}^{\alpha ,0,\beta -1}{\tau }_2\right)\left(x\right)+{\gamma }_2{\left({\displaystyle \frac{m+2}{4}}\right)}^{1-\alpha -\beta }\Gamma (1-\beta )\left(I_{0+}^{1-\beta ,\alpha +\beta -1,\beta -1}{\nu }_2\right)\left(x\right).$$

Substituting $u\left[{\Theta }_0\left(x\right)\right]$ into the boundary condition (7) and applying successively the relations [14]

$$x^{\mu +\rho +\eta }\left(I_{0+}^{\mu ,\rho ,\eta }\phi \right)\left(x\right)=\left(I_{0+}^{\mu ,-\mu -\eta ,-\mu -\rho }\phi \right)\left(x\right),\mu >0,$$

(17)

$$\left(I_{0+}^{\mu ,\rho ,\eta }{I}_{0+}^{\sigma ,\delta ,\mu +\eta }\phi \right)\left(x\right)=\left(I_{0+}^{\mu +\sigma ,\rho +\delta ,\eta }\phi \right)\left(x\right),\mu >0,$$

(18)

after simple calculations, we get

$$k_1\left(I_{0+}^{a+\alpha ,0,\beta -1-a-b}{\tau }_2\right)\left(x\right)+k_2\left(I_{0+}^{a+1-\beta ,\alpha +\beta -1,\beta -1-a-b}{\nu }_2\right)\left(x\right)=g\left(x\right)$$

(19)

where $k_1=A_1{\gamma }_1\Gamma \left(\alpha \right)-A_2,k_2=A_1{\gamma }_2\Gamma (1-\beta ){\left({\displaystyle \frac{m+2}{2}}\right)}^{1-\alpha -\beta }.$

Applying the operator ${\left(I_{0+}^{a+\alpha ,0,\beta -1-a-b}\right)}^{-1}=I_{0+}^{-a-\alpha ,0,\alpha +\beta -1-b}$ to both parts of the resulting equality, taking into account (18), (3), (4) and $\left(D_{0+}^{\alpha }\left(I_{0+}^{\alpha }f\right)\left(t\right)\right)\left(x\right)=f\left(x\right)$ we have

$$k_1{\tau }_2\left(x\right)+k_2\left(I_{0+}^{1-\alpha -\beta }{\nu }_2\right)\left(x\right)=g_1\left(x\right)$$

(20)

where $g_1\left(x\right)=\left(I_{0+}^{-a-\alpha ,0,\alpha +\beta -1-b}g\right)\left(x\right).$

Consider the corresponding homogeneous problem: $g\left(x\right)=0.$

Consider the following two cases:

a) Let $k_1\ne 0$:

$$A_1\Gamma (\alpha +\beta )-A_2\Gamma \left(\beta \right)\ne 0.$$

(21)

Then the ratio (20) takes the form

$${\tau }_2\left(x\right)=k_3\left(I_{0+}^{1-\alpha -\beta }{\nu }_2\right)\left(x\right)+{\displaystyle \frac{1}{k_1}}{g}_1\left(x\right),$$

(22)

where $k_3=-{\displaystyle \frac{k_2}{k_1}}.$

Let’s evaluate the following integral

$$I=\underset{0}{\overset{1}{\int }}{\tau }_2\left(x\right){\nu }_2\left(x\right)dx.$$

Due to the conjugation conditions (8), (9) and ratio (11),(12) we have

$${\tau }_2\left(x\right)=c\left(x\right){\tau }_1\left(x\right),{\nu }_2\left(x\right)=d\left(x\right){\nu }_1\left(x\right),$$

(23)

and therefore, by virtue of ratio (15) we have

$$I={\displaystyle \frac{1}{\Gamma (1+\gamma )}}\underset{0}{\overset{1}{\int }}c\left(x\right){\tau }_1\left(x\right)d\left(x\right){\tau }_1{ }^{\prime \prime }\left(x\right)dx.$$

Integrating in parts and considering that according to (6) and (13) ${\tau }_1\left(0\right)={\tau }_1\left(1\right)=0$, we get

$$I={\displaystyle \frac{1}{\Gamma (1+\gamma )}}\left[{\displaystyle \frac{1}{2}}\underset{0}{\overset{1}{\int }}{\tau }_1^2\left(x\right){\displaystyle \frac{d^2}{d{x}^2}}\left(c\left(x\right)d\left(x\right)\right)dx-\underset{0}{\overset{1}{\int }}{\left({\tau }_1{ }^{\prime }\left(x\right)\right)}^{2}c\left(x\right)d\left(x\right)dx\right].$$

(24)

Hence, due to the conditions (10), we obtain an estimate in domain of $D^{+}$ for the integral:

$$I\le 0.$$

(25)

Now let’s find the estimate of the integral I in domain $D^{-}$.

For $g\left(x\right)=0$, the equality (22) takes the form

$${\tau }_2\left(x\right)=k_3\left(I_{0+}^{1-\alpha -\beta }{\nu }_2\left(t\right)\right)\left(x\right)={\displaystyle \frac{k_3}{\Gamma (1-\alpha -\beta )}}\underset{0}{\overset{x}{\int }}{\nu }_2\left(t\right){(x-t)}^{-\alpha -\beta }dt$$

and therefore,

$$I={\displaystyle \frac{k_3}{\Gamma (1-\alpha -\beta )}}\underset{0}{\overset{1}{\int }}{\nu }_2\left(x\right)dx\underset{0}{\overset{x}{\int }}{(x-t)}^{-\alpha -\beta }{\nu }_2\left(t\right)dt.$$

Next, let’s use the well-known formula for the gamma function $\Gamma \left(\sigma \right)$ [19]

$$\underset{0}{\overset{\infty }{\int }}{s}^{\sigma -1}cos\left(ks\right)ds={\displaystyle \frac{\Gamma \left(\sigma \right)}{k^{\sigma }}}cos\left({\displaystyle \frac{\sigma \pi }{2}}\right),(k>0,0<\sigma <1).$$

Assuming $k=\mid x-t\mid ,\sigma =\alpha +\beta$ to it, we get

$$\mid x-t{\mid }^{-\alpha -\beta }=$$

$$={\displaystyle \frac{1}{\Gamma (\alpha +\beta )cos\left(\pi \frac{\alpha +\beta }{2}\right)}}\underset{0}{\overset{\infty }{\int }}{s}^{\alpha +\beta -1}cos(s\mid x-t\mid )ds,(0<\alpha +\beta <1).$$

Applying this formula and the Dirichlet formula of the permutation of the order of integration in the repeated integral, we arrive at the relation

$$I={\displaystyle \frac{k_{3}sin\left(\pi \frac{\alpha +\beta }{2}\right)}{\pi }}\underset{0}{\overset{\infty }{\int }}{s}^{\alpha +\beta -1}\left[{\left(\underset{0}{\overset{1}{\int }}{\nu }_2\left(x\right)cos\left(sx\right)dx\right)}^2+{\left(\underset{0}{\overset{1}{\int }}{\nu }_2\left(x\right)sin\left(sx\right)dx\right)}^2\right]ds.$$

From the conditions of the theorem we obtain

$$I\ge 0.$$

(26)

It follows from (25) and (26) that $I=0$, and therefore according to (24)

$${\displaystyle \frac{1}{2}}\underset{0}{\overset{1}{\int }}{\tau }_1^2\left(x\right){\displaystyle \frac{d^2}{d{x}^2}}\left(c\left(x\right)d\left(x\right)\right)dx-\underset{0}{\overset{1}{\int }}{\left({\tau }_1{ }^{\prime }\left(x\right)\right)}^{2}c\left(x\right)d\left(x\right)dx=0.$$

Hence, by virtue of the conditions (10) and the equalities ${\tau }_1\left(0\right)={\tau }_1\left(1\right)=0$ we get

$${\tau }_1\left(x\right)=0,x\in \overline{J}.$$

(27)

b) Let $k_1=0,k_2\ne 0$:

$$A_1\Gamma (\alpha +\beta )-A_2\Gamma \left(\beta \right)=0,A_1\ne 0.$$

(28)

Then (20) is a homogeneous Abel equation:

$$k_2\left(I_{0+}^{1-\alpha -\beta }{\nu }_2\right)\left(x\right)=0$$

having only a trivial solution ${\nu }_2\left(x\right)=0$.

Then, by virtue of the second formula (23) ${\nu }_1\left(x\right)=0$, the ratio (15) in the place with the conditions ${\tau }_1\left(0\right)={\tau }_1\left(1\right)=0$ leads to the equality (27). This, according to (14), means that $u(x,y)\equiv 0$ in domain of $\overline{D}$, which proves the uniqueness of the solution to the original problem under the conditions (21) and (28). □

3.2. The Existence of a Solution to Problem A

Theorem 2. 

Let a) $k_1\ne 0,k_2=0;$ b) $k_1=0,k_2\ne 0;$ c) $c\left(x\right)=c=\mathrm{const};$ d) $c\left(x\right)=c=\mathrm{const},$ $d\left(x\right)=d=\mathrm{const}.$ Then there is a solution to problem A.

Proof of Theorem 2. 

According to (14) and (15), to prove the existence of a solution to problem A, it is enough to find ${\nu }_1\left(x\right)$.

By virtue of (23), the equation (20) takes the form

$$k_{1}c\left(x\right){\tau }_1\left(x\right)+k_2\left(I_{0+}^{1-\alpha -\beta }d\left(t\right){\nu }_1\left(t\right)\right)\left(x\right)=g_1\left(x\right).$$

(29)

Consider the case $k_1\ne 0,k_2=0,$ then (29) gives an explicit expression for ${\tau }_1\left(x\right),$ that is, ${\tau }_1\left(x\right)={\displaystyle \frac{g_1\left(x\right)}{k_{1}c\left(x\right)}}$ and ${\nu }_1\left(x\right)$ are found by the formula (15).

If $k_1=0,k_2\ne 0,$ then (29) is an Abel integral equation of the first kind.

$$k_2\left(I_{0+}^{1-\alpha -\beta }d\left(t\right){\nu }_1\left(t\right)\right)\left(x\right)=g_1\left(x\right).$$

(30)

with $0<\alpha +\beta <1.$ According to the condition (10) $g\left(x\right)\in C^1\left(\overline{J}\right)\cup C^2\left(J\right).$ Function $g_1\left(x\right)$ is also continuous [10] and the well-known solution of the equation (30)[13] gives an explicit expression for ${\nu }_1\left(x\right)$ in the form

$${\nu }_1\left(x\right)={\displaystyle \frac{1}{k_{2}d\left(x\right)}}{\displaystyle \frac{d}{dx}}{\displaystyle \frac{1}{\Gamma (\alpha +\beta )}}\underset{0}{\overset{x}{\int }}{(x-t)}^{\alpha +\beta -1}{g}_1\left(t\right)dt.$$

If $c\left(x\right)=c\ne 0,$ then the equation (29) takes the form

$$c{k}_1{\tau }_1\left(x\right)+k_2\left(I_{0+}^{1-\alpha -\beta }d\left(t\right){\nu }_1\left(t\right)\right)\left(x\right)=g_1\left(x\right).$$

(31)

Differentiate both parts of the ratio (31) by x twice and taking into account (5), (15), we get

$$c{k}_1\Gamma (1+\gamma ){\nu }_1\left(x\right)+k_2\left(D_{0+}^{1+\alpha +\beta }d\left(t\right){\nu }_1\left(t\right)\right)\left(x\right)=g_1{ }^{\prime \prime }\left(x\right).$$

(32)

As you know [13] if

$${\nu }_2\left(x\right)=d\left(x\right){\nu }_1\left(x\right)=\underset{y\to 0-}{lim}{(-y)}^{{\beta }_0}{u}_y(x,y)\in C\left([0,1]\right),$$

(33)

then the formula is correct

$$\left(I_{0+}^{1+\alpha +\beta }{D}_{0+}^{1+\alpha +\beta }{\nu }_2\left(t\right)\right)\left(x\right)={\nu }_2\left(x\right)-c_1{x}^{\alpha +\beta }-c_2{x}^{\alpha +\beta -1},$$

(34)

where

$$c_1={\displaystyle \frac{1}{\Gamma (\alpha +\beta +1)}}{\left(I_{0+}^{1-\alpha -\beta }{\nu }_2\right)}^{\prime }(0+),c_1={\displaystyle \frac{1}{\Gamma (\alpha +\beta )}}\left(I_{0+}^{1-\alpha -\beta }{\nu }_2\right)(0+)$$

(35)

If the condition (33) is satisfied, then applying the operator $\left(I_{0+}^{1+\alpha +\beta }\right)$ to both parts of (32) and considering (34) we arrive at the integral equation:

$$k_{2}d\left(x\right){\nu }_1\left(x\right)+c{k}_1\Gamma (1+\gamma )\left(I_{0+}^{1+\alpha +\beta }{\nu }_1\left(t\right)\right)\left(x\right)=g_2\left(x\right),$$

(36)

where

$$g_2\left(x\right)=\left(I_{0+}^{1+\alpha +\beta }{g}_1{ }^{\prime \prime }\left(t\right)\right)\left(x\right)+k_2[c_1{x}^{\alpha +\beta }+c_2{x}^{\alpha +\beta -1}].$$

(37)

If $k_{2}d\left(x\right)\ne 0,$ then (36) Volterra integral equation of the second kind

$${\nu }_1\left(x\right)+\underset{0}{\overset{x}{\int }}K(x,t){\nu }_1\left(t\right)dt=F\left(x\right)$$

(38)

with a continuous core $K(x,t)={\displaystyle \frac{c{k}_1\Gamma (1+\gamma )}{k_2\Gamma (1+\alpha +\beta )d\left(x\right)}}{(x-t)}^{\alpha +\beta }$ and the free member $F\left(x\right)={\displaystyle \frac{1}{k_{2}d\left(x\right)}}{g}_2\left(x\right),$ where function $g_2\left(x\right)$ is given by formula (37), and the constants $c_1,c_2$ are by formula (35).

It is known [4] that the equation (38) has a unique solution ${\nu }_1\left(x\right)$.

If $c\left(x\right)=c\ne 0,$ $d\left(x\right)=d\ne 0$, then the equation (29) reduces to a fractional differential equation [4]:

$$\left(D_{0+}^{1+\alpha +\beta }{\nu }_1\left(t\right)\right)\left(x\right)+k_4{\nu }_1\left(x\right)=\Phi \left(x\right),$$

(39)

where $k_4={\displaystyle \frac{c{k}_1\Gamma (1+\gamma )}{k_{2}d}},\Phi \left(x\right)={\displaystyle \frac{1}{k_{2}d}}{g}_1{ }^{\prime \prime }\left(x\right).$

In [4], an explicit solution of the ${\nu }_1\left(x\right)$ equation (39) is written out, which according to (14) completes the proof of the existence of a solution to the original problem. □

4. Formulation of a Problem

Let ${\alpha }_0=0$, ${\beta }_0=-{\displaystyle \frac{m}{2}}$, then the equation (1) takes the form

$$\left\{\begin{array}{c}{u}_{xx}-D_{0,y}^{\gamma }u=0,\gamma \in (0,1),y>0,\hfill \\ -{(-y)}^m{u}_{xx}+u_{yy}-{\displaystyle \frac{m}{2y}}{u}_y=0,y<0.\hfill \end{array}\right.$$

(40)

In this case, let’s study the following problem.

Problem B. Find a solution $u(x,y)$ of equation (40) satisfying the boundary condition (6) and the condition

$${\displaystyle \frac{d}{dx}}u\left[{\Theta }_0\left(x\right)\right]={\displaystyle \frac{d}{dx}}u(x,0)+\delta \left(x\right),$$

(41)

and the transmission conditions

$$\underset{y\to 0-}{lim}u(x,y)=\underset{y\to 0+}{lim}{y}^{1-\gamma }u(x,y),\forall x\in \overline{J},$$

(42)

$$\underset{y\to 0-}{lim}{(-y)}^{-{\displaystyle \frac{m}{2}}}{u}_y(x,y)=\underset{y\to 0+}{lim}{y}^{1-\gamma }{\left(y^{1-\gamma }u(x,y)\right)}_y,\forall x\in J.$$

(43)

Here $\delta \left(x\right)$ is given function such that

$$\delta \left(x\right)\in C^1\left(\overline{J}\right)\cap C^2\left(J\right).$$

5. Solution Methodology

Solving a modified Cauchy problem with initial data

$$u(x,0)=\tau \left(x\right),x\in \overline{J},\underset{y\to 0-}{lim}{(-y)}^{-{\displaystyle \frac{m}{2}}}{u}_y(x,y)=\nu \left(x\right),x\in J,$$

in domain $D^{-}$ for equation $-{(-y)}^m{u}_{xx}+u_{yy}-{\displaystyle \frac{m}{2y}}{u}_y=0$ is given by the d’Alembert’s formula

$$u(x,y)={\displaystyle \frac{1}{2}}\left[\tau \left(x-{\displaystyle \frac{2}{m+2}}{(-y)}^{{\displaystyle \frac{m+2}{2}}}\right)+\tau \left(x+{\displaystyle \frac{2}{m+2}}{(-y)}^{{\displaystyle \frac{m+2}{2}}}\right)\right]-$$

$$-{\displaystyle \frac{2}{m+2}}{(-y)}^{{\displaystyle \frac{m+2}{2}}}\underset{0}{\overset{1}{\int }}\nu \left(x+{\displaystyle \frac{2}{m+2}}(2t-1){(-y)}^{{\displaystyle \frac{m+2}{2}}}\right)dt.$$

(44)

From (44) we calculate

$$u\left[{\Theta }_0\left(x\right)\right]={\displaystyle \frac{1}{2}}\tau \left(x\right)-{\displaystyle \frac{1}{2}}\underset{0}{\overset{x}{\int }}\nu \left(z\right)dz.$$

Substituting $u\left[{\Theta }_0\left(x\right)\right]$ into the condition (41), we obtain the second functional relation between the unknown functions $\tau \left(x\right)$ and $\nu \left(x\right):$

$${\tau }^{\prime }\left(x\right)+\nu \left(x\right)=-2\delta \left(x\right).$$

(45)

Excluding $\nu \left(x\right)$ from the equations (15) and (45), we obtain

$${\tau }^{\prime }\left(x\right)+{\displaystyle \frac{1}{\Gamma (1+\gamma )}}{\tau }^{\prime \prime }\left(x\right)=-2\delta \left(x\right).$$

(46)

Applying the method of variation of constants to the equation (46), we will have

$$\tau \left(x\right)=C_1+C_2{e}^{-\lambda x}+{\displaystyle \frac{2}{\lambda }}\underset{0}{\overset{x}{\int }}\delta \left(s\right)\left(e^{\lambda (s-x)}-1\right)ds,$$

(47)

where $\lambda =\Gamma (1+\gamma ),C_1,C_2-$ constant values.

From (47), taking into account (45), we get

$$\nu \left(x\right)=\left({\displaystyle \frac{2}{\lambda }}-2\right)\delta \left(x\right)+C_2\lambda e^{-\lambda x}+2\underset{0}{\overset{x}{\int }}{e}^{\lambda (s-x)}\delta \left(s\right)ds,$$

Given that $\tau \left(0\right)=\tau \left(1\right)=0$, from (47) it is easy to show that

$C_1={\displaystyle \frac{2}{1-e^{\lambda }}}\underset{0}{\overset{1}{\int }}\delta \left(s\right)\left(e^{\lambda (s-1)}-1\right)ds,$$C_2=-{\displaystyle \frac{2}{1-e^{\lambda }}}\underset{0}{\overset{1}{\int }}\delta \left(s\right)\left(e^{\lambda (s-1)}-1\right)ds.$

Using the found $\tau \left(x\right)$ and $\nu \left(x\right)$, it is easy to obtain a solution to problem B in each of the areas $D^{+}$ and $D^{-}$, which means that the solution to the problem (40), (6), (41) in a given class of functions in the domain D, satisfying the boundary conditions (6), (41) and the gluing conditions (42)-(43).

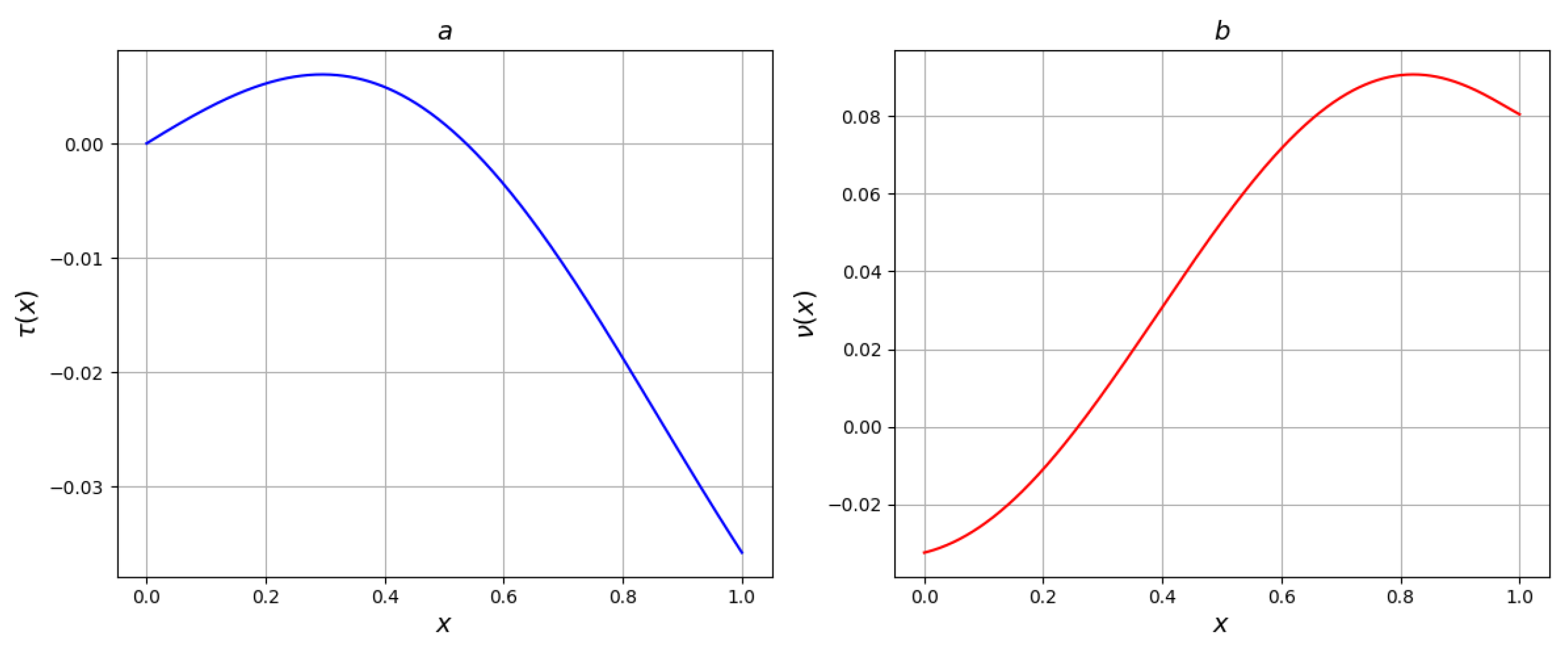
Let’s consider an example of solving problem B for a specific type of function $\delta \left(x\right)$ with its visualization. Visualization was performed using PyCharm software in the Python language.

Example 1. 

Let $\delta \left(x\right)=x^{{\displaystyle \frac{3}{2}}}{(1-x)}^{{\displaystyle \frac{3}{2}}}$.

Then equalities (47), (5) take the following form

$$\tau \left(x\right)=C_1+C_2{e}^{-\lambda x}+{\displaystyle \frac{2}{\lambda }}\underset{0}{\overset{x}{\int }}{s}^{{\displaystyle \frac{3}{2}}}{(1-s)}^{{\displaystyle \frac{3}{2}}}{e}^{\lambda (s-x)}ds,$$

$$\nu \left(x\right)=\left({\displaystyle \frac{2}{\lambda }}-2\right)x^{{\displaystyle \frac{3}{2}}}{(1-x)}^{{\displaystyle \frac{3}{2}}}+C_2\lambda e^{-\lambda x}+2\underset{0}{\overset{x}{\int }}{s}^{{\displaystyle \frac{3}{2}}}{(1-s)}^{{\displaystyle \frac{3}{2}}}{e}^{\lambda (s-x)}ds,$$

where

$$C_1={\displaystyle \frac{2\sqrt{\pi }\Gamma \left(2.5\right)e^{\frac{-\lambda }{2}}{I}_2(-0.5\lambda )}{{\lambda }^2(1-e^{\lambda })}}-{\displaystyle \frac{2B(2.5,2.5)}{1-e^{\lambda }}},C_2={\displaystyle \frac{2\sqrt{\pi }\Gamma \left(2.5\right)e^{\frac{-\lambda }{2}}{I}_2(-0.5\lambda )}{{\lambda }^2(1-e^{\lambda })}}+{\displaystyle \frac{2B(2.5,2.5)}{1-e^{\lambda }}}.$$

Here $I_2\left(x\right)$ is the modified Bessel function, $\Gamma \left(x\right)$ is the gamma function, $B(x,y)$ is the beta function.

Figure 1 shows the graphs of functions $\tau \left(x\right)$ and $\nu \left(x\right)$ for $\gamma =0.9$ and $\delta \left(x\right)=x^{{\displaystyle \frac{3}{2}}}{\left(1-x\right)}^{{\displaystyle \frac{3}{2}}}$.

Using the obtained functions $\tau \left(x\right)$ and $\nu \left(x\right)$, we can obtain a solution to the problem in domain $D^{+}$ and $D^{-}$, respectively, using formulas (14) and (42).

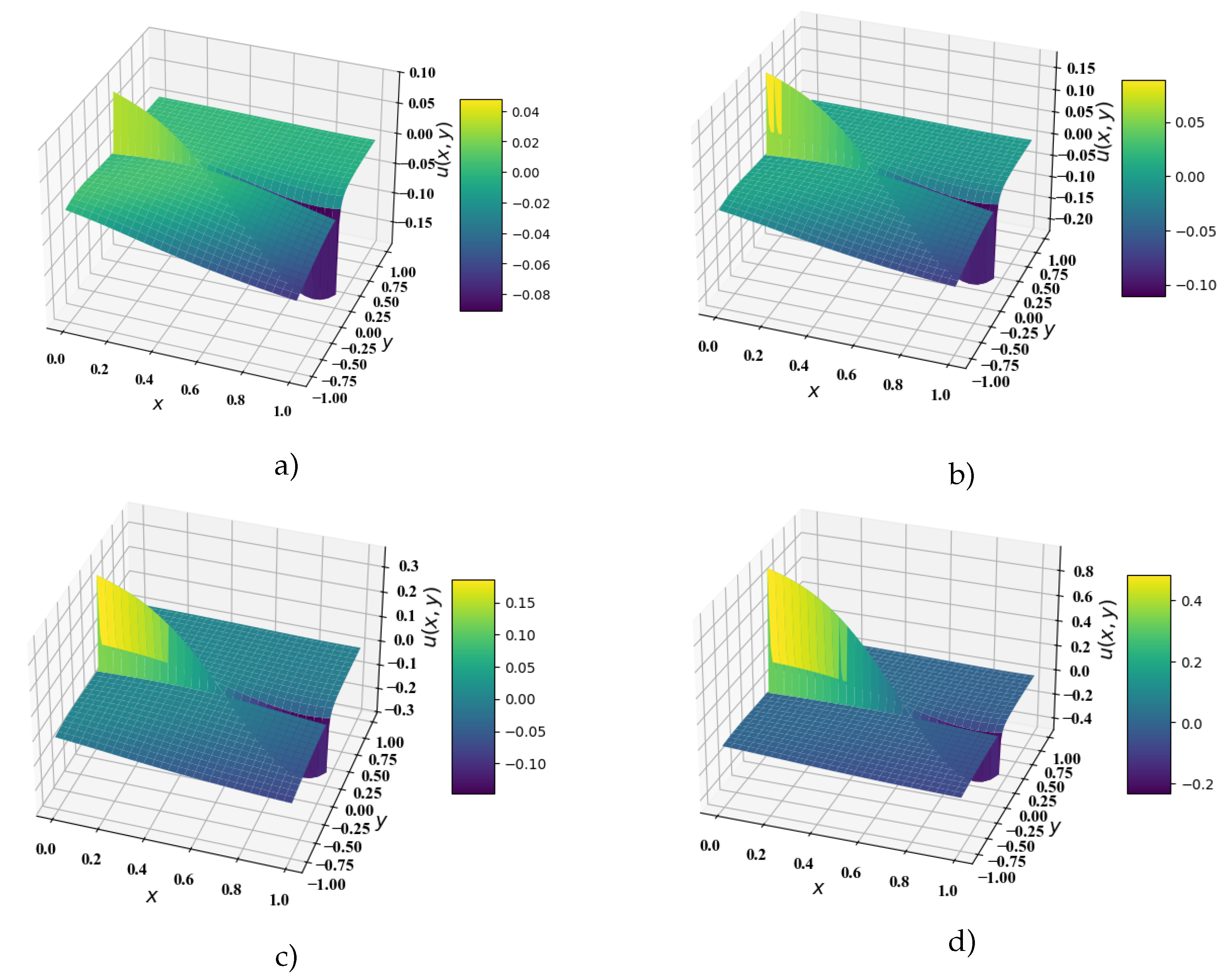
Let us present graphs of the solution $u\left(x,y\right)$ of Problem B using formulas (14) and (42) depending on the values of parameter $\gamma$.

In Figure 2 we can see that when changing the parameter $\gamma$ in domain $D^{+}$ the subdiffusion mode is enhanced due to the fact that the diffusion process proceeds more slowly than normal diffusion. We see that the region of positive values of the solution function $u(x,y)$ expands, and the region of negative values, on the contrary, narrows. In domain $D^{-}$ the wave mode proceeds, the shape of which is also affected by the values of parameter $\gamma$.

6. Discussion

The properties of solution of Equation (1) at $y<0$ essentially depend on coefficients ${\alpha }_0$ and ${\beta }_0$, at the lowest terms of Equation (1). If ${\beta }_0=1$, then the solution to Equation (1) on the parabolic degeneracy line has a logarithmic singularity. In this case boundary value problems for Equation (1) at $y<0$ are studied with different conditions.

7. Conclusions

In this work, we study a boundary value problems for differential equation with partial fractional derivative and degenerate hyperbolic equation. Main results are new. Using these results, we can explore various boundary value problems for differential equations with partial fractional derivative of the second and higher orders.

The paper provides an example of solving a non-local problem in a particular case, and plots the functions. It is shown that the order of the fractional derivative affects the intensity of diffusion, it slows down, which corresponds to subdiffusion. Also, the order of the fractional derivative affects the shape of the wave front.