Submitted:
22 July 2024
Posted:
24 July 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Combinatorial and Group Theoretical Techniques
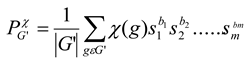
3. Results and Discussions
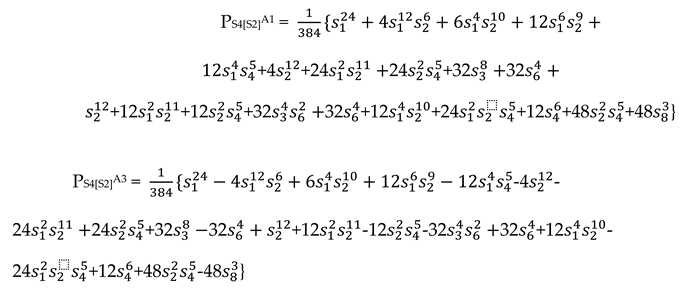
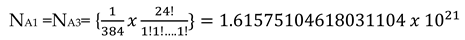
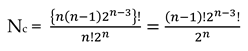
| Color Partition |
No of A1 Coloringsa |
No of A3 Coloringsa |
| 24 0 0 0 | 1 | 0 |
| 23 1 0 0 | 1 | 0 |
| 22 2 0 0 | 5 | 1 |
| 21 3 0 0 | 16 | 6 |
| 20 4 0 0 | 57 | 27 |
| 19 5 0 0 | 169 | 105 |
| 18 6 0 0 | 475 | 335 |
| 17 7 0 0 | 1099 | 866 |
| 16 8 0 0 | 2234 | 1849 |
| 15 9 0 0 | 3843 | 3307 |
| 14 10 0 0 | 5669 | 4967 |
| 13 11 0 0 | 7132 | 6336 |
| 12 12 0 0 | 7725 | 6871 |
| 22 1 1 0 | 5 | 1 |
| 21 2 1 0 | 32 | 13 |
| 20 3 1 0 | 158 | 97 |
| 19 4 1 0 | 688 | 503 |
| 18 5 1 0 | 2396 | 1973 |
| 17 6 1 0 | 6893 | 6025 |
| 16 7 1 0 | 16303 | 14810 |
| 15 8 1 0 | 32156 | 29818 |
| 14 9 1 0 | 53118 | 49918 |
| 13 10 1 0 | 74020 | 70054 |
| 12 11 1 0 | 87278 | 82892 |
| 20 2 2 0 | 244 | 145 |
| 19 3 2 0 | 1331 | 1021 |
| 18 4 2 0 | 5871 | 4986 |
| 17 5 2 0 | 20208 | 18285 |
| 16 6 2 0 | 56090 | 52312 |
| 15 7 2 0 | 126548 | 120340 |
| 14 8 2 0 | 235721 | 226411 |
| 13 9 2 0 | 365096 | 353006 |
| 12 10 2 0 | 473741 | 459377 |
| 11 11 2 0 | 516370 | 501374 |
| 18 3 3 0 | 7674 | 6682 |
| 17 4 3 0 | 33276 | 30591 |
| 16 5 3 0 | 110825 | 105097 |
| 15 6 3 0 | 292629 | 281871 |
| 14 7 3 0 | 623256 | 606096 |
| 13 8 3 0 | 1087220 | 1062760 |
| 12 9 3 0 | 1567505 | 1536897 |
| 11 10 3 0 | 1879494 | 1845178 |
| 16 4 4 0 | 138453 | 131493 |
| 15 5 4 0 | 437694 | 423510 |
| 14 6 4 0 | 1087993 | 1062443 |
| 13 7 4 0 | 2168246 | 2129446 |
| 12 8 4 0 | 3517231 | 3464261 |
| 11 9 4 0 | 4684708 | 4622058 |
| 10 10 4 0 | 5152084 | 5085022 |
| 14 5 5 0 | 1303756 | 1275752 |
| 13 6 5 0 | 3031508 | 2983480 |
| 12 7 5 0 | 5618270 | 5548102 |
| 11 8 5 0 | 8418614 | 8328046 |
| 10 9 5 0 | 10284396 | 10182022 |
| 12 6 6 0 | 6553122 | 6474210 |
| 11 7 6 0 | 11217872 | 11108824 |
| 10 8 6 0 | 15415306 | 15281078 |
| 9 9 6 0 | 17123720 | 16981820 |
| 10 7 7 0 | 17611556 | 17467588 |
| 9 8 7 0 | 22006070 | 21840340 |
| 8 8 8 0 | 24753462 | 24573093 |
| 21 1 1 1 | 51 | 22 |
| 20 2 1 1 | 425 | 281 |
| 19 3 1 1 | 2510 | 2015 |
| 18 4 1 1 | 11325 | 9945 |
| 17 5 1 1 | 39621 | 36528 |
| 16 6 1 1 | 110649 | 104649 |
| 15 7 1 1 | 250736 | 240748 |
| 14 8 1 1 | 467930 | 453070 |
| 13 9 1 1 | 725780 | 706350 |
| 12 10 1 1 | 942226 | 919270 |
| 11 11 1 1 | 1027332 | 1003242 |
| 19 2 2 1 | 3756 | 3061 |
| 18 3 2 1 | 22360 | 20105 |
| 17 4 2 1 | 98101 | 92141 |
| 16 5 2 1 | 329008 | 316265 |
| 15 6 2 1 | 871348 | 847760 |
| 14 7 2 1 | 1859676 | 1822056 |
| 13 8 2 1 | 3247280 | 3194050 |
| 12 9 2 1 | 4684626 | 4618066 |
| 11 10 2 1 | 5618508 | 5544042 |
| 17 3 3 1 | 130170 | 123075 |
| 16 4 3 1 | 546260 | 528355 |
| 15 5 3 1 | 1736268 | 1699440 |
| 14 6 3 1 | 4325880 | 4260540 |
| 13 7 3 1 | 8634420 | 8534760 |
| 12 8 3 1 | 14016130 | 13881320 |
| 11 9 3 1 | 18677240 | 18517190 |
| 10 10 3 1 | 20541952 | 20371606 |
| 15 4 4 1 | 2169038 | 2125858 |
| 14 5 4 1 | 6481828 | 6396668 |
| 13 6 4 1 | 15094180 | 14950100 |
| 12 7 4 1 | 28000166 | 27789946 |
| 11 8 4 1 | 41975340 | 41705670 |
| 10 9 4 1 | 51289438 | 50984818 |
| 13 5 5 1 | 18105486 | 17944878 |
| 12 6 5 1 | 39180892 | 38920964 |
| 11 7 5 1 | 67120260 | 66760032 |
| 10 8 5 1 | 92260524 | 91821066 |
| 9 9 5 1 | 102499670 | 102032840 |
| 11 6 6 1 | 78296512 | 77897372 |
| 10 7 6 1 | 122981972 | 122455864 |
| 9 8 6 1 | 153698290 | 153094910 |
| 9 7 7 1 | 175633880 | 174981580 |
| 8 8 7 1 | 197572890 | 196868820 |
| 18 2 2 2 | 33487 | 30322 |
| 17 3 2 2 | 194912 | 185257 |
| 16 4 2 2 | 818481 | 794136 |
| 15 5 2 2 | 2602172 | 2552704 |
| 14 6 2 2 | 6484766 | 6397066 |
| 13 7 2 2 | 12945012 | 12811992 |
| 12 8 2 2 | 21015167 | 20835247 |
| 11 9 2 2 | 28004836 | 27791786 |
| 10 10 2 2 | 30801270 | 30574296 |
| 16 3 3 2 | 1088655 | 1059945 |
| 15 4 3 2 | 4328656 | 4259696 |
| 14 5 3 2 | 12944976 | 12809676 |
| 13 6 3 2 | 30156640 | 29928140 |
| 12 7 3 2 | 55953912 | 55621272 |
| 11 8 3 2 | 83891030 | 83464690 |
| 10 9 3 2 | 102511416 | 102030166 |
| 14 4 4 2 | 16176465 | 16017675 |
| 13 5 4 2 | 45209956 | 44913056 |
| 12 6 4 2 | 97864801 | 97385171 |
| 11 7 4 2 | 167678736 | 167016576 |
| 10 8 4 2 | 230502306 | 229694856 |
| 9 9 4 2 | 256090630 | 255234030 |
| 12 5 5 2 | 117411604 | 116879096 |
| 11 6 5 2 | 234687752 | 233871724 |
| 10 7 5 2 | 368679660 | 367606632 |
| 9 8 5 2 | 460789280 | 459559450 |
| 10 6 6 2 | 430095214 | 428905586 |
| 9 7 6 2 | 614294660 | 612823960 |
| 8 8 6 2 | 691047030 | 689459130 |
| 8 7 7 2 | 789709860 | 787996500 |
| 15 3 3 3 | 5765010 | 5682726 |
| 14 4 3 3 | 21553380 | 21364620 |
| 13 5 3 3 | 60252960 | 59898540 |
| 12 6 3 3 | 130442733 | 129871167 |
| 11 7 3 3 | 223512780 | 222722100 |
| 10 8 3 3 | 307264170 | 306301230 |
| 9 9 3 3 | 341378584 | 340355686 |
| 13 4 4 3 | 75302150 | 74889430 |
| 12 5 4 3 | 195601766 | 194861566 |
| 11 6 4 3 | 391016740 | 389884220 |
| 10 7 4 3 | 614296776 | 612807816 |
| 9 8 4 3 | 767787880 | 766082150 |
| 11 5 5 3 | 469162776 | 467900988 |
| 10 6 5 3 | 859878528 | 858043860 |
| 9 7 5 3 | 1228207740 | 1225936680 |
| 8 8 5 3 | 1381679430 | 1379231310 |
| 9 6 6 3 | 1432840398 | 1430330262 |
| 8 7 6 3 | 1842059400 | 1839135600 |
| 7 7 7 3 | 2105109000 | 2101948920 |
| 12 4 4 4 | 244472700 | 243610770 |
| 11 5 4 4 | 586400958 | 584936118 |
| 10 6 4 4 | 1074771633 | 1072641603 |
| 9 7 4 4 | 1535163270 | 1532530170 |
| 8 8 4 4 | 1726995915 | 1724156055 |
| 10 5 5 4 | 1289616636 | 1287246912 |
| 9 6 5 4 | 2148984460 | 2145744020 |
| 8 7 5 4 | 2762767590 | 2758994670 |
| 8 6 6 4 | 3223114485 | 3218943735 |
| 7 7 6 4 | 3683411640 | 3678907800 |
| 9 5 5 5 | 2578619766 | 2575009806 |
| 8 6 5 5 | 3867527364 | 3862884864 |
| 7 7 5 5 | 4419870336 | 4414853016 |
| 7 6 6 5 | 5156360952 | 5150820912 |
| 6 6 6 6 | 6015584844 | 6009464868 |
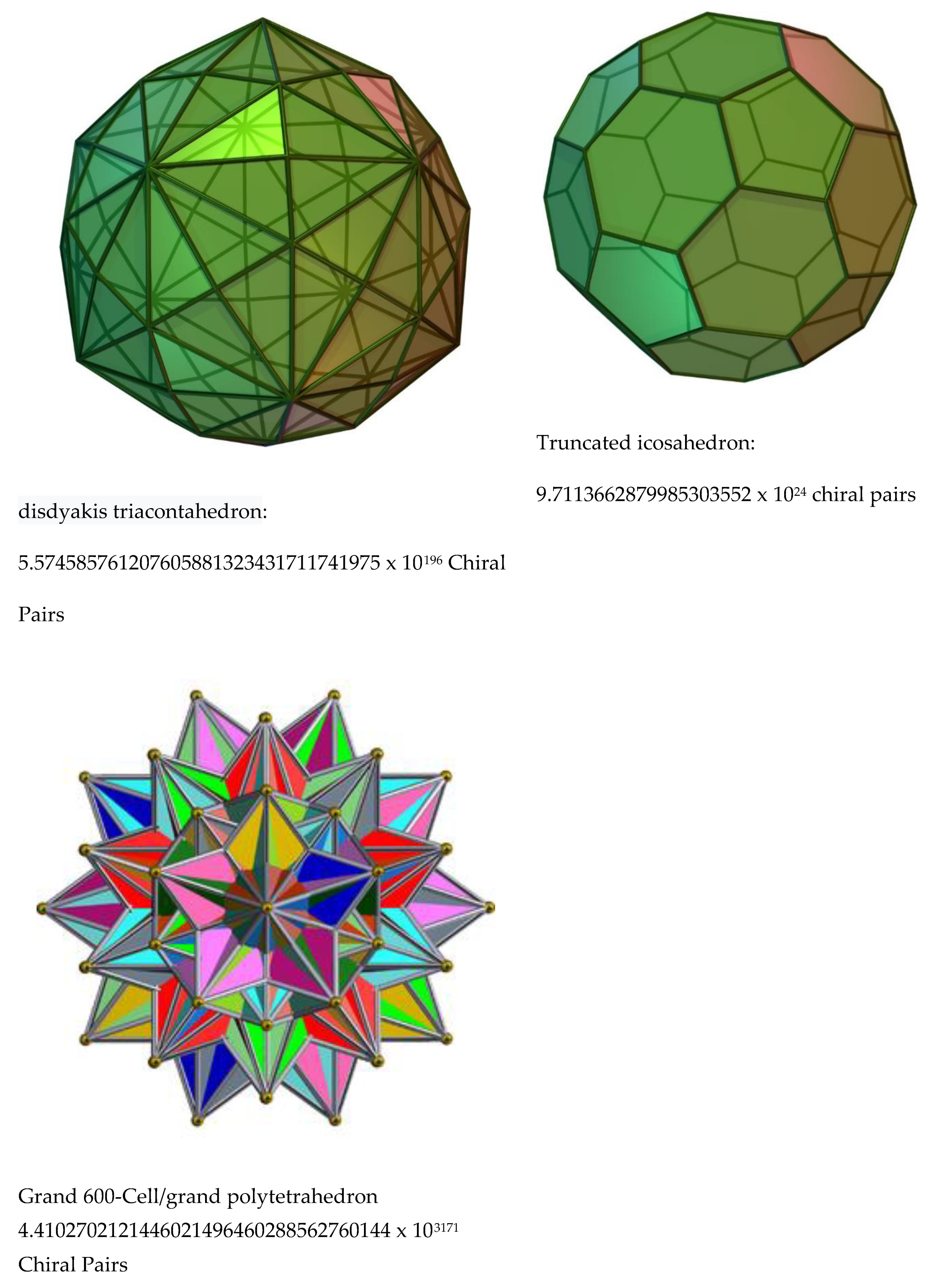
4.4102702121446021496460288562760144 x 103171
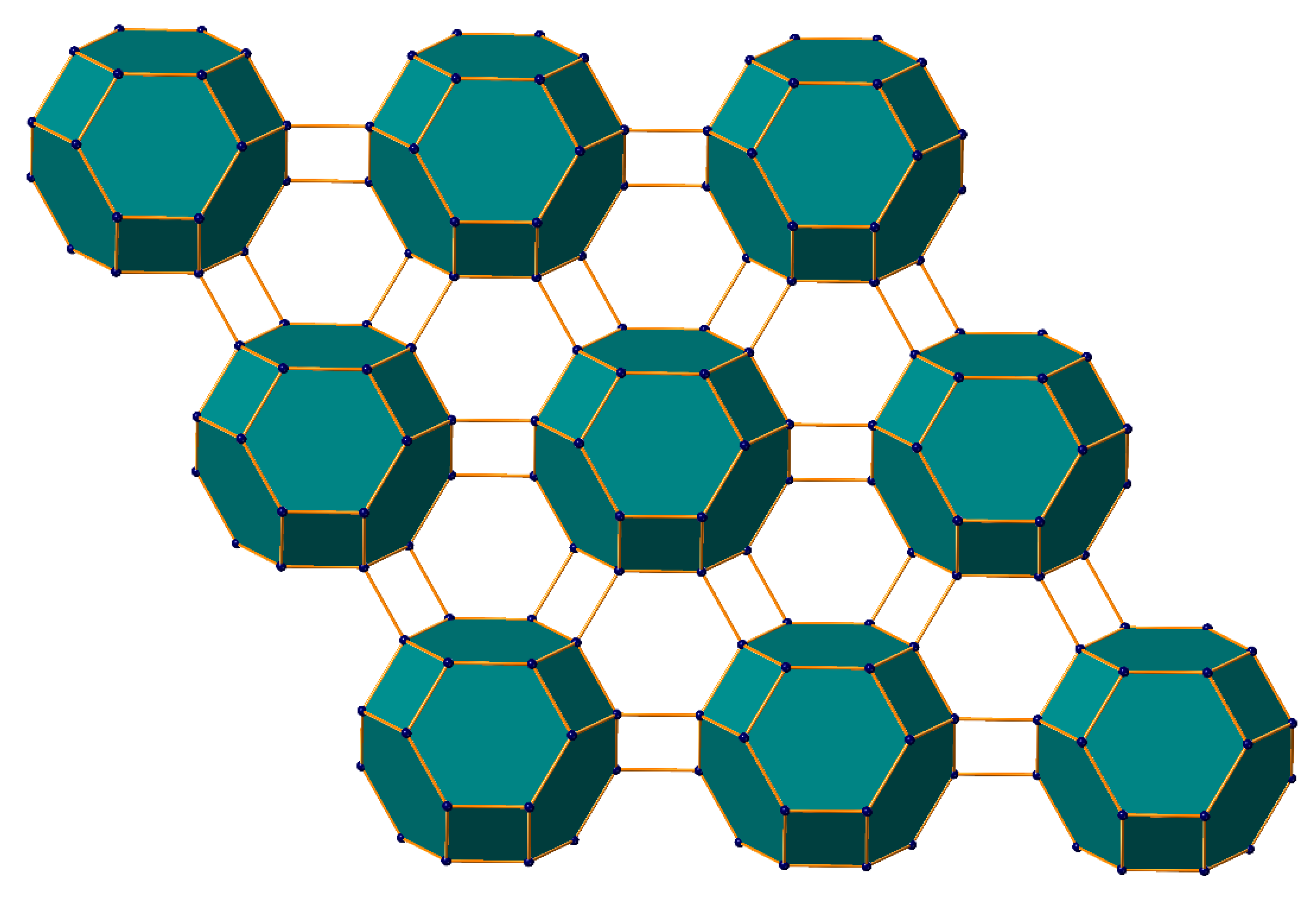
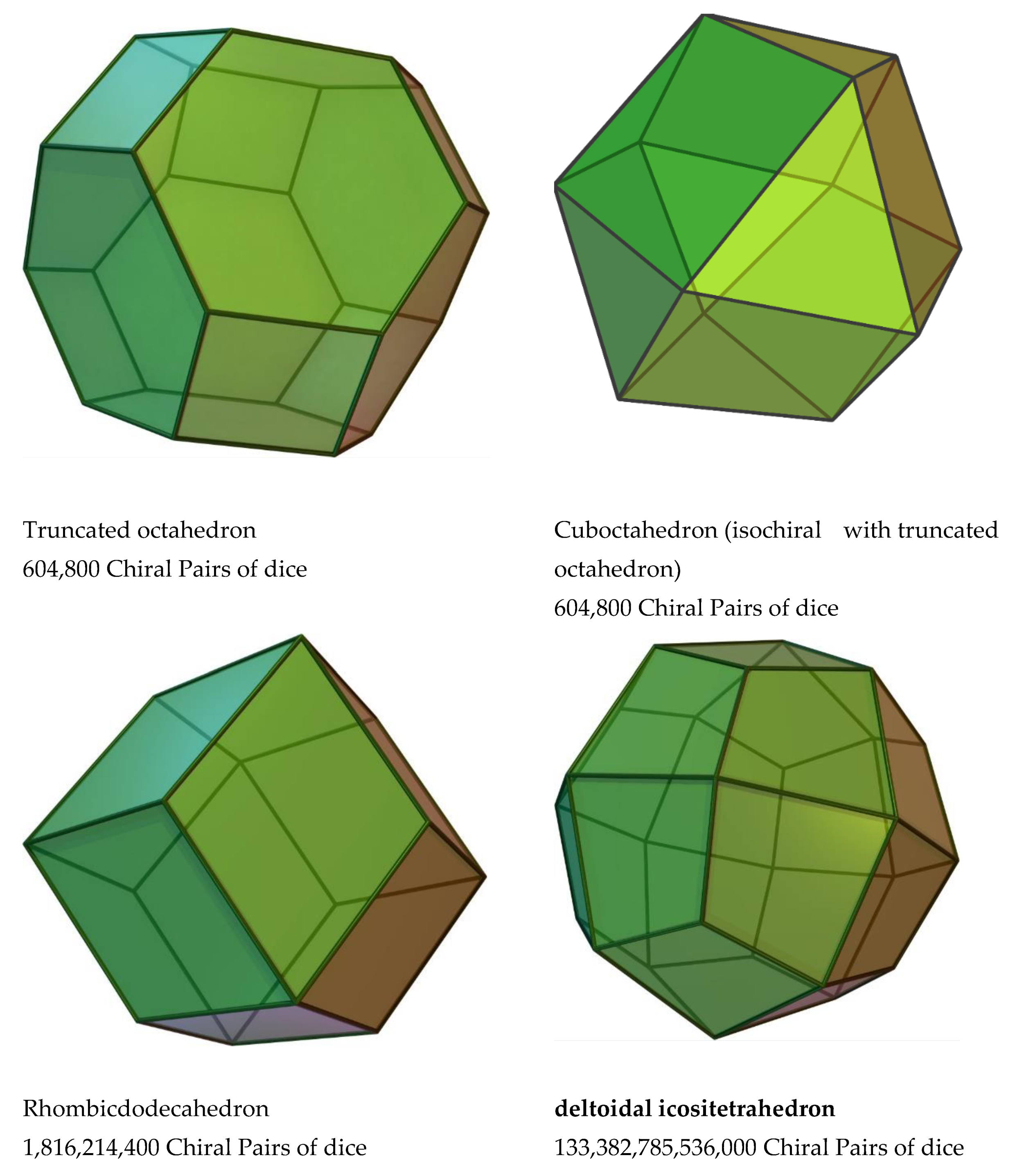
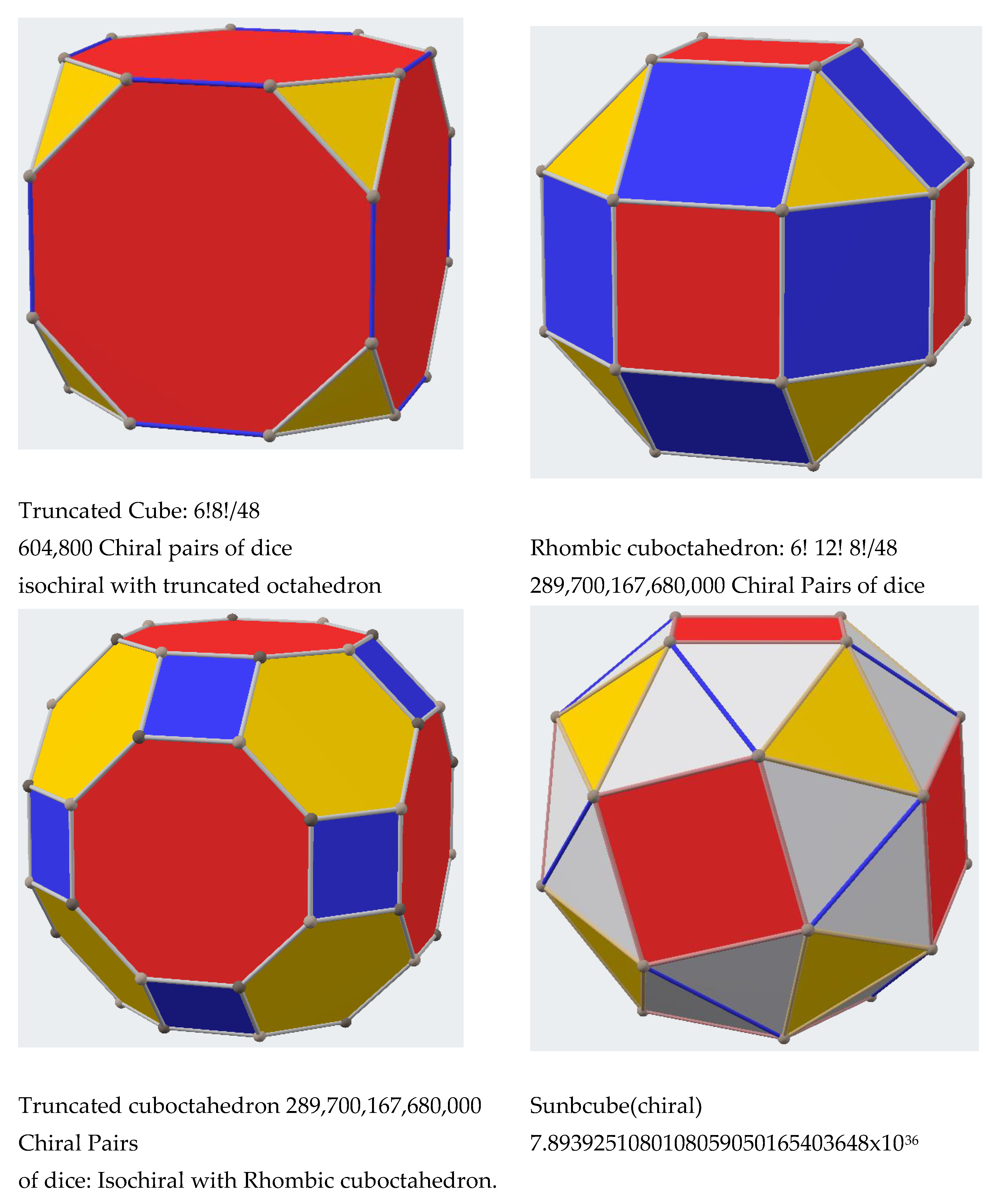
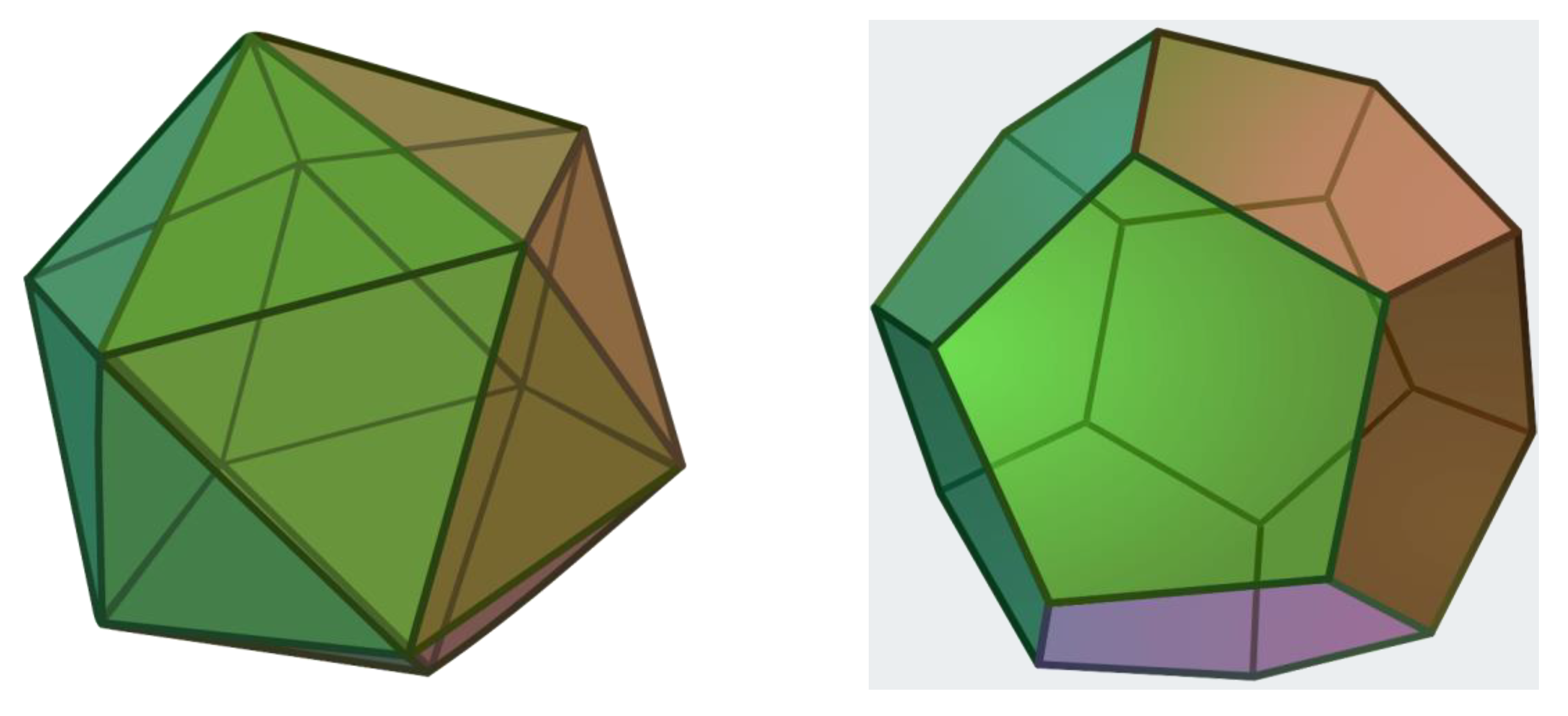
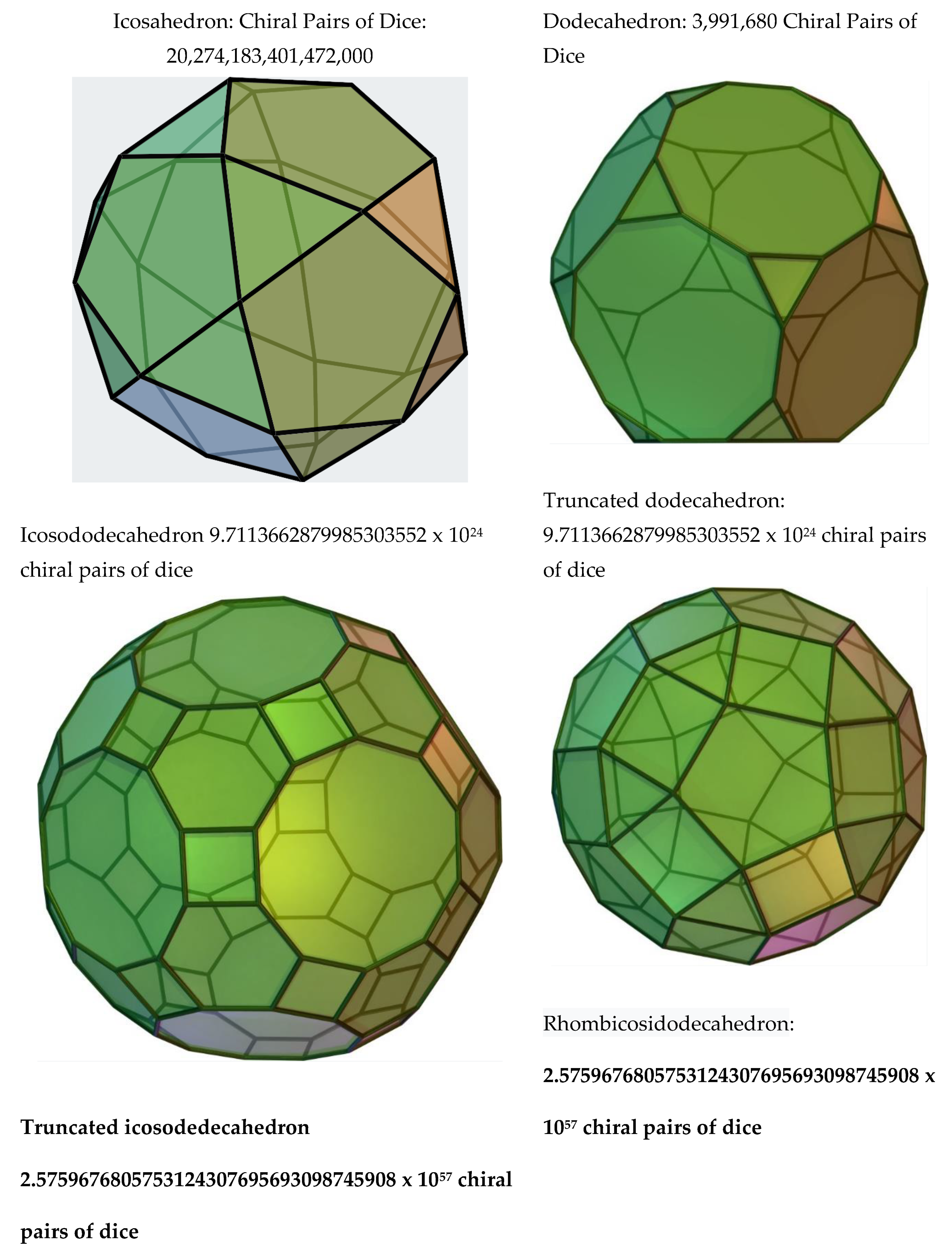
4. Applications: Chirality, Zeolites, mesoporous, nanomaterials and Biological Networks
5. Applications to Cryptography.
 in Wingding font. Note that with the increasing importance of artificial intelligence in the coming years, it is very clear that algorithms with machine learning and AI techniques can be developed to decrypt the messages sent through even such complex pockets of objects, for example, a grand cell-600. Indeed n-dimensional hypercubes and other combinatorially complex shapes considered here provide very compelling objects to generate packets of encrypted messages with face or edge or cell or tesseract or other complex p-dimensional hyperplanes for complex encryption that cannot be easily decrypted without invoking very complex AI algorithms that can unravel puzzles in n-dimensional spaces. Consequently, the present investigation on combinatorics of dice of various shapes in n dimensions indeed opens up such a plethora of applications in cryptography with potentials for defense and other applications.
in Wingding font. Note that with the increasing importance of artificial intelligence in the coming years, it is very clear that algorithms with machine learning and AI techniques can be developed to decrypt the messages sent through even such complex pockets of objects, for example, a grand cell-600. Indeed n-dimensional hypercubes and other combinatorially complex shapes considered here provide very compelling objects to generate packets of encrypted messages with face or edge or cell or tesseract or other complex p-dimensional hyperplanes for complex encryption that cannot be easily decrypted without invoking very complex AI algorithms that can unravel puzzles in n-dimensional spaces. Consequently, the present investigation on combinatorics of dice of various shapes in n dimensions indeed opens up such a plethora of applications in cryptography with potentials for defense and other applications.6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Balasubramanian, K. Recursive Symmetries: Chemically Induced Combinatorics of Colorings of Hyperplanes of an 8-Cube for All Irreducible Representations. Symmetry 2023, 15, 1031. [CrossRef]
- Balasubramanian K. Topological Indices, Graph Spectra, Entropies, Laplacians, and Matching Polynomials of n-Dimensional Hypercubes. Symmetry. 2023; 15(2):557. [CrossRef]
- Balasubramanian, K. Symmetry, Combinatorics, Artificial Intelligence, Music and Spectroscopy. Symmetry 2021, 13, 1850. [CrossRef]
- Carbó-Dorca, R. Boolean hypercubes and the Structure of Vector Spaces, J. Math. Sci. & Model. 2018,1,1-14.
- Carbó-Dorca, R. N-Dimensional Boolean hypercubes and the Goldbach conjecture, J Math Chem. 2016, 54, 1213-1220. [CrossRef]
- Carbó-Dorca, R. DNA unnatural base pairs and hypercubes, J Math Chem. 2018, 56, 1353-1536. [CrossRef]
- Carbó-Dorca, R.; Chakraborty, T. Quantum similarity description of a unique classical and quantum QSPR algorithm in molecular spaces: the connection with Boolean hypercubes, algorithmic intelligence, and Gödel's incompleteness theorems. In Chemical Reactivity 2023, (pp. 505-572), Elsevier.
- Carbó-Dorca, R. Boolean Hypercubes as time representation holders, J Math Chem. 55(2018) 1349-1352. [CrossRef]
- Carbó-Dorca, R.; Chakraborty, T. Divagations about the periodic table: Boolean hypercube and quantum similarity connections. J. Comput. Chem. 2019, 40(30), 2653-2663.
- Kaatz, F.H.; Bultheel, A. Dimensionality of hypercube clusters. J. Math Chem. 2016, 54, 33–43.
- Gowen, A. A.; O’Donnella , C. P.; Cullenb , P. J.; Bell, S. J. Recent applications of chemical imaging to pharmaceutical process monitoring and quality control. European J. Pharmaceutics and Biopharmaceutics, 2008, 69, 10-22.
- Mezey, P. G. Similarity Analysis in two and three dimensions using lattice animals and ploycubes, J. Math. Chem. 1992, 11,27-45.
- Fralov, A.; Jako, E.; Mezey, P. G. Logical Models for Molecular Shapes and Families, J Math Chem. 2001, 30, 389-409.
- Mezey, P. G. Some Dimension Problems in Molecular Databases, J. Math. Chem. 2009, 45, 1.
- Mezey, P. G. Shape Similarity measures for Molecular Bodies: A Three-dimensional Topological Approach in Quantitative Shape-activity Relation, J. Chem. Inf. Comput. Sci. 1992, 32, 650.
- Balasubramanian, K. Combinatorial Multinomial Generators for colorings of 4D-hypercubes and their applications, J. Math. Chem. 2018, 56, 2707-2723.
- Balasubramanian, K. Nonrigid group theory, tunneling splittings, and nuclear spin statistics of water pentamer:(H2O)5." J. Phys. Chem. A 2004,108, 5527-5536.
- Balasubramanian, K. Group-Theory and Nuclear-Spin Statistics of Weakly-Bound (H2O)N, (NH3)N, (CH4)N, and NH4+(NH3)N. J. Chem. Phys. 1991, 95, 8273-8286.
- Clifford, W. K. On the types of compound statement involving four classes, Proc Manchester Literary and Philosophical Soc., 1877, 88-101,.
- Clifford, W. K., Mathematical Papers. Editor: R. Tucker, R.McMillan & Co, London, 1882, Introduction by H. J. Stephen Smith, Reprinted by Chelsea, NY 1968.
- M. A. Harrison and R.G. High, On the cycle index of a product of permutation group, J. Combin. Theory 4 (1968), 277-299.
- Pólya, G.; Read, R. C. Combinatorial Enumeration of Groups, Graphs and Chemical Compounds, Springer, New York 1987.
- Pólya, G. Sur les types des propositions composées, J. Symbolic Logic 1940, 5, 98-103.
- Banks, D. C.; Linton, S. A.; Stockmeyer, P. K. Counting Cases in Substitope Algorithms, IEEE Trans. Visualization & Computer Graphics, 2004, 371-384.
- Bhaniramka, P.; Wenger, R.; Crawfis, R. Isosurfacing in higher Dimension. Proc. of IEEE Visualization 2000, pp.267-270.
- Aichholzer, O. Extremal Properties of 0/1-Polytopes of Dimension 5. Polytopes - Combinatorics and Computation,. Editors: Ziegler, G. & Kalai, G. Birkhäuser, 2000, pp.11-130.
- Perez-Aguila, R. Enumerating the Configurations in the n-Dimensional Polytopes through Pólya’s counting and A Concise Representation, in, 2006, Third International Conference on Electrical and Electronics Engineering, pp1-4, IEEE.
- Banks, D. C.; Stockmeyer, P. K. De Bruijn Counting for visualization Algorithms, Math Found. Sci. Visualization, computer graphics and Massive data exploration, Springer, Berlin 2009, pp 69-88.
- Perez-Aguila, R. Towards a New Approach for volume datasets based on orthogonal polytopes in four-dimensional color space, Engineering Letters 2010, 18:4,326, EL_18_4_02.
- Chen, W. Y. C.; Guo, P. L. Equivalence Classes of Full-Dimensional 0/1-Polytopes with Many Vertices, Jan 2011, https://arxiv.org/pdf/1101.0410.pdf.
- Chen, W. Y. C. Induced cycle structures of the hyperoctahedral group, SIAM J. Disc. Math. 1993, 6, 353-362.
- Ziegler, G. M. Lectures on Polytopes. Graduate Texts in Mathematics, 52, Springer-Verlag, 1994.
- Lemmis, P. W. H. Pólya Theory of hypercubes Geometriae Dedicata 1997, 64,145–15.
- Harary, F.; Palmer, E. M. Graphical Enumeration (Academic press, New York, NY, 1973).
- Liu, M.; Bassler, K. E. Finite size effects and symmetry breaking in the evolution of networks of competing Boolean nodes. J. Phys. A: Mathematical and Theoretical 2010, 44, 045101.
- . Reichhardt, C. J. O; Bassler, K. E. Canalization and symmetry in Boolean models for genetic regulatory networks. J. Phys. A:: Mathematical and Theoretical 40 (2007) 4339.
- Balasubramanian, K. Applications of Combinatorics and Graph Theory to Quantum Chemistry and Spectroscopy, Chem. Rev. 1985, 85,599-618.
- Balasubramanian, K. Symmetry Groups of Nonrigid Molecules as Generalized Wreath-Products and Their Representations, J. Chem. Phys. 1980, 72, 665-677.
- Balasubramanian, K Nonrigid water octamer: Computations with the 8-cube. J. Comput Chem. 2020, 41, 2469- 2484.
- Balasubramanian, K. Computations of Colorings 7D-Hypercube's Hyperplanes for All Irreducible Representations. J. Comput Chem. 2020, 41, 653-686.
- Balasubramanian, K. Relativistic double group spinor representations of nonrigid molecules. J. Chem. Phys. 2004, 120,5524-5535.
- Balasubramanian, K. Generalization of De Bruijn’s Extension of Pólya’s Theorem to all characters, J. Math. Chem. 1993, 14,113-120.
- Balasubramanian, K. Generalization of the Harary-Palmer Power Group Theorem to all Irreducible Representations, J. Math. Chem. 2014,52,703-728.
- Balasubramanian, K., Enumeration of Internal-Rotation Reactions and Their Reaction Graphs. Theor. Chim. Acta. 1979, 53, (2), 129-146.
- Wallace, R. Spontaneous symmetry breaking in a non-rigid molecule approach to intrinsically disordered proteins. Molecular BioSystems, 2012, 8(1), 374-377.
- Wallace, R. Tools for the Future: Hidden Symmetries. In Computational Psychiatry 2017, (pp. 153-165). Springer, Cham.
- Darafsheh, M. R. ; Farjami, Y.; Ashrafi, A. R. Computing the Full Non-Rigid Group of Tetranitrocubane and Octanitrocubane Using Wreath Product. MATCH Commun. Math. Comput. Chem 2005, 54,53.
- Foote, R.; Mirchandani, G.; Rockmore, D. A two-dimensional Wreath Product Transforms. J. Symbolic Computation 2004, 37, 187–207.
- Balasubramanian, K. A Generalized Wreath Product Method for the Enumeration of Stereo and Position Isomers of Polysubstituted Organic Compounds. Theor. Chim. Acta. 1979,51, 37 -51.
- Balasubramanian, K. Symmetry Simplifications of Space Types in Configuration-Interaction Induced by Orbital Degeneracy, Int. J. Quantum Chem. 1981, 20,1255-1271.
- Balasubramanian, K.Nested wreath groups and their applications to phylogeny in biology and Cayley trees in chemistry and physics. J. Math. Chem. 2017, 55, 195-222.
- Nandini, G.K.; Rajan, R.S.; Shantrinal, A.A.; Rajalaxmi, T.M.; Rajasingh, I.; Balasubramanian, K. Topological and Thermodynamic Entropy Measures for COVID-19 Pandemic through Graph Theory. Symmetry 2020, 12, 1992. [CrossRef]
- Rousseau, R. On Certain Subgroups of a Wreath Product”, Match. 1982, 13, 3-6.
- Florek, W.; Lulek, T.; Mucha, M. Hyperoctahedral groups, wreath products, and a general Weyl's recipe. Zeitschrift für Kristallographie-Crystalline Materials, 1988, 184, 31-48.
- Balasubramanian, K. Generators of the Character Tables of Generalized Wreath Product Groups. Theor. Chim. Acta.. 1990, 78,31-43.
- Liu, X. Y.; Balasubramanian, K. Computer Generation of Character Tables of Generalized Wreath Product Groups J. Comput. Chem. 1990, 11, 589-602.
- Balasubramanian, K. A Method for Nuclear-Spin Statistics in Molecular Spectroscopy. J. Chem. Phys. 1981, 74,6824-6829.
- Balasubramanian, K. Operator and algebraic methods for NMR spectroscopy. I. Generation of NMR spin species. J. Chem. Phys. 1983, 78, 6358-6368.
- Coxeter, H. S. M. Regular Polytopes, Dover Publications, New York, 1973.
- T. Ruen, By self - Own work, free public domain work available to anyone to use for any purpose. https://commons.wikimedia.org/w/index.php?curid=11743942.
- Bandelow, C. Inside Rubik’s cube and beyond. 2012, Springer Science & Business Media.
- User: Imk3nnyma, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=79057596.
- Buck, D. K.; Collins, A. A., POV-RAY, https://en.wikipedia.org/wiki/User:Cyp/Poly.pov https://en.wikipedia.org/wiki/User:Cyp/Poly.povPublic Domain, CC BY-SA 3.0.
- Jacob,K.; Clement,J.; Micheal Arockiaraj,M.; Peter, P.; Balasubramanian, K. Distance-based topology and entropy analysis of tetragonal farneseite zeolites, Submitted for Publication, 2024.
- Balasubramanian, K. Double group of the icosahedral group (Ih) and its application to fullerenes. Chem. Phys. Lett. 1996, 260, (3-4), 476-484.
- Kroto, H. W., Heath, J. R.; O'Brien, S. C.; Curl, R. F.; Smalley, R. E. C60:Buckminsterfullerene. Nature 1985, 318, 162-163.
- Kroto, H. W., Heath, J. R.; O'Brien, S. C.; Curl, R. F.; Smalley, R. E. Long Carbon Chain Molecules in Circumstellar Shells, Astrophys. J. 1987, 314, 352–355.
- Balasubramanian, K.; Liu, X. Y. Spectra and Characteristic Polynomials of Polyhedral Clusters. Int. J. Quantum Chem. 1988, 22, (S), 319-328.

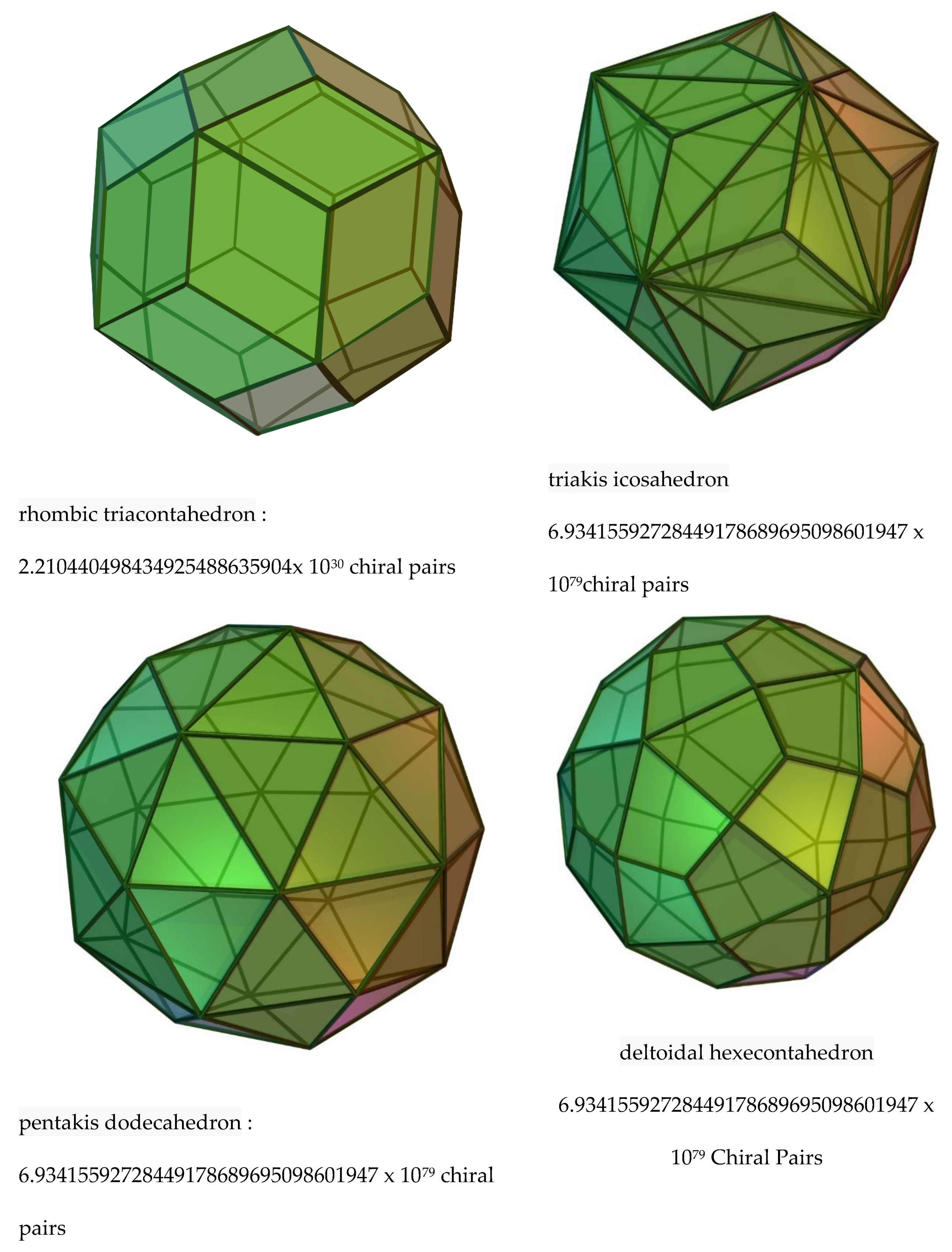
| n | Faces | No of dice | No of Chiral Pairs of dice |
| 3 | 6 | 30 | 15 |
| 4 | 24 | 3.23150209236062208 x 1021 | 1.61575104618031104 x 1021 |
| 5 | 80 | 3.7275758878262397028547673814159646 x 10115 | 1.8637879439131198514273836907079823 x 10115 |
| 6 | 240 | 1.7655752446384800870197812159231254 x 10464 | 8.827876223192400435098906079615627 x 10463 |
| 7 | 672 | 2.8214838544319294796427515741969896 x 101604 | 1.4107419272159647398213757870984948 x 101604 |
| nb | N(A1) |
| 0 | 1 |
| 1 | 1 |
| 2 | 11 |
| 3 | 139 |
| 4 | 4176 |
| 5 | 152635 |
| 6 | 5580266 |
| 7 | 182586993 |
| 8 | 5283117184 |
| 9 | 135891832431 |
| 10 | 3136801139463 |
| 11 | 65570741043751 |
| 12 | 1251192201334018 |
| 13 | 21943233858075034 |
| 14 | 355789263949855043 |
| 15 | 5360531557936453701 |
| 16 | 75382327861202736302 |
| 17 | 993272251366379046339 |
| 18 | 12305535660981459650639 |
| 19 | 143780450498062303705832 |
| 20 | 1588773890867771345864514 |
| 21 | 16644297515678879808798297 |
| 22 | 165686414507591622101552686 |
| 23 | 1570419052306115065132618723 |
| 24 | 14199205570066871577428871140 |
| 25 | 122681136017010754158309432703 |
| 26 | 1014478624347489084027884140426 |
| 27 | 8040682428518284564435181330429 |
| 28 | 61166619897340434689394786752894 |
| 29 | 447149083369066948751292268832796 |
| 30 | 3144948552967196406093283337735784 |
| 31 | 21304490197316629654279247580024508 |
| 32 | 139144951600574592746649080159671056 |
| 33 | 877034846450078628652128896100267264 |
| 34 | 5339594506322238375552079147434465280 |
| 35 | 31427327665763904958336467271605932032 |
| 36 | 178961171429990835258310915317808332800 |
| 37 | 986704837073310196335657862006172680192 |
| 38 | 5271081103312257287838648872443980546048 |
| 39 | 27301496996641809668910837171761665015808 |
| 40 | 137190022408121978237796878411228575170560 |
| 41 | 669219621503025866250112350741134231732224 |
| 42 | 3170826301883363428193286508672704248283136 |
| 43 | 14600549017974504078101835470726548970012672 |
| 44 | 65370639921385716211126737122035700519141376 |
| 45 | 284725453879813021523275240995846178515976192 |
| 46 | 1206988337099206608564703950062943154911313920 |
| 47 | 4982036965898851012606659737835556794489896960 |
| 48 | 20031940300384959298052361807805291335079952384 |
| 49 | 78492500768855341303876241965943810733935427584 |
| 50 | 299841352937027382765902773445578163675698561024 |
| 51 | 1117056020745788242590376169881100544777740353536 |
| 52 | 4060068998479884089705015623755515419238105874432 |
| 53 | 14401754183287135804246166953385408335748576313344 |
| 54 | 49872741338420266137322529195039577022891227611136 |
| 55 | 168660543435384899112410284701246690287995790032896 |
| 56 | 557182152420467968422421922547752056414106468483072 |
| 57 | 1798623088515194841712775021084035912510703835021312 |
| 58 | 5674965951694494062205410635512839112833661296181248 |
| 59 | 17505827173023693533563297554260934909613741294223360 |
| 60 | 52809245305288142132272869107153182169520534320054272 |
| 61 | 155830559917243698043653761141737793516691944388952064 |
| 62 | 449897906857848741029976049141268839915375321375834112 |
| 63 | 1271140117788842474479687792473475435071770769766744064 |
| 64 | 3515496888259767468163216556014840184143394537746726912 |
| 65 | 9518883882057216528608998367914143748380503439084355584 |
| 66 | 25239464838788074127879708050806830413286976339971145728 |
| 67 | 65547266894763058181097740456058221177846743153120378880 |
| 68 | 166759958423441309781250299599634334821117425640231927808 |
| 69 | 415691490562781235971341064888171821804599513259251335168 |
| 70 | 1015474926946222733578581339228367257143428701318056771584 |
| 71 | 2431418839167012178976836276667886688093053146703593472000 |
| 72 | 5707080330822570253408677742000332960960832242019794419712 |
| 73 | 13134102679153312363971846877730573818996158520436289699840 |
| 74 | 29640474965116258983498939796906579169557606545381706956800 |
| 75 | 65604251256123986550051347634863006077799034966669772455936 |
| 76 | 142430282332374444483519754796895120849199732824551463059456 |
| 77 | 303358003928693622016625857618977262242204533973550601601024 |
| 78 | 633940444107398210111331355025827016639517714599813255790592 |
| 79 | 1299979138549348228329063291451252319874543714414110345003008 |
| 80 | 2616208016330563309511496917583731993831663122674685994598400 |
| 81 | 5167818303862841105206809240136218974660614845481150429790208 |
| 82 | 10020525735538923606436025159797456261476584970542687191040000 |
| 83 | 19075217665242770238755496178613251023787049655038318777204736 |
| 84 | 35652490160037082470051758173077553030081498177735400332722176 |
| 85 | 65432805470185704297972943306063050464253178396461240116314112 |
| 86 | 117931219161381211234712613738006405558219054813035950984134656 |
| 87 | 208751813228192029082126716097532138898293814638576077423771648 |
| 88 | 362943493453561141472322840478800602327652562685480290771533824 |
| 89 | 619858550617317904536986031056340852095924421733185407357550592 |
| 90 | 1039984901591277817612034918976099698126465664356715106718973952 |
| 91 | 1714260826798809589470361996501267583138843705609748724712472576 |
| 92 | 2776357208619811182946532139254981696976848855712642666273439744 |
| 93 | 4418288891136903818022397130640910763680489058711583357765943296 |
| 94 | 6909451776565158098396675870686568083843531086171523326916165632 |
| 95 | 10618736414510664024904301130552081477721498205603021838987821056 |
| 96 | 16038716459417148787615793261697627570544461777441421000234237952 |
| 97 | 23810053300578035313573866471631103862233086767820943288313053184 |
| 98 | 34743241040639378059602569562006314113107754712353068755277840384 |
| 99 | 49833739674452441257207592441071504972429917631360631482888486912 |
| 100 | 70265572940977942172662549542368590308742746503025565569864695808 |
| 101 | 97397823878583286179928107075659666820641201605644990708709326848 |
| 102 | 132728407050226242931470451731079405476392486433062572665908232192 |
| 103 | 177830292941079820626630085054867470806112050016763218951307001856 |
| 104 | 234257212816614763710079762418248667308011746087552551552313982976 |
| 105 | 303418866124377217757817320211010493225990120075604352544075153408 |
| 106 | 386429687988593626389672704093941308509024324478124575046739427328 |
| 107 | 483939983088519120899215967419979205493870806825180030389467480064 |
| 108 | 595963127321972621107367481426572082532281766779222667980204670976 |
| 109 | 721716814738535651249288720668083207973311214195686476972126371840 |
| 110 | 859499115734074275578698042830041010298057135266173370496370868224 |
| 111 | 1006620585994861764191267638613753417255640297161311448121542180864 |
| 112 | 1159411210654796139113156147343784043908458958128856461986303574016 |
| 113 | 1313315353662069962889238509921566661821965008467180176968339423232 |
| 114 | 1463079385220025309534502263293078969347233893342480581579761516544 |
| 115 | 1603026109023679904359541354461619193561740429737992388679403831296 |
| 116 | 1727398824378965414180540034621696361312587920268799182661767659520 |
| 117 | 1830747471991382148362281571140508950236269928271495714066772525056 |
| 118 | 1908321517414745798716615408358714803655391352966327587613939073024 |
| 119 | 1956430463231924264230479584872704778184154074936145924234846142464 |
| 120 | 1972734050425523633099066888879877060171554196485690791403223777280 |
| Hexagons | Pentagons | ||||
| Color Partition | Ag | Au | Color Partition | Ag | Au |
| 20 0 0 0 0 0 | 1 | 0 | 12 0 0 0 0 0 0 0 0 0 | 1 | 0 |
| 19 1 0 0 0 0 | 1 | 0 | 11 1 0 0 0 0 0 0 0 0 | 1 | 0 |
| 18 2 0 0 0 0 | 5 | 1 | 10 2 0 0 0 0 0 0 0 0 | 3 | 0 |
| 17 3 0 0 0 0 | 5 | 2 | 9 3 0 0 0 0 0 0 0 0 | 3 | 0 |
| 16 4 0 0 0 0 | 15 | 6 | 8 4 0 0 0 0 0 0 0 0 | 5 | 0 |
| 18 1 1 0 0 0 | 34 | 23 | 10 1 1 0 0 0 0 0 0 0 | 9 | 2 |
| 17 2 1 0 0 0 | 60 | 54 | 9 2 1 0 0 0 0 0 0 0 | 14 | 8 |
| 16 3 1 0 0 0 | 58 | 38 | 8 3 1 0 0 0 0 0 0 0 | 10 | 2 |
| 16 2 2 0 0 0 | 176 | 151 | 8 2 2 0 0 0 0 0 0 0 | 23 | 10 |
| 17 1 1 1 0 0 | 274 | 233 | 9 1 1 1 0 0 0 0 0 0 | 37 | 20 |
| 16 2 1 1 0 0 | 498 | 471 | 8 2 1 1 0 0 0 0 0 0 | 57 | 42 |
| 16 1 1 1 1 0 | 972 | 966 | 8 1 1 1 1 0 0 0 0 0 | 102 | 96 |
| 15 5 0 0 0 0 | 149 | 113 | 7 5 0 0 0 0 0 0 0 0 | 12 | 2 |
| 14 6 0 0 0 0 | 674 | 622 | 6 6 0 0 0 0 0 0 0 0 | 42 | 24 |
| 15 4 1 0 0 0 | 1337 | 1249 | 7 4 1 0 0 0 0 0 0 0 | 80 | 52 |
| 14 5 1 0 0 0 | 2610 | 2562 | 6 5 1 0 0 0 0 0 0 0 | 144 | 120 |
| 15 3 2 0 0 0 | 3928 | 3824 | 7 3 2 0 0 0 0 0 0 0 | 216 | 180 |
| 14 4 2 0 0 0 | 7776 | 7728 | 6 4 2 0 0 0 0 0 0 0 | 408 | 384 |
| 14 3 3 0 0 0 | 15504 | 15504 | 6 3 3 0 0 0 0 0 0 0 | 792 | 792 |
| 15 3 1 1 0 0 | 371 | 310 | 7 3 1 1 0 0 0 0 0 0 | 18 | 6 |
| 14 4 1 1 0 0 | 1984 | 1892 | 6 4 1 1 0 0 0 0 0 0 | 58 | 36 |
| 15 2 2 1 0 0 | 4984 | 4796 | 7 2 2 1 0 0 0 0 0 0 | 142 | 104 |
| 14 3 2 1 0 0 | 9744 | 9636 | 6 3 2 1 0 0 0 0 0 0 | 246 | 216 |
| 14 2 2 2 0 0 | 6557 | 6373 | 6 2 2 2 0 0 0 0 0 0 | 178 | 134 |
| 15 2 1 1 1 0 | 19480 | 19280 | 7 2 1 1 1 0 0 0 0 0 | 488 | 436 |
| 14 3 1 1 1 0 | 38784 | 38736 | 6 3 1 1 1 0 0 0 0 0 | 936 | 912 |
| 14 2 2 1 1 0 | 29352 | 28968 | 6 2 2 1 1 0 0 0 0 0 | 748 | 668 |
| 14 2 1 1 1 1 | 58248 | 58032 | 6 2 1 1 1 1 0 0 0 0 | 1416 | 1356 |
| 13 7 0 0 0 0 | 116304 | 116256 | 5 5 2 0 0 0 0 0 0 0 | 2784 | 2760 |
| 12 8 0 0 0 0 | 693 | 609 | 5 4 3 0 0 0 0 0 0 0 | 5544 | 5544 |
| 13 6 1 0 0 0 | 4597 | 4457 | 4 4 4 0 0 0 0 0 0 0 | 160 | 118 |
| 12 7 1 0 0 0 | 13720 | 13412 | 5 5 1 1 0 0 0 0 0 0 | 296 | 260 |
| 13 5 2 0 0 0 | 27216 | 27048 | 5 4 2 1 0 0 0 0 0 0 | 258 | 204 |
| 12 6 2 0 0 0 | 22802 | 22438 | 4 4 3 1 0 0 0 0 0 0 | 726 | 660 |
| 13 4 3 0 0 0 | 68040 | 67620 | 4 4 2 2 0 0 0 0 0 0 | 1404 | 1368 |
| 12 5 3 0 0 0 | 135744 | 135576 | 5 4 1 1 1 0 0 0 0 0 | 960 | 888 |
| 12 4 4 0 0 0 | 90618 | 90282 | 4 4 2 1 1 0 0 0 0 0 | 1440 | 1332 |
| 13 5 1 1 0 0 | 136024 | 135296 | 4 4 1 1 1 1 0 0 0 0 | 2808 | 2736 |
| 12 6 1 1 0 0 | 271488 | 271152 | 5 3 3 1 0 0 0 0 0 0 | 5544 | 5544 |
| 13 4 2 1 0 0 | 542640 | 542640 | 5 3 2 2 0 0 0 0 0 0 | 4224 | 4092 |
| 12 5 2 1 0 0 | 407400 | 406560 | 4 3 3 2 0 0 0 0 0 0 | 8352 | 8280 |
| 12 4 3 1 0 0 | 814128 | 813792 | 5 3 2 1 1 0 0 0 0 0 | 16632 | 16632 |
| 12 4 2 2 0 0 | 1135 | 1022 | 4 3 3 1 1 0 0 0 0 0 | 33264 | 33264 |
| 13 4 1 1 1 0 | 8501 | 8305 | 5 2 2 2 1 0 0 0 0 0 | 330 | 270 |
| 12 5 1 1 1 0 | 29739 | 29262 | 4 3 2 2 1 0 0 0 0 0 | 1194 | 1116 |
| 12 4 2 1 1 0 | 58917 | 58665 | 4 2 2 2 2 0 0 0 0 0 | 1818 | 1692 |
| 12 4 1 1 1 1 | 59085 | 58497 | 5 2 2 1 1 1 0 0 0 0 | 3510 | 3420 |
| 11 9 0 0 0 0 | 176680 | 176036 | 4 3 2 1 1 1 0 0 0 0 | 6948 | 6912 |
| 10 10 0 0 0 0 | 352800 | 352632 | 4 2 2 2 1 1 0 0 0 0 | 2376 | 2244 |
| 11 8 1 0 0 0 | 74014 | 73286 | 4 2 2 1 1 1 1 0 0 0 | 4656 | 4584 |
| 10 9 1 0 0 0 | 294290 | 293590 | 3 3 3 3 0 0 0 0 0 0 | 7008 | 6852 |
| 11 7 2 0 0 0 | 441952 | 440468 | 3 3 3 2 1 0 0 0 0 0 | 13896 | 13824 |
| 10 8 2 0 0 0 | 882168 | 881412 | 3 3 2 2 2 0 0 0 0 0 | 27720 | 27720 |
| 11 6 3 0 0 0 | 1763664 | 1763496 | 3 3 2 2 1 1 0 0 0 0 | 10572 | 10308 |
| 10 7 3 0 0 0 | 588509 | 587221 | 3 2 2 2 2 1 0 0 0 0 | 20880 | 20700 |
| 10 6 4 0 0 0 | 1175898 | 1175562 | 2 2 2 2 2 2 0 0 0 0 | 41616 | 41544 |
| 11 7 1 1 0 0 | 1764280 | 1762880 | 3 2 2 2 1 1 1 0 0 0 | 83160 | 83160 |
| 10 8 1 1 0 0 | 3527328 | 3526992 | 2 2 2 2 2 1 1 0 0 0 | 166320 | 166320 |
| 11 6 2 1 0 0 | 2647512 | 2644488 | 2 2 2 2 1 1 1 1 0 0 | 3156 | 3012 |
| 10 7 2 1 0 0 | 5291496 | 5289984 | 2 2 2 2 2 2 0 0 0 0 | 9312 | 9168 |
| 10 6 3 1 0 0 | 1466 | 1340 | 3 3 3 1 1 1 0 0 0 0 | 18480 | 18480 |
| 10 6 2 2 0 0 | 12716 | 12478 | 3 3 2 2 2 0 0 0 0 0 | 13992 | 13728 |
| 11 6 1 1 1 0 | 50696 | 50080 | 3 3 2 2 1 1 0 0 0 0 | 27792 | 27648 |
| 10 7 1 1 1 0 | 100944 | 100608 | 3 3 2 1 1 1 1 0 0 0 | 55440 | 55440 |
| 10 6 2 1 1 0 | 118002 | 117162 | 3 3 1 1 1 1 1 1 0 0 | 110880 | 110880 |
| 10 6 1 1 1 1 | 353192 | 352240 | 3 2 2 2 2 1 0 0 0 0 | 41736 | 41424 |
| 9 9 2 0 0 0 | 705600 | 705264 | 3 2 2 2 1 1 1 0 0 0 | 83232 | 83088 |
| 9 8 3 0 0 0 | 176904 | 175812 | 3 2 2 1 1 1 1 1 0 0 | 166320 | 166320 |
| 8 8 4 0 0 0 | 705936 | 704928 | 3 2 1 1 1 1 1 1 1 0 | 332640 | 332640 |
| 9 9 1 1 0 0 | 1059240 | 1057056 | 3 1 1 1 1 1 1 1 1 1 | 665280 | 665280 |
| 9 8 2 1 0 0 | 2116800 | 2115792 | 2 2 2 2 2 2 0 0 0 0 | 62736 | 62184 |
| 8 8 3 1 0 0 | 4232592 | 4232592 | 2 2 2 2 2 1 1 0 0 0 | 124920 | 124560 |
| 8 8 2 2 0 0 | 882504 | 881076 | 2 2 2 2 1 1 1 1 0 0 | 249552 | 249408 |
| 9 8 1 1 1 0 | 1764840 | 1762320 | 2 2 2 1 1 1 1 1 1 0 | 498960 | 498960 |
| 8 8 2 1 1 0 | 3527664 | 3526656 | 2 2 1 1 1 1 1 1 1 1 | 997920 | 997920 |
| 8 8 1 1 1 1 | 5292168 | 5289312 | |||
| 13 3 3 1 0 0 | 10581984 | 10580976 | |||
| 13 3 2 2 0 0 | 2352468 | 2350452 | |||
| 12 3 3 2 0 0 | 7055328 | 7053312 | |||
| 13 3 2 1 1 0 | 14108640 | 14108640 | |||
| 12 3 3 1 1 0 | 10584000 | 10578960 | |||
| 13 2 2 2 1 0 | 21163968 | 21161952 | |||
| 12 3 2 2 1 0 | 31747296 | 31741584 | |||
| 12 2 2 2 2 0 | 1648 | 1510 | |||
| 13 2 2 1 1 1 | 15536 | 15270 | |||
| 12 3 2 1 1 1 | 69812 | 69070 | |||
| 12 2 2 2 1 1 | 138756 | 138378 | |||
| 11 5 4 0 0 0 | 185308 | 184244 | |||
| 10 5 5 0 0 0 | 554856 | 553680 | |||
| 11 5 3 1 0 0 | 1108704 | 1108368 | |||
| 11 4 4 1 0 0 | 324428 | 322888 | |||
| 10 5 4 1 0 0 | 1294012 | 1292612 | |||
| 11 5 2 2 0 0 | 1942136 | 1939000 | |||
| 11 4 3 2 0 0 | 3880632 | 3879120 | |||
| 10 5 3 2 0 0 | 7759920 | 7759584 | |||
| 10 4 4 2 0 0 | 388788 | 387192 | |||
| 10 4 3 3 0 0 | 1940904 | 1938972 | |||
| 11 5 2 1 1 0 | 3881640 | 3878112 | |||
| 11 4 3 1 1 0 | 7760256 | 7759248 | |||
| 10 5 3 1 1 0 | 11641560 | 11637696 | |||
| 10 4 4 1 1 0 | 23279760 | 23278752 | |||
| 11 4 2 2 1 0 | 4853184 | 4848396 | |||
| 10 5 2 2 1 0 | 9700824 | 9698556 | |||
| 10 4 3 2 1 0 | 6468432 | 6464568 | |||
| 10 4 2 2 2 0 | 19401480 | 19397280 | |||
| 11 4 2 1 1 1 | 38799264 | 38798256 | |||
| 10 5 2 1 1 1 | 29105832 | 29096088 | |||
| 10 4 3 1 1 1 | 58200408 | 58195872 | |||
| 10 4 2 2 1 1 | 25866888 | 25864872 | |||
| 9 7 4 0 0 0 | 38802624 | 38794896 | |||
| 9 6 5 0 0 0 | 77598528 | 77596512 | |||
| 8 7 5 0 0 0 | 116400480 | 116392080 | |||
| 8 6 6 0 0 0 | 174608112 | 174588288 | |||
| 9 7 3 1 0 0 | 77370 | 76600 | |||
| 9 6 4 1 0 0 | 154180 | 153760 | |||
| 8 7 4 1 0 0 | 231550 | 230360 | |||
| 8 6 5 1 0 0 | 693500 | 692170 | |||
| 9 7 2 2 0 0 | 1385880 | 1385460 | |||
| 9 6 3 2 0 0 | 462820 | 461000 | |||
| 8 7 3 2 0 0 | 1848420 | 1846740 | |||
| 8 6 4 2 0 0 | 2773160 | 2769520 | |||
| 8 6 3 3 0 0 | 5543520 | 5541840 | |||
| 9 7 2 1 1 0 | 11085360 | 11085360 | |||
| 9 6 3 1 1 0 | 647706 | 645606 | |||
| 8 7 3 1 1 0 | 3234580 | 3231920 | |||
| 8 6 4 1 1 0 | 6468850 | 6464090 | |||
| 9 6 2 2 1 0 | 12933780 | 12932100 | |||
| 8 7 2 2 1 0 | 19402040 | 19396720 | |||
| 8 6 3 2 1 0 | 38799600 | 38797920 | |||
| 8 6 2 2 2 0 | 3881136 | 3878616 | |||
| 9 6 2 1 1 1 | 9702840 | 9696540 | |||
| 8 7 2 1 1 1 | 19400640 | 19398120 | |||
| 8 6 3 1 1 1 | 12935460 | 12930420 | |||
| 8 6 2 2 1 1 | 38801280 | 38796240 | |||
| 9 5 5 1 0 0 | 77597520 | 77597520 | |||
| 9 5 4 2 0 0 | 58204440 | 58191840 | |||
| 8 5 5 2 0 0 | 116398800 | 116393760 | |||
| 9 4 4 3 0 0 | 16169760 | 16162620 | |||
| 8 5 4 3 0 0 | 48502440 | 48494460 | |||
| 8 4 4 4 0 0 | 96998160 | 96995640 | |||
| 9 5 4 1 1 0 | 64667160 | 64662120 | |||
| 8 5 5 1 1 0 | 97004040 | 96989760 | |||
| 9 4 4 2 1 0 | 193996320 | 193991280 | |||
| 8 5 4 2 1 0 | 290998680 | 290982720 | |||
| 8 4 4 3 1 0 | 129334260 | 129324180 | |||
| 8 4 4 2 2 0 | 258658440 | 258658440 | |||
| 9 4 4 1 1 1 | 387992640 | 387982560 | |||
| 8 5 4 1 1 1 | 581995680 | 581967120 | |||
| 8 4 4 2 1 1 | 521000 | 519040 | |||
| 7 7 6 0 0 0 | 2079380 | 2077630 | |||
| 7 7 5 1 0 0 | 3120540 | 3116550 | |||
| 7 6 6 1 0 0 | 6236460 | 6234570 | |||
| 7 7 4 2 0 0 | 12471240 | 12470820 | |||
| 7 6 5 2 0 0 | 832592 | 830212 | |||
| 6 6 6 2 0 0 | 4158480 | 4155540 | |||
| 7 6 4 3 0 0 | 8316680 | 8311360 | |||
| 6 6 5 3 0 0 | 16628880 | 16627200 | |||
| 6 6 4 4 0 0 | 24945000 | 24939120 | |||
| 7 7 4 1 1 0 | 49884960 | 49883280 | |||
| 7 6 5 1 1 0 | 971840 | 969178 | |||
| 6 6 6 1 1 0 | 5821424 | 5818204 | |||
| 7 6 4 2 1 0 | 14555240 | 14546980 | |||
| 6 6 5 2 1 0 | 29100960 | 29097180 | |||
| 6 6 4 3 1 0 | 19402630 | 19396190 | |||
| 6 6 4 2 2 0 | 58201640 | 58194640 | |||
| 7 6 4 1 1 1 | 116397120 | 116395440 | |||
| 6 6 5 1 1 1 | 87308760 | 87291960 | |||
| 6 6 4 2 1 1 | 174598200 | 174590640 | |||
| 11 3 3 3 0 0 | 17463432 | 17455452 | |||
| 11 3 3 2 1 0 | 34920144 | 34917624 | |||
| 10 3 3 3 1 0 | 29103480 | 29094660 | |||
| 11 3 2 2 2 0 | 87302040 | 87292380 | |||
| 10 3 3 2 2 0 | 174595680 | 174593160 | |||
| 11 3 2 2 1 1 | 116398800 | 116393760 | |||
| 10 3 3 2 1 1 | 174603240 | 174585600 | |||
| 11 2 2 2 2 1 | 349191360 | 349186320 | |||
| 10 3 2 2 2 1 | 523792920 | 523773600 | |||
| 10 2 2 2 2 2 | 36382500 | 36369900 | |||
| 9 5 3 3 0 0 | 145500600 | 145490100 | |||
| 9 5 3 2 1 0 | 218260560 | 218234940 | |||
| 9 4 3 3 1 0 | 436491720 | 436480380 | |||
| 8 5 3 3 1 0 | 291000360 | 290981040 | |||
| 9 5 2 2 2 0 | 581983920 | 581978880 | |||
| 9 4 3 2 2 0 | 872982600 | 872961600 | |||
| 8 5 3 2 2 0 | 1309493640 | 1309441560 | |||
| 8 4 3 3 2 0 | 387992700 | 387982620 | |||
| 9 5 2 2 1 1 | 1163967840 | 1163957760 | |||
| 9 4 3 2 1 1 | 1745963520 | 1745924880 | |||
| 8 5 3 2 1 1 | 1109966 | 1107166 | |||
| 8 4 3 3 1 1 | 6652896 | 6649536 | |||
| 9 4 2 2 2 1 | 16632240 | 16623840 | |||
| 8 5 2 2 2 1 | 33257760 | 33254400 | |||
| 8 4 3 2 2 1 | 22174140 | 22167420 | |||
| 8 4 2 2 2 2 | 66515520 | 66508800 | |||
| 7 7 3 3 0 0 | 133024320 | 133024320 | |||
| 7 7 3 2 1 0 | 99776640 | 99759840 | |||
| 7 6 3 3 1 0 | 199539840 | 199533120 | |||
| 7 7 2 2 2 0 | 7761742 | 7757822 | |||
| 7 6 3 2 2 0 | 23284016 | 23274496 | |||
| 6 6 3 3 2 0 | 46560192 | 46556832 | |||
| 7 7 2 2 1 1 | 38804140 | 38793500 | |||
| 7 6 3 2 1 1 | 116402160 | 116390400 | |||
| 6 6 3 3 1 1 | 232794240 | 232790880 | |||
| 7 6 2 2 2 1 | 155198460 | 155191740 | |||
| 6 6 3 2 2 1 | 232803200 | 232781920 | |||
| 6 6 2 2 2 2 | 465588480 | 465581760 | |||
| 7 5 5 3 0 0 | 698389440 | 698365920 | |||
| 7 5 4 4 0 0 | 46563552 | 46553472 | |||
| 6 5 5 4 0 0 | 139680576 | 139670496 | |||
| 7 5 5 2 1 0 | 279351072 | 279351072 | |||
| 7 5 4 3 1 0 | 58205280 | 58191000 | |||
| 6 5 5 3 1 0 | 232797600 | 232787520 | |||
| 7 4 4 4 1 0 | 349203120 | 349174560 | |||
| 6 5 4 4 1 0 | 698382720 | 698372640 | |||
| 7 5 4 2 2 0 | 465595200 | 465575040 | |||
| 6 5 5 2 2 0 | 931170240 | 931170240 | |||
| 7 4 4 3 2 0 | 1396765440 | 1396745280 | |||
| 6 5 4 3 2 0 | 2095161600 | 2095104480 | |||
| 6 4 4 4 2 0 | 290999520 | 290981880 | |||
| 6 4 4 3 3 0 | 581997360 | 581965440 | |||
| 7 5 4 2 1 1 | 1163967840 | 1163957760 | |||
| 6 5 5 2 1 1 | 1745961840 | 1745926560 | |||
| 7 4 4 3 1 1 | 775985400 | 775965240 | |||
| 6 5 4 3 1 1 | 2327935680 | 2327915520 | |||
| 6 4 4 4 1 1 | 3491920320 | 3491856480 | |||
| 7 4 4 2 2 1 | 3103900920 | 3103900920 | |||
| 6 5 4 2 2 1 | 4655871360 | 4655831040 | |||
| 6 4 4 3 2 1 | 27166848 | 27155646 | |||
| 6 4 4 2 2 2 | 54320814 | 54315774 | |||
| 5 5 5 5 0 0 | 54324174 | 54312414 | |||
| 5 5 5 4 1 0 | 162961232 | 162948352 | |||
| 5 5 4 4 2 0 | 325911264 | 325907904 | |||
| 5 4 4 4 3 0 | 67909580 | 67892500 | |||
| 4 4 4 4 4 0 | 271598380 | 271584380 | |||
| 5 5 4 4 1 1 | 407410640 | 407375920 | |||
| 5 4 4 4 2 1 | 814781520 | 814766400 | |||
| 4 4 4 4 3 1 | 543195550 | 543169790 | |||
| 4 4 4 4 2 2 | 1086368700 | 1086361980 | |||
| 9 3 3 3 2 0 | 1629561920 | 1629533920 | |||
| 8 3 3 3 3 0 | 2444369760 | 2444299200 | |||
| 9 3 3 2 2 1 | 81485376 | 81469416 | |||
| 8 3 3 3 2 1 | 325914624 | 325904544 | |||
| 9 3 2 2 2 2 | 488880336 | 488848416 | |||
| 8 3 3 2 2 2 | 977733792 | 977723712 | |||
| 7 5 3 3 2 0 | 407396640 | 407377320 | |||
| 7 4 3 3 3 0 | 814791600 | 814756320 | |||
| 6 5 3 3 3 0 | 1629552960 | 1629542880 | |||
| 7 5 3 2 2 1 | 2444341200 | 2444302560 | |||
| 7 4 3 3 2 1 | 1086375420 | 1086355260 | |||
| 6 5 3 3 2 1 | 3259105920 | 3259085760 | |||
| 6 4 3 3 3 1 | 4888679040 | 4888608480 | |||
| 7 5 2 2 2 2 | 1018503360 | 1018450440 | |||
| 7 4 3 2 2 2 | 2036946240 | 2036923560 | |||
| 6 5 3 2 2 2 | 1357976040 | 1357937400 | |||
| 6 4 3 3 2 2 | 4073890800 | 4073848800 | |||
| 5 5 5 3 2 0 | 6110877360 | 6110769840 | |||
| 5 5 4 3 3 0 | 5431836600 | 5431816440 | |||
| 5 5 5 2 2 1 | 8147778240 | 8147700960 | |||
| 5 5 4 3 2 1 | 10863673020 | 10863632700 | |||
| 5 4 4 3 3 1 | 97780440 | 97765320 | |||
| 5 5 4 2 2 2 | 488871936 | 488856816 | |||
| 5 4 4 3 2 2 | 977743872 | 977713632 | |||
| 4 4 4 3 3 2 | 1955457504 | 1955457504 | |||
| 7 3 3 3 2 2 | 2933201376 | 2933171136 | |||
| 6 3 3 3 3 2 | 1222184880 | 1222137000 | |||
| 5 5 3 3 2 2 | 2444329440 | 2444314320 | |||
| 5 4 3 3 3 2 | 1629563040 | 1629532800 | |||
| 4 4 3 3 3 3 | 4888658880 | 4888628640 | |||
| 4 4 4 4 2 2 | 7333013520 | 7332917760 | |||
| 5 5 3 3 3 1 | 6518191680 | 6518191680 | |||
| 5 5 3 3 2 2 | 9777317760 | 9777257280 | |||
| 5 4 4 4 3 0 | 2036961360 | 2036908440 | |||
| 5 4 4 4 2 1 | 6110833680 | 6110775720 | |||
| 5 4 4 3 3 1 | 8147754720 | 8147724480 | |||
| 5 4 4 3 2 2 | 12221662320 | 12221556480 | |||
| 5 4 3 3 3 2 | 16295509440 | 16295448960 | |||
| 5 3 3 3 3 3 | 21727305720 | 21727305720 | |||
| 4 4 4 4 4 0 | 2546223120 | 2546142480 | |||
| 4 4 4 4 3 1 | 10184706000 | 10184643000 | |||
| 4 4 4 4 2 2 | 15277122000 | 15276958200 | |||
| 4 4 4 3 3 2 | 20369406960 | 20369291040 | |||
| 4 4 3 3 3 3 | 27159162480 | 27159102000 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




