Prerpints.org logo
Preprint
Article

Irreversibility as a Measure of Loss of Working Capacity of a Chemical Reaction as a Thermodynamic Process: Definition With Partial Application of Extreme Values of Internal Energy and Entropy

This version is not peer-reviewed.

Submitted:

05 July 2024

Posted:

09 July 2024

You are already at the latest version

Abstract
Here, we consider a closed composite system consisting of a primary system where the chemical reaction occurs and is located in a p, T reservoir. In the ideal isentropic case (thermodynamic process), the change in the internal energy of the composite system (due to a chemical reaction) is wholly converted into useful work - maximum useful work. Irreversibility - a measure for the degradation of useful work - in a closed system generates entropy, i.e., the thermodynamic process is no longer isentropic. Applying the principle of maximum entropy and minimum internal energy to a part of the system's total volume and applying the elements of the system's volume for which the law of local equilibrium applies useful work and irreversibility can be defined. Suppose the primary system is viewed as a set of black box volume elements in which a chemical reaction occurs. In that case, the criterion of an isentropic process or a process with entropy generation becomes the Gibbs-Duham equation. It has been proven that De Donder's equation of entropy production of a chemical reaction is a particular form of Calen's equation –TdST = dUT where dST is the differential change of total entropy and dUT is the differential change of total internal energy of the composite system.
Keywords: 
Gibbs free energy
;  
isentropic process
;  
maximum non-expansion work
;  
De Donder's equation
;  
local equilibrium
;  
irreversibility
Subject: 
Chemistry and Materials Science  -   Physical Chemistry

1. Introduction

When an isolated system (composite) undergoes a spontaneous, irreversible thermodynamic process, the differential change in its total entropy (dST > 0) is greater than zero. During this process, the differential changes in Gibbs free energy (dG) and Helmholtz free energy (dA) are equal to the negative product of the thermodynamic temperature (T) and the differential change in total entropy (dST), while the total internal energy (UT) of the isolated composite system remains unchanged: d G = − T d S T :   U T , T , p = c o n s t a n t and d A = − T d S T : U T ,   T , V = c o n s t a n t (p is pressure and V is volume; constancy refers both to the primary system - where the chemical reaction takes place - and to the corresponding reservoir of the composite system) [1,2,3].
In a quasi-static reversible (quasi-static isentropic) thermodynamic process [4,5,6] in a closed composite system, dG and dA equal the differential change of the total internal energy (dUT < 0) - while the total entropy is constant [7,8,9]: d G = d U T : S T , T , p = c o n s t a n t and d A = d U T : S T , T , V = c o n s t . For a system to be in equilibrium, whether it is closed or isolated, the values of dG and dA should be equal to zero. For instance, if an isothermal expansion occurs in a closed system and the state of equilibrium exists (meaning the piston in the cylinder does not move), there won’t be any change in the internal energy. Consequently, there will be no differential pressure-volume work on the environment, and neither G nor A will change.
It is natural to wonder what happens when the total internal energy and the total entropy of a composite system change simultaneously. This is a topic of significant importance in the field of thermodynamics and chemical engineering. The goal was to achieve a quasi-static reversible (isentropic) thermodynamic process in the primary system during a chemical reaction of an idealized galvanic or fuel cell. However, some useful work (change in total internal energy) is lost if the chemical reaction in the composite system does not correspond to a hypothetical isentropic process or if the hypothetical chemical reaction in the composite system is isentropic but is coupling with the secondary spontaneous irreversible processes, such as friction during piston movement in a cylinder or resistance when current flows through a conductor. As a result, the composite system is still closed; however, some of the internal energy changes of the quasi-static reversible (isentropic) process, due to the secondary irreversible process, remain as thermal energy within the composite system [10,11,12,13,14,15].
The goal is to describe the thermodynamic process from which the useful work is obtained. This work, in terms of absolute value, is smaller than the absolute value of the maximum useful work obtained from the hypothetical isentropic thermodynamic process. We achieve this by applying the principles of minimum total internal energy and maximum total entropy to the particular volume of the observed system where a thermodynamic process (chemical reaction) takes place. In this context, the system’s volume elements, a key aspect of the principle of local equilibrium, play a crucial role. The discussion focuses on the changes in the Gibbs free energy, the most frequently applied thermodynamic potential. It’s important to note that the change in Gibbs free energy at p, T =constant condition equals the maximum non-expansion work, providing a clear relationship between these two concepts.

2. Discussion

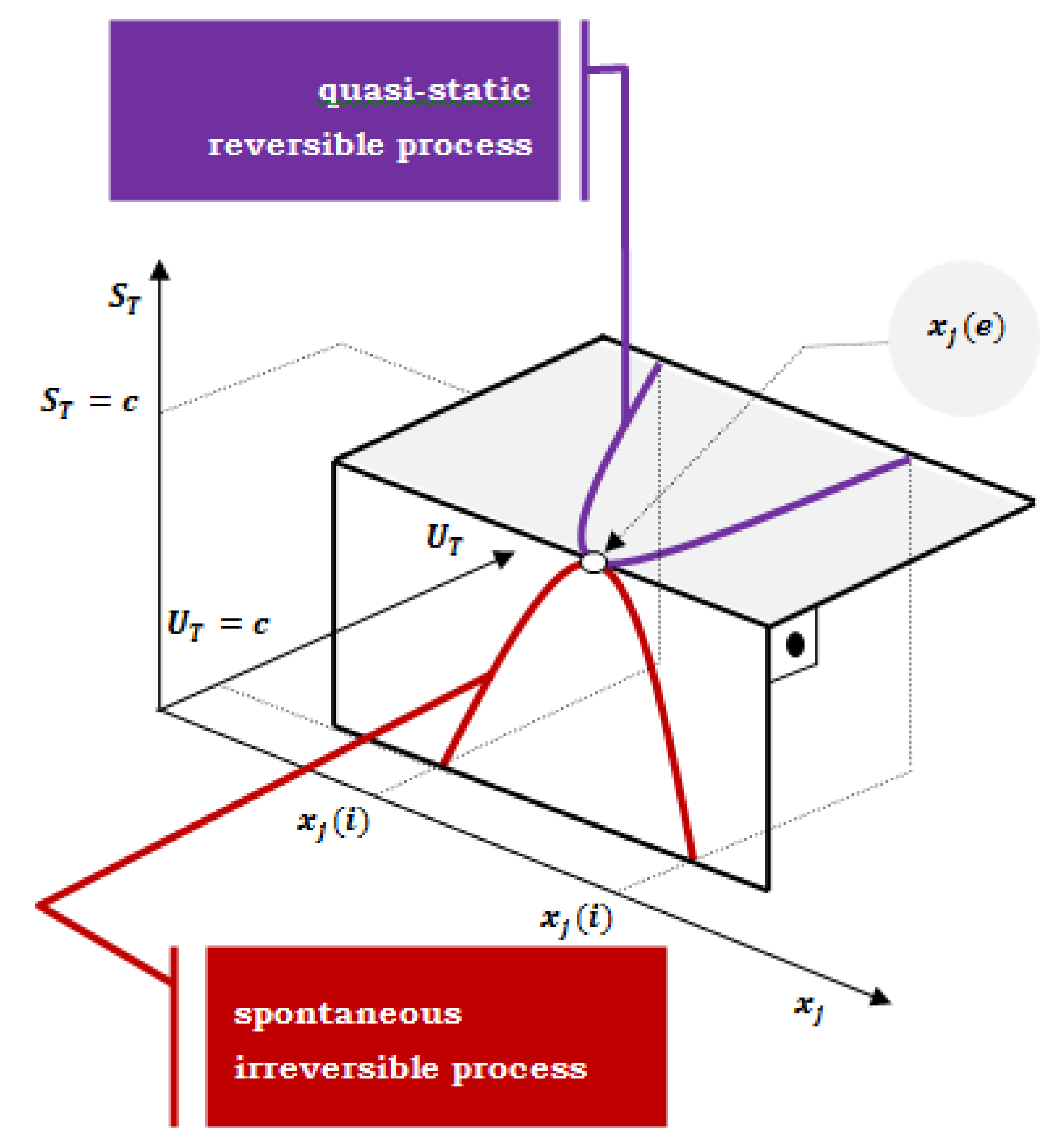
2.1. Two Extremes: Differential Change of Total Internal Energy in a Closed System and Differential Change of Total Entropy in an Isolated System—De Donder’s Equation

Applying the chain rule to the differential change of the total internal energy and the differential change of the total entropy of the composite system (Figure 1) [7,9]:
∂ U T … x j … ∂ x j x i , S T ∂ x j ∂ S T … x j … x i , U T ∂ S T … x j … ∂ U T … x j … x i = − 1
and using identity ∂ f / ∂ x = 1 / ∂ x / ∂ f , the following expression is obtained (xj is an extensive quantity of the state of the system that changes during the thermodynamic transformation and can be the quantity of the state from any compartment of the composite system; in thermodynamic potentials, it is the primary system, i.e., a system for which the thermodynamic parameters that define a given thermodynamic potential apply – or a system in which a chemical reaction takes place):
∂ U T … x j … ∂ x j x i , S T = − ∂ S T … x j … ∂ x j x i , U T ∂ U T … x j … ∂ S T … x j … x i
∂ U T … x j … ∂ x j x i , S T = − T ∂ S T … x j … ∂ x j x i , U T
Multiplied expression (3) by the infinitesimal change of the extensive parameter dxj of the primary system due to the infinitesimal progression of a thermodynamic process (chemical reaction) towards the maximum entropy (equilibrium state) – example for an irreversible process in an isolated composite system (UT=const.); or progression of a quasi-static reversible process towards minimal internal energy (final equilibrium state) – if the rate of change of extensive parameter is negligible small, succession of states of internal equilibrium [4] – in a closed composite system (ST=const.):
∂ U T … x j … ∂ x j x i , S T d x j = − T ∂ S T … x j … ∂ x j x i , U T d x j
d U T = − T d S T ↔ − d U T T = d S T
If the change in the system’s state starts from the xj (i ) initial value of an extensive variable, regardless of whether an isolated composite system with the constant total internal energy is observed (total entropy of the composite system increases to equilibrium) or an isentropically closed composite system (the total internal energy of a composite system decreases to the final equilibrium); the system is reached the same equilibrium state xj (e) (Figure 1).
Equation (5) is actually a more general form of De Donder’s Equation (6) [1,16], which describes the production of entropy in an isolated system during a chemical reaction:
d S = − 1 T ∑ μ i d n i = − 1 T ∑ μ i ν i d ξ = A T d ξ
where μi and νi represent respectively the chemical potential and stoichiometric coefficient of the i-th particle in the observed reaction 0 = ∑ ν i i . In Equation (6) A is the De Donder affinity of the reaction and dξ corresponds to the infinitesimal extent of the chemical reaction [17]. As the chemical potential is the partial molar Gibbs energy, it can then be expressed with the partial molar enthalpy (hi) and entropy (si):
− T d S = ∑ μ i d n i = ∑ h i − T s i d n i = ∑ h i − T s i ν i d ξ = d H r x n − T d S r x n = d G r x n
d S = d S T = d S r x n − d H r x n T = − d G r x n T = − d U T T
In Equation (7), rxn means that the thermodynamic functions change during the progress of the chemical reaction. In an isolated composite system, d H r x n / T represents the differential change of entropy in the pressure-temperature reservoir, while dSrxn corresponds to the differential change of entropy in the primary system where the chemical reaction takes place, which means that De Donder’s differential change of entropy corresponds to the differential change of total entropy ( d S T ) of the isolated composite system. According to Calen, the equality   d G = d U T : S T ,   p , T = c o n s t a n t holds, from which Equation (8) follows. Equality T d S T = − d U T from De Donder’s equation can also be proven under V = constant conditions when the system is without a reservoir of an intensive state parameter, i.e., the system is not composite. Namely, as the chemical potential is, in addition to the partial molar Gibbs energy, also the partial derivative of the internal energy by the amount of the i-th component, it follows that the right-hand side of the equation in expression (7) is also the differential change of the total internal energy (Figure 2):
T d S T = T ∑ ∂ S T ∂ n i U , V , n j d n i = − ∑ ∂ U T ∂ n i S , V , n j d n i = − d U T

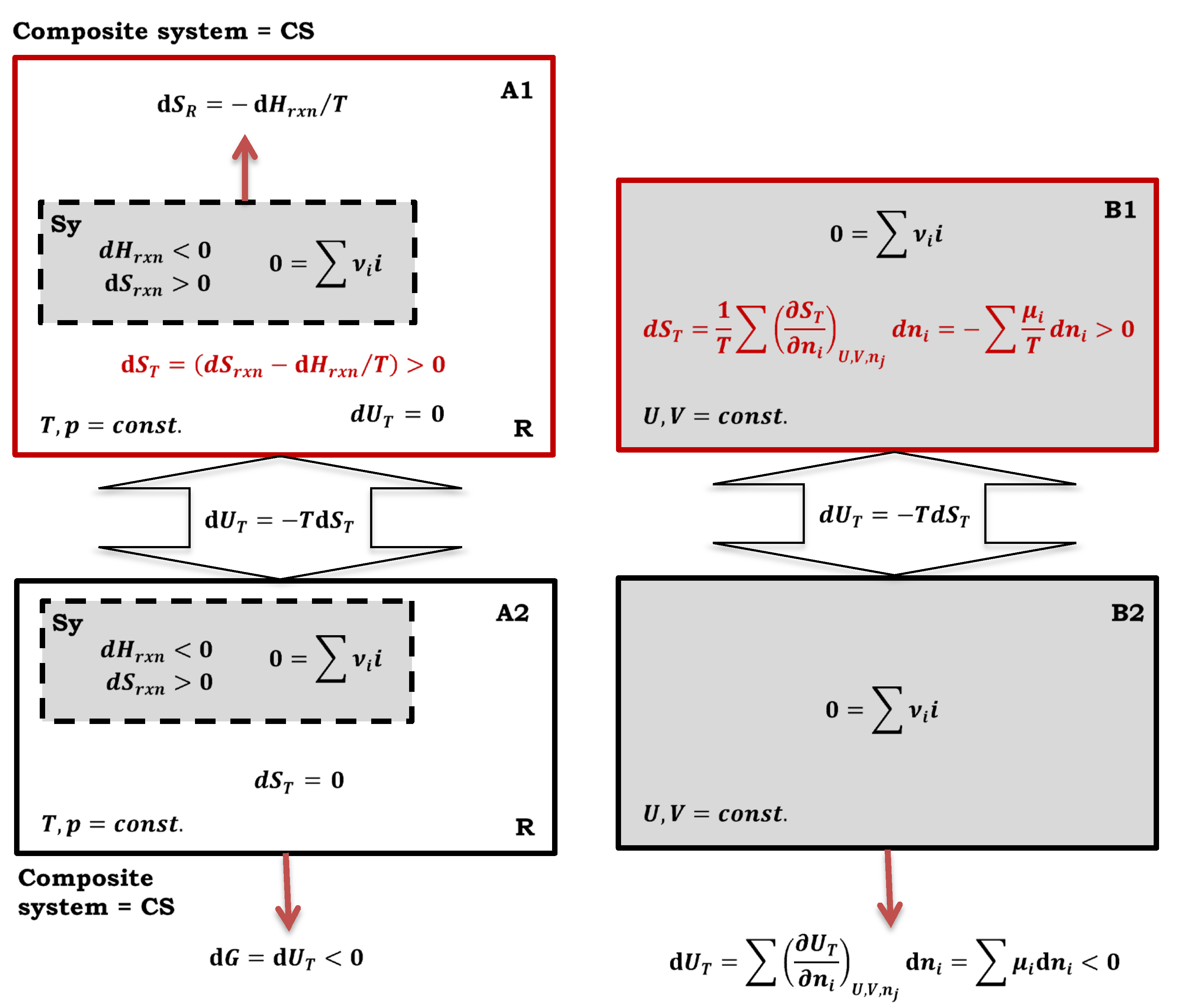
2.2. Irreversibility: as a Loss of Working Capacity of the System in Which the Chemical Reaction Takes Place

Let the observed system be divided into two parts (Figure 3). One part of the system is where the quasi-static reversible (isentropic) process always occurs (at each point of the compartment, the intensive quantities of the state have the same values). In contrast, the other part of the system is where both the quasi-static reversible and irreversible processes can occur (if an irreversible process also occurs, then the intensive state quantities have different values in the distinct places of the compartment). As internal energy and entropy are additives over the elements of an system, where the elements can be real compartments of the composite system or imaginary [7], therefore, at some point in the thermodynamic process the total internal energy of the composite system can be represented as the sum of:
U T = γ r e v U T + γ r e v i r U T = γ r e v U T + 1 − γ r e v U T
In Equation (10), γ r e v represents the fraction of internal energy of the composite (real or imaginary) system where a quasi-static reversible (isentropic process) process takes. Let it be assumed that the fractions γ r e v and γ r e v i r remain constant during the thermodynamic process ( γ r e v + γ r e v i r = 1). Then the differential change of the total internal energy of the composite system due to the infinitesimal progress of a quasi-static reversible thermodynamic process (without an irreversible process in the γ r e v i r part of CS – Figure 2 path a) is:
0 > d U T = γ r e v d U T + γ r e v i r d U T = γ r e v d U T + 1 − γ r e v d U T
Given Equality (5), Equation (11) is:
d U T = γ r e v d U T + γ r e v i r d U T = − T d S T = − T γ r e v d S T + γ r e v i r d S T
Generally, let’s consider a closed composite system (Cs) that becomes isolated. In this scenario, the total internal energy change (11) due to the thermodynamic process remains in the system as thermal energy increases the total entropy (12) - spontaneous, irreversible process.
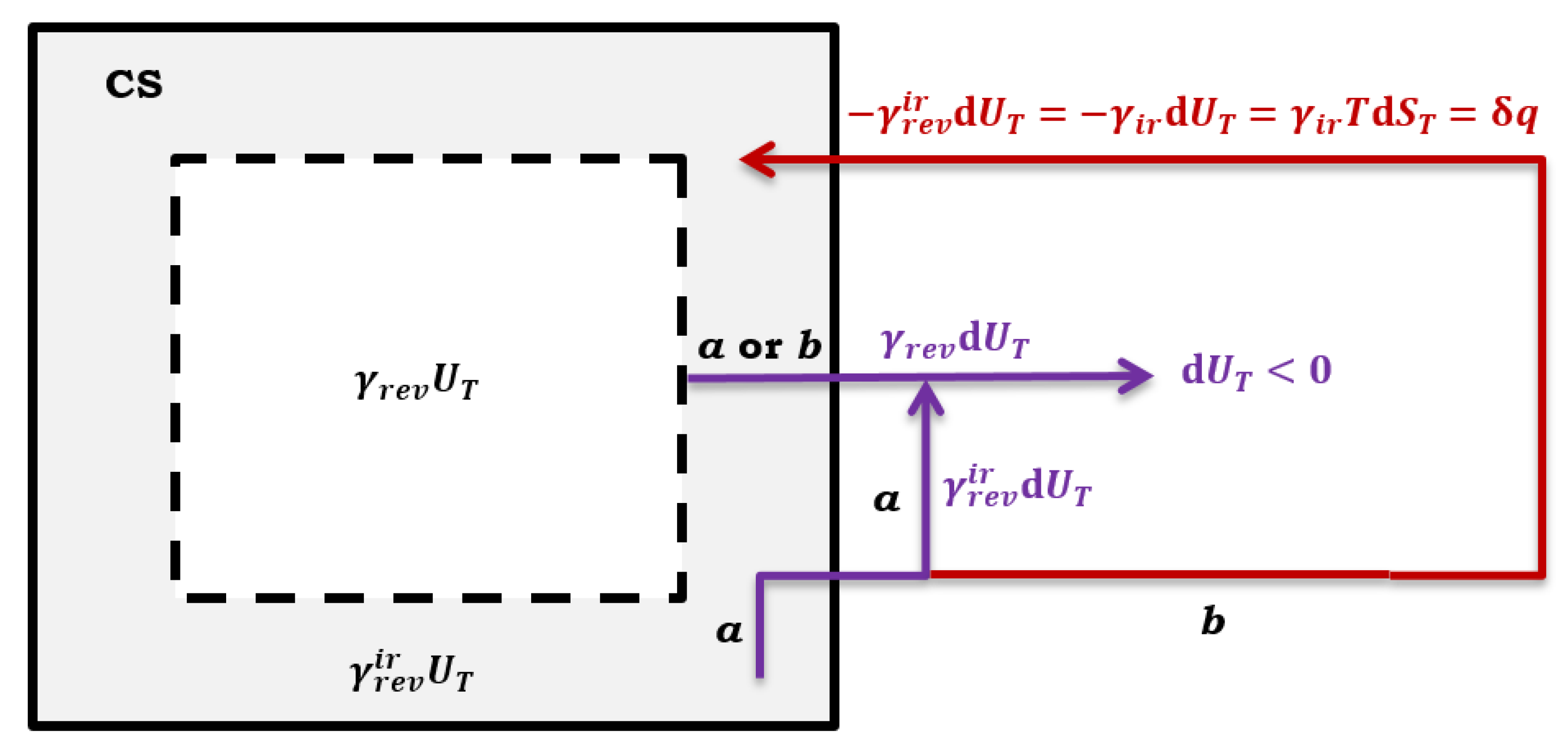
Now, let’s return to the closed (imaginary) composite system shown in Figure 3. For the part of the composite system where the quasi-static reversible process always occurs, the relation:
γ r e v d U T < 0   ⋀   γ r e v T d S T = 0
remains valid. Suppose in the part of the imaginary composite system where both the quasi-static reversible and the irreversible process can occur, the quasi-static reversible process takes place. In that case, it is (Figure 2):
γ r e v i r d U T < 0   ⋀   γ r e v i r T d S T = 0
Presume that a spontaneous irreversible process occurs in   γ r e v i r part of the system CS. In that case, part of the differential change in the total internal energy ( γ r e v i r d U T ) of the hypothetical quasi-static reversible process returns to the system as differential heat ( d U T < 0 refers to a quasi-static thermodynamic process with d S T = 0 , i.e., formally, a quasi-static reversible process first happened and then a spontaneous irreversible process, Figure 3 path b):
δ q = − γ r e v i r d U T = − γ i r d U T > 0
δ q = − γ i r d U T = γ r e v i r T d S T = γ i r T d S T :   d U T < 0   ⋀ − γ i r d U T > 0   ⋀   γ r e v i r T d S T > 0
Since the system is further closed from the part where the quasi-static reversible process exclusively takes place ( γ r e v ), the differential change in internal energy ( γ r e v d U T ) leaves CS without contributing to the differential entropy change of CS (13) (Figure 3). While from part γ r e v i r = γ i r of CS, where it now, in addition to a quasi-static reversible thermodynamic process (which first happened), also takes place spontaneous irreversible process – part of the total internal energy change d U T of a quasi-static reversible thermodynamic process – remains in the imaginary part of the system generating entropy ( T γ r e v i r d S T > 0 ). Therefore, Equation (12) in the case of a system transition from a quasi-static reversible regime to a system where, in addition to a quasi-static reversible process, there is also a spontaneous irreversible process (the system is closed, Figure 3 path b):
d U T = γ r e v d U T + γ r e v i r d U T = − γ r e v T d S T ⏟ 0 − γ r e v i r T d S T = − γ i r T d S T
In Equation (17), d U T refers to the differential change of the total internal energy in CS if a quasi-statically reversible thermodynamic process takes place in each real or imaginary compartment (formally, which occurred before the irreversible process). The actual differential change in total internal energy of CS is γ r e v d U T and leaves the composite system in the form of useful differential work (Figure 2 path b):
− γ r e v d U T − γ i r d U T = 0 + γ i r T d S T
It follows from Equation (17):
d U T − γ r e v d U T = γ r e v i r d U T = − γ r e v i r T d S T = − γ i r T d S T
and taking into account Equation (16):
− d U T − γ r e v d U T = − γ r e v i r d U T = − γ i r d U T = δ q = γ r e v i r T d S T = γ i r T d S T
In the last expression (20), d U T corresponds to the useful differential work, which would be obtained if the thermodynamic process in the composite system were entirely quasi-statically reversible d U T = δ w r e w (Figure 3 path a); γ r e v d U T represents the real useful differential work that is obtained if there is also a parallel irreversible process: γ r e v d U T = δ w (Figure 3 path b). So the difference on the left side of Equation (20) is the differential part of the changes in the total internal energy that is wasted in the form of thermal energy during an irreversible process (wasted work potential – dissipated energy) and leads to the generation of entropy:
δ w r e w − δ w = γ r e v i r d U T = − γ i r T d S T = − δ I
δ I = δ q = − γ r e v i r d U T = − γ i r d U T
In Equation (21) are δ w r e w < 0 and δ w < 0 since these are differential changes in the total internal energy of the composite system that leaves the system in the form of useful work. However, infinitesimal (differential) dissipated energy – differential irreversibility ( δ I ) is δ I > 0 [18]. Namely, irreversibility is part of the change in the total internal energy of the composite system (i.e., the useful work of a quasi-static reversible process when the total entropy change would be zero), which remains in the given composite system – i.e., formally, returns to the composite system during an irreversible process as δ q (Figure 3 path b). If, at every moment of the thermodynamic process in the composite system, there is an internal equilibrium (hypothetical limit case), then a quasi-static reversible process takes place in the entire composite system. Hence, the irreversibility value is equal to zero:
lim γ ir → 0 ⁡ δ w r e v − δ w = γ i r d U T = − γ i r T d S T = − δ I = δ w r e v − δ w r e v = 0
Expression (21) for the final thermodynamic process is:
w r e v − w = γ i r ∆ U T = − γ i r ∆ S T = − I

2.3. Change of Gibbs Free Energy and Irreversibility of a Thermodynamic Process

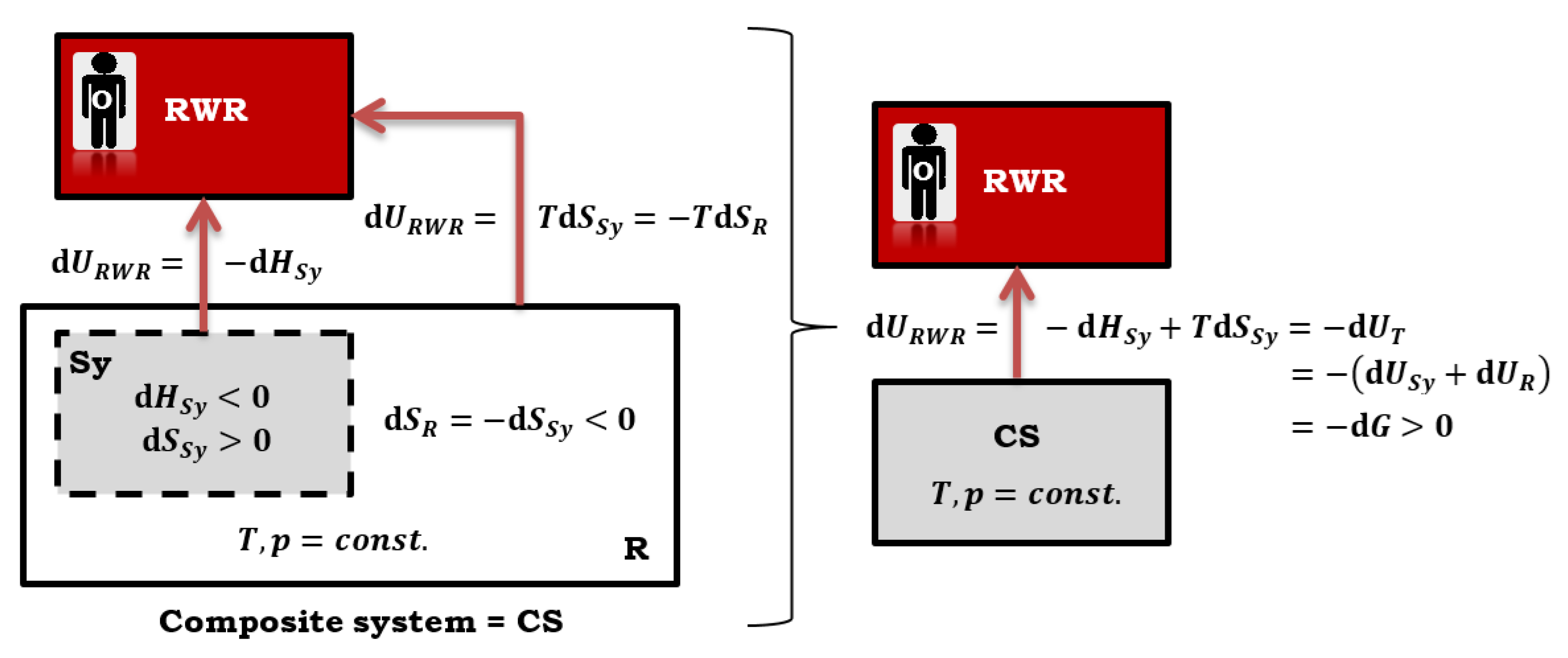
In quasi-static reversible processes, when the temperature and pressure remain constant (isothermal-isobaric conditions), the differential change in Gibbs free energy is equivalent to the maximum differential non-expansion work [3,4,19,20,21]. Additionally, the differential change in the total internal energy of the composite system is also equal to the differential change in Gibbs free energy. This equality is represented by the Equation (25), which holds true when quasi-static reversible (isentropic) processes occur (Figure 4) [7]:
d G = δ w m a x = d U T = d U S y + d U R < 0
In Equation (25), d U S y represents the differential change of internal energy in the primary system (where the main thermodynamic process occurs, for example, a chemical reaction), while d U R represents the differential change of internal energy in the reservoir that provides isothermal-isobaric conditions.
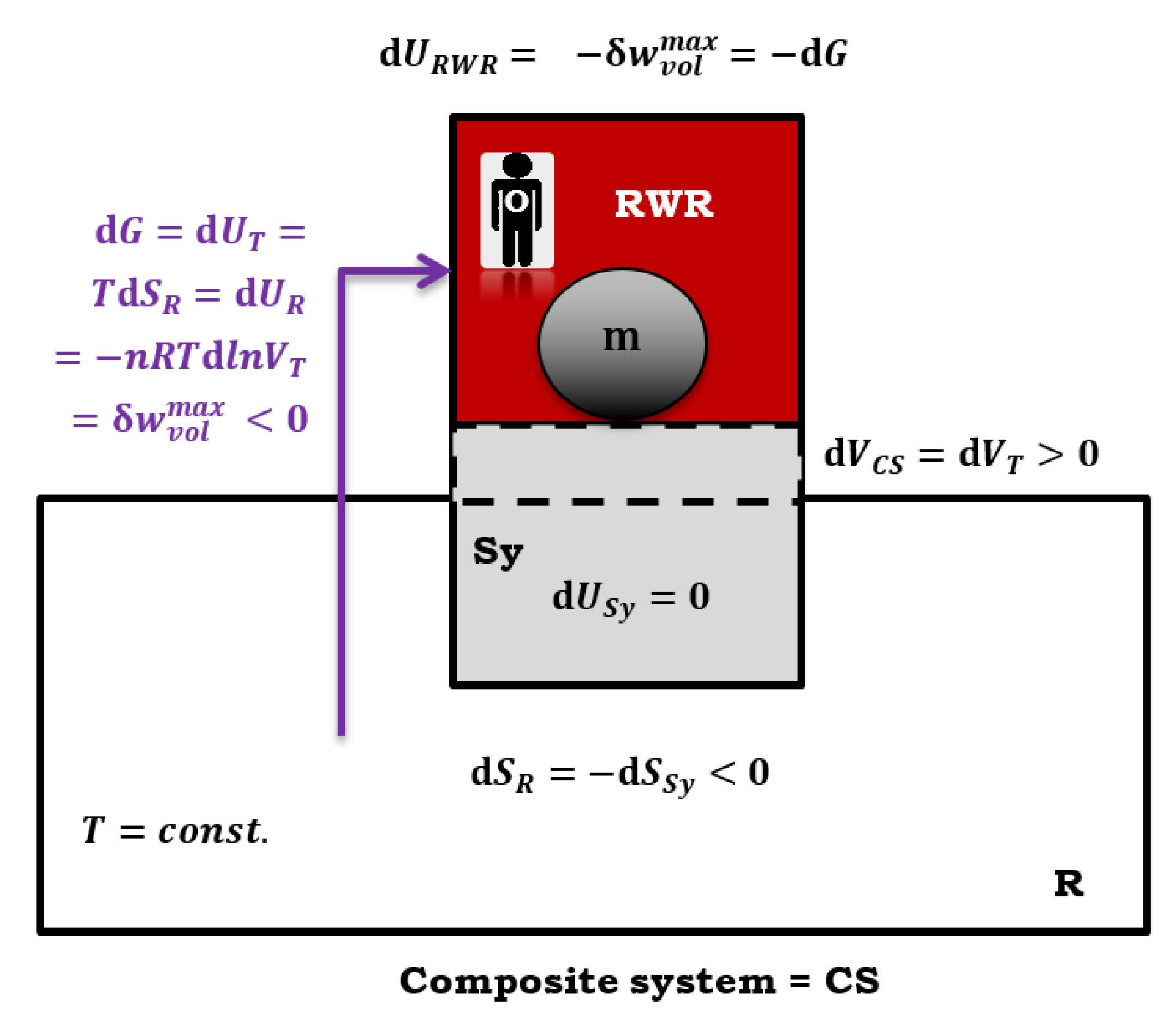
Calen introduced the concept of a reversible work (source) reservoir (RWR), which formally represents a hypothetical auxiliary system where the energy of the change in the total internal energy of the composite system (CS) is "stored", i.e., maximum non-expansion work (in the case of quasi-static reversible processes in the primary system) [7]. Maximum non-expansion work from the CS in the RWR transforms into the potential energy (compression or stretching of the spring). RWR is a fictitious system with a conservative force. In the view of the observer (O) from the RWR, the energy of the change in the internal energy of the composite system, which is the maximum non-expansion work, leaves the CS, resulting in d U T < 0 and δ w m a x < 0 . However, the same energy enters the RWR. Therefore, it is d U R W R > 0 (Figure 4):
− d G = − δ w m a x = − d U T = d U R W R  
If a chemical reaction takes place in the primary system of the composite system CS with T, p reservoir, then the differential change in the internal energy of the primary system Sy is [22]:
d U S y = T d S S y − p d V S y − A d ξ S y
Differentiating Equation (27) by the chemical reaction extent at T, p = const., the following equation is obtained:
∂ U S y ∂ ξ p , T = T ∂ S S y ∂ ξ p , T − p ∂ V S y ∂ ξ p , T − A
Multiplying Equation (28) by the infinitesimal change in the chemical reaction extent gives:
∂ U S y ∂ ξ p , T d ξ = d U r x n = T ∂ S S y ∂ ξ p , T d ξ − p ∂ V S y ∂ ξ p , T − A d ξ
d U r x n = T d S r x n − p d V r x n − A d ξ
d U r x n + p d V r x n − T d S r x n = d H r x n − T d S r x n = d G r x n = − A d ξ S y : p , T = c o n s t .
The thermodynamic parameters of the primary system change due to the chemical reaction ( d U S y = d U r x n , d V S y = d V r x n and d S S y = d S r x n ). The change in the internal energy of the p,T reservoir (R) of the composite system is possible due to volumetric work and thermal energy exchange, so Equation (25) is:
d U T = d U S y + T d S R − p d V R
However, as the total volume of CS is constant, and the chemical reaction is reversible (quasi-static isentropic process), i.e., the CS’s total entropy change is zero, therefore Equation (31) at T, p = const. has the following form:
d U T = d U S y − T d S S y + p d V S y = d U r x n − T d S r x n + p d V r x n = − A d ξ S y = d G r x n
which proves that the change in total internal energy of the composite system is equal to the change in Gibbs free energy resulting from the chemical reaction in the primary system (Figure 4).
If, in a closed composite system, the total entropy change is not zero ( d U T < 0 and d S T ≠ 0 , i.e., d S T > 0 ), then a spontaneous irreversible process occurs during the thermodynamic process. Therefore part of the maximum non-expansion work turns into thermal energy (into a dissipated form of energy) – irreversibility. 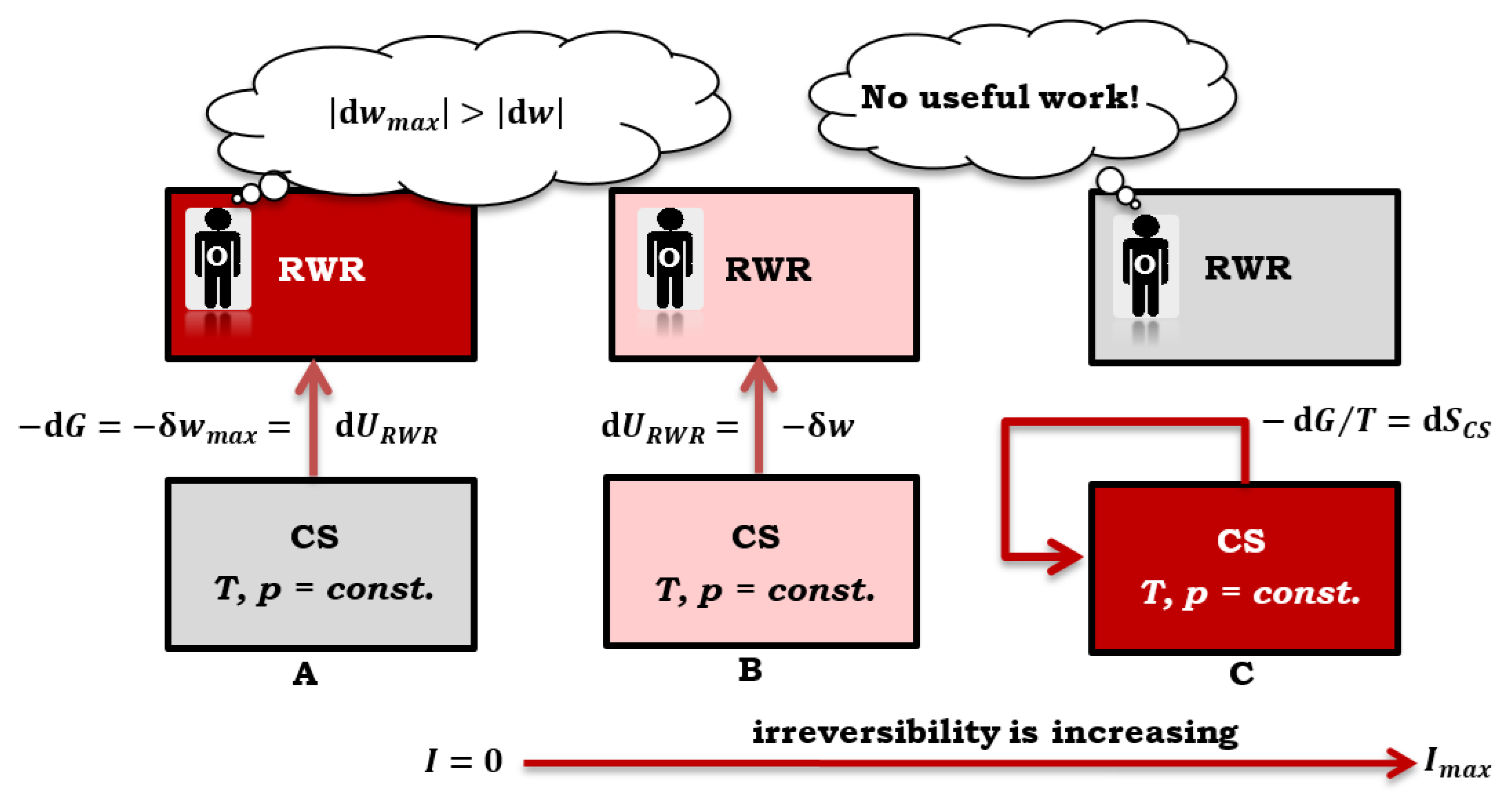Considering Equation (21), the difference between the maximum non-expansion work of a quasi-static reversible process and the real useful non-expansion work whenever a spontaneous irreversible process occurs is (Figure 5):
d G − δ w = δ w m a x − δ w = γ i r d U T = − γ i r T d S T = − δ q = − δ I
The difference (32) represents part of the change in the total internal energy of CS (due to the quasi-static reversible process) that is dissipated in the CS as heat (32) and increases the total entropy of the composite system – entropy is generated in the CS due to an irreversible (secondary) process. The absolute value of the differential non-expansion work δ w is smaller than the absolute value of the maximum differential non-expansion work δ w m a x  (Figure 5).
The criteria for quasi-static reversible (isentropic process) and irreversible spontaneous process in a closed system follow from the Equation (32) (Table 1):
d G − δ w ≤ 0   o r   δ w m a x − δ w ≤ 0
Clausius’s inequality [23,24] is hidden in the above inequality. Namely, the difference − d G − δ w = δ I represents part of the change in the total internal energy of the CS due to the primary thermodynamic process (i.e., chemical reaction), which is dissipated in the form of thermal energy in the CS, i.e., according to Clausius, it represents uncompensated entropy (i.e., entropy production due to an irreversible process). Multiplying the inequality by − 1 / T yields Claussiu’s equation in its most generalized form:
− d G − δ w T = δ I T = d S i r ≥ 0
If a quasi-static reversible process occurs in CS, then δ w = δ w m a x = d G so that the inequality (33) becomes equality (Figure 5A and Table 1):
d G − δ w m a x = 0   a n d   d S T = 0   ⋀ δ I = 0
Within a closed system, a spontaneous irreversible process generates entropy alongside a quasi-static reversible process (33). This entropy, in turn, resulting in less absolute value of negative work. Conversely, a hypothetical quasi-static reversible process within the same system (CS) would result in a higher absolute value of negative work. As such, the negative inequality value signifies that a spontaneous irreversible process has occurred within a closed composite system (36), thereby generating entropy (as depicted in Figure 5B and Table 1).
d G − δ w < 0   a n d   d S T ≠ 0 ⋀ δ I ≠ 0
Suppose the value of δ w in Equation (33) equals zero. In that case, it signifies that the spontaneous irreversible process in the composite system utilizes the complete alteration in the internal energy of the quasi-static reversible process. As a result, the entire change in the Gibbs free energy of the quasi-static process transforms into heat energy – dissipates into the environment (i.e., thermoreservoir). In a closed CS, the maximum irreversibility is attained, which is the highest value of the produced entropy – the closed composite system behaves like an isolated CS, as depicted in Figure 5C (37 and 38). It is crucial to note that no useful work can be extracted from the composite system (CS) in this scenario (Table 1).
d G − 0 = d G < 0   a n d   d S T ≠ 0 ⋀ δ I ≠ 0
S T → S T m a x > 0 ⋀ I → I m a x , ∆ U T = 0
For CS in a natural equilibrium state (without a quasi-static reversible process), d G = 0 and δ w = 0 hold, so inequality (33) is the equality 0 = 0.
Suppose CS is the real isolated system (constant total internal energy). In that case, the total enthalpy change of the spontaneous irreversible thermodynamic process remains in the system ( δ w = 0 ) so that inequality (33) is the equality (37 and 38) or:
d G = − T d S T   a n d   ∆ G = − T ∆ S T m a x  
Bearing in mind Equation (12) for an isolated system with a spontaneous irreversible process, it follows that the coefficient γ i r = 1 , i.e., for a specific change in the CS state the generated entropy have a maximum value (39).
The change in Gibbs free energy (ΔG and dG) represents the thermodynamic potential for the maximum non-expansion work of a quasi-static reversible process in a closed system (ΔST = 0 and dST = 0) or the change in a thermodynamic quantity -G/T (i.e., -ΔG/T or -dG/T) is the thermodynamic potential for the generated maximum total entropy of a spontaneous irreversible process in an isolated system (ΔUT = 0 and dUT = 0).

2.4. Black Box Method Application in the Volume Element of the Primary System of CS: the Gibbs Free Energy and the Irreversibility

Consider the primary system (Sy) - where the chemical reaction takes place intending to obtain useful work - and which (i.e., Sy) is located in the T,p reservoir forming together a composite system (Figure 4). If only a quasi-static chemical reaction takes place in the primary system, then maximum work is obtained from the composite system (isentropic condition, d G = δ w m a x ); while in the primary system, in addition to a quasi-static chemical reaction (isentropic conditions), a non-quasi-static reaction also takes place (or a non-quasi-static thermodynamic process is coupled with a quasi-static chemical reaction) then δ w ( δ w m a x > δ w ) work is obtained from the composite system. Based on the above, the γ r e v i r parameter can be defined:
γ r e v i r = 1 − γ r e v = δ w m a x − δ w / δ w m a x = δ I / δ w m a x
As the internal energy of the primary system ( U S y ) is an additive quantity over real or imaginary elements, Equations (10) and (11) apply, i.e., U S y = γ r e v U S y + γ r e v i r U S y and d U S y = γ r e v d U S y + γ r e v i r d U S y . The internal energy γ r e v U S y in the equilibrium state is a function of the first order:
γ r e v U S y = θ r e v ∆ γ r e v U S y ∆ γ r e v S S y , ∆ γ r e v V S y … = ∆ γ r e v U S y θ r e v ∆ γ r e v S S y , θ r e v ∆ γ r e v V S y …
Therefore, γ r e v U S y can be represented as the product of the parameter θ r e v and the element of the primary system’s internal energy (where the reversible process always takes place) ∆ γ r e v U S y ∆ γ r e v S S y , ∆ γ r e v V S y … , for which the volume element ∆ γ r e v V S y corresponds, where γ r e v V S y = θ r e v ∆ γ r e v V S y holds. The volume element ∆ γ r e v V S y corresponds to the volume for which the law of local equilibrium is valid [1], i.e., that the internal energy and entropy densities are independent of the system’s coordinates and time. 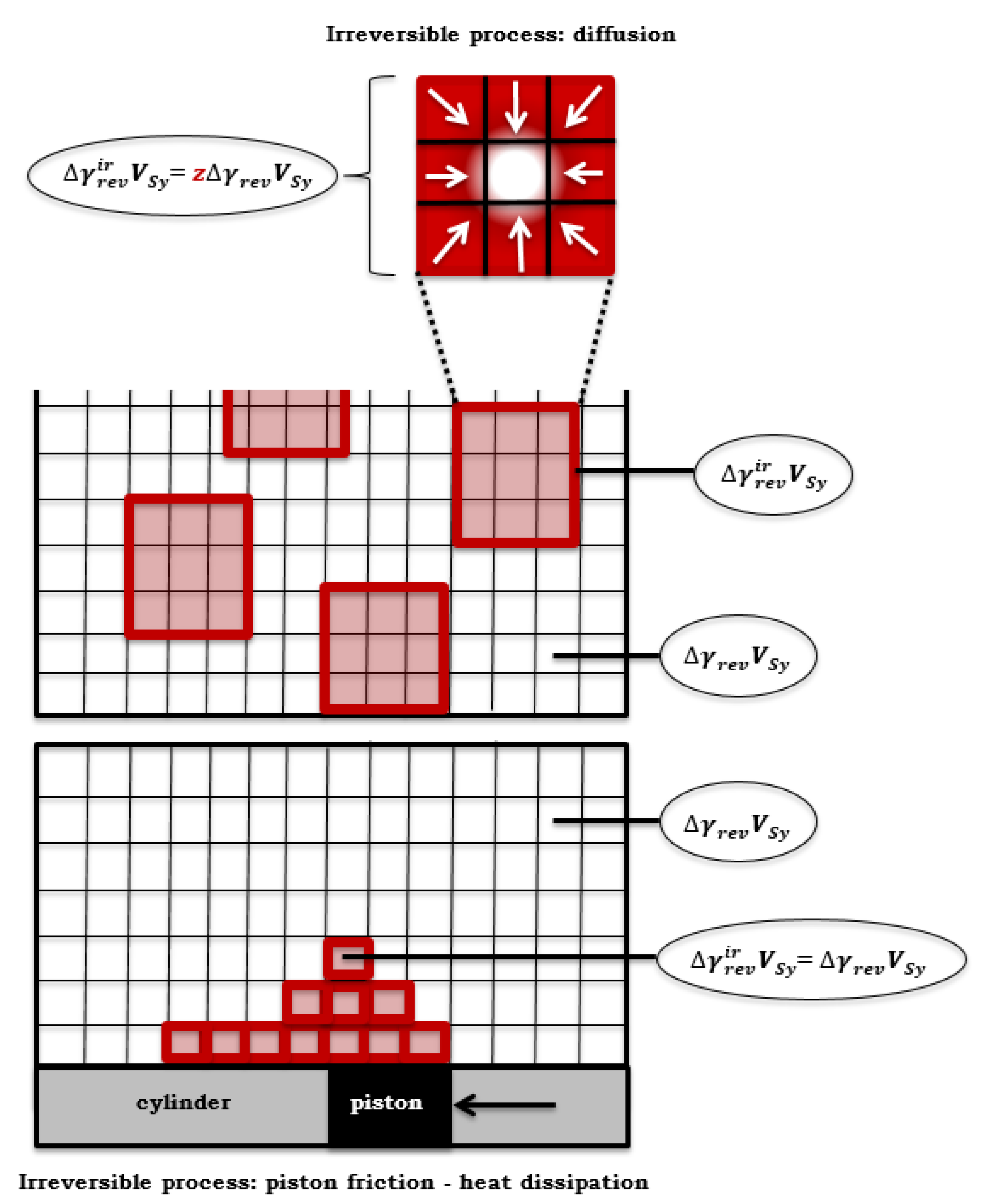Similarly, for the γ r e v i r U S y (part of the primary system where, in addition to the reversible thermodynamic process, an irreversible process can also take place), in the equilibrium state, it is valid that it is a homogeneous function of the first order.
γ r e v i r U S y = θ r e v i r ∆ γ r e v i r U S y ∆ γ r e v i r S S y , ∆ γ r e v i r V S y … = ∆ γ r e v i r U S y θ r e v i r ∆ γ r e v i r S S y ,   θ r e v i r ∆ γ r e v i r V S y …
However, ∆ γ r e v i r V S y ≠ ∆ γ r e v V S y or ∆ γ r e v i r V S y = ∆ γ r e v V S y (which depends on the irreversible process), i.e., the volume element ∆ γ r e v i r V S y , can consist of several volume elements ∆ γ r e v V S y , between which an irreversible thermodynamic process takes place. The volumes γ r e v V S y = θ r e v ∆ γ r e v V S y and γ r e v i r V S y = θ r e v i r ∆ γ r e v i r V S y do not have to be compact, but their elements ∆ γ r e v V S y and ∆ γ r e v i r V S y are randomly distributed over the volume of the primary system (Figure 6).
If the reaction ∑ ν i i = 0 (isothermal-isobaric conditions) takes place in the volume element ∆ γ r e v V S y – black box [25] then after time t from the beginning of the reaction as well as at time t = 0, the internal energy of the observed volume element of the primary system is:
U = ∑ i = 1 C n i u i = ∆ γ r e v V S y ∑ i = 1 C C i u i
Where n i corresponds to the amount of the i-th reactive component at time t, C i corresponds to the concentration of the i-th component in the volume element ∆ γ r e v V S y at time t, and u i represents the partial molar internal energy of component i at time t. Let there be the same state (concentrations, p,T = const.) in each element of the volume ( ∆ γ r e v V S y ) of the primary system at time t = 0, and if the reaction ∑ ν i i = 0 proceeds infinitely slowly. So that the concentrations of the reactive components are equal in each ∆ γ r e v V S y element, then each element of the volume can be viewed as a closed reactive system, i.e., there is no diffusion between volume elements. This means that in each volume element ( ∆ γ r e v V S y ), the amount of the i-th component changes solely due to the reaction:
n i = n i 0 + v i ξ
n i 0 is the amount of the i-th component (reactant or product) at t = 0, and v i is the stoichiometric coefficient of component i in the reaction ∑ ν i i = 0 . The differential change of internal energy in the volume element ∆ γ r e v V S y for the dt time interval is:
d U d t = ∆ γ r e v V S y ∑ i = 1 C u i d C i d t + ∑ i = 1 C C i d u i d t = d q d t + d w d t
As the volume element ∆ γ r e v V S y corresponds to a closed system, it follows that the differential change in internal energy in dt time corresponds to the differential amount of heat exchange ( d q ) and the differential useful work ( d w ). During the differential change of time (dt) based on Equation (44), the change in the amount (concentrate) of the i-th reactive component is:
d n i d t = v i d ξ d t
d C i d t = v i 1 ∆ γ r e v V S y d ξ d t = v i r
Where r represents the chemical reaction velocity ( r = 1 / V d ξ / d t [26], V corresponds to the volume where the reaction takes place). Inserting Equation (47) into Equation (45) yields:
d U d t = ∆ γ r e v V S y r ∑ i = 1 C u i v i + ∑ i = 1 C C i d u i d t = δ q d t + δ w d t
d U = ∑ i = 1 C u i v i d ξ + ∑ i = 1 C n i d u i = δ q + δ w
The Gibbs-Duham equation also appears in equation (49) [25,27]:
− d U d T p , C d T − d U d p T , C d p + ∑ i = 1 C n i d u i = 0
Since the reaction ∑ ν i i = 0 in the volume element ∆ γ r e v V S y takes place at p,T = const. conditions, the Gibbs-Duham equation is:
∑ i = 1 C n i d u i = 0
By introducing the Gibbs-Duham Equation (51) into Equation (49), we get:
d U = ∑ i = 1 C u i v i d ξ = δ q + δ w
If the reaction takes place in a liquid aggregate state, then there is u i ≅ h i (h = partial molar enthalpy) [25], therefore Equation (52) is:
d U = ∑ i = 1 C h i v i d ξ = δ q + δ w
The entropy change in the volume element ∆ γ r e v V S y due to the reaction ∑ ν i i = 0 is (s = partial molar entropy and the volume elements ∆ γ r e v V S y of the primary system are isentropic):
d S = 0 = ∑ i = 1 C s i v i d ξ − δ q T
T ∑ i = 1 C s i v i d ξ = δ q
By introducing Equality (55) into Equation (53), we get:
∑ i = 1 C h i v i d ξ = T ∑ i = 1 C s i v i d ξ + δ w
∑ i = 1 C h i v i d ξ − T ∑ i = 1 C s i v i d ξ = ∑ i = 1 C h i − T s i v i d ξ = ∑ i = 1 C μ i v i d ξ = d G r x n = δ w m a x
Since the volume γ r e v V S y contains the θ r e v number of the element of the volume ∆ γ r e v V S y and since Equation (57) holds for each element of the volume, it follows that the useful (non-expansion) work θ r e v d G r x n = θ r e v δ w m a x is obtained from the volume θ r e v d G r x n = θ r e v δ w m a x .
Let a quasi-static isentropic process (chemical reaction) take place formally in the volume element ∆ γ r e v i r V S y , and then an irreversible thermodynamic process, i.e., Equation (49) is valid with u i ≅ h i :
d U = ∑ i = 1 C h i v i d ξ + ∑ i = 1 C n i d u i = δ q + δ w
In the quasi-static isentropic phase of the thermodynamic process, equality (55) applies, so Equation (58) is:
d U = ∑ i = 1 C h i − T s i v i d ξ + ∑ i = 1 C n i d u i = δ w
However, after an isentropic chemical reaction, an irreversible process formally follows (in reality, both thermodynamic processes occur in parallel), for example due to the friction of a piston, parts of the volume element ∆ γ r e v i r V S y are heated, i.e., useful work is converted into thermal energy of friction ( C p d T = δ I = δ q ), which is in agreement with Lucia’s statement according to which: "at the beginning of the process, the system could be able to use all the energy, while during the process the irreversibility generates a loss of energy" [28]. Therefore, the Gibbs-Duham Equation (50) at constant pressure is:
d U d T p , C d T = C p d T = ∑ i = 1 C n i d u i
By introducing the Gibbs-Duham Equation (60) and d G r x n = ∑ i = 1 C h i − T s i v i d ξ = ∑ i = 1 C μ i v i d ξ into Equation (59), we get:
d G r x n + C p d T = d G r x n + δ I = δ w
When defining the volume element of the primary system ∆ γ r e v i r V S y , it was assumed that with these volume elements, useful work is completely dissipated in an irreversible process, i.e., the equation d U T = − T d S T is valid for each volume element ∆ γ r e v i r V S y – volume element ∆ γ r e v i r V S y for the useful work formally becomes an isolated system:
d G r x n + C p d T = d G r x n + δ I = 0
For the part of the volume of the primary system ( γ r e v i r V S y ) in which, in addition to the quasi-static reaction (with isentropic conditions in the composite system), an irreversible process also takes place, γ r e v i r V S y = θ r e v i r ∆ γ r e v i r V S y applies. In the case of the dissipation of useful work into thermal energy, the equality between the volume elements can be taken ( ∆ γ r e v i r V S y = ∆ γ r e v V S y ) so that γ r e v i r V S y = θ r e v i r ∆ γ r e v V S y (Figure 6). In this way, the maximum useful non-expansion)work ( δ w C S m a x ) that is obtained from the composite system (CS) when a quasi-static chemical reaction (with isentropic conditions) flows in each volume element ∆ γ r e v V S y of the primary system is:
δ w C S m a x = d G r x n θ r e v + θ r e v i r = δ w m a x θ r e v + θ r e v i r
Where d G r x n = δ w m a x corresponds to the differential change of Gibbs free energy per volume element ∆ γ r e v i r V S y = ∆ γ r e v V S y , while θ r e v + θ r e v i r is the total number of volume elements ∆ γ r e v i r V S y = ∆ γ r e v V S y . If in the θ r e v i r number of the volume element ∆ γ r e v i r V S y = ∆ γ r e v V S y , an irreversible process also flows, i.e., Equation (62) applies, then the differential useful non-expansion work from the composite system is:
δ w C S = d G r x n θ r e v + θ r e v i r + δ I θ r e v i r = d G r x n θ r e v                        + d G r x n θ r e v i r + δ I θ r e v i r = d G r x n θ r e v + d G r x n θ r e v i r − d G r x n θ r e v i r = δ w C S m a x     − δ I θ r e v i r = d G r x n θ r e v
In Equation (64) δ I represents irreversibility, i.e., dissipated useful work per volume element of the primary system ( d G r x n < 0 ;   δ I > 0 ;   δ w C S < 0 ). If the elements of the volume are not equal ∆ γ r e v i r V S y ≠ ∆ γ r e v V S y , the equality ∆ γ r e v i r V S y = z ∆ γ r e v V S y applies, i.e., γ r e v i r V S y = θ r e v i r z ∆ γ r e v V S y (Figure 6), then Equation (63) is:
δ w C S m a x = d G r x n θ r e v + z θ r e v i r = δ w m a x θ r e v + z θ r e v i r
that is, Equation (64) is:
δ w C S = d G r x n θ r e v + z θ r e v i r + δ I z θ r e v i r = d G r x n θ r e v                      + d G r x n z θ r e v i r + δ I z θ r e v i r = d G r x n θ r e v + d G r x n z θ r e v i r − d G r x n z θ r e v i r         = δ w C S m a x − δ I z θ r e v i r = d G r x n θ r e v
Exergy is the maximum useful energy obtained from a system that reaches equilibrium with the environment during a hypothetical reversible (quasi-static isentropic) thermodynamic process. In the case of a chemical reaction (for example, in galvanic cells), the equilibrium of chemical potentials with the environment can be replaced by a zero value of De Donder’s affinity (A = 0, Equation (6)). Therefore, Equations (63) and (65) correspond to the maximum non-expansion useful work ( δ w C S m a x ), i.e., exergy that can be obtained from the composite system. Gouy (1889) and Stodola (1905) independently confirmed that the loss of exergy (maximum useful work) is proportional to the generated entropy [29], which follows Equations (64) and (66).
Equation (62) can be generalized, namely since irreversibility is the dissipated useful work then it is: δ I = − d G r x n , i.e.,:
d G r x n − d G r x n = 0
Considering De Donder’s Equations (6) and (8), expression (67) is:
d G r x n + T d S T = d G r x n + T d S D e   D o n d e r = 0
Where d S T = d S D e   D o n d e r = d S i represents the differential production of entropy in an irreversible process per volume element ∆ γ r e v i r V S y ( d S T = d S r x n − d H r x n / T , where d S r x n is the direct entropy change in the volume element ∆ γ r e v i r V S y due to the chemical reaction and − d H r x n / T represents the entropy change in the volume element ∆ γ r e v i r V S y due to reaction heat). The differential entropy change in an irreversible thermodynamic process can be represented as the product of the thermodynamic force (Fk) – proportional to the gradient of some intensive quantity – and an extensive physical quantity (corresponding to the intensive quantity) that is transported during the dt time interval ( d S i = ∑ F k d X k ) [1,30]:
d G r x n + T ∑ F k d X k = 0
Alternatively, taking into account the flux of the extensive variable ( J k = d X k / d t ), i.e., entropy generation per unit of time ( σ = ∑ F k J k ) [30]:
d G r x n d t + T ∑ F k J k = − A d ξ d t + T ∑ F k J k = 0
In this case, Equations (69) and (70) shed light on the volume element ∆ γ r e v i r V S y of the primary system of the composite system, revealing its dynamic nature. For instance, when the volume elements of the primary system experience fluctuations in the chemical reaction velocity, the system’s behavior becomes more complex. In some elements of the volume, the reaction runs faster compared to the hypothetical infinitesimally slow chemical reaction, leading to a deviation from the state with uniform velocities for each element of the volume (Figure 6). This dynamic behavior results in the concentrations of reactive components becoming non-uniform across the volume elements of the primary system. In addition to the thermodynamic force of the chemical reaction A/T (i.e., d G r x n = − A d ξ , Equation (70)), the dynamic system also gives rise to the thermodynamic force of diffusion of reactive components (diffusion between the volume elements of the primary system). ( d n k -differential amount of the k-th reactive component that diffuses in the dt time interval and ∆ μ k is the difference of the k-th component chemical potential between two points of the volume element ∆ γ r e v i r V S y ; for example, if ∆ γ r e v i r V S y = 2 ∆ γ r e v V S y , i.e., z = 2 then the difference ∆ μ k is between the two volume elements ∆ γ r e v V S y ):
d G r x n d t + T ∑ ∆ μ k T d n k d t = d G r x n d t + ∑ ∆ μ k J k = 0
The emergence of the thermodynamic force of diffusion can reduce the chemical potential of a reactive component in some volume element of the primary system. This, in turn, significantly influences the De Donder affinity (A) of the chemical reaction. The result is the absence of d G r x n in some volume elements of the primary system, leading to the absence of useful non-expansion work. However, the most significant impact is the generation of entropy due to the irreversible diffusion process (Equation (71)), a crucial aspect of the system’s behavior.

2.5. Change of the Gibbs Free Energy whiout Non-Expansion Work

Suppose non-expansion work is not obtained from the closed CS, i.e., in that case, no chemical reaction takes place in the primary system Sy, but a quasi-static reversible expansion of the Sy’s volume, during which the Sy’s pressure also changes while T = const. (Figure 7). The change in Gibbs free energy for the isothermal quasi-static reversible process, i.e., an ideal gas’s expansion (no friction between cylinder and piston), is ( T = c o n s t . :     p V = c o n s t .   → p d V + V d p = 0 → − d V / V = d p / p ):
d G = d U T = V d p = n R T d p / p = − n R T d V / V = − n R T d l n V
During the isothermal volume expansion process (pressure-volume work) of an ideal gas in the primary system of CS, the change in internal energy is zero ( d U S y = 0 ). Hence, Equation (72) has the following form:
d G = d U T = d U S y ⏟ 0 + d U R = − n R T d l n V
Let isothermal pressure-volume work first occur (for example, expansion of the primary system from CS), whereby a differential change in the volume of the primary system also means a differential change in the total volume of CS. The transfer of heat from the reservoir toward the primary system follow the expansion of the primary system – the primary system is located in the thermoreservoir, according to which the wall of the primary system is fixed, the wall of the primary system changes according to the RWR (Figure 7). As dSSy = -dSR is valid, Equation (73) is the quasi-static reversible (maximum) differential pressure-volume work:
d G = d U T = T d S R = d U R = − n R T d l n V T = δ w v o l m a x
During expansion, the system performs work on RWR, so that in terms of CS, the maximum differential pressure-volume work has a negative value:
d G = δ w v o l m a x < 0   a n d   d S T = d S S y + d S R = 0
It follows from Equations (73) and (74) that the maximum differential pressure-volume work (expansion) comes from the change in the internal energy of the reservoir. A similar result is obtained starting from the Helmholtz free energy. If friction occurs during the movement of the piston – spontaneous dissipation of pressure-volume work into thermal energy, then a smaller absolute value of the pressure-volume work is obtained, i.e., Equation (32) applies:
d G − δ w v o l < 0   a n d   d G − δ w v o l = γ i r d U T = − γ i r T d S T = − δ I
Of course, even in this case, it is valid that at maximum irreversibility, the pressure-volume work of expansion of the primary system is zero, i.e., the change in Gibbs free energy is dissipated as thermal energy in CS (76). In the state of thermal and mechanical equilibrium of the primary system, i.e., without quasi-static pressure-volume work, dG = 0.
However, it should be emphasized that during the isothermal expansion of the primary system Sy (Figure 7), at every moment of the infinitely slow thermodynamic process, the primary Sy is in mechanical equilibrium with the environment, i.e., in this case with RWR, so the quasi-static process is reversible with a total entropy change that is zero. However, suppose a chemical reaction occurs in the primary system where De Donder’s affinity is not zero ( A = − d G r x n / d ξ ≠ 0 ). In that case, the chemical reaction (and, therefore, the primary system) is not in equilibrium – therefore, it is not a reversible process. According to Calen, if every infinitesimal step of a chemical reaction is described with an expression that refers to a quasi-static process: d G = ∑ μ i d n i = ∑ ν i μ i d ξ (p, T = const.) and, at the same time, the process is isentropic (i.e., the total entropy does not change in the composite system) [7]. This hypothetical reaction in obtaining the maximum non-expansion work is identical to a reversible thermodynamic process.

2.6. Analogy between the Gibbs Free Energy and the Helmholtz Free Energy

If the volume of the primary system (and the thermoreservoir) does not change during the thermodynamic process, then Equation (25) is:
d U T = d U S y + T d S R = d U S y − T d S S y = d U S y − T S S y = d A
From the Equation (77) follows the relations of the differential change of the Helmholtz free energy for a closed and isolated system at V,T = const. – criteria for a quasi-static reversible (isentropic) and spontaneous irreversible process, or an equilibrium state – a system without a thermodynamic process (Table 1) – analogous to the criteria at p,T = const. – differential change of Gibbs free energy (33)-(36) and (39).

3. Conclusions

De Donder’s equation of entropy generation in an irreversible thermodynamic process follows from the equation –TdST = dUT. Irreversibility can be defined as a measure of the lost working capacity of a chemical reaction by partial (per system volume) application of the equation – TdST = dUT. If the primary system of a composite system is viewed as a sum of black box volume elements, then in each of these volume elements, the criterion for an isentropic process and a process (irreversible process) with entropy generation is in the Gibbs-Duham equation.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Kondepudi, D.; Prigogine, I. Modern Thermodynamics, From Heat Engines to Dissipative Structures; John Wiley & Sons: Chichester, GB, 2002; pp. 125–130. [Google Scholar]
  2. Teixeira-Dias, J.J.C. Molecular Physical Chemistry, A Computer-based Approach Using Mathematica® and Gaussian; Springer Nature: Cham, Switzerland, 2017; pp. 47–49. [Google Scholar]
  3. Atkins, P.; Paula, J. Physical Chemistry for the Life Sciences, 2nd ed.; Oxford University Press: Oxford, GB, 2010; pp. 91–100. [Google Scholar]
  4. Engel, T.; Reid, P. Thermodynamics, Statistical Thermodynamics, & Kinetics, 2nd ed.; Pearson Education Inc.: Upper Saddle River, NJ, USA, 2010; pp. 116–119. [Google Scholar]
  5. Glasser, L. Correct Use of Helmholtz and Gibbs Function Differences, ΔA and ΔG: The van’t Hoff Reaction Box. J. Chem. Educ. 2016, 93, 978. [Google Scholar] [CrossRef]
  6. Schmidt-Rohr, K. Expansion Work without the External Pressure and Thermodynamics in Terms of Quasistatic Irrecersible Processes. J. Chem. Educ. 2014, 91, 402–409. [Google Scholar] [CrossRef]
  7. Callen, H.B. Thermodynamics and Introduction to Thermostatistics, 2nd ed.; John Wiley & Sons: Singapore, Singapore, 1985; pp. 153–159. [Google Scholar]
  8. Daily, J.W. Statistical Thermodynamics an Engineering Approach; Cambridge University Press: Cambridge, United Kindo, 2019; pp. 21–27. [Google Scholar]
  9. Keszei, E. Chemical Thermodynamics; An Introduction; Springer-Verlag: Berlin Heidelberg, Germany, 2012; pp. 44–50. [Google Scholar]
  10. Palazzo, P. Chemical and Mechanical Aspect of Entropy-Exergy Relationship. Entropy 2021, 23, 972. [Google Scholar] [CrossRef] [PubMed]
  11. Hladky, P.W. From Bunsen Burners to fuel Cells. J. Chem. Educ. 2009, 86, 582. [Google Scholar] [CrossRef]
  12. Keifer, D. Enthalpy and the Second Law of Thermodynamics. J. Chem. Educ. 2019, 96, 1407. [Google Scholar] [CrossRef]
  13. Noll, R.J.; Hughes, J.M. Heat Evolution and Electrical Work of Batteries as a Function of Discharge Rate: Spontaneous and Reversible Processes and Maximum Work. J. Chem. Educ. 2018, 95, 852. [Google Scholar] [CrossRef]
  14. Osara, J.A.; Bryant, M.D. Thermodynamics of Fatigue: Degradation-Entropy Generation Methodology for System and Process Characterization and Failure Analysis. Entropy 2019, 21, 685. [Google Scholar] [CrossRef] [PubMed]
  15. Osara, J.A.; Bryant, M.D. Methods to Calculate Entropy Generation. Entropy 2024, 26, 237. [Google Scholar] [CrossRef] [PubMed]
  16. Poša, M. Connecting De Donder’s Equation with the Differential Changes of Thermodynamic Potentials: Understanding Thermody-namic Potentials. Found. Chem. 2024, in press. [Google Scholar] [CrossRef]
  17. Moretti, G. The “Extent of Reaction”: a Powerful Concept to Study Chemical Transformation at the First-Year General Chemistry courses. Found. Chem. 2015, 17, 107. [Google Scholar] [CrossRef]
  18. Winterbone, D.E. Advanced Thermodynamics for Engineers; Butterworth-Heineman: Oxford, United Kingdom, 1996. [Google Scholar]
  19. Alberty, R.A. Use of Legendre Transforms in Chemical Thermodynamics. Pure. Appl. Chem. 2001, 73, 1349. [Google Scholar] [CrossRef]
  20. Raff, L.M. Spontaneity and Equilibrium: Why “ΔG < 0 Denotes a Spontaneous Process” and “ΔG = 0 Means the System Is at Equilibrium” Are Incorrect. J. Chem. Educ. 2014, 91, 386. [Google Scholar]
  21. Hanlon, R.T. Deciphering the Physical Meaning of Gibbs’s Maximum Work Equation. Found. Chem. 2024, 26, 179. [Google Scholar] [CrossRef]
  22. De Heer, J. The Principle of Le Chatelier and Braun. J. Chem. Educ. 1957, 34, 375. [Google Scholar] [CrossRef]
  23. Xue, T.-W.; Guo, Z.-Y. What is the Real Clausius Statement of the Second Law of Thermodynamics? Entropy 2019, 21, 926. [Google Scholar] [CrossRef]
  24. Xue, T.-W.; Zhao, T.; Guo, Z.-Y. A Symmetric Form of the Clausius Statement of the Second Law of Thermodynamics. Entropy 2024, 26, 514. [Google Scholar] [CrossRef] [PubMed]
  25. Sandler, S.I. Chemical, Biochemical, and Engineering Thermodynamics, 4th ed.; John Wiley & Sons: Asia, 2006; pp. 791–799. [Google Scholar]
  26. Lente, G. The Connection Between the Second Law of Thermodynamics and the Principle of Microscopic Reversibility. J. Math. Chem. 2010, 47, 1106. [Google Scholar] [CrossRef]
  27. Liu, Y.; Liu, Y.; Drew, M.B.G. Natural Mathematical Derivation of the Gibbs-Duham Equation Related to ΔG and ∂G/∂ξ. Int. J. Thermophys. 2022, 43, 73. [Google Scholar] [CrossRef]
  28. Lucia, U. The Gouy-Stodola Theorem in Bioenergetic Analysis of Living Systems (Irreversibility in Bioenergetics of Living Systems). Energies 2014, 7, 5717. [Google Scholar] [CrossRef]
  29. Lucia, U. Stationary open systems: A brief review on contemporary theories on irreversibility. Phys. A 2013, 392, 1051. [Google Scholar] [CrossRef]
  30. Rastogi, R.P.; Shabd, R. Thermodynamics of Stability of Nonequilibrium Steady States. J. Chem. Educ. 1983, 60, 540. [Google Scholar] [CrossRef]
Preprints 111322 g001
Figure 1. The total entropy (ST) of an isolated system (the total internal energy is constant) increases to the equilibrium state and the total internal energy (UT) in a closed system decreases until the equilibrium state is established. If the change in the system’s state starts from the xj (i) initial value of an extensive variable, regardless of whether an isolated composite system with the constant total internal energy is observed (total entropy of the composite system increases to equilibrium) or an isentropically closed composite system (the total internal energy of a composite system decreases to the final equilibrium); the system is reached the same equilibrium state xj (e).
Figure 1. The total entropy (ST) of an isolated system (the total internal energy is constant) increases to the equilibrium state and the total internal energy (UT) in a closed system decreases until the equilibrium state is established. If the change in the system’s state starts from the xj (i) initial value of an extensive variable, regardless of whether an isolated composite system with the constant total internal energy is observed (total entropy of the composite system increases to equilibrium) or an isentropically closed composite system (the total internal energy of a composite system decreases to the final equilibrium); the system is reached the same equilibrium state xj (e).
Preprints 111322 g001
Preprints 111322 g002
Figure 2. Meaning of De Donder’s equation: A1 isolated composite system (Sy = primary system and R = T, p reservoir), A2 closed composite system, B1 isolated system with constant volume and without a reservoir of intensive thermodynamic parameter, B2 closed system with constant volume and without a reservoir.
Figure 2. Meaning of De Donder’s equation: A1 isolated composite system (Sy = primary system and R = T, p reservoir), A2 closed composite system, B1 isolated system with constant volume and without a reservoir of intensive thermodynamic parameter, B2 closed system with constant volume and without a reservoir.
Preprints 111322 g002
Preprints 111322 g003
Figure 3. Composite system CS with two real or imaginary compartments, in the γ r e v part of the CS, a quasi-static reversible process always takes place, while in the γ r e v i r part of the CS, in addition to the quasi-static reversible process, irreversible thermodynamic processes can also take place; in case of a, a quasi-static reversible process takes place, while in case of b, in addition to a quasi-static reversible thermodynamic process, an irreversible process also takes place.
Figure 3. Composite system CS with two real or imaginary compartments, in the γ r e v part of the CS, a quasi-static reversible process always takes place, while in the γ r e v i r part of the CS, in addition to the quasi-static reversible process, irreversible thermodynamic processes can also take place; in case of a, a quasi-static reversible process takes place, while in case of b, in addition to a quasi-static reversible thermodynamic process, an irreversible process also takes place.
Preprints 111322 g003
Preprints 111322 g004
Figure 4. The change in Gibbs free energy is equal to the change in the total internal energy of the composite system (CS), in the case of a quasi-static reversible process the change in total entropy of CS is equal to zero (Sy = primary system, R = T, p reservoir, RWR = reversible work (source) reservoir).
Figure 4. The change in Gibbs free energy is equal to the change in the total internal energy of the composite system (CS), in the case of a quasi-static reversible process the change in total entropy of CS is equal to zero (Sy = primary system, R = T, p reservoir, RWR = reversible work (source) reservoir).
Preprints 111322 g004
Preprints 111322 g005
Figure 5. In a closed composite system (CS), with an increase in irreversibility (from A to C), a smaller amount of useful work is obtained in absolute value (RWR = reversible work (source) reservoir).
Figure 5. In a closed composite system (CS), with an increase in irreversibility (from A to C), a smaller amount of useful work is obtained in absolute value (RWR = reversible work (source) reservoir).
Preprints 111322 g005
Preprints 111322 g006
Figure 6. Black box method application in the volume element of the primary system of CS.
Figure 6. Black box method application in the volume element of the primary system of CS.
Preprints 111322 g006
Preprints 111322 g007
Figure 7. Composite system CS, which consists of a thermoreservoir (R) and a primary system (Sy), during isothermal quasi-static reversible pressure-volume work, the ball’s (m) potential energy increases in the RWR (reversible work (source) reservoir).
Figure 7. Composite system CS, which consists of a thermoreservoir (R) and a primary system (Sy), during isothermal quasi-static reversible pressure-volume work, the ball’s (m) potential energy increases in the RWR (reversible work (source) reservoir).
Preprints 111322 g007
Table 1. Thermodynamic processes and differential changes of thermodynamic potentials G (Gibbs free energy) and A (Helmholtz free energy) in closed and isolated systems.
Table 1. Thermodynamic processes and differential changes of thermodynamic potentials G (Gibbs free energy) and A (Helmholtz free energy) in closed and isolated systems.
Thermodynamic Processes p , T = c o n s t . V , T = c o n s t .
quasi-static reversible (QSR) or isentropic process in a closed system d G − δ w m a x = 0 1 d A − δ w m a x = 0 1
S T = c o n s t . and d U T = d G = d A < 0
QSR and parallel spontaneous irreversible process in a closed system d G − δ w < 0 ∆ G > w d A − δ w < 0 ∆ A > w
d S T > 0 and d U T = δ w < 0
spontaneous irreversible process in an isolated system or a closed system with Imax – no useful non-expansion work d G − 0 < 0 d A − 0 < 0
d S T = d S T m a x > 0 and U T = c o n s t .
equilibrium state in a closed and isolated system – there is no macroscopically thermodynamic process
d G = 0 d A = 0
d S T = 0 and d U T = 0
1 In the state p,T = const. dwmax represents the differential maximum non-expansion work, also at V,T = const. δwmax represents the differential maximum non-expansion work.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

115

Views

94

Comments

0

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

Email

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated