1. Introduction
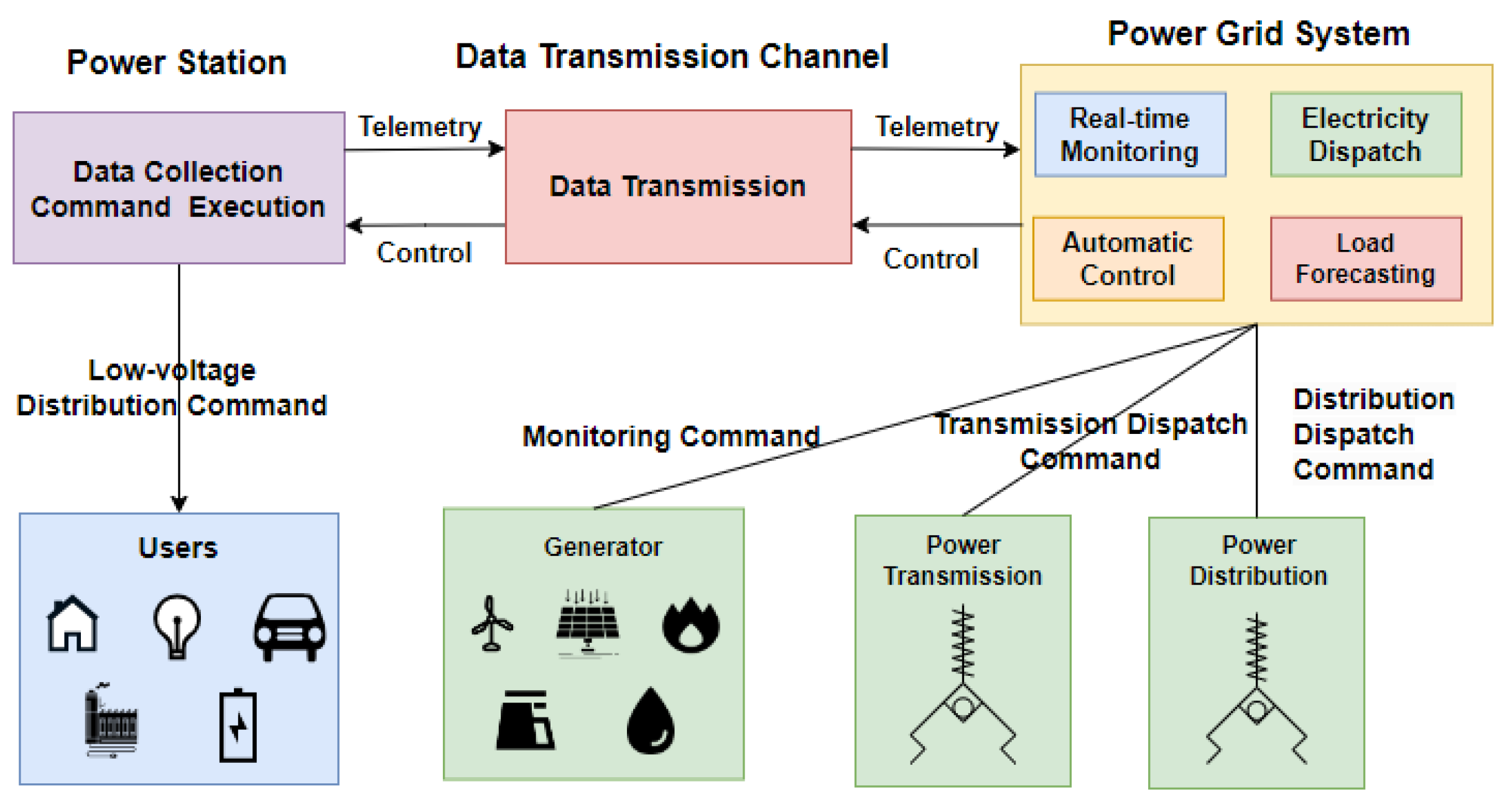
Integrating renewable energy sources into the electricity market has amplified uncertainties in power systems. It is the critical role of electricity load forecasting techniques in efficient power system management, which impacts operation and maintenance activities of transmission and distribution systems. Within competitive electricity markets, the accuracy of load forecasts significantly affects financial, infrastructural, and operational aspects. Notably, even a 1% increase in STLF error could potentially lead to an additional
$10 million in annual operational costs [
1]. As shown in
Figure 1, STLF is important for energy efficiency and sustainability because of its crucial role in balancing power generation and consumption [
2,
3,
4].
Existing prediction models can be primarily categorized into three types: statistical models [
5,
6,
7,
8], AI models [
9,
10,
11,
12,
13,
14,
15,
16], and hybrid models [
17,
18,
19,
20,
21,
22]. Hybrid models are considered highly accurate because they combine the strengths of multiple models while overcoming individual models’ limitations [
23,
24]. However, STLF is often affected by external factors outside the power system, such as temperature, electricity prices, and others [
25,
26]. However, hybrid models in previous studies consider very few such factors. To make the prediction models work in realistic conditions, it is critical to consider a wide range of factors, particularly external factors [
27]. Furthermore, the model combining methods in existing studies are often simple, e.g., the reciprocal of errors method to combine long short-term memory network (LSTM) and XgBoost models based on the weight of MAPE [
18]. Therefore, stacking techniques have been proposed for STLF without thorough analysis and discussion [
28].
We propose a novel hybrid model called the stacked model that leverages the stacking technique to enhance prediction accuracy by considering multiple external factors. The stacking technique is chosen for its ability to combine the strengths of various base models, thereby improving the overall predictive performance. Our model integrates XgBoost, LSTM, Bi-LSTM, and stacked LSTM as base learners, each contributing unique strengths: XgBoost handles structured data and captures non-linear relationships effectively, LSTM and Bi-LSTM excel at learning long-term dependencies in sequential data, and stacked LSTM further improves the depth of temporal feature extraction. Lasso regression is used as the meta-learner to combine the outputs of these base models, ensuring robust and sparse predictions. By considering factors such as temperature, rainfall, and daily electricity prices, the model aims to more accurately reflect real-world conditions and improve prediction accuracy under both stable and unstable load conditions. This paper makes several significant contributions to accurate load forecasting for helping power system planning and dispatch and reducing economic loss. Our contributions are summarized as follows:
Based on different AI model’s complementary strengths in handling non-linear relationships, long-term dependencies, and temporal feature extraction, our model outperforms five single AI models (ANN, XgBoost, LSTM, two-layer LSTM, and Bi-LSTM) and two hybrid models (ANN-WNN and LSTM-XgBoost).
To address the varying load characteristics in different regions, we enhanced the prediction accuracy under both stable and unstable load conditions.
Integrating external factors to simulate real-world conditions and maintain high enhance the accuracy, such as minimum and maximum temperature, electricity price, and rainfall level.
We validate the novel application of the stacking technique by integrating a broader diversity of AI models, demonstrating its superior capability in improving prediction accuracy.
The rest of this paper is structured as follows:
Section 2 provides an overview of recent relative literature on STLF. The relative methodology and the framework of the proposed model are discussed in
Section 3. We describe the case study and experimental results in
Section 4. The effect and limitation of the proposed model are presented in
Section 5, and the paper is concluded in
Section 6.
2. Literature Review
In this section, we provide a comprehensive review of various models utilized in STLF using various models.
2.1. Statistical Models
A statistical model is based on the mathematical function that leverages sample data to make projections about broader phenomena, grounded on a mix of mathematical functions and statistical principles. Many statistical models exist, including the auto-regressive integrated moving average (ARIMA), its extension auto-regressive integrated moving average with explanatory variable (ARIMAX), the Kalman Filter (KF), and multiple linear regression (MLR) models [
29]. The ARIMA model is proposed to predict peak load, and it has better performance than the auto-regressive moving average (ARMA) model [
8]. An improved KF model has been proposed to further enhance the accuracy of peak load forecasting [
6].
Additionally, the ARIMAX model, considering the varying consumer behavior during weekdays, weekends, and holidays, has outperformed the ARMA model [
7,
30]. A seasonal auto-regressive integrated moving average (SARIMA) model was proposed to address the nonlinear relationships among variables and determine relevant time lag patterns [
5]. However, when the forecasting process incorporates multiple variables, statistical models encounter difficulties due to extended computation times, increased processing demands, and limited scope for generalization [
28].
2.2. Artificial Intelligence Models
AI models are considered more advanced due to their ability to unravel complex, nonlinear relationships between load and influencing factors [
31]. Artificial neural network (ANN) models are often employed in STLF for their self-learning and error tolerance abilities, but their limited generalizability led to the development of the support vector machines (SVM) model to address these limitations [
9]. Comparative studies have demonstrated the superiority of the XgBoost model over the back-propagation neural network in prediction accuracy when considering seasonal patterns [
10]. A window-based XgBoost Model was proposed, incorporating real-time electricity pricing, maintaining an impressive MAPE of 0.35% [
16]. Furthermore, an advanced Xgboost model is used to identify extreme weather for determining the range of peak load occurrence [
11].
Furthermore, two LSTM models with different uses are proposed, one for predicting single-step ahead load and the other for multi-step intraday rolling horizons. These models have demonstrated superior performance compared to the generalized regression neural network (GRNN) model and extreme learning machine (ELM) [
12]. Considering the excellent performance and diversity of the LSTM model, [
14] compared the performance of Bi-directional long short-term memory (Bi-LSTM) and stacked LSTM, showing that the Bi-LSTM is better than the stacked LSTM due to the lowest MAPE of 0.22%. Besides, the Bi-LSTM model is validated to have excellent peak value prediction capability [
13]. However, superior performance of stacked LSTM over Bi-LSTM was observed [
15]. This performance discrepancy could be attributed to differences in the datasets used, but it is undeniable that various LSTM models perform consistently well in STLF problems.
2.3. Hybrid Models
A hybrid model combines two or more models into a whole, and it leverages the advantages of individual models [
32,
33]. To make accurate predictions, data processing algorithms have been combined with artificial neural networks, resulting in the creation of hybrid models. [
21] proposed a hybrid STLF model using a grasshopper optimization algorithm (GOA) to optimize parameters and a support vector network (SVN) for prediction. It achieves higher accuracy than SVM models when considering temperature and humidity. However, [
21] acknowledged the potential for improvement by considering additional influential variables. Another proposed hybrid model uses wavelet neural networks (WNN) for decomposing the load and influenced factors into several components and predicting by ANN, resulting in a lower MAPE than that of ANN [
22].
Hybrid models have been proposed using the k-means method for data grouping and ANN-WNN for prediction exhibiting extraordinary results [
17]. This model applies WNN to forecast residuals from the ANN model. This integration enhances data variance and the forecasting accuracy of the model, leading to better performance than standalone ANN or WNN models. Furthermore, an LSTM-XgBoost model uses a reciprocal error method for improved accuracy, achieving a MAPE of 0.57 [
18]. Despite the demonstrated effectiveness of these hybrids, the stacking method is viewed to be more effective in integrating models, but the discussions are limited [
28]. One hybrid model combines a stacking technique with an improved artificial fish swarm algorithm to unite multiple support vector regression (SVR) models, considering previous day temperature data [
19]. In addition, a hybrid model combining multiple deep neural network (DNN) models as base models were developed in [
20], utilizing principal component regression (PCR) to construct a meta-model. These hybrid models highlight the potential of ensemble learning for improving prediction accuracy.
3. Methodology and Framework
This section describes the related methodology and the structure of the proposed model.
3.1. Related Methodology
3.1.1. XgBoost
XgBoost [
34] stands for Extreme Gradient Boosting, which is a machine learning system based on Gradient Boosting design with higher performance. Moreover, it demonstrates a robust capacity for accurately capturing dynamic trends in short-term power loads, proving particularly effective in tackling STLF problems [
10]. It mainly uses the gradient-boosting decision tree to improve speed and performance. It tries to correct the residuals of all previous weak learners by adding new weak learners because one learner may not be enough to get good results. When these learners are combined together for the final prediction, the accuracy is higher than that of individual learners. The final prediction is the sum of each learner’s scores [
35,
36].
The computational procedure of the XgBoost is as follows [
35]:
1: The sample weights and model parameters are first initialized by assigning the same weights to all samples in the training set.
2: We need to use Equation (
1) to calculate the classification error rate at each iteration:
where
is the weight of the i-th sample,
is the c-th classifier.
3: In the
iteration, we need to calculte the weight of the
sample as Equation (
2):
where
= log((1-
)/
)
4: Training XgBoost involves reducing the loss of the dataset’s goal function. To balance the decay of the goal function with the model’s complexity, a second-order Taylor expansion is performed on the loss function, and a regular term is added to the objective function to prevent overfitting. Use of Equation (
3) to compute the objective function:
where n is the dimension of the feature vector, L(
,
) is the loss function,
is the true value,
is the predicted value,
(
) is a regular term, used to control the complexity of the tree structure.
5: As for the complexity, we use Equation (
4) to calculate:
where N is the number of leaf nodes,
is the decreasing value of the minimum loss function for node splitting, which is used to control the degree of conversation. The representation of the weight L2 regularization is
. The square L2 modulus of w is used to regulate the tree’s complexity and prevent overfitting.
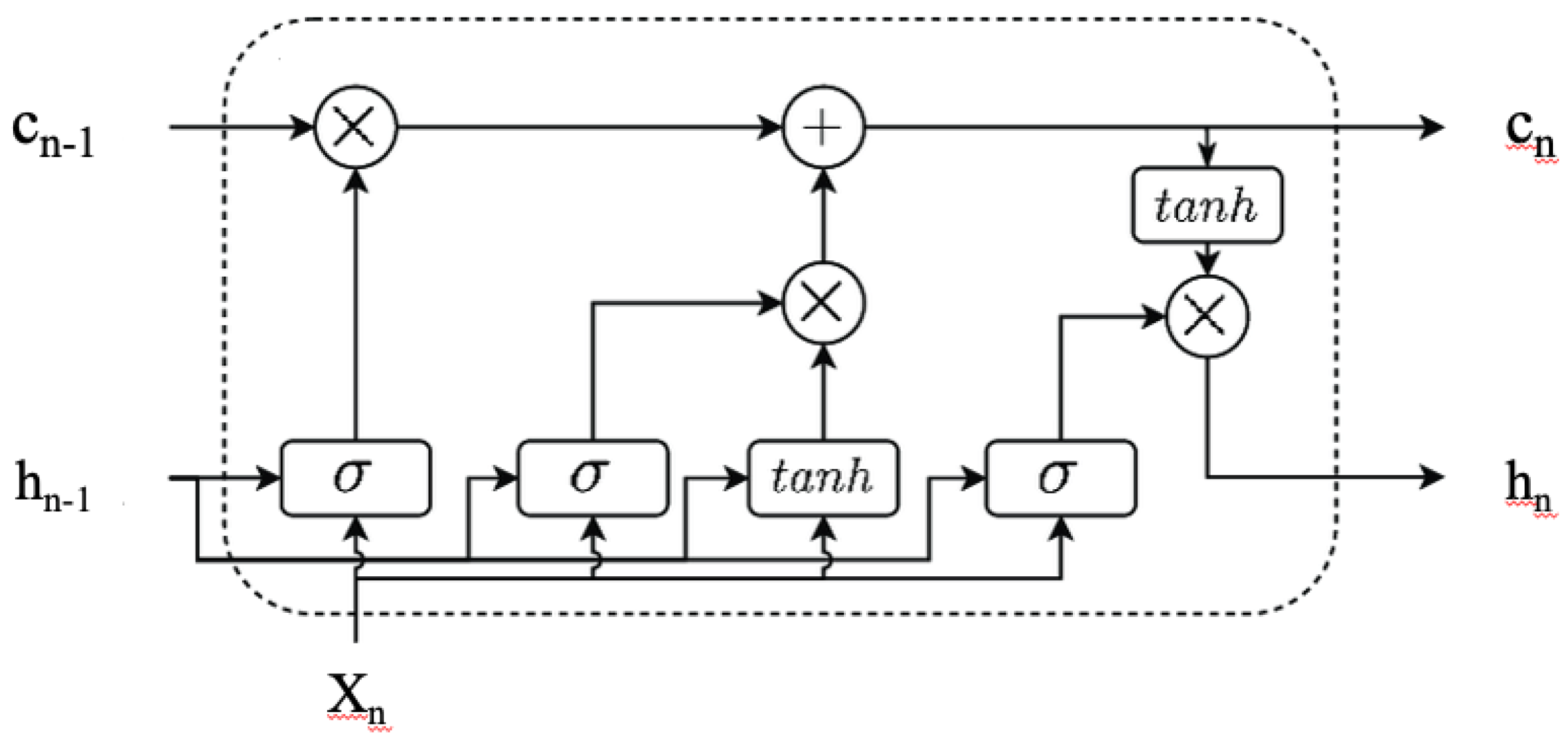
3.1.2. LSTM
LSTM is a recurrent neural network (RNN) architecture to address the challenges posed by processing long-time sequences in RNNs. LSTM tackles the gradient explosion or disappearance problem encountered by traditional RNNs due to their single-state hidden layer [
37]. LSTM introduces a memory cell and three types of gates: input gate, output gate, and forget gate. The memory cell serves as a long-term storage location capable of retaining information over extended periods, while the gates regulate the flow of information into and out of the cell. This architecture allows LSTM to store and propagate errors backward through time and layers, facilitating the learning process across multiple time steps [
38]. In the STLF problem, LSTM can handle input sequences of variable lengths, where historical load data have different lengths [
13]. Moreover, LSTM is adept at capturing sequential patterns and long-term dependencies in historical load data, including daily cycles and seasonal trends [
39]. The architecture of LSTM cell is shown in
Figure 2. The calculation process of each cell in LSTM is shown below[
37].
Forget Gate:
It determines what information to discard and how much useful information to retain from a prior cell state by assigning a value between 0 and 1 to the previous cell state in comparison to the current cell input with the help of the sigmoid activation function.
where
is the sigmoid function,
signifies the forget gate’s weight matrices,
indicates the bias terms of the forget gate, and [
,
]denotes combining two vectors into a single vector.
Input Gate:
Two vectors of the current unit are generated by applying the sigmoid activation function and the tanh activation function, respectively, to the output information of the previous unit and the input information of the current unit, and then these vectors are multiplied together to generate the final input information.
where
is the output information,
is the input information,
and
represent the input gate and cell state weight matrices, respectively, and
and
denote the bias terms of the input gate and cell state.
Cell Status:
Long-term memory updates by mixing previous data with new inputs. It updates by dot-producting the prior state and the forget gate, then adds the product of the input gate and current cell’s state.
Output Gate:
It assigns values between 0 and 1 to regulate information flow in its current state, using the sigmoid function for previous cell output data and processing current cell input data inversely. Next, it applies the tanh function to the cell state’s output, right before executing a dot product operation."
where
is the output information of the previous cell,
is the input information of current cell,
indicates the output gate weight matrices, and
denote the bias terms of output gate.
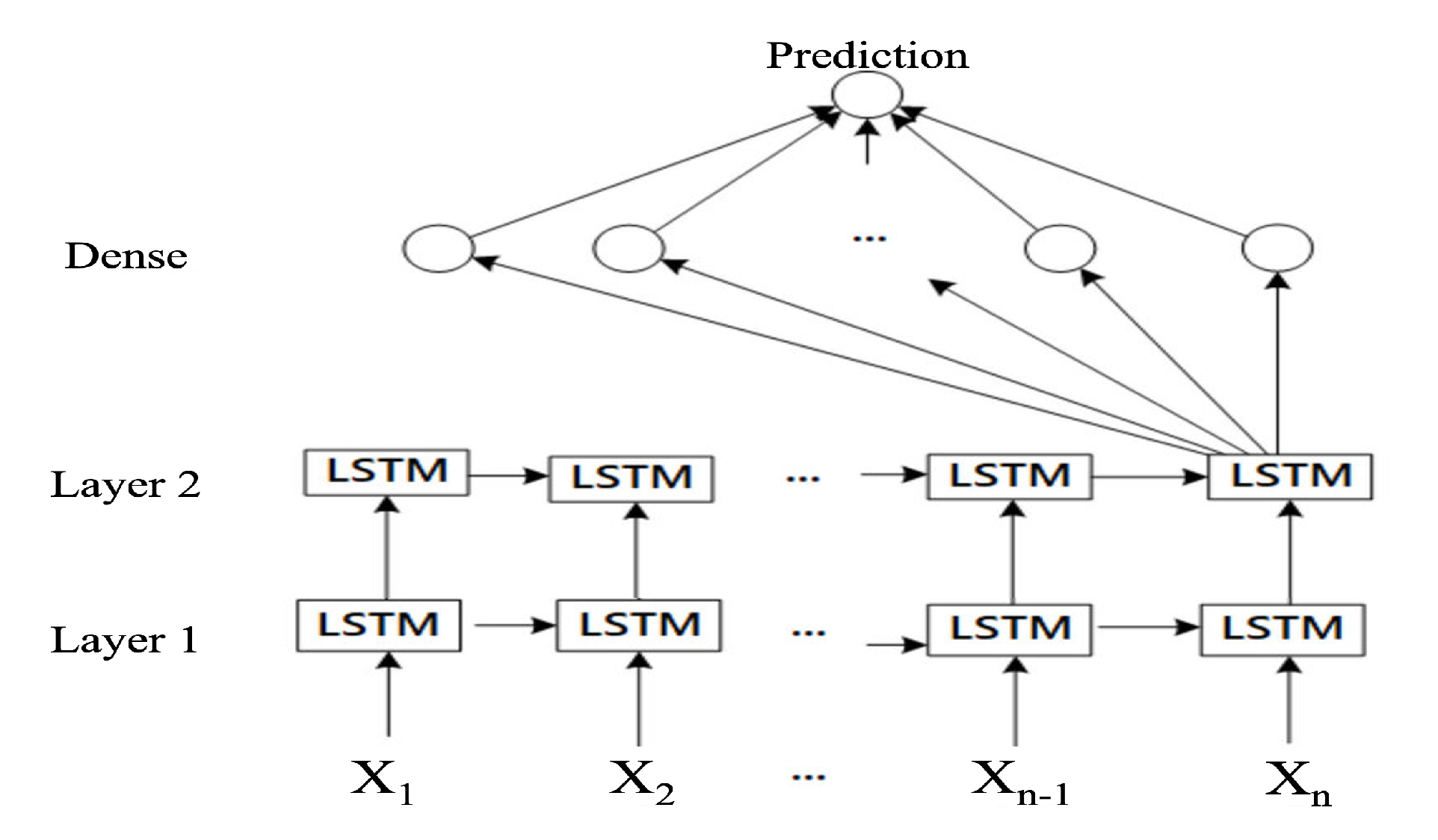
3.1.3. Stacked LSTM
Multiple layers of LSTM units comprise the stacked LSTM model, an extension of the LSTM model. Each layer of a stacked LSTM consists of multiple LSTM units, with the output of one layer as the input for the following layer [
15]. The layers are layered atop one another to form the architecture of a deep neural network. The architecture of the stacked LSTM is shown in
Figure 3. Using a stacked LSTM is intended to enhance the capacity and ability of the model to learn complex patterns in sequential data. Each stack layer can capture distinct levels of abstraction and learn distinct temporal dependencies [
20]. Lower layers can concentrate on capturing local patterns and short-term dependencies, whereas higher layers can learn more abstract and long-term dependencies.
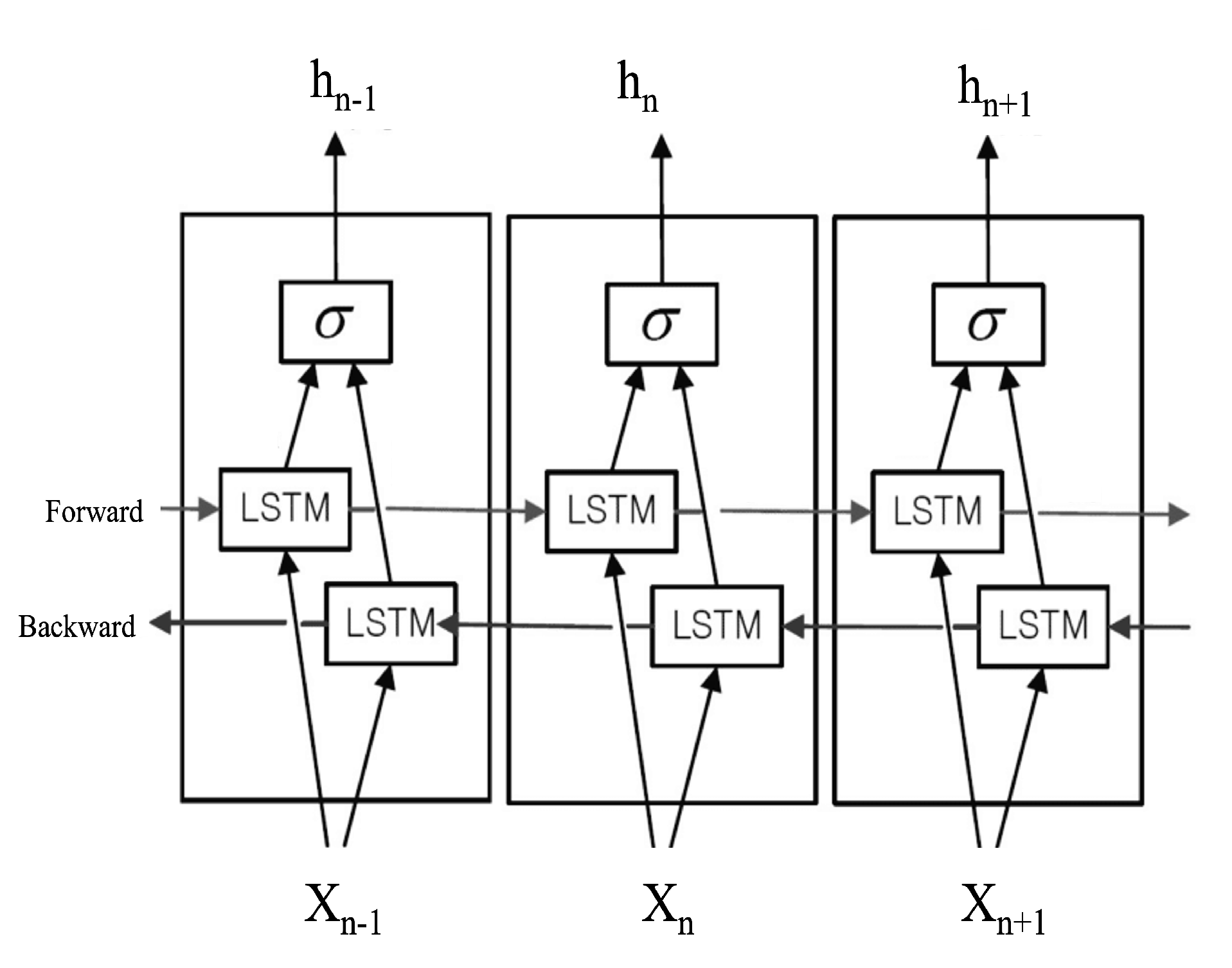
3.1.4. Bi-LSTM
The bidirectional LSTM (Bi-LSTM) is an extension of the traditional LSTM model that incorporates both forward and backward information flow. Bi-LSTM consists of a forward LSTM layer and a backward LSTM layer. During the forward pass, the forward LSTM processes the input sequence from the beginning to the end, capturing past information. Simultaneously, the backward LSTM processes the input sequence in reverse, capturing future information [
13]. The outputs of the two layers are combined to obtain the final output sequence. It allows the model to capture contextual information from both the forward and backward perspectives, reducing reliance on any single time step and improving model robustness [
14].
Figure 4.
The architecture of the Bi-LSTM
Figure 4.
The architecture of the Bi-LSTM
3.1.5. Lasso Regression
The Lasso regression algorithm is a linear regression approach adapted to L1-regularization function, it performs shrinkage and variable selection simultaneously for better prediction [
40]. As for feature selection, it can change the weight of useless features to zero to solve the multicollinearity problem among various features. The Lasso regression aims to identify the subset of important features that minimize response variables’ prediction error. The Lasso regression aims to minimize the loss function:
where
is the observed outcome for the
observation,
is the
feature value for the
observation,
is the coefficient for the
feature, and
is the regularization parameter. By increasing the value
, the coefficients of less important features are shrunk towards zero, and the model will become sparser and more interpretable.
3.1.6. Stacking Technique
The stacking technique is an ensemble learning method combining multiple models to improve machine learning performance. It is used to leverage the strengths of different models and minimize the weaknesses of each model. It is usually composed of two layers, a series of base models considered as the first layer, and a meta-model, which is usually only one and considered the second layer. The output of the base model will be input to the meta-model as new features, and the output of the meta-model is considered the final prediction result. As for the first layer, more base models are helpful for feature learning because they can obtain the learning ability of different models for features. As for the second layer, the regression algorithm is demonstrated to be effective [
20].
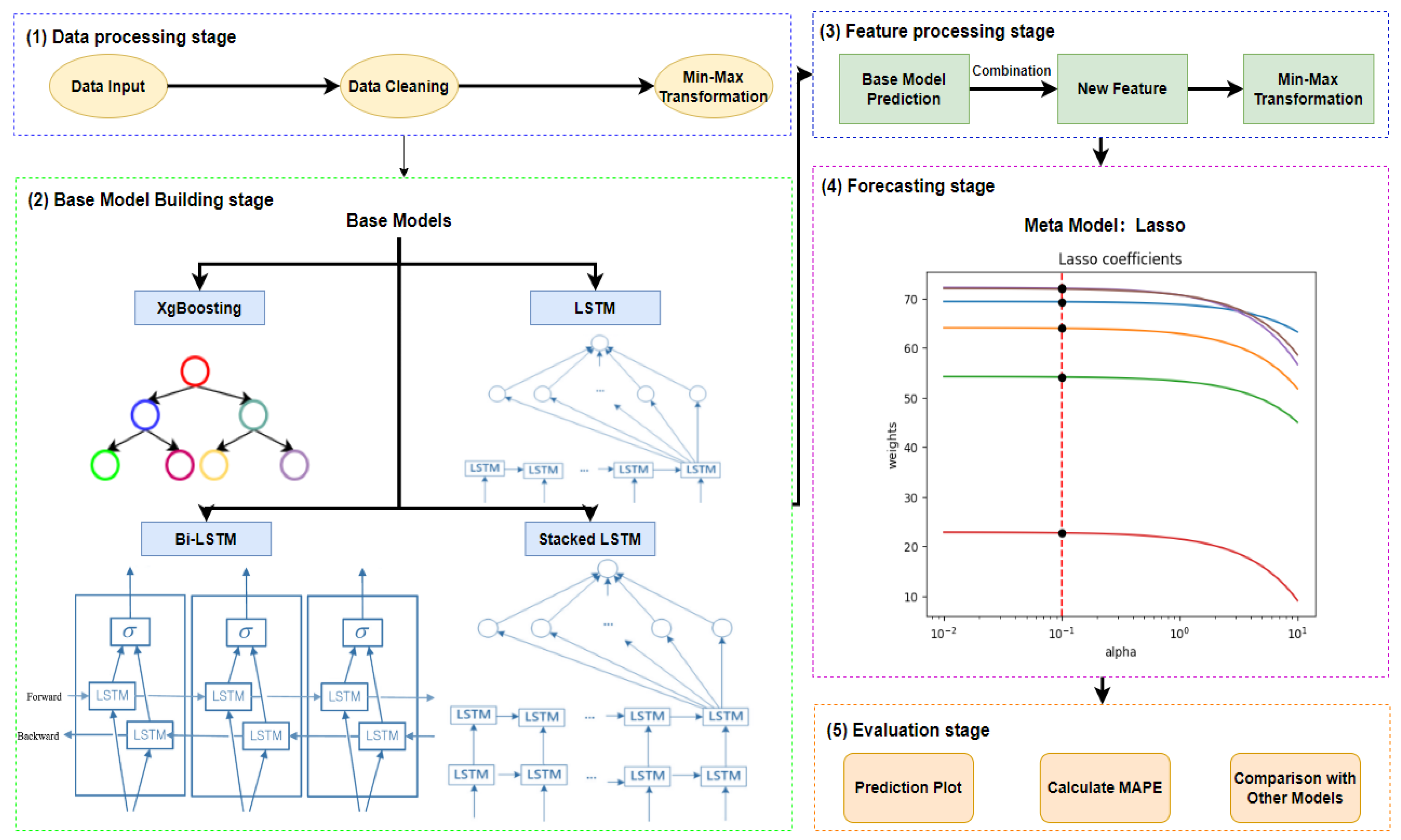
3.2. The Framework of the Proposed Model
The innovation of this study mainly lies in developing and applying a new load forecasting model using staking technology. Compared to other stacked models, it integrates some AI models as base models and considers more influencing factors in STLF. In addition to load factors, our dataset considers the highest and lowest temperatures, the amount of precipitation, and the daily electricity price. We aim to make more accurate predictions on stable and unstable load datasets under conditions closer to the natural environment.
The framework of the proposed model is shown in
Figure 5, it uses the stacking technique to combine the strengths of the models shown for an optimal load forecast. In the architecture of the model, XgBoost, LSTM, Bi-LSTM, and stacked LSTM act as the base model. The predictions of each model will be combined and used for the final prediction of the meta-model lasso regression. These base models create the first computational layer, each possessing unique capabilities in terms of processing data and recognizing patterns. Using a meta-model to integrate the predictions from multiple models, we can achieve a more comprehensive and robust forecast that considers diverse patterns and relationships within the data.
During the base model selection process, we chose the XgBoost model due to its capacity to model complex nonlinear relationships, its resistance to over-fitting, and its inbuilt regularization. The ability to capture temporal dependencies makes LSTM a base model for this task. The reason we chose stacked LSTM is for a better understanding of the underlying complexities within the data, we expect to capture more abstract features within sequences of data. As for the Bi-LSTM, it allows the model to capture patterns that future data points influence. Moreover, the grid search technique determines the selection of parameters within these models. This rigorous procedure ensures good performance by selecting the best combination of parameters for each model.
The process of building this model is summarized in the following four steps:
Transforming the training dataset by the min-max normalization. Standardizing the scaling of data is essential for reducing the likelihood of irregularities caused by heterogeneous data ranges.
Individually applying the four fundamental models to generate predictive outputs. These outputs are then merged to produce a comprehensive set of input features for the meta-model to train.
Adopting the min-max normalization for combined input features. It ensures that the input features presented to the meta-model are scaled appropriately, thereby improving the accuracy and reliability of final output predictions.
Utilizing the meta-model to generate the final prediction. The prediction is based on the input features that have been processed.
Validating the final prediction result by MAPE based on the testing dataset. It is helpful for evaluating the accuracy of the proposed model.
3.3. Measurement Method
This paper uses the MAPE to evaluate the performance and difference between the proposed model and previous models, it clearly provides the disparity between the predicted and actual values and facilitates the analysis of the impact brought about by precise predictions. The measurement method is defined as follows:
where
represents the actual load in one day respectively, and
is the value predicted by the model. A high MAPE indicates that the predictions of the model are significantly off from the actual values. To achieve the highest level of accuracy, the ideal objective in model prediction is to minimize the MAPE value.
4. Performance Evaluation
In this section, we conduct two real case studies to compare the performance of the proposed model with two hybrid modes proposed before and five AI models in stable and unstable load datasets. It has two hybrid models: ANN-ANN [
17], LSTM-XgBoost [
18], and five AI models: ANN, XgBoost, LSTM, Stacked LSTM, Bi-LSTM, which are the component of the hybrid model.
4.1. Data Exploration & Pre-Processing
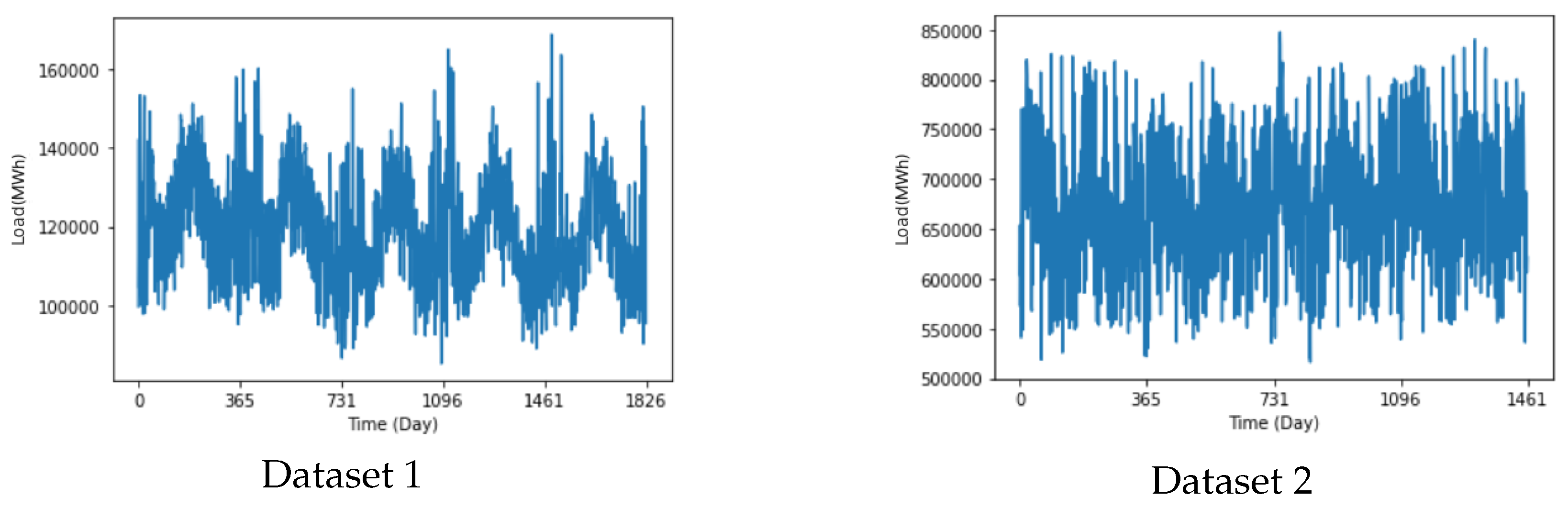
The robustness and accuracy of the proposed model were examined through the implementation of two real case studies. The primary case study used data acquired from Victoria, Australia, from 1 January 2015 to 31 December 2019 [
41]. The secondary case study utilized a dataset drawn from Spain, which integrated four consecutive years of data from 1 January 2015 to 31 December 2018 [
42]. Each dataset is plotted in
Figure 6. The Australian dataset manifests a stable and evident seasonal pattern, whereas the Spanish dataset, in contrast, demonstrates notable load fluctuations, indicating a more volatile nature.
To effectively simulate the impact of multiple influencing factors on the power load in real-world scenarios, our dataset comprehensively includes the daily electric load quantities, a wide spectrum of meteorological elements, and the concurrent daily electricity prices. The features of our datasets are shown in
Table 1. We anticipate that our model will maintain its capacity to generate accurate predictions even with the integration of more factors.
Before the model learning, we split 70% of the dataset for training and the remaining 30% for validation and testing. Given the substantial range inherent in several features that this study considers, we adopt the min-max normalization approach. This procedure uniformly adjusts each feature to fit a standard range of [0,1]. The definition of normalization function is as follows:
where
represents the processed data, and
is a data point.
and
represent the minimum and the maximum value of the sequence
, respectively.
4.2. Experimental Results
4.2.1. Australia Dataset Experiments
We analyzed the Australian dataset to evaluate the performance of proposed model exhibits a stable trend and distinct seasonal patterns. The dataset is compiled from daily samples taken over five years, resulting in 1826 data points.
Table 2 lists MAPE values for the proposed model and benchmarks. The MAPE of our proposed model demonstrates admirable accuracy, averaging around 5.99%. Compared to other forecasting models, this score is lower. One important finding is that while the LSTM-XgBoost model performs better than its XgBoost and LSTM component models individually, but it falls short of our proposed model. The better performance of Bi-LSTM and Stacked LSTM models compared to ANN-WNN and LSTM-XgBoost models can be attributed to the parameters set according to their original design.
Specifically, compared to the ANN-WNN model, the proposed model exhibits a significant improvement with a reduction of 45.65% in MAPE, representing the largest improvement of the proposed model. Similarly, compared to the LSTM-XgBoost model, the proposed model also achieves a reduction of 15.28% in MAPE. Furthermore, compared to the Bi-LSTM model, which already achieves the lowest MAPE among the other models, the proposed model achieves a notable reduction of approximately 9.2% in MAPE. Evaluating the remaining AI models, the improvement of the proposed model in terms of MAPE ranges between 10.6% and 45.46%. These results strongly highlight the potential advantages of the proposed model, as it combines the strengths of different models and effectively identifies complex relationships between variables.
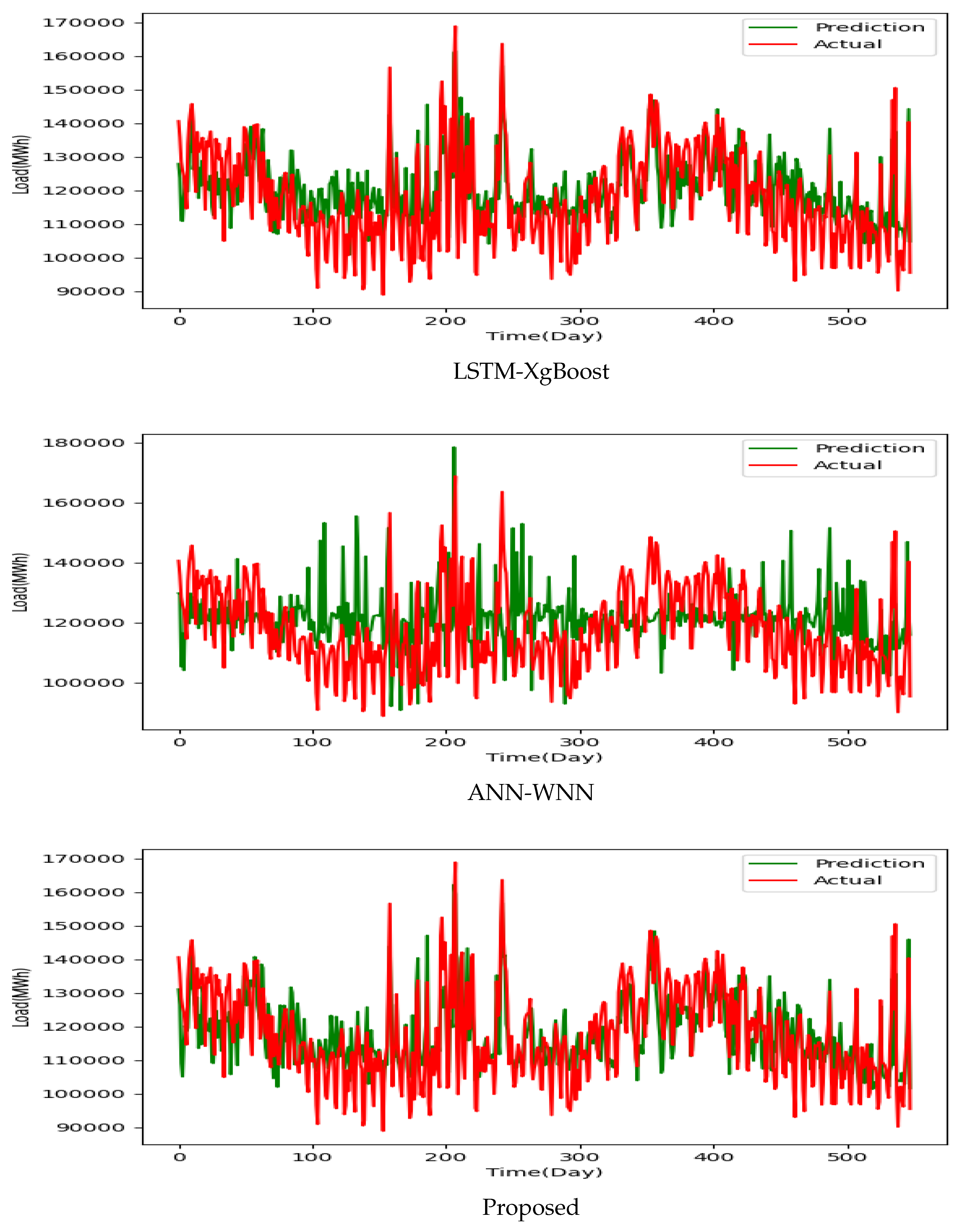
Figure 7 provides a graphical representation of the predicted and actual lines of the hybrid models and the proposed model. The proposed model demonstrates alignment with the actual data because it displays a laudable ability to accurately identify increased loads and corresponding peak values, even though fluctuations exist. The model adeptly recognizes seasonal patterns, contributing to an accurate representation of the overall load trend. However, it has drawbacks in identifying low values. Conversely, the LSTM-XgBoost and ANN-WNN hybrid models do not meet the anticipated performance standards. Instances arise where these models generate forecasts that starkly deviate from the actual data, and a consistent pattern of load overestimation is discernible. Such consistent overestimation could potentially instigate substantial resource wastage. The results highlight the accuracy and efficiency of the proposed model in identifying seasonal patterns and understanding the overall load trend. Consequently, the proposed model outperforms other models in terms of prediction accuracy and trend identification.
4.2.2. Spain Dataset Experiments
To verify the proposed model still applies to the unstable load dataset, we conducted a case study of the Spain dataset, sampled once daily for a total of 1,461 samples for four years. In contrast to the Australian dataset, this dataset lacks evident seasonal patterns and is marked by substantial very short-term fluctuations. Thus, we designate it as an unstable dataset. The efficacy of the proposed model and benchmarks are displayed in
Table 3. The proposed model continues to have the lowest MAPE in the unstable load dataset, at 7.8%, compared to other models. The predictive performance of hybrid models is superior to that of individual AI models because the performance of hybrid models exceeds that of the foundation models that compose them. Based on the results, we can conclude that the proposed model reduced the MAPE of the LSTM-XgBoost and ANN-WNN models by 11.3% and 16.4%, respectively. MAPE can increase by up to 24% compared to the ANN model with the worst performance.
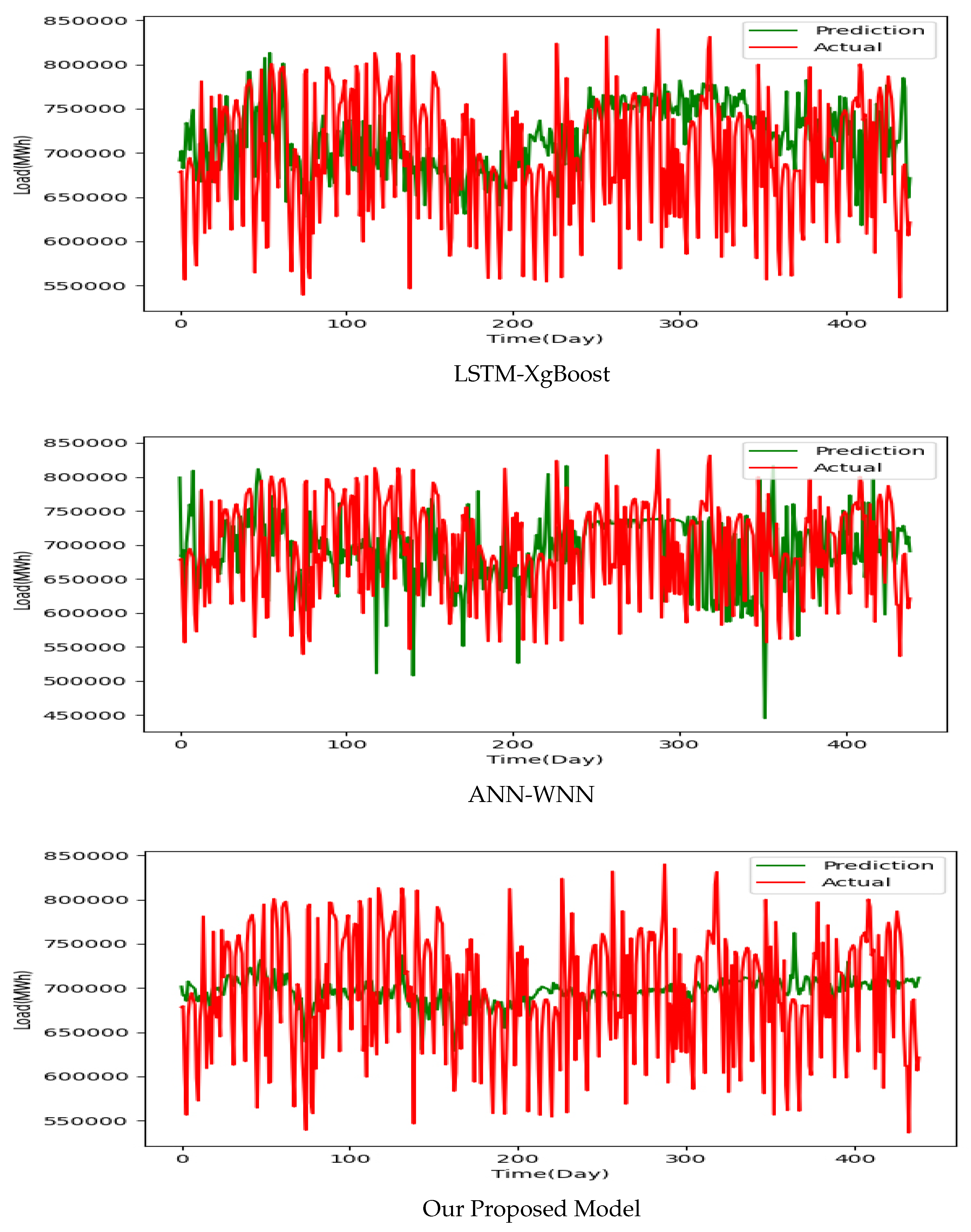
As shown in
Figure 8, the prediction line of the proposed model closely aligns with the actual line, effectively identifying both upward and downward trends in most situations. This trend consistency underscores the model’s capacity to capture load variations accurately. In contrast, other hybrid models demonstrate drawbacks in trend identification, particularly during extreme conditions, where their predictions frequently deviate considerably from actual values. A significant advantage of this model is that it does not produce outliers, whereas predictions from other models present multiple outliers. Furthermore, it resists the tendency to overestimate the load encountered with the LSTM-XgBoost model. Our proposed model effectively avoids scenarios of severe resource wastage and shortages, and it is helpful for dispatch and generation. Despite the noted improvement in trend identification, the proposed model exhibits some limitations in accurately forecasting the load due to the observed gap between actual and predicted values.
5. Discussion
In this section, we will provide a detailed explanation of the implications of the proposed model in real-world scenarios. Additionally, we will discuss the model’s limitations and provide recommendations for further improvement.
5.1. The Effect on Economy
Based on the above evaluation, our proposed hybrid approach using the stacking technique has been proven accurate in predicting non-linear, volatile, stationary, and seasonally fluctuating electricity demand. The accurate STLF leads to significant economic benefits, as a reduction of 1% in prediction errors can result in a cost reduction of
$10 million [
1]. It means the proposed model is beneficial for saving costs due to the higher accuracy. Besides, it will also help power companies make efficient generation decisions and properly plan maintenance schedules, resulting in substantial savings in operational and maintenance costs.
5.2. The Effect on Power Grid
Due to the inherent instability of electricity load and the difficulty of storing electricity, the stability of the power grid is frequently challenged, leading to various extreme scenarios, such as power shortages and wastage [
43]. In this regard, our proposed predictive model identifies variation trends of electricity accurately. It is beneficial for conducting electricity production and scheduling planning, thereby maintaining the system’s stability. Furthermore, the stacking model empowers our model to consider more factors, making it more representative of real-world environments. It has stronger adaptability and helps operators in power transmission and dispatch decisions, as losses can occur during this process due to weather conditions.
5.3. Limitation and Recommendation
The effectiveness of the proposed hybrid model utilizing the stacking technique has been demonstrated. However, predicting minimum values in stable and unstable load datasets encounters challenges. In addition, it only partially predicts the load in an unstable electricity load environment. Therefore, selecting a robust base model is required to enhance the applicability of our forecasting model. Hence, we need to explore further utilization of hybrid models with higher accuracy as base models or to incorporate a broader range of models into the base model to enhance the forecasting model’s applicability. Furthermore, testing the proposed model with a larger dataset, a smaller time interval, or load data for different locations is a good approach to validate effectiveness.
6. Conclusion
STLF is an important research topic that helps minimize prediction errors by leveraging historical load data and relevant influencing factors. In this paper, we have developed a novel hybrid model that integrates multiple AI models using the stacking technique to predict load under various influencing factors, including daily minimum and maximum temperatures, electricity prices, and rainfall. To assess the robustness and accuracy of our model, we conducted comparative analyses with diverse models using load datasets from Australia and Spain. Our results demonstrate significant improvements in MAPE compared to the WNN-ANN [
17] and LSTM-XgBoost [
18] hybrid and five AI models. Our experimental findings show the effectiveness of our proposed model in facilitating proactive power planning, mitigating extreme events such as power outages and excess generation, and advancing the overall reliability and efficiency of power systems.
Furthermore, our experimental results confirm the effectiveness of using the stacking technique to combine different models, outperforming traditional statistical approaches. Our novel approach, which leverages the strengths of individual models and integrates diverse perspectives, improves the accuracy of STLF. Future work could focus on integrating more accurate and advanced hybrid models using the stacking technique. Selecting suitable base models is crucial, as their accuracy directly affects the predictive performance of the meta-model. Additionally, improving the prediction of extreme load points helps in conducting reliable power line inspections, which are essential for ensuring grid stability and security [
44].
Author Contributions
Conceptualization, Guo.F, Wu.J and Pan.L.; methodology, Guo.F and Mo.H.; software, Guo.F and Zhang.Z.; validation, Guo.F. and Mo.H, Li.L. and Huang.F.; formal analysis, Guo.F and Wu.J; investigation, Guo.F and Pan.L.; resources and data curation, Wu.J and Pan.L; writing—original draft preparation, Guo.F and Zhou.H.; writing—review and editing, Mo.H and Zhou.H.; visualization, Zhang.Z.; supervision, Pan.L.; project administration, Mo. H and Wu.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
In this section you can acknowledge any support given which is not covered by the author contribution or funding sections. This may include administrative and technical support, or donations in kind (e.g., materials used for experiments).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| STLF |
Short-term load forecasting |
| AI |
artificial intelligence |
| ARIMA |
Auto-regressive integrated moving average |
| ARIMAX |
Auto-regressive integrated moving average with explanatory variable |
| KF |
Kalman Filter |
| GOA |
Grasshopper optimization algorithm |
| LSTM |
Long short-term memory network |
| MAPE |
Mean Absolute Percentage Error |
| SARIMA |
Seasonal auto-regressive integrated moving average |
| GRNN |
Generalized regression neural network |
| ELM |
Extreme learning machine |
| ANN |
Artificial neural network |
| WNN |
Wavelet neural networks |
| SVM |
Support vector machines |
| SVN |
Support vector network |
| SVR |
Support vector regression |
| DNN |
Deep neural network |
| PCR |
Principal component regression |
References
- Peng, L.; Lv, S.X.; Wang, L.; Wang, Z.Y. Effective electricity load forecasting using enhanced double-reservoir echo state network. Engineering Applications of Artificial Intelligence 2021, 99, 104132. [Google Scholar] [CrossRef]
- Fan, G.F.; Zhang, L.Z.; Yu, M.; Hong, W.C.; Dong, S.Q. Applications of random forest in multivariable response surface for short-term load forecasting. International Journal of Electrical Power & Energy Systems 2022, 139, 108073. [Google Scholar]
- Yang, D.; e Guo, J.; Sun, S.; Han, J.; Wang, S. An interval decomposition-ensemble approach with data-characteristic-driven reconstruction for short-term load forecasting. Applied Energy 2022, 306, 117992. [Google Scholar] [CrossRef]
- Habbak, H.; Mahmoud, M.; Metwally, K.; Fouda, M.M.; Ibrahem, M.I. Load Forecasting Techniques and Their Applications in Smart Grids. Energies 2023, 16. [Google Scholar] [CrossRef]
- Maldonado, S.; González, A.; Crone, S. Automatic time series analysis for electric load forecasting via support vector regression. Applied Soft Computing 2019, 83, 105616. [Google Scholar] [CrossRef]
- Sharma, S.; Majumdar, A.; Elvira, V.; Chouzenoux, E. Blind Kalman filtering for short-term load forecasting. IEEE Transactions on Power Systems 2020, 35, 4916–4919. [Google Scholar] [CrossRef]
- N, S.G.; Sheshadri, G.S. Electrical load forecasting using time series analysis. In Proceedings of the 2020 IEEE Bangalore Humanitarian Technology Conference; 2020; pp. 1–6. [Google Scholar]
- Nepal, B.; Yamaha, M.; Yokoe, A.; Yamaji, T. Electricity load forecasting using clustering and ARIMA model for energy management in buildings. Japan Architectural Review 2020, 3, 62–76. [Google Scholar] [CrossRef]
- Ye, N.; Liu, Y.; Wang, Y. Short-term power load forecasting based on SVM. Proceedings of the World Automation Congress 2012, 2012, pp. 47–51. [Google Scholar]
- Xu, J. Research on power load forecasting based on machine learning. In Proceedings of the 2020 7th International Forum on Electrical Engineering and Automation (IFEEA); 2020; pp. 562–567. [Google Scholar]
- Deng, X.; Ye, A.; Zhong, J.; Xu, D.; Yang, W.; Song, Z.; Zhang, Z.; Guo, J.; Wang, T.; Tian, Y.; Pan, H.; Zhang, Z.; Wang, H.; Wu, C.; Shao, J.; Chen, X. Bagging–XGBoost algorithm based extreme weather identification and short-term load forecasting model. Energy Reports 2022, 8, 8661–8674. [Google Scholar] [CrossRef]
- Hossain, M.S.; Mahmood, H. Short-term load forecasting using an LSTM neural network. Proceedings of the 2020 IEEE Power and Energy Conference at Illinois (PECI). IEEE, 2020, pp. 1–6.
- Mughees, N.; Mohsin, S.A.; Mughees, A.; Mughees, A. Deep sequence to sequence Bi-LSTM neural networks for day-ahead peak load forecasting. Expert Systems with Applications 2021, 175, 114844. [Google Scholar] [CrossRef]
- Atef, S.; Eltawil, A.B. Assessment of stacked unidirectional and bidirectional long short-term memory networks for electricity load forecasting. Electric Power Systems Research 2020, 187, 106489. [Google Scholar] [CrossRef]
- Ren, H.; Li, Q.; Wu, Q.; Zhang, C.; Dou, Z.; Chen, J. Joint forecasting of multi-energy loads for a university based on copula theory and improved LSTM network. Energy Reports 2022, 8, 605–612. [Google Scholar] [CrossRef]
- Zhao, X.; Li, Q.; Xue, W.; Zhao, Y.; Zhao, H.; Guo, S. Research on ultra-short-term load forecasting based on real-time electricity price and window-based XGBoost model. Energies 2022, 15. [Google Scholar] [CrossRef]
- Aly, H.H. A proposed intelligent short-term load forecasting hybrid models of ANN, WNN and KF based on clustering techniques for smart grid. Electric Power Systems Research 2020, 182, 106191. [Google Scholar] [CrossRef]
- Li, C.; Chen, Z.; Liu, J.; Li, D.; Gao, X.; Di, F.; Li, L.; Ji, X. Power load forecasting based on the combined model of LSTM and XGBoost. Proceedings of the 2019 the International Conference on Pattern Recognition and Artificial Intelligence; Association for Computing Machinery: New York, NY, USA, 2019; PRAI’19, pp. 46–51. [Google Scholar]
- Tan, Z.; Zhang, J.; He, Y.; Zhang, Y.; Xiong, G.; Liu, Y. Short-term load forecasting based on integration of SVR and stacking. IEEE Access 2020, 8, 227719–227728. [Google Scholar] [CrossRef]
- Moon, J.; Jung, S.; Rew, J.; Rho, S.; Hwang, E. Combination of short-term load forecasting models based on a stacking ensemble approach. Energy and Buildings 2020, 216, 109921. [Google Scholar] [CrossRef]
- Barman, M.; Dev Choudhury, N.; Sutradhar, S. A regional hybrid GOA-SVM model based on similar day approach for short-term load forecasting in Assam, India. Energy 2018, 145, 710–720. [Google Scholar] [CrossRef]
- El-Hendawi, M.; Wang, Z. An ensemble method of full wavelet packet transform and neural network for short term electrical load forecasting. Electric Power Systems Research 2020, 182, 106265. [Google Scholar] [CrossRef]
- Li, J.; Deng, D.; Zhao, J.; Cai, D.; Hu, W.; Zhang, M.; Huang, Q. A novel hybrid short-term load forecasting method of smart grid using MLR and LSTM neural network. IEEE Transactions on Industrial Informatics 2021, 17, 2443–2452. [Google Scholar] [CrossRef]
- Tayab, U.B.; Zia, A.; Yang, F.; Lu, J.; Kashif, M. Short-term load forecasting for microgrid energy management system using hybrid HHO-FNN model with best-basis stationary wavelet packet transform. Energy 2020, 203, 117857. [Google Scholar] [CrossRef]
- Azeem, A.; Ismail, I.; Jameel, S.M.; Harindran, V.R. Electrical load forecasting models for different generation modalities: A review. IEEE Access 2021, 9, 142239–142263. [Google Scholar] [CrossRef]
- Akhtar, S.; Shahzad, S.; Zaheer, A.; Ullah, H.S.; Kilic, H.; Gono, R.; Jasiński, M.; Leonowicz, Z. Short-Term Load Forecasting Models: A Review of Challenges, Progress, and the Road Ahead. Energies 2023, 16. [Google Scholar] [CrossRef]
- Yin, C.; Mao, S. Fractional multivariate grey Bernoulli model combined with improved grey wolf algorithm: Application in short-term power load forecasting. Energy 2023, 269, 126844. [Google Scholar] [CrossRef]
- Massaoudi, M.; Refaat, S.S.; Chihi, I.; Trabelsi, M.; Oueslati, F.S.; Abu-Rub, H. A novel stacked generalization ensemble-based hybrid LGBM-XGB-MLP model for short-term load forecasting. Energy 2021, 214, 118874. [Google Scholar] [CrossRef]
- Moradzadeh, A.; Mansour-Saatloo, A.; Nazari-Heris, M.; Mohammadi-Ivatloo, B.; Asadi, S. Introduction and literature review of the application of machine learning/deep learning to load forecasting in power system. In Application of Machine Learning and Deep Learning Methods to Power System Problems; 2021; pp. 119–135. [Google Scholar]
- Xiao, X.; Mo, H.; Zhang, Y.; Shan, G. Meta-ANN—A dynamic artificial neural network refined by meta-learning for short-term load forecasting. Energy 2022, 246, 123418. [Google Scholar] [CrossRef]
- Solyali, D. A comparative analysis of machine learning approaches for short-/long-term electricity load forecasting in Cyprus. Sustainability 2020, 12. [Google Scholar] [CrossRef]
- Wu, Z.; Zhao, X.; Ma, Y.; Zhao, X. A hybrid model based on modified multi-objective cuckoo search algorithm for short-term load forecasting. Applied Energy 2019, 237, 896–909. [Google Scholar] [CrossRef]
- Moradzadeh, A.; Zakeri, S.; Shoaran, M.; Mohammadi-Ivatloo, B.; Mohammadi, F. Short-term load forecasting of microgrid via hybrid support vector regression and long short-term memory algorithms. Sustainability 2020, 12, 7076. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; Association for Computing Machinery: New York, NY, USA, 2016; KDD’16, pp. 785–794. [Google Scholar]
- Suo, G.; Song, L.; Dou, Y.; Cui, Z. Multi-dimensional short-term load forecasting based on XGBoost and fireworks algorithm. In Proceedings of the 2019 18th International Symposium on Distributed Computing and Applications for Business Engineering and Science (DCABES); 2019; pp. 245–248. [Google Scholar]
- Nobre, J.; Neves, R.F. Combining principal component analysis, discrete wavelet transform and XGBoost to trade in the financial markets. Expert Systems with Applications 2019, 125, 181–194. [Google Scholar] [CrossRef]
- Lv, L.; Wu, Z.; Zhang, J.; Zhang, L.; Tan, Z.; Tian, Z. A VMD and LSTM based hybrid model of load forecasting for power grid security. IEEE Transactions on Industrial Informatics 2022, 18, 6474–6482. [Google Scholar] [CrossRef]
- Patterson, J.; Gibson, A. Deep learning: A practitioner’s approach; O’Reilly Media, Inc., 2017. [Google Scholar]
- Hossain, M.S.; Mahmood, H. Short-term load forecasting using an LSTM Neural network. In Proceedings of the 2020 IEEE Power and Energy Conference at Illinois (PECI); 2020; pp. 1–6. [Google Scholar]
- Tibshirani, R. Regression shrinkage and selection via the Lasso. Journal of the Royal Statistical Society: Series B (Methodological) 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Kozlov, A. Daily electricity price and demand data, 2020.
- Jhana, N. Hourly energy demand generation and weather, 2019.
- Li, S.; Kong, X.; Yue, L.; Liu, C.; Khan, M.A.; Yang, Z.; Zhang, H. Short-term electrical load forecasting using hybrid model of manta ray foraging optimization and support vector regression. Journal of Cleaner Production, 2023; 135856. [Google Scholar]
- Li, Y.; Ni, M.; Lu, Y. Insulator defect detection for power grid based on light correction enhancement and YOLOv5 model. Energy Reports 2022, 8, 807–814, 2022 The 5th International Conferenceon Electrical Engineering and Green Energy. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).