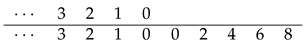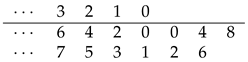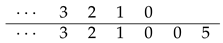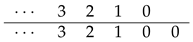Arithmetic Sequences without Arithmetic Operations

Md. Shouvik Iqbal

doi:10.20944/preprints202406.0985.v1

Preprint

Article

Arithmetic Sequences without Arithmetic Operations

This version is not peer-reviewed.

Md. Shouvik Iqbal^*

This version is not peer-reviewed.

Downloads

118

Views

139

Comments

Submitted:

13 June 2024

Posted:

14 June 2024

You are already at the latest version

Abstract

The generation of arithmetic sequences involves arithmetic operations. However, is it possible to generate such sequences without being subject to any arithmetic or related operations, all by just hand? The answer may be negative, as the very rule defining these sequences itself relies on arithmetic operations. Nonetheless, this paper presents a few results demonstrating that the exact sequences of $an$, where, $a \in \{ 2,3,\cdots,9,10\}$ and $n \in \mathbb N \cup \{0\}$, can indeed be generated up to any desired number of terms without relying on any arithmetic operations and others derived from such. This is done by the formation of a specialized table that leverages numerical patterns and the notion of concatenation.

Keywords:

Number patterns

;

Arithmetic sequence

;

Concatenation

;

Multiplication table

;

Arithmetic operations

;

Times table

Subject:

Computer Science and Mathematics - Mathematics

1. Introduction

0, 3, 6, 9, 12, 15, 18, 21, 24, 27, \dots

The sequence above is obtained by multiplying 3 with the natural numbers1 (see the sequence A008585 in the OEIS [1]). This process involves the arithmetic operation of multiplication. Should one be tasked to achieve this without being subject to any arithmetic operations, the solution may seem impossible. Because the sequence of

3 n

extends endlessly, beyond what can be generated by the memory of a human or a computer. Thus, it may generally be agreed upon that the sequence of

3 n

, where

n \in N \cup {0}

, cannot be obtained without the use of any arithmetic operations. This assumption is reasonable. For each input n in the function

f (n) = 3 n

, the corresponding output is three times that of the input n. The function may be broken as

f (n) = n + n + n

, to convert the problem of multiplication into one of addition, indicating the method of counting by an increment2 along the number line, yet fundamentally, the problem remains unchanged.

Therefore, the general assumption is left to be declared true that the sequence of

3 n

cannot be generated without being subject to any arithmetic operations.

Should such a claim be put forward, then it is false — the paper now opposes the general view.

From this point onwards, this paper shall present a method to generate the sequence of

3 n

up to endless terms without being subject to any arithmetic operations. Moreover, it shall also show for sequences of

2 n, 4 n, 5 n, 6 n, 7 n, 8 n, 9 n,

and

10 n

, under the same conditions. By doing so, the efficiency of sequence generation may be optimized, potentially inspiring new algorithms to embrace this approach. Furthermore, it holds firm promise for educational settings. From antiquity, the decimal multiplication table3 had a great concern [2,5,8]. Nowadays, it’s often advised — if not forced — to memorize it. In fact, it is believed that having fluency in recalling multiplication tables proves beneficial for handling other mathematical tasks, and thus learning it is an essential part of thriving in higher education [3]. However, some do believe the opposite [7]. Nevertheless, by the approach of this paper, the pain of memorizing the multiplication tables may potentially be abandoned, while still maintaining efficient recall. Therefore, the explanation of the method shall commence shortly. Prior to that, it is necessary to clearly define the issue being addressed and outline a few considerations regarding it. As a result, a few definitions and considerations are outlined in the following section.

2. Definition and Considerations

Definition 1

(Arithmetic Operation). An arithmetic operation is a mathematical operation that manipulates number(s) once performed.

Remark 1.

The following are the fundamental arithmetic operations:

Addition $(+)$
Subtraction $(-)$
Multiplication $(\times)$
Division $(\div)$

Definition 2

(Natural numbers). The set of numbers

{0, 1, 2, 3, 4, 5, \dots}

is the set of natural numbers and is often denoted by

N

([4] p. 66).

In this paper, the symbol

N \cup {0}

shall be used to denote the set of natural numbers to avoid any potential confusion about whether to include 0.

Remark 2.

Later in this paper, the sequence of natural numbers shall be used and be taken from a predetermined complete set of natural numbers that is independent of any arithmetic operations involved in its generation such as beginning with 0 and incrementing by 1. Therefore, had there been any arithmetic operations used to derive the set of natural numbers itself, they would’ve been trivially ignored.

Definition 3

(Counting by an increment). Let

a_{0}

be the initial value and let d be the fixed value added to each term in the sequence. Then the sequence obtained by

a_{n} = a_{0} + n \cdot d

is defined as counting by an increment. Where,

a_{0}, n \in N \cup {0}

and

d \in N ∖ {0}

In order to address the issue, it is essential to clearly define it. Therefore, the issue to be addressed is defined below by the term “Problem”.

Problem. Generate the sequences of

a n

, where

a \in {2, 3, \dots, 9, 10}

and

n \in N \cup {0}

, up to any desired number of terms, ensuring adherence to the provided guidelines, which may include but are not limited to:

No arithmetic operations noted in Remark 1 can be used.
The terms generated must be done manually, without reliance on any calculating device (i.e., solely by hand).
The sequence must be generated without any prior influence or dependency on the sequence supposed to be generated.
The use of number incrementation other than 1 (i.e., skip counting, as noted in Definition 3) to generate the sequence is prohibited, as it involves the use of arithmetic operations, whether directly or indirectly.
The terms generated must directly correspond to the original terms in the sequence supposed to be generated, one by one, in the same order. That is, strict correspondence between the terms generated and the original terms in the sequence must be met. For example, the sequence 0, 6, 3, 9, 12, 18, 20, 21, 15, 24, ⋯ would be an invalid generation of the sequence 0, 3, 6, 9, 12, 15, 18, 21, 24, ⋯
Besides the arithmetic operations noted in Remark 1, the use of any other arithmetic operations that can be derived from or are similar to those four, are prohibited (such as exponents, logarithms, roots, etc.).

Having the definition and considerations set forth, the following section now delves into an explanation of the method by which the problem can be addressed.

3. The Methodology for Generating the Sequence of $3 n$ , $n \in N \cup {0}$

In order to generate the sequence of

3 n

, where,

n \in N \cup {0}

, a specialized table is used. The process of constructing such is outlined below.

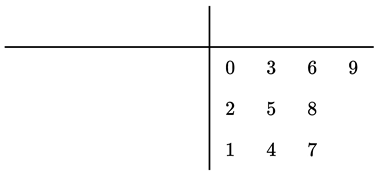
First, begin with the following, Preprints 109270 i001

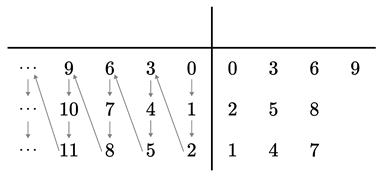
Now, write the natural numbers starting from 0 in the following order, Preprints 109270 i002

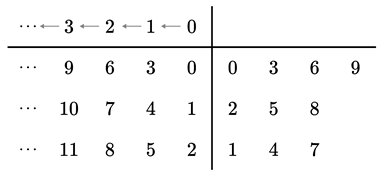
Then, write the natural numbers once again, starting from 0, above the horizontal line and to the left of the vertical line. Note that, this row is for counting the number of repetitions, which is used when division is performed and is NOT the focus of this paper at all4. Preprints 109270 i003

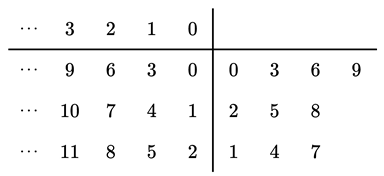
Accordingly, the following table is created. Preprints 109270 i004

Now that the table has been created, careful observation is made. In the table, it is apparent that the number in the first column of the first row to the left of the vertical line and under the horizontal line is 0. When it is distributed to concatenate by preceding the digits in the first row to the right of the vertical line (that is, distributed with the digits 0, 3, 6, and 9), we get 00, 03, 06, and 09, which are the first four terms of the sequence

3 n

or the terms of the sequence

3 n

for

n = 0, 1, 2, 3

, respectively, as shown below, Preprints 109270 i005

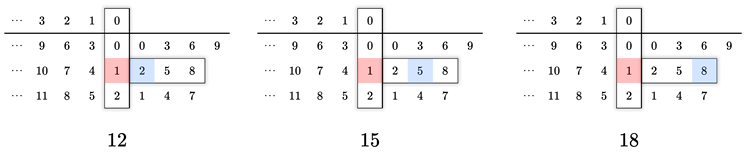
Next, the number in the first column of the second row to the left of the vertical line is distributed to concatenate by preceding the digits in the second row to the right of the vertical line. That is, 1 is distributed to precede the digits 2, 5, and 8 to form 12, 15, and 18 by concatenation. These are the terms of the sequence

3 n

, for

n = 4, 5, 6

, respectively, as shown below, Preprints 109270 i006

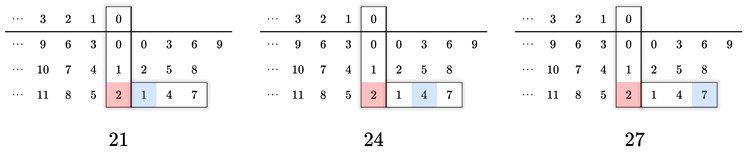
Next, the number in the first column of the third row to the left of the vertical line is distributed to concatenate by preceding the digits of the third row to the right of the vertical line. That is, 2 is distributed to precede the digits 1, 4, and 7 to form 21, 24, and 27 by concatenation. These are the terms of the sequence

3 n

, for

n = 7, 8, 9

, respectively, as shown below, Preprints 109270 i007

When all the numbers in the first column are distributed, we move to the second column to the left of the vertical line. That is, the number in the second column of the first row to the left of the vertical line and below the horizontal line is distributed to concatenate by preceding the digits of the first row to the right of the vertical line. That is, 3 is distributed to precede the digits 0, 3, 6, and 9 to form 30, 33, 36, and 39 by concatenation. These are the terms of the sequence

3 n

, for

n = 10, 11, 12

, respectively, as shown below, Preprints 109270 i008

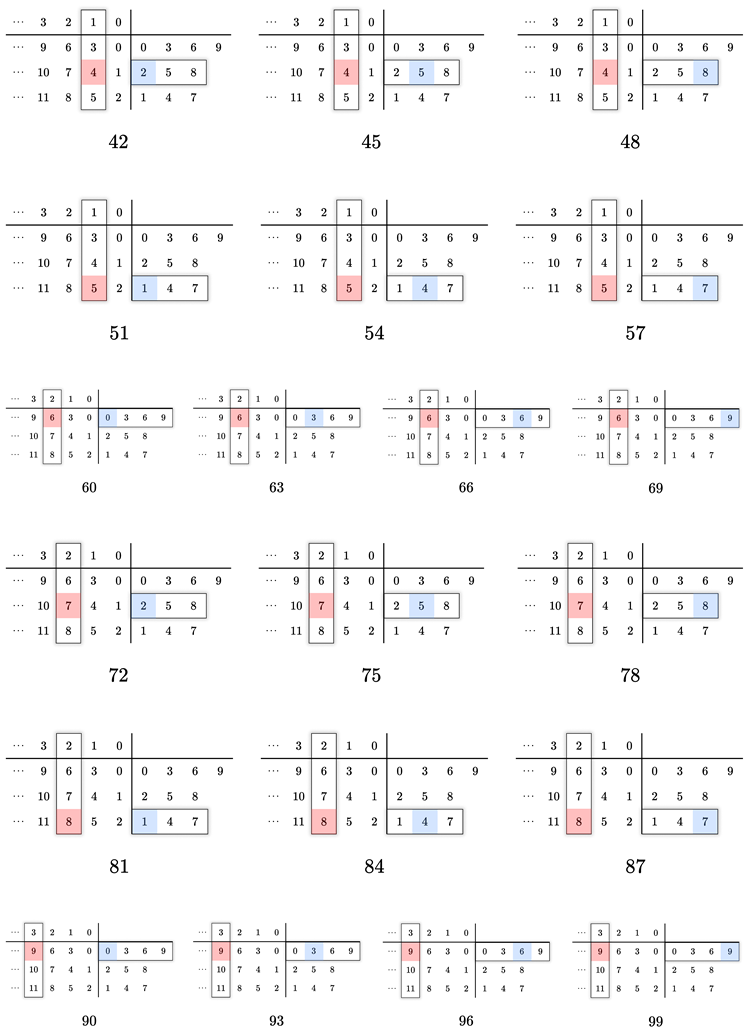
The subsequent steps follow the same process as before as shown in the following figures (recommended to be viewed as an animation). Preprints 109270 i009

Having outlined the methodology for generating the sequence of

3 n

, where

n \in N \cup {0}

, the process for generating sequences of

2 n, 4 n, 5 n, \dots, 9 n, 10 n

follows a similar pattern5. As a result, the table of these sequences is presented in the following section.

4. The Table for the Sequence of $2 n, 3 n, \dots, 9 n, 10 n$ , where $n \in N \cup {0}$

4.1. The Table for $2 n$ , Where $n \in N \cup {0}$

The sequence of

2 n

, where

n \in N \cup {0}

, (see the sequence A005843 in the OEIS [1]) is:

2 n = 0, 2, 4, 6, 8, 10, 12, 14, 16, 18, \dots

The sequence above can be generated manually without the use of any arithmetic operations by the following table, Preprints 109270 i010

4.2. The Table for $3 n$ , Where $n \in N \cup {0}$

The sequence of

3 n

, where

n \in N \cup {0}

, (see the sequence A008585 in the OEIS [1]) is:

3 n = 0, 3, 6, 9, 12, 15, 18, 21, 24, 27, \dots

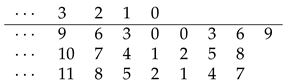
The sequence above can be generated manually without the use of any arithmetic operations by the following table, Preprints 109270 i011

4.3. The Table for $4 n$ , Where $n \in N \cup {0}$

The sequence of

4 n

, where

n \in N \cup {0}

, (see the sequence A008586 in the OEIS [1]) is:

4 n = 0, 4, 8, 12, 16, 20, 24, 28, 32, 36, \dots

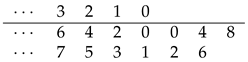
The sequence above can be generated manually without the use of any arithmetic operations by the following table, Preprints 109270 i012

4.4. The Table for $5 n$ , Where $n \in N \cup {0}$

The sequence of

5 n

, where

n \in N \cup {0}

, (see the sequence A008587 in the OEIS [1]) is:

5 n = 0, 5, 10, 15, 20, 25, 30, 35, 40, 45, \dots

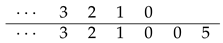
The sequence above can be generated manually without the use of any arithmetic operations by the following table, Preprints 109270 i013

4.5. The Table for $6 n$ , Where $n \in N \cup {0}$

The sequence of

6 n

, where

n \in N \cup {0}

, (see the sequence A008588 in the OEIS [1]) is:

6 n = 0, 6, 12, 18, 24, 30, 36, 42, 48, 54, \dots

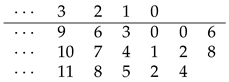
The sequence above can be generated manually without the use of any arithmetic operations by the following table, Preprints 109270 i014

4.6. The Table for $7 n$ , Where $n \in N \cup {0}$

The sequence of

7 n

, where

n \in N \cup {0}

, (see the sequence A008589 in the OEIS [1]) is:

7 n = 0, 7, 14, 21, 28, 35, 42, 49, 56, 63, \dots

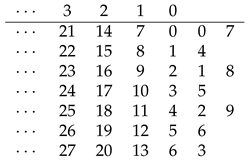
The sequence above can be generated manually without the use of any arithmetic operations by the following table, Preprints 109270 i015

4.7. The Table for $8 n$ , Where $n \in N \cup {0}$

The sequence of

8 n

, where

n \in N \cup {0}

, (see the sequence A008590 in the OEIS [1]) is:

8 n = 0, 8, 16, 24, 32, 40, 48, 56, 64, 72, \dots

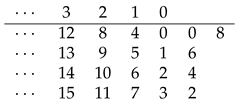
The sequence above can be generated manually without the use of any arithmetic operations by the following table, Preprints 109270 i016

4.8. The Table for $9 n$ , Where $n \in N \cup {0}$

The sequence of

9 n

, where

n \in N \cup {0}

, (see the sequence A008591 in the OEIS [1]) is:

9 n = 0, 9, 18, 27, 36, 45, 54, 63, 72, 81, \dots

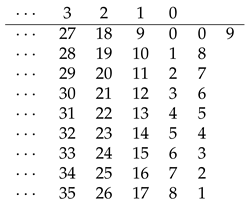
The sequence above can be generated manually without the use of any arithmetic operations by the following table, Preprints 109270 i017

4.9. The Table for $10 n$ , Where $n \in N \cup {0}$

The sequence of

10 n

, where

n \in N \cup {0}

, (see the sequence A008592 in the OEIS [1]) is:

10 n = 0, 10, 20, 30, 40, 50, 60, 70, 80, 90, \dots

The sequence above can be generated manually without the use of any arithmetic operations by the following table, Preprints 109270 i018

References

N. J. A. Sloane et al. The On-Line Encyclopedia of Integer Sequences. Available at https://oeis.org. 2024. (accessed: 23 Apr. 2024.).
Jeremy Berlin. World’s Oldest Decimal Times Table Found in China. Available at https : / / www . nationalgeographic . com / science / article / 140405- chinese- oldest- multiplication- table- decimal. 2014. (accessed: 23 Apr. 2024.).
Educationhub.blog.gov.uk. What is the multiplication tables check and why is it important? Available at https://educationhub.blog.gov.uk/2022/ 11/22/what-is-the-multiplication-tables-check-and-why-is-itimportant. 2022. (accessed: 23 Apr. 2024.).
Herbert B., Enderton. Elements of Set Theory; Academic Press, 1977. [Google Scholar]
Guinnessworldrecords.com. Oldest decimal multiplication table. Available at https://www.guinnessworldrecords.com/world-records/452049- oldest-decimal-multiplication-table. (accessed: 23 Apr. 2024.).
Silvestre Fran¸cois Lacroix. An Elementary Treatise on Arithmetic: Taken Principally from the Arithmetic of S.F. Lacroix, and Translated from the French with Such Alterations and Additions as Were Found Necessary in Order to Adapt it to the Use of American Students. 3rd ed. Hilliard and Metcalf, 1825.
Sophie Mann. California’s updated math curriculum may not require children to memorize times tables DESPITE huge public opposition. Available at https:/ /www.dailymail.co.uk/news/article-13170341/Californias - updated - math - curriculum - not - require - children - memorize - times - tables - DESPITE - huge - public - opposition . html. 2024. (accessed: 23 Apr. 2024.).
Jane Qiu. Ancient times table hidden in Chinese bamboo strips. Available at https://www.nature.com/articles/nature.2014.14482. 2014. (accessed: 23 Apr. 2024.). [CrossRef]

1	including 0
2	also known informally as “skip counting”
3	also known informally as “times table” or sometimes as the “table of Pythagoras” ([6] p. 17)
4	as such, readers are welcome to disregard it completely.
5	Note that the sequences exceeding $10 n$ can also be generated if number incrementation other than 1 is allowed. However, since this paper primarily focuses on the incrementation of 1, it therefore restricts itself to sequences of up to $10 n$

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

118

Views

139

Comments

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Arithmetic Sequences without Arithmetic Operations

Abstract

Keywords:

Subject:

1. Introduction

2. Definition and Considerations

3. The Methodology for Generating the Sequence of 3 n , n ∈ N ∪ { 0 }

4. The Table for the Sequence of 2 n , 3 n , ⋯ , 9 n , 10 n , where n ∈ N ∪ { 0 }

4.1. The Table for 2 n , Where n ∈ N ∪ { 0 }

4.2. The Table for 3 n , Where n ∈ N ∪ { 0 }

4.3. The Table for 4 n , Where n ∈ N ∪ { 0 }

4.4. The Table for 5 n , Where n ∈ N ∪ { 0 }

4.5. The Table for 6 n , Where n ∈ N ∪ { 0 }

4.6. The Table for 7 n , Where n ∈ N ∪ { 0 }

4.7. The Table for 8 n , Where n ∈ N ∪ { 0 }

4.8. The Table for 9 n , Where n ∈ N ∪ { 0 }

4.9. The Table for 10 n , Where n ∈ N ∪ { 0 }

References

MDPI Initiatives

Important Links

Subscribe

3. The Methodology for Generating the Sequence of $3 n$ , $n \in N \cup {0}$

4. The Table for the Sequence of $2 n, 3 n, \dots, 9 n, 10 n$ , where $n \in N \cup {0}$

4.1. The Table for $2 n$ , Where $n \in N \cup {0}$

4.2. The Table for $3 n$ , Where $n \in N \cup {0}$

4.3. The Table for $4 n$ , Where $n \in N \cup {0}$

4.4. The Table for $5 n$ , Where $n \in N \cup {0}$

4.5. The Table for $6 n$ , Where $n \in N \cup {0}$

4.6. The Table for $7 n$ , Where $n \in N \cup {0}$

4.7. The Table for $8 n$ , Where $n \in N \cup {0}$

4.8. The Table for $9 n$ , Where $n \in N \cup {0}$

4.9. The Table for $10 n$ , Where $n \in N \cup {0}$