Prerpints.org logo
Preprint
Article

Optimal Design of I-PD and PI-D Industrial Controllers Based on Artificial Intelligence Algorithm

This version is not peer-reviewed.

Submitted:

04 June 2024

Posted:

06 June 2024

Read the latest preprint version here

A peer-reviewed article of this preprint also exists.

Abstract
The aim of this research is to apply artificial intelligence (AI) methods, specifically artificial immune systems (AIS), in order to design an optimal control strategy for a multivariable control plant. Two specific industrial control approaches are investigated: I-PD (Integral-Proportional Derivative) and PI-D (Proportional-Integral Derivative) control. The study results in a novel solution to the control synthesis problem for the industrial system. In particular, the research addresses the synthesis of I-P control for a two-loop system in the technological process of a distillation column. This synthesis is accomplished using the AIS algorithm, making it the first application of this technique to this specific context. Methodological approaches are proposed to enhance the performance of industrial multivariable control systems through effective utilization of optimization algorithms by establishing modified quality criteria. The problem of synthesis of multi-input multi-output (MIMO) control system is solved, taking into account the interconnections due to the decoupling procedure.
Keywords: 
optimal design
;  
I-PD controller
;  
PI-D controller
;  
artificial intelligence algorithm
;  
artificial immune system
;  
industrial applications
;  
multivariable systems
Subject: 
Engineering  -   Control and Systems Engineering

1. Introduction

The optimal synthesis of I-PD (Integral-Proportional Derivative) and PI-D (Proportional-Integral Derivative) industrial controllers is connected with the development of effective process control systems [1,2]. At present, the synthesis of only PID controllers is well developed. The process of developing and implementing optimal I-PD and PI-D controllers can lead to improvements in the accuracy and performance of control systems, which is important for various industrial and technical applications. The development of efficient optimization algorithms used in optimal I-PD and PI-D controllers is an important research.
Technological processes are characterized by multivariable complexity, large amounts of data and the use of microprocessor technologies [3]. Using the latest advances in artificial intelligence (AI) can significantly improve optimal control algorithms for MIMO control systems. These algorithms can be used for tuning the parameters of I-PD and PI-D controllers to achieve optimal results according to specific performance criteria or given requirements.
Artificial intelligent algorithms such as artificial immune systems (AIS), genetic algorithms (GA), particle swarm (PSO), or optimization algorithms using artificial neural networks can work with a variety of criteria, which allows you to adjust the controls taking into account several aspects of performance [4,5]. In particular, artificial immune systems (AIS) are based on a natural immune system with the ability to learn and adapt to changing conditions. This property gives an advantage to AIS algorithms over other AI algorithms.
The primary objective of this research is to develop more efficient methods for tuning I-PD and PI-D controllers of multivariable industrial systems through the use of AI algorithms such as the AIS algorithm.
The following research questions were considered, which are essential when developing optimal I-PD and PI-D controllers by leveraging AIS technology for controlling systems:
  • What optimality criteria should be considered in the synthesis of I-PD and PI-D controllers using intelligent algorithms?
  • Which models of MIMO processes and control systems in the industry can be used for the synthesis of I-PD and PI-D controllers?
  • What are the advantages and limitations of I-PD and PI-D controllers compared to other types of controllers?
  • What advantages do AIS algorithms offer in solving problems related to the synthesis and tuning of I-PD and PI-D controllers?
The successful integration of industrial artificial intelligence has become an important factor, especially within multivariable sectors like the oil and gas industry [6,7]. The proposed approach involves the development of more efficient intelligent algorithms based on artificial immune systems for the optimal control of multivariable industrial processes in the oil and gas industry. Research on applying AIS for tuning controllers of multivariable systems has the potential to bring significant benefits to both industry and the academic community, contributing to increased efficiency and automation of control processes.
The structure of the paper is organized as follows. Section 1 provides an overview of the research questions and objectives of the present study. Section 2 examines previous studies on AI technology. Section 3 describes the AI algorithm methods for industrial controllers. Section 4 introduces the mathematical model of а MIMO distillation column process control system and details the findings and results of the optimal design of controllers for the distillation column. Section 5 discusses the obtained results. Section 6 concludes the paper and identifies avenues for future exploration.

2. Literature Review

Among the promising frontiers for artificial intelligence in the oil and gas sector, modeling and optimizing various processes hold significant potential [8]. This involves employing artificial intelligence to regulate technological processes, including the pursuit of optimal solutions. Achieving these objectives involves harnessing artificial intelligence optimization algorithms, which are extensively documented in contemporary literature [9]. Intelligent algorithms such as the Dragonfly Algorithm (DA) [10], Genetic Algorithm (GA), Ant Colony Optimization (ACO) [11], Particle Swarm Algorithm (PSA) [12], and Cuckoo Search (CS) [13] have been successfully applied to synthesizing optimal controllers for automatic control systems.
These intelligent algorithms encompass a wide spectrum of capabilities, each with its own strengths and limitations. Their selection should be contextually driven by factors like the specific oil and gas industry process, desired system dynamics and quality, and the optimization problem at hand. For instance, these algorithms are adept at parametrically tuning standard PID controllers to synthesize optimal controls aimed at minimizing selected performance criteria.
While AI algorithms are extensively employed for setting PID controllers in single-input single-output system (SISO), there is a particular interest in utilizing artificial intelligence techniques to fine-tune variable structure controllers. These controllers, including I-PD, PD-PI, and PI-D, present intriguing challenges. Methods for synthesizing I-PD and PD-PI controllers have emerged, leveraging intelligent techniques such as Particle Swarm Optimization (PSO) [14], Cuckoo Search (CS) [15], and Swarm Intelligence [16].
Among the array of algorithms, the artificial immune system (AIS) algorithms have demonstrated notable efficacy in intelligent PID-controllers adjustment [17,18]. These algorithms, which are based on the clonal selection principle, exhibit several distinctive characteristics, including accuracy calculations, convergence rate, and robustness in situations where information about the plant under control is incomplete [19,20]. Notably, the AES algorithm excels in discovering global optimal solutions, outperforming conventional tuning methods in metrics like rise time, control time, steady-state tracking error, and overshoot [21]. This effectiveness has been demonstrated for SISO systems and holds even greater significance for MIMO systems [22].

3. Methods the AI Algorithm for Industrial Controllers

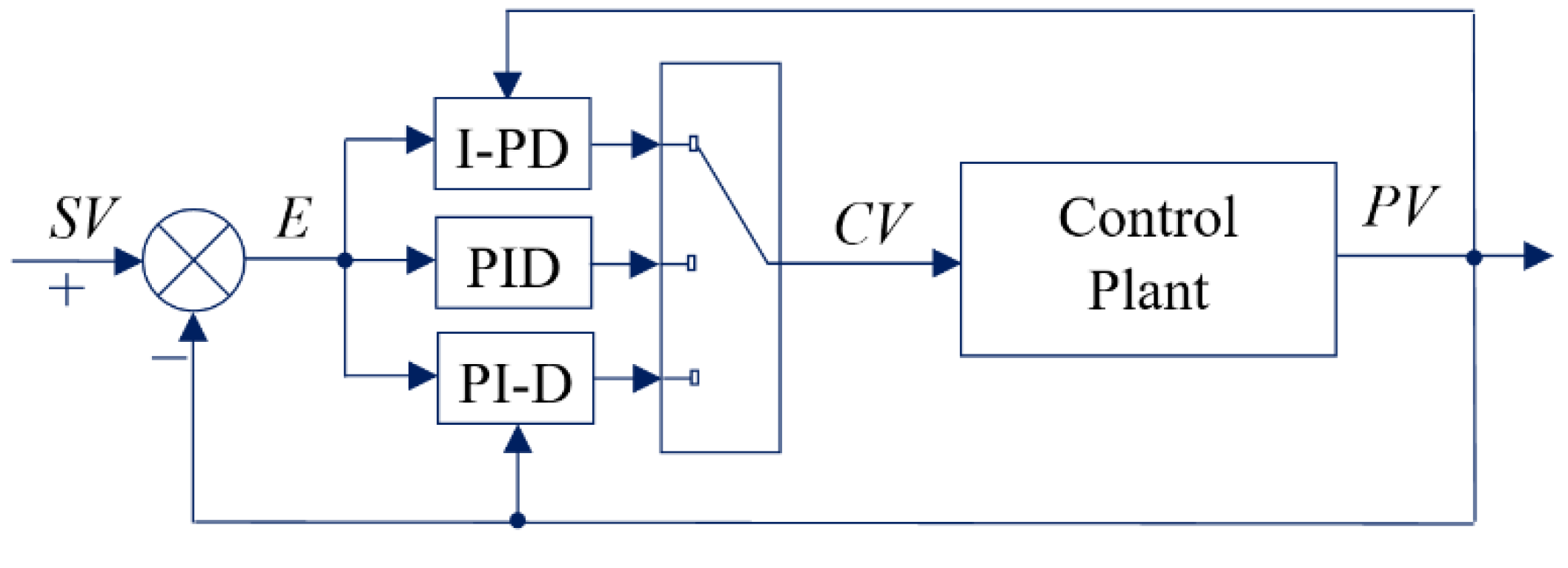
In the application of microprocessor-based process control methodologies within the oil and gas sector, the integration of controllers into the control system is a common practice. In the architecture of automated control systems developed by different companies for microprocessor-driven technology, the array of components extends beyond mere PID controllers to encompass controllers like I-PD and PI-D, as illustrated (see Figure Error! Reference source not found.).
Preprints 108316 g001
Figure 1. Scheme of an industrial control system with a variable controller.
Figure 1. Scheme of an industrial control system with a variable controller.
Preprints 108316 g001
The control strategies applied by these controllers encompass not only the tracking error, denoted as E, but also incorporate the real-time value of the output signal, PV. This specific design of the controller configuration leads to an enhancement in system performance. It facilitates the generation of requisite control actions, CV, which are then directed toward the control plant to attain the predetermined operational modes, SV. During the operation of the control system, a seamless transition occurs between different controller types: PID, I-PD, and PI-D. This dynamic switching contributes to the controller's adaptable structure. The control law governing the I-PD configuration of the control system takes on the following expression:
C V I − P D t = K P · P V t + 1 T I ∫ t = 0 t 1 E t d t + T D d P V t d t ,
where KP is a proportional gain of the controller; TI is a time constant of the integral term of the controller; TD is a time constant of the derivative term of the controller.
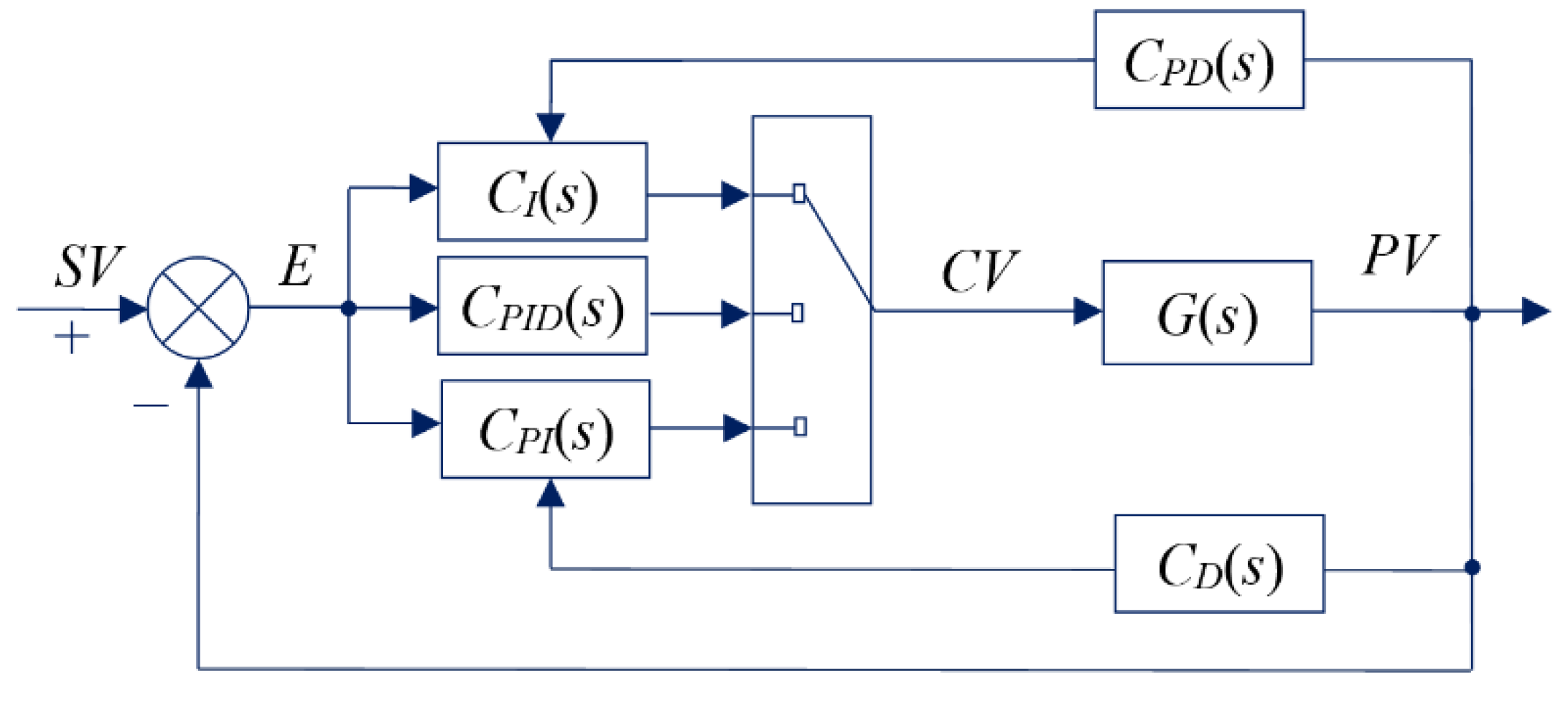
The formation of the closed-loop control system transfer function, involving the controller (1), follows the configuration outlined in the diagram illustrated in Figure Error! Reference source not found.:
T I − P D s = C I ( s ) G ( s ) 1 + G ( s ) C I s + C P D s ,
C I s = 1 T I · 1 s ,   C P D s = K P + T D · s ,
where G(s) is a transfer function of the control plant; CI is a transfer function I-controller in the forward circuit of the block diagram of the control system, to the input of which a tracking error is applied; CPD is a transfer function of the PD controller in the feedback circuit of the control plant, the input of which is supplied with the current value of the output signal.
Preprints 108316 g002
Figure 2. Scheme of an industrial control system with a variable controller.
Figure 2. Scheme of an industrial control system with a variable controller.
Preprints 108316 g002
Let also consider the PI-D control law, in which the control action is formed based on the tracking error, E, and the change in the output signal PV:
C V P I − D t = K P · E ( t ) + 1 T I ∫ t = 0 t 1 E ( t ) d t + T D d P V ( t ) d t
In this case, the expression for the transfer function of the closed-loop control system has the following form:
T P I − D s = C P I ( s ) G ( s ) 1 + G ( s ) C P I s + C D s ,   C P I s = K P + 1 T I · 1 s ,   C D s = T D · s .
To adjust the variable controller, it is necessary to find the controller parameters that provide the extremum of the fitness function – the Integral Square Error (ISE) [17]:
I S E = ∫ t = 0 t 1 E 2 ( t ) d t = ∫ t = 0 t 1 S V − P V t 2 d t → m i n .
The integration range is bounded by the simulation time of the process, denoted as t1.
With the principles outlined above, we establish the problem formulation for the design of optimal control actions, CV. For the control system illustrated in Figure Error! Reference source not found., the task involves determining the parameter settings for the variable controller. This is done with the aim of ISE minimizing (6) while attaining the predetermined values of the output signals, SV. This optimization task is approached through the application of the AIS intelligent search optimization algorithm.
In line with the findings of [21], the AIS algorithm entails the conventional stages of an evolutionary search algorithm, inspired by the mechanisms of the biological immune system. These stages encompass the initialization phase, involving the establishment of initial values for controller parameters, followed by affinity calculations for the parameters with respect to the fitness function. Subsequent steps include the selection, cloning, mutation, and the identification of the most promising clone to explore controller parameter sets that yield the fitness function minimum.
The AIS algorithm that is compatible with these processes is the clonal selection algorithm (CLONALG). The application of the CLONALG algorithm to address the synthesis of standard controllers for MIMO systems is conceptually underpinned by ideas akin to immune system theory. In the context of formulating a control system challenge, the generalized representation of antibodies corresponds to the array of output variables: Ab=(kp,TI,TD,CV), constituting a collection of solutions. The quality criterion (6), expressed in functional form, serves as the antigens: Ag=(E,kp,TI,TD,CV).
The clonal selection algorithm, designed to solution of this problem, includes the following operators: [20,21]:
C L O N A L G = A g , A b , G , S , M , d , t ,
where Ag is a subset of antigens; Ab is an antibody population; G is a set representation; S is a selection operator; С is a clone operator; M is a mutation operator; d is a number of antibodies to be replaced with new ones; t is a generation number.
Steps of the clonal selection algorithm for searching for controller parameters to minimize the quality criterion:
Step 1. Initialization: generation of the initial Ab population.
Population cycle:
Step 2. Affinity (Abt): for each antibody in the population, calculate the fitness function value and determine the affinity.
Step 3. Selection (Gs): select the subset of antibodies with the highest affinity.
Step 4 Cloning (Gc): obtain a population of C clones from Ab.
Step 5. Mutation (GM): obtain a population of changed clones.
Step 6. Re-selection (GS): selection of the best clone.
Step 7. Replacement of antibodies with high affinity clones (Abt+1).
Step 8. If the stop rule is not met, then go to step 2.
Step 9. Output optimal values.
At the initialization stage, the initial set of solutions that satisfy criterion (6) is generated randomly. The next step is the selection of n antibodies with the best affinity, after which the selection of antibodies suitable for cloning is carried out [21]:
N C = ∑ i = 1 n r o u n d β N i ,
where β is a multiplier that controls the number of clones; N is total number of antibodies.
Following the cloning process, which involves duplicating high-affinity antibodies, a set denoted as x is generated. This set subsequently experiences random mutations with a predetermined probability pm. When the degree of affinity is elevated, the mutation rate tends to be reduced:
x i = x i + A · r a n d − 1 ; 1 · x m a x − x m i n ,
where А is an affinity dependent factor and decreases with increasing affinity.
The low affinity antibodies are replaced with new randomly generated antibodies represented by the expression:
x i = x m i n + r a n d 0 ; 1 · x m a x − x m i n .
The repetition of the population cycle continues either until a predefined stopping criterion is satisfied or until a specific number of generations has occurred, referred to as gen. Due to the use of the CLONALG algorithm, a number of solutions with a high degree of similarity are generated. These solutions include controller parameters (kp, TI, TD) that achieve a minimum value of ISE (6).
In the context of applying AIS algorithms to optimize ISE (6), the primary fitness function typically focuses on a cumulative assessment of the difference between SV and PV. In essence, the discrete formulation of criterion (6) is employed. Consequently, the operation of these intelligent search algorithms unfolds as follows: within a predefined timeframe, the current PV values are input and compared against the SV. The resulting disparity is assessed using the ISE. However, these algorithms tend to identify and halt at a relative local minimum, contingent upon the initial population provided.

4. Findings Results Optimal Design of Controllers for Distillation Column

To practically apply the method, a two-loop control system is employed for the operations of a tray-type distillation column. This type of column holds paramount importance in industries such as oil, gas, and chemicals, as it's designed to purify liquids and gases. To implement the method in practice, a two-loop control system is used for the operation of a tray-type distillation column. These columns are of great importance in industries such as oil and gas, where they are used to purify liquids and gases.
A typical distillation column consists of a vertical structure that contains trays or packing material. It includes a reboiler that provides heat in the form of steam to the bottom of the column, a condenser, and a liquid reflux tank that stores the condensed vapor returning from the top of the column. The input material entering the column consists of primary components (for example, butane and pentane for raw gas), along with impurities from other components [24]. It is important to minimize or eliminate these impurities from the final product. Key components can be categorized into heavier and lighter fractions. The heavier components accumulate at the bottom of the column, while the lighter components are collected as the distillate at the top. The internal structures of the column facilitate the flow of liquids and vapors. These structures can be plates, nozzles, or other devices.
Currently, a significant body of literature explores the modeling and control of distillation columns, taking into account internal structures, specific process conditions, and requirements. Numerous studies focus on binary control structures that govern changes in reflux flow rates and reboiler heat loads to regulate the composition of components in the distillate and bottoms.
Within this context, liquid flow rates (L) and vapor flow rates (V) are inputs, while product concentrations χD and χB are outputs. The L−V configuration is a typical control structure for distillation with composition control. In this setting, the control system's objective is to maintain the desired product concentrations χD and χB at the output of the unit using industrial controllers.
Various mathematical models have been developed to describe the L−V configuration, including the Wood-Berry distillation column model [25], a simplified model proposed by Morari and Zafiriou [26], and a detailed model for ethanol-water separation presented in Luyben [27]. For this study, we utilize the model proposed by Minh et al. [24] for a tray-type distillation column with 14 trays.
The distillation column can be described as a system with two input and output variables, making it a two-input, two-output system (TITO). This type of system is commonly referred to as a two-dimensional control system:
d χ D t d t = − 1 1.9588 · χ D t + 0.0042 1.9588 · L t − 0.0062 1.9588 · V t , d χ B t d t = − 1 1.9588 · χ B t + 0.0072 1.9588 · V t − 0.0052 1.9588 · L t ,
where L is reflux rate; V is vapor boil-up rate; χ D is the distillate composition; χ B is the bottom composition.
Let us introduce two column vectors of input, CV1, CV2 and output, PV1, PV2, signals:
P V 1 ( s ) P V 2 ( s ) = χ D ( s ) χ B ( s ) ,   C V 1 ( s ) C V 2 ( s ) = L ( s ) V ( s ) .
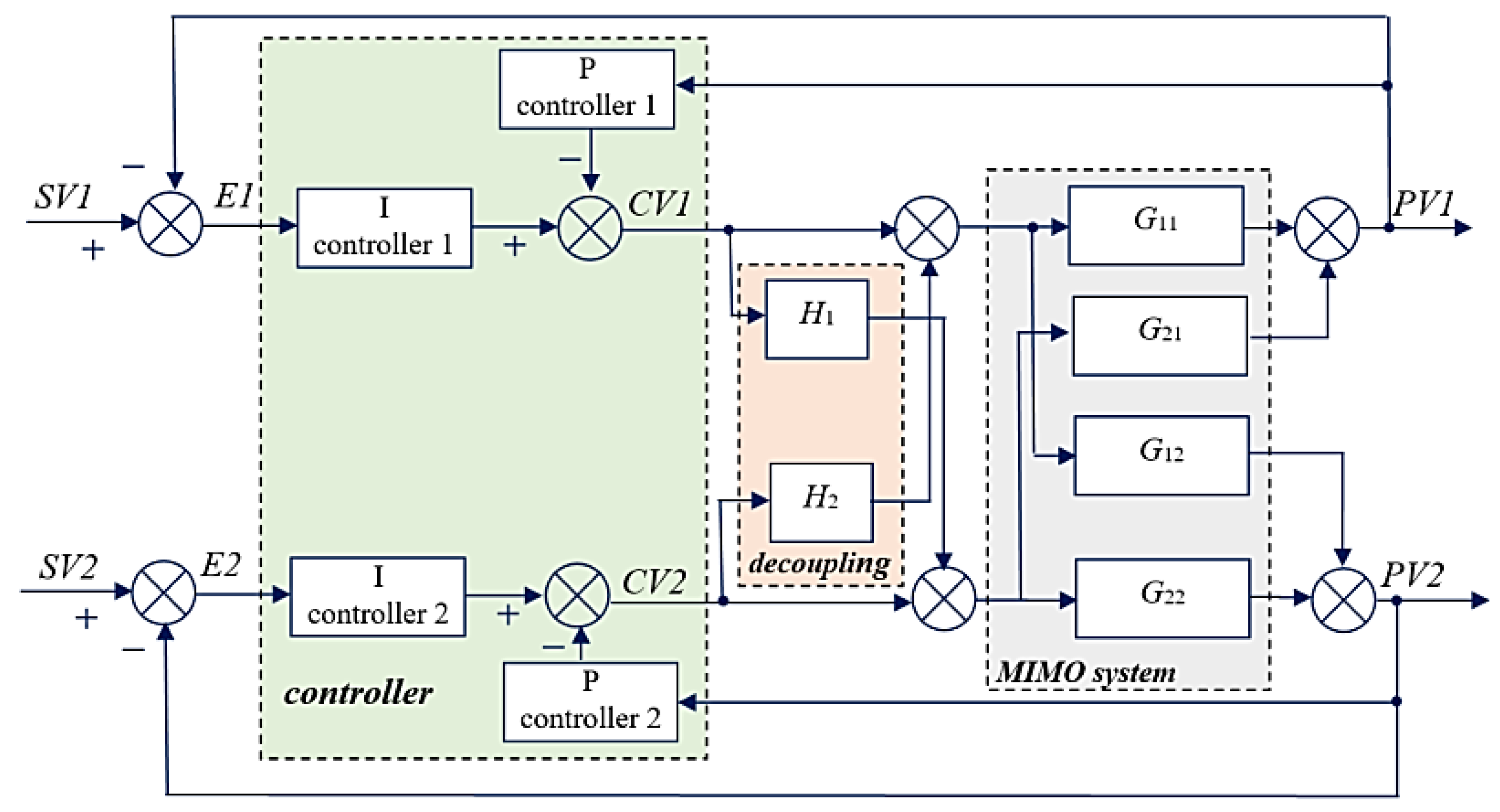
In accordance with the introduced vectors, the expression for the model of a TITO process control system of a distillation column has the form:
P V 1 ( s ) P V 2 ( s ) = G 11 ( s ) G 12 ( s ) G 21 ( s ) G 22 ( s ) C V 1 ( s ) C V 2 ( s ) ,
where G11, G22 are transfer functions of isolated subsystems; G12, G21 are transfer functions of interconnections between subsystems (see Figure Error! Reference source not found.).
Preprints 108316 g003
Figure 3. Scheme for modeling a TITO system with controllers.
Figure 3. Scheme for modeling a TITO system with controllers.
Preprints 108316 g003
We will now derive the results from simulating the transfer functions of isolated circuits by applying a decoupling technique, ensuring that there are no interconnections. To determine the necessary system dynamics, transient simulations were performed (see Figure Error! Reference source not found.), with PV1 and PV2 representing the current output values of the two circuits. In these simulations, a unit step signal, SV, was used as the desired input.
Preprints 108316 g004
Figure 4. Step responses of the of two control loops: (a) First control loop; (b) Second control loop.
Figure 4. Step responses of the of two control loops: (a) First control loop; (b) Second control loop.
Preprints 108316 g004
Upon analyzing the transient processes, it is evident that the system's behavior is characterized by monotonicity. Consequently, for the two circuits described by equation (17), the control law (1), incorporating the time constant, is selected, thus opting for the I-P controller. In accordance with expression (2), the transfer functions for the closed-loop system with I-P controllers can be expressed as:
T I − P 1 s = 0.0042 · 1 T I 1 1 T I 1 + 0.0042 · T D 1 · s 2 + K P 1 + 1 · s + K P 1 · 1 T I 1 ,
T I − P 1 s = 0.0072 · 1 T I 2 1 T I 2 + 0.0072 · T D 2 · s 2 + K P 2 + 1 · s + K P 2 · 1 T I 2 .
To achieve the desired dynamics described as (SV), we introduce a fitness function designed for optimization purposes. In order to address this challenge, this study proposes a methodology that is similar to the approach described in [17]. This methodology is based on deriving a quality criterion without an integration function from formula (6). For clarification, consider the transfer function of a closed-loop control system with a second-order controller in the form of a transfer function:
T s = b 0 a 0 · s 2 + a 1 · s + a 2 ,   m = 0 ,   n = 2 .
In this case, the ISE has the form:
I S E = 1 2 · a 2 2 · Δ · B 0 · Δ 0 → m i n .
According to the model (11):
B 0 = b 0 2 ,   ∆ 0 = d e t a 1 − a 0 a 2 a 1 = a 1 2 + a 0 · a 2 ,   ∆ = d e t a 2 − a 0 0 a 1 = a 1 · a 2 .  
Then
I S E = b 0 2 · a 1 2 + a 0 · a 2 2 · a 2 2 · a 1 · a 2 → m i n .
This quality criterion is effectively utilized in this work as a fitness function, the minimization of which is achieved through a search algorithm based on clonal selection for artificial immune systems.
Therefore, the task can be simplified to the following challenge: identifying the elusive parameters of controllers KP1, TI1, KP2, TI2, that yield the minimum value for the quality criterion (14) through the use of the CLONALG algorithm. This approach results in a unique quality criterion for each subsystem:
I S E I − P 1 = 1 + 0.0084 · K P 1 + 0.0042 2 · K P 1 2 + 1.9588 · 0.0042 · 1 T I 1 0.0084 · 1 T I 1 + 2 · 0.0042 2 · K P 1 · 1 T I 1 ,
I S E I − P 2 = 1 + 0.0144 · K P 2 + 0.0072 2 · K P 2 2 + 1.9588 · 0.0072 · 1 T I 2 0.0144 · 1 T I 2 + 2 · 0.0072 2 · K P 2 · 1 T I 2 .
When formulating quality criteria, several constraints must be taken into account. First, simulation time and, consequently, integration range are limited by the simulation time required for the technological process. Second, controller parameters, which are solutions to an optimization problem, must be strictly positive:
K P 1 > 0 ,   T I 1 > 0 ,   K P 2 > 0 ,   T I 2 > 0
The procedures of the CLONALG algorithm, which are designed to optimize ISE (20) and (21), are implemented within the MATLAB software environment as a program for minimizing the fitness function. During the implementation of the algorithm, an initial population is generated. This population consists of controller parameter values that are selected from a range of feasible values, ensuring both stability of the closed-loop control system and feasibility from a technical perspective. Subsequently, a complete calculation cycle is carried out, following the steps defined in the search algorithm described in section 3 of this document.
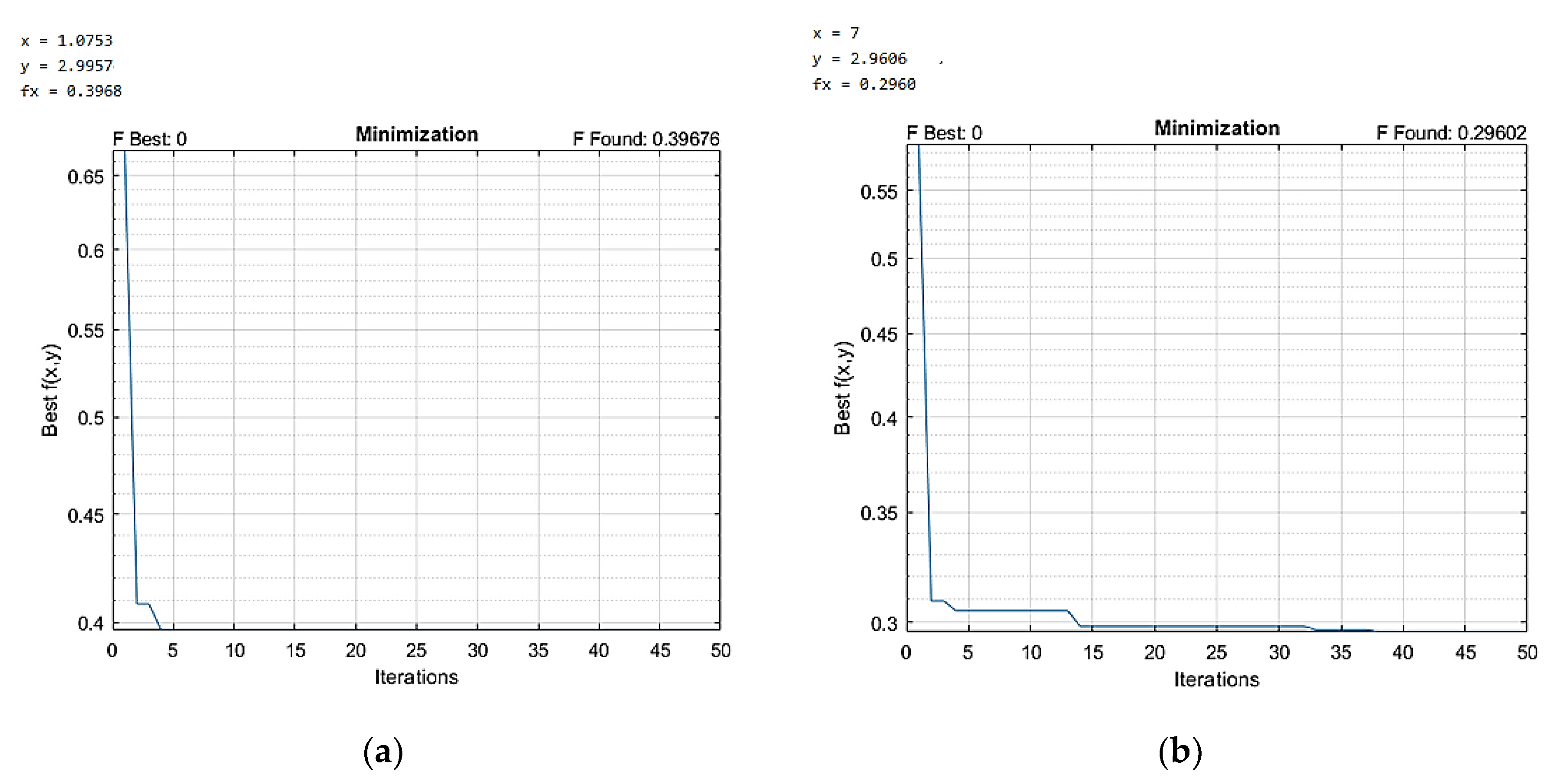
General algorithm settings: N=100 is population size; Ab=cadeia(n,44) is antibody population; gen=50 is number of generations; pm=0.5 is mutation probability; d=0.3 is the population that is subjected to random permutations; β=0.5 is multiplier that controls the number of clones. During the implementation of the algorithms within the MATLAB environment, the following results were obtained for the first and second iterations (see Figure Error! Reference source not found.):
  • evaluations of the effectiveness of applying the algorithm in minimizing ISE;
  • the parameters of typical controllers as a solution to the problem.
Preprints 108316 g005
Figure 5. AIS algorithm evaluation: (a) First control loop; (b) Second control loop.
Figure 5. AIS algorithm evaluation: (a) First control loop; (b) Second control loop.
Preprints 108316 g005
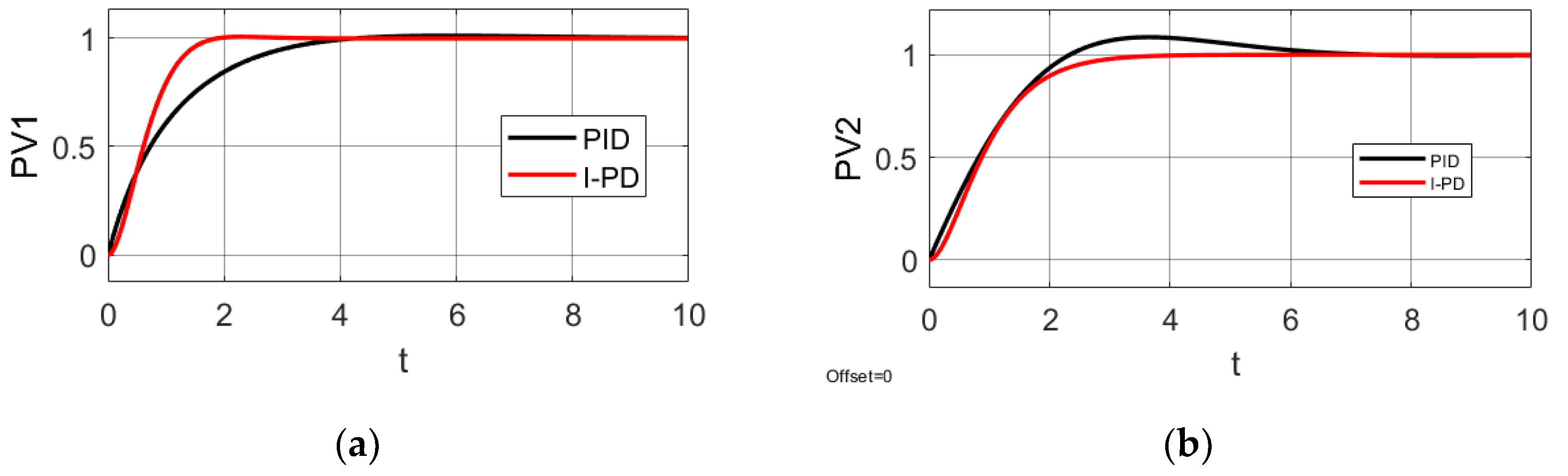
In order to conduct a comparative analysis, parameters of PID controllers were derived using the AIS algorithm. Simulation results for the two control systems, employing PID and IP controllers, are shown in Figure Error! Reference source not found..
Preprints 108316 g006
Figure 6. Step responses of the control system with controllers: (a) First control loop; (b) Second control loop.
Figure 6. Step responses of the control system with controllers: (a) First control loop; (b) Second control loop.
Preprints 108316 g006
Upon examining the step response of the control system using the respective controllers (see Figure Error! Reference source not found.), specifications can be provided:
  • The settling time for processes using an IP controller is significantly shorter compared to those using a PID controller.
  • The overshoot observed in processes with an I-P controller is lower compared to processes with a PID controller.
  • The rise time for the primary circuit's process using an I-P controller is faster than that with a PID controller.
Based on the simulation results obtained, it is possible to draw conclusions about the effectiveness of the intelligent controllers that were fine-tuned using the CLONALG algorithm.
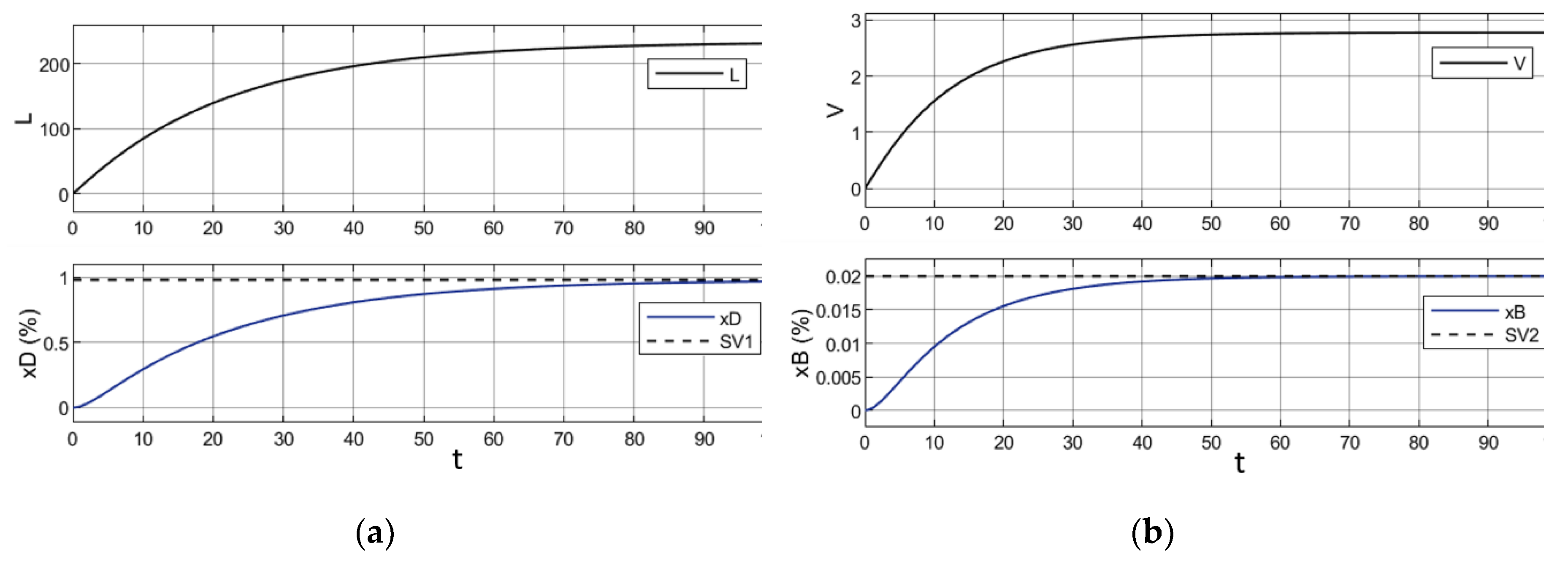
To achieve stabilization of the distillation process, specific target values need to be set. These values include the purity of the distillate, defined as the percentage of isobutane and butane in the product, which is 0.98, and the purity of material from the bottom of the column, also defined in terms of the percentage of these components, at 0.02.
The simulation results of the two control loops using these designated signals are presented in Figure Error! Reference source not found.. Based on the analysis of the graphs, it can be concluded that the desired dynamics have been achieved. Over time, the values of χD and χB have converged towards the predefined values of 0.98 and 0.02, respectively. In addition, Figure Error! Reference source not found. illustrates the control action values of L and V required to achieve the desired system performance.
Preprints 108316 g007
Figure 7. Simulation results of two control loops with reference signals: (a) First control loop; (b) Second control loop.
Figure 7. Simulation results of two control loops with reference signals: (a) First control loop; (b) Second control loop.
Preprints 108316 g007
However, the achieved results are indicative of the output values generated by individual circuits. In order to account for the effect of interactions between components, Figure Error! Reference source not found. provides a representation of a diagram in which the simulated transfer functions from the mathematical model (15) are depicted.
The issue of addressing and compensating for interconnections, arising from the presence of the coupling devices H1 and H2, has been thoroughly explored in [28]. While this current work focuses on the development of controllers based on AIS, a comprehensive explanation of the decoupling process and the calculation of matrices H1 and H2 will not be presented herein. Sufficient to say, decoupling matrices are used to counteract the effects of these relationships, enabling the determination of output values for a MIMO system as illustrated in Figure Error! Reference source not found..

5. Discussion

The research presented in this paper focuses on the application of AI techniques, specifically AIS, to develop an optimal control strategy for a MIMO system. The objective of the study is to improve the control of a distillation column in the context of the oil and gas industry in order to achieve desired operational states efficiently. This optimization process is achieved through the use of the AIS clonal selection algorithm (CLONALG), which iteratively refines the control strategy.
The research successfully addresses the challenge of optimizing the operation of the distillation column by introducing innovative approaches based on the principles of AIS and CLONALG. Traditional control strategies often rely on static rules and fixed parameters, which may not be adaptable to the complex and dynamic nature of industrial systems. In contrast, the use of AIS, inspired by the immune system's mechanisms, provides a dynamic and self-adjusting approach to optimize control.
One of the significant strengths of this research is its incorporation of relevant control laws and a fitness function. Through the integration of these components, the researchers have ensured that the optimized control strategy not only minimizes tracking errors but also considers real-time input signals. This integrated approach acknowledges the significance of real-world feedback in enhancing the control strategy and leading to enhanced system performance and stability.
Furthermore, the study examines control strategies within the context of a distributed industrial control system. This approach is particularly pertinent in modern industrial environments, where interconnected systems necessitate coordinated and efficient control measures. The research investigates the development of control strategies that can efficiently manage distributed components, thereby enhancing the flexibility and scalability of the proposed techniques.
Two specific control strategies, the PID controller and the I-PD controller, have been evaluated in detail. A comparison and analysis of these strategies contributes to a broader understanding of the advantages and limitations of various control approaches in relation to the operational requirements of the oil and gas industry. This comparative analysis provides insight into the feasibility and effectiveness of each strategy, helping practitioners select the most suitable approach based on specific needs.
In conclusion, the study presented in this paper demonstrates the potential and efficacy of employing artificial immune systems, specifically the AIS clonal selection algorithm, in enhancing the control strategy of MIMO systems. By focusing on optimizing a distillation column in the oil and gas industry, this research provides valuable insights into industrial process control.The incorporation of real-time output signals, consideration of distributed control, and comparison of different control strategies enrich the significance and applicability of the study. The findings not only contribute to a better understanding of control optimization, but also pave the way for further research and refinement of AI-based control techniques in complex industrial settings.

6. Conclusions

This article presents an innovative approach to addressing the challenge of designing optimal industrial controllers using intelligent techniques. This approach considers typical controller configurations such as PID, I-PD, and PI-D controllers, which are commonly used in distributed control systems. The proposed approach is tested and evaluated using a MIMO distillation column control system, which is a common application in the oil and gas industry. To solve this problem, a novel search algorithm based on the clonal selection principle of artificial immune systems is used. These systems are known for their ability to adapt to changing conditions.
The significance of this work lies in the introduction of a novel approach to the formulation of the objective function for optimal control, which is intricately integrated with intelligent search algorithms. This research has implications for practical applications, where these intelligent methods can be used to solve diverse problems. Therefore, the findings of this study have the potential to serve as a valuable resource for future implementation in various practical settings.

Author Contributions

Conceptualization, O.S., B.S. and E.K.; methodology, O.S. and B.S.; software, O.S.; validation, O.S., B.S. and E.K.; formal analysis, O.S. and E.K.; investigation, O.S., B.S., and E.K.; resources, B.S. and E.K.; data curation, O.S. and E.K.; writing—original draft preparation, O.S.; writing—review and editing, B.S. and E.K.; visualization, O.S. and E.K.; supervision, B.S.; project administration, B.S.; funding acquisition, B.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Science Committee of the Ministry of Education and Science of the Republic Kazakhstan, grant number АР19674691.

Data Availability Statement

No new data were created.

Acknowledgments

In this section, you can acknowledge any support given which is not covered by the author contribution or funding sections. This may include administrative and technical support, or donations in kind (e.g., materials used for experiments).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Cokmez, E.; Kaya, I. Optimal design of I-PD controller for disturbance rejection of time delayed unstable and integrating-unstable processes. International Journal of Systems Science 2024, 55, 2314215. [CrossRef]
  2. Raja, G.L.; Ali, A. New PI-PD controller design strategy for industrial unstable and integrating processes with dead time and inverse response. J. Control Autom. Electr. Syst. 2021, 32, pp. 266–280. [CrossRef]
  3. Bin Roslan , M.N.; Bingi, K.; Devan, P.A.M.; Ibrahim, R. Design and Development of Complex-Order PI-PD Controllers: Case Studies on Pressure and Flow Process Control. Appl. Syst. Innov. 2024, 7, 33. [CrossRef]
  4. Lee, J.H.; Davari, H.; Singh, J.; Pandhare, V. Industrial Artificial Intelligence for industry 4.0-based manufacturing systems. Manufacturing Letters 2018, 18, pp. 20–23. [CrossRef]
  5. Arinez, J.F.; Chang, Q.; Gao, R.X.; Xu, Ch.; Zhang, J. Artificial Intelligence in Advanced Manufacturing: Current Status and Future Outlook. Journal of Manufacturing Science and Engineering 2020, 142, 110804. [CrossRef]
  6. Koroteev, D.; Tekic, Z. Artificial intelligence in oil and gas upstream: Trends, challenges, and scenarios for the future. Energy and AI, 2021, 3, 10. [CrossRef]
  7. Li, H.; Yu, H.; Cao, N.; Tian, H.; Cheng, Sh. Applications of artificial intelligence in oil and gas development. Archives of Computational Methods Engineering 2021, 28, pp. 937–949. [CrossRef]
  8. Abdelhamid, K.; Touat, A.B.; Kenioua, L. Artificial Intelligent in Upstream Oil and Gas Industry: A Review of Applications, Challenges and Perspectives. International Conference on AIAP: Artificial Intelligence and its Applications, LNNS 2021, 413, pp. 262–271.
  9. Xing, B.; Gao, W. Innovative computational intelligence: A rough guide to 134 clever algorithms. Intelligent Systems Reference Library (Springer) 2014, 62, 469.
  10. Kouba, N.; Menaa, M.; Hasni M.; Boudour, M. A novel optimal combined fuzzy PID controller employing dragonfly algorithm for solving automatic generation control problem. Electric Power Components and Systems 2018, 46, 2054–2070. [CrossRef]
  11. Amar, M.N.; Zeraibi, N.; Redouane, K. Optimization of WAG process using dynamic proxy, genetic algorithm and ant colony optimization. Arabian Journal for Science and Engineering 2018, 43, pp. 6399–6412.
  12. Wang, J. ; Song, N.; Jiang, E.; Xu, D.; Deng, W.; Mao, L. The Application of the Particle Swarm Algorithm to Optimize PID Controller in the Automatic Voltage Regulation System. ICSEE/LSMS (Springer Singapore) 2017, 763, pp. 529–536.
  13. Sethi, R.; Panda, S.; Sahoo, B.P. Cuckoo search algorithm based optimal tuning of PID structured TCSC controller. Springer, Computational Intelligence in Data Mining 2015, 1, pp. 251–263.
  14. Kumar, D.; Meenakshipriya, B.; Ram, S.S. Design of PSO based I-PD Controller and PID Controller for a Spherical Tank System. Indian Journal of Science and Technology 2016, 9, pp. 1–5. [CrossRef]
  15. Puangdownreong, D.; Nawikavatav, A. Thammarat. Optimal Design of I-PD Controller for DC Motor Speed Control System by Cuckoo Search. Procedia Computer Science 2016, 86, pp. 83–86.
  16. Jain, T.; Nigam, M.Optimization of PD-PI Controller using Swarm Intelligence. International Journal of Computational Cognition 2008, 6, pp. 55–59.
  17. Sahraoui, M., Salem, M. Application of artificial immune algorithm-based optimization in tuning a PID controller for nonlinear systems. International Journal of Automation and Control 2015, 9, pp. 186–200.
  18. Saleh, M.; Saad, S. Artificial Immune System based PID Tuning for DC Servo Speed Control. International Journal of Computer Applications 2016, 155, 2, pp. 23–26.
  19. Castro, L.; Zuben, F. The Clonal Selection Algorithm with Engineering Applications. Workshop Proceedings of GECCO’00 2000, pp. 36–37.
  20. Castro, L.; Zuben, F. Learning and Optimization Using the Clonal Selection Principle. IEEE Transactions on evolutionary computation 2002, 6, pp. 239–251. [CrossRef]
  21. Padmanabhan, S.; Chandrasekaran, M.; Ganesan, S.; Khan M.; and Navakant, P. Optimal Solution for an Engineering Applications Using Modified Artificial Immune System. Materials Science and Engineering 2017, 183, pp. 1–65. [CrossRef]
  22. Wang, M.; Feng, Sh.; He, Ch.; Li, Zh.; Xue, Yu. An Artificial Immune System Algorithm with Social Learning and Its Application in Industrial PID Controller Design. Mathematical Problems in Engineering 2017, 2017, 13.
  23. Allwright, D.J. A note on Routh-Hurwitz determinants and integral square errors. International Journal of Control 1980, 31, pp. 807–810. [CrossRef]
  24. Minh, V.T.; Rani, A.A. Modeling and control of distillation column in a petroleum process. Perak.: Hindawi Publishing Corporation, Mathematical Problems in Engineering 2009, 2009, 14. [CrossRef]
  25. Wood, R.K.; Berry, M.W. Terminal composition control of a binary distillation column. Chemical Engineering Science 1973, 28, pp. 1707–1717. [CrossRef]
  26. Morari, Z.; Zafiriou, E. Robust Process Control, Publisher: Prentice-Hall, Inc., Englewood Cliffs, NJ, 1989; 488 p.
  27. Luyben, W.L. Simple Method for tuning SISO controllers in multivariable systems. Ind. Eng. Chem. Process Des. Dev. 1986, 25, pp. 654–660. [CrossRef]
  28. Samigulin, T.I.; Shiryayeva, O.I. Development of a SMART-system for a complex industrial object control based on metaheuristic algorithms of swarm intelligence. WSEAS Transactions on Power Systems 2021, 16, pp. 231–240. [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

166

Views

63

Comments

0

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

Email

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated