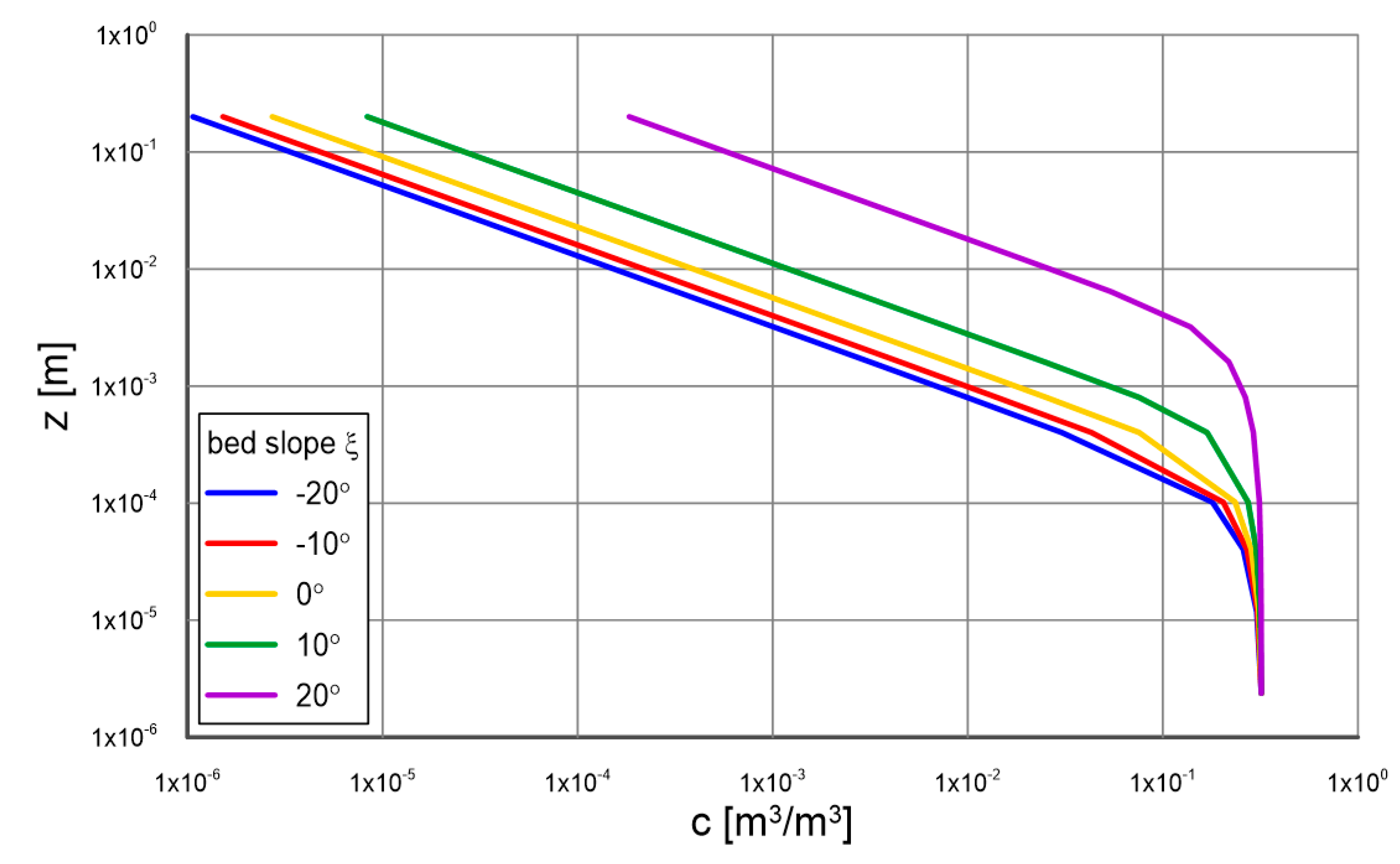
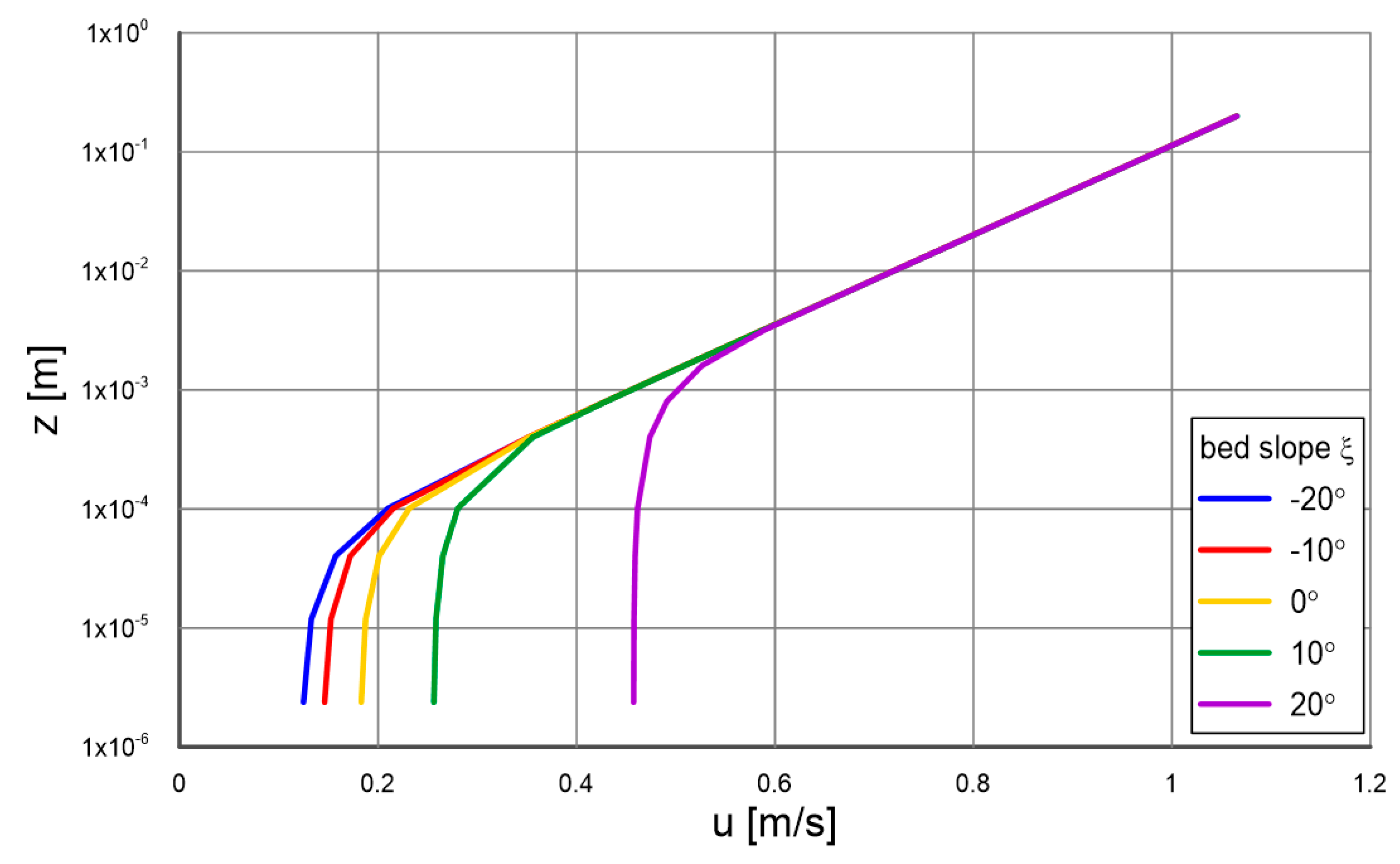
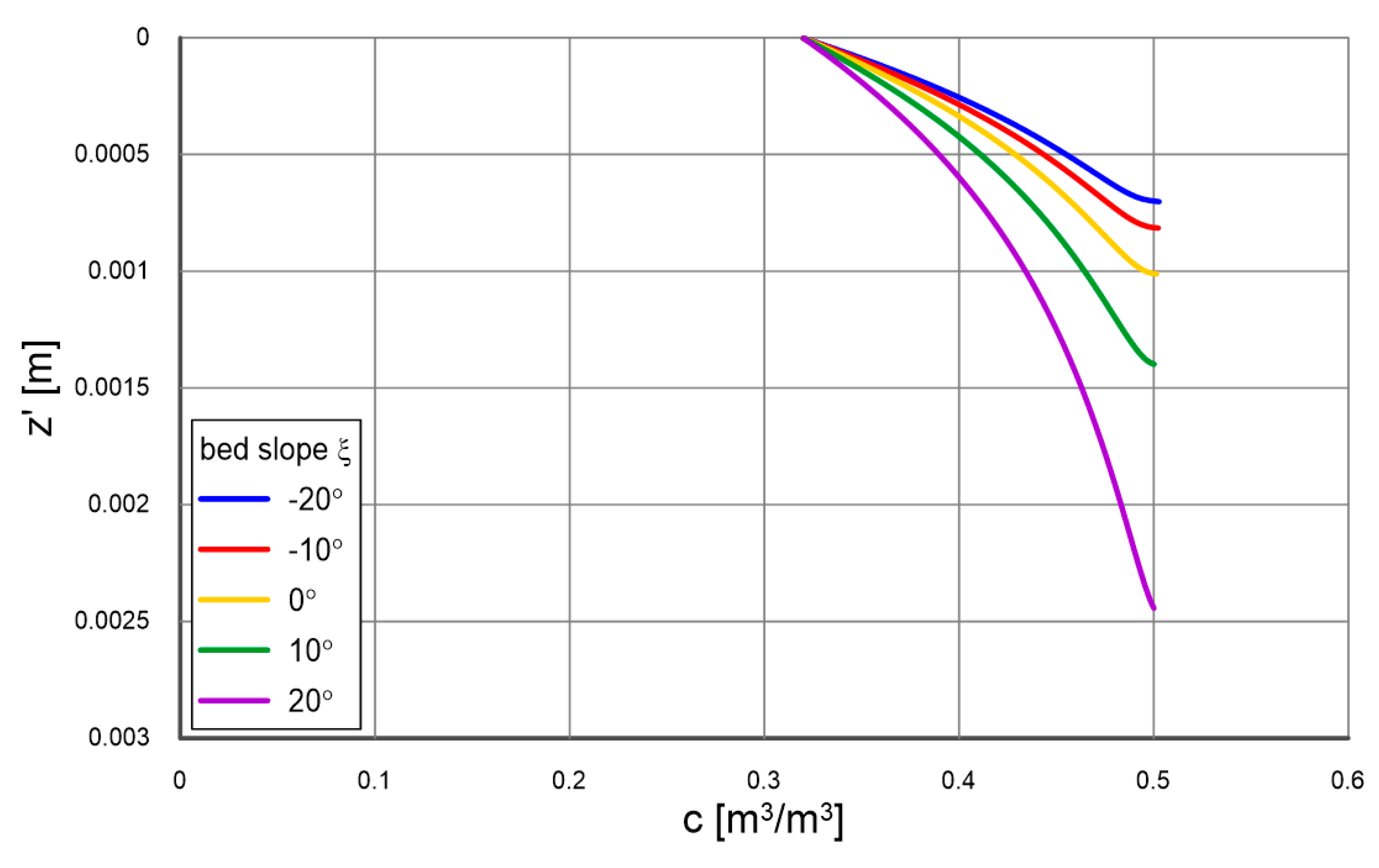
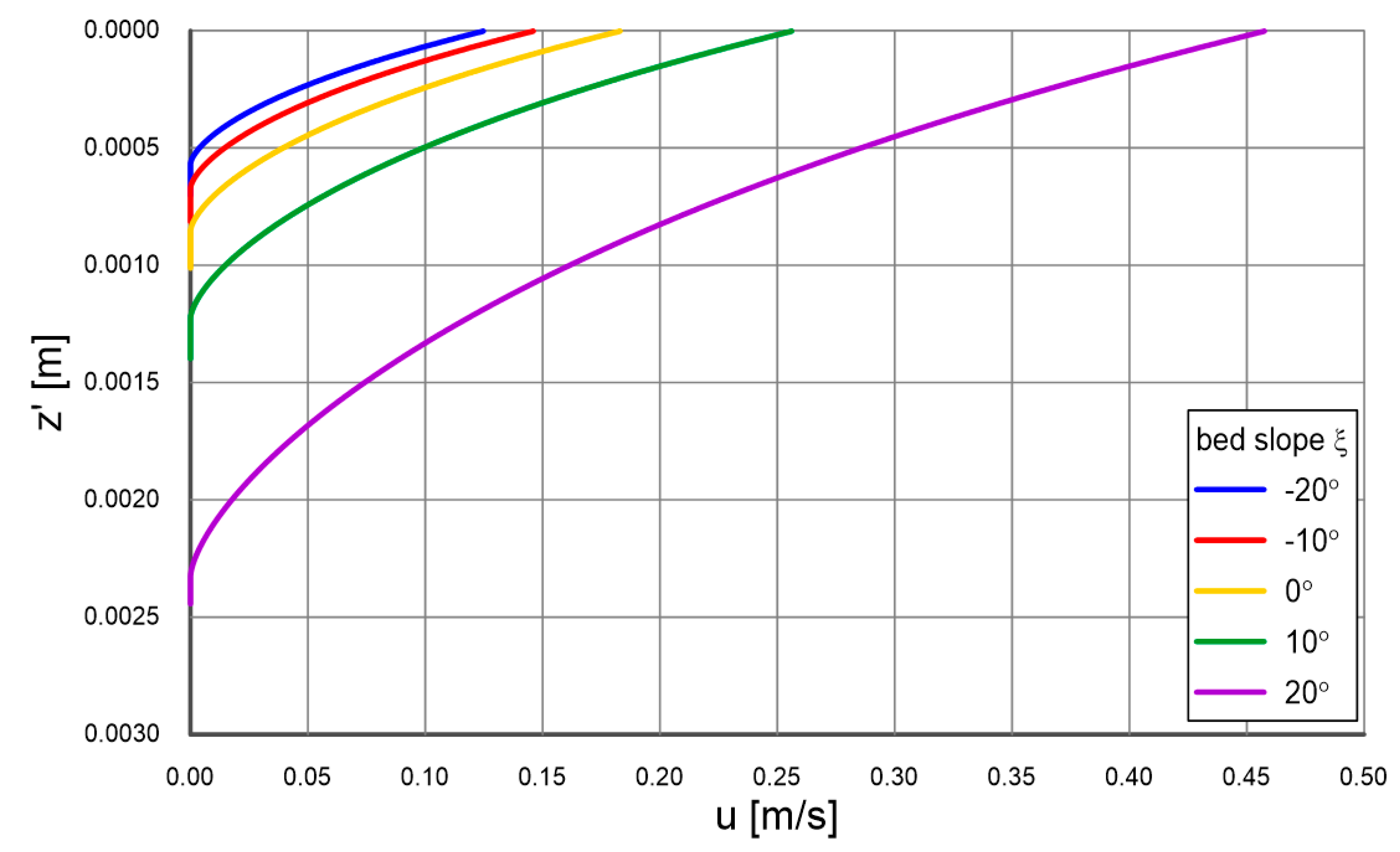
4.1. Vertical Profiles of Velocity, Concentration and Grain Size Distribution
This section may be divided by subheadings. It should provide a concise and precise description of the experimental results, their interpretation, as well as the experimental conclusions that can be drawn.
Frey [
32] conducted measurements under laboratory conditions for homogeneous surrogate sediment consisting of glass beads with a diameter of
at a constant gradient of
, under flow intensities corresponding to dimensionless friction in the range
. He carried out the observations using a special camera that allows recording images at 130 frames per second. However, in order to record individual grains selectively, the width between the vertical panes of flow channel walls was chosen to ensure that there was only one “vertical” layer of beads.
In order to compare the measurement results with calculations for specific conditions, calculations were carried out with the three-layer model presented in this paper.
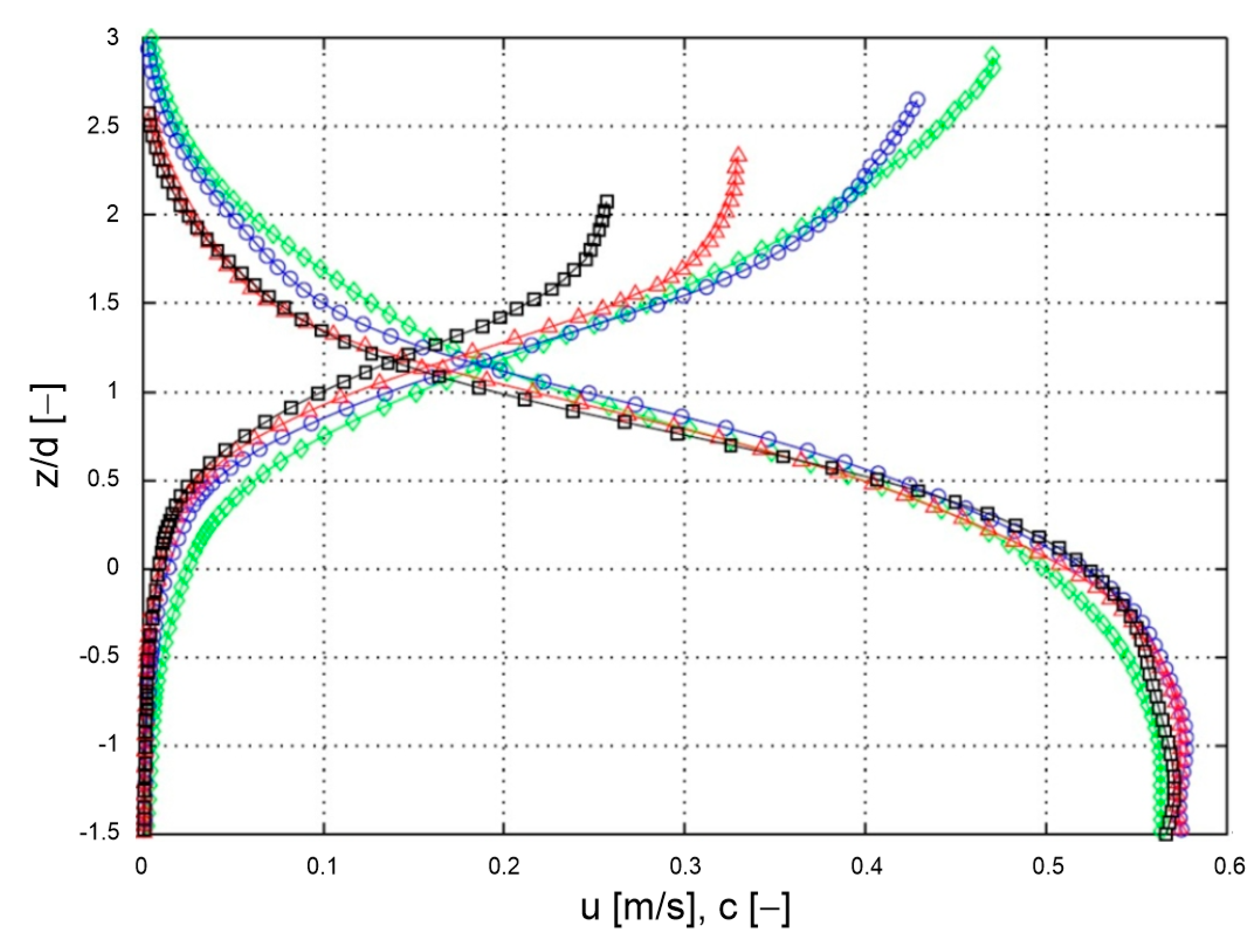
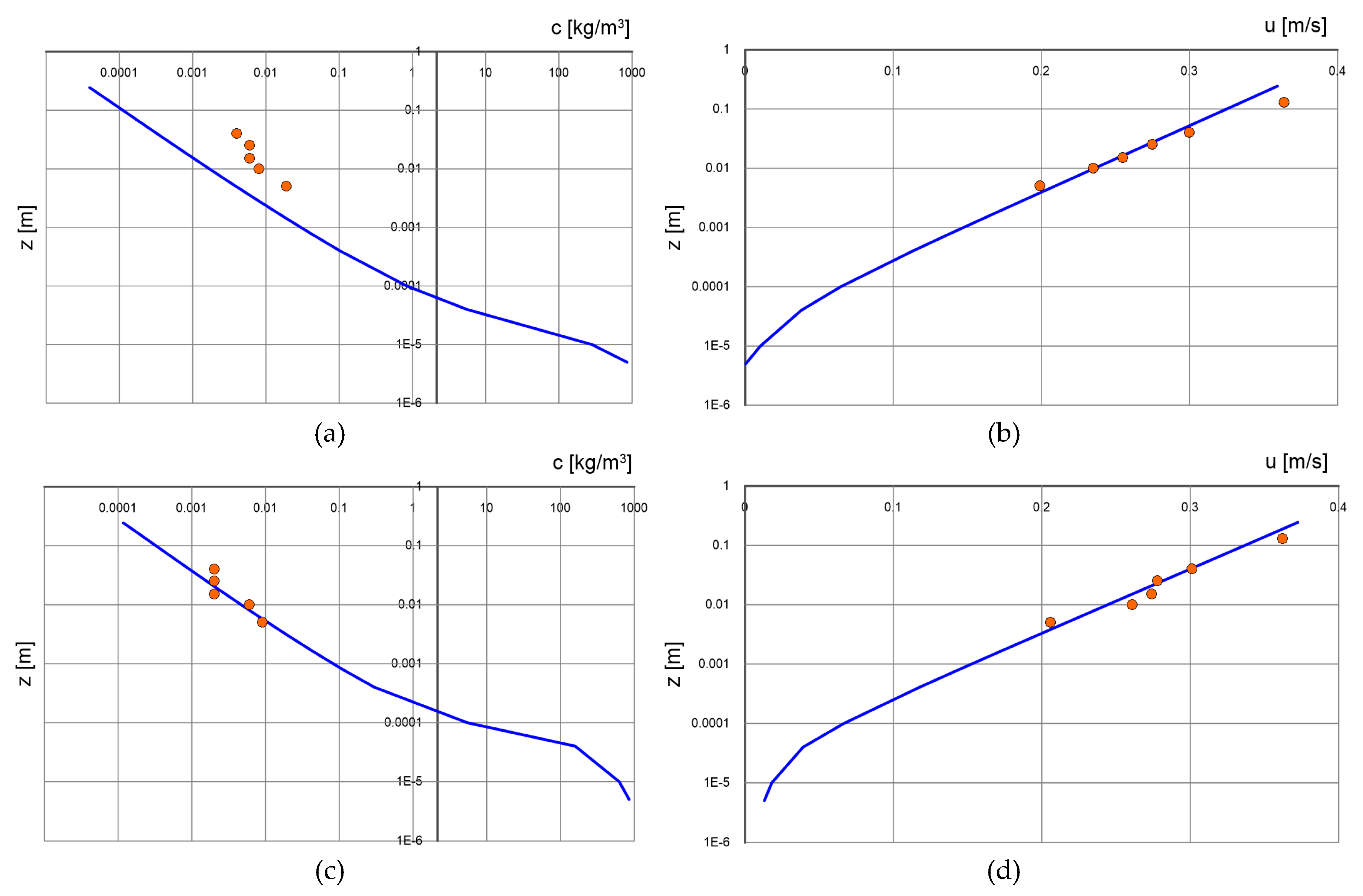
Figure 6a (following [
30]) shows the original vertical distributions of both velocity and concentration presented by Frey [
32] for four measurement series, designated by the author as N10-x, where 10 stands for the bottom slope in percentage and
is the designation of the specific measurement series under given conditions. Calculation results of these quantities with the multilayer model for selected series are shown in
Figure 6b. The calculated concentration and velocity distributions for two measurement series are shown: N10-6 for
and N10-16 for
, with fixed diameter
and bottom slope of 10%. The data presented are calculation results in 3 layers of the model, i.e. in the dense layer (
axis pointing downward) and in the contact layer and upward (
axis pointing upward).
Figure 6a.
Vertical distributions of velocity and concentration determined by Frey [
32] for four measurement series: N10-6 (black points), N10-8 (red points), N10-16 (blue points) and N10-20 (green points).
Figure 6a.
Vertical distributions of velocity and concentration determined by Frey [
32] for four measurement series: N10-6 (black points), N10-8 (red points), N10-16 (blue points) and N10-20 (green points).
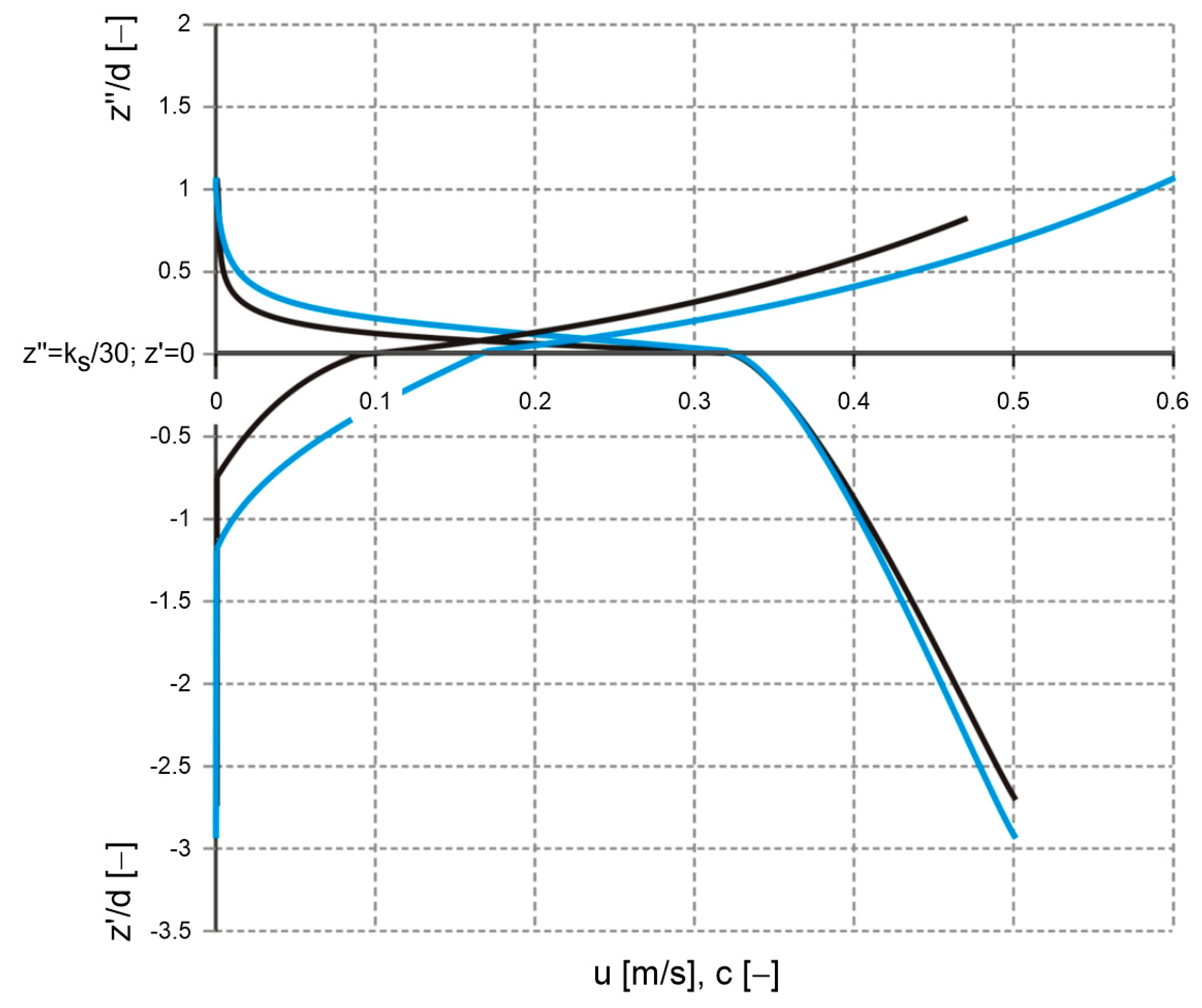
Figure 6b.
Calculated velocities and sediment concentrations with the multilayer model for parameters corresponding to tests N10-6 (black lines) and N10-16 (blue lines).
Figure 6b.
Calculated velocities and sediment concentrations with the multilayer model for parameters corresponding to tests N10-6 (black lines) and N10-16 (blue lines).
It should be noted that the maximum concentration boundary values adopted for the calculations differ slightly from the measured values at the lower boundary of dense layer
. However, this does not fundamentally affect the transport due to the zero sediment velocities occurring in this area. Comparing the calculation results (
Figure 6b) with the corresponding distributions determined by Frey [
32], shown in
Figure 6a, it can be seen that the nature of velocity and concentration distributions are very similar. This confirms the validity of theoretical assumptions made for the lowest layers of the model, from the motionless zone, through the layer to the suspension zone.
There are, of course, some differences, with the model’s overestimation of sediment velocity in the upper zone shown in the figure being particularly noticeable. However, it is difficult to clearly address the model’s errors, as the tests took place on surrogate sediment of balls of equal diameter transported in a single vertical layer. Under such conditions, the real dynamics of grains (here – glass balls) is greatly influenced by the channel walls in the immediate vicinity.
Sediment velocities and concentrations in the dense layer are mapped much better than in the contact layer. This may be related to the fact that this area is dominated by strong interactions between grains. Therefore, the above-mentioned effect of wall influence is most likely no longer as important as it is during fusion and faster grain movement. In the contact layer and upward, the calculated grain velocities are overestimated, because under natural conditions grains collide with other grains, with similar velocities – while in the laboratory measurements described by Frey [
32], grains transported in one vertical layer “bump” against the channel walls, which are at rest. Therefore, friction is of great importance here under laboratory conditions and has the effect of slowing down the beads.
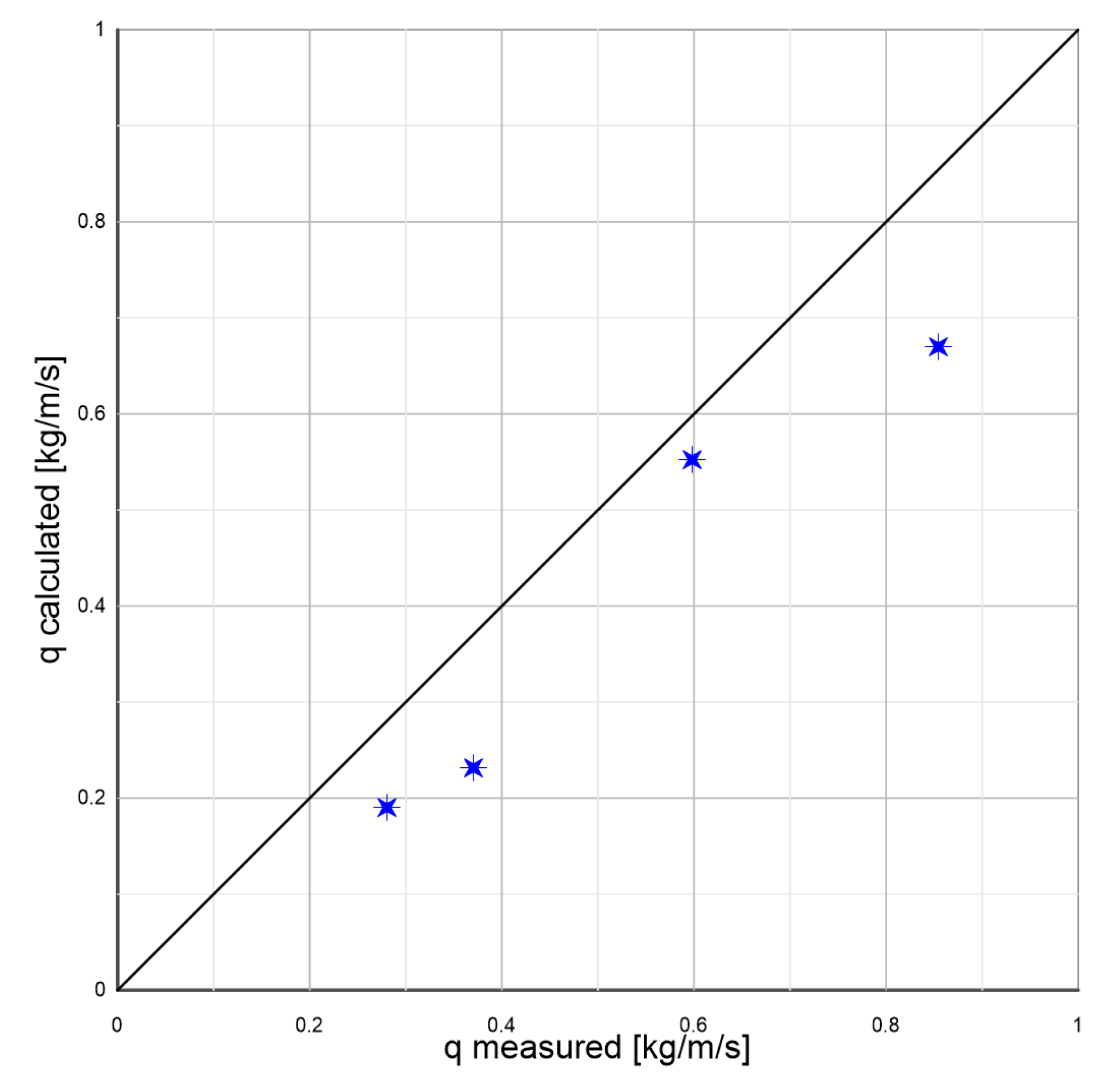
The calculated concentration values in the contact layer seem to decrease much more intensively with the distance from the boundary of two layers. However, it should be noted that the transport intensities calculated with the presented model in comparison with the transports calculated on the basis of Frey’s measurements [
32] (
Figure 7) provide satisfactory results.
In summary, when taking into account the measurement conditions, as well as the fact of replacing real sediment with glass beads, it can be stated that the consistency of measurement results with calculations is satisfactory.
One of the more interesting papers describing the vertical distribution of sediment concentration and segregation is the study by Damgaard et al. [
33], who conducted measurements of fine sand transport by determining concentration and velocity profiles in a channel that allows the implementation of a bottom slope. They made measurements using granulometrically heterogeneous sediments with a median
under conditions of dimensionless friction
, varying the bottom slope from
.
Figure 7.
Example transports of sediments represented by 6 mm diameter glass beads measured by Frey [
32] under 10% bottom slope conditions against the results of calculations (following [
30] with the presented multilayer model. The points from lowest to highest represent successive tests for dimensionless friction values, respectively:
,
,
and
.
Figure 7.
Example transports of sediments represented by 6 mm diameter glass beads measured by Frey [
32] under 10% bottom slope conditions against the results of calculations (following [
30] with the presented multilayer model. The points from lowest to highest represent successive tests for dimensionless friction values, respectively:
,
,
and
.
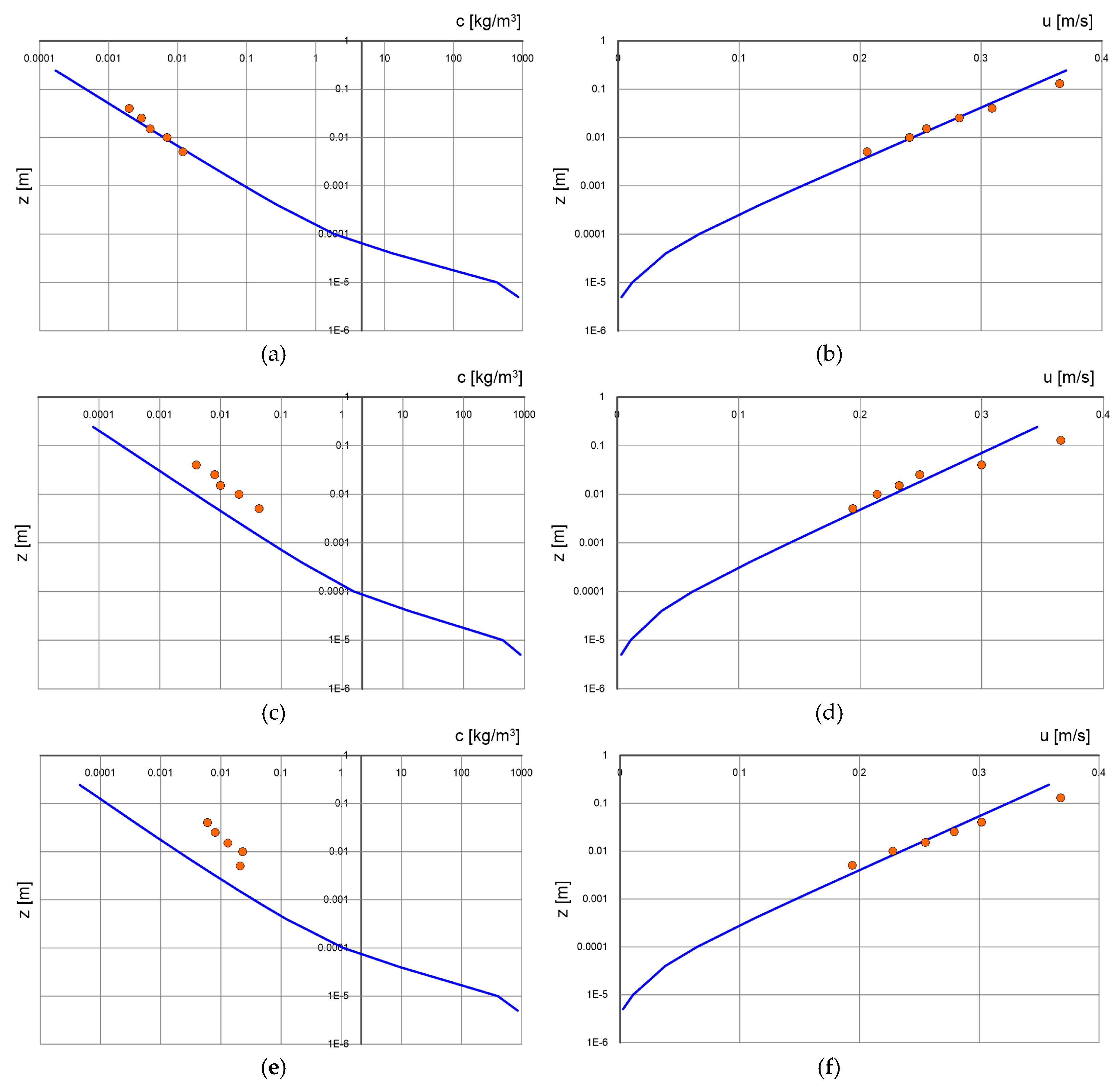
Figure 8 and
Figure 9 show a comparison of calculation results with measurements of velocity and concentration distributions for conditions defined by the dimensionless friction
. The first figure shows results for gradients consistent with the direction of flow, and the second figure shows results for opposite gradients (marked with
“-”). It can be seen that the model reflects sediment velocities very well and reproduces concentration distributions well. The highest concentration correspondences are found for significant gradients (
), while for smaller gradients (
) relatively large differences are observed, which are most likely due to the presence of bottom forms (ripples), which are particularly strong at smaller gradients.
Figure 8.
Comparison of calculated with three-layer model (lines, contact layer and outer layer) and measured (points) by Damgaard et al. [
33] distributions of velocity and sediment concentration for different bottom slopes
. (
,
): (
a), (
b)
; (
c), (
d)
; (
e), (
f)
.
Figure 8.
Comparison of calculated with three-layer model (lines, contact layer and outer layer) and measured (points) by Damgaard et al. [
33] distributions of velocity and sediment concentration for different bottom slopes
. (
,
): (
a), (
b)
; (
c), (
d)
; (
e), (
f)
.
Figure 9.
Comparison of calculated with multilayer model (lines, contact layer and outer layer) and measured (points) by Damgaard et al. [
33] distributions of velocity and sediment concentration for bottom slopes
opposite the flow direction (
,
): (
a), (
b)
; (
c), (
d)
.
Figure 9.
Comparison of calculated with multilayer model (lines, contact layer and outer layer) and measured (points) by Damgaard et al. [
33] distributions of velocity and sediment concentration for bottom slopes
opposite the flow direction (
,
): (
a), (
b)
; (
c), (
d)
.
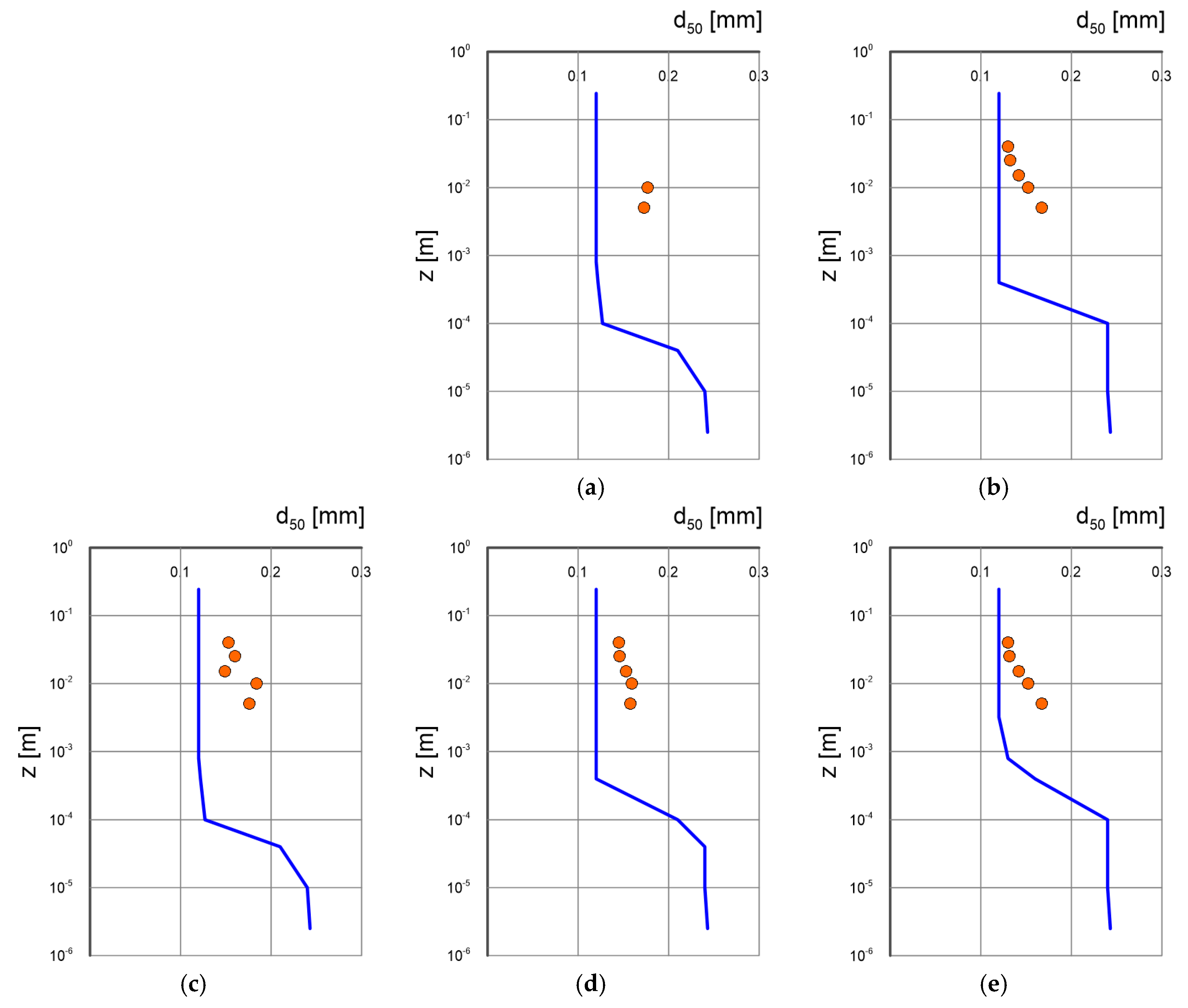
Damgaard et al. [
33] also devoted attention to the vertical segregation structure of heterogeneous sediments under conditions of different bottom slopes. The authors measured the concentration of individual sediment fractions at different distances from the bottom and presented the results in the form of vertical variation of the characteristic diameter
. The parameters corresponding to each test (values of dynamic velocity, dimensionless friction and bottom slope) are shown in
Table 1. Calculation results against the measurement results for selected series are shown in
Figure 10 and
Figure 11, with the vertical variation of the median
of suspended sediments at height
was calculated from the obtained concentration distributions according to the equations:
Knowing the calculated fractional content at a given level it is easy on this basis to estimate the median .
The lines represent the calculation results, and the points represent the values of d50 from measurements, i.e. obtained from the measured concentrations of individual fractions. The lowest value of the lines representing calculation results (), corresponds to the characteristic diameter of the sediment at the bottom. As can be seen in figures, the quality of prediction of the vertical structure d50 in the area above the intensive sorting zone is a test of the validity of theoretical assumptions and the adopted sorting model in the layers below.
Figure 10.
Calculated vertical distributions of the variation of characteristic diameter
(lines) against the measurement results by Damaard et al. [
33] (points) for conditions of bottom slope
(tests 1, 2, (
a), (
b)) and
(tests 4, 5, 6, (
c), (
d), (
e)) for different conditions of dimensionless friction /see Tab. 3[M1] /. The measured diameter of sediment at the bottom
.
Figure 10.
Calculated vertical distributions of the variation of characteristic diameter
(lines) against the measurement results by Damaard et al. [
33] (points) for conditions of bottom slope
(tests 1, 2, (
a), (
b)) and
(tests 4, 5, 6, (
c), (
d), (
e)) for different conditions of dimensionless friction /see Tab. 3[M1] /. The measured diameter of sediment at the bottom
.
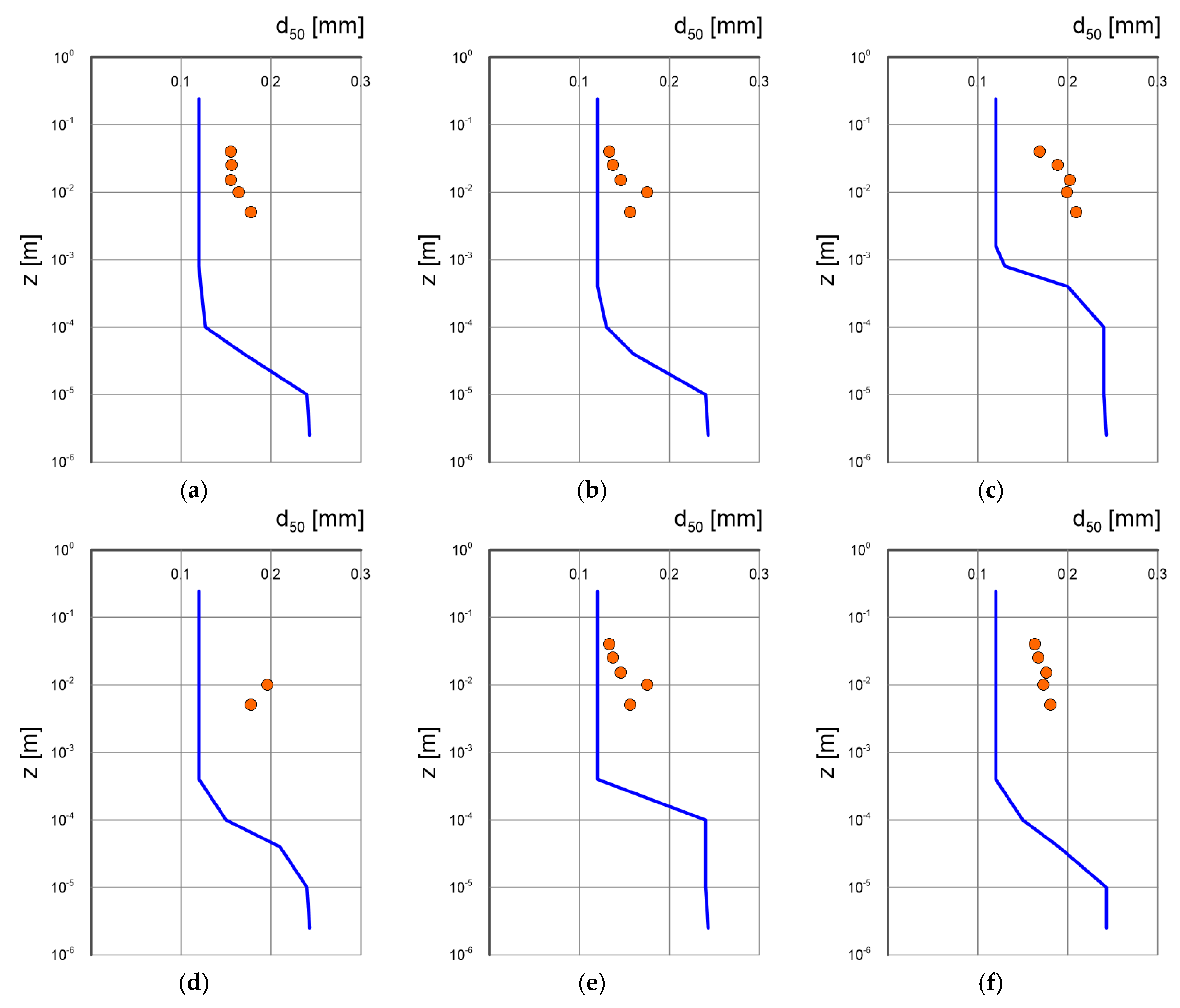
Figure 11.
Calculated vertical distributions of the variation of characteristic diameter
(lines) against the measurement results of Damaard et al. [
33] (points) for conditions of bottom slope
(tests 10, 11, 12, (
a), (
b), (
c)) and
(tests 13, 14, 15, (
d), (
e), (
f)) for different conditions of dimensionless friction /see Tab. 3/. The measured diameter of sediment at the bottom
.
Figure 11.
Calculated vertical distributions of the variation of characteristic diameter
(lines) against the measurement results of Damaard et al. [
33] (points) for conditions of bottom slope
(tests 10, 11, 12, (
a), (
b), (
c)) and
(tests 13, 14, 15, (
d), (
e), (
f)) for different conditions of dimensionless friction /see Tab. 3/. The measured diameter of sediment at the bottom
.
4.2. Sediment Transport
Luque [
34] conducted a series of measurements of sediment transport in a channel 8m long, 20cm high and 10cm wide with a design that allowed for a bottom slope. Flow in the channel was generated using a pump. Measurements were conducted for flow with no slope (0º) and three different bottom slopes: 12º, 18º and 22º under conditions of dimensionless friction in the range
. The author studied transport of heterogeneous sediments, which he described by characteristic diameters
. Measurements for the verification of presented model are very interesting, as Luque [
34] used a wide range of materials representing sediments both in terms of not only diameters, but also density:
sand with density and diameters and ;
gravel with density and diameter ;
particles of shelled walnut with density and diameter ;
magnetite grains with density and diameter .
To calculate shear stresses, the authors measured water velocity distributions. Sediment transport was determined using an optical method, based on analysis of recorded films made for grains traveling a certain distance in a given time.
For the direct values of shear stress and sediment and bottom slope characteristics presented by Luque [
34], calculations were conducted with the model presented in this paper. Comparisons of calculated and measured transport intensities expressed in terms of dimensionless transport
are shown in
Figure 13,
Figure 14,
Figure 15,
Figure 16 and
Figure 17. The solid lines indicate a
correspondence of the calculation results with the measured data, while the dashed lines indicate the limits of double determination error. The dimensionless transport
according to equation (6) is defined as follows:
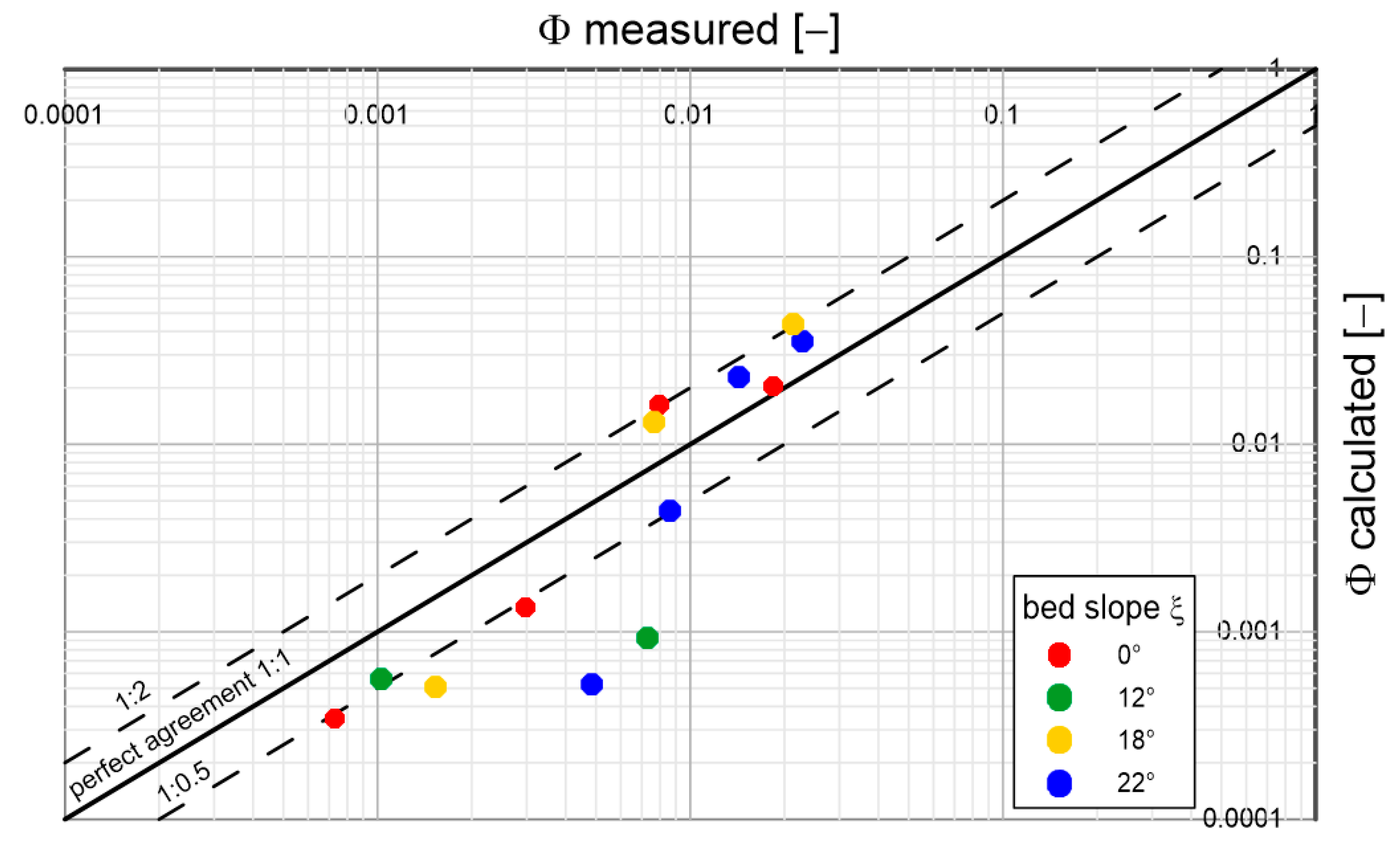
Figure 12.
Comparison of calculated and measured transport intensities for sandy sediment with a diameter
and density
under conditions of different bottom slopes;
(based on Luque’s laboratory studies [
34]).
Figure 12.
Comparison of calculated and measured transport intensities for sandy sediment with a diameter
and density
under conditions of different bottom slopes;
(based on Luque’s laboratory studies [
34]).
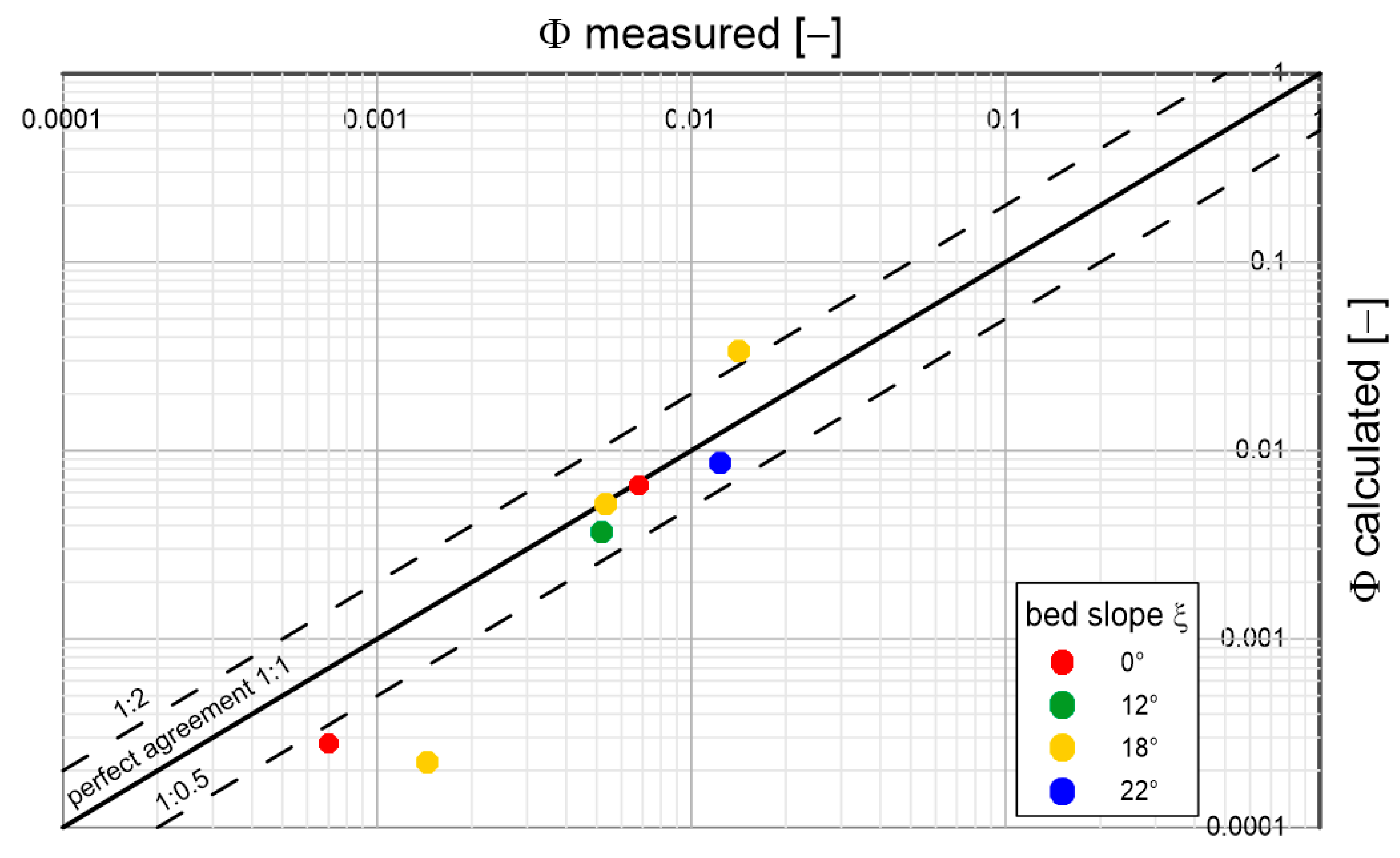
Figure 13.
Comparison of calculated and measured transport intensities for sandy sediment with a diameter
and density
under conditions of different bottom slopes;
(based on Luque’s laboratory studies [
34]).
Figure 13.
Comparison of calculated and measured transport intensities for sandy sediment with a diameter
and density
under conditions of different bottom slopes;
(based on Luque’s laboratory studies [
34]).
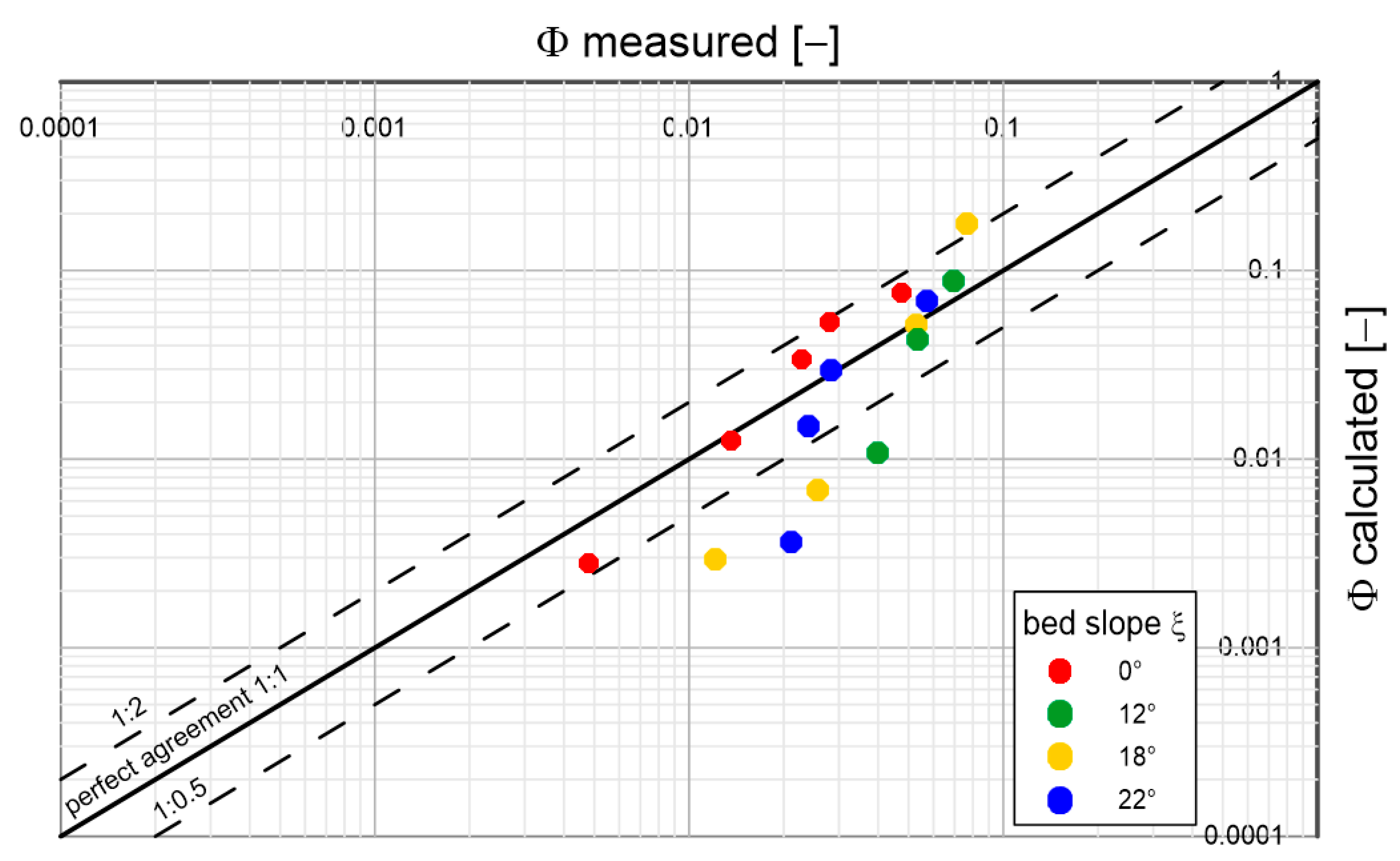
Figure 14.
Comparison of calculated and measured transport intensities for sandy sediment with a diameter
and density
under conditions of different bottom slopes;
(based on Luque’s laboratory studies [
34]).
Figure 14.
Comparison of calculated and measured transport intensities for sandy sediment with a diameter
and density
under conditions of different bottom slopes;
(based on Luque’s laboratory studies [
34]).
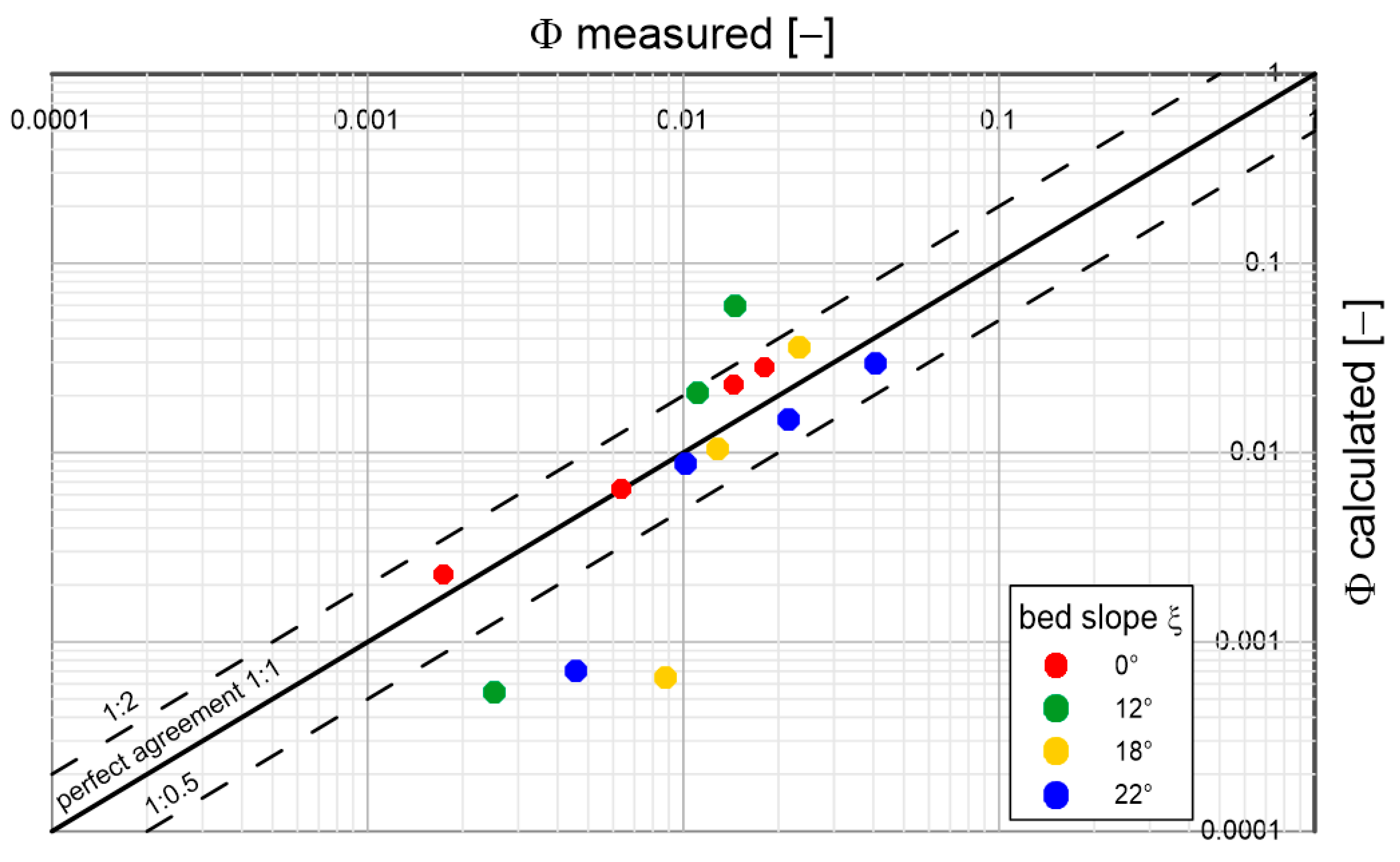
Figure 15.
Comparison of calculated and measured transport intensities for sandy sediment with a diameter
and density
under conditions of different bottom slopes;
(based on Luque’s laboratory studies [
34]).
Figure 15.
Comparison of calculated and measured transport intensities for sandy sediment with a diameter
and density
under conditions of different bottom slopes;
(based on Luque’s laboratory studies [
34]).
Figure 16.
Comparison of calculated and measured transport intensities for sandy sediment with a diameter
and density
under conditions of different bottom slopes;
(based on Luque’s laboratory studies [
34]).
Figure 16.
Comparison of calculated and measured transport intensities for sandy sediment with a diameter
and density
under conditions of different bottom slopes;
(based on Luque’s laboratory studies [
34]).
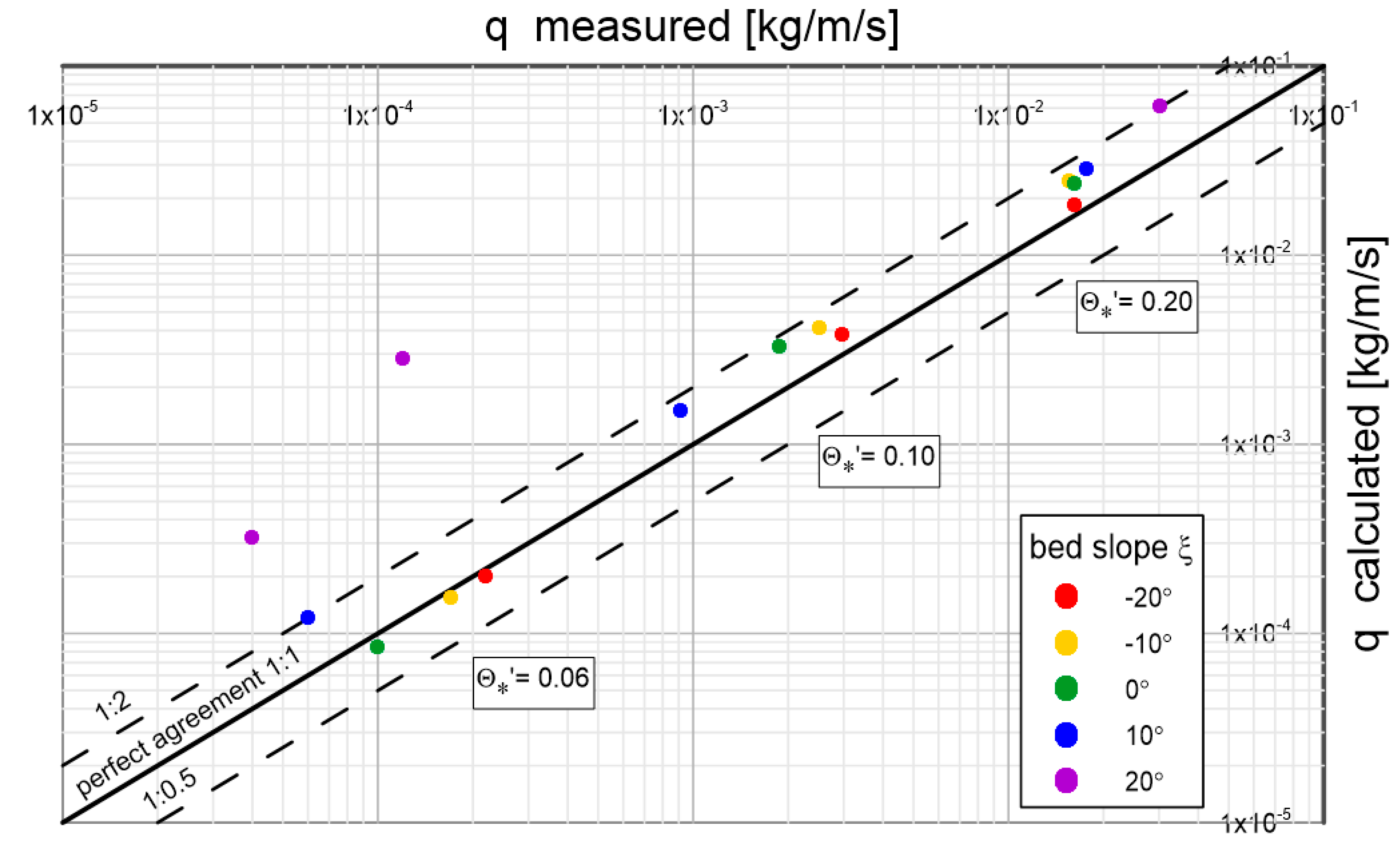
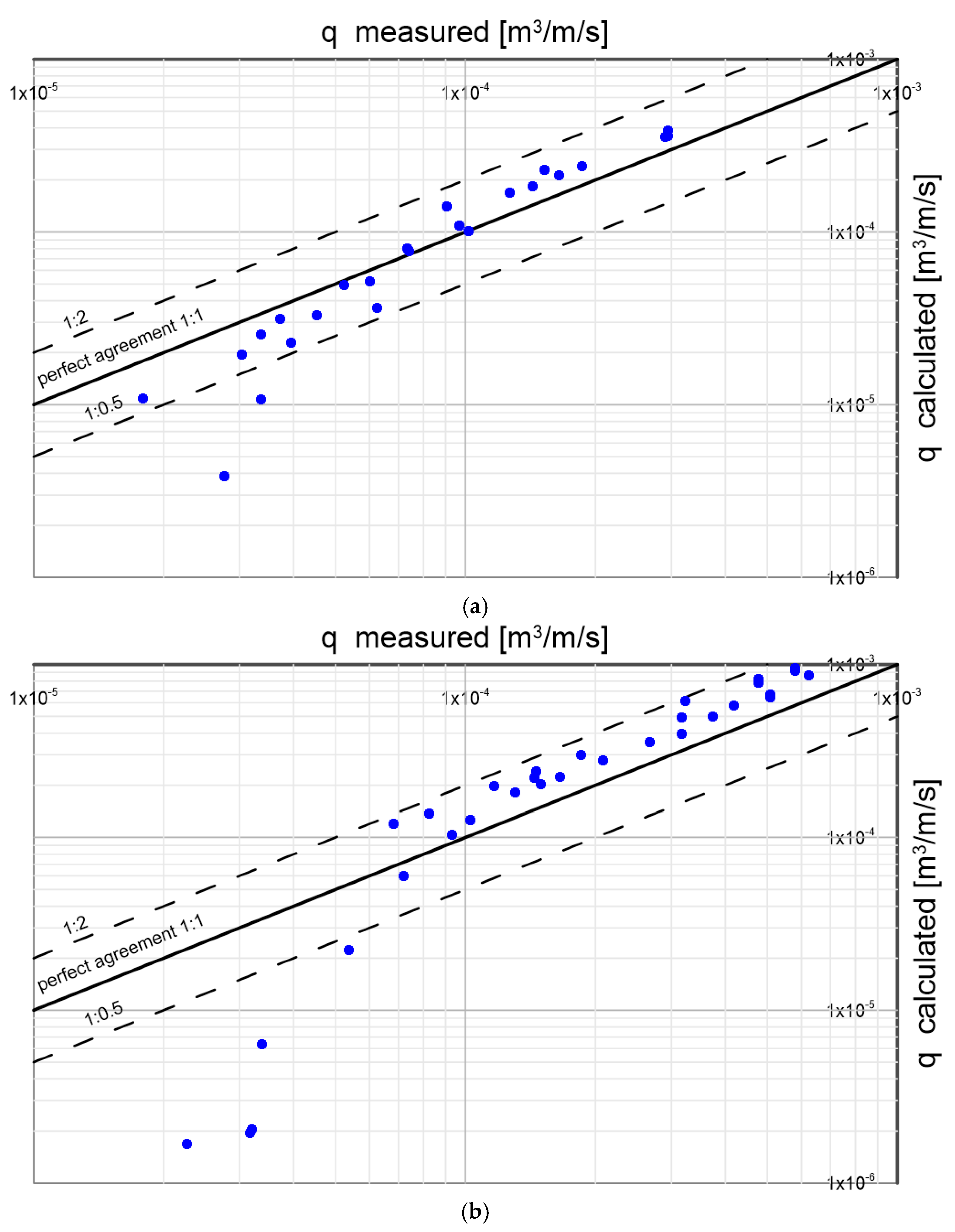
Figure 17.
Results of sediment transport calculations compared with measured data by Damgaard et al. [
33] for sediment with diameter of
under conditions of dimensionless friction
with gradients ranging from -20º to 20º.
Figure 17.
Results of sediment transport calculations compared with measured data by Damgaard et al. [
33] for sediment with diameter of
under conditions of dimensionless friction
with gradients ranging from -20º to 20º.
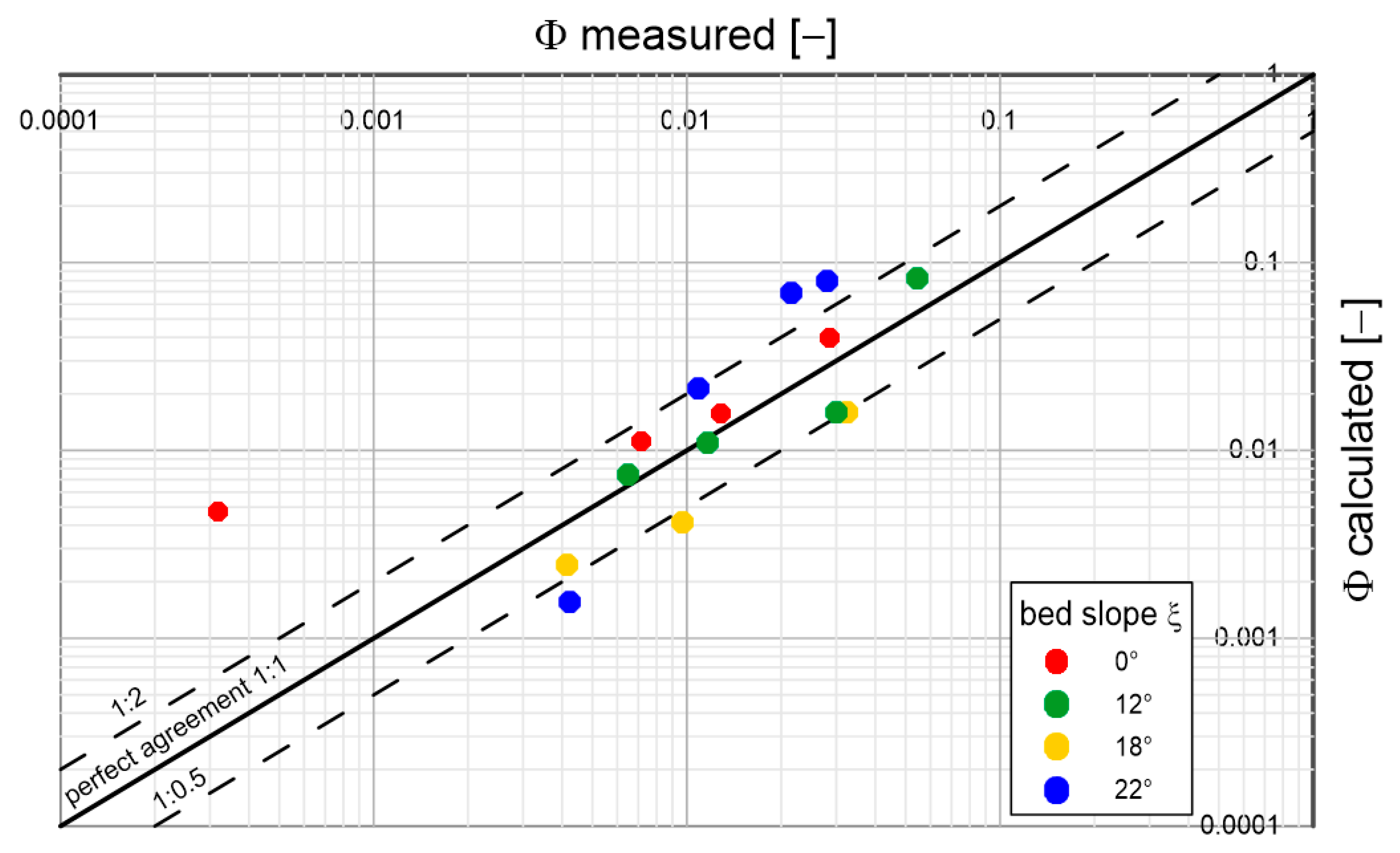
Analysing the results shown in the above graphs, it can be concluded that the model reproduces sediment transports quite well, regardless of diameter and density, over the full range of bottom slopes used in the experimental studies. Most of the prediction results do not exceed double determination errors. It is worth mentioning that the results of Lugue measurements [
34] are characterised by significant deviations from the average values of measurement series. Under conditions close to the beginning of sediment movement, such deviations are typical. Therefore, it is not possible to speak unequivocally about the error of calculation results here. It is interesting to note that there is no decisive difference in the quality of prediction of typical (sandy) sediments from substitute sediments with atypical densities (several times lower or higher). This is a good indication of the model, which may consequently have important implications for future engineering applications.
Figure 17 shows a comparison of calculated sediment transport values with selected measured data from Damgaard et al. [
33] for heterogeneous sediment with diameter
under conditions of dimensionless friction
with gradients ranging from
to
. From
Figure 17, it can be seen that the data in the graph are arranged in three groups, corresponding to 3 different flow conditions according to the dimensionless friction values described in the graph
. A very good consistency between calculation results and measurements was obtained.
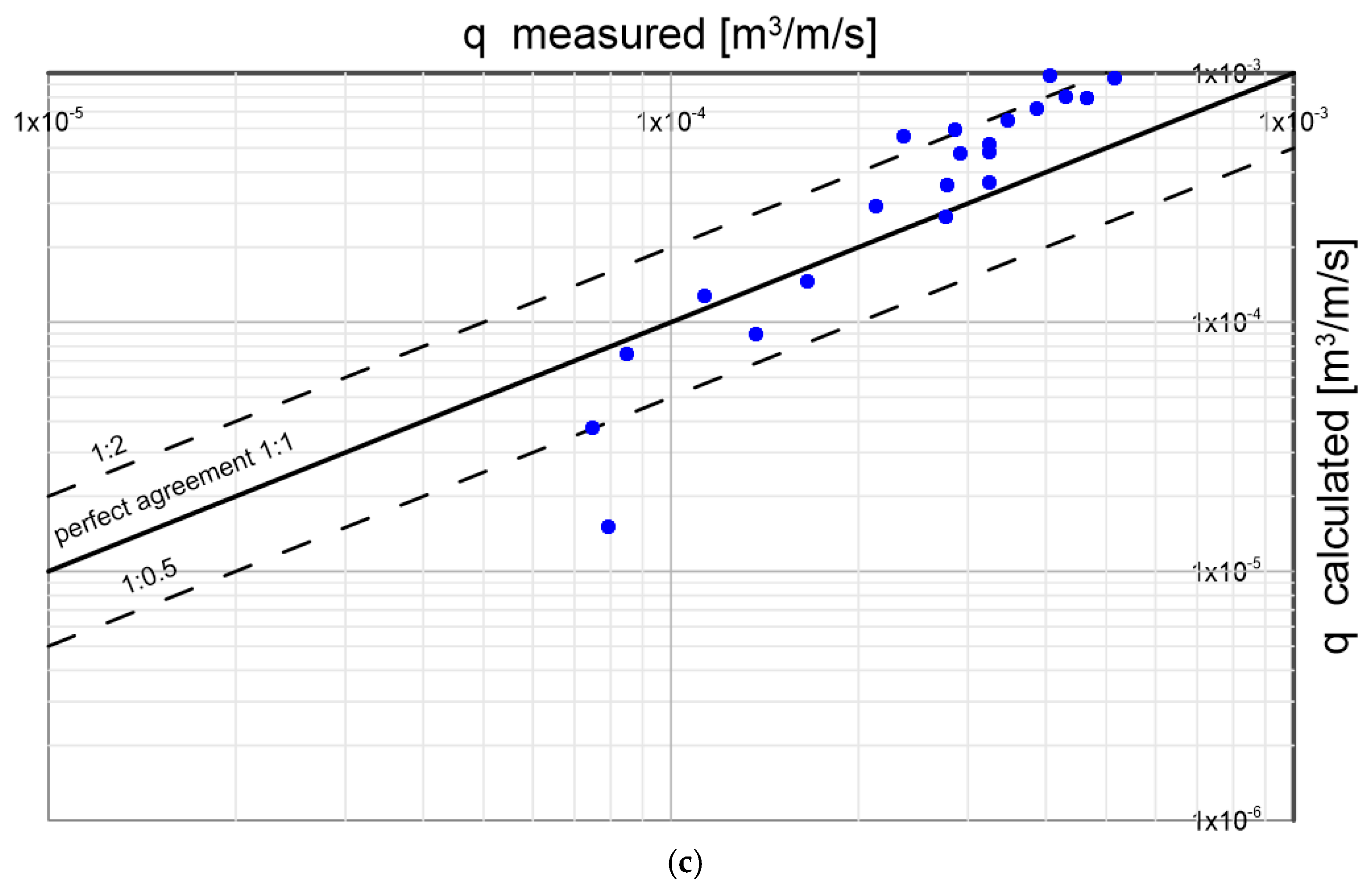
Further results of laboratory measurements that were used to verify the presented model under conditions of higher gradients were published by Smart and Jaeggi [
35]. The authors conducted measurements of dragged sediment transport using a design that allowed the bottom to slope up to 40º.
Smart and Jaeggi [
35] conducted transport measurements of four types of gravels with the following parameters:
and density
,
and density
,
and density
,
and density
, with bottom slopes of 3, 5, 7, 10, 15 and 20% for different values of dimensionless friction in the range
.
A comparison of calculation results with measurements is shown in
Figure 18. Satisfactory conformity was obtained, and in the case of the finest sediments (
) very good conformity. It should be noted that the most deviating results (
, the lowest extreme point on the graph) were achieved for conditions at the boundary of the beginning of the movement, where concentrations are very small, and the measurements are usually characterized by significant scatterings of the results (single grains starting movement).
Larionov et al. [
36] published the measurement results of sediment transport, which they conducted in a channel that allowed the realisation of slopes up to
In the experiments they used 4 different heterogeneous sediments with characteristic diameters
. Tests were carried out for the full range of dimensionless friction in the range from values close to the onset of grain motion (
), with small bottom slopes close to
, to strongly developed, intensive transport (max. value
with bottom slopes up to
).
Figure 19 shows a comparison of the measured results with the values calculated with the three-layer model. The consistency is satisfactory. In most cases, the results are within double determination error.
Aziz and Scott’s [
37] measurement results were also used to verify the presented three-layer model under bottom slope conditions.
Figure 20 shows a comparison of calculated sediment transport intensities for selected measurement results carried out by the authors for sediment with a diameter of
, with bottom slopes of 3% and 10%, corresponding to two groups of dimensionless friction values in the range
and
. Again, very good conformity of calculation results with measured values was obtained.
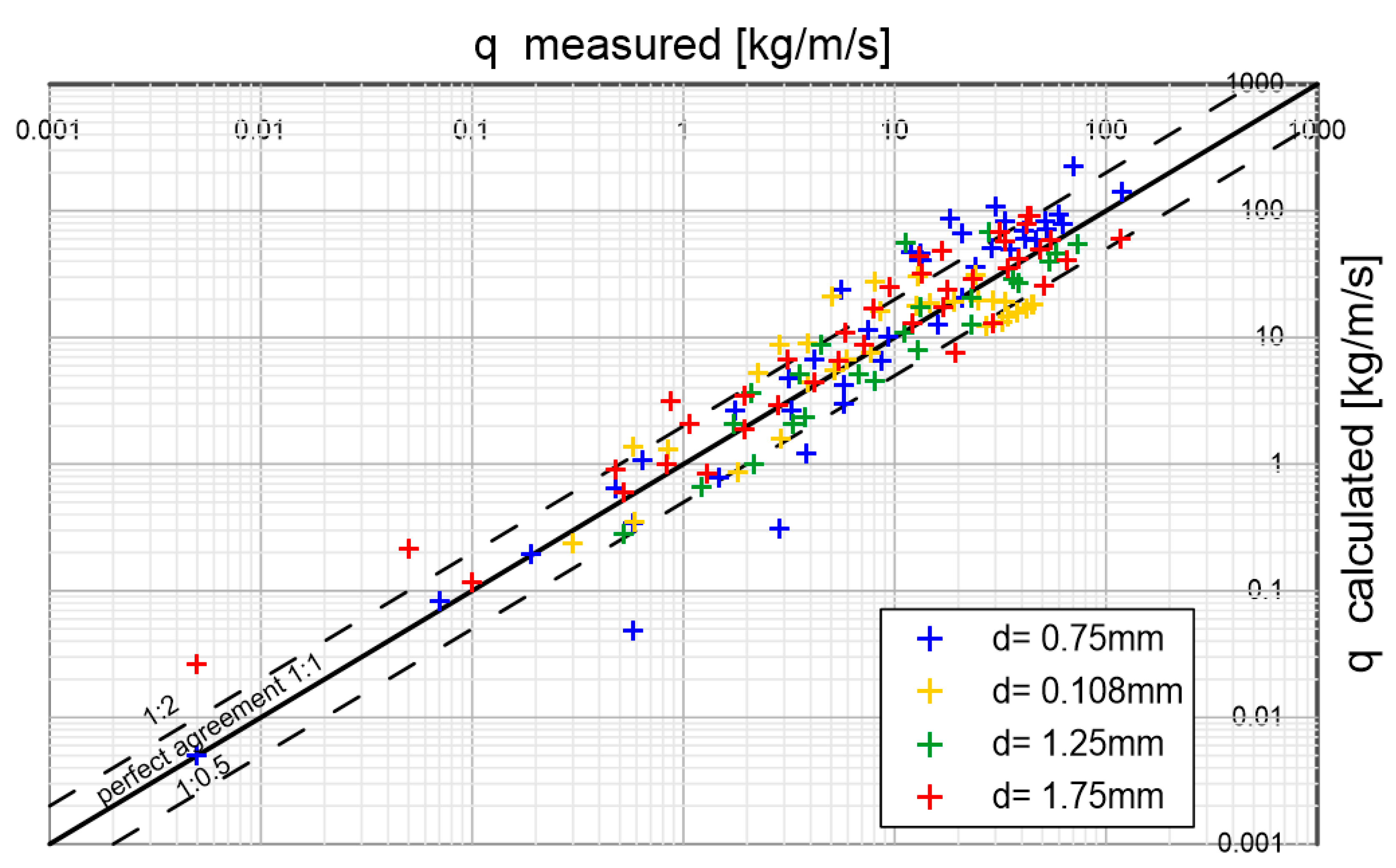
Recking et al. [
11] conducted measurements of homogeneous sediment transport granulometric in a circulation channel for bottom slopes of 0-10% in the range of conditions from the beginning of movement (
) to developed transport (
). Calculation results against measured data for selected 3 diameters (
) are shown in
Figure 21. The model reproduces the measured transport values very well. The exceptions are the lowest points, concerning measurements under conditions close to the beginning of debris movement (
close to the value of
0.06), when practically single grains are mobile. However, under such conditions, there are also significant discrepancies in the measurements.
Figure 18.
Comparison of sediment transport values calculated by three-layer model with the results of Smart and Jaeggi’s measurements [
35] for four different diameters and different values of dimensionless friction in the range
in the range of bottom slopes from 3 to 20%.
Figure 18.
Comparison of sediment transport values calculated by three-layer model with the results of Smart and Jaeggi’s measurements [
35] for four different diameters and different values of dimensionless friction in the range
in the range of bottom slopes from 3 to 20%.
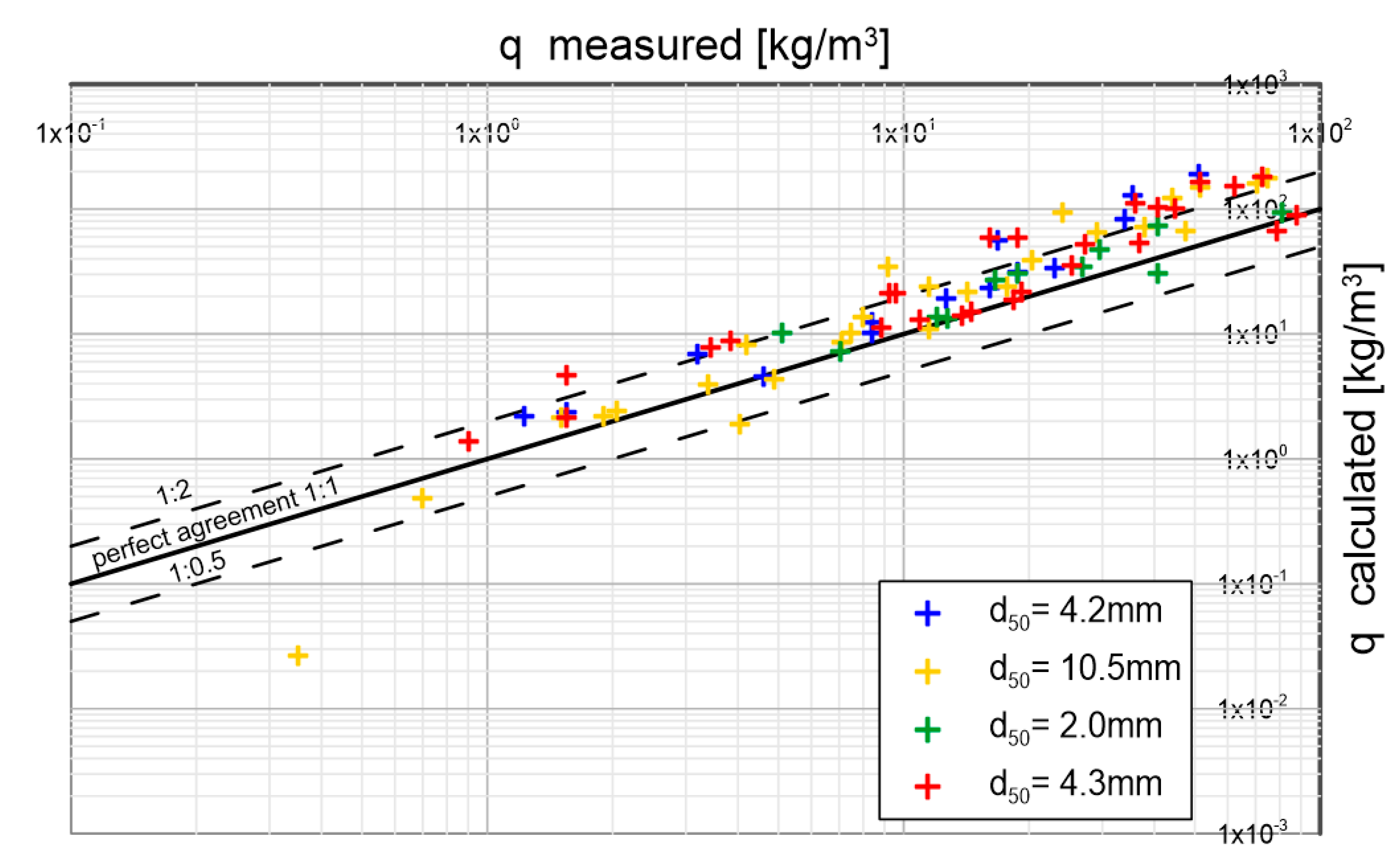
Figure 19.
Measurement results of Larionov et al. [
36] in relation to sediment transport values calculated with the presented three-layer model for four selected diameters in the range of variation of dimensionless friction
under conditions of bottom slopes from 0.5% to 35%.
Figure 19.
Measurement results of Larionov et al. [
36] in relation to sediment transport values calculated with the presented three-layer model for four selected diameters in the range of variation of dimensionless friction
under conditions of bottom slopes from 0.5% to 35%.
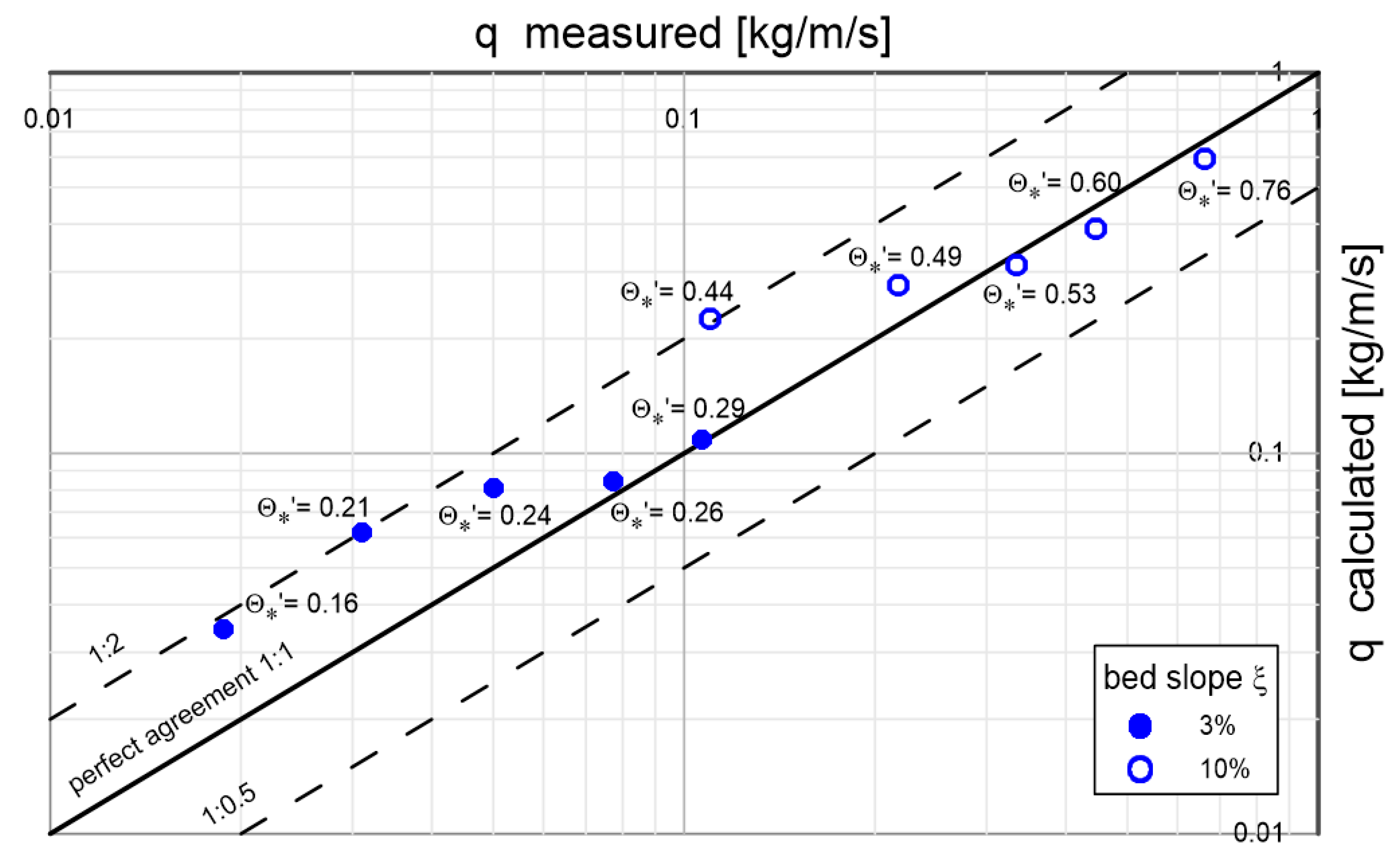
Figure 20.
Comparison of example results of Aziz and Scott [
37] measurements of
diameter sediment transport intensity for two different bottom slopes: 3% (black dots) and 10% (circles) in the dimensionless friction range
with the results of three-layer model calculations.
Figure 20.
Comparison of example results of Aziz and Scott [
37] measurements of
diameter sediment transport intensity for two different bottom slopes: 3% (black dots) and 10% (circles) in the dimensionless friction range
with the results of three-layer model calculations.
Figure 21.
Comparison of measured by Recking et al. [
11] values of sediment transport for three diameters under conditions of slopes from 0% to 10% in the range of dimensionless friction
with the results of calculations with the multilayer model: (
a)
; (
b)
; (
c)
.
Figure 21.
Comparison of measured by Recking et al. [
11] values of sediment transport for three diameters under conditions of slopes from 0% to 10% in the range of dimensionless friction
with the results of calculations with the multilayer model: (
a)
; (
b)
; (
c)
.